首页
登录
注册
下载:
-
弛豫现象是金属玻璃(非晶态合金)中非常关键的物理过程, 它与材料的微观组织结构演化密切相关[1]. 在弛豫过程中, 自由体积的减少会导致结构中可用的自由间隙显著变小, 使材料内部结构发生调整以达到能量更低的较稳定状态[2]. 金属玻璃中的弛豫过程对其微观组织结构具有重要影响, 其内部的原子或原子团在弛豫过程中会发生微观尺度上的移动和重新排列, 这种重新排列通常发生在短程有序区域内或短程有序区域之间[3–6]. 局部的短程有序团簇或者扩展团簇在驰豫过程中逐渐形成并增长, 甚至导致金属玻璃中出现晶态相或者局部晶化现象, 从而改变材料的微观组织结构, 直接影响材料的性能[7–9].
浓度是影响材料结构和性能的重要因素之一, 浓度变化可以显著地改变材料的结构和相变行为等[10,11]. Laws等[12]通过比较几种Mg基非晶合金的室温老化过程, 发现弛豫动力学与元素浓度含量等因素密切相关, Mg含量的增加会导致弛豫焓的增加, 同时减缓弛豫速度, 并降低体系在室温下结晶的可能性. Fernández等[13]对(Cu50Zr50)100–xAlx (原子百分比x = 0, 2.5%, 5%, 7.5%, 10%)的结晶过程进行研究, 发现Al含量直接影响体系的非晶形成能力, 增加Al的含量, 能够提高体系的结晶激活能, 导致结晶需要更高的能量门槛, 影响体系的结晶过程. Chen等[14]发现提高La-Al体系中La原子的浓度会导致体系中Al原子的牢笼效应增强, 由于Al原子的第一近邻La原子个数增加, 导致非高斯参数的异常峰峰值增大. 调整浓度会导致合金体系中元素之间的扩散速率出现差异, 从而引起元素在不同区域出现不均匀的分布[15]. 这种不均匀性可能表现为局部组分变化、局部结构弛豫或者局部应力集中等, 这些因素会影响非晶材料的变形特性[16,17]. 因此, 通过调控合金成分, 可以实现对非晶材料内部动力学行为的精确控制, 进而优化材料的性能和应用.
深入探究浓度对非晶合金动力学不均匀性的影响有利于加深对非晶材料本质和弛豫动力学行为的理解. 本文选取典型的金属-非金属合金材料——Pd-Si作为研究对象, 在共晶点(Pd100–xSix (x = 17.5))附近调整体系中的元素比例[18,19], 从原子扩散以及体系微结构变化的角度探究Pd-Si非晶合金中动力学非均匀性.
-
采用分子动力学方法模拟了不同浓度的Pd100–xSix (x = 18, 20, 24, 26)液态合金在0 GPa下的快速凝固过程与等温弛豫过程. 50000个原子(按照比例分配原子个数)被随机放置在给定周期性边界的三维立方盒子中, 并给每个原子都设定唯一的编号. 让体系在等温等压系综下运行, 采用Verlet速度算法计算原子运动的数值积分[20], 运动方程积分所用的时间步长为2 fs, 并采用嵌入原子势(EAM)来描述原子之间的相互作用[21]. 首先, 让体系在2100 K的恒定温度下弛豫106步(2 ns), 以达到熔化和平衡. 随后, 再让平衡熔体以1012 K/s的冷却速率将温度降低至300 K. 最后, 让每个体系在300 K的恒定温度下弛豫10 ps. 每5步记录一次温度、原子坐标、势能和其他信息.
-
动力学非均匀性在非晶材料中普遍存在, 并且影响着非晶合金的形成和变形过程. 均方位移(mean square displacement, MSD)是研究材料中原子、分子或粒子扩散行为的重要参数之一[22,23]. 通过计算原子的均方位移随时间的变化关系, 可以得到原子的运动模式, 以及原子之间的相互作用情况. 其计算表达式为
其中
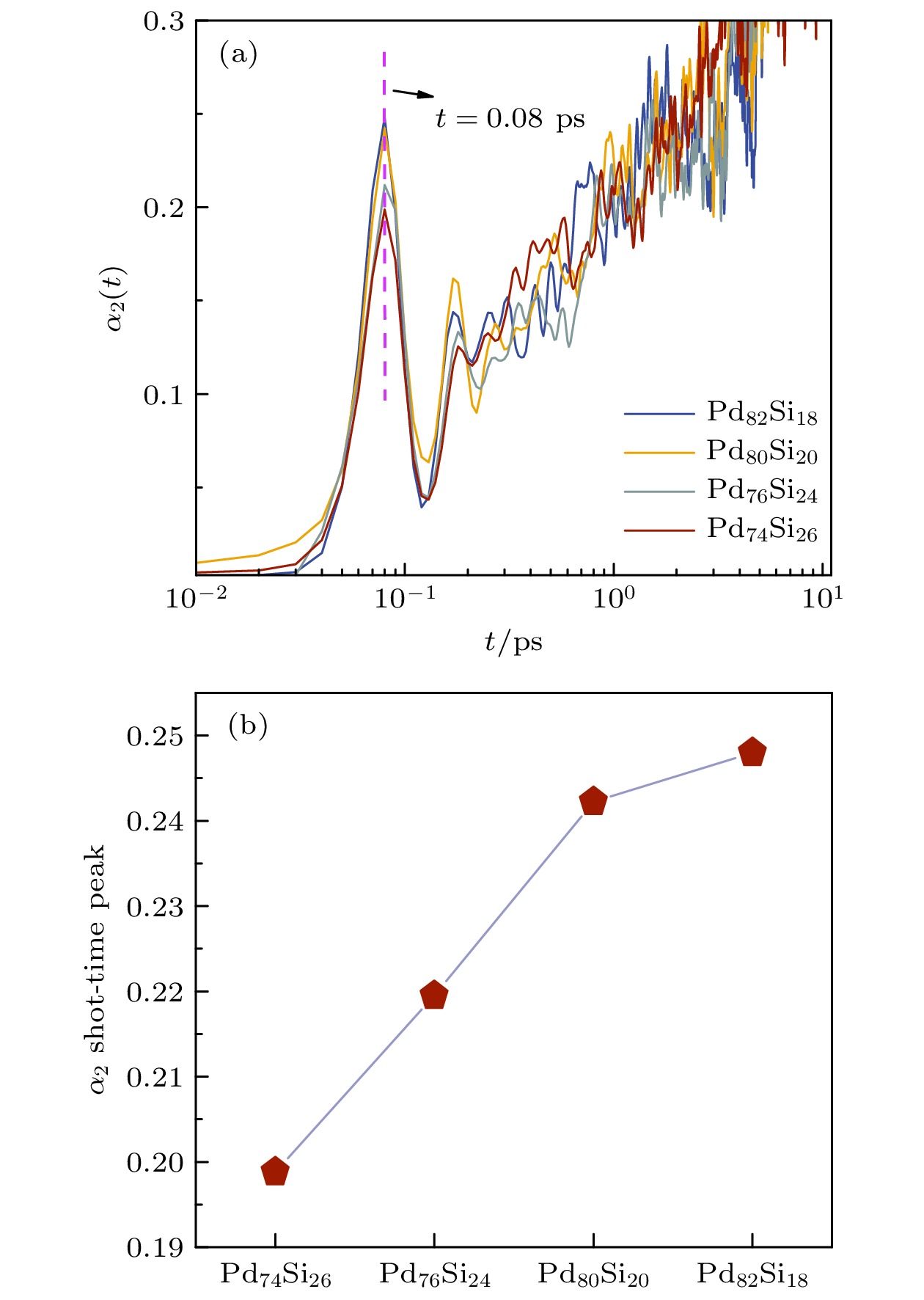
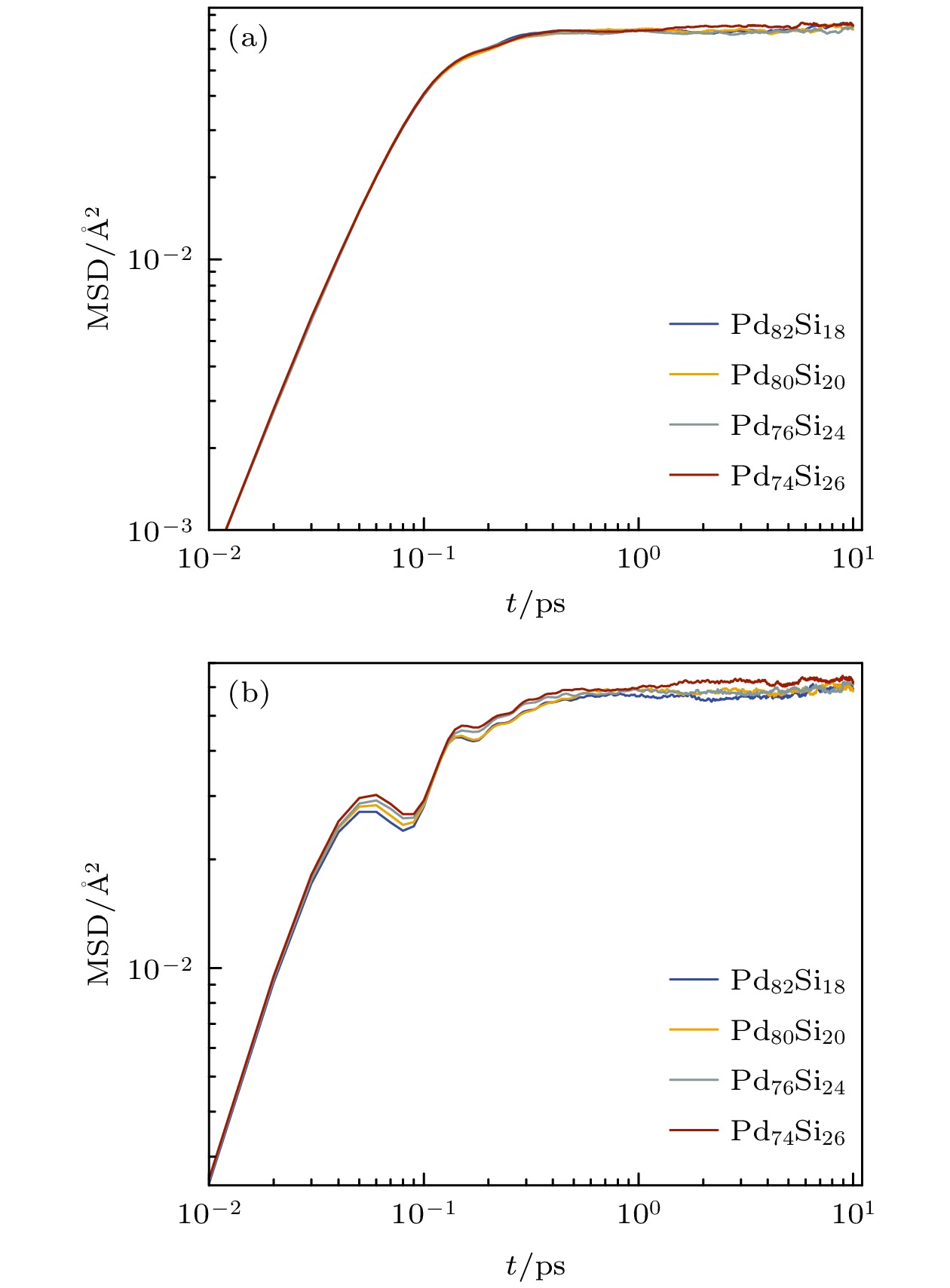
$ {r_j}({t_0}) $ 为粒子在初始时刻的位置,$ {r_j}(t + {t_0}) $ 为粒子在一段时间t后的位置. 图1给出了在300 K进行等温弛豫过程中, 不同浓度的Pd100–xSix非晶合金中Pd原子和Si原子的MSD随时间的演化关系. 由图1可知, 各浓度体系中Pd原子在弛 豫过程中MSD随时间变化符合普遍规律, 而所 研究的各体系中的Si原子在弛豫过程中都出现 了异常显著的牢笼效应, 且随着Pd原子浓度的增多, Si原子的弹道区位移减小, 其牢笼效应更早发生.常采用非高斯参数(non-Gaussian parameter, NGP)描述非晶体系的动力学非均匀性[24], 其计算公式:
其中
$ r(t) $ 表示体系原子在t时刻的位移. 图2给出了不同浓度非晶合金中Si原子的非高斯参数随时间的变化. 由图2(a)可知, Si原子的非高斯参数在0.08 ps处均出现了异常峰, 表明Si原子的动力学行为的分布存在不均匀性. 当扩散情况满足高斯分布时, 体系中原子发生布朗扩散[25]. 图2(b)给出了不同浓度体系中的非高斯参数异常峰峰值, 随Pd原子浓度的增加, Si原子的非高斯参数异常峰峰值增大, 即Si原子运动偏离布朗扩散程度更大, Si原子扩散受到周围原子的阻碍越明显, 这意味着Si原子的动力学行为与体系中Pd原子的浓度密切相关.Von Hove相关函数描述了在给定时间间隔内, 位于某一位置的粒子在另一位置的概率分布情况, 计算随时间变化的Von Hove相关函数的自部分可以揭示物质内部原子或分子的运动特性和动力学行为, 可以得知原子的运动范围以及可能存在的聚集现象[26]. 其计算公式如下:
其中N表示体系中原子的总数,
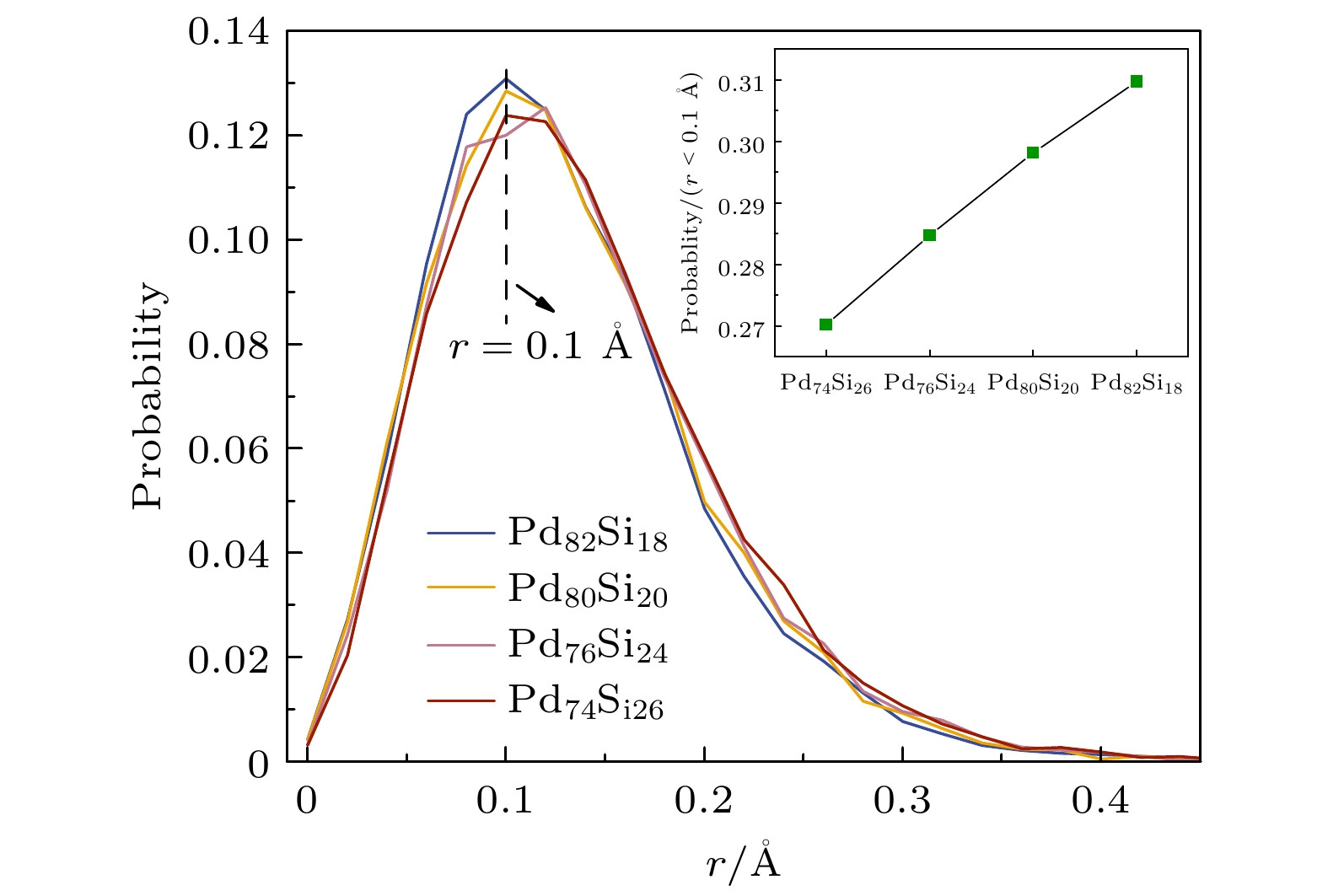
${r_j}(0)$ 为j原子的初始位置,${r_j}(t)$ 为j原子在t时刻的位置. 图3给出了不同浓度Pd-Si非晶合金中Si在0.08 ps内的位移分布情况. 由图3可知, 不同浓度d-Si非晶合金中的Si原子在0.08 ps内位移分布峰值大概都在0.1 Å左右, 且随Pd原子浓度的提高, 曲线的峰值增大. 这表明在0.08 ps内, Pd原子浓度越高Si原子的位移分布在0.1 Å的概率越大, 即大部分的Si原子的位移集中在1 Å. 图3中插图给出了不同体系中Si原子位移小于0.1 Å的占比. Pd浓度最高的Pd82Si18合金体系中, 0.08 ps内位移小于0.1 Å的Si原子占比最大, 表明增加Pd原子浓度会明显地阻碍并减缓Si原子的扩散运动, 表现出更加明显的牢笼效应.通过对不同浓度体系中Si原子的位移分布进行分析, 进一步对原子的位移离散程度或波动大小进行讨论. 图4给出了不同浓度Pd-Si非晶合金体系在出现异常非高斯峰前的平均位移和位移标准差, 对Si原子的扩散作定量分析. 其中平均原子位移的计算式:
其中
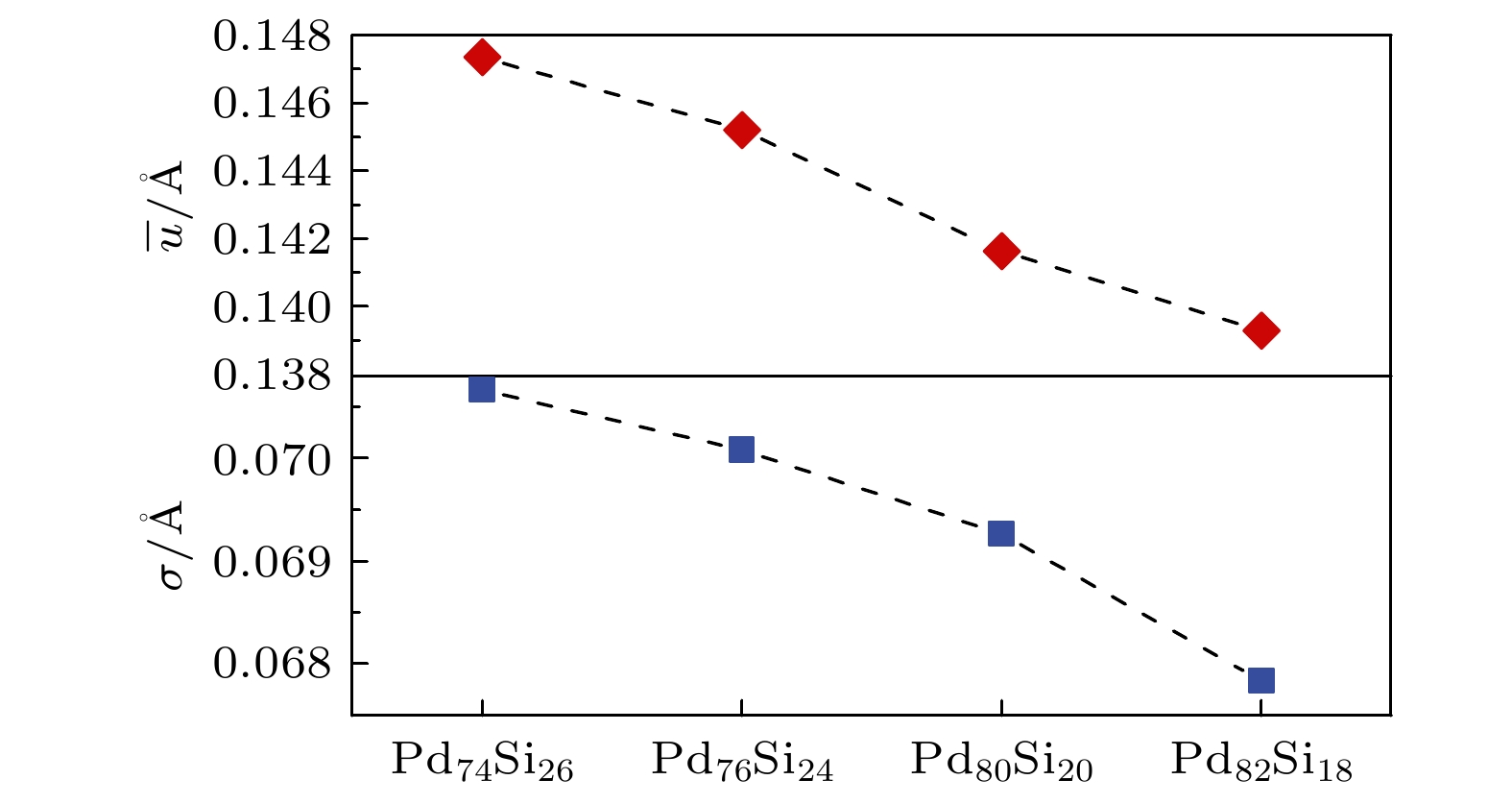
${r_i}(t)$ 表示在t时刻i原子的坐标,${r_i}(0)$ 表示初始时刻i原子的坐标. 位移标准差的计算式:其中xi表示i原子的位移. 标准差可用来衡量体系内原子的离散程度或者波动大小. 标准差越大, 表示数据点越分散或者波动越大, 体系中的原子的位移分布极值越多, 原子受力或扩散大小越无序. 由图4可知, 在Pd原子浓度较高的体系中, Si原子的平均位移较小, 且Si原子的位移标准差也较小. 这表明Pd原子浓度的增加导致体系中Si原子受到更多的来自周围Pd原子的阻碍. 弛豫过程中Si原子的非高斯参数在短时间内出现异常峰, 且有更大比例的Si原子由于受阻发生非高斯扩散, 因此体系中的Si原子运动范围大小较集中, 原子的动力学行为更为有序.
-
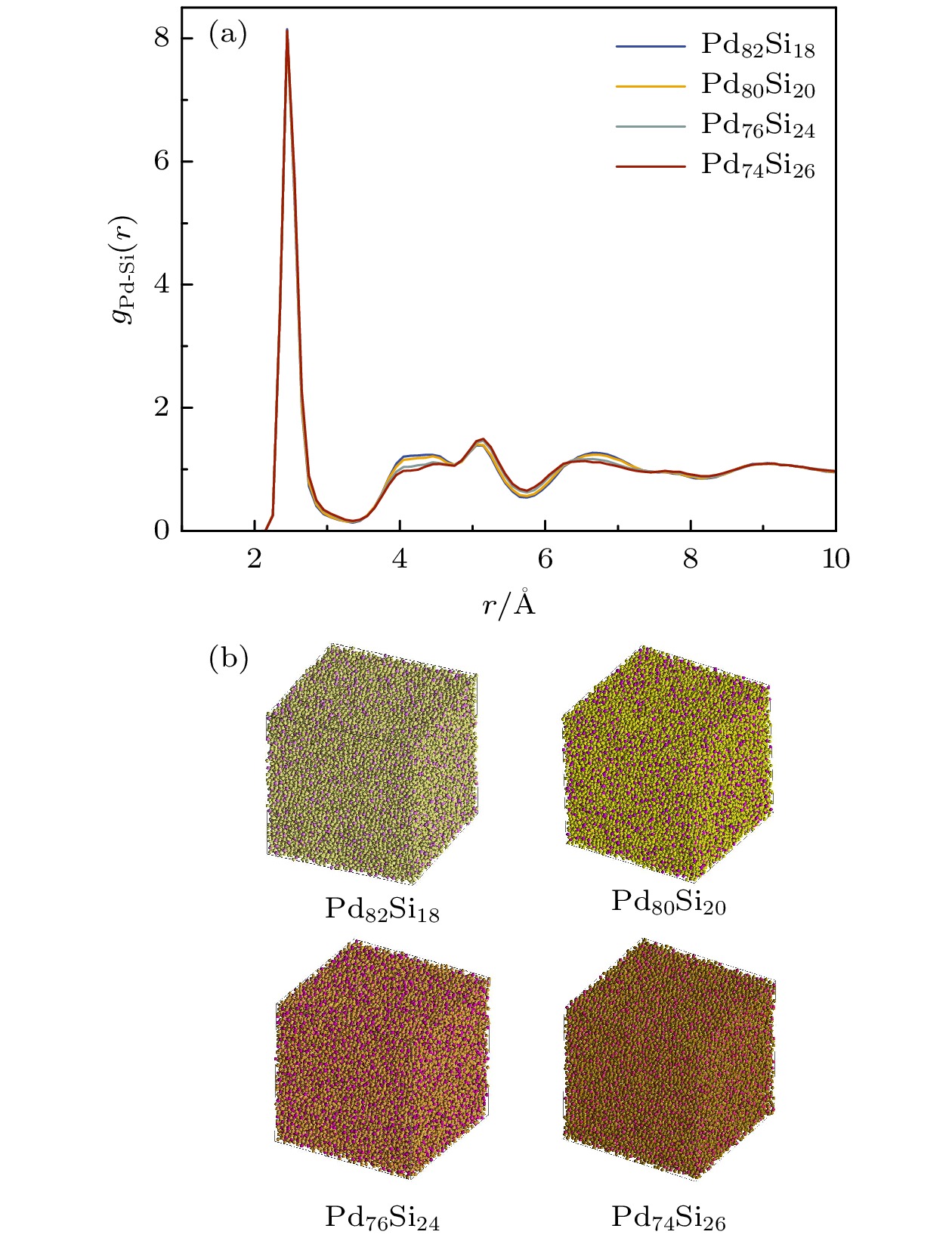
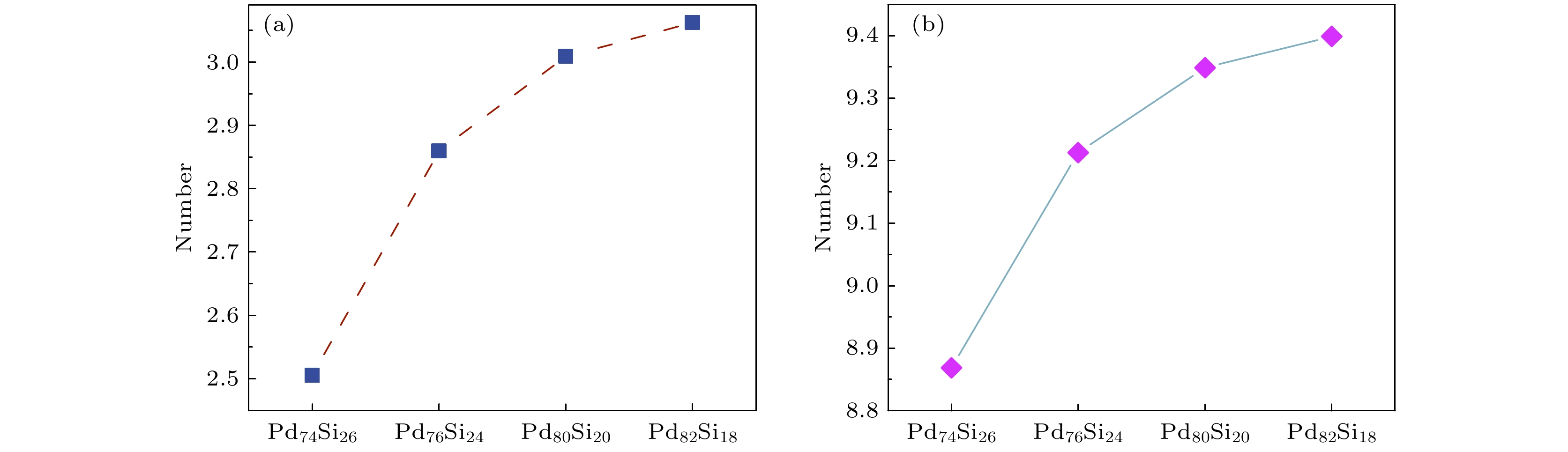
径向分布函数是分析液态、晶态、非晶态体系微结构特征的常用手段之一[27]. 图5(a)给出了300 K时Pd100–x Six非晶合金体系的偏双体分布函数gPd-Si(r). 据图5(a)可知, 四个体系的第二峰均发生了明显的劈裂, 表明这些体系均呈非晶结构特征. 图5(b)进一步给出了不同浓度的Pd-Si体系在300 K时的结构示意图, 可见体系中的原子排列方式呈无序状态. 随着Pd原子浓度的增高, gPd-Si(r)的第二峰劈裂得更加明显, 且左峰峰值明显增大, 表明体系的中程有序结构增强. 图6进一步给出了以第一谷和第一峰为截断距离, 各体系中Si原子的第一近邻Pd原子个数. 可以看出, 随着Pd原子浓度的增加, Si原子的第一近邻Pd原子的数目增多, 在Si原子周围存在更多的大尺寸Pd原子阻碍它们的扩散运动, 导致Si原子的牢笼效应更加明显.
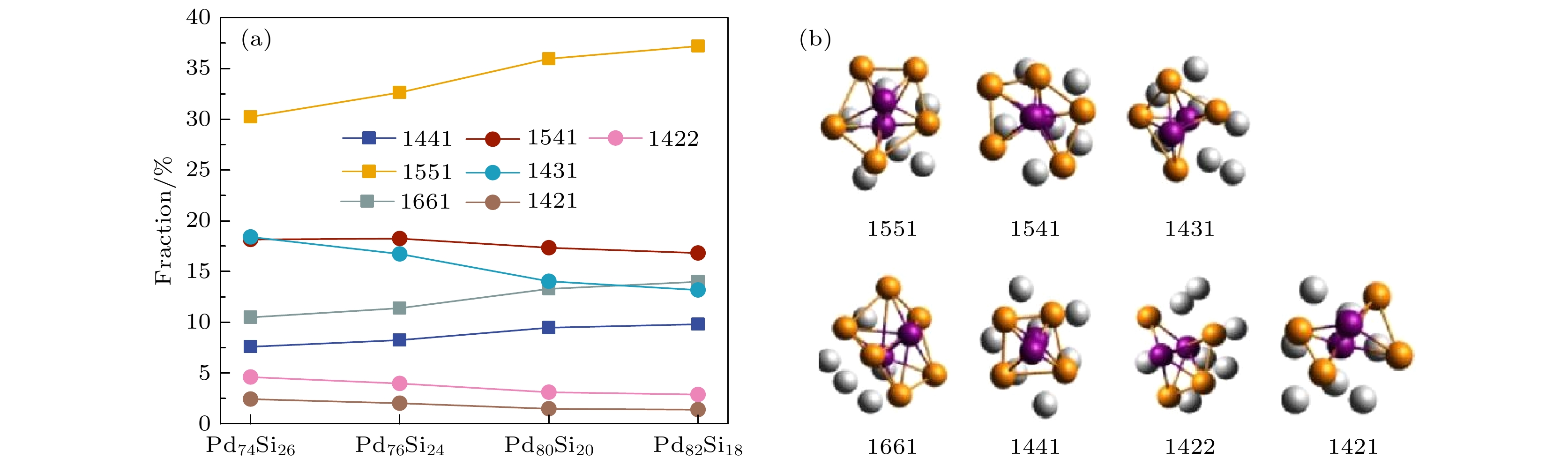
H-A键型指数法通常用于研究非晶材料的局域结构和原子之间的有序性征[28], 可帮助理解非晶材料的结构-性能关系. 为进一步理解局域对称性对Si原子的笼式动力学的影响, 图7给出了弛豫开始时快凝Pd100–xSix非晶合金体系中典型H-A键型所占百分比及典型H-A键型示意图. 分析图7(a)可知, 随着Pd原子浓度的升高, 具有高对称性的饱和键型(1441, 1551, 1661)所占百分比均有所增加, 1551键型所占百分比最多且增长得最为明显. 相反具有较低对称性的非饱和键型(1541, 1431, 1422, 1421)所占百分比均有所下降, 这些低对称性的键型具有较高的位错密度和能量, 因此 具有更加明显的液态特性, 更加不稳定, 非饱和键型在材料中的排列方式更加松散, 容易在弛豫过程中发生形变[29]. 对称性的增多会导致体系中形成更多的相对稳定的封闭网络结构, 导致原子所处的笼状结构能够完好存在更长时间, Si原子的运动受到更多、更强的来自高局域对称性键型的阻碍, 导致其出现明显的牢笼效应. 因此, 增加Pd原子浓度能够明显增加体系的饱和键所占百分比, 提高了体系的局域对称性.
Si原子由于受到周围Pd原子的较大阻碍, 而出现了明显的牢笼效应, 为了清晰地认识不同浓度Pd-Si非晶合金中Si原子的局域结构的差异性, 采用CTIM方法搜索和表征Si原子的局域结构[30]. 对各体系中典型以Si原子为中心的团簇数目进行分析比较, 如图8(a)所示. 图8(b)给出了这些团簇结构的示意图. 由图8(b)可知, Pd原子浓度的增高, 会导致体系中的以Si原子为中心的饱和键组成的典型团簇数目增多, 例如(9 3/1441 6/1551), (10 2/1441 8/1551), (11 2/1441 8/1551 1/1661), (12 2/1441 8/1551 2/1661), 体系中非饱和键参与组成的团簇数目减少, 如(9 1/1441 4/1551 4/1431)和(10 1/1441 5/1551 1/1541 3/1431). 表明提高Pd-Si合金中Pd原子的浓度, 由不饱和键参与组成的Si心团簇会向由饱和键组成的Si心团簇转化, 形成了更多封闭性更高、对称性更高、结构更加紧凑的团簇结构, 束缚Si原子的扩散, 明显增强Si原子的牢笼效应.
-
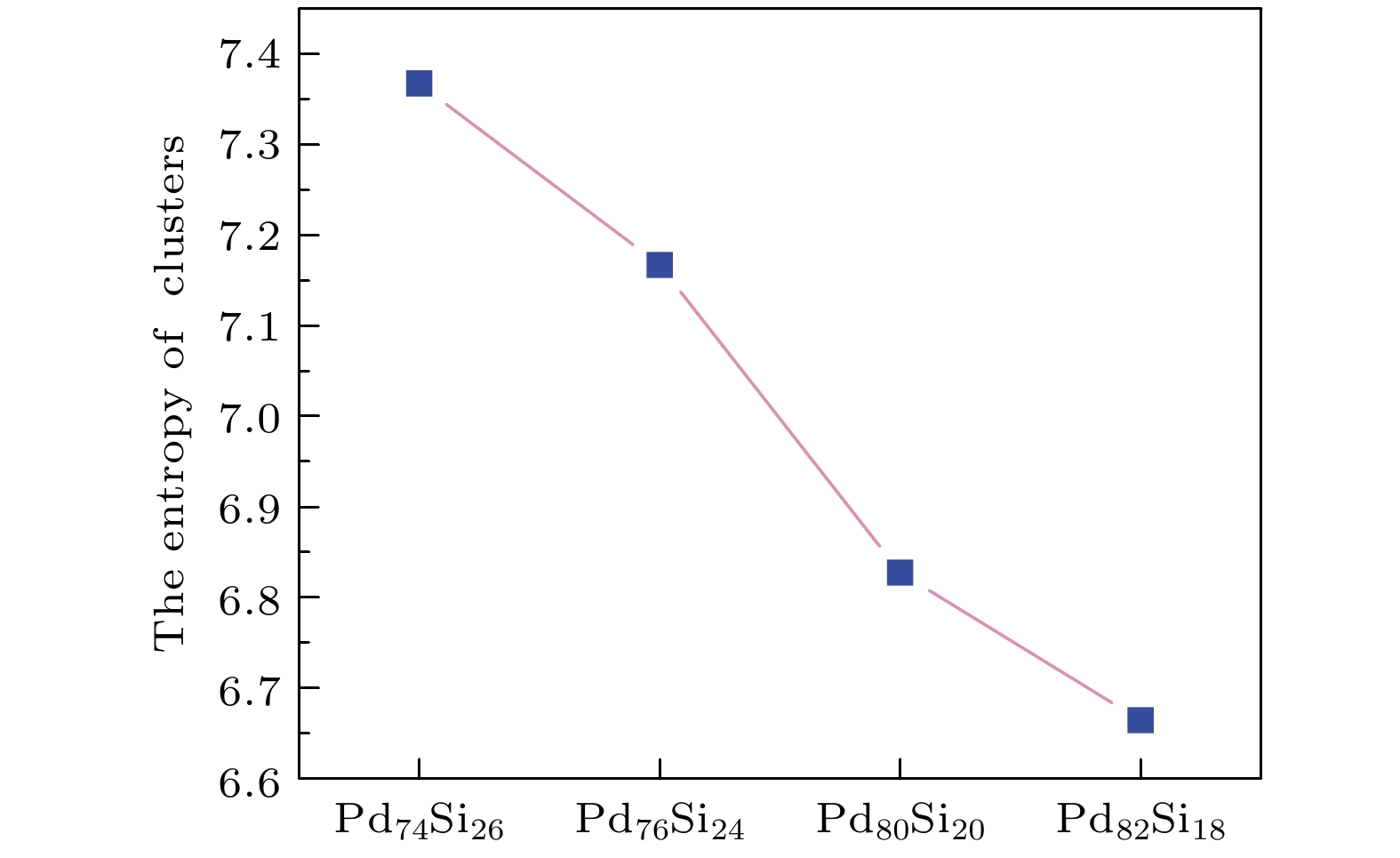
构型熵是一种分析体系结构有序性的辅助方法[31], 可以建立局域结构与体系有序度之间的联系, 常用于非晶合金中与体系有序度相关的研究分析, 构型熵越小, 体系的有序度越大. 其函数定义为
其中Pi是i构型在体系中所占的比例. 由于此处仅考虑构型概率, 故省略了玻尔兹曼常数. 对于仅由面心立方(FCC)、体心立方(BCC)等单一构型组成的系统, 其构型熵S = 0. 体系的构型越多, Pi越小, S越大, 体系的无序程度越大. 图9给出了四种不同浓度的Pd-Si非晶合金在等温弛豫开始时体系的构型熵. 由图9可知构型熵随着Pd原子浓度的增加而减小, Pd82Si18体系中的构型熵最小, 体系的团簇构型数最少, 意味着有更多的Si原子被束缚在相同的牢笼之中. 综上分析可知, 增加Pd原子浓度, 有利于提高体系的对称性增加和有序度.
-
采用分子动力学模拟方法研究了不同成分浓度的Pd-Si合金体系在等温弛豫过程中体系中Si原子牢笼效应. 得出如下主要结论:
1) 增加Pd原子浓度, Si原子的非高斯参数异常峰峰值变大, 其扩散受阻更严重. 同时Si原子的平均位移与位移标准差减小, 有更多的Si原子位移分布在小距离范围内, Si原子的牢笼效应更明显;
2) 增加Pd原子浓度, Si原子的Pd第一近邻增多, 饱和键型增多, 不饱和键型减少, 不饱和键型的Si心团簇向完全由饱和键型构成的Si心团簇转化, 束缚Si原子的扩散, 增强了Si原子的牢笼效应;
3) Pd原子浓度增加使体系构型熵降低, 增加了体系的对称性和有序性, 更多的Si原子处于相同的团簇中心, Si原子的局域原子环境对称性和有序度的明显提升.
Pd-Si非晶合金动力学非均匀性的对称与有序
Symmetry and order of kinetic heterogeneity in Pd-Si amorphous alloys
-
摘要: 微结构特征和结构演化机制是非晶态材料的研究重点, 非晶合金的动力学行为可以揭示非晶合金的形成过程和结构演化机制. 本文采用分子动力学模拟方法探讨了在Pd-Si非晶合金体系中, Pd原子的浓度对Si原子扩散的阻碍作用及其对体系对称性和有序度的影响. 并对与原子扩散、体系的对称性及有序度有关的参数进行了分析, 结果表明, 增加Pd原子的浓度会导致Si原子的扩散受到更明显的阻碍, 表现为Si原子的非高斯参数异常峰的峰值增大和位移的标准差减小. 这一现象表明, 增加Pd原子浓度会增强了Si原子的牢笼效应, 限制Si原子的扩散. 此外, Pd原子浓度的增加促进了Pd-Si非晶合金中不饱和键型向饱和键型的转变, 且体系的构型熵降低, 提高了Pd-Si非晶合金的局域对称性和有序度, 使得Si原子处于封闭性更强、对称性更高、结构更加紧凑的团簇结构中, 增强了其牢笼效应和局域对称性. 本文探讨了Pd原子浓度对Si原子的扩散行为及局域环境的影响机制, 为深入理解非晶合金的结构演化提供了新的视角.Abstract: In amorphous alloys, the atomic arrangement exhibits short-range order while lacking long-range order. Despite the lack of long-range order, the local atomic arrangements and interactions can still significantly affect the motion of atoms. The microstructural features and structural evolution mechanisms of amorphous materials are key areas of research, and the dynamics of amorphous alloys can provide insights into their formation process and structural evolution. The cage effect refers to the phenomenon where atoms are trapped by their surrounding atoms, making them difficult to migrate or diffuse freely. This leads to slower diffusion rates and higher viscosities in these materials. Atomic concentration is one of the crucial factors that influence the structures and properties of amorphous materials. Variation in concentration can significantly change the material’s structure. Adjusting the atomic concentration can lead to the difference in diffusion rate between elements in the amorphous alloys, resulting in heterogeneous distributions of elements in different regions, which in turn affects the deformation characteristics of amorphous materials. This study aims to investigate the effect of Pd atomic concentration on the diffusion hindrance of Si atoms, as well as its influence on the local symmetry and order of the system. To achieve this objective, molecular dynamics simulations are employed to explore the relaxation process of atoms in Pd-Si amorphous alloys at different Pd atomic concentrations, and parameters related to atomic diffusion, displacement distribution, system symmetry, and order are analyzed. The results show that increasing the concentration of Pd atoms leads to a more significant hindrance to the diffusion of Si atoms, manifested as an increase in the abnormal peak values of the non-Gaussian parameters and a decrease in the standard deviation of the displacement. This indicates that a higher Pd atom concentration enhances the cage effect of Si atoms, thus restricting their diffusion. Additionally, the increase in Pd concentration promotes the transition from unsaturated to saturated bond type in the Pd-Si amorphous alloy, and also leads the system’s configurational entropy to decrease. This consequently enhances the local symmetry and order of the Pd-Si amorphous alloys, leading Si atoms to be located in the center of more closed, higher-symmetry, and more compact cluster structure, which strengthens their cage effect and local symmetry. This study investigates the influence of Pd atom concentration on the diffusion behavior and local environment of Si atoms, providing a new insight into the structural evolution of amorphous alloys.
-
Key words:
- molecular dynamics /
- Pd-Si amorphous alloys /
- atomic concentration /
- cage effect /
- local symmetry .
-
-
图 1 Pd-Si非晶合金弛豫过程中Pd原子和Si原子的均方位移随时间的变化 (a) Pd; (b) Si
Figure 1. Time-dependent evolution of mean square displacement of Pd and Si atoms during the relaxation in Pd-Si amorphous alloys: (a) Pd; (b) Si.
图 2 Pd-Si非晶合金弛豫过程中Si原子的非高斯参数随时间的变化 (a) 不同浓度体系Si原子的非高斯参数; (b) 不同浓度体系Si原子非高斯参数异常峰峰值
Figure 2. Variation of non-Gaussian parameters of Si atoms in different systems during the relaxation of Pd-Si amorphous alloys: (a) Non-Gaussian parameters; (b) abnormal peak values of non-Gaussian parameters.
图 3 Pd-Si非晶合金中Si原子在0.08 ps内的Von Hove相关函数的自部分
Figure 3. Self-part of the Von Hove correlation function for the time evolution of Si atoms in Pd-Si amorphous alloys during 0.08 ps.
图 4 Pd-Si非晶合金中Si原子的平均位移与位移标准差
Figure 4. Average displacement and displacement standard deviation of Si atoms in Pd-Si amorphous alloys.
图 5 Pd-Si非晶合金在300 K时的结构特征 (a) 偏双体分布函数gPd-Si(r); (b) 结构示意图
Figure 5. Structural characteristics of Pd-Si amorphous alloys at 300 K: (a) The pair distribution function; (b) visual displays.
图 6 Si原子的近邻Pd原子个数 (a) 以第一峰为截断距离; (b) 以第一谷为截断距离
Figure 6. Number of neighboring Pd atoms for Si atoms: (a) The first peak value as the truncation distance; (b) the first valley value as the truncation distance.
图 7 Pd-Si非晶合金在300 K时的H-A键型分析 (a) 典型H-A键型所占百分比; (b) 典型H-A键型结构示意图
Figure 7. Analysis of H-A bond types of Pd-Si amorphous alloys at 300 K: (a) Percentage of typical H-A bond types; (b) visual displays of H-A bond types.
图 8 Pd-Si非晶合金中在300 K时体系中以Si原子为中心的典型团簇分析 (a) 团簇数目; (b) 团簇结构示意图
Figure 8. Analysis of typical cluster centered on Si atoms in Pd-Si amorphous alloys at 300 K: (a) Number of clusters; (b) visual displays of cluster structure.
-
[1] Qiao J C, Pelletier J M 2014 J. Mater. Sci. Technol. 30 523 doi: 10.1016/j.jmst.2014.04.018 [2] Abrosimova G E 2011 Phys. Usp. 54 1227 doi: 10.3367/UFNe.0181.201112b.1265 [3] Cornet A, Garbarino G, Zontone F, Chushkin Y, Jacobs J, Pineda E, Deschamps T, Li S, Ronca A, Shen J, Morard G, Neuber N, Frey M, Busch R, Gallino I, Mezouar M, Vaughan G, Ruta B 2023 Acta Mater. 255 119065 doi: 10.1016/j.actamat.2023.119065 [4] Zella L, Moon J, Keffer D, Egami T 2022 Acta Mater. 239 118254 doi: 10.1016/j.actamat.2022.118254 [5] 陈贝, 邓永和, 祁青华, 高明, 文大东, 王小云, 彭平 2024 物理学报 73 026101 doi: 10.7498/aps.73.20231101 Chen B, Deng Y H, Qi Q H, Gao M, Wen D D, Wang X Y, Peng P 2024 Acta Phys. Sin. 73 026101 doi: 10.7498/aps.73.20231101 [6] Gao M , Wen D D, Cao G Q, Zhang Y W, Deng Y H, Hu J H 2023 Appl. Surf. Sci. 640 158286 doi: 10.1016/j.apsusc.2023.158286 [7] Faruq M, Villesuzannea A, Shao G S 2018 J. Non-Cryst. Solids 487 72 doi: 10.1016/j.jnoncrysol.2018.02.016 [8] Zhou Z Y, Yang Q, Yu H B 2024 Prog. Mater Sci. 145 101311 doi: 10.1016/j.pmatsci.2024.101311 [9] Deng Y H, Chen B, Qi Q H, Li B B, Gao M, Wen D D, Wang X Y, Peng P 2024 Chin. Phys. B 33 047102 doi: 10.1088/1674-1056/ad1d4e [10] Raya I, Chupradit S, Kadhim M M, Mahmoud M Z, Jalil A T, Surendar A, Ghafel S T, Mustafa Y F, Bochvar A N 2022 Chin. Phys. B 31 016401 doi: 10.1088/1674-1056/ac3655 [11] Jiang J, Sun W F, Luo N 2022 Mater. Today Commun. 31 103861 doi: 10.1016/j.mtcomm.2022.103861 [12] Laws K J, Granata D, Löffler J F 2016 Acta Mater. 103 735 doi: 10.1016/j.actamat.2015.08.077 [13] Fernández R, Carrasco W, Zúñiga A 2010 J. Non-Cryst. Solids 356 1665 doi: 10.1016/j.jnoncrysol.2010.06.016 [14] Chen Y X, Pan S P, Lu X Q, Kang H, Zhang Y H, Zhang M, Feng S D, Ngai K L, Wang L M 2022 J. Non-Cryst. Solids 590 121699 doi: 10.1016/j.jnoncrysol.2022.121699 [15] Gao Q, Jiang Y, Liu Z, Zhang H, Jiang C, Zhang X, Li H 2020 Mater. Sci. Eng., A 779 139139 doi: 10.1016/j.msea.2020.139139 [16] Liu C Y, Maaß R 2018 Adv. Funct. Mater. 28 1800388 doi: 10.1002/adfm.201800388 [17] Pourasghar A, Kamarian S 2015 J. Vib. Control 21 2499 doi: 10.1177/1077546313513625 [18] Celtek M, Sengul S, Domekeli U, Guder V 2023 J. Mol. Liq. 372 121163 doi: 10.1016/j.molliq.2022.121163 [19] Nandam S H, Adjaoud O, Schwaiger R, Ivanisenko Y, Chellali M R, Wang D, Albe K, Hahn H 2020 Acta Mater. 193 252 doi: 10.1016/j.actamat.2020.03.021 [20] Verlet L 1967 Phys. Rev. 159 98 doi: 10.1103/PhysRev.159.98 [21] Available at https://www.google.com/site/eampotentials/Table/PdSi [22] Priezjev N V 2020 Comput. Mater. Sci. 174 109477 doi: 10.1016/j.commatsci.2019.109477 [23] Moon J 2021 J. Appl. Phys. 130 055101 doi: 10.1063/5.0043597 [24] Sun L, Peng C, Cheng Y, Song K, Li X, Wang L 2021 J. Non-Cryst. Solids 563 120814 doi: 10.1016/j.jnoncrysol.2021.120814 [25] Li Y G, Suleiman K, Xu Y 2024 Phys. Rev. E 109 014139 doi: 10.1103/PhysRevE.109.014139 [26] Wen T Q, Sun Y, Ye B L, Tang L, Yang Z J, Ho K M, Wang C Z, Wang N 2018 J. Appl. Phys. 123 045108 doi: 10.1063/1.5019681 [27] Deng Y H, Wen D D, Li Y, Liu J, Peng P 2018 Philos. Mag. 98 2861 doi: 10.1080/14786435.2018.1510188 [28] Wen D D, Deng Y H, Liu J, Tian Z A, Peng P 2017 Comput. Mater. Sci. 140 275 doi: 10.1016/j.commatsci.2017.07.040 [29] Feng S D, Chan K C, Zhao L, Pan S P, Qi L, Wang L M, Liu R P 2018 Mater. Des. 158 248 doi: 10.1016/j.matdes.2018.08.040 [30] Liu R S, Liu H R, Dong K J, Hou Z Y, Tian Z A, Peng P, Yu A B 2009 J. Non-Cryst. Solids 355 541 doi: 10.1016/j.jnoncrysol.2009.02.001 [31] Zhou Y, Liang Y C, Zhou L L, Mo Y F, Wu R L, Tian Z A 2023 J. Non-Cryst. Solids 612 122354 doi: 10.1016/j.jnoncrysol.2023.122354 -
计量
- 文章访问数: 111
- HTML全文浏览数: 111
- PDF下载数: 3
- 施引文献: 0