缩孔和缩松是铸件凝固过程产生的主要缺陷, 其成因是合金在凝固过程中发生收缩, 最后凝固的区域得不到有效的液态金属补缩而产生的. 缩孔缩松会明显降低铸件的力学性能, 缩短服役寿命, 因此需要采取恰当的工艺加以消除. 利用数值模拟技术可以有效预测凝固过程中铸件的收缩情况, 并根据模拟结果对工艺进行优化, 从而减少缩孔缺陷的出现, 是一种低成本高效率的方法.

对铸件缩孔缩松缺陷预测的数值模拟研究可以追溯到20世纪初期^[1], 早期的研究主要依赖于经验公式和简单的物理模型^[2], 主要有等温曲线法、等固相率法、收缩量法、温度梯度法、流导法等, 这些方法可以在一定程度上预测缺陷产生的位置和大小, 但都有局限性, 如等温曲线法和等固相率法是通过判断等温线和等固相率小于某一临界值时, 将其内部单元认定为收缩缺陷, 但在等温线或等固相率闭合回路出现开口时则难以判断. 再如流导法则需要根据不同合金获得其适合的透过率才能进行预测. 20世纪60年代, Piwonka 和Flemings^[3]一起提出了基于达西定律流动模型的缩孔预测方法, 采用达西定律描述糊状区中液态金属的流动, 通过计算流动受阻导致的压力降来预测缩孔的形成, 然而该模型假设条件过于理想化, 难以应用于复杂几何形状的铸件模拟, 尽管如此, 这一模型为后续研究奠定了基础. 1981年, Niyama等^[4]提出了基于温度梯度和冷却速率的经验公式, 即Niyama判据, 该判据在一定范围内不受铸件的材料和形状的影响, 能够有效地对铸钢件进行缩松缩孔预测. 1996年, 贾宝仟和柳百成^[5]通过对铝铜合金的一次枝晶间距的计算公式推导得到新的判据公式, 证明了Niyama判据的正确性, 然而该模型本质仍然依赖于经验公式, 受限于特定的材料和工艺参数, 预测精度在某些情况下受到限制. 20世纪90年代, Stefanescu等^[6]结合热传导、液态金属流动和固态金属三者的耦合构建了热-流-固耦合模型, 通过同时考虑三场耦合提供了更为全面的预测方法, 尽管这一模型大大提高了预测精度, 但也增加了计算复杂度和时间成本. 21世纪初, Carlson和Beckermann^[7]将氢扩散和固相微观结构考虑进随机孔隙形核模型, 提出CS模型. 2001年Lee等^[8]通过模拟晶粒形核和生长的元胞自动机方法, 结合扩展到三维的CS模型模拟孔隙和晶粒的生长模拟缩松缩孔, 但是由于元胞自动机方法本身的模拟尺度较小, 导致计算时间过长, 难以应用到大规模工业生产中去. 最近几年的研究包括Khalajzadeh等^[9]于2017年提出一种孔隙中心模型, 2020年进行了改进, 用于描述金属合金在凝固过程中由于气体和收缩引起的孔隙形成, 该模型采用理想气体定律和Laplace方程, 结合液体压力变化、气体扩散和冷却速率, 描述了孔隙的生长动力学. 通过计算孔隙半径随冷却速度、热梯度、气体扩散和收缩的时间演变, 进行孔隙形成和液体流动的双向耦合, 从而详细分析了孔隙的形核和生长过程. 该算法的缺点如下: 1)该模型假设冷却速率为常数, 并将孔隙假设为理想球形, 但实际铸造过程中冷却速率可能变化, 实际孔隙的形状可能更复杂, 尤其是在收缩和气体同时作用的情况下; 2)该模型强依赖于多个参数的精确值, 如表面张力、气体扩散系数等, 而这些参数在不同材料和工艺条件下可能有所不同, 获取这些参数困难且不准确; 3)对初始条件和边界条件非常敏感, 任何微小的误差都可能导致最终结果的显著偏差; 4)该模型涉及多个非线性方程的求解, 计算复杂度较高, 尤其是处理大规模复杂铸件时, 可能会导致计算时间过长.

目前对铸件收缩数值模拟的研究取得了显著进展, 研究者们正在探索新兴的技术和方法, 以提高铸件收缩模拟的精度和效率, 例如, 机器学习和人工智能技术正在逐渐应用于铸件过程数值模拟中. 通过训练大量的实验数据, 机器学习模型可以识别和优化铸造工艺中的关键参数, 提高模拟的准确性和实时性. 此外, 并行计算和高性能计算技术的发展也为复杂铸件的模拟提供了强有力的支持. 然而在实际应用中仍面临诸多挑战: 1)现有的模型虽然能够准确模拟收缩孔隙的形成过程, 但其计算复杂度较高, 求解时间耗时长, 对计算资源要求高, 尤其是在处理复杂的铸件几何形状和多变的工艺参数时更是如此. 这严重限制了现有模型在实际工业生产中的应用; 2) 许多模型具有较强的参数依赖性, 即对物理场参数过于敏感, 细微的参数差距会导致计算结果截然不同, 而这些参数的获取往往困难且不准确; 3)缩孔形成过程中涉及复杂的质量传输、热传导和相变耦合, 这些过程的精确模拟仍然具有很大的难度等.

为了解决上述问题, 本文在元胞自动机算法模拟铸锭凝固过程的基础上, 提出了一种动态求解凝固过程收缩的思路. 将元胞的位置矢量随凝固过程的位移变化作为求解对象, 应用动网格技术求解每个时刻下的位置矢量. 在动网格中, 网格的动态调整通常依赖于复杂的物理特征数据, 如流体速度、压力、网格温度等, 支持向量机(support vector machines, SVM)算法擅长分类这些特征数据^[10], 在动网格中可以帮助确定何时以及如何调整网格位置, 例如: 在多相流的模拟中, SVM可以用来识别不同流体相边界或不同流动模式下的区域, 从而在这些区域计算网格位置的变化. 动网格技术的本质是解决非线性问题, 径向基函数(radial basis function, RBF)算法^[11]擅长处理该问题, RBF可以通过对网格节点间的关系进行非线性映射, 预测流体力学中的细微变化, 例如: 在模拟气流绕过机翼的过程中, RBF可以帮助精确建模机翼变形的非线性行为, 使网格位置或形状随物体运动、边界变化或者流体特征改变而更新, 从而提高对复杂流体、结构运动或者多相系统的模拟精度. 故本文提出两种分别基于RBF算法和SVM算法的动网格技术, 来模拟铸件凝固过程中缩孔形成的动态过程.

动网格技术是一种在数值计算中广泛应用的方法, 旨在通过随时间动态调整网格的位置或形状, 以更精确地模拟流体、固体或其他物理系统中的变化过程. 该技术常用于处理包含移动边界、变形物体或更大范围运动的复杂问题, 如流体力学中的波浪传播、结构动力学中的形变分析以及空气动力学中飞行器的运动模拟^[12].

动网格技术的核心在于通过调整网格节点的位置, 使得网格能够灵活适应几何形状和物理特性的动态变化, 不仅可以提高计算精度, 还能有效减少计算资源的浪费, 使得计算集中在物理场中变化距离的区域, 提高整体模拟的效率.

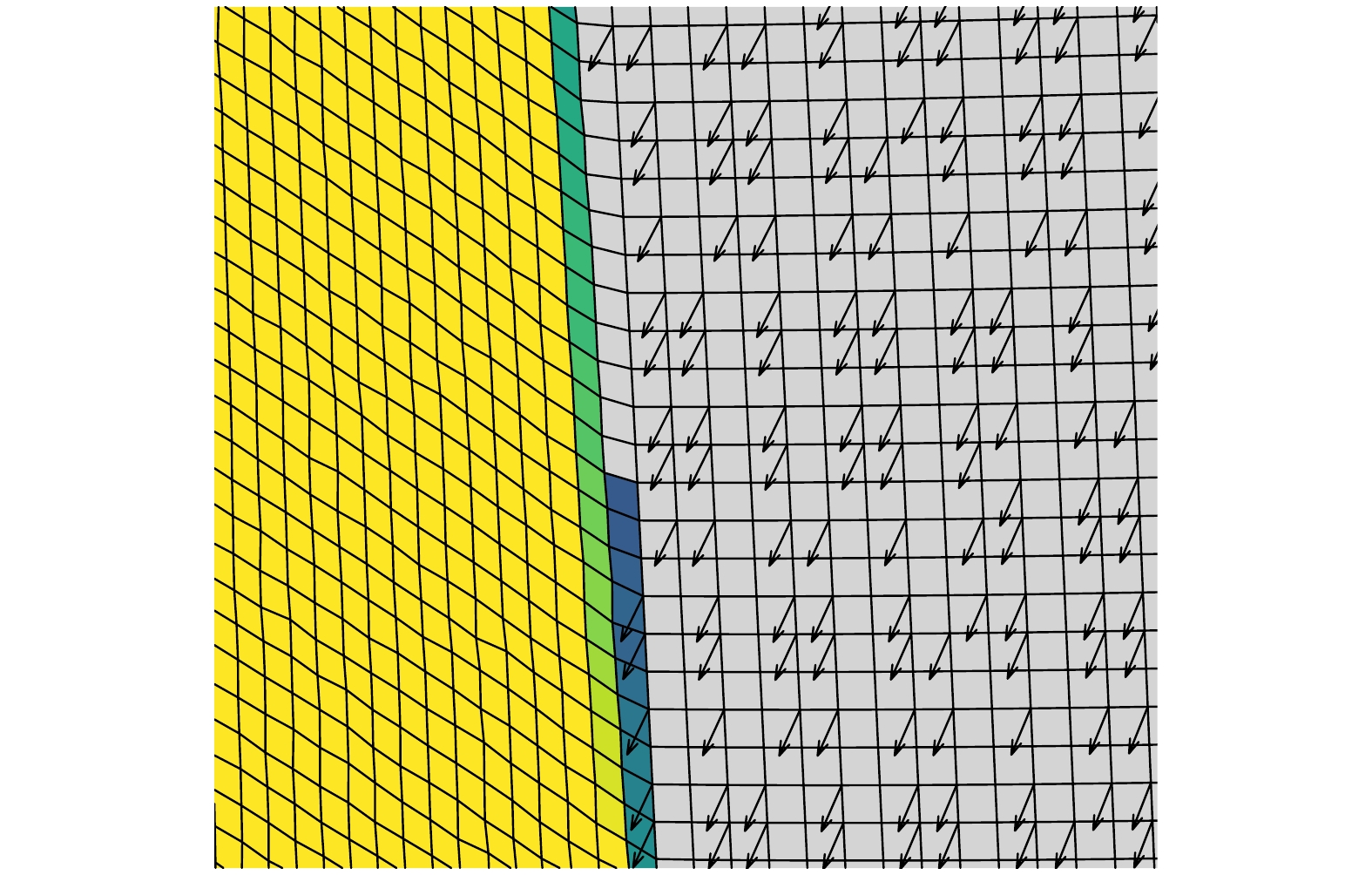
以二维平面向下压缩顶部网格为例, 将顶层网格作为边界, 模拟开始时, 对边界层施加大小为$d_{i, j}^y = - {\text{d}}x \cdot \sin \Big(\dfrac{i}{{{L_x}}} \cdot {\text{d}}x \cdot {\text{π}}\Big)$的应变, 其中${L_x} = {\text{d}}x \cdot {N_x}$, 所得的t = 5, t = 10的计算结果如图1所示.

从图1可以看到, 网格在中央区域产生了明显的形变, 且伴随着顶部网格所施加的应变越大中央区域的形变越剧烈. 动网格的优势就在于此, 当物体移动或者变形时, 网格会随着物体的边界形状的变化进行自适应重构, 使得计算精度能够跟随物理现象的演化而提高^[13]. 正因如此, 可以将动网格技术应用于铸件凝固过程中的收缩模拟. 凝固过程中金属的冷却往往伴随体积的收缩, 这种收缩会导致应力集中、裂纹或者孔洞的产生, 动网格技术能够帮助准确捕捉铸件在冷却过程中的几何变换和应力分布, 根据金属的收缩特性对网格位置进行调整, 实时适应铸件的几何形状, 这样随着铸件冷却, 网格节点也会移动, 使得网格在形变区域保持高精度, 更不必重新生成网格. 董士虎等^[14]基于界面追踪-动网格技术模拟了凝固收缩下Fe-C合金的宏观偏析, 通过收缩量追踪空气-熔钢及铸锭界面并由动网格技术重构计算区域, 利用变形的网格实现合金凝固体积收缩的计算, 较好地预测了收缩腔形状, 但美中不足在于该算法的本质是求解整体的收缩总量之后再施加到顶部网格, 再经过动网格技术计算各自网格的变形量, 这并不是动态追踪收缩的动态过程, 没有反映出凝固收缩的物理本质, 即内部网格的收缩变形驱动了顶部的凹陷. 所以本文着重于还原动态凝固收缩过程, 将凝固过程与收缩过程进行耦合计算, 通过计算内部网格的收缩来反映出顶部收缩腔的动态形成过程. 计算分为两个部分: 1) 动态标记边界点并计算边界点的位移; 2) 通过动网格技术动态地将边界点的位移传播给所有网格.

本文采用元胞自动机(cellular automaton)耦合格子玻尔兹曼方法 (lattice Boltzmann method, LBM)进行铸件凝固模拟. 其思想是将三维空间中的实体抽象为一组可以描述实体单位物理信息的质点集合, 一个元胞的活动受到相邻元胞活动的影响, 宛如人体的细胞一样彼此交流, 共同构成人体的组织. 在铸件凝固中, 本文将元胞的状态分为0, 1, 2, 分别代表液相元胞、界面元胞以及固相元胞并采用D2Q9模型来耦合流场、温度场和溶质场. 大量工作已经验证了该物理模型的可靠性与稳定性^[15–21]. 本文对该模型进行了改进, 将在下文详细介绍. 元胞的收缩可以体现为元胞中心质点的位移, 而铸件凝固过程中收缩主要是由于相变和温度下降, 由于内部网格的温度无时无刻不在发生微小变化, 若将发生温度变化的元胞都标定为边界点则失去了动网格算法本身的意义, 故本文仅将已经凝固完全的固相元胞以及处于半凝固状态的界面元胞标定为边界点, 需要强调的是边界点的概念是动网格计算中的概念, 与CA中的界面元胞不属于同一个概念. 边界点的运动会带动整体的运动, 通过计算边界网格的位移矢量与其位置作为机器学习算法的训练数据集, 进而求得该时刻其他元胞的位置偏移量. 对于一个边界元胞总的收缩位移为

(1) 式右边第1项为元胞因凝固放出显热引起收缩的位移, 结合LBM的离散方式, 具体实现为

其中, $ {\text{d}}{\boldsymbol{s}}_i^{\text{T}} $是将空间进行LBM离散后, 利用线性膨胀公式计算各个方向上的膨胀量后进行的矢量求和, 具体表示为

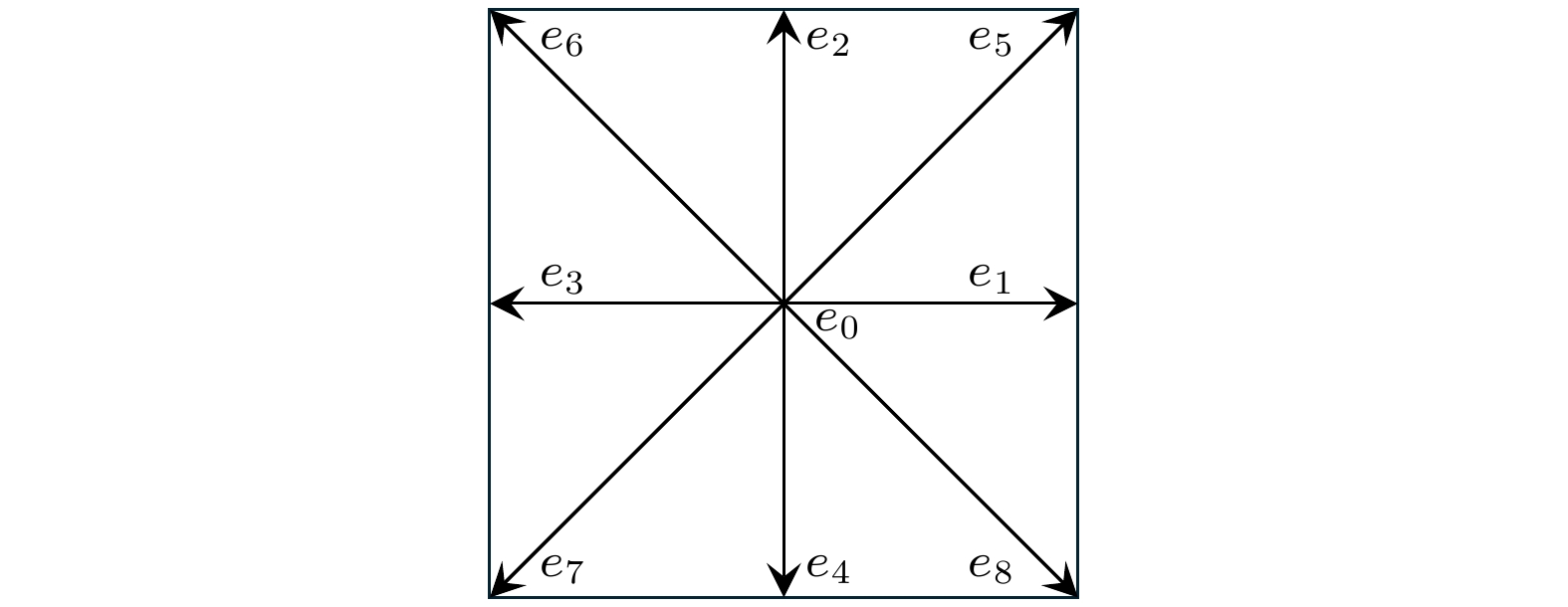
式中, ${\boldsymbol{r}}$是元胞的位置编码, 为元胞计算平面的矢量位置, f_i为格子Boltzmann方程中的离散分布函数, 此处代表温度的分布函数, T_l是合金液相线, T_s是合金固相线, ${{\varepsilon }}\left( {\text{T}} \right)$为热膨胀系数, ${{P}}\left( {\boldsymbol{r}} \right)$为元胞的物理平面的实际矢量位置, ${{\boldsymbol{e}}_i}$为离散方向:

本文的计算平面为二维平面, 采用D2Q9离散模式, 如图2所示.

上文所述的物理平面是指计算流体力学(CFD)中物流体的实际行为. 物理平面关注的是如何将实际的物理过程准确地建模, 以便于在计算中尽可能真实地再现这些过程. 与物理平面相对的是计算平面, 涉及的是如何在计算机上实现和解决物理平面中描述的流体问题, 计算平面关注的是如何将物理问题转化为计算问题, 并通过计算机模拟这些问题.

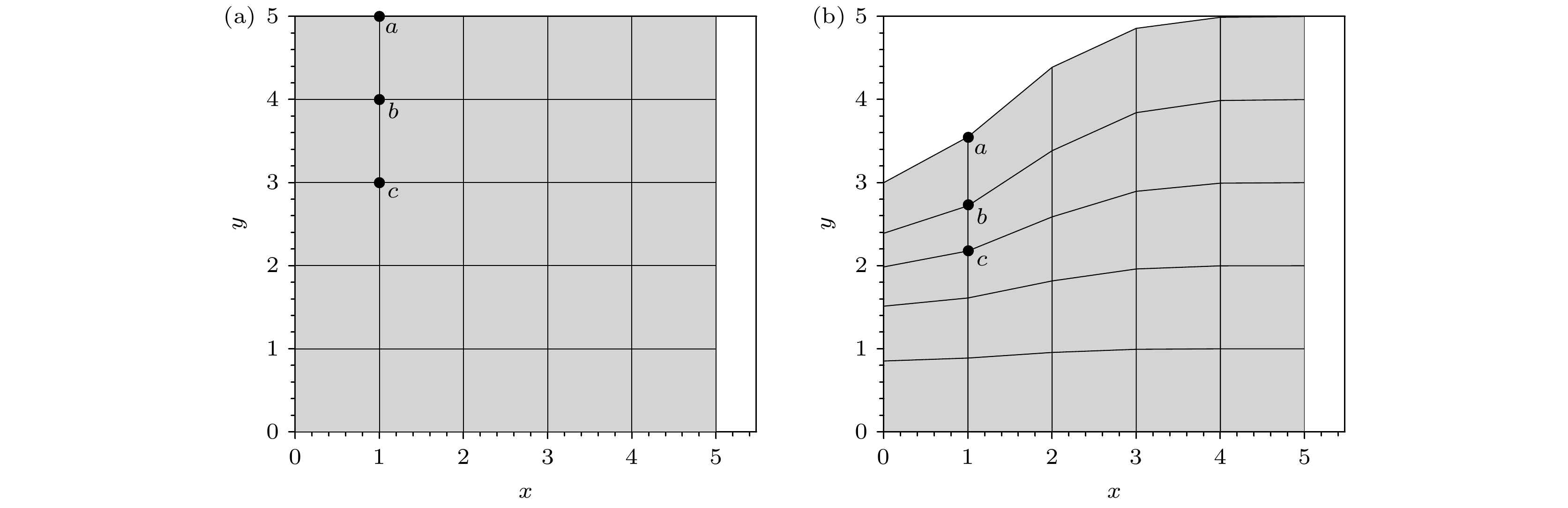
这里以图3为例说明计算平面和物理平面的关系. 图3(a)为所计算模型的实际计算平面, 图3(b)为所计算模型的实际物理平面, 是动网格在某个时间点的计算结果. 图3(b)中的点a, b, c是其中真实的质点位置, 将物理平面映射到图3(a)所示的规则的计算平面, 这个平面的坐标系是正交的, 便于离散方程和编写程序, 其中的点a, b, c是由物理平面相对应的点的映射.

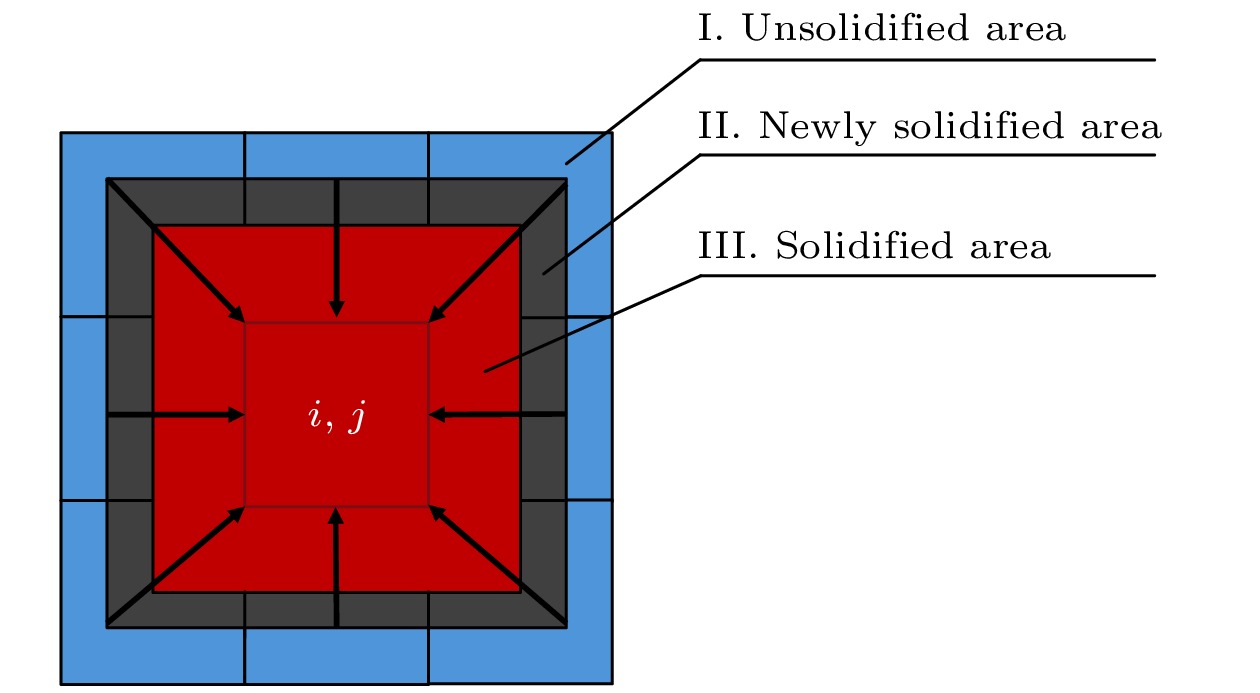
(1)式等号右边第2项是界面元胞的凝固收缩对整体网格位移的影响项, 对于凝固收缩的处理, 本文基于元胞自动机zigzag捕获原理提出一种新的收缩模型. 在LBM的DnQm格式中, 若处于${\boldsymbol{r}} + {{\boldsymbol{e}}_i}$位置的液态元胞被r处的元胞捕获, 沿${{\boldsymbol{e}}_i}$方向生长, 则其收缩方向是沿着${{\boldsymbol{e}}_i}$方向的反方向, 以D₂Q₉八元胞捕获(图4)为例.

图4中, I区域为液相区, II区域是在当前时间步长内增长的固相分数${\text{d}}{f_{\text{s}}}$, III区域是已经凝固的固相区域. 元胞i, j凝固结束后捕获周围8个元胞, 图4中箭头所指方向为每个被捕获元胞的收缩方向, 则被捕获元胞在一个时间步长内由于凝固收缩形成的位移${\text{d}}{{\boldsymbol{s}}^{\text{P}}}$为

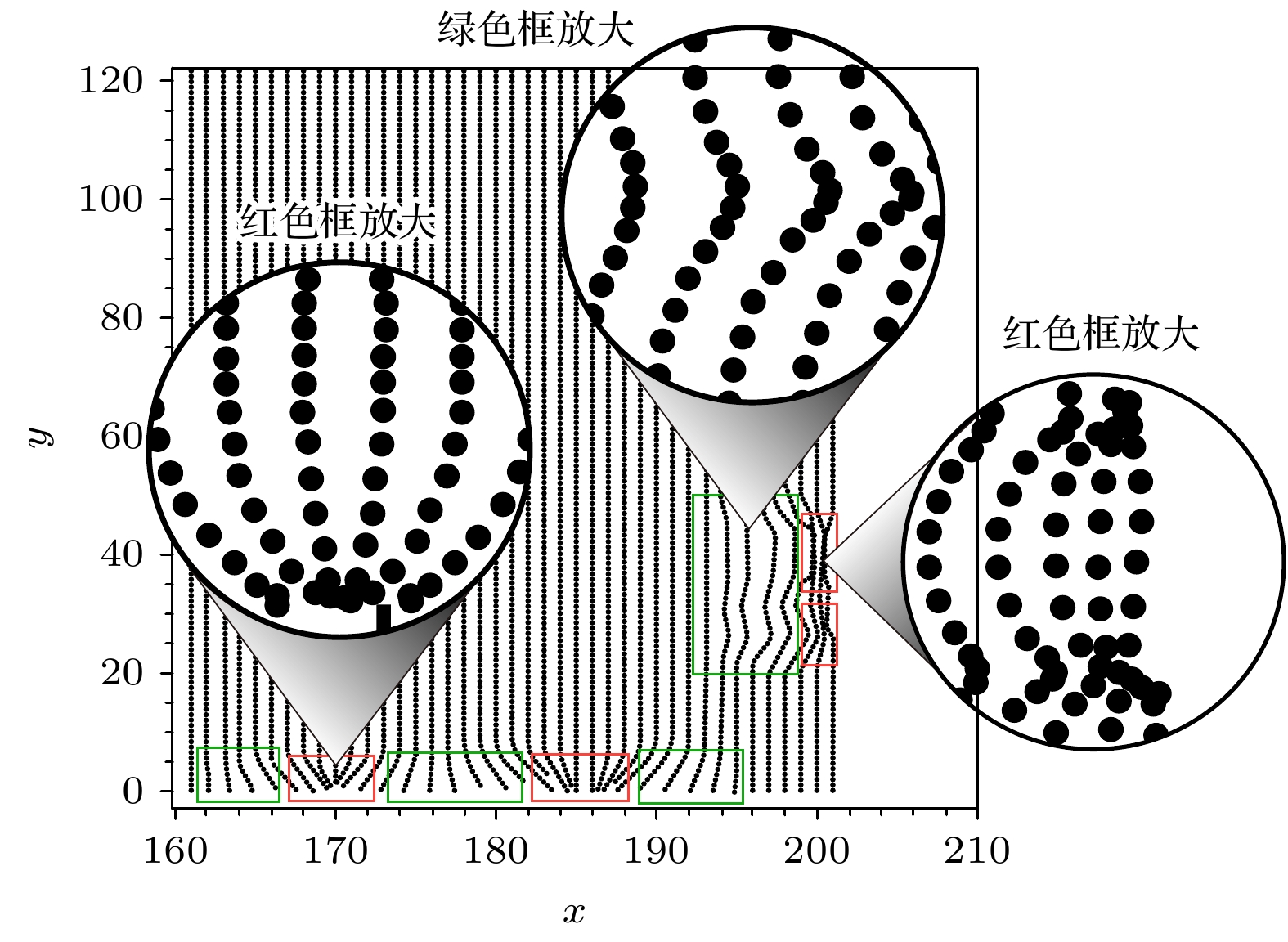
其中, ${\text{σ }}$为凝固收缩系数, 是通过实验测定的参数, df_s是单个时间步长内的增长固相率. 图5所示为被捕获元胞如何“吸引”液相元胞靠近以及如何影响周围元胞的位移的过程, 图5中每个质点代表一个元胞, 红色框中的部分为正在生长的固相枝晶部分, 可从局部放大图中看出其中的元胞密度较高, 已完成凝固的固相元胞在移动的同时带动了周围未凝固元胞向其靠拢, 在图5中绿色框的放大图显示了其中的元胞位置偏向了元胞密集的红色框中已经凝固的元胞. 该方法有效地再现了铸造过程中材料收缩的物理现象, 特别是在材料冷却及凝固过程中表现出与实际情况趋势一致的收缩行为.

与传统的铸件凝固元胞自动机算法不同的地方在于, 本研究重点关注顶部收缩腔的计算, 是处于介观维度的, 该算法在理论上可以计算带有二次枝晶的微观收缩以及应力分布, 将于今后的研究中进行. 故本研究中将元胞的尺寸进行较大幅度的扩大以达到完全可以模拟真实大小的铸锭, 且不会大幅度增加计算时间的程度, 实现思路是忽略传统元胞自动机中形状参数的影响从而将计算建立在完全介观的基础上, 扩大每个元胞的体积使得其每一步的固相增量df_s只是温度和液相浓度的函数${\text{d}}{f_{\text{s}}}\left( {T, {c_{\text{l}}}} \right)$, 通过LBM耦合计算流场、温度场以及溶质场. 由于本文在构建Boltzmann模型时, 采用了郭照立等^[21]提出的基于Bossiness假设的耦合双分布函数, 故做出如下假设: 1) 流体流动过程中的黏性热耗散忽略不计; 2) 除密度外其他物性参数为常数; 3) 对密度仅考虑与体积力有关的项, 其他各项中的密度均为常数.

本文中耦合三场边界条件为反弹边界条件, 为确保在模拟过程中保证动量、质量以及热量严格守恒, 将LBM演化方程修正为

式中, ${f_i}\left( {x, t} \right)$, ${g_i}\left( {x, t} \right)$, ${m_i}\left( {x, t} \right)$分别表示流场、温度场和溶质场粒子的i方向上的分布函数. ${\tau _{\text{f}}}$, ${\tau _{\text{T}}}$, ${\tau _{\text{c}}}$分别为Chapman-Enskog分析得到的流体的流场、温度场及溶质场的松弛时间, ${f_{\text{s}}}\left( {x, t} \right)$是元胞固相率, $m_i^{{\text{eq}}}\left( {x, t} \right)$是元胞在i方向上的平衡分配函数, ${\text{inv}}\left( i \right)$是i方向的反方向, ${\omega _i}$为i方向上的平衡分配系数.

当边界网格的位移可以被计算后, 还需要选择合适的算法将边界网格的位移辐射到整个计算区域. 在微观尺度上, 凝固收缩源于金属从液态向固态转变时, 原子排列方式的根本性改变. 原子排列由液态中的无序转变为固态中的有序, 这种转变导致了体积的收缩, 而动网格技术可以通过实时调整计算网格, 灵活适应固液界面位置的不断变化, 从而精准捕获凝固收缩引起的形貌演化, 更准确地模拟铸件凝固过程中的复杂变形.

神经网络算法是一种广泛应用于模式识别、函数逼近和机器学习领域的强大工具. RBF算法是采用了径向基函数作为激活函数的神经网络, 其对噪声和数据分布的变化具有较好的鲁棒性, 具有良好的泛化能力和较强的拟合能力, 尤其是在处理非线性问题时表现突出. RBF算法的核心是径向基函数, 径向基函数是一种以距离为自变量的函数, 其值仅依赖于输入向量与中心点之间的距离. 作为一种3层的前馈神经网络, RBF神经网络除了输入输出之外仅有一个隐藏层, 早期的RBF网络隐藏层中的转化函数是局部响应的高斯函数, 而其他的向前神经网络, 转换函数一般都是全局响应函数, 这正是RBF优于其他网络的原因, 它的网络模型更精简, 训练时间更短, 同时对函数的逼近也是最优的: 可以以任意精度逼近任意连续函数, 其逼近的准确度随着隐藏层层中的神经元数量增多而提高. 如图6所示, RBF神经网络的训练过程包括3个步骤.

1) 确定隐含层中心. 常用的方法包括随机选择训练数据中的点或者使用聚类算法来选择边界点.

2) 计算径向基函数输出. 对于每一个输入向量, 计算其到各个边界点的距离, 并通过径向基函数计算输出值.

3) 权重学习. 通常使用线性回归或者最小二乘法来确定隐含层和输出层之间的连接权重.

对于网格变形的实现, 可以令其在每个三维坐标方向上采用一个RBF插值函数, 用来描述整个计算域内任意位置在该方向上的偏移量. 一般表达形式如下:

其中${g^{\left( k \right)}}\left( {\boldsymbol{x}} \right)$表示在${\boldsymbol{x}}$位置处网格当前时刻的位移偏移量, 其中k代表方向, $\phi $是插值基函数, 参数为两点之间的欧氏距离$\parallel \cdot\parallel $, ${{\boldsymbol{x}}_i}$是已知的网格的边界点, ${N_{\text{b}}}$代表网格边界点的总数, 系数$\alpha _i^{\left( k \right)}$为k方向上插值函数的系数, 通过边界点已知的位移量相互确定, 即有

$d_i^{\left( k \right)}$是$i$节点$k$方向上的已知位移量, (8)式中$p ({\boldsymbol{x}})$为精确恢复网格平移运动的线性多项式, Estruch等^[22]比较了带有和不带有$p\left( {\boldsymbol{x}} \right)$项的RBF算法, 结果表明$p\left( {\boldsymbol{x}} \right)$项对结果的影响很小, 网格质量差异不大, 故本文省略$p\left( {\boldsymbol{x}} \right)$项. (8)式的全局形式如下:

其中

另外

其中径向基函数目前可分为全局作用函数和局部作用函数, 其本质区别为某边界点位移对内部节点位移的影响范围, 考虑到铸件凝固过程中节点的紧凑性以及各材料补缩能力的不同, 本文选取的径向基函数为可调节半径R的紧支撑型径向基插值函数${\text{CP}}{{\text{C}}^2}$, 取$\xi = \dfrac{{{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}}}{R}$, 则有

更多RBF函数信息及其收敛性可参考文献[23]. 采用上述方案, 矩阵M是严格正定且对称的, 且可以根据R的大小调节作用范围, 使得大部分情况下M为稀疏矩阵, 本文采用预条件共轭梯度算法进行求解(10)式, 可以保证在N次迭代内收敛, N为边界点的个数.

SVM算法最早由Vapnik等^[24]在1979年基于统计学习理论提出, 1990年其理论得到进一步发展. 近几年来该机器学习算法已经成功用于多个领域的回归分析、模式识别以及分类工作等, 例如财务预测、文本分类或其他复杂工程的预测等. 该算法主要应用于分类和回归两大类别的应用. 其核心思路是通过非线性核函数将输入空间映射到一个高维特征区间, 将原问题转化为在此高维空间求解一个线性拟合问题, 其分类的目的是在特征空间上寻找间隔最大的超平面, 由于其忽略了通道阈值$\varepsilon $内的数据像本, 所以回归所得到的拟合函数实际上仅依赖部分训练数据, 使SVM算法仅需要少量的训练样本就可以达到很好的效果.

简要介绍SVM回归算法的理论基础: 假设训练数据集为$\left\{ {\left( {{{\boldsymbol{x}}_1}, {y_1}} \right), \cdot \cdot \cdot , \left( {{{\boldsymbol{x}}_n}, {y_n}} \right)} \right\} \subset \chi \times {\mathbb R} $, 当需要拟合的函数为线性函数时候, 其形式可以写作

SVM回归算法是为了寻找函数$f\left( {\boldsymbol{x}} \right)$, 使得所有训练数据${y_i}$与对应的函数值偏差可控在$\varepsilon $之内, 并要求函数曲线越平缓越好, 因此这个问题可以转化为针对${\omega ^2}$的二次规划问题:

为了更有效率地求解上述问题, 可利用拉格朗日乘数法转化为对偶问题, 因为对偶问题更容易扩展到非线性函数. 其拉格朗日函数可以写为

因为${\alpha _i}, \alpha _i^{\text{*}} \geqslant 0$, 因此

满足KKT条件, 故(18)式中min和max交换位置并不影响结果, 即有

所以$\mathcal{L}$函数对$(\omega , b )$的偏导为0, 有

因此对偶优化问题可以转化为

求解(22)式即可求得${\alpha _i}, \alpha _i^{\text{*}}$, 所要求的函数可以写作

SVM算法可以用核技巧将数据映射到一个高维特征空间, 使得在该高维空间中线性回归函数可以具有更高的拟合精度, 具体方法是用核函数$k\left( {{{\boldsymbol{x}}_i}, {\boldsymbol{x}}} \right)$代替原始数据, 相当于将样本扩展到高维后进行点乘, 其得到的结果等同于样本代入该和函数后的值, 由此, 回归函数变为

实际上只需要很少的训练数据就可以得到精度较高的拟合函数, 这些训练数据称为支持向量, 在本文中以边界节点的位置和位移量作为输入, 构造一个非线性函数空间中其他位置节点的偏移量, 使用输入数据训练模型系数, 再用该模型预测每个时步内所有节点的位移量.

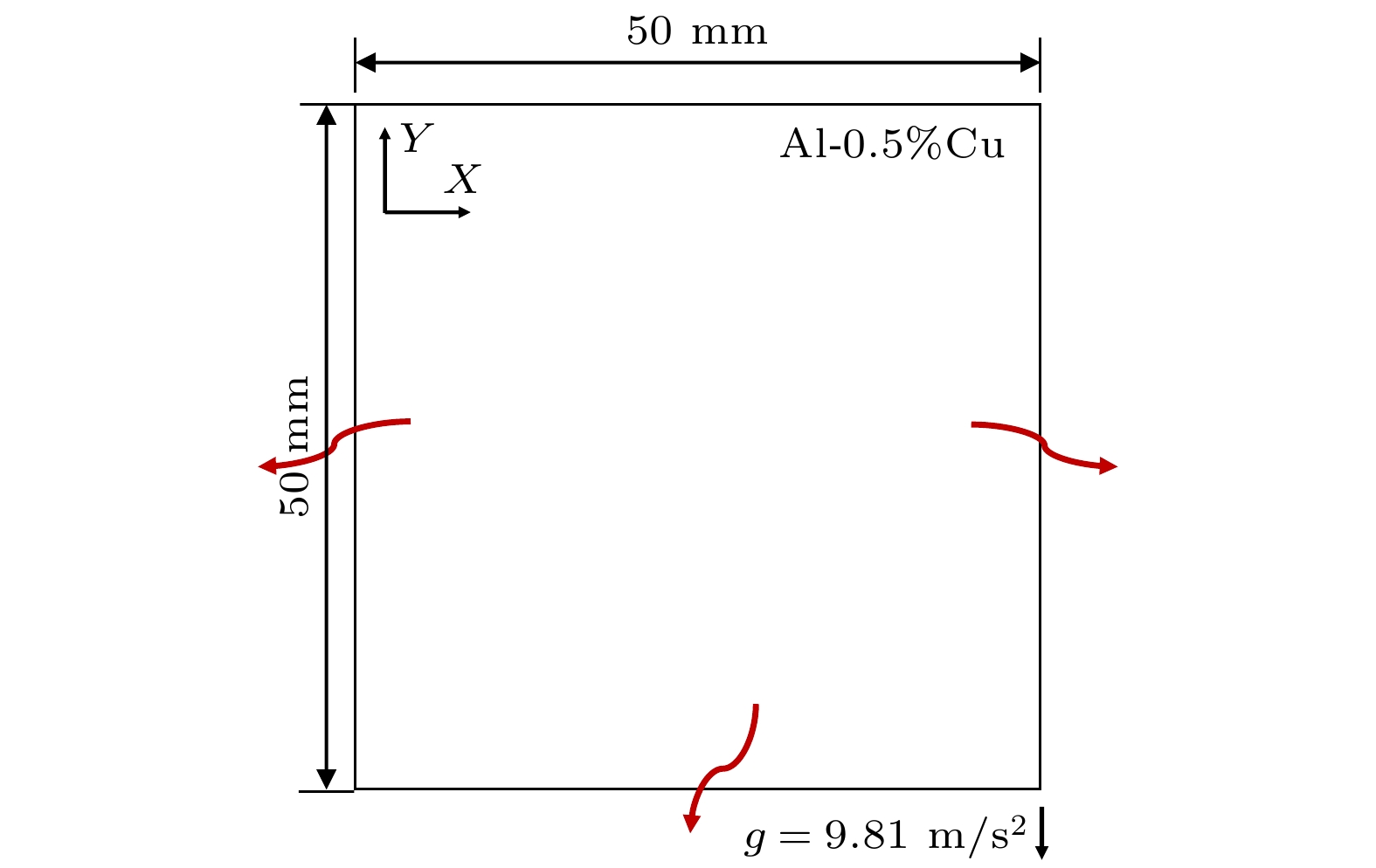
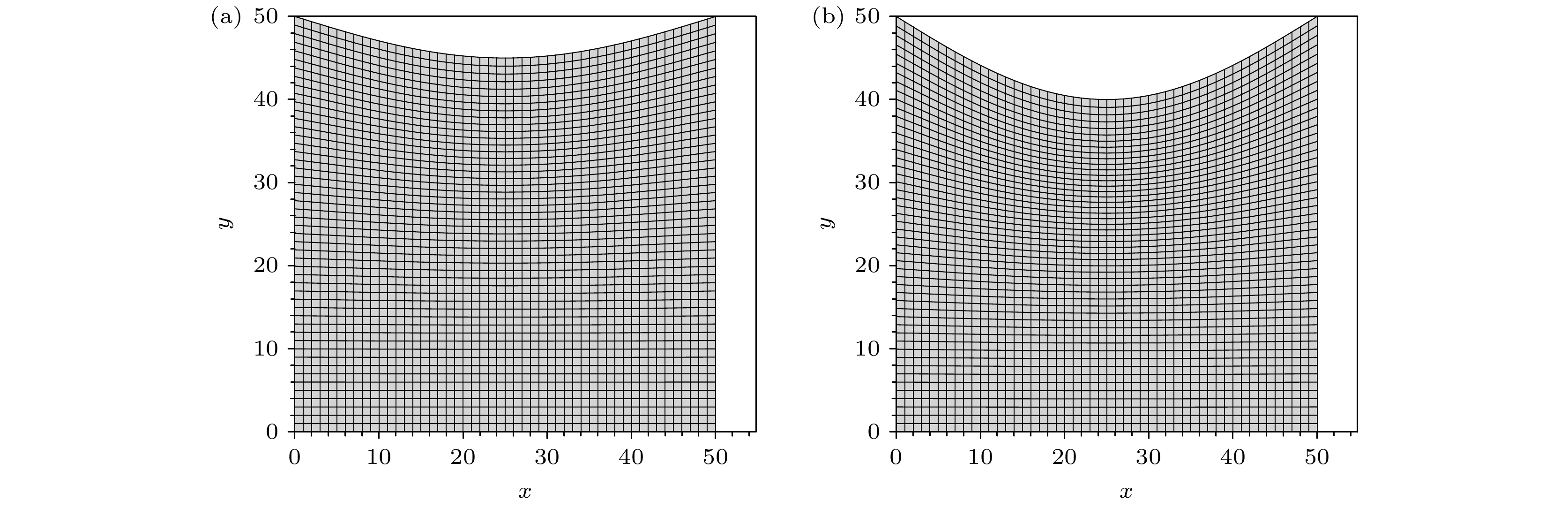
图7是本文数值模拟所用的物理模型, 计算区域为50 mm×50 mm, 划分为$400 \times 400$个均匀结构体网格, 取网格尺寸为$125 {\text{ μm}}$, 重力加速度为$9.81\; {\text{m/}}{{\text{s}}^2}$, 采用第3类边界条件, 铸件的顶部绝热, 周围环境的温度恒定为$300 \;{\text{K}}$, 对流换热系数为300 W/(m²·℃) . 选取合金仍为Al-0.5%Cu, 热物性参数见表1.

在模拟之前, 做出如下假设: 1) 液相为不可压缩牛顿流体; 2) 溶质扩散只存在于液相中, 固相中不存在溶质扩散; 3) 固液两相热扩散系数相同; 4) 不考虑内部等轴晶的形核, 只考虑表层细晶区和中间柱状晶区凝固过程. 模型的LBM边界条件为: 流场的物理边界采用半步长反弹边界条件, 固液边界采用纯反弹边界条件; 温度场边界条件采用非平衡外推格式; 浓度场物理边界采用半步长反弹边界条件, 固液边界采用纯反弹边界格式. 具体的CA模型以及LBM边界格式可见文献[14].

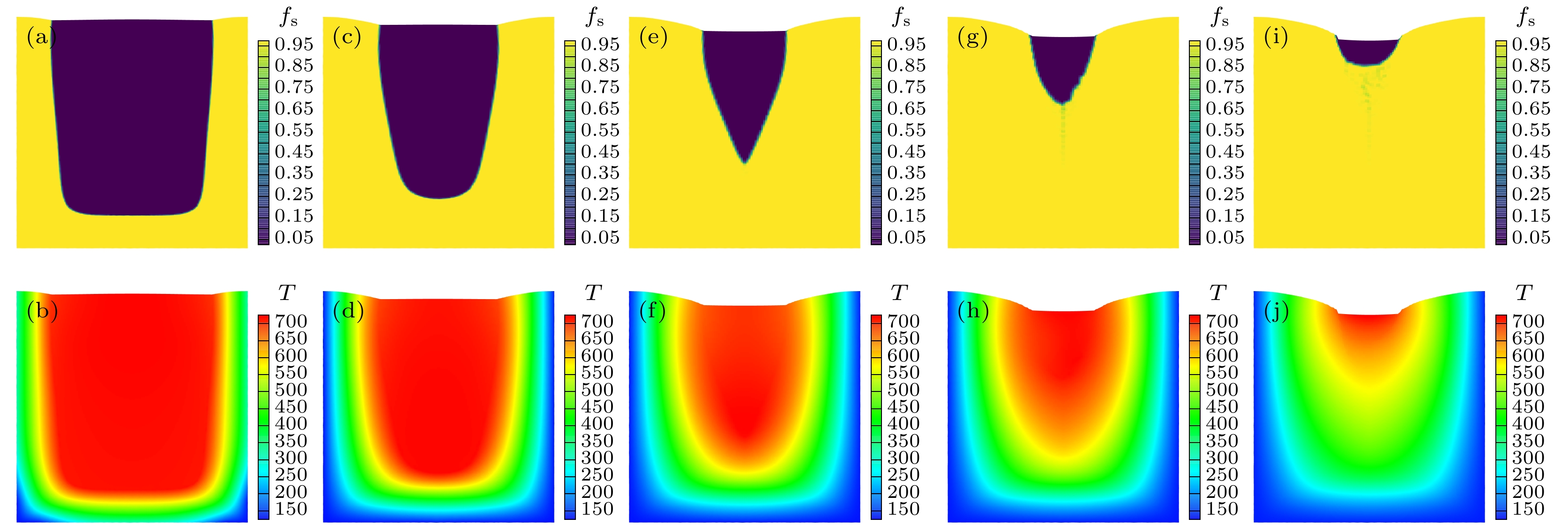
由于RBF算法和SVM算法在视化结果上的相似度较高, 本文选择以RBF算法进行模拟的铸件收缩可视化为例进行深入分析, 图8分别为模拟时间步长分别为step = 25, 50, 75, 100, 125的铸件凝固过程固相分数变化以及温度变化情况, 这些图像清晰地展现了随着时间推移, 铸件内部固相分数和液相分数的转变以及相应时刻温度场的动态演变. 图8右边的色标分别代表了固相分数和温度, 例如, 在图8(a)中, 黄色部分为完全凝固的固相区域, 而紫色部分仍处于液相区域.

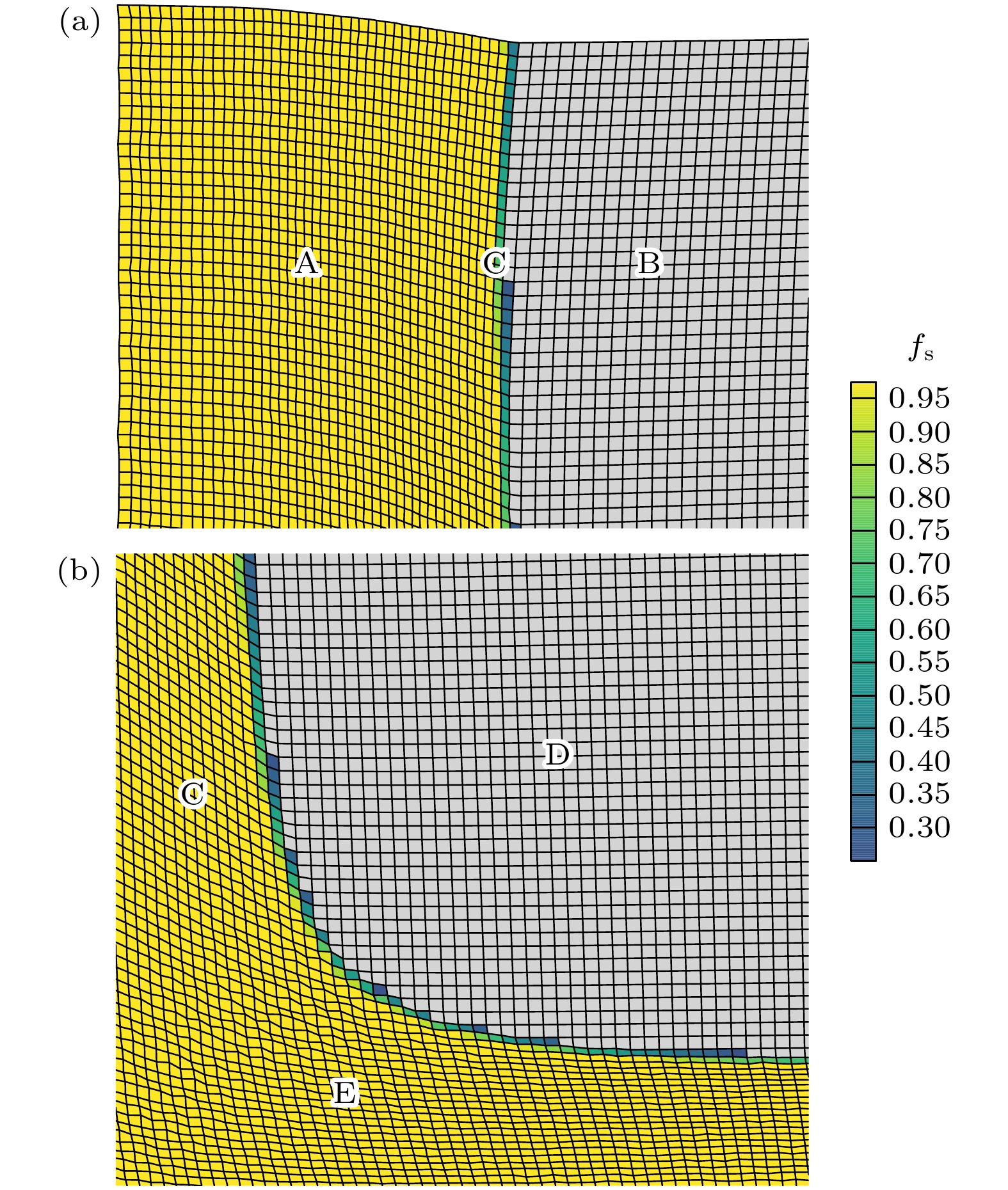
在凝固初期, 由于液态金属与冷却铸型之间存在显著温度差, 热量迅速由液态金属传递到铸型中, 在与铸型的接触面部分形成一层薄的固态金属层, 这个阶段铸件整体的收缩主要受到温度变化的驱动, 正如(1)式中${\text{d}}{s^{\text{T}}}$所示. 顶部液面随体积收缩整体水平下降趋势并不明显, 这是由于收缩方向标定算法是在LBM离散场中的9个方向矢量求和, 而沿壁面方向散热最快, 总体网格在x方向上的收缩率要高于y方向.

图9(a)所示为将t = 25时刻的固相率分布图左上角局部放大的图, 其展示了铸件在该时刻下凝固收缩过程中的网格形状变形情况, 其中A区域是已经完全凝固的固相区域, 与还未凝固的B区域相比可以明显看出其网格在x方向上有明显的压缩, y方向则相差不大, 这是由于此部分网格沿壁面散热最快, 收缩方向也多偏向x方向. 此外, C区域展示了固液相界面处网格的变形情况, 以温度处于${T_{\text{l}}}$到${T_{\text{s}}}$的网格为分界线, 左右两侧网格的形状截然不同, 由液相转变为固相的同时网格会沿热流方向产生压缩.

图9(b)所示为图8(a) t = 25时固相率分布图左下角局部放大图, 可以看到E区域网格在y轴上的压缩明显比C区域界面处的网格要大, 而D区域与图9中的B区域相一致. 从图中可看出经神经网络算法的动网格质量稳定, 网格与网格之间的协调性较好, 在边界处过渡较为自然, 并不会产生网格重叠或者网格节点偏离计算域等问题.

当时间推移至t = 50时, 由于上一阶段优先凝固的元胞起到阻塞潜热释放的作用, 这一阶段中, 此时固液界面的推进速度较之前有所减缓, 此阶段液面的垂直位移量相比第一阶段略有增大, 液面逐渐降低, 固液相界面推进速度趋于稳定; 随着凝固进入稳定推进期, 已完全凝固的固相元胞数量虽然不断增加, 使被标记的边界点数量增加, 但由于收缩率也随温度降低而降低, 使得固相部分的热胀冷缩对顶部缩孔的影响反而是变小的.

图10为图8(e) t = 75时固液相分布的左下角局部放大图, 在这张图上用箭头标注了液相元胞的凝固位移趋势, 可以看出在此局部区域凝固的收缩方向已经与散热方向存在较小差异, 这涉及物理平面与计算平面之间的双向耦合问题, 动网格在物理平面的收缩本质上是元胞生长对元胞网格位移的单向耦合, 而网格之间位置的改变会使计算平面与物理平面之间存在较大差异, 以LBM计算温度场为例: LBM计算温度是在计算平面完成的, 也就意味着元胞和周围8个元胞的间隔始终保持不变, 而在物理平面上元胞之间的距离dx早已发生改变, 所以理论上在计算过程中也需要考虑收缩对生长的耦合, 也就意味着在计算生长中需要时刻调整计算平面中网格间距dx, 但这同时也意味着对无量纲计算的LBM不仅需要更多计算资源, 且在量纲转化中需要添加额外的算法, 这可能会导致原有的算法发散, 最终得不偿失.

到凝固后期, 液相区域大大减小, 由于未凝固的液相区域富集了大量的溶质, 又由于已凝固的元胞数量已经占据大多数元胞, 造成内部液相区域降温速度变慢, 导致最后凝固部分凝固速度缓慢, 凝固收缩对整体收缩的占比减小, 虽然此时各个元胞的收缩率很小, 但是此时大量的固相元胞被标记为边界点, 固相元胞的位移被热收缩主导, 顶部收缩界面反而更加陡峭, 直至凝固结束.

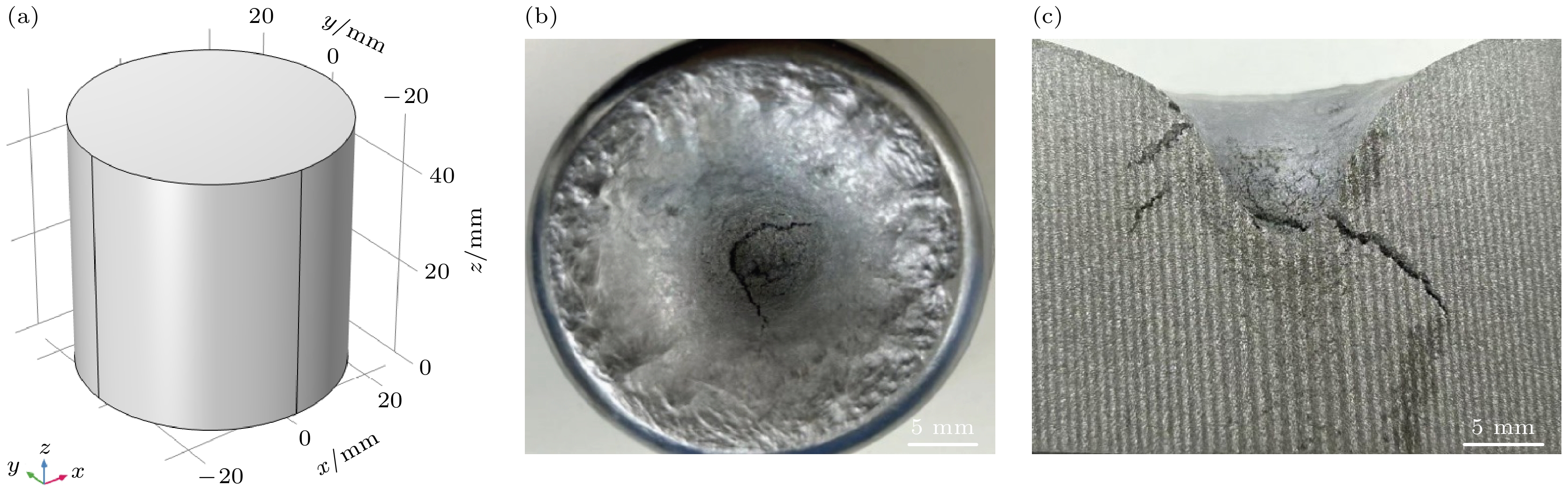
浇注了Al-0.5%Cu铸锭与计算结果相对比. 通过浇注与上述计算铸锭相同的边界条件和初始条件以及尺寸相同的铸锭来验证所建立的数值模型的可靠性.

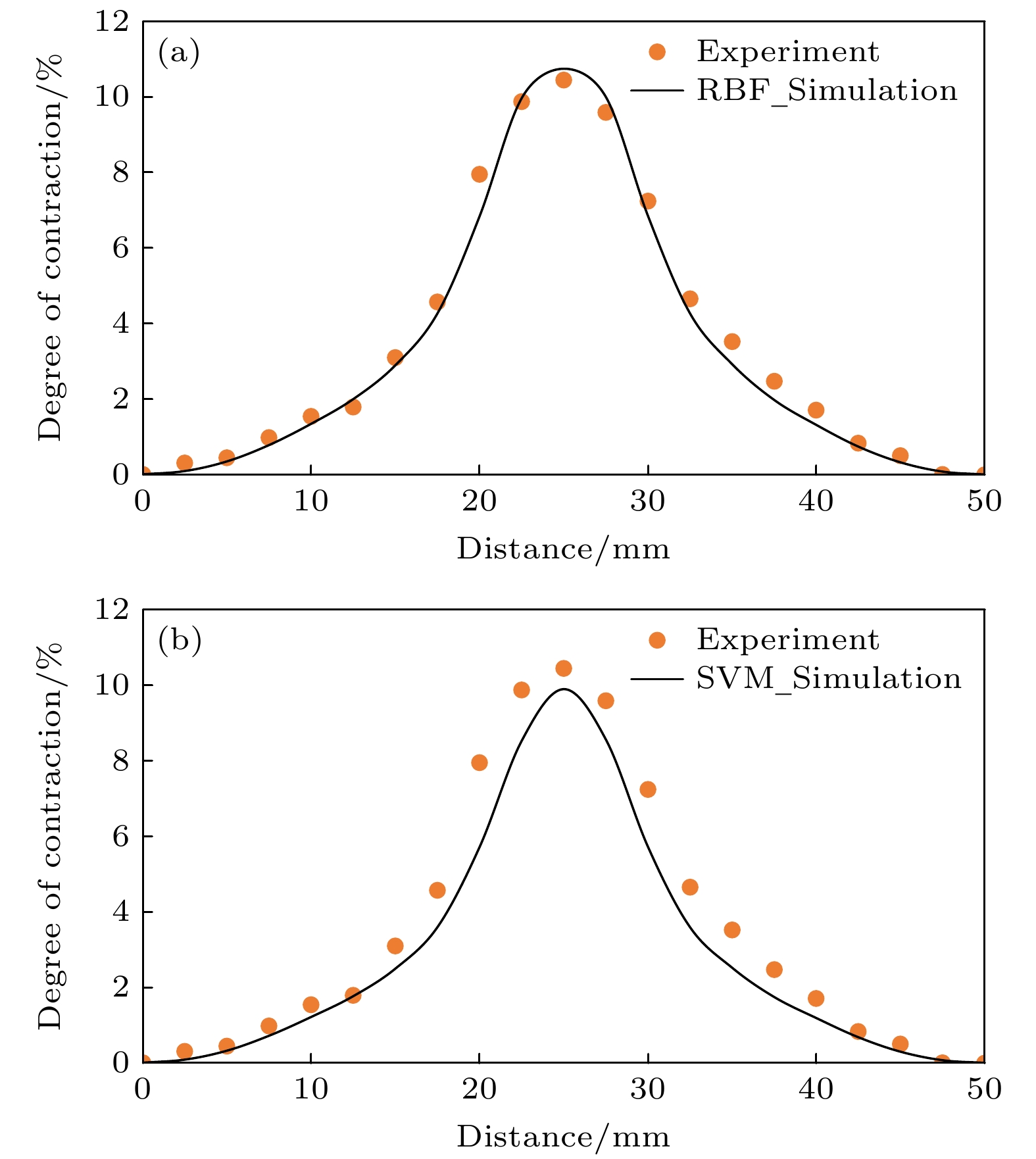
铸件材料仍为Al-0.5%Cu, 实际铸件的几何尺寸与浇铸结果如图11所示. 铸件最大横截面尺寸与模拟尺寸一致, 铸造方式为金属型铸造, 浇铸温度为$\left( {730 \pm 10} \right)$℃.

将实验铸件最大横截面收缩程度与完全凝固后的模拟结果的最顶部网格的收缩程度共同绘制在同一张坐标轴上, 如图12所示.

由于本研究是基于动网格理论来求解铸件凝固收缩情况, 故关键在于边界网格位移的准确性以及所选算法的可靠性. 前期收缩大小主要受温度场影响, LBM可以将流场、溶质场耦合的影响充分考虑, 使得温度场的计算更符合实际情况, 故两种算法在前期的准确度都较好. 而当凝固层厚道达到10 mm左右时, 基于SVM算法的计算结果开始逐渐与实验结果出现差异. 这是由于SVM算法在本质上是拟合高维空间中的函数, 故对边界点的位移准确性具有极强的依赖性, 而本文在计算边界网格位移中有所取舍: 1) 计算铸件凝固过程中没有将收缩对整体凝固的影响耦合进来, 例如在(4)式中, ${\text{σ}}\left( {{T}} \right)$仅是温度的函数, 并没有考虑偏析对边界点收缩程度的影响导致模拟结果的收缩程度比实验结果略小, 在最后凝固区域(x = 25 mm)附近较为明显; 2) 本研究中对流场边界条件的处理为反弹边界条件, 而随着凝固收缩各个节点的位置随之变化, 导致LBM算法中的空间步长也随之发生改变, 正如上文所提到的, 本研究尚未考虑这部分影响, 因为空间步长的改变会破坏LBM平衡分布函数的协调性, 使原有算法严重发散; 3) 本研究在计算过程专注于集中缩孔的计算, 选择的计算域较小, 并未考虑由于补缩不足导致的缩松, 关于缩松和应力的研究将于今后开展. 而RBF算法之所以拟合程度较好是因为相比于SVM算法其考虑了辐射范围R, 相当于是考虑了不同材料液相的补缩能力, 因此在一定程度上可以避免算法本身对数据的依赖度, 这也是RBF算法在训练集较小时优越的原因, 不过补缩能力与R的数值关系还尚未清晰, 针对不同材料的凝固计算需要凭借经验, 这也是RBF算法的不足.

两种网格变形算法其主体是在计算位移过程中以边界节点的位置以及位移信息作为训练集, 构建一个拟合函数, 然后各网格节点利用该函数独立计算各自偏移量, 事实上, 两者在拟合函数的构造部分也有很大的相似度. RBF算法在程序中所消耗的计算资源较小, 是得益于直接求解(11)式的过程中, M矩阵在3个方向上的坐标是一样的, 因此可以只求解一次来提高效率, 且该矩阵是严格正定的, 在上述模型实际求解过程中仅需9 min即可完全求解, 计算收缩程序几乎不增加原程序的运行时间, 而SVM在训练过程中需要解决二次规划问题, 在大规模数据集上可能会非常耗时, 但是SVM计算过程中避免了辐射范围R. 整体来说, 实验结果与RBF算法的模拟结果的误差不超过0.5%, 与SVM算法的模拟结果误差不超过1.2%.

本文提出了两种基于机器学习的铸造过程收缩数值模拟算法, 并给出了两种算法的建模思路以及在凝固收缩计算方面的算例. 通过将基于两种算法的数值模拟结果与实际浇注结果进行对比分析, 最终得到如下结论.

1) 通过将动网格技术与元胞自动机模型耦合, 有效地模拟了铸锭凝固过程中的收缩行为. 研究结果表明, 该耦合方法能够有效捕捉凝固收缩引起的铸件变形, 捕捉固液界面复杂形貌的演变以及铸件内部网格的变形情况. 相较于传统的数值模拟方法, 该方法在处理固液界面大变形方面具有显著优势, 对计算资源需求较少, 与试验结果的误差可控制在2%以内, 为凝固过程的数值模拟提供了一种新的思路.

2) RBF算法在计算的准确率以及计算效率上优于SVM算法, 但RBF算法中辐射范围R对收缩变形情况的影响机理尚未清晰, 需要具备一定经验使用, 而SVM由于对边界网格信息强依赖, 可以避免辐射范围R的考虑, 两种算法各有取舍.

3) 动网格技术与元胞自动机的耦合为铸造过程的数值模拟提供了一种新的工具, 但该方法仍存在一些局限性. 例如: 模型中并未考虑合金元素的偏析对收缩的耦合, 模型是CA对动网格的单向耦合, 这可能会导致模拟结果与实际情况存在一定的偏差.