双电子复合(dielectronic recombination, DR)是一种基本的电子-离子复合机制, 决定着各种自然以及人造等离子体内部的电荷态分布与电离平衡, 其反应截面和速率系数是等离子体演化建模的关键数据, 对于深入认识宇宙天体以及聚变等离子体具有重要意义^[1–7]. 目前, 双电子复合共振实验已经发展成为一种十分重要的技术手段, 可用来研究高电荷态离子的能级结构以及双激发态离子的退激通道^[8,9], 并检验基本的原子物理理论, 如量子电动力学(quantum electrodynamics, QED)效应^[10]、相对论效应^[11,12], 提取原子核结构信息^[13]. 高电荷态离子的双电子复合过程最早由Bates和Massey^[14]于1943年从理论上提出, 随后经Badnell等^[15]、LaGattuta和Hahn^[16]的发展而逐步完善, 直到1978年才首次在实验上予以证实^[17].

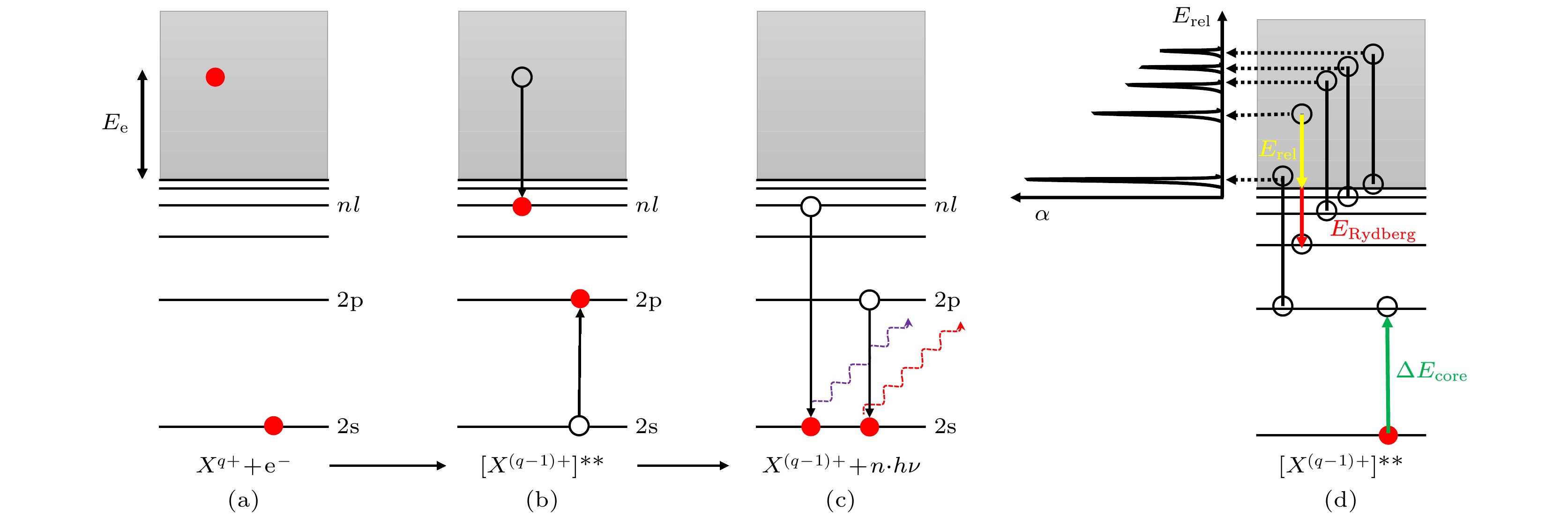
双电子复合过程是一个两步共振过程, 其反应过程可以写成以下形式^[18]:

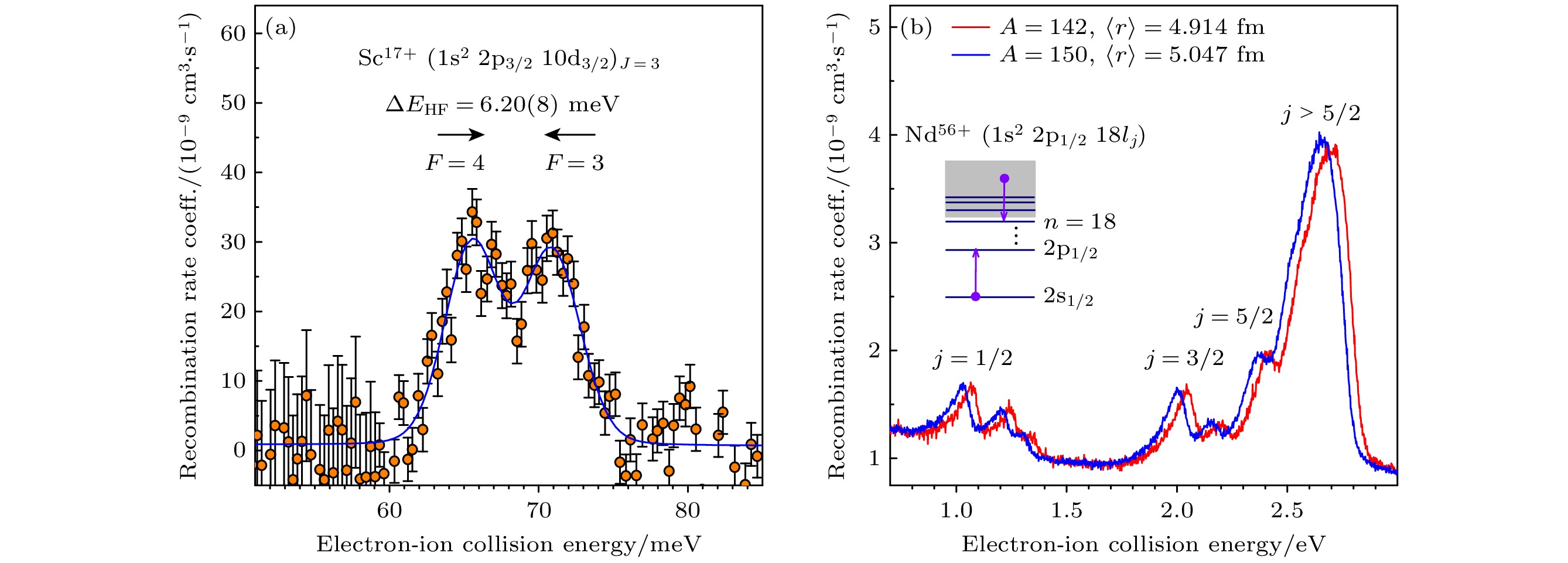
这两个步骤分别为: I 共振俘获过程, 其对应于俄歇的逆过程, 即一个自由电子e^–被俘获到离子X^q+的束缚态, 同时离子X^q+的一个束缚电子被共振激发, 形成中间双激发态[X^(q–1)+]^**, 此过程无任何能量放出; II 辐射稳定过程, 双激发态离子[X^(q–1)+]^**通过放出一个或者多个光子退激发到低于电离阈的稳定态. 图1是类锂离子双电子复合过程的示意图, 其中双电子复合共振的条件是$ {\Delta E}_{{\mathrm{c}}{\mathrm{o}}{\mathrm{r}}{\mathrm{e}}}={E}_{{\mathrm{r}}{\mathrm{e}}{\mathrm{l}}}+ {E}_{{\mathrm{Rydberg}}} $, 因此通过测量双电子复合共振谱可以提取高电荷态离子的能级结构信息.

基于重离子冷却储存环的高电荷离子的双电子复合实验具有多项显著优势, 它能够研究单一电荷态离子的复合过程, 具有极高的能量分辨率, 允许大范围精细调节电子与离子的相对能量, 并且是唯一能够精确测量低能碰撞复合绝对截面关键数据的实验手段^[8]. 国际上开展双电子复合实验研究的重离子冷却储存环包括: 德国海德堡马克斯·普朗克核物理研究所的储存环 (test storage ring, TSR)^[19], 亥姆霍兹重离子研究中心(GSI)的实验储存环 (experimental storage ring, ESR)^[20]; 瑞 典斯德哥尔摩的CRYRING^[21] (已经搬迁至GSI, CRYRING@ESR^[13]), 中国科学院近代物理研究所的储存环CSRm^[22]和CSRe^[23]. 以下几项实验技术的进步显著提升了实验的分辨率、精确度和应用范围: 1) CRYRING通过绝热膨胀技术首次发展了超冷电子束^[24], 极大地提高了双电子复合实验的精度, 这项技术在TSR中也得到了应用^[25]; 2)通过在TSR中使用电子冷却器和专用电子靶, 实现了束流冷却和测量的解耦, 提高了实验效率 和分辨^[25]; 3)在ESR中通过随机冷却快速冷却热离子束, 而将电子冷却器用作电子靶, 拓展了双电子复合实验的质心系碰撞能量与离子种类^[12]. 与这些改进技术相关的代表性工作包括: 2007年, Schippers等^[26]在TSR上使用双电子复合实验观测到了⁴⁷Ti¹⁸⁺离子的超精细诱导跃迁$ \left(2{\mathrm{s}}2{\mathrm{p}}{}^{3}{{\mathrm{P}}}_{0}\to 2{{\mathrm{s}}}^{2}{}^{1}{{\mathrm{S}}}_{0}\right) $; 2008年, Lestinsky等^[25]通过在TSR上引入单独的光阴极电子靶, 观测到了Sc¹⁸⁺离子的超精细分裂, 进一步得到了2s→2p跃迁能量, 精度达到4.6×10^–6, 是迄今为止精度最高的DR实验, 如图2(a)所示; 同年, Brandau等^[27]在ESR上使用双电子复合的方法测定了¹⁴²Nd⁵⁷⁺和¹⁵⁰Nd⁵⁷⁺的同位素位移, 如图2(b)所示, 从中推算出了原子核电荷均方根半径.

基于兰州重离子加速器冷却储存环(CSR)上自主发展的双电子复合精密谱学实验平台, 我们完成了类铍⁴⁰Ar^14+[28], ⁴⁰Ca^16+[29], 类氟⁵⁸Ni^19+[30,31]和类钠⁷⁸Kr^25+[32,33]等高电荷态离子的双电子复合精密谱学实验研究^[23], 在高电荷态离子精细结构、实验室天体物理等方面开展了较为系统的研究工作. 需要说明的是, 这些实验的精度受到了离子束品质和电子束温度等因素的限制; 此外, CSR上的电子冷却器同时用于冷却离子并作为电子靶, 这不仅限制了双电子复合实验的效率, 而且无法进行类氢、类氦和放射性束等高电荷态离子的双电子复合实验.

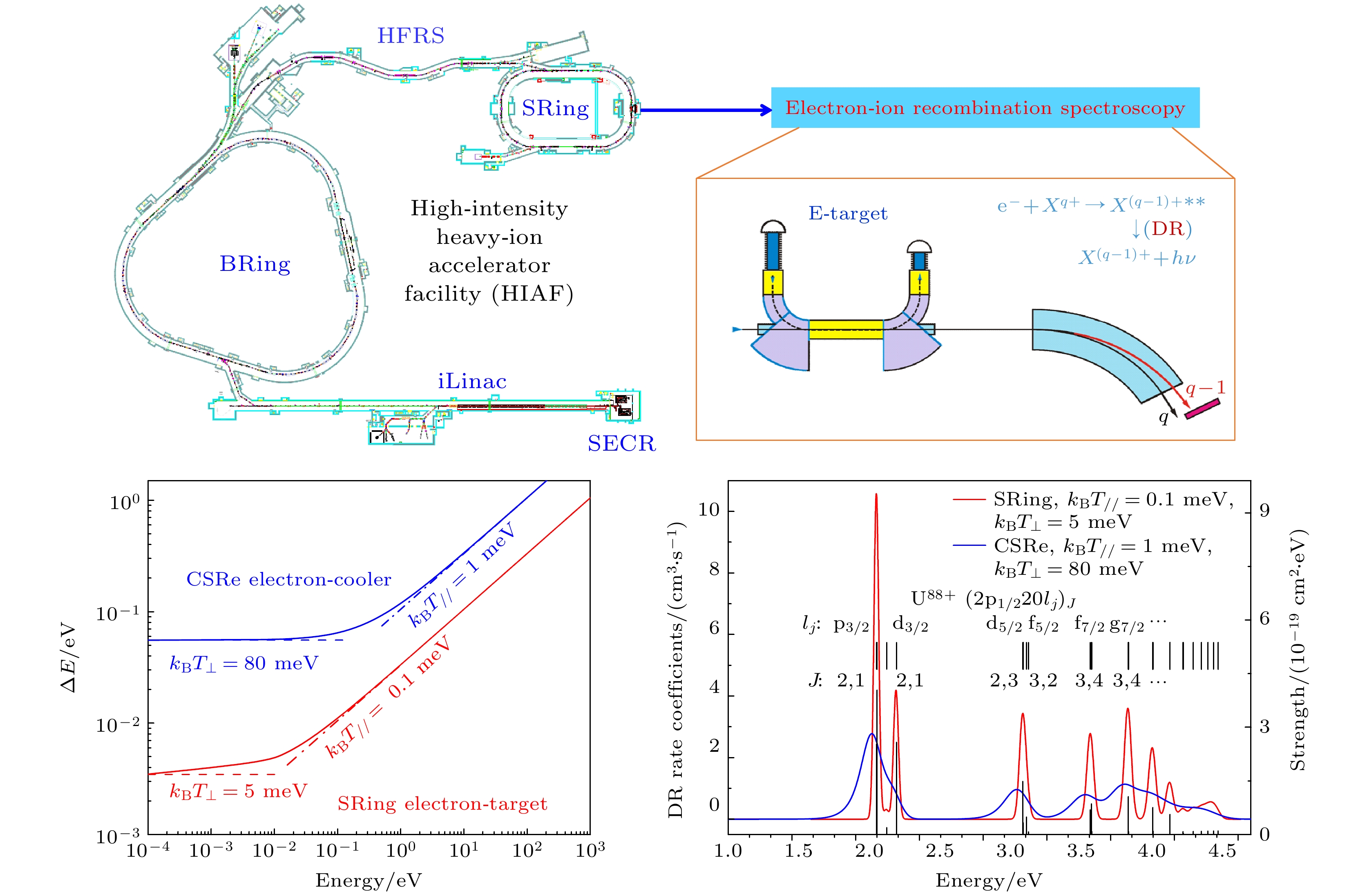
强流重离子加速器装置(high intensity heavy ion acceleration facility, HIAF)是我国正在建设的中高能量、高束团密度的重离子加速器综合研究设施^[34]. 该装置中的高精度环形谱仪(spectrometer ring, SRing)旨在累积和储存高品质的放射性次级束流和稳定离子束流, 并用于原子物理和核物理的前沿实验研究. 在HIAF-SRing上, 将安装一台450 kV的电子冷却器和一台80 kV的低温电子靶装置. 电子冷却器通过压缩储存束流的相空间体积来提升束流品质, 而电子靶装置则用于产生能量快速可调的低温电子束开展电子-离子碰撞实验. 利用绝热膨胀和加速原理可以制备超冷电子靶, 其绝热展开系数高达30, 实现极低的电子束温度, 从而可以大幅提高实验的分辨率, 为高电荷态离子的双电子复合精密谱学研究提供极佳的实验环境. 此外, 通过电子冷却器与独立电子靶技术的结合, 可以开展质心能量范围内从meV到几十keV的双电子复合实验, 从而对类氢、类氦以及放射性束的高电荷态离子进行精密谱测量, 这在目前的CSR上无法实现^[35,36]. 为了深化对实验条件的理解, 本文运用经典分子动力学方法模拟了超冷电子靶的电子束温度, 分析了超冷电子靶的电子束温度对双电子复合实验中共振峰的半高全宽(能量分辨)的影响, 并选取类锂体系的$ {}_{~\,54}^{129}{{\mathrm{X}}{\mathrm{e}}}^{51+} $和$ {}_{~\,92}^{238}{{\mathrm{U}}}^{89+} $重离子作为研究对象, 通过双电子复合模拟谱, 探讨了在SRing上进行高电荷态重离子双电子复合精密谱测量所展现的高分辨率特性, 为开展强场QED效应和提取原子核结构信息等前沿研究提供了重要支撑.

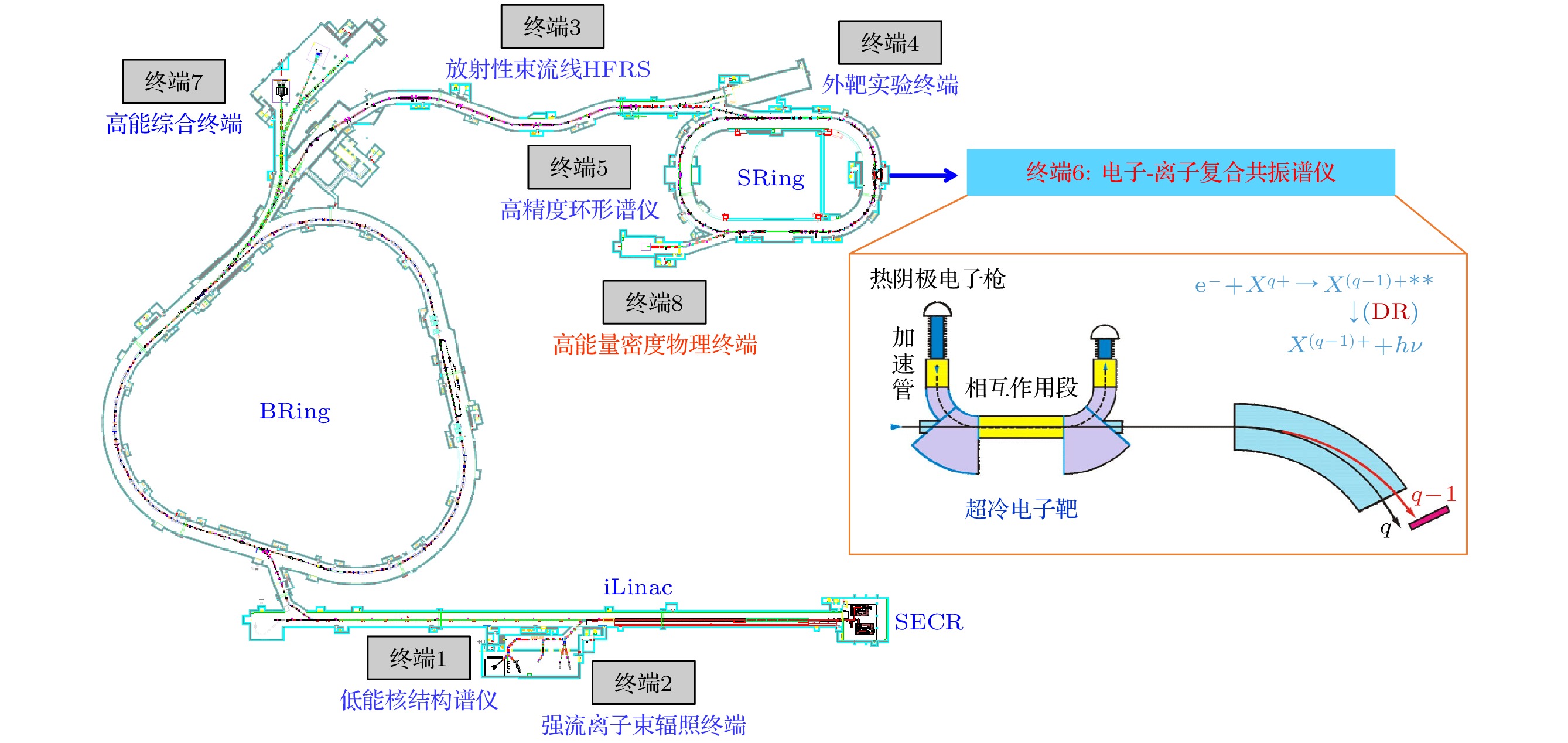
图3为基于HIAF-SRing装置开展双电子复合实验的示意图, 具体细节可参阅Huang等^[36]报道, 此处仅作简要说明. 首先使用超导回旋共振离子源(SECR)产生高电荷态离子束, 经由超导直线加速器iLinac (Superconducting Linac)加速后, 离子束被注入BRing (Booster Ring)中, 累积加速后将束流经HFRS (High Energy Fragment Separator)注入到高精度环形谱仪SRing中开展实验. 在双电子复合实验过程中, SRing中450 kV的电子冷却器专门负责冷却离子束流, 提升束流品质, 而80 kV的电子靶提供能量快速可调的低温电子束用于电子-离子复合实验. 在电子靶的相互作用区域, 超冷电子束与运动中的离子束发生复合反应, 复合后的离子被安装在第二块磁铁之后的复合离子探测器所探测. SRing上的电子-离子复合共振谱仪具有两种工作模式: 1)电子冷却器在冷却点负责持续冷却离子束流, 电子靶的工作电压浮置在电子冷却器的高压上, 通过精密调节电子靶的调制电压以开展高精度的双电子复合精密谱学研究; 2)电子冷却器持续在冷却点工作, 而电子靶则在远离冷却点的位置调制高压, 从而实现质心系中大碰撞能量的双电子复合测量, 例如进行类氢和类氦重离子的双电子复合实验研究.

根据储存环电子-离子合并束实验的原理, 测量到的双电子复合速率系数$ \alpha $为电子速度分布$ f\left({\upsilon }_{{\mathrm{d}}}, \upsilon \right) $和双电子复合共振截面$ \sigma $的卷积^[37]:

其中$ f\left({\upsilon }_{0}, \upsilon \right) $是电子靶电子束的温度分布; 电子靶上电子束温度分布则需根据电子靶的物理设计参数进行模拟计算, 见2.2节, 最终电子束的温度分布呈现扁平的麦克斯韦分布:

其中$ {k}_{{\mathrm{B}}}{T}_{\perp }, {{k}_{{\mathrm{B}}}T}_{/ / } $分别为电子束的横向温度、纵向温度, 而k_B为玻尔兹曼常数, $ {v}_{\perp }, {v}_{/ / } $分别表示电子束的横向、纵向速度. 而双电子复合共振截面呈现洛伦兹峰型:

其中$ {E}_{{\mathrm{d}}} $为共振能量; $ {\varGamma }_{{\mathrm{d}}} $为自然线宽; $ {\widehat{\sigma }}_{{\mathrm{d}}} $为共振截面对能量的积分, 即共振强度. 当双电子复合共振截面是$ \delta $型函数, 可以得到单个共振峰形的解析表达式^[37]:

其中,

误差函数为

因此双电子复合速率系数不仅与双电子复合共振位置和强度有关, 还与电子束温度相关. 在本工作的模拟中, 为了快速而准确地模拟双电子复合共振谱, 误差函数$ {\mathrm{e}}{\mathrm{r}}{\mathrm{f}}\left(x\right) $的数值计算通过文献[38]中的算法实现, 而双电子复合共振结构的位置和强度则通过全相对论组态相互作用程序FAC (flexible atomic code)计算, 具体的计算细节可参考文献[39, 40].

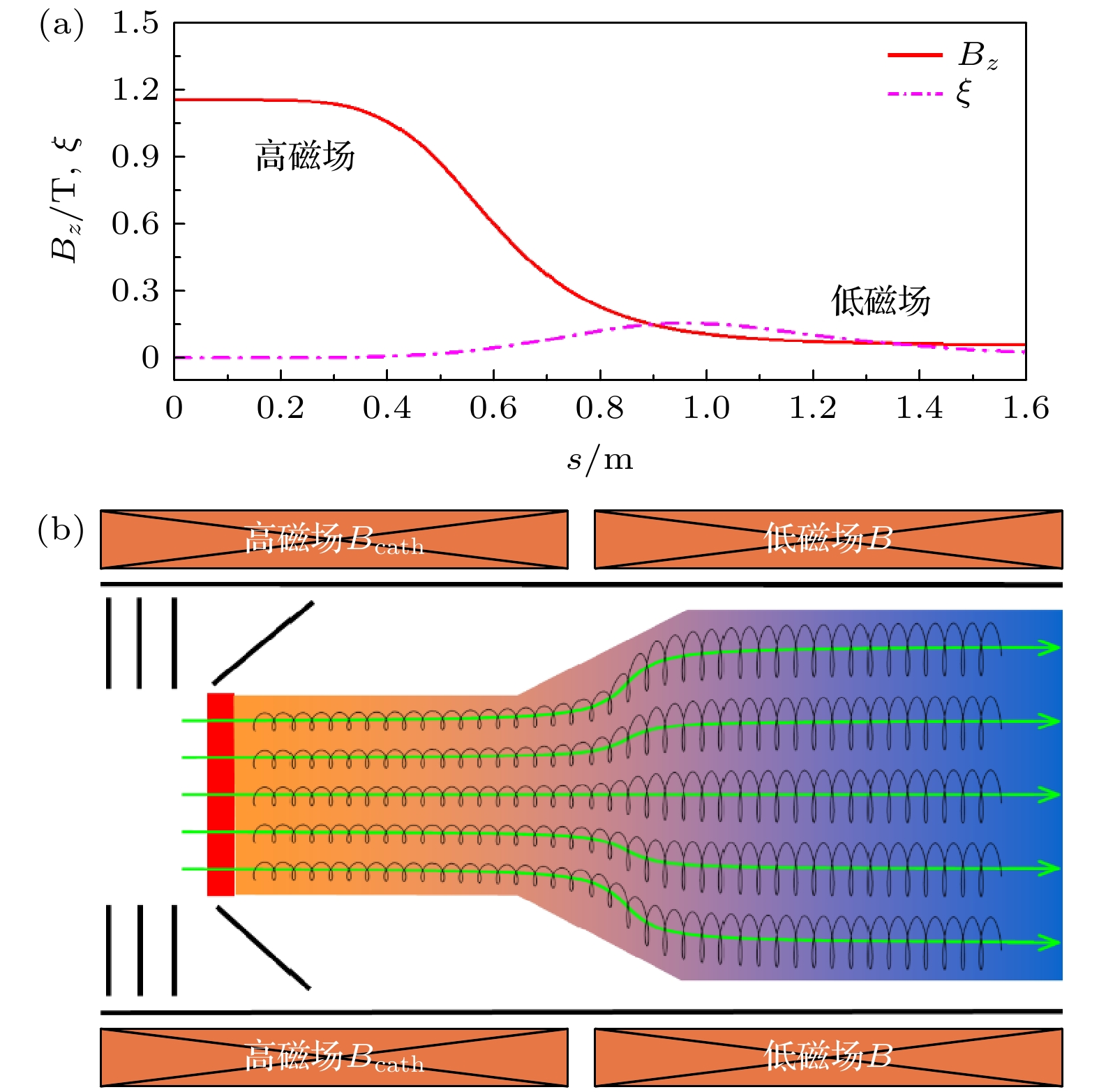
HIAF-SRing上双电子复合实验终端配备的超冷电子靶主要在其加速管区使用绝热膨胀和加速的原理获得极低的电子束温度^[24,41], 如图4所示. 超冷电子靶的主要物理设计参数详见表1. 该电子靶使用热阴极电子枪, 电子束发射最大流强约为0.2 A. 电子束的半径约为$ r=4\;{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{m}}{\mathrm{m}} $, 初始温度约为$ {{k}_{{\mathrm{B}}}T}_{{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}{\mathrm{h}}}=0.1\;{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{e}}{\mathrm{V}} $, 速度分布遵循麦克斯韦分布. 为了降低横向温度, 我们设计了绝热膨胀磁场来约束和引导电子运动, 实现绝热降温. 磁场由超导线圈产生, 形成一个轴对称的绝热磁场, 最高场强可达$ {B}_{{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}{\mathrm{h}}}= $1.2 T, 而电子靶相互作用段的磁场约为B = 0.04 T. 绝热展开因子α定义为$ {B}_{{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}{\mathrm{h}}}/B $, 其值最大可达30. 通常用绝热参数$ \xi $来表征绝热展开过程磁场变化的快慢:

其中λ为电子的拉莫尔波长, 即电子在z方向运动一个拉莫周期的距离, 其中U为加速电压, q为电子的电荷量. 绝热条件要求$ \xi \ll 1 $, 设计中通常要求绝热参数$ \xi $< 0.2, 如图4(a)中红色曲线所示. 电子的横向动能为

磁矩为

当电子从一个高磁场区域$ {B}_{{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}{\mathrm{h}}} $绝热地运动到低磁场区域B时, 磁矩是个守恒量, 因此电子的横向动能$ {W}_{\perp } $变为原来的$ {1}/{\alpha } $. 电子束的横向温度的统计定义为

其中符号$ \left\langle{\cdots }\right\rangle $代表取平均. 因此, 根据(7)式—(9)式, 可以推导出横向温度将从$ {k}_{\mathrm{B}}{T}_{\perp}=100\;{\mathrm{meV}} $降低到$ {k}_{{\mathrm{B}}}{T}_{\perp}/\alpha \approx 3.3\;{\mathrm{meV}} $.

为了验证上述理论推导并获得更精确的数值结果, 采用经典分子动力学方法模拟了超冷电子靶的电子束横向温度经过绝热膨胀后的变化情况. 电子在磁场中的运动方程为

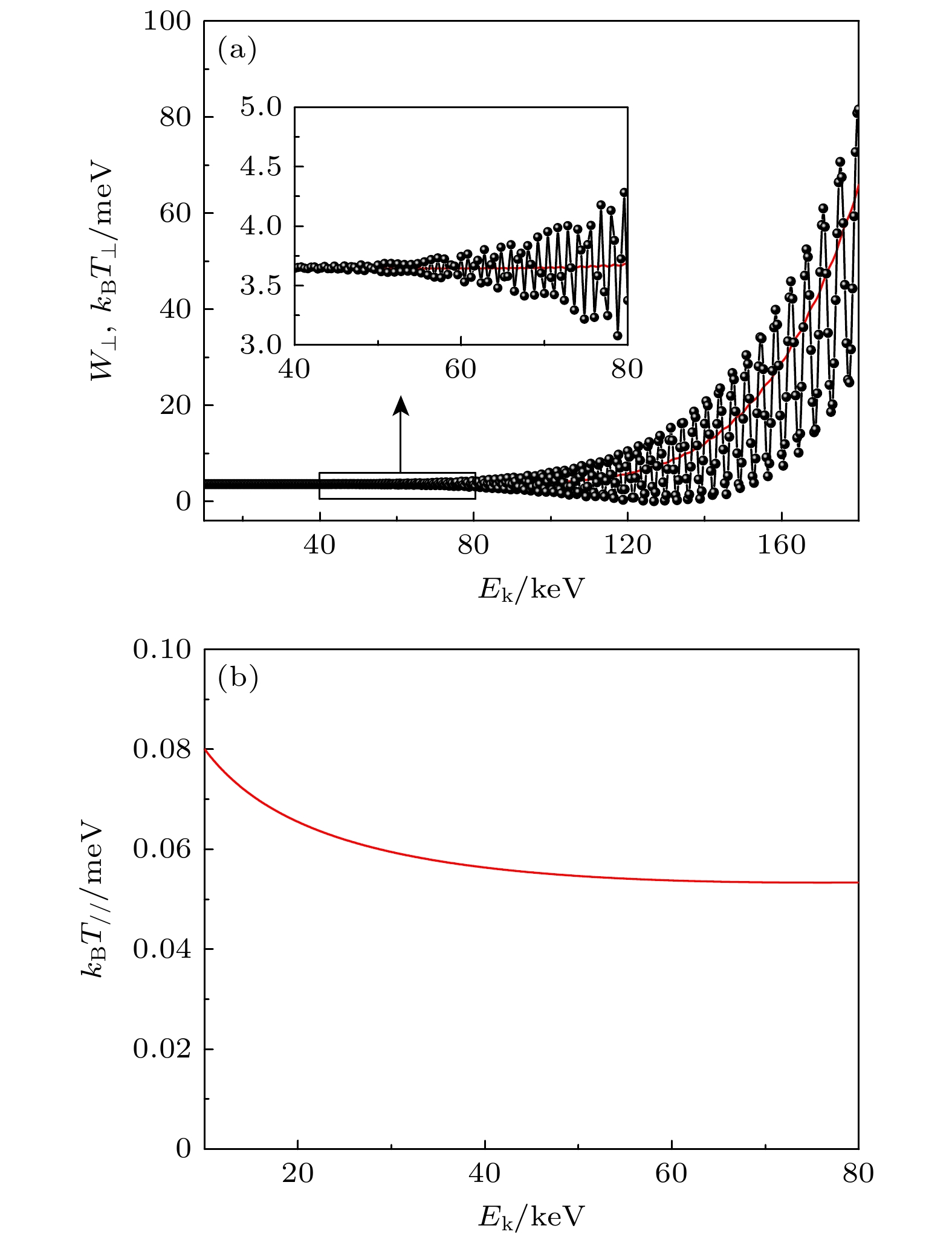
其中γ是电子的相对论洛伦兹因子, $ {E}_{x, y, z} $是所加的加速电场. 我们采用四阶龙格库塔方法求解这 些方程^[42]. 单个电子经过加速管后横向动能随电子束能量变化的关系如图5(a)黑色点线所示, 而红色曲线代表了10⁵个电子的横向温度, 即统计 意义上的温度. 模拟结果表明, 当电子束的能量低于80 keV时, 电子束在磁场中保持绝热运动, 横向温度小于5 meV的设计指标. 然而, 当电子束的能量超过80 keV时, 电子束的运动从绝热转变为非绝热, 横向温度急剧增大, 因此实验时调制电压应避免超出80 kV.

对于纵向温度, 从阴极发射的电子具有初始纵向温度$ {k}_{{\mathrm{B}}}{T}_{/ / }=0.1\;{\mathrm{ }}{\mathrm{e}}{\mathrm{V}} $. 通过施加加速电压$ U $, 电子获得动能$ {E}_{{\mathrm{k}}} $. 由于动能与速度平方成正比, 速度展宽随之减小, 导致纵向电子温度降低至$ {k}_{{\mathrm{B}}}{T}_{/ / }= \dfrac{{\left({k}_{{\mathrm{B}}}{T}_{{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}{\mathrm{h}}}\right)}^{2}}{\left(\gamma +1\right){E}_{{\mathrm{k}}}}\sim {\text{μ}}{\mathrm{eV}} $, 基本可以忽略不计. 此外, 高压纹波$ {\Delta U}/{U}\sim2\times10^{-5} $对纵向温度的贡献也很小. 纵向温度的增加主要由纵-纵弛豫引起, 即加速中由于电子束密度分布的变化, 使得电子之间将通过静电库仑场建立新的平衡态, 这将引起纵向温度的增加, 其大小为$ C\dfrac{{e}^{2}}{4{\mathrm{\pi }}{\varepsilon}_{0}}{n}^{1/3}, $ 其中常数$ C\leqslant 1.9 $, 与绝热加速因子、磁场相关^[43], $ n $为加速后的电子束密度. 当加速时间快于弛豫过程的时间, 即绝热加速, 此时纵向温度的增长将会得到抑制^[43]. 最终纵向温度的表达式为

图5(b)展示了纵向温度随电子束能量的变换关系, 当电子束的能量低于80 keV时, 纵向温度不超过0.1 meV.

实验能量分辨又称能量展宽, 指在给定能量下探测器响应的半高全宽值, 即双电子复合共振峰的半高全宽. 为了得到能量分辨与电子束温度、电子离子相对能量的关系的定量的表达式, 对单个共振的双电子复合速率系数(5)式或(2)式分别取极限$ {k}_{{\mathrm{B}}}{T}_{/ / }, {k}_{{\mathrm{B}}}{T}_{\perp }\to 0 $, 将会导致双电子复合共振峰型有不同的线型, 从而得到能量分辨^[37].

1)当$ {k}_{{\mathrm{B}}}{T}_{/ / }\to 0 $时, $ \xi =(1-{T}_{/ / }/{T}_{\perp }{)}^{1/2}\to 1 $, 当$ {E}_{0} > {E}_{{\mathrm{d}}} $时, 即$ {\upsilon }_{0} > {\upsilon }_{{\mathrm{d}}} $:

因此代入(5)式可得:

而当$ {E}_{0}\leqslant {E}_{{\mathrm{d}}} $时, 即$ {\upsilon }_{0}\leqslant {\upsilon }_{{\mathrm{d}}} $:

因此由(5)式可得:

综上, 双电子复合共振峰型为

该共振峰型为不对称峰型, 因此横向温度导致的半高全宽为

2)当$ {k}_{{\mathrm{B}}}{T}_{\perp }\to 0 $, 即$ {T}_{\perp }\to 0 $时, 由δ函数的极限表达式:

其中$ x = {{m}_{{\mathrm{e}}}{v}_{\perp }^{2}}/({2{k}_{{\mathrm{B}}}}) $, 代入$ f\left({\upsilon }_{0}, \upsilon \right){{\mathrm{d}}}^{3}\upsilon $, 然后积分, 有

再根据(2)式容易得到双电子复合共振峰型为高斯型:

因此纵向温度导致的半高全宽为

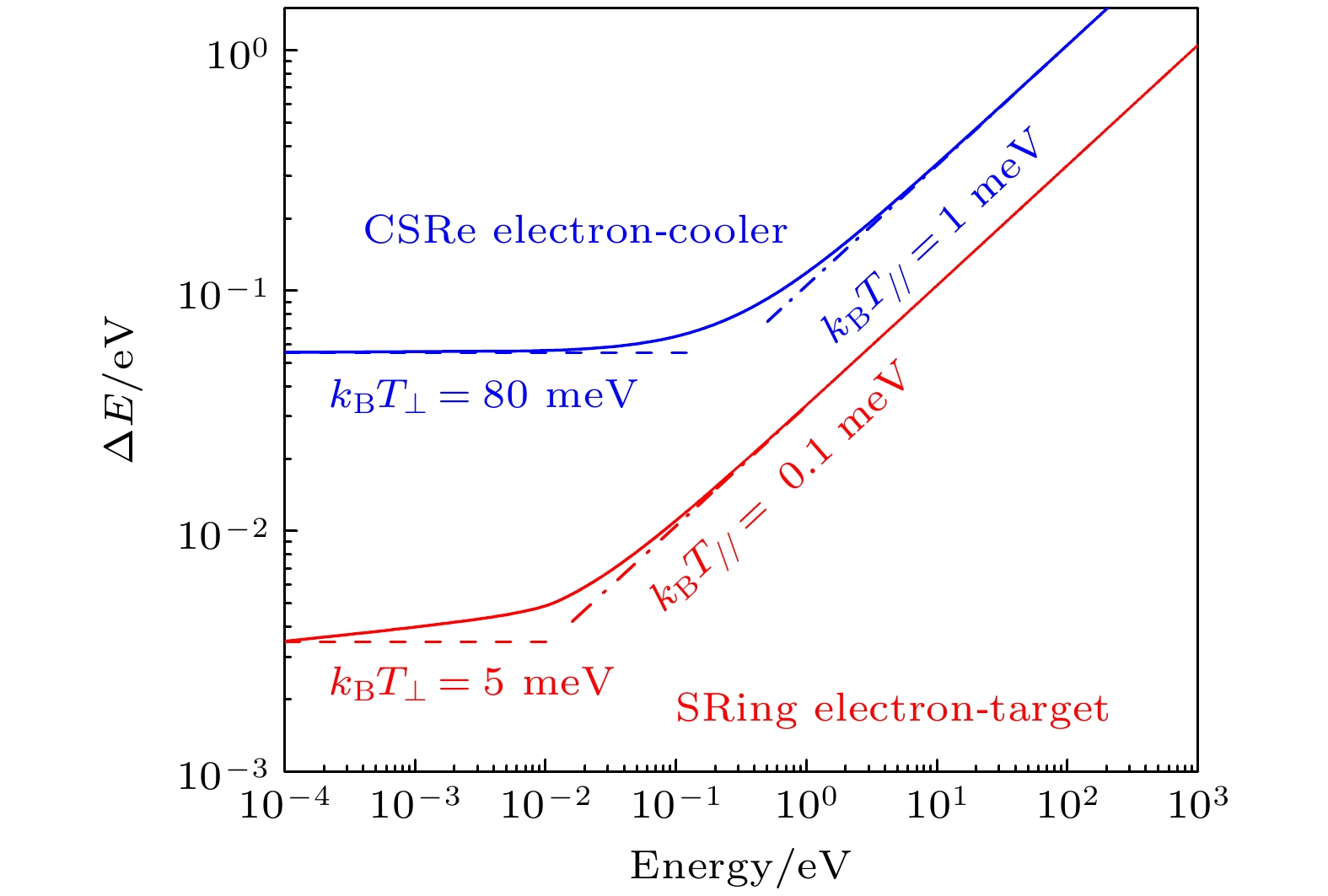
综上, 双电子复合的实验能量分辨$ {{\Delta }}E $为

图6展示了SRing和CSRe上的双电子复合实验能量分辨随碰撞能量的关系. 与CSRe相比, SRing上的双电子复合实验在能量分辨上实现了1—2个量级的显著提升, 并且在低能电子离子碰撞(meV级)区域展现出极高的能量分辨, 约3.5 meV. 因此, 实验的能量分辨在低碰撞能量区域达到最高, 这主要受横向温度的影响, 此时共振结构表现为非对称峰型. 随着碰撞能量的增加, 能量分辨率下降, 主要受纵向温度和碰撞能量的共同影响, 此时共振结构表现为对称峰型.

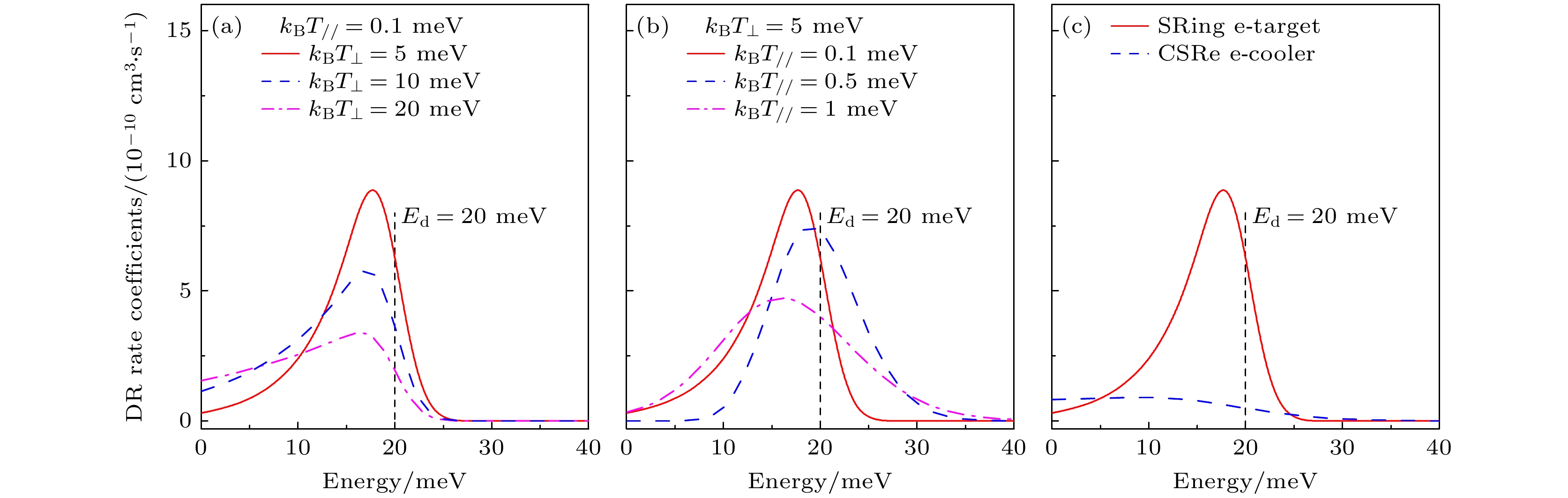
图7(a)和图7(b)展示了不同的电子束温度对双电子复合共振峰型和速率系数的影响, 其中模拟选取的共振峰的能量$ {E}_{{\mathrm{d}}}=20\;{\mathrm{meV}} $, 强度$ S=1\times 10^{-18}~\mathrm{cm^2 {\cdot} eV} $. 当电子束的纵向温度$ {{k}_{{\mathrm{B}}}T}_{/ / } = 0.1\;{\mathrm{meV}} $不变, 横向温度$ {k}_{{\mathrm{B}}}{T}_{\perp }=5\;{\mathrm{meV}} $增大到为10和20 meV时, 共振峰的展宽将逐渐变宽, 峰值逐渐下降; 当电子束的横向温度$ {k}_{{\mathrm{B}}}{T}_{\perp }= 5\;{\mathrm{meV}} $不变, 纵向温度$ {{k}_{{\mathrm{B}}}T}_{/ / }=0.1\;{\mathrm{meV}} $增大到0.5和1 meV时, 共振峰的展宽将逐渐变宽, 峰值逐渐下降. 图7(c)展示了SRing与CSRe在特定共振位置上的峰值对比. 结果显示, 由于SRing双电子复合实验的能量分辨比CSRe提升了1—2个数量级, 因此在SRing上能够清晰地观察到共振峰, 而CSRe无法观测到这一现象. 这一对比突显了SRing在能量分辨率方面的巨大优势.

下面以类锂重离子$ {}_{~\,54}^{129}{{\mathrm{X}}{\mathrm{e}}}^{51+} $和$ {}_{~\,92}^{238}{{\mathrm{U}}}^{89+} $为例, 探讨SRing上进行的双电子复合实验所展现的高分辨率特性. 类锂高电荷态离子的$ {{\Delta }}n=0 $的双电子复合反应通道为

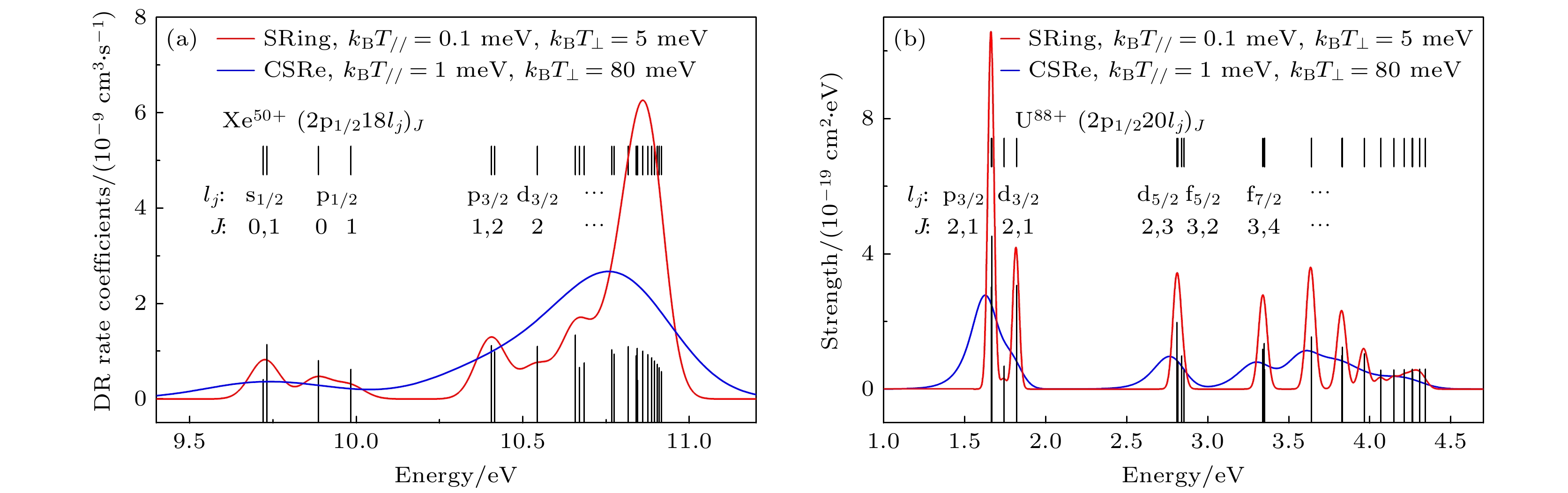
在我们的模拟计算中, 双电子复合共振结构的位置和强度是通过程序FAC计算获得的, 然后与SRing上的电子靶和CSRe上的电子冷却器的电子束温度进行卷积, 得到双电子复合速率系数模拟谱. 对于类锂$ {}_{54}^{129}{{\mathrm{X}}{\mathrm{e}}}^{51+} $离子, 如图8(a)所示, 低能区的双电子复合共振峰是双激发态$ {\left(2{{\mathrm{p}}}_{1/2}18{l}_{j}\right)}_{J} $. 由于SRing的双电子复合实验预计在低能区具有极高的能量分辨率, 能够分辨CSRe上无法识别的一些精细结构, 如双电子复合共振精细结构$ 18{{\mathrm{s}}}_{1/2}, {\mathrm{ }}18{{\mathrm{p}}}_{1/{{2, 3}}/2}, {\mathrm{ }}18{{\mathrm{d}}}_{3/2} $. 对于类锂$ {}_{92}^{238}{{\mathrm{U}}}^{89+} $离子的对比如图8(b)所示, 类锂$ {}_{92}^{238}{{\mathrm{U}}}^{89+} $离子低能区的双电子复合共振峰是双激发态$ {\left(2{{\mathrm{p}}}_{1/2}20{l}_{j}\right)}_{J} $. 同样, 其双电子复合谱能比CSRe上观测到更多的精细结构, 如$ {\left(2{{\mathrm{p}}}_{1/2}20{f}_{j}\right)}_{J} $.

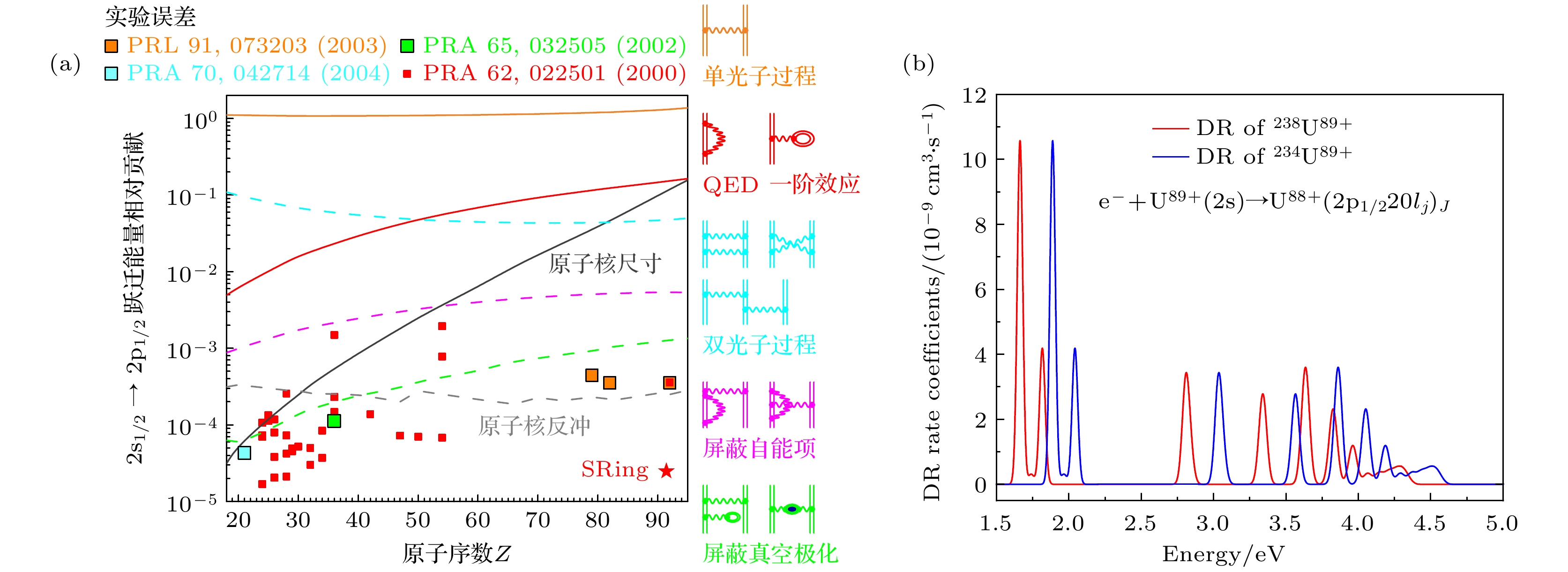
基于HIAF-SRing上超冷电子靶的双电子复合精密谱学实验具有高分辨的特点, 为类氢、类氦、类锂等少电子体系高电荷态离子的双电子复合精密测量带来了新的机遇. 图9(a)展示了类锂离子$ {2{\mathrm{s}}}_{1/2}—{2{\mathrm{p}}}_{1/2} $能级跃迁中的各种效应贡献以及相关实验测量结果, 当前的实验主要集中于低Z元素, 具有较高的测量精度, 而针对高Z元素的实 验相对较少且精度较低^[11], SRing上的超冷电子靶为开展类锂高电荷态离子精密谱测量提供了新的实验平台, 其开展类锂²³⁸U⁸⁹⁺离子双电子复合实验的精度如图9(a)所示, 精确测量$ {2{\mathrm{s}}}_{1/2}—{2{\mathrm{p}}}_{1/2} $等 跃迁过程中从低激发态至里德伯态的系列双电子复合共振峰, 可获得高精度的跃迁能量. 通过与 国际最先进的理论计算结果对比, 提取出兰姆位 移, 从而研究量子电动力学效应^[13]. 此外, 理论计算表明^[44], 类锂的高电荷态离子^{232, 230}Th⁸⁷⁺, ^{238, 236}U⁸⁹⁺和^{238, 234}U⁸⁹⁺的$ {2{\mathrm{s}}}_{1/2}—{2{\mathrm{p}}}_{1/2} $跃迁能级同位素位移分别为–111.9 meV, –114.3 meV和–225.6 meV, 由于双电子复合共振结构对原子核均方根半径高度敏感, SRing上的双电子复合精密谱学方法特别适合于这些放射性重离子的同位素位移测量. 基于SRing超冷电子靶开展类锂^{238, 234}U⁸⁹⁺同位素离子双电子复合的模拟谱如图9(b)所示, 结果表明, 尽管两个同位素的原子核均方根半径差仅为0.028 fm, 但DR共振峰的位移达到了–225.6 meV, DR谱上能够显著观测到这一位移. 因此, SRing能够开展发射线核素重离子的双电子复合精密谱实验, 并结合精确理论计算, 提取核电荷分布等重要核结构信息^[45].

我国正在建设的“十二五”大科学装置强流重离子加速器HIAF, 配备了高精度冷却储存环SRing, 该储存环上装备有450 kV电子冷却器和80 kV超冷电子靶装置, 能够在宽质心能量范围(从meV到几十keV)内对高电荷重离子的双电子复合谱进行精密测量. 本文结合理论推导和模拟分析对基于HIAF-SRing超冷电子靶开展高电荷态离子双电子复合精密谱实验测量进行了比较系统的研究和讨论, 主要结论如下.

1)基于经典分子动力学方法的模拟结果表明, 高精度环形谱仪SRing上配备的独立超冷电子靶10—80 kV工作范围内其电子束的横向温度不超过5 meV, 纵向温度不超过0.1 meV.

2)实验的能量分辨在低碰撞能量区域达到最高约3.5 meV, 主要受横向温度的影响, 导致共振结构呈现出非对称峰型. 随着碰撞能量的增加, 能量分辨降低, 这主要受纵向温度和碰撞能量的共同影响, 此时共振结构表现为对称峰型.

3)以类锂$ {}_{54}^{129}{{\mathrm{X}}{\mathrm{e}}}^{51+} $和$ {}_{92}^{238}{{\mathrm{U}}}^{89+} $重离子为例, 模拟了储存环HIAF-SRing与CSRe上低能区的双电子复合谱. 结果表明, 更高的能量分辨能使我们观测到更精细的双电子复合共振结构, 可以在更高精度上检验强场QED效应, 并通过测量放射性重离子的同位素位移提取原子核电荷均方根半径等原子核结构信息.

本文对HIAF-SRing上独立电子靶的电子束温度分布、双电子复合实验能量分辨和模拟谱的研究, 将为未来SRing电子-离子复合共振谱仪开展高电荷态离子双电子复合精密测量提供重要的支持和参考.