高级搜索

双振荡场空间分离对真空中电子-正电子对产生的影响

,  ,  , 

downloadPDF

上一篇

下一篇

赵文呈, 江淼, 徐妙华, 李英骏. 双振荡场空间分离对真空中电子-正电子对产生的影响[J]. 物理学报, 2025, 74(5): 054201-1. doi: 10.7498/aps.74.20241443
引用本文: 赵文呈, 江淼, 徐妙华, 李英骏. 双振荡场空间分离对真空中电子-正电子对产生的影响[J]. 物理学报, 2025, 74(5): 054201-1. doi: 10.7498/aps.74.20241443
shu
Wencheng ZHAO, Miao JIANG, Miaohua XU, Yingjun LI. Research on electron-positron pair production in vacuum induced by spatially separated dual oscillating fields[J]. Acta Physica Sinica, 2025, 74(5): 054201-1. doi: 10.7498/aps.74.20241443
Citation: Wencheng ZHAO, Miao JIANG, Miaohua XU, Yingjun LI. Research on electron-positron pair production in vacuum induced by spatially separated dual oscillating fields[J]. Acta Physica Sinica, 2025, 74(5): 054201-1. doi: 10.7498/aps.74.20241443
shu

双振荡场空间分离对真空中电子-正电子对产生的影响

  • 1.

    中国矿业大学(北京)理学院, 北京　100083

  • 2.

    中国矿业大学(北京), 隧道工程灾变防控与智能建养全国重点实验室, 北京　100083

    • 通讯作者: E-mail: mjiang@cumtb.edu.cn;  E-mail: mhxu@cumtb.edu.cn;  E-mail: lyj@aphy.iphy.ac.cn

  • 中图分类号: 42.25.Bs, 12.20.Ds, 03.65.-W

Research on electron-positron pair production in vacuum induced by spatially separated dual oscillating fields

  • 1.

    School of Science, China University of Mining and Technology Beijing, Beijing 100083, China

  • 2.

    State Key Laboratory for Tunnel Engineering, China University of Mining and Technology Beijing, Beijing 100083, China

    • Corresponding authors: E-mail: mjiang@cumtb.edu.cn;  E-mail: mhxu@cumtb.edu.cn;  E-mail: lyj@aphy.iphy.ac.cn

  • MSC: 42.25.Bs, 12.20.Ds, 03.65.-W

  • 摘要: 当两个次临界振荡场在空间上发生交叠时, 可以高效促进真空中正负电子对的产生. 本研究旨在探究两场在交叠方向上的间距变化对电子对产生的影响. 模拟结果显示, 随着间距的增大, 产率逐渐降低. 通过对不同频率组合的比较, 还发现空间分离时产率的变化快慢与频率组合密切相关. 此外, 在间距变化时, 电子能谱结构的变化也表现出不同的特征. 通过结合粒子跃迁能量分布概率对能谱图的结构进行了详细分析, 发现高阶跃迁概率随距离增加的衰减速度大于低阶跃迁. 此外, 随着间距的增大, 两个组合场共同作用的多光子效应逐渐减弱, 而单个场通过多光子效应产生正负电子对的概率则逐渐增强. 上述结果和规律均得到了很好的解释, 它帮助我们更深入地理解空间局域化对电子对产生的影响, 并对实验设计提供一定的指导.
    Abstract: This work investigates the combination of two partially overlapping oscillating fields, aiming to analyze the effect of the separation distance between the fields on the production of electron-positron pairs in a vacuum. The process is simulated using computational quantum field theory (CQFT) method and the split-operator technique, which is based on the spacetime-dependent Dirac equation. The main focus is to analyze the influence of separation distance and frequency combination on the pairwise production rate and energy spectrum.The research results show that partially overlapping sub-critical oscillating fields can still effectively generate electron-positron pairs at small separation distances. The variation in separation distance along the overlapping direction significantly affects the pairwise production rate. For two oscillating fields with a fixed sum of frequencies, the separation distance has a notable effect on the pairwise production rate, with different frequency combinations exhibiting varying degrees of dependency.Further analysis of the energy spectrum reveals that the number and positions of spectral peaks are differently affected by the separation distance. Models with smaller frequency differences exhibit more concentrated energy distributions, generally presenting a single-peak structure. In contrast, models with larger frequency differences show more dispersed energy distributions, typically presenting a dual-peak structure. As the separation distance increases, the energy spectrum structure varies with different frequency combinations, especially for larger separation distances. In the case of larger frequency difference, the high-energy peak declines rapidly with separation distance increasing, leading to a lower proportion of high-energy electrons, while in the case of smaller frequency difference the change is relatively small. This phenomenon is further analyzed using energy transition probability distribution diagrams of particles.By analyzing the probability distribution diagrams of particle energy transitions, we obtain a preliminary understanding of the differences in various frequency combinations with respect to separation distance, and explain the changes in energy spectrum structure from the perspective of multiphoton transitions. Additionally, a more detailed analysis of these diagrams based on the law of conservation of energy, enables us to extract particle production trends corresponding to various multiphoton transition effects. It is found that for the same frequency combination, the trends of second- and third-order effects with varying separation distances are different, with higher-order effects decaying more rapidly.By analyzing the variation of probability of multiphoton transitions in a combined field with separation distance, as well as the variation of the probability of multiphoton transitions in a single field, we conclude that when the separation distance is small, the combined fields with larger frequency differences have advantages in the generation of electron-positron pair. However, when the separation distance is large, the combined fields with smaller frequency differences begin to play an important role and exhibit better stability, owing to their inherent multiphoton effects. For different cases under the combined influence of two fields, we conduct a more in-depth analysis of the differences between different orders within the same frequency combination and between the same order transitions under different frequency combinations. By proposing hypotheses and conducting computational verification, it is found that under the same conditions, the trend of normalized overlapping photon numbers changing with separation distances is consistent with the trend of corresponding particle production numbers, providing a more convenient method for testing the trend of particle production under separation distance.This study not only enriches our understanding of the generation of vacuum electron-positron pairs in strong fields, but also provides theoretical guidance and reference for designing experimental devices for generating pairs.
  • 加载中

  • 图 1  组合场分开不同间距D时的场强图象　(a)$ D = 2/c $; (b)$ D = 4/c $; (c)$ D = 6/c $; (d)$ D = 12/c $. 两场场宽均为$ W = 2/c $

    Figure 1.  The field strength diagrams for combined fields separated by different distances D: (a) $ D = 2/c $; (b) $ D = 4/c $; (c) $ D = 6/c $; (d) $ D = 12/c $. The width of both fields is $ W = 2/c$.

    下载: 全尺寸图片 幻灯片

    图 2  (a)产率$ {k} $随$ {D} $的变化趋势, 频率差渐变的过程中, $ {D} $从$ 0 $到$ 10/{c} $的下降趋势; (b)归一化产率$ {k/k_{{\mathrm{max}}}} $随间距$ {D} $的变化趋势

    Figure 2.  (a) The trend of the electron pair production rate $ {k} $ as the frequency difference gradually changes, showing a decreasing trend of $ {D} $ from $ 0 $ to $ 10/{c} $; (b) the trend of normalized electron pair production rate $ {k/k_{{\mathrm{max}}}} $ with respect to the change in distance $ {D} $.

    下载: 全尺寸图片 幻灯片

    图 3  $ {\rm{(a)}}\;\omega_1 = 0.5{c}^2, \;\omega_2 = 1.9{c}^2 $时不同$ {D} $对应的产生粒子能量分布概率; $ ({\mathrm{b}})\;\omega_1 = 1.1{c}^2,\; \omega_2 = 1.3{c}^2 $时不同$ {D} $对应的产生粒子的能量分布概率. 演化时间均为$ {t} = 0.003 \; {{\mathrm{a.u.}}} $, 势高$ {{\cal{V}}_1={\cal{V}}_2 = 2.0 c^2} $, 场宽$ {W = 2/c} $

    Figure 3.  $ {\rm{(a)}} $ Energy spectrum for different $ {D} $ values when $ \omega_1 = 0.5{c}^2,\; \omega_2 = 1.9{c}^2 $; $ {({\mathrm{b}})} $ energy spectrum for different $ {D} $ values when $ \omega_1 = 1.1{c}^2,\; \omega_2 = 1.3{c}^2 $. Evolution time is $ {t} = 0.003 \; {{\mathrm{a.u.}}} $ with potential heights $ {{\cal{V}}_1={\cal{V}}_2 = 2.0 c^2} $ and field width $ {W = 2/c} $

    下载: 全尺寸图片 幻灯片

    图 4  两种组合场参数下的粒子跃迁能量概率分布　(a) $ \omega_1 = 0.5\, c^2 $和$ \omega_2 = 1.9\, c^2 $; (b) $ \omega_1 = 1.1\, c^2 $和$ \omega_2 = 1.3\, c^2 $. 其中子图$ {\rm{(a1)}}\rightarrow {\rm{(a4)}} $和$ {\rm{(b1)}}\rightarrow {\rm{(b4)}} $分别对应空间参数D从$ 0 $到$ 6/c $的变化. 场宽为$ W_1 = W_2 = 2/c $, 势场高度为$ {\cal{V}}_1 = {\cal{V}}_2 = 2.0\, c^2 $

    Figure 4.  Particle transition energy probability distribution for combined fields: (a) $ \omega_1 = 0.5\, c^2 $ and $ \omega_2 = 1.9\, c^2 $; (b) $ \omega_1 = 1.1\, c^2 $ and $ \omega_2 = 1.3\, c^2 $. The subfigures $ {\rm{(a1)}}\rightarrow {\rm{(a4)}} $ and $ {\rm{(b1)}}\rightarrow {\rm{(b4)}} $ correspond to the spatial parameter D varying from $ 0 $ to $ 6/c $, respectively. The field widths are $ W_1 = W_2 = 2/c $, and the potential heights are $ {\cal{V}}_1 = {\cal{V}}_2 = 2.0\, c^2 $.

    下载: 全尺寸图片 幻灯片

    图 5  (a) $ \omega_1 = 0.5{c}^2, \;\omega_2 = 1.9{c}^2 $, (b) $ \omega_1 = 1.1{c}^2,\; \omega_2 = 1.3{c}^2 $条件下各阶多光子跃迁效应对应的归一化粒子数对比, 纵轴为归一化粒子数, 演化时长$ {(t = 0.003 \; {\mathrm{a.u.}} )} $, 不同的线条样式代表不同的跃迁阶级

    Figure 5.  (a) $ \omega_1 = 0.5{c}^2,\; \omega_2 = 1.9{c}^2 $, (b) $ \omega_1 = 1.1{c}^2, \;\omega_2 = 1.3{c}^2 $, under these conditions, the normalized particle numbers corresponding to various order multiphoton transition effects are compared. The vertical axis represents the normalized particle numbers, and different line styles represent different transition orders, with an evolution time of $ {(t = 0.003 \; {\mathrm{a.u.}} )} $.

    下载: 全尺寸图片 幻灯片

    图 6  不同频率组合的低阶跃迁效应随间距变化趋势对比　(a)组合场二阶以及部分三阶跃迁效应粒子数; (b)独立场的二阶以及部分三阶跃迁效应粒子数; (c)各阶主要成分相加的粒子数比较, 且进行了归一化处理

    Figure 6.  Comparison of trends in low-order transition effects with varying separation distances for different frequency combinations: (a) Particle numbers for second-order and partial third-order transition effects of combined fields; (b) particle numbers for second-order and partial third-order transition effects of independent fields; (c) comparison of particle numbers for the main components of each order, with normalization applied.

    下载: 全尺寸图片 幻灯片

    图 7  频率组合$ {\rm{(a1)}}\text{—}{\mathrm{(a4)}} $ $ 0.5{c}^2+1.9{c}^2 $和$ {\rm{(b1)}}\text{—}{\mathrm{(b4)}} $ $ 1.1{c}^2+1.3{c}^2 $下的交叠光子数随间距$ {D} $的变化. 子图的角标(1, 2, 3, 4)分别对应间距$ {D} $的值为$ {0} $, $ {2/c} $, $ {4/c} $, $ {6/c} $. 场宽$ W = 2/c $, 势高$ {\cal{V}} = 2 c^2 $

    Figure 7.  Variation of overlapping photon numbers with distance $ {D} $ under frequency combinations of (a1)–(a4) $ 0.5{c}^2+1.9{c}^2 $ and (b1)–(b4) $ 1.1{c}^2+1.3{c}^2 $. The subscripts of the subplots (1, 2, 3, 4) correspond to distance $ {D} $ values of $ {0} $, $ {2/c} $, $ {4/c} $, and $ {6/c} $ respectively. Field width $ W = 2/c $, potential height $ {\cal{V}} = 2 c^2 $.

    下载: 全尺寸图片 幻灯片

    图 8  频率组合分别为$ 0.5{c}^2+1.9{c}^2 $与$ 1.1{c}^2+1.3{c}^2 $时的归一化-交叠光子数随间距$ {D} $变化趋势

    Figure 8.  The trend of the normalized overlapping photon number with the change of distance $ {D} $ when the frequency combinations are respectively $ 0.5{c}^2+1.9{c}^2 $ and $ 1.1{c}^2+1.3{c}^2 $.

    下载: 全尺寸图片 幻灯片
  • [1] Schwinger J 1951 Phys. Rev. 82 664 doi: 10.1103/PhysRev.82.664
    [2] Kohlfürst C, Ahmadiniaz N, Oertel J, Schützhold R 2022 Phys. Rev. Lett. 129 241801 doi: 10.1103/PhysRevLett.129.241801
    [3] Marinov M S, Popov V S 1977 Fortschr. Phys. 25 373 doi: 10.1002/prop.19770250111
    [4] Brezin E, Itzykson C, 1970 Phys. Rev. D 2 1191 doi: 10.1103/PhysRevD.2.1191
    [5] Popov V S, 1971 Zh. Eksp. Teor. Fiz. 61 1334
    [6] 朱兴龙, 王伟民, 余同普, 何峰, 陈民, 翁苏明, 陈黎明, 李玉同, 盛政明, 张杰 2021 物理学报 70 085202 doi: 10.7498/aps.70.20202224 Zhu X L, Wang W M., Yu T P, He F, Chen M, Weng S M, Chen L M, Li Y T, Sheng Z M, Zhang J 2021 Acta Phys. Sin. 70 085202 doi: 10.7498/aps.70.20202224
    [7] 沈百飞, 吉亮亮, 张晓梅, 步志刚, 徐建彩 2021 物理学报 70 084101 doi: 10.7498/aps.70.20210096 Shen B F, Ji L L, Zhang X M, Bu Z G, Xu J C 2021 Acta Phys. Sin. 70 084101 doi: 10.7498/aps.70.20210096
    [8] Kluger Y, Eisenberg J M, Svetitsky B, Cooper F, Mottola E 1991 Phys. Rev. Lett. 67 2427 doi: 10.1103/PhysRevLett.67.2427
    [9] Alkofer R., Hecht M B, Roberts C D, Schmidt S M, Vinnik D V 2001 Phys. Rev. Lett. 87 193902 doi: 10.1103/PhysRevLett.87.193902
    [10] Schmidt S, Blaschke D, Röpke G, Prozorkevich A V, Smolyansky S A, Toneev V D 1999 Phys. Rev. D 59 094005 doi: 10.1103/PhysRevD.59.094005
    [11] Blinne A, Strobel E 2016 Phys. Rev. D 93 025014 doi: 10.1103/PhysRevD.93.025014
    [12] Kohlfürst C, Alkofer R 2018 Phys. Rev. D 97 036026 doi: 10.1103/PhysRevD.97.036026
    [13] Gies H, Klingmüller K 2005 Phys. Rev. D 72 065001 doi: 10.1103/PhysRevD.72.065001
    [14] Ilderton A, Torgrimsson G, Wårdh J 2015 Phys. Rev. D 92 065001 doi: 10.1103/PhysRevD.92.065001
    [15] Dumlu C K, Dunne G V 2011 Phys. Rev. D 83 065028 doi: 10.1103/PhysRevD.83.065028
    [16] Dumlu C K 2010 Phys. Rev. D 82 045007 doi: 10.1103/PhysRevD.82.045007
    [17] Krekora P, Cooley K., Su Q, Grobe R 2005 Phys. Rev. Lett. 95 070403 doi: 10.1103/PhysRevLett.95.070403
    [18] Xie B S, Li Z L, Tang S, Liu J 2017 Physics 46 713
    [19] Lv Q Z, Liu Y, Li Y J, Grobe R, Su Q 2013 Phys. Rev. Lett. 111 183204 doi: 10.1103/PhysRevLett.111.183204
    [20] Bulanov S S, Mur V D, Narozhny N B, Nees J, Popov V S 2010 Phys. Rev. Lett. 104 220404 doi: 10.1103/PhysRevLett.104.220404
    [21] Di Piazza A, Müller C, Hatsagortsyan K Z, Keitel C H 2012 Rev. Mod. Phys. 84 1177 doi: 10.1103/RevModPhys.84.1177
    [22] 罗蕙一, 江淼, 徐妙华, 李英骏 2023 72 021201 doi: 10.7498/aps.72.20221660 Luo H Y, Jiang M, Xu M H, Li Y J 2023 Acta Phys. Sin. 72 021201 doi: 10.7498/aps.72.20221660
    [23] Braun J W, Su Q, Grobe R 1999 Phys. Rev. A 59 604 doi: 10.1103/PhysRevA.59.604
    [24] Wagner R E, Ware M R, Shields B T, Su Q, Grobe R 2011 Phys. Rev. Lett. 106 023601 doi: 10.1103/PhysRevLett.106.023601
    [25] Wang L, Wu B, Xie B S 2019 Phys. Rev. A 100 022127 doi: 10.1103/PhysRevA.100.022127
    [26] Cheng T, Su Q, Grobe R 2010 Contemp. Phys. 51 315 doi: 10.1080/00107510903450559
  • 加载中
图( 8)
计量
  • 文章访问数:  88
  • HTML全文浏览数:  88
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-10-16
  • 刊出日期:  2025-03-05

双振荡场空间分离对真空中电子-正电子对产生的影响

    通讯作者: E-mail: mjiang@cumtb.edu.cn; 
    通讯作者: E-mail: mhxu@cumtb.edu.cn; 
    通讯作者: E-mail: lyj@aphy.iphy.ac.cn
  • 1. 中国矿业大学(北京)理学院, 北京　100083
  • 2. 中国矿业大学(北京), 隧道工程灾变防控与智能建养全国重点实验室, 北京　100083
  • 收稿日期:  2024-10-16

摘要: 当两个次临界振荡场在空间上发生交叠时, 可以高效促进真空中正负电子对的产生. 本研究旨在探究两场在交叠方向上的间距变化对电子对产生的影响. 模拟结果显示, 随着间距的增大, 产率逐渐降低. 通过对不同频率组合的比较, 还发现空间分离时产率的变化快慢与频率组合密切相关. 此外, 在间距变化时, 电子能谱结构的变化也表现出不同的特征. 通过结合粒子跃迁能量分布概率对能谱图的结构进行了详细分析, 发现高阶跃迁概率随距离增加的衰减速度大于低阶跃迁. 此外, 随着间距的增大, 两个组合场共同作用的多光子效应逐渐减弱, 而单个场通过多光子效应产生正负电子对的概率则逐渐增强. 上述结果和规律均得到了很好的解释, 它帮助我们更深入地理解空间局域化对电子对产生的影响, 并对实验设计提供一定的指导.

English Abstract

    全文HTML

    1.   引　言

    • 量子电动力学(QED)结合了量子力学和狭义相对论, 预言了强场下真空中电子对产生现象, 如施温格效应(Schwinger effect)[1]和多光子跃迁效应[2-5]. 对正负电子对产生的研究对基础物理学的发展以及深化人类对宇宙初始物质形成的认识有重要意义. 在实验领域, 由于激光场强的限制, 真实的施温格效应尚未被直接观测到, 但是随着激光技术的不断进步, 不久的将来在实验室实现施温格强场环境将成为可能[6,7].

      在理论模拟研究中, 人们发展了多种方法探索电子对的产生机制, 包括量子动理学方法和半经典近似法. 量子动理学方法如量子Vlasov方程和实时Dirac-Heisenberg-Wigner形式[8-12]等. 量子Vlasov方程适用于分析均匀空间含时电场中的粒子动力学; 实时Dirac-Heisenberg-Wigner方法为非微扰粒子对产生提供了全面框架. 此外, 依赖于高性能环境的半经典近似法, 如世界线瞬子技术[13,14]和广义WKB近似[15,16]也被应用于模拟粒子相互作用. 计算量子场论(CQFT)提出了一种高效方法, 能够解决在任意不均匀含时局域化电场中正负电子对产生的问题, 精确分析在特定空间局部化电场中正负电子对的产生特性, 并实时描述真空中产生的正负电子对的瞬态特征[17-19].

      本研究利用计算量子场论对真空中电子对产生机制进行了深入探讨, 利用精确的数值模拟方法, 旨在为未来的实验提供关键的模拟参数和设计方向. 在当前实验室单场激光强度不能达到电子对产生阈值的条件下, 利用多束激光叠加的共同作用来产生电子对是一个理想的方案[20,21]. 根据文献[22]的研究我们了解到, 组合场振荡频率对电子对产率具有显著的影响, 特定的频率组合会使得产率大大提升. 然而这种方案也面临一个挑战, 即实验中多个激光场是否可以在空间位置上保持完全重合. 本文通过数值模拟进一步研究了组合场的场中心分离一定距离时, 对电子对产率的具体影响, 并对其背后的物理机制提出了理论上的解释. 这项工作不仅丰富了我们对强场QED现象的理解, 也为实验物理学家在设计未来实验时提供了理论上的指导和参考.

    2.   计算量子场论方法

    • 本文采用计算量子场论(CQFT)方法[23,24], 通过数值求解一维狄拉克方程, 以描述真空中正负电子对的产生过程. 通过推导可以得出, 费米系统中表征粒子数变化的场算符随时间的演化遵循狄拉克方程[25]. 此外可以证明, 在一维情况下, 若只考虑z方向上的分量, 则在该表象下的四分量中的两个分量的结果完全相同. 因此, 可以将其简化为二分量形式:

      在方程(1)中, $ {\boldsymbol{\sigma}}_1 $和$ {\boldsymbol{\sigma}}_3 $为泡利$ {\rm{X}} $矩阵和泡利$ {\rm{Z}} $ 矩阵. 本文采用高斯单位制和原子单位制, $ \hbar = m = e = 1 $, 光速$ c = 137.036 $. 在一维情况下, 无需考虑磁场效应, 且势能$ V(z, t) $在空间上只与坐标z相关.

      场算符$ \hat{\psi}(z, t) $可以通过产生湮灭算符展开:

      其中,$ |p(z)\rangle $和$ |n(z)\rangle $分别代表无外场时正负能级上的自由粒子态. $ \hat{b}_p(t) $是作用在正能态上的产生算符, 而$ \hat{d}^\dagger_n(t) $是作用在负能态上的产生算符. 利用 Bogoliubov 变换得到如下形式:

      式中, $ |p(z, t)\rangle $和$ |n(z, t)\rangle $分别代表以自由粒子态为初态, 后随时间演化的正负能级单粒子态. 将场算符中对应电子(即正能态)的部分定义为

      利用数学变换以及空间中电子密度的性质可以得到其几率密度算符在真空态$ | {vac}\rangle\rangle $的平均值如下:

      通过推导可得, t时刻粒子数算符在真空态中的平均值表达式为

      式中, 时间演化矩阵$ {\boldsymbol{U}}_{p, n}(t) $为t时刻的含时负能态$ | n(z, t)\rangle $与自由正能态$ |p(z)\rangle $的内积. 因此, 为了计算总粒子数$ N(t) $, 首先需要计算$ U_{p, n}(t)= \langle p(z)|n(z, t)\rangle $. 而含时演化态$ |n(z, t)\rangle $可以利用劈裂算符方法[26]数值求解.

    3.   外场间距对多光子跃迁过程的影响

    • 两束高度重合激光场可以通过多光子跃迁效应高效地产生正负电子对. 然而, 在实验中实现两束激光场在空间上完全重合, 具有一定的难度. 因此, 本节将研究当两束激光场存在一定间距, 并且该间距D大于或等于一个单位的康普顿波长($ D\geqslant1/c $)时, 对产生正负电子对过程的影响.

      对于双振荡场模型, 其通用表达式为$ V(z,t)= V_1(z)\sin(\omega_1t)+V_2(z)\sin(\omega_2t) $. 为了表示两场存在一定的间距, 将势能的空间部分设置为

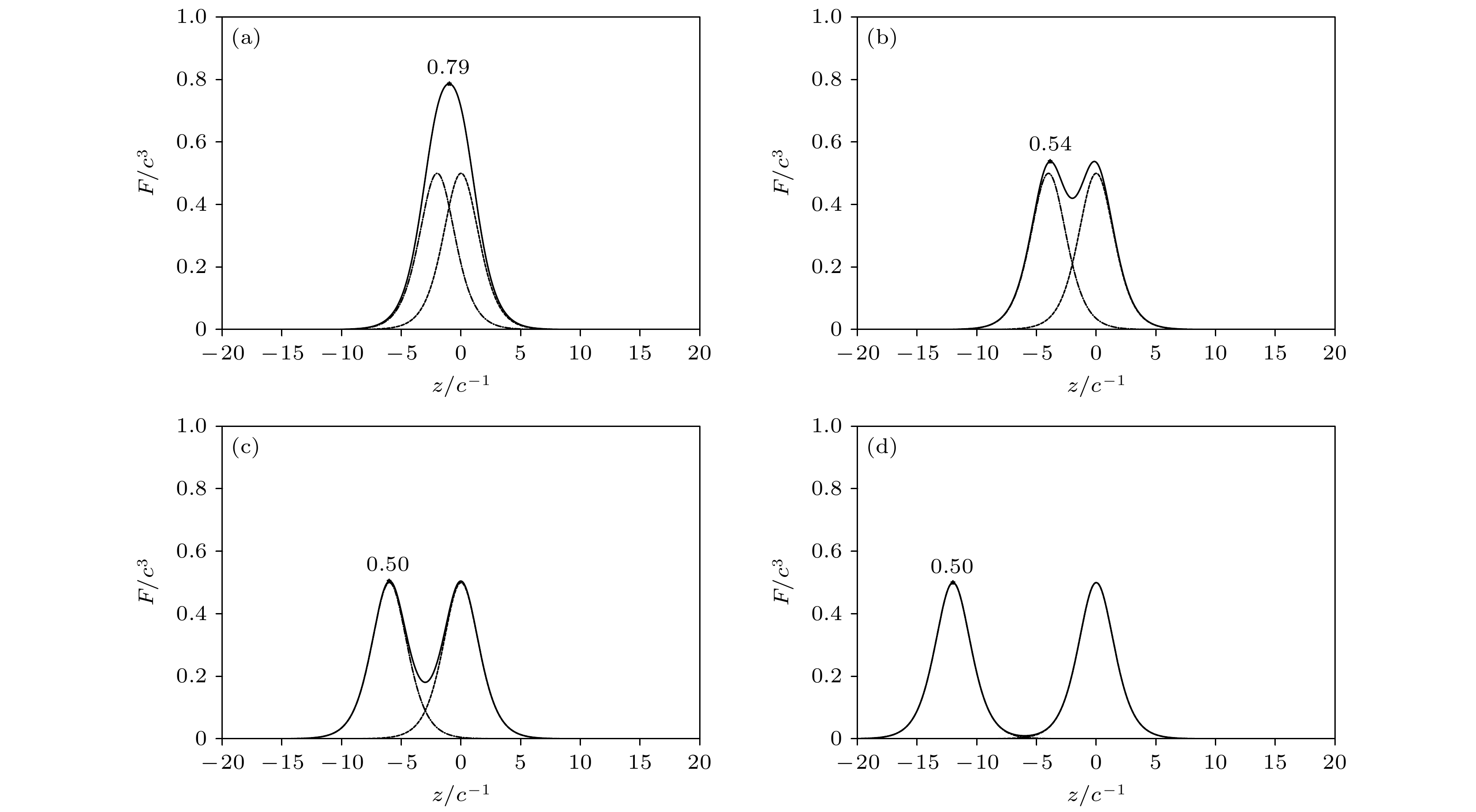
      这里设定两场势高度相等, 即$ {\cal{V}}_1 ={\cal{V}}_2 $, 振荡场场宽均为W, 势场中心为$ z_0 $. 参数D代表了两场之间在空间上的距离. 采用Sauter势$ S(z) $, 将振荡势场$ V(z, t) $代入一维狄拉克方程(1). 然后, 利用CQFT方法对全空间的狄拉克方程进行数值求解, 可以定义一系列量子场论观测量, 包括粒子数与粒子能谱等.

      图1中首先给出了组合场在空间中的场强分布, 不考虑时间上的振荡, 其中$ F = {\mathrm{d}}V(z)/{\mathrm{d}}z $, $ V(z) = V_1(z)+V_2(z) $, 场宽设置为$ W = 2/c $, 势高选取为$ 2 c^2 $. 从图1可以看出, 在$ D = 2/c $时, 两场在空间中依然存在大量交叠部分, 合成场强体现为一个单一的峰, 其峰值约为$ 0.79 c^3 $; 随着间距D的增大, 两场在空间中的重叠区域逐渐减少, 合成场强分裂为两个等高峰, 峰值约为$ 0.54 c^3 $. 当$ D = 12/c $时, 两场在空间上已经完全分开, 不存在叠加. 合成场强变为两个等高峰, 峰值为$ 0.5 c^3 $.

      • 3.1.   双振荡场间距对产生粒子数的影响

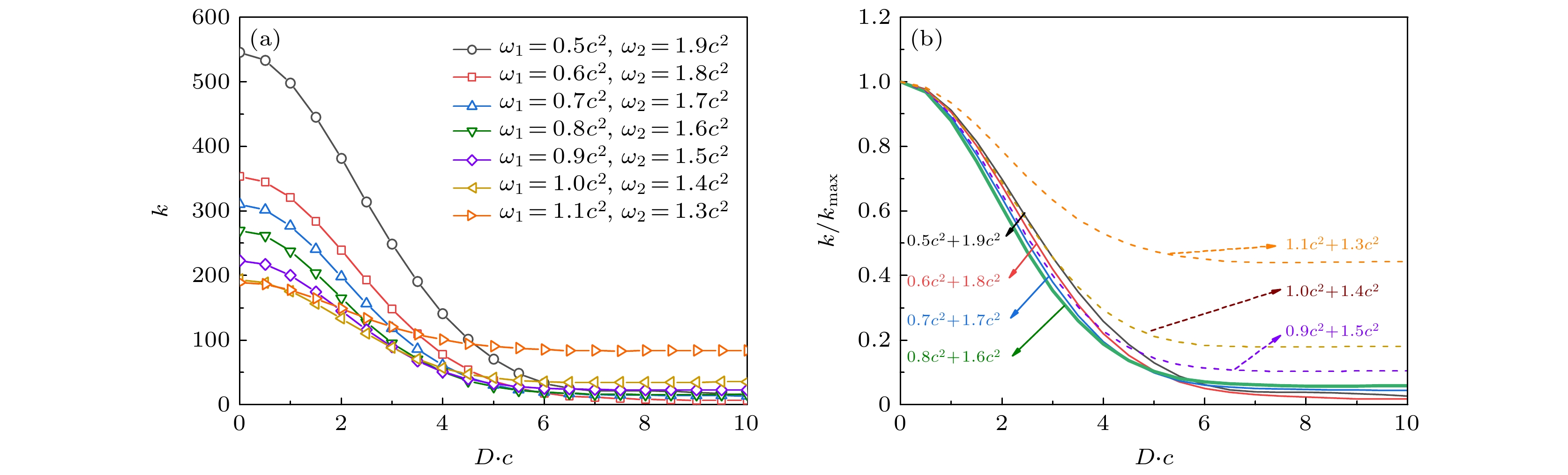
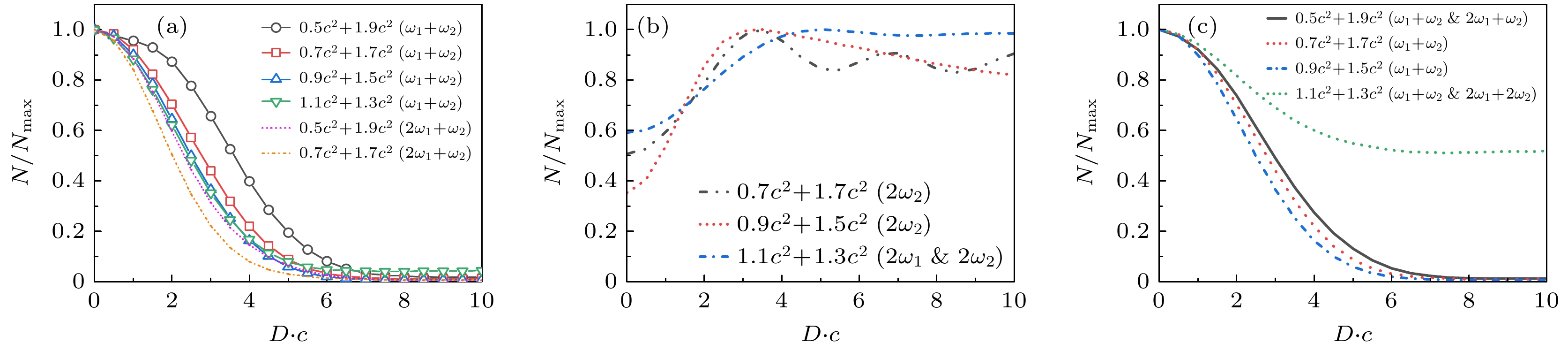
    • 在频率为次临界的振荡组合场(两场的空间位置完全重合)中, 已有研究表明当组合场频率之和约为$ {2.2 c^2} $—$ 2.3 {c}^2 $时, 电子对产量会达到峰值[22]. 本节将探究在组合场分开间距$ {D} $的情况下粒子数产生情况. 模拟中引入粒子数产率$ k\approx \Delta N/\Delta t $用于表征粒子数随时间增长的快慢. 在模拟中, 频率组合范围从$ 0.5 c^2+1.9 c^2 $到$ 1.1 c^2+ 1.3 c^2 $(每次增减单位为$ 0.1 c^2 $).

      图2(a)给出了不同频率组合下产率k随间距D的变化曲线. 从图2(a)可知, 当$ {D = 0} $时, 不同频率组合的产生率并不相同. 对于频率差最大的情况($ \omega_1 = 0.5{c}^2 $, $ \omega_2 = 1.9{c}^2 $)产率最大. 随着频率之差逐渐变小, 产率随之减小. 当D增大时, 所有频率组合的产率均随着D的增加而递减, 这是由于随着场间距增大, 两场之间耦合减弱, 交叠区域的大小和场强均减小, 从而导致产率降低. 当频率组合为$ {1.1 c^2+1.3 c^2} $时, 其产率下降趋势较缓, 在间距约为$ {4.25/c} $时, 与差频较大的($ \omega_1 = 0.5{c}^2 $, $ \omega_2 = 1.9{c}^2 $)产率相等.

      由于各频率组合所对应k-D曲线的初始值$ {k_{{\mathrm{max}}}} $不同, 为了仅比较$ {k} $随$ {D} $变化的趋势, 对各组数据进行归一化处理. 结果如图2(b)所示, 图中横轴表示间距$ {D} $, 单位为$ [1/c] $. 纵轴表示归一化的产率$ {K}={k}/{k_{{\mathrm{max}}}} $.

      通过观察图2(b)可以发现, 不同频率组合随D下降的趋势虽然相似, 但对D的响应存在一定的差异. 随着组合场频率差的减小, k随D衰减趋势并非单调变化, 整体来看呈现出先变快后变缓的趋势, 体现出一定的复杂性. 本文的后续内容中将分析这一现象的原因.

      • 3.2.   两场间距对电子能谱的影响

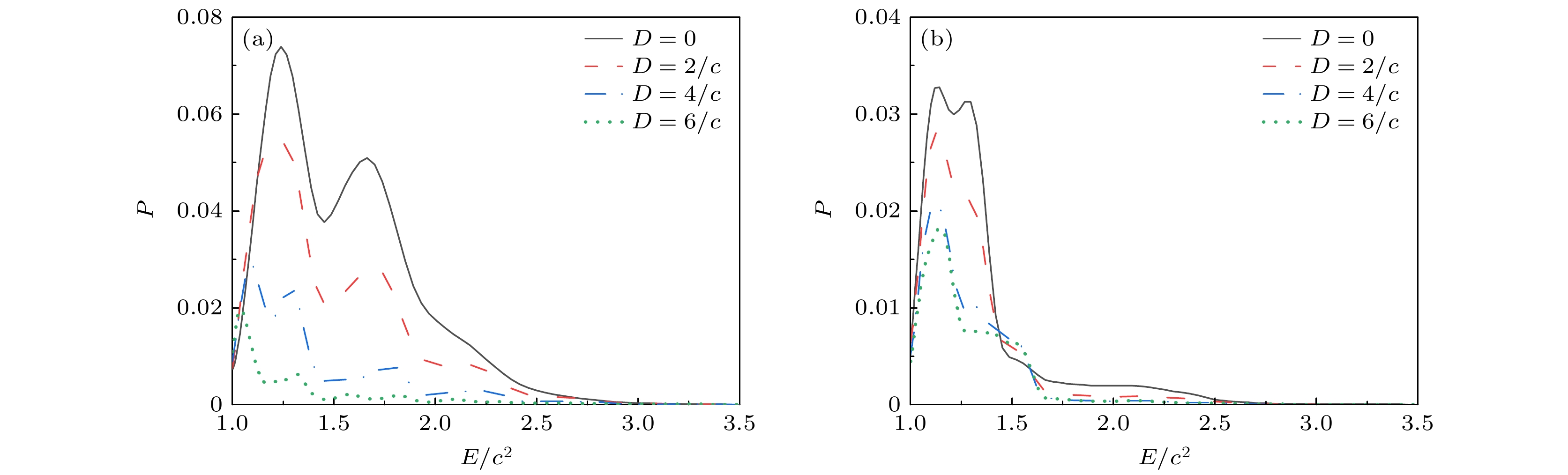
    • 本节研究两场间距$ {D} $对电子对能谱的影响. 图3给出$ {t} = 0.003\; {{\mathrm{a.u.}}} $时, 两种频率组合(a) ($ \omega_1 = 0.5{c}^2,\; \omega_2 = 1.9{c}^2 $)和(b) ($ \omega_1 =1.1{c}^2, \;\omega_2 = 1.3{c}^2 $)在不同间距时粒子的能量分布概率, 其中横轴表示正能态能量, 纵轴表示对应的概率.

      从图3可以看出, 对于差频较大($ \omega_1 = 0.5{c}^2, \omega_2 = 1.9{c}^2 $)情形(见图3(a)), 当两场在空间中完全重合时, 能谱分布宽度较大, 基本呈现双峰结构. 而对于差频较小($ \omega_1 = 1.1{c}^2, \omega_2 = 1.3{c}^2 $)情形, 其能谱分布比较集中, 产生的粒子能量主要集中在低能$ {1.2 c^2} $附近, 基本呈现单峰结构. 随着间距$ {D} $增加, 在间距$ {D} $小于$ {2/c} $时, 两种情形的能谱变化皆不显著. 在间距$ {D} $大于$ {2/c} $后, 对于频率为$ 0.5 c^2+ 1.9 c^2 $情形, 其能谱分布发生显著变化, 双峰结构中的高能峰迅速降低, 高能电子占比降低, 能谱分布整体呈现向低能方向移动. 而对于频率为$ 1.1 c^2+ 1.3 c^2 $, 对应能谱仍然基本集中在$ {1.0 c^2 \text{—}1.5^2} $之间, 低能峰内发生了一些细微的变化. 后文将结合跃迁能量概率分布图对以上现象进一步分析.

      考虑到在模拟中采用的是非均匀分布的局域外场, 粒子将发生动量不守恒的非对称跃迁. 因此, 仅依赖正能部分的能量分布难以准确推断粒子从负能态跃迁到正能态时的概率. 通过观察负能态能量为$ {E_{\mathrm{n}}} $和正能态能量为$ {E_{\mathrm{p}}} $之间的重叠概率, 能够更深入地理解电子对产生过程.

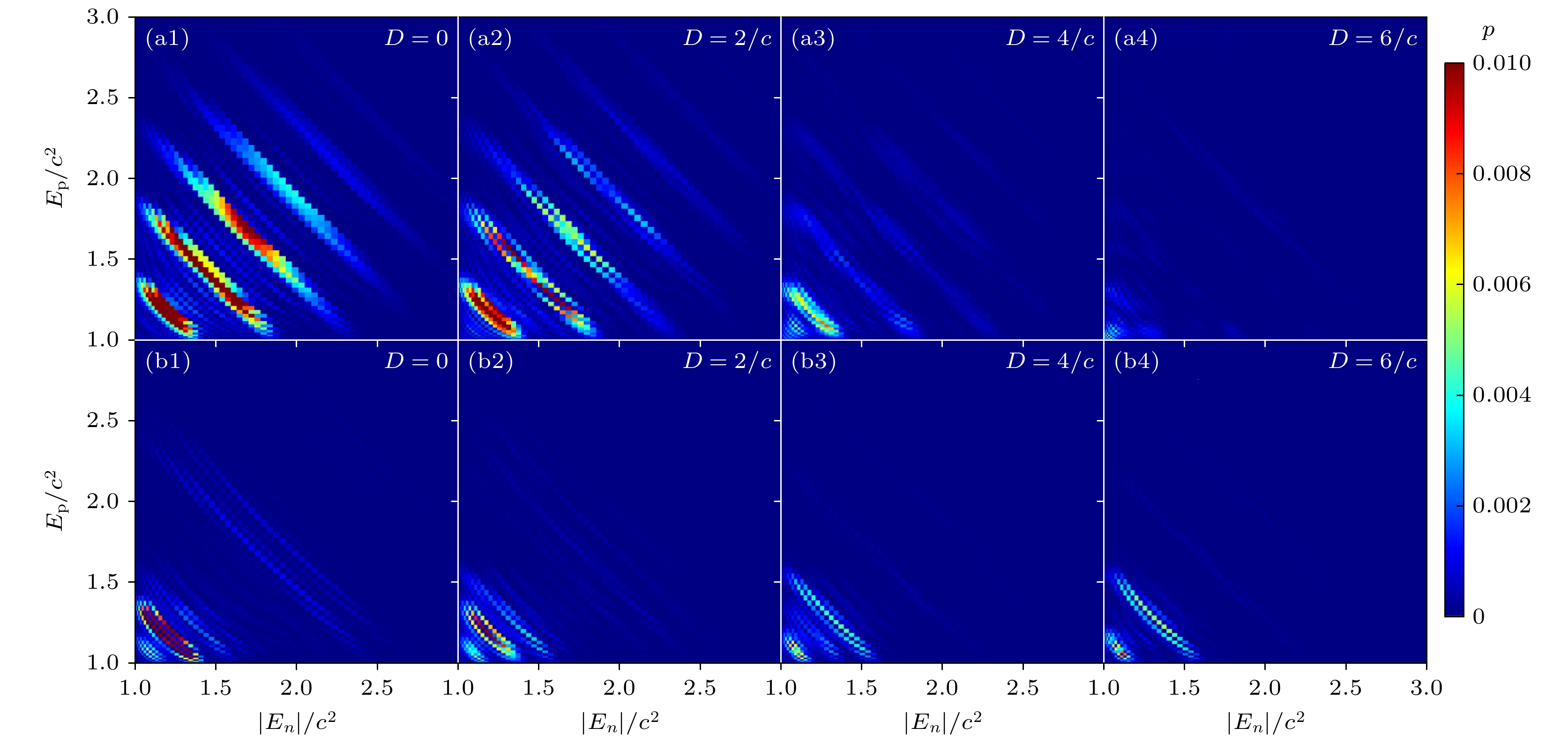
      图4(a1)—(a4)给出了$ \omega_1 = 0.5{c}^2 $, $ \omega_2 = 1.9{c}^2 $时, 随着间距$ {D} $的不同($ {D} = 0,\; 2/{c},\; 4/{c}, 6/{c} $), 粒子的跃迁能量概率分布的变化. 图4(b1)—(b4)则给出了在$ \omega_1 = 1.1{c}^2,\; \omega_2 = 1.3{c}^2 $条件下, 不同间距$ {D} $(分别为$ {D} = 0, \;2/{c}, \;4/{c},\; 6/{c} $)对应的粒子跃迁能量概率分布情况.

      跃迁能量概率分布图的横轴与纵轴分别代表负能态和正能态, 其中横轴与纵轴的交点对应从某一负能态到某一正能态之间的跃迁, 交点上的颜色表示跃迁的概率大小. 在图4中, 与图形反对角线平行的各个亮色条纹代表能量守恒的多光子跃迁效应. 按照远离坐标初始点(1, 1)的方向, 能量之和依次增大, 分别对应从低阶到高阶的多光子跃迁效应. 具体来说, 以图4(a1)为例, 最靠近坐标初始点的较亮条纹满足能量和为$ {2.4 c^2} $, 对应二阶多光子跃迁效应, 组合为$ {0.5 c^2+1.9 c^2} $, 该条纹的相邻条纹为三阶跃迁效应, 能量为$ 2.9{c}^2 $, 对应$ 2\omega_1+\omega_2 $, 其余条纹依次类推. 当两个场在空间中完全重叠时, 对于$ \omega_1 = 0.5{c}^2, \;\omega_2 = 1.9{c}^2 $的情况(图4(a)), 由于最小光子能量为$ \omega_1 = 0.5{c}^2 $, 相邻阶次的条纹较为接近, 高阶多光子跃迁效应更显著且形式更丰富. 因此在图3(a)中形成的能谱宽度也更宽. 而对于$ \omega_1 = 1.1{c}^2, \;\omega_2 = 1.3{c}^2 $的情况(图3(a)), 最小光子能量为$ \omega = 1.1{c}^2 $, 所以各阶跃迁在图4(a)上的间隔较远, 其粒子产量主要来自于最靠近原点的二阶多光子跃迁过程, 与能谱图中的主峰对应.

      当两场间距为$ 2/c $时, 从图4(a2)(b2)中可以看出, 相较于图4(a1)(b1), 条纹整体变暗, 即包括低阶与高阶跃迁在内的跃迁概率整体下降. 然而, 条纹结构基本保持不变, 这是由于两场场宽为$ 2/c $, 此时两场还有较大区域发生重叠. 随着场间距继续增大, 对于频率差较大的情况, 条纹发生显著变化, 较高阶条纹几乎消失. 而在两场间距增大到$ 6/c $时, 二阶效应基本消失, 且在能量为$ {2 c^2} $附近出现一个较小的亮条纹, 该条纹根据能量守恒计算, 对应一阶的单光子跃迁$ \omega_2 $, 由单个场独立提供. 对比间距为0时(图4(a1)), 在该能量处却没有条纹. 这说明在场重合较好时, 两场耦合较强, 单个场独立的光子跃迁效应受到抑制.

      对于差频较小的情况, 贡献其粒子产量的二阶过程包括三种跃迁形式, 分别对应能量为$ \omega_1+ \omega_2={2.4 c^2} $(两个场各自贡献一个光子), $ 2\omega_1={2.2 c^2} $以及$ 2\omega_2={2.6 c^2} $(各个场单独的二阶多光子效应), 在图4(b1)中体现为, 左下角$ 2.4 c^2 $处的亮条纹以及两侧两条弱条纹, 随着场间距逐渐增大, 由两场同时提供一个光子的二阶效应($ \omega_1+\omega_2 $)削弱, 条纹逐渐变暗直至消失, 由两个振荡场各自独立振荡所对应的条纹反而变得显著, 对应能量为$ 1.1 c^2+ 1.1 c^2 $以及$ {1.3 c^2+1.3 c^2} $. 说明两场耦合的二阶跃迁进一步减小到消失, 而两场各自独立的二阶效应增强.

      为了量化分析粒子跃迁能量概率的变化, 本文提取了图4中各级跃迁对应的粒子数, 并做归一化处理(除以最大值). 如图5所示, 横轴代表场间距$ {D} $, 纵轴代表各阶跃迁所产生的归一化粒子数, 图5(b)还给出了场自身的二阶跃迁($ {2\omega_1} $与$ {2\omega_2} $), 分别用紫色、绿色短点线表示. 利用该图可以分析组合场各阶跃迁随着间距变化的趋势. 图5(a)对应差频较大情形, 可以直观地看出: 随着$ {D} $的增加, 高阶跃迁的概率下降速度大于二阶效应的下降速度. 这是由于高阶非线性效应需要更高的场强才能发生, 当$ {D} $增大时, 交叠区域的场强减小, 使得高阶效应的发生变得更加困难. 因此正负电子对能谱中高能端电子的比例显著减少, 能量分布逐渐地集中在低能端. 对于频率差较小的情况(图5(b)), 随着$ {D} $值增加, 三阶跃迁概率的下降速度同样显著快于二阶效应. 因而, 能量分布仍主要聚焦于$ {1.0 c^2} $至$ {1.5 c^2} $区间. 此外还发现, 二阶效应中的三种跃迁类型——$ \omega_1+\omega_2 $, $ 2\omega_1 $以及$ 2\omega_2 $的比重随间距发生变化. 由两场共同引起的二阶效应$ \omega_1+\omega_2 $随间距增大显著降低, 而各场独立产生的二阶效应则相对增强, 整体上使得场自身的二阶占比增大. 这一变化最终导致了$ {1.0 c^2} $—$ {1.5 c^2} $能量区间内能谱分布的微调.

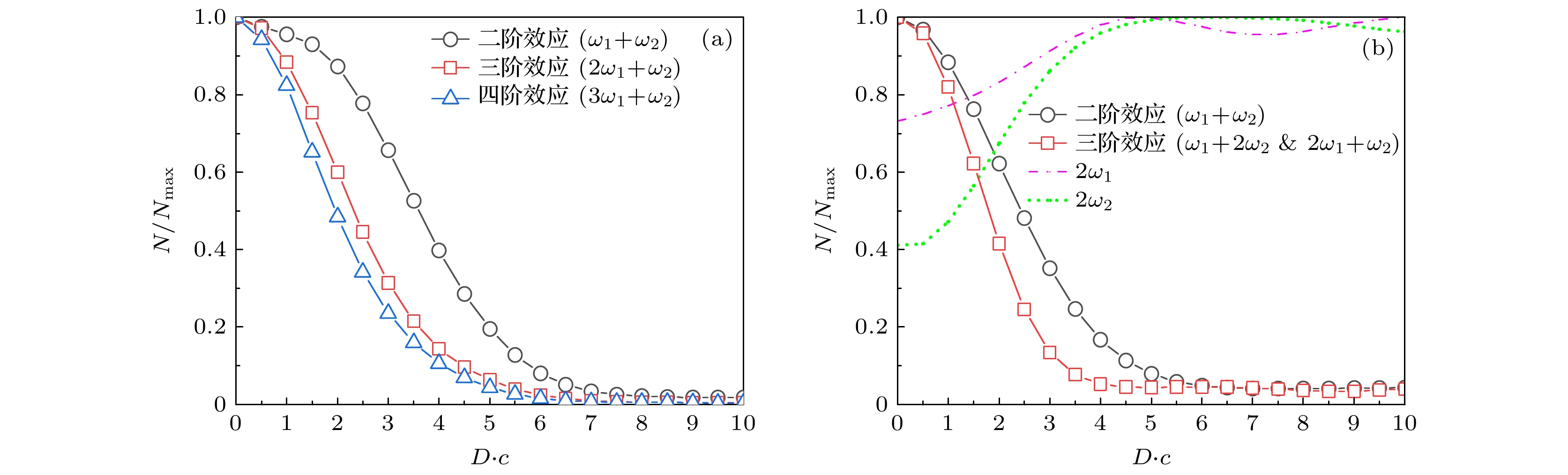
      考虑比较不同频率组合下, 由两场共同激发的跃迁效应(如$ \omega_1+\omega_2 $或$ 2\omega_1+\omega_2 $等)以及外场存在下其中单个场激发(如$ 2\omega_1 $或者$ 2\omega_2 $)的跃迁效应随着间距的变化, 计算了两场共同激发的二阶效应$ \omega_1+\omega_2 $及粒子数占比较大的三阶效应$ 2\omega_1+\omega_2 $所对应的粒子数随间距变化趋势, 并进行归一化, 结果在图6(a)中给出. 图6(b)给出仅由场自身激发的二阶效应所对应的归一化粒子数变化. 在图6(c)中, 将由两场共同激发和由自身场激发的主要跃迁形式的贡献相加, 然后进行归一化处理, 比较其随间距的变化趋势.

      从图6(a)可以看出, 对于不同频率的组合, 由两场共同作用的双光子跃迁过程($ \omega_1+\omega_2 $)中, 频率差减小, 两场共同作用的产生粒子数随间距的下降趋势加快. 两场共同作用的三阶效应($ 2\omega_1+ \omega_2 $)也体现出同样的规律. 对于图6(b)中描述的两场环境中, 由单个场独立激发的二阶效应随场间距的增大发生变化. 在间距从0逐渐增大到约$ {{3/c}} $期间, 基本呈上升趋势, 后随着间距继续增大到场完全分开后逐渐趋于稳定. 正是在图6(a)所示的 由两场共同作用的多光子跃迁贡献, 以及图6(b)所示由单个场多光子跃迁贡献的共同作用下, 使得图2(b)中不同频率组合的K-D曲线体现出一定的复杂性. 从图6(c)可以看出, 将各频率组合的主导阶跃迁粒子数相加之后, 趋势与图2(b)中K-D曲线基本一致. 上述结果同时也表明: 当两场间距较小时, 频率差较大的频率组合对于正负电子对产生来说具有优势. 而随着间距的增大, 频率差较小的频率组合具有更大的稳定性. 这是由于随着两场逐渐分开, 单个场内部的多光子效应开始发挥主要作用.

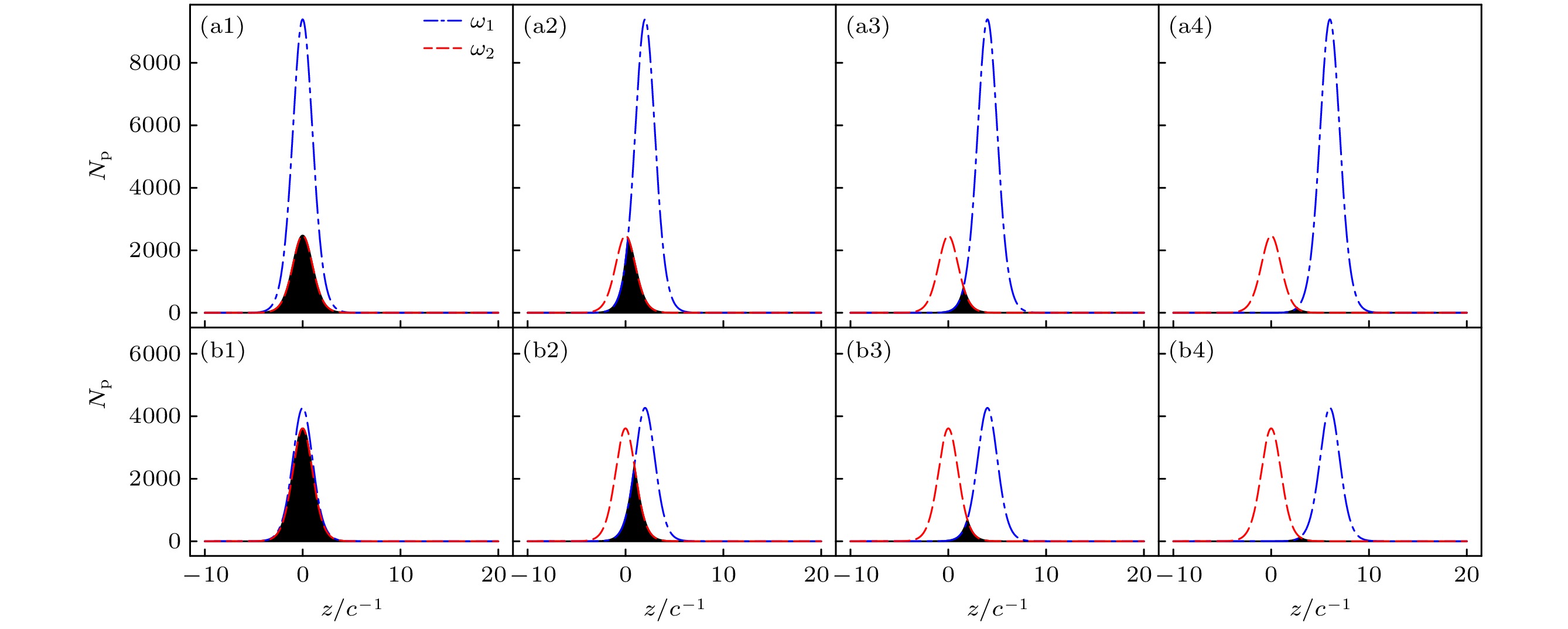
      下面对图6(a)中展现的现象, 即在多光子跃迁过程中, 由两场共同作用所贡献的电子数产率对于频率差越小的组合随D下降得越快的原因进行分析. 根据量子化的概念, 电磁场的能量可以表示为光子数乘以每个光子的能量($ {E}={N_{\mathrm{p}}}{\hbar} \omega $). 当场强$ {F} $保持不变时, 单位时间内频率为 ω 的振荡场所贡献的光子数$ {N_{\mathrm{p}}} $满足$ {N_{\mathrm{p}}}\propto{F}^2/\omega $. 这反映了在给定场强下, 光子频率越高, 对应光子数越少. 对于由两个频率$ \omega_1 $和$ \omega_2 $构成的双振荡场, 每个单独场对应的光子数可记为$ {N_{{\mathrm{p}}_1}} \propto {F}^2/\omega_1 $和$ {N_{{\mathrm{p}}_2}} \propto {F}^2/\omega_2 $. 图7展示了在两种频率组合下, 随着D的增大, 两场交叠的光子数减少的情况(交叠区域用黑色部分表示).

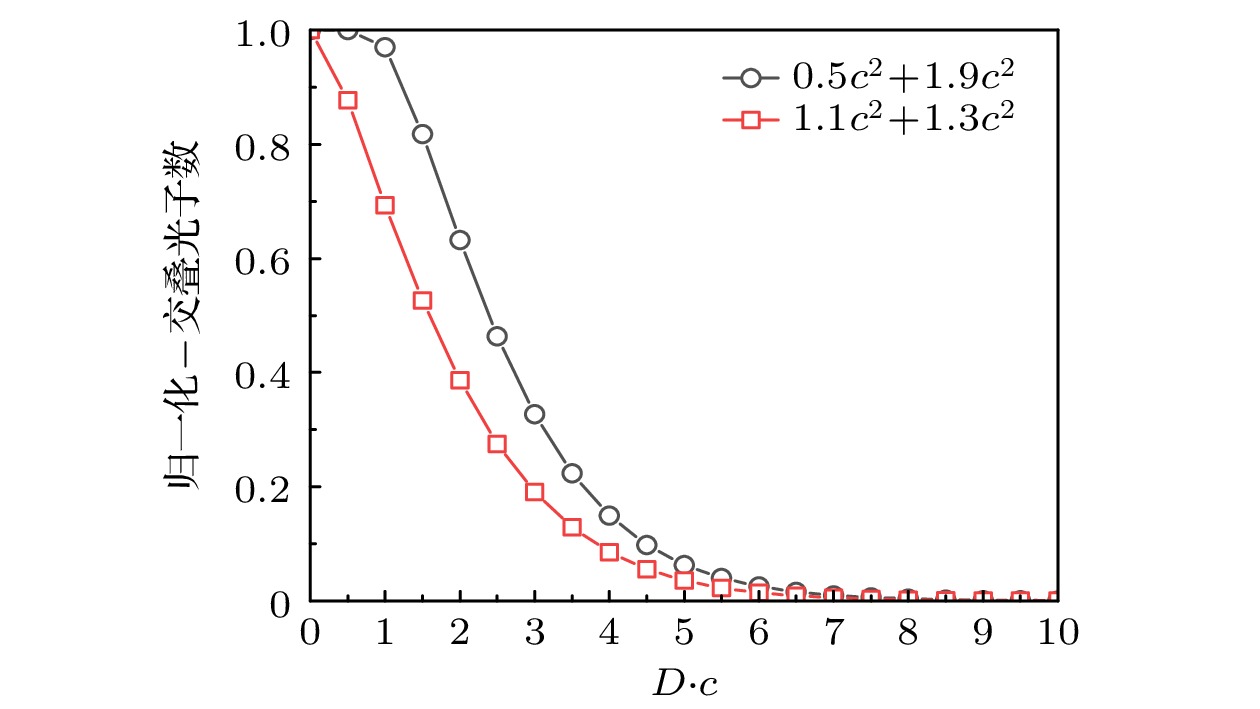
      各种间距下两种频率组合在交叠区域内的光子数计算结果如图8所示, 展示了频率组合$ 0.5{c}^2 + 1.9{c}^2 $与$ 1.1{c}^2 + 1.3{c}^2 $对应的归一化交叠光子数随间距的变化趋势. 从图中可以看出, 差频较大的$ 0.5{c}^2 + 1.9{c}^2 $所对应的交叠光子数下降趋势较缓, 而差频较小的$ 1.1{c}^2 + 1.3{c}^2 $所对应的交叠光子数下降趋势较快. 这是由于在相同的场强下, $ 0.5 c^2 $对应的光子数显著大于$ 1.9 c^2 $对应的光子数. 即使在两场分开一定间距的情况下, $ 0.5 c^2 $对应的场仍为$ 1.9 c^2 $的光场提供了相当数量的光子数, 用于实现两场共同作用下的多光子跃迁过程. 因此频率差越大, 两场共同作用贡献的粒子数随间距变化越缓慢, 图6(a)体现出的规律也得到了很好的解释, 交叠光子数与两场共同作用的各阶多光子效应整体呈正相关.

    4.   结　论

    • 本研究通过计算量子场论(CQFT)方法, 探讨了在双振荡场模型中, 空间局域化对正负电子对产生率的影响. 研究发现, 在两个次临界振荡场空间交叠的情况下, 交叠方向的分离间距在一定范围内依然可以有效促进真空中电子-正电子对的产生. 当两场在交叠方向上的间距变化时, 对电子对产生率的影响呈现出显著的差异. 此外, 电子能谱在间距变化时也发生了变化, 且不同频率组合模型对应的能谱随间距变化不同. 之后结合粒子跃迁能量概率分布进行了进一步的分析, 从多光子跃迁的角度解释了能谱结构的变化, 同时截取了各主要阶次的多光子跃迁效应对应的粒子数, 并展示其随着间距变化的趋势, 发现对于同一频率组合, 其二阶与三阶效应随着间距变化的趋势不同, 高阶的下降速度更快. 此外, 通过分析组合场多光子跃迁概率随间距的变化, 以及自身场的多光子跃迁概率随间距的变化, 得到以下结论: 当两场间距较小时, 频率差较大的组合场在正负电子对产生上具有优势; 而当间距较大时, 频率差较小的振荡场组合由于自身的多光子效应开始发挥主要作用, 从而体现出更好的稳定性. 对于由两场共同作用下的不同情况, 分别对同一频率组合下不同阶次之间的差异, 以及相同阶次跃迁之间在不同频率组合下的差异, 进行了更为深入的分析. 通过提出假设并计算验证, 发现相同条件下的归一化-交叠光子数变化趋势与所对应的产生粒子数变化趋势基本一致, 为考察产生粒子数随间距变化的趋势提供了一种更为便捷的方式.

    参考文献 (26)

目录

/

返回文章
返回