高级搜索

大密度比气泡在多孔介质通道内上升行为的三维介观数值模拟

,  , 

downloadPDF

上一篇

下一篇

赵兹卿, 严裕, 娄钦. 大密度比气泡在多孔介质通道内上升行为的三维介观数值模拟[J]. 物理学报, 2025, 74(5): 054701-1. doi: 10.7498/aps.74.20241678
引用本文: 赵兹卿, 严裕, 娄钦. 大密度比气泡在多孔介质通道内上升行为的三维介观数值模拟[J]. 物理学报, 2025, 74(5): 054701-1. doi: 10.7498/aps.74.20241678
shu
Ziqing ZHAO, Yu YAN, Qin LOU. Three-dimensional mesoscopic numerical simulation of the rising behavior of bubbles with large density ratio in porous media channels[J]. Acta Physica Sinica, 2025, 74(5): 054701-1. doi: 10.7498/aps.74.20241678
Citation: Ziqing ZHAO, Yu YAN, Qin LOU. Three-dimensional mesoscopic numerical simulation of the rising behavior of bubbles with large density ratio in porous media channels[J]. Acta Physica Sinica, 2025, 74(5): 054701-1. doi: 10.7498/aps.74.20241678
shu

大密度比气泡在多孔介质通道内上升行为的三维介观数值模拟

  • 上海理工大学能源与动力工程学院, 上海　200093

    • 作者简介: 赵兹卿.E-mail: zazaqing@126.com .
    通讯作者: E-mail: qlou@usst.edu.cn.

  • 中图分类号: 47.56.+r, 47.85.Dh, 47.55.D-

Three-dimensional mesoscopic numerical simulation of the rising behavior of bubbles with large density ratio in porous media channels

  • School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China

    • Corresponding author: E-mail: qlou@usst.edu.cn.

  • MSC: 47.56.+r, 47.85.Dh, 47.55.D-

  • 摘要: 本文基于格子Boltzmann方法, 使用三维数值模拟研究了复杂多孔介质中大密度比气泡运动行为, 重点探讨Eötvös数 (Eo)、接触角 (θ) 和Reynolds数(Re)耦合作用对气泡速度、形态演化及停滞现象的影响规律. 研究发现, 在多孔介质中, 接触角增大降低了气泡速度, 并加剧速度波动, 使气泡趋于扁平化. Eo的增大则可显著抑制扁平化趋势, 稳定气泡速度, 使其形态更接近子弹头状. 当接触角较大且Eo较小时, 黏附力增强会导致气泡停滞于多孔介质内部. 此外, Re与接触角在阻力构成中呈竞争关系, 对气泡的平均速度具有相互增强的作用, 而在较大接触角下, Re增大会导致气泡尾部不稳定并易断裂. 研究还表明, 低Eo和低Re条件下气泡速度随Eo增大而下降, 而在高Eo和高Re条件下则呈相反趋势, 这一现象源于气泡形态的不稳定性对浮力和速度的影响.
    Abstract: In this paper, a three-dimensional numerical simulation of the motion behavior of bubbles in complex porous medium channels in a large density ratio gas-liquid system is conducted based on the lattice Boltzmann method. The Eötvös number (Eo), contact angle (θ) and Reynolds number (Re) are systematically discussed with emphasis on the law of their coupling effect affecting bubble velocity, morphological evolution and stagnation phenomenon. The results show that the increase of contact angle will reduce the bubble velocity but intensify the velocity fluctuations, making the bubbles tend flat, while the increase of Eo number significantly suppresses the influence of the contact angle, stabilizes the bubble velocity, and makes its shape close to a bullet head shape. When the contact angle is large (θ > 90°) and the Eo number is small (Eo < 10), the adhesion force is significantly enhanced and the bubbles will stagnate inside the porous medium. Re number and contact angle compete in the generation of resistance, and have mutually reinforcing effects on the average velocity of bubbles and interface evolution. The larger contact angle makes the deformation of the bubble tail intensify and becomes unstable, and as the Re number further increases, the tail tentacles are more likely to break, forming residual bubbles. It is also found in this work that the coupling between Eo number and Re number significantly affects bubble behavior in motion and morphological evolution. Under the conditions of high Eo number (Eo ≥ 25) and high Re number (Re ≥14), the bubble velocity increases with the Eo number rising, and the trend becomes more significant as the Re number increases; while under the conditions of low Eo number (Eo < 25) and low Re number (Re < 14), the speed change pattern is completely opposite. This phenomenon is due to the high instability of bubble morphology under the conditions of high Eo number and high Re number, which affects the buoyancy and speed performance. The research results provide important guidance for optimizing the flow behavior of bubbles in porous medium.
  • 加载中

  • 图 1  三维物理模型　(a) 示意图; (b) y方向正视图

    Figure 1.  3D physical model (a) Schematic diagram; (b) front view in the y direction.

    下载: 全尺寸图片 幻灯片

    图 2  不同网格下气泡在y = Ly/2和z = h3切面上轮廓变化　(a) t* = 2.19时刻气泡在y = Ly/2切面的轮廓; (b) t* = 3.69时刻气泡在z = h3切面的轮廓

    Figure 2.  The contour changes of the bubble on the y = Ly/2 and z = h3 sections under different grids: (a) The contour of the bubble on the y = Ly/2 section at t* = 2.19; (b) the contour of the bubble on the z = h3 section at t* = 3.57.

    下载: 全尺寸图片 幻灯片

    图 3  不同Eo与接触角组合下的气泡形态变化

    Figure 3.  Changes in bubble morphology under different combinations of Eo numbers and contact angles.

    下载: 全尺寸图片 幻灯片

    图 4  不同工况下未通过多孔介质的气泡形态

    Figure 4.  The morphology of bubbles that do not pass through porous media under different working conditions.

    下载: 全尺寸图片 幻灯片

    图 5  气泡平均速度${v_{{\text{ave}}}}$在(a)不同Eo与(b)接触角θ工况下的变化趋势

    Figure 5.  Variation trend of average bubble velocity under (a) different Eo numbers and (b) contact angle θ conditions.

    下载: 全尺寸图片 幻灯片

    图 6  瞬时速度v* 在不同Eo下随θ的变化　(a) Eo = 10; (b) Eo = 100

    Figure 6.  Variation of instantaneous velocity v* with θ at different Eo numbers: (a) Eo = 10; (b) Eo = 100.

    下载: 全尺寸图片 幻灯片

    图 7  气泡在 (a)绿色圆点、(b) 蓝色方块、(c) 红色三角处的位置与形态

    Figure 7.  The position and shape of bubbles at (a) green dots, (b) blue squares, and (c) red triangles.

    下载: 全尺寸图片 幻灯片

    图 8  气泡在(a)不同Re与(b)不同θ工况下vave的变化趋势

    Figure 8.  Variation trend of bubble vave under (a) different Re and (b) different θ conditions.

    下载: 全尺寸图片 幻灯片

    图 9  不同Re与接触角耦合作用下气泡的形态变化

    Figure 9.  Changes in bubble morphology under the coupling effect of different Re and contact angle.

    下载: 全尺寸图片 幻灯片

    图 10  气泡在(a)不同Eo和(b)不同Re组合下vave的变化情况

    Figure 10.  Changes in the bubble vave under (a) different Eo numbers and (b) different Re number combinations.

    下载: 全尺寸图片 幻灯片

    图 11  不同Re与Eo耦合作用下气泡的形态变化

    Figure 11.  Changes in bubble morphology under the coupling of different Re and Eo numbers.

    下载: 全尺寸图片 幻灯片
  • [1] Lichtschlag A, Haeckel M, Olierook D, Peel K, Flohr A, Pearce C R, Marieni C, James R H, Connelly D P 2021 Int. J. Greenh. Gas Control 109 103352 doi: 10.1016/j.ijggc.2021.103352
    [2] 张沐安, 王进卿, 吴睿, 冯致, 詹明秀, 徐旭, 池作和 2023 物理学报 72 164701 doi: 10.7498/aps.72.20230695 Zhang M A, Wang J Q, Wu R, Feng Z, Zhan M X, Xu X, Chi Z H 2023 Acta Phys. Sin. 72 164701 doi: 10.7498/aps.72.20230695
    [3] Ajayi T, Gomes J S, Bera A 2019 Petrol. Sci. 16 1028 doi: 10.1007/s12182-019-0340-8
    [4] Liu H B, Xu H, Pan L M, Zhong D H, Liu Y 2019 Int. J. Hydrogen Energy 44 22780 doi: 10.1016/j.ijhydene.2019.07.024
    [5] 王季康, 李华, 彭宇飞, 李晓燕, 张新宇 2022 物理学报 71 158802 doi: 10.7498/aps.71.20212015 Wang J K, Li H, Peng Y F, Li X Y, Zhang X Y 2022 Acta Phys. Sin. 71 158802 doi: 10.7498/aps.71.20212015
    [6] Zhang D, Li Y, Yuan H 2023 Desalination 566 116902 doi: 10.1016/j.desal.2023.116902
    [7] Haris S, Qiu X, Klammler H, Mohamed M M A 2020 Groundw. Sustain. Dev. 11 100463 doi: 10.1016/j.gsd.2020.100463
    [8] Li Y F, Yang G Q, Yu S L, Mo J K, Li K, Xie Z Q, Ding L, Wang W T, Zhang F Y 2021 Electrochim. Acta 370 137751 doi: 10.1016/j.electacta.2021.137751
    [9] Wang C Y, Beckermann C, Fan C 1994 Numer. Heat Transf. Part A: Appl. 26 375 doi: 10.1080/10407789408955999
    [10] Wang H, Lou Q, Liu G, Li L 2022 Int. J. Therm. Sci. 178 107554 doi: 10.1016/j.ijthermalsci.2022.107554
    [11] 张森, 娄钦 2024 物理学报 73 026401 doi: 10.7498/aps.73.20231141 Zhang S, Lou Q 2024 Acta Phys. Sin. 73 026401 doi: 10.7498/aps.73.20231141
    [12] Roosevelt S E, Corapcioglu M Y 1998 Water Resour. Res. 34 1131 doi: 10.1029/98WR00371
    [13] Corapcioglu M Y, Cihan A, Drazenovic M 2004 Water Resour. Res. 40 4
    [14] Ma Y, Kong X Z, Scheuermann A, Galindo-Torres S A, Bringemeier D, Li L 2015 Water Resour. Res. 51 4359 doi: 10.1002/2014WR016019
    [15] Ghasemian S, Ahmadzadegan A, Chatzis I 2019 Transp. Porous Media 129 811 doi: 10.1007/s11242-019-01307-w
    [16] Liu N, Ju B, Yang Y, Brantson E T, Wang J, Tian Y 2019 J. Petrol. Sci. Eng. 180 396 doi: 10.1016/j.petrol.2019.05.057
    [17] Qian Y H, D'Humières D, Lallemand P 1992 Europhys. Lett. 17 479 doi: 10.1209/0295-5075/17/6/001
    [18] 郭照立, 郑楚光 2009 格子Boltzmann方法的原理及应用(北京: 科学出版社) 第42页 Guo Z L, Zheng C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) p42
    [19] Shi J, Ma Q, Chen Z 2019 Microgravity Sci. Technol. 31 207 doi: 10.1007/s12217-019-9681-6
    [20] Sattari E, Zanous S P, Farhadi M, Mohamad A 2020 J. Power Sources 454 227929 doi: 10.1016/j.jpowsour.2020.227929
    [21] Inamuro T, Ogata T, Ogino F 2004 Future Gener. Comput. Syst. 20 959 doi: 10.1016/j.future.2003.12.008
    [22] Yu K, Yong Y M, Yang C 2020 Processes 8 1608 doi: 10.3390/pr8121608
    [23] Fakhari A, Bolster D 2017 J. Comput. Phys. 334 620 doi: 10.1016/j.jcp.2017.01.025
    [24] Alizadeh M, Seyyedi S M, Rahni M T, Ganji D D 2017 J. Mol. Liq. 236 151 doi: 10.1016/j.molliq.2017.04.009
    [25] Chen G Q, Huang X, Zhang A M, Wang S P, Li T 2019 Phys. Fluids 31 097104 doi: 10.1063/1.5115097
    [26] Zhang A, Guo Z P, Wang Q G, Xiong S M 2019 Phys. Fluids 31 063106 doi: 10.1063/1.5096390
    [27] Zhang A, Su D B, Li C M, Zhang Y, Jiang B, Pan F S 2022 Phys. Fluids 34 043312 doi: 10.1063/5.0085217
    [28] Gunstensen A K, Rothman D H, Zaleski S, Zanetti G 1991 Phys. Rev. A 43 4320 doi: 10.1103/PhysRevA.43.4320
    [29] Shan X, Chen H 1993 Phys. Rev. E 47 1815 doi: 10.1103/PhysRevE.47.1815
    [30] Shan X, Chen H 1994 Phys. Rev. E 49 2941 doi: 10.1103/PhysRevE.49.2941
    [31] Swift M R, Osborn W R, Yeomans J M 1995 Phys. Rev. Lett. 75 830 doi: 10.1103/PhysRevLett.75.830
    [32] Swift M R, Orlandini E, Osborn W R, Yeomans J M 1996 Phys. Rev. E 54 5041 doi: 10.1103/PhysRevE.54.5041
    [33] He X, Luo L S 1997 Phys. Rev. E 55 6333 doi: 10.1103/PhysRevE.55.R6333
    [34] He X, Luo L S 1997 Phys. Rev. E 56 6811 doi: 10.1103/PhysRevE.56.6811
    [35] Liang H, Xu J R, Chen J X, Wang H L, Chai Z H, Shi B C 2018 Phys. Rev. E 97 033309 doi: 10.1103/PhysRevE.97.033309
    [36] Chiu P H, Lin Y T 2011 J. Comput. Phys. 230 185 doi: 10.1016/j.jcp.2010.09.021
    [37] Unverdi S O, Tryggvason G 1992 J. Comput. Phys. 100 25 doi: 10.1016/0021-9991(92)90307-K
    [38] Wei Y K, Li Y M, Wang Z D, Yang H, Zhu Z C, Qian Y H, Luo K H 2022 Phys. Rev. E 105 015103 doi: 10.1103/PhysRevE.105.015103
    [39] Jeon D H, Kim S, Kim M, Lee C, Cho H S 2023 J. Power Sources 553 232322 doi: 10.1016/j.jpowsour.2022.232322
    [40] Yi T H, Zhang W Y, Qiu Y N, Lei G, Yu Y Z, Wu J Y, Yang G 2023 Int. J. Multiphase Flow 169 104601 doi: 10.1016/j.ijmultiphaseflow.2023.104601
    [41] 娄钦, 汤升, 王浩原 2021 计算物理 38 289 Lou Q, Tang S, Wang H Y 2021 J. Comput. Phys. 38 289
  • 加载中
图( 11)
计量
  • 文章访问数:  130
  • HTML全文浏览数:  130
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-04
  • 刊出日期:  2025-03-05

大密度比气泡在多孔介质通道内上升行为的三维介观数值模拟

    通讯作者: E-mail: qlou@usst.edu.cn.
    作者简介: 赵兹卿.E-mail: zazaqing@126.com
  • 上海理工大学能源与动力工程学院, 上海　200093
  • 收稿日期:  2024-12-04

摘要: 本文基于格子Boltzmann方法, 使用三维数值模拟研究了复杂多孔介质中大密度比气泡运动行为, 重点探讨Eötvös数 (Eo)、接触角 (θ) 和Reynolds数(Re)耦合作用对气泡速度、形态演化及停滞现象的影响规律. 研究发现, 在多孔介质中, 接触角增大降低了气泡速度, 并加剧速度波动, 使气泡趋于扁平化. Eo的增大则可显著抑制扁平化趋势, 稳定气泡速度, 使其形态更接近子弹头状. 当接触角较大且Eo较小时, 黏附力增强会导致气泡停滞于多孔介质内部. 此外, Re与接触角在阻力构成中呈竞争关系, 对气泡的平均速度具有相互增强的作用, 而在较大接触角下, Re增大会导致气泡尾部不稳定并易断裂. 研究还表明, 低Eo和低Re条件下气泡速度随Eo增大而下降, 而在高Eo和高Re条件下则呈相反趋势, 这一现象源于气泡形态的不稳定性对浮力和速度的影响.

English Abstract

    全文HTML

    1.   引　言

    • 气泡在含多孔介质管道中上升是一种典型的两相流行为, 其存在于大量的工业应用中, 如CO2驱替与封存技术[1–3]、燃料电池开发[4,5]、海水淡化[6]、地下水修复和氢能开发[7,8], 金属泡沫强化沸腾传热[9–11]等, 尤其在CO2注入地下盐水层的过程中, CO2气泡穿过岩心多孔结构的速度与形变断裂行为对封存效率起着关键作用. 然而, 这一问题的研究面临多重挑战. 一方面, 气液间存在复杂的质量交换、动量交换和能量交换, 且界面极易在表面张力的作用下出现变形、断裂和合并等不稳定的现象; 另一方面, 多孔介质表面引发的机械挤压与润湿作用进一步增大了研究难度. 深入分析气泡在多孔介质中的运动规律与界面演化行为, 不仅具有重要的科学价值, 也为上述实际应用的优化提供了理论支持.

      实验研究是探索多孔介质内气泡行为的重要手段. Roosevelt和Corapcioglu [12]使用图像增强的可视化技术, 首次量化了气泡终端速度与时间的关系, 发现气泡在多孔介质内的垂直上升速度与时间呈线性关系. 基于此, Corapcioglu等[13]提出了评估粗糙多孔介质内气泡上升速度的模型, 研究表明, 单个气泡在水饱和多孔介质中经过很短的运动时间和上升距离后达到平衡, 其终端上升速度上限为18.5 cm/s. 随后, Ma等[14]系统研究了二维饱和水多孔介质内气泡的输运特性, 发现空气喷射造成的气泡柱特征宽度和突破时间与气体释放率呈正比关系, 而孔隙水的横截面平均流速也与气体释放率正相关. Ghasemian等[15]采用不同仰角的玻璃微模型研究了气泡在均匀几何水湿多孔介质内的运移, 发现气泡平均速度与气泡长度和模型倾角呈正弦线性关系, 同时气泡介质渗透率随气泡长度的增大而升高. Liu等[16]同样采用了玻璃微珠构成的多孔介质模型来分析气泡的上升行为, 发现气泡平均速度随气泡长度和微珠尺寸的增大先升后稳, 而随着模型倾角和液体黏度的增大, 气泡平均速度则持续上升.

      数值模拟方法由于能够有效模拟实验研究中难以处理的复杂多孔结构, 也成为研究含多孔介质两相流问题的重要手段. 其中, 格子Boltzmann方法[17,18] (lattice Boltzmann method, LBM)作为一种介观数值模拟方法, 凭借其易于处理边界条件, 不需要追踪气液界面以及有良好的并行性能, 得到了广泛应用. 目前, LBM已经实现了对气液界面的精确跟踪和气泡动力学的有效预测. Shi等[19]使用Shan-Chen模型[18]分析了微重力条件下方孔结构中气泡的运动和聚并行为. 研究表明, 平行排列结构能降低气泡逃逸阻力, 而相邻气泡间距和气泡与障碍物间距对气泡聚并时间有显著影响. Sattari等[20]使用Inamuro等[21]提出的多相LBM模型, 研究了交错排列结构中气泡的分裂与聚并, 发现亲气表面增强了气泡的黏附与分裂倾向, 中等Eötvös数 (Eo)条件下气泡传输性能最佳, 而低Eo时易发生气泡堆积阻塞. Yu等[22]采用Fakharie等[23]提出的基于相场的LBM模型, 模拟了高密度比工况下气泡穿过球形和半球形障碍物的行为, 结果表明通道宽度、气泡直径和表面张力对气泡阻力系数有重要影响, 并在此基础上划分出了不同Reynolds数(Re)和Eo条件下的气泡流型. Alizadeh等[24]基于LBM指数函数模型模拟了单个气泡穿过三维圆形截面管的行为, 准确捕获了气液间尖锐界面演化, 并发现改变圆柱管间距和直径会导致气泡形态显著变化. Chen等[25]使用浸润边界LBM模型研究了气泡绕过球形障碍物的动力学特性, 发现气泡在障碍物间受挤压后呈花生形, 而在两障碍物大小不同的情况下, 气泡倾向偏向较小障碍物一侧. 此外, Zhang等[26,27]采用LBM保守相场模型模拟了大密度下障碍物对气泡变形的影响, 并引入两个形状指标用于系统评估障碍物中的气泡形状, 发现气泡形状对流动参数和障碍物的几何布置有很强的依赖性, 而单侧障碍物对气泡形状的影响更为显著.

      综上所述, 多孔介质中气泡上升行为的数值模拟已经取得了许多重要进展, 尤其在结构和排列对气泡形态影响的研究中展现了丰富的规律. 然而, 现有研究在以下方面仍存在不足. 首先, 大多数研究集中于二维模拟, Zhang等[27]提到相较三维模拟的中央纵剖面, 二维模拟可能在预测精度上存在偏差, 难以全面反映复杂孔隙结构中的气液系统动态, 因此复杂孔隙结构中气液系统的三维瞬时模拟是有必要的. 然而, 目前针对多孔介质中气泡行为的三维模拟研究较为有限, 主要集中在研究多孔介质结构和排列的影响, 缺乏对影响参数的系统分析, 气泡形态分析不够全面; 其次, 在研究变量方面, 现有研究多聚焦于单一因素(如Re, Eo或润湿性)对气泡行为的影响, 未能考虑复杂两相流环境下的多因素耦合作用. 气泡在含多孔介质通道中的上升过程中, 浮力、黏性阻力、表面张力和黏附力之间既存在相互对抗, 也存在彼此协同. 因此, 应着重探索相关无量纲数在不同组合条件下对气泡动态行为的影响, 以全面揭示复杂环境下的气泡动力学规律.

      基于上述背景, 本文采用基于相场法的LBM模型, 研究大密度比条件下气泡穿越复杂多孔介质的三维瞬态运动. 重点分析气泡在与均匀分布的球形障碍物接触过程中, 宏观运动特性和界面动力学的变化, 探讨不同Eo, Re和接触角θ的组合对气泡变形、断裂及界面演化规律的共同影响, 并揭示气泡穿越速度的动态变化.

    2.   数值方法

    • 目前, 基于对不同相互作用力的处理方式, 提出了多种两相LBM模型, 如颜色梯度模型[28]、伪势模型[29,30]、自由能模型[31,32]和基于相场的LBM模型[33,34]. 其中, Liang等[35]提出的基于相场的LBM模型在处理大密度问题时稳定性较好, 两相间界面的过渡平滑. 因此, 本文将采用该模型对大密度比下气泡在含多孔介质通道内的运动行为进行模拟. 这一模型含界面演化函数和流场演化函数两个分布函数, 分别用于求解Allen-Cahn方程[36]和Navier-Stokes方程[37]. 其中, 界面演化函数形式如下:

      流场演化函数形式则为

      其中, i为离散速度的方向个数, x和t分别表示粒子的空间位置和演化时间, ${\tau _{\text{f}}}$和${\tau _{\text{g}}}$各代表两个演化函数的无量纲松弛时间, ${\delta _{\text{t}}}$代表时间步长, ${F_i}({\boldsymbol{x}}, t)$为源项的分布函数, $ {G_i}({\boldsymbol{x}}, t) $为外力项的分布函数, $f_i^{{\text{eq}}}({\boldsymbol{x}}, t)$和$g_i^{{\text{eq}}}({\boldsymbol{x}}, t)$是两个函数各自的平衡态分布函数. 界面演化函数的无量纲时间${\tau _{\text{f}}}$与迁移率M相关, 关系式为

      流场演化函数的无量纲时间${\tau _{\text{g}}}$同运动黏度相关, 关系式为

      平衡态分布函数$f_i^{{\text{eq}}}({\boldsymbol{x}}, t)$和$g_i^{{\text{eq}}}({\boldsymbol{x}}, t)$的表达式为

      其中, $\rho $为密度, p为压力, u为流体运动速度, ${c_{\text{s}}}$为格子声速, ${c_{\text{s}}} = c/\sqrt 3 $, ${c_i}$为离散速度, ${\omega _i}$为对应的权重系数. ${c_i}$和${\omega _i}$在不同的格子模型中有所不同, 本文采用三维D3 Q19模型[38], 对应的权重${\omega _i}$为

      相应的离散速度${c_i}$为

      式中$c = {\delta _x}/{\delta _{\text{t}}}$为格子速度, ${\delta _x}$表示格子步长, 这里取${\delta _x} = {\delta _t} = 1$. 源项${F_i}({\boldsymbol{x}}, t)$和外力项$ {G_i}({\boldsymbol{x}}, t) $表达式分别为

      式中, ${\rho _{\text{l}}}$和${\rho _{\text{g}}}$表示液相和气相密度, ${\boldsymbol{n}} = \nabla \phi /|\nabla \phi |$表示界面法向运动方向, $\lambda = 4\phi (1 - \phi )/W$, W为界面厚度, 取4个格子单位. Fs和G分别表示表面张力项和重力项. 表面张力项Fs表达式为

      其中${\mu _\phi }$为化学势, 定义为

      $\kappa $和$\beta $为与界面厚度W和表面张力系数$\sigma $相关的物理参数, 关系式如下:

      重力项$G = \rho g$, 其中g为重力加速度.

      根据Chapman-Enskog展开统计分布函数, 可计算得到流场的宏观量如下:

      式中, 物理量$\phi $为序参数, 用于描述两相及两相界面位置, 气相时$\phi = 0$, 液相时$\phi = 1$, $\phi $ = 0.5为气液两相界面. 关于该模型更详细的信息可参考Liang等[35]的工作.

    3.   物理模型

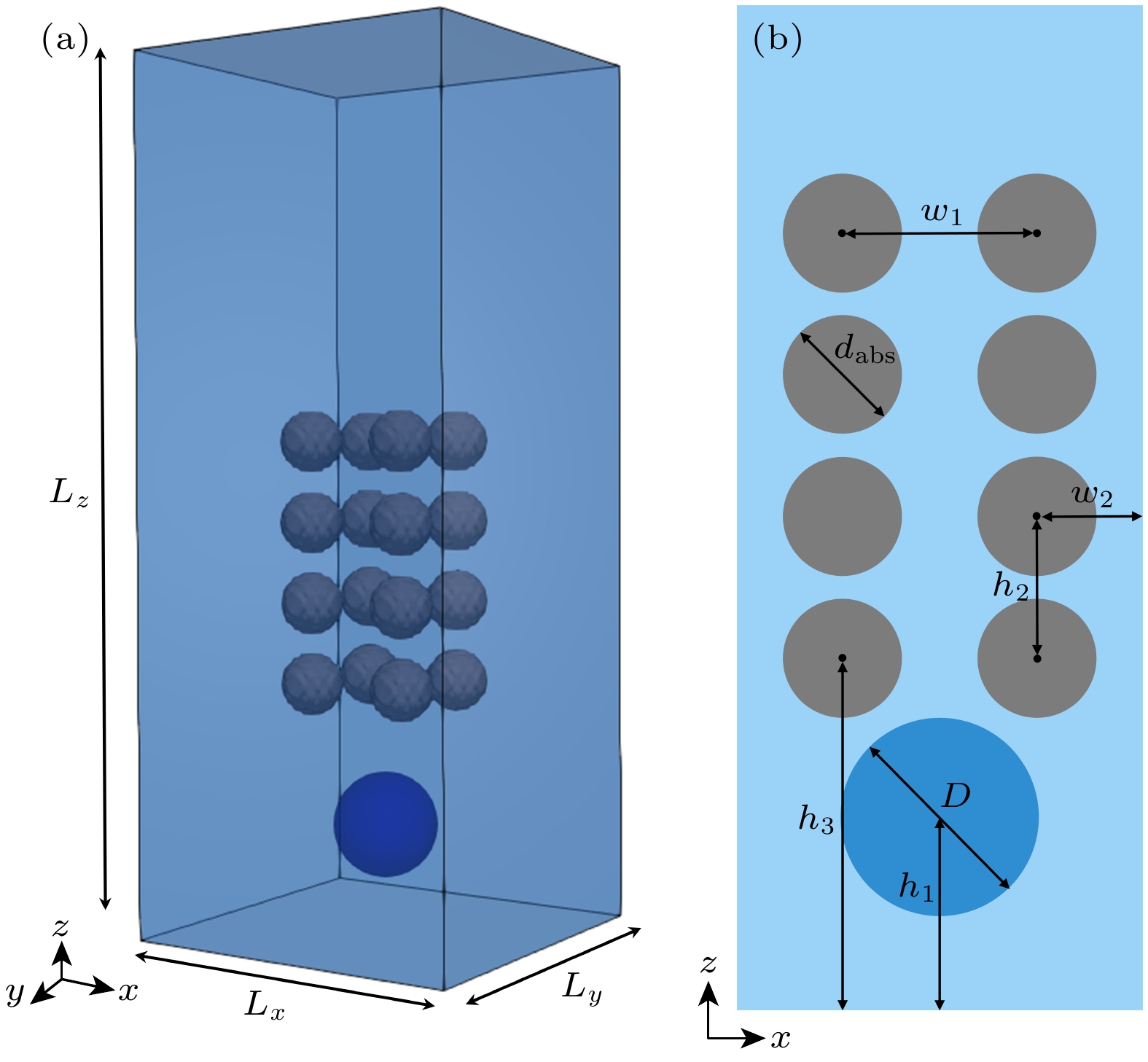
    • 本文所研究物理模型如图1所示, 在大小为Lx×Ly×Lz的计算域下方水平面中心(50, 50)处放置有一个直径为D的圆形气泡, 气泡圆心距底部边界间距为h1. 在气泡上方存在由多个圆球障碍物组成的多孔介质区域, 层与层间障碍物圆心间距均为h2, 最底层障碍物圆心距底部边界间距为h3, 每层铺有4个彼此中心对称的障碍物, 同层相邻障碍物的圆心间距为w1, 障碍物圆心与最近两个垂直边界间距w2, 球形障碍物直径设置为dabs, 区域孔隙率为$\varepsilon $. 计算域除障碍物与气泡外的其余空间均充满液体.

      在数值模拟中, 计算域设置为Lx×Ly×Lz = 100×100×250, 气泡直径D为30个格子单位, 气泡中心距底部边界间距h1 = 30. 由四层圆球形障碍物组成的多孔介质放置于61 < Lz < 150区域, 层间圆心间距h2 = 20, 底层气泡圆心距下边界间距h3 = 20, 同层相邻障碍物圆心间距w1 = 30, 底层障碍物圆心距下边界的最小间距w2 = 25, 障碍物直径dabs = 10, 孔隙率$\varepsilon $ = 0.928. 气液系统参数设置为气相密度$ {\rho _{\text{g}}} = 1 $, 运动黏度${\nu _{\text{g}}} = 1$, 液相密度${\rho _{\text{l}}} = 1000$, 运动黏度${\nu _{\text{l}}} = 0.1$, 界面厚度取W = 4, 重力加速度g给定为4.0×10–5. 计算域前后左右均采用无滑移边界条件, 上下采用周期边界条件, 多孔介质表面采用无滑移润湿边界条件.

      本文在分析气泡运动过程中的参数主要包括接触角θ, Eo以及Re, 其中无量纲数Eo表征浮力与表面张力相对大小, 表达式为

      其中$\sigma $表示气液两相间的表面张力系数, D为特征长度, 这里选择气泡的直径. Re为表征黏性阻力和浮力相对大小的无量纲数, 表达式为

      数值模拟中不同Eo和Re可分别通过调节表面张力系数和流体的运动黏度而得到.

      为了便于计算结果的对比和分析, 下文中变量均采用无量纲形式, 其中, 无量纲时间${t^*}$和无量纲速度${v^*}$转化公式如下:

      式中t为时间步数, v为宏观速度.

    4.   网格无关性验证

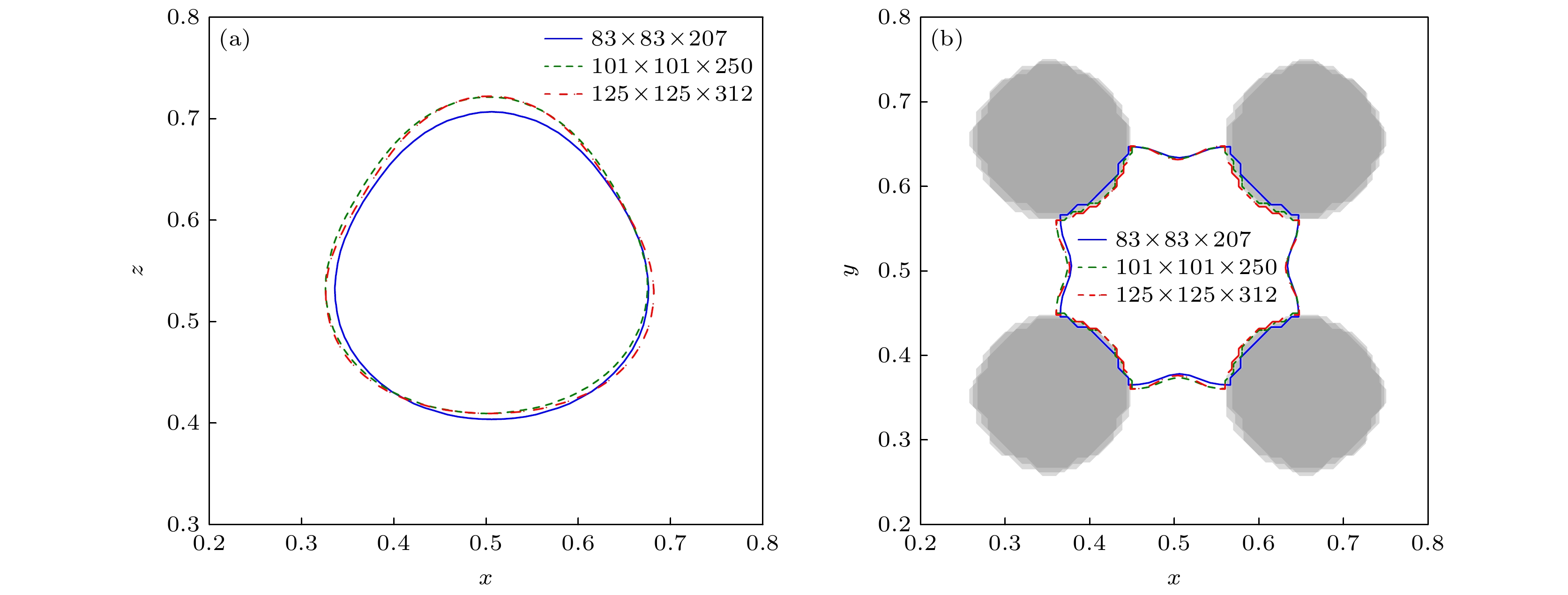
    • 为保证在最小的计算资源下得到最合理的结果, 首先对模型进行网格无关性验证, 这里针对图1描述的物理问题选取了83×83×207, 101×101×250, 125×125×312三种不同尺寸的网格测试网格大小对模拟结果的影响. 为了保证网格无关性验证结果的通用性, 我们选取了较大的Re数(Re = 100)进行数值研究.

      图2展示了气泡在不同网格下y = Ly/2和z = h3切面上的形状, 分别对应气泡顶端接触多孔介质(t* = 2.19)和气泡穿过多孔介质(t* = 3.69)这两个典型时刻. 如图所示, 101×101×250和125×125×312网格下的气泡形状几乎完全一致, 而83×83×207网格下的气泡轮廓与前两者存在明显偏差. 以125×125×312网格下的结果为基准, 计算得83×83×207和101×101×250网格下气泡表面积的平均相对误差为2.8%和0.9%. 其中, 101×101×250的误差是可以接受的. 因此, 考虑到数值精度和计算成本, 本文采用了101×101×250尺寸的网格进行模拟.

    5.   计算结果与分析

      5.1.   Eo与接触角θ耦合对气泡运动的影响

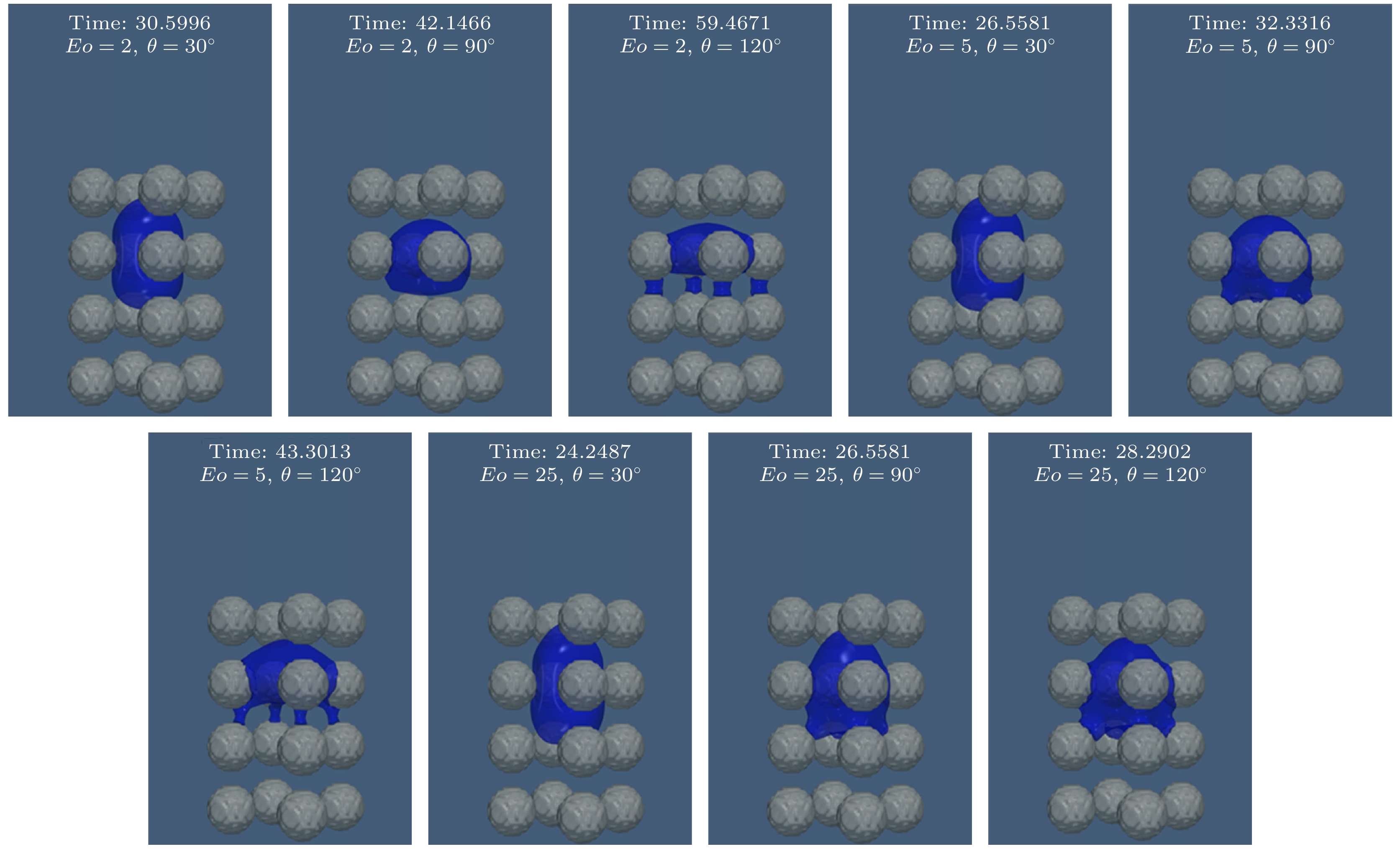
    • Eo和接触角θ是影响气泡在含多孔介质内运动行为的两个关键因素. 文献[20]分别研究了Eo和θ对气泡运动路径和上升速度的影响, 然而Eo和θ耦合作用对气泡运动过程的影响规律尚不清晰. 本节选取不同Eo (Eo = 2, 5, 10, 25, 50, 100)与不同接触角$\theta $($\theta $ = 30°, 60°, 90°, 120°, 150°), 研究两者共同作用下气泡穿过多孔介质的上升运动行为以及受力情况. 对于本节研究的所有工况, Re给定为3.5, 其余参数与第3节相同.

      图3所示为不同Eo和接触角θ条件下气泡在多孔介质内的运动过程. 如图3所示, 在低润湿性条件(θ = 30°)下, 气泡始终保持细长状态, 对Eo依赖性较小. 当接触角增大至中润湿性(θ = 90°)时, 不同Eo下气泡形状较低润湿性发生显著变化. 对于Eo = 2, 气泡不再表现为细长状, 而是收缩为球状, 随着Eo增大, 气泡尾部受到障碍物黏附而逐渐拉长, 至Eo = 25时最终演化为子弹头状. 值得注意的是, 此形态虽与低润湿性条件下的细长状气泡相似, 但成因不同: 低润湿性下, 气泡受多孔介质通道的机械挤压而形成细长状; 而中润湿性下, 气泡与多孔介质的接触面积增大, 黏附力显著增大, 导致气泡在重力和黏附力的共同作用下演化为子弹头状. 当接触角进一步增大至高润湿条件(θ = 120°)时, 不同Eo下气泡形态差异更为显著. 如在低Eo (Eo = 2)条件下, 气泡完全扁平并伴随气泡断裂现象, 部分断裂气泡填充进多孔介质的孔隙中, 表现为鞍状. 鞍状气泡在孔隙内受到固体表面黏附力和表面张力共同作用, 难以依靠自身浮力脱离, 这种现象与不考虑润湿性时断裂气泡散落于流体中的行为显著不同[22], 表明接触角增大引发的黏附力在填充行为中发挥了关键作用. 随着Eo增大至Eo = 5时, 气泡扁平化趋势减弱, 顶端逐渐呈现球形, 此时, 鞍状断裂气泡缩小, 填充现象显著减弱. 当Eo进一步增大至Eo = 25, 气泡受尾部的拉伸作用形成不规则的子弹头状, 同时断裂气泡填充现象消失. 这表明表面张力同样在断裂气泡填充孔隙的过程中发挥了关键作用, 只有当表面张力和黏附力共同作用时, 才会出现断裂气泡填充进多孔介质的现象. 综上所述, 接触角的增大显著强化了气泡的扁平化趋势, 而Eo的增大则有效抑制了这一趋势, 尤其在高接触角条件下, Eo对气泡扁平化的抑制作用更加显著. 此外, 在高接触角与低Eo的组合工况下, 表面张力和黏附力较大, 气泡更容易发生断裂并填充多孔介质孔隙中. 这些发现为深入理解气泡在多孔介质中的界面演化规律提供了依据, 并对优化气泡流动行为的控制策略具有重要参考价值.

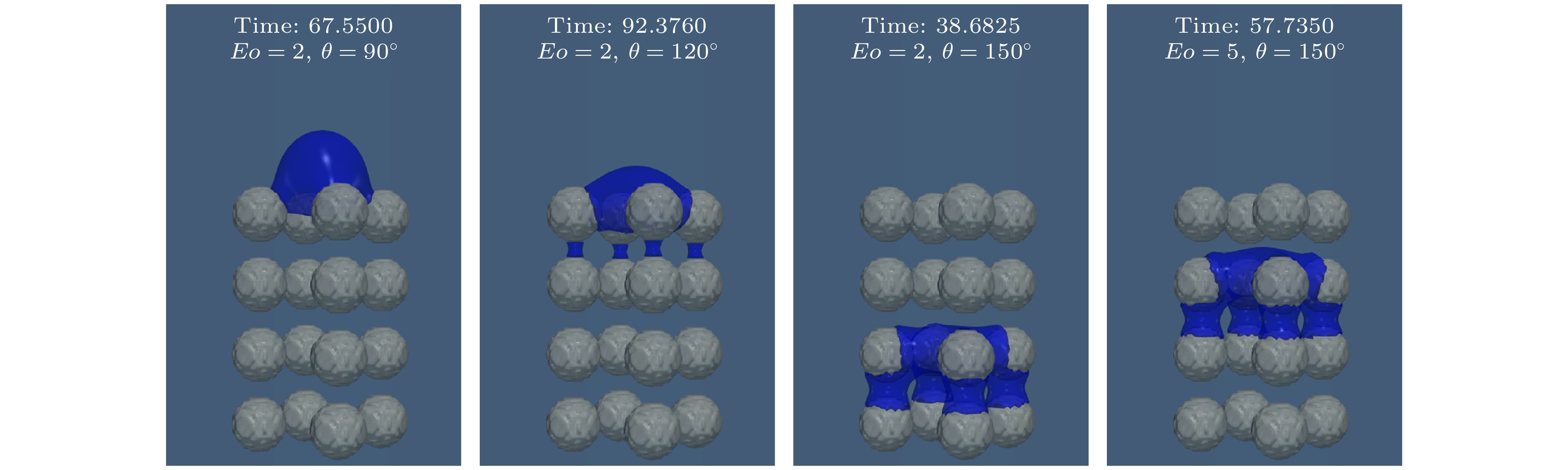
      接触角和Eo不仅影响气泡在多孔介质内的界面演化, 还对气泡能否穿过多孔介质通道起到了关键作用. 在低Eo与高接触角的条件下, 气泡往往无法通过多孔介质, 而是停滞在多孔介质中. 图4展示了这些气泡的停滞位置和最终形态. 与文献[19,20,39]观察到的气泡堵塞现象不同, 本文发现气泡并未在多孔介质入口处发生堵塞, 而是在穿越多孔介质的过程中因黏附力作用而停滞于障 碍物表面. 这一差异主要源于力学机制的不同. 过去的气泡堵塞现象通常由于多孔结构施加给气 泡的接触压力和表面张力过大, 导致气泡被拦截 在多孔介质之外, 尤其是在Eo较小或多孔介质孔隙度较高时. 相比之下, 本文观察到的气泡停滞现象则主要依赖接触角带来的黏附力, 因而气泡可以进入多孔介质, 但会在穿越过程中因黏附力阻碍, 最终动能耗尽而停滞. 随着接触角的增大, 黏滞 力也不断加强, 停滞位置逐渐远离出口. 例如, 在Eo = 2, θ = 90°时, 气泡头部已经穿过了多孔介质, 但由于总阻力与气泡浮力处于临界平衡状态, 同时气泡动能耗尽, 最终黏附在多孔介质的最外层. 而当接触角增大至θ = 120°时, 更强的黏附力导致气泡在第2层就已停滞. 这是由于接触角增 大显著增强了指向壁面的黏附力, 从而加速了气泡速度的衰减[40], 使其更易停滞. 此外, Eo的增大显著降低了气泡停滞的可能性. 如当Eo从Eo = 2增至Eo = 5时, 气泡基本均能够顺利穿过多孔介质, 仅在超疏水条件(θ = 150°)下出现停滞. 这是因为随着Eo增大, 浮力主导作用增强, 气泡更易克服多孔介质内的黏附力影响. 综上, 可以发现接触角增大显著强化了气泡黏附停滞的趋势, 而Eo增大则通过增强浮力削弱了接触角的负面作用. 因此, 在实际应用中, 适当减小接触角或增大Eo可有效降低气泡堵塞现象的发生, 提高气泡的流动效率.

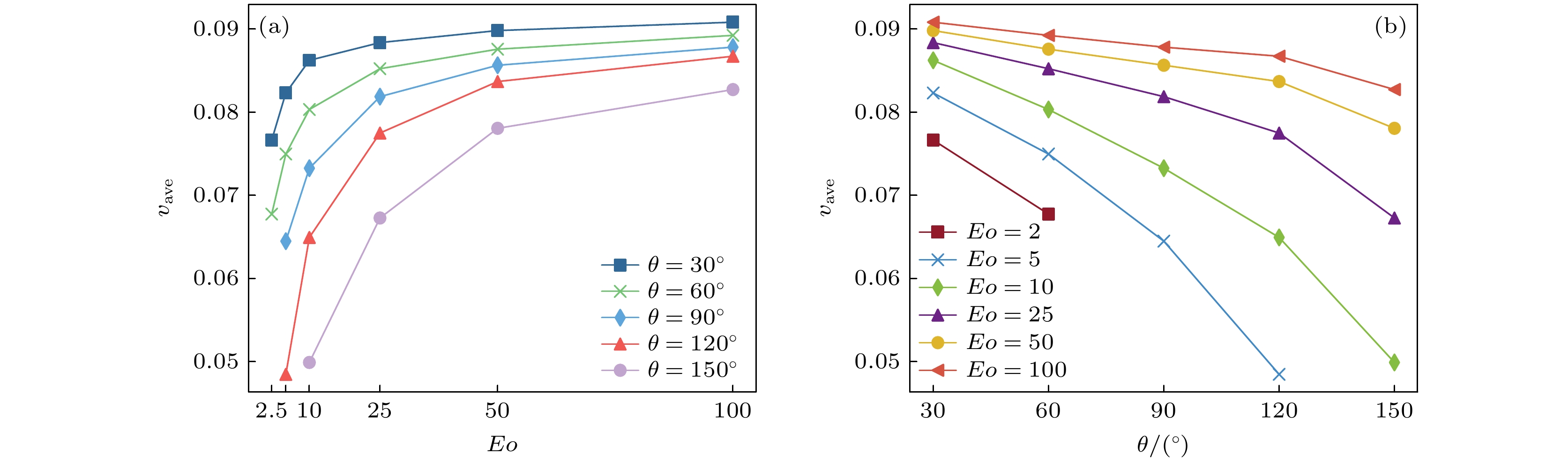
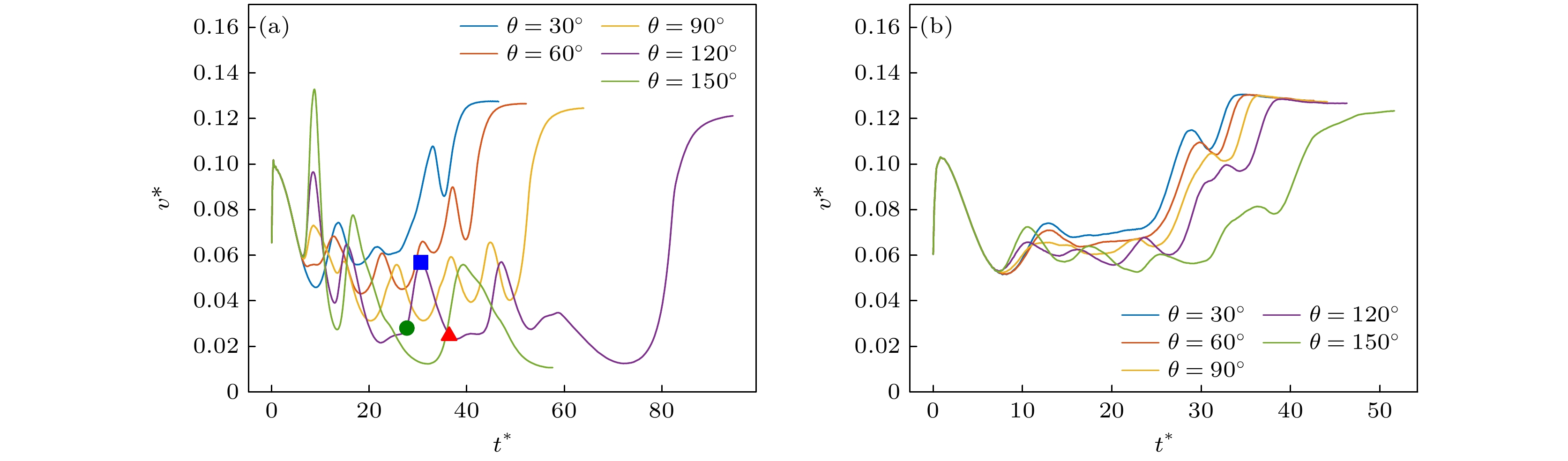
      气泡速度是气泡动力学的重要研究内容, 而在含多孔介质微通道中, Eo和接触角θ是影响速度的关键因素. 图5展示了不同Eo和接触角θ条件下, 气泡平均速度随时间的变化趋势. 这里, 平均速度${v_{{\text{ave}}}}$定义为气泡从初始时刻到达计算域顶端的期间所有气相格点宏观速度的平均值. 从图5可以看出, 气泡平均速度${v_{{\text{ave}}}}$随Eo增大呈现先快速上升, 再缓慢上升的趋势, 与前人研究揭示Eo数对气泡平均速度影响逐渐减弱的规律一致[41]. 然而, 不同Eo数下气泡平均速度的变化幅度会因润湿性不同而表现出显著差异. 当Eo从Eo = 5增大至Eo = 100, 在低润湿(θ = 30°)时, ${v_{{\text{ave}}}}$从0.083增大至0.091, 速度增量为0.008; 在高润湿(θ = 120°)时, ${v_{{\text{ave}}}}$从0.048增大至0.085, 速度增量为0.037, 约为低润湿情况下增量的4倍. 这一差异主要源于Eo对黏附力的调节. 在低Eo下, 黏附力是气泡上升的主要阻力之一, 且其强度随接触角增大而显著提升, 因此接触角对速度的影响较为显著. 然而, 在高Eo下, 浮力主导了气泡的上升过程, 黏附力的相对影响减弱, 导致不同接触角条件下的平均速度逐渐趋于一致. 这表明, Eo通过削弱黏附力对速度的影响, 显著抑制了接触角对气泡运动速度的调控作用.

      为进一步探究Eo和润湿性对气泡运动的动态影响, 本文统计了气泡上升过程中瞬时速度v*的时间变化趋势. 瞬时速度v*定义为当前时刻所有气相格点的平均宏观速度. 为突出对比, 将小Eo (Eo = 10)和大Eo (Eo = 100)条件下的瞬时速度v*分别展示于图6中. 图中显示, 在小Eo (Eo = 10)条件下, 气泡瞬时速度v*呈现多次波动, 即速度周期性地先上升后下降. 这一变化规律与Chen等[25]研究问题中观察到的气泡速度变化趋势一致. 进一步研究发现, 接触角θ越大, 单次波动的持续时间越长, 波动幅度也越显著. 这是由于气泡在穿过多孔介质时, 其与障碍物表面的接触与分离引发了黏附力突然出现和消失. 而接触角θ越大, 黏附力突变对速度的促进和削弱作用也越明显. 相比之下, 在大Eo (Eo = 100)条件下, 气泡瞬时速度v* 波动的幅度与频次显著降低, 不同θ条件下的瞬时速度v* 趋于一致. 其中在疏水工况下, t* = 15.526到t* = 23.684时, 气泡在多孔介质内部运动, 瞬时速度保持平稳, 几乎没有波动, 这是由于气泡在多孔介质内部运动时, 浮力很大程度上被阻力平衡[13], 而黏附力则被较大的Eo所抑制. 在亲水和中性工况下, 瞬时速度依旧存在一定波动, 表明Eo仅能抑制黏附力的影响, 但无法消除黏附力对瞬时速度波动的影响. 总的来说, 瞬时速度随Eo增大而波动减缓, 这与平均速度的变化规律相一致, 进一步验证了Eo通过削弱黏附力突变对气泡运动速度的调控作用, 从而显著抑制了接触角的影响. 通过对平均速度与瞬时速度的综合分析可以看出, Eo对接触角的抑制作用, 不仅使不同接触角条件下的气泡平均运动规律趋于一致, 还平滑了速度的动态波动特性, 使瞬时速度特性更加平稳.

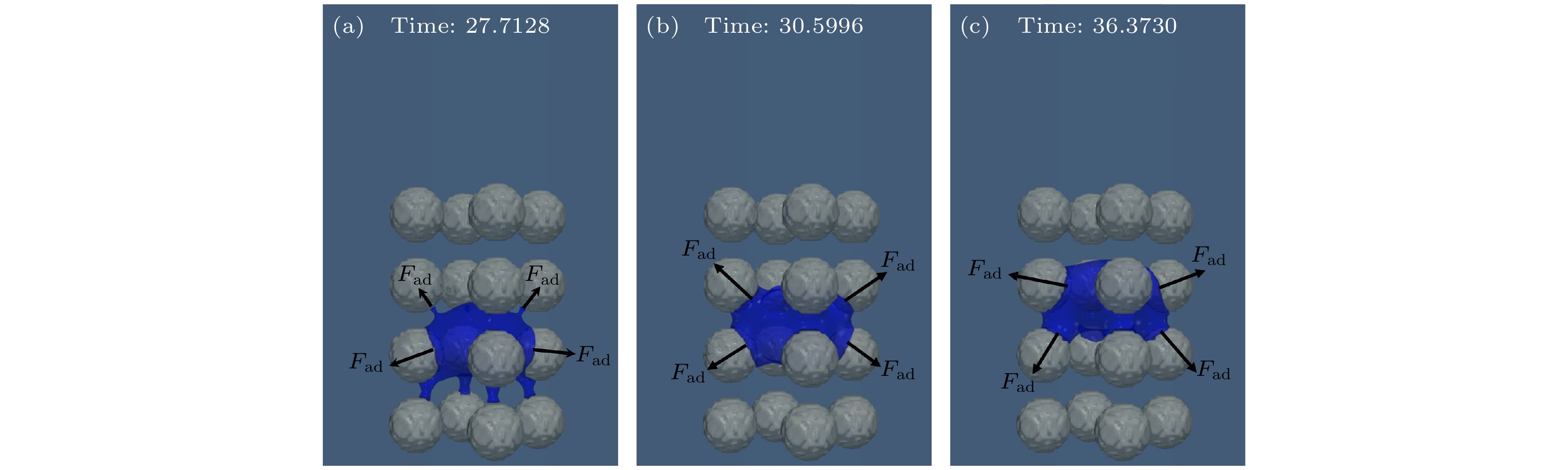
      图6显示, 一个v* 波动周期存在3个关键节点, 分别为起点、峰值和终点, 代表黏附力的突然出现、平衡与突然消失. 以Eo = 10, θ = 120°工况为例, 图7中展示了这3个节点对应的气泡形态与黏附力Fad作用方向的变化. 如图7(a)所示, 气泡上升至第2层障碍物(自下而上)时, 黏附力指向下方. 然而, 随着气泡与第3层障碍物的接触, 气泡上方突然出现指向上方的黏附力, 导致总阻力突然减少, 气泡上升速度随之增大, 这对应速度波动的上升阶段. 随后, 气泡质心逐渐远离第2层障碍物, 两层障碍物的黏附力的方向也随之改变, 指向上的分力不断减小, 指向下的分力不断增大. 这一趋势持续至图7(b)所示的平衡状态, 此时气泡的上下分力与浮力实现平衡, 但气泡动能使其继续上升, 导致黏附力向上分力进一步减小, 总阻力大于浮力, 气泡速度开始下降. 最终, 在图7(c)时刻, 当气泡即将脱离第2层障碍物时, 速度降至最低, 完成一个波动周期. 当气泡彻底脱离障碍物, 向下的黏附力突然消失时, 气泡进入下一个波动周期. 需要指出的是, 图4中观察到的气泡停滞现象通常出现在一个波动周期结束后, 此时总升力小于总阻力, 且气泡动能达到最低. 在气泡穿过顶层障碍物时, 由于缺乏向上黏附力的突然作用, 气泡更易停滞, 难以继续上升.

      • 5.2.   Re与接触角θ耦合对气泡运动的影响

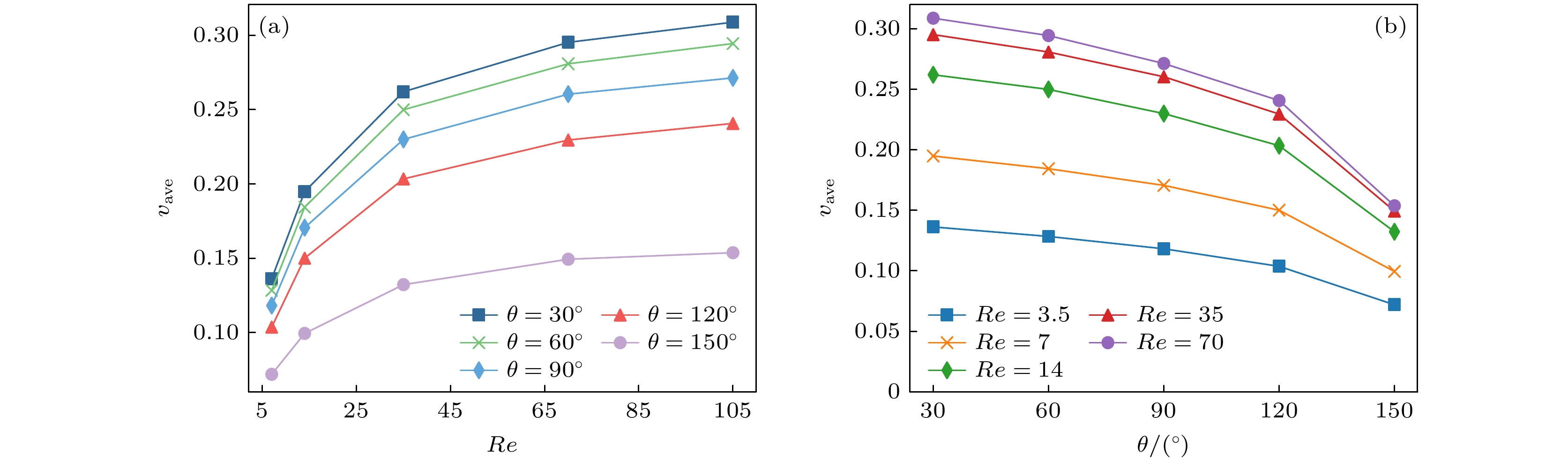
    • 黏性阻力Fd和黏附力都是总阻力的重要组成部分, 两者的相互竞争对气泡运动行为有较大的影响. Re是影响黏性阻力Fd的重要参数, θ是影响黏附力的重要参数, 本节通过模拟不同Re (Re = 3.5, 7, 14, 35, 70, 105)与不同接触角($\theta $ = 30°, 60°, 90°, 120°, 150°)下, 气泡在多孔介质中的运动行为, 分析这一竞争关系对气泡行为动力学的影响. 这里不同的Re通过改变流体的运动黏度${\nu _{\text{l}}}$得到. Eo取10, 其余参数与前文保持一致.

      图8展示了在不同Re与接触角工况下, 气泡平均速度vave的变化情况. 如图8(a)所示, 随着Re增大, vave先快速增大再缓慢增大, 这与vave和Eo之间的变化规律一致. 然而, 接触角增大使所有Re条件下的平均速度vave均下降, 且下降趋势加快. 尤其在接触角从θ = 120°增大至θ = 150°时, 平均速度vave下降幅度最大. 这一现象可由黏性阻力Fd和黏附力在总阻力中的竞争关系解释: 接触角增大显著增强了黏附力, 使其逐渐在与Fd的竞争中占优, 导致vave加速下降. 当接触角增大至θ = 150°时, 黏附力完全主导总阻力, 导致vave出现 骤降. 这一趋势在图8(b)同样显现. 图中表明, 接触角增大对高Re(如Re = 105)下的vave影响更为显著, 相较较低Re时(如Re = 7)表现出更大幅度的下降趋势, 这一现象与Eo增大时接触角对汽泡上升速度影响减弱的趋势相反. 此外, 随着Re的增大, 接触角在总阻力中的影响逐渐增强, 但vave并未出现明显突变. 这可能由于黏性阻力Fd减小幅度较有限, 导致Re的增大并未直接赋予黏附力主导地位.

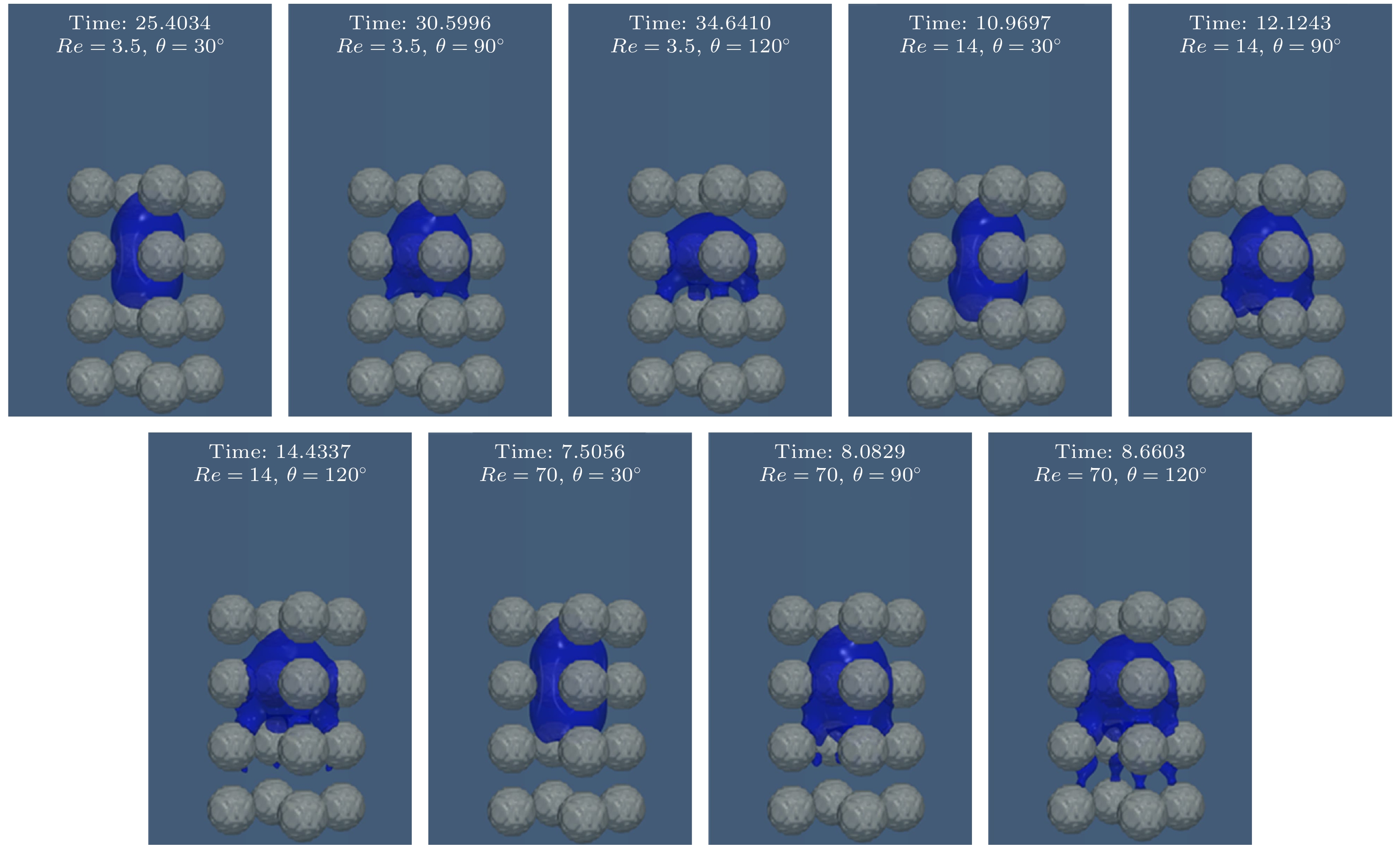
      如图9所示, Re与接触角的耦合作用也对气泡形态变化影响显著. 在θ = 30°时, 尽管Re从Re = 3.5增大至Re = 70, 气泡上升速度显著提高, 但其形态始终保持柱状. 这表明在小接触角条件下, 接触角对气泡形态的影响较弱. 随着接触角提升至θ = 90°, 黏附力增大, 气泡也由柱状演化为子弹头状, 并在尾部产生4个触手. 当Re从Re = 3.5提升至Re = 70后, 气泡与多孔介质接触面积增大, 尾部的触手也逐渐加粗, 同时在下方障碍物表面出现明显的气泡残留. 进一步增大接触角至θ = 120°后, 不同Re下气泡形态变化更为复杂. 如在Re = 3.5时, 由于速度较低, 黏附力作用占优, 导致气泡尾部触手加粗加长, 而在Re = 14, 70时, 速度较高, 黏附力和气泡动能之间的对抗加剧, 气泡尾部触手变得细长并趋于不稳定, 更易产生气泡断裂和气泡残留. 这表明, 较大的接触角增强了Re对气泡形态的影响, 表现为气泡尾部触手的形变加剧及气泡断裂现象与质量损失的增大.

      • 5.3.   Re与Eo耦合对气泡运动的影响

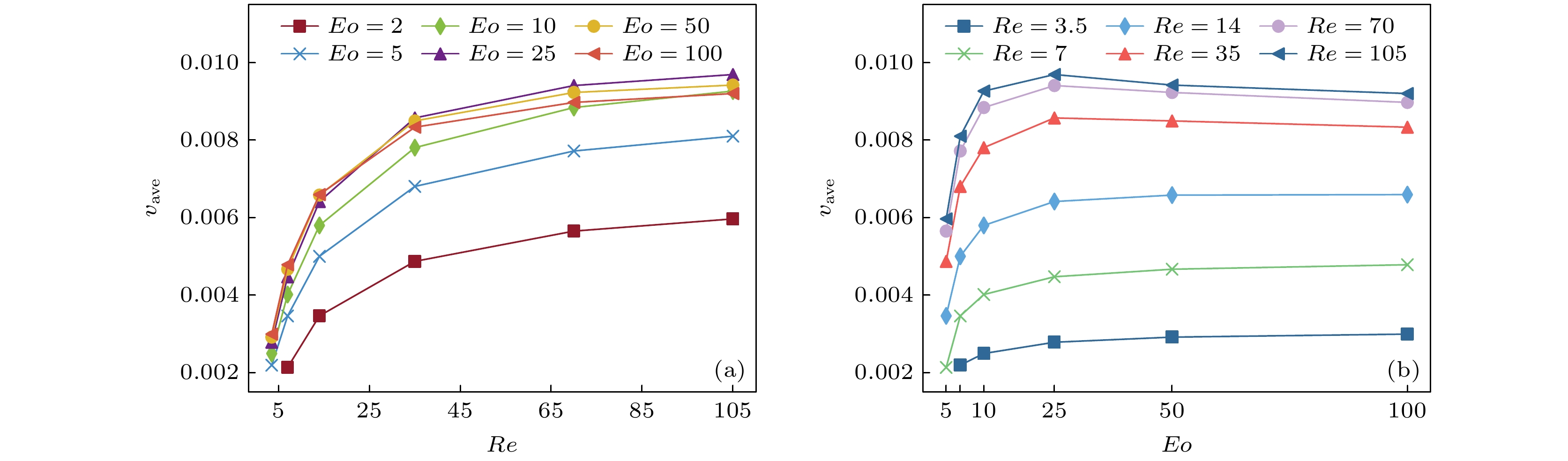
    • 如前文结果所示, Eo和Re分别和接触角之间的耦合作用对气泡运动和形态带来的影响与机理不同, 本节选择研究Re和Eo耦合对气泡运动行为的影响. Eo与Re的取值范围和调节方式与上文相同, 接触角选择θ = 90°, 其余参数同第3节.

      首先分析Re与Eo对气泡平均速度vave的影响. 如图10所示, 气泡平均速度vave随Re和Eo增大而增大, 但增速逐渐减缓. 其中, 与Re相比, Eo增速变化更为剧烈, 尤其在Eo = 25前后. 如图10(b)所示, 当Eo < 25时, vave随Eo增大而显著提升在显著提升, 而当Eo > 25时, vave增长则趋于平缓甚至略有下降. 这是由于较高的Eo抑制了黏滞力的作用, 当Eo > 25时, 黏滞力在总阻力中的占比已大幅降低, 导致气泡速度增幅趋于零. 类似的现象也体现在在Re的变化中, 如图10(b)所示, 当Re>14时, 随Re增大而产生的速度增幅迅速减小, 当Re达到Re = 70和Re = 105时, 两者的平均速度接近一致, 表明此时黏性阻力对气泡运动的影响已显著减弱. 值得注意的是, 不同Re与Eo条件下vave对Eo的响应呈现出相反趋势. 当Re ≥ 14且Eo ≥ 25时, vave随Eo增大而下降, 且这一趋势随着Re的增大更加明显; 在Re < 14且Eo < 25时, vave则随Eo增大而上升, 且同样随着Re的增大更加显著. 这种相反趋势可能是因为气泡在多孔介质中的形态随着Re和Eo的变化发生了显著变化, 从而改变了其运动机制.

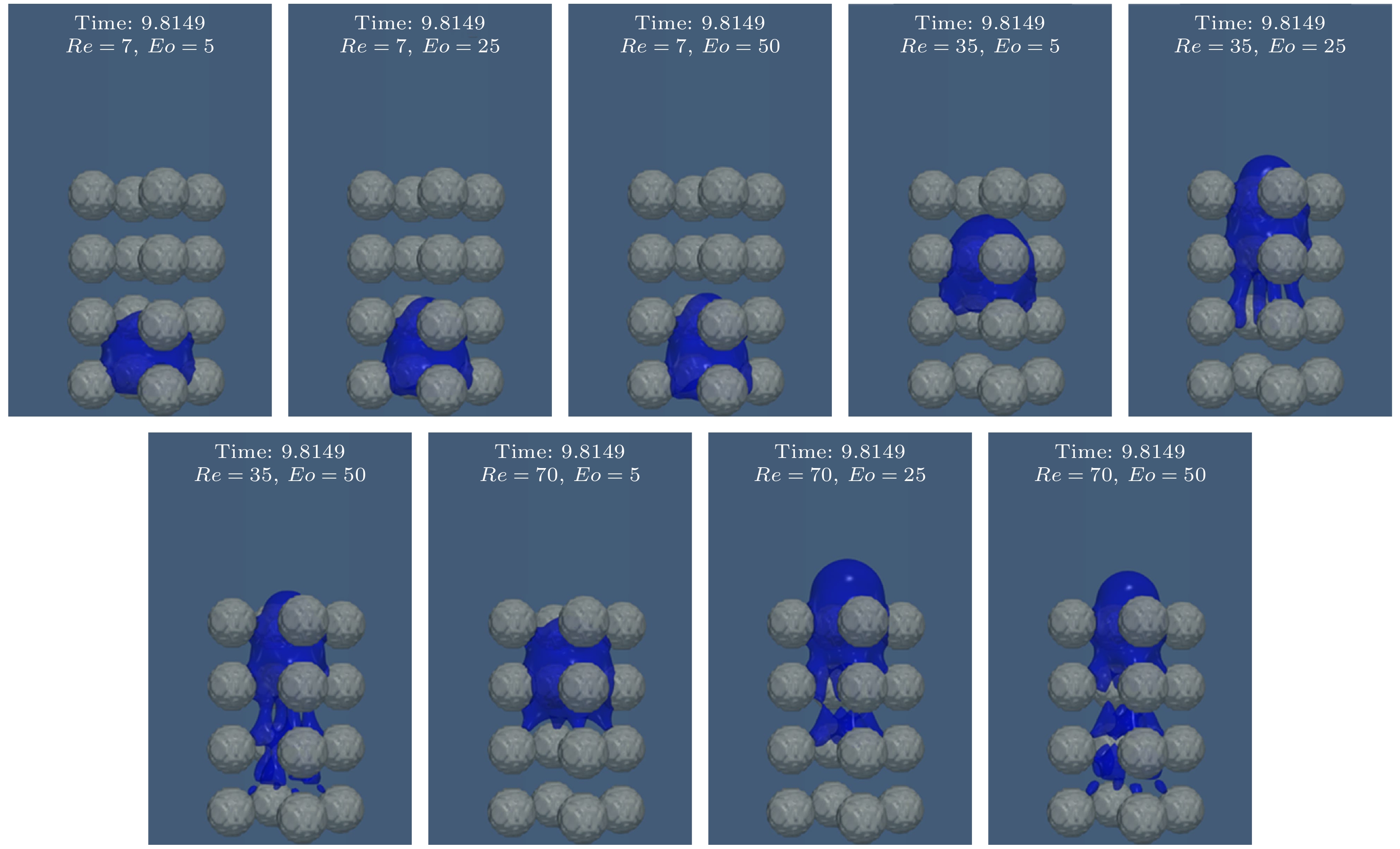
      为更好地分析这一现象的原因, 图11展示了气泡在不同Eo与Re组合下的形态变化. 从图11可观察到, 在大Eo和Re条件下(尤其是Re ≥ 14, Eo ≥ 25), 气泡更容易发生断裂和质量损失. 如Re = 70, Eo = 25情况所示, 该条件下气泡会因尾部形变而断裂为多个部分: 最上方气泡是主要部分, 占据大部分体积; 其余气泡仅占少量体积, 为残余部分. 在Yu等[22]的研究中同样能发现这一现象. 这是由于随着表面张力减小, 气泡维持表面形状的能力变差, 尾部更容易随着气泡动能的增大而产生速度差, 进而发生断裂. 进一步分析发现, 当Eo ≥ 25时, 同一Re下气泡断裂次数越多, 质量损失越严重, 则其上升速度越缓慢, 气泡顶端越低. 如在Eo = 25时, 尾部仅发生一次断裂, 在Eo = 50时, 气泡尾部发生3次断裂, 其气泡顶端则相比Eo = 25略低. 结合图像分析, 这种现象源于气泡的体积减小和质量损失. 较少的断裂和质量损失意味着更大的主体气泡体积, 这为气泡提供了更大的浮升力以克服各种阻力, 使气泡顶端更快到达计算域顶部. 因此, 当Re ≥ 14, Eo ≥ 25时, 尽管Eo与Re增大能够降低阻力, 但同样会带来严重的质量损失, 另外此时黏性阻力与黏附力对速度影响较弱, 无法完全弥补气泡断裂引起的浮力损失, 最终引起速度下降. 在Re ≥ 14, Eo ≥ 25外, 明显的气泡断裂和质量损失几乎不出现, 而Eo的增大显著削弱了气泡在多孔介质表面所受黏附力, 最终表现出随Eo的增大, Re对平均速度影响加强的规律.

    6.   结　论

    • 本文采用基于相场的LBM模型, 对大密度比气泡在含多孔介质通道内的运动变形行为进行三维模拟, 主要研究了在不同润湿性、Eo和Re相互耦合的工况下气泡上升过程中界面变形、破裂以及上升速度的变化情况, 主要得出以下结论.

      1) Eo增大对接触角带来的影响有显著的抑制作用, 一方面θ增大减小气泡的平均速度, 并加剧瞬时速度的波动, 而Eo的增大则使不同θ下平均速度趋于一致, 瞬时速度的波动接近消失. 另一方面在气泡形态上, θ增大会导致气泡扁平化, Eo增大则缓解了扁平化趋势.

      2) 当接触角较大(θ > 90°)且Eo较小(Eo < 10)时, 较强的黏附力使总阻力超过气泡浮力, 导致气泡在多孔介质中停滞. 适当减小接触角或增大Eo, 可以有效避免气泡堵塞现象的发生, 提高气泡流动效率.

      3) Re与θ在总阻力构成中呈现一定的竞争关系, 这种竞争关系表现在Re与接触角对气泡平均速度的相互增强作用上. 在气泡界面的演化上, 较大的θ和Re会使气泡尾部触手形变更为细长并趋于不稳定, 气泡残留也随之增加.

      4) Eo和Re组合中存在两个作用相反的区域. 当Eo ≥ 25且Re ≥ 14时, vave随Eo增大而下降, 而在Re < 14且Eo < 25时, vave则随Eo增大而上升. 这种相反的趋势源于Eo ≥ 25且Re ≥ 14条件下气泡形态的高度不稳定, 使得气泡极易发生断裂, 主体气泡质量损失, 最终引起速度下降.

    参考文献 (41)

目录

/

返回文章
返回