首页
登录
注册
-
水下无线通信是打通空天地海一体化信息网络“最后一公里”的关键技术. 水下无线通信网络的建立可有效提升海洋综合感知能力, 这在海洋资源勘测、海洋灾害预防以及海洋军事预警等方面有着重要的意义[1,2]. 现有水下无线通信技术主要包括水下无线声通信、电磁波通信以及水下无线光通信(underwater wireless optical communication, UWOC)等方式[3]. 其中, UWOC技术具有高码率、低延时、跨介质以及定向传输等优势而受到研究人员的广泛关注[4,5].
目前, UWOC技术已经取得了长足的发展, 水下光通信距离已从米量级提升至了数百米, 且传输速率也已从Mbps提升到Gbps[6]. 2021年, Yan等[7]开发了水下光子互相关光通信技术, 实现了120.1 dB衰减信道的光通信, 等效于Jerlov I型水质下883 m的无线光通信. 2022年, Fei等[8]提出一种基于宽带光电倍增管的UWOC技术, 传输距离与速率分别达到了100.6 m和3 Gbps. 与此同时, UWOC的安全性也受到越来越多的关注. 相较于水下无线声通信, 光束传输具有良好的方向性, 其在安全性方面具有一定优势. 然而, 光子在传播过程中, 由于水中悬浮颗粒与微生物对光子的散射作用, 部分光子会不可避免地偏离预设信道路径[9,10]. 散射光子的存在导致UWOC系统的信息传输存在一定的安全隐患. 2017年, Kong等[11]通过向水下光波传输路径中插入窃听分束器的方法实现了对UWOC系统的窃听. 然而, 该窃听方式具有侵入性, 极易被合法接收端察觉. 本文聚焦于非侵入信道安全性分析, 重点评估散射光子带来的信息泄漏风险, 这对于设计安全传输的UWOC系统至关重要.
针对水中散射光子导致的信息泄漏风险, 本文基于搭线窃听信道模型提出一种UWOC物理层安全性分析模型. 该模型通过计算UWOC系统中合法信道与窃听信道的容量差值, 来评估通信系统的安全性. 具体而言, 该模型首先基于蒙特卡罗模拟与实验测量方法分析信道中散射光子的三维分布, 然后从信息论角度分析合法通信双方信道容量以及窃听信道容量, 最终获得安全保密容量的三维空间分布, 从而评估散射光子所造成的信息泄漏风险. 本研究成果为UWOC定量安全性分析提供了解决策略, 能够为UWOC系统和编解码方案设计提供有力支撑.
-
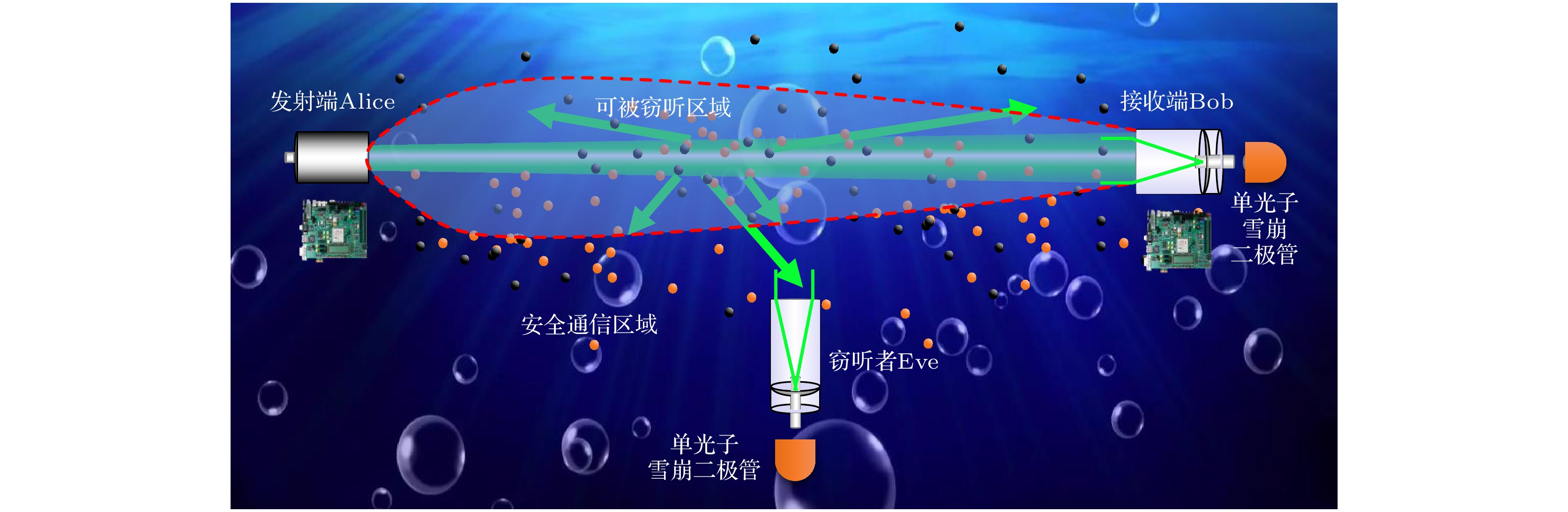
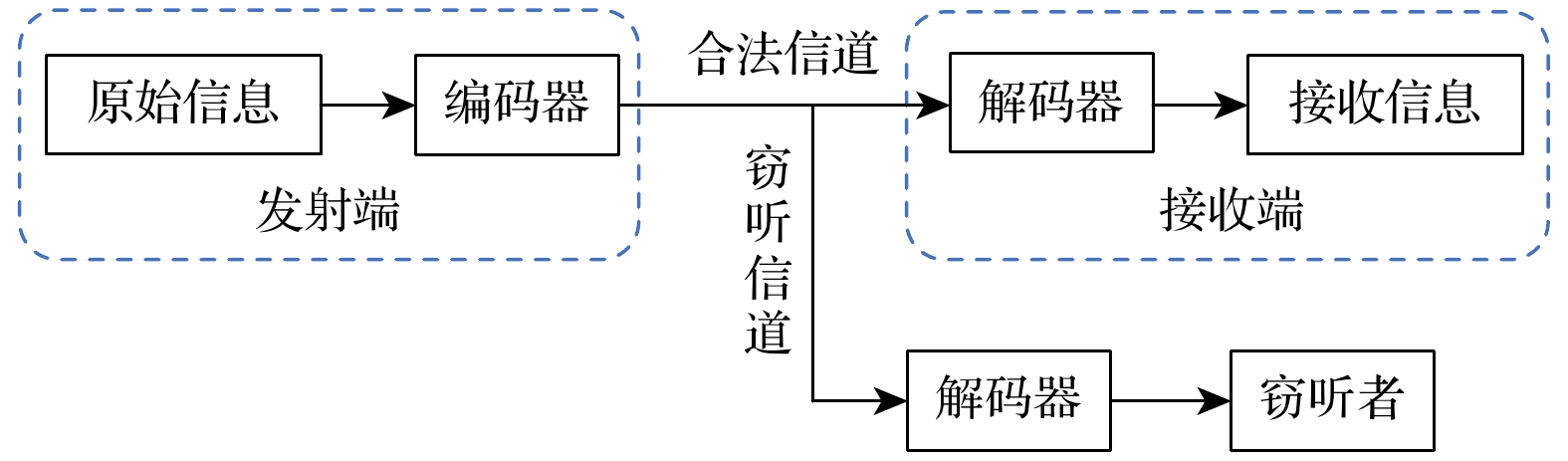
基于计算复杂性的公钥密码、一次一密的私钥体系以及物理层保密通信体系是当前典型的安全通信体系[12–14], 其中基于计算复杂性的公钥体系随着计算机的发展已经有部分加密方式被破解. 此外, 基于一次一密的加密算法虽然能够达到信息论安全性(即可证明安全性), 但需要消耗大量的密钥. 由于水下信道高损耗的特点, 一次一密的私钥体系并不具备实用性. 因此, 本文提出了基于搭线窃听模型的UWOC物理层安全性分析模型以分析UWOC系统的安全性. 搭线窃听信道模型由Wyner[15]于1975年提出, 主要应用于无线电通信领域. 该模型的核心思想是通过波束传输的指向性构建一个优于窃听信道的合法信道, 利用合法信道和窃听信道的信息量差来实现信息论安全性, 是一种无密钥安全通信方式, 如图1所示. 在该模型中, 如何证明合法信道相较于窃听信道的优越性, 是确保其安全性的核心所在. 在经典通信中, 我们可以始终设想, 窃听者掌握着更加灵敏的探测器, 得以拥有与合法接收方等同的信道容量. 但是, 本研究将光量子概念引入通信模型, 且合法与窃听双方均具有光子级探测灵敏度. 鉴于光子具有不可再分的特性, 因此从物理学定律上限制了窃听者所能够获得的最大信道容量, 保证了模型的理论安全性.
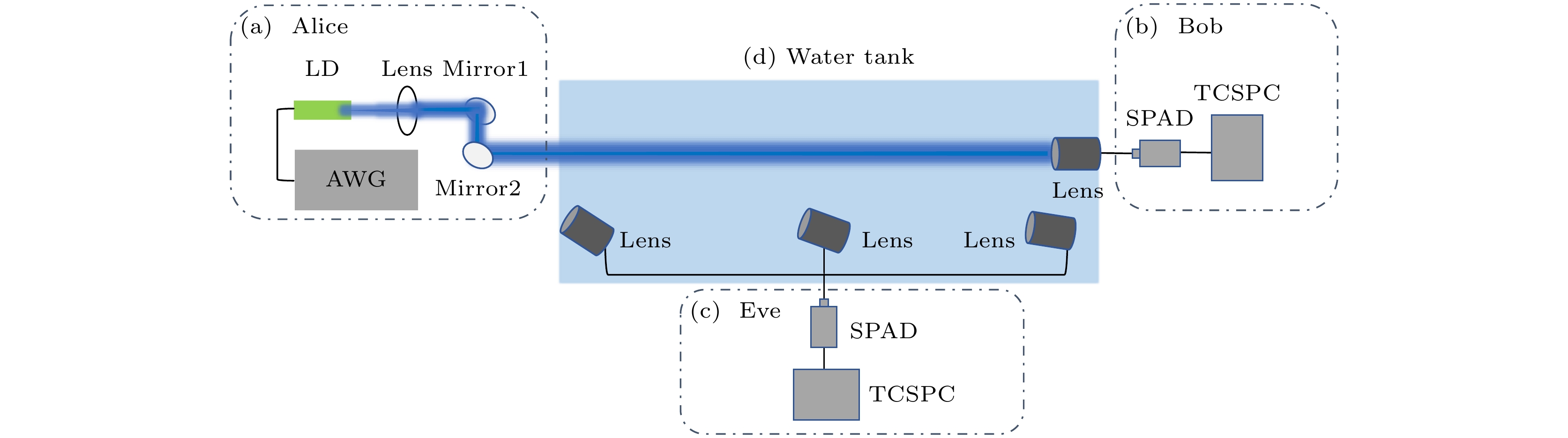
基于搭线窃听信道模型的思想, 本研究设计了如图2所示的UWOC物理层系统, 其中包括发射端(Alice)、接收端(Bob)和窃听者(Eve). 发射端采用相干光作为光源信号, 具有优异的准直性和方向性. 合法接收端与窃听者均采用单光子雪崩二极管作为探测设备. 该UWOC物理层系统中部分信号光子经合法信道可传输至接收端, 接收端通过解码后完成信息传输. 此外, 由于光信号在水下传输过程中不可避免地受到散射效应的影响, 部分光子将无规则的向四周扩散, 从而被窃听端收集, 产生信息泄漏风险.
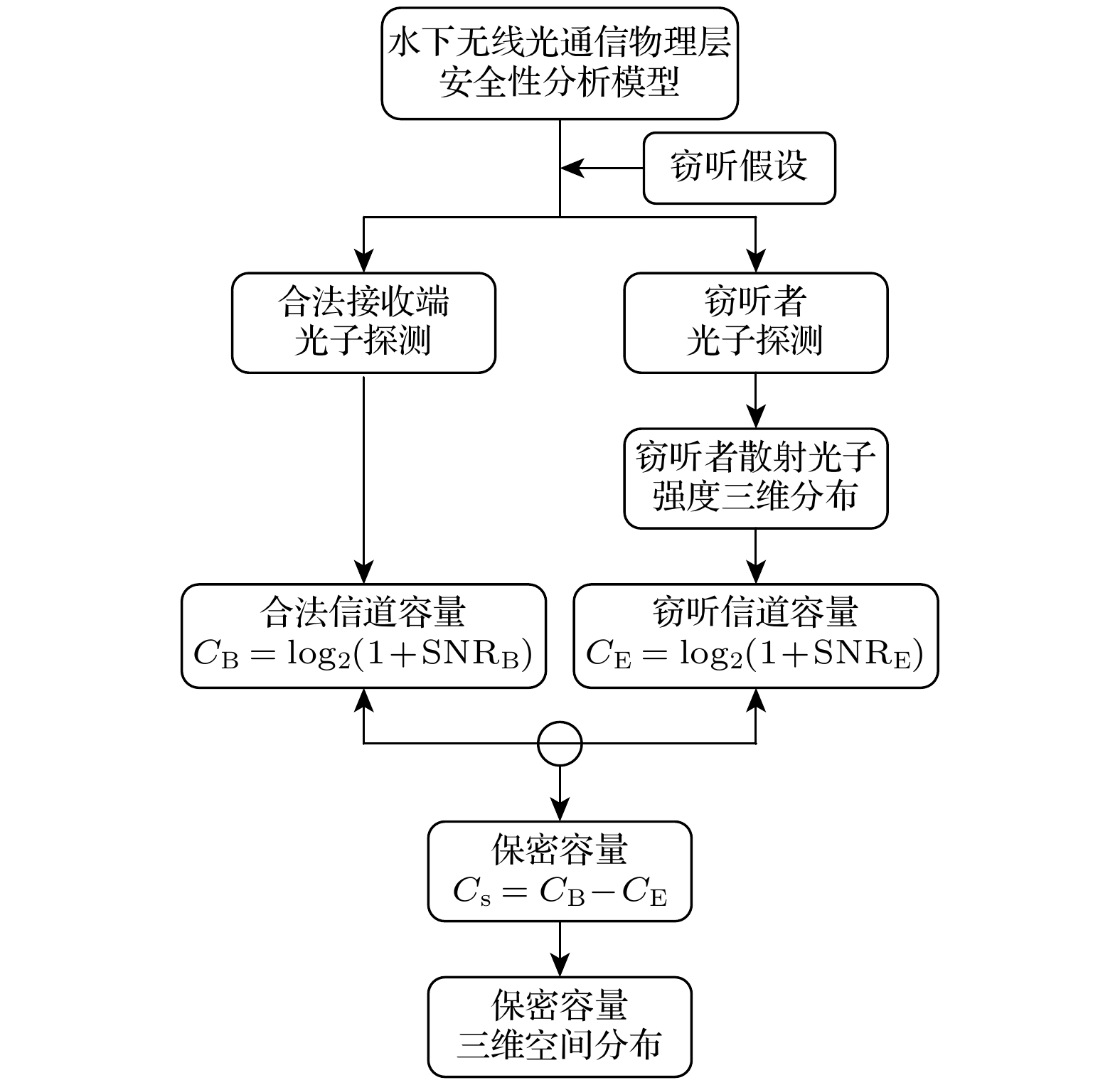
基于如上的物理层配置, 我们提出如图3所示的UWOC物理层安全性分析模型. 在该模型中, 首先基于蒙特卡罗模拟与实验测量方法分析信道中散射光子的三维分布, 然后从信息论角度分析合法通信双方信道容量(CB)以及窃听信道容量(CE), 最终获得安全保密容量(CS)的三维空间分布, 从而评估散射光子所造成的信息泄漏风险与系统的通信安全性. 保密容量是合法信道容量和窃听信道容量之差, 即合法接收端能有效接收的信息量减去窃听者能窃取的信息量[16,17]. 当CS＞ 0时, 通信系统理论上可实现物理层保密通信, 而当CS = 0时, 系统则存在被窃听风险. 通过该模型, 可辨别出不同水文条件以及不同通信条件下, 水下信道中可被窃听区域(CS = 0)与安全通信区域(CS ＞ 0), 如图2中红色虚线划分的区域. 分析结果可为UWOC物理层系统设计提供指导, 确保水下通信的安全性. 在第3, 4, 5节中, 将应用该模型对远洋清澈海水环境下(衰减系数: 0.26 m–1, 即Jerlov II型海水[18])的UWOC系统物理层安全性进行分析.
-
在非侵入合法信道前提下, 散射光子是窃听者获得传输信息的主要途径. 因此, 定量的分析散射光子强度分布对于分析窃听者获得的信息量具有重要指导作用. 本文基于蒙特卡罗模拟方法对光子的产生、传播、散射、吸收以及接收等过程进行了仿真[19], 并获得了散射光子的三维分布图.
-
光子在水中传输时会经历多次散射, 蒙特卡罗方法能够自然地处理多散射现象. 因为每个光子被独立模拟, 它的每一次散射事件都根据预定的概率分布进行. 此外, 蒙特卡罗方法还能够有效处理光子在水中的吸收效应, 通过比较每次步进后光子权值是否低于预设光子阈值, 可以判断光子是否被介质吸收, 以准确模拟吸收过程对光子传输的影响. 吸收与散射效应的叠加表现为光的衰减, 衰减系数可以表示为吸收系数和散射系数之和:
其中a, b, c分别为水质的吸收系数、散射系数以及衰减系数[20].
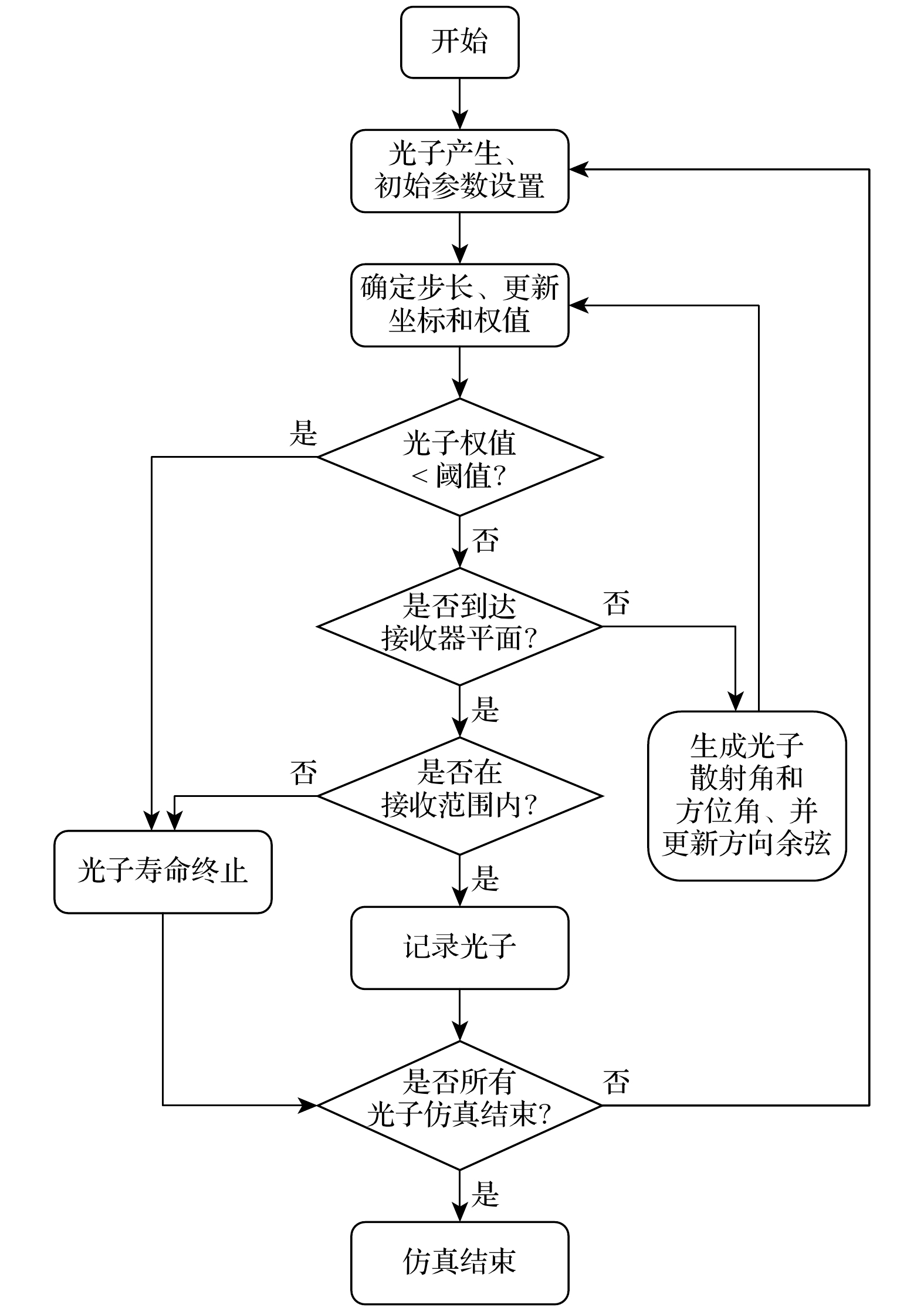
图4所示为水下光子传输的蒙特卡罗仿真流程图.
-
首先随机生成光子, 并设定其初始参数, 包括光子位置、方向及光子权值. 光子位置使用坐标表示, 方向则以方向余弦表示, 初始光子权值为1. 光子位置与方向均在直角坐标系中确定. 由于发射端光源出射方向通常正对合法接收端, 因此通常约定发射端与合法接收端间的连线为z轴, 且光源中心为原点. 基于这些设定, 光子初始状态由位置(x, y, 0)与方向余弦μx = cos(θx), μy = cos(θy)以及μz = cos(θz)表示. 初始光子坐标中的x与y需处于初始光斑面积当中, 且θx, θy以及θz分别代表光子运动方向与x, y, z轴的夹角.
-
确定光子初始参数后随即发射光子, 光子会在海水中前进一段距离直到与海水中的粒子相互作用, 这一距离称为步长. 步长通常由以下公式确定:
其中, R为[0, 1]的随机数, c为衰减系数. 根据步长以及初始坐标与方向信息更新光子坐标. 此外, 由于吸收效应的存在, 光子每传播一定步长后其光子权值都会有所降低, 光子权值的更新可由以下公式计算:
其中, wpost和wpre分别为衰减后与衰减前的光子权值, a为吸收系数.
当光子权值小于光子阈值时, 认为该光子寿命终止, 已被介质吸收, 结束该光子的跟踪. 若光子权值大于光子阈值, 进一步判断光子坐标z轴位置是否到达接收器平面. 若光子到达接收器平面, 则进一步判断其是否在接收范围内. 若其在接收器范围内, 则记录该光子, 若未在接收器范围内, 则认为该光子寿命终止.
若光子权值大于阈值且未到达接收器平面, 则进一步考虑海水的散射效应. 通过生成方位角与散射角来更新光子的方向余弦, 其中方位角(φ)为光子散射后的方向在x -y平面的投影与x轴正方向的夹角, 散射角(θ)为散射后光子的运动方向与原方向之间的夹角. 光子碰撞后的方位角通常表示为
其中, ξ为[0, 1]之间的随机数. 光子发生碰撞后的散射角则使用Henyey-Greenstein (HG)散射相函数来描述[21], 具体计算公式如下:
其中, g为HG散射相函数中的不对称因子, 如果g趋向于1, 则表示光子前向散射作用明显; 如果g趋向于–1, 则表示光子后向散射作用明显, 本研究中g参量的取值为0.924, 该值适用于准直光束条件下大部分的水质环境[22]. 根据方位角与散射角, 光子发生碰撞后的方向余弦可表示为
然后, 重新执行光与物质相互作用模拟操作直至该光子寿命终止或被记录.
-
当光子权值小于阈值或到达接收器平面但超出接收范围则认定光子寿命终止, 当光子到达平面且可被接收时则判定光子能够被探测. 出现上述两种情况之一, 则停止该光子的跟踪.
-
海洋中绝大部分海域为远洋清澈海水环境, 因此本研究对远洋清澈海水环境下的散射光子强度三维空间分布进行了模拟仿真[18,23]. 发射端参数、窃听者接收器参数、光子阈值以及水质参数如表1所列.
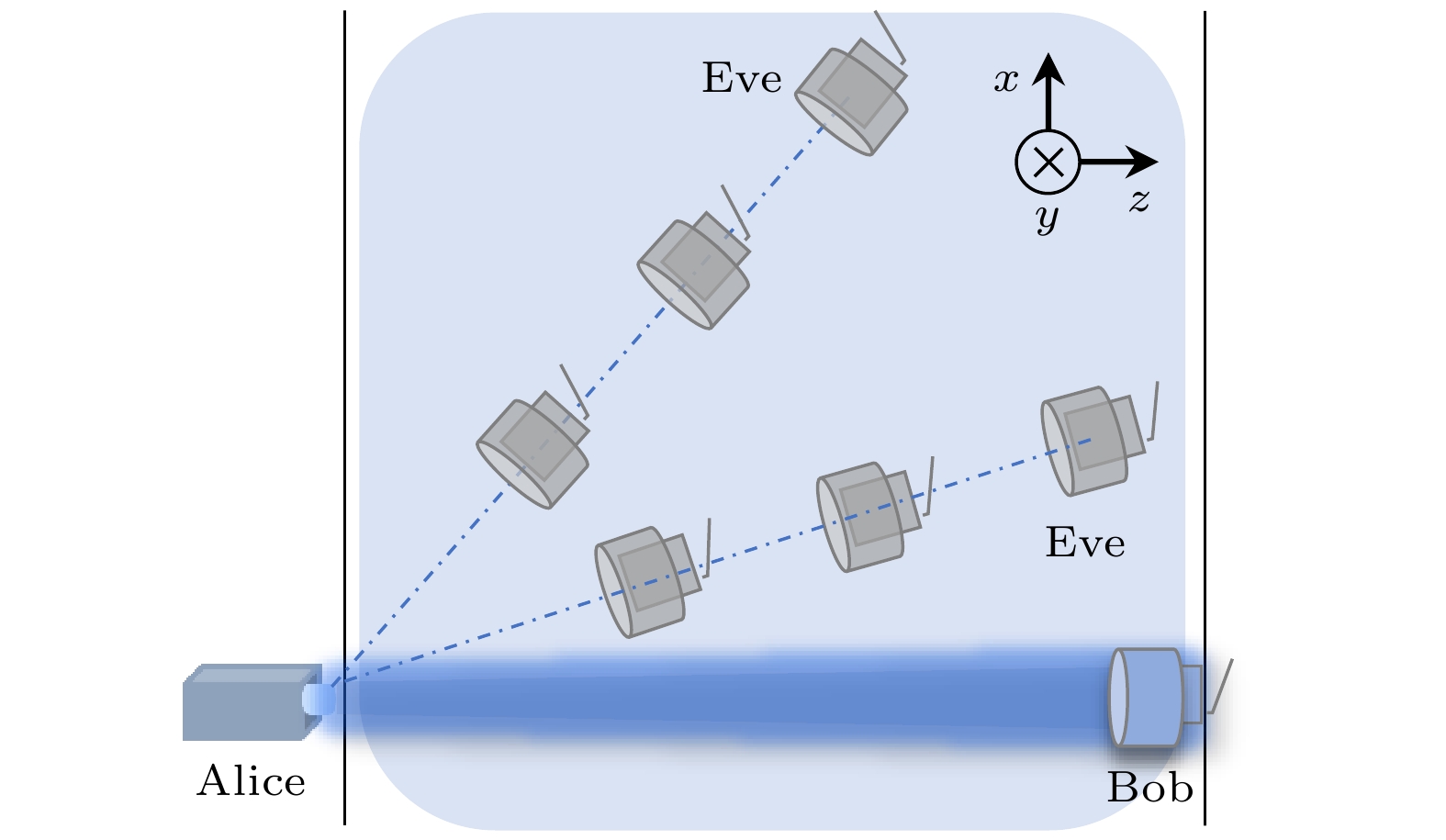
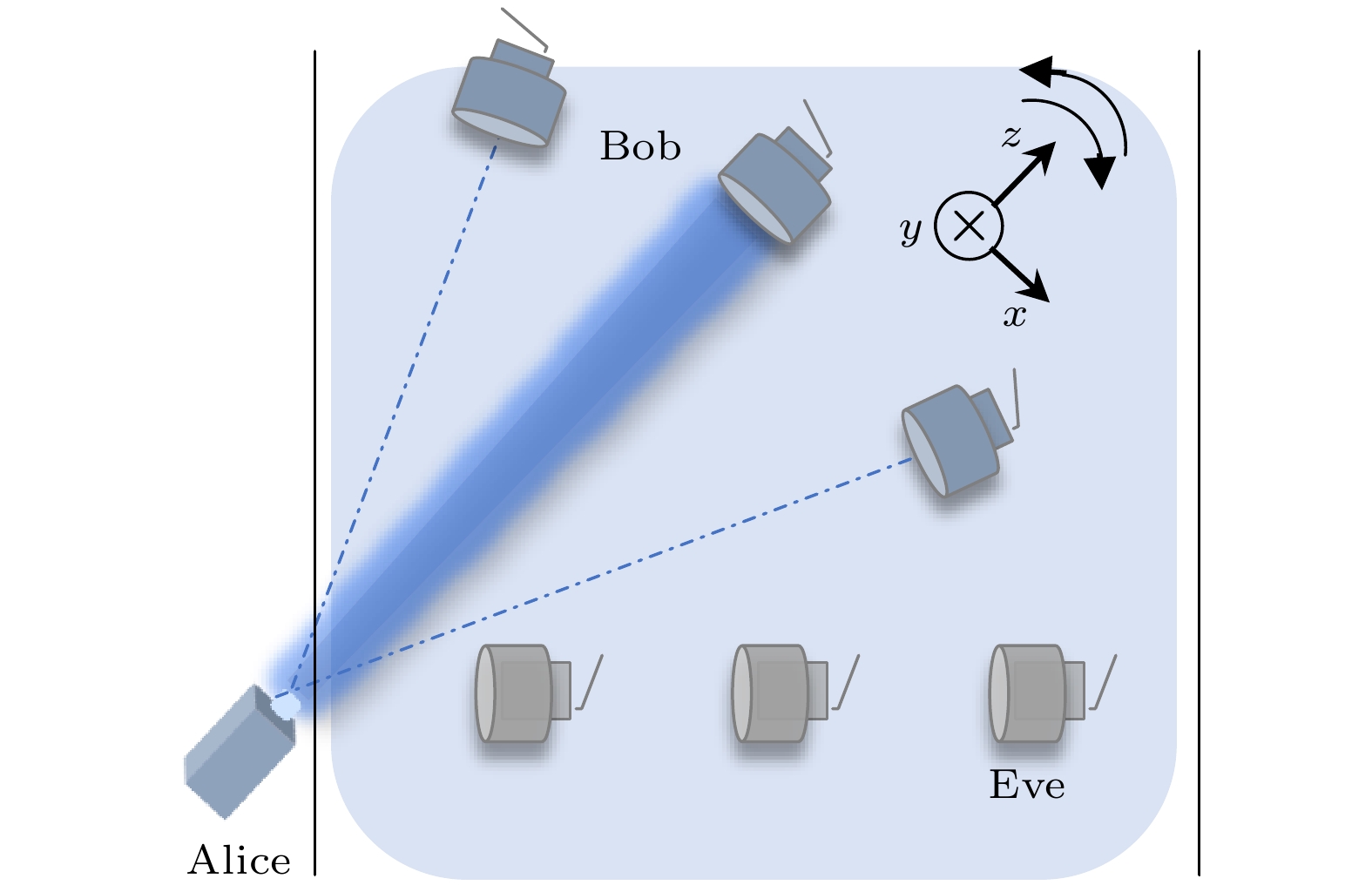
为获取散射光子强度的空间分布, 需将窃听者接收器布置在不同空间位置以获得强度分布信息. 图5所示为窃听者接收器空间位置排布示意图. 窃听者接收器的具体排列方式为在x -z平面中每隔1°设置一条径向直线, 并在每条径向直线上每隔1 m设置一个窃听者接收器.
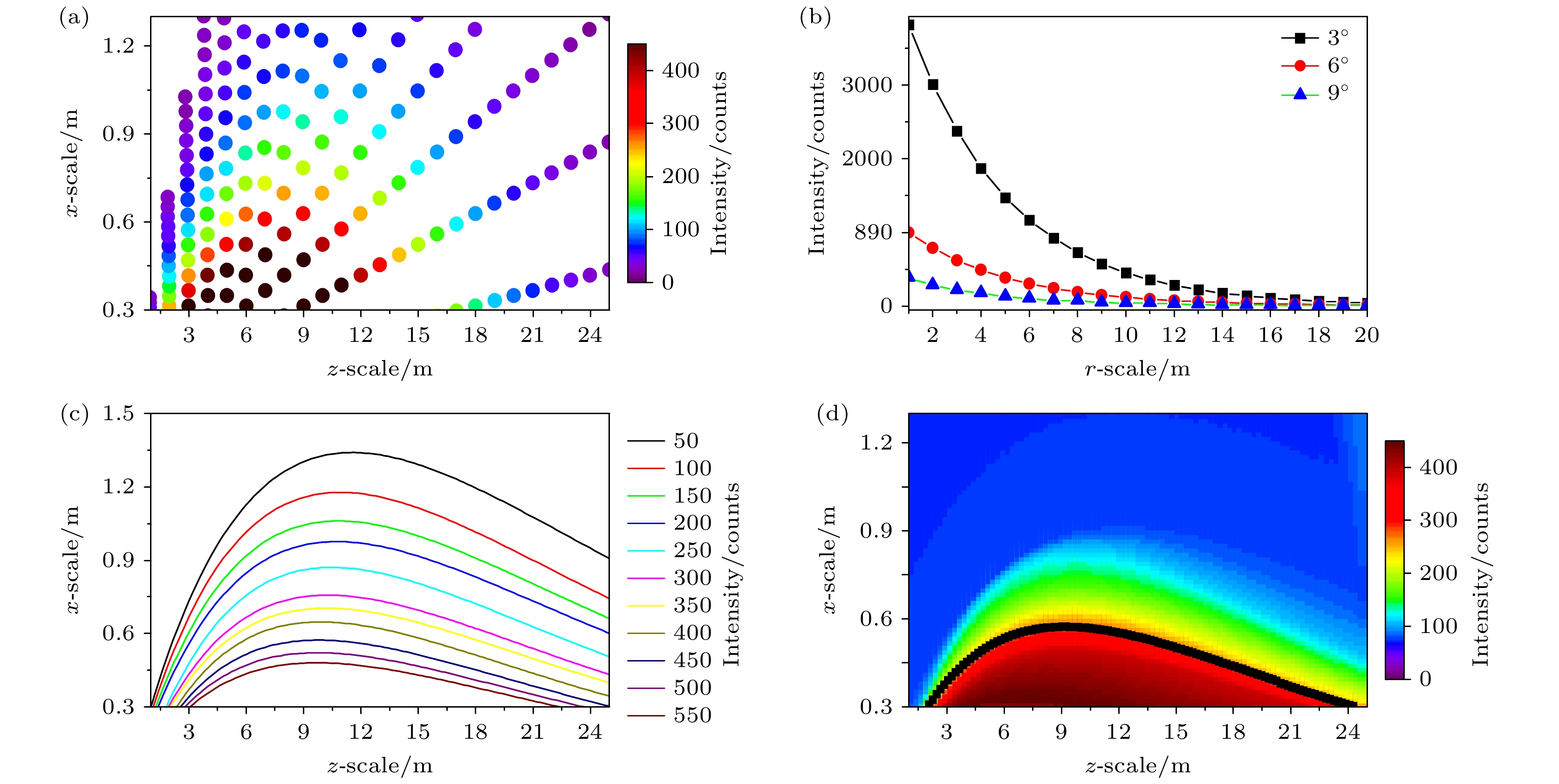
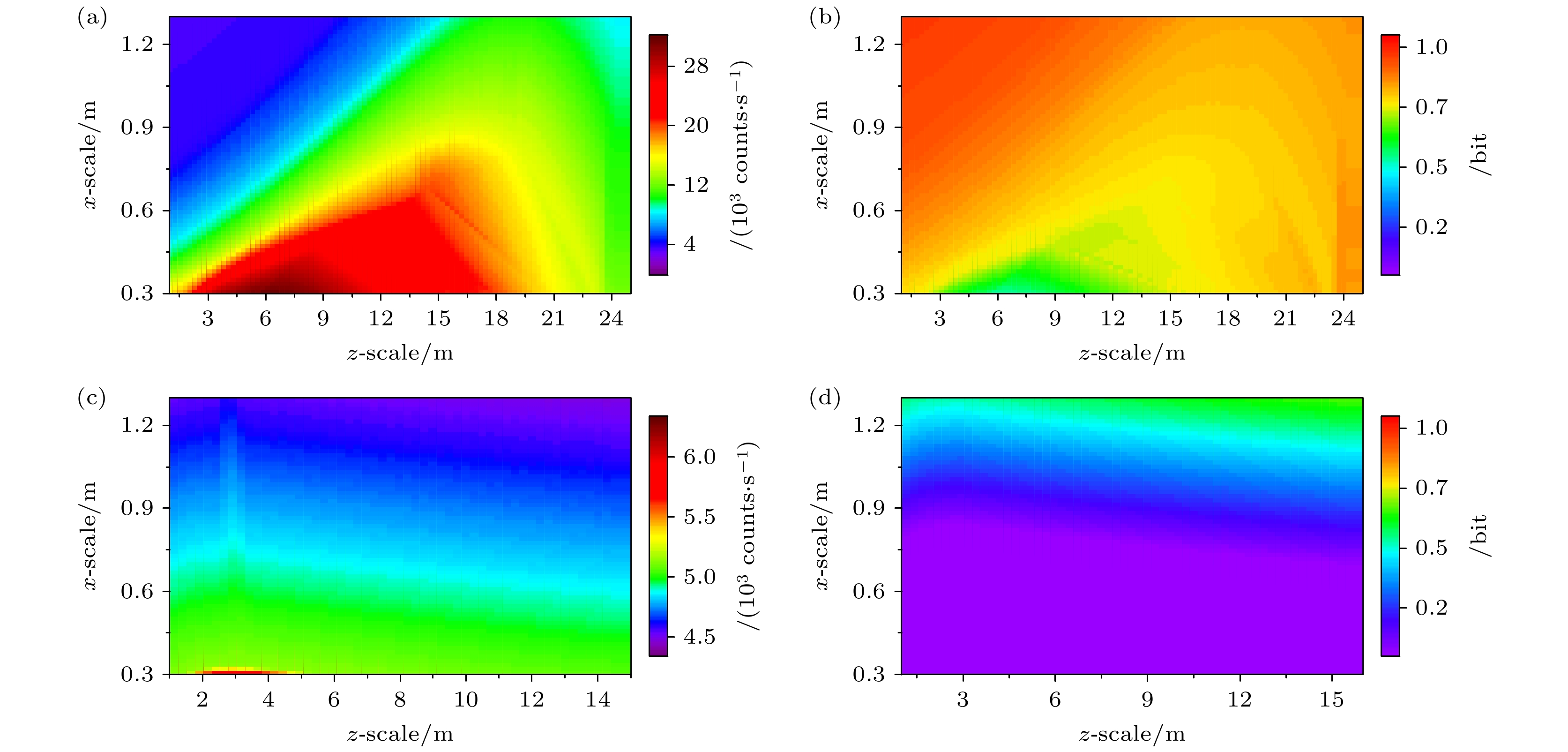
对所有窃听者接收器的散射光子强度进行蒙特卡罗仿真后, 可获得水下窃听者散射光子的三维强度分布散点图, 如图6(a)所示. 由于光子分布沿光束传输方向具有轴对称性, 因此, 图中以二维剖面图的形式展示光子的三维分布. 进一步地, 通过对散点分布图进行插值拟合可获得散射光子的三维连续强度分布图像. 然而, 原始散点分布图的数据点密度不足以支撑获得精确的插值拟合结果, 因此在插值拟合前还需对原始数据进行预拟合处理, 以提升原始数据点的密度. 这一过程包含两个步骤, 分别为径向散射光子强度衰减曲线拟合与散射光子等光强曲线拟合. 径向上不同距离处窃听者散射光子强度的衰减服从指数衰减规律, 可利用单指数函数进行拟合, 如下式所示:
其中, r为径向上的光子传输距离, I0为初始位置散射光子强度, c为衰减系数. 图6(b)所示为远洋清澈海水环境中3°, 6°和 9°径向下散射光子强度的单指数衰减函数拟合结果. 在获得各个径向上的单指数衰减曲线后, 提取每条衰减曲线上的等光强位点, 并利用经验函数对这些等光强位点进行拟合. 在本研究中, 采用的经验函数为双指数函数, 虽然该函数没有理论支撑, 但其能够有效描述散射光子的等光强曲线, 如下式所示:
其中, k, l, m, n为拟合参数. 图6(c)所示为散射光子等光强曲线拟合结果, 拟合光强区间为50—550 counts, 光强间隔为50 counts. 然后, 对一系列等光强曲线进行插值拟合, 获得散射光子强度的三维连续分布图像, 如图6(d)所示. 插值拟合时z轴网格大小为25 cm, x轴网格大小为1.5 cm, 插值拟合算法为三次样条插值算法. 由于发射机光束本身具有一定宽度与发散角, 因此散射光子强度分布插值拟合的起点并非原点, 而是从x = 0.3 m, z = 1 m位置处开始.
此外, 通过在(0, 0, 40)处设置合法接收端, 还对比了合法接收端与窃听者接收信号的强弱, 从而评估散射光子的强度水平. 合法接收端接收器的光学参数与窃听者接收器光学参数一致. 在相同仿真参数下, 合法接收端信号光子强度为 310 counts. 根据合法接收端的信号光子强度, 可以在散射光子强度分布图中框选出与接收端信号强度相当以及信号更强的区域, 如图6(d)中黑色实线框选的区域. 结果显示, 在近发射端的非信号传输路径上有相当大的区域其散射光子强度可与合法接收端相当甚至更强.
-
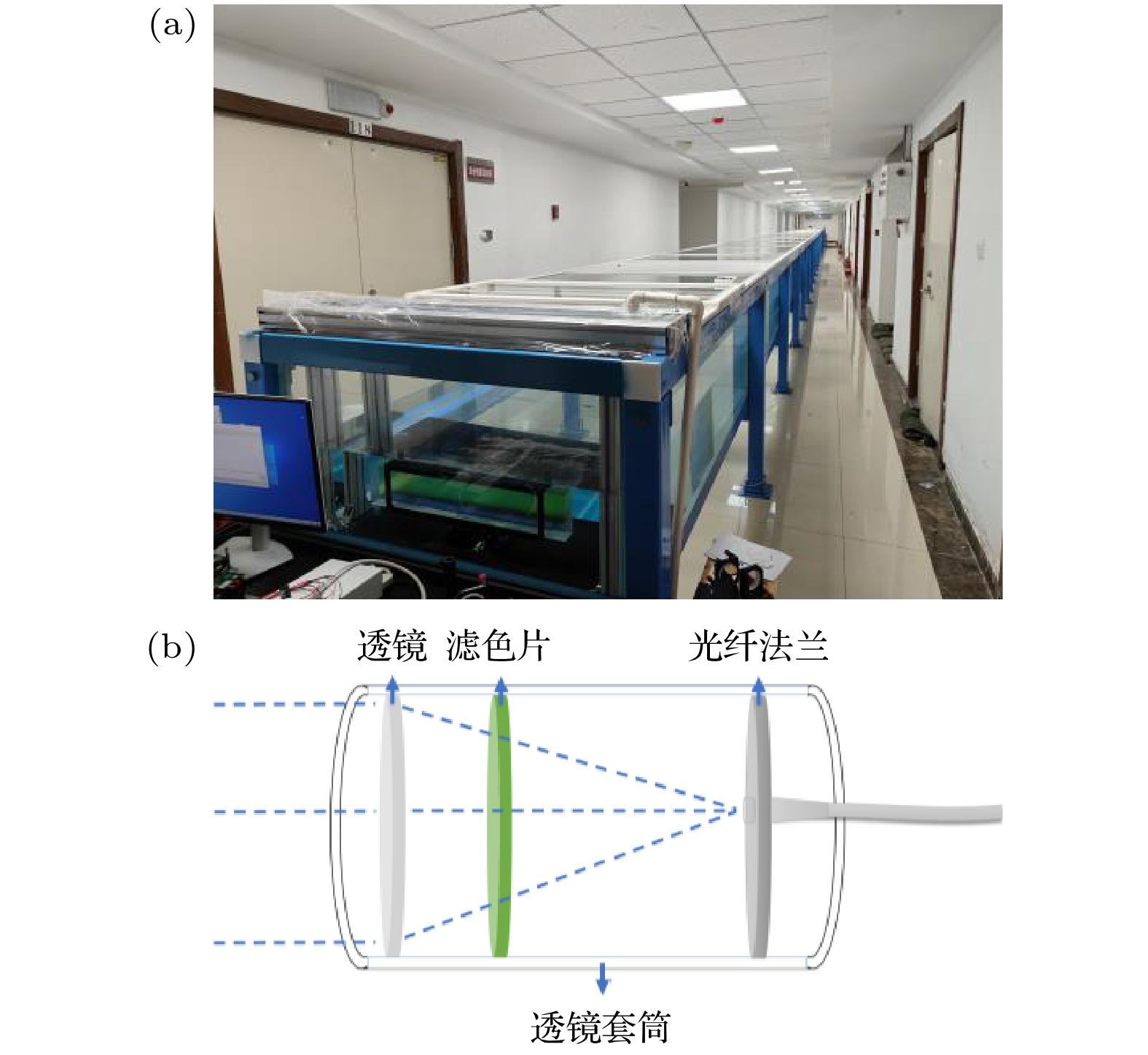
进一步地, 通过实验测量方法对仿真获得的散射光子空间分布图像进行了验证. 图7所示为本研究UWOC系统装置示意图, 该系统包括4个部分: 发射端、合法接收端、非法窃听者以及水下光程池. 本系统采用的编解码方案为多通道频率编解码方案[24,25], 该方案通过对发射端激光进行强度调制实现信息加载, 通过对接收端采集的光子到达时间序列进行傅里叶变换来恢复频率信息, 从而实现信息的传输. 在该UWOC系统中, 发射端包括任意波形发生器(Tektronix, AFG3102C)与激光二极管(北京敏光, LSFLD450-30), 激光被任意波形发生器进行单一频率强度的调制, 强度调制频率为10 MHz. 随后, 激光经透镜和反射镜准直后射入水下光程池. 图8(a)所示为水下光程池实物图, 其长为46 m, 宽1 m, 高0.8 m. 测量过程中, 整个光程池由黑色遮光布遮蔽, 以避免环境光噪声对测量结果产生影响. 激光在水下光程池中传播一定距离后到达合法接收端. 合法接收端接收器由探测镜头、单光子雪崩二极管(EXCELITAS, SPCM-AQRH)以及时间相关单光子计数采集卡(上海星秒, FT1010)构成, 其中通过探测镜头收集光子, 光子通过宽带多模光纤传输并由末端的单光子雪崩二极管探测, 单光子雪崩二极管所产生的电信号最终由时间相关单光子计数采集卡所记录, 以获取光子到达时间序列. 图8(b)所示为探测镜头结构示意图, 其由透镜(增透波长为400—700 nm)、带通滤色片((450± 10) nm)、光纤法兰以及外部的透镜套筒组成, 透镜直径为1 in (1 in = 2.54 cm), 视场角范围为4°. 此外, 置于非信号传输路径上的窃听者接收器其光学参数以及信号采集设备均与合法接收端相同. 需要强调的是, 受限于水池的宽度, 对散射光子强度分布的实验测量并不能按照图5所示的方案进行. 在实验测量时, 我们采用偏转激光入射角度的方式替代窃听者角度的变化, 从而实现散射光子强度分布的测量, 如图9所示.
-
针对模拟仿真过程中所考虑的远洋清澈海水水质, 我们在实验室中通过向超纯水中添加适量的海盐与二氧化硅散射小球构建了衰减系数相近的水质环境. 基于前述的测量系统与方案, 对该水质中的散射光子强度三维散点分布图进行了测量, 并通过相同的插值拟合方法构建了三维连续分布图像, 如图10(a)所示.
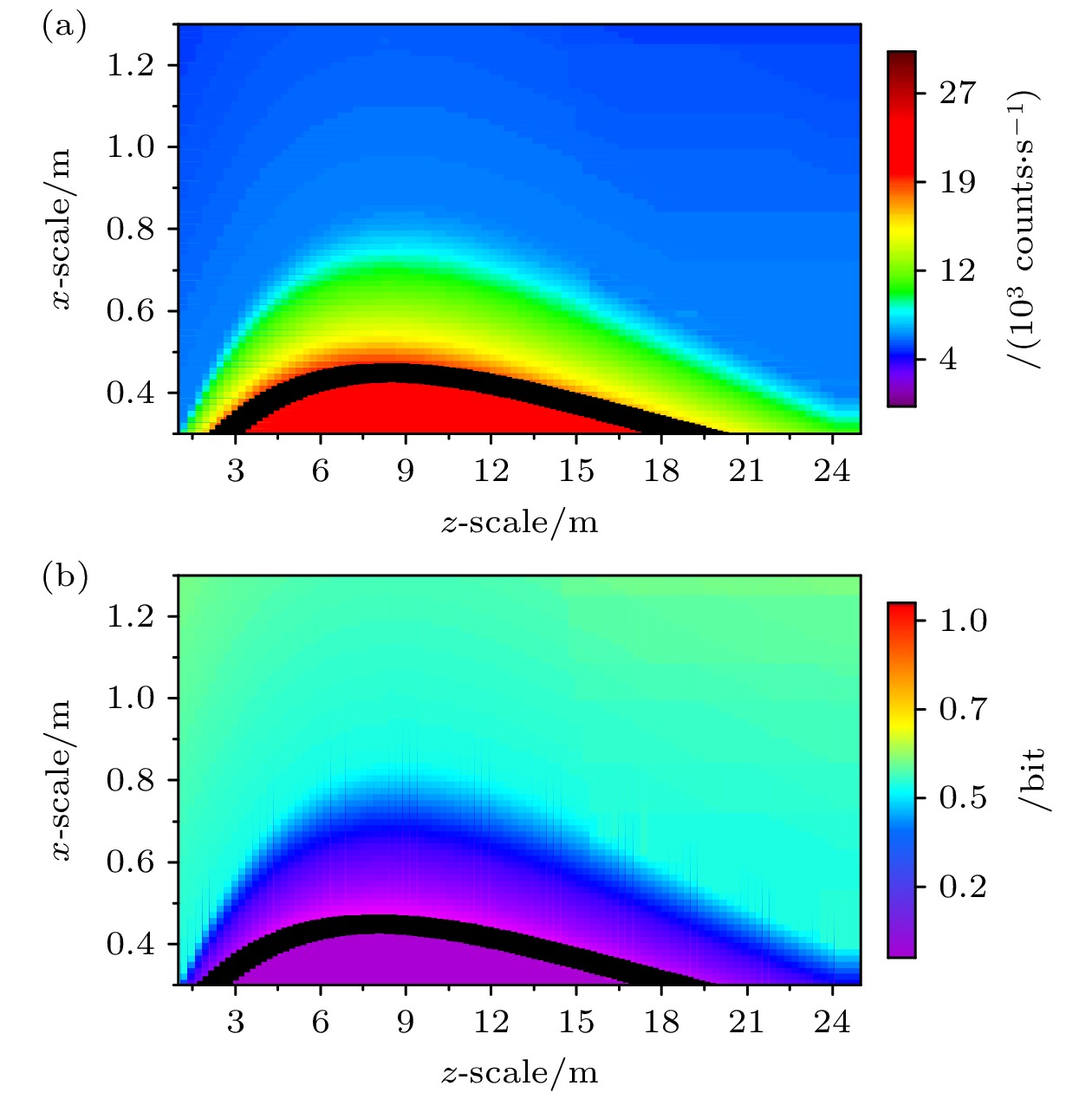
实验测量所得的散射光子强度分布特征基本与理论模拟结果一致. 此外, 通过在(0, 0, 40)处设置合法接收端, 同样也对比了预设合法接收端与窃听者接收信号的强弱. 合法接收端的信号光强为21000 counts/s. 根据合法接收端的信号光强, 同样可以在散射光子强度分布图中框选出与接收端光子强度相当以及更强的区域, 如图10(a)中黑色实线框选的区域.
-
在明确光子计数后, 还不足以评估UWOC系统的安全性, 还需进一步明确合法信道与窃听信道解码信噪比来获得保密容量(CS), 从而评估系统通信安全性[17]. 保密容量是指在安全传输条件下合法信道中无误码传输的最大通信容量, 其通过以下公式计算:
其中, CB和CE分别代表合法信道容量与窃听信道容量[26,27]. 二者由以下公式定义:
其中, SNRB和SNRE分别为合法信道和窃听信道的解码信噪比. 解码信噪比计算公式如下:
其中, IS和IN分别表示信号与噪声强度. 针对于我们所采用的多通道频率编解码方案, 提取傅里叶变换频谱中发射端频率对应的频谱峰值作为信号强度, 提取频谱的基底噪声平均值为噪声强度(主要源于单光子雪崩二极管的暗计数)[28]. 此外, 由于本文采用的传输方式是一次传输方式, 并不涉及具体的带宽. 因此, 本文中信道容量与保密容量的单位为bit[29].
对实验中所有空间位点的保密容量进行计算, 并进行插值拟合获得如图10(b)所示的保密容量分布图像. 在当前通信环境下, 由于合法接收端解码信噪比保持不变以及噪声强度的空间分布保持不变, 因此保密容量与散射光子强度的空间分布趋势呈现反相关的关系. 根据香农信息论, 当CS＞ 0时, 通信系统理论上可实现保密通信; 而当CS = 0时, 系统则存在被窃听风险. 图10(b)中黑色实线为保密容量为0的分界线, 当窃听者空间位置位于界线以内深紫色区域时其可通过散射光子获得通信的全部秘密信息. 当窃听者位于界线以外时, 合法通信双方可以通过防窃听编码使得窃听者获得的秘密信息无限接近于0, 且窃听者距离传输路径越远, 合法通信双方的保密容量越大, 即可实现的安全传输码率越高.
本研究还对其他不同水质环境的散射光子强度分布和保密容量分布进行实验测量与分析. 图11(a), (b)分别为衰减系数为0.02 m–1与0.60 m–1水质下的散射光子强度分布图, 图11(c), (d)则是对应的保密容量分布图像. 这两种水质衰减系数分别接近于纯净海水(即Jerlov I型海水[30])与沿岸海水(即Jerlov 1C型海水[18]). 对比3种水质实验结果发现, 不同水质下散射光子强度与保密容量的空间分布服从相同的变化趋势. 当水质衰减系数逐渐降低时散射光子在非预设路径区域的强度将逐渐增大. 然而, 虽然散射光子强度在弱衰减水质中更强, 但其保密容量却更大, 这归因于弱衰减水质中预设合法接收端(40 m处)的解码信噪比显著大于强衰减水质.
需要强调的是, 除吸收和散射效应, 作为三大退化效应之一的水下湍流效应也是影响水下光子传输的重要因素. 然而, 在本项研究中, 我们旨在提出一种UWOC物理层安全性的分析模型, 因而并未完全构建真实的水下环境. 因此, 本项研究中并未考虑水下湍流对光子传输造成的影响. 然而, 当前水下湍流效应的模拟仿真与实验室复现的方法与技术已相对成熟[19,31], 有助于我们在下一步工作中开展湍流效应方面的相关研究.
此外, 本文所提出的物理层安全性分析模型不仅适用于多通道频率编解码方案, 也可应用于其他编解码方式. 由于不同编解码方式具有不同的抗噪能力, 因此它们的解码信噪比会有所不同, 从而 导致在不同编解码方式下的保密容量也有所差异. 然而, 尽管解码信噪比和保密容量的绝对值不同, 不同编解码方式下散射光子与信号光子的强度分布仍然保持一致. 若假设噪声强度的空间分布不发生变化, 则不同编解码方式下解码信噪比和保密容量的空间变化趋势将保持一致.
-
本文基于搭线窃听信道模型提出一种UWOC物理层安全性分析模型. 该模型通过分析水下信道中散射光子的三维分布, 并从信息论角度分析合法通信双方信道容量以及窃听信道容量, 最终获得安全保密容量的三维空间分布, 从而评估通信系统安全性. 对常见远洋清澈海水环境下UWOC系统的理论模拟和实验结果表明, 在信号传输路径附近一定范围内系统的保密容量为零, 证明散射光子的存在会造成信息的泄漏. 因此, 在实际应用中, 为了保证通信的安全, 需对近发射端附近的非信号传输区域进行监视以确保通信的安全性. 本研究成果为UWOC定量安全性分析提供了解决策略, 能够为UWOC系统和编解码方案设计提供有力支撑.
水下无线光通信物理层安全性研究
Physical-layer security of underwater wireless optical communication
-
摘要: 水下无线光通信(UWOC)具有定向传输的特点, 相较于声呐、无线电等广播式传输模式具有更高的安全性. 然而, 由于海水散射效应部分光子在传输过程中会被散射出预设路径, 从而造成信息泄漏风险. 本文基于搭线窃听信道模型提出一种UWOC物理层安全性分析模型以评估信息泄漏风险. 该模型通过计算UWOC系统中合法信道与窃听信道的容量差值, 来评估通信系统的安全性. 具体而言, 该模型首先基于蒙特卡罗模拟与实验测量方法分析信道中散射光子的三维分布, 然后从信息论角度分析合法通信双方信道容量以及窃听信道容量, 最终获得安全保密容量的三维空间分布, 从而评估散射光子所造成的信息泄漏风险与系统的通信安全性. 本文应用该模型对清澈海水环境下的UWOC系统的安全性进行了分析, 研究发现传输路径附近一定范围内系统的保密容量为零, 证明散射光子会造成信息泄漏. 本研究成果为UWOC系统定量安全分析提供了解决策略, 能够为UWOC系统和编解码方案设计提供有力支撑.Abstract: Underwater wireless optical communication (UWOC) possesses significant advantages, such as high bandwidth, low latency, and low power consumption, making it a key technology for building information networks in marine environments. However, due to the scattering effect of seawater, some photons carrying information inevitably scatter out of their predetermined paths, leading to the possibility for information leakage. Therefore, we propose a physical-layer security analysis model for UWOC systems based on the wiretap channel model. The model evaluates the security of the communication system by calculating the capacity difference between the legitimate channel and the eavesdropping channel in the UWOC system. Specifically, the model first constructs the three-dimensional intensity distribution of scattered photons in the underwater channel via Monte Carlo simulations and experimental measurements. Then, it calculates the capacities of both the legitimate and eavesdropping channels based on the decoding results. Finally, the three-dimensional distribution of secrecy capacity is derived to assess the security of the communication system. In this work this model is used to analyze the security of the UWOC system in clear seawater environments. The results show that the secrecy capacity of the system is zero within a certain range near the transmission path, demonstrating that scattered photons can cause information leakage. We recommend that, in practical applications, monitoring the non-signal transmission area near the transmitter is essential to ensure communication security. This research provides a solution for analyzing the quantitative security of UWOC, which can strongly support the design of UWOC systems and encoding/decoding schemes.
-
-
图 2 水下无线光通信(UWOC)物理层系统示意图
Figure 2. Schematic diagram of the physical-layer system for underwater wireless optical communication (UWOC).
图 4 水下光子传输蒙特卡罗仿真流程
Figure 4. Monte Carlo simulation process for underwater transmission of photons.
图 5 窃听者接收器空间位置排布示意图
Figure 5. Schematic diagram of the spatial arrangement of eavesdropper.
图 6 远洋清澈海水环境下窃听者散射光子强度的模拟仿真 (a) 散射光子的三维散点分布图; (b) 3°, 6°, 9°径向下散射光子强度的衰减曲线, 其可通过单指数衰减函数拟合; (c) 散射光子等光强曲线, 其可通过双指数函数拟合; (d) 散射光子强度三维空间分布图, 由于光子分布沿光束传输方向具有轴对称性, 图中以二维剖面图的形式展示光子的三维分布
Figure 6. Simulation of scattered photon intensity in clear seawater: (a) Scatter plot of scattered photon intensity; (b) intensity decay curves of scattered photon at radial angles of 3°, 6°, and 9°, which can be fitted by single exponential decay function; (c) contours of scattered photon intensity, which can be fitted by double exponential function; (d) intensity distribution map of scattered photons by simulation, the three-dimensional spatial distribution of scattered photon intensity is represented in the form of a two-dimensional profile due to the axial symmetry of photon distribution along the beam propagation direction.
图 7 UWOC系统装置示意图 (a) 发射端模块; (b) 接收端模块; (c) 窃听者模块; (d) 水下光程池; LD为激光二极管, AWG为任意波形发生器, SPAD为单光子雪崩二极管, TCSPC为时间相关单光子计数采集卡
Figure 7. UWOC system: (a) Transmitter; (b) receiver; (c) eavesdropper; (d) water tank. LD represents laser diode, AWG represents arbitrary waveform generator, SPAD represents single-photon avalanche diode, TCSPC represents time-correlated single photon counting.
图 8 (a) 水下光程池实物图; (b) 探测镜头示意图
Figure 8. (a) Photograph of water tank; (b) schematic diagram of the lens.
图 9 散射光子强度三维空间分布图实验测量方案
Figure 9. Experimental measurement scheme for the intensity distribution map of scattered photons.
图 10 (a) 远洋清澈海水条件下窃听者散射光子强度分布图实验测量结果; (b) 系统保密容量分布图
Figure 10. (a) Intensity distribution map of scattered photons by experimental measurement in clear seawater; (b) secrecy capacity distribution map in clear seawater.
图 11 (a), (b) 纯净海水与沿岸海水条件下窃听者散射光子强度分布图; (c), (d) 纯净海水与沿岸海水条件下系统保密容量分布图
Figure 11. (a), (b) Intensity distribution maps of scattered photons in pure seawater and coastal seawater; (c), (d) secrecy capacity distribution maps in pure seawater and coastal seawater.
表 1 蒙特卡罗仿真参数
Table 1. Parameters for the Monte Carlo simulation.
参数 数值 参数 数值 光子数 107 接收孔径/mm 50 光斑直径/mm 25 接收器视场角/(°) 4 光束发散角/rad 10–4 光子阈值 10–5 吸收系数a/m–1 0.065 散射系数b/m–1 0.195 
下载: 导出CSV
-
[1] Qi Z R, Zhao X Y, Pompili D 2023 IEEE Trans. Commun. 71 7163 doi: 10.1109/TCOMM.2023.3315313 [2] Naik R P, Salman M, Bolboli J, Shetty C S, Chung W Y 2024 IEEE Trans. Veh. Technol. 73 8420 doi: 10.1109/TVT.2024.3357838 [3] Esmaiel H, Sun H X 2024 Sensors 24 7075 doi: 10.3390/s24217075 [4] 郑晓桐, 郭立新, 程明建, 李江挺 2018 物理学报 67 214206 doi: 10.7498/aps.67.20181112 Zheng X T, Guo L X, Cheng M J, Li J T 2018 Acta Phys. Sin. 67 214206 doi: 10.7498/aps.67.20181112 [5] Abd El-Mottaleb S A, Singh M, Armghan A, Atieh A, Aly M H 2025 Opt. Commun. 574 131204 doi: 10.1016/j.optcom.2024.131204 [6] Zhang L, Wang Z M, Wei Z X, Chen C, Wei G D, Fu H Y, Dong Y H 2020 Opt. Express 28 31796 doi: 10.1364/OE.405417 [7] Yan Z Q, Hu C Q, Li Z M, Li Z Y, Hang Z, Xian M J 2021 Photonics Res. 9 2360 doi: 10.1364/PRJ.438275 [8] Fei C, Wang Y, Du J, Chen R L, Lv N F, Zhang G W, Tian J H, Hong X J, He S L 2022 Opt. Express 30 2326 doi: 10.1364/OE.448448 [9] Nath N, Chouhan S 2024 IEEE Internet Things J. 11 39721 doi: 10.1109/JIOT.2024.3450541 [10] Li S, Wang P, Li G, Zhang X, Li H, Zhou B, Yang T 2023 Opt. Express 31 34729 doi: 10.1364/OE.500703 [11] Kong M W, Wang J L, Chen Y F, Ali T, Sarwar R, Qiu Y, Wang S L, Han J, Xu J 2017 Opt. Express 25 21509 doi: 10.1364/OE.25.021509 [12] Fu X Q, Li H W, Shi J H, Li T, Bao W S 2025 Sci. China-Phys. Mech. Astron. 68 210314 doi: 10.1007/s11433-024-2510-x [13] Li Z F, Kong X H, Zhang J, Shao L D, Zhang D J, Liu J, Wang X, Zhu W R, Qiu C W 2022 Laser Photon. Rev. 16 2200113 doi: 10.1002/lpor.202200113 [14] Wang H M, Zhang X, Jiang J C 2019 IEEE Wirel. Commun. 26 32 doi: 10.1109/mwc.001.1900045 [15] Wyner A D 1975 Bell Syst. Tech. J. 54 1355 doi: 10.1002/j.1538-7305.1975.tb02040.x [16] Guan K, Cho J, Winzer P J 2018 Opt. Commun. 408 31 doi: 10.1016/j.optcom.2017.07.078 [17] Shannon C E, Weaver W 1949 The Mathematical Theory of Information (Urbana: University of Illinois Press) p145 [18] Williamson C A, Hollins R C 2022 Appl. Opt. 61 9951 doi: 10.1364/AO.470464 [19] Zhang J L, Kou L L, Yang Y, He F T, Duan Z L 2020 Opt. Commun. 475 126214 doi: 10.1016/j.optcom.2020.126214 [20] Ramley I, Alzayed H M, Al-Hadeethi Y, Chen M G, Barasheed A Z 2024 Mathematics 12 3904 doi: 10.3390/math12243904 [21] Wen H, Yin H X, Ji X Y, Huang A 2023 Appl. Opt. 62 6883 doi: 10.1364/AO.498451 [22] Gabriel C, Khalighi M A, Bourennane S, Léon P, Rigaud V 2013 J. Opt. Commun. Netw. 5 1 doi: 10.1364/JOCN.5.000001 [23] Hollins R C, Williamson C A 2023 Appl. Opt. 62 6218 doi: 10.1364/AO.493186 [24] Hu J Y, Yu B, Jing M Y, Xiao L T, Jia S T, Qin G Q, Long G L 2016 Light Sci. Appl. 5 e16144 doi: 10.1038/lsa.2016.144 [25] Hu J Y, Jing M Y, Zhang G F, Qin C B, Xiao L T, Jia S T 2018 Opt. Express 26 20835 doi: 10.1364/OE.26.020835 [26] Hoang T M, Vahid A, Tuan H D, Hanzo L 2024 IEEE Commun. Surv. Tutor. 26 1830 doi: 10.1109/COMST.2024.3363639 [27] Illi E, Qaraqe M, Althunibat S, Alhasanat A, Alsafasfeh M, de Ree M, Mantas G, Rodriguez J, Aman W, Al-Kuwari S 2024 IEEE Commun. Surv. Tutor. 26 347 doi: 10.1109/COMST.2023.3327327 [28] 韩彦睿, 李伟, 臧延华, 杨昌钢, 陈瑞云, 张国峰, 秦成兵, 胡建勇, 肖连团 2023 物理学报 72 160301 doi: 10.7498/aps.72.20230398 Han Y R, Li W, Zang Y H, Yang C G, Chen R Y, Zhang G F, Qin C B, Hu J Y, Xiao L T 2023 Acta Phys. Sin. 72 160301 doi: 10.7498/aps.72.20230398 [29] Rioul O, Magossi J C 2014 Entropy 16 4892 doi: 10.3390/e16094892 [30] Solonenko M G, Mobley C D 2015 Appl. Opt. 54 5392 doi: 10.1364/AO.54.005392 [31] Liu X Y, Yang S H, Gao Y Z, Li J, Li C F, Xu Z, Fan C Y 2024 Opt. Commun. 569 130747 doi: 10.1016/j.optcom.2024.130747 -
计量
- 文章访问数: 134
- HTML全文浏览数: 134
- PDF下载数: 1
- 施引文献: 0