本研究采用轧制AZ31B镁合金，具体成分见表1。该材料适用范围广、性能稳定，具有很强的代表性，且合金元素含量较少，可以很好地反映金属 Mg的本质，合金元素对变形机制的影响也较小^[17]。

为了确定本构模型中AZ31B镁合金的材料硬化参数及失效参数，进行了AZ31B镁合金准静态拉伸试验和异形剪切试验。试验在WDW-100微控电子万能试验机（图1）上进行，参照的国家标准为 GB/T 228.1—2021《金属材料拉伸试验 第 1 部分：室温试验方法》。

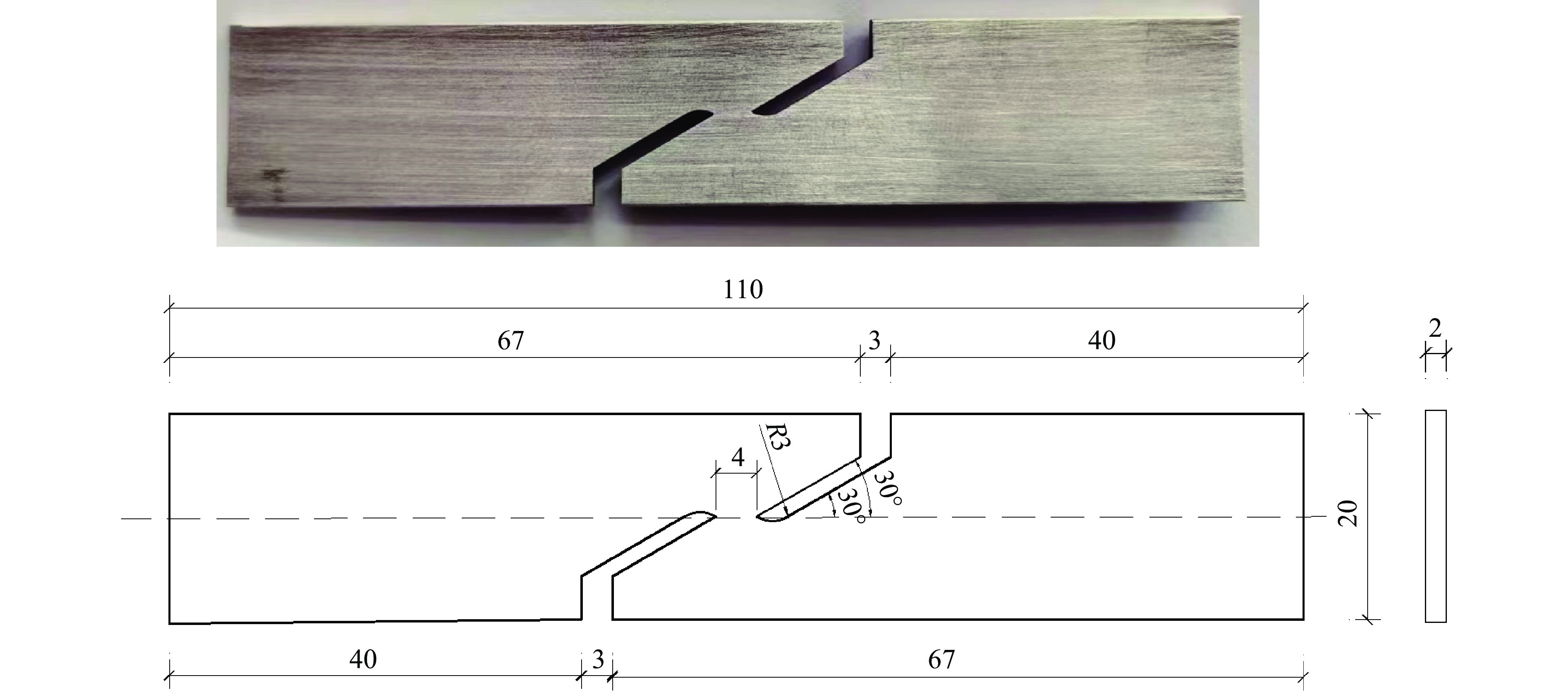
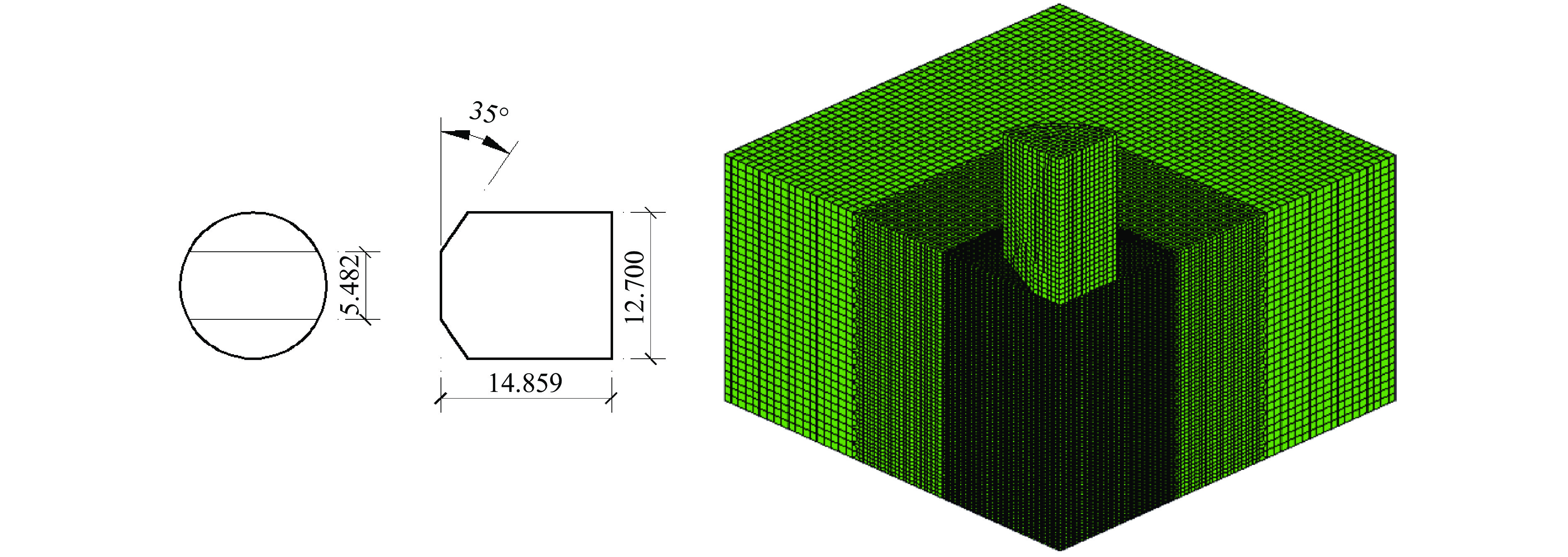
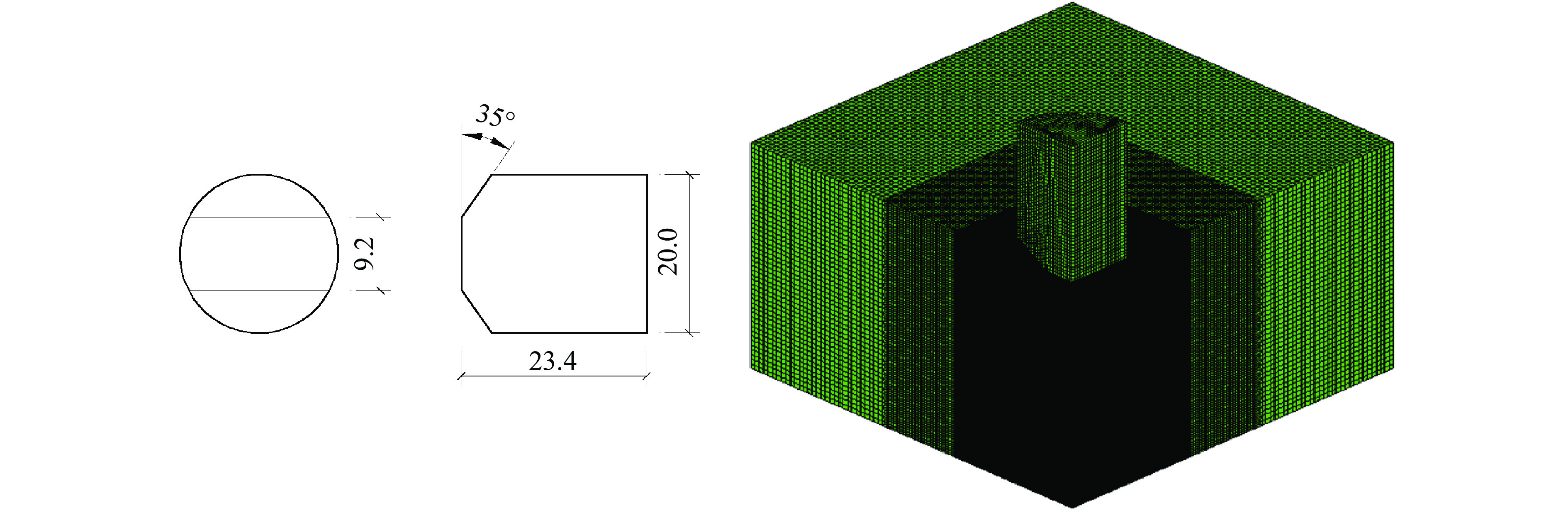
设AZ31B镁合金板的轧制方向为x方向，横截面的方向为y方向，厚度方向为z方向。如图2所示，将xy 面定义为轧制面，xz面定义为纵截面， yz 面定义为横截面。试验中所有加载方向均沿着垂直于镁合金材料横截面的方向进行，即图2中x方向。准静态拉伸试样和异形剪切试样的照片及尺寸如图3和图4所示。

研究人员对AZ31B镁合金开展了一系列动态试验研究^[18–28]，结果表明，AZ31B镁合金具有明显的应变率效应，并且温度对AZ31B镁合金的屈服强度、极限抗拉强度和延性等力学性能有显著影响。综合以上研究结果，本研究提出可以反映AZ31B镁合金在大变形、高温、高应变率下的强度模型，表达式如下

式中：$ {\sigma }_{\rm{eq}} $为等效应力；$ \varepsilon $为等效塑性应变；$ \xi $为Lode 角参数；$ \dot{\varepsilon } $为应变率；$ T $为当前温度；$ {A}_{\rm t}\left[{\left(1+{B}_{\rm t}\varepsilon \right)}^{{n}_{\rm t}}+D-1\right] $ 描述了材料的准静态拉伸行为和应变率的影响，$ {A}_{\rm t} $、$ {B}_{\rm t} $、$ {n}_{\rm t} $为拟合参数，可通过最小二乘法拟合室温、准静态条件下的真实应力-真实应变关系得到，$ D $为塑性应变为零时的动态增长因子；$ 1-\left(1-{\gamma }_{\text{p}}\right)\sqrt{1-{\xi }^{2}} $ 描述了材料的准静态剪切行为和Lode 角参数对材料强度的影响，$ {\gamma }_{\text{p}} $为剪切强度与拉伸强度之比；$ {\left(1-{{T}^{*}}^{{m}_{1}}\right)}^{{m}_{2}} $描述了温度的影响，$ {T}^{\mathrm{*}}$为无量纲温度，m₁、m₂为通过高温材料试验确定的材料参数。

D可由某一具体塑性应变（$ {\varepsilon }_{x} $）时的动态增长因子（$ {D}_{x} $）得到，即

$ {D}_{x} $可以通过以下函数形式对材料动态试验数据拟合得到，即

式中：$ {W}_{x} $、$ {B}_{y} $、$ {W}_{y} $、$ S $为通过材料动态试验确定的材料参数；$ {\dot{\varepsilon }}_{0} $为参考应变率，通常$ {\dot{\varepsilon }}_{0} $=1 s⁻¹，$ {\dot{\varepsilon }}_{\text{quasi}} $为准静态下的应变率，通常小于10⁻³ s⁻¹。

γ_p的具体形式为

式中：A_s、B_s、n_s为剪切参数，A_t、B_t、n_t为拉伸参数。Lode 角参数$ \xi $的定义为

式中：$ \overline{\sigma } $ 为等效应力，$ {J}_{2} $、$ {J}_{3} $ 为偏应力张量的第二和第三不变量，$ {\sigma }_{{\text{m}}}=\left({\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}\right)/3 $ 为平均应力，$ {\sigma }_{1} $、$ {\sigma }_{2} $、$ {\sigma }_{3} $ 为主应力。

$ T^* $表示为

式中：$ {T}_{{\text{a}}} $为环境温度，一般取室温293 K；$ {T}_{{\text{m}}} $为参考温度，一般取熔点。

失效准则参考周琳等^[29]的工作，考虑了应力三轴度 $ \eta $、Lode 角参数$ \xi $、应变率$ {\dot{\varepsilon }} $和温度T的影响，具体形式为

式中：$ {\varepsilon _{\rm f}} $为断裂应变，$ {C}_{1} $、$ {C}_{2} $、$ {C}_{3} $、$ {C}_{4} $ 为材料参数。应力三轴度 $ \eta $的定义为

式中：$ {I}_{1}={\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3} $，表示应力张量的第一不变量。

在冲击问题的研究过程中，局部区域往往出现塑性功转化为热量的现象。通常，将温度的增量ΔT表示为

式中： $ \rho $ 为靶板密度，$ {c}_{p} $ 为材料的比定压热容，$ \chi $ 为塑性功转化为热量的系数。

考虑到冲击波的传播， 通常采用 Grüneisen 状态方程来描述，该方程的形式为

式中： $ p$ 为静水压力；$ {C}_{0} $、$ {S}_{1} $、$ {\varGamma }_{0} $为材料参数；$ {E}_{{\text{m}}} $为材料的比内能；$ \mu =1-V/{V}_{0} $，$ V $、${V}_{0} $分别为当前比容和初始比容。

拉伸试验中，材料达到极限抗拉强度时会出现颈缩失稳，试件截面的应力不再均匀分布，如单轴拉伸时轴线处的单元处于三向拉伸应力状态，真实应力的理论计算需要进行Bridgman修正^[30]，真实应变需通过最小截面面积获得，然而，由于理论模型假设的局限性，修正后的结果仍有误差。因此，需要通过数值模拟进一步修正，以获得精确的应力-应变关系和断裂应变。

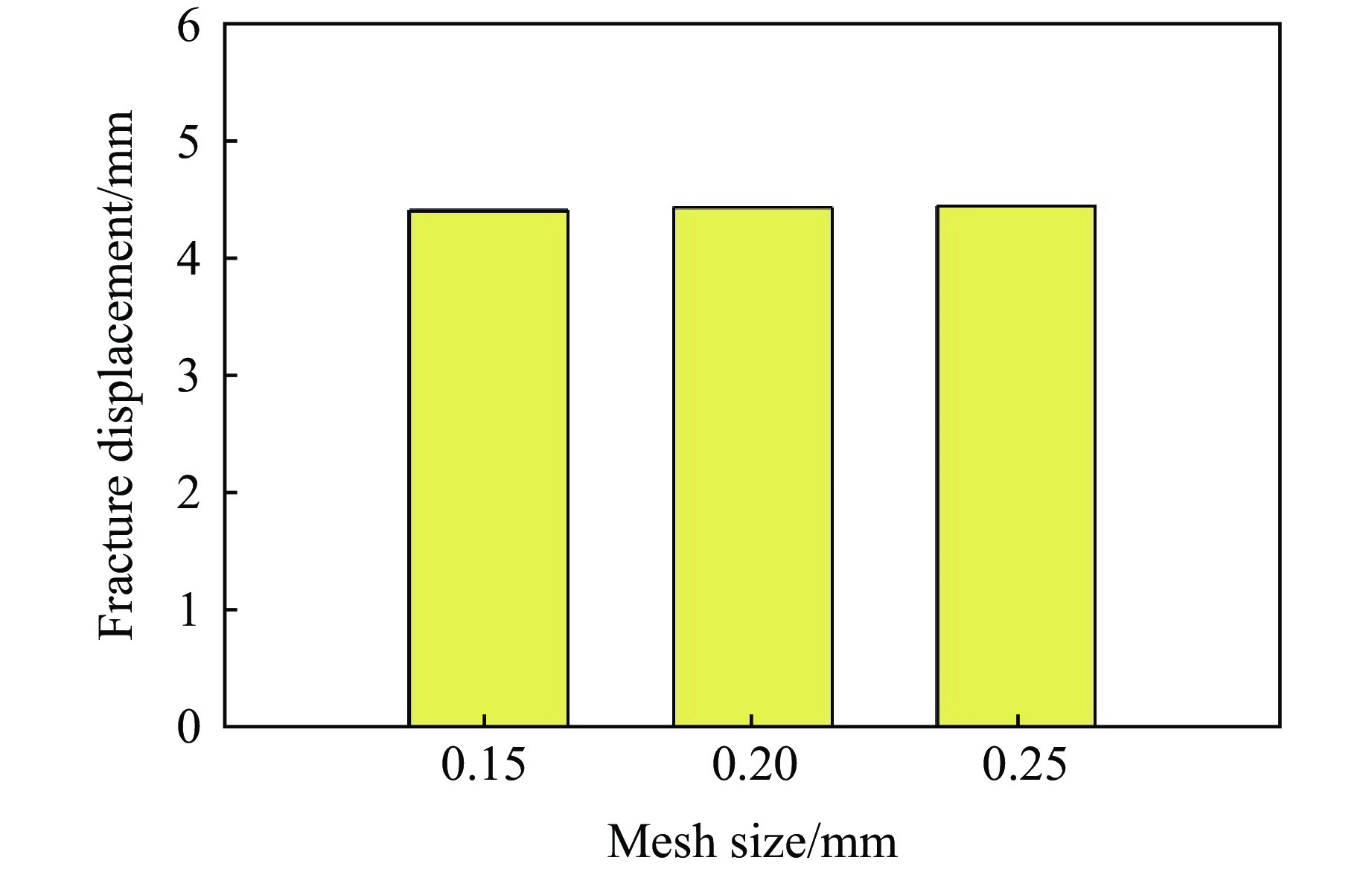
为了评估AZ31B镁合金有限元模型的网格依赖性，基于光滑圆棒试验构建有限元模型。图5给出了在不同网格尺寸（0.15、0.20和0.25 mm）下准静态拉伸数值模拟得到的断裂位移。由图5可知，3种网格尺寸的计算结果已经趋于稳定，表明模型已经达到收敛。鉴于此，在权衡计算效率与计算精度的基础上，选择0.20 mm×0.20 mm×0.20 mm作为有限元模型的网格尺寸。

图6和图7分别显示了AZ31B镁合金光滑圆棒和异形剪切样品的准静态拉伸有限元模型。考虑到光滑圆棒试件的对称性，建立1/4模型，并设置对称边界条件。异形剪切试件采用全模型计算。2种试件均一端固定，另一端拉伸，直至试件断裂，试件中间的主要力学响应区域采用细网格（0.20 mm×0.20 mm×0.20 mm），其余区域逐渐过渡到较粗的网格（0.40 mm×0.40 mm×0.40 mm）。

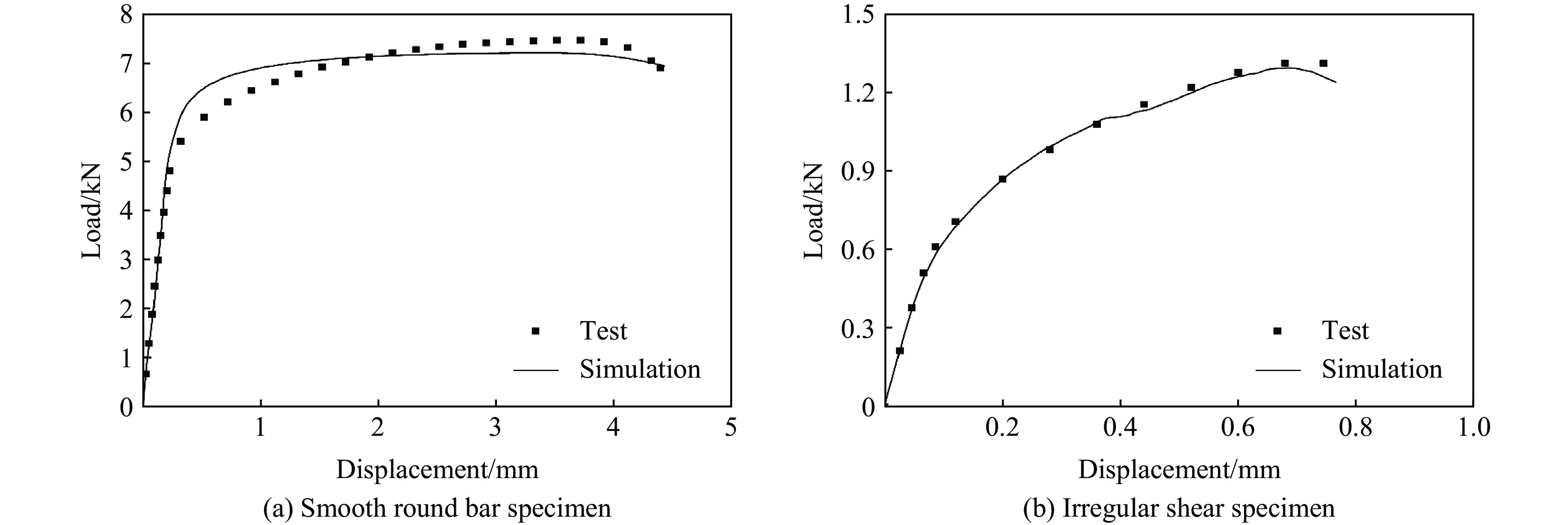
数值模拟标定的强度模型参数$ {A}_{\text{t}} $、$ {B}_{{\text{t}}} $、$ {n}_{{\text{t}}} $、$ {A}_{{\text{s}}} $、$ {B}_{{\text{s}}} $、$ {n}_{{\text{s}}} $分别为170 MPa、56740、0.058、70 MPa、255、0.358，失效准则参数$ {C}_{1} $、$ {C}_{2} $分别为0.40 、0.32。

图8为准静态工况下光滑圆棒试样和剪切试样的数值模拟结果与试验荷载-位移曲线的对比。由图8可知，当前模型能够较好地预测AZ31B镁合金在不同应力状态下的响应。

由图8(a)可知：在弹性阶段，光滑圆棒的数值模拟结果与试验数据高度一致；而在材料强化阶段，两者吻合度略有下降，最大相对偏差为8.5%；在材料颈缩阶段吻合较好，最大相对偏差为3.7%。试验观察发现：在加载初期，试件发生均匀变形，截面上应力分布均匀；当荷载达到最大值（即试件的抗拉强度）时，截面出现颈缩，随后失效破坏。

从图8(b)可以看出，剪切试样的数值模拟结果与试验数据的吻合度较高，最大相对偏差不超过3%。在加载初期，材料变形均匀，荷载随时间均匀增加；当材料达到线弹性剪切强度后，进入强化阶段，荷载呈现非线性变化；当加载到极限荷载时，材料出现局部变形，发生不均匀的塑性变形，伴随着剪切失稳，随后断裂。

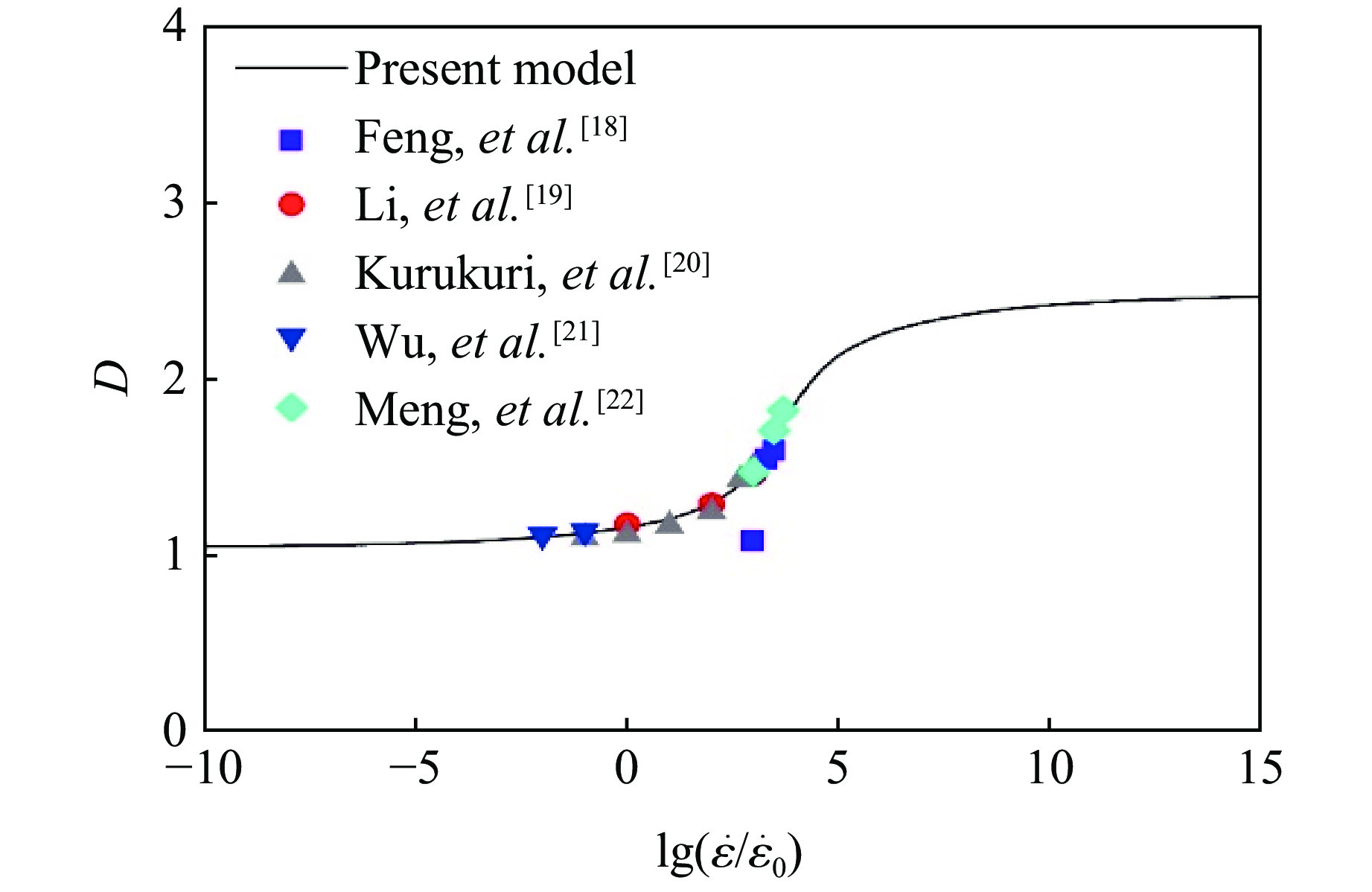
研究表明，在AZ31B镁合金的塑性变形过程中，滑移和孪生机制扮演着重要角色^[18–22]。在描述动态增强因子时，本模型采用非线性函数（见式(3)），并且综合考虑了塑性应变对动态增强因子的影响（见式(2)）。计算中，所用材料参数 $ {W}_{x} $、$ {B}_{y} $、$ {W}_{y} $、$ S $、$ {\dot{\varepsilon }}_{\text{quasi}} $ 和塑性应变 $ {\varepsilon }_{x} $ 分别为3.657、4.671、1.064、0.2013、0.001 s⁻¹、0.08。图9 给出了模型预测的室温下AZ31B镁合金的动态增强因子$ D $随无量纲应变率 $ \mathrm{l}\mathrm{g}\left(\dot{\varepsilon }/{\dot{\varepsilon }}_{0}\right) $ 的变化关系。当 $ \mathrm{l}\mathrm{g}\left(\dot{\varepsilon}/\dot{\varepsilon}_0\right) < 2 $ 时，AZ31B镁合金的应变率敏感性较低，$ D $呈线性缓慢增长；当 $ 2\leqslant\mathrm{l}\mathrm{g}\left(\dot{\varepsilon}/\dot{\varepsilon}_0\right)\leqslant6 $ 时，AZ31B镁合金表现出显著的应变率增强效应，$ D $随 $ \rm {lg}\left(\dot{\varepsilon }/{\dot{\varepsilon }}_{0}\right) $ 的增加而快速上升；当无量纲应变率 $ \mathrm{l}\mathrm{g}\left(\dot{\varepsilon}/\dot{\varepsilon}_0\right) > 6 $ 时，$ D $再次呈线性缓慢增长。

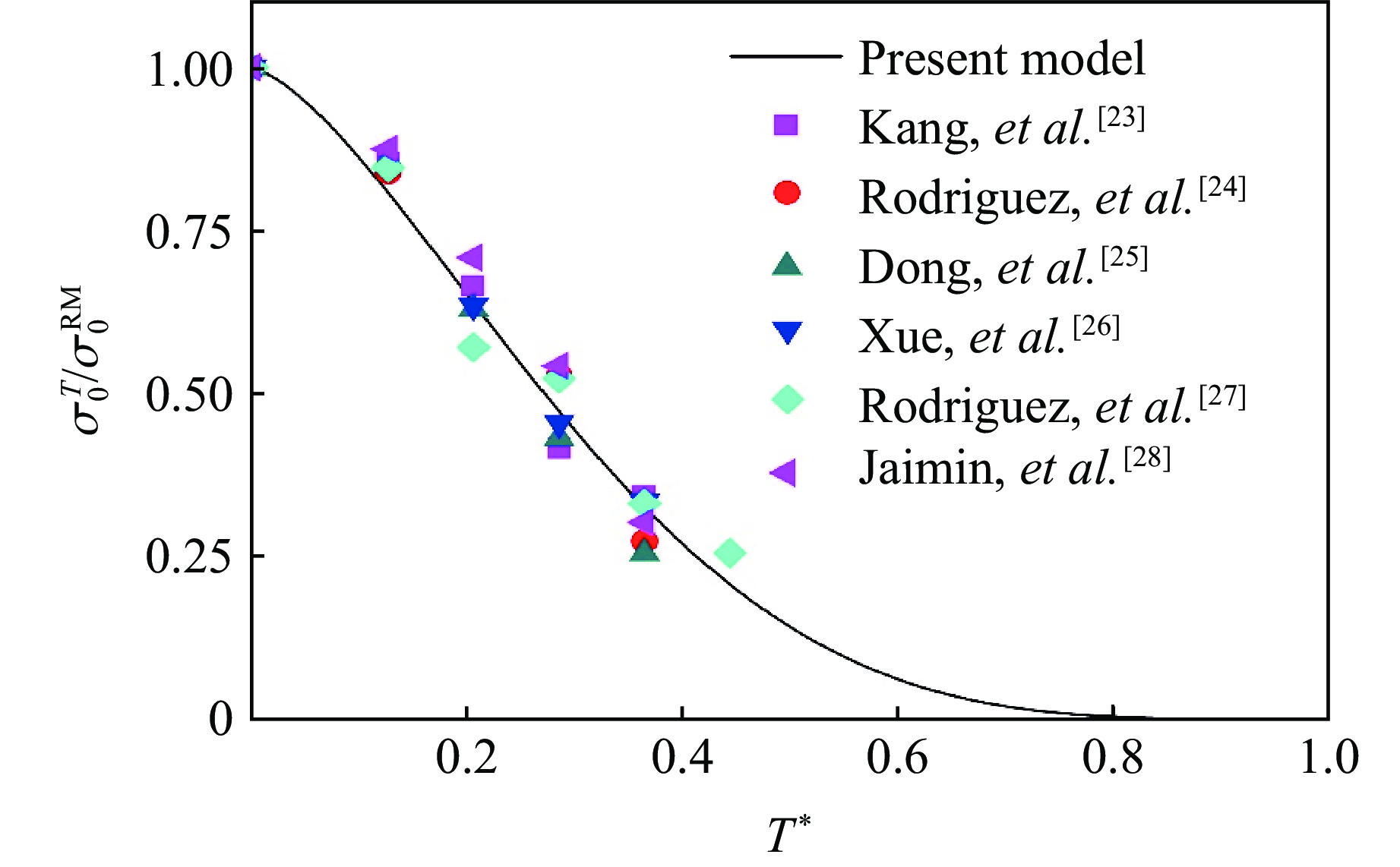
在描述温度对材料强度的软化效应方面，本研究的本构模型采用以无量纲温度为变量的指数函数形式，见式(1)。计算过程中使用的材料参数 $ {m}_{1} $、$ {m}_{2} $ 分别为1.476、4.384。图10 给出了模型预测的AZ31B镁合金在准静态条件下的高温强度与室温强度比$ {\sigma }_{0}^{T}/{\sigma }_{0}^{\text{RM}} $ 随无量纲温度$ {T}^{\mathrm{*}} $的变化趋势。可以看出：AZ31B镁合金的强度高度依赖温度；进入塑性变形阶段后，随着温度升高，AZ31B镁合金的流动应力明显降低。

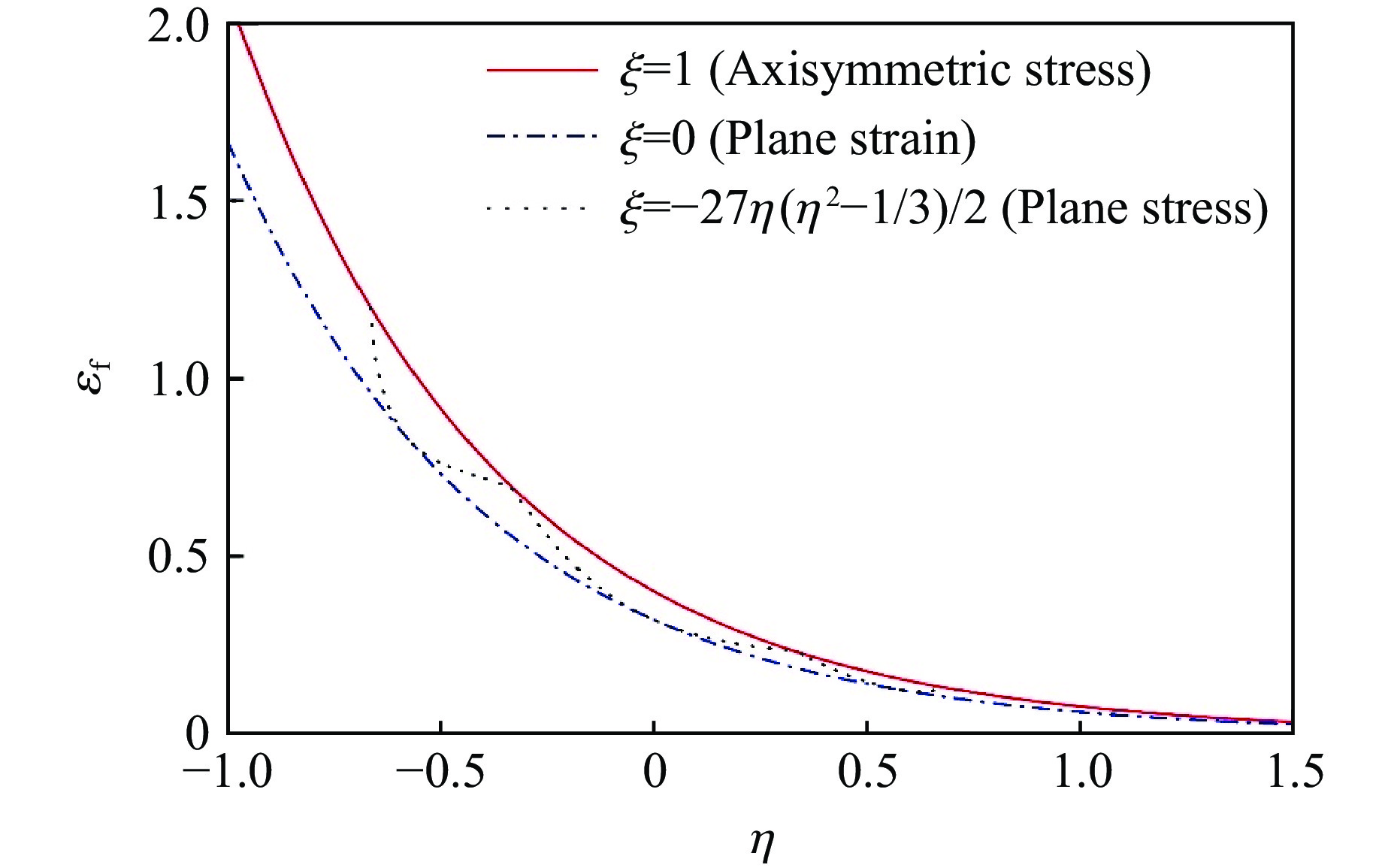
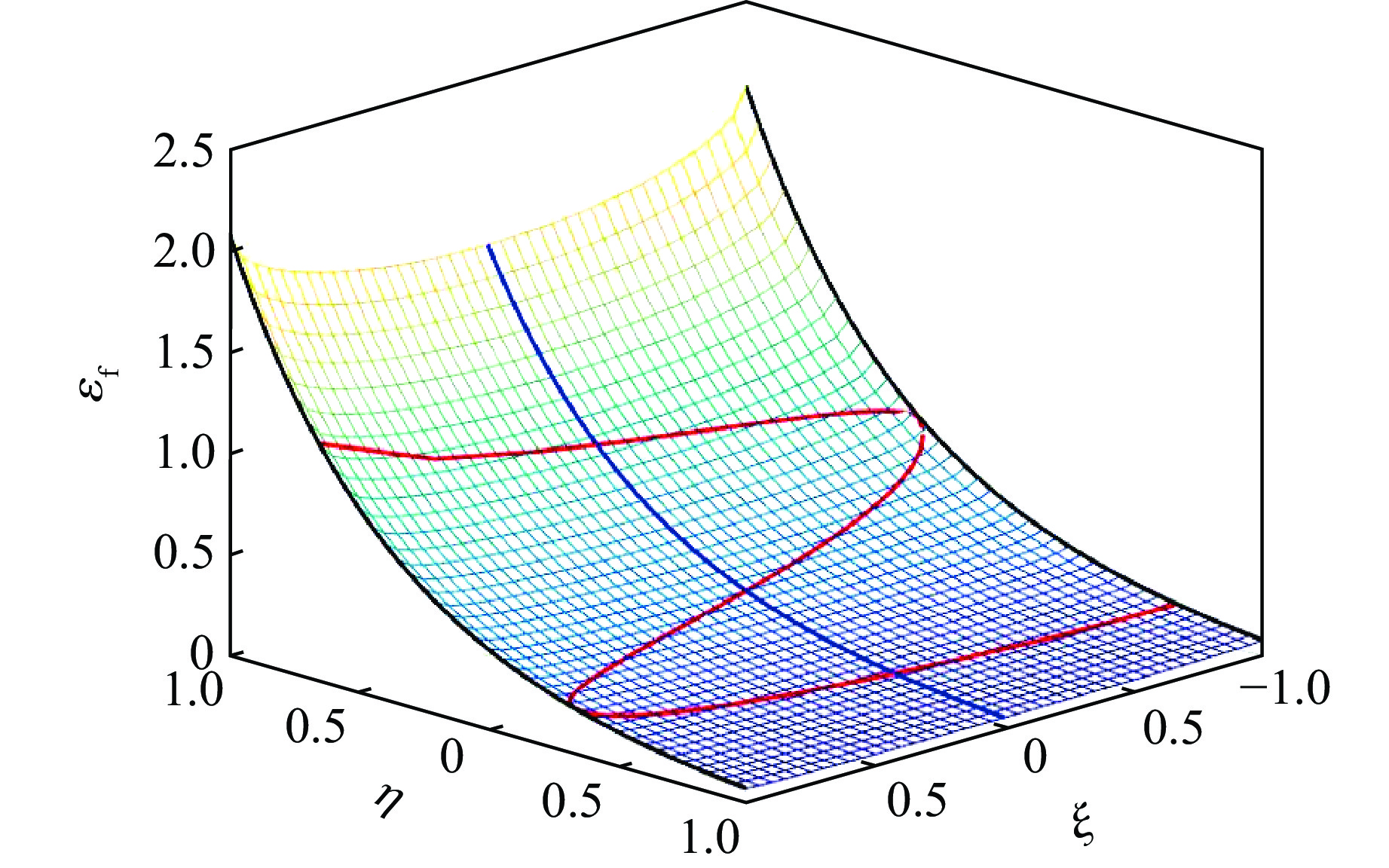
图11给出了不同 Lode 角参数下AZ31B镁合金的断裂应变随应力三轴度的变化关系，其中：实线代表轴对称应力状态，此时 $ \xi =1 $；点划线代表平面应变状态，此时 $ \xi =0 $；虚线代表平面应力状态，此时 $ \xi =-27\eta \left({\eta }^{2}-1/3\right)/2 $。图12为断裂应变与应力三轴度、Lode角的三维空间图，其中：黑色实线代表轴对称应力状态，此时 $ \xi=\pm1 $；蓝色实线代表平面应变状态，此时 $ \xi =0 $；红色实线代表平面应力状态，此时 $ \xi =-27\eta \left({\eta }^{2}-1/3\right)/2 $。失效准则中采用的材料参数 $ {C}_{1} $、$ {C}_{2} $ 是通过3.1.1节中准静态光滑圆棒拉伸试验和剪切试验并结合数值模拟确定的，分别为0.40和0.32。Jia等^[31]通过试验确定的参数 $ {C}_{3} $、$ {C}_{4} $ 在T<573 K时为0.020 和−1.803，在T≥573 K时为−0.113和2.544。

基于Jones等^[32]的0.5-cal FSP子弹撞击AZ31B镁合金靶板试验建立有限元模型，如图13所示， 其中：靶板厚度为25 mm；0.5-cal FSP子弹的直径为12.70 mm，质量为13.4 g。考虑到子弹和靶板的对称性，选取靶板的1/4进行建模。在撞击区域附近（25 mm×25 mm×25 mm）采用细尺寸网格（单元尺寸为0.20 mm×0.20 mm×0.20 mm），其余区域逐渐过渡到较粗的网格（单元尺寸为0.80 mm×0.80 mm×0.80 mm）。在模拟弹丸与靶板的接触时，采用Surface-to-Surface接触算法，弹体与靶板之间的摩擦力忽略不计。忽略弹丸在冲击过程中的形变，将其视为刚体。

基于Jones等^[32]的20 mm口径FSP子弹撞击AZ31B镁合金靶板试验，建立有限元模型，如图14所示，其中：靶板厚度为38.784 mm；弹丸的直径为20 mm，质量为53.8 g。同样建立1/4模型进行分析。在撞击区域附近（40.000 mm×40.000 mm×38.784 mm）采用细尺寸网格（单元尺寸为0.20 mm×0.20 mm×0.20 mm），其他区域逐渐过渡到较粗的网格（单元尺寸为0.80 mm×0.80 mm×0.80 mm）。采用Surface-to-Surface接触算法模拟子弹与靶板之间的相互作用，忽略摩擦力的影响。此外，忽略弹丸在冲击过程中的形变，将其视为刚体。

为了进一步检验子程序能否真实反映理论模型，构建了一个单单元模型，数值模拟准静态加载条件下的拉伸和剪切行为，检验其能否复现AZ31B镁合金在试验中标定的真实应力-真实应变关系。计算所用的材料参数见表2，其中：ρ₀为AZ31B镁合金的密度，E为弹性模量，ν为泊松比。

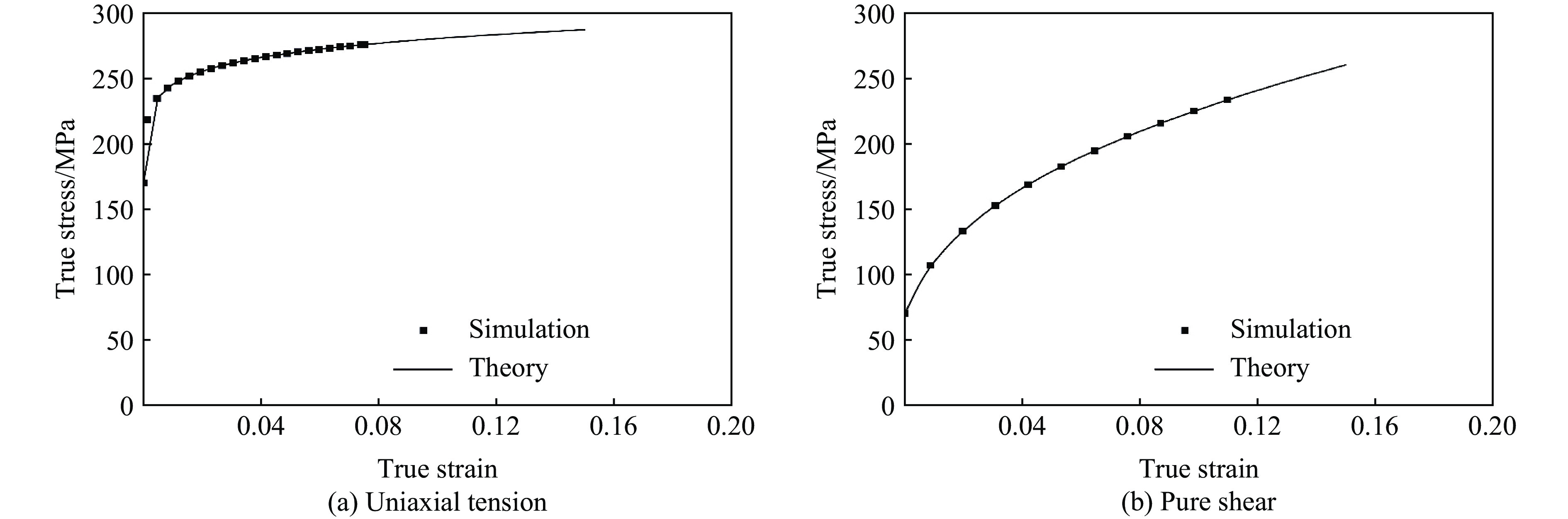
图15给出了模型预测的AZ31B镁合金材料在拉伸模式和剪切模式下的真实应力-真实应变曲线与理论结果的对比。可见，模型预测结果与理论结果一致，用户子程序能够正确执行。

弹道极限是衡量靶板抗弹性能的关键指标之一。通常情况下，采用Recht等^[35]提出的R-I公式拟合弹体初始撞击速度与残余速度之间的关系，以确定弹道极限。该公式的具体表达式为

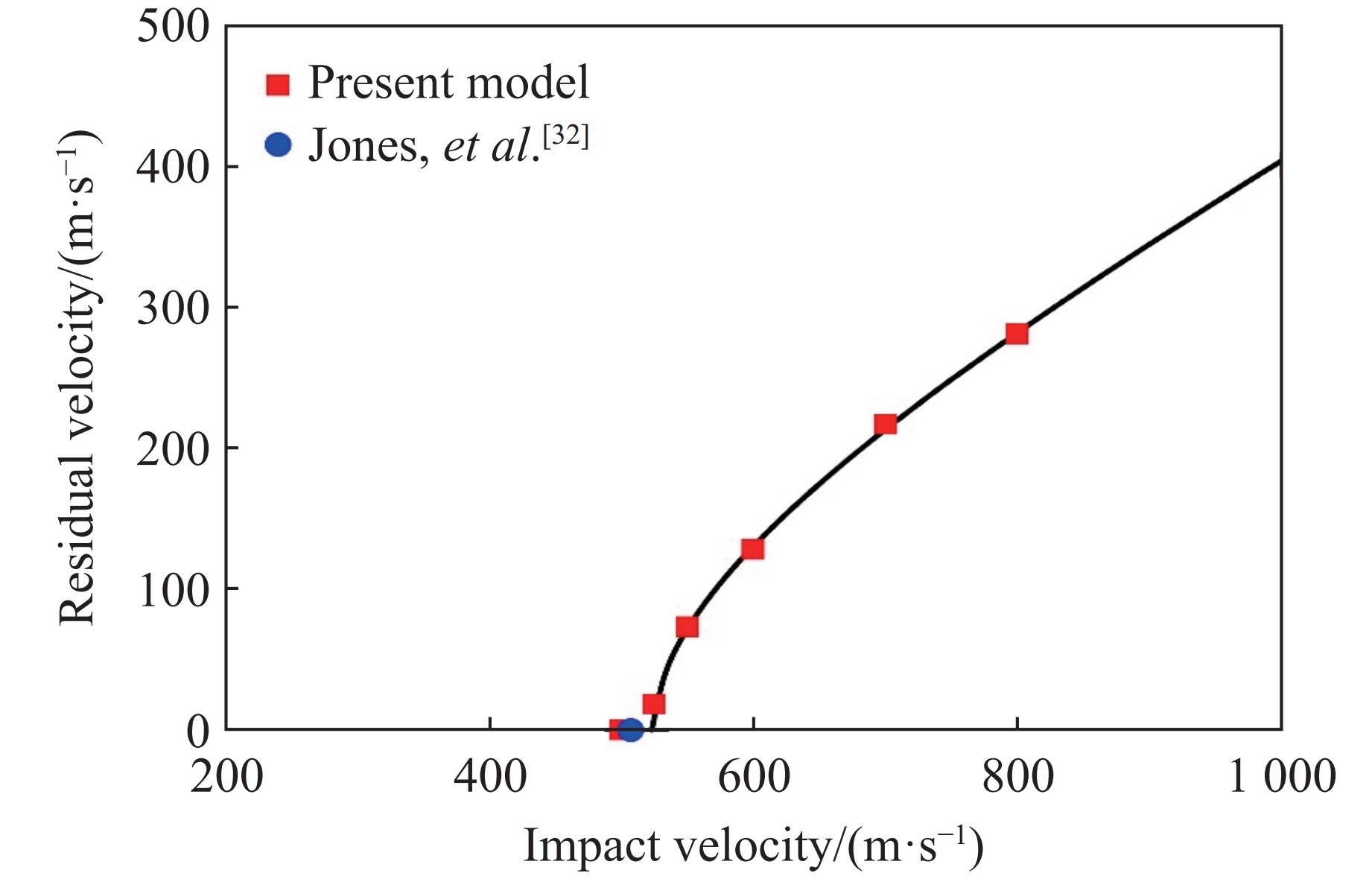
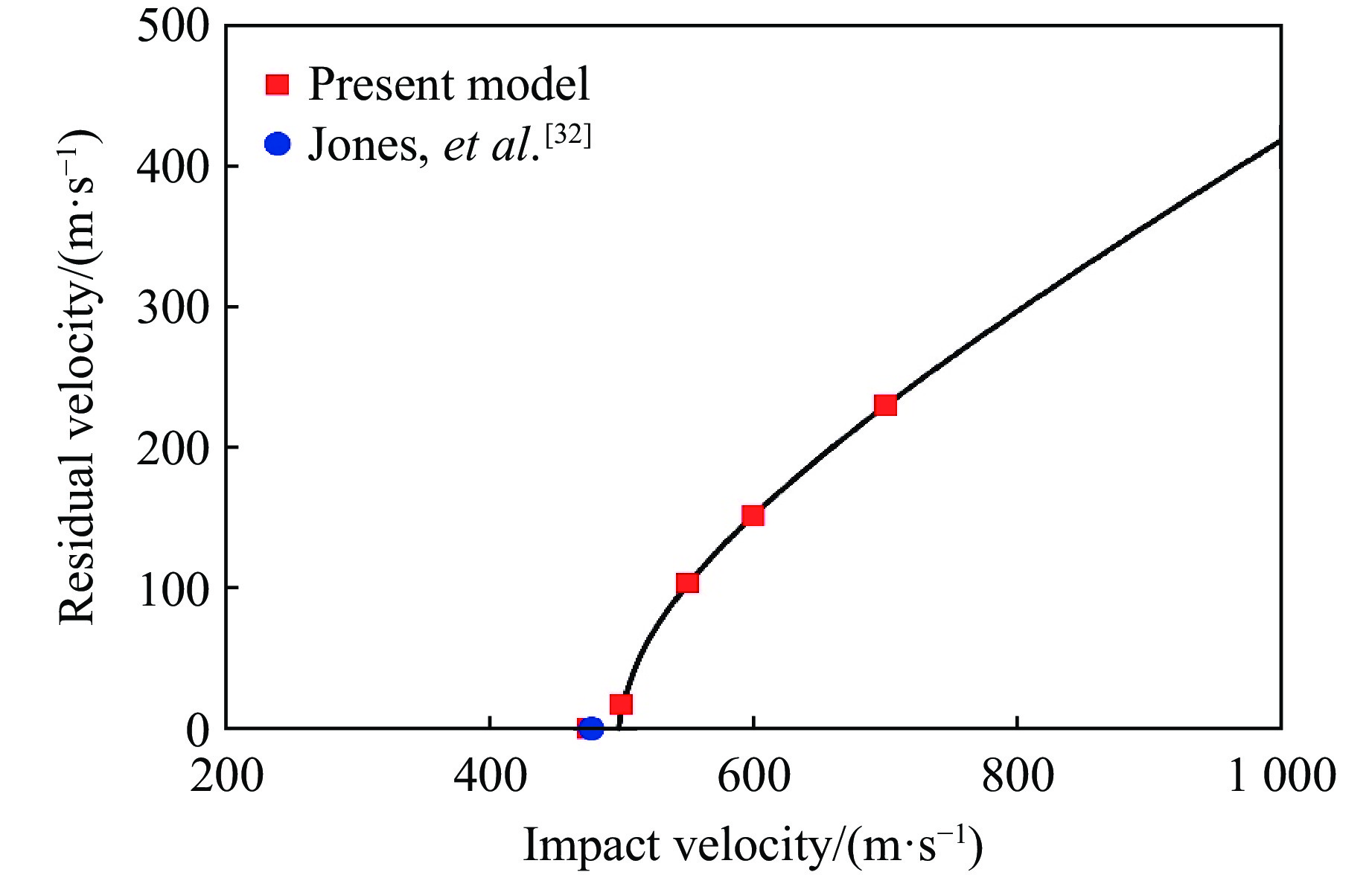
式中：$ {v}_{\rm i} $为子弹的初始速度，$ {v}_{\text{r}} $为子弹的残余速度，$ {v}_{\text{bl}} $为弹道极限，$ a $和$ P $为待定常数。$ {v}_{\rm {bl}} $ 通过最小二乘法拟合子弹残余速度与初始速度间的关系来确定。

数值模拟0.5-cal FSP子弹以不同初始速度冲击25 mm厚的AZ31B镁合金靶板的过程，可以得到对应的残余速度，拟合式(13)得到弹道极限。图16 给出了数值模拟预测的弹道极限与试验数据之间的比较。由图16可知，本构模型预测的弹道极限与试验数据基本吻合。表3给出了采用本构模型对0.5-cal FSP子弹撞击25 mm厚AZ31B镁合金靶板情况预测的弹道极限以及试验数据。模型预测的弹道极限为523 m/s，试验测定的弹道极限为507 m/s，两者之间的相对偏差仅为3.2%。

图17 为数值模拟预测的0.5-cal FSP子弹撞击AZ31B镁合金靶板的破坏模式与试验结果^[32]的对比。试验中0.5-cal FSP子弹以639 m/s的速度撞击25 mm厚的AZ31B镁合金靶板，靶板在此过程中主要以绝热剪切破坏为主，可以看出，数值模拟预测的破坏形貌与试验结果吻合较好。同时还可以看出，靶板正面的弹孔边缘产生了“唇”状凸起，靶板背面被贯穿后，弹坑周边出现了微小的凸起。

图18为数值模拟预测的20 mm FSP子弹撞击38 mm厚AZ31B镁合金靶板的弹道极限与试验数据的比较。可以看出，本构模型预测的弹道极限与试验结果基本吻合。模型预测的弹道极限为498 m/s，试验得到的弹道极限为477 m/s，两者之间的相对偏差仅为4.4%，见表4。

图19 给出了数值模拟得到的20 mm FSP子弹以472 m/s的速度撞击38 mm厚AZ31B镁合金靶板时靶板的破坏形貌与试验结果的对比。试验结果显示，靶板正面的弹孔边缘产生“唇”状凸起，靶板背面出现明显鼓包，并伴随裂纹的形成。由图19可知，数值模拟预测的破坏形貌与试验观测现象的契合度较高。

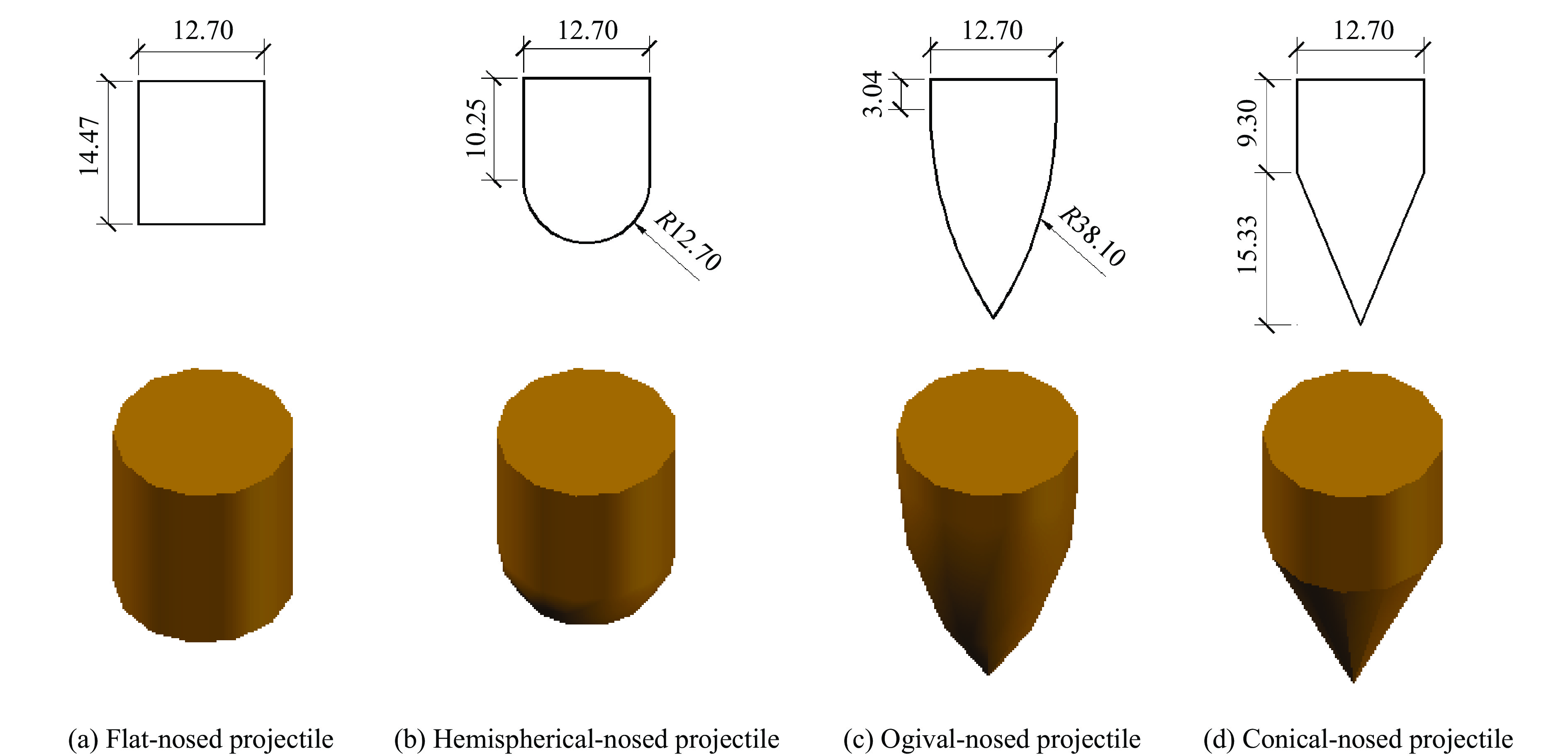
不同类型的子弹会对弹丸的飞行特性和效果产生一定影响，因此，在弹道设计和分析过程中必须充分考虑这一因素。图20展示了4种不同形状的弹头，包括平头弹、半球头弹、卵形弹和锥形弹。这些弹头在试验研究、理论分析和数值模拟中经常被使用。需要指出的是，这些弹头拥有相同的直径、密度和质量，但是形状差异导致了它们在长度上存在轻微的差别。本研究选取的弹头直径为12.70 mm, 弹头质量为13.4 g，AZ31B镁合金靶板的厚度为25 mm。直径为12.70 mm、质量为13.4 g的0.5-cal FSP子弹对25 mm厚的AZ31B镁合金靶板的冲击情况^[32]已在4.2节中进行了数值模拟验证。

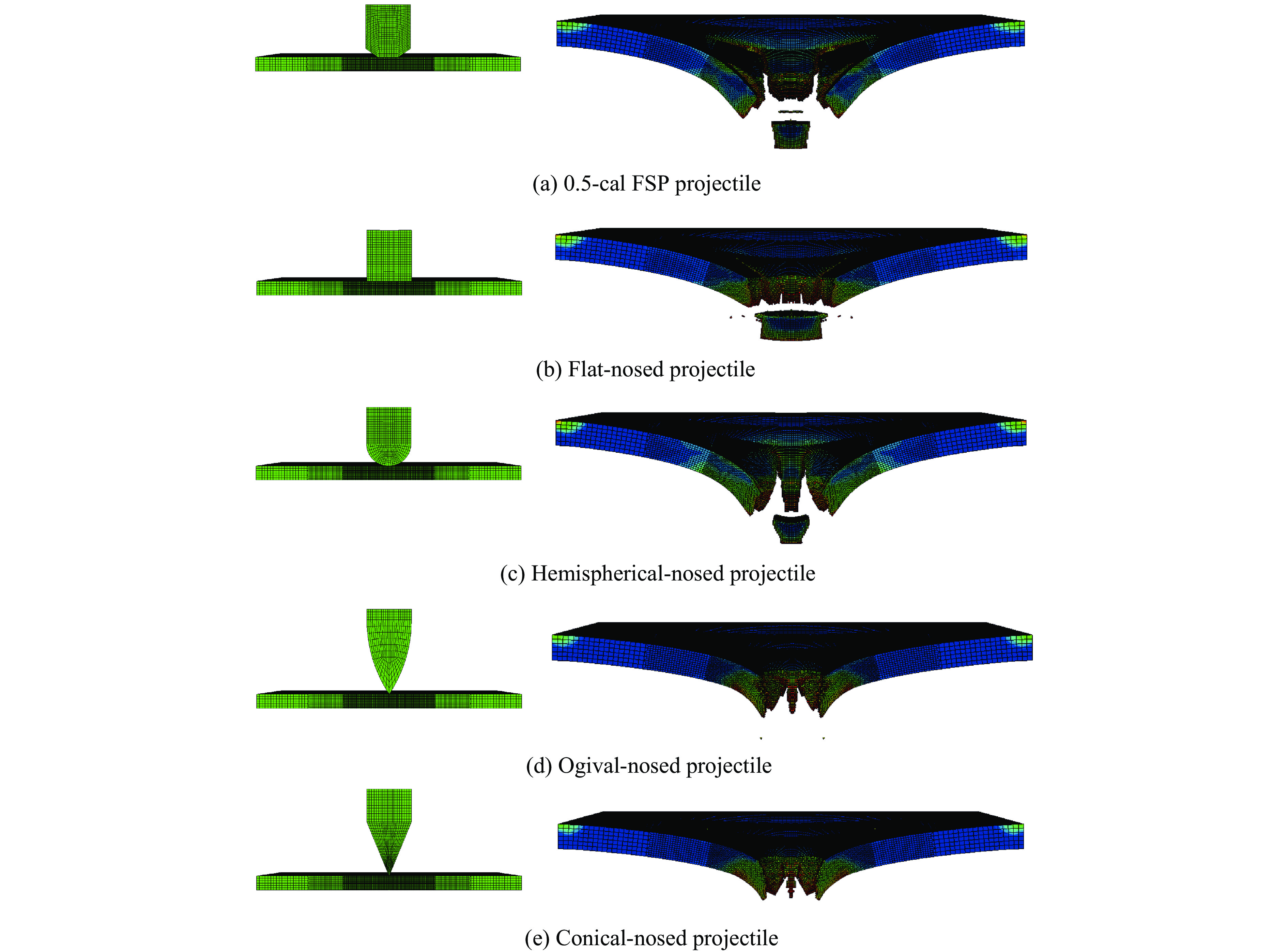
图21 给出了数值模拟预测的不同形状弹头在639 m/s速度下冲击靶板时横截面的破坏形貌。可见，不同形状弹头产生的破坏形貌不同：平头弹撞击靶板形成的冲塞体直径约为弹体直径，半球头弹造成的冲塞体直径约为弹体直径的1/2，卵形弹和锥形弹在撞击点附近引起靶板大面积整体性变形，形成延性扩孔。4种子弹的冲击模拟结果表明：平头弹冲击导致靶板发生剪切冲塞，弹体周边材料容易发生剪切失效，冲塞体厚度远小于靶板厚度，说明撞击初期为延性扩孔过程，直到弹体达到一定深度后失效机制才转变为剪切冲塞；半球头弹、卵形弹和锥形弹则通过推开靶板材料实现贯穿，靶板前后形成“唇”状边缘，但半球头弹在贯穿过程中会在弹体前方形成一个小冲塞体，“唇”状边缘特征并不显著。

表5列出了不同类型子弹冲击下弹道极限的数值模拟预测结果。平头弹对应的弹道极限最大（560 m/s），锥头弹对应的弹道极限最小（414 m/s），这种差异主要源于不同子弹冲击靶板时产生不同的失效机制。撞击初期，材料的失效主要受延性扩孔影响，子弹头部形状越尖锐，受到的阻力越小，弹道极限越低。平头弹和半球头弹在冲击响应后期会形成冲塞体，冲塞体吸收部分弹体动能，导致弹丸需要更多的动能才能穿透靶板。因此，平头弹和半球头弹的弹道极限相对较高，且平头弹的弹道极限最高。卵形弹和锥形弹的弹道极限几乎一致，表明子弹头部形状细节对弹道极限的影响并不显著。

薄靶和厚靶在冲击荷载作用下的失效模式存在显著差异，为此，采用数值模拟进一步分析了厚度为4 mm的薄靶的抗冲击性能。图22给出了数值模拟预测的不同形状弹头冲击下靶板横截面的破坏形貌，所有弹丸的撞击速度均为150 m/s。

由图22可知，不同类型的子弹撞击4 mm厚薄靶时，靶板产生较大弯曲变形，贯穿区域出现了盘状的凹陷，破坏形貌主要为花瓣状撕裂。由于靶板发生了弯曲变形，这部分变形也会消耗弹体能量，因此，在研究中是不可忽略的。此外，0.5-cal FSP子弹、平头弹和半球头弹与前面研究的25 mm厚靶板一样，均保留了剪切冲塞破坏的特征，但由于存在靶板弯曲变形，卵形弹和锥形弹的延性扩孔行为表现得不太明显。

本研究建立了金属动态本构模型，并编译成VUMAT用户子程序，采用万能试验机开展了AZ31B镁合金准静态光滑圆棒拉伸和异形剪切试验，校准了AZ31B镁合金本构模型的相关参数，研究了弹头形状、靶板厚度对弹丸高速侵彻AZ31B镁合金的影响，得出以下结论：

(1) 基于准静态单轴拉伸和纯剪切试验及数值模拟校验结果表明，AZ31B镁合金的拉伸和剪切力学行为不一致，拉伸强度明显高于剪切强度；

(2) 模型能够较好地预测AZ31B靶板在不同弹丸（包括0.5-cal FSP子弹和20 mm FSP子弹）冲击下的弹道极限、穿孔破坏形貌（包括靶板冲击面的“唇”状凸起、背面贯穿后弹孔附近的微小凸起和背面未贯穿的鼓包）；

(3) AZ31B镁合金靶板在不同形状弹丸冲击下的失效机制不同，通过模拟平头弹、半球头弹、卵形弹和锥形弹撞击25 mm厚AZ31B镁合金靶板，发现平头弹对应的弹道极限最大，锥形弹对应的弹道极限最小；

(4) 冲击荷载作用下，薄靶与厚靶的失效模式存在显著差异，薄靶（4 mm）以弯曲变形和花瓣形撕裂破坏为主，厚靶（25 mm）以剪切破坏为主。