首页
登录
注册
-
罗茨泵是利用两个相同凸转子的非接触旋转所产生的进口真空吸力，将介质输送到出口的一类容积泵，动力由轴向串联的齿轮副提供，最早用于罗茨真空泵，具有高效、强自吸、低脉动和耐磨损等性能，广泛应用于石油化工、医药、食品等行业领域[1-2]。其中，转子叶上工作轮廓线的形状及其形状系数直接决定了泵的轻量化、脉动、运行稳定性等诸多性能[3-4]，总体上工作轮廓线所采用的曲线类型决定了转子能取得的最大形状系数，形状系数越大，轻量化效果越好，但脉动和稳定性能相对越差[5]，因此往往也采用较小的形状系数来提高脉动质量和工作稳定性，并通过增大转子宽度来弥补较小形状系数带来的排量损失。目前，新型轮廓线形状的采用和组合轮廓线的设计仍是轮廓构造的主要研究方向，在圆弧[6]、渐开线[7]和摆线[8]等传统轮廓线研究的基础上，还包括了双曲线[9-10]、抛物线[11]、椭圆弧[12-13]、直线[14]、弦线[15]甚至单点[16]等非常规轮廓线的探讨与应用。由于转子副不承担动力传递，所以轮廓构造上采用1的重合度，且以节圆为界将转子半叶轮廓划分为节圆外和节圆内具有互构关系[17]的两部分工作轮廓段，并以其中某一工作轮廓段所采用的曲线类型加以命名，例如，圆弧、渐开线、摆线转子（泵）等。截止目前为止，转子轮廓多采用基于由节圆外已知轮廓确定节圆内待定轮廓的顶轮廓对称轴（简称为顶轴）的构造法，由此构造出的节圆外工作轮廓段具有凸曲线特征，导致转子叶的截面积惯性矩相对较大，易带来工作稳定性等动力学性能方面的问题[18]。如何缓解这一问题，或者说如何实现节圆外工作轮廓段具有构造上的凹曲线特征，鲜见相关文献[5]报道，现有的顶轴外构造法也难于实现。鉴于抛物线轮廓构造的复杂性[19-20]，拟就其工作轮廓段基于中轴（即过转子中心和轮廓与节圆交点的轴）的节圆外和节圆内的两种构造新方法展开深入的通用性研究，以期更好地拓展罗茨泵的潜在性能，和进一步完善现有罗茨转子的轮廓构造方法，并为其它曲线类型的应用提供技术方案。
-
图1中，o为转子中心，半叶轮廓asped由圆心为ps的顶过渡圆弧as，节圆外、内工作轮廓段sp、pe，圆心为pe的根过渡圆弧ed共四部分相切相连组成，p为半叶轮廓的中点，也是转子副的共轭节点，oa为顶轴，op为中轴，od为根轴，xpy为坐标系，ps、pe为顶轴、根轴分别与节圆的交点；∠aop=∠dop=τ= 0.5π/N，N为转子叶数，ε=oa长度/节圆半径R为形状系数。注：所有长度尺寸均采用实际尺寸除以R的无量纲长度，例r=R/R=1的无量纲节圆半径。
当sp或pe为抛物线时，分别称之为中轴外或中轴内抛物线的轮廓构造，m为其上任一点，对应曲率的中心、半径为om、rm；法线mom与中轴的交点、交角为g、θ，mg、pg的长度为rg、h；端点s、e的横坐标xs(k)、xe(k)，均由抛物线系数k唯一确定。
由抛物线的定义及其上m(xm, ym)的坐标方程
得ym对xm的一阶导数ym'
和二阶阶导数ym''
式中，xe≤xm≤0、0<xm≤xs为中轴内、外的构造区间。
则，以xm、k为变量的抛物线共性特征量为
-
图2中，N=3，m为抛物线sp上任一点，待定轮廓段pe上与m具有互构关系的点为m'，pm、pm'为m、m'的位于节圆上的相对速度瞬心。由共轭原理知m和m'处具有相同的节圆相位角σ、传动角φ(σ)和啮线距ρ(σ)[5]。其中，φ(σ)和ρ(σ)关于σ的解析函数，渐开线等能直接得到，而抛物线等则不能，故采用xm代替σ来间接得到，由此也看出抛物线转子轮廓构造的复杂性就在于φ(σ)和ρ(σ)的非直接得到。
在△pmgo中，由
得
就pm(xpm, ypm)的横坐标xpm，另由
得
及
当式（8）中xm=xs(k)时，再由
得xs(k)，例N=3、k=2时，xs = 0.4104。
则，ps(xps, yps)和pe(xpe, ype)的互构方程为
本体转子上m与配对转子上m'的凹−凸共轭关系，如图3所示。其中，o'为配对转子中心，m'处的曲率中心、曲率半径分别为om'、rm'。
由凹−凸轮廓外共轭的欧拉一萨瓦里共轭方程
得
时才不会出现轮廓干涉现象[20]。
N=3、k=2、xs=0.4104时，rm、r'm随xm的变化规律，如表1所示。由此推断出rm最大化的位置为s处；r'm最小化的位置为e处。
当式（13）中xm=xs(k)时，由
得k的最小值kmin及其对应的最大形状系数εmax为
当k=kmax=∞时，图2中sp变成位于x轴的直线段，对应的最小形状系数εmin为
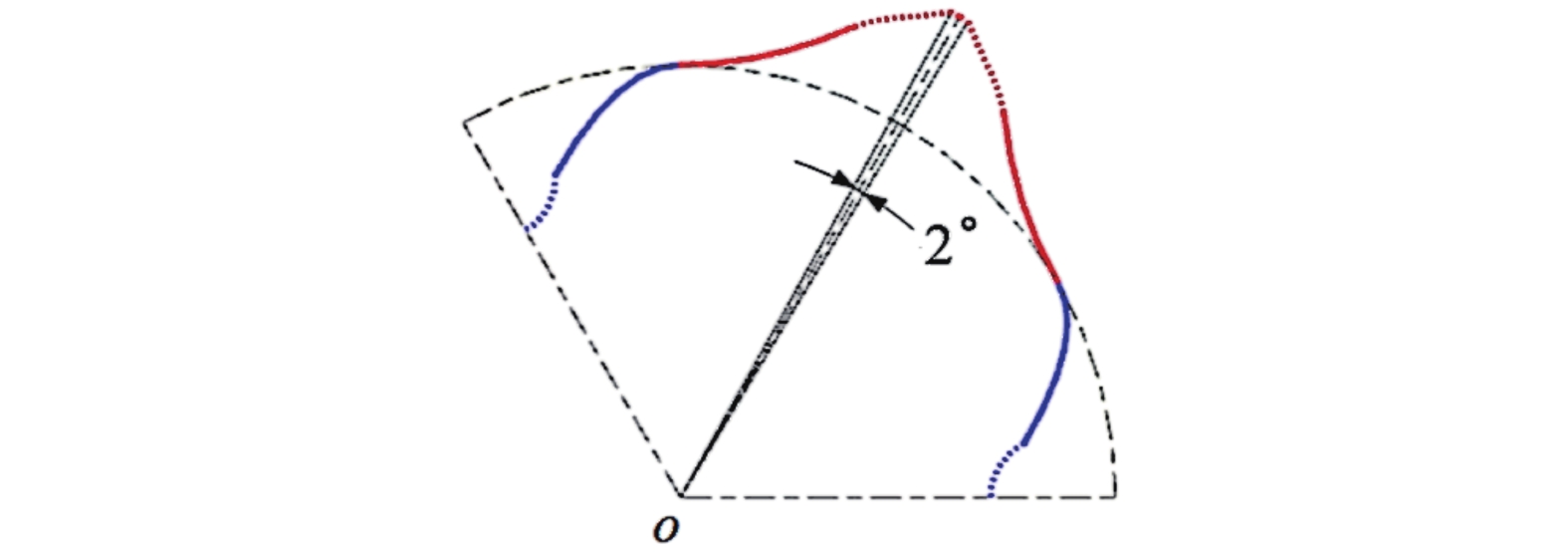
由此可见，εmax由待定轮廓pe不发生干涉的零最小曲率半径条件所决定，εmax一般较小，选用范围也较窄，例2叶时ε=1.134~1.244，此时在不改变抛物线凹曲线特征的前提下，可通过进一步的高形化技术[20]来增大转子的形状系数达1.313，且因顶部2°的与o同心的圆弧能减少径向泄漏，如图4所示。
-
图5中，N=3，m为抛物线pe上任一点，sp上的互构点为m'，相应的相对速度瞬心分别为p'm、pm。
在△pmgo中，由
得
就pm(xpm, ypm)的横坐标xpm，另由
得
及
当式（20）中xm=xe(k)时，再由
得xe(k)。例N=3、k=0.2时xe = −0.226。
则，ps(xps, yps)和pe(xpe, ype)的互构方程为
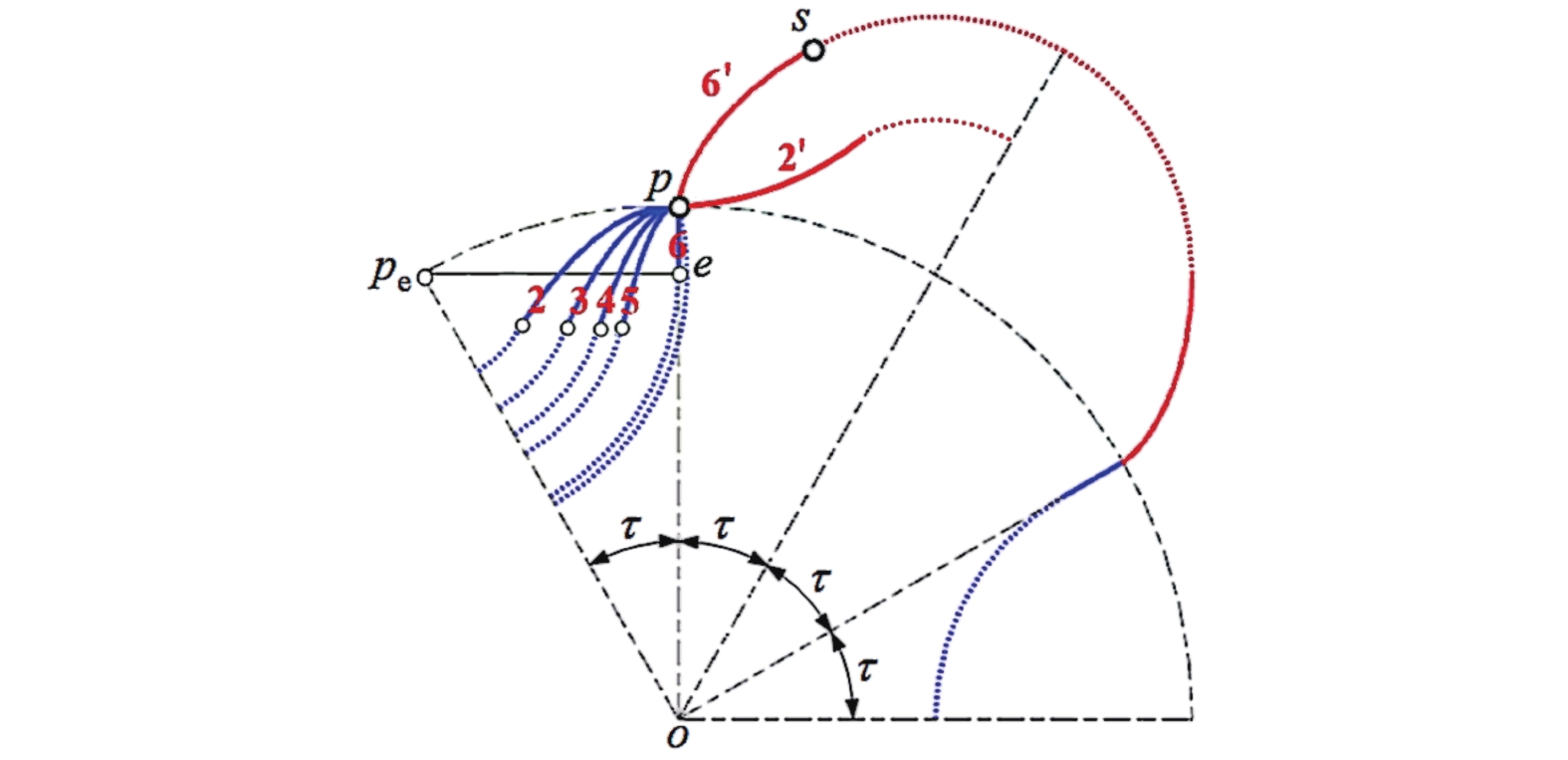
图6中，k=40、20、10、5、0下的pe分别以2、3、4、5、6标识，k=40、0下的ps以2'、6'标识，如所示。其中，k越小，ε越大，尤其k=kmin=0时，pe将变成位于中轴上直线段6，相应的εmax为
由此可见，εmax由抛物线轮廓的自身形态所决定，ε的选用范围很大，不过待定轮廓ps也将由凹曲线2'变成为凸曲线6'，轮廓构造柔性好。
-
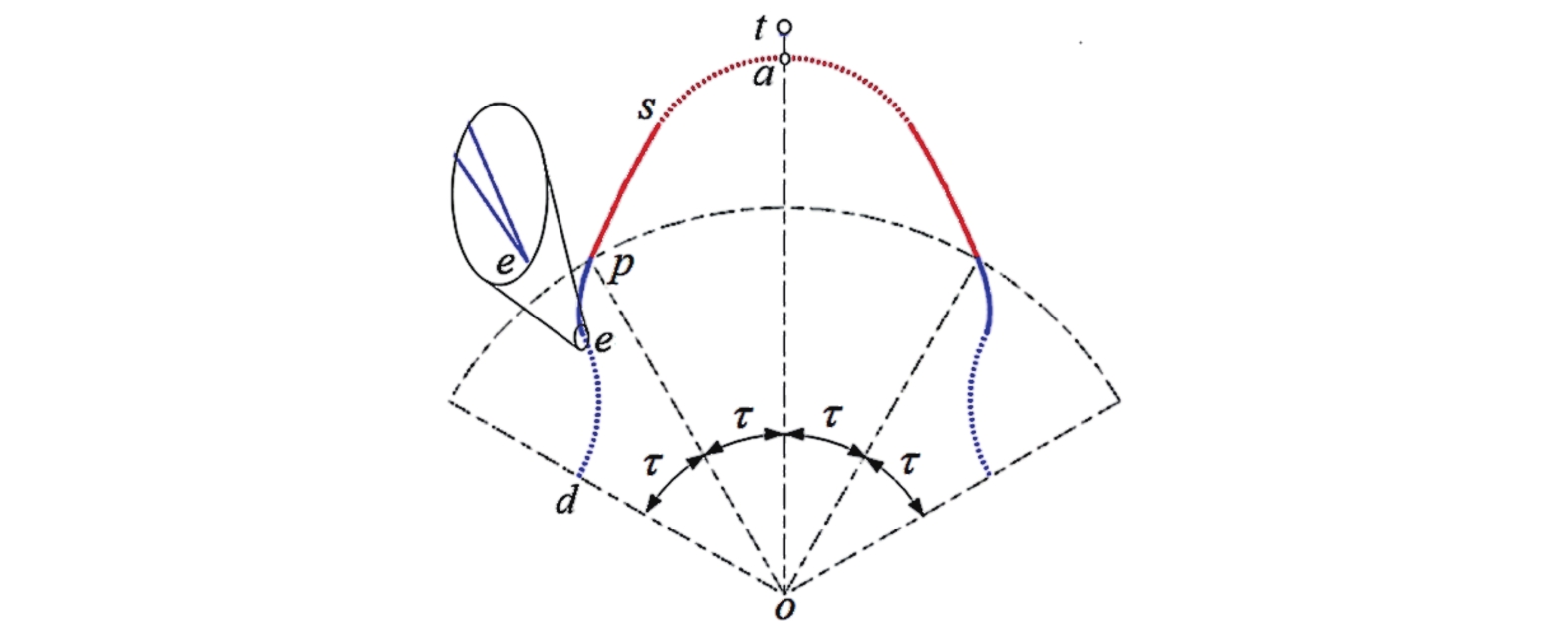
图7中，N=3，t为抛物线顶点，ot为顶轴及其长度为ho，sp为抛物线。
在图7直角坐标系xty中，由p(xp, yp)的坐标
得
在△pmgo中，由
得
就pm(xpm, ypm)的横坐标xpm，另由
得
及
就式（4）中的h(xm, k)，当xm=xs(k)时，由
得
例N=3，k=0.55时xs=−0.1583。
则，ps(xps, yps)和pe(xpe, ype)的互构方程为
由式（33）根号内大于等于0的有解要求，得
则最大抛物线系数kmax及其最小形状系数εmin为
例N=3，k=kmax=0.586时的叶轮廓，如图8所示。其中，无顶、根过渡圆弧段as、ed。
采用与前述同样的推断方法，得rm最大化的位置为s处，r'm最小化位置为e处，得k的最小值kmin及其对应的最大形状系数εmax为
k(3)=kmin(3)-0.0014=0.418的微小变化时，端点e处出现了轮廓干涉，如图9所示。由此验证式（25）~（37）的正确性，同时也说明εmax也由待定轮廓pe不发生干涉的零最小曲率半径条件所决定。
-
图1-图9均由所涉公式通过UGNX的规律曲线绘制，xs、xe均由EXCEL的规划求解得出，由图1-图9的合理性，说明所建式（1）~式（37）的正确性。
图10中，c1、c2、c3分别为顶轴外、中轴内、中线外3叶抛物线转子的叶轮廓，因c3如式（15）所示的εmax=1.244，c1如式（36）所示的εmin=1.293，c2的ε=1.0~1.5可选范围大，所以通过ε=1.244的c2、c3和ε=1.293的c1来比较这三种构造方法下的叶截面属性。
由此计算出各自的k、xe(k)或xs(k)，并构建出基于UGNX软件的叶轮廓，及创建出厚度1 mm的3D模型，再通过测量面得出叶截面积，测量体得出叶的质心位置，如表2所示。其中，测量坐标系为xoy。
以c1的叶截面积惯性矩E=叶截面积×y2为比较基准，则c2、c3的叶截面积惯性矩降低9.77%、12.00%，c3较c2降低2.48%。一般来说，叶截面积惯性矩越小，工作稳定性等动力学性能相对越好。
因为共轭处存在较大的非接触间隙，由图10还可以看出，c1、c2、c3分属于凸−凸、近似凸−平、凸−凹型的共轭模式，所以c1的共轭泄漏量相对最大，c2的居中，c3的相对最小。
-
(1) 传动角和啮线距关于节圆相位角的函数解析性决定了轮廓构造的繁简程度，渐开线等轮廓线能显性解析则简，抛物线等轮廓线只能隐性解析则繁，优选抛物线轮廓点的横坐标代替节圆相位角的构造变量，能化繁为简。
(2) 抛物线系数越小，形状系数越大，最小抛物线系数由待定共轭轮廓不发生干涉的最小曲率半径为零所决定。中轴外构造法下2、3、4叶的最小抛物线系数/最大形状系数为19.52/1.32、1.81/1.24、0.75/1.08；中轴内构造法下的为0/1.71、0/1.50、0/1.38，顶轴外构造法下的为0.60/1.49、0.42/1.39、0.31/1.32。
(3) 中轴外、中轴内较顶轴外构造法易于实现节圆外工作轮廓的凹函数特征，导致案例中轴外、中轴内较顶轴外叶截面积惯性矩下降分别9.77%、12%，从而有效降低共轭泄漏和提高旋转稳定性。
罗茨轮廓的中轴构造法及其叶属性分析
Median-Axis Construction Method of Roots Contour and Its Lobe Nature Analysis
-
摘要: 为进一步提升罗茨泵的潜在性能和完善转子轮廓的现有顶轴构造法，提出了基于中轴的两种构造新方法；以抛物线的应用为例，首先以任一共轭点处的啮线距和传动角为构造参数，共轭点的横坐标为构造变量，建立出共轭轮廓的互构方程；其次由待定轮廓上出现零最小曲率半径的特殊情况，确定出最小抛物线系数及其最大形状系数，最后对比分析中轴外/中轴内/顶轴外构造法下的叶截面属性及其潜在性能。结果表明构造参数关于构造变量的函数解析性决定了轮廓构造的繁简程度，优选抛物线轮廓点的横坐标为构造变量能化繁为简；最大形状系数由最小抛物线系数所决定，最小抛物线系数由待定轮廓上出现零曲率半径的极限条件所决定，中轴外/中轴内/顶轴外构造法下的最小抛物线系数为2叶的19.52/0/0.60，2叶的1.81/0/0.42，4叶的0.75/0/0.31，最大形状系数为2叶的1.32/1.71/1.49，3叶的1.24/1.50/1.39，4叶的1.08/1.38/1.32；中轴外、中轴内较顶轴外构造法易于实现节圆外工作轮廓的凹函数特征，叶截面积惯性矩分别下降9.77%、12%等，得出中轴构造法更能降低共轭泄漏和提高旋转稳定性的重要结论。Abstract: In order to further expand roots pump potential performance and improve the rotor-contour construction method based on the current top-axis, two new methods of contour construction based on the median-axis are proposed; with the application of parabolic contour as an example, from the contacting-line and transmission-angle on either conjugate point as constructing parameters, the abscissa of the conjugate point is the construction variable, the inter-construction equations for the lobe contour are derived firstly; from the minimum curvature radius on lobe contour being zero, the minimum parabolic coefficient and following maximum shape coefficient are derived secondly; the lobe cross section natures and following potential performances under three different construction methods of outer median-axis and inner median-axis and outer top-axis are compared and analyzed finally. The results show that the functional analysis of constructing parameters determines the complexity of the contour construction, and the abscissa of the parabolic contour point as the construction variable can simplify the complexity. The maximum shape coefficient is determined by the minimum parabolic coefficient, and the minimum parabolic coefficient is determined by the zero minimum curvature radius on the pending contour. For the three different construction methods of outer median-axis and inner median-axis and outer top-axis, the minimum parabolic coefficient is 19.52/0/0.60 under two lobes, 1.81/0/0.42 under three lobes, 0.75/0/0.31 under four lobes; the maximum shape coefficient is 1.32/1.71/1.49 under two lobes, 1.24/1.50/1.39 under three lobes, 1.08/1.38/1.32 under four lobes; the concave function features of the outer working contour are easier to be realized by the inner and outer median-axis construction method than the top-axis construction method, and the lobe cross-sectional area inertia moment is decreased by 9.77% and 12%, etc. It is concluded that the construction method based on the median-axis can better reduce the conjugate leakage and improve the rotational stability than the current top-axis construction method.
-
-
图 1 中轴内外轮廓的抛物线特征
Figure 1. Structural features of inner and outer-parabola-contour based on median-axis
图 2 中轴外抛物线转子的轮廓构造
Figure 2. Rotor-contour-structure of outer-parabola-contour based on median-axis
图 3 中轴外抛物线转子副的轮廓共轭关系
Figure 3. Rotor-pair contour-conjugation-relation with outer-parabola based on median-axis
图 4 中轴外抛物线的高形化转子轮廓
Figure 4. Highly formalized rotor-contour with outer-parabola based on median-axis
图 5 中轴内抛物线转子的轮廓构造
Figure 5. Rotor-contour-structure of inner-parabola-contour based on median-axis
图 6 中轴内抛物线轮廓随抛物线系数的变化规律
Figure 6. Variation-law of inner-parabola-contour based on median-axis with the parabolic-factor
图 7 顶轴外抛物线转子的轮廓构造
Figure 7. Rotor-contour-structure of outer-parabola based on top-axis
图 8 顶轴外抛物线转子的最小形状系数轮廓构造
Figure 8. Rotor-contour-structure of outer-parabola based on top-axis with minimum shape-factor
图 9 顶轴外抛物线转子的轮廓干涉
Figure 9. Rotor-contour- interference of outer-parabola based on top-axis
图 10 三种构造方法下的叶轮廓比较
Figure 10. Lobe-profiles comparison under the three construction methods
表 1 中轴内外共轭轮廓曲率半径的变化规律
Table 1. Curvature-radius changes of inner or outer conjugation-contour based on median-axis
xm 0 xs/6 xs/3 xs/2 2xs/3 5xs/6 xs σ/° 0.00 3.94 8.01 12.38 17.23 22.89 30.00 rm 1.00 1.01 1.03 1.06 1.11 1.18 1.26 r'm 0.33 0.33 0.31 0.28 0.23 0.15 0.02 
下载: 导出CSV
表 2 三种构造方法下的叶截面数据
Table 2. Lobe cross-section data under the three construction methods
轮廓 ε k 质心位置y 叶截面积 c1 1.293 0.586 0.645 1.076 c2 1.244 0.325 0.616 1.065 c3 1.244 1.806 0.610 1.061
下载: 导出CSV
-
[1] Burmistrov A, Raykov A, Isaev A, et al. Efficiency improvement of Roots vacuum pump working process: Computational fluid dynamics methods modeling[J]. Vakuum in Forschung und Praxis,2022(3):34−41 [2] Nguyen T T, Tuyen B N, Tran V T. Analyzing rotor profile's effects to performance of roots vacuum pump applied the CFD method[J]. Applied Mechanics and Materials,2019(9):87−95 [3] 肖荣和, 李玉龙. 基于罗茨泵平均理论流量的转子容积利用系数反求法[J]. 机械传动,2022,46(6):73−77 (in Chinese) Xiao R H, Li Y L. Inverse method on volume utilization factors of rotor based on average theoretical flow of roots pump[J]. Journal of Mechanical Transmission,2022,46(6):73−77 [4] 权太喜, 杨艳. 高扭转子的全共轭轮廓构造及其流量脉动式[J]. 机械传动,2021,45(9):164−169 (in Chinese) Quan T X, Yang Y. Full conjugate contour constructing of helical rotor with higher and its flow ripple formula[J]. Journal of Mechanical Transmission,2021,45(9):164−169 [5] 李玉龙, 孙付春, 刘萍. 泵用凸转子的轮廓设计方法[M]. 上海: 上海交通大学出版社, 2022: 33−41 (in Chinese) Li Y L, Sun F C, Liu P. Contour design method of convex rotor for pumps[M]. Shanghai: Shanghai Jiaotong University Press, 2022: 33−41 [6] 李正清, 李小金, 杨建斌, 等. 罗茨真空泵偏心大圆弧转子型线设计及分析[J]. 真空与低温,2022,28(6):699−704 (in Chinese) Li Z Q, Li X J, Yang J B, et al. Design and analysis of eccentric large arc rotor profile of Roots vacuum pump[J]. Vacuum and Cryogenics,2022,28(6):699−704 [7] 蔡玉强, 孟欣. 渐开线罗茨压缩机转子型线的改进研究与动态仿真[J]. 制造业自动化,2015,37(2):80−82 (in Chinese) Cai Y Q, Meng X. Study improvement and dynamic simulation on rotor profiles for involute roots compressor[J]. Manufacturing Automation,2015,37(2):80−82 [8] 陈庆红, 李玉龙, 张平山. 凸轮转子外摆线轮廓的3种特定形态及其性能分析[J]. 机械传动,2022,46(10):99−103 (in Chinese) Chen Q H, Li Y L, Zhang P S. Three special forms of epicycloid contours of cam rotors and their performance analysis[J]. Journal of Mechanical Transmission,2022,46(10):99−103 [9] 李玉龙, 李秀荣, 赵岩, 等. 罗茨转子双曲线轮廓构造的探索与分析[J]. 真空科学与技术学报,2020,40(10):942−946 (in Chinese) Li Y L, Li X R, Zhao Y, et al. Construction and analysis of hyperbolic rotor profile for roots vacuum pump: an analytical study[J]. Chinese Journal of Vacuum Science and Technology,2020,40(10):942−946 [10] 李玉龙, 赵岩, 刘萍. 一类罗茨泵用的双曲线转子[P]. 江苏省: CN201911206039.8, 2023-09-15 (in Chinese) Li Y L, Zhao Y, Liu P. Hyperbolic rotor for Roots pump[P]. Jiangsu Province: CN201911206039.8, 2023-09-15 [11] 李玉龙, 孙付春, 冉光泽. 泵用顶突抛物线转子的高能组合型线构造方法[J]. 真空科学与技术学报,2019,39(3):226−229 (in Chinese) Li Y L, Sun F C, Ran G Z. Construction of parabolic rotor contour with rostellum geometry for roots pump: a simulation study[J]. Chinese Journal of Vacuum Science and Technology,2019,39(3):226−229 [12] 杨向莙, 孙付春. 椭圆弧凸转子的型线构造及进一步高形技术[J]. 机械传动,2020,44(1):163−167 (in Chinese) Yang X J, Sun F C. Profile shaped-configuration of convex ellipse rotor and its following high shape technology[J]. Journal of Mechanical Transmission,2020,44(1):163−167 [13] 李玉龙. 一种具有高有效容积率的椭圆弧型罗茨泵转子[P]. 江苏省: CN201811380402.3, 2020-09-01 (in Chinese) Li Y L. An elliptic-arc Roots rotor with a high effective volume-ratio[P]. Jiangsu Province: CN201811380402.3, 2020-09-01 [14] 刘萍. 平-凸罗茨转子的高形化及轻量化研究[J]. 真空科学与技术学报,2020,40(5):400−404 (in Chinese) Liu P. Novel high shape rotor with flat-convex profile for lightweight roots-pump: an analytical study[J]. Chinese Journal of Vacuum Science and Technology,2020,40(5):400−404 [15] 邹旻, 乔永强, 任爽, 等. 双啮合弦线转子泵的设计与受力分析[J]. 液压与气动,2020(5):184−189 (in Chinese) Zou M, Qiao Y Q, Ren S, et al. Design and force analysis of double-meshing string rotor pump[J]. Chinese Hydraulics & Pneumatics,2020(5):184−189 [16] 陈曦, 刘嘉. 凸转子定点共轭的极限轮廓构造及轻量化分析[J]. 机床与液压,2022,50(17):137−141 (in Chinese) Chen X, Liu J. Extreme contour construction with fixed-point conjugating of roots rotor and following lightweight analysis[J]. Machine Tool & Hydraulics,2022,50(17):137−141 [17] 李玉龙, 秦运栋, 张安民, 等. 罗茨转子轮廓的双对称图解构造法[J]. 液压与气动,2021,45(9):96−100 (in Chinese) Li Y L, Qin Y D, Zhang A M, et al. A graphic method with bi-symmetric axis used for contour structure of Roots rotor[J]. Chinese Hydraulics & Pneumatics,2021,45(9):96−100 [18] 冯海生, 肖永强, 吴保国, 等. 齿轮-转子-轴承系统复合故障振动特性研究[J]. 机械传动,2022,46(7):7−16 (in Chinese) Feng H S, Xiao Y Q, Wu B G, et al. Research of vibration characteristics of gear-rotor-bearing system with compound faults[J]. Journal of Mechanical Transmission,2022,46(7):7−16 [19] 刘宏杰, 曾超, 刘伦伦, 等. 一种抛物线型转子及机油泵[P]. 山东省: CN201811115856.8, 2020-09-29 (in Chinese) Liu H J, Zeng C, Liu L L, et al. A parabolic rotor for an oil-pump[P]. Shandong Province: CN201811115856.8, 2020-09-29 [20] 李玉龙, 刘萍, 臧勇, 等. 泵用新抛物线转子的型线研究与轻量化设计[J]. 真空科学与技术学报,2019,39(11):969−973 (in Chinese) Li Y L, Liu P, Zang Y, et al. Novel parabolic rotor of roots pump: a theoretical study[J]. Chinese Journal of Vacuum Science and Technology,2019,39(11):969−973 -
计量
- 文章访问数: 28
- HTML全文浏览数: 28
- PDF下载数: 0
- 施引文献: 0