随着引力波探测技术的发展, LIGO-Virgo-KAGRA^[1–4]联合观测台站目前已经成功探测到近百个引力波事件, 直接验证了爱因斯坦关于引力波存在的预言. 受大地脉动干扰以及地面干涉仪基线长度的制约, 地面引力波探测天线对低于10 Hz的引力波信号难以实现高灵敏的响应^[5]. 然而在1 Hz以下的频段中, 蕴含着包括大质量黑洞并合、极端质量比双星系统绕转, 以及宇宙及早期相变的随机引力波遗迹等极为丰富的波源信息^[6]. 相比之下, 空间环境更加稳定, 噪声水平低, 可实现百万公里距离超高精度星间激光干涉测距, 从而可实现更低频段的引力波信号探测^[7,8]. 鉴于此, 国际研究团队相继提出了中低频空间引力波探测计划, 包括欧空局主导的LISA计划^[9,10]、日本发起的DECIGO计划^[11,12]、我国发起的太极计划^[13,14]与天琴计划^[15]等. 这些任务在科学目标与顶层指标设计上各有侧重, 其中太极计划是由中国科学院发起的绕日轨道空间引力波探测任务, 该任务包含3颗卫星编队飞行, 构成绕日运行的近似等边三角形星座, 其星间测量基线约300万公里, 探测目标频段为0.1 mHz—1 Hz^[16,17].

对空间引力波探测任务而言, 探测器探测能力由惯性传感器测试质量残余加速度噪声水平和激光测距精度两个顶层指标共同决定. 惯性传感器测试质量残余加速度噪声是测试质量在激光测距(敏感轴)方向偏离引力场中自由下落运动的加速度噪声, 是制约中低频段引力波探测灵敏度水平的关键因素. 测试质量是星间距离测量的端点, 惯性传感器系统的主要作用是尽可能屏蔽来自空间环境与卫星内部环境的干扰与杂散耦合, 保障测试质量尽可能的在引力场中沿测地线运动^[16]. 当引力波信号经过时, 引力波引起的潮汐效应将导致不同卫星上的作为惯性基准的测试质量之间相对距离发生变化^[18]. 通过超高精度星间激光干涉测距技术, 可以实现星间测试质量间微弱相对位移信号的精密读出, 进而可实现引力波信号的有效探测. 对于太极计划而言, 为实现科学观测目标, 惯性传感器的测试质量残余加速度噪声指标需达到小于3×10^–15 m/(s²·Hz^1/2)@3 mHz的水平^[19].

星载超高精度惯性传感器是一个在复杂干扰力与补偿控制力共同作用下的多自由度动力学系统. 高精度惯性传感器的测量数据的准确读出与评估, 都高度依赖于惯性传感器系统相关物理参数(运行参数)的精确定标测量结果. 惯性传感器关键运行参数包括静电驱动标度因数, 以及测试质量平衡质心位置与卫星质心偏差矢量. 由于地面测试环境、定标测量方法与在轨实际运行空间环境及运行模式存在较大差异, 地面初步运行参数定标值与在轨真值之间会产生偏差, 这将导致空间引力波探测任务数据产品的精度下降, 影响最终的科学产出. 因此在空间引力波探测任务试运行阶段以及科学运行阶段, 都需要按计划定期开展惯性传感器关键运行参数的在轨定标工作^[20].

基于同类技术精度10^–10—10^–12 m/(s²·Hz^1/2)的静电悬浮惯性传感器, 以加速度计模式广泛应用于现有的地球重力卫星任务中, 例如CHAMP^[21], GRACE/GFO^[22], GOCE^[23], 以及我国重力卫星任务^[15]等. 针对GRACE任务, Wang^[24]提出利用磁力矩器驱动卫星绕特定轴向往复摆动, 产生惯性力信号来标定质心偏差, 并通过比较质心调节块移动前后的输出变化标定标度因数的技术方案, 该方案成功应用于GRACE及其后续卫星GFO, 以及我国的重力卫星任务. Zhang等^[25]在“太极一号”技术实验卫星中通过基于磁力矩器驱动的卫星机动实验, 系统地完成了其惯性传感器标度因数与质心偏差的精确定标. 这些已完成的实验为太极计划超高精度惯性传感器的定标设计提供了宝贵的经验. 对于太极计划而言, 三星编队中每颗卫星都将搭载两套独立的惯性传感器系统, 其感探头的结构设计、运行模式与GRACE/GFO, 及“太极一号”的惯性传感器相比存在明显差异, 且仪器指标提升3—5个量级, 要求噪声小于3×10^–15 m/(s²·Hz^1/2), 这对定标方案和定标精度均提出了更为严苛的要求.

本文面向空间引力波探测太极任务所配置的超高精度静电悬浮惯性传感器, 针对其在轨定标需求, 提出了包含标度因数与质心偏差矢量在内的关键运行参数定标方案, 通过理论分析与数值仿真实验验证了这一新方案的可行性与稳健性.

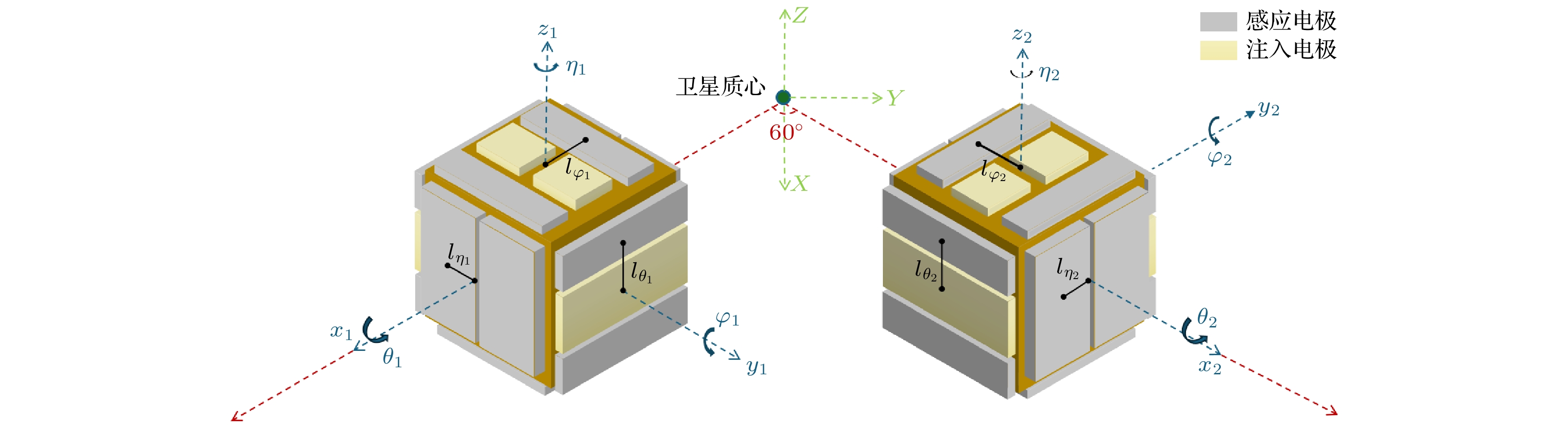
空间引力波探测任务所配置的超高精度惯性传感器^[19]主要由敏感探头、电容位移传感及静电伺服控制系统(前端电子学系统)、锁紧与释放系统、电荷管理系统^[26]以及真空腔组成. 其中, 敏感探头包括测试质量和电极笼. 电极笼上装配有12个感应控制电极, 形成6对感应控制电极, 实现对测试质量6个自由度的驱动和控制, 作为电容位移传感和静电驱动的执行元件. 此外, 电极笼中还包括3对注入电极, 用于施加激励电压, 如图1所示.

惯性传感器存在两种工作模式: 加速度计模式和无拖曳控制模式. 在加速度计模式下, 静电力对测试质量进行六自由度闭环控制, 使其稳定悬浮在电极笼的标称中心位置, 测试质量所受的静电力反映了卫星所受到的非引力扰动. 在无拖曳控制模式下, 惯性传感器电容位移传感电路检测测试质量与电极板之间的相对运动, 并通过无拖曳与姿态控制器驱动微推进器产生补偿推力, 控制卫星跟随测试质量运动, 实现无拖曳控制.

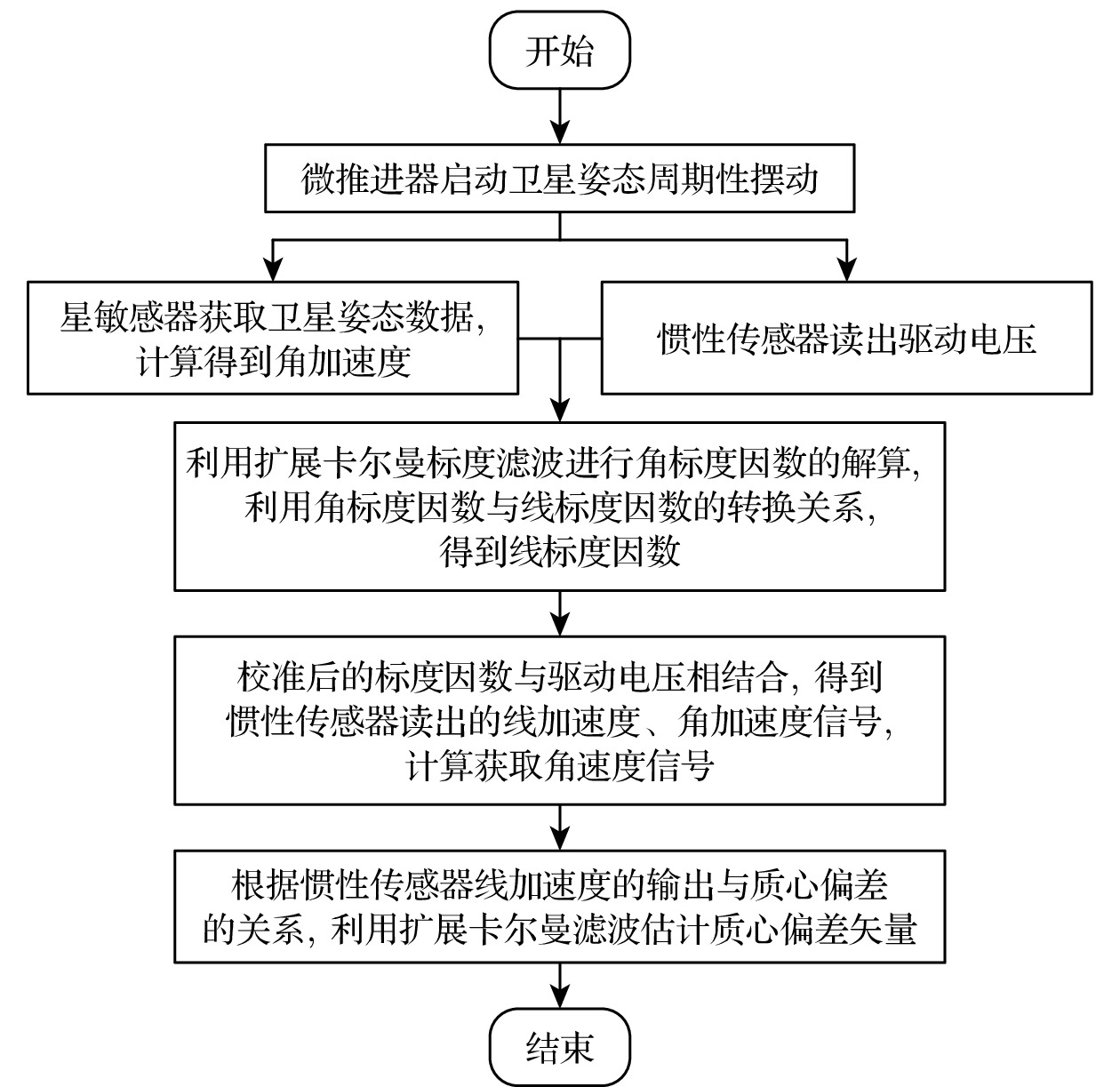
由于无拖曳控制系统具有快速响应能力, 能够迅速识别并补偿任何非引力引起的卫星摆动, 这种快速响应会减小卫星摆动的幅度和持续时间. 而在加速度计模式下, 卫星的控制策略相对灵活, 可以根据需要进行特定的机动, 进而完成科学测量、校准测试或姿态调整等需求. 我们设计了主动施加卫星持续摆动的机动方案, 以提高惯性传感器加速度输出信号的信噪比, 进而快速实现在轨参数标定. 因此, 针对惯性传感器六自由度静电驱动控制标度因数在轨定标问题以及测试质量平衡位置质心偏差在轨定标问题, 本文研究并设计了加速度计模式下的定标方案, 并将定标后的惯性传感器数据应用于无拖曳控制模式, 以实现科学探测.

标度因数与质心偏差的总体定标流程如图2所示.

由于地面测试环境、定标测量方法与在轨实际运行空间环境及运行模式存在较大差异, 惯性传感器标度因数地面定标值与在轨真值之间会存在一定偏差. 此外, 在轨运行过程中电子器件的性质的缓慢改变也会导致的标度因数漂移. 惯性传感器标度因数的定标误差与电压读出耦合, 会引入惯性传感器读数偏差, 对惯性传感器性能评估和电荷管理系统实时电荷评估带来影响, 需要定期开展惯性传感器标度因数参数的在轨定标工作.

惯性传感器在加速度计模式下工作时, 作用在测试质量上的静电驱动补偿加速度可通过驱动电压和标度因数求得, 详见表1. 其中$ {\dot{\omega }}_{i}(i=x, y, z) $和$ {a}_{i}(i=x, y, z) $分别代表沿3个轴向的角加速度和线加速度, $ {V}_{i, 1}, {V}_{i, 2}(i=x, y, z) $代表垂直$ i $轴的两块感应电极板的驱动电压读数, $ {k}_{i}(i=x, y, z) $和$ {\beta }_{i}(i=x, y, z) $ 分别代表线标度因数和角标度因数, 其理论值可通过下式计算:

其中, $ {\varepsilon }_{0} $表示真空介电常数, $ {S}_{i} $表示垂直$ i $轴电极笼表面感应电极板的面积, $ {d}_{i} $表示沿$ i $轴方向感应电极板与测试质量块的间隔, M表示测试质量的质量, $ {J}_{\theta }, ~{J}_{\varphi }, ~{J}_{\eta } $分别表示测试质量块沿$ x, y, z $轴的转动惯量, $ {l}_{\theta }, ~{{l}_{\varphi },~ l}_{\eta } $为3个转动轴静电力力臂, $ {V}_{{\mathrm{P}}} $表示预载电压.

太极任务配置有高精度星敏感器, 可以实现独立的卫星姿态精密测量. 基于这一测量数据输入, 本文提出了一种依靠高精度卫星姿态估计信息对惯性传感器标度因数进行定标的方案. 利用高精度星敏感器读出卫星姿态信号, 由于在加速度计模式下测试质量姿态与固定在卫星平台上的电极笼锁死, 从而可将其转化为惯性传感器坐标系下测试质量的角加速度的独立测量信号, 结合惯性传感器读出的驱动电压, 根据表1关系式, 构造扩展卡尔曼滤波器, 完成角标度因数的定标. 定标角标度因数后, 根据角标度因数与线标度因数的转换关系, 可以获得线标度因数:

式中, 测试质量的质量、转动惯量、电极的等效力臂并不会在发射前后或者跟随环境而改变, 因此上述基于角标度因数获得线标度因数的方法具有可行性.

获取卫星的姿态信号与惯性传感器的驱动电压后, 采用扩展卡尔曼滤波算法定标角标度因数, 估计量$ \boldsymbol{X} = {[{\beta }_{x}\;\; {\beta }_{y}\;\; {\beta }_{z}]}^{{\mathrm{T}}} $, 测量值$ \boldsymbol{Y} = {\left[{\dot{\omega }}_{x}\;\; {\dot{\omega }}_{y}\;\;{\dot{\omega }}_{z}\right]}^{{\mathrm{T}}} $, 系统的状态方程及观测方程为

其中, 观测矩阵$ {\boldsymbol{H}}_{k} $为

因为标度因数没有动态特性, 因此状态转移矩阵$ \boldsymbol{\varPhi }=\boldsymbol{I} $. 测量噪声$ {V}_{k} $满足:

在滤波过程中, 需要迭代更新的变量包括卡尔曼增益:

后验估计:

以及误差协方差矩阵:

在加速度计模式下, 惯性传感器通过电容差分测量测试质量与电极笼之间的相对位移与姿态, 并通过控制电压将测试质量推回到标称位置, 控制电压与作用于测试质量的加速度呈线性关系, 根据控制电压读出, 结合标度因数$ k $, 可以计算得到卫星受到的非引力加速度, 如表1所示. 测试质量与卫星之间的相对加速度波动$ {S}_{{\mathrm{a}}} $与控制电压波动$ {S}_{{\mathrm{V}}} $满足如下关系:

在加速度计模式下开展卫星机动试验, 利用表1即可计算得到标度因数的标定值. 标度因数标定值与真值的误差记为$ \delta k $.

在科学观测模式下, 当标度因数存在标定误差时, 惯性传感器测量数据中会包含由标定误差$ \delta k $与电压耦合引入附加的加速度误差$ {\Delta a}_{\_{\mathrm{\delta }}k}=\delta k{S}_{{\mathrm{V}}} $, 根据惯性传感器性能指标要求, $ {S}_{\Delta a\_{\mathrm{\delta }}k} $需要满足

将(11)式代入(10)式, 可知线标度因数定标的相对精度须满足:

测试质量与卫星之间的相对加速度波动主要由卫星受到的非引力扰动——太阳光压的波动引起. 参考LISA PathFinder和LISA任务卫星设计^[27], 以及太极任务卫星的前期初步设计方案, 卫星在太阳直射方向截面面积为14—15 m², 质量约为2 t. 在距离太阳1 AU处太阳辐射功率约为1367 W/m², 在mHz频段辐射功率涨落约为$ {1.2\times 10}^{-3}{({3 \;{\mathrm{mHz}}}/{f})}^{1/3} $ Hz^–1/2. 考虑卫星表面太阳能板吸收比率, 在太极任务目标mHz频段, 太阳光压波动引起的扰动加速度满足$ {S}_{{\mathrm{a}}}\lesssim 1.1\times {10}^{-11}{\left({3\; {\mathrm{mHz}}}/{f}\right)}^{1/3} $ m/(s²·Hz^1/2). 因此, 线标度因数的定标相对精度要求满足: $ {\delta k}/{k} < 0.03\% $.

在卫星发射与长期在轨运行过程中, 推进剂及其他工质的消耗会导致卫星的质心偏差与地面定标值之间存在差异. 一方面, 质心偏差是姿态与无托曳控制中自由度耦合相关的重要参数. 另一方面, 惯性传感器评估中需要扣除质心偏差产生的惯性力, 质心偏差标定误差会影响惯性传感器性能评估的可靠性. 因此, 需定期对卫星质心偏差进行定标.

太极计划任务每颗卫星配置有两套独立惯性传感器系统, 其中测试质量的平衡位置与卫星质心的实际偏移矢量记为$ {\boldsymbol{r}}_{{i}}\;(i=1, 2) $ (后文中黑斜体符号代表矢量), 见图1. 因此, 当卫星绕特定轴摆动时, 测试质量受到惯性力产生加速度:

其中, $ \dot{\boldsymbol{\omega }} $, $ \boldsymbol{\omega } $分别表示卫星的角加速度和角速度. 机动过程中惯性传感器处于加速度计模式, 惯性传感器通过施加控制电压, 抵消因测试质量受到惯性力、以及卫星受到的非引力干扰所引起的测试质量与电极笼之间的相对加速, 使得测试质量与卫星平台运动同步, 同步位移精度$\sim2\;{\mathrm{n}}{\mathrm{m}}/{\mathrm{H}}{{\mathrm{z}}}^{1/2} $. 因此卫星的角加速度与角速度与测试质量一致. 惯性传感器通过静电控制实际输出的加速度数据为

式中$ {\boldsymbol{a}}_{{\mathrm{n}}{\mathrm{g}}} $表示卫星受到的非引力加速度扰动, 对于太极计划的轨道而言, $ {\boldsymbol{a}}_{{\mathrm{n}}{\mathrm{g}}} $以太阳光压为主. 同时, 如上文所述, 加速度计模式下测试质量被精确控制跟随卫星平台运动, 因此(14)式中正比于$ {\dot{\boldsymbol{r}}}_{{i}},\; {\ddot{\boldsymbol{r}}}_{{i}} $的项可以忽略.

在定标时段内(~10⁴ s水平), 太阳轨道的空间环境变化极为缓慢, 方程(14)中$ {\boldsymbol{a}}_{{\mathrm{n}}{\mathrm{g}}} $主导的太阳光压部分$ {\boldsymbol{a}}_{{\mathrm{s}}{\mathrm{r}}} $后文将通过数值仿真生成模拟数据, 其他潜在的空间环境干扰则基于时间的线性函数来近似, 由此(14)式可简化为

式中

在完成惯性传感器标度因数的定标结果之后, 基于标度因数测定值, 通过控制电压数据可以获得测试质量的角速度$ \boldsymbol{\omega } $、角加速度$ \dot{\boldsymbol{\omega }} $以及线加速度$ \boldsymbol{a} $. 上述质心偏差测量数据全部为卫星本体坐标系下的数据, 通过构建扩展卡尔曼滤波器来定标质心偏移矢量$ {\boldsymbol{r}}_{{i}} $.

质心偏差与标度因数估计方法相同, 通过构造扩展卡尔曼滤波器对质心偏差进行定标, 其中, 测量值$\boldsymbol Y $、估计量$\boldsymbol X $和观测矩阵$\boldsymbol H $分别为

在科学运行模式下, 卫星角速度、角加速度与测试质量质心偏差耦合, 会产生惯性力加速度, 需要根据卫星速度、角加速度和测试质量质心偏差的定标结果$ \boldsymbol{r} $扣除耦合惯性力加速度, 确保惯性传感器输出数据的准确性和可靠性. 如果质心偏差的定标结果存在误差$ {\mathrm{\delta }}\boldsymbol{r} $, 那么质心偏差的定标误差会引入额外的加速度噪声:

太极计划编队建立星间干涉测量链路进入科学运行模式后, 卫星指向抖动噪声需控制在$ \leqslant 10\;{\mathrm{ }}{\mathrm{n}}{\mathrm{r}}{\mathrm{a}}{\mathrm{d}}/{{\mathrm{H}}{\mathrm{z}}}^{1/2} $水平, 其对应的角加速度噪声$ {S}_{\dot{\boldsymbol{\omega }}}\leqslant 40 $prad/(s²·Hz^1/2)@10 mHz. 基于太极计划测试质量在敏感轴上残余加速度噪声小于3 × 10^–15 m/(s²·Hz^1/2)的要求, 可以推导出质心偏差矢量$ \boldsymbol{r} $的分量的定标精度$ \delta \boldsymbol{r} $必须优于75 μm.

太极计划任务每颗卫星配置冷气或离子微推进器执行无拖曳与姿态控制. 微推进器的标称推力范围为0.1—100 μN, 推力分辨率要求为0.1 μN, 依据太极卫星的初步设计, 可产生的力矩范围为$ {10}^{-7}—{10}^{-4}\;{\mathrm{N}}{\cdot} {\mathrm{m}} $. 惯性传感器在轨定标阶段, 为提升定标精度, 应尽可能获得幅值更大的卫星机动所引起的惯性加速度信号(见(12)式), 同时需保证测试质量与卫星间的相对加速度在惯性传感器量程范围之内(即≤10^–9 m/s²). 因此, 考虑到质心偏差的设计值|r|在25—30 cm, 本文选择微推进器施加扭矩幅值为$ {10}^{-6}—{10}^{-5}\;{\mathrm{N}}{\cdot} {\mathrm{m}} $量级的方波机动信号. 太极计划惯性传感器设计性能在3 mHz附近存在拐点, 3 mHz以下性能出现下降, 但同时考虑到更长的机动周期可以获得幅值更大卫星机动角度, 从而提升卫星姿态信号的信噪比, 因此本文定标工作频率设计为4 mHz. 目前, 国内外甚高精度星敏感器的观测精度已经达到了$ {0.2}''\left(3\sigma \right) $的先进水平^[28,29]. 为了确保扩展卡曼滤波器在估计标度因数和质心偏差时能够达到预期的精度, 本研究设计并执行持续10000 s的卫星机动仿真实验, 可同时对这两个参数进行精确定标. 本文用Matlab软件仿真.

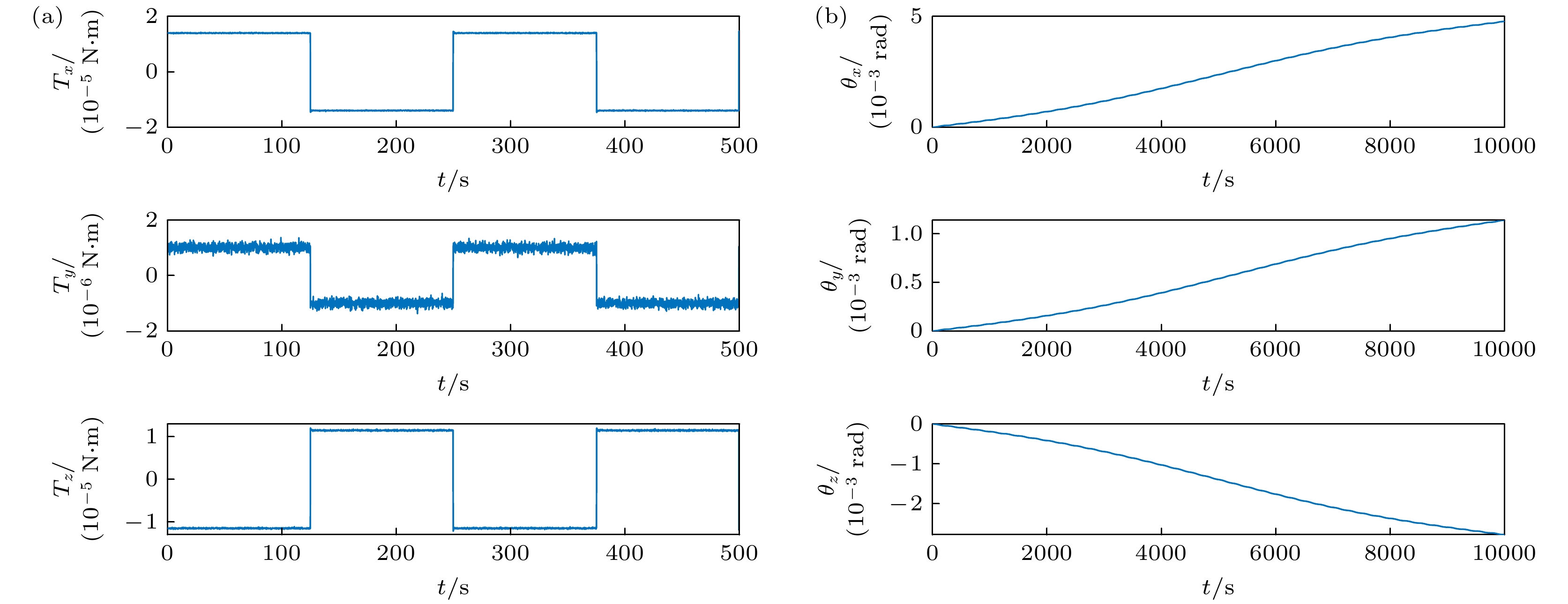
在卫星机动行为的数值仿真过程中, 考虑微推进器工质供应不稳定、控制系统中传感器的测量误差和控制算法的误差、结构振动、热效应等效应, 在推力信号中叠加$\sim0.1\;{\text{μ}}{\mathrm{N}}/{\mathrm{H}}{{\mathrm{z}}}^{1/2} $的噪声信号, 推力调节响应时间小于5 ms^[30,31]. 同时, 在仿真过程中, 为模拟实际机动行为, 完整考虑了推进器推力的不稳定性引起的信号占空比改变、幅值抖动以及推力过冲等效应. 考虑上述因素后, 作用于卫星上的总力矩模拟信号如图3所示, 图3(a)是参数定标期间推进器作用于卫星上力矩仿真信号 , 为了清晰可见只展示前500 s的仿真信号, 图3(b) 是微推进器推动卫星产生的角度$ \theta $仿真信号, 显示了卫星在微推进器作用下的姿态变化. 角度变化的幅度和速率直接关联到惯性传感器输出信号的信噪比, 这对于后续的标度因数和质心偏差的定标至关重要.

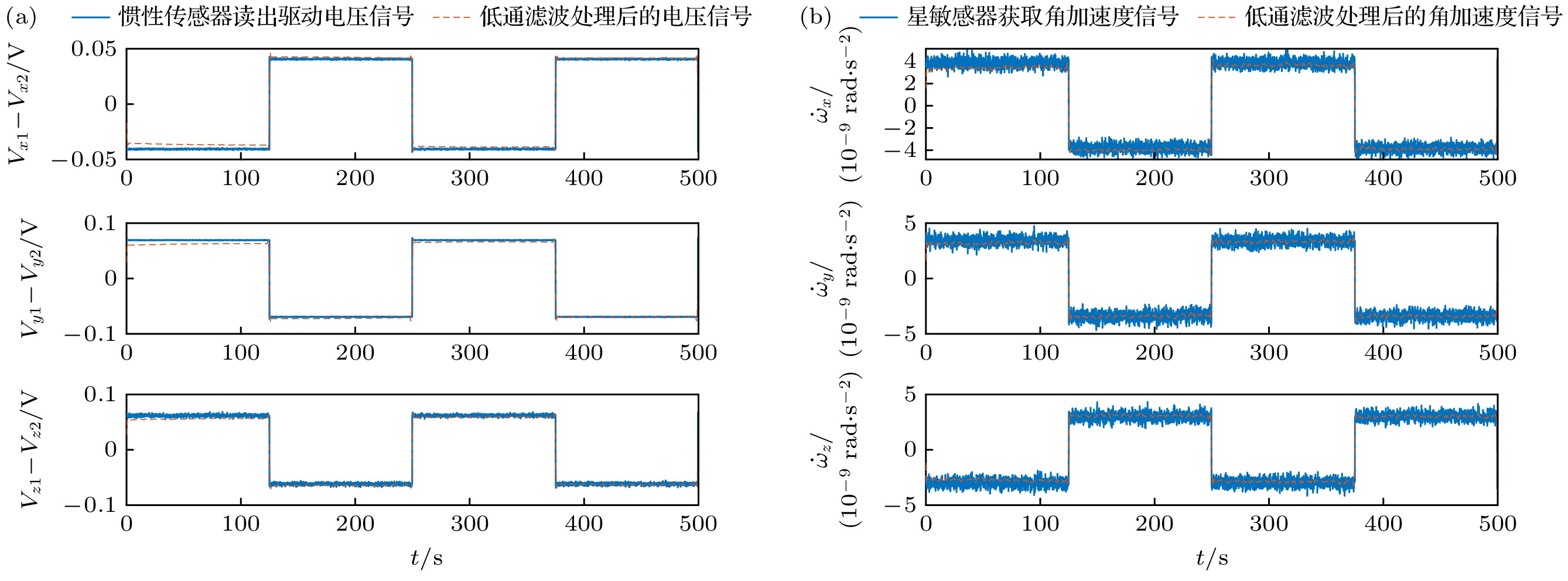
标度因数定标需要的测量数据包括星敏感器观测得到的卫星姿态角数据和惯性传感器在加速度计模式下的控制电压数据, 图4给出单套惯性传感器在惯性传感器坐标系下的角加速度以及控制电压数据仿真结果. 仿真数据中, 静电驱动控制电压纹波噪声满足$ {\delta V}/{V} \lesssim 8\times {10}^{-6}/{\mathrm{H}}{{\mathrm{z}}}^{1/2} $, 星敏感器读出噪声$ {\sim0.2}''\left(3\sigma \right) $^[32].

图4中蓝线为星敏感器与惯性传感器获取的测量数据, 红线为对应的低通滤波处理后的仿真信号. 通过对比分析, 可以发现星敏感器获取的角加速度信号存在较为显著的测量噪声, 这是影响标度因数在轨定标精度的主要原因. 采用截止频率为0.05 Hz的低通滤波器平滑处理上述仿真测量数据, 在保障信号保真度的同时有效地抑制了星敏感器的测量噪声, 进而提高标度因数的定标精度.

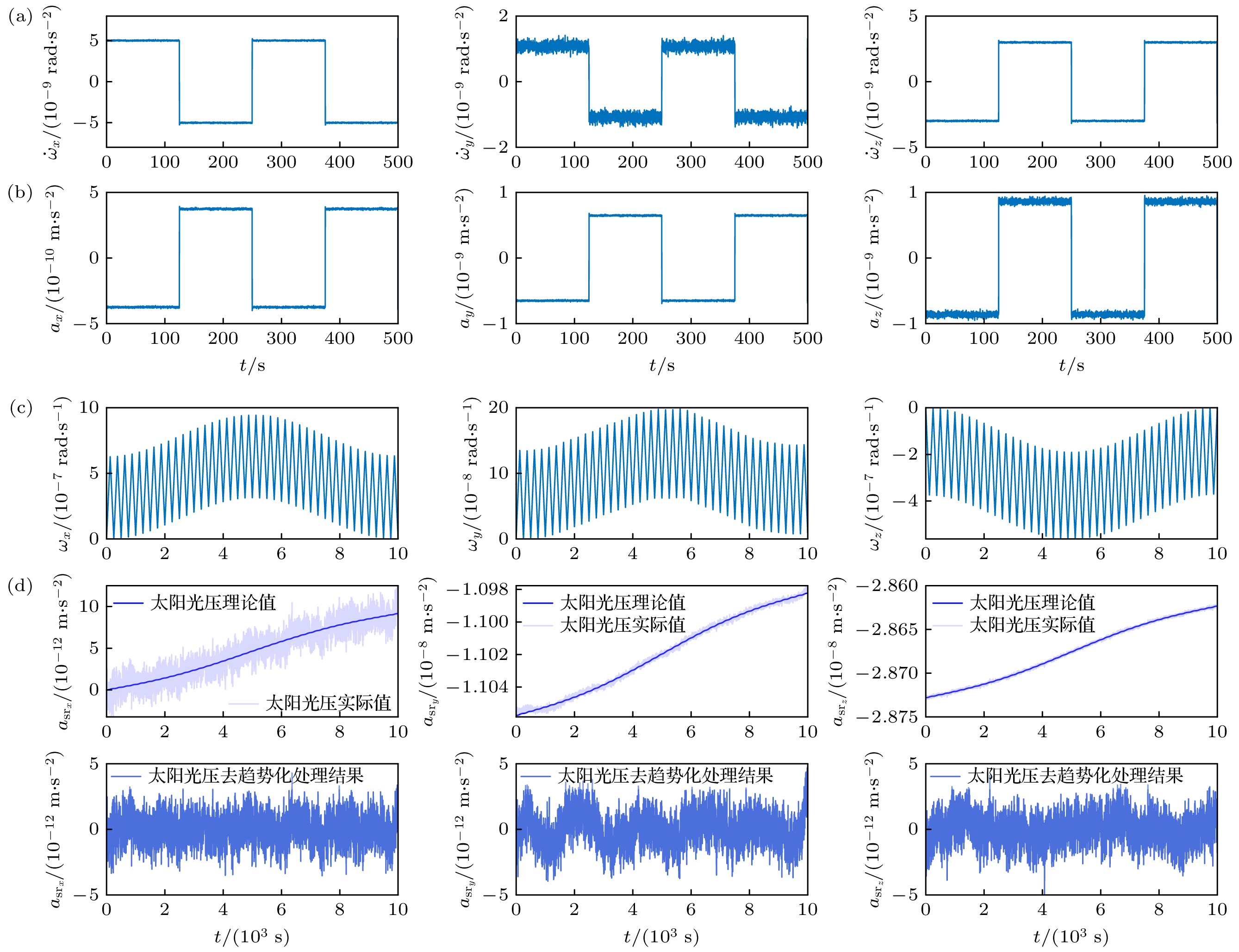
质心偏差定标所需的测量数据包括卫星本体坐标系下惯性传感器测量的测试质量的角加速度信号$ \dot{\boldsymbol{\omega }} $, 角速度信号$ \boldsymbol{\omega } $, 线加速度信号$ \boldsymbol{a} $. 图5(a)—(c) 给出单套惯性传感器中以上测量数据的仿真 信号, 其中, 线加速度、角加速度本底噪声水平分别为$ {3 \times 10}^{-15} $ m/(s²·Hz^1/2), ~$ 1 \times 10^{-14} $ rad/(s²·Hz^1/2). 对于太极计划的轨道而言, 定标时段内卫星受到的非引力加速度扰动中以太阳光压为主导项. 图5(d) 展示了定标时段内线加速度信号$ \boldsymbol{a} $中太阳光压随着卫星姿态变化引起的加速度噪声项$ {\boldsymbol{a}}_{{\mathrm{s}}{\mathrm{r}}} $, 并对其进行去趋势化处理的结果. 太阳光压直流部分及 其波动引起的测量频段内加速度扰动幅度谱密 度$ \lesssim 1.1\times {10}^{-11}{\left({3~{\mathrm{mHz}}}/{f}\right)}^{1/3}\cdot $m/(s²·Hz^1/2), 基于文献[33]研究结果评估得到.

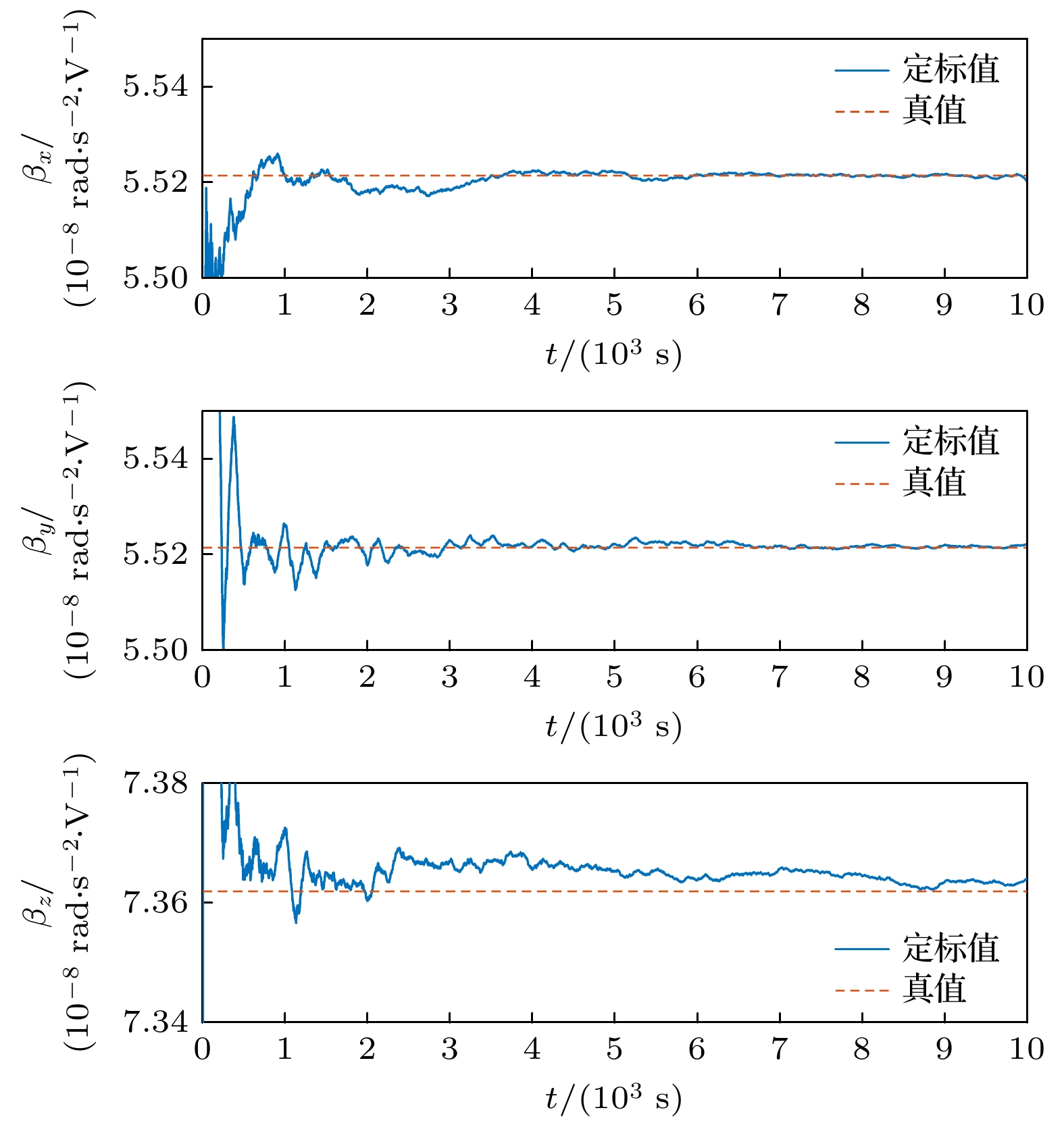
根据2.1节的标度因数定标方案, 基于卫星的角加速度模拟信号和惯性传感器的电压读出模拟信号, 构造扩展卡尔曼滤波器进行标度因数的定标, 定标结果如图6所示.

图6所示为角标度因数$ {\beta }_{i}=[{\beta }_{x}, {\beta }_{y}, {\beta }_{z}] $的定标估计的收敛过程, 通过扩展卡尔曼滤波算法进行参数估计. 星敏感器在获取角加速度信号过程中引入的测量噪声相对较大. 为了降低这一噪声对定标精度的影响, 采用低通滤波算法对测量信号进行平滑处理, 以有效抑制高频噪声成分. 尽管如此, 为了确保标度因数的相对精度能够稳定地收敛至$ 0.03\% $以内, 定标过程仍需持续10000 s. 具体结果如表2所示.

表2中, 角标度因数定标相对精度分别为$ 0.0033\% $, $ 0.0027\% $, $ 0.0173\% $, 优于$ 0.03\% $的预期精度要求, 验证了标度因数在轨定标方案的可行性. 通过角标度因数与线标度因数的转换关系, 即(2)式, 得到线标度因数的定标值. 标度因数是将惯性传感器的输出电压转换为加速度测量值的关键参数, 本文的定标结果确保了测量值与实际加速度之间的正确对应关系, 从而提高惯性传感器的测量精度与数据质量.

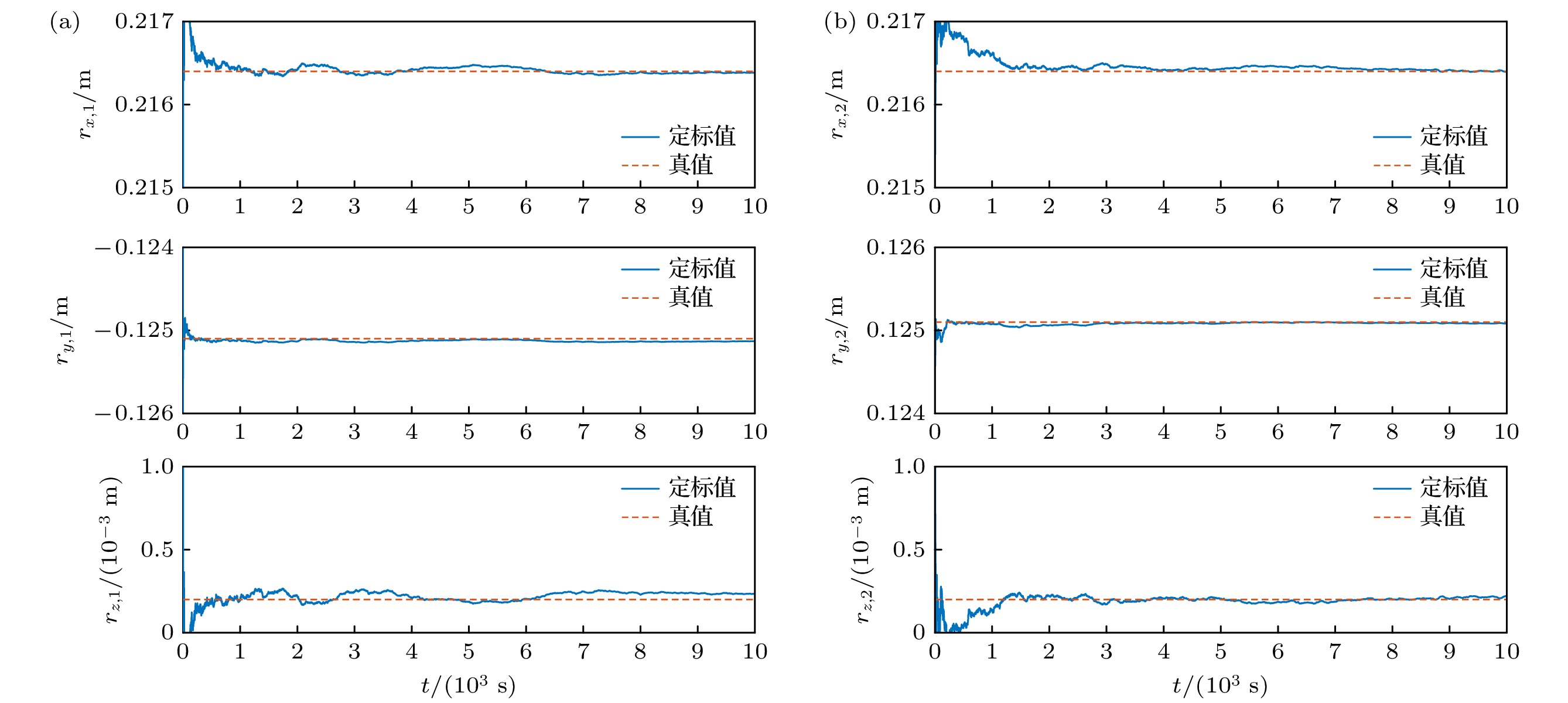
根据2.2节的质心偏差定标方案, 基于惯性传感器获取的质心偏差定标所需的测量数据模拟信号, 构造扩展卡尔曼滤波器进行质心偏差的定标, 定标结果如图7所示.

图7所示为质心偏差$ {\boldsymbol{r}}_{1}, {\boldsymbol{r}}_{2} $的定标估计的收敛过程, 通过扩展卡尔曼滤波算法进行参数估计. 太阳光压的扰动被视为影响质心偏差在轨定标精度的主要因素. 为了准确评估其影响, 我们对太阳光压波动项进行了去线性趋势化处理, 得到了其噪声幅度约为$ 2\times {10}^{-12} $m/s². 这一关键数据被纳入扩展卡尔曼滤波算法的误差协方差矩阵中, 以实现对定标过程中误差的精确矫正. 通过将标度因数定标实验与质心偏差定标实验进行迭代积分, 我们能够在10000 s的时间内, 实现两个参数定标精度的稳定收敛. 质心偏差定标的具体结果见表3.

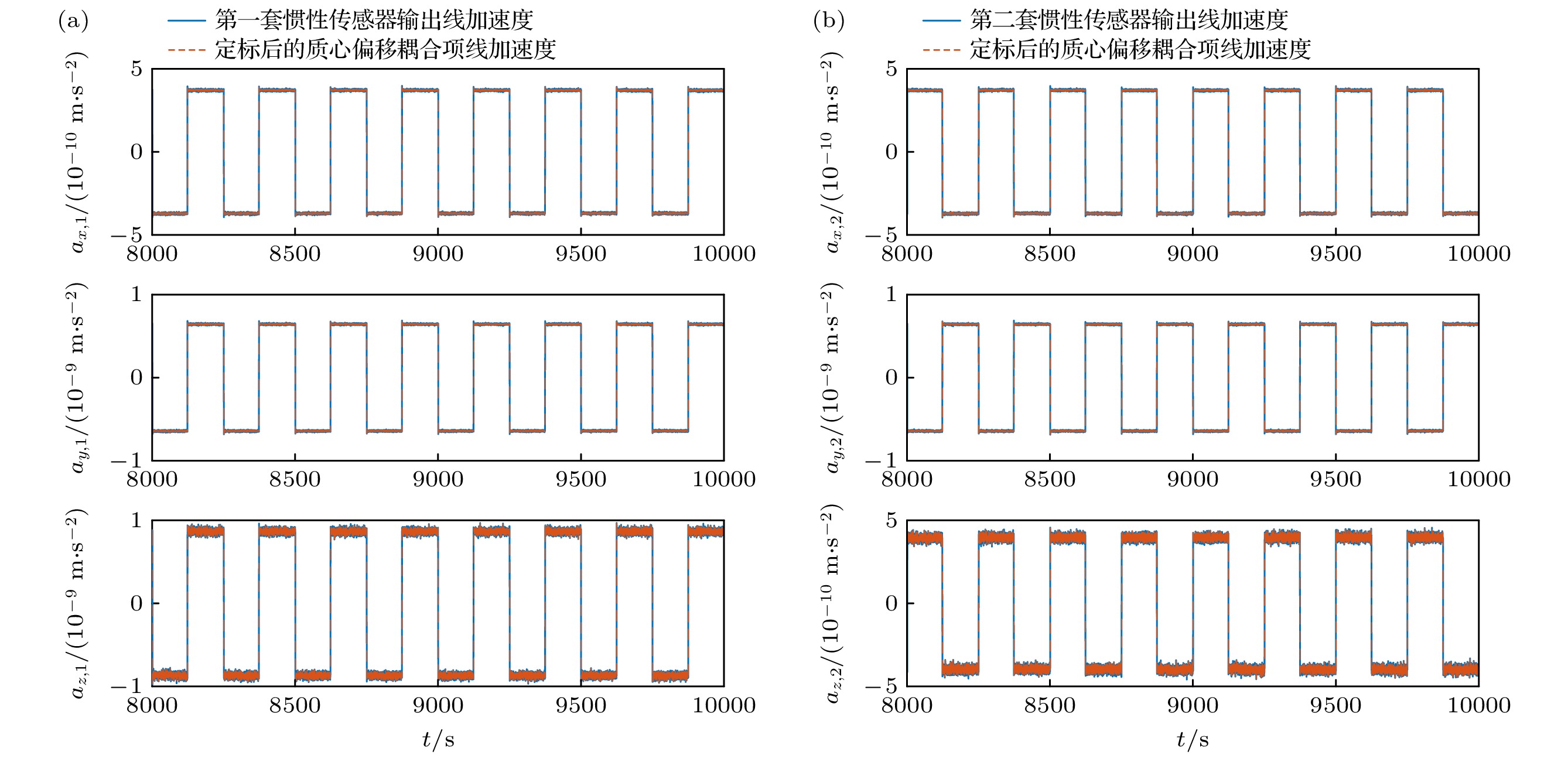
由表3可知, 质心偏差三轴定标误差为 $ {\delta }_{{\boldsymbol{r}}_{1}}= $[15 μm, 31 μm, 34 μm], $ {\delta }_{{\boldsymbol{r}}_{2}} $=[5 μm, 15 μm, 13 μm], 达到了优于75 μm的定标精度要求, 两套惯性传感器敏感轴方向的定标结果更是达到了5 μm和15 μm的高精度水平. 如图8所示, 惯性传感器输出的线加速度与其识别的质心偏差耦合加速度高度吻合, 这是由于我们主动对卫星施加摆动, 从而增大卫星角加速度的幅值, 以此提高信号的信噪比, 提升标定精度. 科学运行模式下, 卫星处于“超静超稳”状态, 不会发生较大抖动, 但质心偏差耦合项仍会引入系统误差, 需要根据质心偏差的定标结果完成耦合加速度的扣除, 确保惯性传感器输出数据的准确性和可靠性.

为了满足太极计划惯性传感器测试质量加速度噪声$ < $3×10^–15 m/(s²·Hz^1/2)@3 mHz的指标要求, 惯性传感器标度因数相对误差要求小于0.03%, 质心偏差在轨定标单轴误差要求控制在75 μm以内. 本文结合太极计划全新的惯性传感器设计布局以及实际噪声环境设计了主动施加卫星摆动的定标方案, 并给出了参数的定标原理、估计算法和精度需求分析. 通过仿真实验模拟卫星机动过程, 模拟惯性传感器和星敏感器测量数据, 并采用扩展卡尔曼滤波算法估计参数, 得到标度因数的三轴定标相对误差分别为0.0033%, 0.0027%, 0.0173%, 质心偏差定标误差$ {\delta }_{{\boldsymbol{r}}_{1}}= $[15 μm, 31 μm, 34 μm], $ {\delta }_{{\boldsymbol{r}}_{2}} $ = [5 μm, 15 μm, 13 μm], 满足太极二号惯性传感器标度因数和质心偏差在轨标定要求. 在后续工作中, 我们将继续完善太极计划惯性传感器在轨定标方案, 提供更多设备参数的定标设计, 建立一套完备、高效、超高精度的在轨定标系统.