首页
登录
注册
-
里德伯原子是一种主量子数很高的特殊原子, 具有寿命长[1]、电偶极矩大[2]、电极化率大[3–5]等诸多特点. 由于其大的电极化率特性, 基于里德伯原子的电场传感器受到了广泛关注. 相比传统的电场测量方法, 基于里德伯原子的电场测量无需校准, 可直接溯源至国际单位制[6], 同时具备高精确度和良好的稳定性, 这些特性使其在量子传感领域展现出巨大的应用潜力[7–9].
利用里德伯原子的特性, 可以实现低功率下的微波场精确测量, 这在需要高灵敏度检测微弱电场的场合非常有价值[10–13]. 除微波场外, kHz量级以下的低频电场测量也成为研究者关注的课题. 然而, 在直流(DC)电场或者低频电场的研究中, 由于里德伯原子最外层电子的束缚能小, 易于被电离, 电离产生的自由电荷在气室内表面附着, 在外界低频电场作用下, 表面自由电荷会重新分布, 形成附加电场并对外界低频电场产生屏蔽效应[14]. 研究者们采用多种方法来消除或者减小这种屏蔽效应, 例如加载射频(RF)电场的低频电场实验测量[15], 使用电导率更小的蓝宝石晶体[16]作为气室材料, 直接将极板引入气室内部[17,18]等. 目前, 基于里德伯原子的直流或低频电场测量技术正日益引起科研人员和相关行业的关注.
Floquet理论是一种用于分析具有时间周期性特征的系统的理论, 利用该理论可以有效地研究在周期性射频场调制下的原子系统的特性. 通过引入MHz量级的RF电场作为驱动场, 对里德伯原子能级进行调制, 从而形成里德伯暗态[19], 并在EIT光谱两侧形成多个边带. 利用这一机制可以实现对电场强度、频率及相位的高精度测量[20–22]. Miller等[23]采用外置极板施加RF电场, 得到铷原子的Floquet-EIT光谱, 研究了偶数阶边带与RF电场的关联特性, 并实现了相对不确定度为±0.35%的RF电场测量. Song等[24]利用奥特勒-汤斯(AT)分裂和Floquet-EIT, 实现了连续可调谐的微波场测量. 目前, 采用Floquet理论对RF电场的测量研究较多, 对DC电场与RF电场同时作用下Floquet-EIT光谱特性的研究较少.
本文基于Floquet-EIT微扰理论, 在内置极板的铯原子气室内部施加RF电场和DC电场, 产生Floquet-EIT光谱的一阶边带, 实验研究了一阶边带的幅值以及半高全宽(FWHM)与DC电场强度的对应关系, 并比较了Floquet-EIT光谱和DC-Stark光谱对直流电场的相对标准偏差. 此研究结果为基于里德伯原子的微弱直流或低频电场测量提供了新思路.
-
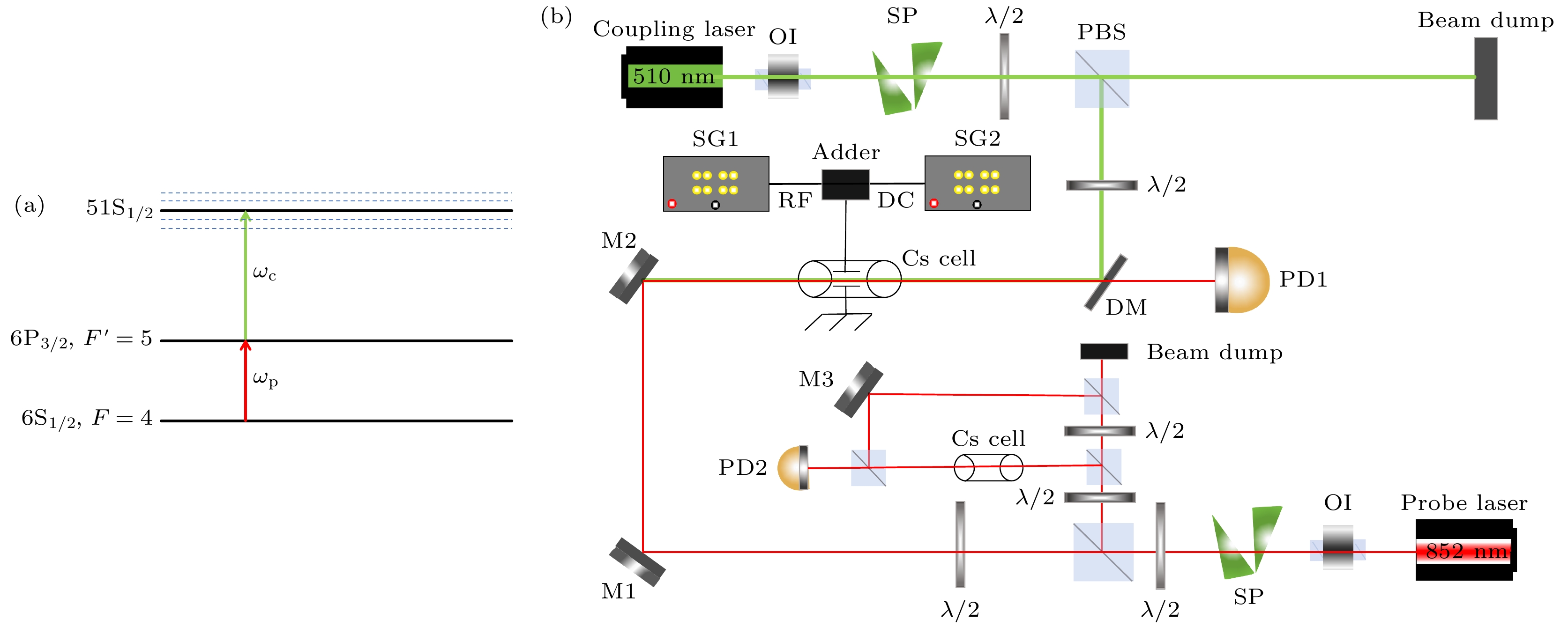
图1(a)为里德伯原子阶梯型EIT的能级示意图, 其中
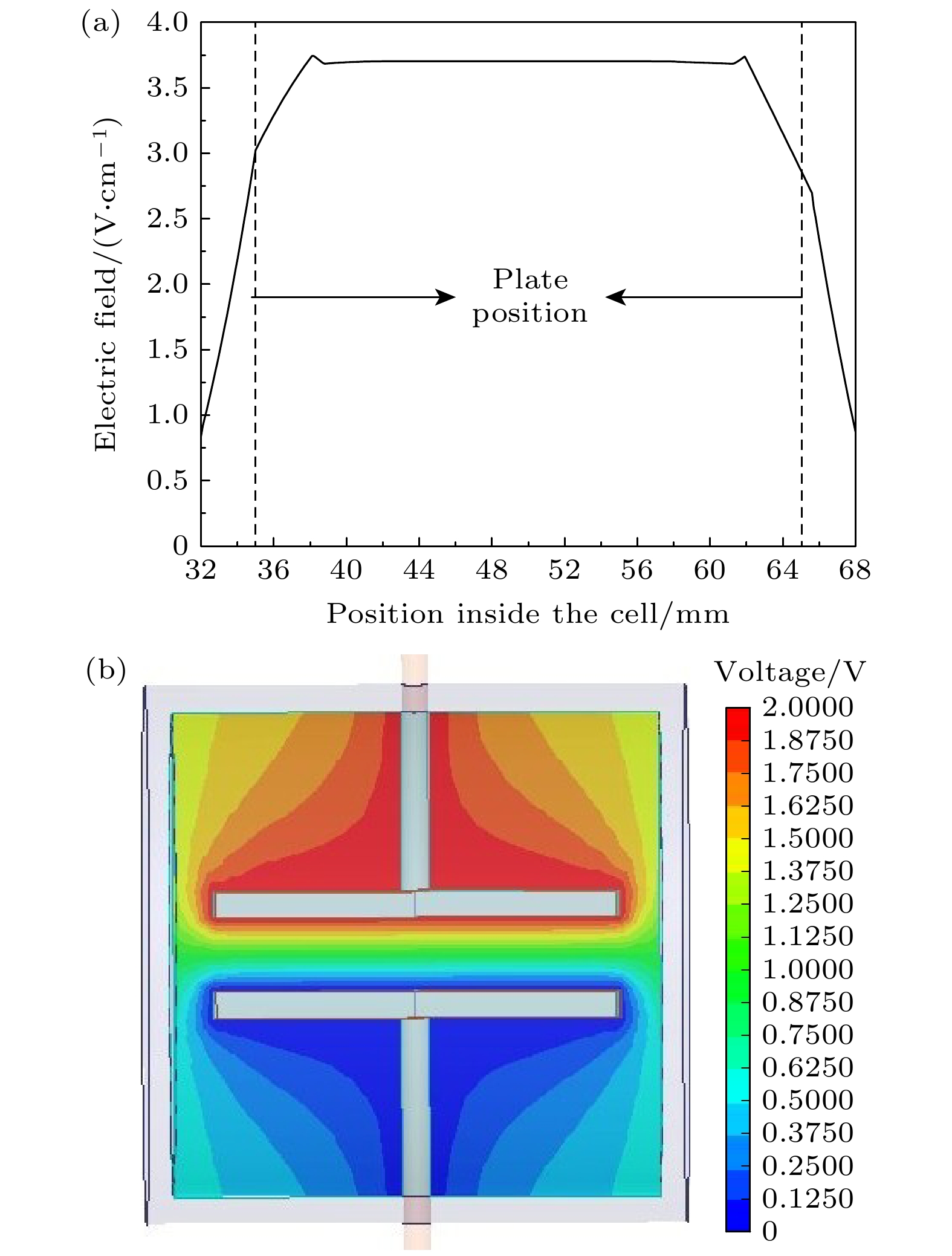
${\omega _{\mathrm{p}}}$ 和${\omega _{\mathrm{c}}}$ 分别为探测光和耦合光的频率. 通过搭建饱和吸收光谱, 将一台852 nm激光器(探测光)频率锁定在铯原子$ 6{{\text{S}}_{{1 {/ } 2}}}, F = 4 \to 6{{\text{P}}_{{3 {/ } 2}}}, F' = 5 $ 跃迁线. 如图1(b)所示, 探测光通过Cs原子气室并被探测器(PD1)探测, 在原子气室处激光功率为150 μW, 光斑直径为1.2 mm. 510 nm激光(耦合光)与探测光在铯原子气室内重合并反向传输, 在原子气室处激光功率为50 mW, 光斑直径为1.5 mm. 在能级跃迁$ 6{{\text{P}}_{{3 {/ } 2}}}, F' = 5 \to 51{{\text{S}}_{{1 {/ } 2}}} $ 频率附近扫描耦合光频率, 记录探测光光强变化, 获得EIT光谱信号.EIT光路中采用内置极板的原子气室, 其内部安装间距为5.4 mm的平行电极板以施加RF电场和DC电场. 实验中调节波片使探测光和耦合光的偏振方向与极板电场方向相同. 首先利用Maxwell电磁仿真软件对内置平行极板的原子气室进行电磁仿真. 电压由铜柱引入内部, 设定上下极板间电压差为2 V, 得到的两个平行极板间的模拟电场和电压分布如图2所示. 其中图2(a)为极板中心位置处的模拟电场分布, 极板处于图示35—65 mm位置, 图2(b)为气室内的模拟电压云图. 可以发现, 除了极板边缘区域外, 极板内部的电场分布均匀, 在极板中央处电场
$E = {U}/{d}$ ≈3.7 V/cm. 这种内置极板设计有效避免了屏蔽效应对实验的影响. -
施加的外部电场
$E\left( t \right)$ 可以表达为其中,
${E_{\mathrm{dc}}}$ 为DC电场强度,${E_{{\mathrm{rf}}}}$ 为RF电场强度,${\omega _{{\mathrm{s}}}}$ 为RF电场频率.在Floquet微扰理论中, 考虑旋波近似并且忽略其他快速振荡的非共振项后, 形成的Floquet-EIT第n阶边带的有效哈密顿量的矩阵形式可以表示为[25]
其中:
式中,
$\hbar $ 为约化普朗克常量,$ {\varOmega _{\mathrm{p}}} $ 和$ {\varDelta _{\mathrm{p}}} $ 分别为探测光的拉比频率和失谐量,$ {\varOmega _{\mathrm{c}}} $ 和$ {\varDelta _{\mathrm{c}}} $ 分别为耦合光的拉比频率和失谐量,$ \varOmega _{\mathrm{c}}^n $ 和$ \varDelta _{\mathrm{c}}^n $ 分别为耦合光在n阶边带处的有效拉比频率和失谐量,$ \varOmega _{\mathrm{p}}^ * $ 和$ \varOmega _{\mathrm{c}}^{n * } $ 分别为$ {\varOmega _{\mathrm{p}}} $ 和$ \varOmega _{\mathrm{c}}^n $ 的复共轭项,$ {{\text{J}}_k} $ 和$ {{\text{J}}_{n - 2 k}} $ 为k阶贝塞尔函数和n–2k阶贝塞尔函数,$\alpha $ 为里德伯原子极化率. 通过Atom calculator计算软件[26], 可得到$ 51{{\text{S}}_{{1 {/ } 2}}} $ 态的极化率$\alpha $ 约为66.1 MHz·cm2/V2.由(3)式可以得到, DC电场和RF电场诱导的Stark频移量分别为
-
实验首先研究不同DC电场强度下
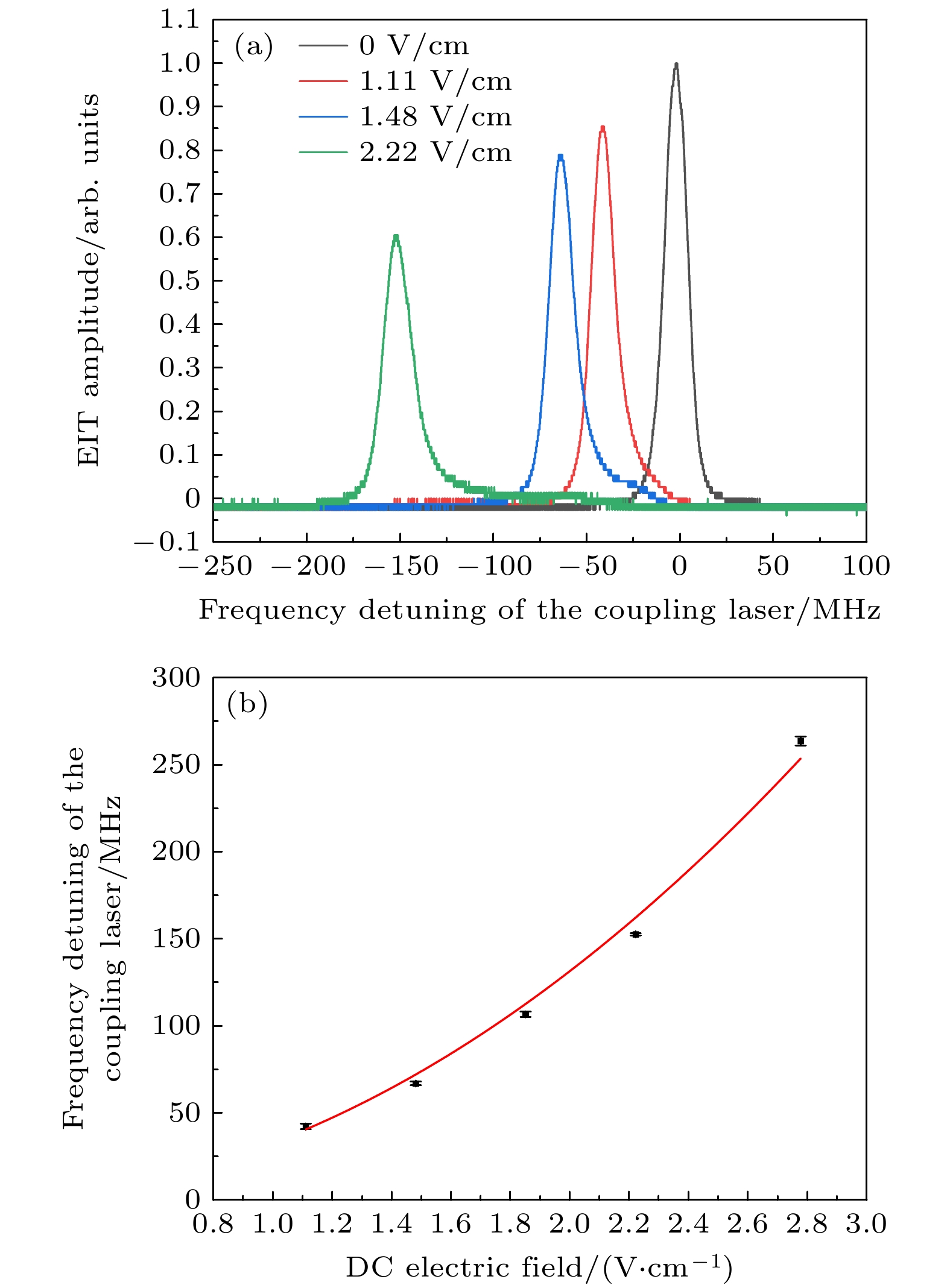
$51{{\text{S}}_{{1 {/ } 2}}}$ 态的里德伯原子EIT光谱. 如图3(a)所示, 随着DC电场强度增大, EIT光谱出现偏移, 同时幅值减小、线宽加宽, 该实验现象是由DC电场引起的Stark效应所致. 图3(b)是用(6)式对实验数据进行拟合的结果, 得到$\alpha $ = (65.72±1.58) MHz·cm2/V2, 与Atom calculator计算的极化率基本一致. 实验误差主要来源于极板间距的不均匀性以及平行电极板的边缘效应.如图4所示, 研究了不同RF电场强度作用下
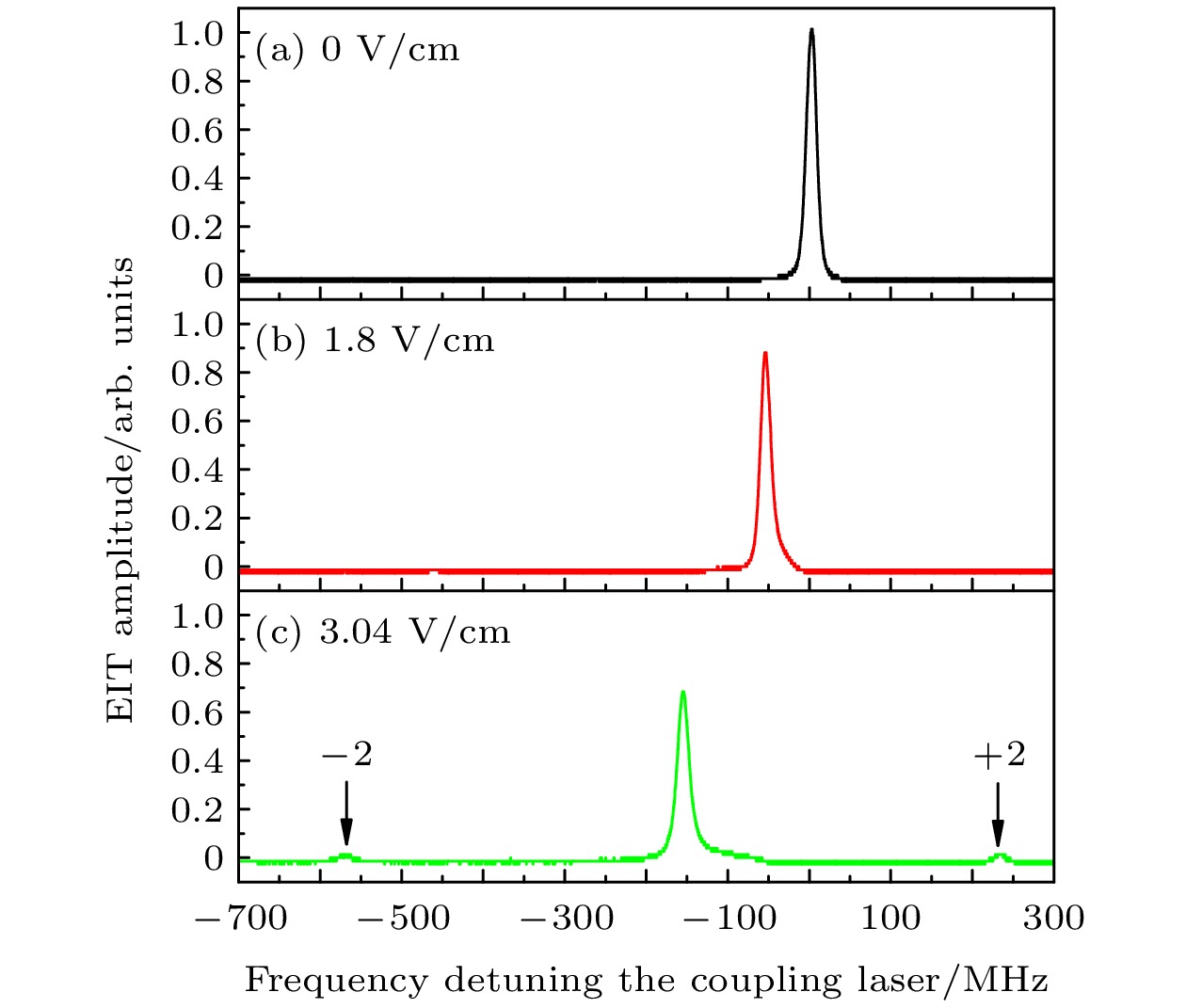
$51{{\text{S}}_{{1 {/ } 2}}}$ 态的EIT光谱. 其中图4(a)为无外场时$51{{\text{S}}_{{1 {/ } 2}}}$ 态的EIT光谱, 将此光谱峰值频率位置作为频率失谐零点. 由于实验中的RF电场频率远小于激发态原子到里德伯态原子的能级跃迁频率, 所以RF电场下的里德伯原子极化率可以认为与DC电场下的极化率相等. 当RF电场施加在极板上时, 由于RF信号与平行电极板间存在阻抗匹配, 会导致实际电场强度与设定电场强度存在一定的偏差. 因此实验中利用EIT光谱的AC-Stark频移量, 即(7)式校准RF实际电场强度. 图4(b), (c)分别为Erf = 1.8 V/cm, Erf = 3.04 V/cm时的EIT光谱. 可以清晰地看到随着RF电场强度增大, EIT光谱发生Stark频移现象并在主峰两侧产生Floquet二阶边带, 这是因为RF电场引入了一个周期性驱动, 使得原子的能级分裂为多个Floquet边带的里德伯暗态. 实验中ωs = 200 MHz, 所以由RF电场引起的二阶边带与主峰之间的频率差为2×ωs = 400 MHz.由Floquet理论, 仅施加RF电场时,
${E_{\mathrm{dc}}} = 0$ , 根据(5)式可以得到:此时, 耦合光在奇数阶边带处的有效拉比频率为0, 因此, 图4中的EIT光谱只出现偶数阶边带.
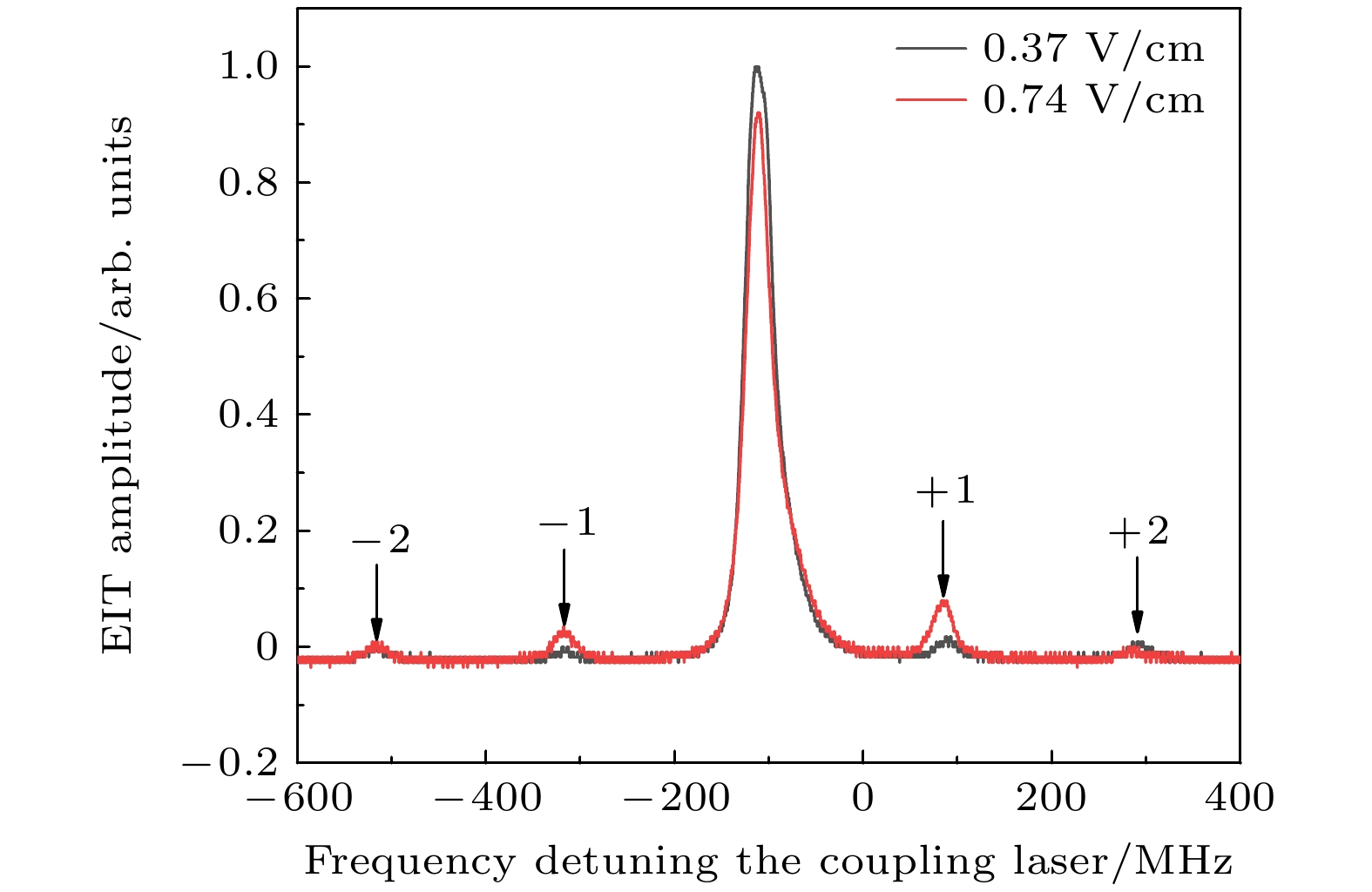
为了进一步研究DC电场作用下的Floquet-EIT光谱特性, 固定Erf = 2.58 V/cm, 将DC电场和RF电场同时接入平行电极板, 实验结果如图5所示. 此时EIT光谱两侧各呈现出2个小峰, 从左到右分别对应–2阶边带、–1阶边带、+1阶边带以及+2阶边带. 并且由(4)式和(5)式可知,
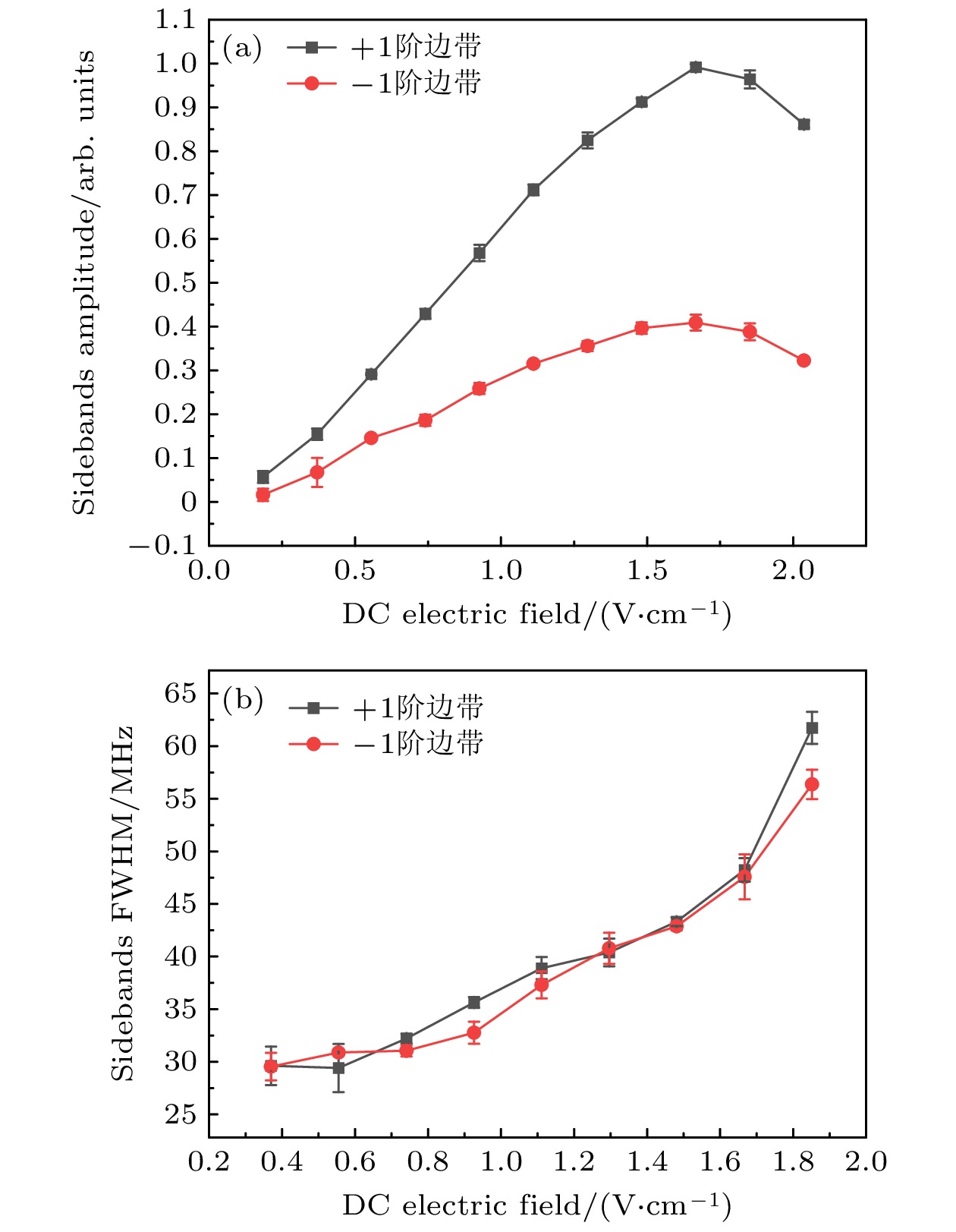
$\varOmega _{\text{c}}^n$ 不再为0, 这表明DC电场的引入改变了电场与里德伯原子的相互作用机制, 从而产生了奇数阶边带. 实验结果与基于DC电场测量的Floquet理论预测一致[25].图5中EIT主峰两侧的±1阶边带存在不对称性, 这是由于每个边带所对应的耦合光的有效拉比频率和失谐量不同所导致. 实验结果表明当DC电场强度增大时, 一阶边带的幅值显著升高. 为了进一步探究DC电场强度对Floquet-EIT的影响, 实验研究了DC电场强度与Floquet-EIT一阶边带的对应关系. 图6(a), (b)所示为ωs = 200 MHz, Erf = 2.58 V/cm时, DC电场强度与一阶边带幅值和半高全宽(FWHM)的关系. 在DC电场强度较小时, 一阶边带的幅值与FWHM均呈现出随电场强度单调递增的关系, 当电场增大至约1.67 V/cm时, 一阶边带幅值降低, FWHM明显增宽, 这是由于DC-Stark效应导致的频率偏移与边带间隔接近时, 相邻边带彼此出现串扰, 并且强电场引入的非线性效应, 使EIT光谱出现高阶边带以及复杂的态混合, 形成复杂的Floquet边带, 此时微扰下的Floquet理论近似不再适用[8], 此时的DC电场强度为Floquet-EIT的最大可测量值Emax.
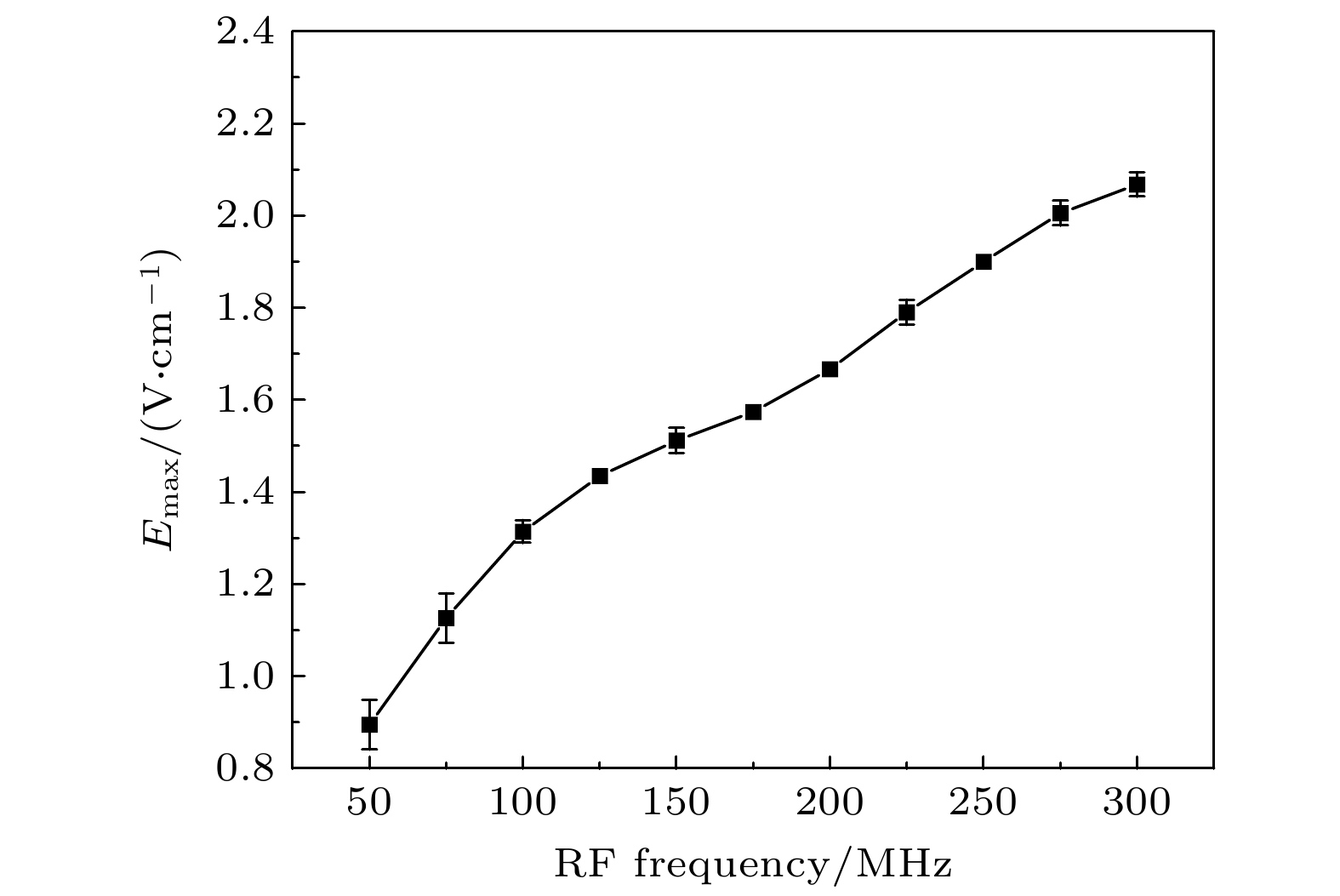
为了进一步研究RF频率对Floquet-EIT一阶边带的影响, 实验保持RF电场强度不变, 使Erf = 2.58 V/cm, 改变RF频率
${\omega _{{\mathrm{s}}}}$ 范围为50—300 MHz, 获得的DC电场强度最大可测量值Emax如图7所示. 可以发现, Emax随RF频率的增大而增大.为了比较DC-Stark频移与Floquet-EIT边带幅值在微弱电场下的测量精确度, 通过向极板内部施加DC电压, 并使
${E_{\mathrm{dc}}}$ = 0.56 V/cm保持不变, 测量多组数据, 得到该电场基于DC-Stark效应的EIT偏移量$\bar \varDelta $ 为10.42 MHz, 标准偏差$\sigma $ 为0.89 MHz, 其相对标准偏差${\text{RSD}} = {\sigma }/{{\bar \varDelta }} = 8.5{\text{%}} $ . 改变DC电场强度为1.11 V/cm和1.48 V/cm, 得到其相对标准偏差分别为3.8%和1.4%. 同样地, 对Floquet-EIT的一阶边带幅值进行类似测量计算, 得到其相对标准偏差, 结果如表1所示.实验结果表明, 在测量微弱电场时, Floquet-EIT边带幅值的相对标准偏差低于DC-Stark效应的频率相对标准偏差. 这是由于在微弱电场下, 外界环境的扰动对频率测量的影响大于对信号幅值测量的影响, 进而导致更大的电场强度测量误差. 并且我们发现随着电场强度的增大, DC-Stark方法的RSD减小, 这是由于DC-Stark方法的标准偏差
$\sigma $ 不随电场强度变化, 而偏移量$\bar \varDelta $ 随着电场强度增大而增大, 使得RSD减小. -
实验通过构建里德伯原子的阶梯型三能级结构, 开展了基于射频电场缀饰下Floquet-EIT光谱的特性研究. 实验发现, 在仅施加射频电场时, AC-Stark效应导致EIT光谱偏移并且EIT光谱两侧产生偶数阶边带, 同时施加DC电场后, 除了偶数阶边带信号外, 还能够探测到Floquet-EIT光谱的奇数阶边带信号. 基于此现象, 实验研究了一阶边带幅值及半高全宽与直流电场强度的关系. 研究表明, 随着直流电场强度增大, 一阶边带幅值和半高全宽也增大. 然而, 当直流电场达到一定强度时, 由于边带串扰和非线性效应等影响, 光谱出现了边带幅值下降和半高全宽加宽明显等现象. 我们进一步研究了不同RF频率下的DC电场最大可测量值. 结果表明, 增大RF频率, 可以提升DC电场的测量范围. 最后通过比较Floquet-EIT与DC-Stark的相对标准偏差, 发现Floquet-EIT光谱对微弱低频电场的测量精确度高于传统的DC-Stark法. 本实验展示了Floquet-EIT在射频和直流电场同时作用下的光谱特性, 并为基于里德伯原子的高灵敏度直流电场测量提供了实验依据.
感谢重庆大学物理系汪涛老师和深圳技术大学工程物理学院韩婴婴老师的有益讨论.
射频场缀饰的直流电场Floquet-电磁诱导透明光谱特性研究
Spectral characteristics of Floquet-electromagnetically induced transparency dressed by radio frequency field in a direct current electric field
-
摘要: 在室温铯原子气室中利用探测光(852 nm)与耦合光(510 nm)构建的里德伯阶梯型结构, 实现了基于射频场缀饰的直流电场Floquet-电磁诱导透明(Floquet-electromagnetically induced transparency, Floquet-EIT)光谱, 并研究了直流电场下的Floquet-EIT光谱特性. 实验发现, 仅射频电场作用时, EIT光谱只呈现偶数阶边带, 而当射频场与直流电场同时作用时, 实验观测到Floquet-EIT的一阶边带信号. 随着直流电场强度增大, 一阶边带幅值逐渐升高. 然而, 当直流电场增大到一定强度时, 强电场会导致边带间相互串扰, 使边带幅值下降, 但增大射频频率可以延缓直流电场对一阶边带的串扰影响. 最后对比Floquet-EIT光谱的边带幅值与DC-Stark光谱的频率偏移在微弱直流电场下的相对标准偏差, 发现前者在微弱电场下的测量精确度明显优于后者. 本文工作为直流电场和低频电场的量子传感测量提供了新思路.
-
关键词:
- 里德伯原子 /
- 电磁诱导透明 /
- Floquet-电磁诱导透明边带 /
- 射频调制
Abstract:A Rydberg atom is a special type of atom characterized by a high principal quantum number. Electric field sensors based on Rydberg atoms have received widespread attention due to their high polarizability. However, there is currently little research on the use of Rydberg atoms for direct current (DC) or low-frequency electric fields, mainly due to the shielding effect of atomic vapor cells in low-frequency electric fields, which makes accurate measurement of the electric fields extremely challenging. In this paper, we construct a Rydberg ladder configuration by using probe laser at 852 nm and coupling laser at 510 nm in a room-temperature cesium vapor cell with integrated electrode plates, thereby enabling the realizing of a Floquet-EIT (electromagnetically induced transparency) spectrum dressed by a radio frequency (RF) field in the presence of a DC electric field. We further study the influence of DC electric field on spectral characteristic. Experimentally, it is observed that when only the RF electric field is applied, the EIT spectrum displays solely even-order sidebands. Furthermore, when both the RF field and the DC electric field are simultaneously present, the first-order sideband signal of the Floquet-EIT is observed. As the intensity of the DC electric field increases, the amplitude of the first-order sideband gradually increases. However, increasing the DC electric field to a sufficient magnitude induces sideband interference, which leads the sideband amplitudes to decrease. Furthermore, increasing the RF frequency can alleviate the interference effects induced by the DC electric field on the first-order sideband. Finally, comparing the relative standard deviation of the sideband amplitudes of the Floquet-EIT spectra with the frequency shifts of the DC-Stark spectra under weak DC electric fields, we find that the measurement accuracy of the former is significantly superior to that of the latter. This work makes use of a Cs atomic vapor cell with an integrated electrode to avoid shielding effects. By observing Floquet-EIT spectra, the response of the spectra to DC electric fields is investigated. This experiment provides novel insights into the quantum sensing measurements of DC and low-frequency electric fields. -
-
图 1 里德伯原子EIT能级示意图 (a)和实验装置图(b) OI, 光隔离器;
${\lambda {/ } 2}$ , 半波片; PBS, 偏振分光棱镜; M, 852 nm高反镜; SG, 信号发生器; DM, 二向色镜; PD, 光电探测器; SP, 整形棱镜Figure 1. Schematic diagram of Rydberg EIT energy levels (a) and experimental setup diagram (b). OI, optical isolator;
${\lambda {/ } 2}$ , half-wave plate; PBS, polarization beam splitter; M, 852 nm high reflectivity mirror; SG, signal Generator; DM, dichroic mirror; PD, photodiode; SP, shaping prism.
图 2 原子气室中内置极板间的电场模拟分布(a)和模拟电压云图(b)
Figure 2. Simulated distribution of electric field between the built-in plates in the atomic cell (a) and simulated voltage cloud map (b).
图 3 基于DC-Stark效应的EIT光谱频移图 (a)不同DC电场强度下的EIT光谱; (b) DC电场强度和EIT光谱频移的关系
Figure 3. EIT Spectral frequency shift based on DC Stark effect: (a) EIT spectra with different DC electric field intensity; (b) the relationship between DC electric field intensity and EIT spectral frequency shift.
图 4 在200 MHz下基于AC-Stark效应, 不同RF电场强度的EIT光谱 (a)Erf = 0 V/cm; (b) Erf = 1.8 V/cm; (c) Erf = 3.04 V/cm
Figure 4. EIT spectra based on the AC-Stark effect at 200 MHz with different RF electric field intensity: (a) Erf = 0 V/cm; (b) Erf = 1.8 V/cm; (c) Erf = 3.04 V/cm.
图 5 Erf为2.58 V/cm的RF电场与DC电场同时作用产生的Floquet-EIT边带, 黑线和红线分别代表Edc为0.37 V/cm和0.74 V/cm的实验结果
Figure 5. Floquet-EIT sidebands generated by the simultaneous action of RF electric field with Erf is 2.58 V/cm and DC. The black and red lines represent the experimental results with Edc values of 0.37 V/cm and 0.74 V/cm, respectively.
图 6 不同DC电场强度对一阶边带的影响 (a) DC电场强度与一阶边带幅值的对应关系; (b) DC电场强度与一阶边带FWHM的对应关系
Figure 6. The effect of different DC electric fields on the first-order sidebands: (a) The correspondence between DC electric field intensity and first-order sideband amplitude; (b) the correspondence between DC electric field intensity and first-order sideband FWHM.
表 1 DC-Stark频移与Floquet-EIT边带幅值在不同DC电场下的相对标准偏差对比
Table 1. Comparison of the RSD of DC-Stark shift and Floquet-EIT sideband amplitude with different DC electric fields.
不同方法的RSD DC电场强度/(V·cm–1) 0.56 1.11 1.48 DC-Stark的频移/% 8.5 3.8 1.4 Floquet-EIT的
+1阶边带幅值/%0.9 1.7 0.8 
下载: 导出CSV
-
[1] Prajapati N, Robinson A K, Berweger S, Simons M T, Artusio-Glimpse A B, Holloway C L 2021 Appl. Phys. Lett. 119 214001 doi: 10.1063/5.0069195 [2] Teale C, Sherman J, Kitching J 2022 AVS Quantum Sci. 4 024403 doi: 10.1116/5.0090892 [3] Liu X B, Jia F D, Zhang H Y, Mei J, Liang W C, Zhou F, Yu Y H, Liu Y, Zhang J, Xie F 2022 Chin. Phys. B 31 090703 doi: 10.1088/1674-1056/ac6dbb [4] Viteau M, Radogostowicz J, Bason M G, Malossi N, Ciampini D, Morsch O, Arimondo E 2011 Opt. Express 19 006007 doi: 10.1364/OE.19.006007 [5] Li L, Jiao Y C, Hu J L, Li H Q, Shi M, Zhao J M, Jia S T 2023 Opt. Express 31 29228 doi: 10.1364/OE.499244 [6] Holloway C L, Gordon J A, Jefferts S, Schwarzkopf A, Anderson D A, Miller S A 2014 IEEE Trans. Antennas Propag. 62 6169 doi: 10.1109/TAP.2014.2360208 [7] Kai Y L, Hai T T, Shu Z Y, Chang J C, Xiao H L, Jie L, Xin D Z, Hui Y, Shi L Z 2020 Phys. Rev. A 101 053432 doi: 10.1103/PhysRevA.101.053432 [8] 韩玉龙, 刘邦, 张侃, 孙金芳, 孙辉, 丁冬生 2024 物理学报 73 113201 doi: 10.7498/aps.73.20240355 Han Y L, Liu B, Zhang K, Sun J F, Sun H, Ding D S 2024 Acta Phys. Sin. 73 113201 doi: 10.7498/aps.73.20240355 [9] 王延正, 武博, 付云起, 安强 2025 激光与光电子学进展 62 0302001 doi: 10.3788/LOP240998 Wang Y Z, Wu B, Fu Y Q, An Q 2025 Laser Optoelectron. Prog. 62 0302001 doi: 10.3788/LOP240998 [10] Kumar S, Fan H, Kübler H, Jahangiri A J, Shaffer J P 2017 Opt. Express 25 8625 doi: 10.1364/OE.25.008625 [11] 吴逢川, 林沂, 武博, 付云起 2022 物理学报 71 207402 doi: 10.7498/aps.71.20220972 Wu F C, Lin Y, Wu B, Fu Y Q 2022 Acta Phys. Sin. 71 207402 doi: 10.7498/aps.71.20220972 [12] Liu B, Zhang L H, Liu Z K, Zhang Z Y, Zhu Z H, Gao W, Guo G C, Ding D S, Shi B S 2022 Phys. Rev. Appl. 18 014045 doi: 10.1103/PhysRevApplied.18.014045 [13] Hao J H, Jia F D, Cui Y, Wang Y H, Zhou F, Liu X B, Zhang J, Xie F, Bai J H, You J Q, Wang Y, Zhong Z P 2024 Chin. Phys. B 33 050702 doi: 10.1088/1674-1056/ad1a8f [14] 杨智伟, 焦月春, 韩小萱, 赵建明, 贾锁堂 2017 物理学报 66 093202 doi: 10.7498/aps.66.093202 Yang Z W, Jiao Y C, Han X X, Zhao J M, Jia S T 2017 Acta Phys. Sin. 66 093202 doi: 10.7498/aps.66.093202 [15] 李伟, 张淳刚, 张好, 景明勇, 张临杰 2021 激光与光电子学进展 58 1702002 Li W, Zhang C G, Zhang H, Jing M Y, Zhang L J 2021 Laser Optoelectron. Prog. 58 1702002 [16] Jau Y Y, Carter T 2020 Phys. Rev. Appl. 13 054034 doi: 10.1103/PhysRevApplied.13.054034 [17] Holloway C L, Prajapati N, Sherman J A, Rufenacht A, Artusio-Glimpse A B, Simons M T, Robinson A K, David S L M, Norrgard E B 2022 AVS Quantum Sci. 4 034401 doi: 10.1116/5.0097746 [18] Ouyang K, Shi Y S, Lei M W, Shi M 2023 Appl. Phys. Lett. 123 264001 doi: 10.1063/5.0186065 [19] Luo X B, Li L P, You L, Wu B 2014 New J. Phys. 16 013007 doi: 10.1088/1367-2630/16/1/013007 [20] Rotunno A P, Berweger S, Prajapati N, Simons M T, Artusio-Glimpse A B, Holloway C L, Jayaseelan M, Potvliege R M, Adams C S 2023 J. Appl. Phys. 134 134501 doi: 10.1063/5.0162101 [21] Veit C, Epple G, Kübler H, Euser T G, Russell P S J, Löw R 2016 J. Phys. B 49 134005 doi: 10.1088/0953-4075/49/13/134005 [22] Bason M G, Tanasittikosol M, Sargsyan A, Mohapatra A K, Sarkisyan D, Potvliege R M, Adams C S 2010 New J. Phys. 12 065015 doi: 10.1088/1367-2630/12/6/065015 [23] Miller S A, Anderson D A, Raithel G 2016 New J. Phys. 18 053017 doi: 10.1088/1367-2630/18/5/053017 [24] Song D N, Jiao Y C, Hu J L, Yin Y W, Li Z H, He Y H, Bai J X, Zhao J M, Jia S T 2024 Appl. Phys. Lett. 125 194001 doi: 10.1063/5.0227250 [25] Liu W X, Zhang L J, Wang T 2023 Chin. Phys. B 32 053203 doi: 10.1088/1674-1056/aca6db [26] Šibalić N, Pritchard J D, Weatherill K J, Adams C S 2017 Comput. Phys. Commun. 220 319 doi: 10.1016/j.cpc.2017.06.015 -
计量
- 文章访问数: 61
- HTML全文浏览数: 61
- PDF下载数: 1
- 施引文献: 0