首页
登录
注册
下载:
-
能级之间的跃迁现象是量子力学的核心研 究内容, 尤其是在周期性外场调制下的跃迁行为. 1932年, Landau[1], Zener[2], Stückelberg[3]和Majorana[4]的开创性工作揭示: 二能级系统的含时驱动导致在免交叉区域发生能级之间的跃迁, 该跃迁被称为Landau-Zener (LZ)跃迁, 用于描述该现象的LZ模型已广泛应用于量子比特[5,6]、玻色爱因斯坦凝聚[7–10]及量子计算[11–15]等领域. 当系统受到周期性调制而反复经过免交叉点时, 能级跃迁过程中的相位累积可导致相长干涉或相消干涉, 该现象即为Landau-Zener-Stückelberg-Majorana (LZSM)干涉[16–20]. 然而, 现实中由于各种不可避免的环境噪声和退相干效应, 驱动量子系统的相干时间通常是有限的, 使实验观察和研究时域LZSM干涉面临很大挑战. 2014年, 在氮空位(NV)色心系统中首次实验观测到LZ Rabi振荡[21], 持续时间达到数微秒. 光晶格钟作为高精度的测量设备[22], 且量子相干时间在秒量级[23], 非常适合观测时域LZSM干涉. 此外, 光晶格钟的稳定度达到了10–18[24], 为研究噪声对LZ跃迁的影响创造了良好条件. 2021年, 刘伟新等[17]理论研究了基于光晶格钟的时域LZSM干涉现象-时域LZ Rabi振荡和时域LZSM干涉, 为实验实现时域LZSM干涉提供了指导. 最近, 本课题组[16]基于87Sr光晶格钟, 实验观测到时域LZ Rabi振荡. 然而, 原子系统内时域LZSM干涉边带谱的实验测量尚未见公开报道.
本文基于87Sr光晶格钟, 通过周期性调制698 nm钟激光频率和优化系统参数, 实验测量了时域LZSM干涉边带谱, 并分析了钟激光作用时间对LZSM干涉边带谱的影响. 实验测得的高激发率时域LZSM干涉边带谱, 对于量子模拟和LZ跃迁的研究具有重要意义.
-
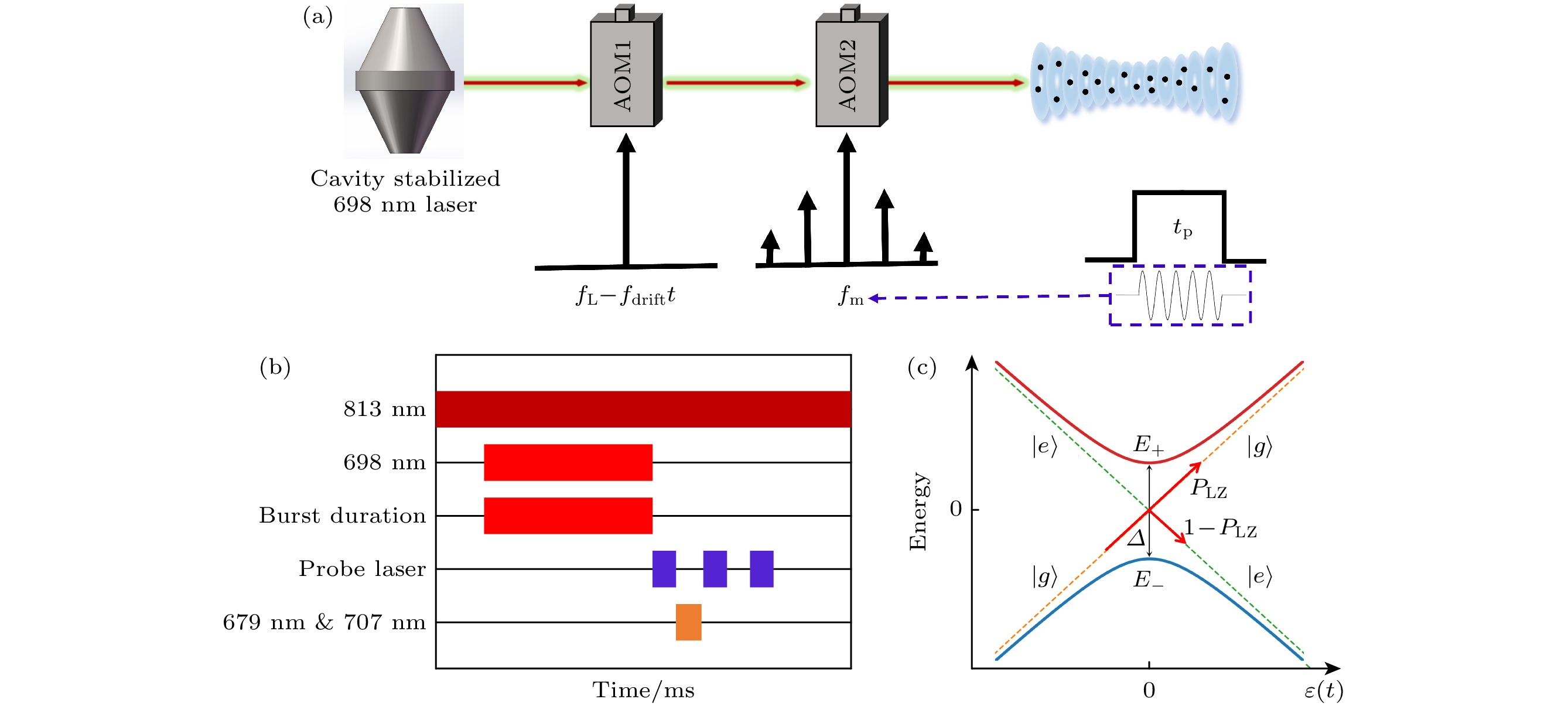
基于87Sr光晶格钟实验平台[25]的实验装置及时序如图1(a)和图1(b)所示. 经两级激光冷却后, 约10000个原子被装载到一维水平光晶格中, 813 nm的晶格光通过Pound-Drever-Hall (PDH)锁频技术稳定到10 cm的超低膨胀腔(Stable Laser System, 18 JSD00111393). 利用周期性频率调制的698 nm钟激光探测制备好的量子参考体系, 实现激光与原子的(5s2)1S0(F = 9/2) — (5s5p)3P0 (F = 9/2)跃迁共振.
周期性调制是LZ跃迁发生的必要条件, 本实验借助声光调制器(acousto-optic modulator, AOM)实现698 nm钟激光频率的周期性调制. 采用射频信号发生器的Burst模式生成余弦调制信号并作用至AOM2(AA OPTO-ELECTRONIC, MT80-A1-VIS). 通过698 nm探测光时序信号进行同步触发, 使调制后的698 nm钟激光在钟探测时保持相同的初始调制相位, 确保原子感受到相同的初始加速度, 从而实现稳定的LZ跃迁. 此外, 698 nm钟激光的偏振严格对准AOM晶体的光轴, 以减少AOM晶体温度变化导致的偏振退化效应, 并防止698 nm激光通过偏振元件时产生的功率抖动影响激光与原子之间的耦合强度. 最终, 利用AOM2扫描698 nm钟激光的中心频率, 并通过归一化探测原子的激发率.
698 nm钟激光的超低膨胀腔受外界温度、湿度和噪声的影响, 钟激光的中心频率产生约0.1 Hz/s的频率漂移. 而本实验需长时间扫描钟激光的中心频率, 频率漂移会导致谱线产生频率误差, 需对其进行补偿. 在钟激光频率无调制的情况下, 通过光钟自比对的方式, 利用AOM2作为频率反馈装置, 将钟激光的频率锁定在原子跃迁谱线上. AOM2反馈输出的频率显示钟激光的频率漂移呈线性关系, 因此使用AOM1 (AA OPTO-ELECTRONIC, MT110-B50A1-VIS)以相反的速率线性扫描钟激光的频率, 实现线漂的补偿. 当补偿时间超过两小时, 受环境等因素的影响, 钟激光的频率漂移以0.05—0.1 Hz/s的速率发生变化, 因此需重新测量钟激光的线漂, 以调整频率补偿速度.
调制后的钟激光频率可表示为[26]
其中A为调制幅度; ωs为调制频率; ωp为平均钟激光频率. 由此可知调制周期T = 2π/ωs. 通过旋转波近似, 则系统的哈密顿量可表示为
其中h为普朗克常数; δ为钟激光与原子共振跃迁的频率失谐;
$ {g_{\boldsymbol{n}}} = g{L_{{n_z}}}(\eta _z^2){L_{{n_x}}}(\eta _x^2){{\mathrm{e}}^{ - {{\eta _z^2} {/ } 2}}}{{\mathrm{e}}^{ - {{\eta _x^2} {/ } 2}}} $ 为修正的钟激光与外态$ {\boldsymbol{n}} = ({n_z}, {n_x}) $ 的耦合强度,$ {\eta _x} = {{\Delta \theta } {/ } {{\lambda _{\text{P}}}}}\sqrt {{h {/ } {(2 m{v_{\text{r}}})}}} $ 和$ {\eta _z} = {1 {/ } {{\lambda _{\text{P}}}}}\sqrt {{h {/ } {(2 m{v_z})}}} $ 分别为横向和轴向Lamb-Dicke参数, Δθ为钟激光与晶格光之间的夹角, vr和vz分别为横向和轴向囚禁频率,$ {L_n}( \cdot ) $ 是n阶拉盖尔多项式.图1(c)为二能级系统免交叉区域附近的LZ跃迁示意图. 当系统的驱动信号为零时, 免交叉点处绝热能级之间的能隙最小. 在远离免交叉点的区域, 由于能隙较大, 可认为系统为绝热演化. 接近免交叉点时, 若外部扫描速率足够慢, 系统将沿绝热路径(图1(c)实线)演化, 假设初态为
$|E_- \rangle =|g \rangle $ , 系统的布居将绝热地由$|E_- \rangle = |g \rangle $ 态演化为$|E_- \rangle =| e \rangle $ 态. 当扫描速率过快使得绝热条件在免交叉区域附近被破坏, 量子态经历LZ哈密顿量的上下瞬时本征态的混合过程, 该过程类似于光学实验上分束器的操作, 最终将在绝热态之间发生跃迁, 即由$|E_- \rangle =|g \rangle $ 态跃迁到$|E_+ \rangle =|g \rangle \rangle $ 态, 对应原子的跃迁概率可由LZ模型给出, 即其中
$ \chi = g_n^2/(4 v) $ 为绝热参数;$ v = A\omega _{\text{s}}^2 $ 为扫描速率. 当$\chi \gg 1$ 时,$ {P_{{\text{LZ}}}} \approx 0 $ , 系统处于慢通道极限(slow-passage limit, SPL). 当$\chi \ll 1$ 时,$ 1 - {P_{{\text{LZ}}}} \ll 1 $ , 系统处于快通道极限(fast-passage limit, FPL). 因此, 实验中除了周期性调制钟激光的频率外, 还需选择合适的耦合强度g, 以确保系统满足时域LZSM干涉条件. -
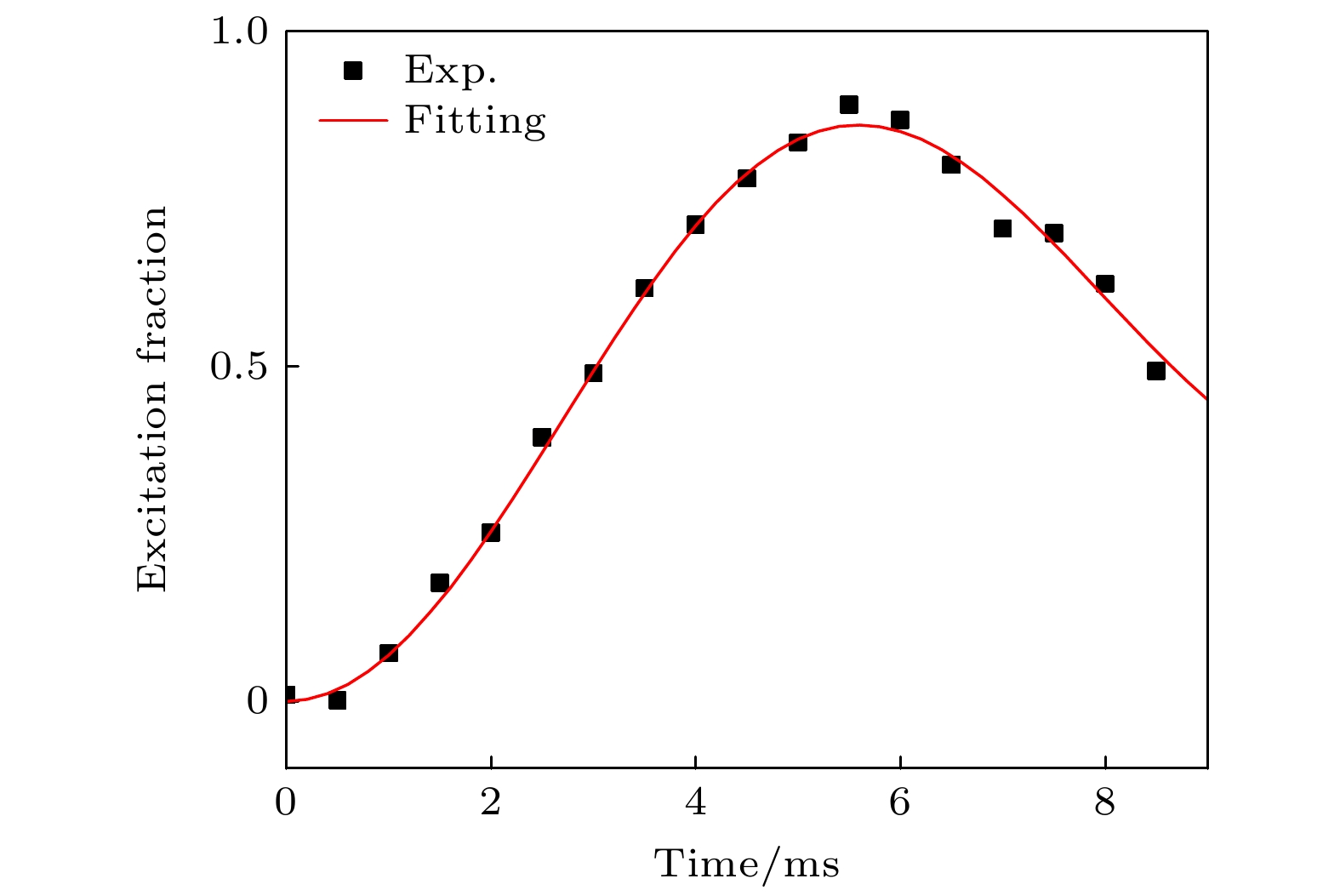
通过探测边带可分辩的钟跃迁Rabi谱, 确定晶格阱深约为157Er (Er为反冲能量)、vz = 86 kHz, vr = 250 Hz、轴向温度Tz = 5.1 μK、径向温度Tr = 9.0 μK[27]. 为了获得激光与原子之间的耦合强度, 在无调制的情况下, 测量了Rabi谱激发率随698 nm钟激光探测时间的变化, 如图2所示, 并对数据进行拟合, 最终确定g = 119, Δθ = 6.5 mrad, ηx = 0.027和ηz = 0.24.
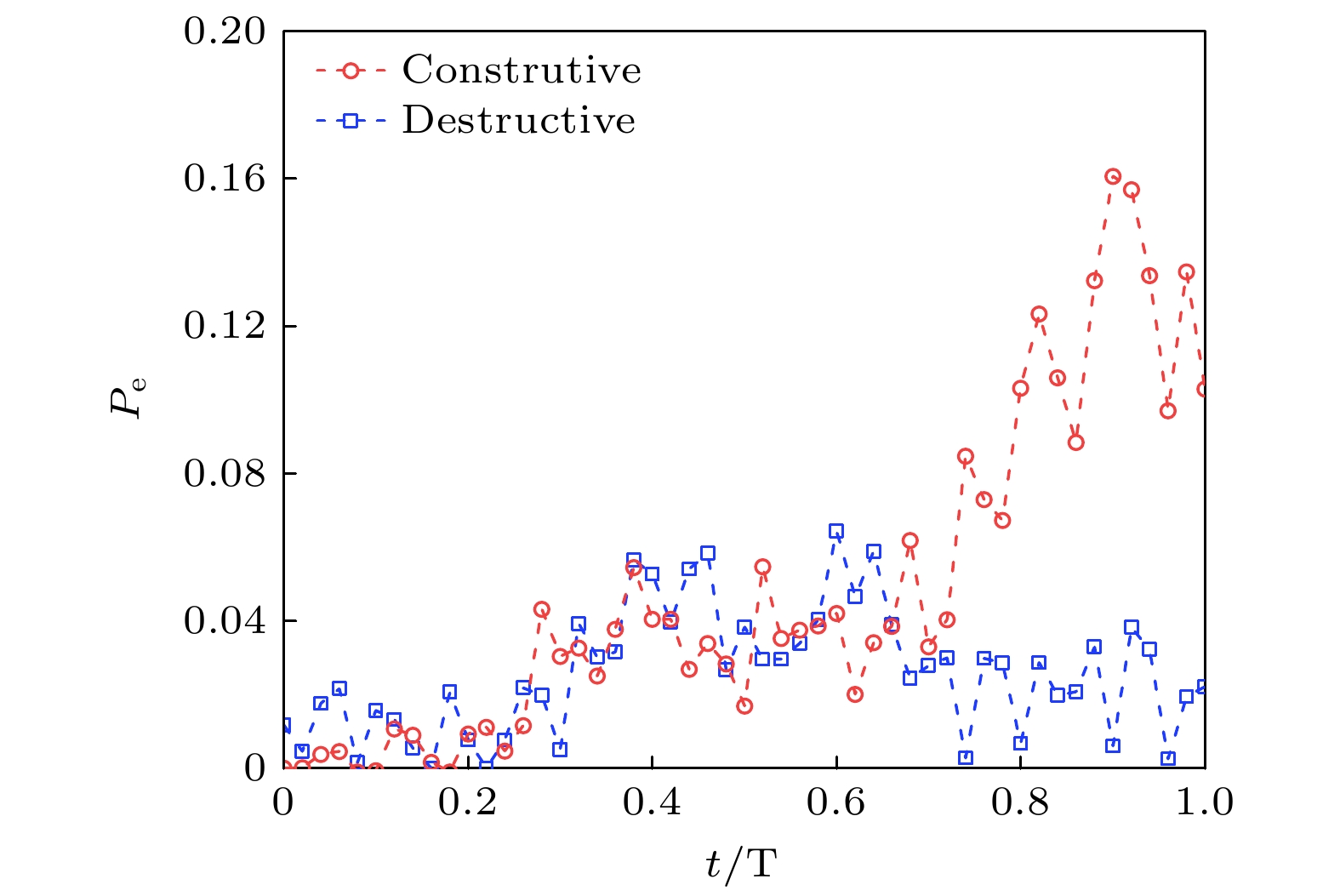
设置钟激光的调制频率为ωs = 2π×200 Hz (即2πg/ωs ≈ 0.6), 固定钟激光与原子共振跃迁频率的失谐为δ = 0 Hz, 测量一个调制周期下的LZSM干涉谱线. 当调制幅度为A = 6.25和A = 5.15, LZSM干涉谱线分别表现出相长干涉和相消干涉的特性, 如图3所示, 且出现台阶状结构, 并伴随着小幅高频振荡. 这些振荡的原因在于, 即使远离免交叉点, 哈密顿量中的
$ {\hat \sigma _x} $ 项仍在基态布居中产生动力学行为. 具体而言, 在相邻的两个LZ跃迁之间, 原子在绝热表象下沿着绝热基态演化, 保持其布居状态不发生改变. 此外, SPL条件下的相消干涉也对应着相干抑制隧穿(CDT). 在调制作用下, 系统保持未被激发, 但由于温度耗散效应的影响, 在周期的后半部分, 激发率较前半部分略有上升. 这些实验现象与Liu等[17]的模拟计算结果相一致. 然而, 由于实验中原子的温度较高以及钟激光的非线性漂移, 导致激发率的测量存在较大波动. -
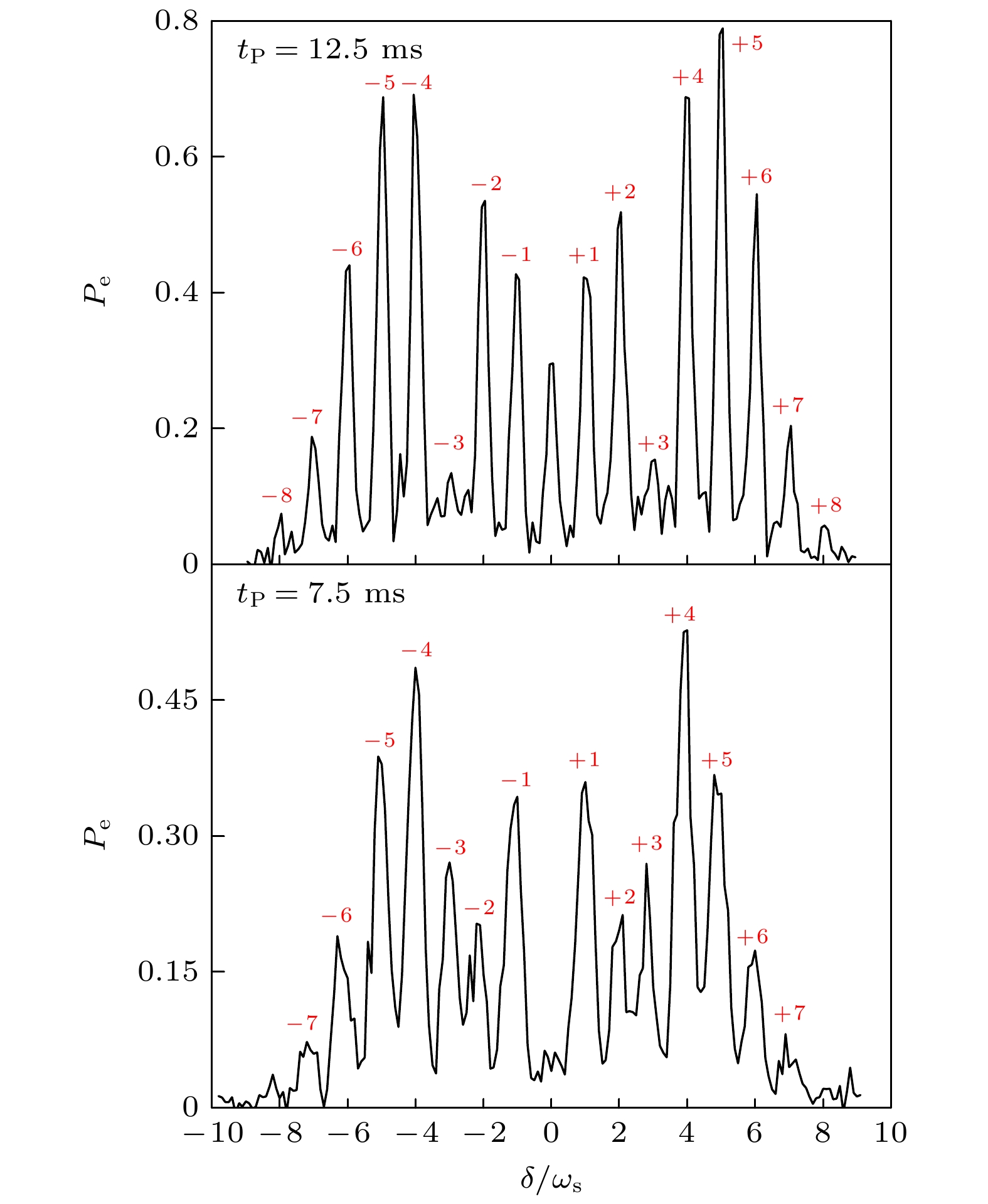
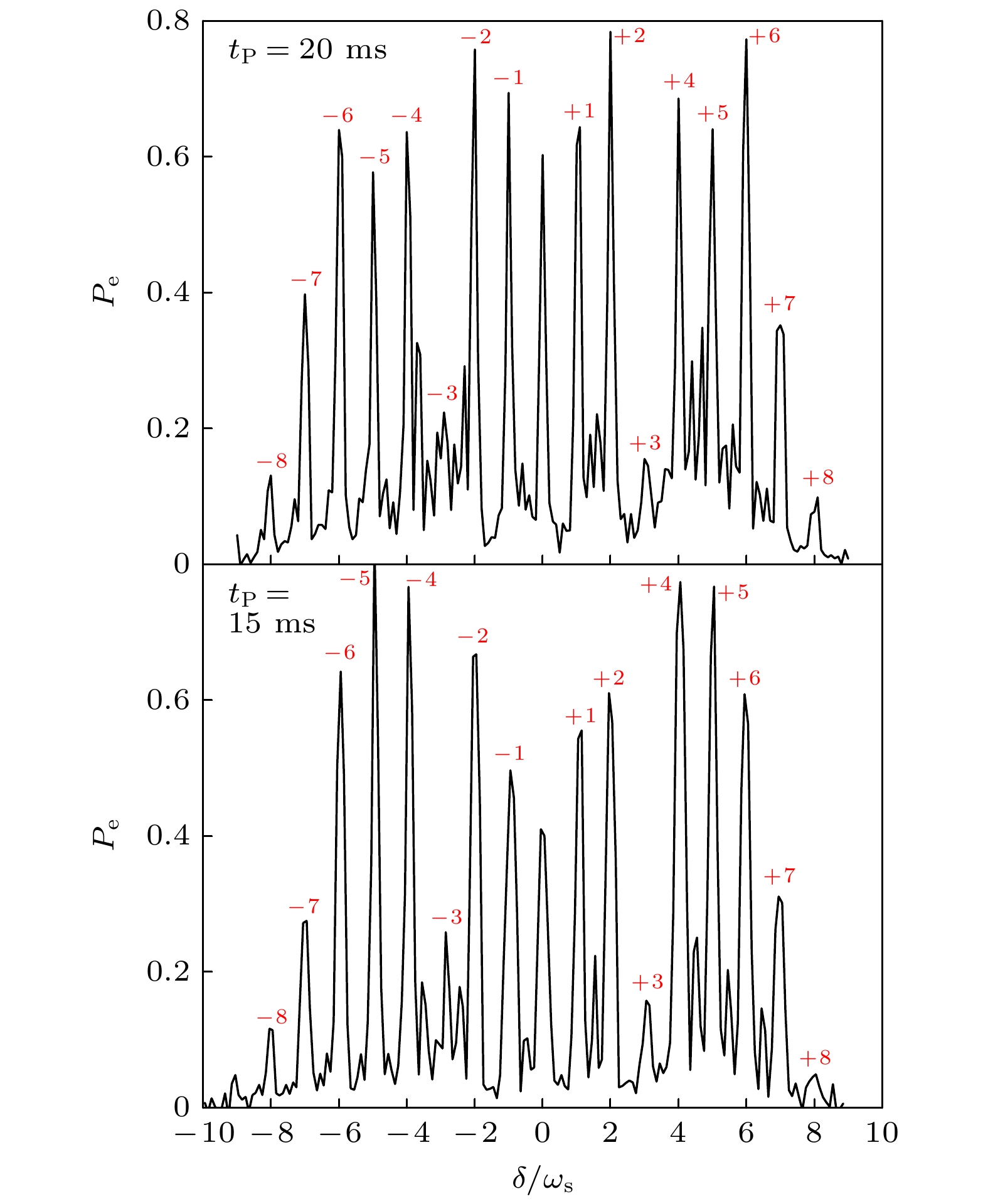
由图3的测量结果可知, 在FPL条件下, 保持其他系统参数不变, A在区间[5.15, 6.25]均满足LZ跃迁. 因此, 设置A = 6, 扫描钟激光的频率失谐δ, 测量时域LZSM干涉边带谱, 实验结果如图4和图5所示. 时域LZSM干涉边带谱存在多个边带, 其中δ/ωs = k (k为整数)时对应±k阶边带, 表明只有调制频率的整数倍位置会发生相长干涉. 此外, 各阶边带的激发率也存在差异, 原因在于不同边带对应的LZ Rabi振荡周期不同, 当钟激光作用时间相同时, 边带对应的激发率将不同. 实验结果与Liu等[17]理论模拟结果一致.
设置钟激光的作用时间为调制周期的半整数倍, 即tp = 7.5 ms (即3T/2)和tp = 12.5 ms (即5T/2). 实验结果(图4)显示, LZSM干涉边带谱呈现对称性. 当干涉时间为3T/2时, 中心载波的激发率被显著抑制. 而干涉时间为5T/2时, ±3阶边带被抑制. 随着LZSM干涉时间的增加, 边带的线宽逐渐减小. 以–1阶边带为例, 通过洛伦兹曲线拟合, 其线宽由248 Hz减小到196 Hz.
设置钟激光的作用时间为调制周期的整数倍, 即tp = 15 ms (即3T)和tp = 20 ms (即4T), 实验结果如图5所示. +1, +4, +5、+6, –3和–4阶边带旁出现明显的干涉小峰, 且这些小峰均位于边带的右侧, 导致LZSM干涉边带呈现非对称分布. 此外, 钟激光作用时间为调制周期的整数倍时, 谱线的整体激发率高于调制周期的半整数倍时对应的激发率, 谱线信噪比更高. 同样, 边带线宽随LZSM干涉时间增加而减小, 其中–1阶边带的线宽由183 Hz降到了89 Hz.
在FPL条件下, 钟激光作用时间为调制周期的半整数倍时, 边带谱呈现对称分布; 而当作用时间为调制周期的整数倍时, 则表现为非对称分布. 该现象可通过Liu等[17]报道中的(12)式加以解释, 其中激发态的布居概率仅与LZ跃迁概率PLZ、斯托克斯相位
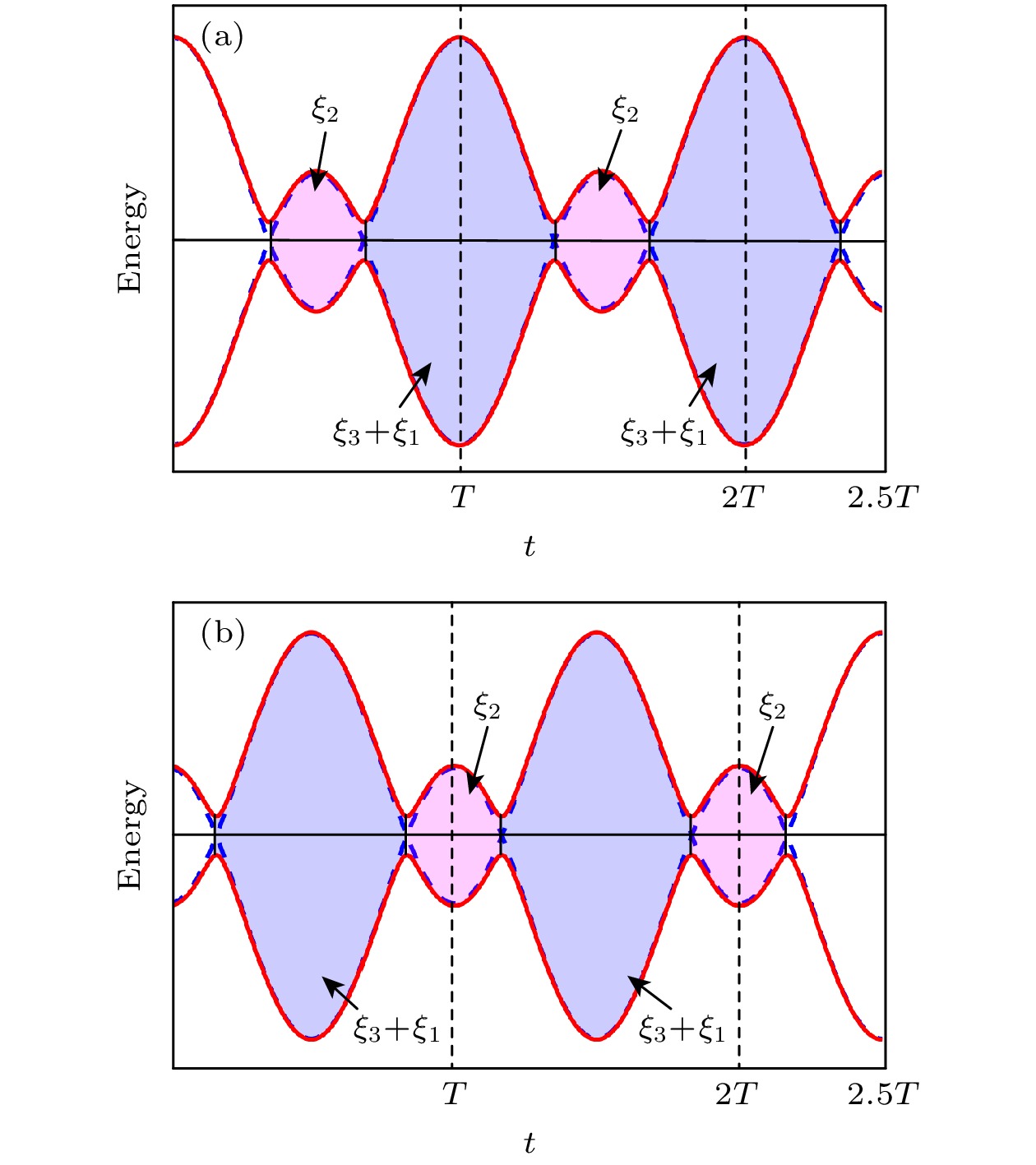
$ \phi $ 和两个免交叉点之间量子态演化积累的相位$ {\xi _2} $ 有关. 依据文献[17]中的(6)式, 钟跃迁过程中量子态演化积累的有效动力学相位如图6所示. 当钟激光作用时间为NT (其中N为正整数)时, 积累的有效动力学相位为$ N{\xi _2} + (N - 1) ({\xi _1} + {\xi _3}) $ ; 而当作用时间为$ (N + {1 {/ } 2}){{T}} $ 时, 积累的有效动力学相位为$ N{\xi _2} + N({\xi _1} + {\xi _3}) $ . 改变钟激光与原子跃迁共振频率的失谐, 将其由δ转变为–δ时, 相位的累积情况也会发生变化. 作用时间为$ (N + {1 {/ } 2}){{T}} $ 时, 有效动力学相位保持不变, 仍为$ N{\xi _2} + N({\xi _1} + {\xi _3}) $ , 因此, 当固定钟激光的作用时间, 扫描钟激光频率得到的时域LZSM干涉谱呈现对称分布, 理论上对称边带的激发率也应相同, 但由于实验过程中存在噪声和退相干效应, 实际测量的对称边带激发率可能会存在差异. 而钟激光作用时间为$ NT $ 时, 积累的有效动力学相位变为$ N({\xi _1} + {\xi _3}) + (N - 1){\xi _2} $ , 从而使时域LZSM边带谱呈现非对称分布. -
基于87Sr光晶格钟较长的系统相干时间, 通过补偿钟激光的频率漂移并精确选择系统参数, 周期性调制698 nm钟激光的频率, 在快通道极限下测量了时域LZSM干涉边带谱, 实验结果揭示了钟跃迁过程中量子态演化积累的有效动力学相位对时域LZSM干涉边带谱对称性的影响. 此外, 当钟激光作用时间为调制周期的整数倍时, 与钟激光作用时间为调制周期的半整数倍相比, 谱线激发率和信噪比更高, 在态制备研究中具有潜在的应用价值. 实验结果与理论模拟[17]高度一致, 验证了光晶格钟平台进行时域LZSM干涉研究的可行性. 未来, 通过进一步抑制钟激光噪声, 光晶格钟将为研究噪声对LZ跃迁的影响提供理想的实验平台.
基于87Sr光晶格钟的时域Landau-Zener-Stückelberg-Majorana干涉边带谱的测量
Measurement of the time-domain Landau-Zener-Stückelberg-Majorana interference sidebands in an 87Sr optical lattice clock
-
摘要: 时域Landau-Zener-Stückelberg-Majorana干涉在量子态操控、延长量子态寿命和抑制系统退相干方面具有重要应用价值. 本文基于87Sr光晶格钟平台, 通过周期性调制698 nm钟激光频率并优化光钟系统参数, 在快通道极限下实现了Landau-Zener跃迁, 并测量了不同实验参数下的时域Landau-Zener-Stückelberg-Majorana干涉边带谱. 由于调制后的激光与原子相互作用在时域上展现出干涉现象, 因此, 通过改变激光失谐可以探测不同钟激光作用时间下的时域干涉边带谱. 实验结果表明, 当钟激光作用时间为调制周期的整数倍时, 扫描钟激光的频率失谐, 干涉边带谱关于零失谐频率呈非对称分布. 而当作用时间为调制周期的半整数倍时, 干涉边带谱则呈对称分布. 该现象源于钟跃迁量子态演化过程中积累的有效动力学相位. 时域Landau-Zener-Stückelberg-Majorana干涉谱的研究为未来基于光晶格钟平台的态制备和研究噪声对Landau-Zener跃迁的影响奠定了实验基础.Abstract:
Landau-Zener-Stückelberg-Majorana (LZSM) interference has significant application value in quantum state manipulation, extending quantum state lifetime, and suppressing decoherence. Optical lattice clock, with a long coherence time, increases the likelihood of experimentally observing time-domain LZSM interference. Although time-dominant Landau-Zener (LZ) Rabi oscillations have already been observed in optical lattice clock, the time-dominant LZSM interference sidebands in optical lattice clock remain unexplored. This study is based on an 87Sr optical lattice clock. By periodically modulating the frequency of the 698-nm clock laser and optimizing the parameters of the optical clock system, LZ transitions are achieved under the fast-passage limit (FPL). During the clock detection, two acoustic optical modulators (AOMs) are employed: AOM1 that compensates for the frequency drift of the clock laser and operates continuously throughout the experiment, and AOM2 that performs traditional clock transition detection and generates a cosine modulation signal by using an external trigger from the RF signal generator in Burst mode. Ultimately, the periodically modulated 698-nm clock laser with a frequency of $\omega (t) = \cos \left[ {\displaystyle\int {\left( {{\omega _{\text{p}}} - A{\omega _{\text{s}}}\cos {\omega _{\text{s}}}t} \right){\mathrm{d}}t} } \right]$ is used to probe atoms, and the Hamiltonian is $ {\hat H_n}(t) = \dfrac{h}{2}[\delta + A{\omega _{\text{s}}}\cos ({\omega _{\text{s}}}t)]{\hat \sigma _z} + \dfrac{{h{g_n}}}{2}{\hat \sigma _x} $. As the modulated laser interacts with the atoms, the interference phenomenon is exhibited in the time domain; adjusting the clock laser detuning allows for probing the time-domain LZSM interference sideband spectra at different detection times. The results show that the time-domain LZSM interference sideband consists of multiple sidebands. Specifically, ±kth order sidebands can be observed at δ/ωs = k, where k is an integer, representing constructive interference. Additionally, due to the different LZ Rabi oscillation periods for each sideband, the excitation fractions of different sidebands are also different, resulting in different excitation fractions for sidebands at the same clock detection time. When scanning the frequency of the clock laser, small interference peaks will appear next to the +1st, +4th, +5th, +6th, –3th and –4th order sidebands when detection time is an integer period. These peaks all appear on the right side of the sidebands, thus breaking the symmetry of LZSM interference sidebands. In contrast, when the detection time is a half-integer period, the interference sidebands exhibit symmetric distribution. This phenomenon mainly arises from the effective dynamical phase accumulated during the LZSM interference evolution. Moreover, the excitation fraction is higher than that at half-integer period, which holds potential application value in state preparation research. The experimental results are in excellent agreement with theoretical simulations, confirming the feasibility of conducting time-domain LZSM interference studies on the optical lattice clock. In the future, by further suppressing clock laser noise, the optical lattice clock will provide an ideal experimental platform for studying the effects of noise on LZ transition. -
-
图 1 实验原理图 (a), (b)分别为LZSM干涉实验装置图和时序图; (c)二能级系统免交叉点附近的LZ跃迁示意图. 实线代表绝热表象下的能级E±, 虚线表示非绝热表象下的能级
$|g \rangle $ 和$|e \rangle $ Figure 1. Experimental diagram: (a), (b) The experimental setup and timing sequences of LZSM interference, respectively; (c) schematic diagram of LZ transition at the avoided crossing point of two-level system. The solid lines represent the adiabatic levels E±, and the dashed lines represent the diabatic levels
$|g \rangle $ and$|e \rangle $ .
图 3 FPL条件下一个调制周期的LZSM干涉谱线. 其中红色带圆形标记的虚线为A = 6.25时的相长干涉谱线, 蓝色带正方形标记的虚线为A = 5.15时的相消干涉谱线
Figure 3. LZSM interference in FPL at one period. The red dashed line with circle markers represents constructive interference at A = 6.25, and the blue dashed line with square markers represents destructive interference at A = 5.15.
图 4 FPL条件下钟激光作用时间为调制周期的半整数倍时(tP = 7.5和12.5 ms)的时域LZSM干涉边带谱
Figure 4. Time-dominant LZSM interference sidebands in FPL at half-integer period (tP = 7.5 and 12.5 ms).
图 5 FPL条件下钟激光作用时间为调制周期的整数倍时(tP = 15和20 ms)的时域LZSM干涉边带谱
Figure 5. Time-dominant LZSM interference sidebands in FPL at integer period (tP = 15 and 20 ms).
图 6 钟跃迁能级随钟激光作用时间变化的示意图 (a), (b)分别代表钟激光频率失谐为δ和–δ时的有效动力学相位累积. 其中红色实线为绝热能级, 蓝色虚线为非绝热能级, 填充区域为绝热演化过程积累的有效动力学相位
Figure 6. Time evolution of energy levels of clock transition with (a) δ and (b) –δ. The red solid lines and the blue dashed lines represent the adiabatic levels and the diabatic levels, respectively. The shade areas represent collected effective dynamic phases during the adiabatic evolution.
-
[1] Landau L D 1932 Phys. Z. Sowjetunion 2 46 [2] Zener C 1932 Proc. R. Soc. London, Ser. A 137 696 doi: 10.1098/rspa.1932.0165 [3] Stückelberg E C G 1932 Helv. Phys. Acta 5 369 [4] Majorana E 1932 Nuovo Cimento 9 43 doi: 10.1007/BF02960953 [5] Xu K B, Xie T Y, Shi F Z, Wang Z Y, Xu X K, Wang P F, Wang Y, Plenio M B, Du J F 2019 Sci. Adv. 5 eaax3800 doi: 10.1126/sciadv.aax3800 [6] Fuchs G D, Burkard G, Klimov P V, Awschalom D D 2011 Nat. Phys. 7 789 doi: 10.1038/nphys2026 [7] Thalhammer G, Winkler K, Lang F, Schmid S, Grimm R, Denschlag J H 2006 Phys. Rev. Lett. 96 050402 doi: 10.1103/PhysRevLett.96.050402 [8] Zenesini A, Lignier H, Tayebirad G, Radogostowicz J, Ciampini D, Mannella R, Wimberger S, Morsch O, Arimondo E 2009 Phys. Rev. Lett. 103 090403 doi: 10.1103/PhysRevLett.103.090403 [9] Tayebirad G, Zenesini A, Ciampini D, Mannella R, Morsch O, Arimondo E, Lörch N, Wimberger S 2010 Phys. Rev. A 82 013633 doi: 10.1103/PhysRevA.82.013633 [10] Uehlinger T, Greif D, Jotzu G, Tarruell L, Esslinger T, Wang L, Troyer M 2013 Eur. Phys. J. Spec. Top. 217 121 doi: 10.1140/epjst/e2013-01761-y [11] Teranishi Y, Nakamura H 1998 Phys. Rev. Lett. 81 2032 doi: 10.1103/PhysRevLett.81.2032 [12] Saito K, Kayanuma Y 2004 Phys. Rev. B 70 201304(R doi: 10.1103/PhysRevB.70.201304 [13] Gaudreau L, Granger G, Kam A, Aers G C, Studenikin S A, Zawadzki P, Pioro-Ladrière M, Wasilewski Z R, Sachrajda A S 2012 Nat. Phys. 8 54 doi: 10.1038/nphys2149 [14] Cao G, Li H O, Tu T, Wang L, Zhou C, Xiao M, Guo G C, Jiang H W, Guo G P 2013 Nat. Commun. 4 1401 doi: 10.1038/ncomms2412 [15] Gaitan F 2003 Phys. Rev. A 68 052314 doi: 10.1103/PhysRevA.68.052314 [16] Tan W, Liu W X, Chen Y X, Zhou C H, Zhao G D, Chang H, Wang T 2025 Phys. Rev. A 111 033102 doi: 10.1103/PhysRevA.111.033102 [17] Liu W X, Wang T, Zhang X F, Li W D 2021 Phys. Rev. A 104 053318 doi: 10.1103/PhysRevA.104.053318 [18] Shevchenko S N, Ashhab S, Nori F 2010 Phys. Rep. 492 1 doi: 10.1016/j.physrep.2010.03.002 [19] Sen A, Sen D, Sengupta K 2021 J. Phys. Condens. Matter 33 443003 doi: 10.1088/1361-648X/ac1b61 [20] Liu H Y, Dai M C, Wei L F 2019 Phys. Rev. A. 99 013820 doi: 10.1103/PhysRevA.99.013820 [21] Zhou J W, Huang P, Zhang Q, Wang Z X, Tan T, Xu X K, Shi F Z, Rong X, Ashhab S, Du J F 2014 Phys. Rev. Lett. 112 010503 doi: 10.1103/PhysRevLett.112.010503 [22] Aeppli A, Kim K, Warfield W, Safronova M S, Ye J 2024 Phys. Rev. Lett. 133 023401 doi: 10.1103/PhysRevLett.133.023401 [23] Boyd M M, Zelevinsky T, Ludlow A D, Foreman S M, Blatt S, Ido T, Ye J 2006 Science 314 1430 doi: 10.1126/science.1133732 [24] Bloom B, Nicholson T L, Williams J, Campbell S, Bishof M, Zhang X, Zhang W, Bromley S L, Ye J 2014 Nature 506 71 doi: 10.1038/nature12941 [25] Guo F, Tan W, Zhou C H, Xia J, Chen Y X, Liang T, Liu Q, Liu Y, He D J, Zhou Y Z, Wang W H, Shen Y, Zou H X, Chang H 2021 AIP Adv. 11 125116 doi: 10.1063/5.0064087 [26] Yin M J, Wang T, Lu X T, Li T, Wang Y B, Zhang X F, Li W D, Smerzi A, Chang H 2021 Chin. Phys. Lett. 38 073201 doi: 10.1088/0256-307X/38/7/073201 [27] Blatt S, Thosen J W, Campbell G K, Ludlow A D, Swallows M D, Martin M J, Boyd M M, Ye J 2009 Phys. Rev. A 80 052703 doi: 10.1103/PhysRevA.80.052703 -
计量
- 文章访问数: 65
- HTML全文浏览数: 65
- PDF下载数: 0
- 施引文献: 0