首页
登录
注册
-
激波与物质内部杂质、孔洞和缺陷等密度间断界面的相互作用广泛存在于惯性约束核聚变[1–2]、水下爆炸[3]、超声速燃烧[4–5]等工程技术领域。从流体力学视角来看，这种相互作用涉及激波的折射与反射[6]、旋涡的产生和输运[7–8]、湍流混合[9]等丰富的现象，具有重要的学术意义。在相关研究中，为突出重点、分解难点，通常将杂质、孔洞和缺陷等结构简化为圆形气柱/球形气泡等几何构型，以充分利用气体介质的透明特性及相对简单的物理性质，开展激波与气柱/气泡相互作用（shock-bubble interactions，SBI）的机理探究[10]，从而为实际应用提供参考。此外，SBI还被视作一种有限界面振幅条件下的Richtmyer-Meshkov不稳定性（Richtmyer-Meshkov instability, RMI）[10–12]，因而成为研究RMI的标准构型之一。
Rudinger等[13]较早开展了SBI研究，利用纹影技术，探究了受冲击气柱/气泡与环境气体之间的相对运动特征。随后，Haas等[6]借助激波管实验，细致考察了SBI的界面演化和波系结构，并应用几何声学理论描述波系形态，研究表明：SBI的界面演化和波系结构与气柱/气泡内部气体相对于环境气体的声阻抗比紧密相关；特别地，当气柱/气泡内部气体的声阻抗低于环境气体的声阻抗时，此类SBI被定义为发散类型，其内部透射波系呈发散状态，受冲击的气柱/气泡演化出涡环结构；反之，重气柱/气泡情形被定义为收敛类型，其内部透射波系呈汇聚状，受冲击的气柱/气泡演化为涡对结构，汇聚波系则在气柱下游极点附近聚焦，可能诱发射流。自Rudinger等[13]和Haas等[6]的开创性研究后，SBI便引起了国内外学者的广泛关注，研究范畴涉及射流形成机制[14–16]、波系演化规律[17]、流场环量沉积[18–19]、湍流混合机理[20–22]等诸多方面。
在SBI诱导射流形成机制研究中，激波聚焦导致的压力扰动被视作关键因素。Zou等[23]和Zhai等[17]研究了气体类型和入射激波强度对SBI的影响，揭示了激波聚焦位置和压力幅值对射流形成与演化的显著影响。Geogievskiy等[24]深入分析了平面激波与不同长短轴比椭球形重气泡的相互作用，总结了激波聚焦位置和压力幅值在不同条件下的变化规律。朱跃进等[16]采用数值模拟方法研究了平面激波与SF6气泡的相互作用，指出激波聚焦产生的压力扰动和斜压涡量共同主导射流演化。Ou等[25]结合激波管实验和数值模拟，研究了激波冲击不同组分SF6气柱的演化规律，证实了斜压机制在射流演化中的促进作用。Fan等[26]通过数值模拟研究了平面激波作用下三角形、四边形和圆形气柱的射流形成机制，研究发现，射流由气柱内部波系聚焦形成的马赫反射波系冲击气柱下游界面产生，射流宽度由马赫杆尺度决定，并提出了利用马赫反射波系滑移线内部楔形区的出现及楔形区顶点位置作为射流产生机制的定性判据。在流场环量演化方面，Picone等[7]提出了预测界面环量沉积的PB模型，而Yang等[27]结合数值模拟和理论分析发展了预测气柱环量的YKZ模型。Samtaney等[28]利用激波极曲线理论推导了预测圆形气柱环量的SZ模型，该模型已成功应用于高马赫数激波冲击气泡及激波冲击椭圆气柱等多种情形的界面环量预测[8]。需要说明的是，传统的SBI研究一般基于连续介质假设，主要关注界面演化的速度场以及温度、密度等热力学平衡量的分布。Zhang等[15]、Xu等[29]将离散玻尔兹曼方法引入SBI研究中，给出了更丰富的流场参数，为考察SBI演化过程中的非平衡效应提供了良好的契机。
在SBI研究领域，除了关注激波对单个气柱/气泡的单次冲击外，部分研究涉及更为复杂的情形，包括激波多次冲击气柱/气泡[30]、激波冲击多气柱[31]、激波单次冲击多层气柱[32–33]等问题，并获得了丰富的物理认识。总体来看，已有研究大多数集中在无限大空间中的SBI问题。然而，在诸多实际问题中，SBI经常发生在平面重-轻界面（入射激波从高阻抗介质向低阻抗介质传播）附近，而且这种界面邻近效应对SBI的演化具有重要影响。以冲击压缩工程领域为例，激波与金属近表面层的杂质、孔洞相互作用时，有可能导致部分物质高速脱离基体，进而引发微喷射现象[34]。在此情形下，金属表面另一侧一般为空气或真空条件，因此，金属表面为典型的重-轻界面。Li等[35]借助分子动力学模拟发现，激波诱导的单晶铜近表面氦泡塌缩能够显著提升微喷射速度和质量；Flanagan等[36]的研究同样表明，单晶铜近表面氦泡影响激波阵面的均匀性，进而增加微喷射量。然而，在这些问题中，波系与界面作用所引发的流体力学效应与金属材料的复杂性质相互耦合，致使其中的关键物理机制难以辨识。因此，有必要从流体力学的视角出发，对该问题进行简化研究。在实际问题中，金属内部杂质的阻抗可能高于或低于基体，并且这2种情况对激波冲击的响应不同[34]。本研究将主要聚焦杂质阻抗高于基体的情形，为简化问题，在忽略杂质形状影响的基础上，将杂质简化为重气柱，把金属表面简化为平面重-轻界面，使问题转化为耦合下游平面重-轻界面的平面激波与重气柱相互作用问题；采用数值模拟方法，深入探究多种下游平面重-轻界面距离条件下激波冲击诱导重气柱的演化发展规律，并与无下游界面条件下的模拟结果进行对比分析，以期揭示界面邻近效应对SBI的影响机制，为实际应用提供规律性认知和支撑。
-
采用基于有限体积法的VAS2D（2 dimensional and axisymmetric vectorized adaptive solver）程序[35]求解二维多组分Euler方程。该程序利用MUSCL-Hancock格式[37]实现时间和空间的二阶精度，利用HLL黎曼求解器[38]计算物理通量。对于激波冲击气柱这种大密度梯度、强间断问题，该程序采用自适应网格加密技术，可以在诸如激波、流体界面和滑移线等大密度梯度区域自动进行网格细化，并且在流场平滑区域进行网格稀疏。该程序在捕捉复杂激波结构和界面演化方面的可靠性已经在诸如非均匀激波冲击平面界面[39]、平面激波冲击气柱[17]等问题中得到了充分的验证。
-
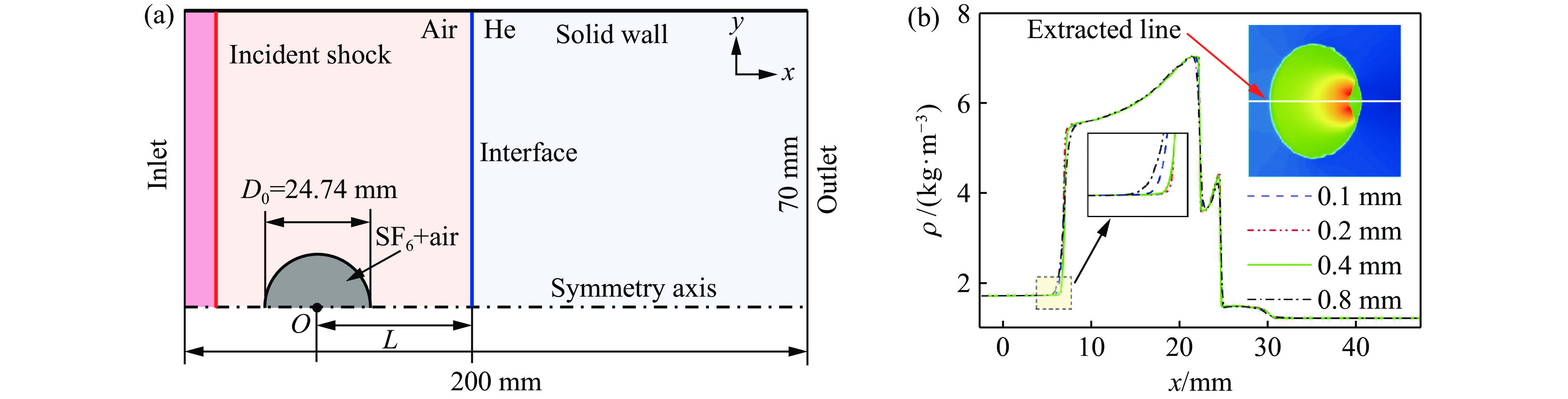
数值模拟计算域如图1(a)所示，将入射激波传播方向设为x方向，与之垂直的方向设为y方向。考虑到来流和几何具有对称性，为节约计算资源，仅选取上半部分流场区域（0≤x≤200 mm，0≤y≤70 mm）进行模拟。同时，在x轴处设置对称边界条件，流场的左、右边界为开口边界条件，上边界为固壁边界条件。流场参数依照Ou等[25]的激波管实验进行设定，激波马赫数Ms= 1.22，重气柱中心O点位于流场对称轴x=12.37 mm处，直径D0 = 24.74 mm；重气柱内为SF6-空气混合气体，其中，SF6和空气的质量分数分别为49%和51%，周围环境气体为空气；流场的初始压力为
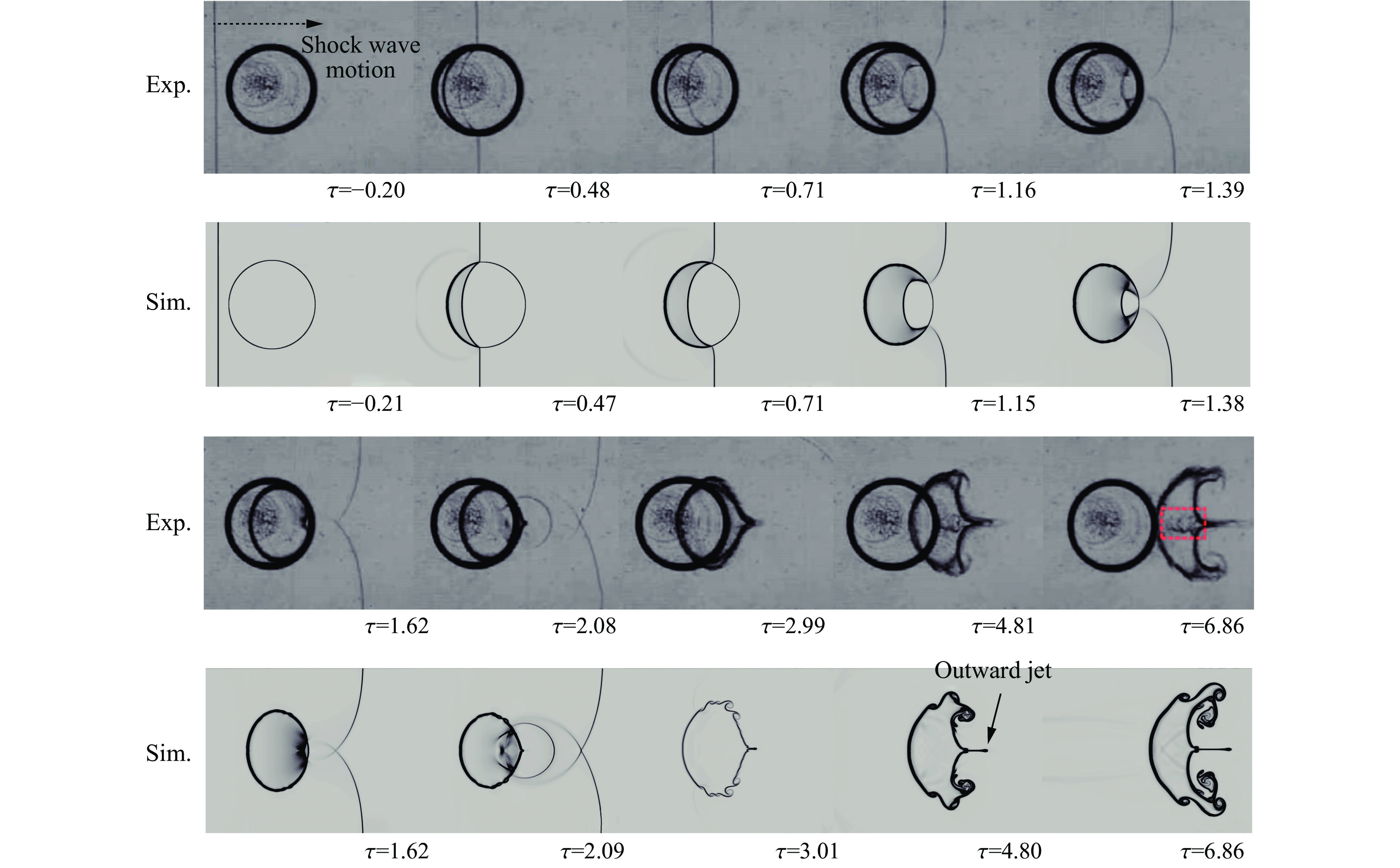
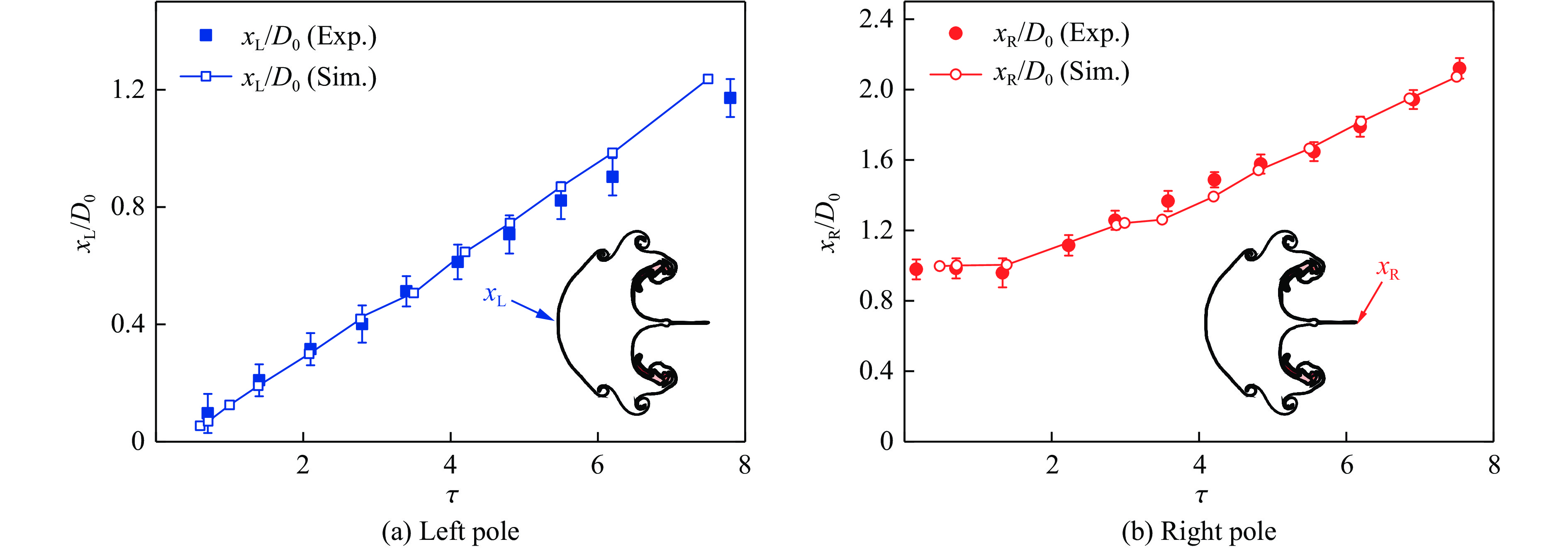
101.325 kPa，初始温度为293 K。为探究下游平面重-轻界面对激波与重气柱相互作用的影响，在距气柱中心下游L处设置平面重-轻界面，界面下游的轻气体设为氦气（He）。下游平面重-轻界面对重气柱演化的影响则通过流场波系与界面耦合效应实现。改变界面间距，考察这2种因素的影响。本研究考虑的4种工况参数设置如表1所示，其中：工况Ⅰ为无下游界面的参考工况，与Ou等[25]的实验保持一致；工况Ⅱ和工况Ⅳ的L差别较大，以突出流场波系对气柱演化的影响；工况Ⅱ与工况Ⅲ的L比较接近，主要用于考察界面耦合效应对气柱演化的影响。为了验证数值程序的可靠性，并检验网格的收敛性，首先采用初始尺寸分别为0.8、0.4、0.2、0.1 mm的4套网格对工况Ⅳ开展数值模拟。选取平面激波接触重气柱左极点的时刻为零时刻（t=0 μs），图1(b)显示了不同初始网格条件下t=110 μs时沿流场对称轴的密度分布。可以看出，初始网格尺寸为0.2和0.1 mm时，计算结果吻合得较好，验证了网格的收敛性。在保证计算精度的同时，为减少计算量，后续数值模拟采用0.2 mm的初始网格尺寸，经3层自适应加密后，流场的最小网格尺寸约为25 μm。采用0.2 mm的初始网格尺寸模拟得到的数值纹影图像与Ou等[25]的实验纹影图像对比如图2所示，定义无量纲时间τ = tWi/D0，其中，Wi为入射激波速度。可以看出，数值模拟准确捕捉到了激波与气柱相互作用产生的波系、旋涡及射流等结构，与实验结果高度吻合。进一步定量提取气柱上下游极点位置随时间的变化规律，并与实验结果进行对比，如图3所示。可见，二者的一致性良好，验证了本研究中数值模拟的可靠性。
-
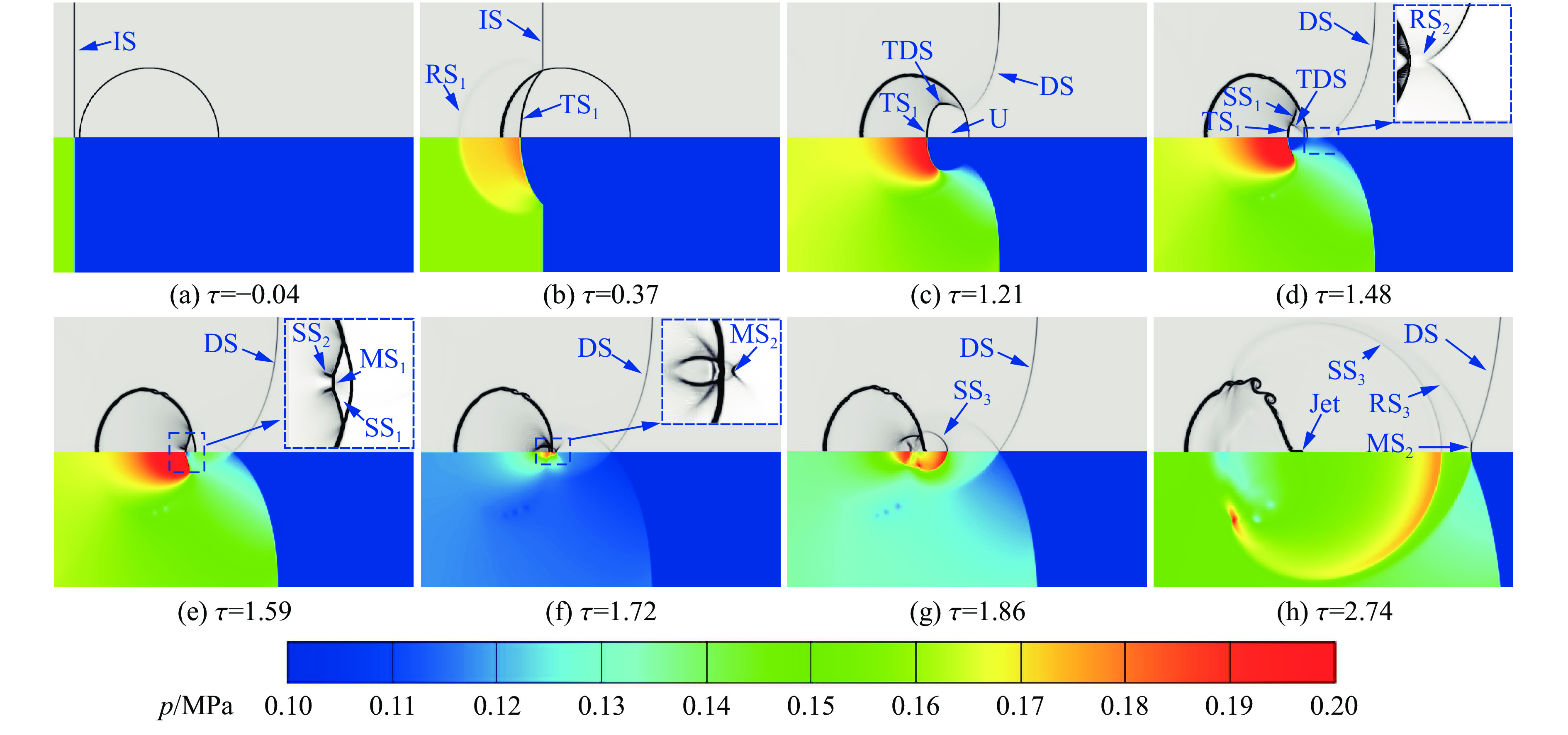
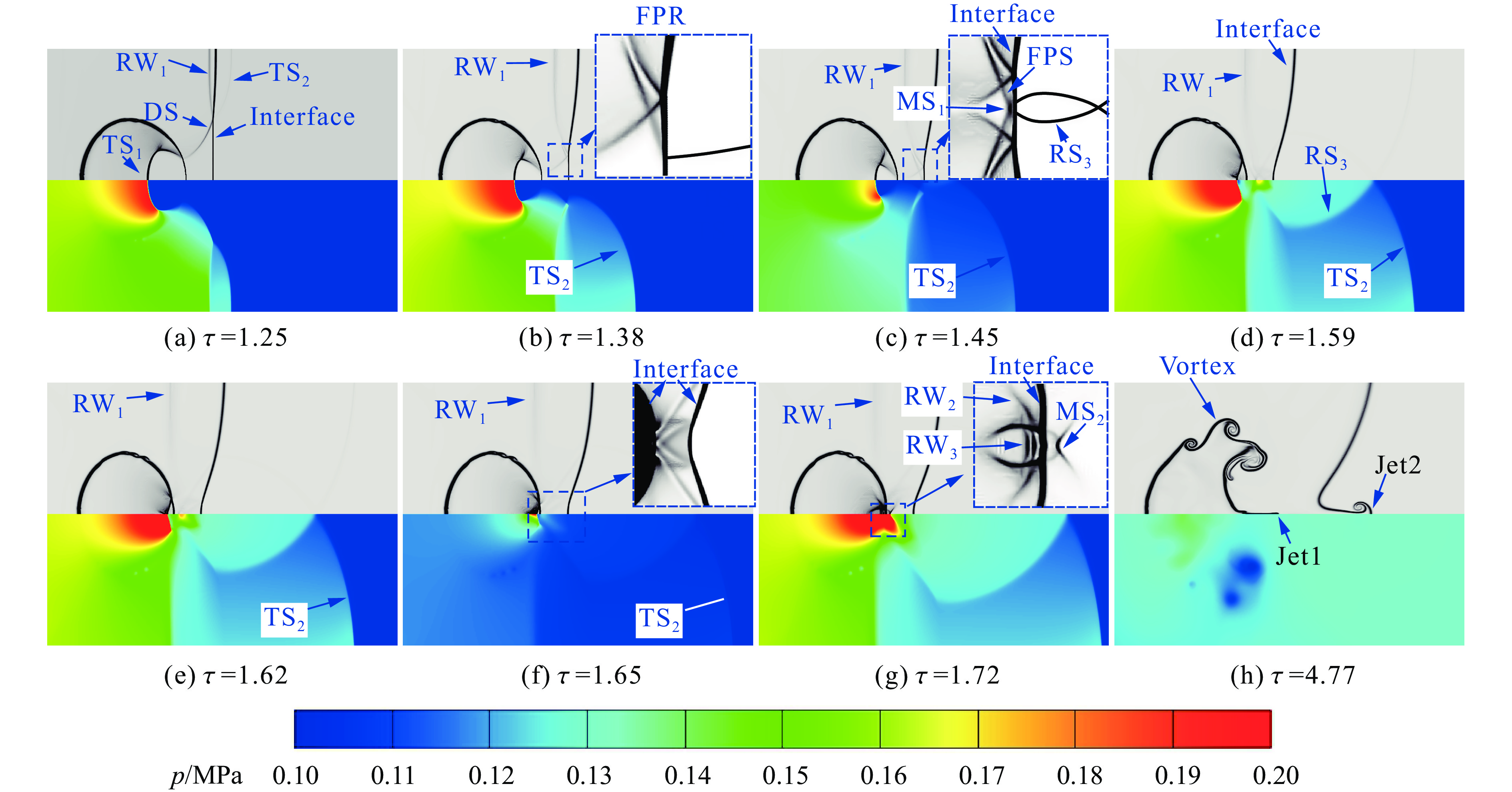
在探讨下游平面重-轻界面对激波诱导重气柱演化的影响前，首先对无下游界面的工况Ⅰ予以讨论。图4以流场密度（ρ）纹影图与压力（p）云图相结合的方式展示了工况Ⅰ的流场和波系结构。如图4(a)和图4(b)所示，平面入射激波IS从左向右传播，当接触气柱的上游界面时，会产生向气柱内部传播的透射激波TS1和向气柱上游运动的反射激波RS1。由于气柱内部气体的声阻抗大于环境气体的声阻抗，透射激波TS1的传播滞后于平面入射激波IS，且TS1的波阵面呈汇聚状分布。随着入射激波IS越过气柱上极点，气柱外部形成了弯曲的衍射激波DS，同时DS向气柱内部折射产生透射衍射激波TDS。由图4(c)可知，此时透射激波TS1、透射衍射激波TDS以及气柱下游界面之间存在一个未受波系扰动的区域U。随着流场的进一步演化，透射衍射激波TDS与透射激波TS1之间的强度差异逐渐增大。为了平衡流场压力差，两者之间形成新的激波SS1，如图4(d)所示。此外，从图4(d)还能看出，气柱外部的衍射激波DS已越过气柱右极点，并在气柱下游的流场对称轴上发生规则反射，进而产生新的反射激波RS2。在图4(e)所示的τ=1.59时刻，气柱内部由透射衍射激波TDS、透射激波TS1和激波SS1组成的波系完成向流场对称轴的汇聚过程，形成由马赫杆MS1、激波SS1和SS2组成的马赫反射波系。与此同时，气柱内部的未扰动区U完全消失。随后，在气柱内部波系聚焦形成的马赫反射波系穿过气柱下游界面，并驱动气柱界面变形。在图4(f)的局部放大图中，能够清晰地辨别该马赫反射波系与气柱右极点附近界面作用后形成的复杂反射和透射波系。由于该透射波系呈发散状态，其波阵面扰动在传播过程中逐渐衰减，到图4(g)时，已演变为波阵面较为光滑的弧形发散激波SS3。随着波系进一步演化，在图4(h)中，气柱外部衍射波系已从规则反射波系转变为马赫反射波系。同时，由气柱内部聚焦波系透射产生的弧形发散激波SS3逐渐趋近该马赫反射波系。此外，气柱内部激波聚焦产生的局部高压驱动的气柱射流清晰可辨。
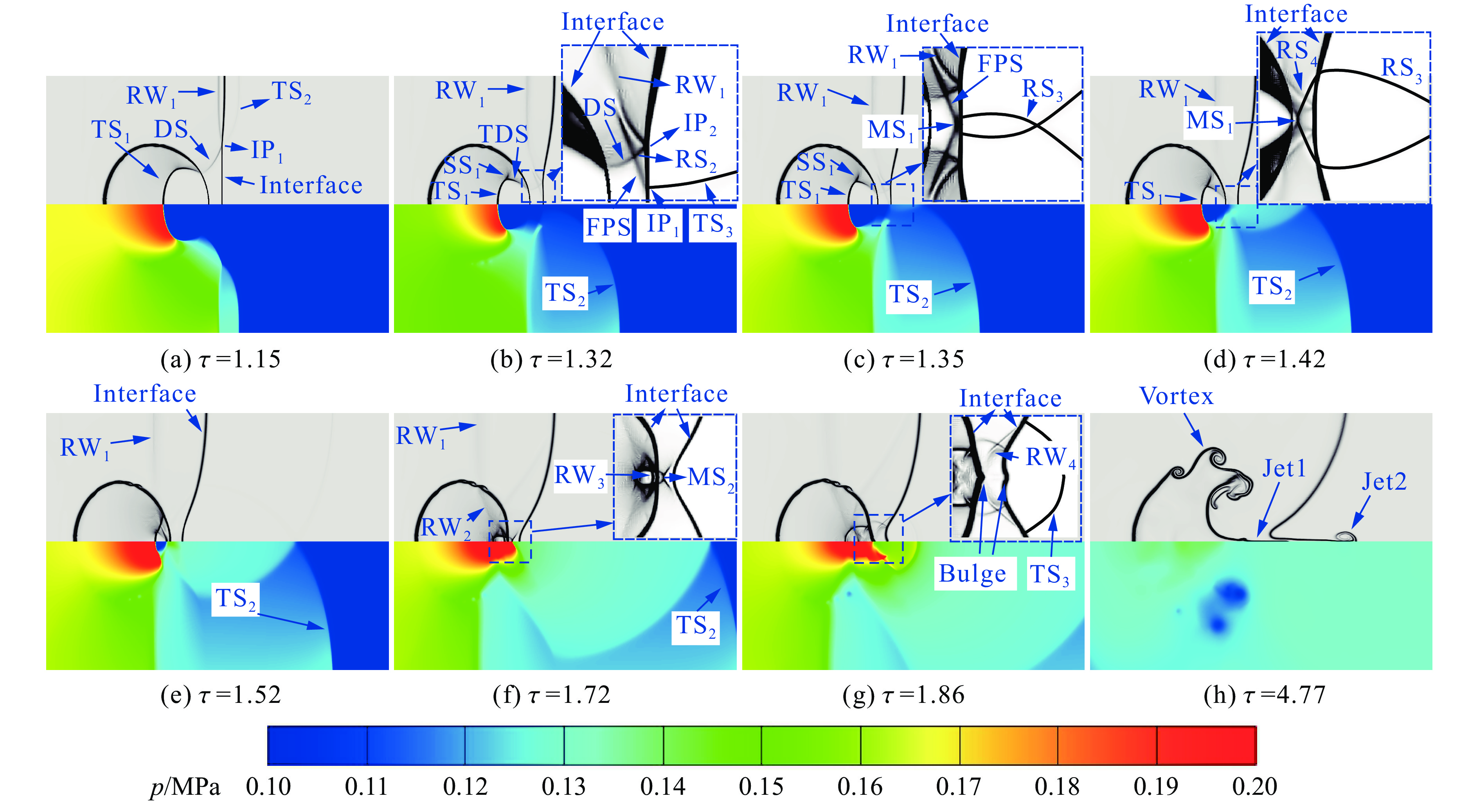
在气柱衍射波系冲击下游平面重-轻界面前，工况Ⅱ、工况Ⅲ和工况Ⅳ的流场及波系结构与工况Ⅰ相同。因而，图5重点展示气柱衍射波系接触下游平面界面后工况Ⅱ的流场与波系演化情况。如图5(a)所示，衍射激波DS首先与下游平面界面相交于IP1，并发生规则折射，形成透射激波TS2和反射稀疏波RW1。随着DS向下游运动，其与下游平面界面间的夹角逐渐增大。由于下游平面界面为重-轻界面，TS2沿界面的运动速度逐渐超过DS沿界面运动的速度。于是，DS在界面上的折射类型由规则折射转变为自由前驱激波折射，并形成自由前驱激波FPS和透射激波TS3，如图5(b)所示。同时，FPS继续与DS相互作用，产生激波RS2。激波RS2在IP2处与平面重-轻界面相交，形成反射稀疏波RW1。随着流场进一步演化，自由前驱激波FPS在流场对称轴上发生马赫反射，生成向上游运动的马赫杆MS1，如图5(c)和图5(d)所示。在τ=1.52时刻，见图5(e)，该马赫反射波系已从气柱右极点附近进入气柱内部。与此同时，下游平面界面的反射稀疏波RW1也抵达气柱的下游界面，二者发生相互作用。随后，如图5(f)所示，气柱内部波系完成聚焦过程，在气柱右极点附近诱发局部高压区，并向外透射以MS2为马赫杆的马赫反射波系。在τ=1.86时刻，见图5(g)，运动变形后的下游平面界面受到该透射马赫反射波系的二次冲击而发生局部凸起，并产生透射激波TS3和反射稀疏波RW4。其中，反射稀疏波RW4在传播过程中与气柱右极点附近界面相互作用，再次加速该界面。从图5(g)还可以看出，在气柱内部聚焦波系的作用下，气柱右极点附近界面也发生了局部凸起。随后，这两处界面凸起分别发展为气柱射流Jet1和下游界面射流Jet2。值得注意的是，在图5(h)中，气柱射流Jet1已穿透气柱与下游平面界面之间的间隙流体，嵌入下游平面界面射流Jet2内部，两者相互耦合，并共同演化。
如图6所示，工况Ⅲ条件下的流场和波系演化与工况Ⅱ相似。在图6(a)～图6(e)中，可以依次观察到与工况Ⅱ中一致的衍射激波DS在下游平面重-轻界面的自由前驱折射（free precursor shock refraction，FPR）现象以及自由前驱激波FPS在流场对称轴上的马赫反射现象等。只不过因2种工况的L稍有差异，导致这些波系的强度和角度稍有不同。2种工况较为显著的差别体现在气柱内部聚焦波系以及气柱外部衍射波系在下游平面重-轻界面上的反射波系抵达气柱右极点的先后次序上。如前所述，因为工况Ⅱ的L较小，所以气柱外部衍射波系在下游平面界面的反射波系先于气柱内部聚焦波系到达气柱的右极点，如图5(e)～图5(g)所示。由于工况Ⅲ的L稍大，其气柱外部衍射波系在下游平面重-轻界面的反射波系与气柱内部聚焦波系几乎同时抵达气柱的右极点，如图6(f)所示。在图6(g)所示的τ=1.72时刻，气柱内部聚焦波系向下游透射产生以激波MS2为马赫杆的马赫反射波系；同时，由RW2和RW3等组成的反射稀疏波系已经产生。随后，受气柱内部聚焦波系及其透射波系诱导产生的气柱射流Jet1以及下游界面射流Jet2相继形成，如图6(h)所示。值得注意的是，与工况Ⅱ的情形相比，工况Ⅲ的L更大，此时Jet1未能穿透气柱与下游平面界面之间的间隙流体，即Jet1与Jet2未能形成耦合结构。
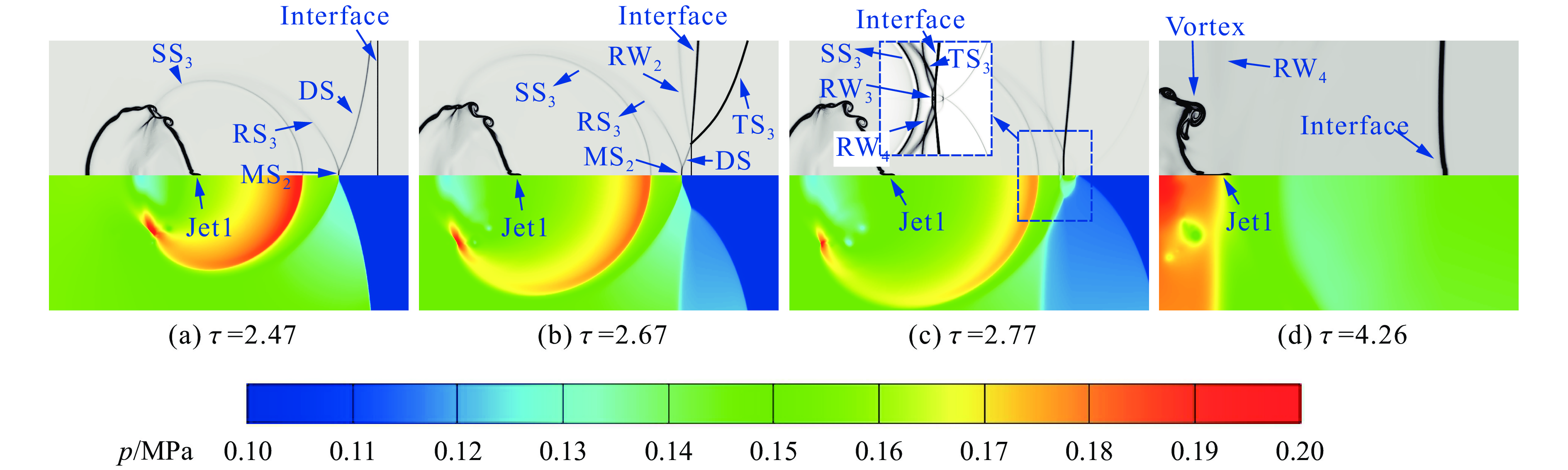
对于工况Ⅳ，因其L较大，气柱内部聚焦波系会先于气柱外部衍射波系在下游平面界面的反射波系到达气柱右极点，使得其流场及波系演化与工况Ⅱ和工况Ⅲ显著不同。如图7(a)所示，在到达下游平面界面前，气柱衍射波系已演变为由激波DS、MS2和RS3组成的马赫反射波系。与此同时，气柱射流已完全形成，气柱内部聚焦波系向气柱下游透射的弧形发散激波SS3也清晰呈现。随着流场进一步演化，气柱衍射波系的波阵面上靠前的激波DS率先冲击下游平面界面，由于两者之间的夹角较小，因此，DS在界面上发生规则折射，形成透射激波TS3和反射稀疏波RW2，如图7(b)所示。在τ=2.77时刻，见图7(c)，气柱衍射波系的马赫杆MS2已完全穿过下游平面界面，形成由稀疏波RW3和RW4组成的反射波系。随后，如图7(d)所示，该反射稀疏波系到达气柱界面，并依次与气柱射流、气柱涡结构以及气柱的上游界面发生相互作用。
-
图8通过SF6气体的流场密度云图展示了4种工况下气柱界面的演化形态。可以看到，在演化早期，气柱受激波压缩而宽度减小。随后，很快有旋涡从气柱上下极点附近卷起，并发展为涡对结构。与此同时，受气柱内部聚焦波系的诱导，气柱射流也逐渐发展演化。在气柱演化后期，受下游平面界面的影响，4种工况下的界面形态呈现显著差异，以下通过气柱宽度W、气柱高度H和射流长度LJ量化这些差异。
图9显示了4种工况下气柱宽度、气柱高度和射流长度随时间的变化情况，均采用气柱初始直径D0进行无量纲化。如图9(a)所示，在演化早期，4种工况下气柱宽度受激波压缩而减小，并且在τ=1.64附近被压缩至最窄。随后，伴随着气柱射流和涡对的发展演化，4种工况的气柱宽度呈现出不同的变化趋势。在演化中期（工况Ⅰ：1.64<τ≤5.98，工况Ⅱ：τ>1.64，工况Ⅲ：1.64<τ≤3.66，工况Ⅳ：1.64<τ≤6.22），气柱宽度由气柱左极点和射流头部位置决定，随着射流的形成与演化，4种工况的气柱宽度均逐渐增大。由于工况Ⅱ和工况Ⅲ的气柱界面还同时受到下游平面界面反射稀疏波系的拉伸作用，气柱宽度的增长速率大于工况Ⅰ和工况Ⅳ。之后，由于环境气体对射流发展的阻碍作用，除工况Ⅱ以外，其他工况的气柱射流发展均趋于饱和，气柱宽度开始减小。在演化晚期（工况Ⅰ：τ>5.98，工况Ⅲ：τ>3.66，工况Ⅳ：τ>6.22），工况Ⅰ、工况Ⅲ和工况Ⅳ的气柱涡对前端在流向上的位置逐渐超过射流头部，气柱宽度转换为由气柱左极点和涡对右边界决定，气柱宽度演化最终进入线性增长阶段。值得注意的是，由于工况Ⅱ的气柱射流与下游平面界面射流形成耦合结构，使得气柱射流头部位置一直领先于涡对右边界，因而，其气柱宽度持续增大，并始终大于其他工况。
对于气柱高度的演化规律，在入射激波冲击气柱的早期阶段，气柱高度保持不变。当入射激波越过气柱上极点后，入射激波在气柱外部转化为衍射激波，使得气柱在展向上被压缩，高度随之减小。随后，气柱涡对在自诱导作用下逐渐发展演化，气柱高度逐渐增大。从τ=2.45附近开始，由于下游平面界面反射稀疏波系的作用，工况Ⅱ和工况Ⅲ的气柱在展向上被拉伸，加之其涡对发展更为充分，因而这2种工况下的气柱高度大于工况Ⅰ和工况Ⅳ。
气柱射流长度的演化规律如图9(c)所示，以无下游平面界面的工况Ⅰ为基准，下游平面界面对工况Ⅱ和工况Ⅳ的气柱射流发展有促进作用，对工况Ⅲ的气柱射流发展起抑制作用。对于工况Ⅱ，下游平面界面对气柱射流的促进作用是通过复杂波系作用引起的界面耦合实现的。首先，气柱外部衍射波系及气柱透射波系先后两次冲击下游平面界面，诱导其产生射流，为界面耦合创造条件；随后，下游平面界面的反射稀疏波系促进气柱射流发展，使其更容易穿透气柱与下游平面界面之间的间隙流体，从而形成界面耦合。对于工况Ⅳ，当下游平面界面反射稀疏波系与重气柱作用时，气柱射流已充分发展，因此，气柱射流是被稀疏波的拉伸作用促进的。下游平面界面对工况Ⅲ气柱射流的抑制机理可从图8中τ=8.08时刻气柱涡对的演化图像得以解释。可以发现，由于下游平面界面反射稀疏波系的作用，工况Ⅲ的气柱涡对结构比工况Ⅰ发展得更为充分，并且在展向上更加靠近气柱射流。由于该涡对在流场对称轴附近诱导的流体速度方向与射流运动方向相反，因此，射流发展受到抑制，这也解释了为何工况Ⅲ与工况Ⅰ的射流长度差异在气柱演化早期并未显现，直到τ=5.12之后才开始出现。
-
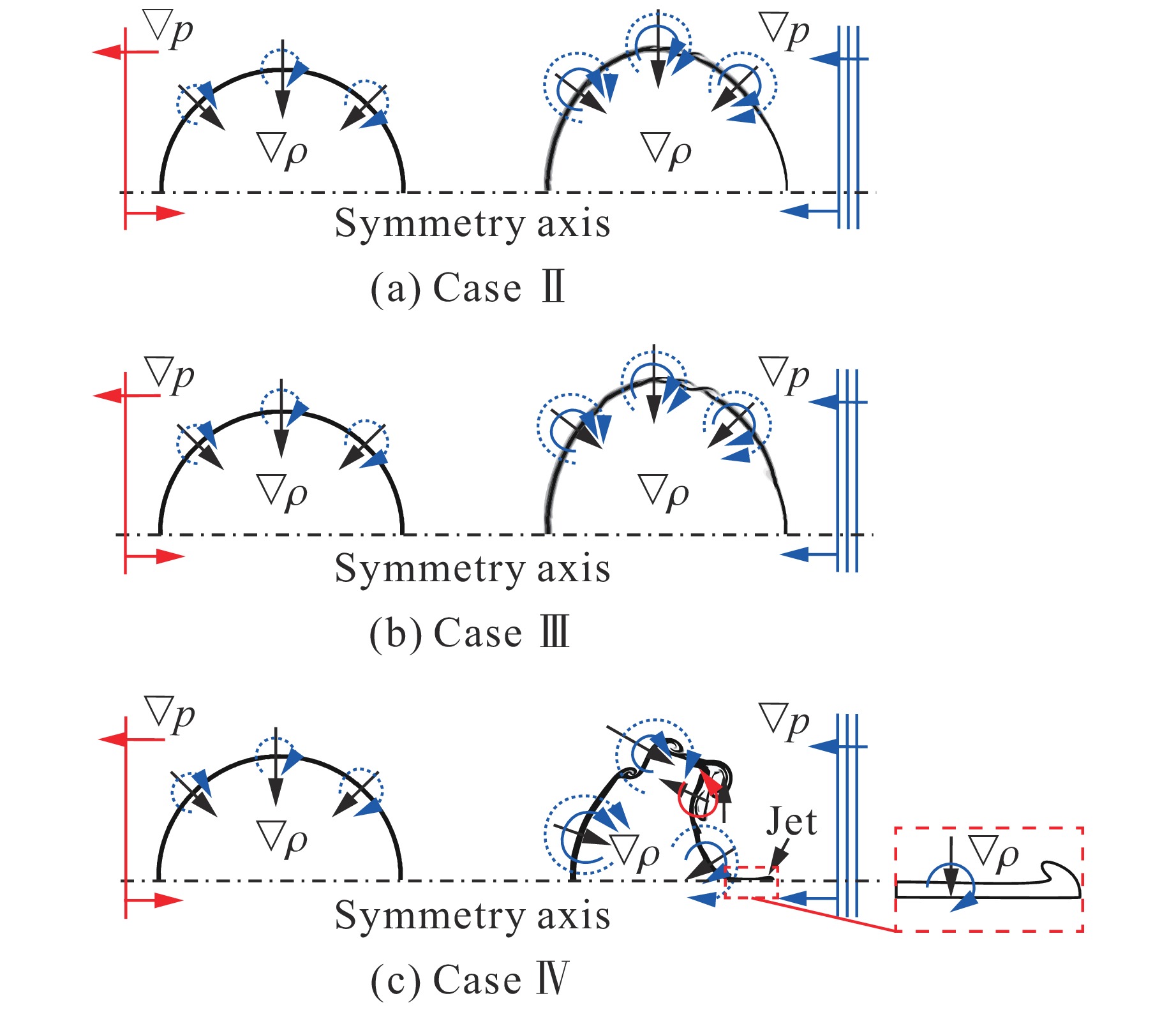
在激波及稀疏波与气柱相互作用过程中，压力梯度与密度梯度不共线导致斜压效应，界面上会沉积斜压涡量。图10为工况Ⅱ、工况Ⅲ和工况Ⅳ斜压涡量沉积示意图，其中：带箭头的虚线表示由入射激波诱导的斜压涡量，带箭头的实线则代表反射稀疏波系诱导的斜压涡量。为简化起见，图10中忽略了下游平面界面反射波系的复杂结构，将其简化为均匀稀疏波。由图10可知，3种工况下入射激波与气柱界面作用会在流场上半平面诱导出负的斜压涡量（顺时针方向）。反射稀疏波作用时，由于3种工况的气柱形态存在差异，因此，在界面上诱导的斜压涡量不同。如图10(a)和图10(b)所示，当反射稀疏波作用于气柱界面时，工况Ⅱ和工况Ⅲ的流场上半平面气柱界面均沉积负的斜压涡量。对于工况Ⅳ，反射稀疏波与气柱作用时气柱界面形态已发生较大变化，因而反射稀疏波除了在大部分区域诱导负的斜压涡量外，还在气柱右侧界面靠近涡对的少部分区域诱导正的斜压涡量（逆时针方向）。
环量是定量表征流场旋涡强度的关键参数。本研究通过对上半平面的气柱涡量进行积分，得到气柱环量随时间变化情况。图11展示了4种工况下上半平面气柱界面沉积的正环量Г+、负环量Г−以及总环量Г 随时间的变化规律。如图11(a)所示，在τ=1.64之前，负环量的绝对值呈线性增长趋势，并在τ=1.64左右达到最大值，随后缓慢减小。不同工况下，下游平面界面反射波系存在差异，其与气柱发生作用的时刻也不同，使得界面上沉积的负环量出现差异。就工况Ⅱ和工况Ⅲ而言，下游重-轻界面的反射稀疏波与气柱作用后，界面负环量的绝对值显著增大，并逐渐趋于稳定。而工况Ⅳ中，因下游重-轻界面反射稀疏波较晚与气柱界面发生作用，其负环量绝对值增大的时刻也相应推迟。根据Ou等[25]的研究，上半平面的气柱正环量主要聚集于射流和涡对附近的小范围区域，故而正环量的绝对值远低于负环量的绝对值。从图11(b)可以看出，4种工况下气柱正环量在初期缓慢增长，之后在下游平面重-轻界面反射稀疏波系的作用下工况Ⅱ和工况Ⅲ进入快速增长期。鉴于工况Ⅱ的射流持续发展，聚焦其内部的正环量也最大。至于工况Ⅳ，如图10(c)中的局部放大图所示，由于下游平面界面反射稀疏波系与气柱射流作用并诱发涡量反向，使其正环量出现降低。4种工况下气柱的总环量随时间的变化规律如图11(c)所示，工况Ⅱ、工况Ⅲ和工况Ⅳ的气柱总环量最终所达到的饱和值比较接近，并且都显著高于无下游平面重-轻界面的工况Ⅰ。这一现象表明，下游平面重-轻界面有助于气柱界面的环量沉积，并且界面间距对气柱界面总环量沉积的影响并不显著。
-
综合上述分析可知，下游平面重-轻界面的存在对重气柱演化产生重要影响。首先，平面入射激波与重气柱作用后，会形成超前的外部衍射波系和相对滞后的内部透射波系。外部衍射波系在气柱下游的流场对称轴上碰撞，进而发生从规则反射到马赫反射的转变；内部透射波系则在气柱内部右极点附近聚焦，诱导气柱产生射流，同时向下游透射马赫反射波系，该波系最终发展为弧形发散激波。随后，气柱的衍射波系和透射波系依次冲击下游平面界面，在诱导下游平面界面产生射流结构的同时，向流场上游反射稀疏波系。这些稀疏波系与气柱相互作用，促进了气柱宽度和高度的演化，以及界面环量沉积。此外，当界面间距较小时，气柱射流能够穿透气柱与下游平面重-轻界面之间的间隙流体，与下游平面界面的射流形成耦合，极大地促进气柱射流的演化发展。
上述研究结果对于激波与金属近表面层杂质相互作用引发的微喷射现象理论研究具有重要启示，表明在相关理论建模中，需要将杂质与金属表面的距离作为重要参数予以考虑。此外，激波与杂质缺陷的相互作用会导致激波阵面出现非均匀性。当这种非均匀激波作用于金属表面时，会诱导金属表面失稳，进而产生微喷射。在后续研究中，需要重点关注这种由非均匀激波诱导的界面失稳现象[39–40]，深入探究其作用机制和影响规律。
-
采用VAS2D程序，通过数值模拟研究了耦合下游平面重-轻界面的激波与重气柱相互作用问题，重点考察了界面间距对重气柱演化的影响，得到以下结论。
(1) 入射激波冲击重气柱后会形成超前的外部衍射波系和相对滞后的气柱内部透射波系，其中：外部衍射波系会在流场对称轴上碰撞，发生从规则反射到马赫反射的转变；而内部透射波系于气柱右极点附近聚焦，并向下游透射产生马赫反射波系，该马赫反射波系在传播过程中逐渐衰减，最终发展为弧形发散激波。
(2) 根据界面间距不同，气柱外部衍射波系在下游平面重-轻界面的反射波系及该反射波系到达气柱右极点的时间存在差异。当界面间距较小时，外部衍射波系在下游平面重-轻界面发生从规则折射向自由前驱激波折射转变，并产生向上游传播的马赫反射波系。此时，平面重-轻界面的反射稀疏波系到达气柱右极点的时间早于气柱内部聚焦波系。随着界面间距逐渐增大，外部衍射波系的反射稀疏波系到达气柱右极点的时间先与气柱内部聚焦波系的到达时间一致，之后滞后于气柱内部聚焦波系的到达时间。
(3) 下游平面重-轻界面的存在对重气柱射流的演化产生重要影响。气柱的衍射波系及透射波系依次冲击下游平面重-轻界面，并诱导该界面演化形成射流。当界面间距较小时，重气柱射流穿透气柱与下游平面重-轻界面之间的间隙流体，与下游重-轻界面的射流发生耦合，显著促进重气柱射流的演化发展。随着界面间距逐渐增大，初始阶段重气柱射流因气柱演化涡对的影响而受到抑制，随后，又因下游重-轻界面反射稀疏波系的稀疏拉伸作用而被轻微促进。
(4) 在气柱外部衍射波系的反射稀疏波二次作用界面过程中，引起了斜压涡量和稀疏拉伸效应等，因而下游平面重-轻界面的存在促进了重气柱的宽度、高度演化及环量沉积。
界面邻近效应对激波诱导重气柱演化的影响
Interface Proximity Effect on the Evolution of a Shock-Accelerated Heavy Gas Cylinder
-
摘要: 针对实际应用中激波与物质近表面杂质及孔洞等相互作用中的界面邻近效应，通过数值模拟开展了下游平面重-轻界面对激波诱导重气柱演化影响的简化机理研究。结果表明，激波冲击气柱形成的衍射和透射波系依次冲击下游界面，在气柱与下游界面之间形成来回反射的波系结构，这些波系不仅影响气柱的界面演化，而且在下游界面诱导产生射流。在不同的界面间距条件下，气柱外部衍射波系在下游界面的反射波系不同，这些反射波系及气柱内部聚焦波系冲击气柱右极点的先后顺序也存在差异。当界面间距较小时，气柱射流可以穿透气柱与下游界面之间的间隙流体，并与下游界面射流耦合，显著促进气柱射流的演化。随着界面间距的增大，射流耦合现象逐渐减弱，重气柱演化涡对抑制了气柱射流的发展。当界面间距进一步增大时，气柱射流又会因下游界面反射稀疏波系的拉伸作用而被促进。此外，在不同的界面间距条件下，下游界面的存在均对气柱界面宽度、高度的发展及环量沉积起到促进作用。Abstract: To uncover the interface proximity effect arising from the interaction between shock wave and near-surface impurity and hole of material in practical applications, a simplified mechanism study on the influence of downstream planar heavy-light interfaces on the evolution of a shock-accelerated heavy gas cylinder was carried out through numerical simulation. The findings reveal that the diffracted and transmitted wave systems formed by the incident shock impacting the heavy gas cylinders successively interact with the downstream planar slow-fast interface, leading to the formation of wave systems that reflect back and forth between the gas cylinder and the downstream planar slow-fast interface. Significantly, these wave systems not only govern the evolution of the gas cylinder interface but also trigger the generation of jets at the downstream planar slow-fast interfaces. Under diverse interfacial spacing conditions, the type of reflected waves originating from the diffracted wave system outside the gas cylinder varies at the downstream interface, and the sequence of the reflected wave system and the focused wave system inside the gas cylinder interacting with the right pole of the gas cylinder is different. When the interfacial distance is narrow, the gas cylinder jet can permeate the gap fluid sandwiched between the gas cylinder and the downstream slow-fast interface and couple with the jet at the downstream planar slow-fast interface, which significantly promotes the evolution of the gas cylinder jet. As the interfacial distance increases, the jet coupling phenomenon progressively wanes, and the gas cylinder jet succumbs to the inhibitory effect of the vortex pair within the gas cylinder. With a further augmentation in interfacial distance, the gas cylinder jet will be promoted by the stretching effect of the reflected rarefaction wave system at the downstream interface. In addition, under different interface spacing conditions, the presence of a downstream planar slow-fast interface invariably augments the development of interfacial width, height, as well as circulation deposition.
-
Key words:
- shock wave /
- Richtmyer-Meshkov instability /
- gas cylinder /
- jet /
- micro-jet /
- circulation .
-
-
图 1 数值模拟计算域示意图 (a)及网格收敛性验证 (b)
Figure 1. (a) Schematic diagram of the computational domain, (b) grid convergence validation
图 2 激波冲击重气柱的实验和数值模拟纹影图像对比
Figure 2. Comparison of experimental and numerical schlieren sequences of the shock-accelerated heavy gas cylinder
图 3 重气柱左、右极点x坐标（xL/D0和xR/D0）的实验与数值模拟结果定量比较
Figure 3. Quantitative comparison of experimental and numerical results of x coordinates of left and right poles (xL/D0, xR/D0) of the shock-accelerated heavy gas cylinder
图 4 工况Ⅰ条件下激波与重气柱作用过程的数值纹影图（上）和压力云图（下）（IS、DS、TS1和TDS分别代表入射激波、衍射激波、透射激波和透射衍射激波，RS1和RS2代表反射激波，SS1、SS2和SS3代表流场横波，MS1和MS2代表马赫杆，U代表未扰动区）
Figure 4. Numerical schlieren (upper) and pressure contour (lower) of the flow field resulting from the interaction between a planar incident shock wave and a heavy gas cylinder for case Ⅰ (Here IS, DS, TS1 and TDS, respectively, denote the incident shock, the diffracted shock, the transmitted shock and the transmitted diffracted shock; RS1 and RS2 represent the reflected shocks; SS1, SS2, and SS3 denote the transverse shocks; MS1 and MS2 represent the Mach stems; U denote the undisturbed flow region.)
图 5 工况Ⅱ条件下激波与气柱作用过程的数值纹影图（上）和压力云图（下）（TS1、TS2和TS3代表透射激波，RS1、RS2、RS3和RS4代表反射激波，RW1、RW2、RW3和RW4代表反射稀疏波，SS1代表流场横波，FPS代表自由前驱激波，IP1和IP2代表激波与界面交点）
Figure 5. Numerical schlieren (upper) and pressure contour (lower) of the flow field resulting from the interaction between a planar incident shock wave and a heavy gas cylinder for case Ⅱ (Here TS1, TS2 and TS3 denote the transmitted shocks; RS1, RS2, RS3 and RS4 denote the reflected shocks; RW1, RW2, RW3 and RW4 denote the reflected rarefaction waves; SS1 denotes the transverse shock; FPS denotes the free precursor shock wave; IP1 and IP2 represent the shock-interface intersection points.)
图 6 工况Ⅲ条件下激波与气柱作用过程的密度纹影图（上）和压力云图（下）（FPR代表自由前驱激波折射）
Figure 6. Numerical schlieren (upper) and pressure contour (lower) of the flow field resulting from the interaction between a planar incident shock wave and a heavy gas cylinder for case Ⅲ (Here FPR denotes the free precursor shock refraction.)
图 7 工况Ⅳ条件下激波与气柱作用过程的密度纹影图（上）和压力云图（下）
Figure 7. Numerical schlieren (upper) and pressure contour (lower) of the flow field resulting from the interaction between a planar incident shock wave and a heavy gas cylinder for case Ⅳ
图 8 4种工况下重气柱界面的演化形态
Figure 8. Evolution of heavy gas cylinder morphology for four cases
图 9 4种工况下重气柱无量纲宽度、高度及射流长度随时间的变化
Figure 9. Evolution of the non-dimensional width, height and jet length of the shock-accelerated heavy gas cylinder for four cases
图 10 工况Ⅱ、工况Ⅲ和工况Ⅳ下波系与气柱界面作用过程的涡量沉积示意图
Figure 10. Sketch diagrams of the vorticity deposition induced by the interaction between shocks and the gas cylinders for cases Ⅱ, Ⅲ and Ⅳ
图 11 4种工况下上半平面气柱界面负环量、正环量和总环量随时间演化规律
Figure 11. Evolution of the negative, positive and total circulation deposited on the shock-accelerated heavy gas cylinder at the upper half plane for four cases
表 1 初始条件设置
Table 1. Setting of initial conditions
Case Gas combinations of downstream planar heavy-light interfaces Ms L/mm Ⅰ Air-He 1.22 ∞ Ⅱ Air-He 1.22 0.6D0 Ⅲ Air-He 1.22 0.7D0 Ⅳ Air-He 1.22 2.0D0 
下载: 导出CSV
-
[1] ZHOU Y, SADLER J D, HURRICANE O A. Instabilities and mixing in inertial confinement fusion [J]. Annual Review of Fluid Mechanics, 2025, 57: 197–225. doi: 10.1146/ANNUREV-FLUID-022824-110008 [2] BETTI R, HURRICANE O A. Inertial-confinement fusion with lasers [J]. Nature Physics, 2016, 12(5): 435–448. doi: 10.1038/nphys3736 [3] BOKMAN G T, BIASIORI-POULANGES L, MEYER D W, et al. Scaling laws for bubble collapse driven by an impulsive shock wave [J]. Journal of Fluid Mechanics, 2023, 967: A33. doi: 10.1017/jfm.2023.514 [4] REN Z X, WANG B, XIANG G M, et al. Supersonic spray combustion subject to scramjets: progress and challenges [J]. Progress in Aerospace Sciences, 2019, 105: 40–59. doi: 10.1016/j.paerosci.2018.12.002 [5] YANG H X, RADULESCU M I. Dynamics of cellular flame deformation after a head-on interaction with a shock wave: reactive Richtmyer-Meshkov instability [J]. Journal of Fluid Mechanics, 2021, 923: A36. doi: 10.1017/jfm.2021.594 [6] HAAS J F, STURTEVANT B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities [J]. Journal of Fluid Mechanics, 1987, 181: 41–76. doi: 10.1017/S0022112087002003 [7] PICONE J M, BORIS J P. Vorticity generation by shock propagation through bubbles in a gas [J]. Journal of Fluid Mechanics, 1988, 189: 23–51. doi: 10.1017/S0022112088000904 [8] LI D D, WANG G, GUAN B. On the circulation prediction of shock-accelerated elliptical heavy gas cylinders [J]. Physics of Fluids, 2019, 31(5): 056104. doi: 10.1063/1.5090370 [9] BALAKUMAR B J, ORLICZ G C, RISTORCELLI J R, et al. Turbulent mixing in a Richtmyer-Meshkov fluid layer after reshock: velocity and density statistics [J]. Journal of Fluid Mechanics, 2012, 696: 67–93. doi: 10.1017/jfm.2012.8 [10] RANJAN D, OAKLEY J, BONAZZA R. Shock-bubble interactions [J]. Annual Review of Fluid Mechanics, 2011, 43: 117–140. doi: 10.1146/annurev-fluid-122109-160744 [11] RICHTMYER R D. Taylor instability in shock acceleration of compressible fluids [J]. Communications on Pure and Applied Mathematics, 1960, 13(2): 297–319. doi: 10.1002/cpa.3160130207 [12] MESHKOV E E. Instability of the interface of two gases accelerated by a shock wave [J]. Fluid Dynamics, 1969, 4(5): 101–104. doi: 10.1007/BF01015969 [13] RUDINGER G, SOMERS L M. Behaviour of small regions of different gases carried in accelerated gas flows [J]. Journal of Fluid Mechanics, 1960, 7(2): 161–176. doi: 10.1017/S0022112060001419 [14] 邹立勇, 刘仓理, 庞勇, 等. 激波作用下SF6气泡界面演化和射流发展的数值模拟 [J]. 高压物理学报, 2013, 27(1): 90–98. doi: 10.11858/gywlxb.2013.01.013 ZOU L Y, LIU C L, PANG Y, et al. A numerical study on interface evolution and jet development of a shocked SF6 gas bubble [J]. Chinese Journal of High Pressure Physics, 2013, 27(1): 90–98. doi: 10.11858/gywlxb.2013.01.013 [15] ZHANG D J, XU A G, SONG J H, et al. Specific-heat ratio effects on the interaction between shock wave and heavy-cylindrical bubble: based on discrete Boltzmann method [J]. Computers & Fluids, 2023, 265: 106021. doi: 10.1016/j.compfluid.2023.106021 [16] 朱跃进, 于蕾, 潘剑锋, 等. 激波冲击SF6重气泡引发射流的数值模拟 [J]. 爆炸与冲击, 2018, 38(1): 50–59. doi: 10.11883/bzycj-2016-0135 ZHU Y J, YU L, PAN J F, et al. Simulation on jet formation induced by interaction of shock wave with SF6 bubble [J]. Explosion and Shock Waves, 2018, 38(1): 50–59. doi: 10.11883/bzycj-2016-0135 [17] ZHAI Z G, SI T, ZOU L Y, et al. Jet formation in shock-heavy gas bubble interaction [J]. Acta Mechanica Sinica, 2013, 29(1): 24–35. doi: 10.1007/s10409-013-0003-8 [18] ZOU L Y, LIAO S F, LIU C L, et al. Aspect ratio effect on shock-accelerated elliptic gas cylinders [J]. Physics of Fluids, 2016, 28(3): 036101. doi: 10.1063/1.4943127 [19] BAI J S, ZOU L Y, WANG T, et al. Experimental and numerical study of shock-accelerated elliptic heavy gas cylinders [J]. Physical Review E, 2010, 82(5): 056318. doi: 10.1103/PhysRevE.82.056318 [20] LI P, BAI J S, WANG T, et al. Large eddy simulation of a shocked gas cylinder instability induced turbulence [J]. Science China Physics, Mechanics and Astronomy, 2010, 53(2): 262–268. doi: 10.1007/s11433-009-0269-9 [21] 柏劲松, 王涛, 邹立勇, 等. 可压缩多介质粘性流体和湍流的大涡模拟 [J]. 爆炸与冲击, 2010, 30(3): 262–268. doi: 10.11883/1001-1455(2010)03-0262-07 BAI J S, WANG T, ZOU L Y, et al. Large eddy simulation for the multi-viscosity-fluid and turbulence [J]. Explosion and Shock Waves, 2010, 30(3): 262–268. doi: 10.11883/1001-1455(2010)03-0262-07 [22] ORLICZ G C, BALASUBRAMANIAN S, VOROBIEFF P, et al. Mixing transition in a shocked variable-density flow [J]. Physics of Fluids, 2015, 27(11): 114102. doi: 10.1063/1.4935183 [23] ZOU L Y, ZHAI Z G, LIU J H, et al. Energy convergence effect and jet phenomenon of shock-heavy spherical bubble interaction [J]. Science China Physics, Mechanics & Astronomy, 2015, 58(12): 124703. [24] GEORGIEVSKIY P Y, LEVIN V A, SUTYRIN O G. Interaction of a shock with elliptical gas bubbles [J]. Shock Waves, 2015, 25(4): 357–369. doi: 10.1007/s00193-015-0557-4 [25] OU J F, DING J C, LUO X S, et al. Effects of Atwood number on shock focusing in shock-cylinder interaction [J]. Experiments in Fluids, 2018, 59(2): 29. doi: 10.1007/s00348-018-2492-5 [26] FAN E, GUAN B, WEN C Y, et al. Numerical study on the jet formation of simple-geometry heavy gas inhomogeneities [J]. Physics of Fluids, 2019, 31(2): 026103. [27] YANG J, KUBOTA T, ZUKOSKI E E. A model for characterization of a vortex pair formed by shock passage over a light-gas inhomogeneity [J]. Journal of Fluid Mechanics, 1994, 258: 217–244. doi: 10.1017/S0022112094003307 [28] SAMTANEY R, ZABUSKY N J. Circulation deposition on shock-accelerated planar and curved density-stratified interfaces: models and scaling laws [J]. Journal of Fluid Mechanics, 1994, 269: 45–78. doi: 10.1017/S0022112094001485 [29] XU A G, ZHANG D J, GAN Y B. Advances in the kinetics of heat and mass transfer in near-continuous complex flows [J]. Frontiers of Physics, 2024, 19(4): 42500. doi: 10.1007/s11467-023-1353-8 [30] 廖深飞, 邹立勇, 刘金宏, 等. 激波两次冲击下重气柱Richtmyer-Meshkov不稳定性的粒子图像测速研究 [J]. 高压物理学报, 2016, 30(6): 463–470. doi: 10.11858/gywlxb.2016.06.005 LIAO S F, ZOU L Y, LIU J H, et al. A particle image velocimetry study of Richtmyer-Meshkov instability in a twice-shocked heavy gas cylinder [J]. Chinese Journal of High Pressure Physics, 2016, 30(6): 463–470. doi: 10.11858/gywlxb.2016.06.005 [31] ZOU L Y, HUANG W B, LIU C L, et al. On the evolution of double shock-accelerated elliptic gas cylinders [J]. Journal of Fluids Engineering, 2014, 136(9): 091205. doi: 10.1115/1.4026439 [32] FENG L L, XU J R, ZHAI Z G, et al. Evolution of shock-accelerated double-layer gas cylinder [J]. Physics of Fluids, 2021, 33(8): 086105. doi: 10.1063/5.0062459 [33] 郑纯, 何勇, 张焕好, 等. 激波诱导环形SF6气柱演化的机理 [J]. 爆炸与冲击, 2023, 43(1): 013201. doi: 10.11883/bzycj-2022-0226 ZHENG C, HE Y, ZHANG H H, et al. On the evolution mechanism of the shock-accelerated annular SF6 cylinder [J]. Explosion and Shock Waves, 2023, 43(1): 013201. doi: 10.11883/bzycj-2022-0226 [34] 朱建士, 胡晓棉, 王裴, 等. 爆炸与冲击动力学若干问题研究进展 [J]. 力学进展, 2010, 40(4): 400–423. doi: 10.6052/1000-0992-2010-4-J2009-144 ZHU J S, HU X M, WANG P, et al. A review on research progress in explosion mechanics and impact dynamics [J]. Advances in Mechanics, 2010, 40(4): 400–423. doi: 10.6052/1000-0992-2010-4-J2009-144 [35] LI B, WANG L, E J C, et al. Shock response of He bubbles in single crystal Cu [J]. Journal of Applied Physics, 2014, 116(21): 213506. doi: 10.1063/1.4903732 [36] FLANAGAN R M, HAHN E N, GERMANN T C, et al. Molecular dynamics simulations of ejecta formation in helium-implanted copper [J]. Scripta Materialia, 2020, 178: 114–118. doi: 10.1016/j.scriptamat.2019.11.005 [37] SUN M, TAKAYAMA K. Conservative smoothing on an adaptive quadrilateral grid [J]. Journal of Computational Physics, 1999, 150(1): 143–180. doi: 10.1006/jcph.1998.6167 [38] TORO E F. Riemann solvers and numerical methods for fluid dynamics: a practical introduction [M]. Berlin: Springer, 2009. [39] ZHANG E L, LIAO S F, ZOU L Y, et al. Refraction of a triple-shock configuration at planar fast-slow gas interfaces [J]. Journal of Fluid Mechanics, 2024, 984: A49. doi: 10.1017/jfm.2024.245 [40] 张恩来, 廖深飞, 邹立勇, 等. 马赫反射波系冲击诱导平面界面失稳的数值模拟 [J]. 中国科学: 物理学 力学 天文学, 2024, 54(10): 104704. ZHANG E L, LIAO S F, ZOU L Y, et al. Numerical simulation of the instability of a planar interface subjected to a Mach reflection wave configuration [J]. Scientia Sinica Physica, Mechanica & Astronomica, 2024, 54(10): 104704. -
计量
- 文章访问数: 34
- HTML全文浏览数: 34
- PDF下载数: 0
- 施引文献: 0