首页
登录
注册
-
爆破作为一种高效、经济、环保的岩石破碎手段，在现代矿业生产中发挥着不可替代的作用。然而，在露天转井下联合开采过程中，随着露天矿的不断剥离，露天台阶距离井下巷道越来越近，露天台阶爆破对井下巷道产生的不利影响也越来越大。在频繁的爆破扰动荷载下，井下邻近巷道上部围岩内部微裂隙发育，结构弱面延伸扩展，巷道结构的物理力学性能降低。随着巷道围岩损伤累积，容易诱发巷道结构变形开裂、失稳垮塌等安全事故，从而影响矿山生产。
近年来，国内外学者针对爆破荷载对小净距邻近隧道结构动力的影响进行了广泛而深入的研究。在爆破振动安全准则和安全允许准则研究方面，早在20世纪20年代，美国科研人员就开始研究了爆破振动控制准则[1]。Jiang等[2]以铁路隧道顶部附近开挖爆破为例，采用数值模拟分析了隧道衬砌和围岩在爆破振动下的振动速度和有效应力，根据最大抗拉强度理论和数值计算结果，确定了峰值振速的安全准则。Xu等[3]基于Mohr-Coulomb强度准则，利用响应振动速度的Fourier-Bessel展开法，建立了圆形隧道围岩爆破振动安全判据，提出了确定安全判据的最大径向振速。Li等[4]通过拟合爆破振动速度与最大主应力的关系，得到了基于抗拉强度的安全振速判据，得出振速的安全阈值为19.62 cm/s。Xue等[5]根据爆破前后衬砌裂缝变化与峰值粒子速度（peak particle velocity，PPV）之间的统计关系，提出了隧道不同部位PPV的安全阈值。Hou等[6]对隧道振动进行了监测，利用瞬时最大输入能量衡量隧道损伤，提出第一次隧道结构破坏的能量阈值为200 J、塑性累计损伤阈值为
3000 J的安全判据。凌同华[7]基于小波时间-能量密度法建立了时间-能量密度积分（integral of the time-energy density，TEDI），以此作为爆破振动损伤的统一安全准则，并通过神经网络确定了TEDI大于15的损伤阈值。近年来，关于单段药量较小的隧道爆破对邻近既有隧道动力响应影响的研究较多，而对单段药量较大的露天深孔台阶爆破对井下邻近既有巷道影响的研究较少，并且，很多研究仅采用理论分析、现场监测或数值模拟中的单一方法。由于露天台阶爆破与隧道爆破在爆源特性方面存在差异，隧道结构在爆破振动作用下的能量响应受爆破地震波特性和结构本身固有特性的影响，仅基于爆破地震波特性或结构固有性质的安全准则显然不能完全描述工程结构在爆破地震波作用下的真实危害。为此，本研究以拉拉铜矿露天转井下过渡开采阶段为工程背景，采用现场爆破振动监测和数值模拟研究露天台阶爆破荷载作用下邻近既有巷道的振动响应规律，以期弥补以往爆破振动危害效应评价方法的不足，指导爆破参数调整，保证工程的顺利进行。
-
拉拉铜矿为露天+地下联合开采矿山。目前，矿山已进入露天转地下的联合开采过渡阶段，设计露天开采最低平台为
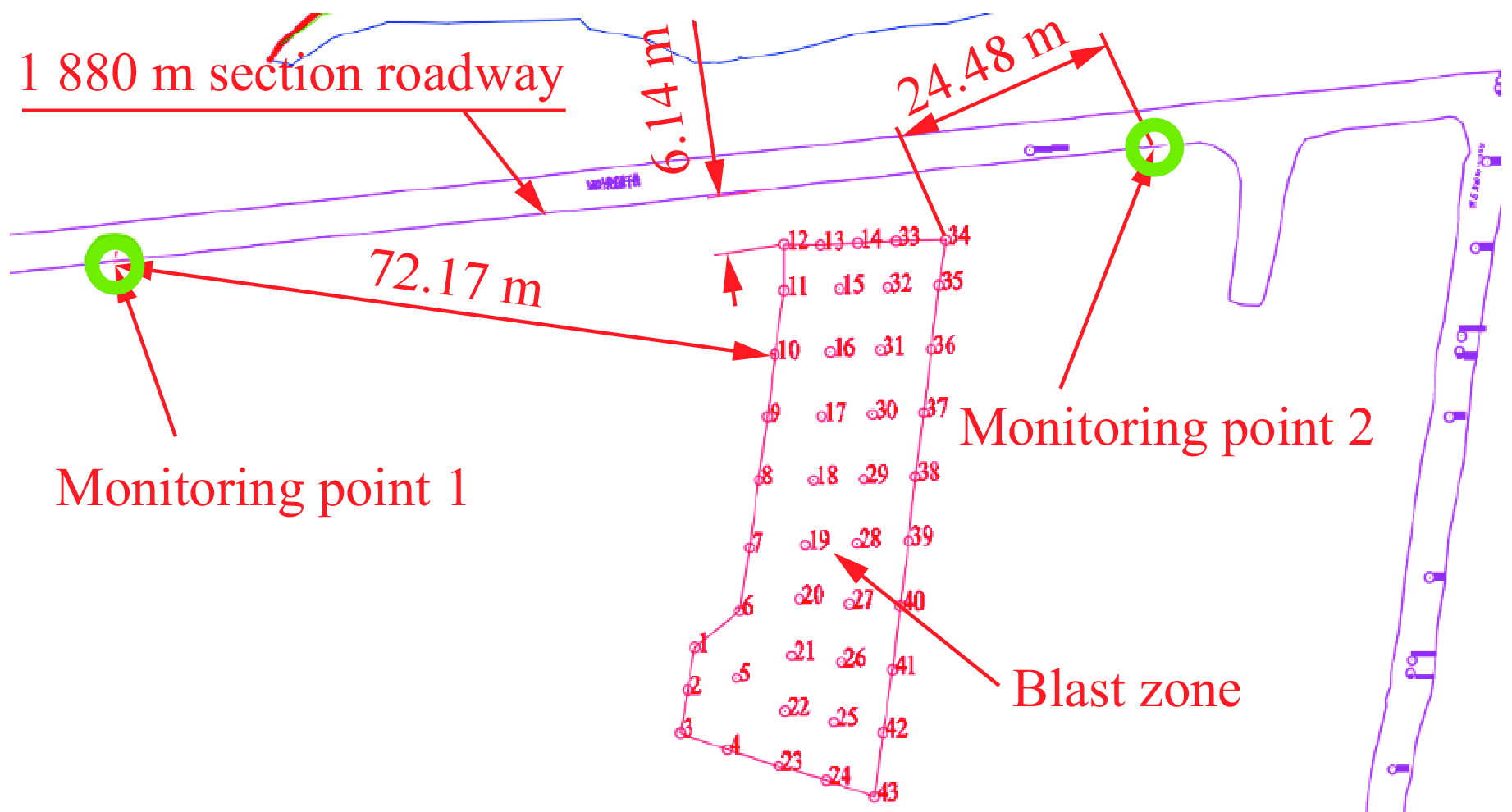
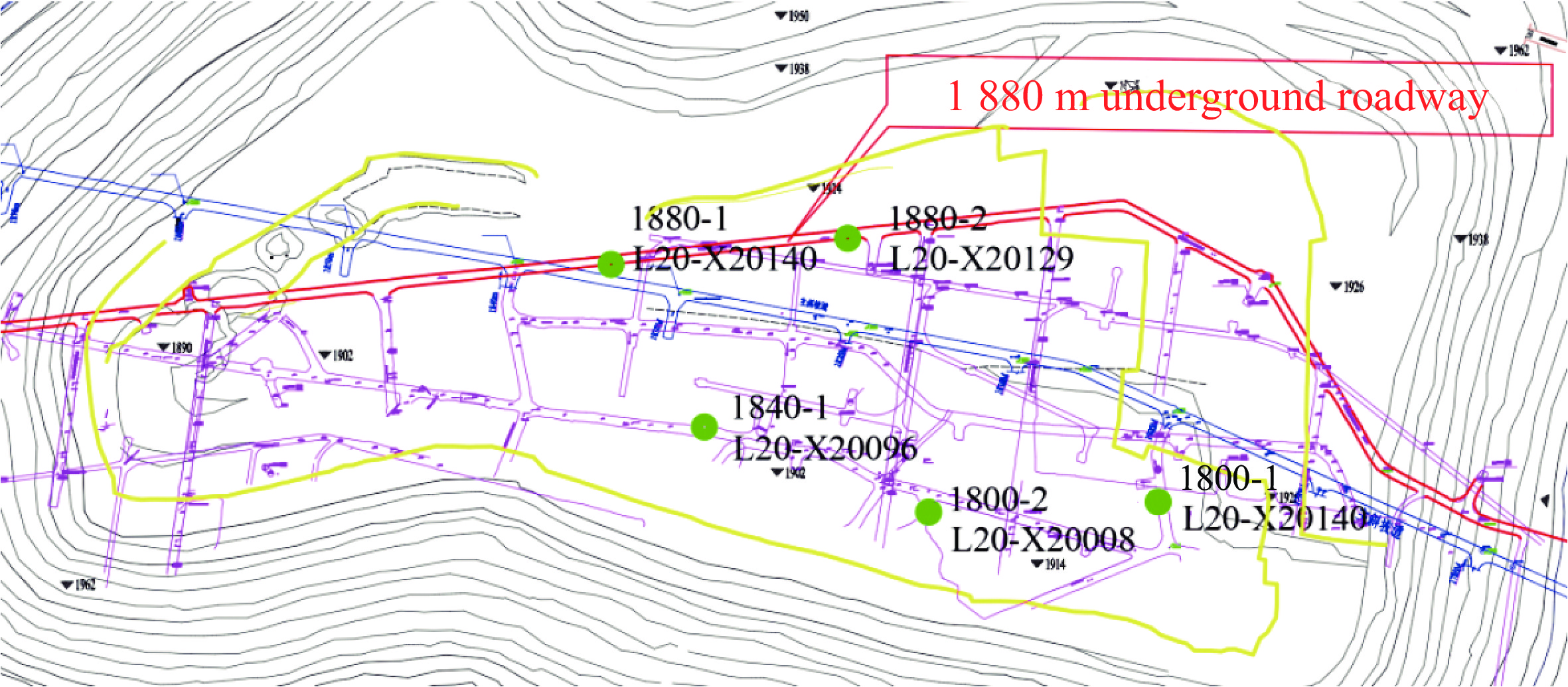
1890 m，1890 m平台以上采用露天开采，1890 m以下采用地下开采，露天采场台阶高度为12 m。露天孔深一般为12～14 m，超深0～2.5 m，使用现场混装乳化炸药车进行耦合装药，单孔药量为240～400 kg。开采境界下方1880 m分段布置一条基建采准巷道，全长1170 m，巷道位置如图1中红色标注位置所示。自露天1890 ～1902 m平台开沟爆破后，终了境界1890 m下部1880 m分段已建成的巷道工程出现顶板、边帮开裂，局部发生垮落，如图2所示。由于落凼井下充填管路主线布置在1880 m巷道，该巷道工程还承担着井下材料运输、通风、水电和通讯等功能，因此，该巷道的稳定对于落凼井下生产有重要作用。 -
为分析露天台阶爆破荷载作用下井下巷道工程的动力响应特性以及振动衰减规律，根据《爆破振动监测技术规范》（T/CSEB 0008—2019）6.1.4中的规定：当需分析爆破振动传播规律时，应先选择代表性监测断面，并使每个监测点至爆源的距离按近密远疏的对数规律布置，每次监测取得的有效数据应不少于5个；监测点布置范围应大于最近一个监测点到爆心距离的1个数量级。根据拉拉铜矿井下工程巷道的重要性，在井下
1880 、1840 、1800 m 3个分段布置5台测振仪。1880 m分段巷道作为充填管路主线，与露天开采境界平台1890 m的距离最近，布置2台测振仪，间隔100 m；1840 和1800 m分段作为主要的探矿工程，且采区值班硐室也布置在1800 m分段，所以1840 m分段布置1台测振仪，1800 m分段布置2台测振仪。5个振动监测点的位置如图1中绿色圆圈所示，爆破区域为黄色线以内区域。爆破振动测试仪器选用L20-X网络测振仪，量程为5～500 Hz，精度为0.001～35 cm/s（±2%），符合国家监管要求和爆破行业标准。该测振仪与传感器为一体式，可通过网络连接实时监测振动数据并上传至云平台以便分析。在安装过程中，根据现场情况，调整灵敏度、采样频率、采样时长、幅值范围、触发阈值等参数，并对测振仪进行零点校准。为了确保仪器不被路过的台车、人车等碾压或撞击，保证监测数据准确有效，在巷道边墙侧壁上钻凿一个方形洞，如图3所示，将传感器放入洞中，并用水泥将其与基岩紧密粘接以形成刚性连接。 -
该工程中，巷道位于爆源下方，且测振仪传感器的x、y方向指向是固定的，由于爆区位置随时变化，传感器指向爆源的水平方向可能是x向或y向，因此，根据每次测点与爆区位置的关系进行调整，将传感器y方向指向爆心水平方向的数据纠正为水平径向数据。同理，将传感器x方向指向爆心水平切向的数据纠正为水平切向数据。z方向始终竖直向上，不需要调整。共获得42组有效监测数据，其中
1880 m巷道共采集20组数据。监测结果如表1所示，其中：vp为峰值振速，f为主振频率，L为测点至爆源的水平距离，H为测点与爆源的高程差，R为测点至爆源的距离（爆心距），mm为单孔最大药量。由于数据较多，表1仅展示了1880 m巷道测到的振动数据。 -
俄罗斯科学家萨道夫斯基给出了最大单段装药量Q与质点峰值振速vp及爆心距R之间的经验公式
式中：K为与爆破场地有关的系数，
$ \alpha $ 为与地质条件有关的参数，$ {{Q^{1/3}}/{R}} $ 为比例药量。将式(1)两边同时取对数，得到
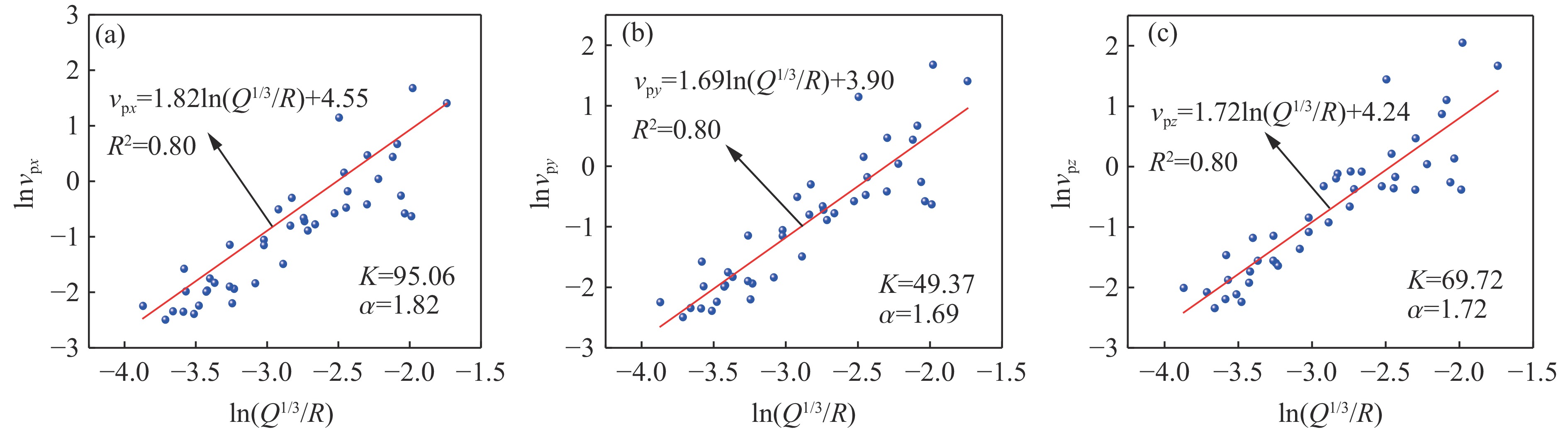
通过式(1)对表1中实测振动数据进行回归分析，得到井下振动衰减拟合结果，如图4所示，其中：vpx、vpy、vpz分别为x、y、z方向的峰值振速。3个方向的峰值振速衰减拟合系数R2均为0.80，拟合效果较好。
目前，常用爆破远区拟合的振动规律来评估爆破振动对近区的影响。然而，研究发现，利用爆破远区振动规律预测爆破近区振动的精度不高[8]，为此，采用移动式测振仪对15～48 m区域内的振动进行监测。对比发现，对于本研究工况，采用拟合公式预测15～48 m区域内的误差在16.55%～33.45%之间，因此，确定巷道振动安全阈值时，应保留一定的安全余量。经推导，得到3个方向质点峰值振速（vpx、vpy、vpz）衰减规律的经验公式
根据式(1)可以反推出最大安全单段药量的计算公式
根据《爆破安全规程》（GB 6722—2014）规定的矿山巷道爆破振动评价标准（结构物的固有频率f0≤10 Hz时，安全振速为15～18 cm/s；10 Hz<f0<50 Hz时，安全振速为18～25 cm/s；f0≥50 Hz时，安全振速为20～30 cm/s），安全振速取18 cm/s。对实测数据进行拟合，得到爆破振动控制标准下最大单响药量随距离的变化规律，如表2所示。本研究中，巷道顶板与开采境界平台的最小距离为10 m，取3个方向中的预测最小值作为最大单段药量，根据计算确定当装药中心与巷道轮廓边界的最小距离为10 m时，露天台阶爆破允许的最大单段药量为64.37 kg。然而，随着装药中心与巷道轮廓边界之间距离的增大，巷道所能承受的爆破最大单段药量也急剧增大，由于矿山现场采用逐孔起爆方式，且装药结构为连续耦合装药，最大单段药量即单个炮孔的最大装药量，因此，在确定各个炮孔的单孔装药量时，可根据炮孔装药中心与巷道结构之间的距离来调整。为保证矿岩的爆破效果，可适当调整距离巷道较近的几个炮孔之间的间距，以降低大块及根底对生产的影响。
-
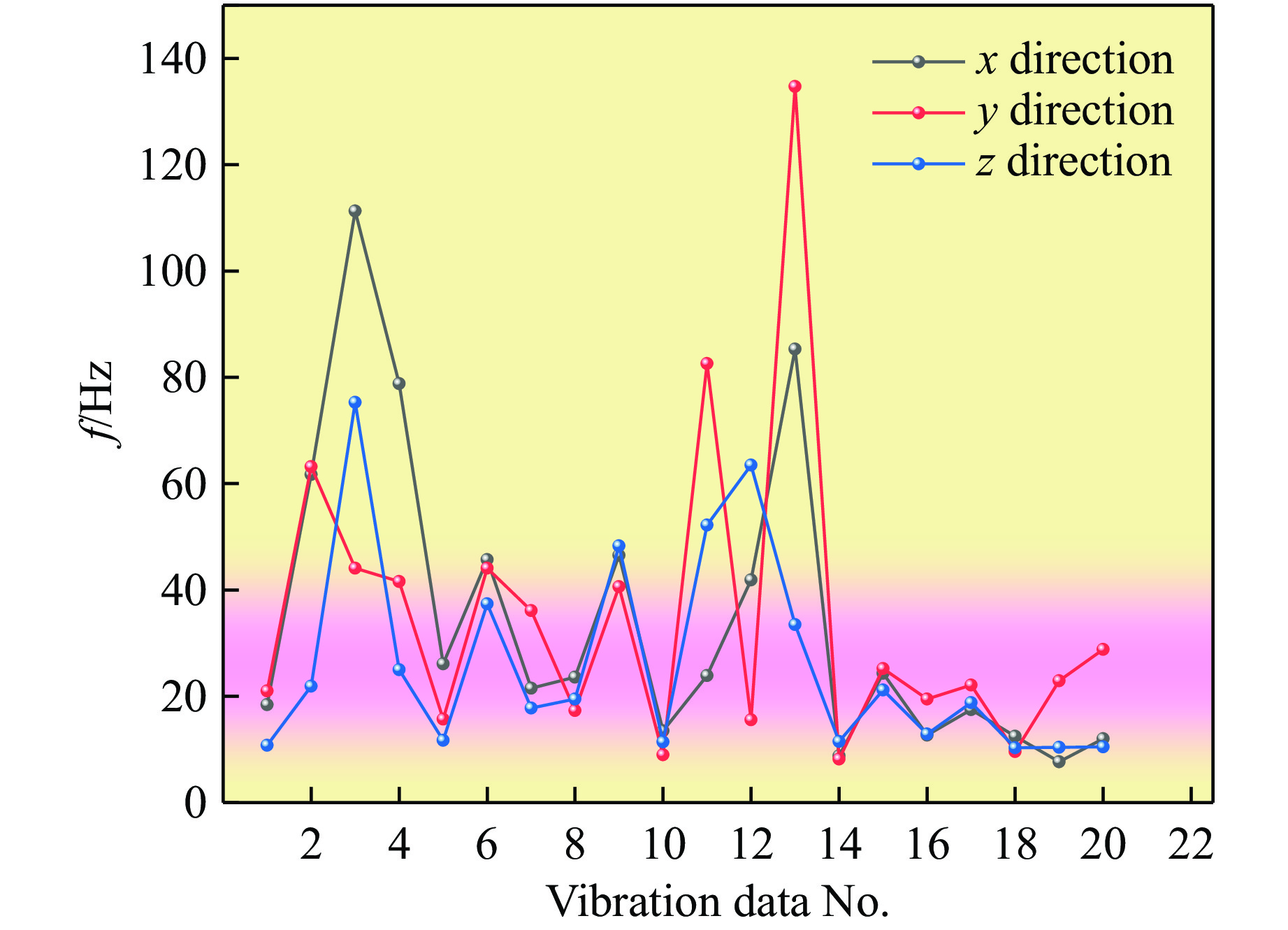
当爆破振动主振频率接近受保护结构物的固有频率时，可能诱发共振，从而引发破坏。因此，近些年来学者们都结合结构物的固有频率，将“振速-频率”作为结构物的双因素判据[9–10]。为直观分析监测振动数据的主振频率分布特征，对表1中20组数据的主振频率分布进行分析，如图5所示。露天深孔台阶爆破致使91.67%的巷道振动主振频率大于10 Hz，主要分布在10～65 Hz范围内，因此，邻近井下巷道爆破振速控制阈值范围为18～25 cm/s。
-
基于希尔伯特黄变换，对爆破振动信号进行能量分析。选取露天某次台阶爆破中的井下振动数据进行分析，在
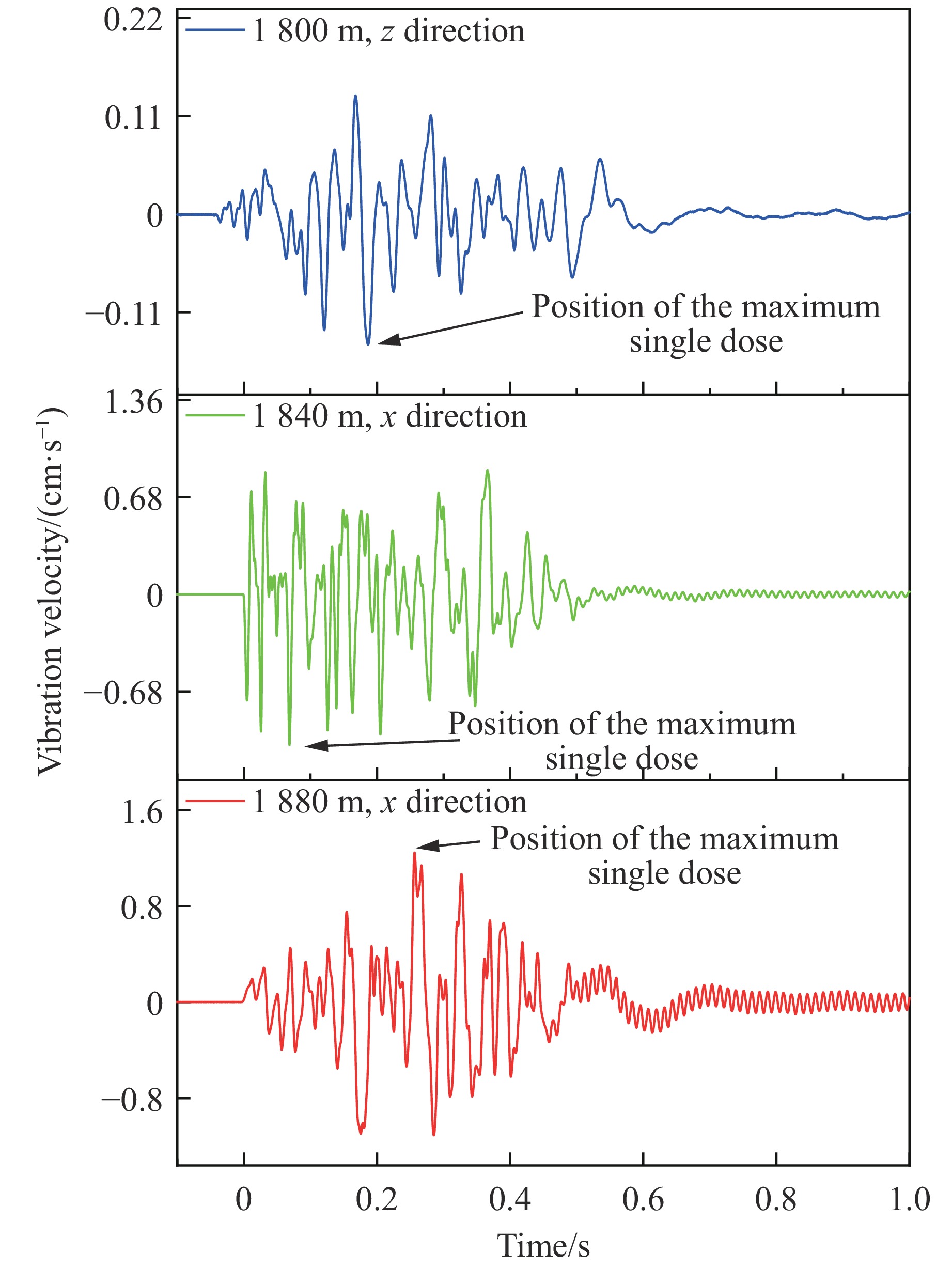
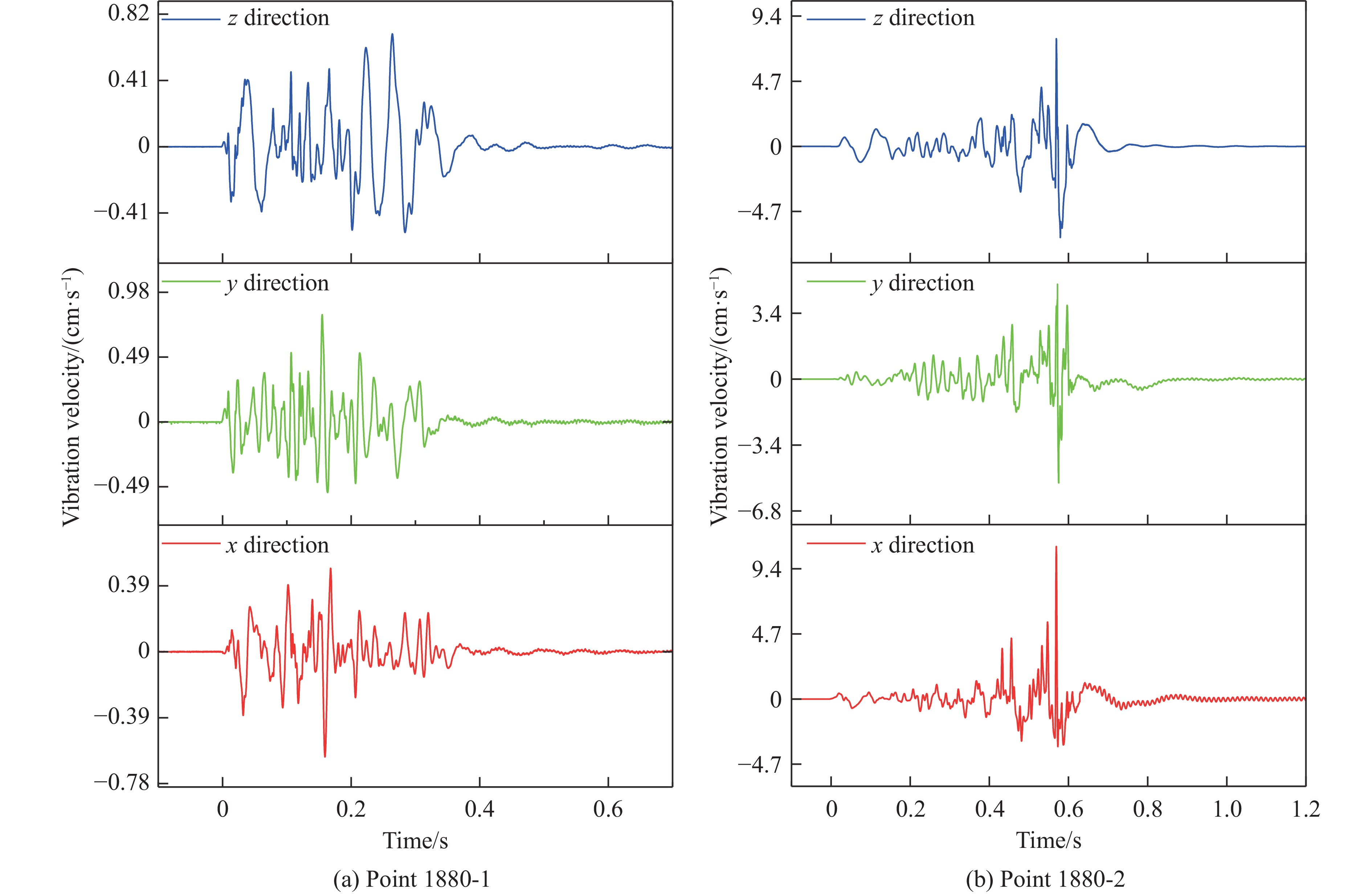
1880 、1840 和1800 m分段各选取1个测点的振动数据，对比发现：1880 和1840 m分段在x方向上的峰值振速最大，1800 m分段在z方向上的峰值振速最大。选取3个分段测点峰值振速方向的振动信号进行能量分析，振动信号波形如图6所示，三维能量分布如图7所示。从图7可以看出：随着井下监测点所处深度的增加，露天爆破振动频率不断衰减；在
1880 m分段，较大振动能量对应的频率主要分布在50～110 Hz区间，最大能量对应的频率为80～100 Hz；在1840 m分段，纵向深度增加了20 m，振动能量较大的频率区间集中在50～80 Hz，多个频带能量相近；到1800 m分段时，振动能量主要分布在18～40 Hz区间，随着纵向深度的增加，振动主频也朝低频方向衰减。 -
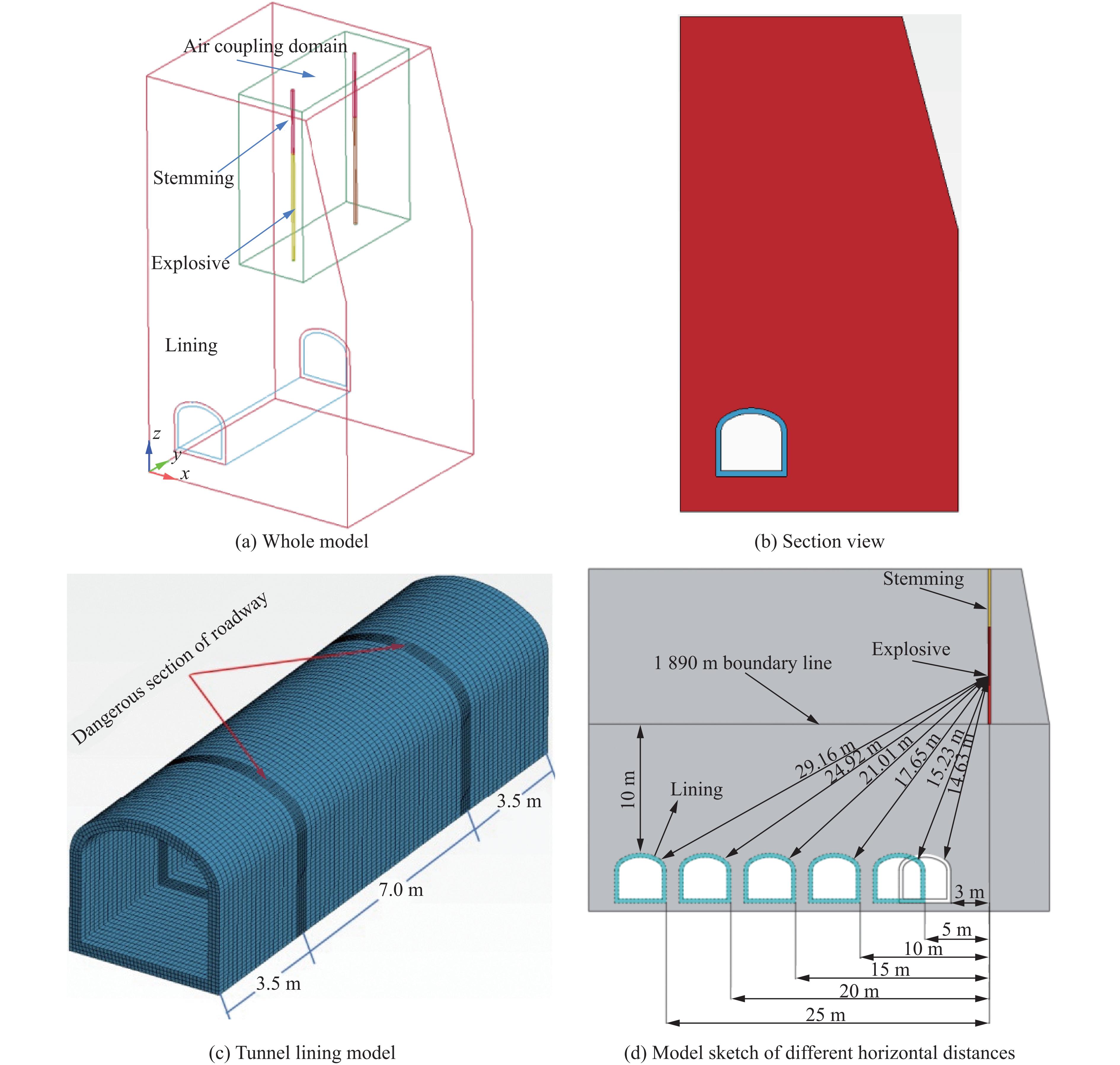
为进一步研究露天台阶爆破作用下不同空间位置邻近既有巷道的动力响应特征，采用动力有限元软件ANSYS/LS-DYNA进行数值模拟。模型由岩体、邻近巷道衬砌、炸药和填塞组成，台阶高度为12 m，巷道顶部到最终开采境界的垂直距离为10 m。岩体采用Lagrange网格划分，炸药和填塞物均采用Euler网格划分，采用多物质任意拉格朗日-欧拉（arbitrary Lagrangian-Eulerian，ALE）算法，计算单元采用3D-SOLID164实体单元，数值模型采用cm-g-μs单位制。在LS-PrePost后处理软件中，通过NON_REFLECTED_BOUNDAY选项卡，对模型边界设置无反射边界条件。根据现场实际情况，将台阶上部表面、台阶坡面以及巷道壁面设置为自由边界，其余面均设置为无反射边界条件，以模拟无限域。围岩与巷道衬砌采用共节点接触方式[11–12]。根据炮孔与巷道右边界的水平距离S0（3、5、10、15、20和25 m），建立了6个三维模型。计算模型如图8所示。
-
岩体材料本构模型采用MAT_PLASTIC_KINEMATIC模型，该材料模型考虑了岩石材料的弹塑性，其应力-应变关系为
式中：
$ {\sigma _{\text{Y}}} $ 为屈服应力，$ \dot \varepsilon $ 为应变率，C、P为应变率参数，$ {\sigma _0} $ 为初始屈服应力，β为硬化系数，$ {E_{\mathrm{p}}} $ 为塑性硬化模量，$ \varepsilon _{\mathrm{p}}^{{\mathrm{eff}}} $ 为有效塑性应变。该材料模型能够描述材料的强化效应（随动强化和各向同性强化）和应变率效应，同时带有失效应变，但鉴于其未考虑岩石材料的抗拉强度，使用MAT_ADD_EROSION选项卡设置岩石的抗拉强度，使之强制性失效[13–14]。根据矿山地质资料及岩石力学试验报告，
1880 m巷道上方的岩性较为单一，大部分为钠长岩，只有少部分片岩，岩石波速为3800 ～4100 m/s，为此，岩石的物理力学参数选用钠长岩的物理力学参数，如表3所示，其中：ρ0为岩石材料的密度，E为弹性模量，ν为泊松比，σc为屈服强度，Et为切线模量。 -
巷道衬砌采用MAT_JOHSON_HOLMQUIST_CONCRETE材料模型。该模型适用于混凝土、岩石及其他脆性材料在高应变率下的行为模拟，可反映强度、应变率与损伤之间的关系[15]，表达式为
式中：
$ {\sigma ^*} $ 为等效应力与静态屈服强度之比；$ {\dot \varepsilon ^*} = \dot \varepsilon /{\dot \varepsilon _0} $ 为无量纲应变率，$ {\dot \varepsilon _0} $ 为参考应变率；$ A $ 、$ B $ 、$ n $ 、$ c $ 为材料常数；$ {p^{{*^{}}}} $ 为无量纲压力；D为损伤因子，0≤D≤1。材料参数如表4所示，其中：ρ1为衬砌材料密度，G为材料模量，Smax为归一化最大强度，μ1为压实体积应变，μc为压碎体积应变，pl为压实体积压力，pc为压碎体积压力，fc为抗压强度，T为最大拉伸静压力，εfmin为最小失效应变，K1、K2、K3为压力常数，D1和D2为损伤因子。 -
炸药采用Jones-Wilkens-Lee（JWL）高能炸药模型，其爆轰压力状态方程为
式中：pe为爆炸产生的压力，V为爆炸产物的相对体积，E0为炸药的初始内能，Ae、Be、R1、R2和ω为JWL状态方程参数。
-
选用MAT_SOIL_AND_FOAM材料进行填塞，填塞材料的相关参数来自文献[16]，具体取值如表5和表6所示，其中：γsat为饱和容重，Gs为土的剪切模量，Ks为土的体积模量，A0、A1、A2为屈服函数常数，ptc为拉伸断裂的压力阈值。
-
采用*MAT_NULL模型定义空气材料，用*EOS_LINEAR_POLYNOMIAL关键字描述空气的状态方程[17]，其线性多项式状态方程为
式中：μ为比体积，μ=ρ/ρ0−1，ρ、ρ0分别为空气的当前密度和参考密度；C0～C6为状态方程参数；Ea为空气的单位体积内能。如果μ<0，则设
$ {C_2}{\mu ^2} $ 和$ {C_6}{\mu ^2} $ 为零。对于空气，可用γ定律状态方程模拟。设置式中：
$ \gamma $ 为理想气体等熵绝热指数。理想气体压力为 -
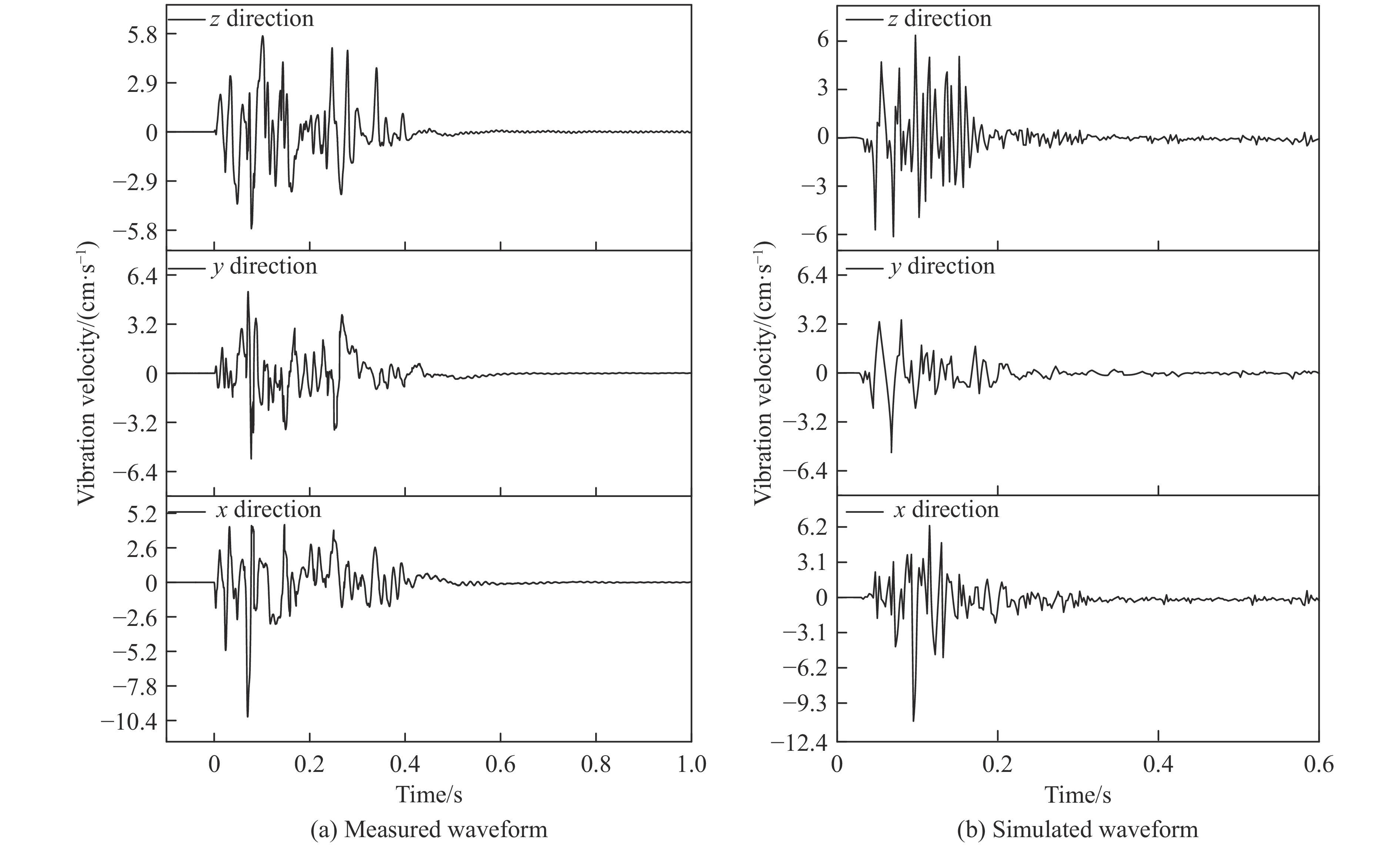
通过对比测点振速的现场监测数据与模拟结果，验证数值模拟的合理性。选取现场测试与数值模拟中爆心距（药柱中心与巷道边界的距离）相近的一次振动数据进行对比验证，实测波形与模拟波形如图9所示。表7给出了监测点的峰值振速。可见，数值模拟与现场监测的x、y、z方向的峰值振速之间的最大相对误差为8.3%。因此，基于数值计算模型研究邻近井下巷道在露天台阶爆破荷载作用下的动力响应是可靠的。
-
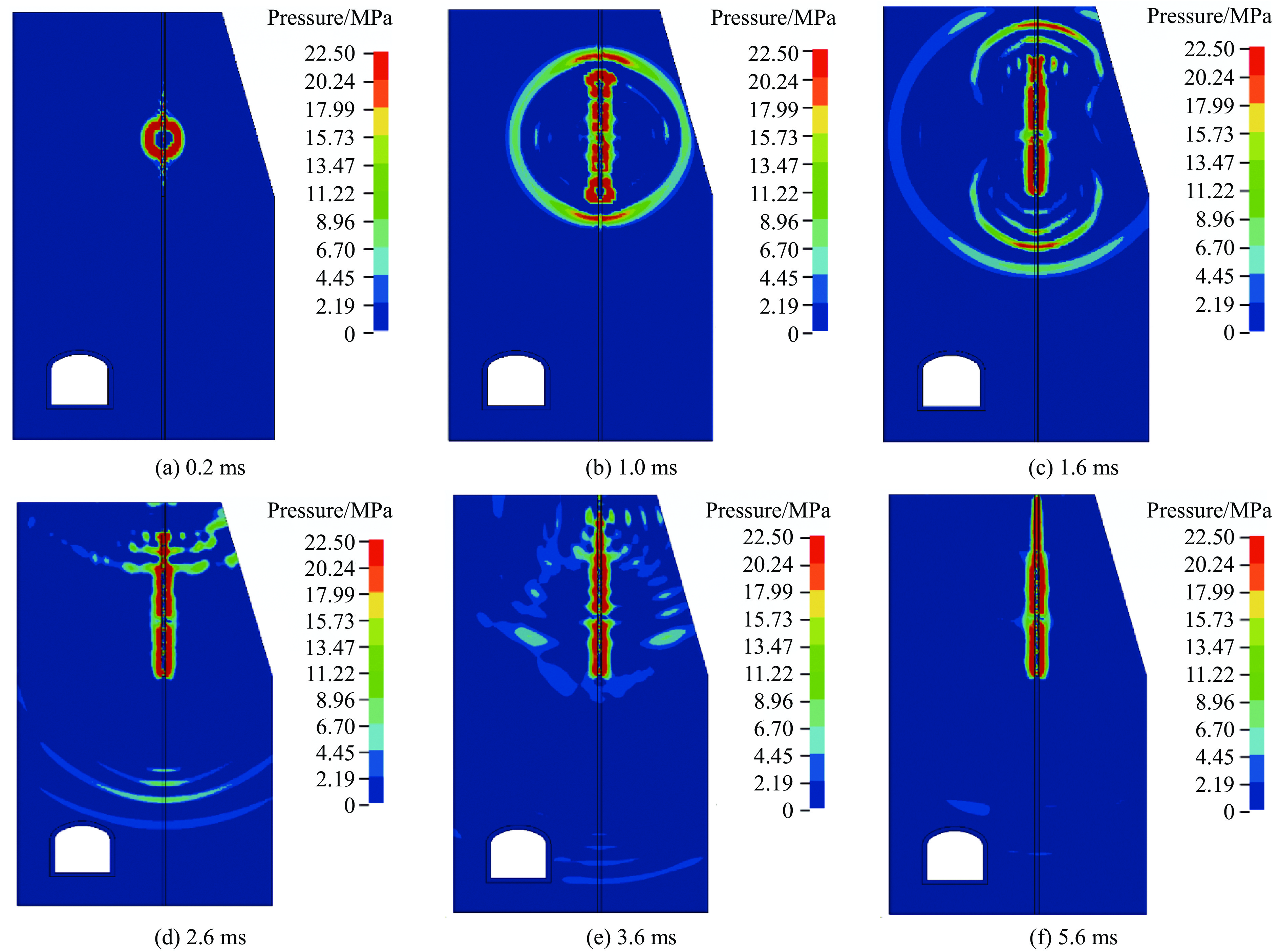
图10给出了不同时刻爆破地震波在岩石介质中的传播。柱状炸药的能量释放沿其轴向分布，可能引发非对称的能量分布。与点源爆炸不同，地震波的传播可能并非球形，而是更接近柱形或椭球形，如图10(a)所示。表面波的面积随着爆破地震波的传播而增加；t=2.6 ms时，爆破地震波传播到巷道顶部边界；t=3.6 ms时，爆破地震波传播到巷道底部；在巷道顶部附近，地震波被反射和传输，其中一部分被反射回岩层并在岩石中传播，另一部分则穿过巷道轮廓界面向巷道底部岩层传输。
不同时刻衬砌的有效应力变化如图11所示。1.9 ms时，应力波传到既有巷道拱腰处，有效应力为0.1 MPa；2.4 ms时，应力波传播到既有巷道拱顶处，最大有效应力为0.63 MPa；2.8 ms时，应力波从拱腰处向四周扩散传播，最大有效应力为0.76 MPa；4.8 ms时，应力波遍布巷道衬砌的各个部位，最大值为1.72 MPa，出现在左拱腰位置。
-
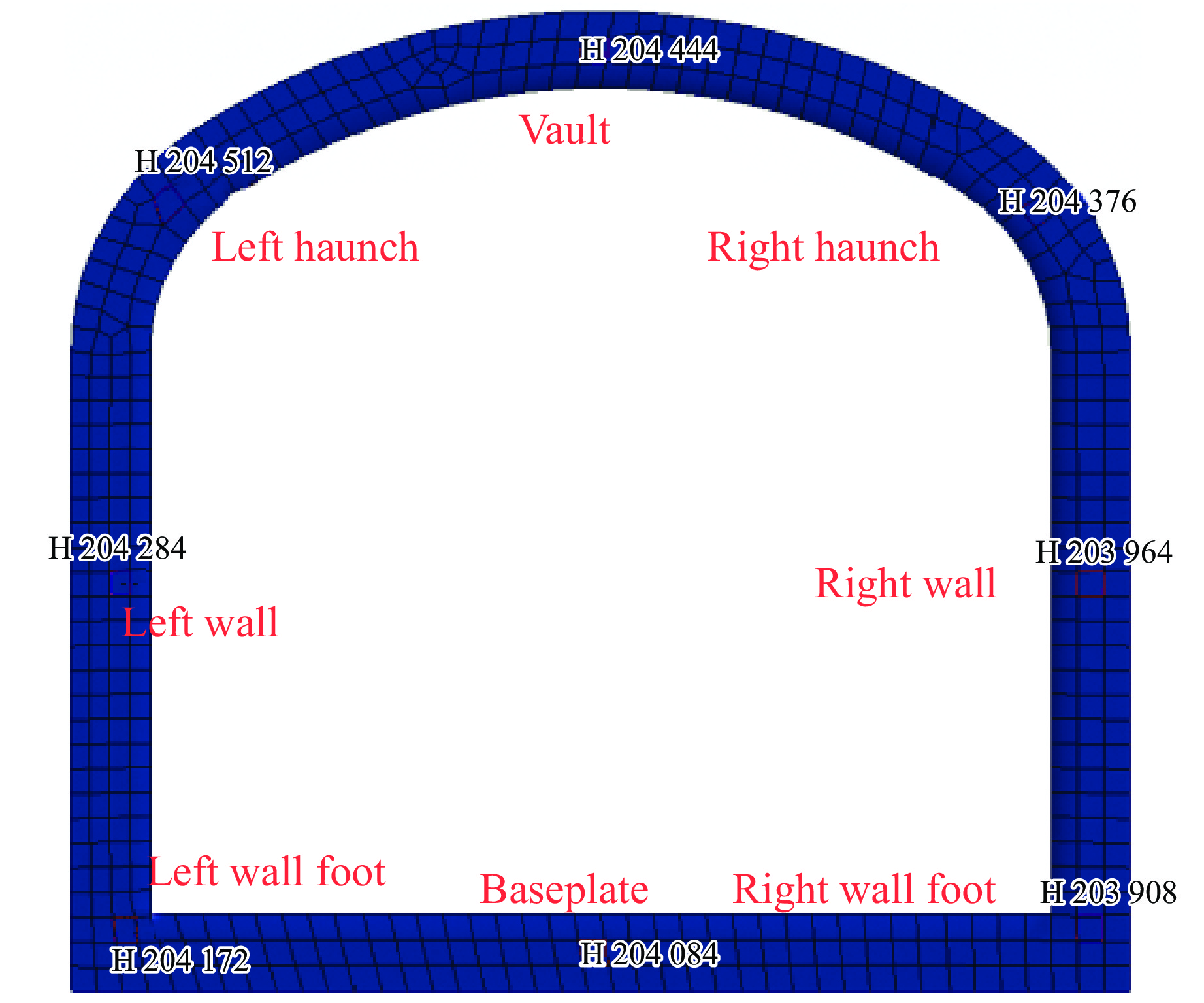
地下结构的振动响应主要通过结构的峰值振速和拉应力来分析[18]。选取离炮孔最近的巷道截面的不同位置分析巷道结构的峰值振速和峰值拉应力变化规律，对炮孔距巷道截面S0为3、5、10、15、20、25 m的动力响应进行研究，对巷道截面不同部位共8个测点的峰值振速及峰值应力进行分析，选取的测点如图12所示，模拟结果如图13所示。
从图13可以看出，在S0不同的情况下，由于爆炸应力波传播到巷道结构各个部位的时间差异以及在巷道结构周围反射和透射等原因，巷道结构在不同方向和不同部位的振速有较大的差别。随着S0的增大，巷道各个部位的振速不断变化，以S0=15 m为界限，在S0<15 m的工况下竖直方向的峰值振速相比于水平径向和切向更大，S0>15 m后水平方向的峰值振速更大，并且处于迎爆侧的巷道结构峰值振速比背爆侧峰值振速大，但随着S0的增大，巷道两侧的振速差距逐渐缩小，峰值振速基本都出现在拱顶。
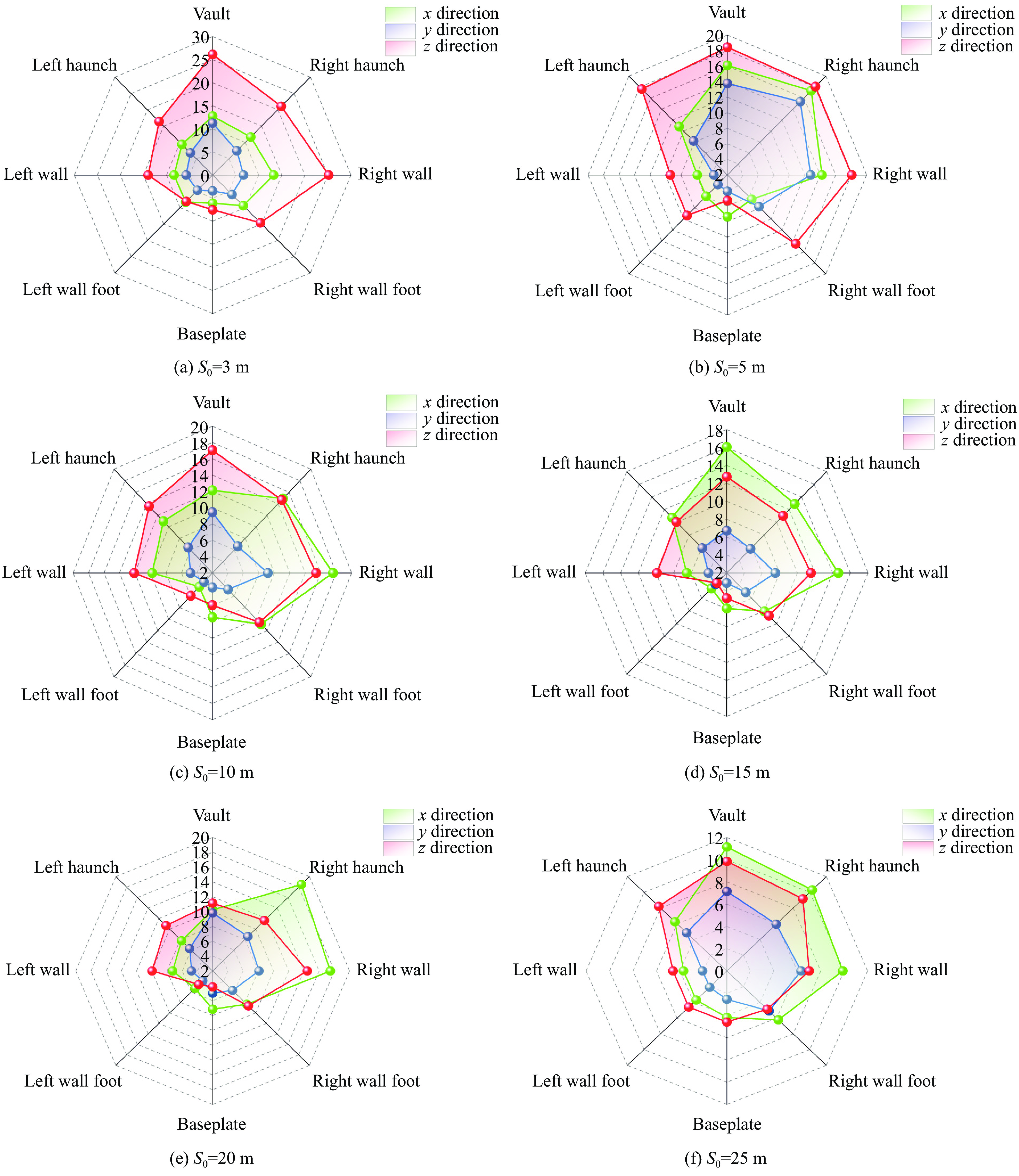
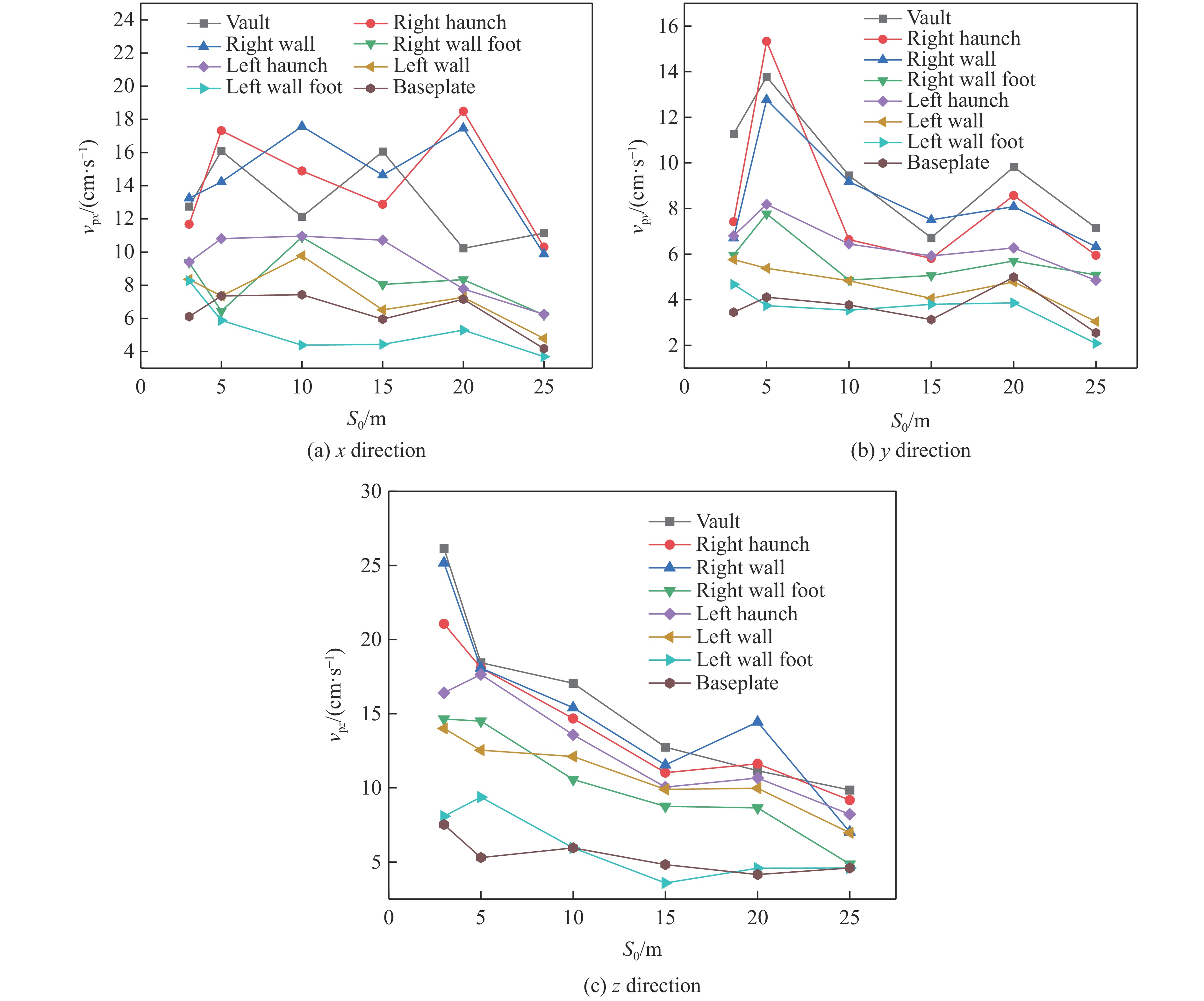
图14显示了不同S0下巷道各个部位3个方向的峰值振速变化。在拱顶、右拱腰和右边墙处，x方向的峰值振速随S0的增大呈振荡变化，而其他部位则整体呈下降趋势；除了拱顶、右拱腰和左拱腰在S0=5 m时y方向的峰值振速出现激增外，其他部位的y方向峰值振速整体随着S0的增大而逐渐衰减；巷道各个部位的z方向峰值振速随着S0的增大而不断衰减，衰减幅度相比y方向更加剧烈。
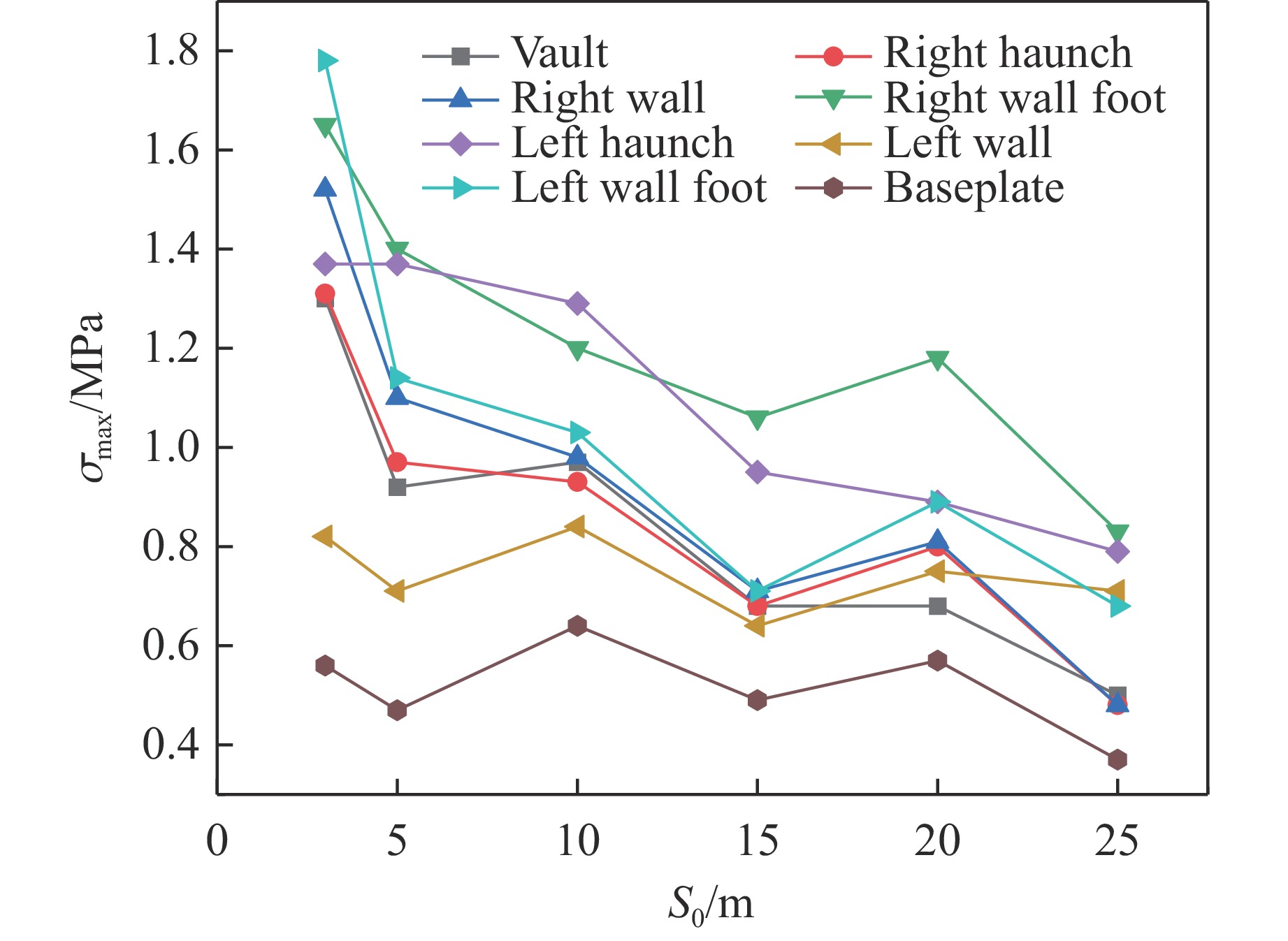
动态应力是研究巷道动力学响应的一个重要控制参数。当巷道结构的动态应力达到其极限抗拉强度时，巷道结构发生破坏。图15显示了不同S0下巷道结构各个部位的峰值有效应力（σmax）变化情况。从图15中可以看出：随着S0的增大，巷道结构所承受的σmax整体呈减小趋势；当S0较小时，峰值应力较大的位置主要出现在左右边墙脚、拱腰和迎爆侧边墙等位置。
-
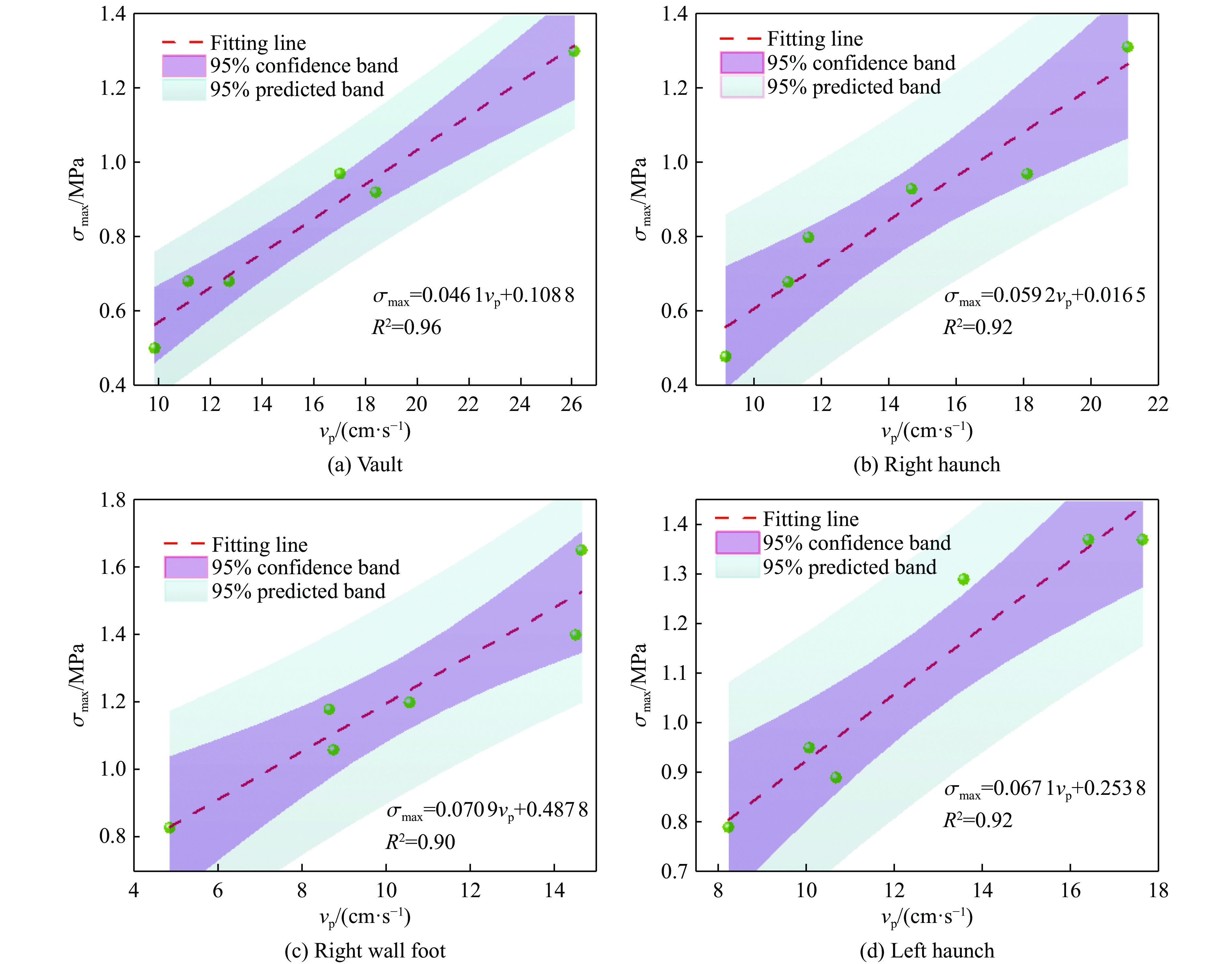
巷道的主要结构是顶板、两帮、底板，三者是独立的，但又相互依存。巷道的整体稳定性取决于三者联合作用形成的稳定体系，其中任何一部分出现破坏都会影响巷道整体的稳定性[19]。结合图13和图15可以发现，当S0较小时，巷道结构各个部位的z方向峰值振速相比其他2个方向的峰值振速更大，峰值振速较大的位置主要出现在拱顶、左右拱腰、右边墙脚4个位置，且σmax也较大，因此，对这4个位置的σmax与z向峰值振速建立关系，从而最大程度地降低后续工程对巷道的影响。如图16所示，巷道结构关键部位的σmax与峰值振速vp之间存在明显的线性关系，拟合得到的线性方程如表8所示。
研究发现，岩石在高应变率下的动力强度会有所增大[20]。在爆破振动作用下巷道混凝土衬砌的极限抗拉强度得到一定程度的提高，这是因为爆破振动会产生强烈的动载荷和振动效应，对混凝土结构产生强烈的冲击力，从而促进混凝土内部颗粒之间的摩擦减小，使混凝土更加密实，提高其力学性能[21]。具体来说，在爆破振动的作用下，混凝土中的颗粒会产生相对位移，颗粒之间的摩擦力减小，从而减小内部的摩擦阻力。因此，在外荷载作用下，混凝土更容易产生位移和变形，使内部应力分布更加均匀。由于混凝土的抗拉强度与其内部应力分布有关，当应力分布更加均匀时，混凝土的极限抗拉强度可能提高，即
式中：
$ {\sigma _{\text{t}}} $ 为岩石的动态抗拉强度；$ {\sigma _{{\text{t}}0}} $ 为岩石的静态抗拉强度；$ {\bar K_{\text{D}}} $ 为岩石的强度增大系数，通常取1.24～1.48，考虑到巷道前期频繁受露天爆破荷载的影响，本研究取1.32。C20混凝土的单轴抗拉强度为1.54 MPa，代入式(14)，可得巷道衬砌的动态抗拉强度为2.03 MPa；将动态抗拉强度代入表8中的拟合方程，可得巷道衬砌拱顶、右拱腰、右边墙脚、左拱腰部位的振速阈值分别为41.74、34.06、21.79、26.52 cm/s，取其中最小值21.79 cm/s作为巷道衬砌的安全振速阈值，考虑到工程的重要程度和既有衬砌在运营期间的安全性损减，以及2.3.1节中用中远区振动规律预测15～48 m区域的振速时存在一定的误差，需预留一定的安全余量，因此，本研究取安全振动速度为19 cm/s。
-
通过上述现场振动监测数据分析得到爆区场地相关系数和地震波衰减指数，通过数值模拟得出该矿山井下巷道的安全振速为19 cm/s。依据萨道夫斯基公式，可以得到露天台阶爆破炮孔的安全最大单段药量。以下以某次现场爆破过程中爆区离巷道较近的情况进行爆破参数调整，爆区与巷道位置的平面关系如图17所示。
爆区处在
1902 m平台，巷道处在1880 m分段，距离巷道较近的炮孔取消超深，并适当缩小炮孔间距，炮孔底端距巷道的垂向距离为10 m；1880 m巷道距离爆区最近孔的水平距离为6.14 m，计算可得最近炮孔的爆心距为15.29 m。经计算，3个方向允许的最大单段药量的最小值为251.55 kg。由于现场只有$ \varnothing $ 200 mm的钻头，孔径均为200 mm，采用混装乳化炸药进行径向耦合装药，因此，在保证炸药单耗的前提下：对于离巷道较近的炮孔（12、13、14、33和34），采取间隔装药方式，以降低单孔装药量，实际单孔装药量为250 kg；对于其余炮孔，预测峰值振速均在安全振速阈值以内，孔网参数和装药量不变。调整前后的参数如表9所示。爆破后2个监测点测得的振速时程曲线如图18所示。可以看出，最大峰值振速为11 cm/s，均在安全阈值以内。
-
综合露天台阶开挖爆破现场振动速度监测及数值计算，分析了井下邻近巷道爆破振动响应特性，得到以下结论。
(1) 通过对露天台阶爆破荷载作用下邻近井下巷道围岩质点振动进行跟踪监测，全面分析了测点的峰值振速、主振频率、能量，通过回归分析，得到了地震波井下衰减规律，获得了爆区的振动衰减系数K、α，为优化爆破参数提供了参考依据。
(2) 通过数值模拟得到了不同空间位置的爆源爆炸荷载下邻近既有巷道结构不同部位的峰值振速和有效应力的响应情况，得出了巷道结构的峰值有效应力与峰值振速之间的关系，计算得出巷道振动的安全阈值为19 cm/s。
(3) 结合现场监测数据拟合的衰减系数与数值模拟得出的安全阈值计算安全最大单段药量。对于邻近巷道炮孔，通过间隔装药方式降低单孔装药量、缩小孔网参数等措施，既保证了该区域矿岩的破碎需求，又降低了爆破荷载对邻近既有巷道的破坏。
露井联采台阶爆破对井下巷道振动的影响
Effect of Bench Blasting on Vibration in Underground Roadways during Open Pit-Underground Combined Mining
-
摘要: 在露井联采过程中，为了控制露天台阶爆破振动对井下邻近既有巷道衬砌的破坏，以拉拉铜矿露天转井下过渡开采阶段为背景，采用现场振动监测、理论计算、数值模拟方法，研究既有邻近巷道的动力响应规律。通过对监测数据进行回归分析，得出井下振动衰减规律，并对振动主频及瞬时能量进行了分析。采用LS-DYNA数值模拟软件，对露天台阶和井下巷道建立6种不同相对空间位置的模型，进而建立双孔延期爆炸模型，研究了爆破荷载作用下邻近井下既有巷道的动态响应规律。结果表明：露天台阶爆破过程中，爆源下方邻近既有巷道产生的最大振速主要出现在拱部和迎爆侧的边墙部；巷道与爆源的相对空间位置不同，峰值振速所在的方向和位置也不同；在巷道拱顶与炮孔底部竖直方向距离固定为10 m的情况下，巷道边墙与炮孔水平距离在15 m以内时，炸药起爆后巷道结构竖直方向振速较大，超过15 m后，巷道结构水平径向振速较大。通过拟合应力与振速之间的关系，利用巷道极限动态抗拉强度推导出振速阈值为19 cm/s。基于安全阈值调整爆破参数后，可以保证邻近既有巷道的安全。Abstract: In order to control the lining damage of underground roadways induced by the vibration effect of bench blasting in an open-pit quarry, the dynamic response of the existing adjacent roadway at the transition mining stage from open pit to underground in Lara Copper Mine were studied by means of field vibration monitoring, theoretical calculation and numerical simulation. Through regression analysis of the monitoring data, the vibration attenuation law was obtained, and the dominant frequency and instantaneous energy of the vibration were analyzed. Six models with different relative spatial positions between the open-pit bench and underground roadway were established using the LS-DYNA software. Subsequently, double-hole delayed blasting models were developed to investigate the dynamic response of adjacent existing roadways under blasting loads. The results show that for the existing roadway located below the explosion source of the open pit bench, its maximum vibration velocity mainly appears in the arch and the side wall on the explosion-facing side. The direction and position of the peak vibration velocity change with the different relative spatial position of the roadway and the explosion source. When the vertical distance between the roadway vault and the bottom of the blast hole is fixed at 10 m, and the horizontal distance between the roadway sidewall and the blast hole is less than 15 m, the vibration velocity in the vertical direction of the tunnel structure is greater after explosion. Beyond this 15 m horizontal distance, the vibration velocity in the horizontal and radial directions of the tunnel structure is larger. By fitting the relationship between peak effective stress and peak particle velocity and utilizing the ultimate dynamic tensile strength of the roadway, a vibration velocity threshold of 19 cm/s was derived. After adjusting blasting parameters according to the safety threshold, the safety of adjacent existing roadway can be ensured.
-
-
图 1 井下巷道及振动监测点位置
Figure 1. Underground roadway and the location of vibration monitoring points
图 13 不同水平距离下巷道结构的峰值振速（单位：cm/s）
Figure 13. PPVs of tunnel structure at different horizontal distances (Unit: cm/s)
图 14 不同水平距离下各方向的峰值振速变化
Figure 14. PPVs in each direction at different horizontal distances
图 15 不同水平距离下峰值有效应力的变化
Figure 15. Variations of peak effective stress at different horizontal distances
图 16 巷道关键部位的峰值振速-峰值有效应力拟合曲线
Figure 16. Fitting curves of peak vibration velocity-peak effective stress in key positions of roadway
图 18 2个监测点测得的振速时程曲线
Figure 18. Time-history curves of vibration velocity obtained by two measuring points
表 1 现场实测振动数据
Table 1. On-site measured vibration data
Test
No.Measuring
pointL/m H/m R/m mm/kg vp/(cm·s−1) f/Hz x direction y direction z direction x direction y direction z direction 1 1880-1 128.06 14 128.82 370 0.23 0.54 0.40 18.4 21.0 10.8 2 1880-1 82.37 14 83.55 380 0.62 0.81 0.70 61.7 63.2 21.9 1880-2 50.48 14 52.39 380 11.00 5.35 7.77 111.3 44.1 75.3 3 1880-1 108.42 14 109.32 380 0.41 0.69 0.69 78.8 41.6 25.0 1880-2 111.01 14 111.89 380 0.68 0.49 0.92 26.1 15.7 11.7 4 1880-1 56.36 14 56.37 400 0.56 0.96 1.14 45.7 44.1 37.4 1880-2 67.80 14 67.81 400 1.24 1.34 1.04 21.5 36.1 17.8 5 1880-1 298.34 26 299.47 390 0.08 0.11 0.12 23.6 17.3 19.5 6 1880-1 88.98 14 90.07 410 3.15 3.34 4.24 46.5 40.6 48.3 7 1880-1 208.52 26 210.13 380 0.16 0.23 0.21 13.5 9.0 11.4 8 1880-1 39.54 14 41.95 400 4.08 8.07 5.31 23.9 82.6 52.2 9 1880-1 45.74 14 47.83 300 10.12 5.57 5.71 41.9 15.6 63.5 10 1880-1 85.10 14 86.24 400 1.17 1.62 1.24 85.3 134.7 33.5 1880-2 135.91 14 136.63 400 0.60 0.63 0.72 8.8 8.2 11.5 11 1880-1 337.01 14 338.01 350 0.14 0.11 0.13 24.3 25.2 21.2 1880-2 252.08 14 253.42 350 0.27 0.21 0.23 12.7 19.5 12.9 12 1880-1 235.25 26 236.68 390 0.13 0.20 0.11 17.5 22.1 18.8 1880-2 147.76 26 150.03 390 0.32 0.38 0.34 12.5 9.6 10.3 13 1880-1 183.98 26 185.81 360 0.16 0.15 0.21 7.7 22.9 10.4 1880-2 85.07 26 88.95 360 0.56 0.69 0.72 12.0 28.8 10.5 
下载: 导出CSV
表 2 不同距离下最大单段药量
Table 2. Maximum charge per delay at different distances
R/m Q/kg Horizontal radial Horizontal tangential Vertical 10 64.37 166.78 94.24 13 141.42 366.42 207.06 16 263.67 683.14 386.04 19 441.53 1143.95 646.44 22 685.43 1775.89 1003.55 25 1005.81 2605.95 1472.62
下载: 导出CSV
表 3 岩石材料模型参数
Table 3. Parameters of the rock material model
ρ0/(kg·m−3) E/GPa ν σc/MPa Et/GPa β 2700 71.25 0.24 75.5 0.4 0.5
下载: 导出CSV
表 4 衬砌材料参数
Table 4. Parameters of the lining material
ρ1/(g·cm−3) G/GPa A B Smax c n μ1 μc pl/GPa 2.40 10.63 0.23 1.84 7 0.005 0.88 0.12 0.005 0.8 pc/MPa fc/MPa T/MPa $ {\dot \varepsilon _0} $ /s−1εfmin D1 D2 K1/GPa K2/GPa K3/GPa 10 20 2.8 1×10−6 0.01 0.04 1 85 −171 208
下载: 导出CSV
γsat/(kN·m−3) Gs/MPa Ks/MPa A0/MPa A1/MPa A2/MPa ptc/MPa 17 2.524 4673 0.0010 0.0049 0.0079 −0.005
下载: 导出CSV
Pressure/MPa Volumetric strain Pressure/MPa Volumetric strain 0 0 800 − 0.1878 100 − 0.0216 1000 − 0.2408 200 − 0.0437 2000 − 0.5586 400 − 0.0895 3000 − 1.0272 600 − 0.1374 4000 − 1.9380
下载: 导出CSV
表 7 测点峰值振速对比
Table 7. Comparison of peak particle velocities of measured points
Direction vmax/(cm·s−1) Error/% Simulation Test x 10.89 10.12 7.6 y 5.11 5.57 8.3 z 6.13 5.71 7.4
下载: 导出CSV
表 8 巷道关键部位峰值有效应力-峰值振速拟合方程
Table 8. Fitting equations of peak effective stress-peak vibration velocity in key positions of roadway
Part of the roadway Fitting equation Vault $ {\sigma _{\max }} = 0.046\,1{v_{\text{p}}}+0.108\,8 $ Right haunch $ {\sigma _{\max }} = 0.059\,2{v_{\text{p}}}+0.016\,5 $ Right wall foot $ {\sigma _{\max }} = 0.070\,9{v_{\text{p}}}+0.487\,8 $ Left haunch $ {\sigma _{\max }} = 0.067\,1{v_{\text{p}}}+0.253\,8 $
下载: 导出CSV
表 9 调整前后参数
Table 9. Parameters before and after adjustment
Adjustment Blast hole
diameter/mmHole
spacing/mArray
pitch/mInterval
length/mLength of
charge/mCharge per
hole/kgBefore 200 7.0 5.5 0 8.5 360 After 200 4.0 4.0 2.5 6.0 250
下载: 导出CSV
-
[1] DOWDING C H. Suggested method for blast vibration monitoring [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1992, 29(2): 145–156. doi: 10.1016/0148-9062(92)92124-U [2] JIANG N, ZHOU C B. Blasting vibration safety criterion for a tunnel liner structure [J]. Tunnelling and Underground Space Technology, 2012, 32: 52–57. doi: 10.1016/j.tust.2012.04.016 [3] XU T. Blasting vibration safety criterion of surrounding rock of a circular tunnel [J]. Geotechnical and Geological Engineering, 2019, 37(4): 3077–3084. doi: 10.1007/s10706-019-00826-z [4] LI Y X, WANG Z B, LUO Q Q, et al. Stability analysis of civil air defense tunnel under blasting vibration [J]. Journal of Vibroengineering, 2024, 26(4): 892–903. doi: 10.21595/jve.2024.23892 [5] XUE F, XIA C C, LI G L, et al. Safety threshold determination for blasting vibration of the lining in existing tunnels under adjacent tunnel blasting [J]. Advances in Civil Engineering, 2019(1): 8303420. doi: 10.1155/2019/8303420 [6] HOU S J, XIE F, TIAN S K, et al. Effects of blasting vibrations on an arch in the Jiaohuayu tunnel described by energy response spectrum analysis [J]. Applied Sciences, 2022, 12(22): 11395. doi: 10.3390/app122211395 [7] 凌同华. 爆破震动效应及其灾害的主动控制 [D]. 长沙: 中南大学, 2004. LING T H. Blast vibration effect and initiative control of vibrational damage [D]. Changsha: Central South University, 2004. [8] 张在晨, 林从谋, 黄志波, 等. 隧道爆破近区振动的预测方法 [J]. 爆炸与冲击, 2014, 34(3): 367–372. doi: 10.11883/1001-1455(2014)03-0367-0 ZHANG Z C, LIN C M, HUANG Z B, et al. Prediction of blasting vibration of area near tunnel blasting source [J]. Explosion and Shock Waves, 2014, 34(3): 367–372. doi: 10.11883/1001-1455(2014)03-0367-0 [9] 杨润强, 严鹏, 王高辉, 等. 地应力水平对深埋隧洞爆破振动频谱结构的影响 [J]. 爆炸与冲击, 2019, 39(5): 055201. YANG R Q, YAN P, WANG G H, et al. Effect of in-situ stress level on frequency spectrum of blasting vibration in a deep-buried tunnel [J]. Explosion and Shock Waves, 2019, 39(5): 055201. [10] 刘家明, 张俊儒, 王智勇, 等. 硬质地层下近接隧道爆破振动影响分区及动力响应研究 [J]. 现代隧道技术, 2023, 60(2): 125–137. doi: 10.13807/j.cnki.mtt.2023.02.014 LIU J M, ZHANG J R, WANG Z Y, et al. Impact zoning and dynamic response to blasting vibration in adjacent tunnel under hard rock strata [J]. Modern Tunnelling Technology, 2023, 60(2): 125–137. doi: 10.13807/j.cnki.mtt.2023.02.014 [11] 薛方方, 胡广柱, 张建伟, 等. 深埋倾斜式压力钢管壁厚与间隙参数的敏感性分析 [J]. 华北水利水电大学学报(自然科学版), 2021, 42(6): 8–13. doi: 10.19760/j.ncwu.zk.2021074 XUE F F, HU G Z, ZHANG J W, et al. Sensitivity analysis of wall thickness and clearance parameters of deep buried inclined penstock [J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2021, 42(6): 8–13. doi: 10.19760/j.ncwu.zk.2021074 [12] 苏凯, 杨逢杰, 年夫喜, 等. 超深埋隧洞防渗排水措施与衬砌外水压力分布规律 [J]. 中南大学学报(自然科学版), 2024, 55(6): 2222–2235. doi: 10.11817/j.issn.1672-7207.2024.06.015 SU K, YANG F J, NIAN F X, et al. Anti-seepage and drainage measures of ultra-deep buried tunnel and distribution law of external water pressure of lining [J]. Journal of Central South University (Science and Technology), 2024, 55(6): 2222–2235. doi: 10.11817/j.issn.1672-7207.2024.06.015 [13] 费鸿禄, 郭玉新. 基于LS-DYNA的交错扇形深孔崩落法排间间隔时间优化研究 [J]. 中国安全生产科学技术, 2022, 18(4): 127–134. doi: 10.11731/j.issn.1673-193x.2022.04.018 FEI H L, GUO Y X. Study on optimized selection for row interval time of staggered sector deep-hole caving method based on LS-DYNA [J]. Journal of Safety Science and Technology, 2022, 18(4): 127–134. doi: 10.11731/j.issn.1673-193x.2022.04.018 [14] 金键, 侯海量, 陈鹏宇, 等. PMT水下内爆冲击波强度与传播特性研究 [J]. 振动与冲击, 2018, 37(13): 100–104, 122. doi: 10.13465/j.cnki.jvs.2018.13.015 JIN J, HOU H L, CHEN P Y, et al. Shock wave intensity and propagation features of a PMT’s underwater implosion [J]. Journal of Vibration and Shock, 2018, 37(13): 100–104, 122. doi: 10.13465/j.cnki.jvs.2018.13.015 [15] 刘江超, 高文学, 张声辉, 等. 水间隔装药孔壁爆炸应力分布规律 [J]. 兵工学报, 2021, 42(12): 2646–2654. doi: 10.3969/j.issn.1000-1093.2021.12.012 LIU J C, GAO W X, ZHANG S H, et al. Distribution law of explosion stress on hole wall of water interval charge [J]. Acta Armamentarii, 2021, 42(12): 2646–2654. doi: 10.3969/j.issn.1000-1093.2021.12.012 [16] XIE L X, LU W B, ZHANG Q B, et al. Damage evolution mechanisms of rock in deep tunnels induced by cut blasting [J]. Tunnelling and Underground Space Technology, 2016, 58: 257–270. doi: 10.1016/j.tust.2016.06.004 [17] LIU K, LI Q Y, WU C Q, et al. A study of cut blasting for one-step raise excavation based on numerical simulation and field blast tests [J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 109: 91–104. doi: 10.1016/j.ijrmms.2018.06.019 [18] 管晓明, 傅洪贤, 王梦恕, 等. 隧道爆破振动下砌体结构局部动力反应研究 [J]. 现代隧道技术, 2017, 54(3): 135–141. doi: 10.13807/j.cnki.mtt.2017.03.019 GUAN X M, FU H X, WANG M S, et al. Local dynamic response of a masonry structure to the vibrations of tunnel blasting [J]. Modern Tunnelling Technology, 2017, 54(3): 135–141. doi: 10.13807/j.cnki.mtt.2017.03.019 [19] 左壮壮. 露天矿爆破作用下邻近巷道围岩的振动控制及损伤规律研究 [D]. 阜新: 辽宁工程技术大学, 2023: 13–14. ZUO Z Z. Study on vibration control and damage law of surrounding rock of adjacent roadway under open-pit blasting [D]. Fuxin: Liaoning Technical University, 2023: 13–14. [20] 曹明星, 严松宏, 郑永强, 等. 邻近隧道爆破振动响应分析 [J/OL]. 工程爆破(2023-10-25)[2024-10-29]. https://doi.org/10.19931/j.EB.20230100. CAO M X, YAN S H, ZHENG Y Q, et al. Analysis of blasting vibration response of adjacent tunnel [J/OL]. Engineering Blasting (2023-10-25)[2024-10-29]. https://doi.org/10.19931/j.EB.20230100. [21] CAO H Q, WANG D Y, GUO J F, et al. Blasting safety criterion of existing high speed railway tunnel over tunnel [J]. Journal of Vibroengineering, 2024, 26(7): 1670–1685. doi: 10.21595/jve.2024.24186 -
图( 18) 表( 9)
计量
- 文章访问数: 23
- HTML全文浏览数: 23
- PDF下载数: 0
- 施引文献: 0