高级搜索

高温超导约瑟夫森结技术及应用于液氮温区量子电压标准的可能性

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

陈紫雯, 朱珠, 康焱, 焦玉民, 张力丹, 张焱, 马平. 高温超导约瑟夫森结技术及应用于液氮温区量子电压标准的可能性[J]. 物理学报, 2025, 74(9): 090304-1. doi: 10.7498/aps.74.20241262
引用本文: 陈紫雯, 朱珠, 康焱, 焦玉民, 张力丹, 张焱, 马平. 高温超导约瑟夫森结技术及应用于液氮温区量子电压标准的可能性[J]. 物理学报, 2025, 74(9): 090304-1. doi: 10.7498/aps.74.20241262
shu
Ziwen CHEN, Zhu ZHU, Yan KANG, Yumin JIAO, Lidan ZHANG, Yan ZHANG, Ping MA. High-temperature superconducting Josephson junction technology and its potential application to quantum voltage standards in liquid nitrogen temperature range[J]. Acta Physica Sinica, 2025, 74(9): 090304-1. doi: 10.7498/aps.74.20241262
Citation: Ziwen CHEN, Zhu ZHU, Yan KANG, Yumin JIAO, Lidan ZHANG, Yan ZHANG, Ping MA. High-temperature superconducting Josephson junction technology and its potential application to quantum voltage standards in liquid nitrogen temperature range[J]. Acta Physica Sinica, 2025, 74(9): 090304-1. doi: 10.7498/aps.74.20241262
shu

高温超导约瑟夫森结技术及应用于液氮温区量子电压标准的可能性

  • 1.

    北京无线电计量测试研究所, 北京　100039

  • 2.

    北京大学应用超导研究中心, 北京　100871

  • 3.

    北京大学, 人工微结构和介观物理全国重点实验室, 北京　100871

  • 4.

    北京大学物理学院, 北京　100871

    • 作者简介: 陈紫雯: 934023769@qq.com .
    通讯作者: E-mail: hrb_zz@sina.com.;  E-mail: zhang_yan@pku.edu.cn.;  E-mail: maping@pku.edu.cn.

  • 中图分类号: 03.75.Lm, 74.72.-h, 06.20.-f

High-temperature superconducting Josephson junction technology and its potential application to quantum voltage standards in liquid nitrogen temperature range

  • 1.

    Beijng Institute of Radio Metrology & Measurement, Beijing 100039, China

  • 2.

    Applied Superconductivity Research center, Peking University, Beijing 100871, China

  • 3.

    State Key Laboratory for Artificial Microstructure and Mesoscopic Physics, Peking University, Beijing 100871, China

  • 4.

    School of Physics, Peking University, Beijing 100871, China

    • Corresponding authors: E-mail: hrb_zz@sina.com;  E-mail: zhang_yan@pku.edu.cn;  E-mail: maping@pku.edu.cn

  • MSC: 03.75.Lm, 74.72.-h, 06.20.-f

  • 摘要: 本文对液氮温区约瑟夫森电压标准的物理原理、相关应用研究的发展历史、研究现状以及未来发展方向进行了综述. 液氮温区工作的约瑟夫森电压标准具有移动性强、能耗小等特点, 便于应用推广. 本文描述了目前约瑟夫森量子电压标准的研究现状, 重点探讨了基于高温超导体发展液氮温区量子电压标准可能性, 以及目前在芯片制备方面存在的各种挑战. 在此基础上, 介绍了超导约瑟夫森结阵列的一种新型制备技术, 即聚焦氦离子辐照技术, 其在高一致性约瑟夫森结阵列的制备上可能具有优势, 是未来探索实现液氮温区量子电压计量标准的一种可能技术路线.
    Abstract: This paper reviews the physical principles, development history of related application research, current research status and prospects of the Josephson voltage standard (JVS) working at liquid helium temperatures. The JVS working at liquid helium temperature has advantages of high mobility and low-energy consumption, and has a broad application prospect. This paper describes the research status of Josephson voltage standards, focusing on the possibility of developing a JVS based on high-temperature superconductors, and the challenges in chip preparation. In addition, a newly developed preparation technology for Josephson junction, namely the focused helium ion beam, is introduced. It has advantages in the preparation of high consistent Josephson junction arrays in high consistency. Therefore, it is a possible technical route for exploring the realization of JVS working at liquid helium temperature in the future.
  • 加载中

  • 图 1  约瑟夫森结的示意图

    Figure 1.  Schematic representation of a Josephson junction.

    下载: 全尺寸图片 幻灯片

    图 2  相位粒子在约瑟夫森势阱中运动的示意图　(a)随着I增大, 约瑟夫森势阱逐渐倾斜, 相位粒子滑动到下一个极小值处; (b)随着I减小, 约瑟夫森势阱恢复水平, 相位粒子在一个局部极小值上振荡

    Figure 2.  Schematic diagram of the motion of phase particle in the Josephson potential well: (a) As I increases, the Josephson potential well gradually tilts, and the phase particle slides to the next minimum; (b) as I decreases, the Josephson potential well returns, and the phase particle oscillates at a new local minima.

    下载: 全尺寸图片 幻灯片

    图 3  N4-21量子电压的桌面测控部分, 包括: 1. 制冷模块, 2. 测试模块, 3. 控制与电源模块, 4. 电脑[42]

    Figure 3.  Photo of the cryocooler-based table top Josephson voltage standard N4-21. 1. cryocooler unit, 2. measuring unit, 3. control and power supply unit and 4. laptop[42].

    下载: 全尺寸图片 幻灯片

    图 4  双晶晶界约瑟夫森结列拓扑结构微观结构图[43], 该串联阵列由一条垂直穿过晶界的曲折线连接而成. 图中标记1为双梳齿结构, 它们构成了一个半波长谐振器. 中间的虚线表示晶界, 在该处形成晶界结[43]

    Figure 4.  Schematic representation of the topology of a chain of bi-crystal Josephson junctions. The array is connected by a meandering line passing vertically through the grain boundary. Label 1 indicates the double comb tooth structure, which constitutes a half wavelength resonator. The position of grain boundaries is indicated by the dashed line[43]

    下载: 全尺寸图片 幻灯片

    图 5  (a) 161个串联双晶结在77 K时, 75.2 GHz微波辐照下的伏安特性曲线; (b)子阵列伏安特性曲线中在12.5 mV电压处的台阶[42]

    Figure 5.  (a) Current-voltage characteristic of the HTS array containing 161 junctions under irradiation at frequency 75.2 GHz; (b) current-voltage trace of step at approximately 12.5 mV of the sub array[42].

    下载: 全尺寸图片 幻灯片

    图 6  聚焦氦离子束辐照写入超导约瑟夫森结的示意图[78]

    Figure 6.  Schematic representation of a focused helium ion beam creating a Josephson junction[78].

    下载: 全尺寸图片 幻灯片

    图 7  (a)聚焦氦离子束制备阵列的光学显微镜图, 周围是电极, 连接了中间的弯曲微带线[84]; (b)阵列的三个分支, 黑色代表了超导薄膜上蒸镀的金[84]; (c)氦离子显微镜成像模式下的100 nm间距结阵放大图[84]

    Figure 7.  (a) Optical image of the array pattern. Large bonding pads attached to a centered meandering microstrip[84]. (b) Three branches of the meander are enlarged. Dark color lines are Au covered superconducting film[84]. (c) Zoomed view of single tracks of He+ irradiation at 100 nm inter-spacing imaged in HIM[84].

    下载: 全尺寸图片 幻灯片

    图 8  T = 24 K时的I-V特性　(a)在不同微波功率下无微波辐射和微波辐射(f = 11.79 GHz)的单结[84]; (b)在不同微波功率下无微波辐射和有微波辐射(f = 11.76 GHz)的50个串联结阵列, 其中台阶的相邻步长之间的电压是单个结的60倍[84]; (c)在不同输入功率电平下无微波辐射和有微波辐射(f = 12.35 GHz)的60个结串联的阵列, 其中台阶的相邻步长之间的电压是单个结的60倍[84]

    Figure 8.  Current-voltage characteristics at T = 24 K for (a) single junction without and with microwave radiation of f = 11.79 GHz at different input power levels[84]. (b) 50-JJ series array without and with microwave radiation of f = 11.76 GHz at different input power levels. The space between adjacent steps in voltage is 50 times of that for an individual junction[84]. (c) 60-JJ series array without and with microwave radiation of f = 12.35 GHz at different input power levels. The space between adjacent steps in voltage is 60 times of that for an individual junction[84].

    下载: 全尺寸图片 幻灯片
  • [1] Josephson B D 1962 Phys. Lett. 1 251 doi: 10.1016/0031-9163(62)91369-0
    [2] Clarke J, Braginski A I 2003 The SQUID handbook (Volume II. ed.) (Weinheim: Wiley-VCH
    [3] Hamilton C A 2000 Rev. Sci. Instrum. 71 3611 doi: 10.1063/1.1289507
    [4] Kohlmann J, Behr R, Funck T 2003 Meas. Sci. Technol. 14 1216 doi: 10.1088/0957-0233/14/8/305
    [5] Shapiro S 1963 Phys. Rev. Lett. 11 80 doi: 10.1103/PhysRevLett.11.80
    [6] Klushin A M, Lesueur J, Kampik M, Raso F, Sosso A, Khorshev S K, Bergeal N, Couëdo F, Feuillet-Palma C, Durandetto P, Grzenik M, Kubiczek K, Musiol K, Skorkowski A 2020 IEEE Instrum. Meas. Mag. 23 4 doi: 10.1109/mim.2020.9062678
    [7] Mccumber D E 1968 J. Appl. Phys. 39 3113 doi: 10.1063/1.1656743
    [8] Jain A K, Lukens J E, Tsai J S 1987 Phys. Rev. Lett. 58 1165 doi: 10.1103/PhysRevLett.58.1165
    [9] Degennes P G 1964 Rev. Mod. Phys. 36 225 doi: 10.1103/RevModPhys.36.225
    [10] Gurvitch M, Washington M A, Huggins H A 1983 Appl. Phys. Lett. 42 472 doi: 10.1063/1.93974
    [11] Niemeyer J, Hinken J H, Kautz R L 1984 Appl. Phys. Lett. 45 478 doi: 10.1063/1.95222
    [12] Primary Voltage Standard Josephson Junction Arrays, Hypres https://www.hypres.com/products/ [2024-8-7]
    [13] Schulze H, Behr R, Muller F, Niemeyer J 1998 Appl. Phys. Lett. 73 996 doi: 10.1063/1.122064
    [14] Schulze H, Behr R, Kohlmann J, Müller F, Niemeyer J 2000 Supercond. Sci. Technol. 13 1293 doi: 10.1088/0953-2048/13/9/301
    [15] Zhong Q, Zhong Y, He Q, Zhang J 2008 Cryog. Supercond. 36 32 doi: 10.3969/j.issn.1001-7100.2008.12.009
    [16] SRI 6000 Series Programmable Josephson Voltage Standard (PJVS), NIST https://www.nist.gov/sri/standard-reference-instruments/ [2024-8-7]
    [17] AC Quantum Voltmeter Cooler, Supracon http://www.supracon.com/en/ [2024-8-7]
    [18] Rüfenacht A, Flowers-Jacobs N E, Benz S P 2018 Metrologia 55 S152 doi: 10.1088/1681-7575/aad41a
    [19] Dresselhaus P D, Elsbury M M, Olaya D, Burroughs C J, Benz S P 2011 IEEE Trans. Appl. Supercond. 21 693 doi: 10.1109/TASC.2010.2079310
    [20] Mueller F, Behr R, Weimann T, Palafox L, Olaya D, Dresselhaus P D, Benz S P 2009 IEEE Trans. Appl. Supercond. 19 981 doi: 10.1109/TASC.2009.2017911
    [21] Yamamori H, Ishizaki M, Shoji A, Dresselhaus P D, Benz S P 2006 Appl. Phys. Lett. 88 042503 doi: 10.1063/1.2167789
    [22] 曹文会, 李劲劲, 钟青, 郭小玮, 贺青, 迟宗涛 2012 物理学报 61 170304 doi: 10.7498/aps.61.170304 Cao W W, Li J J, Zhong Q, Guo X W, He Q, Chi Z T 2012 Acta Phys. Sin. 61 170304 doi: 10.7498/aps.61.170304
    [23] Cao W H, Li J J, Zhong Y, He Q 2015 Chin. Phys. B 24 127402 doi: 10.1088/1674-1056/24/12/127402
    [24] Yu H F, Cao W H, Zhu X B, Yang H F, Yu H W, Ren Y F, Gu C Z, Chen G H, Zhao S P 2008 Chin. Phys. B 17 3083 doi: 10.1088/1674-1056/17/8/052
    [25] Cao W H, Yu H F, Tian Y, Yu H W, Ren Y F, Chen G H, Zhao S P 2009 Chin. Phys. B 18 5044 doi: 10.1088/1674-1056/18/11/072
    [26] Xu W N, Ying L L, Lin Q, Ren J, Wang Z 2021 Supercond. Sci. Technol. 34 085002 doi: 10.1088/1361-6668/ac086e
    [27] Li X, Tan J R, Zheng K M, Zhang L B, Zhang L J, He W J, Huang P W, Li H C, Zhang B, Chen Q, Ge R, Guo S Y, Huang T, Jia X Q, Zha Q Y, Tu X C, Kang L, Chen J, Wu P H 2020 Photonics Res. 8 637 doi: 10.1364/PRJ.377900
    [28] 李春光, 王佳, 吴云, 王旭, 孙亮, 董慧, 高波, 李浩, 尤立星, 林志荣, 任洁, 李婧, 张文, 贺青, 王轶文, 韦联福, 孙汉聪, 王华兵, 李劲劲, 屈继峰 2021 物理学报 70 018501 doi: 10.7498/aps.70.20202121 Li C G, Wang J, Wu Y, Wang X, Sun L, Dong H, Gao B, Li H, You L X, Lin Z R, Ren J, Li J, Zhang W, He Q, Wang Y W, Wei L F, Sun H C, Wang H B, Li J J, Qu J F 2021 Acta Phys. Sin. 70 018501 doi: 10.7498/aps.70.20202121
    [29] 李劲劲 2021 科技成果管理与研究 16 72 doi: 10.3772/j.issn.1673-6516.2021.02.024 Li J J 2021 Management and Research on Scientific & Technological Achievements 16 72 doi: 10.3772/j.issn.1673-6516.2021.02.024
    [30] 朱珠, 康焱, 王路, 胡毅飞 2018 宇航计测技术 38 12 doi: 10.12060/j.issn.1000-7202.2018.04.03 Zhu Z, Kang Y, Wang L, Hu Y F 2018 J Astronaut. Metrol. Meas. 38 12 doi: 10.12060/j.issn.1000-7202.2018.04.03
    [31] 李红晖, 王曾敏, 徐晴, 田正其, 段梅梅, 王磊 2023 计量学报 44 1564 doi: 10.3969/j.issn.1000-1158.2023.10.12 Li H H, Wang Z M, Xu Q, Tian Z Q, Duan M M, Wang L 2023 Acta. Metrol. Sin. 44 1564 doi: 10.3969/j.issn.1000-1158.2023.10.12
    [32] Trinchera B, Durandetto P, Serazio D 2024 Measurement 233 114747 doi: 10.1016/j.measurement.2024.114747
    [33] 段梅梅, 赵双双, 徐晴, 王磊, 贾正森, 黄洪涛, 潘仙林 2022 电测与仪表 59 100 doi: 10.19753/j.issn1001-1390.2022.02.014 Duan M M, Zhao S S, Xu Q, Wang L, Jia Z S, Huang H T, Pan X L 2022 Electr. Meas. Instrum. 59 100 doi: 10.19753/j.issn1001-1390.2022.02.014
    [34] Wu M K, Ashburn J R, Torng C J, Hor P H, Meng R L, Gao L, Huang Z J, Wang Y Q, Chu C W 1987 Phys. Rev. Lett. 58 908 doi: 10.1103/PhysRevLett.58.908
    [35] 赵忠贤, 陈立泉, 杨乾声, 黄玉珍, 陈赓华, 唐汝明, 刘贵荣, 崔长庚, 陈烈, 王连忠, 郭树权, 李山林, 毕建清 1987 科学通报 32 412 doi: 10.1360/csb1987-32-6-412 Zhao Z X, Chen L Q, Yang Q S, Huang Y Z, Chen G H, Tang R M, Liu G R, Cui C G, Chen L, Wang L Z, Guo S Q, Li S L, Bi J Q 1987 Chin. Sci. Bull. 32 412 doi: 10.1360/csb1987-32-6-412
    [36] Hilgenkamp H, Mannhart J 2002 Rev. Mod. Phys. 74 485 doi: 10.1103/RevModPhys.74.485
    [37] Hamilton C A, Burroughs C J, Benz S P, Kinard J R 1997 IEEE Trans. Instrum. Meas. 46 224 doi: 10.1109/19.571818
    [38] Chaudhari P, Mannhart J, Dimos D, Tsuei C C, Chi J, Oprysko M M, Scheuermann M 1988 Phys. Rev. Lett. 60 1653 doi: 10.1103/PhysRevLett.60.1653
    [39] Klushin A M, Prusseit W, Sodtke E, Borovitskii S I, Amatuni L E, Kohlstedt H 1996 Appl. Phys. Lett. 69 1634 doi: 10.1063/1.117055
    [40] Klushin A M, Weber C, Darula M, Semerad R, Prusseit W, Kohlstedt H, Braginski A I 1998 Supercond. Sci. Technol. 11 609 doi: 10.1088/0953-2048/11/7/002
    [41] Klushin A M, Behr R, Numssen K, Siegel M, Niemeyer J 2002 Appl. Phys. Lett. 80 1972 doi: 10.1063/1.1458072
    [42] Khorshev S K, Pashkovsky A I, Subbotin A N, Rogozhkina N V, Gryaznov Y M, Levichev M Y, Pestov E E, Galin M A, Maksimov V Y, Zhezlov D A, Katkov A S, Klushin A M 2019 IEEE Trans. Instrum. Meas. 68 2113 doi: 10.1109/TIM.2019.2896011
    [43] Klushin A M, Pestov E E, Galin M A, Levichev M Y 2016 Phys. Solid State 58 2196 doi: 10.1134/S1063783416110184
    [44] Khorshev S K, Pashkovsky A I, Rogozhkina N V, Levichev M Y, Pestov E E, Katkov A S, Behr R, Kohlmann J, Klushin A M 2016 Proceedings of the Conference on Precision Electromagnetic Measurements (CPEM), Ottawa, CANADA, Jul 10–15, 2016 pp1–l2
    [45] Jin, Y R, Jia, Q J, Deng H, Wang N, Jiang F Y, Tian Y, Gao M Y, Zheng D N 2015 IEEE Trans. Appl. Supercond. 25 1 doi: 10.1109/TASC.2014.2363630
    [46] Linghu K, Guo Z, Wu Q, Luo W, Nie R, Jin Y, Zheng D, Wang F, Gan Z 2019 IEEE Trans. Appl. Supercond. 29 1 doi: 10.1109/TASC.2018.2880318
    [47] Li Y L, Xu T Q, Wang Y, Wang F R, Gan Z Z 2023 Sensors 23 4434 doi: 10.3390/s23094434
    [48] 马平, 姚坤, 谢飞翔, 张升原, 邓鹏, 何东风, 张凡, 刘乐园, 聂瑞娟, 王福仁, 王守证, 戴远东 2002 物理学报 51 224 doi: 10.7498/aps.51.224 Ma P, Yao K, Xie F X, Zhang S Y, Deng P, He D F, Zhang F, Liu L Y, Nie R J, Wang F R, Wang S Z, Dai Y D 2002 Acta Phys. Sin. 51 224 doi: 10.7498/aps.51.224
    [49] 刘新元, 谢柏青, 戴远东, 王福仁, 李壮志, 马平, 谢飞翔, 杨涛, 聂瑞娟 2005 物理学报 54 1937 doi: 10.7498/aps.54.1937 Liu X Y, Xie B Q, Dai Y D, Wang F R, Li Z Z, Ma P, Xie F X, Yang T, Nie R J 2005 Acta Phys. Sin. 54 1937 doi: 10.7498/aps.54.1937
    [50] 王倩, 马平, 华宁, 陆宏, 唐雪正, 唐发宽 2010 物理学报 59 2882 doi: 10.7498/aps.59.2882 Wang Q, Ma P, Hua N, Lu H, Tang X Z, Tang F K 2010 Acta Phys. Sin. 59 2882 doi: 10.7498/aps.59.2882
    [51] Yu M, Geng H F, Hua T, An D Y, Xu W W, Chen Z N, Chen J, Wang H B, Wu P H 2020 Supercond. Sci. Technol. 33 025001 doi: 10.1088/1361-6668/ab5e13
    [52] 尤立星, 冯一军, 潘俊, 吉争鸣, 周赣东, 康琳, 左景萍, 杨森祖, 吴培亨, 陈国新, 王牧 1999 低温物理学报 21 372 doi: 10.3969/j.issn.1000-3258.1999.05.013 You L X, Feng Y J, Pan J, Ji Z M, Zhou G D, Kang L, Zuo J P, Yang S Z, Wu P H, Chen G X, Wang M 1999 Chin. J. Low Temp. Phys. 21 372 doi: 10.3969/j.issn.1000-3258.1999.05.013
    [53] 王争, 岳宏卫, 周铁戈, 赵新杰, 何明, 谢清连, 方兰, 阎少林 2009 物理学报 58 7216 doi: 10.7498/aps.58.7216 Wang Z, Yue H W, Zhou T G, Zhao X J, He M, Xie Q L, Fang L, Yan S L 2009 Acta Phys. Sin. 58 7216 doi: 10.7498/aps.58.7216
    [54] 王华兵, 许伟伟, 吴培亨 2017 物理 46 528 doi: 10.7693/wl20170805 Wang H B, Xu W W, Wu P H 2017 Physics 46 528 doi: 10.7693/wl20170805
    [55] 高吉, 马平, 戴远东 2007 物理 36 869 doi: 10.3321/j.issn:0379-4148.2007.11.009 Dai Y D, Gao J, Ma P 2007 Physics 36 869 doi: 10.3321/j.issn:0379-4148.2007.11.009
    [56] 张骏, 张辰, 张焱, 马平, 王越 2015 低温物理学报 37 423 Zhang J, Zhang C, Zhang Y, Ma P, Wang Y 2015 Chin. J. Low Temp. Phys. 37 423
    [57] Xu T Q, Li Y L, Wang H Z, Wang Y, Wang F R, Gan Z Z 2023 Physica C 615 1354390 doi: 10.1016/j.physc.2023.1354390
    [58] Klushin A M, Weber C, Borovitskii S I, Starodubrovskii R K, Lauer A, Wolff I, Kohlstedt H 1999 IEEE Trans. Instrum. Meas. 48 274 doi: 10.1109/19.769581
    [59] Rao C N R, Raveau B 1989 Acc. Chem. Res. 22 106 doi: 10.1021/ar00159a004
    [60] Hao L, Macfarlane J C, Pegrum C M 1996 Supercond. Sci. Technol. 9 678 doi: 10.1088/0953-2048/9/8/010
    [61] Hao L, Macfarlane J C 1997 Physica C 292 315 doi: 10.1016/S0921-4534(97)01747-4
    [62] Mcdaniel E B, Gausepohl S C, Li C T, Lee M, Hsu J W P, Rao R A, Eom C B 1997 Appl. Phys. Lett. 70 1882 doi: 10.1063/1.118720
    [63] Klushin A M, Borovitskii S I, Weber C, Sodtke E, Semerad R, Prusseit W, Gelikonova V D, Kohlstedt H 1997 3rd European Conference on Applied Superconductivity (EUCAS), Veldhoven, Netherlands, June 30–July 03, 1997 p587
    [64] Tinchev S S 1990 Supercond. Sci. Technol. 3 500 doi: 10.1088/0953-2048/3/10/005
    [65] Simon R W, Bulman J B, Burch J F, Coons S B, Daly K P, Dozier W D, Hu R, Lee A E, Luine J A, Platt C E, Schwarzbek S M, Wire M S, Zani M J 1991 IEEE Trans. Magn. 27 3209 doi: 10.1109/20.133894
    [66] Kang D J, Burnell G, Lloyd S J, Speaks R S, Peng N H, Jeynes C, Webb R, Yun J H, Moon S H, Oh B, Tarte E J, Moore D F, Blamire M G 2002 Appl. Phys. Lett. 80 814 doi: 10.1063/1.1446998
    [67] Cybart S A, Chen K, Cui Y, Li Q, Xi X X, Dynes R C 2006 Appl. Phys. Lett. 88 012509 doi: 10.1063/1.2162669
    [68] Sharafiev A, Malnou M, Feuillet-Palma C, Ulysse C, Wolf T, Couëdo F, Febvre P, Lesueur J, Bergeal N 2018 Supercond. Sci. Technol. 31 035003 doi: 10.1088/1361-6668/aa9d48
    [69] Cybart S A, Anton S M, Wu S M, Clarke J, Dynes R C 2009 Nano Lett. 9 3581 doi: 10.1021/nl901785j
    [70] Cybart S A, Cho E Y, Wong T J, Wehlin B H, Ma M K, Huynh C, Dynes R C 2015 Nat. Nanotechnol. 10 598 doi: 10.1038/nnano.2015.76
    [71] Cho E Y, Zhou Y W, Cho J Y, Cybart S A 2018 Appl. Phys. Lett. 113 022604 doi: 10.1063/1.5042105
    [72] Cai H, Lefebvre J C, Li H, Cho E Y, Yoshikawa N, Cybart S A 2024 Appl. Phys. Lett. 124 212601 doi: 10.1063/5.0206445
    [73] Li H, Cai H, Sarkar N, Lefebvre J C, Cho E Y, Cybart S A 2024 Appl. Phys. Lett. 124 192603 doi: 10.1063/5.0206821
    [74] Lefebvre J C, Cho E Y, Cybart S A 2023 Appl. Phys. Lett. 123 112602 doi: 10.1063/5.0167106
    [75] Goteti U S, Cai H, Lefebvre J C, Cybart S A, Dynes R C 2022 Sci. Adv. 8 eabn4485 doi: 10.1126/sciadv.abn4485
    [76] Cai H, Li H, Cho E Y, Lefebvre J C, Cybart S A 2021 IEEE Trans. Appl. Supercond. 31 7200205 doi: 10.1109/tasc.2021.3069904
    [77] Elswick D, Ananth M, Stern L, Marshman J, Ferranti D, Huynh C 2013 Microsc. Microanal. 19 1304 doi: 10.1017/S1431927613008519
    [78] Chen Z W, Li Y L, Zhu R, Xu J, Xu T Q, Yin D L, Cai X W, Wang Y, Lu J M, Zhang Y, Ma P 2022 Chin. Phys. Lett. 39 077402 doi: 10.1088/0256-307X/39/7/077402
    [79] Zaluzhnyy I A, Goteti U, Stoychev B K, Basak R, Lamb E S, Kisiel E, Zhou T, Cai Z, Holt M V, Beeman J W, Cho E Y, Cybart S, Shpyrko O G, Dynes R, Frano A 2024 ACS Appl. Nano Mater. 7 15943 doi: 10.1021/acsanm.4c00247
    [80] Graser S, Hirschfeld P J, Kopp T, Gutser R, Andersen B M, Mannhart J 2010 Nat. Phys. 6 609 doi: 10.1038/nphys1687
    [81] Yin D L, Cai X W, Xu T Q, Sun R N, Chen Z W, Han Y, Tian L F, Wang Y, Zhang Y, Gan Z Z 2024 Physica C 623 1354532 doi: 10.1016/j.physc.2024.1354532
    [82] Chen Z W, Zhang Y, Ma P, Xu Z T, Li Y L, Wang Y, Lu J M, Ma Y W, Gan Z Z 2024 Chin. Phys. B 33 047405 doi: 10.1088/1674-1056/ad21f7
    [83] Wang X, Chen F, Lin Z, Tian S, Li C, Kornev V, Kolotinskiy N 2024 Electromagn. Sci. 2 1 doi: 10.23919/emsci.2024.0009
    [84] Kasaei L, Melbourne T, Li M J, Manichev V, Qin F, Hijazi H, Feldman L C, Gustafsson T, Davidson B A, Xi X X, Chen K 2019 IEEE Trans. Appl. Supercond. 29 1102906 doi: 10.1109/TASC.2019.2903418
    [85] Karrer M, Wurster K, Linek J, Meichsner M, Kleiner R, Goldobin E, Koelle D 2024 Phys. Rev. Appl. 21 014065 doi: 10.1103/PhysRevApplied.21.014065
  • 加载中
图( 8)
计量
  • 文章访问数:  61
  • HTML全文浏览数:  61
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-08
  • 刊出日期:  2025-05-05

高温超导约瑟夫森结技术及应用于液氮温区量子电压标准的可能性

    通讯作者: E-mail: hrb_zz@sina.com.; 
    通讯作者: E-mail: zhang_yan@pku.edu.cn.; 
    通讯作者: E-mail: maping@pku.edu.cn.
    作者简介: 陈紫雯: 934023769@qq.com
  • 1. 北京无线电计量测试研究所, 北京　100039
  • 2. 北京大学应用超导研究中心, 北京　100871
  • 3. 北京大学, 人工微结构和介观物理全国重点实验室, 北京　100871
  • 4. 北京大学物理学院, 北京　100871
  • 收稿日期:  2024-09-08

摘要: 本文对液氮温区约瑟夫森电压标准的物理原理、相关应用研究的发展历史、研究现状以及未来发展方向进行了综述. 液氮温区工作的约瑟夫森电压标准具有移动性强、能耗小等特点, 便于应用推广. 本文描述了目前约瑟夫森量子电压标准的研究现状, 重点探讨了基于高温超导体发展液氮温区量子电压标准可能性, 以及目前在芯片制备方面存在的各种挑战. 在此基础上, 介绍了超导约瑟夫森结阵列的一种新型制备技术, 即聚焦氦离子辐照技术, 其在高一致性约瑟夫森结阵列的制备上可能具有优势, 是未来探索实现液氮温区量子电压计量标准的一种可能技术路线.

English Abstract

    全文HTML

    1.   引　言

    • 约瑟夫森结[1](Josephson junction)是超导电子学的关键元件. 约瑟夫森结的高可靠、可重复制造技术是超导电子学发展的重要基础. 目前, 约瑟夫森结的最成功应用是超导量子干涉器件[2](superconducting quantum interference device, SQUID)和量子电压标准[3]. 前者由于SQUID磁强计具有地球磁场大小数十亿分之一的分辨率而在弱磁信号探测应用上发挥着重要作用. 后者是源自于交流约瑟夫森效应的量子电压与时间的比例关系只涉及基本物理常数(电子电荷$ e $和普朗克常数$ h $), 且现在频率测量可达到极高精度(从原子钟得到的频率不确定度优于1.7×10–16), 基于约瑟夫森结的电压频率关系设计的电压标准能够以非常高的精度在世界上任何地方复现. 约瑟夫森电压标准(Josephson voltage standards, JVS)已经成为世界所有国家都在使用的电压标准[4].

      在直流偏置和微波辐照共同作用下, 约瑟夫森结和微波感应电流会发生相互作用, 并在约瑟夫森结的直流伏安特性曲线上的电压$ {V}_{{\mathrm{e}}}=n(h/2 e)f $(h是普朗克常数, e是电子电荷, $ f $是频率, $ n $是整数)位置上发生电流跳跃, 并且这些跳跃处电流的大小$ {I}_{n}=2{I}_{{\mathrm{c}}}\left|{{\mathrm{J}}}_{n}\left[\left(2 e/h{f}_{}\right){V}_{{\mathrm{e}}}\right]\right| $(其中$ {I}_{{\mathrm{c}}} $是临界电流, $ {{\mathrm{J}}}_{n} $是第n阶Bessel函数, $ {V}_{{\mathrm{e}}} $是约瑟夫森结上微波电压的幅度)[5]. 跳跃电流是跳变点的电压决定的约瑟夫森时变电流和微波感应电流间发生相位锁定的结果. 交流约瑟夫森效应的实验验证就是通过对这种跳跃电流的观测完成的. 这个方法及其实验设计不但构成了超导电子学技术领域中的重要元件——如约瑟夫森混频器、参量放大器以及约瑟夫森电压标准的工作基础, 也是测量分析约瑟夫森结性能参数的常用方法[6].

      传统电压基准中使用的标准电池产生的标准电压受到温度、振动、充放电的影响, 数值会随时间漂移, 各个国家复现的数值难以统一. 虽然约瑟夫森电压标准不是从国际单位制SI出发, 但它非常稳定且精度极高, 可以在任何地方复制, 不需要进行任何人为校准, 也不受环境或制造约瑟夫森结的超导材料的影响, 因此在20世纪90年代被国际计量组织确立为世界范围内用于电压量值复现与传递的标准. 本文将主要分为如下几个部分: 第2节首先对量子电压生成的基本物理原理进行介绍; 第3和第4节对基于低温超导体和高温超导体的量子电压基准的发展现状进行介绍, 其中重点从芯片制备技术角度对用于实现液氮温区工作量子电压的高温超导约瑟夫森结技术进行介绍, 探讨了目前高温超导量子电压基准发展面临的挑战; 第5节介绍了近几年新发展出的高温超导约瑟夫森结制备技术, 有望在未来实现高密度、高可控性和一致性的高温超导量子电压芯片. 第6节对全文进行总结, 并作展望.

    2.   量子电压的基本原理

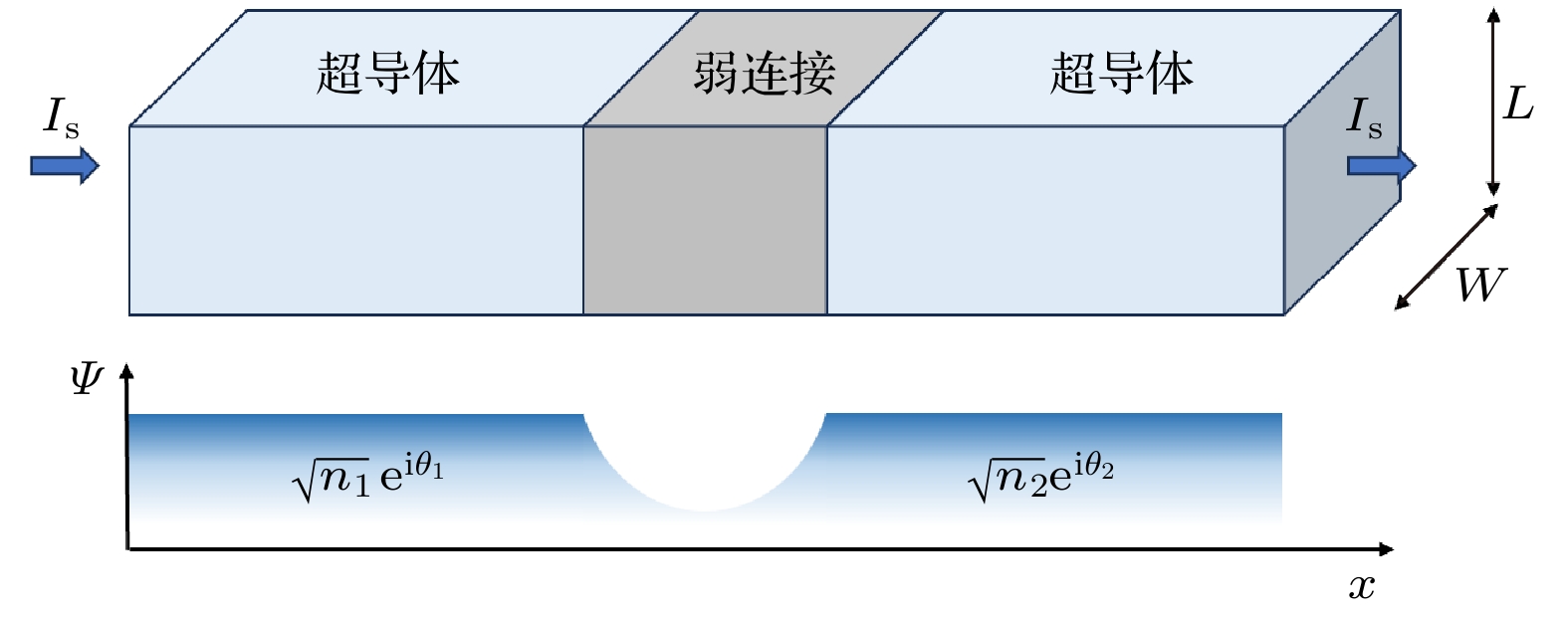
    • 约瑟夫森效应是一种宏观量子现象, 是超导电子学领域发展的重要物理基础. 在该现象发生的结构, 即约瑟夫森结(如图1所示)中, 被中间弱连接层分隔的两侧超导体之间发生弱耦合, 库珀对在两侧超导体之间转移使得它们的相位发生一定联系. 图中Ψ代表超导电子的波函数, n代表序参量, θ代表两侧超导体超导波函数的相位. 约瑟夫森效应是由两侧超导体超导态电子波函数的相位差$ \varphi $产生的, 本节将从约瑟夫森效应的基本理论出发, 结合“相位粒子在约瑟夫森势阱中运动”的物理图像, 解释量子标准电压的产生原理. 在原理的基础上, 给出了高质量量子电压芯片的制备对约瑟夫森结具体参数的一般要求.

      约瑟夫森结中的电流包括超导电流(库珀对)和正常态电流(被拆散的库珀对). 电阻电容分路(resistively and capacitively shunted junction model, RCSJ)模型是一种用并联的电阻电容来等效约瑟夫森结的电路模型, 可以用来定量描述约瑟夫森结的基本性质. 该电路的总电流即经过结的电流由约瑟夫森电流$ {I}_{{\mathrm{s}}} $、流经电阻$ {R}_{{\mathrm{n}}} $的正常态电流$ {I}_{{\mathrm{N}}} $以及结电容$ C $贡献的位移电流$ {I}_{{\mathrm{D}}} $三部分构成[7]. 经过一系列推导即可得出描述约瑟夫森结的基本方程:

      其中$ i=I/{I}_{{\mathrm{c}}} $和$ \tau =2 e{I}_{{\mathrm{c}}}Rt/{\mathrm{\hbar }} $分别为归一化的偏置电流(外加的电流驱动)和时间, $ {\beta }_{{\mathrm{c}}}={(2 e/{\mathrm{\hbar }})I}_{{\mathrm{c}}}{R}_{{\mathrm{n}}}^{2}C $被称为麦克坎勃参量. 除此之外, 对高温超导约瑟夫森结来说, 还需要额外需要考虑电流噪声的贡献. 电流噪声的功率谱密度由Jonson-Nyquist公式$ {S}_{{\mathrm{I}}}\left(f\right)=\left(4{k}_{{\mathrm{B}}}T\right)/{R}_{{\mathrm{n}}} $给出, 其会直接引起临界电流$ {I}_{{\mathrm{c}}} $的涨落. 另外, 高温超导器件的工作温度限制了结临界电流$ {I}_{{\mathrm{c}}} $不能过小, 否则热能$ {k}_{{\mathrm{B}}}T $将会与结零电流状态对应的能量($ {I}_{{\mathrm{c}}}{\varPhi }_{0}/2{\mathrm{\pi }} $)相当, 热涨落将会破坏约瑟夫森结的宏观量子效应. 对于工作在液氮温区的量子电压芯片, 临界电流一般在毫安(mA)量级.

      约瑟夫森结的量子电压台阶出现在其电压态, 而电压态的动力学特性由约瑟夫森结的特征频率($ {f}_{{\mathrm{c}}}={I}_{{\mathrm{c}}}{R}_{{\mathrm{n}}}/{\varPhi }_{0} $)和麦克坎勃参量$ {\beta }_{{\mathrm{c}}} $决定. $ {f}_{{\mathrm{c}}} $可认为是RCSJ电路的截止频率, 其决定了约瑟夫森结输出响应的特征时间; 而$ {\beta }_{{\mathrm{c}}} $与RCSJ电路的品质因子有关, 其大小区分了约瑟夫森结具有的回滞和非回滞特性, 决定了结的输运性质.

      结电压态的动力学行为可以用上述RCSJ的基本模型结合“相位粒子在势阱中的运动”这一物理图像来描述. (1)式的二阶非线性微分方程可以用质量为$ M $, 阻尼系数为$ \eta $粒子在倾斜的约瑟夫森势阱$ {U}_{}\propto 1-{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\varphi -i\varphi $(或形象称为“搓衣板势阱”)中的运动来类比, (1)式可改写为

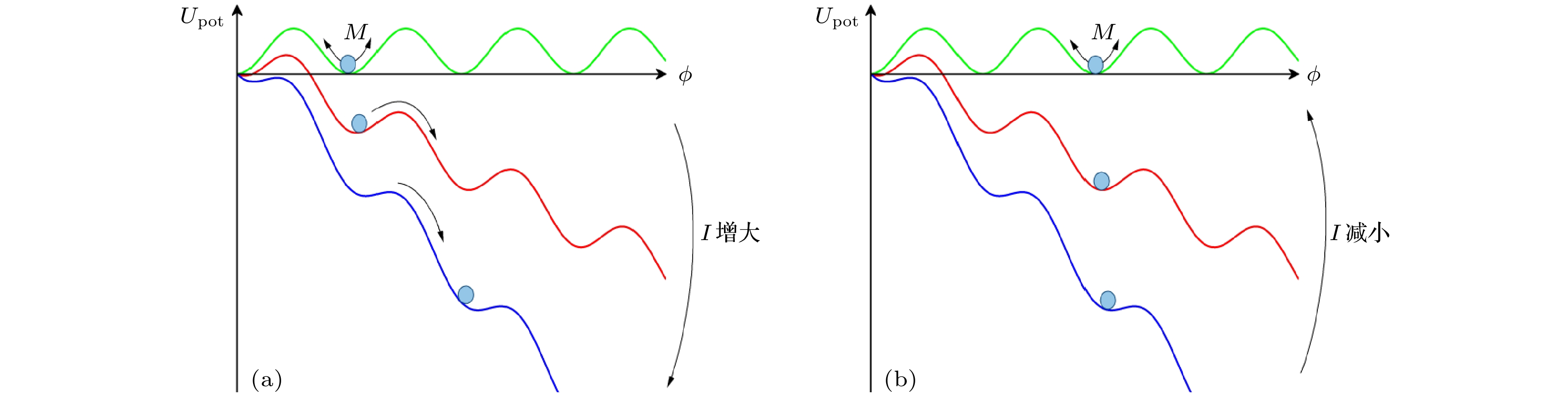
      其中$ \varphi $为两侧超导体的相位差.

      图2展示了由(2)式描绘的相位粒子在约瑟夫森势阱中的运动, 其中横坐标$ \phi =\varphi /{\varPhi }_{0} $为约化的结相位, $ {\varPhi }_{0} $为一个磁通量子. 当偏置电流$ I $为0时, 约瑟夫森势阱如图2绿色曲线所示, 在相位间隔为2$ {\mathrm{\pi }} $的整数位置势阱将出现极小值, 相位粒子被束缚在势阱中的某一极小值附近振荡. 当偏置电流$ I $小于临界电流$ {I}_{{\mathrm{c}}} $时, 随着$ I $的增大, 约瑟夫森势阱开始出现倾斜, 如图2蓝色曲线所示, 但是相位粒子仍然被束缚在这一极小值附近, 直到$ I $大于临界电流$ {I}_{{\mathrm{c}}} $, 势阱倾斜大到相位粒子开始出现滑动, 约瑟夫森结开始出现电压态, 直至滑动到下一个极小值处. 此时若$ I $减小, 相位粒子将会被重新束缚在这一新的极小值位置处.

      基于上述图像, 当约瑟夫森结上同时流经直流偏置电流和正弦变化的偏置电流$ {I}_{{\mathrm{r}}{\mathrm{f}}} $时, 结在过阻尼状态下, 相位粒子将按照2π的整数倍在约瑟夫森势阱中运动. 直流偏置电流决定了约瑟夫森势阱的平均斜率, 而$ {I}_{{\mathrm{r}}{\mathrm{f}}} $则会引起势阱斜率在平均值附近的来回振荡, 因此在某一偏置电流范围内, 相位粒子将会在几个局部极小值之间发生振荡(结处于电压态). 相位粒子发生的2π的整数倍变化的平均值将反映在结输运性质上, 即在伏安特性曲线上出现特定数量的量子化电压台阶$ {V}_{n}=nf{K}_{{\mathrm{J}}} $(或称为“夏皮罗台阶”), 其中$ {K}_{{\mathrm{J}}}\equiv 2 e/h $为约瑟夫森常数, 这一电压台阶的数值只与频率和物理常数(约瑟夫森常数)有关. 借助原子钟, 与时间常数相关的频率不确定度目前可达到10–16量级, 是7个国际单位制的基本物理常数中精度是最高的, 比其他基本单位精度要高出10个数量级左右, 其他物理常数通常需要寻找跟时频的直接计算关系来建立精度更高的基准. 而在低温试验下得到约瑟夫森常数的相对不确定度可以达到10–19量级[8], 被各个国家统一设定为固定值($ {K}_{{\mathrm{J}}}=483{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}597.848{\mathrm{ }}4{\mathrm{ }}\;{\mathrm{G}}{\mathrm{H}}{\mathrm{z}}/{\mathrm{V}} $). 因此, 利用交流约瑟夫森效应产生的量子化电压可以作为目前最高等级的电压标准. 伏安特性曲线上具有某一特定量子电压值$ {V}_{n} $的电流变化区间被称为量子电压偏置电流的工作裕度, 在此范围内电流的涨落对电压值不会产生明显影响, 因此是量子电压芯片工作稳定性的重要衡量标准. 当存在热涨落时, 在特定量子电压值$ {V}_{n} $的偏置电流工作裕度范围内, 该量子电压台阶实际上将具有一定的斜率, 电压值在此范围内的变化被称为台阶的线宽, 线宽越小, 电压台阶越能被清晰定义. 结本征线宽大小[9]正比于:

      由(3)式可以看出, 台阶线宽与约瑟夫森结的参数以及工作温度密切相关.

      结合上述物理图像以及量子电压基准运行要求, 量子电压芯片上的约瑟夫森结的设计需要满足以下基本原则:

      1)麦克坎勃参量$ {\beta }_{{\mathrm{c}}}\ll 1 $, 即约瑟夫森结应具有非回滞特性.

      2)短结, 结的长度$ L $要小, 以保证交变磁场中结平面内感生的磁通可以小于磁通量子$ {\varPhi }_{0} $ $ ({\varPhi }_{0}\equiv {h}/({2 e})\approx 2.07 \times 10^{-15}\;{\rm V \cdot s}) $, 进而保证偏置电流在结区内均匀分布.

      3)小结, 结的面积($ L\times W $)要小. 结边界的阻抗不匹配将会使结内形成驻波, 此时可将结看作开路的谐振腔, 具有特定的电磁振荡模式. 若微波偏置恰好激发起该模式, 其将会与约瑟夫森电流相互作用, 引起额外的直流电压分量, 影响量子电压台阶的准确性. 由于结的谐振模式的频率反比于结的尺寸, 因此需要减小约瑟夫森结的几何尺寸以使其谐振模式的基频大于微波偏置频率$ f $, 使得微波偏置无法激励这些特定的模式.

      4)结的等离子频率$ {f}_{{\mathrm{p}}} $要小于偏置频率$ f $, 一般取$ f\geqslant {2 f}_{{\mathrm{p}}} $. 由于约瑟夫森结的等离子频率与结的临界电流密度$ {J}_{{\mathrm{c}}}^{1/2} $成正比, 这就要求约瑟夫森结有较低临界电流密度, 对结势垒层的质量和工艺控制提出了很高的要求.

      5)要观测到明显的约瑟夫森效应, 要求$ {I}_{{\mathrm{c}}}{\varPhi }_{0}/2{\mathrm{\pi }} \gg {k}_{{\mathrm{B}}}T $. 这就要求结要具有较大的$ {I}_{{\mathrm{c}}} $, 且$ {I}_{{\mathrm{c}}} $的离散性要小, 以避免噪声导致量子电压在不同电压台阶之间跳变导致输出电压的不稳定.

      不难发现, 上述的要求之间也存在一些矛盾, 例如, 5)要求较大临界电流, 而结临界电流$ {I}_{{\mathrm{c}}}= WL{J}_{{\mathrm{c}}} $, 因此与2), 3), 4)的要求无法同时满足, 这就要求在芯片的设计和制备上对结的尺寸以及具体制备工艺进行综合考虑, 以使得以上要求都得到满足. 此外, 需要根据结参数, 对芯片的其他拓扑结构(如谐振腔、结阵并联金电阻层等)进行合理设计, 以实现结与外部微波驱动耦合的最大化. 同时, 由于约瑟夫森结的临界电流对温度有很强的依赖关系, 温度的涨落会影响量子电压标准的精度, 为了保证量子电压芯片工作时的温度稳定性, 还需要对制冷系统进行优化设计以尽可能地减小漏热.

    3.   约瑟夫森量子电压标准的研究现状

    • 传统液氦温区约瑟夫森电压基准的发展经历了多个阶段, 取得了诸多重要技术突破. 20世纪70年代初, 早期的约瑟夫森电压基准基于几个独立偏置的低温超导约瑟夫森结, 输出电压最大只能到10 mV左右, 需要设计额外的电阻分压器将约瑟夫森标准与当时精度最高的韦斯顿电池进行比较. 为了解决结均匀性的问题, 增加输出电压, 1982年Nb/Al-AlOx/Nb的超导体-绝缘体-正常态金属-绝缘体-超导体(superconductor-insulator -superconductor, SIS)结技术发展成熟[10], 同时将结阵集成到带有鳍线天线的微带线的方案被提出[11], 通过毫米波范围的电磁波辐射实现对了大量串联约 瑟夫森结的同步驱动. 由此开发出首个大规模超导集成电路, 包含14000个SIS铌结, 每个结工作在n = 5的台阶上, 应用于直流约瑟夫森电压标准(conventional dc Josephson voltage standard, CJVS), 输出电压高达10 V, 电流工作裕度约为20 μA, 相对不确定度为达到10–9. 直流电压标准目前已实现商业化[12]. 目前, 低温超导直流电压标准广泛应用于各国计量机构, 用于复现直流伏特, 直接校准1 V和10 V的新型固态电压标准(齐纳二极管)以及精密数字电压表, 取代了基于韦斯顿电池的“实物”初级标准, 并为基于约瑟夫森效应的伏特新定义奠定了基础.

      然而, 早期基于SIS结的直流电压标准存在着局限性. 由于SIS结通常具有欠阻尼的特性, 其伏安特性存在回滞的现象. 当结上偏置电流变化时, 由于欠阻尼约瑟夫森结的回滞特性, 电压值可能维持在原台阶, 导致无法迅速选定特定电压数值. 由此产生的电压稳定性欠佳, 易受电磁干扰影响. 为克服这些问题, 基于过阻尼、无回滞约瑟夫森结的可编程约瑟夫森电压标准(programmable Josephson voltage standard, PJVS)被开发. PJVS由数千个具有单值非滞后伏安特性的超导体-正常层-超导体(superconductor-normal metal-superconductor, SNS)结[13,14]或超导体-正常态金属-超导体(superconductor-normal metal-superconductor, SNS)约瑟夫森结[15]构成, SNS结典型势垒层材料为Nb-NbxSi1–x-Nb. PJVS输出电压稳定, 可以快速进行电压合成, 其芯片上的子结阵设计按照二进制分布, 通过程控实现交直流量子电压信号的输出. 其在国际比对的移动量子电压标准、瓦特天平、量子阻抗和功率标准等众多应用中被证明有效, 能提供超过10 V、高达数kHz的直流和交流峰值电压. PJVS作为量子电压标准中发展相对成熟的一种方案, 已有商用产品出售[16,17].

      对于更高频率的交流量子电压的产生, 一般采用约瑟夫森任意波形合成器(JAWS)技术实现, 由单个阵列组成, 由典型时钟频率为15 GHz的调频脉冲射频(RF)信号驱动, 目前已可实现高达2 V, 1 MHz的频谱纯净交流信号的产生[18]. 使用短脉冲而非正弦射频信号, 可在宽频率范围内有效调制信号, 使结保持在量子化电压台阶上, 输出电压由脉冲重复率精确确定.

      纵观液氦温区量子电压标准发展历程, 其之所以能够突破关键技术, 实现产业化过程, 离不开低温超导约瑟夫森结技术的进步. 要实现如此高精度的电压标准系统, 对用于PJVS标准的芯片中的关键部件, 即约瑟夫森结阵列的设计和制备提出了很高的要求. 如前所述, 在设计上, 要综合结参数和结尺寸, 使得约瑟夫森结区的偏置电流和微波偏置在结区内部均匀分布; 在工艺上, 要求结临界电流$ {I}_{{\mathrm{c}}} $需要尽量大并且离散性小. 目前满足上述要求的液氦温区约瑟夫森结阵列的制备工艺已经比较成熟, 所制备的量子电压芯片可以达到良好的工作性能. 美国NIST[19]、德国PTB[20]以及日本AIST[21]等机构推动了液氦温区量子电压芯片的制备技术的进步, 与此同时, 国内中国计量科学研究院[22,23]、中国科学院物理研究所(简称为物理所)[24,25]和中国科学院上海微系统与信息技术研究所[26](简称为上海微系统所)、南京大学[27]等多家单位在超导集成电路技术上实现了重要突破[28]. 其中计量院课题组[29]攻克了约瑟夫森结大规模集成工艺技术瓶颈, 将Nb/NbxSi1–x/Nb约瑟夫森结物理集成度提升至40万量级, 使我国在量子电压类芯片的研制上跻身国际前列.

      由SIS类型约瑟夫森结到SNS类型约瑟夫森结的研究和探索, 使结阵突破了集成工艺的难题, 在微波辐照下产生出更稳定纯净的量子电压信号, 使得量子计量在低频计量中具备了竞争力. 约瑟夫森结势垒层的改变和优化提高了低温超导量子电压的集成度, 另外在结的制备参数方面, 提高结本身的临界电流、同时减小正常态电阻以提高第一级电压台阶的工作裕度, 有利于提高电压的稳定性, 这为高温超导量子电压中约瑟夫森结的研究提供了宝贵的参考经验.

      2019年5月20日, 国际单位制的七个基本单位基于物理常数进行了重新定义, 这标志着计量单位向常数化和量子化方向的发展迈出了重要一步. 在国内, 北京无线电计量测试研究所与中国计量科学研究院建立的直流约瑟夫森量子电压标准系统能够产生不确定度达到10–9量级的量子基准电压, 共同承担了国家直流量子电压量值传递的任务[30,31]. 液氦温区约瑟夫森电压标准不仅是国家计量机构的电压基准装置, 也在电力系统中尝试被集成到智能电网中, 用于新一代基于量子电压的电能标准装置, 从而减少了量值传递链路的复杂性和不确定性[32,33].

      虽然目前基于低温超导体的量子电压标准系统已经可以实现高精度的商用化应用, 但由于工作温度的限制, 铌基约瑟夫森电压标准只能在液氦沸点温度(4.2 K)温度下运行. 维持这一温度既可以采用装有液氦的杜瓦来实现约瑟夫森结阵芯片的制冷, 也可以把约瑟夫森结阵列芯片固定在免液氦的干式制冷机的冷头上进行冷却, 但由于我国氦气资源极度贫乏并且需要从国外进口, 基于液氦的低温超导量子电压标准系统不但运行成本高, 还存在禁运风险. 而能够维持4 K温度的免液氦制冷机需要功率很大的压缩机, 体积、重量和能耗都很大, 不但使用不易, 还需要复杂的技术支撑. 针对目前量子电压发展的现状, 从实用化的角度出发, 对于量子电压标准的进一步优化, 一方面需要对新型制冷系统进行研制, 另一方面可以通过开发新一代可工作在液氮温区的量子电压芯片的新思路, 来降低能耗, 节约成本, 并提高约瑟夫森电压标准的实用性和便携性.

    4.   液氮温区的量子电压芯片

    • 超导转变温度$ {T}_{{\mathrm{c}}} $超过液氮沸点的高温超导材料的发现[34,35]激发了超导电子学和计量领域研究者对于新一代量子电压标准的应用研究. 由于铜氧化物高温超导材料YBa2Cu3O7–δ(YBCO)约瑟夫森结有很高的工作温度, 液氮温区运行的量子电压标准拥有操作便捷、价格便宜、运行可靠的制冷方案. 除此之外, 高温超导约瑟夫森结具有与电阻分路模型符合很好、无回滞的伏安特性[36], 与计量科学领域中的可编程约瑟夫森电压标准[4]、脉冲驱动的交流约瑟夫森电压标准[37]等对约瑟夫森结伏安特性的要求高度契合, 因此有望发展出一种能在工业部门、军队的校准实验室、大科学装置运行现场使用的量子电压标准. 77 K低温制冷机在相同制冷量要求下(约100 W)有更小的体积、更低的重量和能耗, 可能将目前难以移动的电压标准技术升级为可移动式的小型电压标准系统, 还可能将它纳入商用电压表中. 如果高温超导约瑟夫森结阵列的制造技术能够得到突破, 将会给量子电压标准技术带来更加广阔的应用前景.

      • 4.1.   高温超导量子电压标准芯片的研究现状

    • 高温超导约瑟夫森电压标准发展建立的核心是高温超导约瑟夫森结阵列制备的探索研究. 众多高温超导结阵制备工艺中最成功的是双晶晶界结(以下简称为“双晶结”)技术[36,38]. 在过去二十多年时间内, 国际上和国内对基于该技术的高温超导约瑟夫森电压标准都开展了持续的研究.

      在国际上, 早期德国尤利希研究中心和俄罗斯科学院微结构物理研究所分别对基于双晶结阵技术的高温超导量子电压开展了研究[6]. 1996年, 德国尤利希研究中心率先在氧化钇稳定氧化锆(YSZ)双晶上制备了含有365个高温超导约瑟夫森结的串联阵列. 他们发现, 在没有对微波偏置和器件采取任何优化措施时, 在15 K的温度下, 该高温超导量子芯片上多达39个结可以与K波段微波偏置发生相位锁定[39]. 同时, 针对当时的双晶晶界结工艺导致临界电流和正常态电阻参数具有分布离散性大的问题, Klushin等[39]通过简单的分流电阻设计, 获得了明显的第一级夏皮诺台阶, 台阶处电流跳跃高度大小约为结阵的30%. 这项开创性研究表明了高温超导双晶结技术可以满足液氮温区电压标准的设计要求, 为高温超导约瑟夫森电压标准的发展奠定了基础. 1998年, 德国尤利希研究中心[40]进一步通过减小双晶晶界夹角和增加薄膜厚度的简单方法, 大幅度地提高了分流双晶晶界约瑟夫森结设计的临界电流和第一个恒压处电流阶跃的大小, 首次在80 K获得了$ {I}_{{\mathrm{c}}} > 2\;{\rm mA}$的临界电流和$ \Delta {I}_{1} > 1\;{\rm mA}$的第一阶跳跃电流幅度; 同时在温度等于50 K时, 第一阶跳跃电流的幅度$ \Delta {I}_{1}\approx 2\;{\rm mA}$, 接近阵列的临界电流值. 这项研究结果表明高温超导双晶晶界结技术能够保证电压标准在液氮温度下运行并给出很高的精度. 2002年, 德国尤利希研究中心[41]利用一个工作在4 K温度下的铌基可编程约瑟夫森电压标准对64 K工作的YBCO双晶结阵列输出的量子电压进行了校准, 发现两者间的不确定度在10–8量级(电压测量值在9 mV时). 该结果表明, 高温超导约瑟夫森结阵列可以在液氮温度下正常工作, 抗干扰能力强, 工作稳定性好, 并且能够用于高精度电压校准测量.

      经过对YBCO结阵技术的不断优化改进与积极探索, 俄罗斯科学院微结构物理研究所[42]在2018年报道了一个可移动工作的高温超导约瑟夫森电压标准N4-21. N4-21电压标准系统的运行温度由小型脉管制冷机提供. 集成有高温超导约瑟夫森结阵列的芯片被固定在一台小型液氮低温制冷机的冷头上, 冷头的温度可以维持在65—79 K之间. 图3所示是该液氮温区量子电压的测控部分, 集成了制冷模块、测试模块、控制与电源模块与电脑.

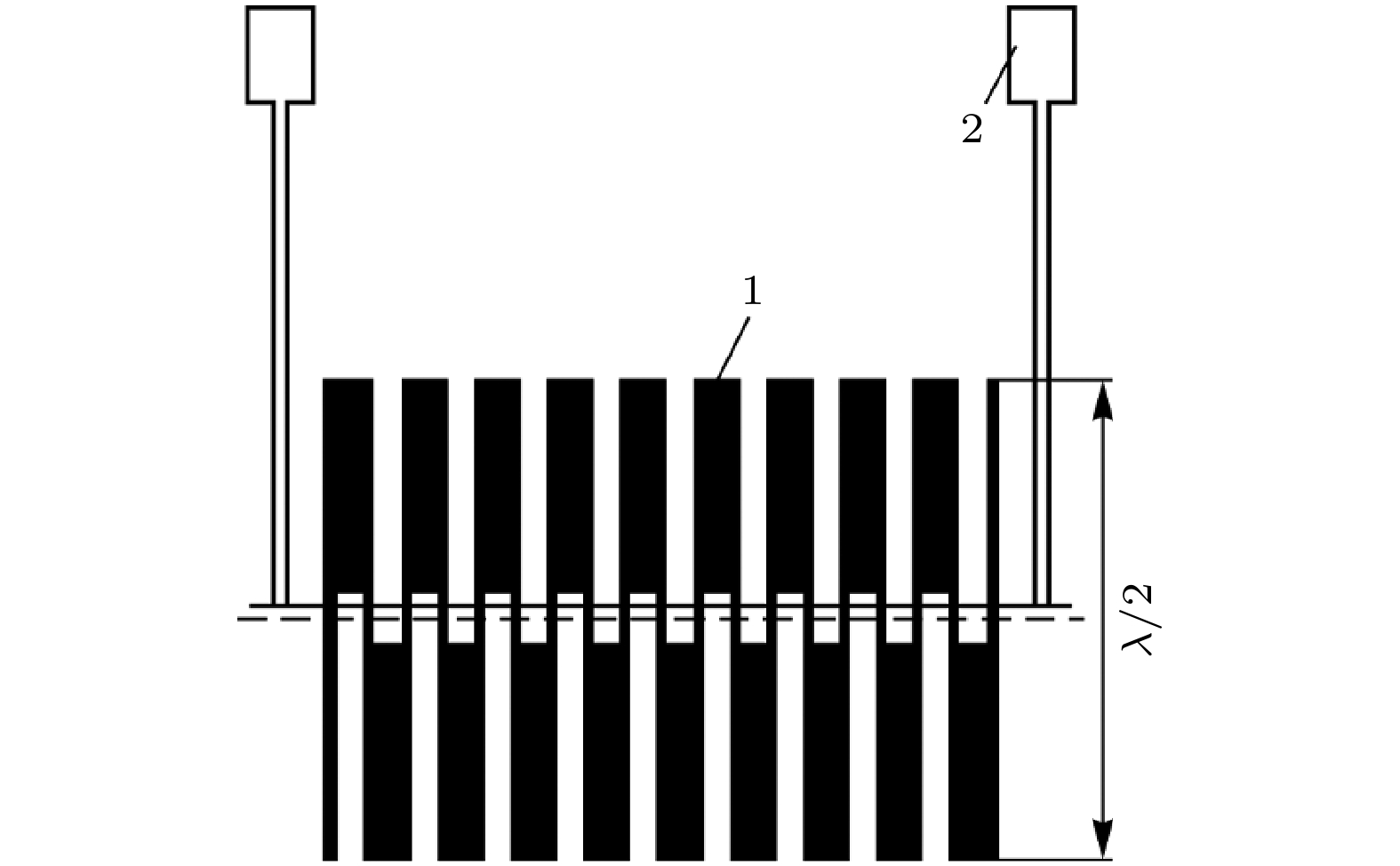
      该电压标准芯片也采用了高温双晶结技术来制备约瑟夫森结阵列[43], 晶界结串联阵列制备在晶界夹角24°, 面积10 mm×10 mm的YSZ双晶衬底上. 结部分采用了分流电阻设计, 使用了厚度150 nm的YBCO外延膜超导薄膜和正常金属组成的双层薄膜结构. 图4所示是该芯片结阵周围的结构示意图, 晶界附近高温超导薄膜形成的曲折线结构与晶界交叉处形成约瑟夫森结, 这些结串联在一起形成阵列. 该阵列结构与和晶界垂直的双梳齿线段构成一个半波长谐振腔, 从而使得约瑟夫森结与驱动微波之间有较好的耦合. 图5为该设计的YSZ双晶晶界结串联阵列的交流和直流伏安特性. 在75 GHz微波偏置下, 量子电压台阶位置上的电流跳跃幅度大于等于$ {I}_{{\mathrm{c}}} $, 伏安特性与电阻分路结(RSJ)模型[2]符合得很好. 为了确定N4-21所能达到的技术指标, 他们用铌基电压标准的输出电压$ {U}_{{\mathrm{J}}{\mathrm{N}}{\mathrm{b}}} $与N4-21的输出电压$ {U}_{{\mathrm{J}}{\mathrm{N}}4{\text{-}}21} $进行了比对[44], 发现在1 V和10 V的电压水平上, 两者间的相对不确定度为10–8量级. 该结果表明高温超导电压标准N4-21在远高于液氦的工作温度下仍然保持高精度, 可以作为伏特标准的一部分在国家计量机构中使用. 同时由于它的可移动性更强、运行成本更低以及有电就能运行等特点, 在标准的计量和测试中心、大公司大企业的计量实验室以及国家军队部门科学研究和计量机构都可以使用. 该标准还可用于校准精密数字电压表和直流电压校准.

      在高温超导量子电压标准的研究领域, 国内起步较晚, 相关的研究较少. 目前, 国内利用高温超导量子芯片开展的应用研究主要集中在弱磁信号探测, 以及微波信号接收等应用上. 例如, 在弱磁探测方面, 物理所和北京大学在早期分别基于高温超导双晶结和台阶结技术进行了高灵敏度的高温超导直流SQUID和射频SQUID器件的研制, 并利用这些对低频磁场灵敏的器件开展了核磁共振相关的实验研究[45,46]. 北京大学利用高温超导SQUID开展了心磁测量和磁感应通信等探索研究[47–50]. 南京大学课题组[51]在YBCO双晶阵列结阵列混频器件上实现了高达154次的谐波混频. 另外, 国内还有大量关于基于双晶结和台阶结相关的研究报道[36,52–57]. 虽然在上述研究工作中已经实现了高质量双晶结以及相关器件, 但作为芯片的关键结构的高温约瑟夫森结一般为单个或数个, 对可用于量子电压标准应用的结阵相关研究目前还比较少, 在大数量串联的高温约瑟夫森结阵芯片的制备研究上仍然缺乏技术积累. 随着近年来低温超导量子电压计量领域的发展成熟, 以及国家对量子技术研发投入的不断加大, 电压计量领域开始关注高温超导量子电压技术的研究, 在这样的支持下, 相信我国未来在这一研究领域一定能有所突破. 然而, 从客观的角度讲, 要最终实现实用化的高温量子电压标准, 我们目前仍然面临着一些需要克服和解决的问题, 其中最主要的就是基于高温超导材料的高质量约瑟夫森结阵芯片的制备. 下一节将从高温超导体本身的材料特性出发, 探讨目前高温约瑟夫森结阵芯片制备所面临的挑战.

      • 4.2.   高温超导量子电压标准芯片面临的挑战

    • 对于基于约瑟夫森效应的量子电压测量基准, 为产生足够大的量子基准电压, 通常需要成千上万个约瑟夫森结串联组成的结阵, 同时还要求结阵尺度在施加微波频率1/4波长范围之内. 这对结参数的一致性以及结阵密度都提出了很高要求. 从芯片制造工艺的角度来看, 在对约瑟夫森结参数进行精准控制的同时保持不同结之间参数的高一致性, 从而实现高质量结阵的制备, 是高温超导量子电压标准能否实现所需要解决的关键问题. 由于约瑟夫森结中的振荡电流会产生热量, 因此在高密度结阵的情况下实现良好的散热也是一个挑战. 目前为止, 虽然基于高温超导约瑟夫森结的量子电压标准的研发取得了一定成功, 例如前文4.1节所述的高温超导电压标准N4-21使用的双晶晶界结技术已经在高温约瑟夫森电压标准技术领域确定了先进性和市场地位[58], 但和能与半导体规模化生产兼容的低温约瑟夫森结制备技术相比, 目前这一高温超导约瑟夫森结制备技术仍不够成熟, 这与高温超导体的物理特性密切相关.

      与传统的各向同性低温超导体不同, 铜氧化物高温超导材料具有很强的各向异性, 同时超导相干长度ξ极短, 如最常用的高温超导材料YBCO, 其在c轴方向的典型值仅为0.2 nm左右, 在ab面内的典型值也只有1.5 nm[35,59], 这一物理特性导致了基于绝缘势垒层的低温超导约瑟夫森结的成熟制备技术难以被直接用于高温约瑟夫森结的制备. YBCO薄膜的制备需要很高的沉积温度(800—900 ℃)以及很高的背景氧压(20—100 Pa), 极短的超导相干长度使得YBCO的超导性对晶体结构和化学组分的变化十分敏感, 因此高质量薄膜的制备对生长条件的微弱变化十分敏感, 最佳条件窗口较窄, 比低温超导材料的生长要困难得多.

      另外, 与三明治结构的低温超导约瑟夫森结不同, 高温约瑟夫森结一般利用晶格中的氧缺陷导致的弱超导性来实现约瑟夫森效应. 如目前YBCO约瑟夫森结制备中最成功和常用的双晶结技术, 就是利用YBCO在双晶衬底上的外延生长, 晶界两侧的YBCO由于晶格不匹配产生的大量的氧空位缺陷. 然而, 晶界的不完美、晶界附近的YBCO化学组分在原子尺度上的微小变化都会导致结的超导临界温度、临界电流等出现巨大改变. 例如晶界的“小面化”现象[60,61], 可能导致双晶结在不同晶界位置处的临界电流$ {I}_{{\mathrm{c}}} $和正常态电阻$ {R}_{{\mathrm{n}}} $有很大不同[62], 此时结将等效为不同临界电流$ {I}_{{\mathrm{c}}} $的分支的并联, $ {I}_{{\mathrm{c}}} $最大的分支起主导作用, 导致不同的双晶结的临界电流出现离散性. 因此, 尽管基于双晶结技术的高温超导双晶约瑟夫森结在电压标准应用上的可行性已经得到了初步验证, 但从实用化和更加广泛的应用需求的角度看, 该技术目前存在着参数一致性较难控制的问题. 另一个高温超导约瑟夫森结常用的台阶结技术, 其依赖于高温超导薄膜的外延生长在衬底台阶边缘附近产生的氧缺陷[36]导致的超导弱连接来形成约瑟夫森结, 前驱衬底上台阶结构的质量直接影响台阶结的质量, 因此也存在着与双晶结技术相似的问题.

      除制备工艺上存在的问题待优化和解决之外, 由于约瑟夫森电压标准的输出电压与微波偏置频率、串联阵列的大小(约瑟夫森结的数量)成正比, 因此能否提高微波偏置频率、提高约瑟夫森结的堆积密度也是高温超导约瑟夫森电压标准进一步发展和推广使用必须突破的关键技术问题. 例如, 为了提高高温双晶结阵的集成度, 可采取高密度曲折线设计来提高双晶晶界结堆积密度. 除此之外, 还可以使用含有一个以上晶界的衬底. 例如, 衬底本身有$ k $个相互平行, 并且间距10—20 μm的晶界, 相同的设计就可以使串联约瑟夫森结阵列中的结数提高$ k $倍[63]. 但是这种双晶价格昂贵, 并且我国目前还没有掌握它的制造技术.

    5.   液氮温区量子电压标准的其他可行性方案

    • 除了高温超导双晶晶界结和台阶结之外, 还可以利用离子辐照损伤技术来制备高温超导约瑟夫森结. 通过离子辐照形成的局部弱化微桥结使用了高质量YBCO外延薄膜, 结的伏安特性基本符合电阻分路结(RSJ)模型, 不但结参数可以比较方便地通过离子辐照剂量进行控制, 长时间室温储藏和多次冷热循环条件下性能可以基本保持不变[55]. 利用辐照损伤技术可以制备与可编程约瑟夫森电压标准、脉冲驱动的交流约瑟夫森电压标准设计要求符合的伏安特性无回滞的SNS约瑟夫森结. Tinchev[64]首次展示了使用这一技术来制造SQUID的效果. 随后, 有许多工作发展、改进了这个工艺[65,66], 相继实现了数十个离子损伤约瑟夫森结的串联阵列[67,68]; 15820个(28×565)约瑟夫森结或15255个(27×565) SQUID的二维阵列[69]. 但是, 由于现代先进的常规离子束损伤技术的抗蚀掩膜的最小尺寸只能达到20 nm, 远远大于c外延YBCO薄膜a-b面上的相干长度. 因此实际上, 制备高温超导约瑟夫森结的常规离子束技术仍然存在许多没有解决的问题.

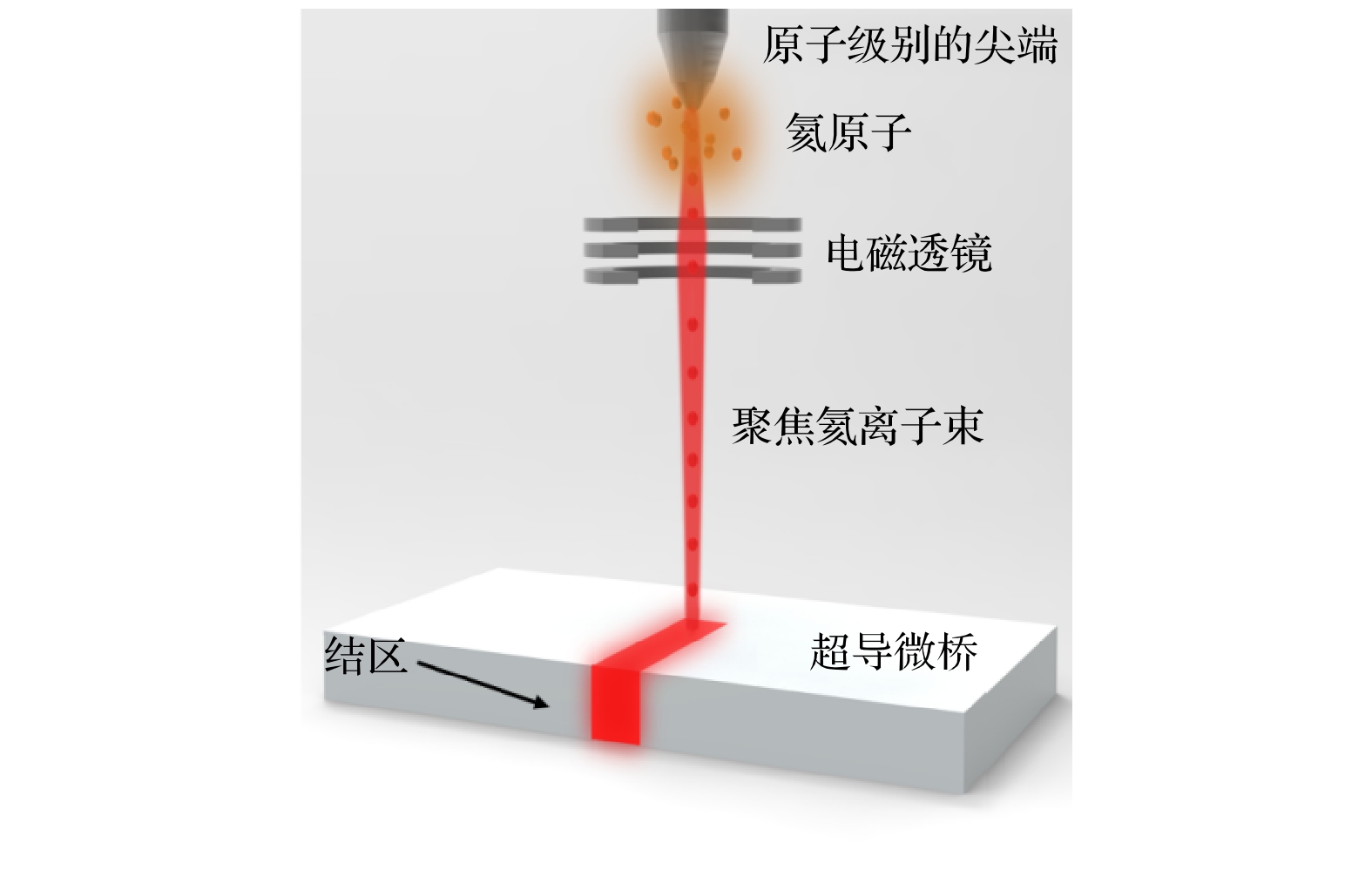
      近年来, 聚焦氦离子束辐照在约瑟夫森结阵列制造上取得的结果[70–76]引起了超导电子学领域和计量科学领域的广泛关注. 所谓聚焦离子束在现代半导体工业中是一种重要装备和常用工艺技术. 其使用的聚焦氦离子束理论上的空间精度能达到0.5 nm, 比电子显微镜使用的电子束具有更高的成像分辨率, 比镓离子束具有更强的聚焦控制能力, 同时还可以对超导体的超导性进行调控, 对高温超导材料的纳米级加工, 尤其是约瑟夫森结的制备具有独特优势[77]. 如图6所示, 利用聚焦氦离子束可以实现高温超导约瑟夫森结的直接“写入”, 是一种工艺更加简便的高温约瑟夫森结制备方法[78]. 纳米区域聚焦X射线衍射实验研究[79]结果表明, 氦离子辐照约瑟夫森结产生的物理起源可能与YBCO常见的约瑟夫森结类型(如双晶晶界结)类似, 即由氧缺陷导致的[36,80]. 聚焦He+辐照会使YBCO晶格结构发生改变, 在铜氧面上产生氧缺陷, 导致YBCO超导性能的下降. 同时, 氧缺陷密度可以通过改变辐照剂量来控制, 因此可以利用这一原理来进行弱超导的YBCO氦离子辐照结的制备, 通过辐照剂量的改变来对约瑟夫森结的性质进行控制. 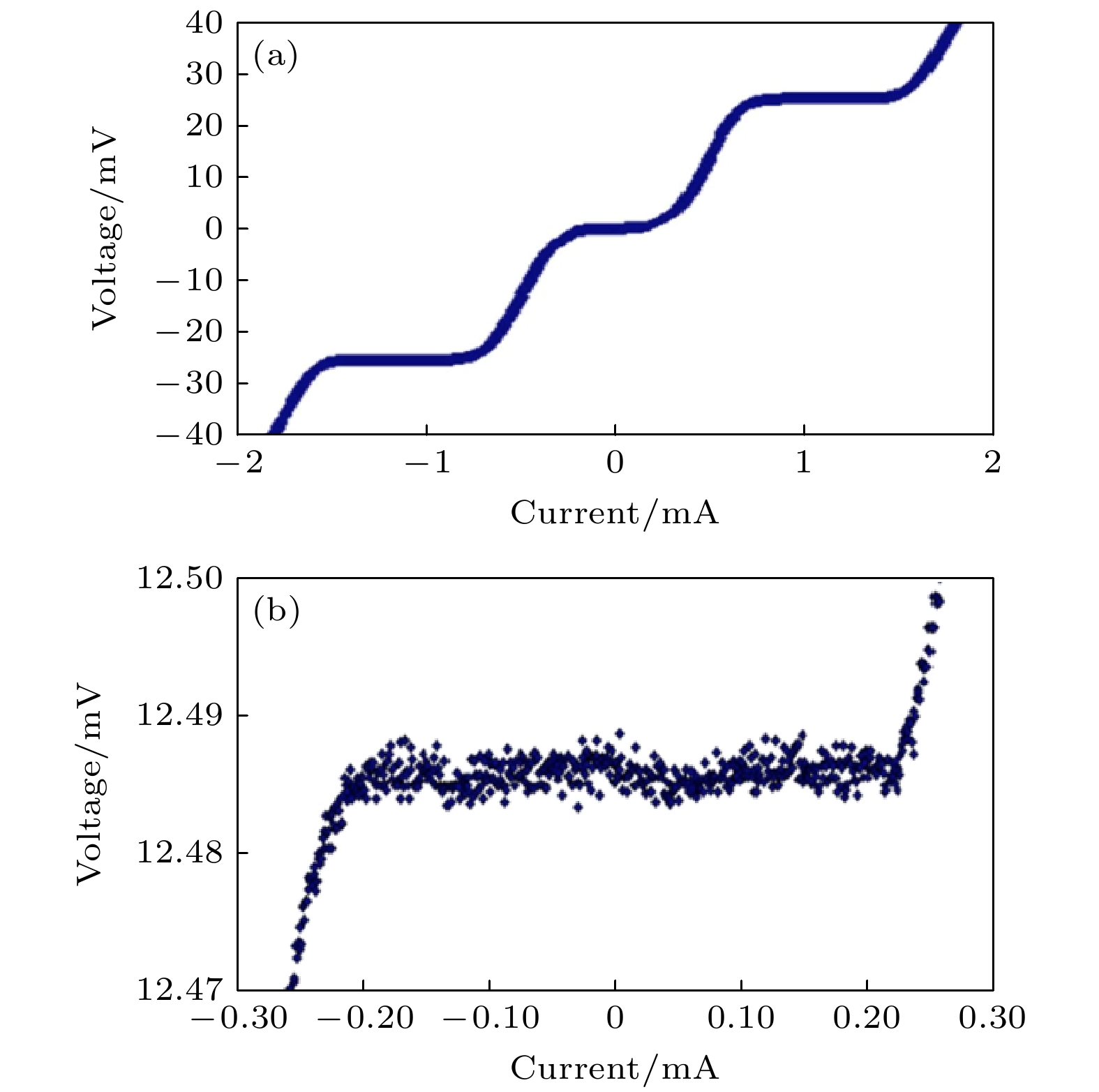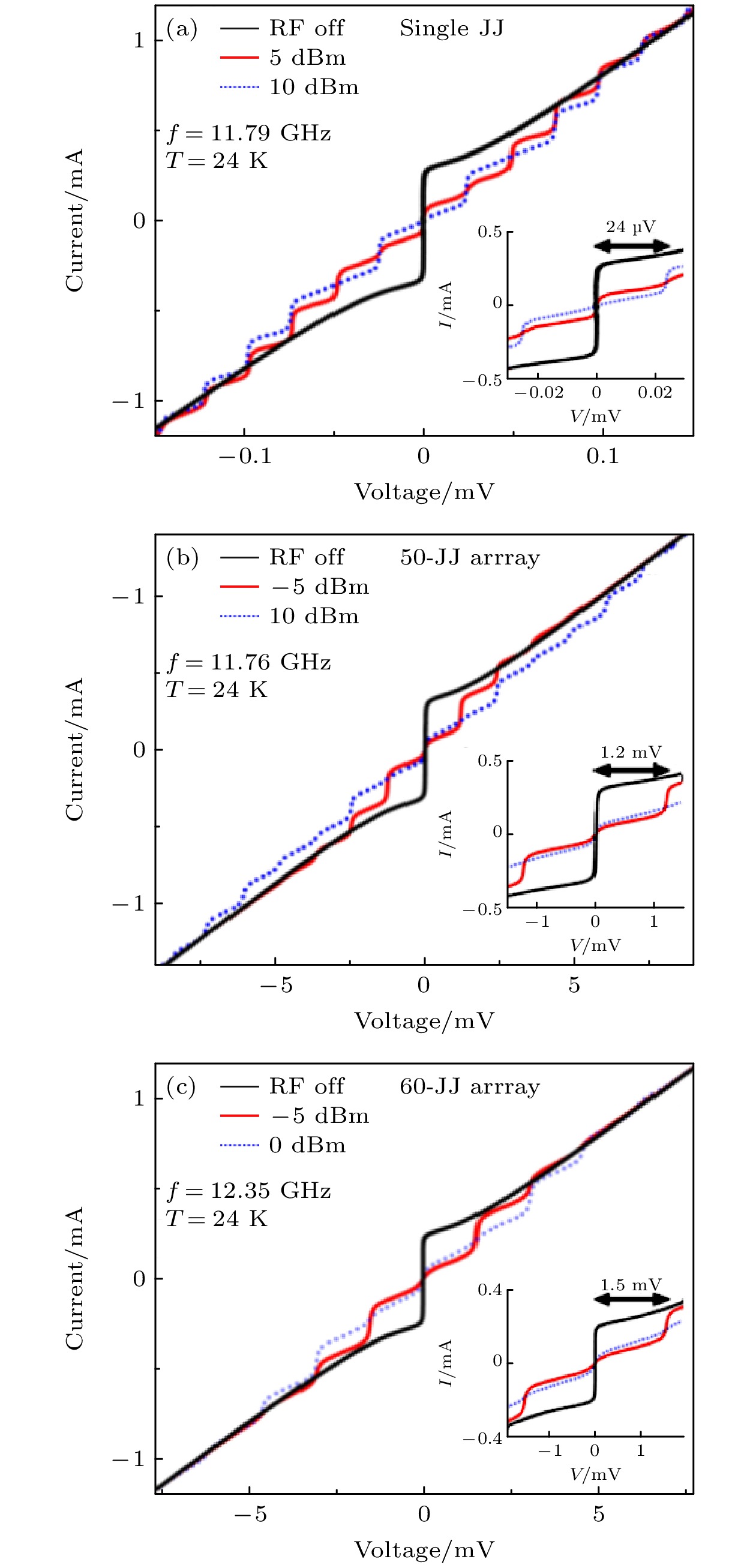与YBCO双晶晶界结类似, 聚焦He+辐照也能够制备出临界电流$ {I}_{{\mathrm{c}}} $很大且正常态$ {R}_{{\mathrm{n}}} $很小的约瑟夫森结, 因此适用于量子电压标准中量子电压芯片的制备.

      国际上, Cybart课题组[70] 首先利用聚焦氦离子束辐照实现了YBCO约瑟夫森结的制备. 近期, 国内的研究单位也对聚焦离子辐照技术十分关注, 对利用该技术制备高温约瑟夫森结开展了大量探索和研究. 北京大学应用超导研究中心与合作团队的相关实验结果表明, 利用聚焦氦离子束技术可以在YBCO[78], MgB2[81], Co掺杂的BaFe2As2[82]等超导材料体系中实现临界电流可控的氦离子辐照结的制备, 且临界电流离散性可稳定在10%以内. 同时, YBCO氦离子辐照结在液氮温区可以展现出明显的微波感应台阶, 有在液氮温区实现大量子电压生成的应用潜力. 此外, 物理所[83]、上海微系统所[72]等单位的相关课题组也利用聚焦氦离子束技术实现了高质量YBCO约瑟夫森结的制备. 上述单个约瑟夫森结的研究结果表明, 氦离子辐照技术理论上可以用于实现大量串联的高温约瑟夫森结阵的制备, 有望用于液氮温区量子电压标准的实现. 实际上, 目前已经有利用氦离子辐照技术、针对电压标准应用开展的相关研究. 例如, Kasaei等[84]使用30 keV聚焦氦离子束技术在MgB2薄膜上制备了间隔紧密的平面约瑟夫森结阵列, 如图7所示, 他们制备的结阵由60个约瑟夫森串联而成, 这些结的临界电流之间的离散性小于3.5%. 结参数的均匀性可以保证与微波偏置的同步, 在该结阵样品他们确实观测到了平坦的大幅度夏皮罗跳跃电流(如图8所示). 该工作显示出了聚焦氦离子束辐照技术在包括量子电压标准在内的约瑟夫森结阵电路应用中的潜力.

      理论上利用聚焦氦离子束辐照制备YBCO超导结阵芯片是实现液氮温区量子电压基准的一种很有潜力的方案. 首先, 辐照结方案相比于晶界结在结一致性和参数可控性上更具优势, 利用He+辐照剂量可以精确调控约瑟夫森结的$ {I}_{{\mathrm{c}}} $, $ {R}_{{\mathrm{n}}} $以及$ {T}_{{\mathrm{c}}} $, 同时通过调节剂量可以制备出不同类型的结. Cybart等[70]研究结果表明, YBCO薄膜厚度在30 nm, He+辐照剂量小于2×1016 ions/cm2时, 所制备的结临界电流随温度变化呈现$ {(1-T/{T}_{{\mathrm{c}}})}^{2} $的关系, 结伏安特性曲线反映出Andreev反射主导了结电输运过程, 表明结是SNS类型结; 而He+辐照剂量大于6×1016 ions/cm2时, 约瑟夫森电流在结输运电流中起主导作用, 表明结是SIS类型结. 其次, 利用辐照结任意写入的特点理论上可以轻松将结的间距做到100 nm以内, 从而实现高密度的结阵, 同时在设计复杂紧凑的二维结阵芯片上具有较高自由度. 通过工艺摸索、芯片设计以及配套量子电压系统的研制, 未来很有可能发展出可以随时随地提供高精度计量校准服务的结构更加紧凑、可在液氮温区运行的约瑟夫森电压标准系统, 在利用更少约瑟夫森结的脉冲驱动的交流量子电压标准、量子电压噪声源甚至约瑟夫森任意波形发生器上发挥作用. 然而, 利用这种方法在YBCO超导材料上实现量子电压标准的可行性目前还未有实验上的验证. 同时, 从量子电压台阶线宽、标准电压数值的不确定度等指标来看, 目前He+辐照结的相关实验结果仍较为初步, 未来还需要通过优化结参数、减少测量噪声、增大微波耦合来实现更优异的电压台阶信号. 除此之外, 实用化的高温量子电压标准需要性能稳定的量子电压芯片. 然而, 有研究指出He+辐照结的性质会随时间改变[85], 具体表现为临界电流随时间而增加并慢慢趋于饱和, 这就可能导致生成的量子电压准确性受到影响. 不过, 该研究也同时指出可以通过原位退火来稳定He+辐照结的参数. 总而言之, 未来对这些问题更加深入全面的研究将会为实用化的高精度高温量子电压标准的实现带来新的可能性.

    6.   结　论

    • 在约瑟夫森电压标准被确立为世界范围内用于电压量值复现与传递标准的三十多年以来, 基于约瑟夫森结阵的量子电压芯片的制备以及电压标准系统的整体研发受到了全世界研究者们的广泛关注和大量的研究. 对于基于低温超导材料的工作在液氦温区的量子电压标准技术, 得益于低温超导材料的特性以及与传统半导体制造技术相兼容的芯片制备技术, 目前低温量子电压标准系统已经可以实现10–9量级或更低的电压不确定度. 对于基于高温超导材料的可工作在液氮温区的量子电压标准, 目前最常用的双晶结技术制备的高温超导量子芯片在1 V和10 V水平上的直流量子电压测量中的最好指标已经可以达到10–8量级的不确定度, 但由于高温超导材料本身超导相干长度极短的物理特性, 这一技术发展仍存在难点与挑战, 主要在于难以实现结临界电流一致性非常好的大规模结阵列的制备. 除了双晶结技术之外, 聚焦氦离子辐照技术由于可以实现直接在超导材料中写入约瑟夫森结, 节省工艺步骤, 同时还可以对目标区域的高温超导材料的临界电流进行精确控制, 因此理论上更容易扩展到大规模、参数一致性好的结阵制备中. 随着针对液氮温区可编程量子电压标准研究的开展, 聚焦氦离子辐照技术制备约瑟夫森结的工艺方法和专门技术将会逐步建立和成熟, 未来有希望利用这一技术实现与低温量子电压芯片相当的约瑟夫森结阵集成度.

      高温超导约瑟夫森电压的发展依赖于切实的应用需求和相关技术的进步, 而高温超导体的物理特性直接限制了其标准的快速发展和相关应用. 尽管如此, 国内外研究机构依然在对高温超导量子电压进行持续研究, 积累了宝贵的理论和实验的相关经验, 该领域实现了螺旋上升式的发展. 我们相信, 有了前人对于高温超导电子学领域的相关沉淀和探索, 结合现如今半导体工艺的快速发展, 未来基于高温超导的约瑟夫森电压表标准一定会在更广阔的领域实现应用和落地, 从而满足科学研究、现代工业以及国防尖端装备研制中对计量装置的可移动、高精度的要求.

    参考文献 (85)

目录

/

返回文章
返回