首页
登录
注册
-
磁约束核聚变是解决人类能源问题的根本途径之一[1]. 托卡马克是当前国内外广泛研究的可控磁约束核聚变装置. 偏滤器靶板热流控制与芯部约束兼容性是托卡马克等离子体研究的前沿关键物理问题. 它是一个非平衡态复杂系统[2], 宏观磁流体不稳定性与微观不稳定性同时存在, 且时间、空间尺度跨度巨大. 它所涉及不同区域物理现象的物理机制十分复杂, 包含复杂磁场位形下的粒子输运、多粒子碰撞、电磁湍流等物理过程. 目前单个物理模型难以定性描述这种多尺度、复杂的系统性行为, 因此需要采用集成模拟方法开展相关物理研究. 通过向偏滤器靶板区注入杂质等方法实现偏滤器脱靶是偏滤器靶板热流控制的主要手段之一, 偏滤器脱靶能够有效降低靶板热负荷, 延长靶板材料使用寿命. 研究脱靶与芯部等离子体的兼容性, 为探索新的聚变堆运行模式和物理机制提供了重要的研究方向.
在实验方面, 在DIII-D装置上进行了边界局域模ELM控制与偏滤器脱靶的研究[3], EAST装置上已开展了在高极向比压
$ {\beta }_{{\mathrm{p}}} $ 条件下完全脱靶与芯部约束能力改善的实验研究[4]. 偏滤器脱靶期间的能量沉积测量很重要, 孟令义[5]分析了能量沉积烧蚀对靶板探针诊断测量和杂质注入对脱靶影响的实验研究. HL-2A 装置目前已经开展了多炮包含 ELM与 H 模脱靶相互作用的实验研究[6], 积累了较为丰富的实验数据. 秦晨晨等[7]基于不同三角形变下的平衡位形, 研究了负三角形变位型条件下剥离气球模的非线性演化特征.借助国内外发展成熟的集成模拟平台, 开展集成模拟研究是分析H模脱靶与芯部等离子体兼容性这一多物理过程, 探究其物理机制的重要方法[8]. 针对等离子体核心区域与边缘区域的相互作用机制, Luce等[9]进行了深入探讨与全面总结, 重点分析了湍流输运过程与边界约束条件之间的内在联系. 在众多集成模拟平台中, 由欧洲聚变联盟构建的IMAS(集成建模与分析套件)[10]以及美国研究团队设计的OMFIT(一体化集成建模框架)[11]具有代表性. 在芯边耦合模拟方面, Zheng等[12]研究了EAST装置上芯部与偏滤器等离子体的耦合特性, 提出了改进的边界条件模型. OMFIT是由美国通用原子(General Atomics)使用IDL (interactive data language)语言和 Python 语言开发的开源集成模拟平台, 该平台为各类物理模拟程序提供了标准化的数据交互接口、提升了数据输入输出效率、优化了数据交换机制, 使整体计算流程更为简洁高效. 在DIII-D的kineticEFIT工作流[11]及罗一鸣等[13,14]搭建的工作流中, 使用OMFIT集成模拟平台集成的子模块主要包含ONETWO[15], EFIT[16], TGYRO[17]等大型物理模拟代码. ONETWO程序实现了多个辅助计算程序的功能集成, 包括NUBEAM程序[18]计算中性束注入功率、GENRAY程序[19]处理低杂波加热[20]、TORAY程序[21]模拟电子回旋波加热. 它将辅助加热子程序计算的沉积功率和驱动电流作为输运方程的源项输入, 将辅助加热子程序计算的能量通量、动量通量和粒子通量作为其目标通量.
OMFIT目前虽然集成了多个刮削层和台基程序, 包括EPED[22], UEDGE[23], SOLPS[24]等, 但是它们的物理模型复杂、计算量大、消耗时间长和集成效率低, 亟需发展台基-刮削层边界神经网络快速集成程序. 因此, 迫切需要引入新的技术以提高其计算效率与台基结构预测的准确性, 机器学习方法是一个高效的解决方案. 神经网络模型在磁约束核聚变领域具有广泛的应用前景. Liang等[25]基于HL-2A 装置的高约束H模放电实验数据, 开发了针对高约束模时段的识别算法, 得到了可靠的识别结果. 刘自结[26]在EAST上构建了CAR(conditional autoregressive prior probability model)条件自回归先验概率模型, 实现了等离子体电流密度剖面的重建算法. 汪金鑫[27]利用神经网络方法, 借鉴以往托卡马克装置破裂预测的研究经验, 将机器学习方法成功应用至EAST装置. Zhu等[28]基于深度学习的方法, 在 HL-2A 装置上也开发出了一套鱼骨模识别算法, 经验证该套识别方法识别准确率较高. 本文将自主研发的昆仑台基-刮削层神经网络KLNN模型, 成功集成到OMFIT平台上, 利用全连接神经网络(fully connected neural networks, FCNN)技术训练的边界区域台基结构快速计算程序, 对HL-2A高约束脱靶和芯部约束兼容性开展大规模集成模拟研究.
本文论述结构分为以下5个部分: 第1部分为引言; 第2部分内容主要介绍本文基于OMFIT集成模拟平台所采用的工作流, 及工作流中负责不同区域和时空尺度下程序模块的物理模型; 第3部分内容介绍H模脱靶实验结果; 第4部分主要包含3个方面的研究内容, 即初始等离子体剖面构建、集成模拟计算结果和芯部不稳定性分析; 第5部分为总结和讨论.
-
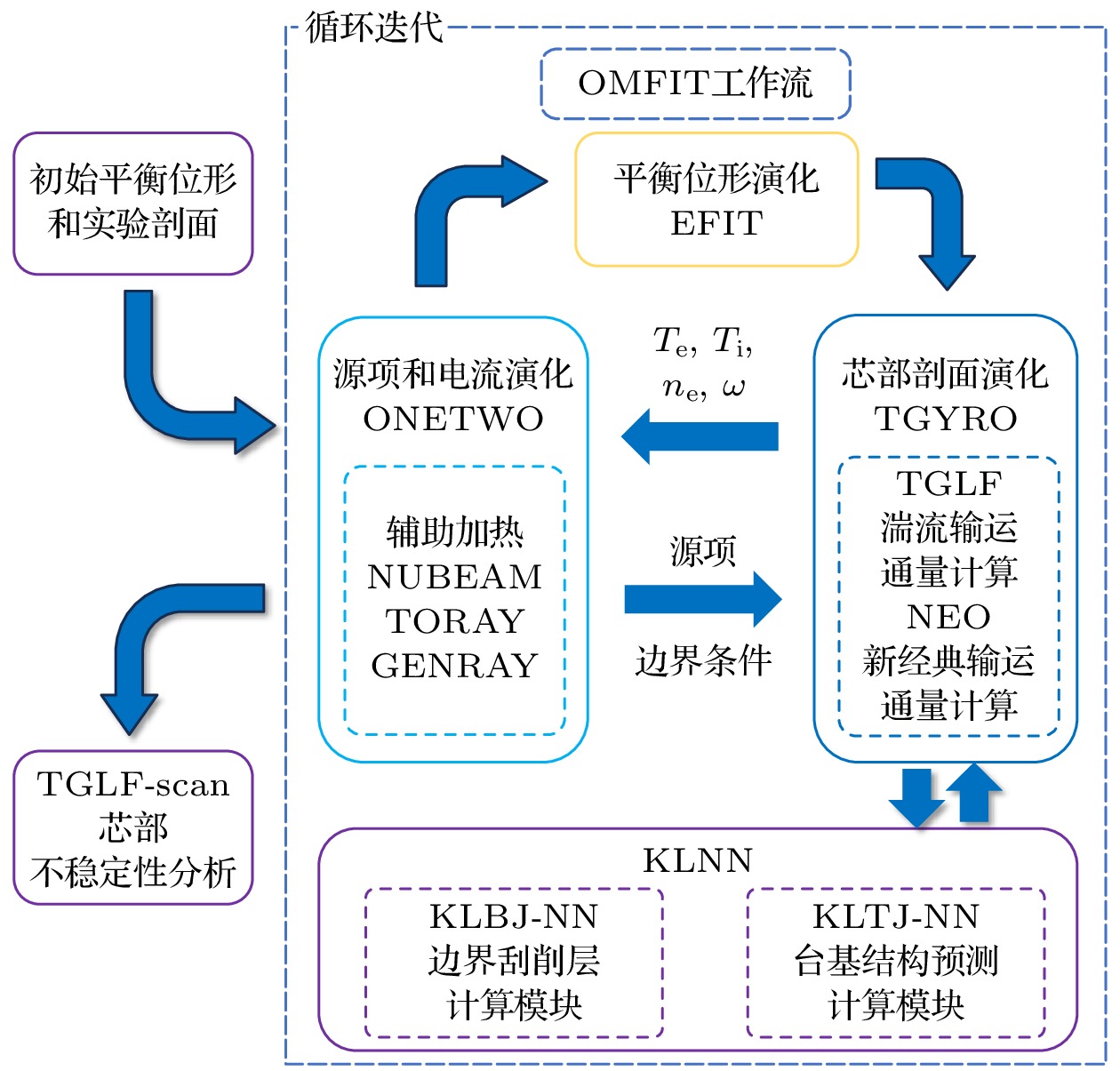
本文基于OMFIT平台搭建的包含KLNN模块的工作流如图1所示. 分成实验数据处理与剖面的构建、整体实验结果的集成模拟迭代计算与验证以及芯部不稳定性分析[29]三部分. 在上述提到的工作流中, 包含电流演化及热源计算程序ONETWO、平衡演化程序EFIT、边界-台基结构计算程序KLNN以及芯部动理学剖面演化程序TGYRO. 本工作流程重点在于H模脱靶条件下的芯部输运、台基和刮削层的集成模拟不稳定性分析.
具体工作流详见图1所示, 将初始的位形、平衡文件及物理参量经合理自洽的处理后作为工作流输入量, ONETWO模块通过调用各项辅助加热程序计算相应的能量、动量及粒子源通量和能量损失, 进而根据上述输出结果计算出等离子体的剖面, 进一步将计算得出的电流剖面和压强剖面信息传递至EFIT平衡演化程序重新对平衡位形进行计算. 然后, 新的平衡位形代入湍性输运程序TGYRO进行动理学剖面演化循环迭代计算直至收敛. 由于TGYRO程序适用于对芯部物理湍性输运[30]分析, 缺乏等离子体边界信息, 因此我们开发的KLNN程序对台基-边界区域的物理量进行计算并输出台基结构(台基高度和宽度)及边界物理量(电子密度、电子温度、台基顶部有效电荷数、台基底部有效电荷数), 为输运程序提供边界条件. ONETWO所计算的热源及电流剖面也进一步为TGYRO和KLNN的计算更新剖面信息.
具体的集成模拟工作流程如下:
1)选取HL-2A装置39007炮放电平顶段的时刻
$ {t}_{0}=1320\;{\mathrm{m}}{\mathrm{s}} $ , 从实验诊断系统获得的主等离子体剖面诊断数据(电子温度$ {T}_{{\mathrm{e}}} $ 、电子密度$ {n}_{{\mathrm{e}}} $ 、离子温度$ {T}_{{\mathrm{i}}} $ 和离子环向旋转速度$ \omega $ ), 经插值与曲线拟合的方法, 将该时刻构建的实验剖面与位形信息导入至OMFIT集成平台;2) ONETWO程序调用1)的剖面与平衡位形信息演化电流分布情况, 同时由ONETWO程序调用辅助加热程序计算热源项与损失项;
3)将ONETWO程序计算得到的粒子压强分布剖面和电流演化分布剖面传递给平衡演化程序EFIT, 由EFIT根据ONETWO 计算得到的极向电流通量和其自身倒数乘积的剖面
$ F{F}' $ 与压强剖面$ {P}' $ 计算新的平衡位形;4)将KLNN程序的昆仑边界神经网络KLBJ-NN程序通过自主搭建的边界神经网络快速计算程序计算所得的台基底部的电子密度和电子温度、台基顶部和台基底部的有效电荷数
$ {Z}_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ 以及昆仑台基神经网络KLTJ-NN程序通过等离子体电流、环向磁场强度和安全因子$ {q}_{95} $ 作为输入量计算得出台基高度和宽度以及台基底部至等离子体边界的剖面;5)将步骤2)得到的电流源和能量源信息和步骤3)得到的新的平衡位形以及步骤4)得到的台基结构信息传递给芯部剖面演化与通量计算程序TGYRO, 由TGYRO程序根据温度密度剖面的小半径方向梯度分别计算新经典输运通量和湍性输运通量, 再根据 ONETWO 计算结果的源项信息计算出目标通量, 通过调节剖面梯度来匹配二者, 以此演化等离子体动理学剖面;
6)将KLNN程序计算的台基区剖面传输至TGYRO程序, 与芯部等离子体剖面相结合, 得到归一化小半径上各主要物理参数完整的等离子体动理学剖面, 并将更新后的主等离子体剖面(电子温度
$ {T}_{{\mathrm{e}}} $ 、电子密度$ {n}_{{\mathrm{e}}} $ 、离子温度$ {T}_{{\mathrm{i}}} $ 和离子环向旋转速度$ \omega $ )传输给ONETWO;7)基于更新后的各项物理参数的动理学剖面和平衡位形, 循环第2)—6)步工作流的操作流程, 在迭代至第N个循环后, 等离子体各参数的动理学剖面计算结果均达到收敛(收敛条件为ONETWO目标通量与TGYRO程序计算的总通量相匹配)后, 得到一个最终稳态的解.
-
在本次工作流中, 通过求解计算Grad-Shafranov方程得到二维的平衡位形, 初始和迭代过程中的压强及电流由电子离子和杂质离子的温度密度计算得到.
ONETWO程序基于离子密度演化方程、电子能量守恒方程、离子能量守恒方程、环向动量平衡方程、法拉第定律计算极向磁场的演化方程计算粒子输运. 自举电流采用Sautor模型[14]计算, 驱动电流由辅助加热程序TORAY计算. ONETWO程序通过由Hinton-Chang公式[14]和GLF23准线性程序[31]来分别计算新经典输运通量和湍性输运通量. 在对粒子源的计算中, 可以计算器壁循环和边界气体(杂质)注入提供的粒子源, 以及在被调用的NUBEAM中计算中性束带来的加料效应. 在能量源的计算中, 需要对欧姆加热、辅助加热、聚变加热以及辐射损失进行计算. 其中, 辅助加热由TORAY, GENRAY和NUBEAM程序模块来计算, 聚变加热采用的是BoschHale公式[32], 辐射损失由平均离子模型来计算. 动量源则来源于中性束注入(neutral beam injection, NBI), 同样由NUBEAM程序计算, 为ONETWO提供动量源项输入. 其中, NUBEAM是计算中性束注入的蒙特卡罗程序. TORAY程序是用来计算电子回旋波驱动电流的射线追踪程序, 该程序采用Cohen简化模型[15], 分别利用格林函数计算射频波电流驱动效率, 用半相对论响应函数计算电流驱动, 碰撞算子采用高速度模型.
在集成模拟工作流中, TGLF程序通常利用准线性程序计算湍性输运通量, TGYRO通过调用其计算得到的结果进行剖面演化计算. 新经典物理程序NEO[33]是直接从第一性原理出发求解漂移动力学方程的初值程序. 它采用线性 Fokker-Planck碰撞算子[34]与漂移-动力学方程(drift-kinetic equation, DKE)[35]相结合推导的方程. 由于考虑了粒子的漂移运动(由于电场、磁场不均匀性等引起的粒子漂移)和碰撞效应, NEO程序可以更准确地描述等离子体粒子的行为, 从而得到分布函数, 进而得到相应的新经典输运系数[36].
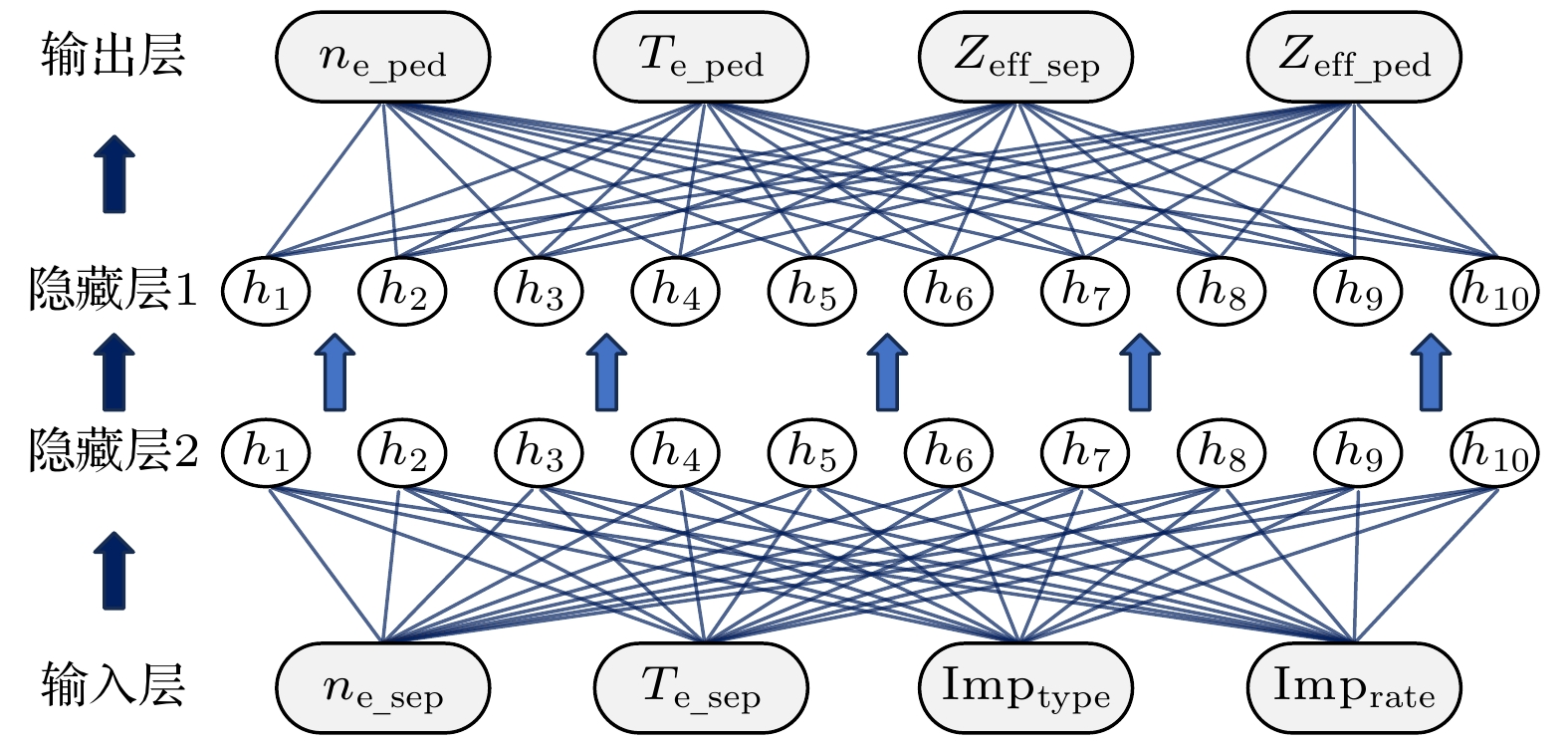
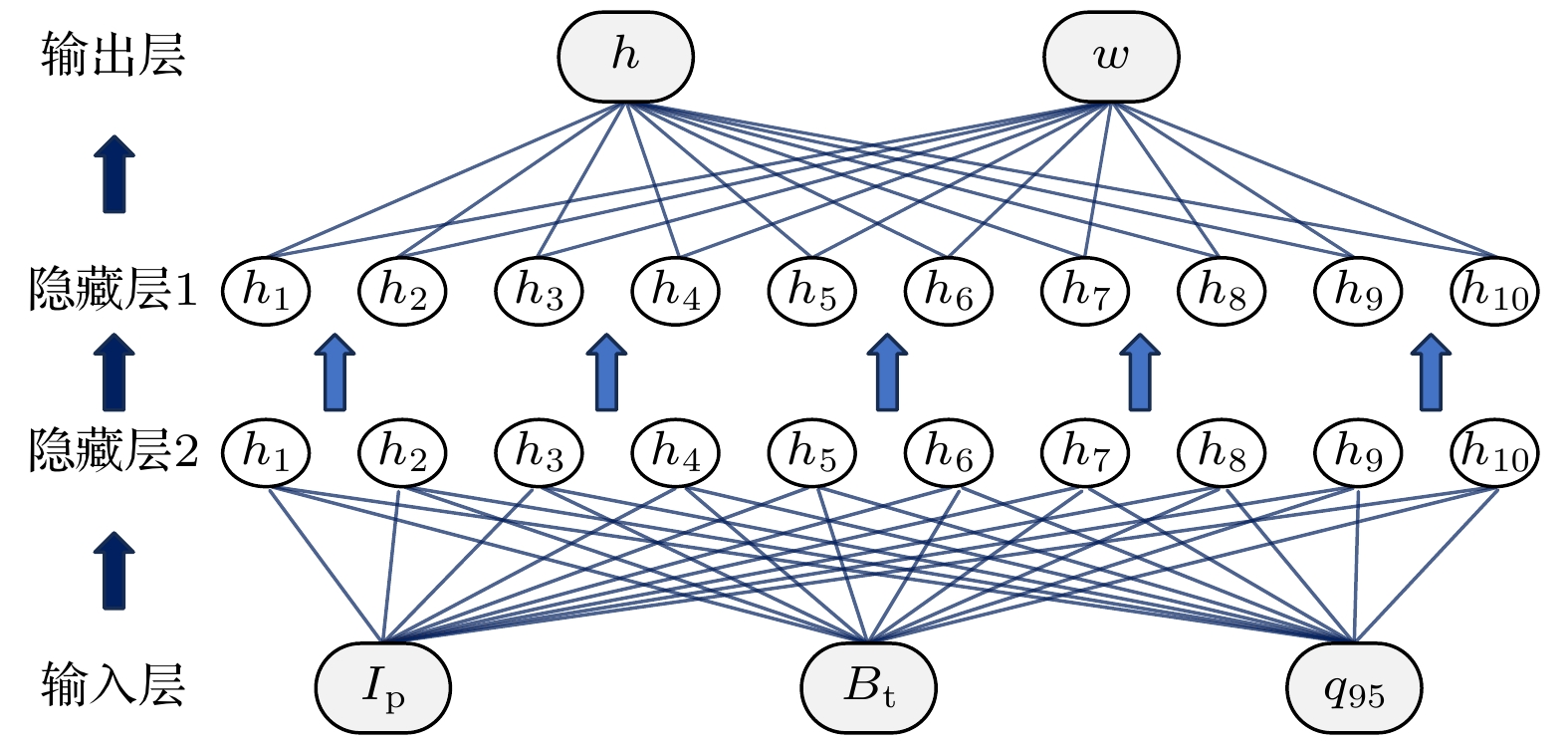
本文自主研发的KLNN程序结合HL-2A装置前期积累的大量实验数据, 针对HL-2A装置的H模脱靶实验数据进行扫描, 形成数据集. KLNN程序作为OMFIT集成模拟的新增模块, 用于计算边界等离子体动理学剖面和台基结构. 该程序为自主研发的一个神经网络快速计算程序, 解决了传统EPED程序计算速度慢、迭代模拟时间长、极大耗费计算机时的问题, 以及国内缺少访问EPED程序权限等客观制约问题. 它分别基于BOUT++和SOLPS模拟程序获得台基和刮削层等离子体参量, 然后分别提供给KLTJ-NN程序和KLBJ-NN程序. SOLPS程序提供扫描后的杂质种类
$ {{\mathrm{I}}{\mathrm{m}}{\mathrm{p}}}_{{\mathrm{t}}{\mathrm{y}}{\mathrm{p}}{\mathrm{e}}} $ 、杂质注入速率$ {{\mathrm{I}}{\mathrm{m}}{\mathrm{p}}}_{{\mathrm{r}}{\mathrm{a}}{\mathrm{t}}{\mathrm{e}}} $ 、边界电子密度$ {n}_{{\mathrm{e}}\_{\mathrm{s}}{\mathrm{e}}{\mathrm{p}}} $ 和边界电子温度$ {T}_{{\mathrm{e}}\_{\mathrm{s}}{\mathrm{e}}{\mathrm{p}}} $ 等数据. 参照Kates-Harbeck等[37]搭建的全连接神经网络结构及方法, 训练边界区域快速计算程序KLBJ-NN的物理参数训练集数据, 经不断优化超参数后将计算得到的台基顶部电子温度$ {T}_{{\mathrm{e}}\_{\mathrm{p}}{\mathrm{e}}{\mathrm{d}}} $ 、密度$ {n}_{{\mathrm{e}}\_{\mathrm{p}}{\mathrm{e}}{\mathrm{d}}} $ 、台基顶部有效电荷数$ {Z}_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}\_{\mathrm{p}}{\mathrm{e}}{\mathrm{d}}} $ 、台基底部有效电荷数$ {Z}_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}\_{\mathrm{s}}{\mathrm{e}}{\mathrm{p}}} $ . 结合BOUT++程序提供的等离子体总电流$ {I}_{{\mathrm{P}}} $ 、环向磁场强度$ {B}_{{\mathrm{t}}} $ 、边界安全因子$ {q}_{95} $ 作为全连接神经网络技术训练的边界区域台基结构快速计算程序KLTJ-NN的输入. KLTJ-NN同样参照Kates-Harbeck等[37]搭建的神经网络全连接层结构与数据处理方法, 基于HL-2A装置H模实验积累的实验数据库(包含每炮实验总电流$ {I}_{{\mathrm{P}}} $ 、环向磁场强度$ {B}_{{\mathrm{t}}} $ 、边界安全因子$ {q}_{95} $ 参数下对应的台基高度和宽度)进行训练, 经平滑插值拟合快速计算得到边界区域台基结构(台基高度h和台基宽度w)作为输出. KLBJ-NN程序用于计算边界等离子体动理学剖面, SOLPS程序根据HL-2A装置超过2000个H模脱靶的算例数据(包含以下边界物理量: 中平面电子密度剖面、中平面电子温度剖面、中平面有效电荷剖面、中平面杂质密度剖面、台基底部充气位置、粒子种类、充气速率、抽气位置、抽气速率、环向磁场强度、等离子体电流、安全因子)进行参数扫描. SOLPS程序固定芯部边界输入功率为588 kW、抽气速率$ {12\;{\mathrm{m}}}^{3}/{\mathrm{s}} $ 、氘气注入速率为$ 2\times {10}^{19}{\mathrm{个}}/{\mathrm{s}} $ , 进而扫描其他参数范围如下: 芯部边界电子密度$ (0.5—2.8) \times 10^{19} \; {\rm m}^{-3} $ 、杂质注入速率($ 2{\times 10}^{19}{\mathrm{个}}/{\mathrm{s}} $ 、$ 4\times {10}^{19}{\mathrm{个}}/{\mathrm{s}} $ 、$ 6\times {10}^{19} {\mathrm{个}}/{\mathrm{s}} $ )、杂质种类分别为氮气和氖气、杂质注入位置分别为内靶板和外靶板. KLBJ-NN程序与KLTJ-NN程序的神经网络结构分别如图2和图3所示. -
HL-2A装置主要的运行参数如下: 大半径
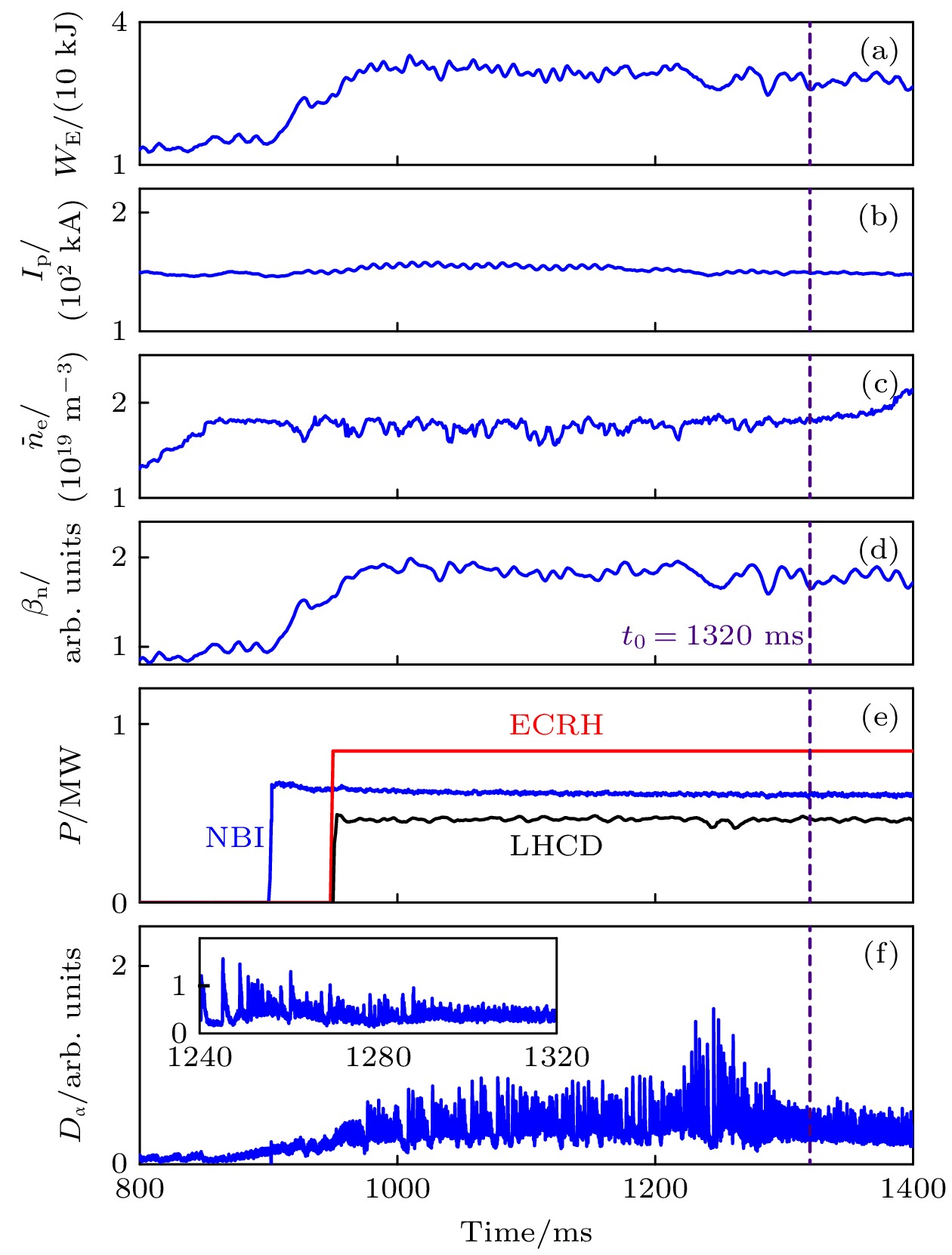
$ R = 1.65\;{\mathrm{m}} $ , 小半径$ a = 0.4\;{\mathrm{m}} $ , 电流平顶时间$ (1000— 3000)\;{\mathrm{m}}{\mathrm{s}} $ , 等离子体电流$ {I}_{{\mathrm{P}}}=(100—250)\;{\mathrm{k}}{\mathrm{A}} $ , 环向磁场$ {B}_{{\mathrm{t}}}=(1.0—1.8)\;{\mathrm{T}}, $ 等离子体密度$ (0.3—4.5)\times {10}^{19}\;{{\mathrm{m}}}^{-3} $ , ECRH加热功率为$ (1—2)\;{\mathrm{M}}{\mathrm{W}}(68{\mathrm{ }}\;{\mathrm{G}}{\mathrm{H}}{\mathrm{z}}) $ , 具备两条中性束束线, 加热功率为$ (1—2)\;{\mathrm{M}}{\mathrm{W}} $ , 低杂波耦合功率为$ (0.8—1)\;{\mathrm{M}}{\mathrm{W}} $ . 本节基于HL-2A的第39007炮高约束模脱靶放电进行模拟验证, 辅助加热方式有NBI加热、电子回旋波加热和低杂波耦合. 该炮下的等离子体主要放电参数如图4所示. 根据放电参数, 选取稳态运行阶段的等离子体平顶阶段下的某一时刻作为模拟时刻, 这里选取进入H模脱靶后$ 1320\;{\rm ms} $ 时刻. 该时刻具体放电参数见表1, 包括等离子体电流、纵场强度、芯部离子温度、芯部电子温度、芯部电子密度、电子线平均密度、Greenwald密度极限比值、安全因子q95、归一化比压$ {\beta }_{{\mathrm{n}}} $ 等, 实验值和集成模拟的初始输入值基本一致. 第39007炮采用常规偏滤器下单零位形放电, 采用加热系统: 两道总加热功率0.6 MW的NBI、0.85 MW加热功率的电子回旋波(electron cyclotron resonance heating, ECRH)、0.45 MW加热功率的低杂波电流驱动(lower hybrid current drive, LHCD).该实验于
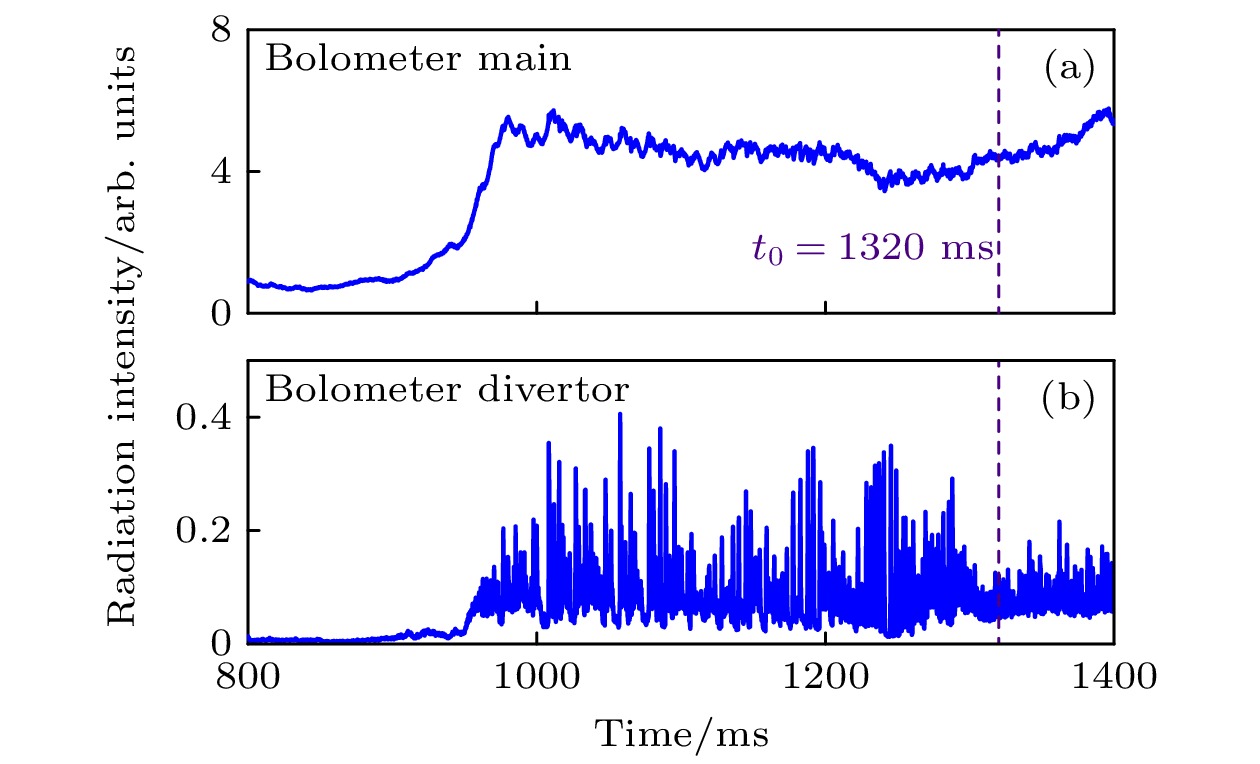
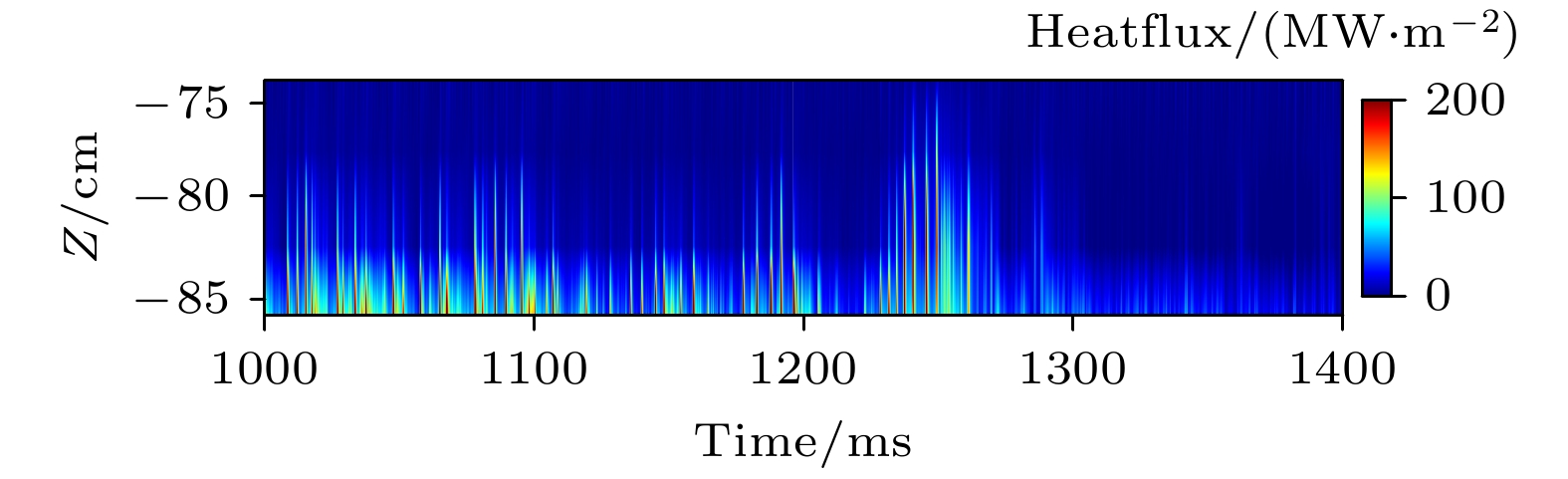
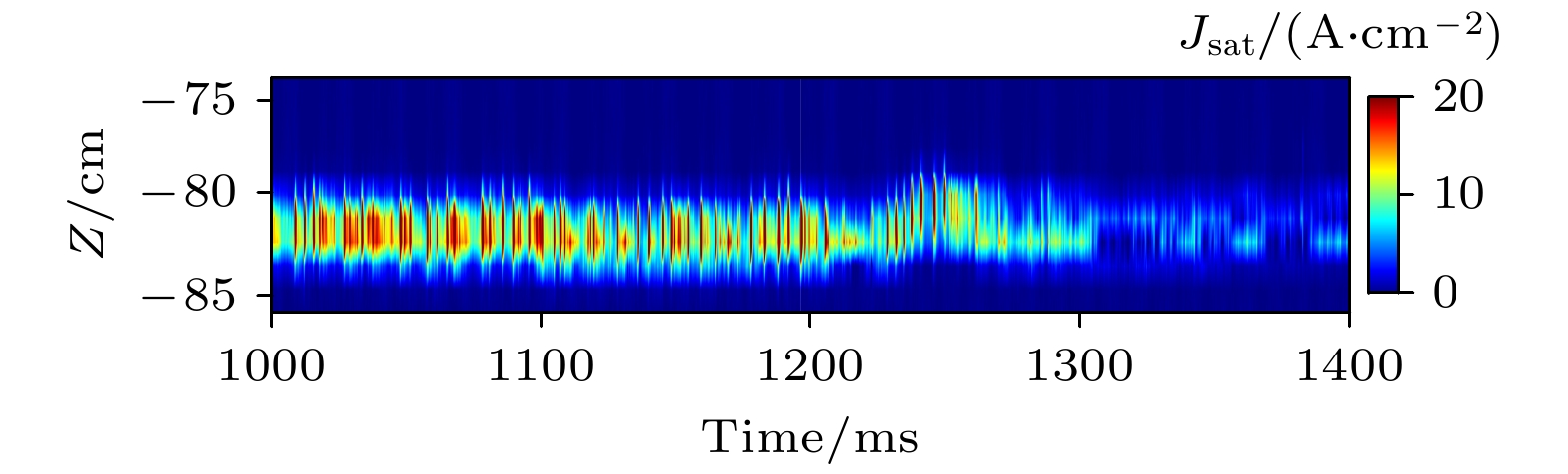
$ t=800{\mathrm{ }}\;{\mathrm{m}}{\mathrm{s}} $ 时刻开始持续不断注入杂质脉冲直至进入H模脱靶状态. 结合图4中辅助加热注入功率时间演化图4(e), 观察到等离子储能(图4(a))、电子线平均密度(图4(c))以及归一化比压$ {\beta }_{n} $ (图4(d))在$ t=950{\mathrm{ }}\;{\mathrm{m}}{\mathrm{s}} $ 时刻后得到明显提高,$ {D}_{{\mathrm{\alpha }}} $ 信号(图4(f))幅度明显增强. 上述实验现象表明在$ t=950{\mathrm{ }}\;{\mathrm{m}}{\mathrm{s}} $ 时刻等离子体开始进入H模放电运行模式. 图4(f)中$ {D}_{{\mathrm{\alpha }}} $ 信号在$ {t}_{0}= 1320{\mathrm{ }}\;{\mathrm{m}}{\mathrm{s}} $ 时刻变化幅度明显减弱、图5显示Bolometer辐射功率测量系统测得的辐射强度在偏滤器靶板区$ {t}_{0}=1320\;{\mathrm{m}}{\mathrm{s}} $ 时刻明显减弱, 进入H模后的$ (900— 1400)\;{\mathrm{m}}{\mathrm{s}} $ 时段内主真空室区辐射强度基本不变. 图6显示等离子体边界靶板探针测得的偏滤器靶板区的热流通量在约$ t=1300\;{\mathrm{m}}{\mathrm{s}} $ 时刻显著降低, 以及图7显示等离子体边界靶板探针测得的偏滤器靶板区的离子饱和流在约$ t=1300\;{\mathrm{m}}{\mathrm{s}} $ 时刻显著降低. 综合以上实验数据可以得到$ t=1300\;{\mathrm{m}}{\mathrm{s}} $ 开始进入H模脱靶状态. 进入脱靶后, 发现ELM的幅度有明显的减小, 可见脱靶对ELM的抑制有积极的作用. 如图4(a), (c), (d)中储能、电子线平均密度、归一化比压$ {\beta }_{{\mathrm{n}}} $ 的时间演化所示, 这些物理量在脱靶前后基本保持不变. 为了进一步分析脱靶前后芯部约束性能的变化, 选取H模脱靶后的$ 1300—1380\;{\mathrm{m}}{\mathrm{s}} $ 时段和脱靶前的$ 1100—1180\;{\mathrm{m}}{\mathrm{s}} $ 时段, 对储能、能量约束时间以及$ {H}_{98} $ 因子进行数据处理, 获得平均值+随机误差值(如脱靶后储能为27.8 ± 1.883). 对比发现脱靶后储能、能量约束时间以及$ {H}_{98} $ 因子较脱靶前略有降低, 其中储能、能量约束时间和$ {H}_{98} $ 因子分别下降4.8%, 4.5%和3.8% (表2). 由此可见, H模脱靶后偏滤器热负荷得到显著降低, 但是等离子体芯部约束性能并没有降低很多, 实现了偏滤器脱靶与芯部约束的兼容性. 为了进一步开展H模脱靶物理研究, 本文选取脱靶后$ {t}_{0}=1320{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}\;{\mathrm{m}}{\mathrm{s}} $ 时刻的实验数据, 开展H模脱靶状态下集成模拟和芯部不稳定分析研究. -
针对HL-2A装置第39007炮脱靶与芯部约束兼容性的实验结果, 选取脱靶后
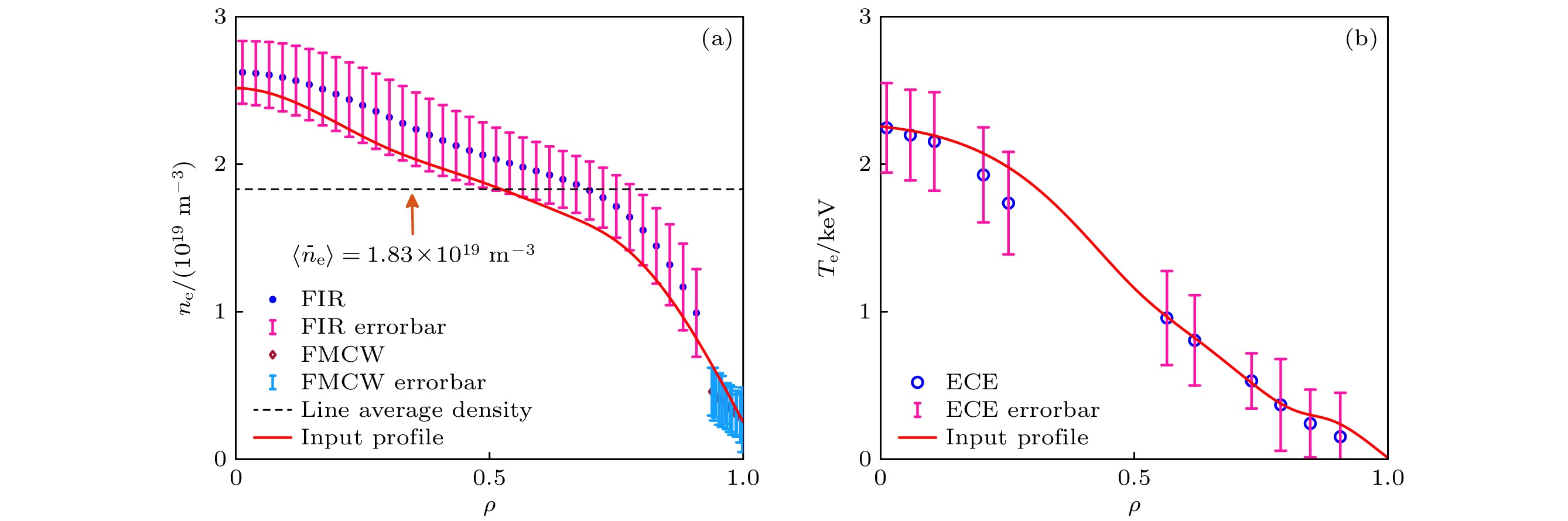
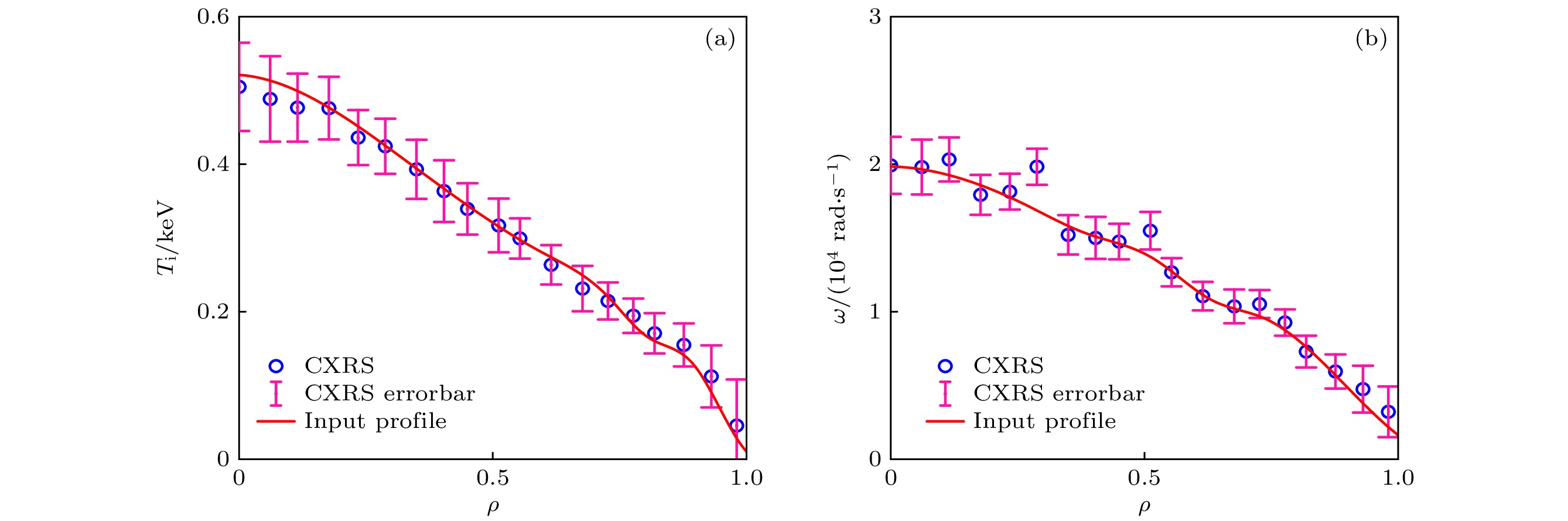
$ {t}_{0}=1320\;{\mathrm{m}}{\mathrm{s}} $ 时刻的等离子体参数诊断数据, 综合考虑多种诊断数据的物理自洽性, 合理构建了等离子体动理学剖面主要包含: 电子温度$ {T}_{{\mathrm{e}}} $ 、电子密度$ {n}_{{\mathrm{e}}} $ 、离子温度$ {T}_{{\mathrm{i}}} $ 和离子环向旋转角速度$ \omega $ . 各个物理参量的实验数据及其误差棒获取方式如下: 1)芯部电子密度误差棒实验数据来源于远红外激光干涉仪(FIR, 时间分辨率为1 ms)基于第220—2420 ms时段内每间隔1 ms产生的2200个时间切片下的实验数据, 经统计计算后95%置信区间下修正的随机误差; 2)边界电子密度误差棒实验数据来源于微波调频反射计(FMCW, 时间分辨率为0.1 ms)基于第1240—1400 ms时段内每间隔0.1 ms产生的1600个时间切片下的实验数据, 经统计计算后95%置信区间下修正的随机误差; 3)电子温度误差棒实验数据来源于电子回旋辐射(ECE, 时间分辨率为1 μs)基于第1319—1321 ms时段内, 每间隔1 μs产生的2000个时间切片测得的实验数据, 经统计计算后95%置信区间下修正的随机误差; 4)离子温度和旋转速度的实验数据误差棒是基于电荷交换复合光谱诊断系统(CXRS, 时间分辨率为5—50 ms)的实验误差棒, 在95%置信区间下修正的误差棒数据. 为使得各个实验参量总体误差保持在较小范围内, 等离子体温度密度实验剖面的自洽构建方法如下: 1) FIR测得的电子线平均密度与芯部电子密度剖面以及FMCW测得的边界电子密度剖面经平滑插值后构建出完整的初步电子密度剖面; 2) CXRS系统测量得到的等离子体离子温度数据和旋转速度经平滑插值后得到其剖面; 3)结合磁测量系统的逆磁线圈测得的归一化比压$ {\beta }_{{\mathrm{n}}} $ 、储能以及ECE诊断系统测得的电子温度实验数据, 自洽构建出电子温度剖面. 对第39007炮1320 ms时刻的电子密度、电子温度数据处理结果及自洽构建的剖面如图8所示, 离子温度和旋转速度的数据处理结果及自洽构建的剖面如图9所示. -
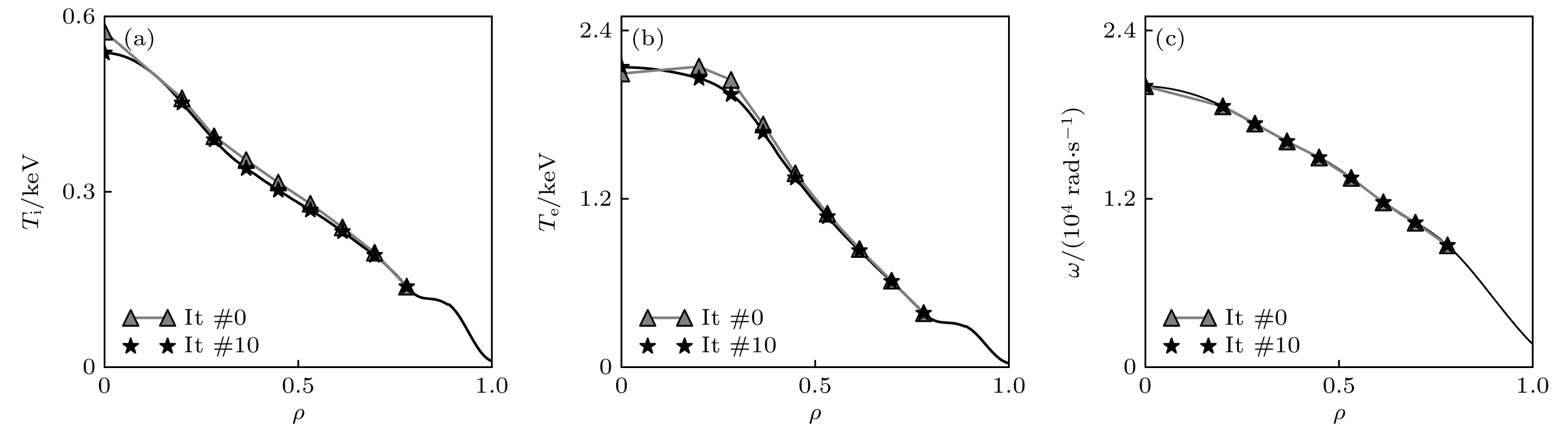
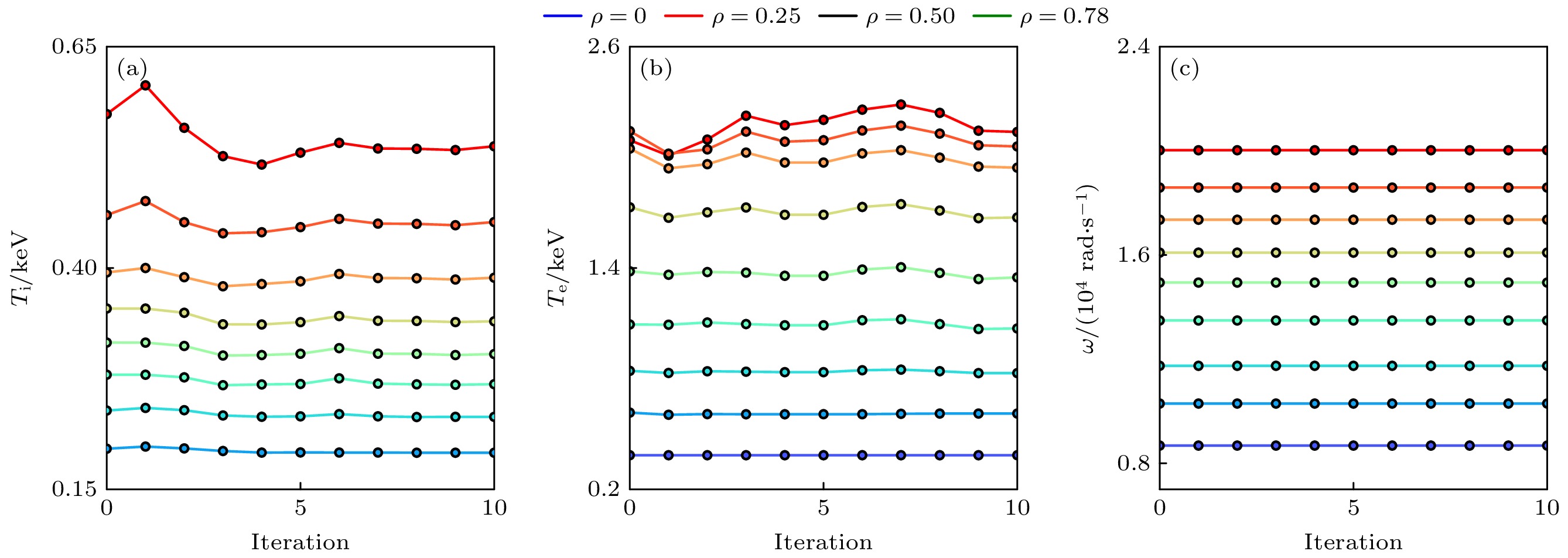
基于图1搭建的集成模拟工作流, 对HL-2A装置第39007炮
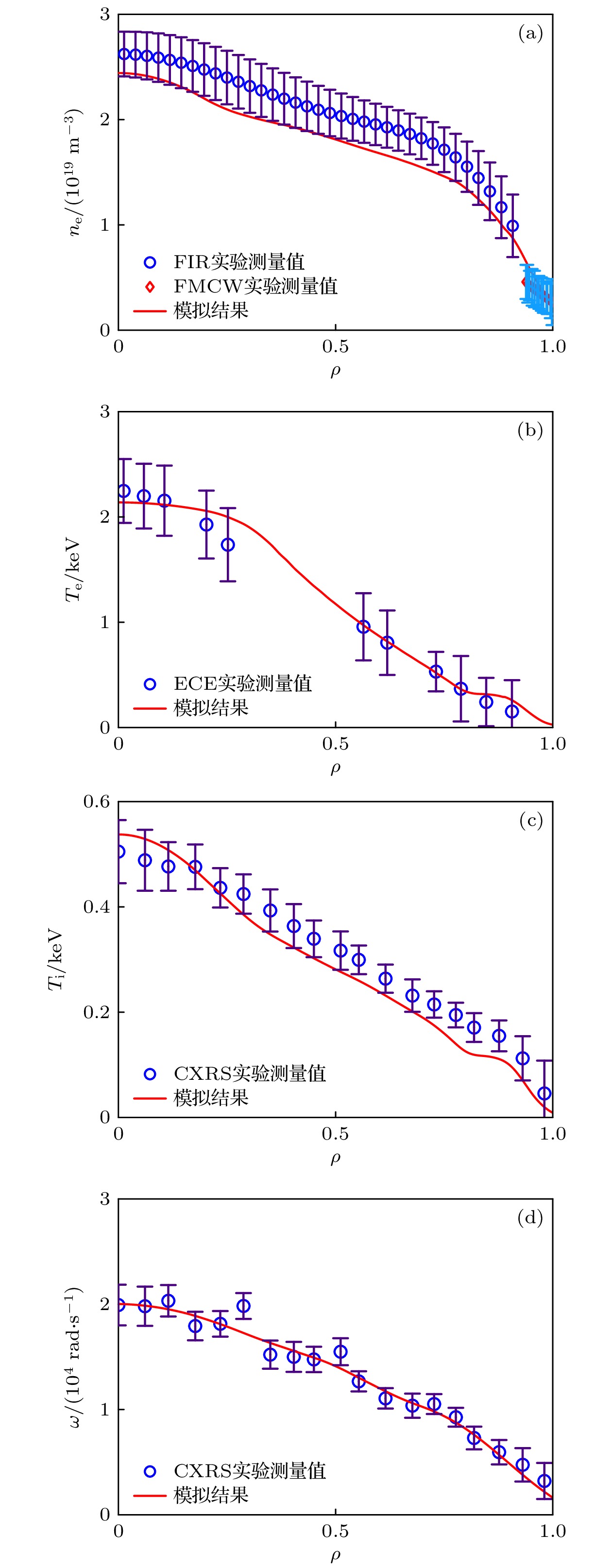
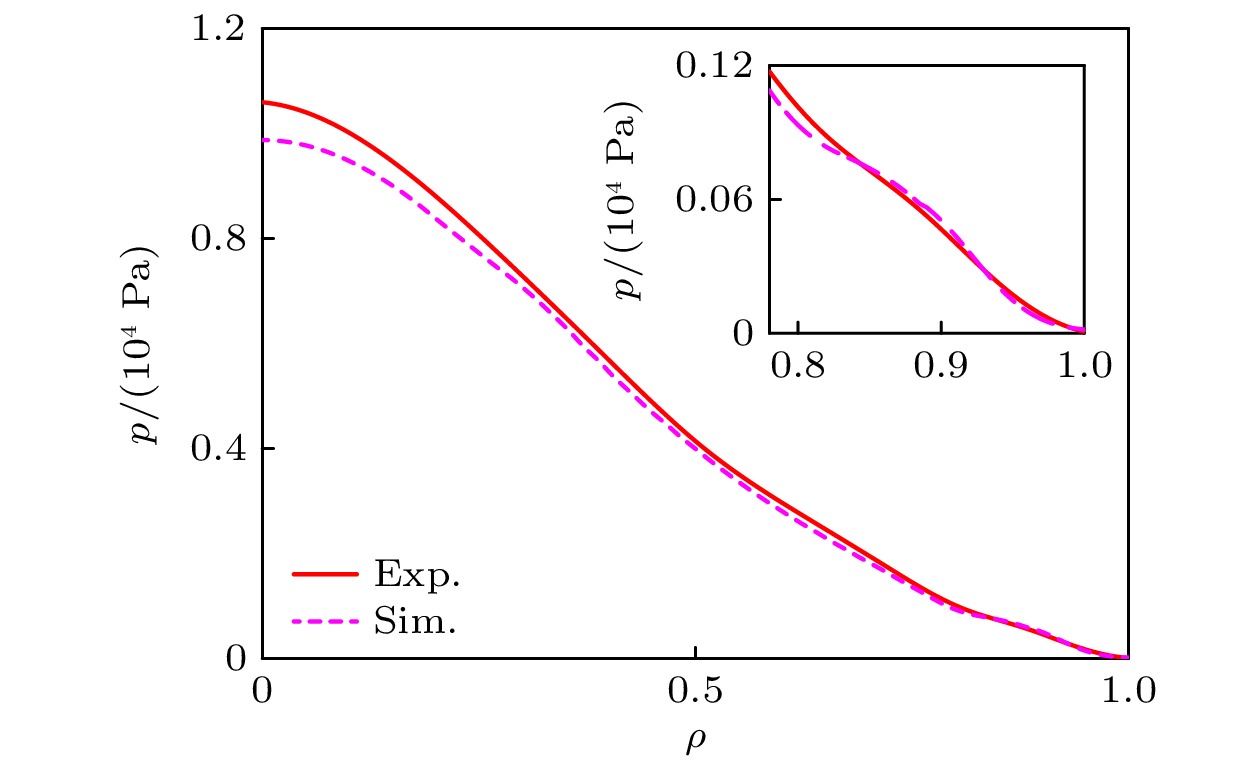
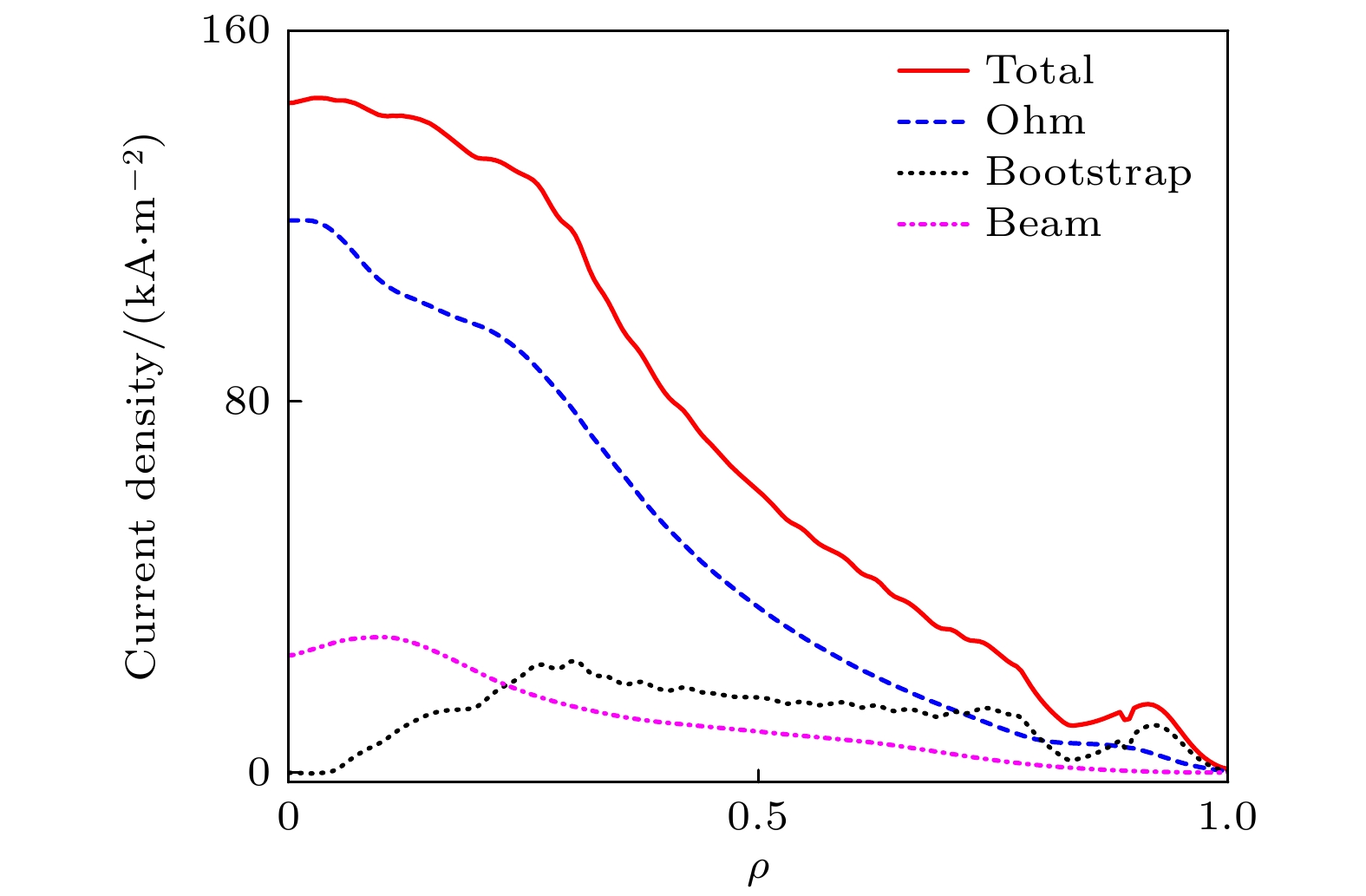
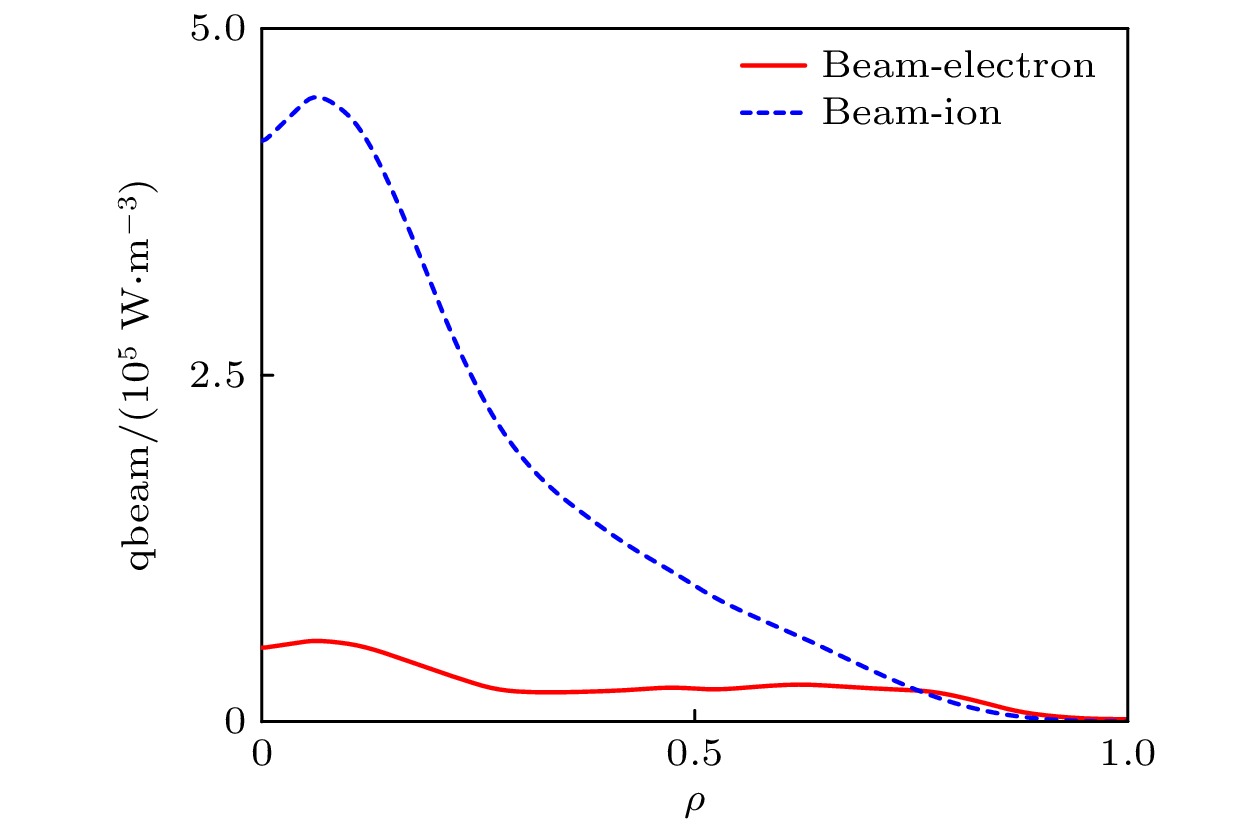
$ 1320\;{\mathrm{ }}{\mathrm{m}}{\mathrm{s}} $ 各剖面进行了实验与模拟的验证. 在确保集成模拟所采用的各种物理参量(如环向等离子体电流、放电位形、辅助加热方法及功率、加料速率、充杂种类、有效电荷数、辐射功率等)与实验严格保持一致的情况下, 开展自洽合理地模拟结果与实验结果对比, 并进一步分析解释实验. 在对第39007炮的模拟中芯部($ \rho \leqslant 0.78) $ 的湍性输运和新经典输运采用TGYRO程序进行迭代计算, 而在边界区域$ (0.78＜\rho \leqslant 1) $ 则通过KLNN程序进行快速计算. 经过多轮迭代后各项参数及动理学剖面如图10所示, 各项参数的初始迭代结果与最终迭代结果基本吻合; 图11中的不同径向位置下的最后10次参数迭代演化结果基本趋于收敛.从图12和图13(exp. 代表实验数据, sim. 代表模拟结果)可以看出, 温度、密度以及压强略有下降, 台基处电子温度、电子密度与实验剖面对照基本吻合, 离子温度模拟结果略微偏离误差棒范围, 但整体上与实验吻合得很好, 充分验证了上述搭建的集成模拟工作流的可信度. 在此基础上, 进一步计算该时刻下的各成分的电流剖面为工程和实验提供参考, 如图14所示(total代表总电流), 欧姆电流(ohm)为60%、自举电流(bootstrap)份额为27%、NBI驱动电流(beam)份额为13%. 在该炮的实验条件中, 由两束同向的 NBI注入对主等离子体同时进行加热, 总加热功率为0.6 MW. 从图15可以看出, 本炮放电采取的是NBI离轴注入方式, NUBEAM程序计算的NBI注入的能量沉积效应主要集中在离子成分, 沉积位置集中在归一化小半径
$ \rho =0.1 $ 位置附近. -
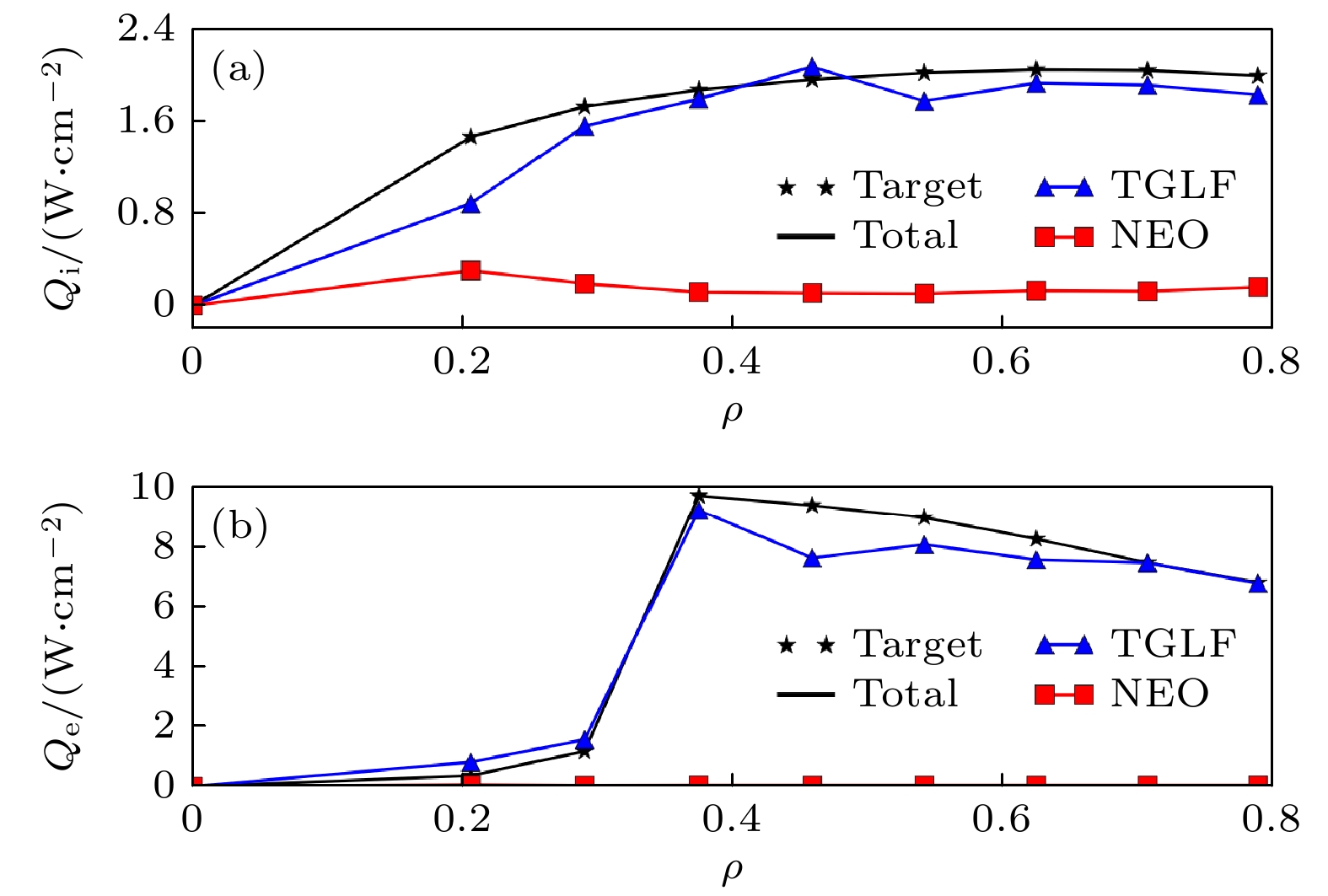
待各项物理模块的迭代计算达到稳态后, 对TGYRO程序计算得到的最终收敛结果开展进一步物理分析, 使用TGYRO计算小半径方向的能量通量如图16所示, TGYRO程序计算得到的总通量(total)与ONETWO程序计算的目标通量(target)相匹配.
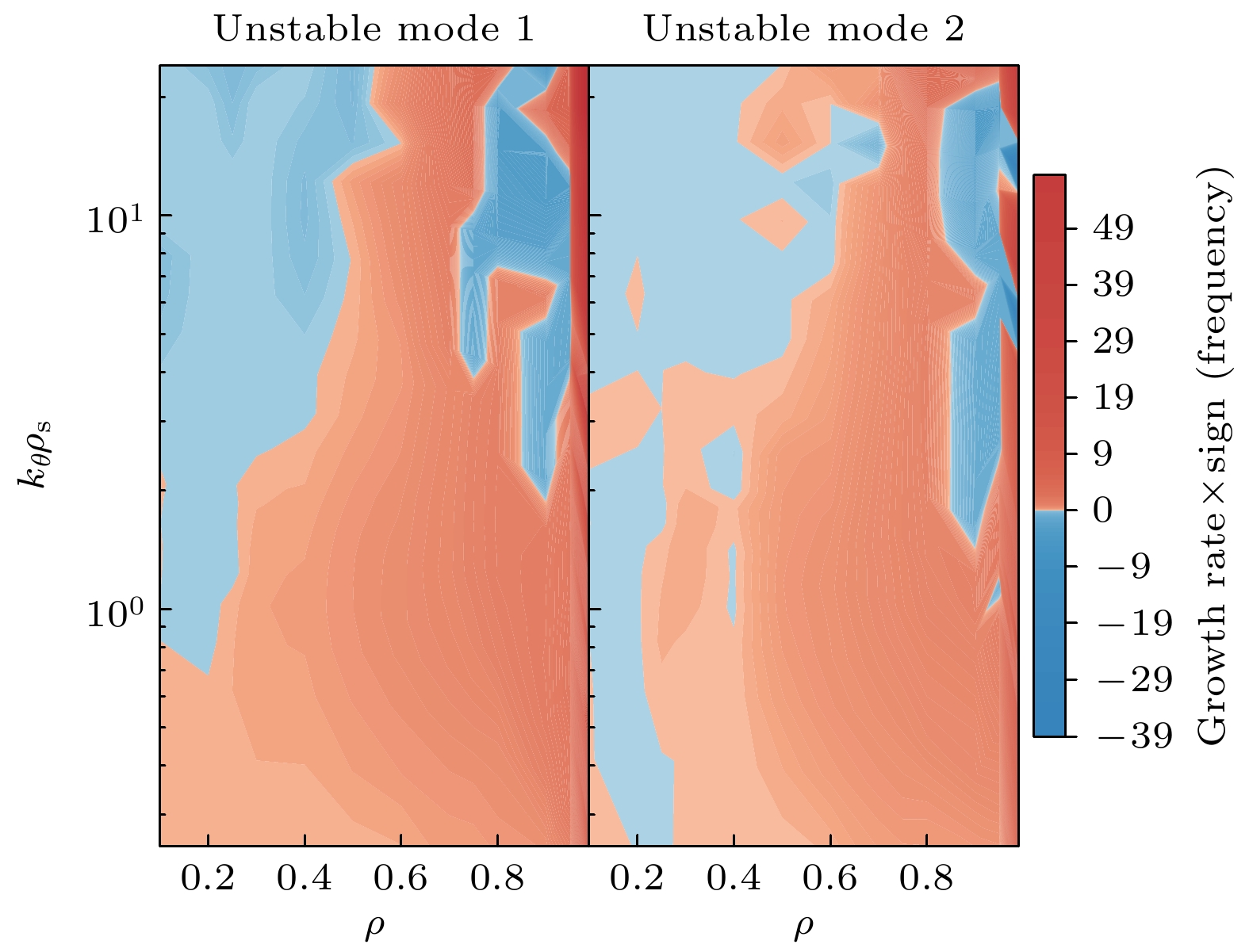
使用TGLF-scan程序扫描不同空间位置的本征模增长率, 得到
$ \rho =0.1—0.99 $ 区间内的两支最不稳定本征模式的图像扫描结果如图17所示, 图中横坐标表示归一化后的小半径ρ, 纵坐标为归一化极向波数$ {k}_{\theta }{\rho }_{s} $ , 颜色的深浅程度对应该区域的不稳定性增长率大小, 电子抗磁漂移方向$ (\omega > 0) $ 为红色(实频为正值$ (\omega > 0) $ 代表电子湍流), 离子抗磁漂移方向$ (\omega < 0) $ 为蓝色(实频为负值$ (\omega < 0) $ 代表离子温度梯度(ITG)湍流). 图17为不稳定性增长率与实频符号乘积的正负是由实频符号决定的. 通过实频符号来区分ITG和电子湍流, 我们可以对湍流进行模式识别. 根据参考文献[38,39], 我们定义归一化极向波数大于1为高模数. 归一化极向波数在1以下的$ 0 < \rho < 1 $ 区域内为电子抗磁漂移方向, 不稳定性以电子湍流为主; 在$ \rho =0.2—0.5 $ 及$ \rho =0.7—0.9 $ 、归一化极向波数$ {k}_{\theta }{\rho }_{{\mathrm{s}}} > 1 $ 区域内主要为离子抗磁漂移方向, 并伴有少量的电子抗磁漂移方向, 不稳定性以ITG为主, 伴有少量高模数的电子湍流; 在$ \rho =0.5—0.7 $ 区域, 以电子抗磁漂移方向为主, 不稳定性主要是以电子湍流主导[40].在经过TGLF-scan程序对不同位置
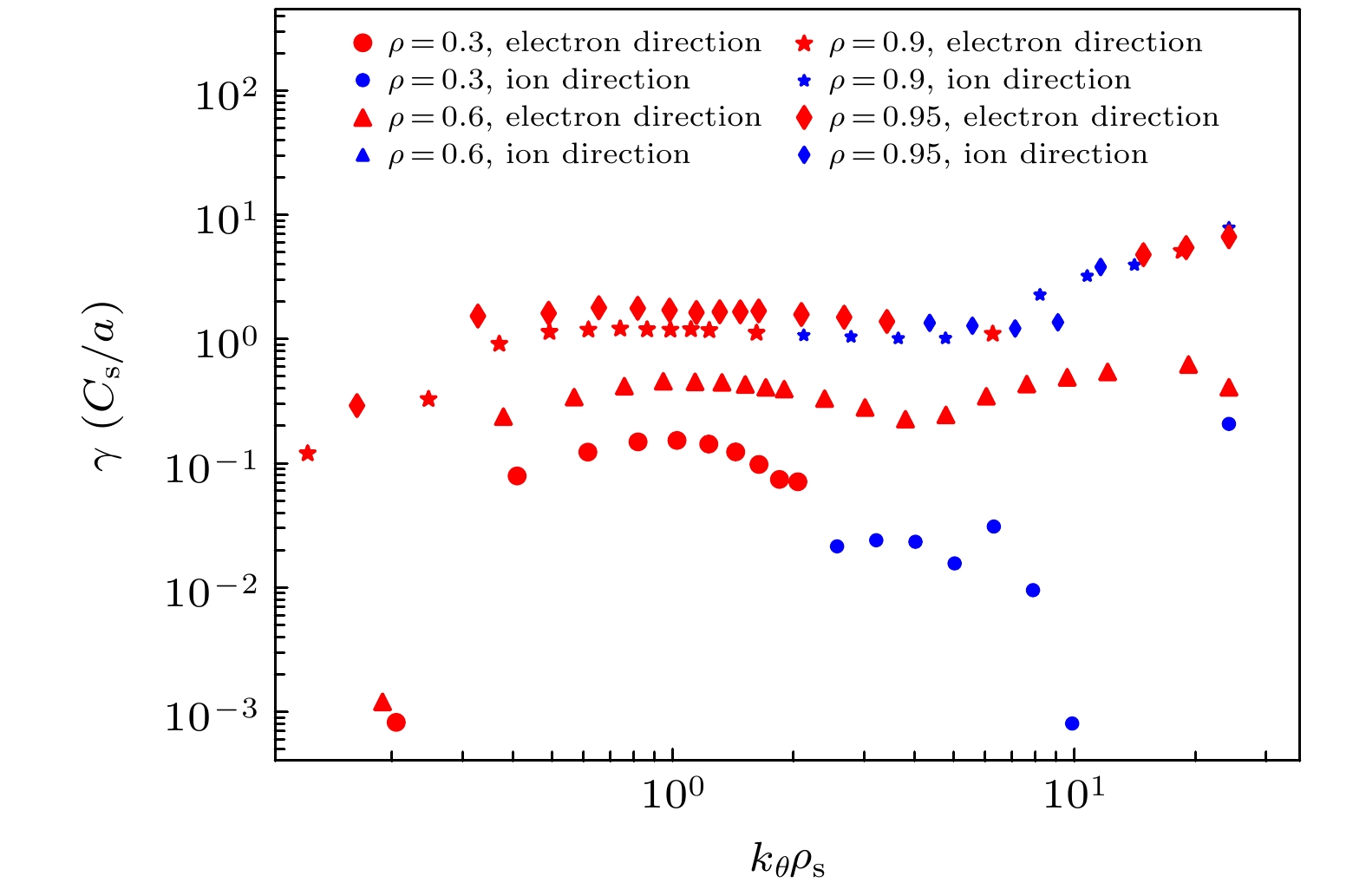
$ (\rho = 0.3, 0.6, 0.9, 0.95) $ 的微观不稳定性和增长率进行扫描后, 得到相应增长率与归一化极向波数的关系如图18所示. 图中横坐标表示归一化的极向波数$ {k}_{\theta }{\rho }_{{\mathrm{s}}} $ , 纵坐标表示归一化的增长率$ \gamma ({c}_{{\mathrm{s}}}/a) $ , 其中$ {c}_{{\mathrm{s}}} = \sqrt{{T}_{{\mathrm{e}}}/{m}_{{\mathrm{i}}}} $ ,$ {\rho }_{{\mathrm{s}}}={c}_{{\mathrm{s}}}/{\varOmega }_{{\mathrm{s}}} $ ,$ {\varOmega}_{{\mathrm{s}}}=eB/{(m}_{{\mathrm{i}}}c) $ , a为装置小半径. 基于图18的扫描结果进行线性分析, 高极向波数$ ({k}_{\theta }{\rho }_{{\mathrm{s}}} > 1 $ )模式下在$ \rho =0.3 $ 附近受到抑制, 湍流模式为电子湍流(TEM/ETG)(红色部分)和ITG混合湍流, 且以ITG为主导(蓝色部分). 在$ \rho =0.6 $ 附近, 湍流为电子湍流. 在靠近边界$ \rho =0.9 $ 处,$ {k}_{\theta }{\rho }_{{\mathrm{s}}} < 2 $ 时, 湍流模式为电子湍流与ITG混合型湍流, 这一混合湍流由电子湍流主导;$ {k}_{\theta }{\rho }_{{\mathrm{s}}} > 2 $ 时则以ITG为主, 并伴有少量的TEM/ETG. 而在更靠近边界$ \rho =0.95 $ 处,$ {k}_{\theta }{\rho }_{{\mathrm{s}}} < 3 $ 和$ {k}_{\theta }{\rho }_{{\mathrm{s}}} > 10 $ 时, 湍流模式以电子湍流为主导,$ 3 < {k}_{\theta }{\rho }_{{\mathrm{s}}} < 10 $ 的范围内则以ITG主导. 由此可见, 在脱靶的情况下, 芯部湍性输运以电子湍流为主导, 且在边界$ {k}_{\theta }{\rho }_{{\mathrm{s}}} < 2 $ 的情况下同样由电子湍流主导, 而在$ {k}_{\theta }{\rho }_{{\mathrm{s}}} > 2 $ 的情况下则以ITG为主导, 并伴有少量的TEM/ETG. 基于可见边界的通量向内输运, 而芯部的通量则向外输运, 有利于边界输运垒的形成, 但是不利于芯部输运垒的形成. 基于图12从实验与模拟结果上来看, 在脱靶情况下电子和离子的芯部温度密度剖面较为平坦, 且边界形成了较为清晰的台基结构. 同时, 结合图4(f)中$ {D}_{{\mathrm{\alpha }}} $ 信号的变化幅度明显减弱、图5(b)中Bolometer辐射测量系统测得的边界靶板辐射强度减弱、图6中等离子体边界靶板探针测得的热流通量减弱和图7等离子体边界靶板探针测得的离子饱和流强度减弱的实验结果, 可以得出脱靶情况下, ELM的幅度降低, 可见脱靶对ELM和芯部湍流均有重要的作用, 其内在机制还需要进一步深入研究. -
本文针对偏滤器靶板热流控制下的H模脱靶与芯部约束兼容性开展了实验和集成模拟研究, 获得了HL-2A装置H模等离子体偏滤器脱靶与芯部约束相兼容的实验结果, 并针对该实验结果, 基于OMFIT集成模拟平台创新了边界快速集成模拟方法与实验验证方法, 为开展H模偏滤器热流控制与芯部约束兼容性物理研究提供了一定的集成模拟与实验验证基础. 本文合理自洽地构建了集成模拟初始等离子体输入剖面, 并且率先实现了HL-2A装置#39007炮高约束模式下边界偏滤器脱靶与芯部约束兼容性的集成模拟研究, 经集成模拟多次迭代计算得到的最终收敛结果与实验结果相吻合, 验证了本文集成模拟工作流的可靠性. 芯部不稳定性分析结果进一步显示: 在高极向波数(
$ {k}_{\theta }{\rho }_{s} > 1 $ )模式下的$ \rho =0.3 $ 附近电子抗磁漂移方向上的不稳定性受到抑制, 湍流由ITG主导; 在$ \rho =0.6 $ 附近, 电子湍流成为湍流的主导因素; 在靠近边界$ \rho = 0.9$ 处,$ {k}_{\theta }{\rho }_{{\mathrm{s}}} < 2 $ 时, 湍流由电子湍流TEM/ETG主导,$ {k}_{\theta }{\rho }_{{\mathrm{s}}} > 2 $ 时则以ITG为主, 并伴有少量的电子湍流; 而在更靠近边界$ \rho =0.95 $ 处,$ {k}_{\theta }{\rho }_{{\mathrm{s}}} < 3 $ 或$ {k}_{\theta }{\rho }_{{\mathrm{s}}} > 10 $ 时, 湍流由电子湍流主导,$ 3 < {k}_{\theta }{\rho }_{{\mathrm{s}}} < 10 $ 的范围内则由ITG主导. 由此可见, 在脱靶的情况下, 在芯部$ 0.1 < \rho \leqslant 0.5 $ 的区域内高极向波数($ {k}_{\theta }{\rho }_{{\mathrm{s}}} > 1 $ )模式下的湍性输运以ITG主导, 在芯部$ 0.5 < \rho \leqslant 0.7 $ 的区域内的湍性输运以电子湍流主导, 而边界则是$ {k}_{\theta }{\rho }_{{\mathrm{s}}} < 2 $ 的情况下由电子湍流主导,$ {k}_{\theta }{\rho }_{{\mathrm{s}}} > 2 $ 的情况下则以ITG为主, 并伴有少量的TEM/ETG. 本文所分析时刻的温度密度实验剖面在芯部较为平坦, 边界形成了较为清晰的输运垒结构, 与分析的湍流模式有很好的定性吻合.同时发现进入脱靶后, ELM的爆发幅度得到了抑制, 这与本文自洽模拟得出的较低的台基梯度有密切的关系. 这种导致脱靶ELM运行状态是否为脱靶造成的刮削层返流, 影响了台基乃至芯部的输运和不稳定性的原因, 值得进一步深入研究. 目前的结果考虑了台基和边界区物理, 但由于实验数据集数量的不足导致KLNN边界神经网络快速集成模拟程序无法对边界杂质输运影响进行更多细致分析. 因此, 未来若在本文工作基础上进一步更深入的开展边界杂质输运对台基及芯部约束影响的物理机制分析和探讨, 还需要更为详细准确的实验诊断数据、边界杂质和通量信息作为数据支撑. 托卡马克H模脱靶和非脱靶条件下芯部约束兼容性和输运物理对比分析非常重要, 本文已开展了HL-2A装置H模脱靶实验的集成模拟分析, 我们在下一步工作中将开展脱靶前后的芯部约束兼容性和输运物理对比研究工作. 通过主动注入杂质实现偏滤器脱靶是一种有效降低靶板热负荷的放电运行方案, 但是由于杂质的注入、向内输运和聚芯效应将极大的影响等离子体的芯部约束性能. 托卡马克等离子体偏滤器脱靶是如何影响芯部的、以及脱靶与芯部约束兼容性的物理机理依然是一个关键、复杂问题, 仍需后续开展相关工作进行深入探究, 包括但不限于: 1)偏滤器及刮削层采用吹气、超声分子束注入等方法主动注入杂质对边界区等离子体输运、背景湍流的影响; 2)不同杂质注入对偏滤器靶板能量沉积不对称性的影响、刮削层及靶板区等离子体输运; 3)杂质粒子向内输运对台基结构、边缘局域模的影响; 4)横跨芯部、台基边界的大尺度磁流体动力学不稳定性对芯部与边界耦合的影响; 5)杂质聚芯对高能量粒子驱动不稳定性的影响; 6)发展先进的、基于新一代人工智能大模型(如DeepSeek)的边界快速集成物理模型等.
感谢美国通用原子(General Atomics)提供的OMFIT集成模拟平台支持. 感谢大连理工大学王元震、南华大学谭清懿提供的BOUT++和SOLPS数据支持, 以及大连理工大学刘悦, 核工业西南物理研究院高金明、余德良、王玮、张毅、肖国梁、胡世林、李正吉、沈宇奇、刘逸飞、严一帆、王哲和赵菊对本文工作的指导、建议和帮助.
HL-2A上H模脱靶与芯部约束兼容性的集成模拟与实验验证
Integrated modeling and experimental validation of H-mode divertor detachment and core confinement compatibility on HL-2A tokamak
-
摘要: 托卡马克高约束H模条件下偏滤器脱靶和热流控制是当前磁约束核聚变研究中的关键物理问题. 脱靶对H模边界输运物理尤其是对芯部约束兼容性的影响是研究偏滤器脱靶物理的关键问题. 本文获得了HL-2A装置H模等离子体偏滤器脱靶与芯部约束兼容的实验结果, 采用OMFIT集成模拟平台, 新发展了偏滤器靶板区的神经网络快速集成模拟方法, 率先采用该快速集成模拟方法开展HL-2A第39007炮高约束模式下, 边界偏滤器脱靶与芯部约束兼容性的集成模拟研究, 经验证集成模拟结果与实验结果相吻合. 通过进一步分析发现: HL-2A装置H模脱靶情况下, 在芯部$ 0.1 \lt \rho \leqslant {\mathrm{ }}0.5 $的区域内高极向波数($ {k}_{\theta }{\rho }_{{\mathrm{s}}} $>1)模式下的湍性输运以离子温度梯度(ITG)模主导, 在芯部$ 0.5 \lt \rho \leqslant {\mathrm{ }}0.7 $的区域内的湍性输运以电子湍流主导; 而边界则是在归一化极向波数$ {k}_{\theta }{\rho }_{{\mathrm{s}}} \lt 2 $的情况下由电子湍流主导, $ {k}_{\theta }{\rho }_{{\mathrm{s}}} \gt 2 $的情况下则以ITG为主, 并伴有少量的电子湍流. 本文研究结果为托卡马克装置芯边耦合物理研究提供了一定的集成模拟与实验验证基础.Abstract: The divertor detachment and heat flux control under high-confinement H-mode conditions in tokamaks represent critical physical challenges in current magnetic confinement fusion research. Understanding the influence of detachment on H-mode boundary transport physics, particularly its compatibility with core confinement, is central to resolving divertor detachment physics. In this study, experimental results on divertor detachment and core confinement compatibility in H-mode plasma from the HL-2A tokamak are presented. On the objective magnetohydrodynamic framework for integrated tasks (OMFIT) integrated modeling platform, a novel neural network-based fast integrated modeling method for the divertor target region is developed by integrating a new edge neural network module (Kun-Lun Neural Networks, KLNN) to enhance divertor, scrape-off-layer and edge pedestal fast prediction capability. For the first time, this method is used to conduct integrated simulations of divertor detachment and core confinement compatibility in HL-2A discharge #39007 under high-confinement mode. The simulation results are validated with experimental measurements, demonstrating that they are well consistent. Further analysis reveals that in HL-2A H-mode detachment scenarios, turbulent transport in the core region ($ 0.1 \lt \rho \leqslant 0.5 $) with high poloidal wave numbers $ ({k}_{\theta }{\rho }_{{\mathrm{s}}} \gt 1 $) is dominated by ion temperature gradient (ITG) mode, while electron-driven turbulence prevails in the region $ (0.5 \lt \rho \leqslant 0.7) $. In the boundary region, electron turbulence dominates at low normalized poloidal wave numbers ($ {k}_{\theta }{\rho }_{{\mathrm{s}}} \lt 2 $), whereas ITG modes become predominant at higher wave numbers ($ {k}_{\theta }{\rho }_{{\mathrm{s}}} \gt 2 $), accompanied by minor electron turbulence contributions. The research results of this work provide a certain foundation for integrated simulation and experimental verification in the study of core-edge coupling physics in tokamak devices and some insights for understanding detachment-compatible H-mode scenarios in the next-step fusion devices.
-
Key words:
- tokamak /
- detachment /
- H mode /
- integrated simulation .
-
-
图 1 包含KLNN程序的OMFIT等离子体剖面集成模拟工作流
Figure 1. Integrated simulation workflow of OMFIT plasma profiles incorporating KLNN program.
图 4 HL-2A装置第39007炮等离子体放电参数随时间演化图 (a)等离子体储能; (b)等离子体电流; (c)电子线平均密度; (d)归一化比压
$ {\beta }_{{\mathrm{n}}} $ ; (e) NBI, ECRH和 LHCD辅助加热功率; (f)$ {D}_{{\mathrm{\alpha }}} $ 射线Figure 4. Time evolution of the dischargement parameters of the shot #39007 in HL-2A: (a) Plasma stored energy; (b) plasma current; (c) average electron line density; (d)
$ {\beta }_{{\mathrm{n}}} $ ; (e) auxiliary heating power$ {P}_{{\mathrm{N}}{\mathrm{B}}{\mathrm{I}}} $ ,$ {P}_{{\mathrm{E}}{\mathrm{C}}{\mathrm{R}}{\mathrm{H}}} $ and$ {P}_{{\mathrm{L}}{\mathrm{H}}{\mathrm{C}}{\mathrm{D}}} $ ; (f)$ {D}_{{\mathrm{\alpha }}} $ ray.
图 5 (a)真空室区等离子体辐射强度随时间演化图; (b)偏滤器靶板区等离子体辐射强度随时间演化图
Figure 5. (a) Time evolution of plasma radiation intensity in the vacuum chamber area; (b) time evolution of plasma radiation intensity in the divertor target plate area.
图 6 等离子体边界靶板探针测得的热流通量随时间演化图
Figure 6. Time evolution of heat flux measured by the plasma boundary target plate probe.
图 7 等离子体边界靶板探针测得的离子饱和流强度随时间演化图
Figure 7. Time evolution of ion saturated current intensity measured by the plasma boundary target plate probe.
图 8 第39007炮在1320 ms时的实验值与输入剖面 (a)电子密度剖面; (b)电子温度剖面
Figure 8. Experiment and input profiles of the shot #39007 at the 1320 ms: (a) Electron density; (b) electron temperature.
图 9 第39007炮在1320 ms时刻的实验值与集成模拟初始输入剖面 (a)离子温度
$ {T}_{{\mathrm{i}}} $ ; (b)旋转速度$ \omega $ Figure 9. Experimental values and the initial input profiles of the integrated simulation of the shot #39007 at the 1320 ms: (a) Ion temperature
$ {T}_{{\mathrm{i}}} $ ; (b) rotation$ \omega $ .
图 10 OMFIT集成平台TGYRO程序中不同物理量第0次和第10次迭代结果对比 (a)离子温度
$ {T}_{{\mathrm{i}}} $ ; (b)电子温度$ {T}_{{\mathrm{e}}} $ ; (c)旋转速度$ \omega $ Figure 10. Comparison of the results of the 0th and 10th iterations of different physical quantities in the TGYRO program of the OMFIT integrated platform: (a) Ion temperature
$ {T}_{{\mathrm{i}}} $ ; (b) electron temperature$ {T}_{{\mathrm{e}}} $ ; (c) rotation$ \omega $ .
图 11 OMFIT集成平台TGYRO程序中各物理量不同径向位置最后10次迭代演化结果 (a)离子温度
$ {T}_{{\mathrm{i}}} $ ; (b)电子温度$ {T}_{{\mathrm{e}}} $ ; (c)旋转速度$ \omega $ Figure 11. Evolution results of the last 10 iterations of various physical quantities at different radial positions in the TGYRO program of the OMFIT integrated platform: (a) Ion temperature
$ {T}_{{\mathrm{i}}} $ ; (b) electron temperature$ {T}_{{\mathrm{e}}} $ ; (c) rotation$ \omega $ .
图 12 第39007炮在1320 ms时刻各物理量剖面的模拟结果与实验结果对照 (a)电子密度
$ {n}_{{\mathrm{e}}} $ ; (b)电子温度$ {T}_{{\mathrm{e}}} $ ; (c)离子温度$ {T}_{{\mathrm{i}}} $ ; (d)旋转速度$ \omega $ Figure 12. Comparison between the simulation results and experimental results of the physical quantity profiles of the shot #39007 at the 1320 ms: (a) Electron density
$ {n}_{{\mathrm{e}}} $ ; (b) electron temperature$ {T}_{{\mathrm{e}}} $ ; (c) ion temperature$ {T}_{{\mathrm{i}}} $ ; (d) rotation$ \omega $ .
图 13 第39007炮1320 ms时刻压强剖面的实验与模拟对照
Figure 13. Comparison of experiment and simulation pressure profiles of the shot # 39007 at the 1320 ms.
图 14 第 39007 炮在1320 ms时刻的各成分电流剖面
Figure 14. Current profiles of each composition of the shot #39007 at the 1320 ms.
图 15 第39007炮1320 ms时刻NBI注入的能量密度沉积分布
Figure 15. Energy density deposition distribution of NBI of the shot # 39007 at the 1320 ms.
图 16 第39007炮放电在1320 ms时刻模拟后得到的(a)离子能量通量和(b)电子能量通量
Figure 16. Ion energy flux (a) and electron energy flux (b) of the shot #39007 at the 1320 ms after simulation.
图 17 HL-2A装置第39007炮在1320 ms,
$ \rho =0.1—0.99 $ 区域内最不稳定的两支本征模式的频谱Figure 17. Frequency spectrum of the two most unstable eigenmodes in the
$ \rho =0.1-0.99 $ region of the shot #39007 at the 1320 ms in HL-2A.
图 18 39007炮在1320 ms,
$ \rho =0.3, 0.6, 0.9, 0.95 $ 处线性不稳定性的增长率与波数的关系(蓝色为离子抗磁漂移方向, 红色为电子抗磁漂移方向)Figure 18. Relationship between the growth rate of linear instability and the wave number in the
$ \rho =0.3, {\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}0.6, {\mathrm{ }}0.9, {\mathrm{ }}0.95 $ of the shot #39007 at the 1320 ms (The blue color indicates the direction of the ion diamagnetic drift, the red color indicates the direction of the electron diamagnetic drift).表 1 HL-2A #39007炮1320 ms时刻等离子体参数的实验值与模拟初始输入值对比表
Table 1. Comparison table of experimental values and initial input values of simulation for plasma parameters of the shot #39007 at the 1320 ms in HL-2A.
物理量 实验值 模拟初始输入值 等离子体电流/kA 150 150 纵场强度/T 1.33 1.33 NBI功率/kW 600 600 ECRH功率/kW 850 850 LHCD功率/kW 450 450 欧姆电流占比 — 0.60 NBI驱动电流占比 — 0.13 自举电流占比 — 0.27 芯部离子温度/keV 0.51 0.52 芯部电子温度/keV 2.25 2.26 芯部电子密度/(1019 m–3) 2.62 2.52 电子线平均密度/(1019 m–3) 1.83 1.91 Greenwald密度极限比值 0.42 0.43 q95 3.32 3.07 归一化比压 1.67 1.75 
下载: 导出CSV
表 2 HL-2A #39007炮脱靶前后时段平均的储能、能量约束时间以及H98因子变化对比表
Table 2. Comparison table of changes in average stored energy, average energy confinement time and average H98 factor during the time periods before and after detachment of the shot #39007 in HL-2A.
储能/kJ 能量约束时间/ms $ {H}_{98} $ 因子脱靶前时间段
(1100—1180 ms)29.2 ± 1.699 19.86 ±1.24 1.06 ± 0.069 脱靶后时间段
(1300—1380 ms)27.8 ± 1.883 18.96 ± 1.25 1.02 ± 0.066 下降百分比/% 4.8 4.5 3.8
下载: 导出CSV
-
[1] 孙有文, 仇志勇, 万宝年 2024 物理学报 73 175202 doi: 10.7498/aps.73.20240831 Sun Y W, Qiu Z Y, Wan B N 2024 Acta Phys. Sin. 73 175202 doi: 10.7498/aps.73.20240831 [2] Ida K, Fujita T 2018 Plasma Phys. Control. Fusion 60 033001 doi: 10.1088/1361-6587/aa9b03 [3] Leonard A W 2018 Plasma Phys. Control. Fusion 60 044001 doi: 10.1088/1361-6587/aaa7a9 [4] Wang L, Wang L, Wang H Q, Eldon D, Yuan Q P, Ding S, Li K D, Garofalo A M, Gong X Z, Xu G S, Guo H Y, Wu K, Meng L Y, Xu J C, Liu J B, Chen M W, Zhang B, Duan Y M, Ding F, Yang Z S, Qian J P, Huang J, Ren Q L, Leonard A W, Fenstermacher M, Lasnier C, Watkins J G, Shafer M W, Barr J, Weisberg D, McClenaghan J, Hanson J, Hyatt A, Osborne T, Thomas D, Humphreys D, Buttery R J, Luo G N, Xiao B J, Wan B N, Li J G 2021 Nat. Commun. 12 1365 doi: 10.1038/s41467-021-21645-y [5] 孟令义 2022 博士学位论文 (合肥: 中国科学技术大学) Meng L Y 2022 Ph. D. Dissertation (Hefei: University of Science and Technology of China [6] Wu T, Nie L, Yu Y, Gao J M, Li J Y, Ma H C, Wen J, Ke R, Wu N, Huang Z H, Liu L, Zheng D L, Yi K Y, Gao X Y, Wang W C, Cheng J, Yan L W, Cai L Z, Wang Z H, Xu M, 2023 Plasma Sci. Technol. 25 015102 doi: 10.1088/2058-6272/ac82df [7] 秦晨晨, 牟茂淋, 陈少永 2023 物理学报 72 045203 doi: 10.7498/aps.72.20222138 Qin C C, Mou M L, Chen S Y 2023 Acta Phys. Sin. 72 045203 doi: 10.7498/aps.72.20222138 [8] 龙婷, 柯锐, 吴婷, 高金明, 才来中, 王占辉, 许敏 2024 物理学报 73 088901 doi: 10.7498/aps.73.20231749 Long T, Ke R, Wu T, Gao J M, Cai L Z, Wang Z H, Xu M 2024 Acta Phys. Sin. 73 088901 doi: 10.7498/aps.73.20231749 [9] Luce T C, Challis C D, Ide S, Joffrin E, Kamada Y, Politzer P A, Schweinzer J, Sips A C C, Stober J, Giruzzi G, Kessel C E, Murakami M, Na Y S, Park J M, Polevoi A R, Budny R V, Citrin J, Garcia J, Hayashi N, Hobirk J, Hudson B F, Imbeaux F, Isayama A, McDonald D C, Nakano T, Oyama N, Parail V V, Petrie T W, Petty C C, Suzuki T, Wade M R, the ITPA Integrated Operation Scenario Topical Group Members, the ASDEX-Upgrade Team, the DIII-D Team, JET EFDA Contributors, the JT-60U Team 2014 Nucl. Fusion 54 013015 doi: 10.1088/0029-5515/54/1/013015 [10] Imbeaux F, Pinches S D, Lister J B, Buravand Y, Casper T, Duval B, Guillerminet B, Hosokawa M, Houlberg W, Huynh P, Kim S H, Manduchi G, Owsiak M, Palak B, Plociennik M, Rouault G, Sauter O, Strand P 2015 Nucl. Fusion 55 123006 doi: 10.1088/0029-5515/55/12/123006 [11] Meneghini O, Smith S P, Lao L L, Izacard O, Ren Q, Park J M, Candy J, Wang Z, Luna C J, Izzo V A, Grierson B A, Snyder P B, Holland C, Penna J, Lu G, Raum P, McCubbin A, Orlov D M, Belli E A, Ferraro N M, Prater R, Osborne T H, Turnbull A D, Staebler G M, the ATOM Team 2015 Nucl. Fusion 55 083008 doi: 10.1088/0029-5515/55/8/083008 [12] Zheng J X, Song Y T, Huang X Y, Lu K, Xi W B, Ding K Z, Ye B, Niu E W 2013 Plasma Sci. Technol. 15 152 doi: 10.1088/1009-0630/15/2/15 [13] 罗一鸣, 王占辉, 陈佳乐, 吴雪科, 付彩龙, 何小雪, 刘亮, 杨曾辰, 李永高, 高金明, 杜华荣, 昆仑集成模拟设计组 2022 物理学报 71 075201 doi: 10.7498/aps.71.20211941 Luo Y M, Wang Z H, Chen J L, Wu X K, Fu C L, He X X, Liu L, Yang Z C, Li Y G, Gao J M, Du H R, Kunlun Integrated Simulation and Design Group 2022 Acta Phys. Sin. 71 075201 doi: 10.7498/aps.71.20211941 [14] 罗一鸣 2022 硕士学位论文 (成都: 核工业西南物理研究院) Luo Y M, 2022 M S Thesis (Chendu: Southwestern Institute of Physics [15] John H S, Taylor T S, Lin-Liu Y R, Turnbull A D 1994 Plasma Phys. Controlled Fusion 3 603 doi: 10.2172/10104519 [16] Lao L L, John H S, Stambaugh R D, Kellman A G, Pfeiffer W, 1985 Nucl. Fusion 25 1421 doi: 10.1088/0029-5515/25/10/004 [17] Pan C, Staebler G M, Lao L L, Garofalo A M, Gong X, Ren Q, Smith S P 2017 Nucl. Fusion 57 036018 doi: 10.1088/1741-4326/aa4ff8 [18] Pankin A, McCune D, Andre R, Bateman G, Kritz A 2004 Comput. Phys. Commun. 159 157 doi: 10.1016/j.cpc.2003.11.002 [19] Yang C, Bonoli P T, Wright J C, Ding B J, Parker R, Shiraiwa S, Li M H 2014 Plasma Phys. Control. Fusion 56 125003 doi: 10.1088/0741-3335/56/12/125003 [20] 樊浩, 陈少永, 牟茂淋, 刘泰齐, 张业民, 唐昌建 2024 物理学报 73 095204 doi: 10.7498/aps.73.20240130 Fan H, Chen S Y, Mou M L, Liu T Q, Zhang Y M, Tang C J 2024 Acta Phys. Sin. 73 095204 doi: 10.7498/aps.73.20240130 [21] Kritz A H, Hsuan H, Goldfinger R C, Batchelor D B 1982 Ray Tracing Study of Electron Cyclotron Heating in Toroidal Geometry (Pergamon) pp707-723 [22] Beurskens M N A, Osborne T H, Schneider P A, Wolfrum E, Frassinetti L, Groebner R, Lomas P, Nunes I, Saarelma S, Scannell R, Snyder P B, Zarzoso D, Balboa I, Bray B, Brix M, Flanagan J, Giroud C, Giovannozzi E, Kempenaars M, Loarte A, de la Luna E, Maddison G, Maggi C F, McDonald D, Pasqualotto R, Saibene G, Sartori R, Solano E R, Walsh M, Zabeo L, The DIII-D Team, The ASDEX Upgrade Team, JET-EFDA Contributors 2011 Phys. Plasmas 18 056120 doi: 10.1063/1.3593008 [23] Moscheni M, Wigram M, Wu H, Meineri C, Carati C, De Marchi E, Greenwald M, Innocente P, LaBombard B, Subba F, Zanino R 2025 Nucl. Fusion 65 026025 doi: 10.1088/1741-4326/ada048 [24] Cowley C, Kuang A Q, Moulton D, Lore J D, Canik J, Umansky M, Wigram M, Ballinger S, Lipschultz B, Bonnin X 2023 Plasma Phys. Control. Fusion 65 035011 doi: 10.1088/1361-6587/acb4ba [25] Liang J H, Liu S F, Wang H P, Du Y, Wang Z H, Chen Y H, Xu M, Xia F, Yang Y , Zhong W L 2022 Nucl. Fusion Plasma Phys. 42 164 [梁嘉禾, 刘松芬, 王鸿鹏, 杜月, 王占辉, 陈逸航, 许敏, 夏凡, 杨宗谕, 钟武律 2022 核聚变与等离子体物理 42 164] doi: 10.16568/j.0254-6086.2022s1012 Liang J H, Liu S F, Wang H P, Du Y, Wang Z H, Chen Y H, Xu M, Xia F, Yang Y , Zhong W L 2022 Nucl. Fusion Plasma Phys. 42 164 doi: 10.16568/j.0254-6086.2022s1012 [26] 刘自结 2022 博士学位论文 (合肥: 中国科学技术大学) Liu Z J 2022 Ph. D. Dissertation (Hefei: University of Science and Technology of China [27] 汪金鑫 2022 博士学位论文 (合肥: 中国科学技术大学) Wang J X 2022 Ph. D. Dissertation (Hefei: University of Science and Technology of China [28] Zhu X B, Xia F, Yang Z Y, Liu F W, Gong X W, Liu Y H, Zhang Y, Shi P W, Chen W, Yu L M, Chen Z W, Zhong W L 2024 Nucl. Fusion Plasma Phys. 44 149 [朱晓博, 夏凡, 杨宗谕, 刘锋武, 龚新文, 刘宇航, 张毅, 施培万, 陈伟, 于利明, 陈正威, 钟武律 2024 核聚变与等离子体物理 44 149] doi: 10.16568/j.0254-6086.202402004 Zhu X B, Xia F, Yang Z Y, Liu F W, Gong X W, Liu Y H, Zhang Y, Shi P W, Chen W, Yu L M, Chen Z W, Zhong W L 2024 Nucl. Fusion Plasma Phys. 44 149 doi: 10.16568/j.0254-6086.202402004 [29] Kinsey J E, Staebler G M, Candy J, Waltz R E, Budny R V 2011 Nucl. Fusion 51 083001 doi: 10.1088/0029-5515/51/8/083001 [30] Staebler G M, Candy J, Waltz R E, Kinsey J E, Solomon W M 2013 Phys. Rev. Lett. 110 055003 doi: 10.1103/PhysRevLett.110.055003 [31] Waltz R E, Staebler G M, Dorland W, Hammett G W, Kotschenreuther M, Konings J A 1997 Phys. Plasmas 4 2482 doi: 10.1063/1.872228 [32] Bosch H S, Hale G M 1992 Nucl. Fusion 32 611 doi: 10.1088/0029-5515/32/4/I07 [33] Marin M, Camenen Y, Bourdelle C, Casson F J, Coosemans R, Garzott L, the TCV Team 2025 Nucl. Fusion 65 036015 doi: 10.1088/1741-4326/adb169 [34] Belli E A, Candy J 2012 Plasma Phys. Control. Fusion 54 015015 doi: 10.1088/0741-3335/54/1/015015 [35] Perin M, Chandre C, Tassi E, 2016 J. Phys. A: Math. Theor. 49 305501 doi: 10.1088/1751-8113/49/30/305501 [36] Dudkovskaia A V, Connor J W, Dickinson D, Hill P, Imada K, Leigh S, Wilson H R 2023 Nucl. Fusion 63 126040 doi: 10.1088/1741-4326/acfe8c [37] Kates-Harbeck J, Svyatkovskiy A, Tang W 2019 Nature 568 526 doi: 10.1038/s41586-019-1116-4 [38] Tang W M, Rewoldt G 1993 Phys. Fluids B Plasma Phys. 5 2451 doi: 10.1063/1.860730 [39] Tang W M, Rewoldt G 1978 Nucl. Fusion 18 1089 doi: 10.1088/0029-5515/18/8/006 [40] 李慧 2021 博士学位论文 (大连: 大连理工大学) Li H 2021 Ph. D. Dissertation (Dalian: Dalian University of Technology -
计量
- 文章访问数: 47
- HTML全文浏览数: 47
- PDF下载数: 0
- 施引文献: 0