首页
登录
注册
-
石墨烯是一种由单层碳原子以蜂窝状排列构成的二维材料, 具有优异的力学[1]、电学[2,3]和热学性能[4]. 石墨烯具有极高的杨氏模量和断裂强度, 但其有限的延展性(<0.2)和正泊松比(约为0.168)限制了其在柔性电子产品中的应用[5]. 近年来, 负泊松比(negative Poisson’s ratio, NPR)效应[6]引起了研究人员的高度关注. 负泊松比效应是指材料在受到拉伸时, 横向发生膨胀, 受到压缩时, 横向发生收缩, 这在传统材料中是不可见的. 研究表明, 石墨烯材料可通过巧妙的结构设计实现这一特殊的力学行为, 从而拓展其在柔性电子、智能材料和能源吸收等领域的应用潜力.
石墨烯的力学性质主要来源于其独特的原子排列和共价键结构, 但通过外部结构设计对其进行调控已成为国内外学者的研究重点. 通过在石墨烯中引入结构缺陷或孔隙[7], 特别是通过剪纸(kirigami)技术[8–14]等手段进行石墨烯的切割, 可以产生特定的孔隙结构, 显著改变其应力响应, 使石墨烯表现出负泊松比效应. 例如, Ho等[15]将周期性矩形穿孔引入石墨烯实现了负泊松比效应; Cai等[16]采用周期性凹入蜂窝结构, 通过调整内凹尺寸实现具有特定拉胀性能的石墨烯剪纸. 最近, Pan等[17,18]通过剪纸技术将旋转三角形和工字形图案引入石墨烯, 增强了石墨烯的延展性, 同时也使石墨烯产生了负泊松比. 此外, 功能化石墨烯, 如氧化[19]或氢化[20]石墨烯, 也会表现出负泊松比, 这主要是由于其结构中形成了皱纹.
尽管通过拓扑优化设计可以实现石墨烯的负泊松比效应, 但传统的设计方法通常基于经验或简化的理论模型, 通过剪纸技术进行孔隙化设计实现负泊松比效应时, 涉及的设计参数繁多, 通常需要大量的计算资源和时间, 尤其是在进行大规模的石墨烯分子动力学模拟时, 效率往往较低. 机器学习 (ML) 技术提供了一种新的思路和工具, 可以高效探索设计空间并加速材料结构的正向设计. 已有研究表明, 机器学习可以成功应用于石墨烯的结构设计. 例如, Hanakata等[21]使用卷积神经网络(CNN)设计了具有高延展性的石墨烯剪纸; Wan等[22]则基于机器学习设计了低热导率的多孔石墨烯. 然而, 到目前为止尚未有利用机器学习研究石墨烯负泊松比效应的相关报道.
本文通过引入菱形穿孔缺陷有效地实现了负泊松比石墨烯的结构设计, 并结合机器学习技术构建了一种数据驱动的机器学习模型, 可实现高效预测并设计具有负泊松比的穿孔石墨烯结构. 通过分子动力学模拟构建穿孔石墨烯结构的泊松比数据集, 并通过贝叶斯优化和交叉验证调整模型超参数, 采用反向传播神经网络(back propagation neural network, BPNN)[23]对泊松比进行对比预测分析, 建立从穿孔几何参数到泊松比的隐含映射关系. 在此基础上, 研究了不同穿孔几何参数对石墨烯剪纸结构泊松比的影响规律, 并与分子动力学模拟进行对比. 本研究成果将进一步推动石墨烯结构的智能设计和优化, 为其在柔性电子、智能材料和能源吸收等领域的应用奠定基础.
-
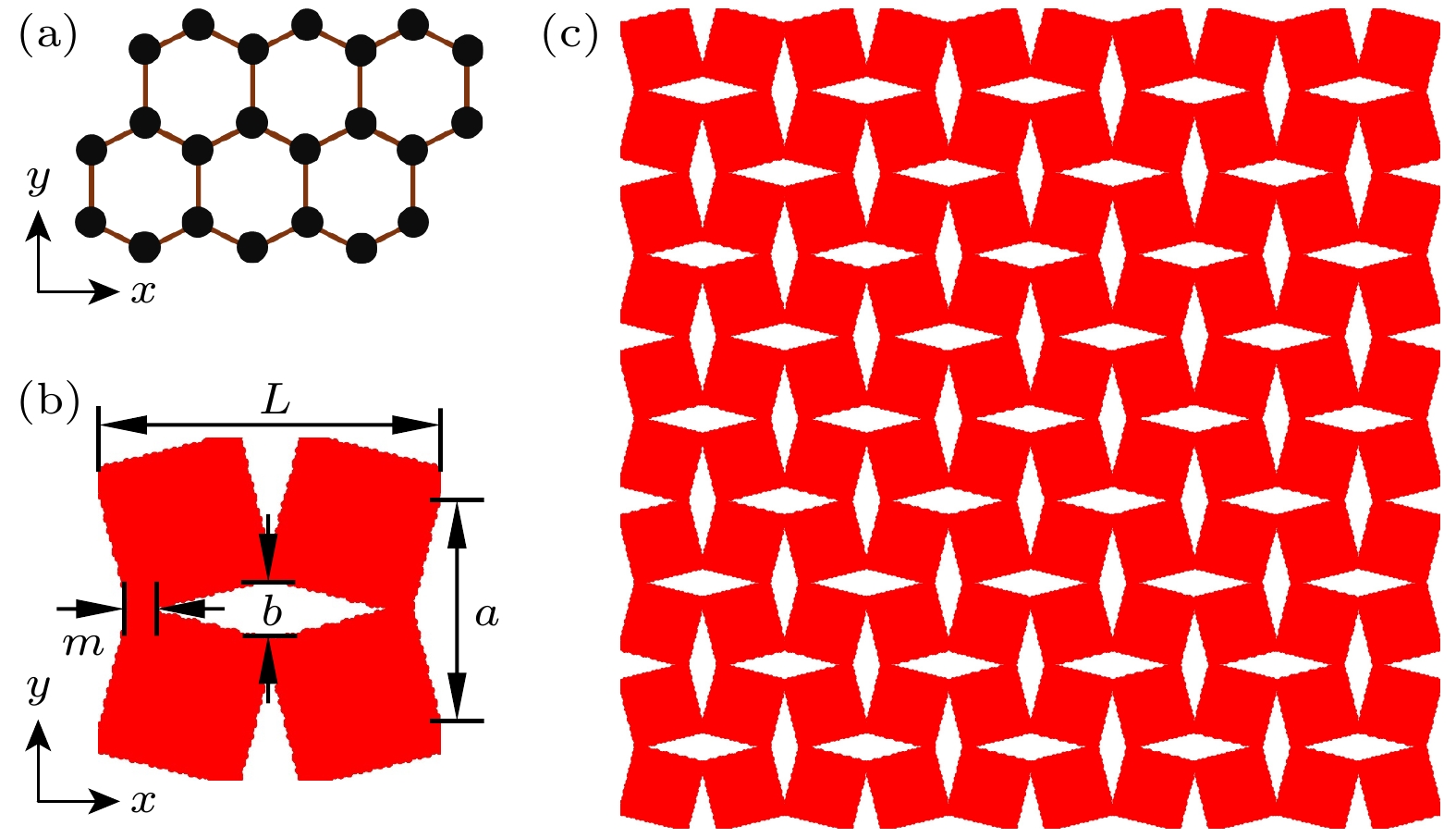
本文采用中心对称穿孔几何设计方法来设计具有对称和周期性的菱形穿孔石墨烯模型, 这种设计方法的核心思想是在材料中引入具有中心对称性的孔洞或结构, 通过精确调控孔洞的微观结构(形状、大小、排列密度等参数), 使其表现出材料本身所不具备的独特物理特性. 图1(a) 为石墨烯晶胞, 其中沿 x 轴和 y 轴分别为锯齿方向和扶手椅方向, C—C 键长为 0.1421 nm. 图1(b) 为菱形穿孔石墨烯剪纸的代表单元晶胞, 该晶胞由3个参数表征[24]: 穿孔纵横比(AR)、穿孔间距比(IS) 和晶胞尺寸. AR和IS的定义如下:
其中, a和b分别为穿孔的长度和宽度, L为晶胞尺寸, m为穿孔间距. L可通过以下公式计算:
为确保计算效率并参考相关实验文献[25], 本文采用了5×5晶胞组装构建石墨烯剪纸, 如图1(c)所示. 通过调整AR, IS 和L参数, 可以控制石墨烯剪纸的结构, 因此, 这3个参数被确定为特征值, 作为后续神经网络的输入参数. 在本研究中, 这些参数的取值范围为: AR ∈ [1, 22], IS ∈ [0.05, 0.3] 和 L ∈ [15, 40] nm, 共生成了432个具有不同几何参数的石墨烯剪纸模型, 作为机器学习模型的输入.
用于机器学习训练的数据集包括菱形穿孔的3个几何参数和石墨烯剪纸的泊松比, 这些数据通过使用分子动力学软件包LAMMPS[26]对石墨烯剪纸进行拉伸测试得到. 在分子动力学模拟中, 采用 AIREBO 势函数[27,28]描述石墨烯剪纸结构中的碳-碳原子间的相互作用, 截止半径设置为 2.0 Å[29,30]. 模拟中, 在 x 和 y 方向应用周期性边界条件. 运动方程积分采用 Velocity-Verlet 算法[31], 时间步长为 1 fs. 在模拟拉伸前, 首先使用共轭梯度法对石墨烯剪纸模型进行能量最小化, 然后在NPT系综下经过充分的弛豫之后, 通过在x或y方向上施加恒定速率以实现单轴拉伸变形. 拉伸过程中采用Nose-Hoover方法[32], 并将压力恒定为0 Pa, 温度保持在1 K. 尽管石墨烯表现出轻微的各向异性, 但本文分子动力学模拟结果表明, 引入周期性的菱形穿孔后, 沿锯齿和扶手椅方向拉伸时得到的泊松比基本一致. 因此, 本文仅沿x方向(锯齿方向)进行单轴拉伸模拟, 以确定穿孔石墨烯剪纸模型的泊松比. 泊松比定义为纵向应变与横向应变的比值, 即
$ {\nu }_{xy}=-{\varepsilon }_{y}/{\varepsilon }_{x} $ , 通过在 0—1% 应变范围内纵向应变-横向应变关系曲线的斜率计算得到[19]. -
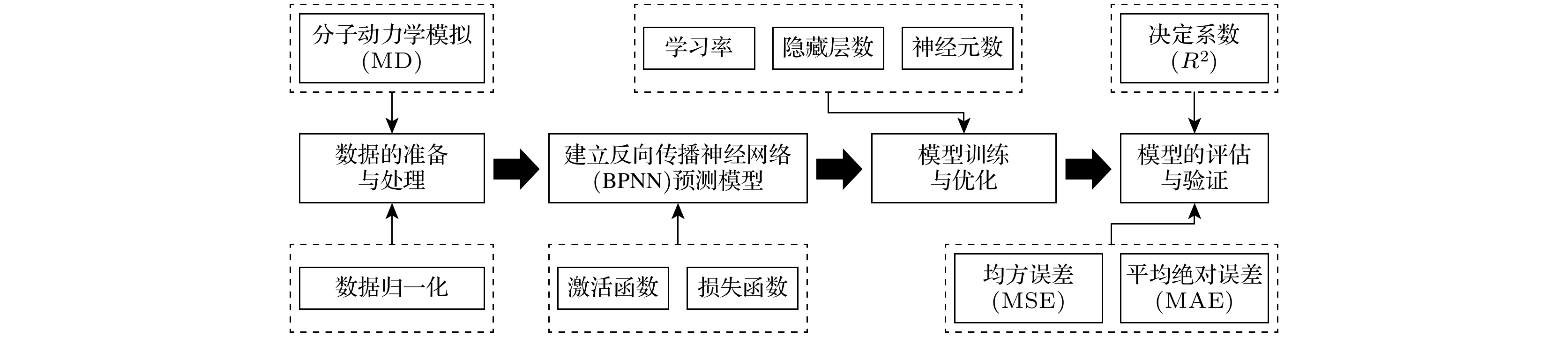
图2是菱形穿孔石墨烯负泊松比预测机器学习模型的构建流程, 主要包括数据集的收集、数据归一化预处理、模型的建立、模型训练与参数优化以及模型的评估与验证. 这一流程旨在通过高效的算法设计和优化方法, 准确捕捉菱形穿孔石墨烯结构参数与负泊松比之间的复杂映射关系.
-
在构建模型之前, 首先收集包含菱形穿孔石墨烯L, IS和AR的结构参数数据, 同时通过分子动力学模拟获得其对应的负泊松比(
$ {v}_{xy} $ )值, 形成原始数据集. 为了提高模型的训练效率并避免特征值量纲对模型训练造成的干扰, 本文采用MinMaxScaler模块对数据进行最大最小归一化处理, 公式如下[33]:其中, X表示原始数据, Xmin和Xmax分别为数据的最小值和最大值. 归一化处理后, 将数据随机划分为训练集(占80%)和测试集(占20%), 训练集用于模型的训练, 测试集用于验证模型的泛化能力.
-
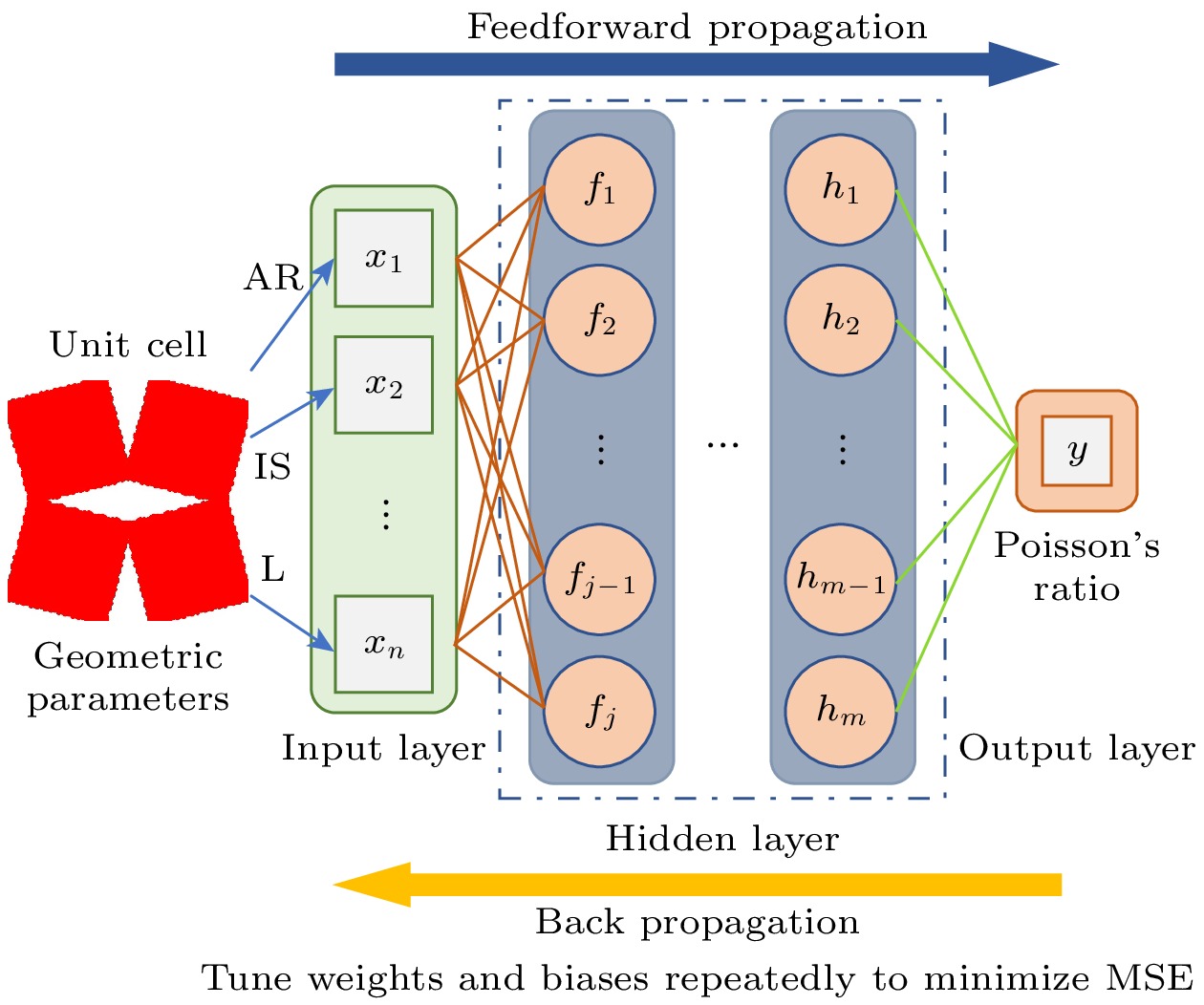
本文采用BPNN作为预测模型. BPNN是一种采用误差反向传播算法训练的多层前馈网络, 具有强大的自学习能力和非线性映射能力, 适用于复杂数据的建模任务. BPNN包括前向传播和反向传播, 其架构如图3所示. 前向传播是神经网络通过层级结构和参数, 将输入数据逐步转换为预测结果的过程, 实现输入与输出之间的复杂映射. 前向传播神经网络由输入层、隐藏层和输出层组成, 其中输入层接收AR, IS和L作为特征变量, 输出层则生成穿孔石墨烯的泊松比的预测值. 隐藏层采用ReLU(rectified linear unit)激活函数, 以增强模型的非线性表示能力, 避免梯度消失问题, 从而加速收敛. 此外, 输出层采用线性激活函数, 以确保模型适用于回归任务.
反向传播算法利用链式法则, 通过输出层向输入层逐层计算误差梯度, 高效求解神经网络参数的偏导数, 以实现网络参数的优化和损失函数的最小化. 依据前向传播的算法, 最终能得到样本的预测值, 预测值和实际值之间的差距用损失函数来表示, 损失函数选用均方误差(mean squared error, MSE), 其表达式为
其中,
$ {y}_{m} $ 是第m个样本的真实值,$ {y}_{m}'$ 是第m个样本的预测值, N为样本数量. MSE 的最小化能够有效提升模型的拟合性能. -
为了进一步优化模型性能, 本文结合贝叶斯优化(Bayesian optimization)[34]与十折交叉验证(10-fold cross-validation)对模型的超参数进行调优. 贝叶斯优化基于高斯过程构建参数性能的概率模型, 通过历史数据不断调整搜索策略, 每次迭代优先评估具有高潜在性能的参数组合, 从而实现高效的参数优化. 优化范围包括隐藏层数量(1—5层)、每层神经元数量(8—128个)以及学习率(0.00001—0.1). 通过交叉验证综合评估不同参数组合的表现, 最终确定最优配置如表1所列. 优化后的模型在复杂非线性映射任务中表现出强大的适用性和鲁棒性.
在模型训练完成后, 通过测试集对其性能进行全面评估. 本文选取均方误差(MSE)、平均绝对误差(mean absolute error, MAE)和决定系数(R2)作为评价指标, 其中MAE的计算公式为
决定系数(R2)则用于衡量模型的拟合优度, 其定义如下:
其中,
$ {{\bar y}_{m}} $ 是所有真实值的平均值. 结果表明, 优化后的 BPNN模型在菱形穿孔石墨烯负泊松比预测任务中具有较高的预测精度. 测试集的MSE和MAE值为0.006755和0.04633, 均显著较低, 准确度(R2)可达98%, 充分验证了模型的泛化能力和预测效果. 这一结果不仅体现了 BPNN在复杂非线性回归问题中的应用潜力, 也为探索材料结构参数与性能间的关联提供了重要的理论支持. 在本文的神经网络建模过程中, 我们使用了Python编程语言及其多种工具和库, 如scikit-learn (sklearn), Keras, pandas, NumPy等. -
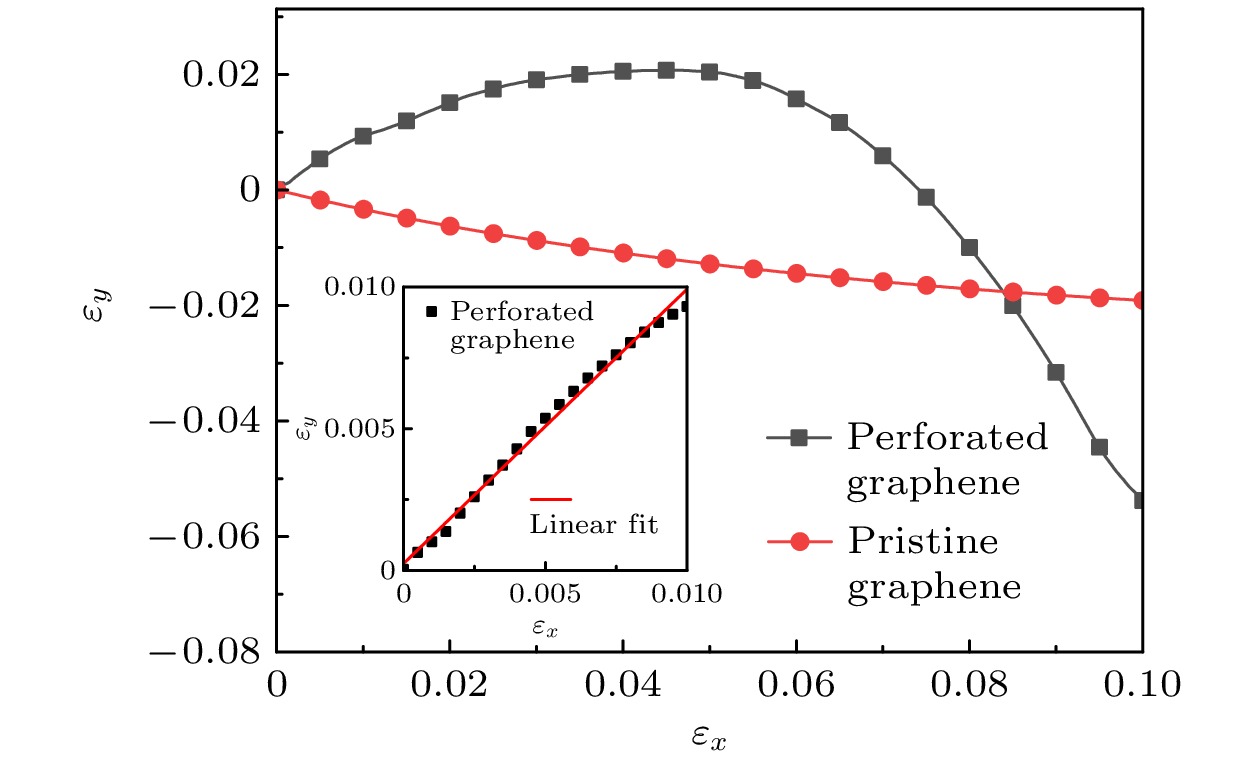
图4为完美无穿孔石墨烯与菱形穿孔石墨烯(AR = 10, IS = 0.1)在加载过程中的纵向应变与横向应变关系曲线. 对于完美无穿孔石墨烯, 纵向应变随着加载应变的增大而减小, 表明其在加载方向伸长的同时, 纵向长度缩短, 呈现正泊松比特性. 而菱形穿孔石墨烯的纵向应变则随加载应变的增大而增大, 直至加载应变达到临界值约0.05. 这说明, 在加载应变小于临界值时, 菱形穿孔石墨烯在加载方向伸长的同时纵向长度也增大, 表现出显著的负泊松比效应. 通过对加载应变范围0—0.01内的曲线进行拟合, 可得该菱形穿孔石墨烯模型的泊松比为–0.96.
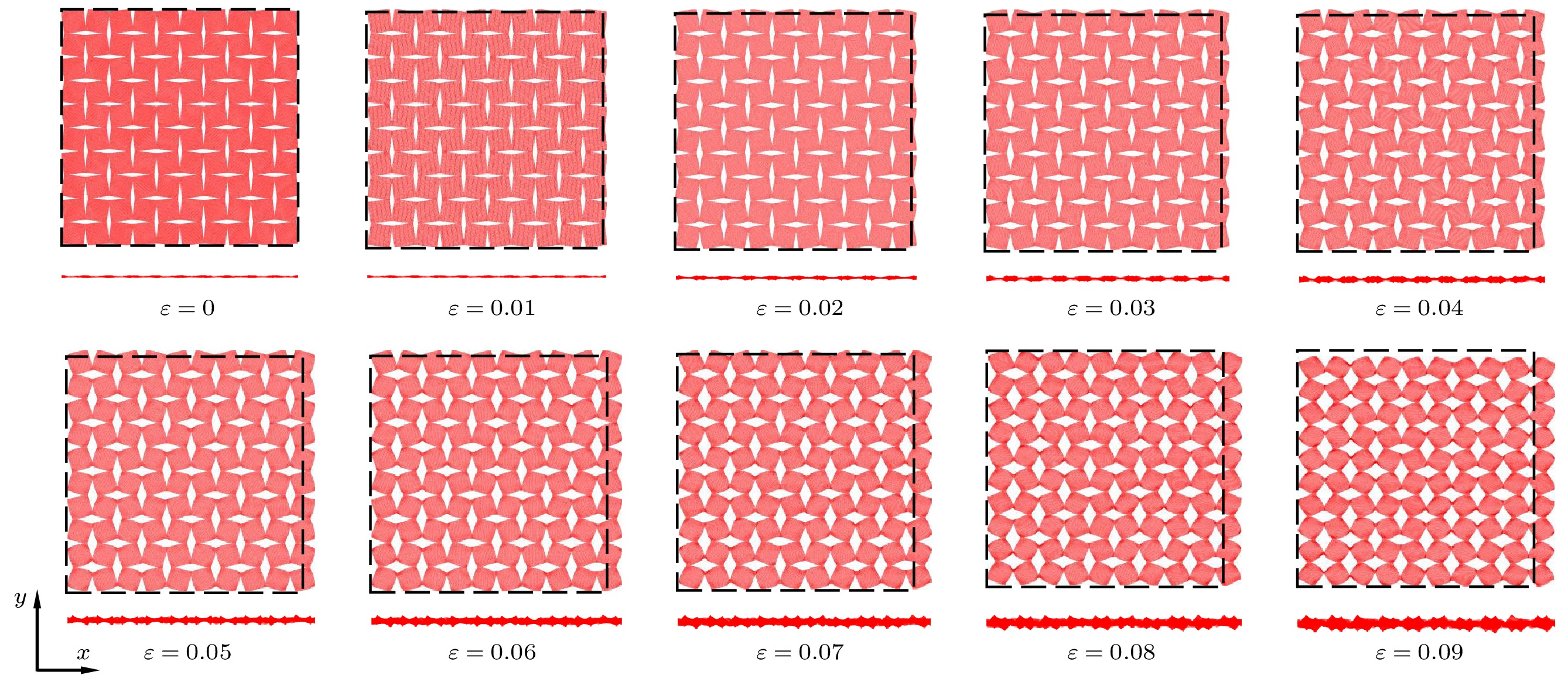
图5为菱形穿孔石墨烯(AR = 10, IS = 0.1)在不同应变下的俯视图和侧视图, 虚线表示未变形时的模型尺寸. 垂直于加载方向的菱形短轴在拉伸作用下延长, 驱动旋转单元发生旋转, 从而使平行于加载方向的菱形短轴也随之增大, 导致穿孔石墨烯在纵向方向发生膨胀. 这一现象类似于宏观尺度下刚性单元的旋转效应机制. 如图5所示, 当应变小于0.05时, 纵向膨胀效应始终存在, 但在应变超过0.05后, 这种膨胀效应逐渐减弱, 最终导致负 泊松比效应消失, 这与图4的分析结果相符. 图4显示含菱形穿孔缺陷石墨烯的泊松比随着应变的增大由负变正, 其物理机制可以归因于上述菱形穿孔石墨烯在不同应变阶段具有不同的变形机制. 当应变小于临界阙值0.05时, 在拉力的作用下, 旋转单元的旋转机制占主导, 从而导致穿孔石墨烯在垂直方向膨胀; 而当应变达到0.05时, 旋转单元旋转结束, 随着应变的增大, 碳-碳键的伸长变形机制将占主导, 此后穿孔石墨烯在垂直方向收缩. 然而, 菱形穿孔石墨烯的旋转机制与宏观材料中的刚性单元旋转机制并不完全相同, 主要体现在以下两个方面: 首先, 菱形孔洞之间并未通过铰链连接, 因此旋转效应较弱; 其次, 由于石墨烯面外刚度较低, 在拉伸过程中, 旋转单元除了发生旋转外, 还会伴随显著的面外变形. 从图5的侧视图中可以清晰观察到这一点, 这进一步削弱了旋转效应. 因此, 菱形穿孔石墨烯的负泊松比效应是旋转单元旋转效应与面外变形耦合作用的结果.
-
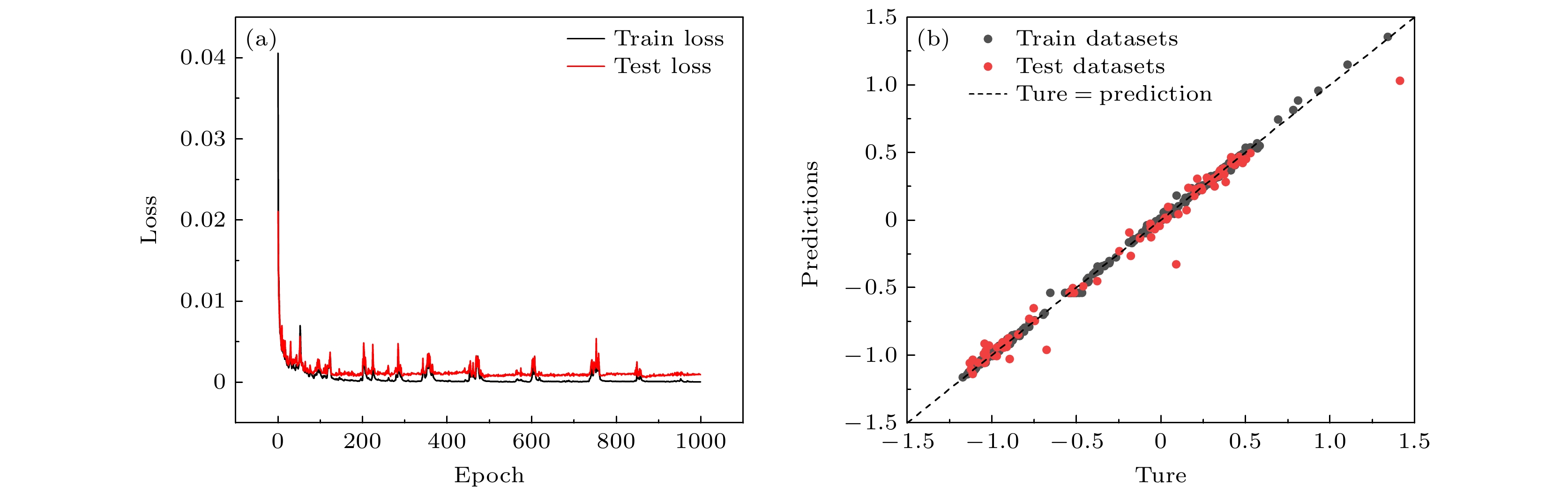
表2列出了BPNN模型在训练集和测试集上的关键性能指标. 训练集的MSE和R²分别为0.000326和0.9990, 而测试集的对应指标为0.006755和0.9813. 该结果表明, BPNN在训练样本的拟合过程中表现出较高的预测精度(接近于完美拟合), 并在测试集上展现了良好的泛化能力, 能够有效适应未见样本.
图6(a)呈现了训练误差与测试误差随训练轮次(epoch)变化的趋势. 结果显示, 在初始阶段, 误差迅速下降, 表明BPNN通过权重和偏差调整实现了高效的收敛. 随着训练过程的推进, 误差逐步趋于平稳, 标志着模型参数的收敛性和训练的完成, 为后续预测任务提供了稳定的优化权重. 图6(b)展示了训练集和测试集的预测结果与真实值的对比情况. 可以看出, 训练集和测试集的数据点大部分集中在“预测值=真实值”这条对角线附近, 拟合效果良好. 这进一步验证了BPNN能够准确捕捉样本之间的规律, 并能有效预测未知样本的优点.
-
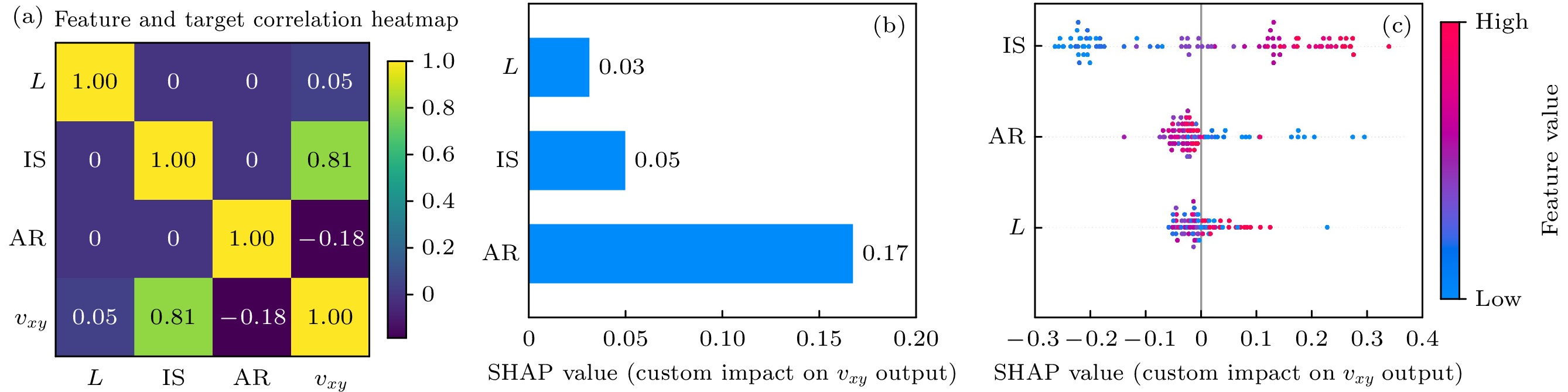
如图7所示, 通过计算每对特征与输出变量之间的Pearson相关性, 研究了各特征对目标变量的线性关系. Pearson相关系数的取值范围为–1—1, 分别表示最强的负相关和正相关. 由图7(a)可见穿孔几何参数IS与泊松比之间存在显著正相关性(相关系数接近1), 表明IS的增大会削弱负泊松效应. 相比之下, AR对泊松比呈现弱负相关性, 其影响程度有限, 说明AR的调控作用可能依赖于其他参数的交互影响. 而L的相关性最弱, 对负泊松比的影响可忽略不计. 这些结果为后续模型解释性分析提供了初步的量化依据.
为了进一步探究机器学习模型的内部机制并量化各特征对输出的贡献, 采用SHAP(SHapley Additive exPlanations)值[35]分析模型的可解释性. 图7(b)通过SHAP值分析展示了各输入特征对输出变量(
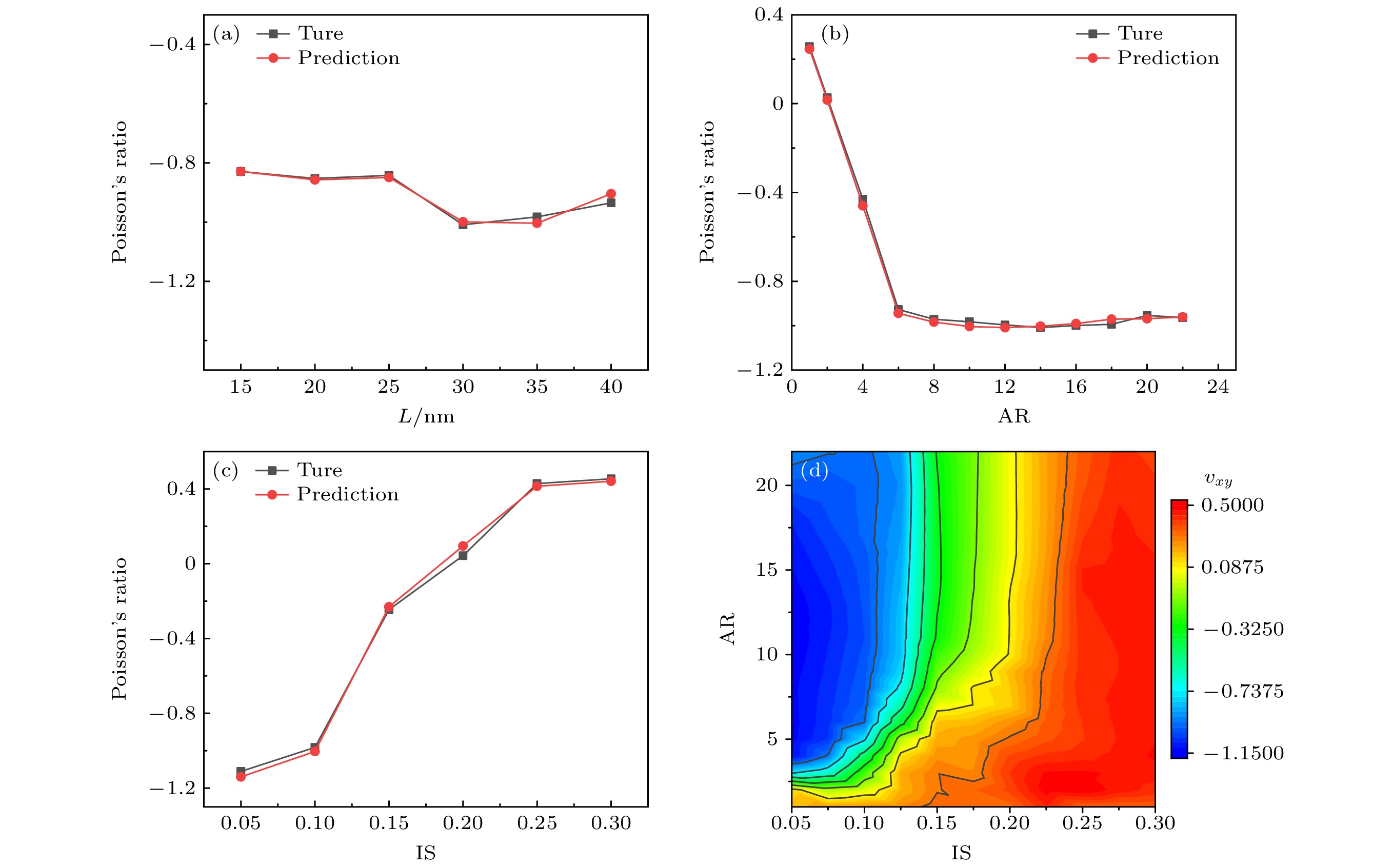
$ {v}_{xy} $ )的相对贡献度. 结果显示, IS的平均SHAP值显著高于其他特征, 表明其是模型预测输出的主要驱动因子. 此外, AR和L的平均SHAP值较低, 提示其对预测结果的影响较为有限. 图7(c)进一步通过SHAP值散点图可视化了各特征对输出的具体影响. 可以观察到, IS的高值对应于较大的正影响, 而AR和L的影响分布则较为分散且幅度相对较小. IS在模型解释性分析中起到了核心作用, 明确了其在调控负泊松比中的主导地位, 并验证了其重要性.为了进一步研究结构参数对负泊松比的影响, 将预测结构与模拟结果进行对比分析, 结果如图8所示. 从整体趋势来看, 预测值与真实值(模拟结果)之间的吻合度较高, 充分验证了机器学习模型在负泊松比预测任务中的准确性和可靠性. 如图8(a)所示, 随着L的增大, 泊松比在较小范围内呈现波动, 整体变化幅度不大. 这一现象表明, L对负泊 松比的影响相对有限, 可能仅在特定的设计参数 范围内对负泊松比具有微弱的调控作用. 相比之下, AR对负泊松比的影响较为显著(图8(b)). 泊松比随着AR的增大迅速降低并趋于平稳, 表现出明显的非线性关系. 这表明增大AR能够有效增强负泊松效应, 但当AR超过一定阈值后, 其效应趋于稳定.
IS的影响(图8(c))则展现出明显的非线性增长趋势. 随着IS的增大, 泊松比显著增大, 反映出IS是影响负泊松效应的关键参数之一. 较高的IS会削弱负泊松效应, 说明优化IS是提升负泊松比性能的重要手段. 为了进一步分析结构参数间的交互作用, 图8(d)通过二维平面图展示了AR和IS的协同影响. 结果表明, 当AR较低且IS较小时, 泊松比保持在较低范围内, 负泊松效应较强. 而随着两者的增大, 泊松比逐渐上升, 负泊松效应逐步减弱. 这一发现揭示了两者之间存在一定的非线性耦合关系.
通过对模型预测值与模拟结果的对比分析, 系统阐明了结构参数对负泊松比的影响规律. 研究表明, AR和IS是调控负泊松效应的关键参数, 而其协同作用进一步丰富了结构设计的理论指导意义, 为负泊松比材料的优化设计提供了重要参考.
-
本文通过引入周期性菱形穿孔缺陷有效地实现了负泊松比石墨烯的结构设计, 并基于BPNN构建了一种数据驱动的机器学习模型, 可实现高效预测并设计具有负泊松比的穿孔石墨烯结构. 本文得到如下结论:
1)通过分子动力学模拟与结构分析, 揭示了菱形穿孔石墨烯产生负泊松比效应的机制. 研究表明, 孔洞结构中的旋转单元在加载过程中产生的旋转效应与面外变形的协同作用是负泊松比效应的主要来源. 此外, 负泊松比效应表现出应变依赖性, 加载应变超过特定阈值后, 效应逐渐减弱直至消失.
2)基于BPNN构建的数据驱动机器学习模型, 可高效预测并设计具有负泊松比的穿孔石墨烯结构. 通过分子动力学模拟生成泊松比数据集, 并结合贝叶斯优化与交叉验证调优模型超参数, 结果显示优化后的模型在预测菱形穿孔石墨烯负泊松比方面具有较高精度和强泛化能力. 这表明, 该模型能够有效捕捉结构参数与负泊松比效应之间复杂的非线性关系.
3)结合机器学习与SHAP值分析, 定量评估了不同穿孔几何参数对负泊松比效应的影响. 研究发现, 减小IS会增强负泊松比效应; 增大AR能够提高负泊松比效应, 但当AR超过一定值时, 该效应趋于稳定; L对负泊松比影响较小. 特征重要性分析进一步表明, IS对负泊松比效应的正向影响最显著, 而AR与L的影响则相对较弱且具有一定非线性特征.
基于机器学习的菱形穿孔石墨烯负泊松比效应预测与优化
Prediction and optimization of negative Poisson’s ratio in rhombic perforated graphene based on machine learning
-
摘要: 通过结构设计调控石墨烯的性能已引起广泛关注. 然而, 结构设计几何参数与性能之间存在复杂的非线性关系, 如何准确预测石墨烯性能参数加快结构设计仍需进一步深入探索. 本文通过引入周期性菱形穿孔缺陷有效地实现了负泊松比石墨烯的结构设计, 分析了负泊松比效应的产生机制, 并基于反向传播神经网络(BPNN)构建了一种数据驱动的机器学习模型, 可实现高效预测并设计具有负泊松比的穿孔石墨烯结构. 通过分子动力学模拟构建菱形穿孔石墨烯结构的泊松比数据集, 采用优化后的BPNN模型对泊松比进行预测分析, 研究发现, 穿孔间距比(IS)对菱形穿孔石墨烯结构泊松比的影响最显著, 而穿孔纵横比(AR)与晶胞尺寸(L)的影响则相对较弱. 本文还研究了不同穿孔几何参数对菱形穿孔石墨烯负泊松比效应的影响规律, 减小IS和增大AR能够增强石墨烯结构的负泊松比效应. 机器学习模型的预测结果与分子动力学模拟结果高度吻合, 验证了机器学习方法在石墨烯泊松比预测中的有效性和可靠性. 本研究通过引入菱形穿孔缺陷, 结合机器学习技术, 实现对石墨烯负泊松比效应的高效预测与优化, 为其在智能材料和柔性电子中的应用提供理论支持.Abstract: Tuning graphene’s properties through structural design has received significant attention. However, the complex nonlinear relationship between geometric parameters of structural design and performance needs further exploring to accurately predict the performance of graphene and speed up the optimization of its structural design. This study introduces periodic rhombic perforations to effectively achieve the structural design of graphene with negative Poisson’s ratio (NPR). The mechanisms underlying the NPR effect are analyzed, and a data-driven machine learning model based on a backpropagation neural network (BPNN) is developed to efficiently predict and design perforated graphene structures exhibiting NPR. By constructing a Poisson’s ratio dataset for rhombic perforated graphene structures through molecular dynamics simulations and employing an optimized BPNN model for predictive analysis, it is found that the perforation spacing ratio (IS) has the most significant effect on the Poisson’s ratio of rhombic perforated graphene, while the perforation aspect ratio (AR) and unit cell size (L) have relatively weak influence. The study further investigates the influence of various perforation geometric parameters on the NPR behavior of graphene. It is found that reducing IS and increasing AR can enhance the negative Poisson’s ratio effect. The machine learning predictions closely align with molecular dynamics simulation results, demonstrating the effectiveness and reliability of this approach for Poisson’s ratio prediction. By integrating rhombic perforation design with machine learning technologies, this research provides an efficient framework for optimizing the NPR effect in graphene, and theoretical support for its application in smart materials and flexible electronics.
-
Key words:
- graphene /
- negative Poisson’s ratio /
- machine learning /
- molecular dynamics .
-
-
图 1 (a) 石墨烯的原子结构; (b) 菱形穿孔代表单元; (c) 5×5菱形穿孔石墨烯剪纸模型
Figure 1. (a) Graphene unit cell; (b) representative unit cell of graphene kirigami with labeled features; (c) perforated graphene kirigami composed of a 5 × 5 array of representative unit cells.
图 2 菱形穿孔石墨烯负泊松比预测的机器学习模型构建流程图
Figure 2. Machine learning constructing workflow for predicting the negative Poisson’s ratio of rhombic perforated graphene.
图 4 完美无穿孔和菱形穿孔石墨烯加载过程中的纵向应变与横向应变关系曲线
Figure 4. Longitudinal versus lateral strains during the loading of pristine and rhombic perforated graphene.
图 5 菱形穿孔石墨烯在不同应变下形貌的俯视图和侧视图, 其中虚线为未变形前模型尺寸
Figure 5. Top and side views of rhombic perforated graphene kirigami at various tensile strains. The dashed box indicates the model dimensions prior to deformation.
图 6 BPNN训练过程和预测结果分析 (a) BPNN损失函数迭代图; (b) 预测值和真实值对比图
Figure 6. Analysis of the BPNN training process and prediction results: (a) Iteration plot of the BPNN loss function; (b) comparison of predicted and actual values.
图 7 特征重要性分析 (a) 特征与目标变量的Pearson相关性热力图; (b) 特征重要性柱状图(基于SHAP值); (c) 特征SHAP值散点图
Figure 7. Feature importance analysis: (a) Heatmap of Pearson correlation between features and the target variable; (b) bar chart of feature importance (based on SHAP values); (c) scatter plot of feature SHAP values.
图 8 菱形穿孔几何参数对穿孔石墨烯泊松比的影响 (a) L; (b) AR; (c) IS; (d) L固定时不同的AR和IS
Figure 8. Influence of rhombic perforation geometric parameters on the Poisson’s ratio of perforated graphene: (a) L; (b) AR; (c) IS; (d) different AR and IS with fixed L.
表 1 调优后的BPNN参数
Table 1. Optimized BPNN parameters after adjustment.
类型 BPNN参数 输入 AR, IS, L 输出 vxy 隐藏层 91-92-27-60 激活函数 Relu 优化器 Adam 学习率 0.006701783312545704 迭代次数 1000 
下载: 导出CSV
表 2 BPNN的性能评估指标
Table 2. Performance evaluation metrics of the BPNN.
评估指标 R2 MSE MAE 训练集 0.9990 0.000326 0.01225 测试集 0.9813 0.006755 0.04633
下载: 导出CSV
-
[1] Lee C, Wei X D, Kysar J W, Hone J 2008 Science 321 385 doi: 10.1126/science.1157996 [2] Zhang Y B, Tan Y W, Stormer H L, Kim P 2005 Nature 438 201 doi: 10.1038/nature04235 [3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 doi: 10.1126/science.1102896 [4] Balandin A A, Ghosh S, Bao W Z, Calizo I, Teweldebrhan D, Miao F, Lau C N 2008 Nano Lett. 8 902 doi: 10.1021/nl0731872 [5] Jang H, Park Y J, Chen X, Das T, Kim M S, Ahn J H 2016 Adv. Mater. 28 4184 doi: 10.1002/adma.201504245 [6] Huang C, Chen L 2016 Adv. Mater. 28 8079 doi: 10.1002/adma.201601363 [7] Grima J N, Winczewski S, Mizzi L, Grech M C, Cauchi R, Gatt R, Attard D, Wojciechowski K W, Rybicki J 2015 Adv. Mater. 27 1455 doi: 10.1002/adma.201404106 [8] Zhai Z R, Wu L L, Jiang H Q 2021 Appl. Phys. Rev. 8 041319 doi: 10.1063/5.0051088 [9] Yu Y, Yin Y Q, Bai R Y, Hu Y Z, Li B, Wang M Y, Chen G M 2023 Appl. Phys. Lett. 123 011702 doi: 10.1063/5.0157978 [10] Sun R J, Zhang B, Yang L, Zhang W J, Farrow I, Scarpa F, Rossiter J 2018 Appl. Phys. Lett. 112 251904 doi: 10.1063/1.5025025 [11] Han D X, Chen S H, Zhao L, Tong X, Chan K C 2022 AIP Adv. 12 035305 doi: 10.1063/5.0084906 [12] Lee J H, Singer J P, Thomas E L 2012 Adv. Mater. 24 4782 doi: 10.1002/adma.201201644 [13] Grima J N, Manicaro E, Attard D 2011 Proc. R. Soc. A: Math. Phys. Eng. Sci. 467 439 doi: 10.1098/rspa.2010.0171 [14] Han T W, Scarpa F, Allan N L 2017 Thin Solid Films 632 35 doi: 10.1016/j.tsf.2017.03.059 [15] Ho V H, Ho D T, Kwon S Y, Kim S Y 2016 Phys. Status Solidi B Basic Res. 253 1303 doi: 10.1002/pssb.201600061 [16] Cai K, Luo J, Ling Y R, Wan J, Qin Q H 2016 Sci. Rep. 6 35157 doi: 10.1038/srep35157 [17] Shi P, Chen Y, Feng J, Sareh P 2024 Phys. Rev. E 109 035002 doi: 10.1103/PhysRevE.109.035002 [18] Shi P, Chen Y, Wei Y, Feng J, Guo T, Tu Y M, Sareh P 2023 Phys. Rev. B 108 134105 doi: 10.1103/PhysRevB.108.134105 [19] Wan J, Jiang J W, Park H S 2017 Nanoscale 9 4007 doi: 10.1039/C6NR08657H [20] Jiang J W, Chang T C, Guo X M 2016 Nanoscale 8 15948 doi: 10.1039/C6NR04976A [21] Hanakata P Z, Cubuk E D, Campbell D K, Park H S 2018 Physi. Rev. Lett. 121 255304 doi: 10.1103/PhysRevLett.121.255304 [22] Wan J, Jiang J W, Park H S 2020 Carbon 157 262 doi: 10.1016/j.carbon.2019.10.037 [23] Rumelhart D E, Hinton G E, Williams R J 1986 Nature 323 533 doi: 10.1038/323533a0 [24] Slann A, White W, Scarpa F, Boba K, Farrow I 2015 Phys. Status Solidi B Basic Res. 252 1533 doi: 10.1002/pssb.201451740 [25] Grima J N, Mizzi L, Azzopardi K M, Gatt R 2016 Adv. Mater. 28 385 doi: 10.1002/adma.201503653 [26] Thompson A P, Aktulga H M, Berger R, Bolintineanu D S, Brown W M, Crozier P S, Veld P J I, Kohlmeyer A, Moore S G, Nguyen T D, Shan R, Stevens M J, Tranchida J, Trott C, Plimpton S J 2022 Comput. Phys. Comm. 271 10817 doi: 10.1016/j.cpc.2021.108171 [27] Dhaliwal G, Nair P B, Singh C V 2019 Carbon 142 300 doi: 10.1016/j.carbon.2018.10.020 [28] Stuart S J, Tutein A B, Harrison J A 2000 J. Chem. Phys. 112 6472 doi: 10.1063/1.481208 [29] Qin H S, Sun Y, Liu J Z, Liu Y L 2016 Carbon 108 204 doi: 10.1016/j.carbon.2016.07.014 [30] Qian C, McLean B, Hedman D, Ding F 2021 APL Mater. 9 061102 doi: 10.1063/5.0052870 [31] Swope W C, Andersen H C, Berens P H, Wilson K R 1982 J. Chem. Phys. 76 637 doi: 10.1063/1.442716 [32] Hoover W G 1985 Phys. Rev. A Gen. Phys. 31 1695 doi: 10.1103/PhysRevA.31.1695 [33] Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay É 2011 J. Mach. Learn. Res. 11 2825 doi: 10.5555/1953048.2078195 [34] Jones D R, Schonlau M, Welch W J 1998 J. Glob. Optim. 13 455 doi: 10.1023/A:1008306431147 [35] Lundberg S M, Lee S I 2017 Proceedings of the 31st Conference on Neural Information Processing Systems Long Beach, California, USA, December 4–9, 2017 pp4768–4777 -
计量
- 文章访问数: 30
- HTML全文浏览数: 30
- PDF下载数: 0
- 施引文献: 0