随着量子信息科学和量子计算技术的飞速发展, 对多体纠缠态的研究已经成为了量子信息处理领域的关键课题. 多体纠缠态在量子密码学^[1]、量子秘密共享^[2]、量子隐形传态^[3-5]、量子密钥分发^[6-9]、量子计算^[10-13]和量子安全直接通信^[14-16]等多个领域中起着至关重要的作用. 其中W态作为一种由多个量子比特纠缠构成的特殊多体纠缠态^[3,17], 其主要特征在于: 当任意一个量子比特丢失时, 剩余的量子比特依然以一定的概率保持纠缠, 这使W态对局部退相干具有较强的鲁棒性^[18-20]. 这种特性赋予了W态在量子信息传输^[21,22]、量子密钥分发^[9,23,24]和量子网络构建^[25,26]等方面的应用潜力. 目前, W态的理论研究已经相对成熟, 那么如何实现高效、可扩展地制备W态就显得十分重要.

近年来, 研究者们积极探索了多种量子体系的纠缠态制备方法^[27-29], 其中, 里德伯超级原子凭借其独特的集体行为成为一种新兴的制备量子纠缠态的工具^[30-32]. 里德伯超级原子不同于单个里德伯原子, 它由里德伯原子系综构成. 在高激发的里德伯态中, 原子间的相互作用强度(1—100 MHz)远高于典型激光的拉比频率(几十 kHz —几 MHz)^[33-35]. 因此, 在里德伯阻塞效应的作用下^[11,36-43], 位于阻塞范围内的里德伯原子系综中仅允许一个原子被激发至里德伯态. 在这种情况下, 系综的行为就像一个多能级“原子”, 即里德伯超级原子. 系综的集体状态用于表示超级原子的有效能级^[30,44-46]. 里德伯超级原子具有诸多优势^[31,47], 比如制备超级原子比制备单个原子容易, 超级原子中基态与激发态之间的耦合强度远大于单个原子基态与激发态的耦合强度; 利用超级原子的能级进行编码对于原子丢失具有鲁棒性等优点. 由于这些优势, 里德伯超级原子展现了在量子信息处理中的巨大潜力. 基于里德伯超级原子平台的量子纠缠态的制备已经成为一个重要的研究方向^[48,49].

迄今为止, 研究者已经提出许多能够在短时间内实现高保真度的纠缠态制备方案^[50-52]. 在众多快速制备量子纠缠态的方案中, 比较令人感兴趣的一种方法是超绝热迭代技术^[27,53,54], 该技术是 Berry^[55]提出的无跃迁量子驱动的扩展, 也是Iañez 等^[56]提出的一种通过迭代交互绘景(结合多个 Schrödinger 绘景)来改进绝热捷径(shortcuts to adiabaticity, STA)的方法. 该方法能够产生一系列不同的哈密顿量, 并允许研究者选择实验中可行且适合特定应用需求的哈密顿量. 后来Song等^[57]则将该方法扩展至三能级系统, 展示了超绝热迭代技术在多能级系统中的应用潜力. 随后Huang等^[58]提出了一种通过迭代相互作用绘景快速生成GHZ态的方案. Wu等^[59]也提出了基于超绝热技术快速制备树型三维纠缠态的方案. 受上述工作的启发, 本文基于超绝热迭代技术, 提出了一种快速制备W态的方案. 与传统方法不同, 该方案无需精确控制实验参数和交互时间, 且反绝热哈密顿 量与有效哈密顿量形式相同, 有利于实验实现. 此外, 实验中也不需要额外的耦合, 从而在保持高保真度的同时具备较高的实验可行性. 本方案还可扩展到利用 N 个里德伯超级原子快速制备W态的情况.

本文结构安排如下: 第2节介绍物理模型, 展示里德伯超级原子能级结构, 并给出在腔场和控制场作用下的哈密顿量表达式. 随后, 通过引入超绝热迭代技术, 得出用于制备W态的脉冲参数的选择. 第3节通过数值模拟验证了该方案的有效性, 分析系统在原子自发辐射、腔体和光纤泄漏等退相干因素下的鲁棒性. 结果显示, 与绝热方案相比, 基于绝热迭代技术的W态演化时间更短. 第4节将方案扩展到N个里德伯超级原子的W态制备, 以探讨方案的可扩展性. 最后, 第5节总结了本文的主要结论与研究意义.

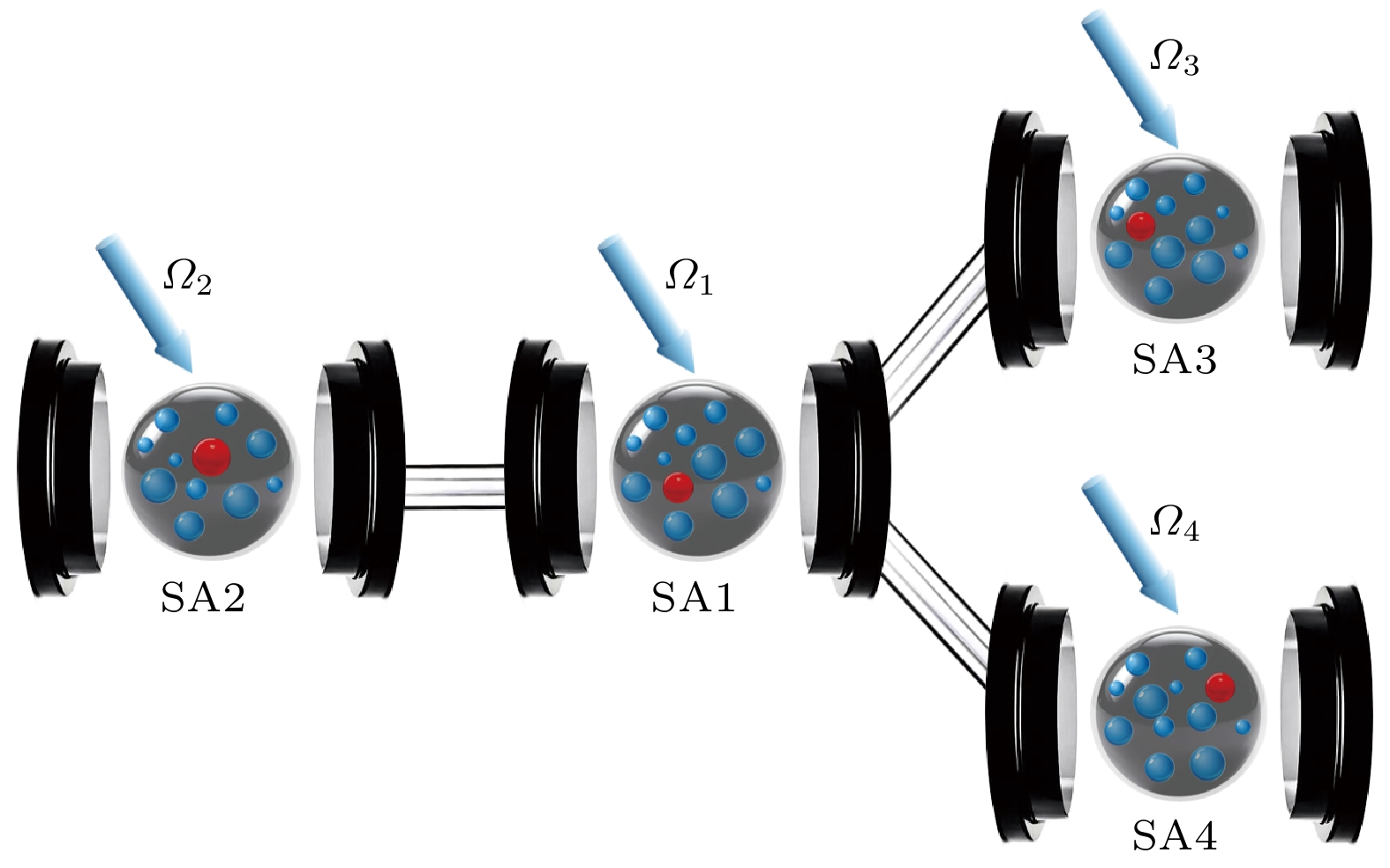
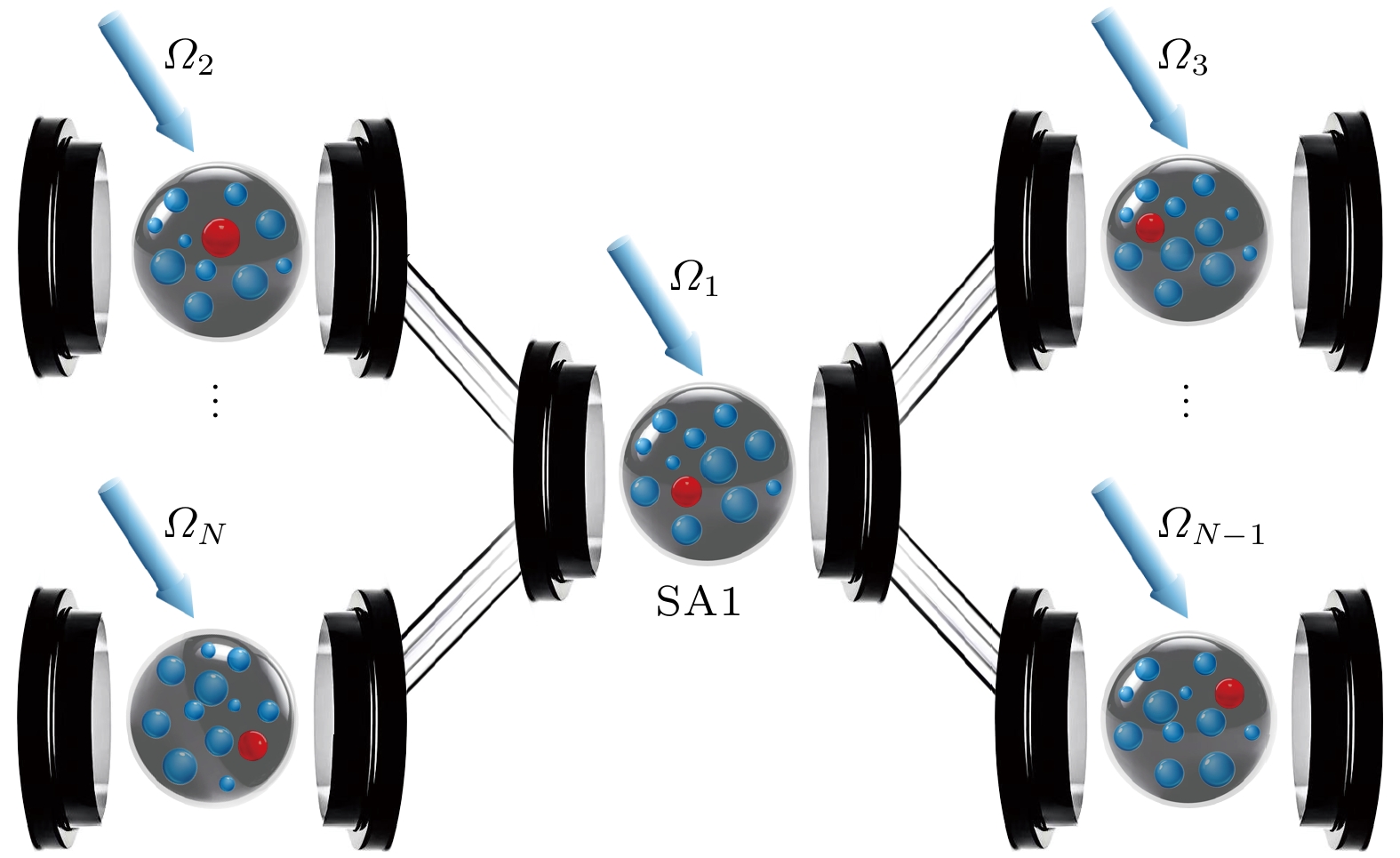
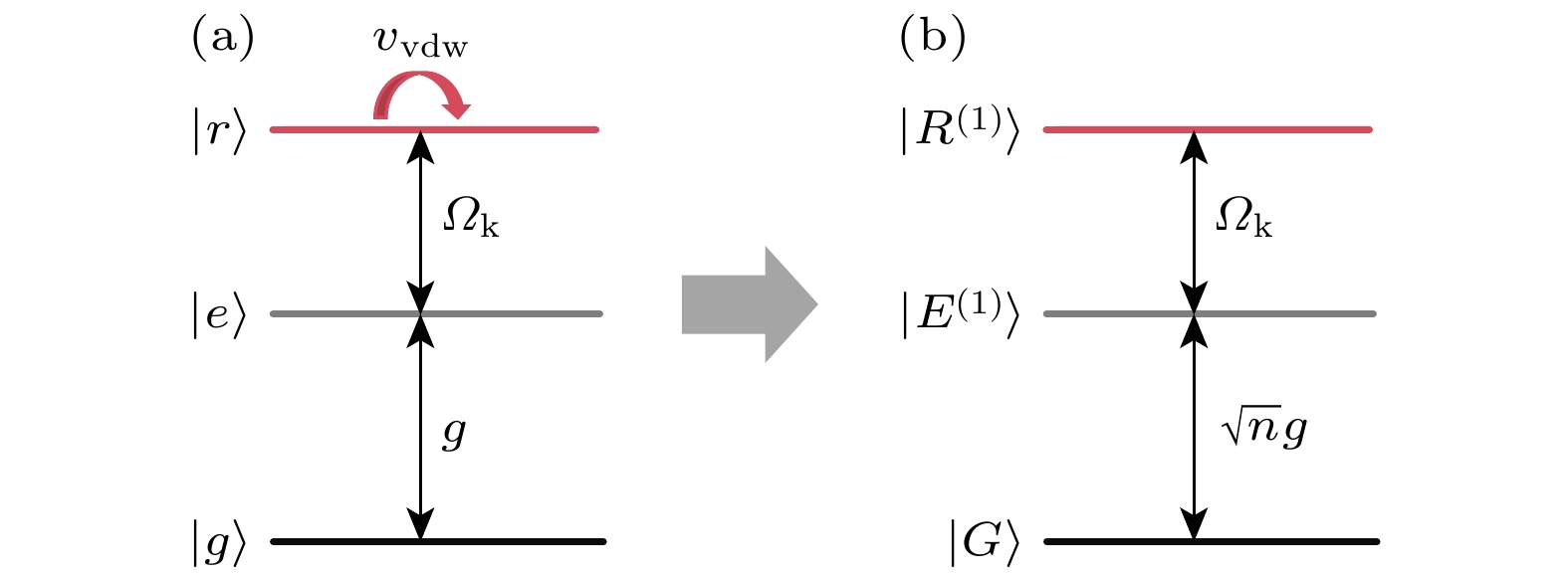
本方案采用$ ^{87}\text{Rb} $原子, 其能级结构如图1所示. 在弱腔场极限下 (平均光子数不超过1) 和外部经典场共同作用下, 冷却的里德伯原子系综被激发, 每个里德伯原子的能级结构如图1(a)所示, 基态 $ |g\rangle\equiv|5 {\mathrm{S}}_{1/2}, F = 2, m_{\mathrm{F}} = 2\rangle $、激发态 $ |e\rangle\equiv|5 {\mathrm{P}}_{3/2}, F = 3, m_{\mathrm{F}} = 3\rangle $以及里德伯态$ |r\rangle\equiv|111 {\mathrm{S}}_{1/2},\; m_{\mathrm{J}} = 1/2\rangle $. 其中, 原子跃迁$ |g\rangle \leftrightarrow |e\rangle $以耦合常数g共振耦合到腔场; 在第k个腔中, 原子跃迁$ |e\rangle \leftrightarrow |r\rangle $ 由拉比频率为$ \varOmega_k(t) $的经典场驱动; $ v_{{\mathrm{vdw}}} $表示两个原子在里德伯态下的范德瓦耳斯相互作用, 该相互作用能够显著改变周围原子的里德伯能级, 从而形成里德伯阻塞效应^[33,60-63]. 在此效应下, 系综会表现为一个等效的里德伯超级原子, 其简化的能级结构如图1(b)所示, $ |G\rangle \leftrightarrow |E^{(1)}\rangle $以耦合常数$ \lambda = \sqrt{n}g $共振耦合到腔场, 经典场以拉比频率$ \varOmega_k(t) $共振驱动 $ |E^{(1)}\rangle \leftrightarrow |R^{(1)}\rangle $的跃迁. 其中,

$ |R^{(1)}\rangle= \displaystyle \sum\nolimits^n_i|g_1 g_2\cdots r_i \cdots g_n\rangle/\sqrt{n} ,$

$ |E^{(1)}\rangle = \displaystyle \sum\nolimits_i^n|g_1 g_2 \cdots e_i \cdots g_n\rangle/ \sqrt{n}, $

$ |G\rangle=|g_1 g_2...g_n\rangle $.

将超级原子分别放置在4个独立的真空腔中, 如图2所示. 在旋转波近似下, 相互作用绘景下的哈密顿量可以表示为 ($ \hbar = 1 $):

其中, $ H_{{\mathrm{ac}}} $表示腔与超级原子之间的相互作用, $ H_{{\mathrm{al}}} $表示经典场与超级原子之间的相互作用, $ H_{{\mathrm{cf}}} $则代表腔与光纤之间的相互作用. $ a_k $为第k个腔中光子的湮灭算符, v表示光纤与腔之间的耦合强度, $ b_{k}^\dagger $是第k个光纤的产生算符. 假设系统的初始态为 $ |\psi_1\rangle=|R^{(1)}GGG\rangle|0\rangle_{{\mathrm{all}}} $, 即第1个超级原子处于态$ |R^{(1)}\rangle $, 其余超级原子处于基态$ |G\rangle $, 此外, 所有腔和光纤都处于真空态. 在此假设下, 系统将在如下空间中演化:

在此空间中, 可以将哈密顿量重新改写为

为了简单起见, 在计算中假设$ v=\lambda $. 根据量子芝诺动力学, 整个希尔伯特空间将被划分为若干子空间. 由于初始态为$ |\psi_1\rangle=|R^{(1)}GGG\rangle|0\rangle_{{\mathrm{all}}} $, 整个演化过程将被限制在由暗态构成的子空间$ \{|\psi_{1}\rangle $, $ |\psi_{7}\rangle $, $ |\psi_{11}\rangle $, $ |\psi_{15}\rangle $, $ |\phi\rangle\} $中, 其中$ |\phi\rangle = 1/ \sqrt{15} (3 |\psi_2\rangle - |\psi_{4}\rangle + |\psi_{6}\rangle - |\psi_{8}\rangle $+$|\psi_{10}\rangle - |\psi_{12}\rangle + |\psi_{14}\rangle) $. 因此有效哈密顿量为

式中, $ P_0 $表示投影算符^[64], $ P_0= \displaystyle\sum\nolimits_m|m\rangle\langle m|, (m\in\{|\psi_1\rangle, |\psi_7\rangle, |\psi_{11}\rangle, |\psi_{15}\rangle, |\phi\rangle\}) $. 由于系统在暗空间中演化, 所以$ \xi_0 = 0 $. 令$ \varOmega'_2(t) = 1/\sqrt{5}\varOmega_2(t) = 1/\sqrt{5}\varOmega_3(t) = 1/\sqrt{5}\varOmega_4(t)$, $\varOmega'_1(t) = 3\varOmega_1(t)/\sqrt{15} $, $ |\varPsi\rangle = 1/\sqrt{3}(|\psi_7\rangle+|\psi_{11}\rangle+|\psi_{15}\rangle), $ 则有效哈密顿量变为

为了方便, 令$ |\psi_1\rangle=\left(1, 0, 0\right)^{\mathrm{T}} $, $ |\phi\rangle=\left(0, 1, 0\right)^{\mathrm{T}} $和$ |\varPsi\rangle= \left(0, 0, 1\right)^{\mathrm{T}} $, 此时有效哈密顿量可以改写为

其中,

该有效哈密顿量的本征值为 $ \zeta_0 = 0 $ 和 $ \zeta_\pm = \pm \varOmega'(t) $, 相应的本征态为

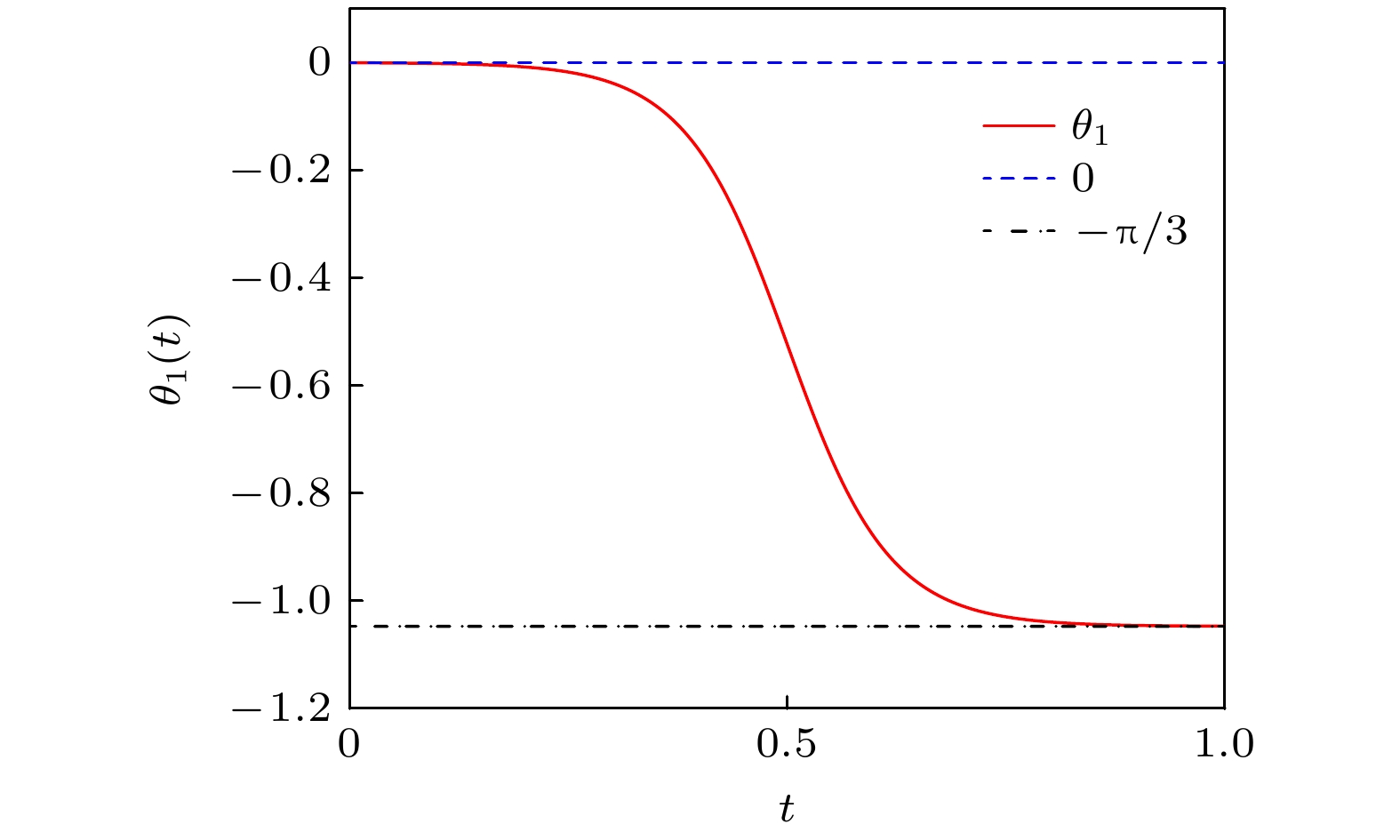
根据绝热演化理论^[65,66], 如果系统的初态处于某个本征态, 那么其可以持续沿该本征态进行绝热演化. 具体来说, 若在初始时刻系统的状态为$ |\psi_1\rangle $, 且处于本征态$ \zeta_0(t) $上, 则该系统将沿着本征态$ \zeta_0(t) $绝热演化. 方案的目标态为W态, 即 $ 1/2 (|\psi_1\rangle + |\psi_7\rangle + |\psi_{11}\rangle + |\psi_{15}\rangle) $, 可以进一步表示为 $ 1/2 |\psi_1\rangle + \sqrt{3}/2 |\varPsi\rangle $. 据此很容易得到关于$ \theta_1 $的边界条件, 即 $ \theta_1(0) = 0 $, $ \theta_1(T)=-\pi/3 $(其中T为系统演化时间). 为了更好地分析哈密顿量, 对其作幺正变换:

通过$ H_1=A_1^{\dagger}H_{{\mathrm{eff}}}A-{\mathrm{i}} A_1^{\dagger} \partial_t A_1 $, 可得

根据(10)式可以得到绝热演化需要满足的绝热近似条件是$ |\varOmega'(t)|\gg {|\dot{\theta}_1}/{\sqrt{2}}| $, 即需要保证不同本征态之间的耦合强度$ |{\dot{\theta}_1}/{\sqrt{2}}| $很小. 一些研究者提出可以增加反绝热项以消除或抑制这一绝热耦合^[59]. 容易看出, 在哈密顿量中添加项$ H^{(1)}_{{\mathrm{CD}}}={\mathrm{i}} A_1^{\dagger} \partial_t A_1 $恰好可以抵消引起绝热耦合的项$ -{\mathrm{i}} A_1^{\dagger} \partial_t A_1 $. 因此, 在原始哈密顿量中增加的反绝热项的形式可表示为

然而, (11)式表明所添加的反绝热哈密顿量要与$ |{\psi_1}\rangle $和$ |{\varPsi}\rangle $直接耦合, 这在实际操作中通常较难实现. 为了找到合适的哈密顿量, 进入超绝热绘景(即进行二次绘景迭代)进行分析. 哈密顿量$ H_{1} $((10)式)的本征值为 $ 0, \; \pm \varOmega'^\prime(t) $, 其中$ \varOmega'^\prime(t)= \sqrt{\varOmega'^2(t)+\dot{\theta}_1^2(t)} $. 对应的本征态分别为

式中$ \theta_2(t)=\arctan |\dot{\theta}_1(t)|/\varOmega'(t) $. 继续进行第2次幺正变换:

通过$ H_2=A_2^{\dagger}H_1 A-{\mathrm{i}} A_2^{\dagger} \partial_t A_2 $, 可以易得

可以求得在超绝热绘景中的反绝热项为$ H^{(2)}_{{\mathrm{CD}}}= {\mathrm{i}} A_2^{\dagger} \partial_t A_2 $, 即(14)式中的第2项. 容易求得其在原始绘景中的具体形式$ H^{(2)}_{{\mathrm{CD}}}={\mathrm{i}}A_1 \partial_t A_2 A_2^{\dagger} A_1^{\dagger} $,

哈密顿量$ H_{{\mathrm{eff}}} $上添加反绝热项, 可以得到修正后的哈密顿量为

由此可见, 添加的反绝热项$ H_{{\mathrm{CD}}}^{(2)} $是对原有脉冲的一种修正, 这种修正在实验中是易于实现的.

根据受激拉曼绝热通道的边界条件, $ \varOmega^{\prime}_{1} $和$ \varOmega^{\prime}_{2} $可以被选择为下面形式:

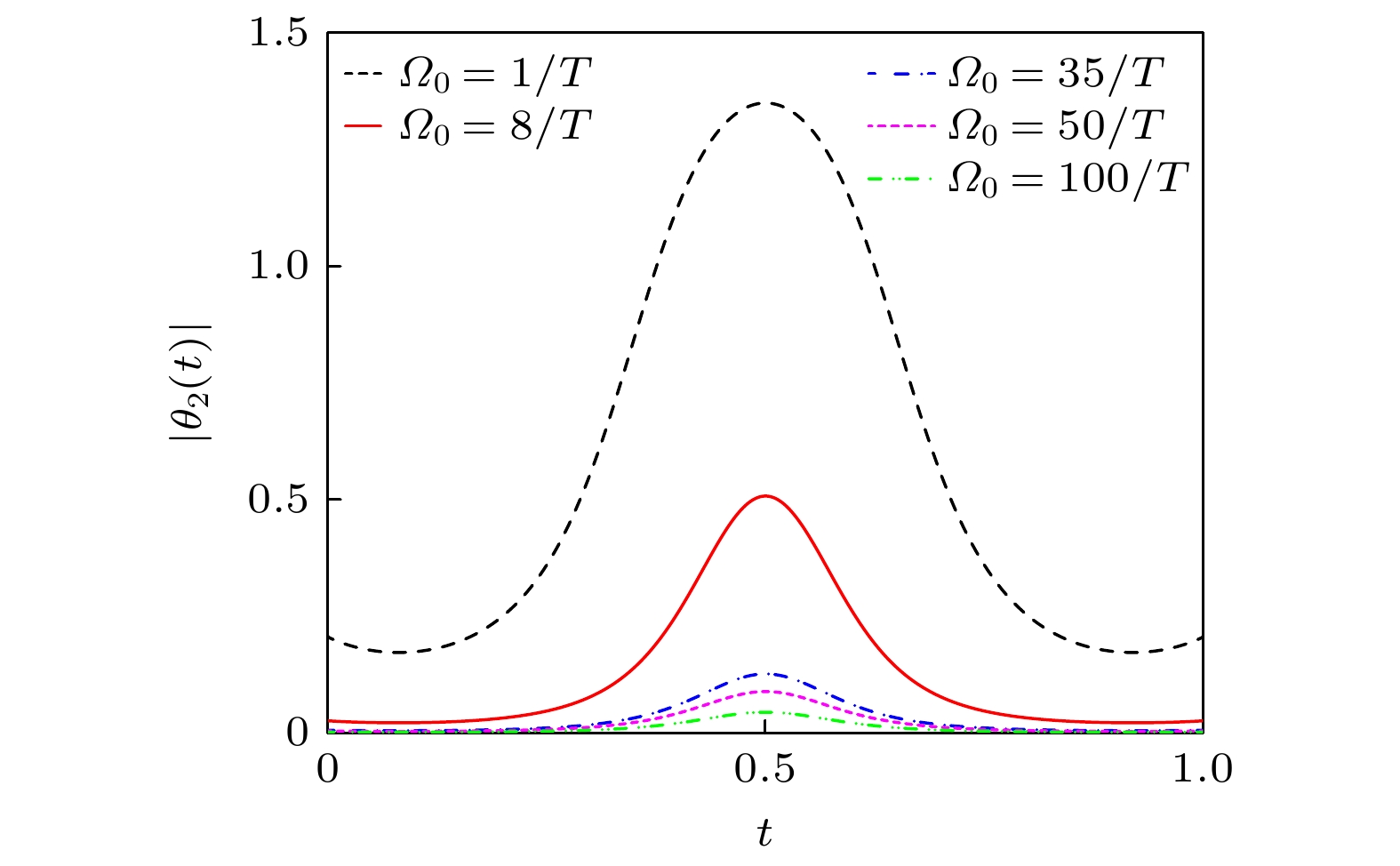
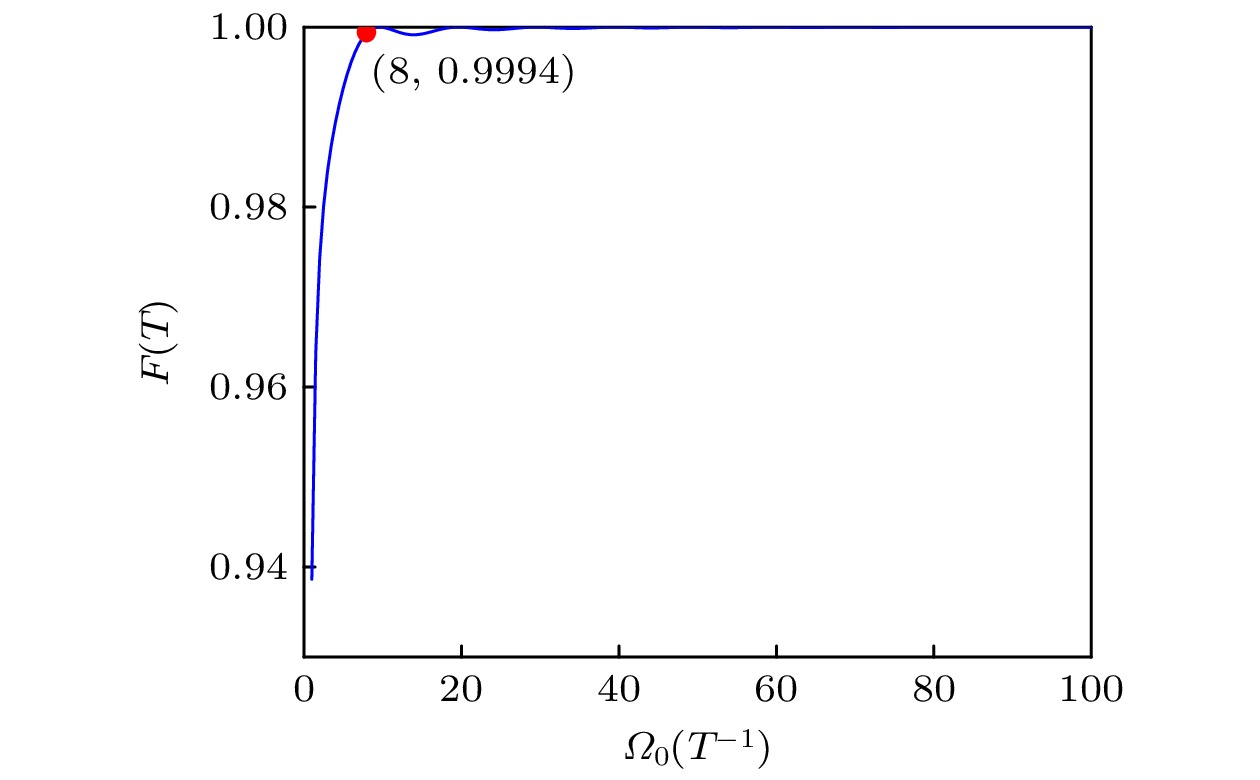
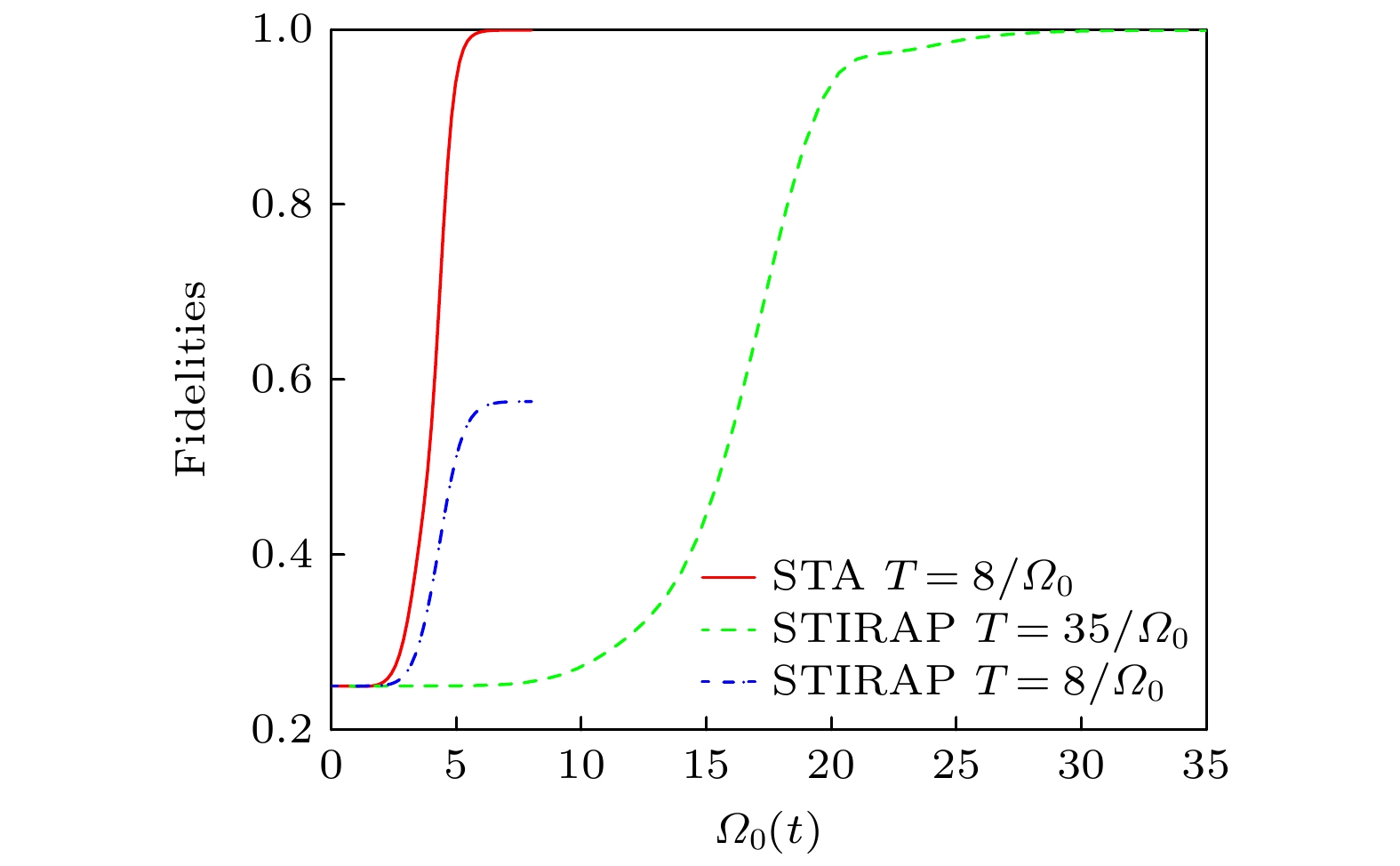
其中, $ \vartheta=-\pi/3 $, $ \varOmega_0 $为脉冲幅值, $ t_0 = 0.14 T $, $ t_{\mathrm{c}} = 0.19 T $, T为演化时间. 对于这两个脉冲, 可以确定$ \theta_1(t) $和$ \theta_2(t) $. 图3为与时间相关的$ \theta_1(t) $. 根据(7)式和(17)式, 可知$ \theta_1(t) $与$ \varOmega_0 $无关. 再结合图3, 可以得出结论, 无论$ \varOmega_0 $取任何值, 均满足条件$ \theta_1(0) = 0 $和$ \theta_1(T) = -\pi/3 $. 图4显示, 当$ \varOmega_0 $足够大时, 条件$ \theta_2(0) = \theta_2(T) $也能得到满足. 然而, 由于本文需满足极限条件$ \varOmega_k(t) \ll \{\lambda, v\}_{{\mathrm{min}}} $, 因此$ \varOmega_0 $不能过大. 为了选择合适的$ \varOmega_0 $, 图5绘制了最终保真度$ F(T) = |\langle{\psi_W}|\psi(T)\rangle|^2 $与$ \varOmega_0 $的关系图, 这里$ \psi(T) $是整个系统的最终状态. 根据图5, 选择$ \varOmega_0 = 8/T $, $ \lambda = 80/T $即可.

由于$ \varOmega'_1(t) $和$ \varOmega'_2(t) $这两个脉冲的形式较为复杂, 为了进一步提高实验的可操作性, 对其进行了高斯拟合. 这两个拟合后的脉冲的表达式为

两脉冲相应的参数为

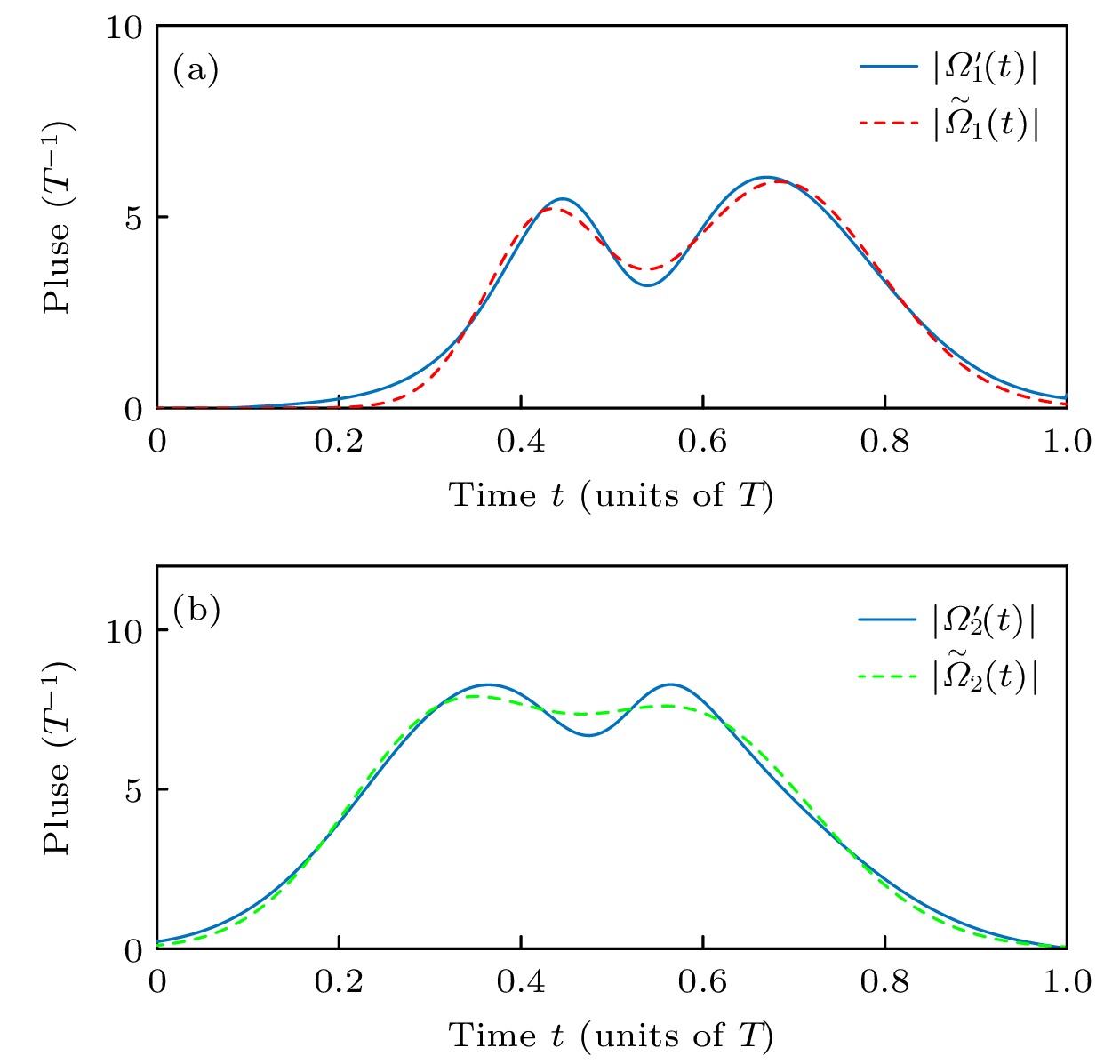
如图6所示, 拟合脉冲$ \widetilde{\varOmega}_1(t) $和$ \widetilde{\varOmega}_2(t) $与原始脉冲$ \varOmega'_1(t) $和$ \varOmega'_2(t) $高度重合, 因此可用拟合脉冲替代原始脉冲进行试验操作. 图7为在不同情况下, W态的保真度随时间的变化. 对比这3种演化, 可得出结论: 超绝热迭代方法演化到W态所需要的时间比绝热演化方法少很多.

此外, 为进一步验证方案的实际效果, 还考虑了原子自发辐射、腔以及光纤中光子的泄漏等退相干因素对方案的影响. 此时, 系统的主方程可以写为

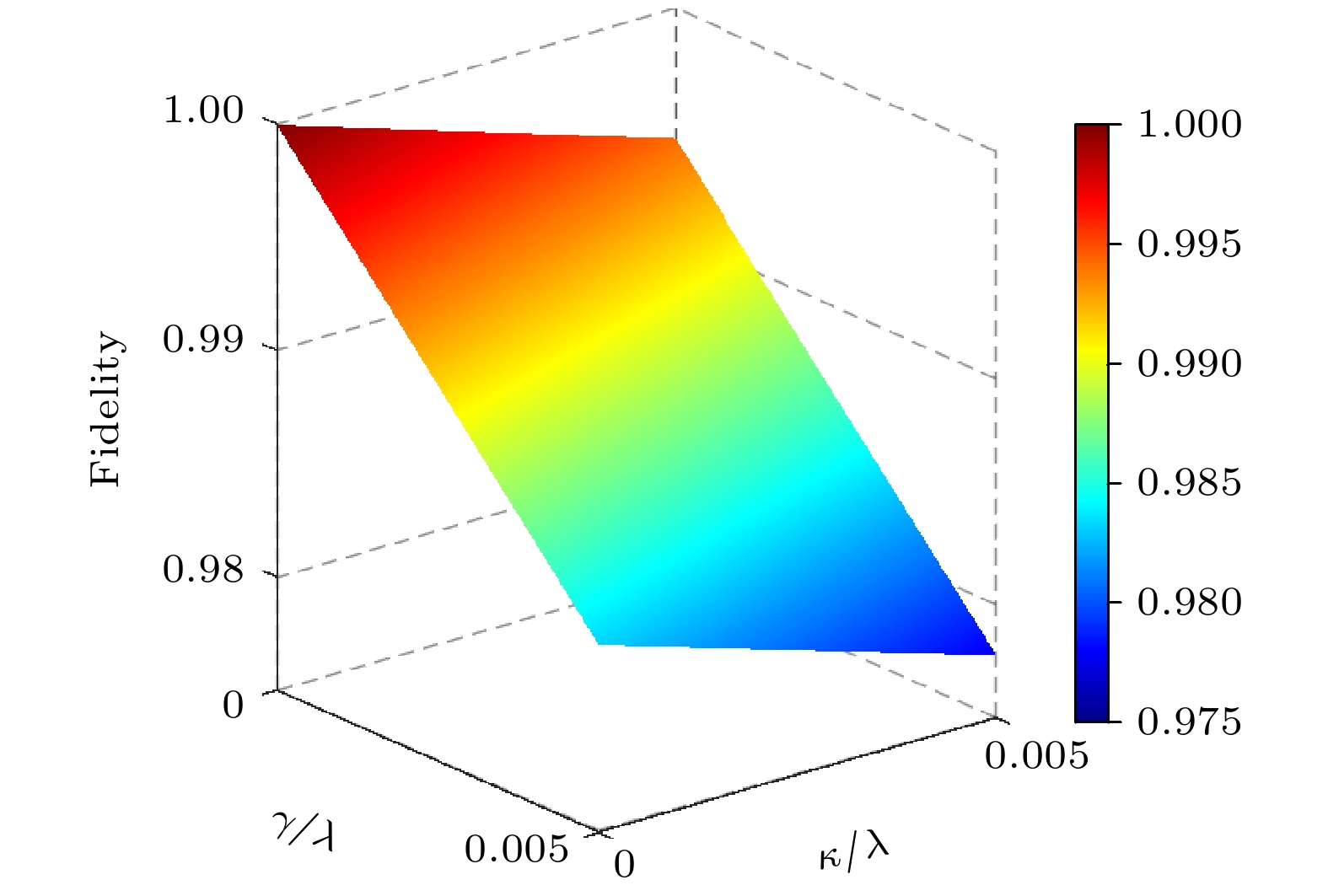
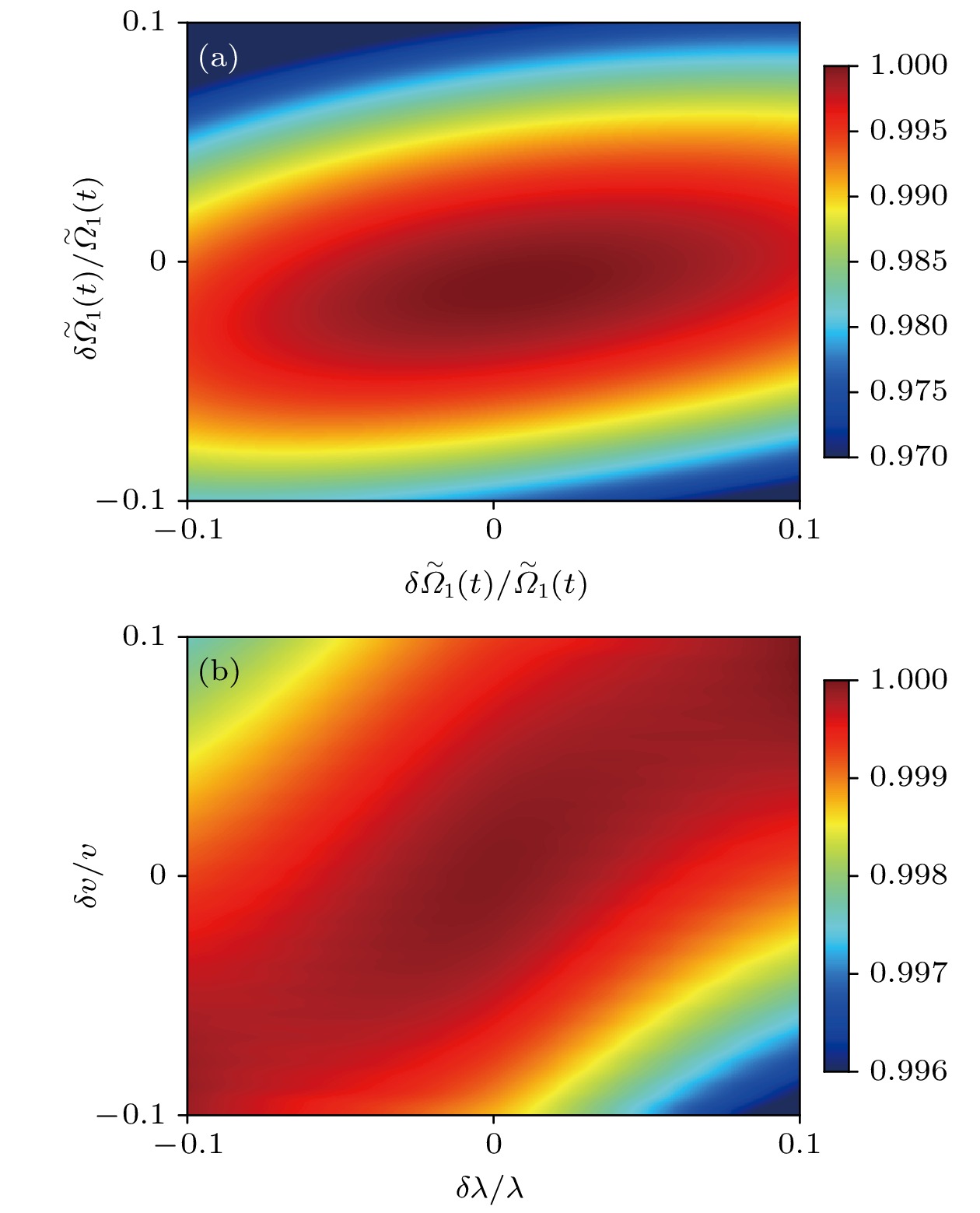
其中, $ L_k $描述了退相干效应, $ L_k^{R}=\sqrt{\gamma_k^{R}}|{E^{(1)}}\rangle_k\times \langle{R^{(1)}}| $是第k个超级原子$ |{R^{(1)}}\rangle\rightarrow |{E^{(1)}}\rangle $的自发辐射, $ L_k^{E}=\sqrt{\gamma_k^{E}}|{G}\rangle_k\langle{E^{(1)}}| $是第k个超级原子$ |{E^{(1)}}\rangle \rightarrow |{G}\rangle $的自发辐射. $ L_k^{c}=\sqrt{\kappa_k^{c}}a $是第k个腔中光子的衰减, $ L_k^{f}=\sqrt{\kappa_k^{f}}b $是第k个光纤中的光子的衰减. 为了便于计算, 令$ \gamma_k^{R} = 0.01\gamma, \; \gamma_k^{E}=\gamma $, $ \kappa_k^{f}= \kappa_k^{c}= \kappa $. 从图8可以看出, 超绝热方案对原子的自发辐射相比于腔-光纤系统中的光子泄漏更为敏感. 但总体而言, 该方案在面对原子自发辐射和光子泄漏引起的退相干效应时具有较强的鲁棒性. 即使在$ \kappa/\lambda=\gamma/\lambda = 0.005 $的情况下, 最终的保真度$ F(T) $也依然高于$ 97.5{\text{%}} $. 在实际操作过程中, 不可避免地会出现操作偏差, 因此我们进一步考虑了拟合脉冲$ \widetilde{\varOmega}_1(t) $和$ \widetilde{\varOmega}_2(t) $以及参数λ和光纤与腔之间耦合强度v的变化对最终保真度的影响. 图9展示了最终保真度随这些参数相对误差变化的关系. 从图9(a), (b)可知, 该方案对拟合脉冲和参数λ和v的波动是鲁棒的.

在实验中, 可将$^{87}{\mathrm{Rb}}$原子系综放在超高真空腔中的磁光阱中来制备里德伯超级原子. 将原子系综进一步冷却后, 最终的原子云可包含25000个原子^[48]. 考虑到实验参数^[67-70], 可选择在磁光阱中制备包含$n = 10^{4}$个$^{87}{\mathrm{Rb}}$原子的里德伯超级原子. 控制场以拉比频率$\sim 2\pi × 10 $ MHz驱动$|e\rangle\leftrightarrow|r\rangle$的跃迁, 中间态的辐射衰减率$\sim2\pi × 3$ MHz, 里德伯态的衰减率$\sim2\pi × 1$ kHz, 腔的衰减率$\sim2\pi × 0.66$ MHz, 在该实验条件下, 方案的保真度可达$ 97.7{\text{%}} $以上.

由于纠缠的量子比特数量越多, 非经典效应越显著, 对量子应用的意义也更为重要, 因此这里将在上述W态制备方法的基础上进一步推广至N粒子W态的制备. 其物理模型如图10所示, 其中N个里德伯超级原子分别置于不同的真空腔中, 第2个到第N个腔均与第1个腔相连, 且每个超级原子的有效能级结构与图1(b)相同. 这个系统下在旋转波近似下的相互作用哈密顿量为

假设初始态为$ |\psi_1\rangle=|R^{(1)}GG\cdots GG\rangle $, 假设$ v=\lambda $, $ \varOmega_k=\varOmega ~(k = 2, 3, 4, \cdots, N) $, 利用与(1)式—(8)式相同的推导方法, 可得最后的有效哈密顿量为

其中, $ |\varPsi\rangle = 1/\sqrt{{N}-1}(|GR^{(1)}G\cdots GG\rangle+ $ $|GGR^{(1)} \cdots GG\rangle + \cdots + |GGG\cdots R^{(1)}G\rangle + |GGG\cdots GR^{(1)}\rangle) $, $ \varOmega'_1(t)=(N-1)/\sqrt{N^2-1}\varOmega_1(t) $, $ \varOmega'_2(t) = 1/\sqrt{N^2-1} \times\varOmega(t) $. 对比(21)式和四粒子情况的(5)式, 它们只有系数上的不同. 显然可以通过类似四粒子 的W态的过程得到所期望的N粒子W 态:

$ 1/\sqrt{N}|R^{(1)}GG\cdots GG\rangle+\sqrt{N-1}/\sqrt{N}|\varPsi\rangle $.

本文提出了一种通过将超绝热迭代技术应用于里德伯超级原子体系且无需精确控制实验参数和交互时间的快速制备W态的方案. 该方案的一个关键特点在于, 反绝热哈密顿量与有效哈密顿量具有相同的形式, 从而简化了实验的实现过程, 降低了实验操作中的难度. 数值模拟结果表明, 该方案不仅能够高效制备W态, 还具有较高的保真度和实验可行性. 数值模拟分析显示, 即便在原子自发辐射和光子泄漏引起的退相干效应下, 方案的保真度依然能够保持较高的鲁棒性. 即使在原子自发辐射和光子泄漏都很大的情况下, 保真度仍然可以保持在97.5%以上, 表明了该方案在实际中的应用潜力. 总的来说, 本文提出的基于超绝热迭代技术的里德伯超级原子W态制备方案, 为未来的多粒子量子系统纠缠态制备提供了新思路, 并展现了较高的可扩展性与实用性.