首页
登录
注册
-
聚变反应需要参与反应的原子核具有足够的能量克服原子核间的库仑势垒. 通过提高燃料温度, 使原子核具有足够的动能穿透库仑势垒进而发生聚变反应是目前可控核聚变广泛采用的技术途径. 在激光驱动惯性约束聚变(inertial confinement fusion, ICF)研究领域, 较主流的点火途径包括中心点火[1,2]、快点火[3,4]、冲击点火[5]、整体点火[6]和双锥对撞点火[7]等实验方案, 而中心点火是目前唯一实现聚变点火的实验方案[8,9]. 中心点火方案在中心点火实验中, 采用激光或者辐射烧蚀燃料靶丸, 使靶丸壳层在烧蚀压的作用下高速向内压缩, 当燃料在中心汇聚时, 动能转变为燃料内能, 创造出高温高密度的等离子体中心热斑引发聚变反应. 因此, 提高中心热斑等离子体的温度是实现惯性约束聚变点火的必要条件. 等离子体中物质处于离化态, 离子和电子的温度既是独立的, 又相互影响. 内爆过程中, 离子主要参与动能转换过程, 电子主要参与辐射能转换过程. 电子和离子温度会在某些阶段发生分离, 又会通过能量交换趋于平衡. 通过内爆热斑温度的空间分布和时间演化, 研究热斑燃料能量积累和耗散过程, 能够帮助校准等离子体热传导模型, 校验辐射流体数值模拟程序; 在点火实验中, 热斑温度的空间分布和时间演化能够揭示热斑的自加热和等离子体燃烧传播过程.
ICF实验中, 热斑的离子温度主要通过核反应产物来诊断, 其中通过测量聚变中子的能谱展宽诊断离子温度的方法应用最为广泛[10–13], 这种方法通常只能给出热斑的时空平均离子温度. 在中心点火实验中, 热斑的尺寸一般仅有几十微米, 持续时间大约一百多皮秒, 测量如此小时空尺度内中子能谱的分布是极为困难的. 时间分辨磁反冲中子谱仪[14,15]和多点中子时间谱测量技术[16,17]是正在发展的两种时间分辨离子温度诊断技术, 离子温度成像技术[18]是目前正在发展的一种可能获得热斑离子温度空间分布的诊断技术, 但这三种技术尚未达到应用水平, 目前还没有能够在实验中直接测量热斑离子温度时空分布的方法. 目前的ICF实验中, 通常可获得总中子产额[19]、中子发射时间历程[20]和热斑中子图像[21–25]这三种与反应速率相关的诊断量. 核反应速率是离子温度的函数, 这三种诊断量再加上热斑的平均离子温度均含有离子温度时间演化和空间分布的信息, 为推算离子温度时空分布提供了约束条件.
本研究提出了一种可通过中子诊断数据推算一维内爆热斑离子温度时空分布的方法. 通过分析内爆离子温度演化的物理过程, 可以建立离子温度时空分布的简化参数模型. 中子产额、平均离子温度、中子发射时间历程和热斑中子图像等实验的主要中子诊断数据都与离子温度时空分布相关联, 以上述诊断数据作为约束条件用于求解出离子温度的时空分布中的未知参数. 本工作中将辐射流体算例作为模拟实验, 利用模拟实验计算出的诊断参数作为优化目标, 采用遗传算法计算出了一组最优化的离子温度时空分布, 优化解与模拟实验的离子温度时空分布符合较好. 验证了方法的有效性.
-
对于球一维分布的热斑, 相对于球心的位置坐标x的等离子体元在时间t的离子温度可以表示为Ti(x, t). 由于发生聚变反应时, 热斑处于阻滞状态, 燃料的运动几乎停滞, 可近似认为等离子元的位置坐标x不随t变化. 对于不同位置x处的体元, 离子温度随时间演化过程是相似的, 可以用相同的函数形式Ti(t, χ)描述, 其中χ是一组未知参数, 对于不同位置的体元, 参数χ不相同. 在聚变发生的时刻离子温度的空间分布存在一定的规律, 因此可以用χ(x, k)来描述参数组χ随位置坐标x的变化, 其中k也是一组未知参数, 这样离子温度的时空分布既可表示为自变量为x和t并含有一组未知参数k的函数Ti(x, t, k). 燃料的聚变反应率等于离子数密度与热核反应截面的乘积, 而热核反应截面是离子温度的函数, 因此实验获得的中子诊断数据都可以表示为离子温度的函数, 将这些诊断数据作为约束, 可以对未知参数k进行求解, 进而获得离子温度的时空分布.
-
内爆的压缩过程存在两种典型的物理机制, 一种是以冲击波传播行为为主导的冲击内爆. 驱动产生的高速冲击波在靶丸中心聚集碰撞使得碰撞位置的等离子体的温度和密度骤然升高, 引发聚变反应. 冲击压缩过程中燃料的温度时空分布与冲击波行为有很强的关联性. 另一种是惯性内爆, 惯性压缩是靶丸压缩的最大时刻, 壳层和燃料的动能几乎完全转化为内能, 整个热斑整体达到较高的温度密度, 进而产生聚变反应. 惯性压缩时燃料的温度空间分布比冲击压缩更加均匀, 变化过程也更为平缓. 在不同实验条件下, 两种压缩机制对聚变反应贡献份额不同, 可能存在其中一种为主导, 也存在两种机制产生的聚变反应数相当的情况. 本节主要以一维冲击压缩内爆为例对离子温度时空分布的建模方法进行了阐述.
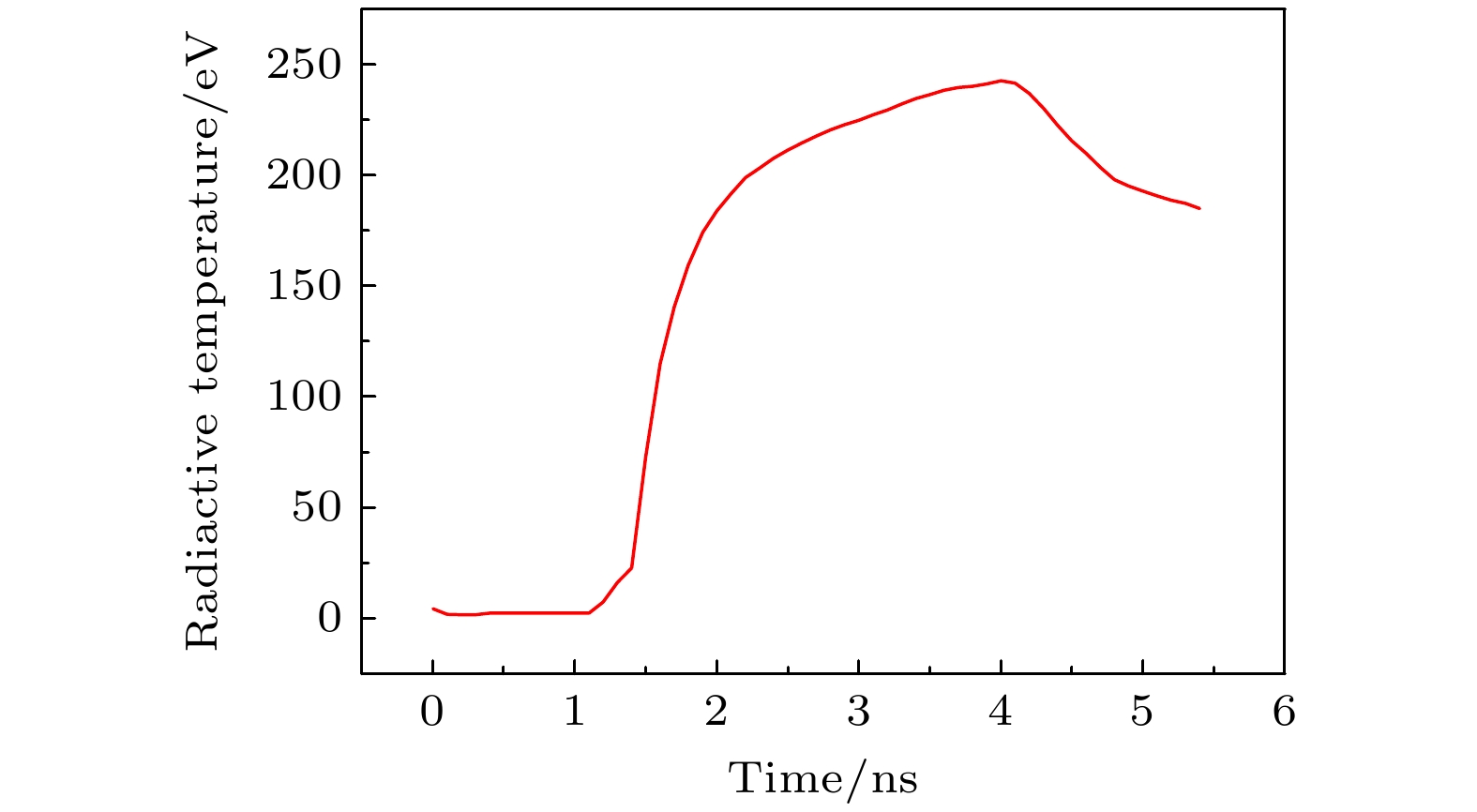
采用一维的辐射流体程序Multi1D[26]对典型的冲击压缩内爆进行了模拟. 典型算例采用了一个球形多层结构靶丸, 靶丸由外向内分别是碳氢(CH)烧蚀层, 玻璃(SiO2)球壳, 氘氚(DT)气体. CH烧蚀层的厚度为18 μm, 算例中将烧蚀层分为了18个体元, SiO2球壳的厚度为2 μm, 分隔为10个体元, DT气体区初始直径为500 μm, 气压为40个大气压, 分隔为50个体元. 靶丸每一层内初始网格等间距划分. 电子限流因子和离子限流因子均为0.06; 电子离子热传导乘子为1. 算例模拟了间接驱动实验方式, 驱动源使用了峰值辐射温度为250 eV的X射线辐射源, 辐射源辐射温度的时间波形如图1所示.
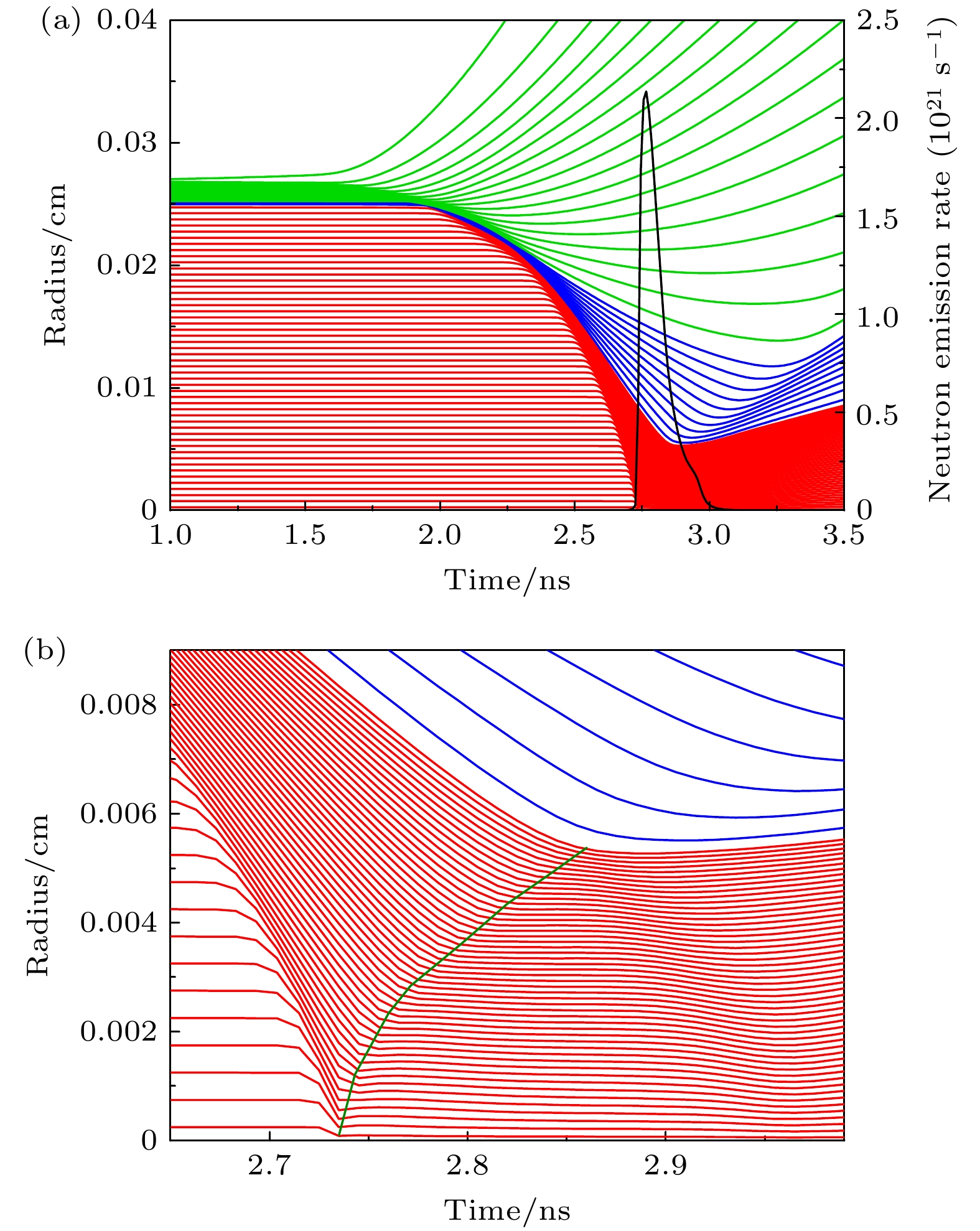
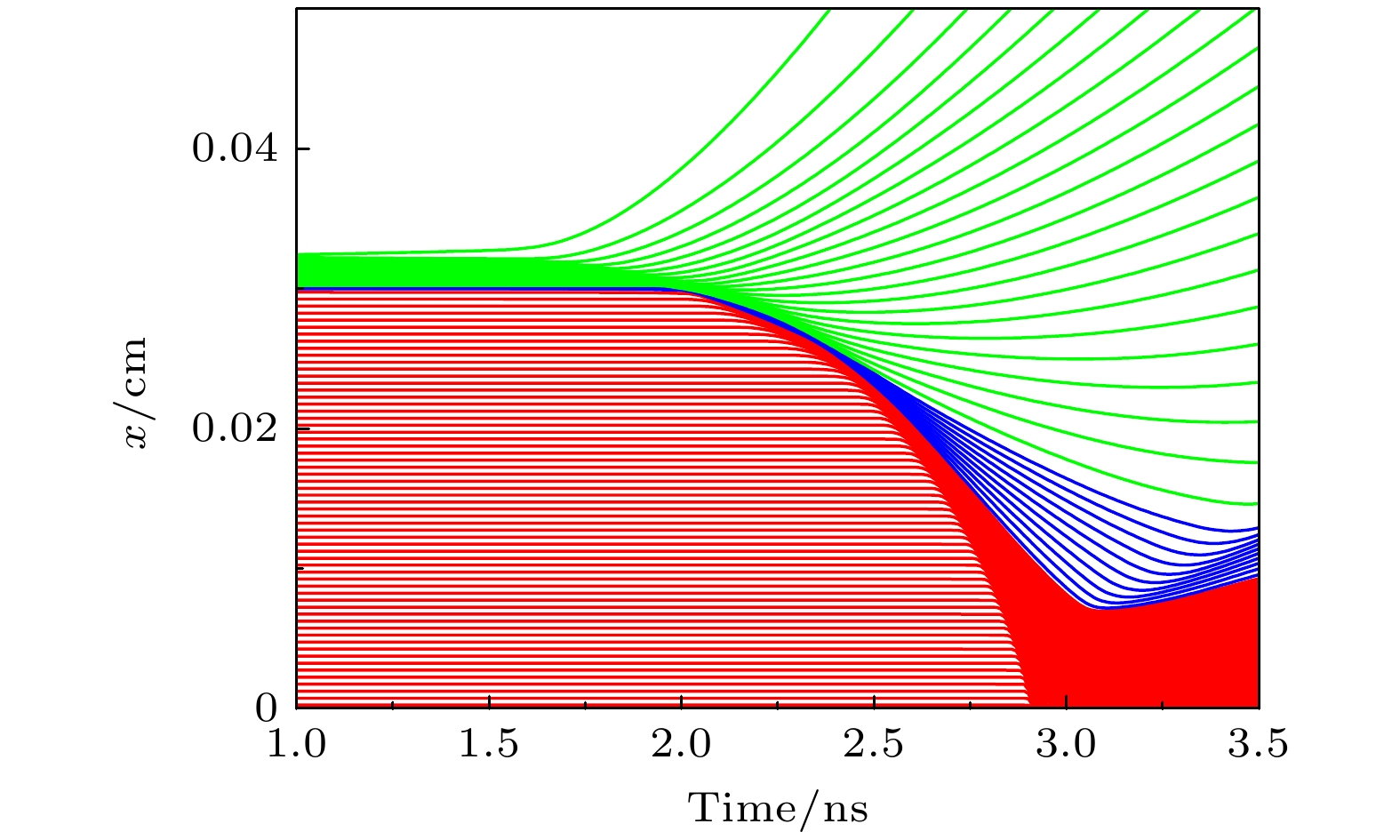
计算的内爆流线如图2(a)所示, 红色曲线是DT燃料, 蓝色曲线是SiO2球壳, 绿色曲线是CH烧蚀层. 辐射从1.5 ns开始烧蚀CH层, 使得外层CH向外膨胀, 将内层物质向内压缩, 压缩产生的冲击波依次经过CH层、SiO2球壳和DT燃料, 冲击波经过物质后使其高速向内压缩. 在2.72 ns时, 冲击波在靶丸中心汇聚, 并形成反射波, 图2(b)中的绿色曲线标示了反射冲击波在燃料中的轨迹, 反射冲击波向外传播过程中与向内汇聚的燃料碰撞, 使燃料减速进入阻滞状态, 并在2.86 ns达到燃料的外边界, 此时燃料压缩到最小尺度, 靶丸的收缩比约为5倍. 图2(a)中的黑色曲线是中子发射率曲线, 可以看出当冲击波聚心后中子发射率迅速上升, 并在2.77 ns时达到峰值之后逐渐衰减, 燃料燃烧时间的半高宽约0.09 ns.
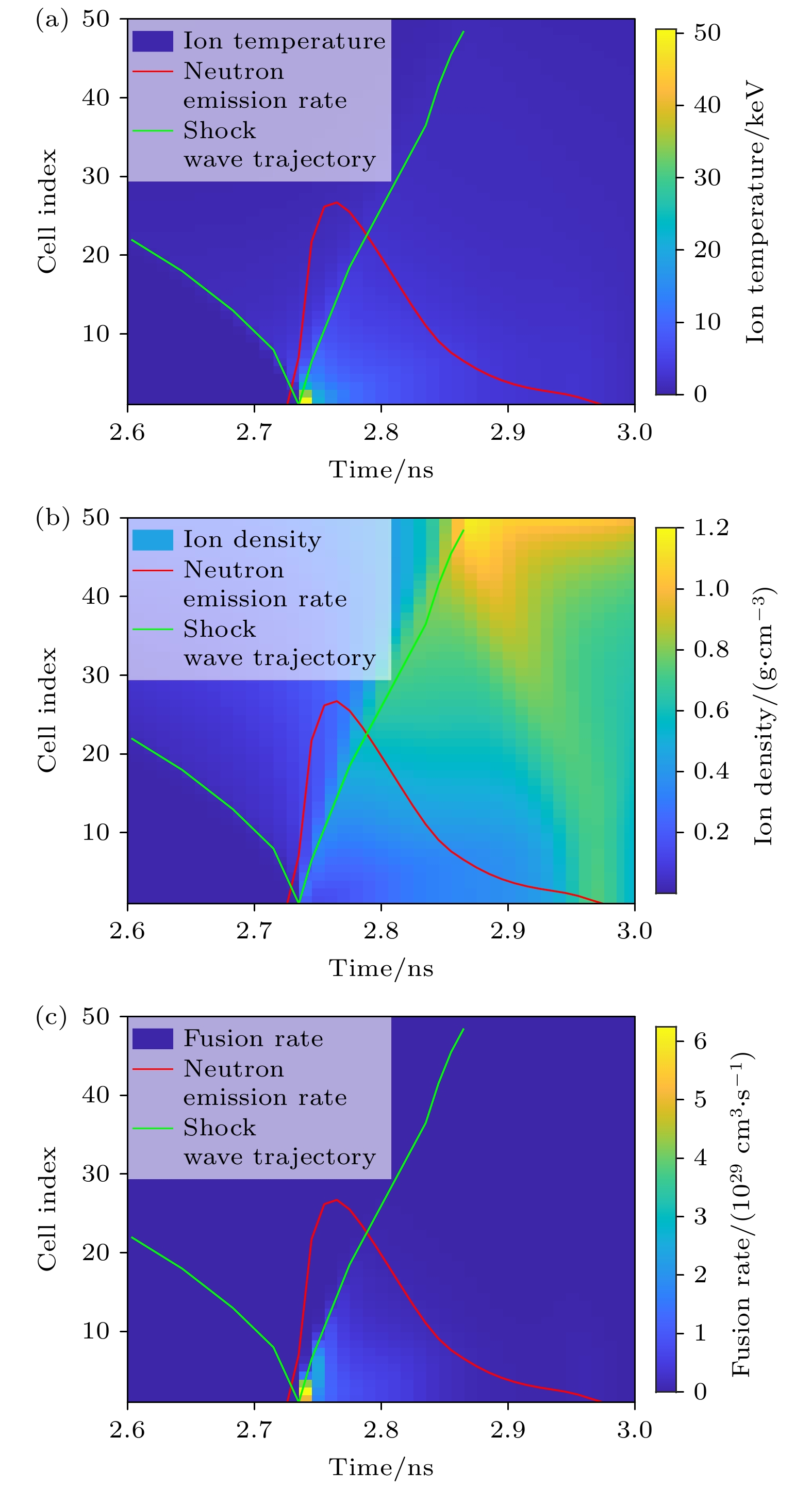
图3给出了热斑离子温度, 离子密度和聚变反应率的时空分布, 图中纵坐标为燃料区网格编号, 中心网格编号为1, 红色曲线是靶丸总的中子发射速率, 绿色曲线是冲击波的位置. 最初辐射烧蚀壳层产生的冲击波从外向内传播, 掠过燃料区, 并在大约2.74 ns时汇聚到靶丸中心, 在此之前燃料没有发生显著的聚变反应. 随后, 冲击波在中心碰撞并开始返回向外传播, 此时燃料仍在向内运动, 当向外的反射冲击波与向内运动的燃料发生碰撞, 使得冲击波波阵面位置处的物质温度和密度迅速上升, 并引发剧烈聚变反应, 随后燃料的离子温度和密度迅速降低. 靶丸在2.97 ns时压缩到最小, 此时燃料密度最高, 但离子温度相比峰值时已经显著降低, 聚变反应较弱. 模拟展示了典型的冲击压缩内爆的物理图像: 由冲击波的传播行为主导的聚变过程. 通常冲击压缩内爆靶丸收缩比较小, 热斑的离子密度不高, 整个聚变过程受离子温度的影响更大, 聚变反应速率与离子温度具有相似的时空演化过程, 它们都在冲击波到达时达到最大, 之后缓慢下降. 因此, 实验中中子发射时间波形和空间分布两种诊断数据, 能够反映离子温度的时空分布.
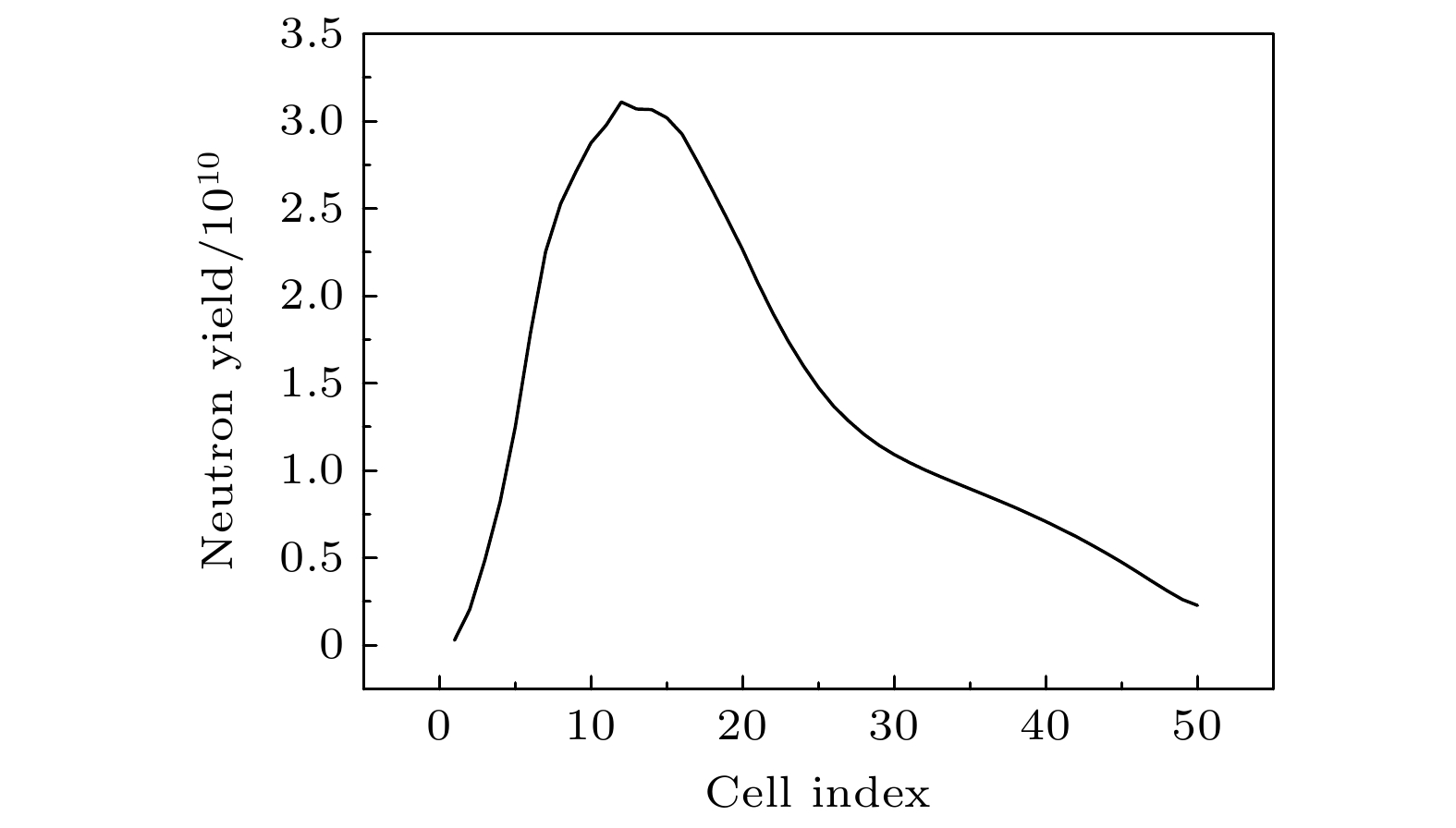
虽然热斑中心部的聚变反应率最大, 但其体积较小, 对中子产额的贡献并不高, 图4展示了不同网格中子产额的统计, 可以看出第5个-第30个网格, 也就是燃料的中间层对中子产额的贡献最大.
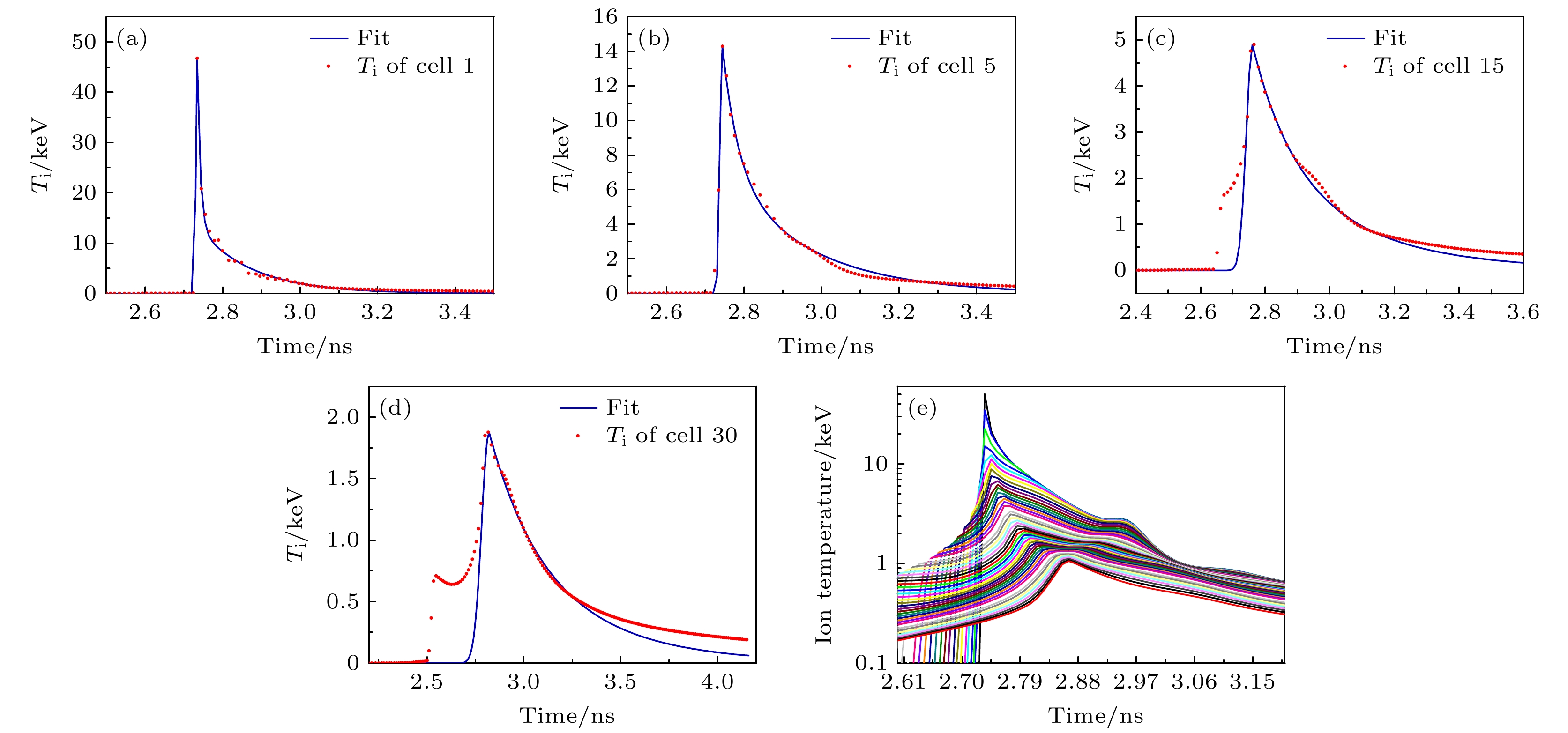
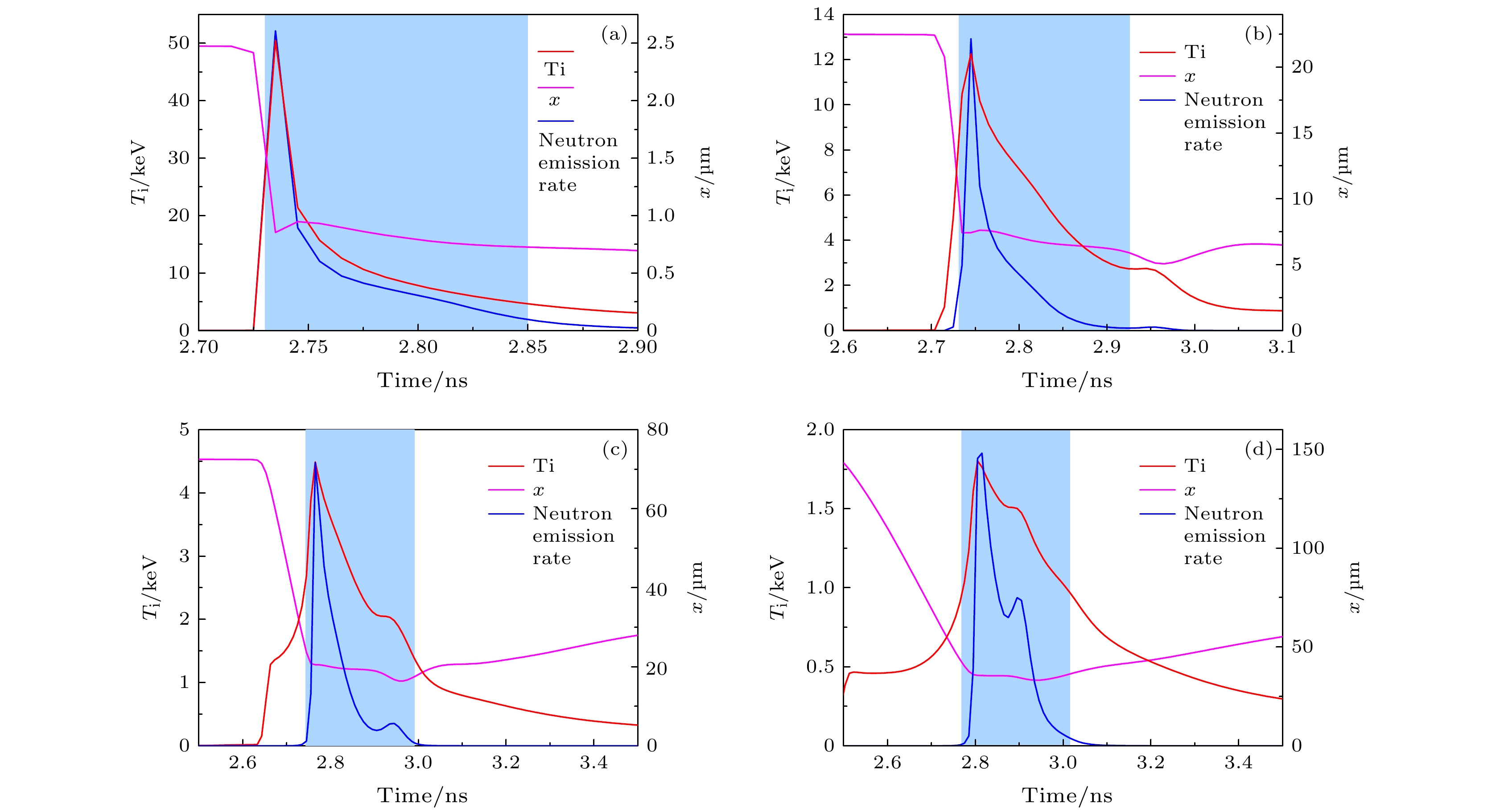
首先分析单一网格内的离子温度时间演化过程. 图5(a)—(d)分别给出了由内向外数第1个、第5个、第15个和第30个网格的离子温度-时间曲线. 离子温度的时间演化分为几个不同的阶段. 当冲击波向内传播首次经过网格时, 离子温度快速上升, 冲击波掠过网格后趋于稳定, 当冲击波在中心折返再到达时温度会第二次快速上升并达到最高点, 随后离子温度缓慢下降, 下降过程中, 当靶丸压缩达到最大时离子温度会稳定一小段时间, 然后继续下降. 不同的网格温度的变化模式是相似的, 不同的是几个过程的发生时间有差异, 对于靠近中心的网格, 冲击波第一次掠过和返回的时间间隔相隔很近, 因此两次温度上升的过程基本融合在一起, 而外层网格这两个过程间隔较长, 可以清晰地分辨. 图5(e)给出了所有网格的离子温度-时间曲线. 可以看出曲线沿半径方向呈一定规律性的变化: 离子温度的峰值沿半径向外递减; 外侧网格的温度峰值时刻晚于内侧; 温度下降阶段, 外侧网格的温度下降更慢; 阻滞阶段离子温度由内向外逐渐降低.
基于离子温度时空分布的规律, 我们可以建立一个含有未知参数的模型对其进行描述, 然后利用实验中得到的中子诊断数据作为约束, 求解出模型中的参数, 过多的模型参数会增加参数求解的难度, 在建立参数模型时需要考虑合理的简化, 使模型数学形式尽量简单, 参数尽量少. 中子的产生主要集中在持续百余皮秒的阻滞阶段, 这给定了诊断方法所能观察的时间窗口, 参数模型仅需要描述诊断时间窗口内温度的分布. 在诊断时间窗内单个网格的升温过程和降温过程由不同的物理因素所主导, 可采用分段函数对这两个温度变化过程分别进行描述. 由于聚变时, 燃料处于阻滞状态, 诊断时间窗内每个网格可视为静止, 因此模型中的位置坐标与时间不相关. 热斑温度变化受冲击波传播过程影响, 因此不同网格之间温度变化过程存在关联, 可在分段函数中引入一些待定参数描述温度的空间分布. 通过以上两个步骤即可建立描述热斑离子温度时空分布的数学模型, 具体的建模过程如下:
如图6所示, 红色曲线是离子温度, 蓝色曲线是中子发射速率, 阴影部分表示诊断数据的观测时间窗口. 虽然在实验过程中, 离子温度经历了多个演化过程, 但在建立离子温度时空分布参数模型时可以只考虑表征聚变反应持续时间内的温度变化. 当冲击波到达位置x时, x处的温度达到峰值, 将温度峰值时刻用tp表示. t ≤ tp时, 离子温度快 速上升, 这个过程可以用一个高斯函数近似描述, t ≥ tp时, 能量会向外层网格传导导致网格温度快速下降, 局域温度趋于平衡后, 温度的下降速度会减慢, 这个过程可以用一个双指数函数描述, 位置为x网格的温度-时间曲线表示如下:
式中, tp表示离子温度的峰值时刻, H表示峰值时刻的温度, υ影响上升沿的宽度, τ1表示下降沿的快衰减过程, τ2表示下降沿的慢衰减过程.
为了检验温度时间曲线的有效性, 在计算算例中挑选了不同位置网格按照(1)式的形式进行拟合, 图5中的蓝色实线是拟合结果, 可以看出在诊断观测窗口内, 拟合曲线与温度-时间曲线符合得较好.
整个实验过程中, 热斑等离子体是流体状态, 燃料的位置是时变的. 从图2可以看出, 等离子体在辐射的驱动下, 不断向内压缩, 当压缩到最大时, 处于短暂的停滞状态, 而聚变反应即发生在这一阶段. 图2(b)是阻滞阶段的网格运动轨迹放大图, 其中绿色曲线是发射冲击波波前的位置. 可以看出当反射冲击波掠过之后, 等离子体收缩的速度骤然减缓, 在一两百皮秒的时间内, 网格位置几乎无变化. 图6中紫红色的线条表示网格坐标随时间的变化, 在聚变反应发生的主要时间内, 网格的位移仅有1—2 μm, 在压缩最大时刻, 网格的最大位移也不超过5 μm, 远小于热斑的半径(约50 μm), 同时这个尺度的变化引起的空间部分差异小于中子成像的分辨率(大于10 μm), 难以反映在诊断数据上, 因此在模型中近似认为发生聚变反应时的热斑等离子体是“静止”的, 即网格的位置x是不含时间t的, 这极大降低离子温度时空分布模型的复杂度.
(1)式将温度-时间曲线在形式上统一起来, 对于不同的x, (1)式中的5个参数是不同的, 显然不同位置的温度存在物理上的关联, 因此我们可以将5个参数用x的函数表示, 以此表征温度的空间分布规律. 前文的分析提到, 温度的时空分布主要由反射冲击波的行为主导. 根据一维球形冲击波的自模拟特性[27], 冲击波R半径随时间t的增长满足以下关系:
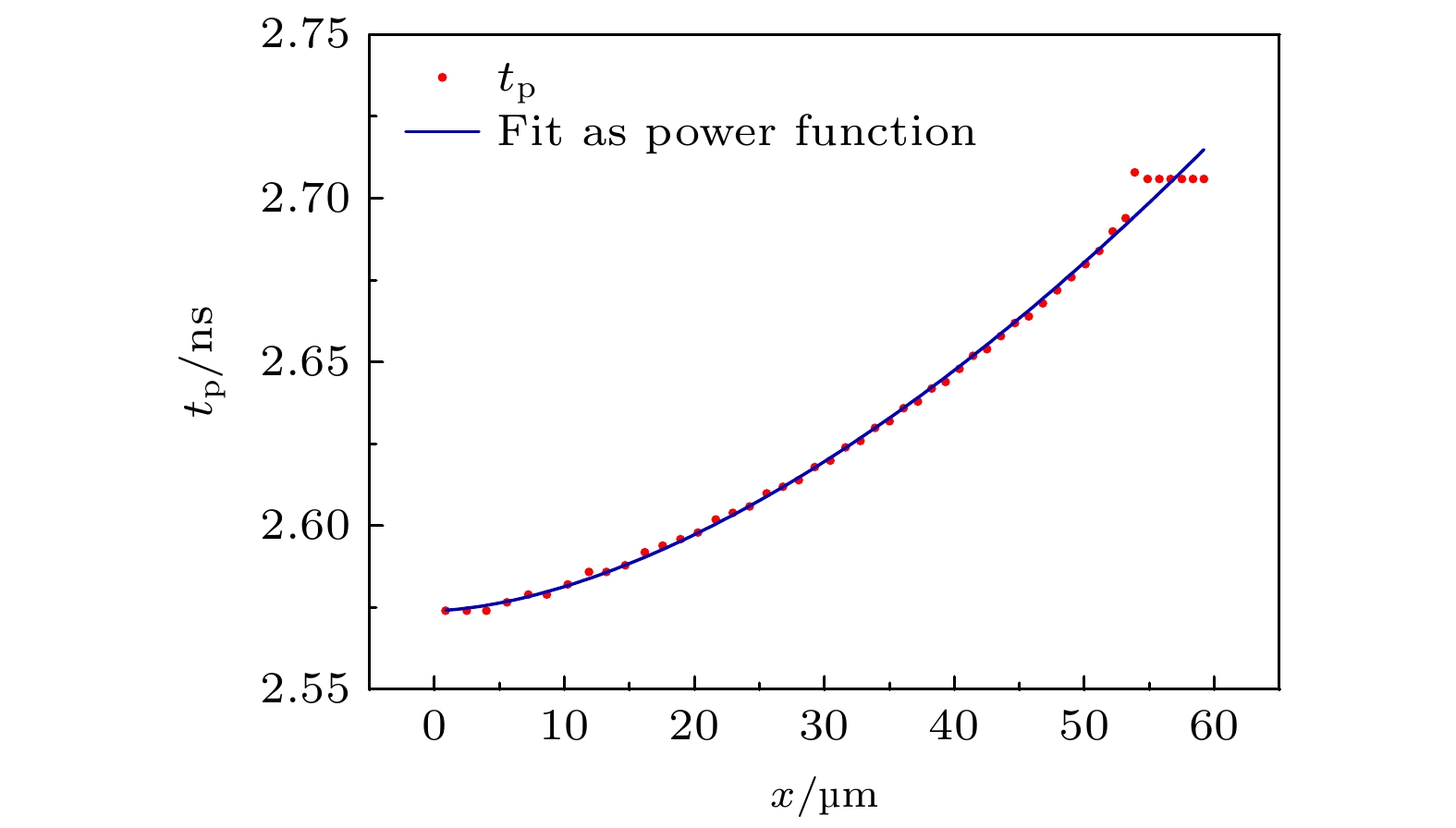
其中B和α是常数, Ti到达峰值的时刻tp即冲击波到达x的时刻, tp可表示为
其中t0是反射冲击波在球心产生的时刻; a1和b1为与实验物理过程有关的常数, 冲击波速度是逐渐降低的, 因此b1 > 1且a1 > 0. 图7是统计了模拟算例不同位置的离子温度峰值时刻, 将它们按照(3)式的形式进行拟合, 可以看出除了最外层的几个网格处于同一时刻, 热斑中大部分网格的tp很好地符合了幂指数形式. 某个网格内温度的上升时间取决于冲击波掠过该网格所用时间, 冲击波掠过网格的时间反比与冲击波在该位置的速度正比于网格的宽度:
2.2节模拟的典型算例中, 冲击波掠过一个网格的时间仅有几个皮秒, 相对整个温度演化过程来说非常短, 因此可以将υ作为常数来处理. H, τ1和τ2均与离子的热传导与温度平衡有关, H是单调减小的, 且变化速率随x降低, τ1表征温度的快速衰减, 越靠近球心的温度越高, 因此τ1是随x单调增加的. 这两个量的参数可以用以下函数表示:
τ2表征的是温度的慢速衰减, 当离子温度快速下降以后, 热斑内不同区域的温度逐步趋于平衡, 不同位置的温度下降趋势是较为相似的, 可将温度下降过程中表征慢成分的τ2当作常数处理. 将(3)式和(5)式代入(1)式, 就可以得到一个含有10个未知参数的离子温度时空分布数学模型.
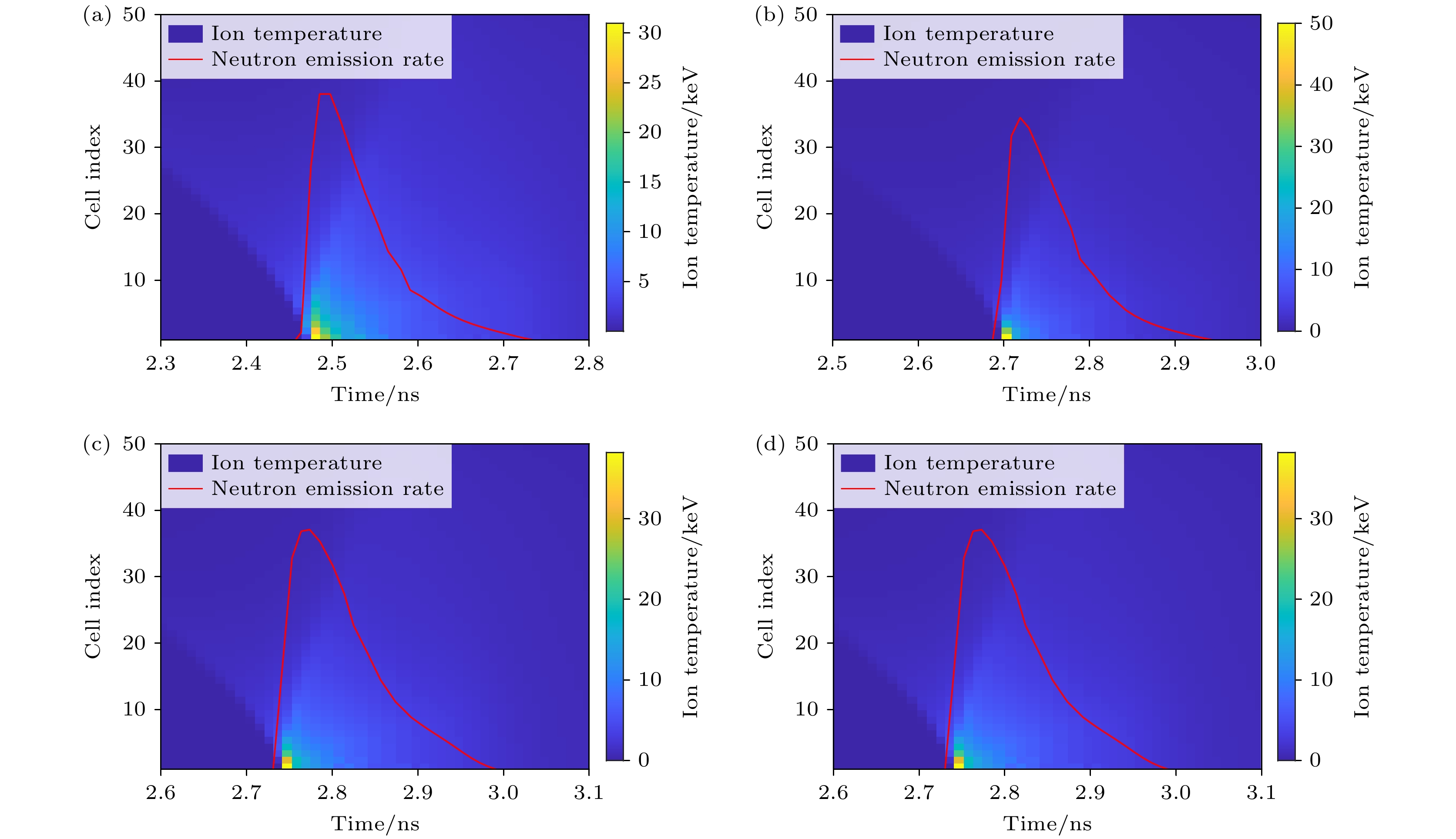
除了上文分析的典型算例, 通过模拟分析了更多不同条件下离子温度的时空分布. 图8分别展示了在标准算例的初始条件下, 辐射强度提升1.2倍(图8(a)), 壳层厚度减薄为16 μm (图8(b)), 燃料气压降低到35 atm (图8(c)), 电子离子热传导率降低20% (图8(d)) 4种情况下离子温度时空分布. 这几个算例中, 聚变反应均主要由冲击压缩引发, 其离子温度时空分布符合相同的特征, 即每一个网格的温度呈快速上升、缓慢下降的演化过程, 冲击波达到的时刻决定了不同网格的温度峰值时刻.
-
在实验中, 获得的中子产额、离子温度、中子发射时间历程和热斑中子图像都与热斑的平均离子温度存在关联, 中子发射时间历程和热斑中子图像含有离子温度的时间和空间分布信息, 将这些诊断量作为约束条件, 可对建立的离子温度时空分布模型的未知参数进行求解. 除了平均离子温度, 其他三个诊断量都与聚变反应率直接相关. 热斑中燃料的聚变反应率可表示为
式中,
$ \left\langle {\sigma v} \right\rangle $ 是该反应的热核反应截面, 它是离子温度Ti(x, t)的函数[16]; n1和n2表示两个聚变核的原子核数密度, 通常两种燃料等比混合, n1 = n2 = 0.5n, n是热斑原子核的总数密度; 由于热斑等离子体在宏观上仍是电中性的, 对于氢的同位素, 离子的数密度与电子的数密度相等, 在实验中, 电子的密度可以通过X光光谱进行诊断.以下讨论以DT实验为例, 每一次聚变反应放出一个中子, 因此F也可以表示中子发射率. 聚变速率曲线可表示为特定时刻聚变反应率在空间的积分:
式中,
$ {\eta _1} $ 是聚变速率测量系统的效率, 表示1个源中子在诊断系统中产生的信号强度.实验的总中子产额等于聚变速率曲线对时间积分:
实验的离子温度可通过实验的中子能谱来计算. 离子温度为Ti的等离子体发生聚变反应产生的中子能谱符合高斯分布:
式中, c是常数, 对DD中子为38.4, DT中子为75.1. 离子温度正比与高斯分布的标准差, 可表示为
从前文的分析可知热斑是温度不均匀的等离子体, 因此整个热斑中子能谱可表示为
式中,
$ {Y_{\text{n}}}({T_{\text{i}}}) $ 表示温度为Ti的等离子产生的中子产额;$ {Y_{{\text{ntotal}}}} $ 表示热斑产生的总中子产额. 热斑的平均离子温度可由以下公式计算:即热斑的平均离子温度等于每个时空格点的离子温度以其中子产额贡献为权重的加权平均值.
对于一维分布的热斑, 可以用以x为自变量的函数V(x)表示热斑单位体积中子发射率随坐标的变化, V(x)由聚变反应率对时间积分得到:
式中,
$ {\eta _2} $ 表示中子成像系统的探测效率. 由于热斑符合一维分布, 根据阿贝尔变换, 热斑中子在一个观测方向上的投影图像分布为式中, R是图像中像素点距热斑中心的距离; xD表示热斑的半径. 由此就将4种重要诊断量表示为时空分布的离子温度为自变量的函数. 利用这些诊断数据就可以对建立的模型中的位置参数进行求解.
-
离子温度模型的待求解参数有10个, 参数的组合数量是相当庞大的, 无法采用遍历的方式获得最优解, 本文采用基于遗传算法的参数优化方法进行参数求解. 现有实验诊断数据集L, 其中也包含n个诊断数据点
$ \left( {{l_1}, {l_2}, \cdots {l_n}} \right) $ , 中子产额和平均离子温度分别给出一个数据点, 聚变速率曲线和中子图像均为一条一维曲线, 可以给出多个数据点. 这一组数据的不确定度为$ \left( {{\sigma _1}, {\sigma _2}, \cdots {\sigma _n}} \right) $ , 对于离子温度时空分布模型的一组给定的参数集合$ \chi $ , 可以通过2.3节的方法计算得到一组诊断数据$ H(\chi ) $ , 给出与诊断数据相对应的n个数据点$ ( {h_1}, {h_2}, \cdots {h_n} ) $ . 则定义适应度函数:输入不同的参数组合
$ \chi $ 计算出f, f越小说明参数越优. 遗传算法在随机搜寻过程中逐步筛选出“优良”的参数, 将其保留组合, 直至获得一组最优解. -
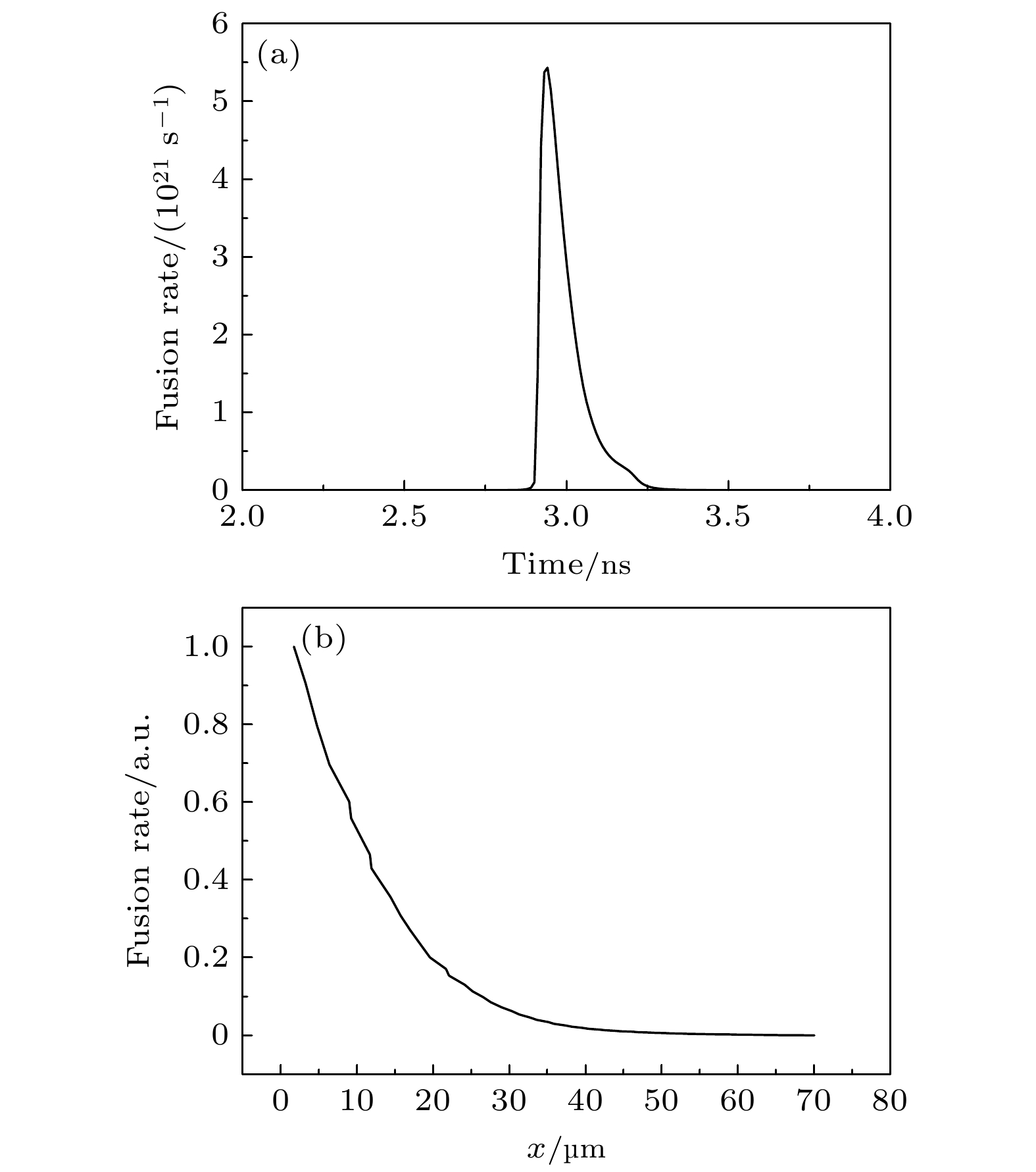
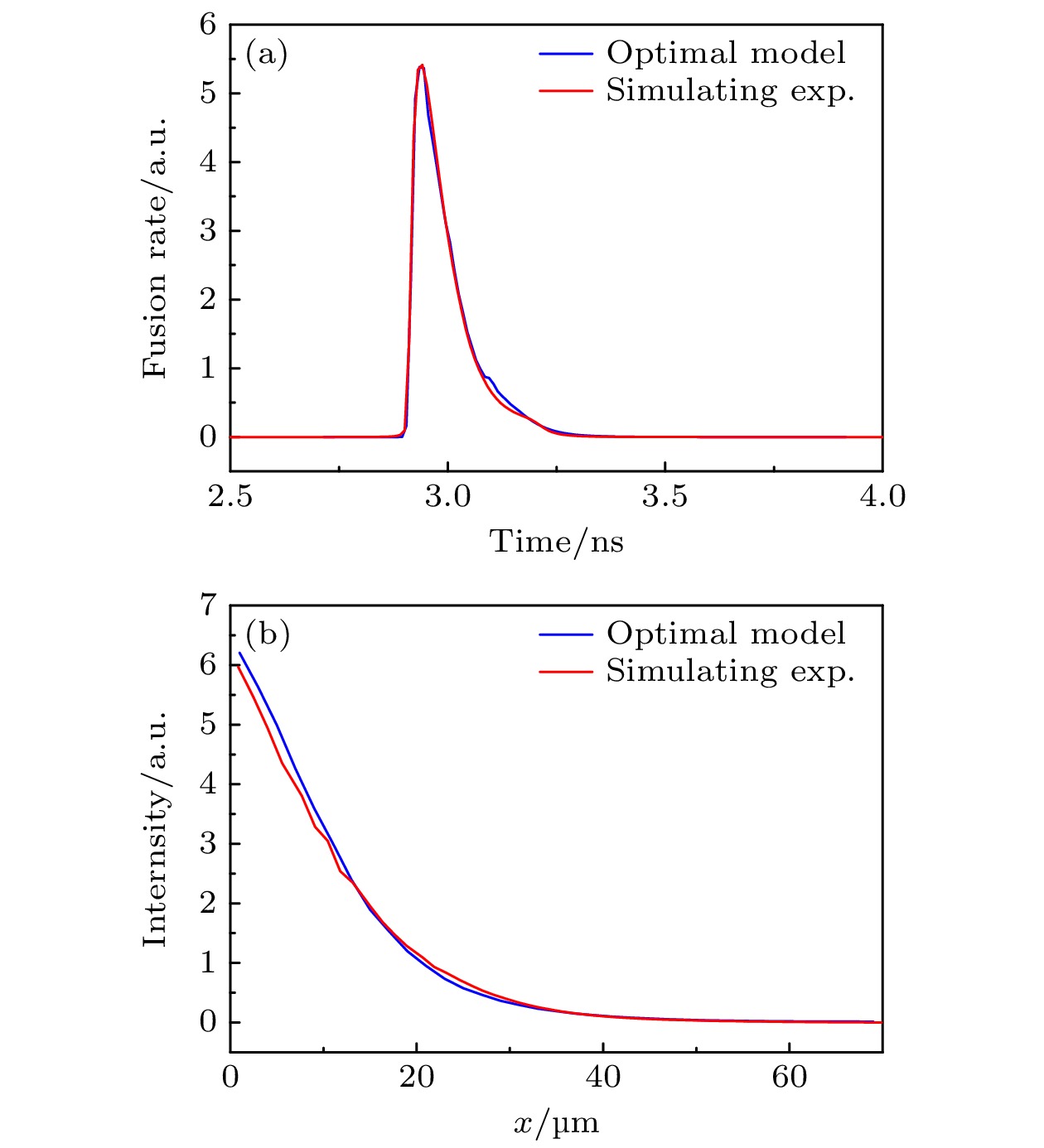
为了验证模型和方法的有效性, 我们采用Multi1D开展一次模拟实验, 利用解析模型计算模拟实验的离子温度时空分布. 模拟实验采用的计算参数如下: 驱动源采用图1的辐射温度曲线; 靶丸内径600 μm, 中间充50个大气压DT气体; 中间为2 μm SiO2, 最外层为22 μm CH, 电子限流因子和离子限流因子为0.06; 电子离子热传导乘子设置为0.7. 将模拟的结果进行处理, 计算出实验中的4种诊断数据: 中子产额为5.89×1011, 平均离子温度为5.3 keV, 聚变速率曲线如图9(a), 中子图像径向强度分布为图9(b). 靶丸网格流线如图10所示. 计算同时给出离子密度的时空分布用于接下来的参数优化求解.
为了提高计算效率, 可以根据已知的信息先给出一组初始的参数, 并给每一个参数划定一定的求解区间, 这组初始参数越接近最优解, 求解区间越小, 计算收敛的速度越快, 计算结果越准确. 为了模拟真实实验数据分析过程, 在给定初始值和参数求解区间时, 仅依据能够在真实实验中可以给出的诊断数据, 而不考虑其他的计算结果. 给定参数的初始值后, 围绕初始值利用遗传算法进行最优解搜索, 在迭代5000次后, 得到表1的最优参数值, 表1参数对应的时间, 长度和温度的单位分别是: ns, cm和eV. 最优参数给出的中子产额为5.92×1011与模拟实验差异小于1%, 平均离子温度为5.8 keV与模拟实验差异约9%, 最优解给出的聚变速率曲线和中子图像空间分布计算结果见图11, 可以看出与模拟实验给出的诊断数据符合得很好.
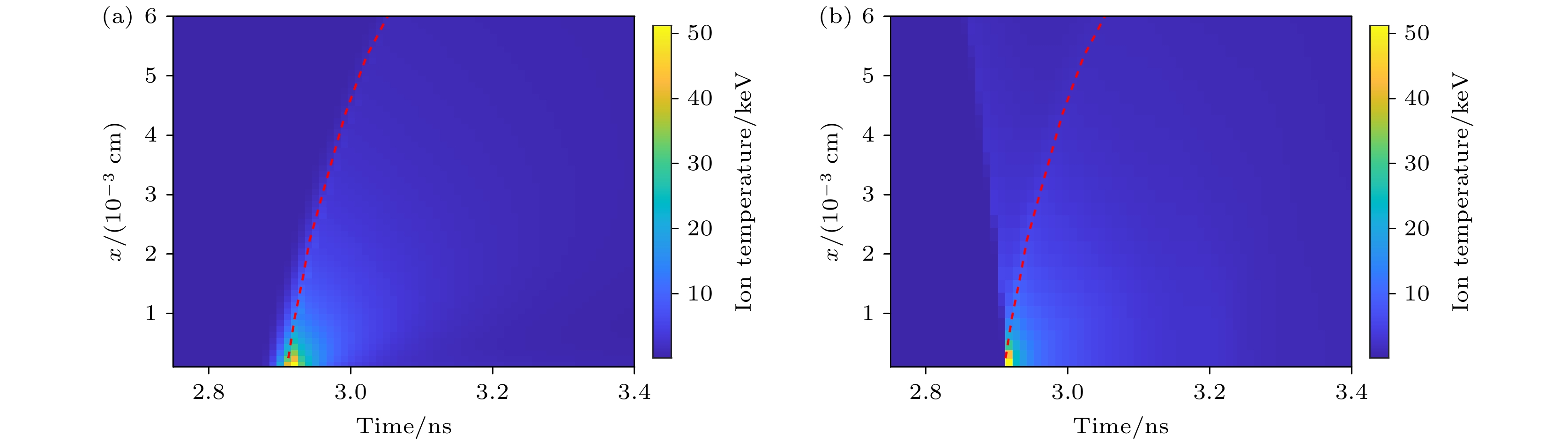
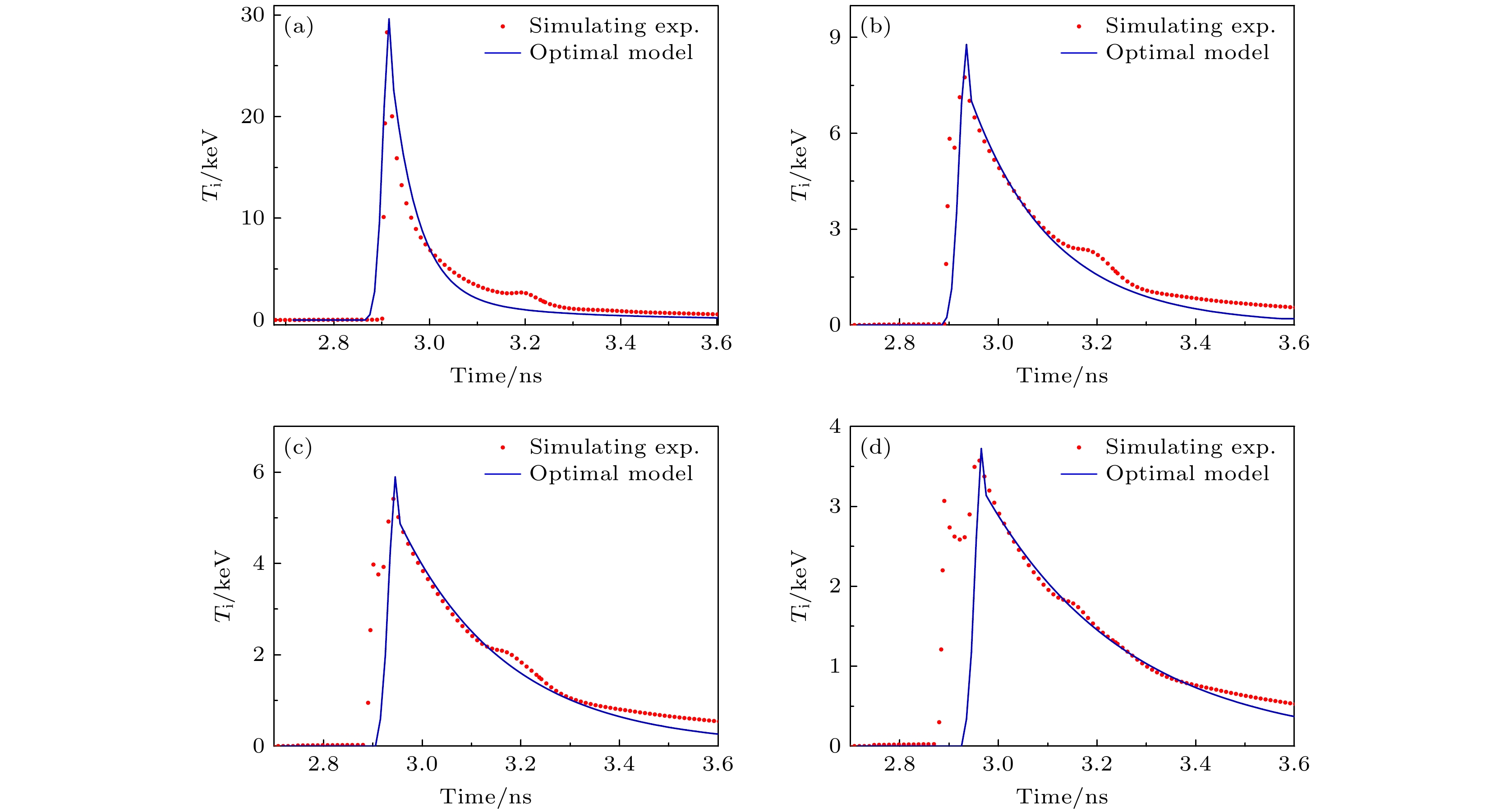
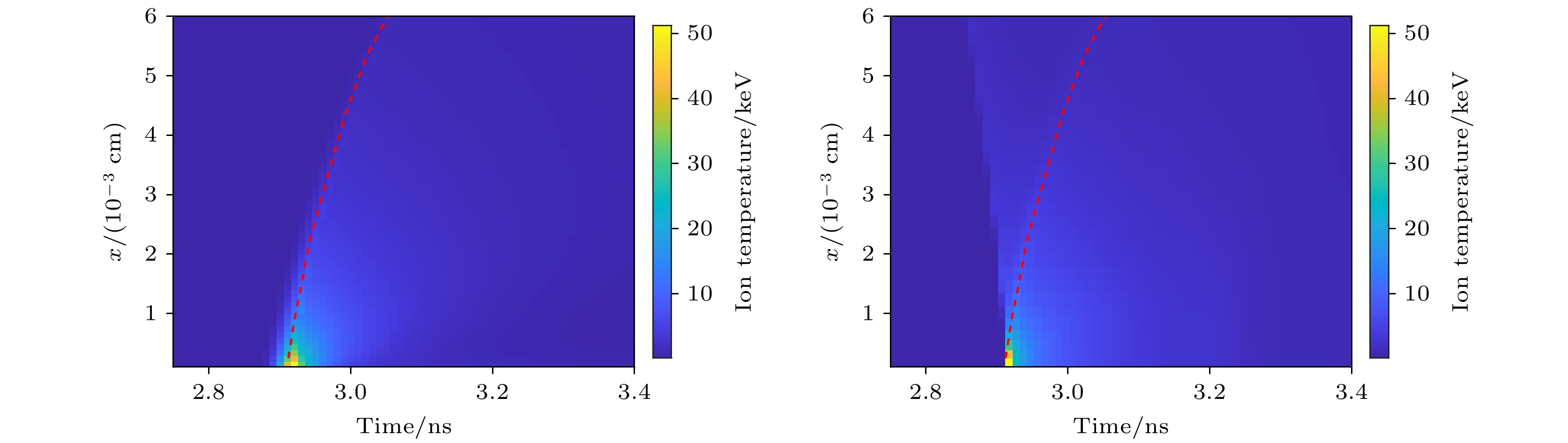
图12是计算出的离子温度时空分布与模拟实验产生的离子温度时空分布对比, 图中红色虚线是冲击波的轨迹, 也对应了每一个体元的温度最大值, 两幅图均采用了相同的色标. 图13是主要聚变反应区几个不同位置的温度曲线的计算值与模拟实验值的比较. 从整体的分布和演化趋势来看, 两者是比较相符的, 大部分区域的峰值温度和峰值时刻两者都符合得很好. 在局部上两者存在差异. 一处位于热斑外层位于图13中红线左侧的区域, 冲击波向内汇聚第一次经过体元时使得温度升高, 并维持了一小段时间, 在2.2节中已经讨论过, 这段时间内的几乎不产生聚变反应, 处于诊断的时间窗口之外, 中子诊断数据并不能反映这一段时间的温度情况, 不在计算的范围之内. 第二处差异是在热斑中心, 计算值的温度上升和下降都比模拟实验值更缓慢. 实际上温度的上升沿和长下降沿在不同区域有一定差异, 但目前模型中采用的σ和τ2两个参数是不随x变化的定值, 热斑中心区域虽然温度较高, 但其质量占比小, 对中子产额的贡献有限, 因此诊断数据对此区域内温度的敏感度不高, 也就出现了计算的诊断数据比较符合, 但中心处温度出现偏差的情况. 采用更复杂的参数模型(例如令σ和τ2随坐标x变化)能够改善这种情况, 但代价是使得模型中的待解参数增加, 进而提高最优参数计算的收敛难度, 在本方法的实践应用中, 待解参数的数量可根据计算精度要求和计算成本进行优化平衡.
-
本文以一维冲击内爆为例, 通过一维辐射流体模拟分析了惯性约束聚变实验聚变反应发生期间离子温度的时空分布规律. 分析表明: 辐射烧蚀靶丸壳层产生向内的强冲击波, 强冲击波在靶丸中心汇聚后产生向外传播的反射冲击波, 反射冲击波与向内汇聚的燃料发生碰撞, 在反射冲击波波阵面的物质被急剧压缩, 使得燃料温度密度骤然提升引发短暂的强聚变反应, 冲击波经过之后燃料的温度和密度逐渐下降, 聚变反应也随之减弱. 当反射冲击波掠过后, 燃料运动基本停滞, 并在聚变反应持续的时间内基本处于静止状态. 在上述物理过程中, 特定位置的离子温度呈一个快速上升, 然后缓慢下降的演化趋势. 离子温度的上升过程随着冲击波的传播由热斑中心向外递次出现. 离子温度的上升速率、峰值时刻、峰值强度取决于冲击波的速度和强度, 离子温度的下降速率则取决于离子的热传导过程. 提取离子温度时空分布的主要特征, 可将其归纳为一个含有10个待定参数的数学模型. 利用与离子温度相关的实验诊断数据给定的约束条件, 可以求解出模型中的待定参数, 给出实验的离子温度时空分布. 由于缺乏计算所需的完整的实验数据, 利用一个仿真算例作为模拟实验对计算方法进行了验证, 验证结果显示离子温度时空分布的计算值与模拟实验值在总体上基本相符, 这说明方法是有效的. 下一阶段, 我们将开展计算方法的应用研究, 完善相关诊断能力, 在近一维的内爆实验中获得离子温度时空分布计算所需的全部诊断量, 实现方法的应用. 本方法不仅适用冲击压缩内爆实验也适用于强惯性压缩的内爆实验, 相比冲击内爆而言, 一维惯性压缩内爆在聚变反应发生时温度上升速率要慢一些, 峰值温度值更低, 不同位置的温度达到峰值的时间较为接近, 可以用相似的方法进行离子温度时空分布的计算. 存在一些更复杂的情况, 冲击和惯性两种物理机制引发的聚变反应强度相当, 此时可以将两种模型结合起来, 但这意味着待解参数的数量在单聚变峰的基础上翻倍, 参数求解会更加困难. 本文的方法可推广到具有二维和三维分布的热斑温度计算, 但在实际应用中仍需解决两个方面的关键问题. 首先是需要提高辐射流体程序对二维和三维内爆模拟的准确性. 辐射流体程序一维内爆模拟的准确性已经经过验证, 程序对实验内爆性能预测的偏离已经可以做到小于10%, 但目前二维和三维内爆涉及的物理过程要复杂得多, 程序模拟的准确性远不如一维模拟, 因此基于数值模拟提炼出的二维和三维热斑离子温度的时空分布规律可能难以完全反映实验的真实物理图像. 其次是二维和三维问题需要更复杂的温度分布模型, 待定参数的求解难度将大幅提高, 同时也需要更多的实验诊断数据支撑, 例如三维的热斑中子图像、三维的离子密度分布, 这些诊断技术还不成熟, 目前大多数实验不具备这样的诊断配套条件. 这些问题需要在以后的研究中进一步解决和改进.
基于多诊断参数分析的一维内爆热斑离子温度时空分布计算方法
A method of calculating spatiotemporal distribution of ion temperature in hot spots of one-dimensional implosions based on multi-diagnostic parameter analysis
-
摘要: 惯性约束聚变中, 热斑离子温度是决定聚变增益的关键参数, 热斑离子温度时空分布能够揭示热斑能量的沉积与耗散过程, 针对此物理研究需求, 提出了一种基于多诊断参数分析的一维内爆热斑离子温度时空分布计算方法. 本文以冲击压缩内爆为例, 分析了离子温度时空分布的特性, 建立了离子温度时空分布数学模型. 利用计算算例作为模拟实验给出了离子温度相关的多个关键诊断量, 以此作为离子温度时空分布求解的约束. 通过遗传算法计算出了模型中的待定参数, 计算参数给出的离子温度时空分布与模拟实验基本相符, 验证了本方法的有效性. 本方法可以应用于近一维内爆实验热斑离子温度时空分布的计算, 为更深入地了解内爆热斑的形成与演化过程提供了实验观测手段.Abstract:
In inertial confinement fusion (ICF), the ion temperature of hot spots is a critical parameter determining fusion gain, and its spatiotemporal distribution provides insights into energy deposition and dissipation processes. However, directly diagnosing such a distribution remains challenging due to the extreme spatiotemporal scales of hot spots (~100 ps, ~100 μm). To cope with this challenge, a computational method of reconstructing the spatiotemporal ion temperature distribution in one-dimensional implosion hot spots through multi-diagnostic parameter analysis is proposed in this work. Taking shock-compressed implosions for example, the physical process is simulated via the one-dimensional (1D) radiation-hydrodynamics code Multi1D. The analysis shows two key mechanisms. One is that the propagation of reflected shock waves governs the rapid temperature rise and spatiotemporal differences in peak temperatures, and the other is that ion-ion conduction and ion-electron thermal conduction dominate the slow temperature decline. These mechanisms are found to be universal under different initial conditions. Based on these characteristics, a mathematical model with 10 parameters is developed to describe the spatiotemporal ion temperature distribution. The relationships between this distribution and experimental diagnostic quantities, including neutron yield, average ion temperature, time-dependent fusion reaction rate, and neutron imaging profile, are rigorously derived. Using computational cases as simulated experiments, key diagnostic parameters related to ion temperature are generated as constraints. Genetic algorithm is employed to optimize the model parameters, and the resulting ion temperature distributions show excellent agreement with simulation results in the fusion phase, thus validating the effectiveness of the method. This approach provides a way to reconstruct the ion temperature distribution in near-one-dimensional ICF experiments by using traditional neutron diagnostics, thus bypassing the limitations of spatiotemporally resolved measurement techniques. Although theoretically extensible to 2D/3D scenarios, challenges such as increased model complexity and insufficient multidimensional diagnostic data must be addressed. This method provides a valuable experimental way for understanding formation and evolution of hot spots, calibrating radiation-hydrodynamics codes, and optimizing implosion designs, which is of great significance for achieving fusion ignition. -
-
图 2 模拟计算的内爆靶丸流线(a)和阻滞阶段燃料的流线(b). 图(a)中红色线条表示DT燃料的运动轨迹, 蓝色线条表示SiO2的运动轨迹, 绿色线条表示CH的运动轨迹, 黑色线条表示聚变速率曲线. 图(b)中红色线条表示DT燃料的运动轨迹, 绿色曲线表示冲击波的轨迹
Figure 2. Streamline of the inertial confinement target capsule (a) and the streamlines of the fuel in the stagnation phase (b) during simulation calculations. In panel (a), the red lines represent the trajectory of the DT fuel, the blue lines indicate the trajectory of SiO2, the green lines show the trajectory of CH, and the black lines represent the fusion rate curve. In panel (b), the red lines depict the trajectory of the DT fuel, while the green curve represents the trajectory of the shock wave.
图 3 一维模拟给出的冲击压缩内爆热斑离子温度(a)、离子密度(b)和聚变反应率(c)的时空分布
Figure 3. The one-dimensional simulation provides the temporal and spatial distributions of ion temperature (a), ion density (b), and fusion reaction rate (c) in the hot spot of the shock-compressed implosion.
图 5 第1个(a)、第5个(b)、第15个(c)、第30个网格(d)以及所有网格(e)的燃料离子温度时间演化过程. Ti为网格的离子温度
Figure 5. Temporal evolution of fuel ion temperature for the 1st (a), 5th (b), 15th (c), and 30th (d) grid, as well as for all grids (e). Ti is the ion temperature of the grid.
图 6 第1个 (a)、第5个 (b)、第15个 (c)和第30个 (d)网格的诊断时间窗口. Ti为网格的离子温度, x是网格的坐标
Figure 6. Diagnostic time windows for the 1 st (a), 5 th (b), 15 th (c), and 30 th grid (d). Ti is the ion temperature of the grid, and x is the coordinate of the grid.
图 7 不同位置离子温度峰值时刻按照幂指数拟合, tp是温度的峰值时刻
Figure 7. Peak ion temperature times at different locations fitted to a power-law model, where tp is the peak time of the ion temperature.
图 8 不同实验条件下离子温度的时空分布 (a)辐射强度提升1.2倍; (b)壳层厚度减薄为16 μm; (c)燃料气压降低到35 atm; (d)电子离子热传导率降低20%. 图中的红色线条是热斑的聚变速率曲线
Figure 8. Spatio-temporal distribution of ion temperature under different experimental conditions is shown as follows: (a) Radiation intensity increased by 1.2 times; (b) shell thickness reduced to 16 μm; (c) fuel gas pressure decreased to 35 atm; (d) electron-ion thermal conductivity reduced by 20%. In all figures, the red lines indicate the fusion rate curve of the hot spots.
图 9 模拟实验的聚变速率曲线(a)和中子成像强度分布(b)
Figure 9. The fusion rate curve (a) and the neutron imaging intensity distribution (b) of simulated experiment.
图 10 模拟实验的流线图, 其中红色线条表示DT燃料的运动轨迹, 蓝色线条表示SiO2的运动轨迹, 绿色线条表示CH的运动轨迹
Figure 10. Simulation experiment’s streamline diagram, red lines represent the motion trajectory of DT fuel, blue lines indicate the motion trajectory of SiO2 and green lines depict the motion trajectory of CH.
图 11 计算值对应的聚变速率曲线(a)和中子图像空间分布(b)与模拟实验诊断数据的比较
Figure 11. Comparison of the calculated fusion rate curve (a) and the spatial distribution of neutron imaging (b) with the diagnostic data from the simulation experiments.
图 12 计算的离子温度时空分布(a)与模拟实验的离子温度时空分布(b). 图中的红色虚线表示冲击波的轨迹
Figure 12. Calculated spatio-temporal distribution of ion temperature (a) compared to that from the simulation experiments (b). The red dashed line indicating the trajectory of the shock wave.
图 13 阻滞时刻距热斑中心4 μm (a)、16 μm (b)、22 μm (c)和31 μm (d) 4个体元离子温度时间曲线的计算值与模拟实验值的比较, Ti为网格的离子温度, x是网格的坐标
Figure 13. Comparison of the calculated ion temperature time curves with the simulation values for four spatial points at distances of 4 μm (a), 16 μm (b), 22 μm (c), and 31 μm (d) from the center of the hot spot at the stagnation moment. Ti is the ion temperature of the grid, and x is the coordinate of the grid.
表 1 利用遗传算法得到的模拟实验离子温度时空分布参数的最优解
Table 1. Optimal solution for the spatio-temporal distribution parameters of ion temperature in the simulation experiments obtained using a genetic algorithm.
tp/ns t0/ns a1/(ns·cm–1) b1 2.915 230 1.45 υ/ns 0.0151 H/eV H0/cm a2/(eV·cm–1) b2 0.00698 0.345 –1.67 τ1/ns τ01/ns a3/(ns·cm–1) 0.0204 88 τ2/ns 0.284 
下载: 导出CSV
-
[1] 张棋, 马积瑞, 范金燕, 张杰 2022 物理学报 71 135202 doi: 10.7498/aps.71.20220199 Zhang Q, Ma J R, Fan J Y, Zhang J 2022 Acta Phys. Sin. 71 135202 doi: 10.7498/aps.71.20220199 [2] 张占文, 漆小波, 李波 2012 物理学报 61 145204 doi: 10.7498/aps.61.145204 Zhang Z W, Qi X B, Li B 2012 Acta Phys. Sin. 61 145204 doi: 10.7498/aps.61.145204 [3] 张家泰, 何斌, 贺贤土, 常铁强, 许林宝 2001 物理学报 50 921 doi: 10.7498/aps.50.921 Zhang J T, He B, He X T, Chang T Q, Xu L B 2001 Acta Phys. Sin. 50 921 doi: 10.7498/aps.50.921 [4] 何民卿, 张华, 李明强, 彭力, 周沧涛 2023 物理学报 72 095201 doi: 10.7498/aps.72.20222005 He M Q, Zhang H, Li M Q, Peng L, Zhou C T 2023 Acta Phys. Sin. 72 095201 doi: 10.7498/aps.72.20222005 [5] 袁强, 胡东霞, 张鑫, 赵军普, 胡思德, 黄文会, 魏晓峰 2011 物理学报 60 015202 doi: 10.7498/aps.60.015202 Yuan Q, Hu D X, Zhang X, Zhao J P, Hu S D, Huang W H, Wei X F 2011 Acta Phys. Sin. 60 015202 doi: 10.7498/aps.60.015202 [6] 赵英奎, 欧阳碧耀, 文武, 王敏 2015 物理学报 64 045205 doi: 10.7498/aps.64.045205 Zhao Y K, Ouyang B Y, Wen W, Wang M 2015 Acta Phys. Sin. 64 045205 doi: 10.7498/aps.64.045205 [7] 高凡, 袁鹏, 黄浩彬, 寇琦, 贾青, 远晓辉, 张喆, 张杰, 郑坚 2023 物理学报 72 175203 doi: 10.7498/aps.72.20230442 Gao F, Yuan P, Huang H B, Kou Q, Jia Q, Yuan X H, Zhang Z, Zhang J, Zheng J 2023 Acta Phys. Sin. 72 175203 doi: 10.7498/aps.72.20230442 [8] Zylstra A B, Hurricane O A, Callahan D A, et al. 2022 Nature 601 542 doi: 10.1038/s41586-021-04281-w [9] Abu-Shawareb H, et al. (Indirect Drive ICF Collaboration) 2022 Phys. Rev. Lett. 129 075001 doi: 10.1103/PhysRevLett.129.075001 [10] Lerche R A, Coleman L Q, Houghton J W, Speck D R, Storm E K 1977 Appl. Phys. Lett. 31 645 doi: 10.1063/1.89509 [11] Lerche R A, Glebov V Y, Moran M J, et al. 2010 Rev. Sci. Instrum. 81 10D319 doi: 10.1063/1.3478680 [12] Glebov V Y, Sangster T C, Stoeckl C, et al. 2010 Rev. Sci. Instrum. 81 10D325 doi: 10.1063/1.3492351 [13] Tang Q, Chen J B, Xiao Y Q, Yi T, Liu Z J, Zhan X Y, Song Z F 2020 Rev. Sci. Instrum. 91 023508 doi: 10.1063/1.5109711 [14] Frenje J A, Hilsabeck T J, Wink C W, Bell P, Bionta R, Cerjan C, Johnson M G, Kilkenny J D, Li C K, Séguin F H, Petrasso R D 2016 Rev. Sci. Instrum. 87 11D806 doi: 10.1063/1.4959164 [15] Kunimune J H, Frenje J A, Berg G P A, et al. 2021 Rev. Sci. Instrum. 92 033514 doi: 10.1063/5.0040745 [16] Moore A S, Schlossberg D J, Eckart M J, Hartouni E P, Hilsabeck T J, Jeet J S, Kerr S M, Nora R C, Kilkenny J 2022 Rev. Sci. Instrum. 93 113536 doi: 10.1063/5.0099933 [17] Meaney K D, Kim Y, Hoffman N M, et al. 2022 Rev. Sci. Instrum. 93 083520 doi: 10.1063/5.0101887 [18] Birge N, Geppert-Kleinrath V, Danly C, et al. 2022 Rev. Sci. Instrum. 93 113510 doi: 10.1063/5.0101820 [19] Bleuel D L, Yeamans C B, Bernstein L A, et al. 2012 Rev. Sci. Instrum. 83 10D313 doi: 10.1063/1.4733741 [20] Stoeckl C, Boni R, Ehrne F, et al. 2016 Rev. Sci. Instrum. 87 053501 doi: 10.1063/1.4948293 [21] Ress D, Lerche R A, Ellis R J, Lane S M, Nugent K A 1988 Science 241 956 doi: 10.1126/science.241.4868.956 [22] Fittinghoff D N, Birge N, Geppert-Kleinrath V 2023 Rev. Sci. Instrum. 94 021101 doi: 10.1063/5.0124074 [23] 余波, 应阳君, 许海波 2010 物理学报 59 5351 doi: 10.7498/aps.59.5351 Yu B, Ying Y J, Xu H B 2010 Acta Phys. Sin. 59 5351 doi: 10.7498/aps.59.5351 [24] 王胜, 邹宇斌, 温伟伟, 李航, 刘树全, 王浒, 陆元荣, 唐国有, 郭之虞 2013 物理学报 62 122801 doi: 10.7498/aps.62.122801 Wang S, Zou Y B, Wen W W, Li H, Liu S Q, Wang H, Lu Y R, Tang G Y, Guo Z Y 2013 Acta Phys. Sin. 62 122801 doi: 10.7498/aps.62.122801 [25] 章法强, 祁建敏, 张建华, 李林波, 陈定阳, 谢红卫, 杨建伦, 陈进川 2014 物理学报 63 128701 doi: 10.7498/aps.63.128701 Zhang F Q, Qi J M, Zhang J H, Li L B, Chen D Y, Xie H W, Yang J L, Chen J C 2014 Acta Phys. Sin. 63 128701 doi: 10.7498/aps.63.128701 [26] Ramis R, Schmalz R, Meyer-Ter-Vehn J 1988 Comput. Phys. Commun. 49 475 doi: 10.1016/0010-4655(88)90008-2 [27] 李维新 2003 一维不定常流与冲击波(北京: 国防工业出版社)第343—355页 Li W X 2003 One-Dimensional Nonsteady Flow and Shock Waves (Beijing: National Defense Industry Press) pp343–355 -
计量
- 文章访问数: 24
- HTML全文浏览数: 24
- PDF下载数: 0
- 施引文献: 0