-
气态分子的热力学性质是物理化学领域中的一个重要研究课题, 其在能源转化[1]、天体物理[2]、生态环境保护[3,4]、光学材料研究[5]等领域都有广泛应用. 2005年, Angelova和Frank[6]使用Morse势研究了HCl, HF, KCl, K2等分子的热力学性质, 分析了影响比热值的因素; 2010年, Halpern[7]通过量子化学和统计力学方法, 成功计算了氩二聚体的结构和热力学性质; 2015年, Liu等[8]用代数方法(algebraic method, AM)计算了溴分子在600—2100 K温度范围内的振动亥姆霍兹自由能、熵和热容, 相比于简单谐振子模型(simple harmonic oscillator, SHO)计算精度提高了近50%; 2017年, Jia等[9]利用改进的Manning-Rosen势函数, 导出包括振动热容和振动熵等热力学函数公式, 并以Li2分子为例讨论了热力学量与温度的关系, 在他们后续的研究中, 利用改进的Rosen-Morse势计算了磷二聚体在298—6000 K的摩尔焓以及通过建立硫二聚体的吉布斯自由能的表达式, 预测了硫二聚体的吉布斯自由能和熵值[10,11]; 2018年, Iko等[12]使用渐进迭代法(asymptotic iteration method, AIM)研究了K2分子在不同振动量子数下配分函数、平均能量、熵、比热容等; 2020年, Okorie等[13]利用改进的变形指数型势(improved deformed exponential-type potential, IDEP)推导得出配分函数和热力学函数, 得到了H2, CO, N2, LiH分子的振动平均能、自由能、熵和比热容; 同年, Bakhti等[14]通过多参数指数型势(multi-parameter exponential-type potential, MPETP)描述分子内部的振动情况, 得到O2和H2分子在5000—120000 K的熵、比热、自由能; 2022年, Oluwadare等[15]通过量子力学模型和Hellmann-Feynman定理, 系统地研究了一维谐振子系统中双原子分子的热力学性质、抗磁磁化率和Massieu函数, 并得出了这些性质与状态数、原子数、振动频率和温度之间的具体关系; 2024年, Strekalov[16]使用乘积近似模型得到的配分函数进一步计算了CO分子的热力学性质. 上述研究为探索双原子分子的热力学性质做出了贡献.
除了以上方法, 还包括密度泛函理论、从头计算、分子动力学等[17–20]理论可用于计算分子的相关热力学性质. 需要注意的是, 构建解析势能函数求得分子体系完全振转能级来获得正确的配分函数, 是计算体系热力学性质的基础. 本文基于课题组扩展的改进多参数指数型(the extended improved multiparameter exponential-type, EIMPET)势能模型[21], 研究获得了基态H2和HD分子的精确势能曲线以及完全振转能级, 然后通过量子统计系综理论计算了H2和HD分子的热力学性质, 并将所得计算结果与美国国家标准与技术研究所(National Institute of Standards and Technology, NIST)[22]数据库数据进行了比较和分析.
-
扩展改进多参数指数型(EIMPET)势能模型是课题组前期从IMEPT势[23]和Morse势[24]导出的变分代数基础上的进一步改进, 表达式如下[21]:
其中
$ \varLambda \left( r \right){\text{δ }}U\left( r \right) $ 为对IMPET函数的扩展项, 该部分旨在改善IMPET势的精度,$ \varLambda \left( r \right) $ ,$ {\text{δ }}U\left( r \right) $ 分别表示为$ {U_{{\text{IMPET}}}}\left( r \right) $ 为IMPET势,$ {U_{{\text{Morse}}}}\left( r \right) $ 为Morse势, 分别表示为这里,
$ \beta = {\left[ {{{{f_2}} {/ } {\left( {2{D_{\mathrm{e}}}} \right)}}} \right]^{\frac{1}{2}}} $ ,$ {f_2} $ 为二阶力常数[25],$ {f_2} = 4{\pi ^2}\mu \omega _{\mathrm{e}}^2{c^2} $ ,$ {D_{\mathrm{e}}} $ 是离解能,$ \mu $ 为分子约化质量,$ h $ 为普朗克常数,$ r $ 是核间距,$ {r_{\mathrm{e}}} $ 是平衡核间距,$ {\omega _{\mathrm{e}}} $ 和$ {\alpha _{\mathrm{e}}} $ 为实验振动和转动光谱常数,$ c $ 为光速. (2)式中$ \lambda $ 为拟合的无量纲参数, 最终的势能曲线由$ \lambda $ 来决定. 而$ \lambda $ 的最优值可以由EIMPET势与RKR 势 (Rydberg-Klein-Rees)数据的最小方均根误差(RMS)来确定:式中,
$ {U_{{\mathrm{RKR}}}} $ 为RKR势能数据,$ N $ 为根据实验光谱获得的RKR势能点个数.通过EIMPET势计算得到分子的势能数据后, 将其代入一维薛定谔方程中进行求解就能得到分子全套的振转能级
$ {E_{v, J}} $ [26]:其中
$ \hbar = {h {/ } {2\pi }} $ ;$ {\varPsi _{v, J}}\left( r \right) $ 为波函数;$ U\left( r \right) $ 是势能函数, 借助Le发布的计算程序LEVEL[26]计算分子的完整振转能级.要求解分子的相关热力学性质, 其中的重中之重就是获得分子在不同温度下的配分函数. 总的配分函数
$ Q\left( T \right) $ 由两部分组成: 一是内部配分函数$ {Q_{{\text{int}}}}\left( T \right) $ , 二是平动配分函数$ {Q_{\mathrm{t}}}\left( T \right) $ 组成, 表示为其中平动配分函数为
$ {Q_{\mathrm{t}}}(T) = {\left( {{{2\pi m{k_{\text{B}}}T}}/{{{h^2}}}} \right)^{{3}/{2}}}V $ ;$ m $ 为分子的质量;$ {k_{\text{B}}} $ 为玻尔兹曼常数;$ T $ 为开尔文温度;$ V $ 为体积.在忽略自旋相互作用下内部配分函数为
其中
$ \sigma $ 是对称因子, 所若算分子是同核分子,$ \sigma= 0.5 $ ; 若所算分子为异核分子, 则$ \sigma $ = 1, 本文中所计算的H2分子为同核分子,$ \sigma $ = 0.5, HD分子为异核分子,$ \sigma $ = 1;$ n $ 为电子量子数;$ \left( {2 - {\delta _{\varLambda , 0}}} \right)\left( {2 S + 1} \right) $ 为电子简并度,$ \varLambda $ 为投射到核间距轴上的电子轨道角动量量子数;$ S $ 为电子自旋角动量量子数;$ \left( {2 J + 1} \right) $ 为旋转简并度;$ {\varepsilon _0} $ 为最低能级.通过量子统计系综理论可以计算分子体系的摩尔热容
$ {C_{\text{m}}}\left( T \right) $ :其中
$ {N_{\text{A}}} $ 为阿伏伽德罗常数; 类似地, 摩尔熵$ {S_{\text{m}}}\left( T \right) $ 与$ Q\left( T \right) $ 关系为摩尔吉布斯自由能
$ {G_{\text{m}}}\left( T \right) $ 为约化摩尔吉布斯自由能
$ {G_{\text{r}}}\left( T \right) $ 为相对摩尔焓
$ \Delta {H_{\text{r}}}\left( T \right) $ 为其中
$ {H_{\text{m}}}\left( {{T_{\text{r}}}} \right) $ 表示在298.15 K温度条件下的摩尔焓. -
准确的配分函数是计算摩尔热容、摩尔熵、摩尔吉布斯自由能等相关热力学性质的重要基础, 而获得配分函数前需要通过精确分子势能来获得可靠的能级数据. 因此, 首先通过EIMPET势能函数来得到分子精确的势能曲线. 势能函数所需的参数列于表1中, 光谱常数来源于文献[27,28]. 对于H2, 计算用到的RKR数据取自文献[29], 而HD的RKR数据是通过表1的实验光谱常数[30,31] (
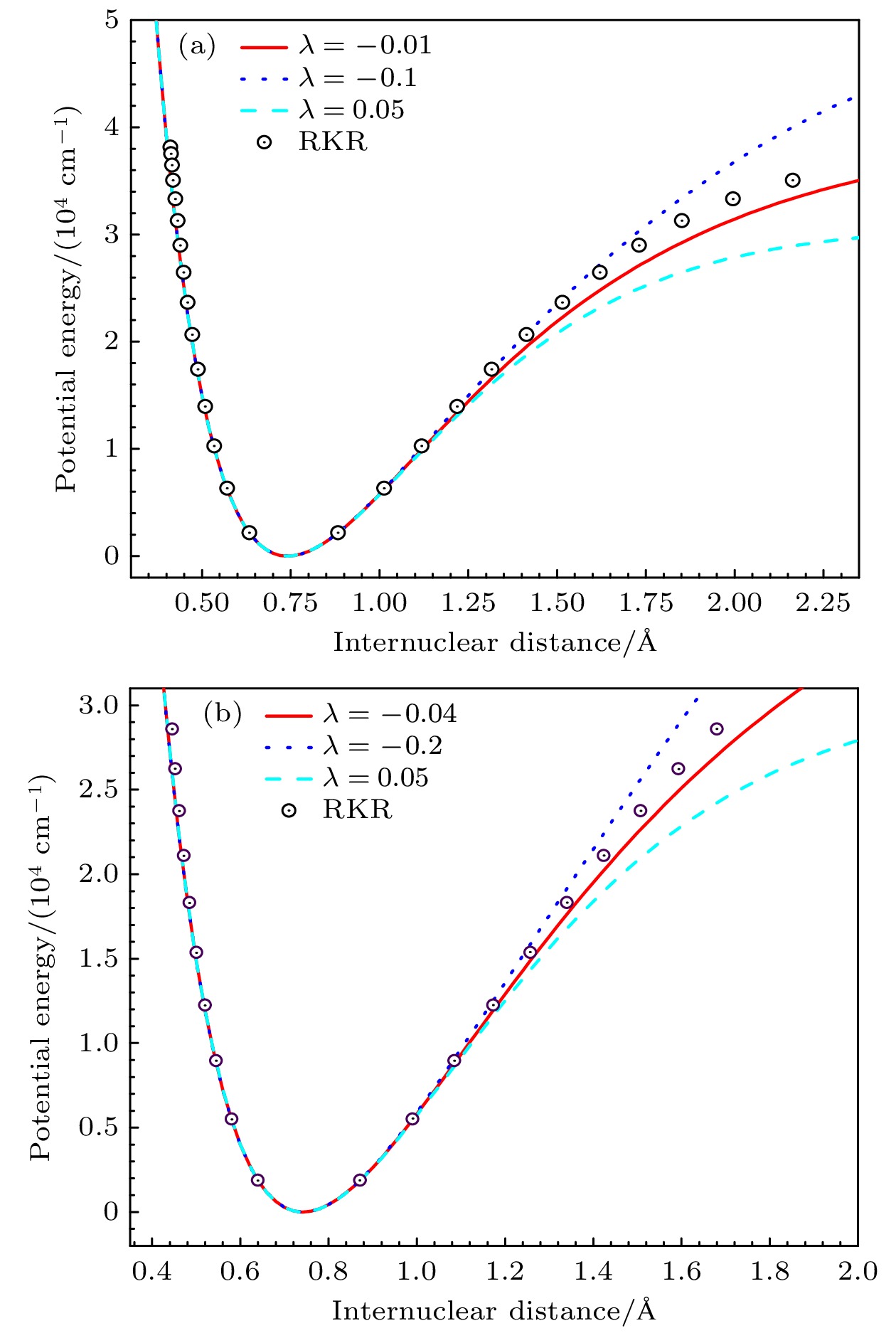
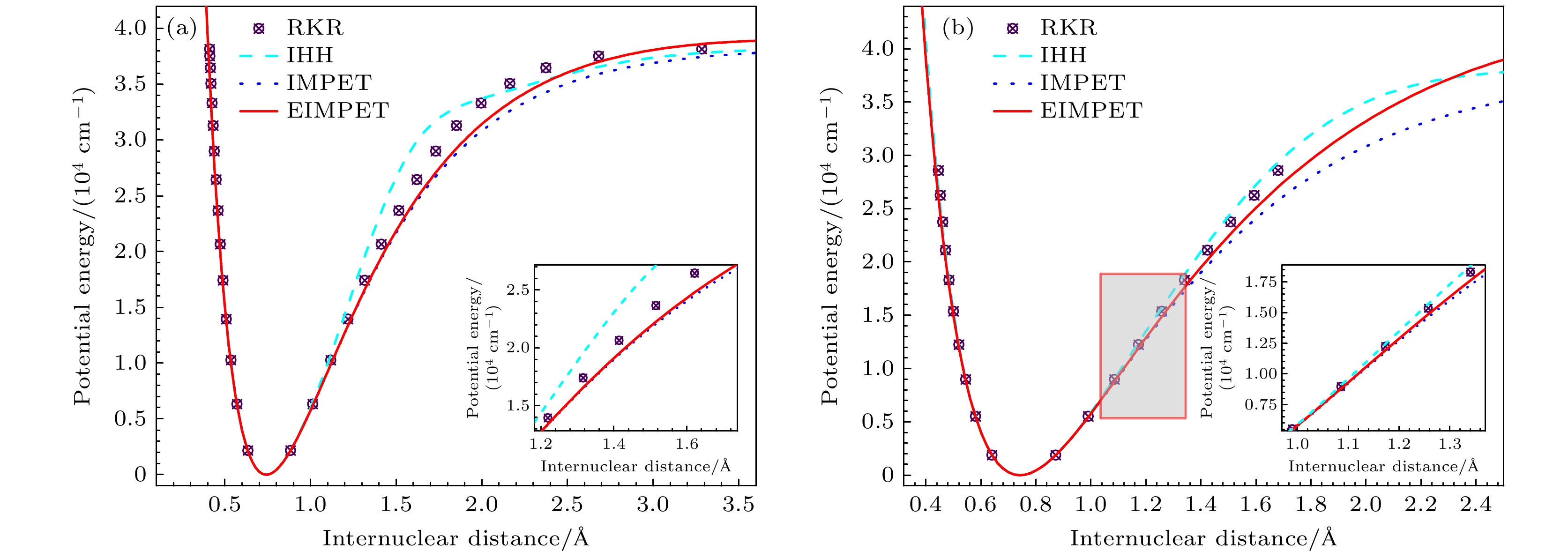
$ {D_{\text{e}}} $ ,$ {r_{\text{e}}} $ ,$ {\omega _{\text{e}}} $ ,$ {\alpha _{\text{e}}} $ )结合RKR程序反演得到.图1为H2和HD分子的势能曲线, 该图对IHH (improved Hulburt-Hirschfelder)[32], IMPET, EIMPET势能模型和RKR数据进行了比较. 由图可知, 与IHH和IMPET势能模型相比, EIMPET势能模型有较高的精度. 值得注意的是, H2和HD分子的EIMPET与IMPET、IHH曲线, 在平衡构型附近, 与RKR值有很大程度上的重叠. 随着核间距的增加, H2和HD分子的势能曲线都逐渐偏离RKR数据; 对于H2分子, 在1.13 Å (1 Å=10–10 m) 处势能曲线与RKR数值点开始出现明显偏差, 而IHH势能曲线在1.02 Å附近出现偏离情况, 在核间距
$ r \geqslant $ 1.2 Å可观察到EIMPET和IMPET曲线的偏差愈加明显, 而EIMPET曲线能更快地收敛于离解能. 类似地, 对于HD分子, 在$ r \geqslant $ 0.99 Å处观察到EIMPET势能数据更接近RKR值. 以上结果表明, H2和HD分子EIMPET势可作为求解薛定谔方程获取可靠能级数据的解析势.另外, 还给出了EIMPET势能在不同
$ \lambda $ 值势能曲线的变化趋势, 如图2所示. 从图2(a)可以看到, 对于H2而言, EIMPET势能曲线取$ \lambda $ = –0.01的结果更接近RKR值; 而取$ \lambda $ = 0.05时, 随着核间距增大, 势能曲线逐渐小于实验值; 当$ \lambda $ = –0.1时, 计算得到的势能曲线结果在核间距r > 1.75 Å却大于RKR值. 而对于HD分子, 如图2(b)所示, 相比于$ \lambda $ 取值为–0.2和0.05的势能结果,$ \lambda $ 值为–0.04的EIMPET势在渐近区附近与RKR值更接近. -
分子热力学性质可由热力学方程(10)—(16)计算获得. 表2展示了计算得到的H2分子摩尔热容
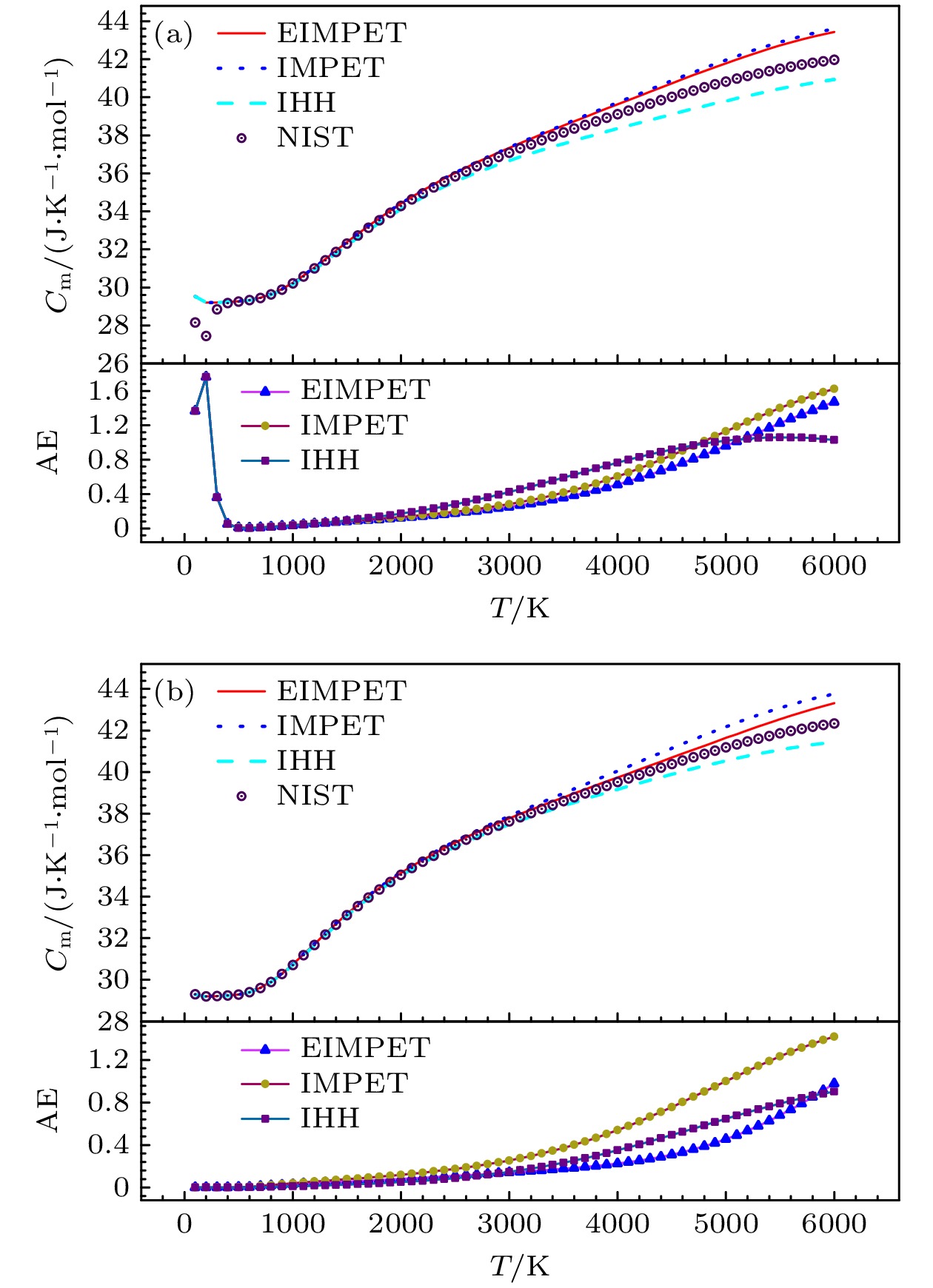
$ {C_{\text{m}}}\left( T \right) $ 以及计算值与NIST数据库[22]中数据的绝对误差$ \Delta {C_{\text{m}}} $ ,$ \Delta {C_{\text{m}}} $ 总体上随着温度的升高而增加, 这是因为H2在较高温度下易解离成两个原子, 从而导致误差的增大, 而在100—500 K的温度区域$ \Delta {C_{\text{m}}} $ 出现由大变小的趋势, 且在低温区域差异很大, 这可能是H2分子在低温区正氢和仲氢的存在比例不同, 低温区以仲氢为主, 随着温度的升高仲氢会向正氢转换, 而纯正氢在气态时的热力学性质与混合态截然不同, 因此出现这样的差异[33]. 对于三种势能模型得到的数据, 在高温区域(T ≥ 900 K), 由IMPET势得到的摩尔热容绝对误差均大于EIMPET势, 另外, IHH势得到的计算结果在100—900 K和5300—6000 K温度区间的误差虽小于EIMPET势(图3), 但EIMPET势的平均绝对误差相对更小. 对于HD分子而言, 它的总体趋势与H2分子相似, 随着温度升高, 误差逐渐增大, 且相对于IHH和IMPET势, HD分子的EIMPET势计算误差更小. 虽然在高温和低温区域$ \Delta {C_{\text{m}}} $ 较大, 但H2和HD分子的EIMPET势平均绝对误差最小, 分别为0.519和0.236 J·K–1·mol–1, 因此, 使用该势计算$ {C_{\text{m}}}\left( T \right) $ 是更好的选择.借助(13)式—(16)式, 进一步计算了分子的
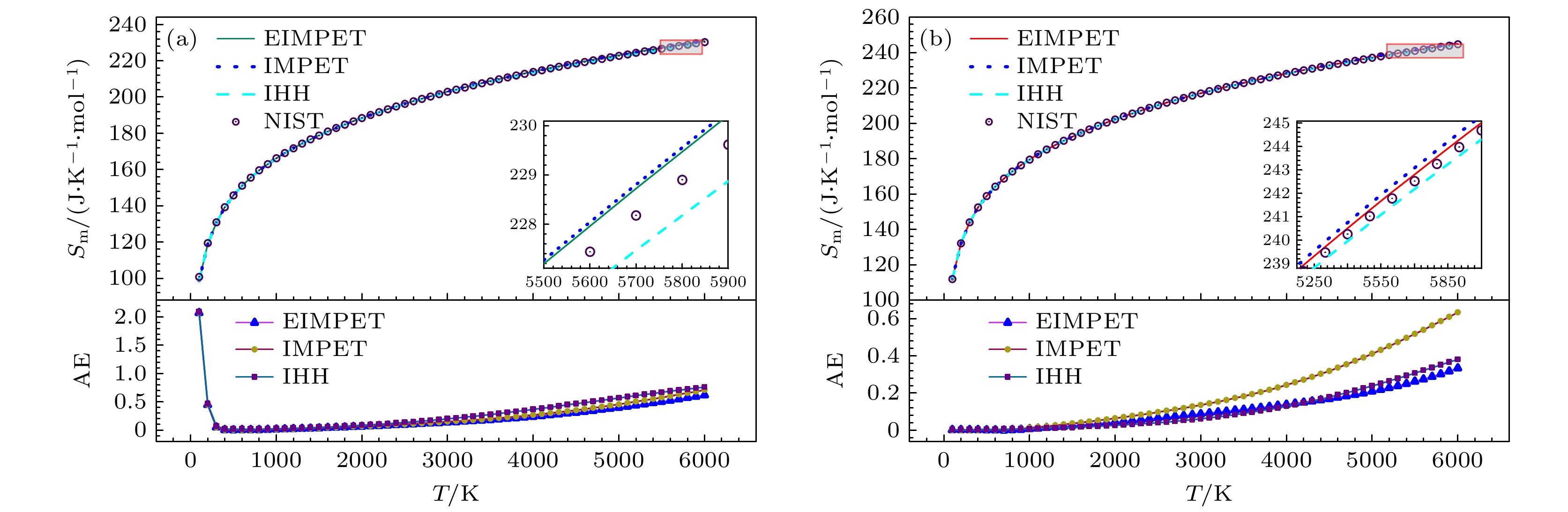
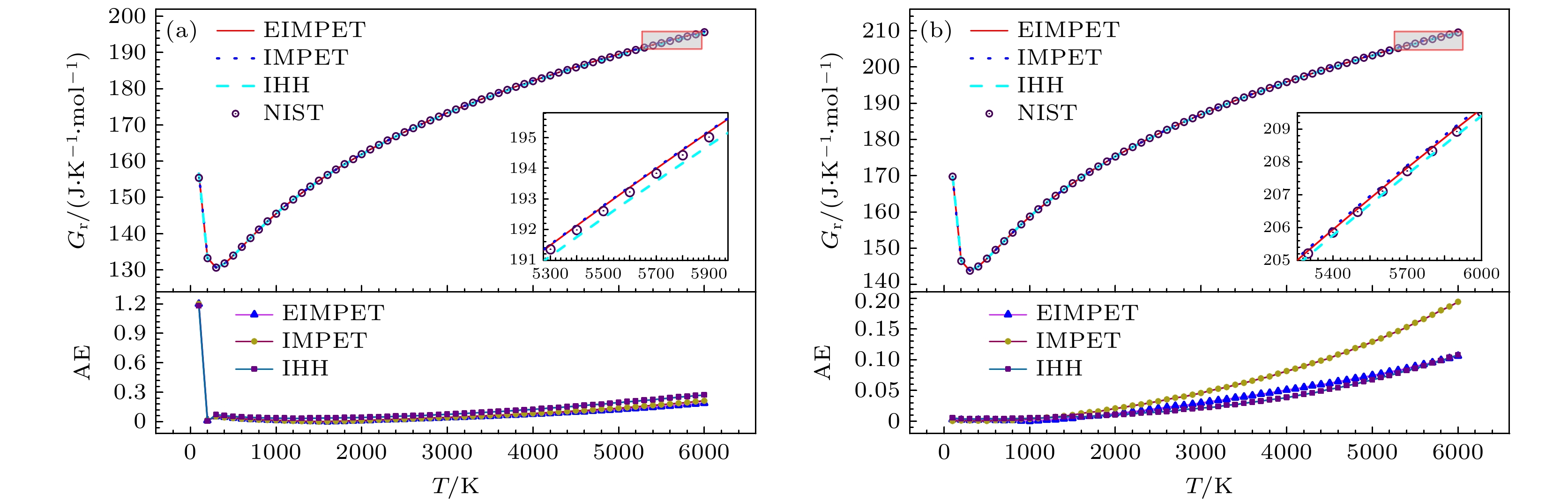
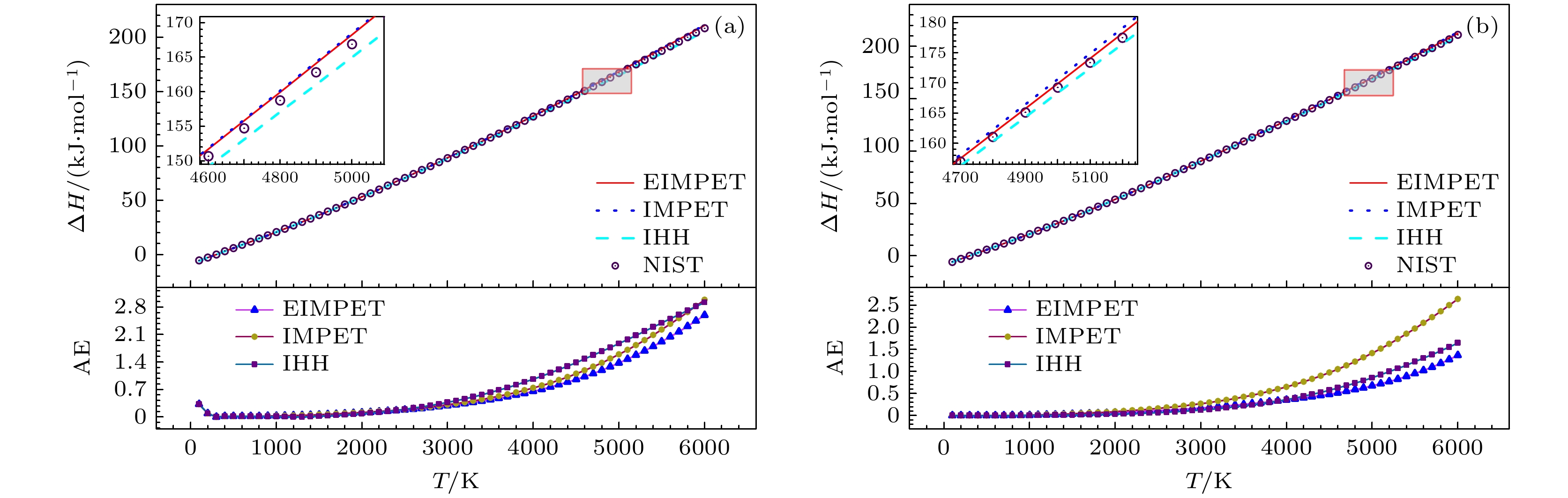
$ {S_{\text{m}}}(T) $ ,$ {H_{\text{r}}}(T) $ 和$ {G_{\text{r}}}(T) $ , 从表3看到, 以EIMPET势能函数为基础的计算模型计算得到的H2和HD分子的$ {S_{\text{m}}}(T) $ 方均根误差为0.3824 J·K–1·mol–1和0.1443 J·K–1·mol–1,$ \Delta {H_{\text{r}}}\left( T \right) $ 分别为0.9586 kJ·mol–1和0.4863 kJ·mol–1,$ {G_{\text{r}}}(T) $ 分别为0.1754 J·K–1·mol–1和0.0495 J·K–1·mol–1. 对于上述四个热力学量, EIMPET势计算H2分子得到的方均根误差值均小于IHH和IMPET势计算所得结果, 而对于HD分子的$ {G_{\text{r}}}(T) $ 而言, 虽然IHH的误差略小于EIMPET势的结果, 但后者仍得到了较为精确的计算值.本研究利用EIMPET势计算得到的摩尔熵、相对摩尔焓和约化摩尔吉布斯自由能等热力学量与温度的关系, 见图4—图6. 图4在100—6000 K温度区间内, 对使用IHH, IMPET和EIMPET势能计算得到的摩尔熵与NIST数据库数据进行了对比. 图上方展示了计算值与NIST数据的比较, 下方显示了三种势能计算所得摩尔熵与NIST数据库数据之间的绝对误差, 结果表明, H2和HD分子的计算值与NIST数据具有良好的一致性. 对于H2分子, IHH势、IMPET势与EIMPET势计算结果在较低温度下的误差几乎一致, 随着温度升高, 特别在3600 K以上, 三种势能模型计算结果之间的差异变得明显, 且EIMPET势所得结果的绝对误差较小; 类似地, HD分子也呈现出相似趋势, 并且三种模型在HD分子上的差异更加显著, 不同的是, IHH势在1100—4200 K温度下误差出现小于其他两种势能的情况. 图5(a), (b)展示了两个分子的相对摩尔焓随温度升高的变化趋势, 总体与NIST数据保持一致. 如图6(a), (b)所示, 分子的约化摩尔吉布斯自由能误差在整个温度区间内较小, 并且H2分子的EIMPET势结果优于IHH和IMPET势, EIMPET势数据的绝对误差在0.187 J·K–1·mol–1以内, 且在低温区域出现较大偏差, 原因与摩尔热容的变化趋势类似; 而HD分子的绝对误差范围在0.001—0.1 J·K–1·mol–1之间. 需要注意的是, 随着温度升高, 分子内部运动剧烈, 分子的高振转能级贡献增加, 进而可能使得振转能级误差引起的热力学量计算值与实验值在高温区域会出现相对较大的偏差. 总体来说, 这些结果仍验证了EIMPET势能模型在计算气体双原子分子热力学性质方面的优势及其实际应用价值.
-
本文基于扩展的改进多参数指数型(EIMPET)势能模型确定了H2和HD分子的解析势能曲线, 并通过数值方法求解了分子的完全振转能级. 此外, 根据量子统计系综理论计算了H2和HD分子的摩尔热容、摩尔熵、约化摩尔吉布斯自由能和相对摩尔焓, 结果与NIST数据库中的数据相吻合. 本文提出了一种以EIMPET势能模型为基础来计算气相双原子分子热力学性质的量子化学方法, 可为进一步研究三原子分子的热力学性质提供参考.
H2和HD分子宏观热力学性质
Macroscopic thermodynamic properties of H2 and HD
-
摘要: 本文通过扩展的改进多参数指数型(the extended improved multiparameter exponential-type, EIMPET)势能模型, 结合实验光谱数据, 研究了H2和HD分子的热力学性质. 首先利用解析势能曲线计算得到分子的振转能级, 其次结合量子统计系综理论计算了分子在100—6000 K温度下的配分函数、摩尔热容、摩尔熵、摩尔焓以及约化摩尔吉布斯自由能. 计算结果与美国国家标准与技术研究所(National Institute of Standards and Technology, NIST)数据库中的数据具有良好的一致性. 本文的理论方法可用于预测某些气态物质的热力学性质.
-
关键词:
- H2分子 /
- HD分子 /
- 扩展的改进多参数指数型势能模型 /
- 热力学性质
Abstract: H2 molecule and their isotopes represent one of the modern clean energy sources. It is imperative to understand their thermodynamic properties for comprehending their behaviors under various conditions. Thereby promoting their more in-depth applications. In this paper, an extended improved multiparameter exponential-type potential (EIMPET) combined with the quantum statistical ensemble theory is used to investigate and analyze the thermodynamic properties of H2 and HD molecules. Firstly, reliable energy level data for molecules are obtained using the EIMPET potential. Subsequently, the one-dimensional Schrödinger equation is solved with the LEVEL program to determine the rovibrational energy levels of the molecules. Finally, the quantum statistical ensemble theory is integrated to determine the partition functions, molar heat capacity, molar entropy, molar enthalpy, and reduced molar Gibbs free energy of H2 and HD in a temperature range of 100–6000 K. The calculation results indicate that compared with IHH potential and IMPET potential, the EIMPET potential is closer to RKR data. A comparison of the calculated thermodynamic properties of the molecules reveals that the results from the EIMPET potential-based method accord well with those from the NIST database. Specifically, for H2, the root mean square (RMS) errors for $ {C_{\text{m}}}\left( T \right) $, $ {S_{\text{m}}}\left( T \right) $, $ {G_{\text{r}}}\left( T \right) $, and $ \Delta {H_{\text{r}}}\left( T \right) $are 0.6894 J·K–1·mol–1, 0.3824 J·K–1·mol–1, 0.1754 J·K–1·mol–1, and 0.9586 kJ·mol–1, respectively, while for HD, the RMS errors are 0.3431 J·K–1·mol–1, 0.1443 J·K–1·mol–1, 0.0495 J·K–1·mol–1, and 0.4863 kJ·mol–1, respectively. All of these results are superior to those obtained using IMPET potential, and to those obtained using IHH potential as a whole. These findings demonstrate the advantages and practical applications of the EIMPET potential in calculating the thermodynamic properties of diatomic gas molecules, providing a foundation for subsequently studying the thermodynamic properties of triatomic molecules. -

-
表 1 H2和HD分子电子基态的实验光谱常数和可调参数
$ \lambda $ 的值Table 1. Experimental spectral constants and adjustable parameter
$ \lambda $ of the ground electronic states of H2 and HD molecules.表 2 H2分子不同温度下的摩尔热容以及绝对误差
Table 2. Molar heat capacity of H2 molecule at different temperatures and absolute errors.
T/K $ {C}_{{\mathrm{m}}}^{{\mathrm{N}}{\mathrm{I}}{\mathrm{S}}{\mathrm{T}}} $
/(J·K–1·mol–1)$ {C}_{{\mathrm{m}}}^{{\mathrm{I}}{\mathrm{H}}{\mathrm{H}}} $
/(J·K–1·mol–1)$ {C}_{{\mathrm{m}}}^{{\mathrm{I}}{\mathrm{M}}{\mathrm{P}}{\mathrm{E}}{\mathrm{T}}} $
/(J·K–1·mol–1)$ {C}_{{\mathrm{m}}}^{{\mathrm{E}}{\mathrm{I}}{\mathrm{M}}{\mathrm{P}}{\mathrm{E}}{\mathrm{T}}} $
/(J·K–1·mol–1)$ \Delta {C}_{{\mathrm{m}}}^{{\mathrm{N}}{\mathrm{I}}{\mathrm{S}}{\mathrm{T}}\text{-}{\mathrm{I}}{\mathrm{H}}{\mathrm{H}}} $
/(J·K–1·mol–1)$ \Delta {C}_{{\mathrm{m}}}^{{\mathrm{N}}{\mathrm{I}}{\mathrm{S}}{\mathrm{T}}\text{-}{\mathrm{I}}{\mathrm{M}}{\mathrm{P}}{\mathrm{E}}{\mathrm{T}}} $
/(J·K–1·mol–1)$ \Delta {C}_{{\mathrm{m}}}^{{\mathrm{N}}{\mathrm{I}}{\mathrm{S}}{\mathrm{T}}\text{-}{\mathrm{E}}{\mathrm{I}}{\mathrm{M}}{\mathrm{P}}{\mathrm{E}}{\mathrm{T}}} $
/(J·K–1·mol–1)100 28.154 29.521 29.520 29.520 1.367 1.366 1.366 300 28.849 29.210 29.212 29.212 0.361 0.363 0.363 500 29.260 29.265 29.270 29.270 0.005 0.010 0.010 700 29.441 29.432 29.452 29.452 0.009 0.011 0.011 900 29.881 29.857 29.910 29.908 0.024 0.029 0.027 1100 30.581 30.535 30.629 30.626 0.046 0.048 0.045 1300 31.423 31.354 31.491 31.487 0.069 0.068 0.064 1500 32.298 32.204 32.384 32.378 0.094 0.086 0.080 1700 33.139 33.017 33.243 33.236 0.122 0.104 0.097 1900 33.917 33.763 34.040 34.031 0.154 0.123 0.114 2100 34.624 34.432 34.768 34.757 0.192 0.144 0.133 2300 35.263 35.029 35.430 35.416 0.234 0.167 0.153 2500 35.842 35.560 36.036 36.018 0.282 0.194 0.176 2700 36.370 36.036 36.595 36.573 0.334 0.225 0.203 2900 36.856 36.464 37.119 37.091 0.392 0.263 0.235 3100 37.311 36.856 37.616 37.581 0.455 0.305 0.270 3300 37.740 37.218 38.096 38.051 0.522 0.356 0.311 3500 38.149 37.558 38.565 38.508 0.591 0.416 0.359 3700 38.544 37.882 39.029 38.958 0.662 0.485 0.414 3900 38.928 38.196 39.491 39.405 0.732 0.563 0.477 4100 39.301 38.502 39.952 39.849 0.799 0.651 0.548 4300 39.665 38.803 40.412 40.292 0.862 0.747 0.627 4500 40.017 39.099 40.868 40.732 0.918 0.851 0.715 4700 40.355 39.388 41.316 41.164 0.967 0.961 0.809 4900 40.676 39.671 41.750 41.585 1.005 1.074 0.909 5100 40.976 39.942 42.163 41.988 1.034 1.187 1.012 5300 41.252 40.199 42.548 42.369 1.053 1.296 1.117 5500 41.498 40.439 42.900 42.721 1.059 1.402 1.223 5700 41.712 40.656 43.211 43.038 1.056 1.499 1.326 5900 41.890 40.849 43.476 43.315 1.041 1.586 1.425 6000 41.965 40.934 43.590 43.436 1.031 1.625 1.471 MAE — — — — 0.564 0.587 0.519 * $ \Delta {C}_{{\mathrm{m}}}^{{\mathrm{N}}{\mathrm{I}}{\mathrm{S}}{\mathrm{T}}\text{-}{\mathrm{m}}{\mathrm{o}}{\mathrm{d}}{\mathrm{e}}{\mathrm{l}}}=|{C}_{{\mathrm{m}}}^{{\mathrm{N}}{\mathrm{I}}{\mathrm{S}}{\mathrm{T}}}-{C}_{{\mathrm{m}}}^{{\mathrm{m}}{\mathrm{o}}{\mathrm{d}}{\mathrm{e}}{\mathrm{l}}}| $ ; MAE: mean absolute error表 3 H2和HD分子不同势能模型下的预测数据与NIST数据的方均根误差
Table 3. Root mean square error of predicted data for H2 and HD molecules under different potential energy models compared to NIST data.
热力学量 H2EIMPET H2IMPET H2IHH HDEIMPET HDIMPET HDIHH Cm/(J·K–1·mol–1) 0.6894 0.7750 0.7019 0.3431 0.6338 0.4055 Sm/(J·K–1·mol–1) 0.3824 0.4096 0.4591 0.1443 0.2732 0.1575 ΔHr/(kJ·mol–1) 0.9586 1.1052 1.2110 0.4863 0.9749 0.5946 Gr/(J·K–1·mol–1) 0.1754 0.1805 0.2005 0.0495 0.0859 0.0452 -
[1] Wang C W, Peng X L, Liu J Y, et al. 2022 Int. J. Hydrogen Energy 47 27821 doi: 10.1016/j.ijhydene.2022.06.105 [2] Fan X, Bañados E, Simcoe R A 2023 Annu. Rev. Astron. Astrophys. 61 373 doi: 10.1146/annurev-astro-052920-102455 [3] Abramowitz S, Chase M W 1991 Pure Appl. Chem. 63 1449 doi: 10.1351/pac199163101449 [4] Grein F 2023 Struct. Chem. 34 317 doi: 10.1007/s11224-022-02007-w [5] Yahiatène I, Hennig S, Huser T 2013 Chem. Phys. Lett. 587 1 doi: 10.1016/j.cplett.2013.08.102 [6] Angelova M, Frank A 2005 Phys. At. Nucl. 68 1625 doi: 10.1134/1.2121908 [7] Halpern A M 2010 J. Chem. Educ. 87 174 doi: 10.1021/ed800049s [8] Liu G Y, Sun W G, Liao B T 2015 Indian J. Phys. 89 1109 doi: 10.1007/s12648-015-0698-4 [9] Jia C S, Zhang L H, Wang C W 2017 Chem. Phys. Lett. 667 211 doi: 10.1016/j.cplett.2016.11.059 [10] Ding Q C, Jia C S, Liu J Z, Li J, Du R F, Liu J Y, Peng X L, Wang C W, Tang H X 2022 Chem. Phys. Lett. 803 139844 doi: 10.1016/j.cplett.2022.139844 [11] Jia C S, Wang C W, Zhang L H, Peng X L, Tang H M, Zeng R 2018 Chem. Eng. Sci. 183 26 doi: 10.1016/j.ces.2018.03.009 [12] Ikot A N, Chukwuocha E O, Onyeaju M C, Onate C A, Ita B I, Udoh M E 2018 Pramana-J. Phys. 90 22 doi: 10.1007/s12043-017-1510-0 [13] Okorie U S, Ikot A N, Chukwuocha E O, Rampho G J 2020 Results Phys. 17 103078 doi: 10.1016/j.rinp.2020.103078 [14] Bakhti H, Diaf A, Hachama M 2020 Comput. Theor. Chem. 1185 112879 doi: 10.1016/j.comptc.2020.112879 [15] Oluwadare O J, Oyewumi K J, Abiola T O 2022 Indian J. Phys. 96 1921 doi: 10.1007/s12648-021-02139-5 [16] Strekalov M L 2024 Chem. Phys. Impact 8 100444 doi: 10.1016/j.chphi.2023.100444 [17] Coveney P V, Wan S 2016 Phys. Chem. Chem. Phys. 18 30236 doi: 10.1039/C6CP02349E [18] Fang Z, Vasiliu M, Peterson K A, Dixon D A 2017 J. Chem. Theory. Comput. 13 1057 doi: 10.1021/acs.jctc.6b00971 [19] Startsev A N 2019 J. Sulfur Chem. 40 435 doi: 10.1080/17415993.2019.1588273 [20] van Speybroeck V, Gani R, Meier R J 2010 Chem. Soc. Rev. 39 1764 doi: 10.1039/b809850f [21] Kang D, Fan Q, Fan Z, Li H, Fu J 2024 Int. J. Quantum Chem. 124 e27373 doi: 10.1002/qua.27373 [22] National Institute of Standards and Technology (NIST), 2017 NIST Chemistry WebBook, NISTS Standard Reference Database Number 69. http://webbook.nist.gov/chemistry/ [23] Xie B J, Jia C S 2020 Int. J. Quantum Chem. 120 e26058 doi: 10.1002/qua.26058 [24] Morse P M 1929 Phys. Rev. 34 57 doi: 10.1103/PhysRev.34.57 [25] Desai A M, Mesquita N, Fernandes V 2020 Phys. Scr. 95 085401 doi: 10.1088/1402-4896/ab9bdc [26] Le Roy R J 2017 J. Quant. Spectrosc. Radiat. Transfer 186 167 doi: 10.1016/j.jqsrt.2016.05.028 [27] Ding Q C, Jia C S, Wang C W, Peng X L, Liu J Y, Zhang L H, Jiang R, Zhu S Y, Yuan H, Tang H X 2023 J. Mol. Liq. 371 121088 doi: 10.1016/j.molliq.2022.121088 [28] Hooydonk G V http://hdl.handle.net/1854/LU-1212652 [2024- 12-18] [29] Tobias I, Vanderslice J T 1961 J. Chem. Phys. 35 1852 doi: 10.1063/1.1732156 [30] Fink E H, Akins D L, Bradley Moore C 1969 Chem. Phys. Lett. 4 283 doi: 10.1016/0009-2614(69)80186-7 [31] Wilkinson P G 1968 Can. J. Phys. 46 1225 doi: 10.1139/p68-156 [32] Tian H, Fan Q, Fan Z, Fu J, Li H, Ma J, Xie F 2022 Int. J. Quantum Chem. 122 e26983 doi: 10.1002/qua.26983 [33] Leachman J W, Jacobsen R T, Penoncello S G, Lemmon E W 2009 J. Phys. Chem. Ref. Data 38 721 doi: 10.1063/1.3160306 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: