高级搜索

应变与电场调控下二维异质结BAs/I-AsP的光电特性

,  ,  ,  , 

downloadPDF

上一篇

下一篇

郝军华, 张德龙, 王正佳, 陈淑鑫, 王玉芳. 应变与电场调控下二维异质结BAs/I-AsP的光电特性[J]. 物理学报, 2025, 74(10): 107102-1. doi: 10.7498/aps.74.20250196
引用本文: 郝军华, 张德龙, 王正佳, 陈淑鑫, 王玉芳. 应变与电场调控下二维异质结BAs/I-AsP的光电特性[J]. 物理学报, 2025, 74(10): 107102-1. doi: 10.7498/aps.74.20250196
shu
Junhua HAO, Delong ZHANG, Zhengjia WANG, Shuxin CHEN, Yufang WANG. Optoelectronic properties of two-dimensional heterostructure BAs/I-AsP under strain and electric field modulation[J]. Acta Physica Sinica, 2025, 74(10): 107102-1. doi: 10.7498/aps.74.20250196
Citation: Junhua HAO, Delong ZHANG, Zhengjia WANG, Shuxin CHEN, Yufang WANG. Optoelectronic properties of two-dimensional heterostructure BAs/I-AsP under strain and electric field modulation[J]. Acta Physica Sinica, 2025, 74(10): 107102-1. doi: 10.7498/aps.74.20250196
shu

应变与电场调控下二维异质结BAs/I-AsP的光电特性

  • 1.

    天津大学精密仪器与光电子工程学院, 光电信息技术教育部重点实验室, 微光机电系统技术教育部重点实验室, 天津　300072

  • 2.

    天津仁爱学院物理教学部, 天津　301636

  • 3.

    哈尔滨工业大学仪器科学与工程学院, 凝聚态科学与技术研究所, 哈尔滨　150080

  • 4.

    天津仁爱学院智算工程学院, 天津　301636

  • 5.

    南开大学物理科学学院, 天津　300071

    • 作者简介: 郝军华.E-mail: nkhjh@mail.nankai.edu.cn .
    通讯作者: E-mail: dlzhang@tju.edu.cn.;  E-mail: zhengjiawang@hit.edu.cn.;  E-mail: shuxinfriend@tju.edu.cn.; 

  • 中图分类号: 71.15.Mb, 73.20.At, 78.20.-e, 68.35.Gy

Optoelectronic properties of two-dimensional heterostructure BAs/I-AsP under strain and electric field modulation

  • 1.

    Key Lab of Micro-Opto-Electro-Mechanical Systems (MOEMS) Technology (Ministry of Education), Key Lab of Optoelectronic Information Technology (Ministry of Education), School of Precision Instrument and Opto-Electronics Engineering, Tianjin University, Tianjin 300072, China

  • 2.

    Department of Physics, Tianjin Ren’ai College, Tianjin 301636, China

  • 3.

    Condensed Matter Science and Technology Institute, School of Instrumentation Science and Engineering, Harbin Institute of Technology, Harbin 150080, China

  • 4.

    School of Intelligent Computing Engineering, Tianjin Ren’ai College, Tianjin 301636, China

  • 5.

    School of Physics, Nankai University, Tianjin 300071, China

    • Corresponding authors: E-mail: dlzhang@tju.edu.cn.;  E-mail: zhengjiawang@hit.edu.cn.;  E-mail: shuxinfriend@tju.edu.cn.; 

  • MSC: 71.15.Mb, 73.20.At, 78.20.-e, 68.35.Gy

  • 摘要: 由两种或多种不同的二维材料组合而产生的层状范德瓦耳斯异质结构具有不同寻常的物理特性, 可用于设计高效光电器件. 本文使用基于密度泛函理论的第一性原理方法系统地研究了由二维砷化硼(BAs)和蓝磷砷(I-AsP)单层形成的异质结的几何结构和光电性能. 研究表明, 4种垂直堆叠的BAs/I-AsP异质结构在基态下具有稳定的结构, 且带隙在0.63—0.86 eV之间. 相较于其组分的单层结构, 该异质结构的光学吸收系数得到提升, 并且具备I型能带排列结构. 另外, 通过施加双轴应变和电场可显著地改变异质结构的带隙和能带类型. 在双轴施加–10%—8%的拉伸或压缩应变下, 带隙也随之增大, 在拉伸大于8%时, 带隙开始减小. 电场在–0.5—0.5 V/Å范围内线性地影响带隙, 随着电场增大, 带隙逐渐减小. 双轴应变和电场都可使材料能带排列在I型和II型之间转变. 同时, BAs/I-AsP异质结具有约13%的理论光电转换效率. 可见, 该二维异质结在光伏和光电领域具有广阔的应用前景.
    Abstract: In recent years, two-dimensional (2D) materials have attracted considerable attention due to their outstanding optical and electronic properties, and they have shown great potential applications in next-generation solar cells and other optoelectronic devices. In this work, density functional theory (DFT) is used to systematically study the electronic and optoelectronic properties of the heterojunction formed by 2D BAs and I-AsP monolayers, as well as the response of this heterojunction under biaxial strain and electric field. The calculation results show that in the ground state, the four vertically stacked BAs/I-AsP heterostructures all have stable geometric structures, and their band gaps range from 0.63 to 0.86 eV. Compared with their constituent monolayers, these heterostructures have the increased optical absorption coefficients (the absorption coefficient in the x-direction reaches 106 cm–1), and they can effectively separate the photogenerated electron-hole pairs. Of the four structures, the A1 structure exhibits the smallest interlayer spacing, the smallest binding energy, and the highest stability. It has a type-I band alignment and a structure of a direct-band-gap semiconductor with band gaps of 0.86 eV (PBE) and 1.26 eV (HSE06), which can be used in the field of light-emitting diodes. The band gap and band type of the heterostructure can be effectively changed by applying biaxial strain and electric field. Under the application of biaxial tensile or compressive strain in a range of –10% to 8%, the band gap increases accordingly. When the tensile strain is greater than 8%, the band gap starts to decrease. When the biaxial strain ε ≤ –3% and ε > 8%, the heterojunction transitions from a type-I band alignment to a type-II band alignment. Under tensile strain, the absorption spectrum undergoes a red shift, while compressive strain leads to a blue shift of the absorption spectrum. Similarly, the externally applied electric field linearly affects the band gap of the BAs/I-AsP heterojunction in a range from –0.5 to 0.5 V/Å, and the band gap decreases as the electric field increases. When a positive electric field with E ≥ 0.2 V/Å is applied, the band alignment of the heterojunction can also transition from type-I to type-II. The BAs/I-AsP heterojunction has strong absorption properties in the ultraviolet and visible light ranges. Based on the Scharber model, the theoretical power conversion efficiency (PCE) η of the BAs/I-AsP heterojunction is found to be greater than 13%, which is higher than those of 2D heterojunction materials such as Cs3Sb2I9/InSe (η = 3.3%), SiPGaS/As (η = 7.3%) and SnSe/SnS (η = 9.1%). This further expands the application scope of the BAs/I-AsP heterojunction, making it expected to play an important role in the field of photodetectors and solar cells.
  • 加载中

  • 图 1  单层(a) I-AsP和(b) BAs的俯视图和侧视图

    Figure 1.  Top and side views of monolayer (a) I-AsP and (b) BAs.

    下载: 全尺寸图片 幻灯片

    图 2  BAs/I-AsP异质结4种堆叠构型的俯视图与侧视图

    Figure 2.  Top and side views of the four stacking configurations of the BAs/I-AsP heterojunction.

    下载: 全尺寸图片 幻灯片

    图 3  在T = 300 K下的AIMD模拟中, BAs/I-AsP异质结构(A1构型)的能量与温度变化情况

    Figure 3.  Variations of energy and temperature of the BAs/I-AsP heterostructure (A1 structure) in the AIMD simulation at T = 300 K.

    下载: 全尺寸图片 幻灯片

    图 4  采用PBE和HSE06方法得到的BAs/I-AsP异质结能带结构和投影态密度

    Figure 4.  Band structures and projected density of states of the BAs/I-AsP heterojunction obtained by using the PBE and HSE06 methods.

    下载: 全尺寸图片 幻灯片

    图 5  (a) BAs/I-AsP异质结界面电位分布; (b)异质结的Bader电荷分析结果(负值代表电荷由BAs层转移至I-AsP层); (c) BAs/I-AsP异质结构沿z方向的平面平均电荷密度差Δρ(z), 其中插图展示了电荷密度差的三维等值面(黄色和蓝色区域分别表示电子增加和减少)

    Figure 5.  (a) The interfacial potential distribution of the BAs/I-AsP heterojunction; (b) results of the Bader charge analysis of the heterojunction, the negative values indicate that the charge is transferred from the BAs layer to the I-AsP layer; (c) the planar average charge density difference Δρ(z) of the BAs/I-AsP heterostructure along the z direction of the surface. The inset shows the three-dimensional isosurface of the charge density difference (the yellow and blue regions represent the increase and decrease of electrons respectively).

    下载: 全尺寸图片 幻灯片

    图 6  BAs/I-AsP异质结构在双轴应变下的变化情况　(a)带隙变化; (b)能带边缘变化; (c), (d) ε = 4% 和–4%的能带结构

    Figure 6.  Variation of the BAs/I-AsP heterostructure under biaxial strain: (a) Variation of the band gap; (b) variation of the band edges; (c), (d) the energy band structures with ε = 4% and –4%, respectively.

    下载: 全尺寸图片 幻灯片

    图 7  BAs/I-AsP异质结构在外加电场下的变化　(a)带隙变化; (b)能带边缘变化; (c), (d) E = 0.2 V/Å和–0.2 V/Å的能带结构

    Figure 7.  Variation of the BAs/I-AsP heterostructure under an externally applied electric field: (a) Variation of the band gap; (b) variation of the band edges; (c) the energy band structure with E = 0.2 V/Å and –0.2 V/Å, respectively.

    下载: 全尺寸图片 幻灯片

    图 8  (a)单层BAs、单层I-AsP与BAs/I-AsP异质结沿x轴和z轴的光吸收系数; (b) BAs/I-AsP异质结在不同双轴应变下沿x轴和z轴的光吸收系数变化情况; (c) BAs/I-AsP异质结在不同外加电场作用下沿x轴和z轴的光吸收系数变化情况

    Figure 8.  (a) The optical absorption coefficients along the x-axis and z-axis of the monolayer BAs, I-AsP and the BAs/I-AsP heterojunction; (b) variations of the optical absorption coefficients along the x-axis and z-axis of the BAs/I-AsP heterojunction under different biaxial strains; (c) variations of the optical absorption coefficients along the x-axis and z-axis of the BAs/I-AsP heterojunction under different applied electric fields.

    下载: 全尺寸图片 幻灯片

    图 9  BAs/I-AsP异质结的光电转换效率随导带偏移量$ \Delta {E}_{{\mathrm{c}}} $和施主带隙$ {E}_{{\mathrm{g}}}^{{\mathrm{d}}} $变化的等高线图

    Figure 9.  Contour plot of the photoelectric conversion efficiency of the BAs/I-AsP heterojunction as a function of the conduction band offset ($ \Delta {E}_{{\mathrm{c}}} $) and the donor band gap ($ {E}_{{\mathrm{g}}}^{{\mathrm{d}}} $).

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  单层BAs、单层I-AsP以及4种堆叠构型的结构参数, 包括晶格常数(其中a = b)、层间距(d)、键长(l)、带隙(Eg)和层间结合能(Eb)

    Table 1.  Structural parameters for monolayer BAs, monolayer I-AsP, and four stacking configurations in heterostructures, include lattice constants (where a = b), interlayer distance (d), bond length (l), band gap (Eg), and interlayer binding energy (Eb).

    a/Å d/Å lB-As/Å(lAs-As/lAs-P/lP-P) Eg/eV Eb/(meV·Å–2)
    PBE HSE06
    BAs 3.39 — 1.96 0.76 1.18 —
    I-AsP 5.87 — 2.49/2.37/2.24 1.63 2.27 —
    A1 5.87 3.44 1.96 (2.49/2.37/2.24) 0.86 1.26 –0.59
    A2 5.87 3.83 1.96 (2.49/2.37/2.24) 0.63 — –0.43
    A3 5.87 3.60 1.96 (2.49/2.37/2.24) 0.79 — –0.52
    A4 5.87 3.81 1.96 (2.49/2.37/2.24) 0.71 — –0.47
    下载: 导出CSV

    表 2  施加双轴应变和外加电场下具有II型能带排列的异质结构的光伏特性相关参数

    Table 2.  Summary of the photovoltaic characteristic parameters of the heterostructures with type-II band alignment under the biaxial strain and the external electric field.

    Strain/% $ {E}_{{\mathrm{g}}}^{{\mathrm{d}}} $/eV $ \Delta {E}_{{\mathrm{c}}} $/eV $ {V}_{{\mathrm{o}}{\mathrm{c}}} $/V $ \eta $/%
    –41.340.6810.35913.14
    –61.010.5580.1527.49
    101.280.6340.33412.72
    Electric field/(V·Å–1)$ {E}_{{\mathrm{g}}}^{{\mathrm{d}}} $/eV$ \Delta {E}_{{\mathrm{c}}} $/eV$ {V}_{{\mathrm{o}}{\mathrm{c}}} $/V$ \eta $/%
    0.21.640.8230.52213.13
    0.31.660.9040.46211.26
    0.41.670.9760.3909.51
    0.51.671.0570.3158.09
    下载: 导出CSV
  • [1] Kazem H A, Chaichan M T, Al-Waeli A H A, Sopian K 2024 Sol. Energy 282 112946. doi: 10.1016/j.solener.2024.112946
    [2] Qu W J, Han D J, Zhang J, Peng K W, Gao Y, Huang S M 2025 Energy 316 134562 doi: 10.1016/j.energy.2025.134562
    [3] Richter A, Hermle M, Glunz S W 2013 IEEE J. Photovolt. 3 1184 doi: 10.1109/JPHOTOV.2013.2270351
    [4] An J R, Zhao X Y, Zhang Y N, Liu M X, Yuan J, Sun X J, Zhang Z Y, Wang B, Li S J, Li D B 2022 Adv. Funct. Mater. 32 2110119 doi: 10.1002/adfm.202110119
    [5] Zhang J, Zhang H, Du Q, Xie X, Fang Y, Tang C, Chen G 2024 Part. Part. Syst. Charact. 41 2300062 doi: 10.1002/ppsc.202300062
    [6] Ullah S, Thonhauser T, Menezes M G 2024 Appl. Mater. Today 41 102495 doi: 10.1016/j.apmt.2024.102495
    [7] Hao J H, Zhang D L, Chen S X, Xu J, Wang Z J, Wang Y F 2025 Surf. Interfaces 58 105837 doi: 10.1016/j.surfin.2025.105837
    [8] Mao Y L, Wu R L, Ding D, He F 2022 Computat. Mater. Sci. 202 110957 doi: 10.1016/j.commatsci.2021.110957
    [9] Lv B, Lan Y C, Wang X Q, Zhang Q, Hu Y J, Jacobson A J, Broido D, Chen G, Ren Z F, Chu C W 2015 Appl. Phys. Lett. 106 074105 doi: 10.1063/1.4913441
    [10] Broido D A, Lindsay L, Reinecke T L 2013 Phys. Rev. B 88 214303 doi: 10.1103/PhysRevB.88.214303
    [11] Xie M Q, Zhang S L, Cai B, Zhu Z, Zou Y S, Zeng H B 2016 Nanoscale 8 13407 doi: 10.1039/C6NR02923J
    [12] Xie M Q, Cai B, Meng Z S, Gu Y, Zhang S L, Liu X H, Gong L Y, Li X A, Zeng H B 2020 ACS Appl. Mater. Interfaces 12 6074 doi: 10.1021/acsami.9b21102
    [13] Mak K F, Shan J 2016 Nat. Photonics 10 216 doi: 10.1038/nphoton.2015.282
    [14] Deng X Q, Sheng R Q, Jing Q 2021 RSC Adv. 11 21824 doi: 10.1039/D1RA03606H
    [15] Li L K, Yu Y J, Ye G J, Ge Q Q, Ou X D, Wu H, Feng D L, Chen X H, Zhang Y B 2014 Nat. Nanotechnol. 9 372 doi: 10.1038/nnano.2014.35
    [16] Zhu Z, Tománek D 2014 Phys. Rev. Lett. 112 176802 doi: 10.1103/PhysRevLett.112.176802
    [17] Song Y H, Muzaffar M U, Wang Q, Wang Y, Jia Y, Cui P, Zhang W, Wang X S, Zhang Z 2024 Nat. Commun. 15 1157 doi: 10.1038/s41467-024-45263-6
    [18] Zhou D C, Meng Q L, Si N, Zhou X, Zhai S W, Tang Q, Ji Q M, Zhou M, Niu T C, Fuchs H 2020 ACS Nano 14 2385 doi: 10.1021/acsnano.9b09588
    [19] Cheng W J, Yao X D, Zhao L X, Li C K, Zheng Q F, Han J, Wang S M, Liu Y, Zhu J L 2024 Phys. Rev. B 109 064507 doi: 10.1103/PhysRevB.109.064507
    [20] Antonatos N, Mazánek V, Lazar P, Sturala J, Sofer Z 2020 Nanoscale Adv. 2 1282 doi: 10.1039/C9NA00754G
    [21] Jamdagni P, Thakur A, Kumar A, Ahluwalia P K, Pandey R 2018 Phys. Chem. Chem. Phys. 20 29939 doi: 10.1039/C8CP06162A
    [22] Zhang S L, Yan Z, Li Y F, Chen Z F, Zeng H B 2015 Angew. Chem. Int. Edt. 54 3112 doi: 10.1002/anie.201411246
    [23] Zhong M Z, He J 2020 J. Semicond. 41 080402 doi: 10.1088/1674-4926/41/8/080402
    [24] Yuan S F, Shen C F, Deng B C, Chen X L, Guo Q S, Ma Y Q, Abbas A, Liu B L, Haiges R, Ott C, Nilges T, Watanabe K, Taniguchi T, Sinai O, Naveh D, Zhou C W, Xia F N 2018 Nano Lett. 18 3172 doi: 10.1021/acs.nanolett.8b00835
    [25] Cai X Y, Chen Y Z, Sun B, Chen J, Wang H Y, Ni Y X, Tao L, Wang H, Zhu S H, Li X M, Wang Y C, Lv J, Feng X L, Redfern S A T, Chen Z F 2019 Nanoscale 11 8260 doi: 10.1039/C9NR01261C
    [26] Blöchl P E 1994 Phys. Rev. B 50 17953 doi: 10.1103/PhysRevB.50.17953
    [27] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758 doi: 10.1103/PhysRevB.59.1758
    [28] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865
    [29] Grimme S, Antony J, Ehrlich S, Krieg H 2010 J. Chem. Phys. 132 154104 doi: 10.1063/1.3382344
    [30] Hao J H, Zhang D L, Wang Z J, Chen S X, Xu J, Wang Y F 2024 Mater. Today Commun. 38 108423 doi: 10.1016/j.mtcomm.2024.108423
    [31] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188 doi: 10.1103/PhysRevB.13.5188
    [32] Nosé S 1984 J. Chem. Phys. 81 511 doi: 10.1063/1.447334
    [33] Tang W, Sanville E, Henkelman G 2009 J. Phys. Condens. Mater. 21 084204 doi: 10.1088/0953-8984/21/8/084204
    [34] Bai H, Qian G L, Liang Q, Feng Y Y, An M Y, Xie Q 2024 Comput. Mater. Sci. 238 112948 doi: 10.1016/j.commatsci.2024.112948
    [35] Cheng K, Xu J K, Guo X, Guo S D, Su Y 2023 Phys. Chem. Chem. Phys. 25 17360 doi: 10.1039/D3CP01290E
    [36] Wu H Y, Yang K, Si Y, Huang W Q, Hu W, Huang G F 2019 Phys. Status Solidi RRL 13 1800565 doi: 10.1002/pssr.201800565
    [37] 孙婷钰, 吴量, 何贤娟, 姜楠, 周文哲, 欧阳方平 2023 物理学报 72 076301 doi: 10.7498/aps.72.20222250 Sun T Y, Wu L, He X J, Jiang N, Zhou W Z, Ouyang F P 2023 Acta Phys. Sin. 72 076301 doi: 10.7498/aps.72.20222250
    [38] Bernardi M, Palummo M, Grossman J C 2012 ACS Nano 6 10082 doi: 10.1021/nn303815z
    [39] Wu M, Meng D 2024 Physics B 680 415847 doi: 10.1016/j.physb.2024.415847
    [40] Behzad S, Chegel R 2023 Sci. Rep. 13 21339 doi: 10.1038/s41598-023-48654-9
    [41] Lin L, Lou M S, Li S F, Cai X L, Zhang Z W, Tao H L 2022 Appl. Surf. Sci. 572 151209 doi: 10.1016/j.apsusc.2021.151209
    [42] 刘晨曦, 庞国旺, 潘多桥, 史蕾倩, 张丽丽, 雷博程, 赵旭才, 黄以能 2022 物理学报 71 097301 doi: 10.7498/aps.71.20212261 Liu C X, Pang G W, Pan D Q, Shi L Q, Zhang L L, Lei B C, Zhao X C, Huang Y N 2022 Acta Phys. Sin. 71 097301 doi: 10.7498/aps.71.20212261
    [43] Xu Y H, Fan Z Q, Zhang Z H, Zhao T 2021 Appl. Surf. Sci. 547 149174 doi: 10.1016/j.apsusc.2021.149174
    [44] 熊祥杰, 钟防, 张资文, 陈芳, 罗婧澜, 赵宇清, 朱慧平, 蒋绍龙 2024 物理学报 73 137101 doi: 10.7498/aps.73.20240434 Xiong X J, Zhong F, Zhang Z W, Chen F, Luo J L, Zhao Y Q, Zhu H P, Jiang S L 2024 Acta Phys. Sin. 73 137101 doi: 10.7498/aps.73.20240434
    [45] Shahid I, Hu X, Ahmad I, Ali A, Shehzad N, Ahmad S, Zhou Z 2023 Nanoscale 15 7302 doi: 10.1039/D3NR00316G
    [46] Zhang R Q, Zhou Z Z, Yao Q, Qi N, Chen Z Q 2021 Phys. Chem. Chem. Phys. 23 3794 doi: 10.1039/D0CP05548D
  • 加载中
图( 10) 表( 2)
计量
  • 文章访问数:  27
  • HTML全文浏览数:  27
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-02-18
  • 刊出日期:  2025-05-20

应变与电场调控下二维异质结BAs/I-AsP的光电特性

    通讯作者: E-mail: dlzhang@tju.edu.cn.; 
    通讯作者: E-mail: zhengjiawang@hit.edu.cn.; 
    通讯作者: E-mail: shuxinfriend@tju.edu.cn.; 
    作者简介: 郝军华.E-mail: nkhjh@mail.nankai.edu.cn
  • 1. 天津大学精密仪器与光电子工程学院, 光电信息技术教育部重点实验室, 微光机电系统技术教育部重点实验室, 天津　300072
  • 2. 天津仁爱学院物理教学部, 天津　301636
  • 3. 哈尔滨工业大学仪器科学与工程学院, 凝聚态科学与技术研究所, 哈尔滨　150080
  • 4. 天津仁爱学院智算工程学院, 天津　301636
  • 5. 南开大学物理科学学院, 天津　300071
  • 收稿日期:  2025-02-18

摘要: 由两种或多种不同的二维材料组合而产生的层状范德瓦耳斯异质结构具有不同寻常的物理特性, 可用于设计高效光电器件. 本文使用基于密度泛函理论的第一性原理方法系统地研究了由二维砷化硼(BAs)和蓝磷砷(I-AsP)单层形成的异质结的几何结构和光电性能. 研究表明, 4种垂直堆叠的BAs/I-AsP异质结构在基态下具有稳定的结构, 且带隙在0.63—0.86 eV之间. 相较于其组分的单层结构, 该异质结构的光学吸收系数得到提升, 并且具备I型能带排列结构. 另外, 通过施加双轴应变和电场可显著地改变异质结构的带隙和能带类型. 在双轴施加–10%—8%的拉伸或压缩应变下, 带隙也随之增大, 在拉伸大于8%时, 带隙开始减小. 电场在–0.5—0.5 V/Å范围内线性地影响带隙, 随着电场增大, 带隙逐渐减小. 双轴应变和电场都可使材料能带排列在I型和II型之间转变. 同时, BAs/I-AsP异质结具有约13%的理论光电转换效率. 可见, 该二维异质结在光伏和光电领域具有广阔的应用前景.

English Abstract

    全文HTML

    1.   引　言

    • 在化石能源危机日益严峻的背景下, 太阳能作为清洁可再生资源, 其开发备受瞩目[1,2]. 硅基光伏太阳能电池凭借硅储量丰富以及成熟的工业制造技术优势, 在能源市场占据着主导地位. 但即便历经大量的改良尝试, 其转换效率目前也已无限趋近于理论上限, 进一步提升的空间极为有限[3]. 高性能太阳能电池新材料的研发迫在眉睫. 二维(2D)层状材料凭借较大的比表面积、出色的载流子迁移率、高强度、高柔韧性和高光学吸收等独特性能, 成为纳米电子、光电子和光伏器件的理想候选材料[4–8].

      硼化砷(BAs)隶属III-V族材料, 在二维物质中以独特热力学性能脱颖而出, 具备超高晶格热导率、高载流子迁移率和高熔点[9–11]. 理论预测表明, 六方单层硼化砷的带隙为1.14 eV[12], 这与硅的带隙非常接近, 而硅已作为叠层太阳能电池材料被成功应用, 这意味着带隙较窄的六方单层硼化砷也可能用作叠层太阳能电池材料. 当BAs作为光电极材料时, 在可见光和紫外线辐射下均展现出光敏特性[13]. Deng等[14]研究发现, 具有II型能带排列的BAs/As结构有助于光生载流子分离, 施加电场时光吸收系数显著变化, 极大拓宽了该异质结的应用范围.

      2014年, 二维黑磷(磷烯)成功合成, 其电子迁移率高达103 cm–2·V–1·s–1, 直接带隙约为2 eV, 从而引发了对更多二维磷同素异形体的探索, 如蓝磷[15,16]. 蓝磷的理论预测带隙可在1.1—2 eV范围内调节, 体相层堆叠类似于石墨, 已分别于2020年和2024年通过分子束外延等方法在Cu3O2/Cu(111)和Cu(111)衬底上成功制备, 并发现其具有高温热稳定性[17,18].

      砷与磷同属V族元素, 共价半径相近, 也存在多种同素异形体, 如黑砷和灰砷. 灰砷(g-As)作为砷最稳定的同素异形体, 具有A7层状相[19,20]. 理论计算和实验表明, 少层灰砷具有可调节的带隙(~2.5 eV), 能通过层数或应力进行调控; 而块状灰砷作为半金属, 展现出超高的载流子迁移率, 以及由补偿机制产生的巨磁阻(GMR)特性[21,22]. 黑砷与黑磷具有相同的晶体结构, 灰砷则在结构上与蓝磷相似, 它们均拥有稳定的层状结构. 同时, 黑砷和灰砷还具备优异的光电和热电性能, 这使得它们成为光电应用领域极具潜力的候选材料[21,23].

      基于黑磷、蓝磷和砷拥有相同的二维结构, 二维二元黑磷砷和蓝磷砷成为新材料开发的重要方向. 近期, 层状黑磷砷(As1–xPₓ)合金已成功合成, 它作为中红外应用领域极具潜力的替代材料备受关注[24]. Cai等[25]运用粒子群优化算法, 系统研究了单层蓝磷砷(AsxP1–x)的低能量结构, 不仅证实了As∶P = 1∶1组成的高稳定性, 还获得了一系列新颖的二维蓝磷砷单层, 为该领域的研究提供了新的思路和材料基础. 其中最稳定的I-AsP单层优势最为显著, 例如具有可调节的直接带隙, 能更好适配不同光电需求; 高吸收系数(×105 cm–1), 在整个可见太阳光谱范围内远超蓝磷; 超高载流子迁移率(约7.4×104 cm2·V–1·s–1), 大幅提升电学性能; 卓越的光伏效率, 30 nm厚的I-AsP薄片基电池光电转换效率可达约12%, 而且I-AsP与CdSe形成异质结后的光电转换效率(PCE)可高达约13%. 这些优势充分表明, I-AsP薄片是极具潜力的高效太阳能电池材料, 在光伏应用领域前景广阔.

      目前尚未发现有关BAs/I-AsP异质结的研究. 因此, 本文将单层BAs垂直置于单层蓝磷砷(I-AsP)之上, 构建BAs/I-AsP异质结. 通过研究异质结的几何结构等性质来确定BAs/I-AsP异质结的稳定性. 计算BAs/I-AsP异质结的电学和光学性质, 以确定异质结的类型及相应的应用领域. 通过施加外部应力和电场, 研究异质结对应力和电场的耐受性, 调控异质结的性能并拓宽其应用范围. 本文的BAs/I-AsP异质结计算结果将对实验研究起指导和促进作用.

    2.   计算方法

    • 本文采用基于密度泛函理论(DFT)的DS-PAW软件包完成[26]. 价电子和芯电子之间的相互作用利用投影增强波(PAW)方法来描述[27]. 电子之间的交换关联效应, 使用广义梯度近似(GGA)中的PBE (Perdew Burke Ernzerhof)方法和杂化泛函HSE06方法[28–30]. 在几何弛豫和电子结构计算时, 布里渊区采用了6×6×1, 11×6×1, 10×6×1的k点网格对单层I-AsP, BAs和异质结BAs/ I-AsP的所有特性进行了优化[31]. 为避免相邻异质结构之间的相互作用, 两个相邻异质结构之间被大于25 Å的真空层隔开. 采用Grimme等[29]提出的DFT-D3方法来描述异质结构层间的范德瓦耳斯力. 计算过程中, 截断能量、最大力和能量的收敛标准分别设置为450 eV, 0.01 eV/Å和10–5 eV. 同时, 为了验证结构的热稳定性, 在NVE系综下从头计算分子动力学(AIMD)模拟[32]. 本次模拟将温度设定在300 K, 总计执行1000步, 每步步长3 fs, 模拟全程持续时长为3000 fs. 此外, 通过Bader电荷方法计算了电荷转移量[33].

      形成能$ {E_{\text{b}}} $的计算表达式为[34]

      其中, $ {E_{{\text{vdW}}}} $, $ {E_{{\text{BAs}}}} $和$ {E_{{\text{I-AsP}}}} $分别代表二维范德瓦耳斯异质结构, 单层BAs以及单层I-AsP的总能量, A代表异质结构的表面积.

      晶格失配率定义为[35]

      其中, a1和a2分别代表BAs和I-AsP的晶格常数.

      功函数的计算公式如下[36]:

      其中, $ {E_{{\text{vac}}}} $表示真空能级, $ {E_{\text{f}}} $表示费米能级.

      平面平均差分电荷密度(Δρ)表达式为[36]:

      其中, $ {\rho _{_{\text{vdW}}}} $, $ {\rho _{_{\text{BAs}}}} $和$ \rho_{_\text{I-AsP}} $分别表示范德瓦耳斯异质结构、单层BAs结构以及单层I-AsP结构的电荷密度.

      施加双轴应变ε定义为[34]

      其中, a和a0分别是应变结构和未应变结构的晶格常数.

      光吸收系数通过以下公式计算[34,37]:

      其中, ω为光的频率, $ {\varepsilon _1}(\omega ) $和$ {\varepsilon _2}(\omega ) $分别为介电函数的实部和虚部.

      光电转换效率(PCE)采用Shockley-Queisser limit方法进行计算[36,38]:

      其中, $ {\beta _{{\text{FF}}}} $代表由Shockley-Queisser极限导出的束缚填充因子, 这里取值为0.65; Voc代表电池的开路电压,

      Jsc代表当外部量子效率达到极限值100%时电池产生的短路电流密度,

      Psolar代表AM1.5的太阳能通量,

      $ E_{\text{g}}^{\text{d}} $代表施主带隙的值, $ {{\Delta }}{E_{\text{c}}} $代表导带偏移(conduction band offset, CBO), e代表基本电荷的电荷量.

    3.   结果与讨论

      3.1.   BAs/I-AsP异质结及其稳定性

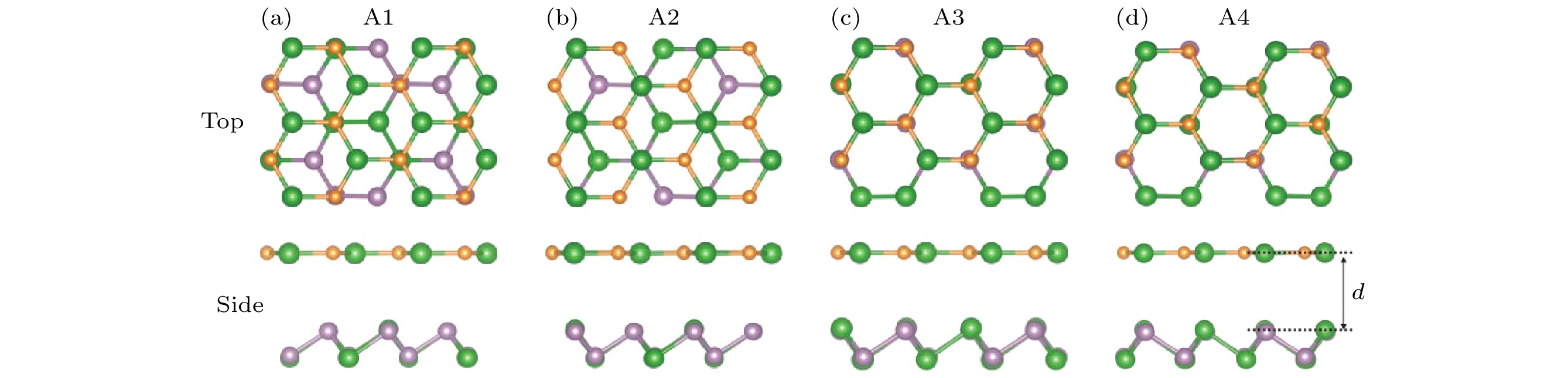
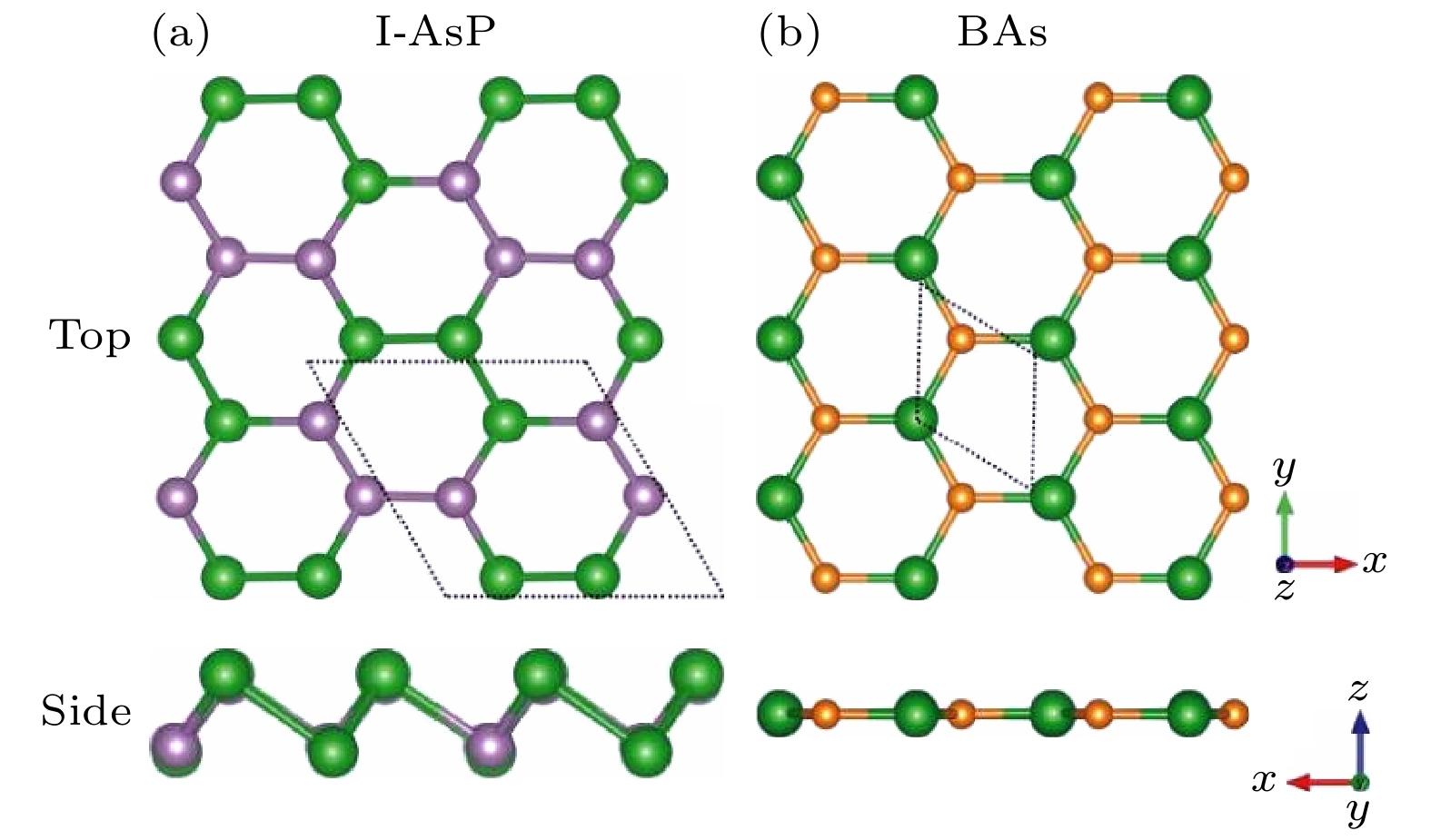
    • 为了构建稳定的BAs/I-AsP异质结构, 首先优化了单层BAs和I-AsP的结构参数, 图1为两种结构优化后的俯视图和侧视图. 绿色球代表As原子, 紫色球代表P原子, 橙色球代表B原子. 虚线内结构为结构原胞. BAs和I-AsP的晶格常数分别为3.39 Å和5.87 Å, 其空间群分别为$ P\bar 6 m2 $和$ P3 m1 $. 从俯视图可以看出, 两种结构原子均呈现蜂窝状排列, 与石墨烯类似. 从侧视图看, BAs比较平整, 而I-AsP则具有锯齿状褶皱的结构且两层原子沿z方向的垂直间距为1.44 Å. BAs为直接带隙半导体, I-AsP为间接带隙半导体, 带隙值分别为0.76 eV(PBE) 和1.63 eV(PBE). 利用HSE06方法得到, BAs和I-AsP的带隙分别为1.18 eV和2.27 eV. 此外, PBE和HSE06方法得到的能带结构在定性上是相同的. 计算结果见表1, 与已有的报道结果相一致[12,39,40].

      综合考虑两种材料的晶格失配率、对称性、建模与计算的可行性, 以及实验操作的可行性等相关因素, 将BAs与I-AsP单层沿着z方向垂直堆叠并进行相对旋转, 进而构建出了4种两两结构相似的BAs/I-AsP异质结构超胞, 如图2所示. 将这些堆叠构型在相同的截断能量、最大力和能量收敛标准下进行优化, 分别标记为A1, A2, A3和A4 . 根据顶层原子和底层原子的相对位置对四种结构进行描述: 在A1构型中, BAs中的As原子位于下层六边形As-P环中心上方; 在A2构型中, BAs中的B原子位于下层六边形As-P环中心上方; 在A3构型中, 俯视两种结构六边形晶格刚好重合, BAs中的B原子与I-AsP中的As和P原子垂直距离最近; 在A4构型中, 俯视两种结构六边形晶格也刚好重合, BAs中的As原子与I-AsP中的As和P原子垂直距离最近. 优化后, 这四种异质结构保持其初始堆叠排列, 层间距d分别为3.44, 3.83, 3.60和3.81 Å, 这意味着与其他构型相比, A1堆叠构型具有最短的层间距离. 此外, 基于(1)式计算得出 A1, A2, A3和A4模式下BAs/I-AsP异质结构的结合能分别为–0.59, –0.43, –0.52和–0.47 meV/Å2. BAs/I-AsP异质结构中的A1堆叠模式拥有最短层间距离和最小结合能, 证实其为能量上最有利的堆叠模式. BAs/I-AsP异质结晶格常数、BAs与I-AsP单层之间的层间距d、键长l、界面结合能Eb以及带隙Eg列于表1中. 结果表明, 键长变化可忽略不计, 这表明原子重排程度较小, 且层间相互作用为较弱的范德瓦耳斯力. A1构型中的单层BAs和单层I-AsP结构相对旋转了150°. 利用(2)式可以计算出晶格失配率为2.22%, 界面应力相对较小, 沿x轴或y轴的应变均为3.33%. 这证明了稳定性和实验合成的可能性.

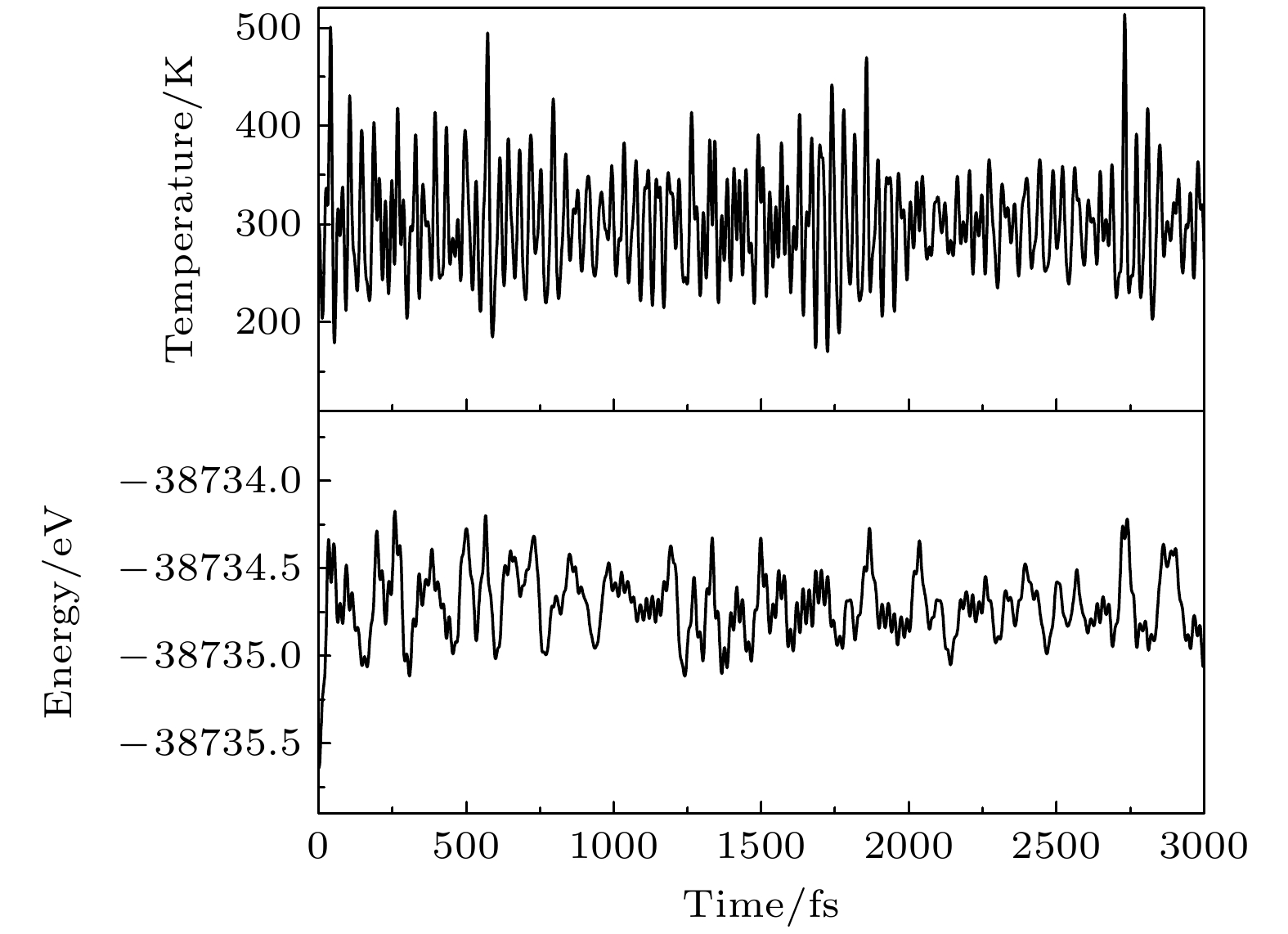
      二维材料的稳定性对实际应用中器件的可靠性和使用寿命有着显著影响. 为研究BAs/I-AsP异质结构的稳定性, 采用从头算分子动力学方法(ab initio molecular dynamics, AIMD), 在300 K的温度下, 以1 fs的时间间隔对BAs/I-AsP异质结构(A1构型)进行3 ps的模拟, 以研究其热稳定性. 从图3可以看到, 随着时间延长, BAs/I-AsP异质结构在温度具有较大波动的情况下, 能量仅有轻微波动, 结构变化并不明显, 这表明BAs/I-AsP异质结构具有热稳定性. 界面结合能列于表1中, 均为负值, 这些负值表明在界面形成过程中存在放热现象, 且相互作用稳定. 这些特征有利于在实验环境下的合成过程. 因此, 本文将通过施加拉伸应变和电场调制, 系统研究BAs/I-AsP异质结A1结构的光电特性.

      • 3.2.   BAs/I-AsP异质结构的电学性质

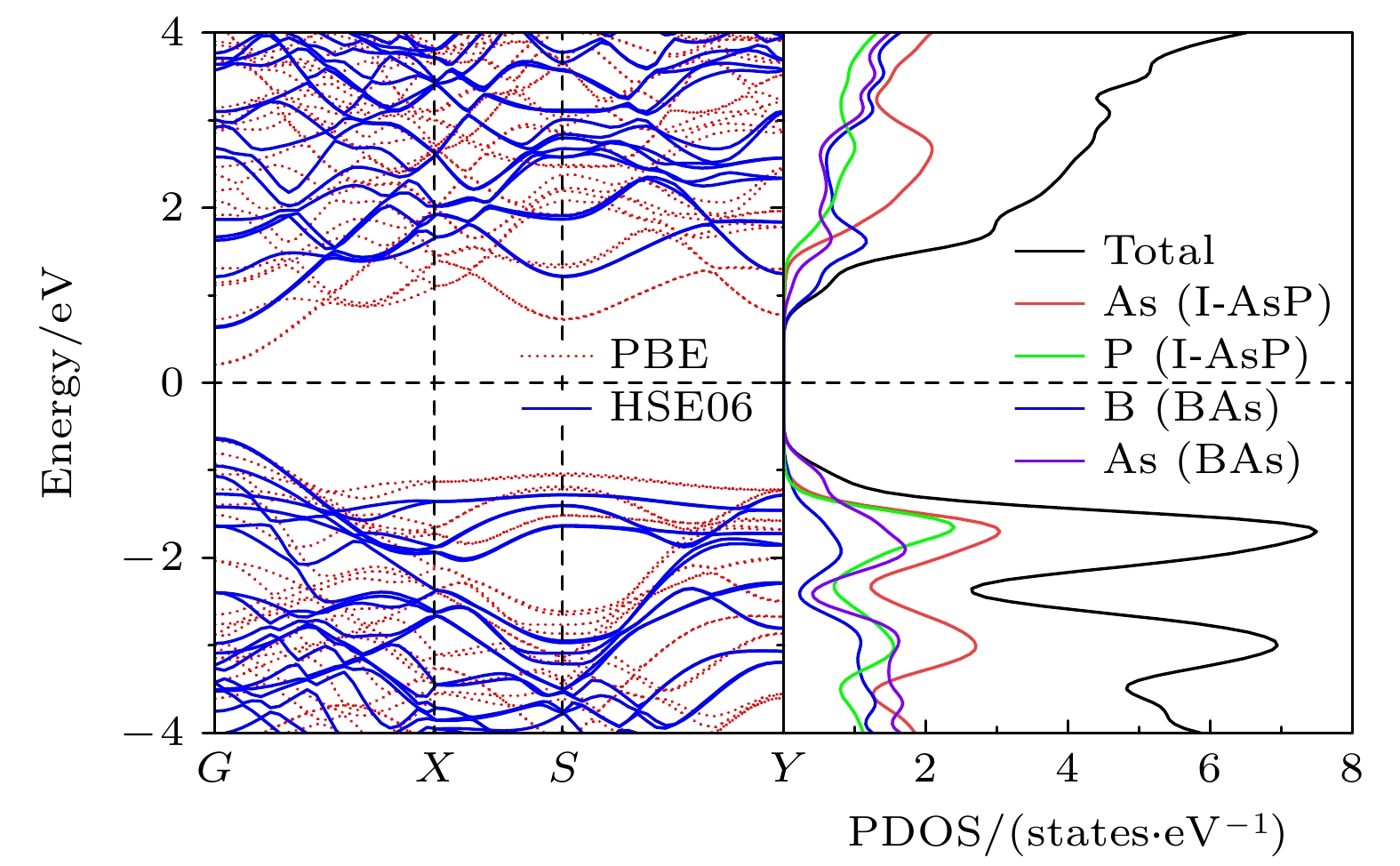
    • 图4为采用 PBE和HSE06泛函杂化计算的二维BAs/I-AsP异质结沿着布里渊区中高对称点G(0, 0, 0)→X(1/2, 0, 0) → S(1/2, 1/2, 0) → Y(0, 1/2, 0)路径的能带结构和投影态密度. 能带结构表明二维BAs/I-AsP异质结为直接带隙, 价带顶和导带底位于G点. 二维BAs/I-AsP异质结的带隙为0.86 eV (PBE)或1.26 eV(HSE06). 与单个单层相比, 形成范德瓦耳斯异质结构后, 带隙变小. 如图4所示, 采用HSE06方法得到的带隙增大, 异质结的价带变化较小, 导带向上平移~0.4 eV. 尽管 PBE 泛函可能会低估带隙, 但其仍能准确预测带隙变化趋势, 并精确阐释物理机制[36]. 从投影态密度曲线可以看出, 价带顶主要来源于BAs中As原子的贡献, 而BAs中的B原子对导带底起主要作用, 这说明了基态BAs/I-AsP异质结为I型能带排列. 本研究的核心目的在于探究BAs/I-AsP异质结构的光电特性, 在受到外加电场作用或双轴应变影响时会产生怎样的响应. 鉴于此, 在后续分析中采用PBE泛函, 针对BAs/I-AsP异质结构(A1构型)展开研究.

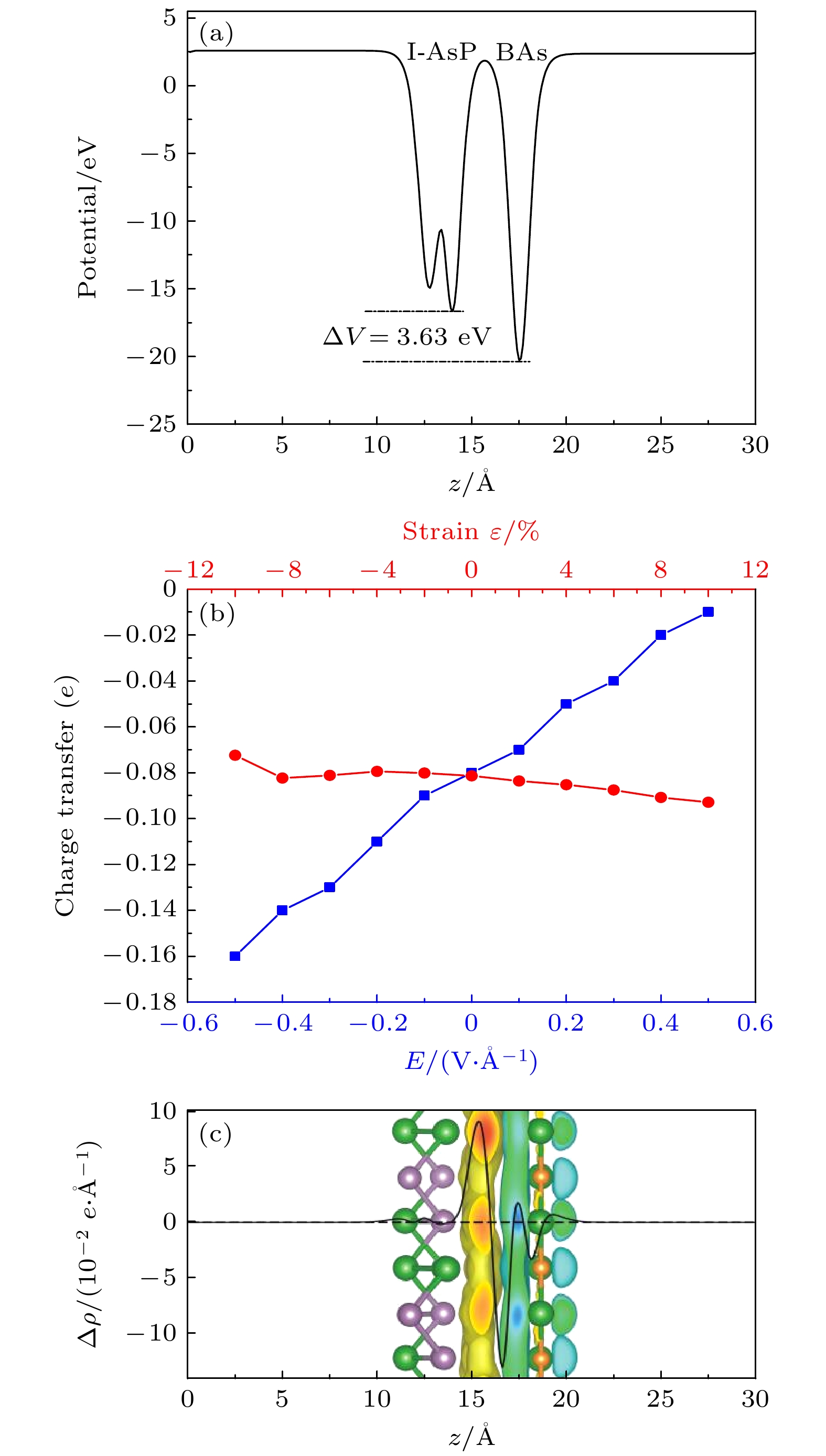
      图5(a)中的黑色实线展示了BAs/I-AsP异质结构沿z方向的平均静电势, 费米能级为–2.39 eV. 利用(3)式计算得出, 单层BAs、单层I-AsP以及BAs/I-AsP范德瓦耳斯异质结构的功函数分别为2.22, 2.68和4.98 eV. 功函数表示真空能级与费 米能级之间的能量差, 其表征了异质结构中电子的束缚强度, 这是描述BAs/I-AsP范德瓦耳斯异质结构能带排列的关键因素. 功函数的增大使得电子更不容易从异质结中逸出, 在一定程度上提高了材料抵抗外界干扰(如热、光、电等)的能力, 使得异质结结构在实际应用中具有更好的稳定性和可靠性. 从图5(a)可以看出, 由于局部电荷分布的差异, 该异质结构在电势分布上呈现多势垒结构, 且在异质结的界面处出现一个高势垒, 其阻止电子从BAs层进一步扩散到I-AsP层, 以使系统达到平衡状态. 界面处BAs层的静电势深度比I-AsP层大约高出3.63 eV. 这种差异源于相关原子不同的电负性, 说明从BAs层到I-AsP层形成内建电场. 根据Bader电荷分析, 约有0.08个电子从BAs层转移至I-AsP层(见图5(b)). 电荷的重新分布产生了一个从 BAs 指向I-AsP的内建电场, 这与功函数和静电势的分析结果相符.

      基于(4)式, 可以计算出异质结沿z方向的平面平均差分电荷密度, 如图5(c)所示, 正、负Δρ(z)分别代表电荷增加与减少. 为了便于观察, 插图中还展示了异质结构及电荷密度差的三维等值面(黄色和蓝色区域分别表示电子增加和减少). 电荷重新分布主要发生在异质结构的界面处, 从图中可以看出电子向I-AsP层聚集, 而空穴被束缚于BAs层, 这与前面的分析结果相一致.

      • 3.3.   双轴应变及电场对BAs/I-AsP异质结构电子性质的影响

    • 机械应变已被证实是一种调控二维材料电子特性的有效方法[37]. 为探究应变对BAs/I-AsP范德瓦耳斯异质结构的影响, 本文系统研究了BAs/I-AsP异质结构在双轴应变下电子特性的演变. 通过不断改变x和y方向的晶格常数来模拟施加机械应变. 双轴应变的大小采用(5)式计算, 应变ε范围在–10%—10%之间, 步长为2%. ε正值表示拉应变, ε负值表示压应变.

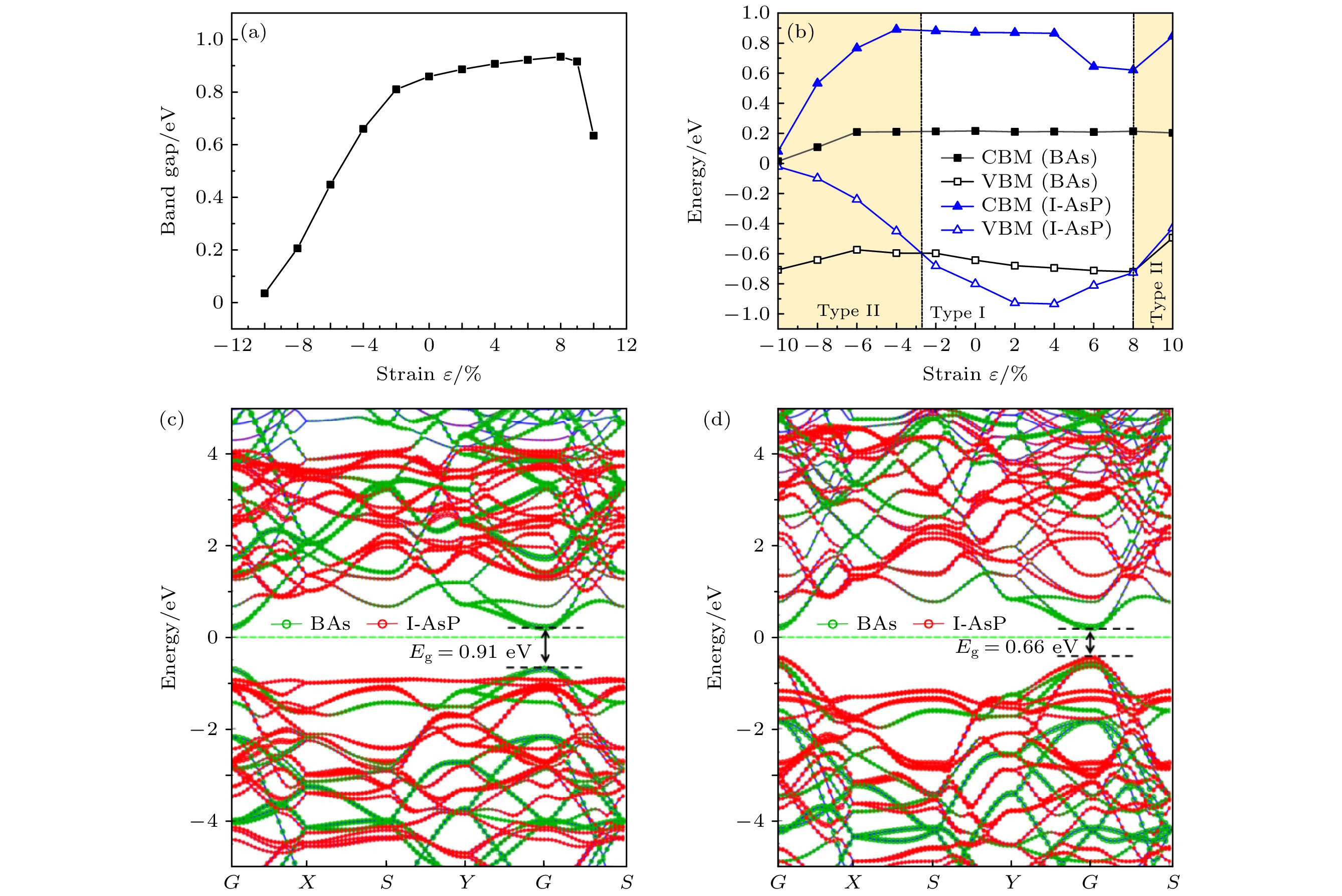
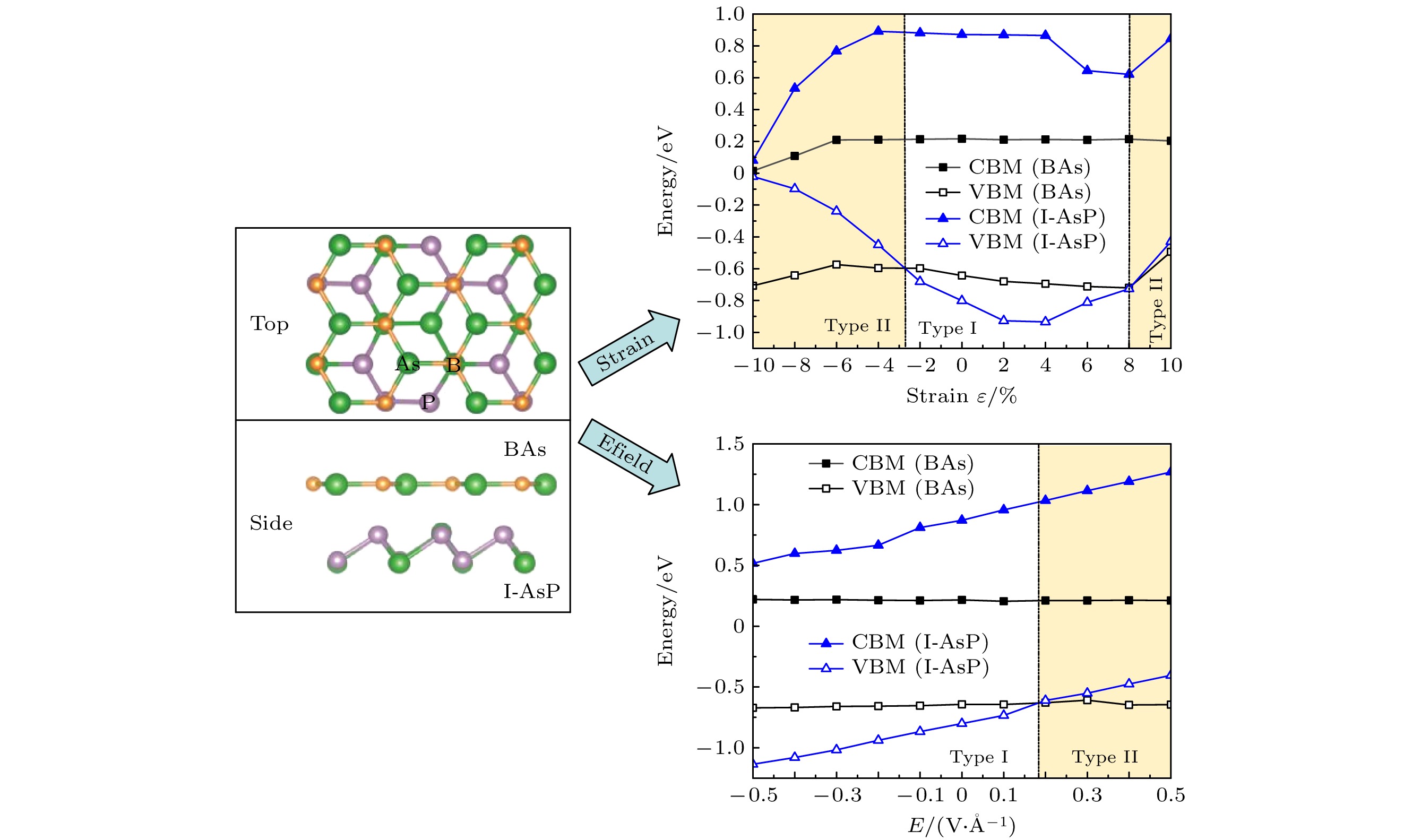
      由图5(b)可以看出, ε从–10%—10%变化过程中, 电荷由BAs层转移至I-AsP层数量缓慢增加, 约0.02e. 图6展示了在双轴应变下的带隙及能带边缘值的变化情况. 如图6(a)所示, 当拉应变从0%增至+8%时, 异质结的带隙值缓慢增加; 拉应变从+8%增至+10%时, 异质结的带隙值急剧减小, 减小约0.3 eV. 这是因为BAs/I-AsP异质结构的价带极小值逐渐靠近费米能级, 导致带隙值下降. 当压应变从0%增至–10%过程中, 异质结的带隙值逐渐减小. 在ε = –10%时, 带隙值最小且仅为0.035 eV, 这表明此异质结已接近半导体-半金属相转变点.

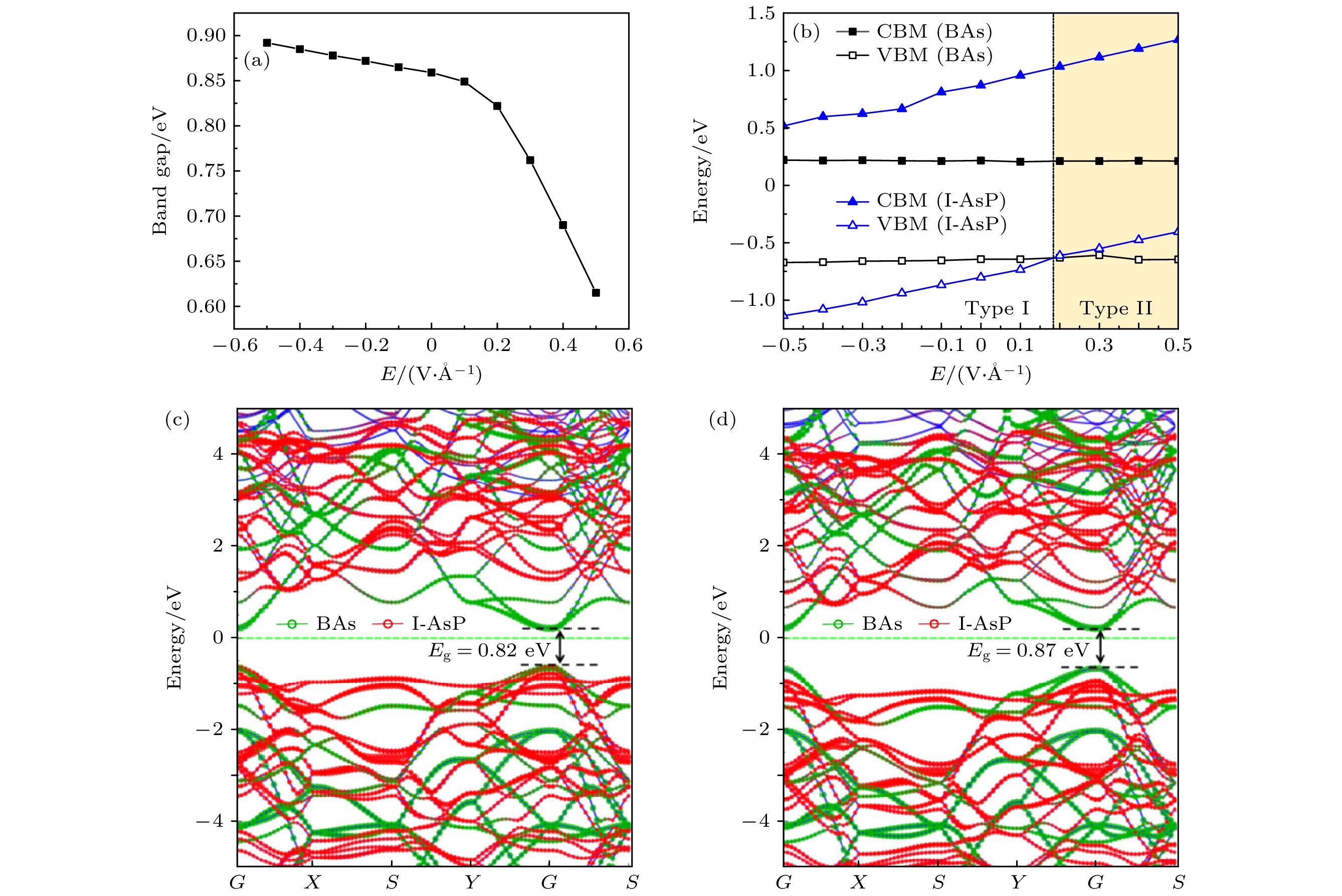
      从图6(b)可以看出, 施加双轴应变后, 导带极小值(CBM)主要来自BAs分子层贡献. 当ε > 8%或ε ≤ –3% 时, BAs的价带顶低于I-AsP, 这意味着异质结构从I型半导体转变为II型半导体, 这确保了有效的载流子分离, 意味着BAs/I-AsP异质结构在合适的应变下可作为太阳能电池的候选材料. 图6(c), (d)分别为ε = ±4%的能带结构, 可以看出ε = 4%时为I型能带排列, 当ε = –4%时转变为II型能带排列(此时, 异质结带隙为$ E_{\text{g}}^{} $= 0.66 eV, 施主材料I-AsP的带隙为$ E_{\text{g}}^{\text{d}} $= 1.34 eV). 双轴应变下能带排列类型变化, 主要原因是价带顶(VBM)贡献的材料发生变化, 同时在拉伸(压缩)应变下, 原子间距离变长(变短), 这导致原子层内电荷密度发生明显变化, 以及层间电荷重新分布, 最终致使异质结构的能带结构发生改变.

      许多研究表明, 在实际应用中异质结的特性会受到外加电场的显著影响[34,37,41,42]. 接下来, 本文将研究电场对BAs/I-AsP异质结构的影响. 电场垂直施加于BAs/I-AsP异质结构上, 强度范围为–0.5—0.5 V/Å, 间隔为0.1 V/Å. 电场正方向定义为从I-AsP指向BAs. 图7展示了BAs/I-AsP异质结A1构型的带隙与沿z向电场之间的函数关系, 可以看出带隙对电场非常敏感. 如图7(a)所示, 在0 > E > –0.5 V/Å范围内, E与带隙之间的函数关系为线性缓慢增大. 而当电场E从0增至0.5 V/Å时, 带隙值随电场增大而线性大幅减小. 缩小的带隙可导致异质结构光吸收产生红移, 有利于开发具有高光学灵敏度的宽带红外探测器[43]. 此外, 从图7(b)可以看出, 当E ≥ 0.2 V/Å时, BAs/I-AsP异质结的能带结构将由I型转变为II型, 电场为0.2 V/Å时其带隙值为0.82 eV. 电场从–0.5 V/Å变化到0.5 V/Å过程中, BAs的价带顶(VBM)和导带底(CBM)几乎不发生变化, 而I-AsP的价带顶(VBM)和导带底(CBM)单调递增. 主要是由于在电场作用下电子从BAs层转移到I-AsP层, 空穴从I-AsP层转移到BAs层, 导致BAs/I-AsP的费米能级向下/向上移动, 其中I-AsP层相应的能带边缘变化最为明显, 最终表现为异质结带隙的不断减小. 对外加电场下, BAs/I-AsP单层之间的电荷转移如图5(b)所示, 负值表示BAs层原子失去电子. 正向电场作用下, BAs转移到I-AsP的电子数线性减少, 相反, 负向电场作用下, BAs转移到I-AsP的电子数线性增加, 进而产生内建电场. 从图7(c), (d)可以看出, 在正负电场作用下, 异质结构的导带极小值(CBM)和价带极大值(VBM)在倒易空间中始终处于G点位置, 即该异质结构始终保持着直接带隙半导体的特性. 随着总电场不断增大, 增强了电子和空穴的漂移特性. 因此, 这些结果表明电场能够有效地调制能带排列和带隙, 且带隙线性变化, 这有利于更精确地操控带隙, 从而动态控制BAs/I-AsP异质结构的电子特性, 使其在太阳能电池材料应用领域发挥更大的作用.

      • 3.4.   BAs/I-AsP异质结构的光学性质

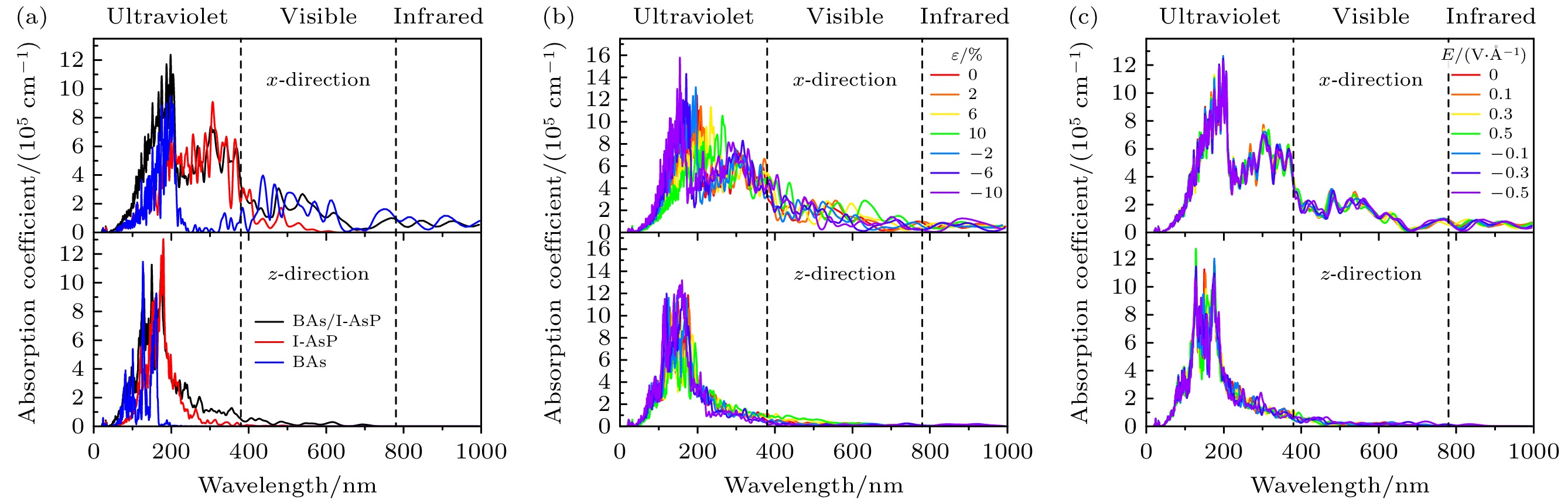
    • 为深入剖析BAs/I-AsP异质结的光学性质, 为其在光学器件中应用提供坚实的理论基础, 依据(6)式对BAs/I-AsP异质结光吸收系数展开精确计算. 由于BAs/I-AsP异质结在x和y方向具有相同的光学性质, 在此分别研究异质结沿x轴和z轴的光学性质. 图8(a)—(c)显示了单层BAs、单层I-AsP与BAs/I-AsP异质结在不同双轴应变和外加电场作用下沿x轴和z轴的光吸收系数变化情况. 显然, 相较于单层材料, 异质结构能够突破单层的局限, 叠加二者的光吸收系数, 如图8(a)所示. 从图8(a)—(c)可以看出, 在x方向和z方向的紫外区域都出现了强吸收峰. 同时, 在任意波段, x方向的吸收系数明显高于z方向, 因此, 我们重点关注x轴方向的光吸收. 在x方向上, BAs/I-AsP异质结在紫外和可见光区域均表现出强光吸收, α值高达106 cm–1, 这使得BAs/I-AsP范德瓦耳斯异质结成为光电器件的潜在候选材料.

      图8(b)为BAs/I-AsP范德瓦耳斯异质结在不同双轴应变下光吸收系数的演变情况. 在紫外-可见光-红外区域, 吸收光谱均发生了显著变化. 在紫外区域, 光吸收系数随着压应变的增大而增大并向波长更短的方向平移; 光吸收系数随着拉应变的增大而降低并向可见光波段方向移动. 在可见光区域, 可以看出拉应变ε = 10%时, 光吸收系数明显增强. 在ε = –10%时, 红外区域光吸收系数明显提高. 即在拉应变下, 光吸收峰出现红移, 在压应变下出现蓝移. 原因是拉应变下, 原子间距增加, 使电子云分布更为弥散, 电子跃迁到激发态后所处能级与基态能级差值进一步减小, 对应光子能量降低, 从而光吸收峰红移; 而压应变时, 虽带隙减小, 但晶体内部电荷分布的重新排列, 改变了电子跃迁的选择定则, 激发态与基态的能级相对位置以特定方式变化, 导致电子跃迁吸收光子能量增大, 进而出现蓝移现象. 在BAs/I-AsP异质结中, x方向(面内)与z方向(面外)应力导致光吸收系数表现为各向异性, 其物理机制源于应力对材料电子结构的差异化调控: 面内应力通过改变BAs和I-AsP的晶格常数, 直接影响其面内电子能带色散关系, 从而调制特定偏振方向的光跃迁概率; 而面外应力则通过调节BAs与I-AsP的层间间距, 改变界面电荷转移效率和激子束缚能, 导致垂直方向的光吸收阈值与跃迁矩阵元显著变化. 这种方向依赖的光学响应为器件设计提供了新路径, 例如利用偏振选择性光吸收开发高灵敏光电探测器, 或通过应变工程优化太阳能电池对特定入射角度光的捕获效率等方面. 图8(c)为外加电场对BAs/I-AsP异质结吸收光谱的影响. 总体而言, 外加电场可以改变可见光和红外区域的光吸收, 而对紫外区域的影响可忽略不计. 在可见光和红外区域, 与未施加电场的情况相比, BAs/I-AsP异质结在负电场和正电场下的光吸收分别发生红移和蓝移. 双轴应变和外加电场可以有效地调控BAs/I-AsP异质结的光学性质, 使其在高效太阳能电池和超薄光电器件中具有巨大的应用潜力.

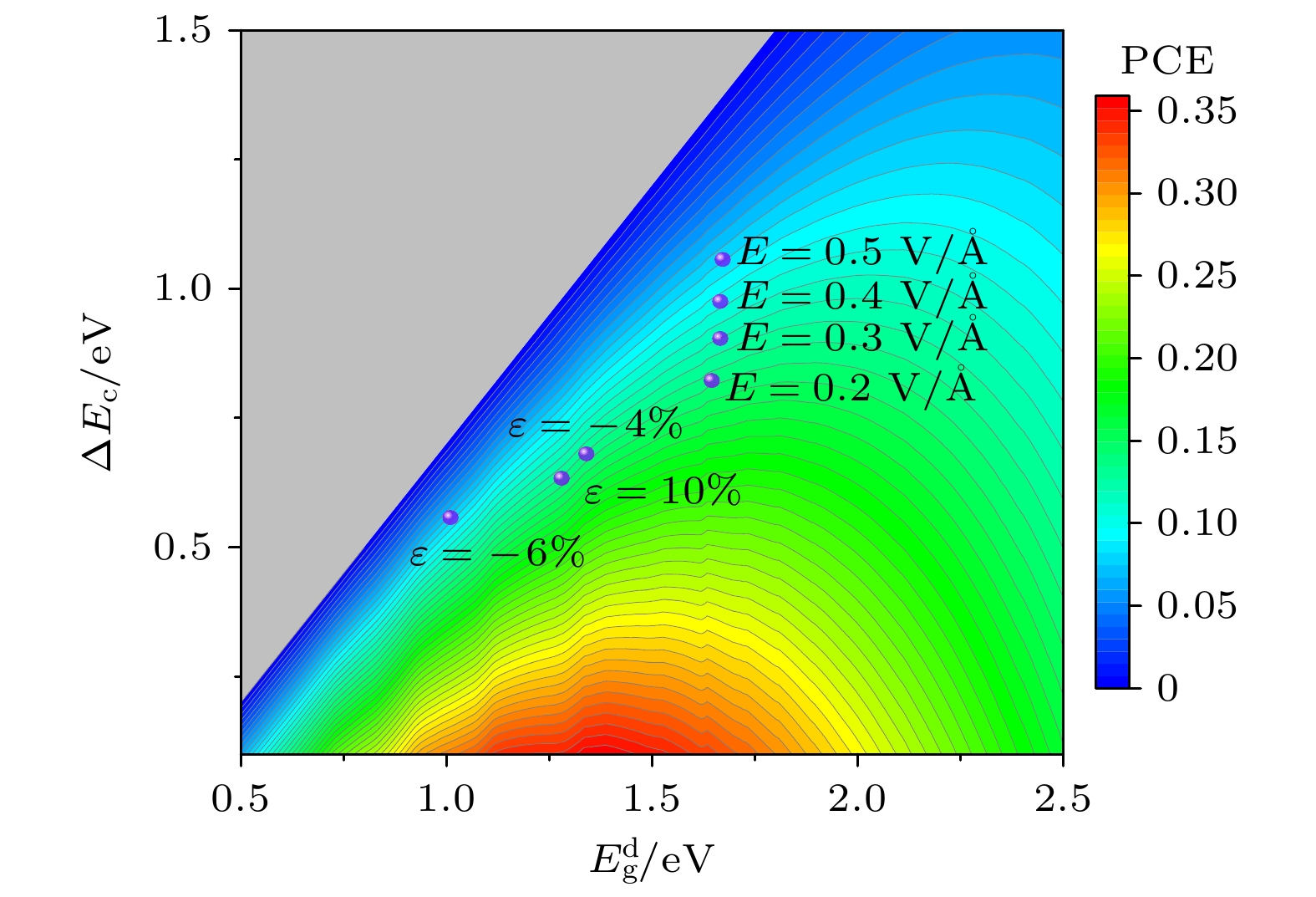
      根据(7)式, 我们计算了在双轴应变和外加电场作用下BAs/I-AsP异质结由I型转变成II型半导体后的光电转换效率η, 如图9所示. 由电子结构分析可知, 异质结中I-AsP为供体, BAs为受体. 通过BAs/I-AsP异质结构在不同双轴应变下的能带结构分析, 发现ε ≤ –3%和ε > 8%的范围内, BAs/I-AsP异质结均为交错型II类能带排列, 确保了有效的载流子分离. 双轴应变ε = –4%, –6%和10%的相关参数及光电转换效率η, 如表2所示. ε = –4%时, 光电转换效率最高(η = 13.14%). 在外部正向电场的控制下且当E ≥ 0.2 V/Å, 异质结由I型转变为II型半导体, 其光电转换效率随着电场增加而减小, 主要归因于以下两方面因素: 1)供体I-AsP的带隙增大, 在光照条件下, 难以产生大量光生载流子; 2)受体与供体之间的导带偏移量过大, 致使开路电压偏低. 正向电场E = 0.2 V/Å时, 光电转换效率最高(η = 13.13%). 由表2可以得到, ε = –4%和E = 0.2 V/Å时, BAs/I-AsP的光电转换效率几乎相等, 并且高于如Cs3Sb2I9/InSe (η = 3.3%), SiPGaS/As (η = 7.3%)和SnSe/SnS (η = 9.1%)等二维异质结材料[44–46]. 可见, BAs/I-AsP异质结构在较小的双轴应变和外加弱电场调控下, 兼具合适的II型能带结构及较宽的光吸收范围等特性, 使其有望成为一种高效的太阳能电池材料.

    4.   结　论

    • 综上所述, 本文应用密度泛函理论系统研究了BAs/I-AsP异质结构的电子和光学特性, 以及它们在双轴应变和电场作用下的响应情况. 研究发现BAs和I-AsP的晶格失配率较小, 并基于它们的对称性探索了4种不同的堆叠构型. 通过研究结合能Eb以及应用分子动力学模拟分析确定了结构的稳定性, 得到A1构型拥有最小的层间距、最小的结合能以及最高的稳定性. BAs/I-AsP异质结构在基态下表现出直接带隙半导体的特性, 并具有I型能带排列, 即导带底和价带顶都位于同一种材料中使得电子和空穴都被限制在同一区域, 有利于载流子的高效复合与辐射跃迁, 可应用于发光二极管领域. 此外, 我们观察到双轴应变和外加电场都能显著改变异质结构的带隙. 特别是当施加双轴应变ε ≤ – 3%和ε > 8%时, 异质结从I型转变为II型能带排列. 同样, 施加正向电场且E ≥ 0.2 V/Å, 异质结能带排列也可以从I型转变为II型. 这进一步拓宽了BAs/I-AsP异质结的应用范围, 使其有望在光电探测器领域发挥重要作用. II型能带排列结构中价带顶(VBM)和导带底(CBM)分别由BAs层和I-AsP层原子占据, 有利于光生电子-空穴对的高效分离, 从而实现高效的光电器件应用和太阳能转换. 研究发现, 该异质结在ε = –4%和E = 0.2 V/Å时, 光电转换效率可达13%. 双轴应变对带隙的影响在–10%—8%的范围内呈现出分段线性增大的趋势. 相反, 电场对带隙的影响在–0.5—0.5 V/Å的范围内呈现出分段线性减小的趋势. 带隙的可控线性变化为可调谐器件提供了一种选择. 与这两种单层材料相比, BAs/I-AsP异质结在紫外和可见光范围具有强烈的吸收性能, 从而有望在紫外探测器和太阳能器件的应用中展现出巨大的潜力. 此外, 在拉伸应变下, 我们观察到吸收光谱发生红移, 而压缩应变则导致吸收光谱发生蓝移. 这些研究结果凸显了BAs/I-AsP范德瓦耳斯异质结构在纳米电子器件和光电器件领域的潜在应用价值. 近期, 实验成功合成了单层蓝磷和黑磷砷合金, 所积累的经验为单层蓝磷砷的合成奠定了良好基础. 然而, 目前存在应变和电场调控精度不足的问题, 将有可能导致异质结类型(如Type-I/II)偏离设计目标, 进而影响在实际光电器件或光伏发电应用中光电转化效率的稳定性. 随着调控精度的不断提高, 本计算结果将为后续相关实验提供理论上的指导, 进一步推动实验的开展.

    参考文献 (46)

目录

/

返回文章
返回