首页
登录
注册
-
氢能作为一种清洁能源, 在使用过程中不会产生CO2等温室气体排放, 是一种真正的零排放能源[1]. 而且, 氢能的利用有助于减少人类活动对环境的负面影响, 为实现可持续发展做出贡献. 氢能可以广泛来源于天然气、煤炭等化石能源, 以及水电、核电和光电等清洁能源, 为能源供给提供了多样化的选择. 光电化学分解水制氢以及电解水制氢是解决氢能来源问题的最有前景的方式之一. 在这一过程中, 气泡的成核、生长、合并和脱离电极表面对水分解效率和设备性能具有重要影响. 在电解水和光电化学水分解中, 气泡覆盖电极表面会降低电极的有效反应面积, 从而减小反应速率. 另外, 气泡的覆盖也会阻碍离子传输途径, 导致电阻的增大[2,3].
为研究电极表面气泡的生长和脱离模式, 已经进行了大量的实验研究. (光)电极表面的单个气泡的生长模式可分为惯性控制生长, 扩散控制生长和化学反应控制生长[4]. 气泡生长可能会经历扩散控制和化学反应控制, 也可能只经历一种. 是扩散控制还是化学反应控制是由电极的活化面积决定的. 许多调控方式被用于改善气泡的生长和脱离模式. 通过表面工程, 构建超亲水电极能减小电极与气泡之间的黏附力, 促进气泡脱离[5]. 纳米阵列电极表现出加速的气泡生长动力学, 具有高的时间系数、最小的气泡分离尺寸和最短的分离时间. 磁场[6,7]、超声场[8]、压力的改变[9,10]也会加速气泡的演化, 增强溶液中的质量传递, 改善反应动力学. 然而, 通过这种主动调控的方式需要消耗额外的能量, 可能会增加电解水的成本和复杂性. 电解质的特性, 如溶质的类型[11]和pH值[12,13]会影响作用于气泡的离子浓度Marangoni力, 从而影响气泡的脱离. 氢气泡脱离模式取决于电解液中阴离子的霍夫迈斯特序列. 一些学者也通过构建活性位点诱导气泡聚并[14,15], 显著提高了反应动力学, 将平均电流提高了2.4倍. 尽管有关气泡演化的许多实验有趣且巧妙, 然而由于实验的局限性, 获取气泡周围物理场分布的详细信息具有较大的难度.
为了揭示电解液中的传质和流动特性, 一些研究使用有限元方法对电解水中的气泡进行数值模拟. Liu等[16]通过流体体积法(Volume of Fluid, VOF)模拟了气泡的演化, 揭示了气泡生长过程中的浓度分布. 然而, 由于气液界面通过气体体积分数区分, 因此无法准确描述气泡的边界和气泡与电解液之间的相互作用. Meulenbroek等[17]数值模拟了铂微电极上的氢气泡周围的热Marangoni对流和浓度Marangoni对流, 揭示了气泡界面顶部停滞的起源. Zhan等[18]对不同生长情况的气泡直径进行稳态模拟, 发现电解液的焦耳热主要在电极表面的微层内产生, 并根据模拟得到的多物理场参数改进了预测气泡脱离直径的力平衡模型. Raman等[19]采用DNS方法模拟了连续电解氢气泡的生长和脱离过程, 发现当气泡超出电解液的溶解氢饱和的区域时, 气泡的气体演化效率被限制. Meulenbroek等[20]通过模拟量化了马兰戈尼力对不同酸性电解质中氢气泡的影响. 以往的模拟研究主要对象是阴极的氢气泡, 对阳极处氧气的研究较少. 而在光电化学水分解中, 在n型半导体上, 主要反应是氧气的演化反应(OER), 因为OER是一个四电子转移反应, 需要高过电位[21].
需要特别指出的是, 光电极表面氧气泡的生长机制与常规沸腾系统中的气泡存在本质差异. 表1系统比较了两种体系的驱动力来源、能质传输及关键控制因素. 理解这些异同对设计高效光电化学系统至关重要.
总之, 电解水无法大规模应用的难题之一是析氧反应的缓慢动力学. 另外以往的模拟研究中, 初始条件对气泡生长的影响也不够深入. 本文通过Comsol软件对阳极上氧气泡的生长过程进行了非稳态模拟研究. 模拟中气泡的边界由动网格控制. 研究了电极上反应区域的大小和电流对气泡生长的影响, 并与我们前期的光电化学分解水的实验数据进行对比, 发现由于生长的气泡对光的散射会造成气泡底部电流密度的降低.
-
在光电化学水分解实验中, 在聚焦激光的照射下, 单个氧气泡在TiO2光电极表面生长. 相较于边长为5 cm的正方体反应池, 附着在光电极表面的单个氧气泡尺寸极小(半径小于350 μm). 表面张力主导下气泡趋近球形, 且激光聚焦形成的圆形光斑使反应区域呈现轴对称特征, 周向浓度梯度可忽略. 在对气泡生长产生较大影响的狭小区域内, 几何特征与物理属性围绕垂直于电极表面的气泡轴线呈对称分布. 低雷诺数(Re
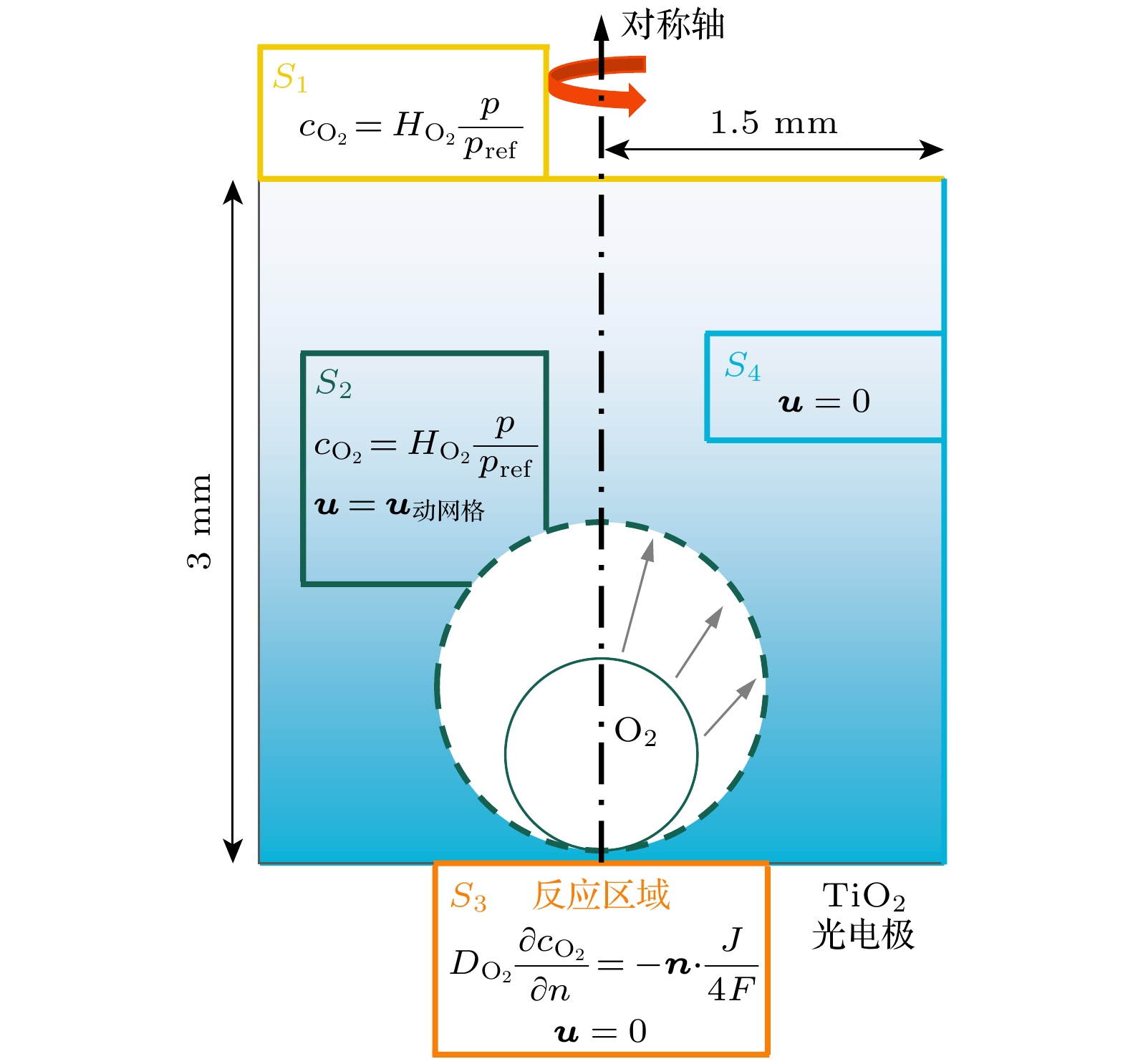
$ \ll $ 1)条件下, 涡流和湍流发展被抑制, 气泡在生长过程中始终保持着良好的轴对称形貌. 基于此, 在模拟研究中可借助二维轴对称模型来表征三维气泡的生长过程. 二维轴对称模型保留了轴向/径向的浓度和流动分布特征, 忽略了由于三维气泡形貌不规则、涡流和湍流及反应池的不对称所引起的非对称浓度梯度和流动, 同时避免了复杂三维计算带来的网格畸变问题, 从而在保证精度的前提下显著简化计算流程.在(r, z)面上使用圆柱形反应单元进行二维模拟. 二维平面模拟的尺寸设定为 1.5 mm×3 mm. 图1为二维轴对称模型的示意图以及边界条件. 光电极被简化为一个平面. 在模型示意图中, 几何尺寸的比例未按实际设定, 仅为展示气泡的几何细节. 模型求解区域不包括气泡内部. 鉴于TiO2纳米棒的芯吸性[22], 纳米材料表面具有吸入并保留液膜的能力, 可以在气泡析出过程中, 在气泡底部保留一层反应溶液, 进一步降低表观接触角. 因此, 在气泡生长过程中, 电极表面的反应区域被简化为固定区域, 不会随着气泡的生长而变化. 另外, 由于TiO2纳米棒电极具有光致亲水性, 在紫外光照下接触角会显著下降. 因此, 气泡与电极表面的接触角设置为0°. 为确保网格质量, 气泡底部与光电极表面始终保持0.02 μm的距离. 初始气泡的半径被设置为15 μm. 在求解过程中耦合了层流和稀物质传递的物理场. 借助动网格技术, 描述溶解氧通过扩散进入气泡内部, 进而引发气泡生长的过程.
-
与电解质浓度相比, 电解液中的氧分子浓度非常低. 为模拟电解液中氧分子的扩散, 采用稀物质传递模型. 模型考虑了电解液中的扩散与对流. 模拟仅仅考虑了阳极的区域, 模型中加入水和氧气两种物质, 没有考虑OH–. 尽管忽略OH–传递会弱化对pH梯度诱导对流的描述, 但气泡生长引起的微对流可稳定局部pH分布[23], 从而减弱由于忽略OH–引起的溶解氧传递过程的误差. 稀物质传递的质量方程:
其中, ci是浓度, Ji是质量扩散通量, u是速度. 下标i表示化学物种, 在本研究中是H2O或者O2. 由于分子扩散, 稀释物种模型包含质量输运. 因此, 扩散通量也可以写成如下:
其中, Di是物种的扩散系数, O2的扩散系数为2.1×10–9 m2/s, 水的扩散系数为2.9×10–9 m2/s.
在求解域顶部S1和气泡界面S2采用浓度边界条件. 依据亨利定律饱和浓度为
其中, Hi为亨利系数, 水中溶解氧的亨利系数为1300 mol/(L·Pa). p为未溶解于水中的氧气的分压, 约为21283 Pa. pref为参考压力, 本文为大气压.
光电极表面的反应区域S3采用扩散通量边界:
其中, Di为扩散系数, 氧气的扩散系数为2.1×10–9 m2/s, j是电流密度, F是法拉第常数, 值为96485 C/mol, rlaser是光斑半径.
通过给定电流I来确定扩散通量, 忽略了电极表面的化学反应过程对气体产生的影响. 例如, 析氧反应涉及到水分子在催化剂表面的吸附、然后失去电子发生氧化反应, 生成氧气、质子和电子等多个步骤, 直接给定扩散通量忽略了这些中间过程对气体产生的影响. 另外, 模型将电极表面简化为平面, 忽略了电极表面的粗糙度对气体在电极表面的吸附和扩散路径的影响. 然而, 本文核心在于揭示气泡生长模式与宏观参数(电流密度、反应区域尺寸)的关联机制, 通过电流I给定扩散通量可有效解耦气泡动力学与复杂电化学反应过程, 显著降低了计算成本. 由于在电极上不反应的区域和壁面上没有通量, 在包括S4在内的其他边界上设置无通量边界.
-
由于气泡生长过程中电解液流速较慢, 采用层流物理场进行计算. 通过不可压缩流体的Navier-Stokes方程求流场分布:
其中, ρ是密度, p是压力, μ是黏度, g是重力加速度. (7)式等号左边是流体元素的动量变化率, 第1个是随时间变化的速度项, 第2个是对流项. 方程等号右边是各种力对流体单元的作用, 包括压力项、黏度控制的速度扩散项和体力项.
在求解区域顶部S1设置为压力出口, 在气泡界面S2设置为滑移边界, 其他区域均设置为无滑移壁面.
在气泡生长过程中, 界面追踪采用了动网格的方式. 对通过气泡界面的溶解氧的通量积分, 计算在每个时间步上界面的生长率和位移, 并将其应用于网格的运动. 根据理想气体定律可得气泡的生长速度:
其中, Rg是理想气体常数, p0是气体内部压力, T是温度, R是气泡半径.
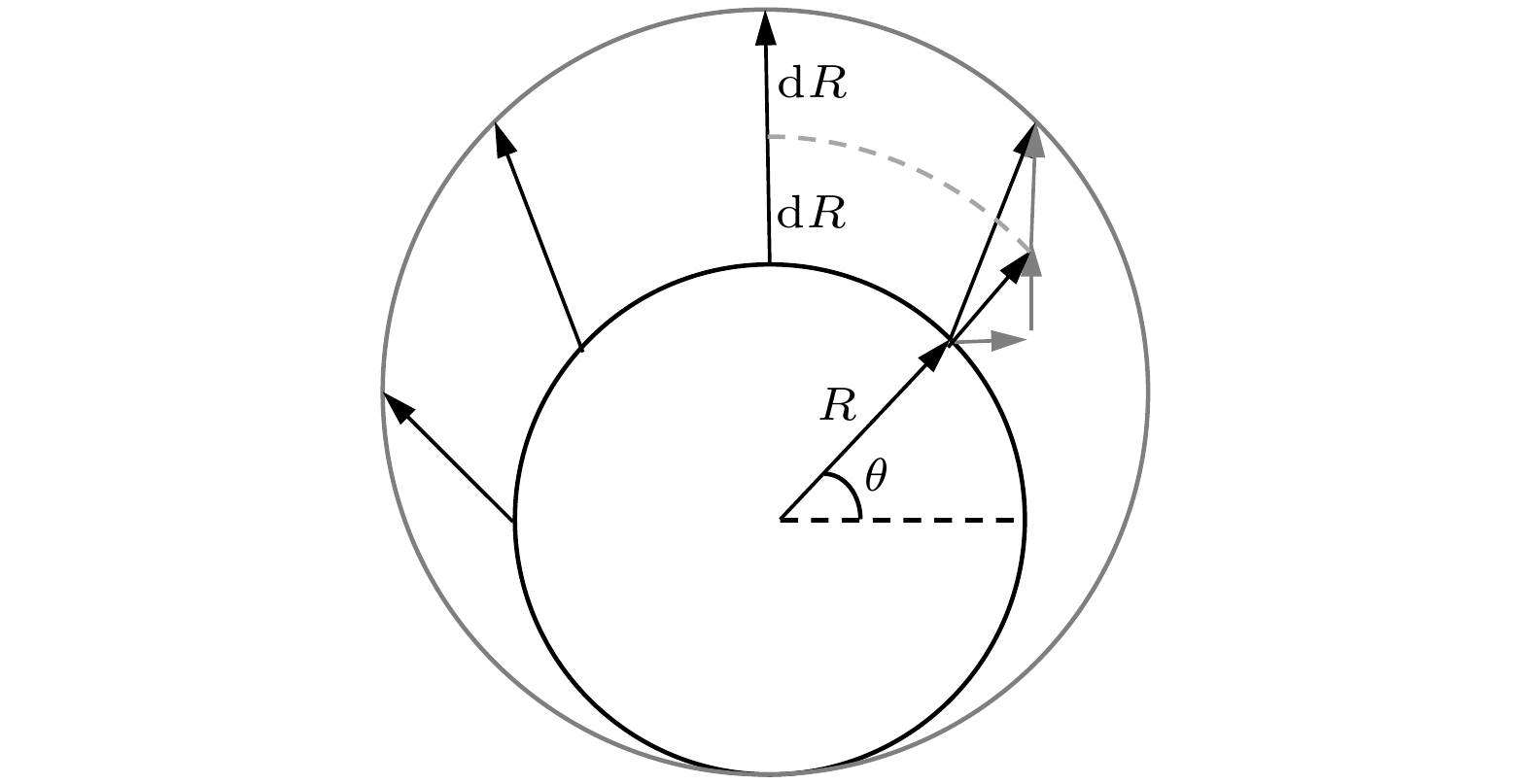
然而, 气泡底部附着于光电极表面. 气泡的界面的更新不仅有径向的生长. 气泡界面的生长可以分解为气泡径向的生长和沿着z方向的上升, 如图2所示. 在一个时间步内, 气泡界面网格的位移在r和z方向的分量分别为
其中, θ依据comsol中的几何坐标系和atan2函数得到, 进入气泡内溶解氧的通量通过检测边界探针获取. 通过检测气泡顶部的点探针计算得到气泡的半径.
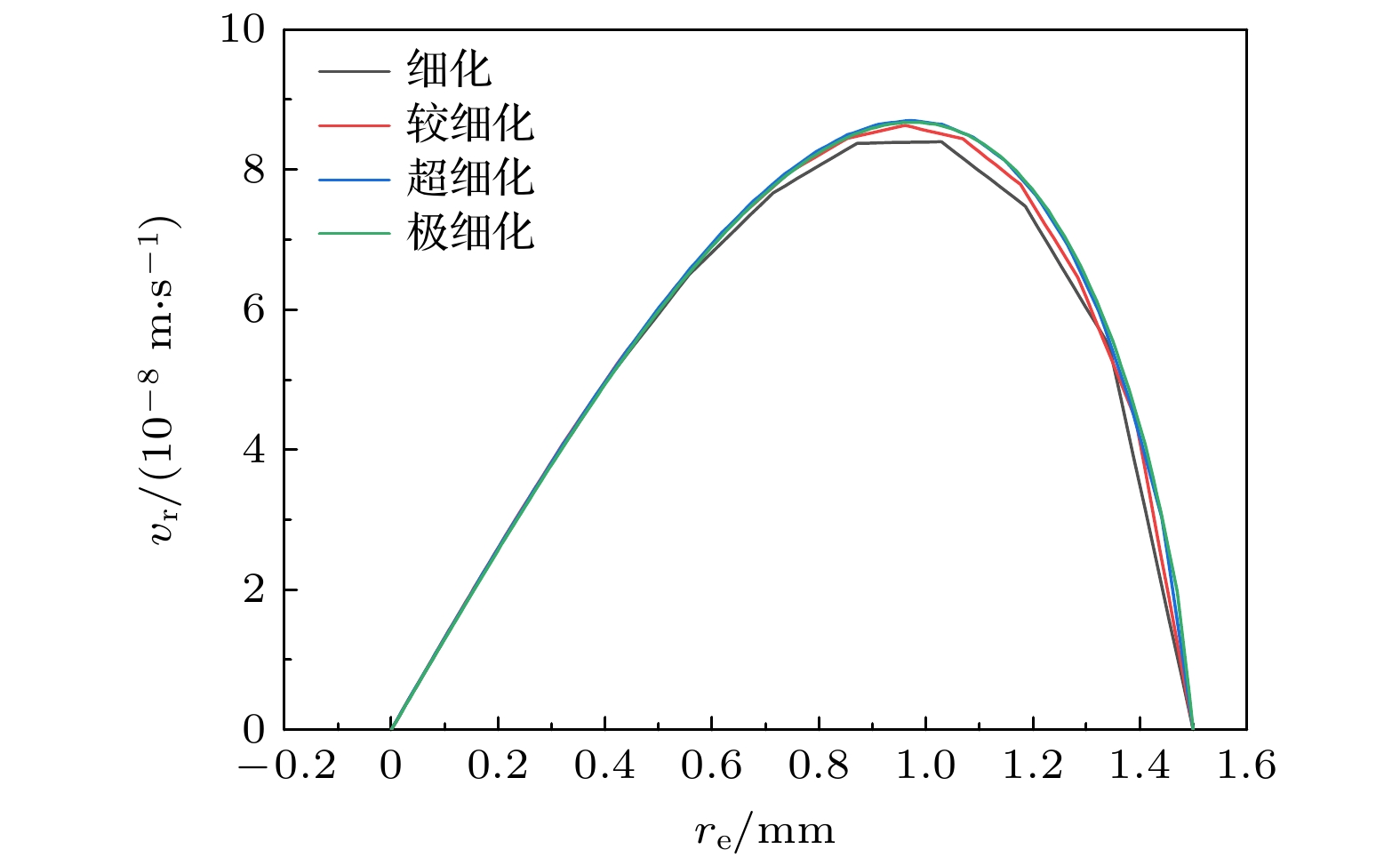
表2列出了模拟用到的参数. 在计算中, 气泡半径从15 μm增至约350 μm. 气泡半径增大了约22倍, 网格的移动会增大网格的偏斜度, 因此在模拟中设置了自动重新划分网格. 监测了网格的质量, 一旦网格质量低于0.2, 则启动重新划分网格程序. 基于Comsol物理场控制进行网格的自动划分, 分为细化、较细化、超细化、极细化4组网格, 4组网格的网格数量分别为14108, 16223, 21144, 40766. 气泡内的网格最大尺寸设置为1 μm. 气泡和电极表面的网格的最大尺寸也设置为1 μm. 最大单元增长率设置为1.01. 采用4组网格计算得到的出口处的流速的r方向分量如图3所示, 细化和较细化均有明显的误差, 而超细化和极细化的差距不大. 因此, 综合考虑计算时间和数据的准确性, 采用超细化的网格进行计算.
-
在(光)电化学水分解中, 已有大量的研究表明, 在微电极上的气泡生长可以分为两个主阶段, 分别是惯性控制阶段和化学反应控制阶段[24]. Cao等[25]在此基础上补充了由扩散控制向化学 反应控制的过渡阶段, 这一阶段处于惯性控制阶 段与化学反应控制阶段之间. 气泡的生长直径与 时间之间的关系为db = βtα (其中α是时间系数, β是生长系数). 不同阶段的区分主要取决于时间系数.
惯性控制阶段大约持续100 ms. 惯性控制阶段的气泡生长直径由以下公式控制:
其中, db是气泡的直径, ρl是电解液密度, ΔPb表示气泡内部和外部之间的压力差抵消表面张力后的残余压力.
化学反应控制阶段占据了气泡生长过程的绝大部分, 这一阶段气泡生长直径表达式为[26,27]
其中, I表示电流, Zs是化学计量数, Rg是通用气体常数, F是法拉第常数, P表示压力, fg代表气体逸出效率, fg = 1 – (1 – Θ)2.5, Θ是气泡覆盖率.
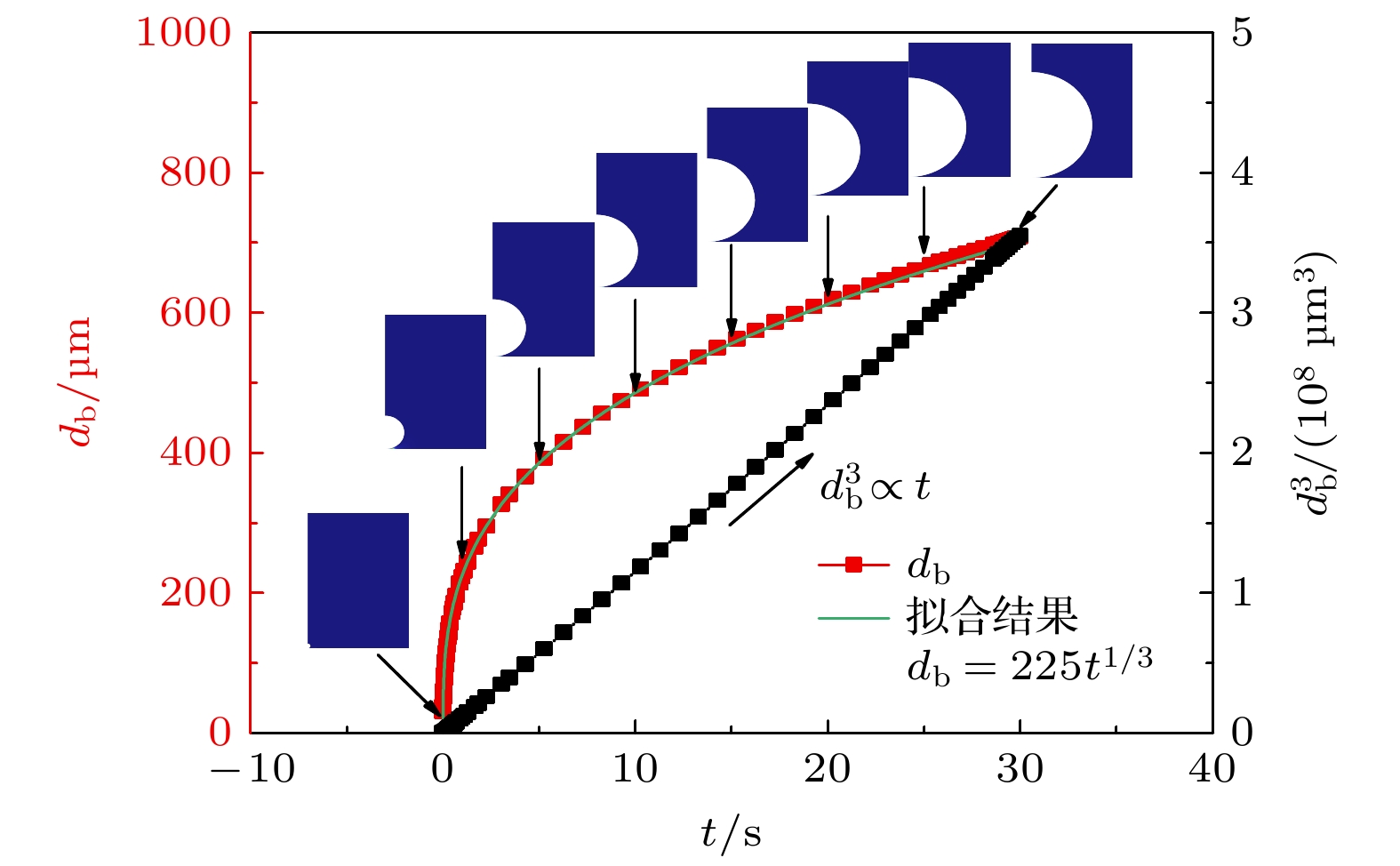
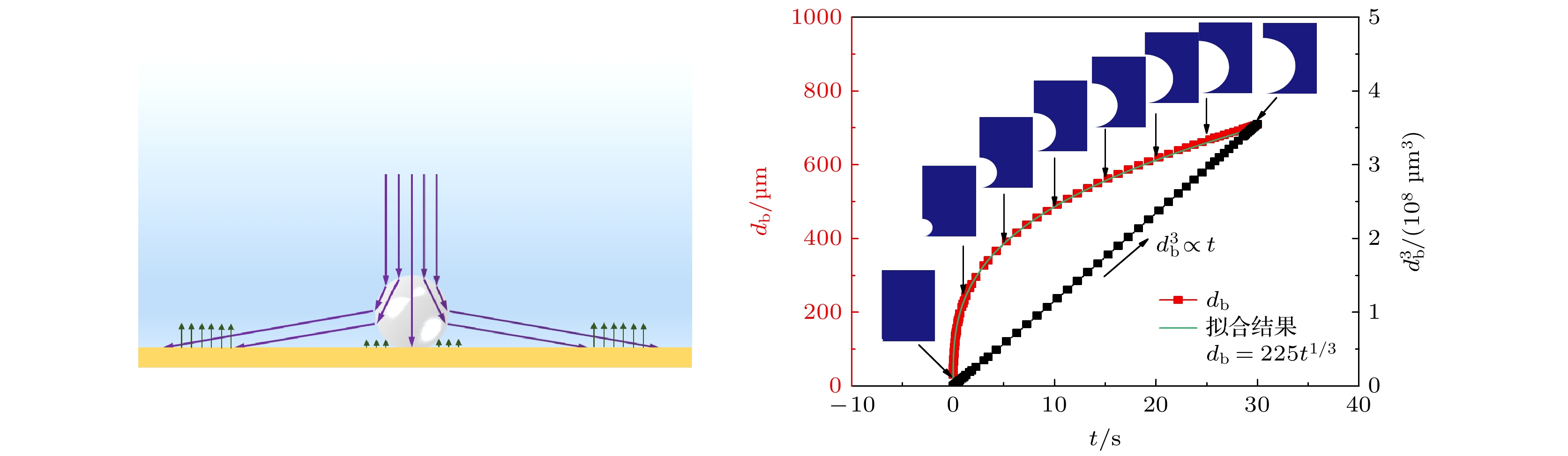
在气泡开始生长前, 进行1.2×10–5 s的模拟. 模拟中只启用稀物质传递和层流, 用以构建电解液中气泡生长至30 μm时的浓度场. 当电流为0.06 mA时, 反应区域直径为0.1 mm的微电极表面生长气泡的直径和快照如图4所示. 气泡生长直径与时间的拟合关系式为db = 225t1/3. 由气泡边界的溶解氧通量计算得到气泡直径与气泡在化学反应控制阶段的生长关系吻合较好, 这也表明了模拟的可靠性.
由于模拟中气泡是从直径为30 μm开始生长, 不是由溶解氧分子聚集成核, 以及气泡在惯性控制阶段的生长与电解液中的浓度分布关系较大, 因此, 气泡在惯性阶段的生长与(11)式具有一定的偏差. 但气泡惯性阶段的生长时间非常短, 对气泡的生长直径影响并不显著.
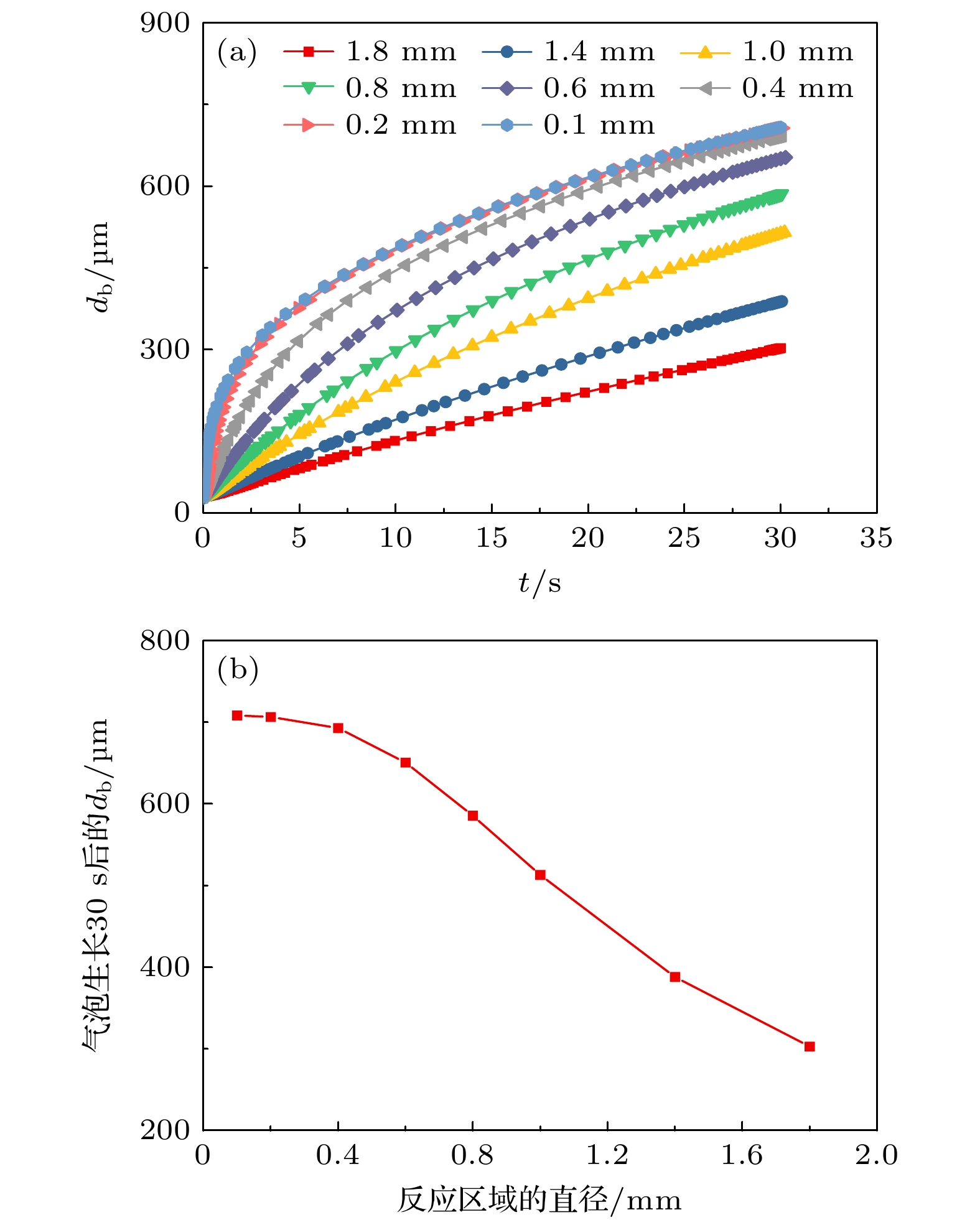
设置不同的反应区域, 得到气泡直径的曲线如图5所示. 较小的反应区域引起了更大的气泡直径. 当反应区域直径超过0.4 mm时, 生长了30 s的气泡直径近似随着反应区域增大线性减小. 在气泡生长早期, 反应区域越小, 气泡生长速率越快. 另外, 相比于反应区域的直径为0.1 mm时, 0.4 mm时的气泡直径一开始虽然明显小于0.1 mm的情况, 但在30 s时气泡生长直径已经与反应区域直径为0.1 mm的情况接近. 尽管反应区域直径为0.1 mm和直径为0.2 mm的电极反应面积相差4倍, 但气泡生长曲线差别非常小. 在前期针对激光光斑尺寸的研究中, 光斑尺寸相差68%, 气泡生长曲线的差异也不大[28]. 这是因为气泡能够迅速生长, 进而超出电极表面的反应区域.
由于气泡的直径与生长时间满足幂律关系, 因此时间系数可以通过以下微分求得:
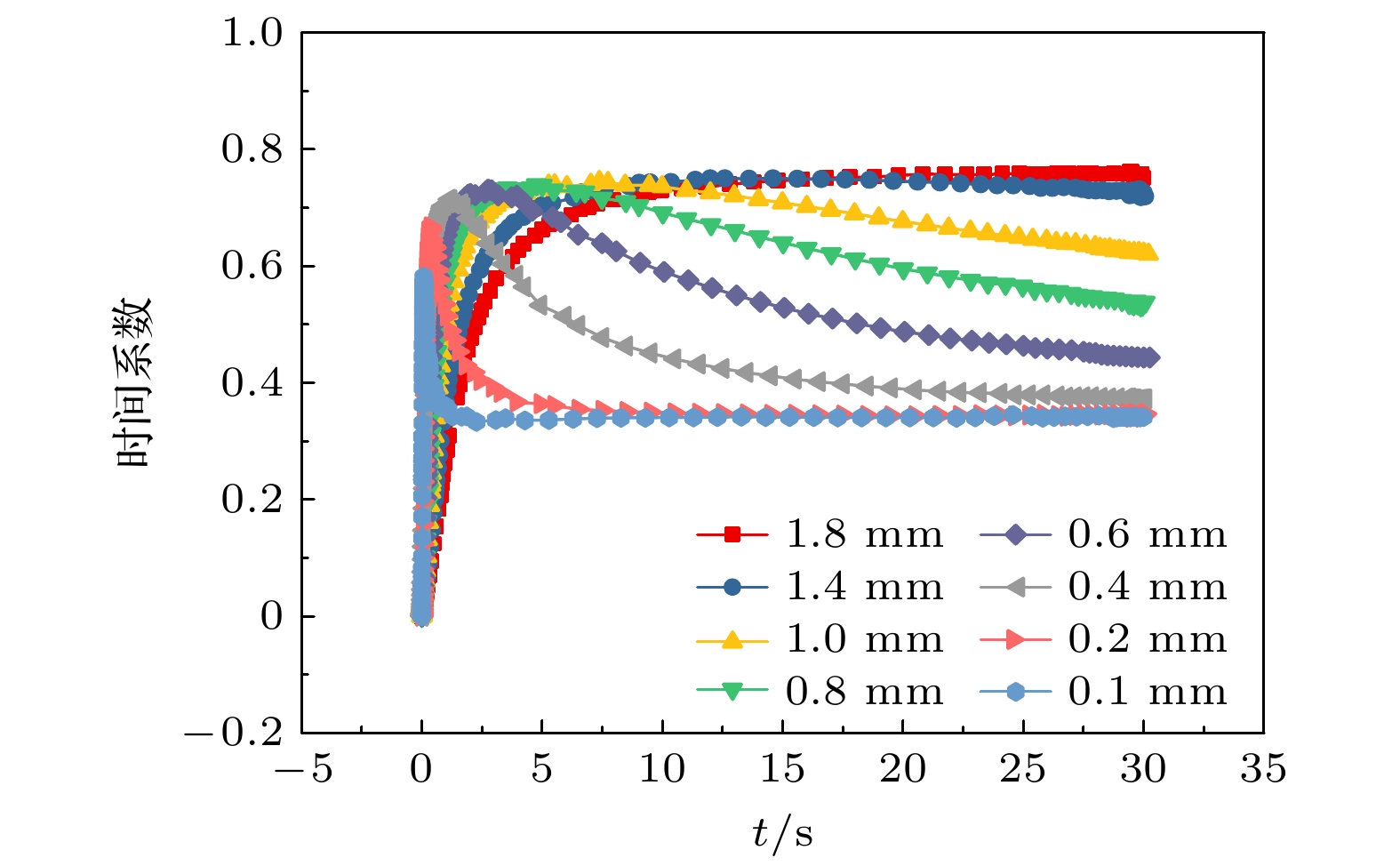
图6给出了由(13)式在不同反应区域下生长的气泡的时间系数. 通过前面的分析可知, 在气泡生长的惯性控制阶段, 时间系数为0.66—1.00[25]. 然而对于惯性控制阶段的直径变化, 模拟呈现并不准确. 但由于这一阶段气泡的生长时间不超过0.1 s, 对于气泡后续的生长影响并不大. 时间系数从0.56降低到0.33的时间段是由扩散控制向化学反应控制过渡阶段. 这一阶段气泡的生长受限于电解液中过饱和的溶解氧. 时间系数为0.33时, 气泡生长受到化学反应控制. 随着反应区域增大, 时间系数的尖峰逐渐变大, 由扩散控制向化学反应控制阶段过渡的时间也变长. 反应区域越大, 从电极扩散进入电解液本体的溶解氧越多. 在气泡生长时, 过饱和的溶解氧又从电解液本体进入气泡, 从而导致时间系数更大. 这与大尺寸电极中气泡生长主要受扩散控制的现象一致[29].
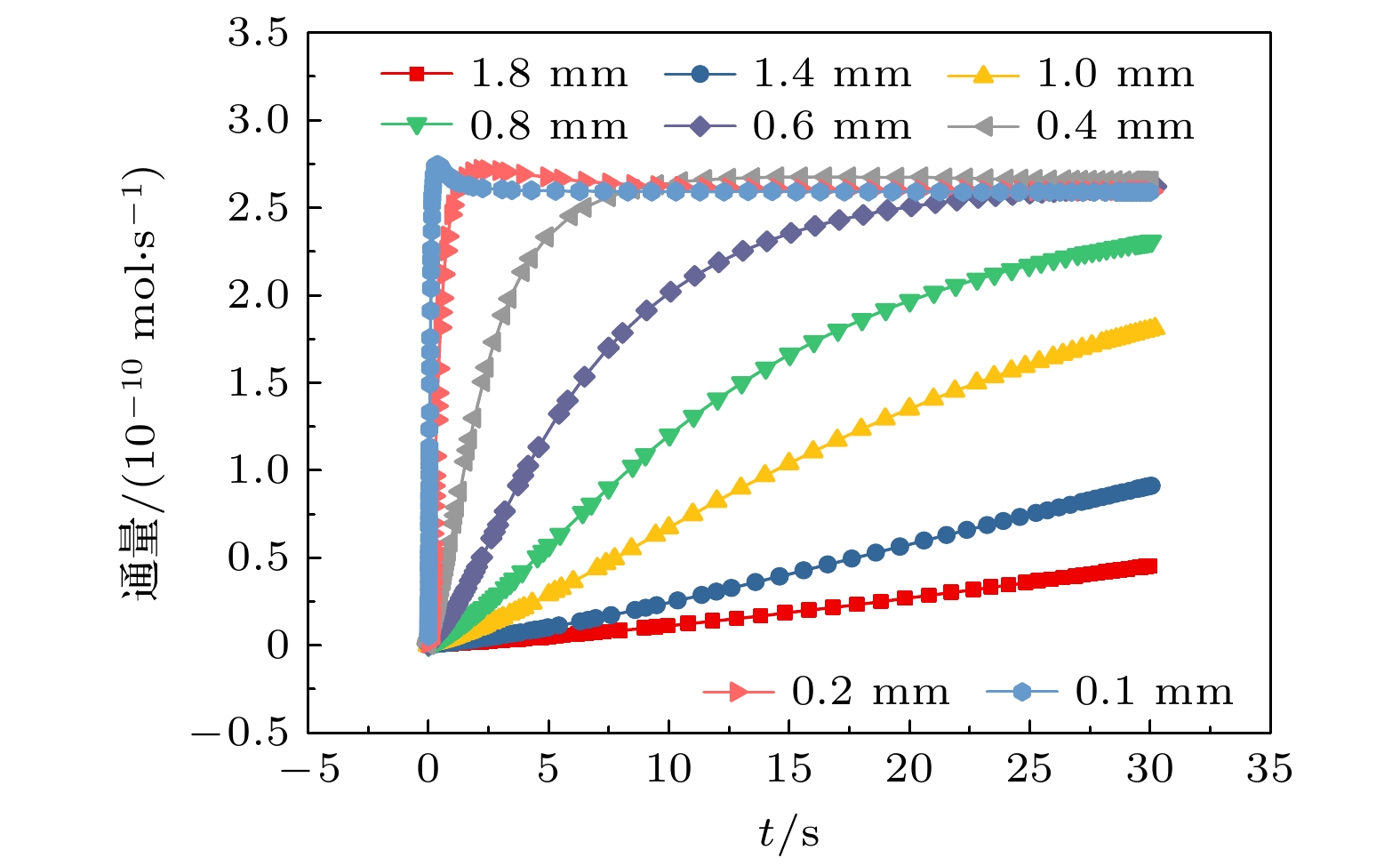
不同反应区域的气泡边界的溶解氧通量如图7所示. 当电极的反应区域较小时, 例如反应区域直径为0.1 mm, 扩散进入气泡内部的溶解氧通量在2 s后就近似与电极表面产生氧气分子的通量相等. 当反应区域直径增加至0.4 mm时, 气泡边界的溶解氧通量在10 s后比直径为0.1 mm的反应区域的通量仍大一些. 超出的通量是由于电解液中过饱和的溶解氧又扩散进入了气泡. 这也是反应区域直径为0.4 mm的电极表面的气泡在30 s时生长至与反应区域直径为0.1 mm的电极表面的气泡一样大的原因, 如图5(a)所示. 对于反应区域直径不低于0.8 mm的情况, 在30 s内, 单位时间进入气泡内的溶解氧通量一直低于电极表面产生的溶解氧. 电极表面产生的溶解氧均有一部分扩散进入电解液本体, 无法被气泡吸收.
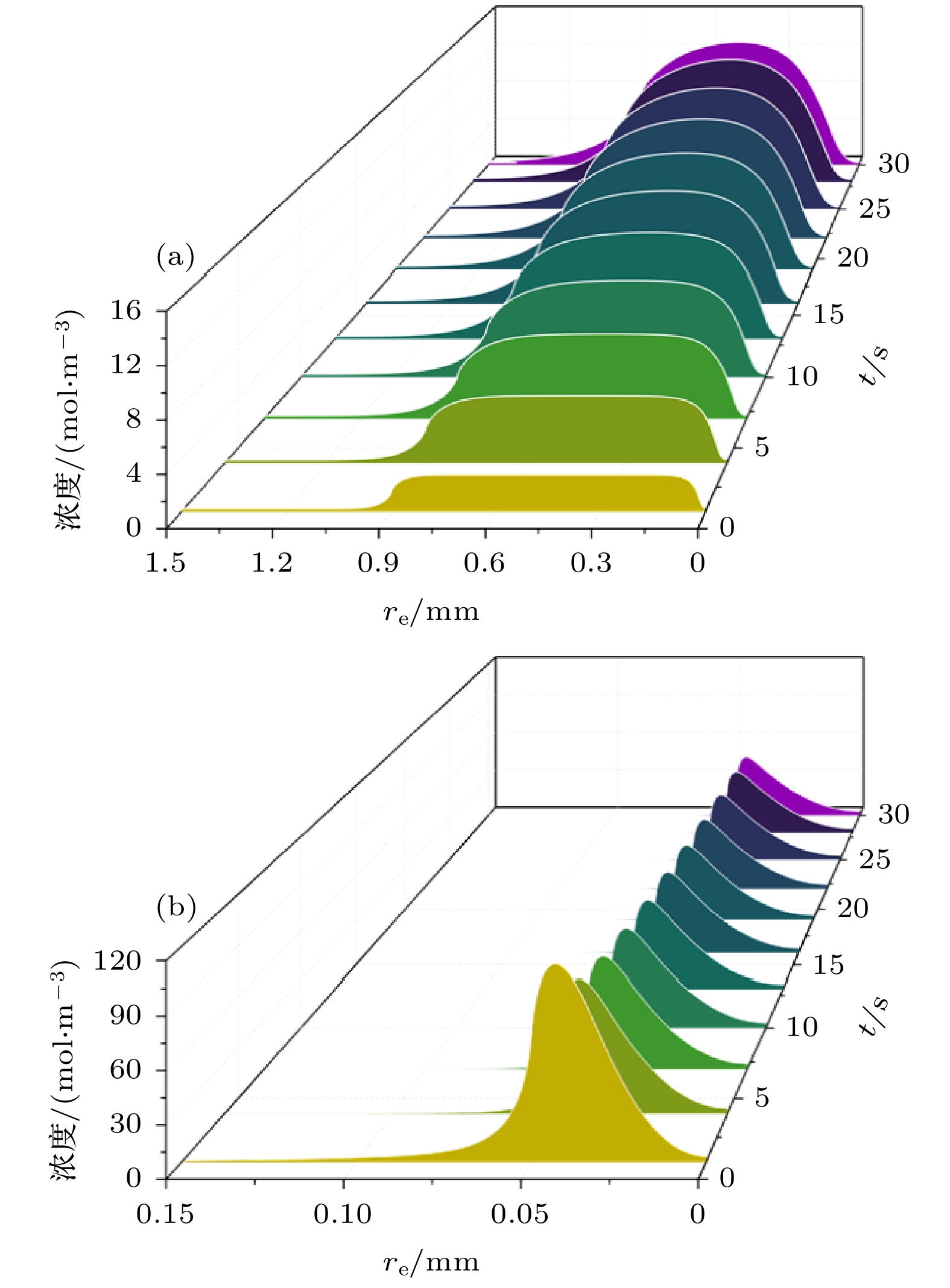
随着气泡的生长, 微电极和大尺寸电极表面浓度的浓度变化也有明显的差别. 如图8所示, 在大尺寸电极表面, 例如当反应区域直径为1.8 mm时, 电极表面浓度随着反应进行不断增大. 而在微电极表面, 当反应区域直径为0.1 mm时, 电极表面浓度随反应进行而减小. 当气泡生长至30 s时, 反应区域直径为1.8 mm和0.1 mm的电极表面的浓度的最大值分别为12.95 mol/m3和46.44 mol/m3. 因此, 微电极表面的浓度峰值显著高于大电极表面的浓度峰值, 从而导致微电极表面与气泡表面之间的浓度梯度更为陡峭.
-
前期的实验研究表明, 同一电流下, 不同光功率气泡的生长满足同一条生长曲线[30]. 而随着电流增大, 气泡的生长速率增大, 气泡直径的曲线向上偏移. 因此, 电流会显著影响气泡的生长直径. 模拟的反应区域的直径设置为0.1 mm, 初始浓度建立时间为1.2×10–5 s. 本节通过模拟, 深入探讨了电极电流对气泡生长的影响.
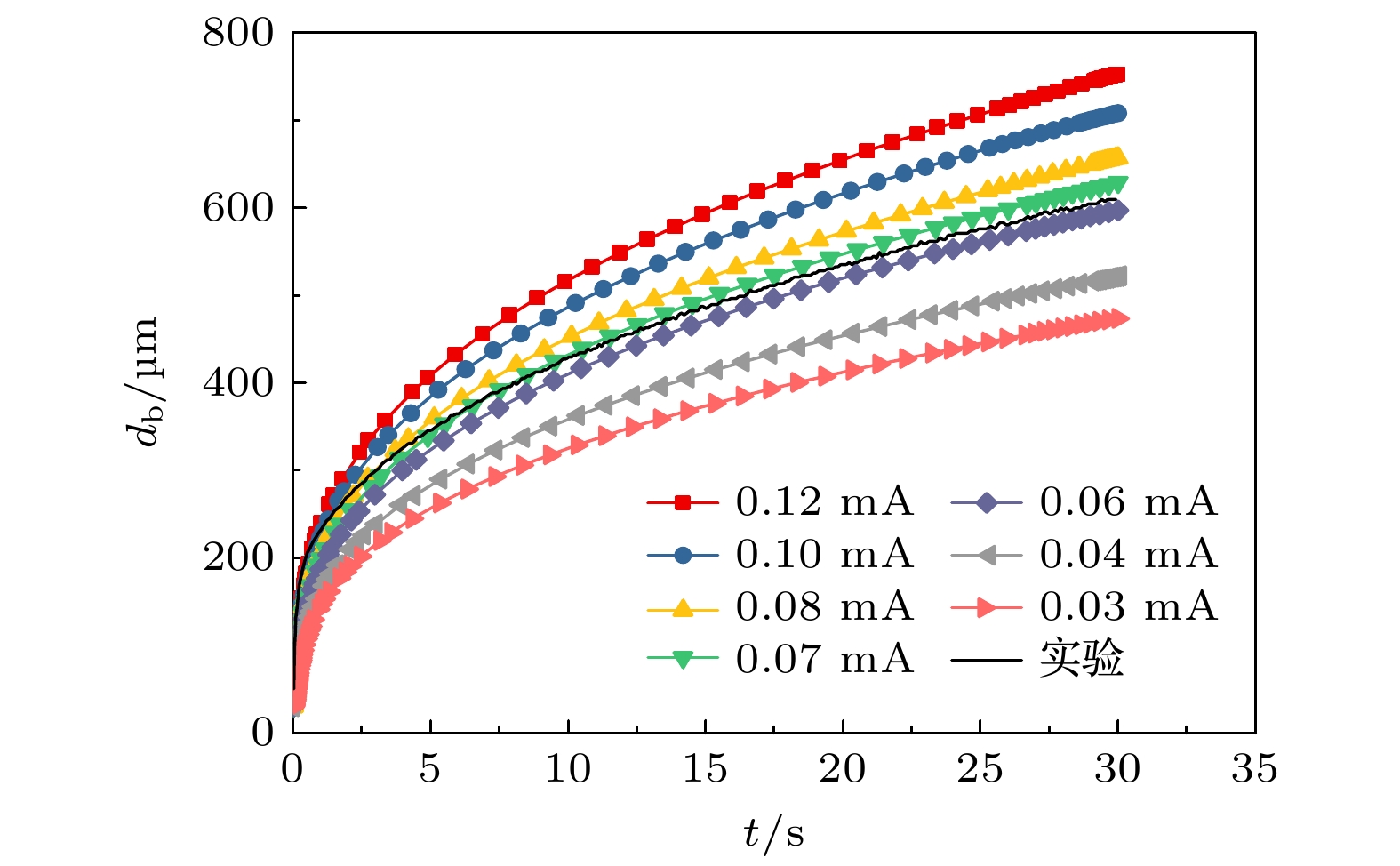
图9为模拟中不同电流下气泡直径的变化. 增大电流会导致气泡直径变大, 与实验中得到的结论一致. 然而, 模拟中电流为0.10 mA时的气泡直径的曲线明显比实验中同样电流下时的气泡直径的曲线高. 电流为0.06 mA时的, 气泡直径的变化与实验中电流为0.10 mA时的比较接近. 而在气泡较小时, 电流为0.10 mA时实验中的气泡直径的生长曲线比模拟得到的电流为0.06 mA的生长曲线要高一些. 这表明在气泡生长早期, 电流为0.10 mA的实验中成核位点附近的溶解氧的浓度应当比电流为0.06 mA时的模拟中要高.
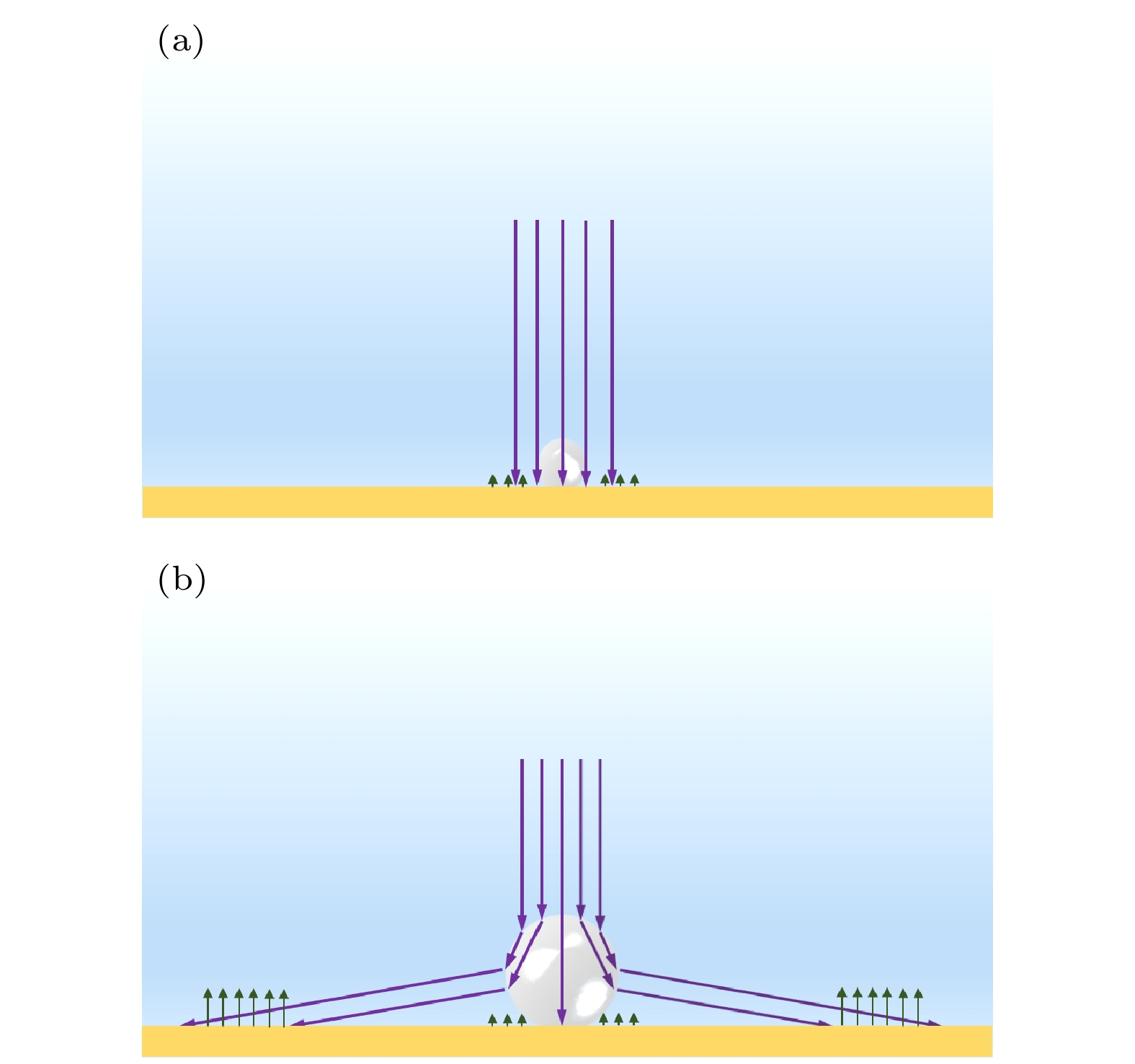
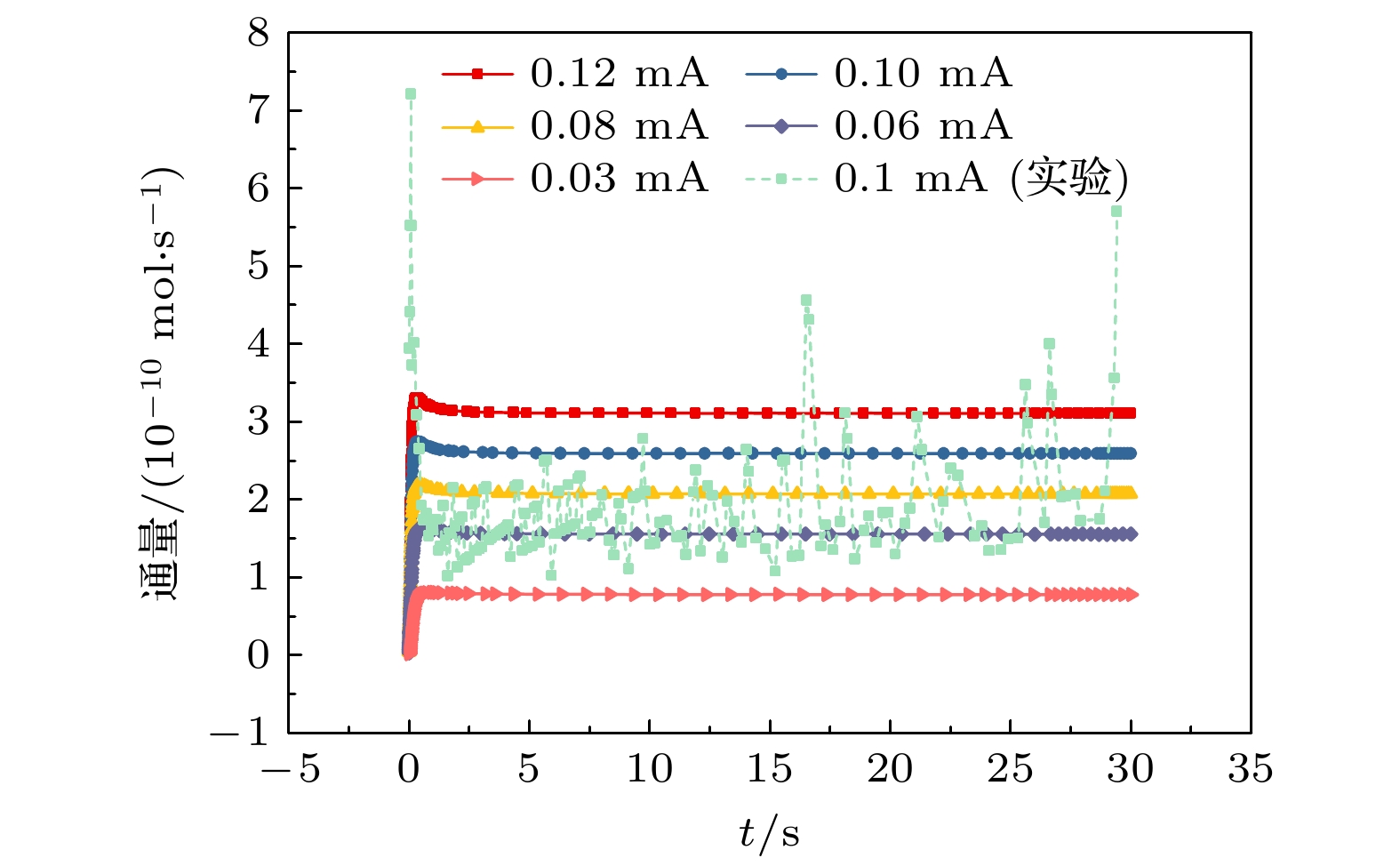
气泡在生长过程中会折射和散射激光光束. 如图10所示, 由小气泡反射和折射的光较少[31,32], 光电极表面的实际反应区域与模拟中的设定接近, 因此电流为0.10 mA时, 在气泡生长的早期, 实验与模拟得到的气泡直径的曲线比较吻合. 而随着气泡生长, 离气泡较远处的表面也开始进行析气反应. 在较远处的表面上产生的气体直接扩散进入电解液本体中, 无法扩散进入气泡中, 导致气泡的生长速率变慢. 此时, 实验中电流为0.10 mA时的气泡生长曲线与模拟中电流为0.06 mA的比较吻合, 即由于气泡生长, 气泡底部光电极表面上的电流密度变小了40%. Dorfi等[31]的研究中, 在532 nm激光照射下, 光电极上的大气泡大约造成的光电流损耗约23%. 这种差异可能是由于实验采用了紫外光, 具有更短的波长和更大的折射率, 从而造成更多的光被折射至电极上的其他区域. 此外, 比较不同电流的模拟与实验中(0.10 mA)气泡边界的溶解氧通量, 如图11所示. 可以看出实验中通过气泡边界的溶解氧通量围绕电流为0.06 mA的模拟曲线上下振荡. 这种振荡是由于实验中气泡直径变化并不是完全平滑的. 实际生长的气泡可能偶尔吸收电极表面直径为几个微米的小气泡导致气泡的直径会有一定的突变. 但实验中的通量围绕电流为0.06 mA的模拟曲线上下振荡已足以表明模拟结果(0.06 mA)与实验数据(0.1 mA)相吻合.
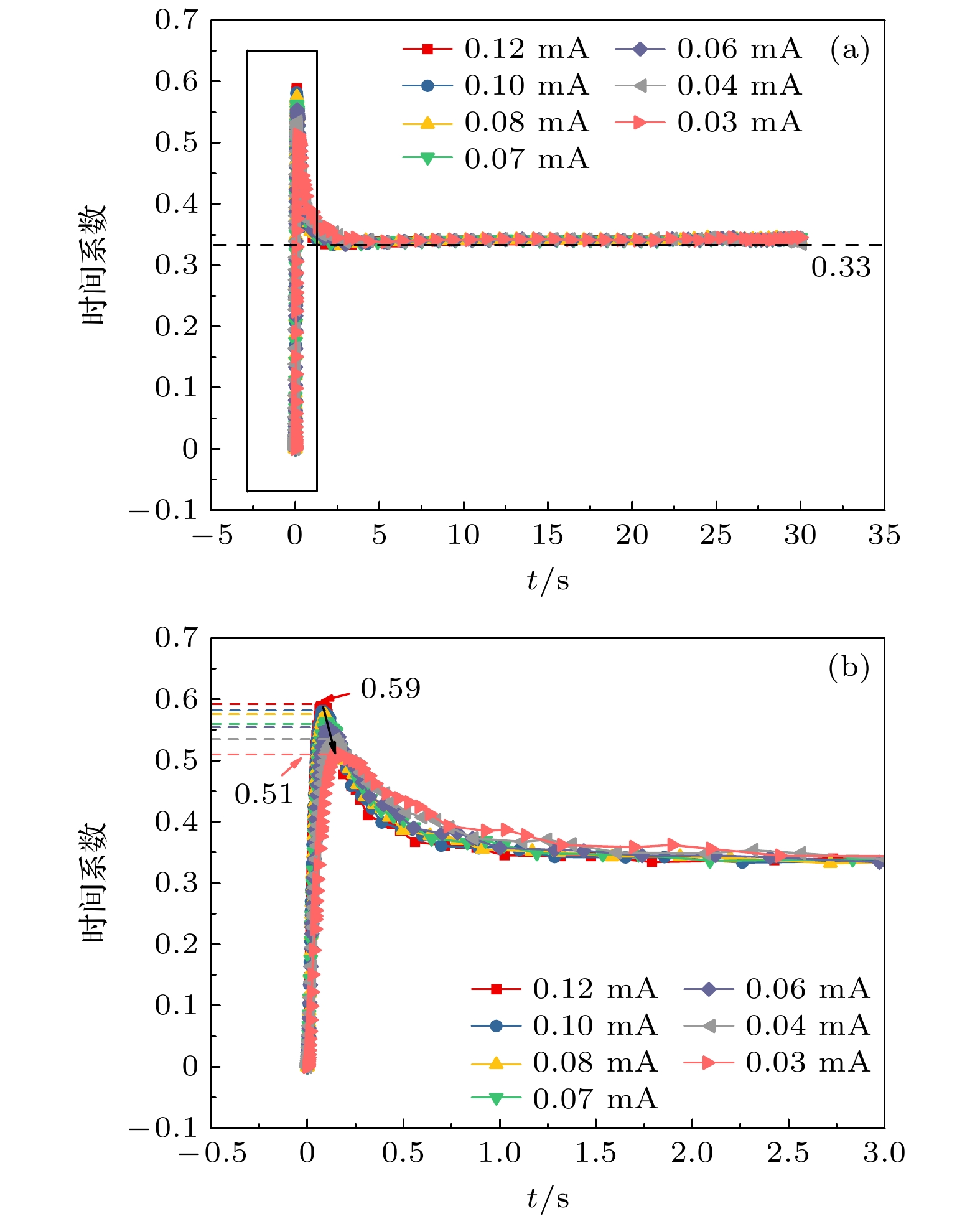
通过微电极的电流大小主要影响气泡生长控制方程中的生长系数, 而对时间系数的影响相对较小. 如图12所示, 不同电流的时间系数都会很快接近0.33, 这表明气泡很快就过渡到只受化学反应控制, 电极表面产生的溶解氧全部进入气泡内部. 电流的增大会导致时间系数的尖峰更高, 电流为0.12 mA时时间系数的尖峰比电流为0.03 mA时大0.08, 这是因为在初始浓度构建阶段, 更大的电流会增加电解液中溶解氧的过饱和. 当气泡开始生长时, 电解液中的过饱和度越大, 气泡生长得越快. 另外, 快速生长的气泡吸收了电解液本体中过饱和的溶解氧, 会导致气泡更快地转变为化学反应控制生长. 因此, 电流越大, 时间系数降低得越快.
-
本研究采用数值软件Comsol模拟了电极表面单个氧气泡的生长过程, 比较了不同反应区域和电流对气泡生长的影响. 同时, 对比了光电化学分解水中的单气泡动力学的实验数据, 主要结论如下.
随着反应区域增大, 时间系数的尖峰逐渐变大, 由扩散控制向化学反应控制阶段过渡的时间也变长. 这是因为反应区域增大会导致从电极扩散进入电解液本体的溶解氧越多. 在气泡生长时, 过饱和的溶解氧又从电解液本体进入气泡, 从而导致时间系数更大. 这与大尺寸电极中气泡生长主要受到扩散控制的现象一致. 另外, 与反应区域较大的电极表面相比, 反应区域较小的微电极表面的浓度峰值明显更高, 从而导致微电极表面与气泡表面之间的浓度梯度更加陡峭.
随着电流增大, 气泡的生长速率增大, 时间系数降低得越快. 实验中电流为0.10 mA时的气泡生长曲线与模拟中电流为0.06 mA吻合较好. 这是因为在实验中, 随着气泡生长, 离气泡较远处的表面也开始进行析气反应. 在较远处的表面上产生的气体直接扩散进入电解液本体中, 无法扩散进入气泡中, 导致气泡的生长速率变慢.
水分解中氧气泡生长动力学研究
Kinetics of oxygen bubble growth in water decomposition
-
摘要: 理解电极表面氧气泡演化对提升大规模水分解的效率具有重要意义. 本文提出了一种基于气泡边界的溶解氧通量的电极表面氧气泡生长的数值模型, 研究了反应区域和电流的大小对气泡生长的影响. 结果表明, 由气泡边界的氧通量计算得到气泡直径与气泡在化学反应控制阶段的生长关系吻合较好. 随着反应区域增大, 在气泡生长过程中, 由扩散控制向化学反应控制阶段过渡的时间也变长. 微电极表面的浓度峰值明显高于大电极表面的浓度峰值, 从而导致微电极表面与气泡表面之间的浓度梯度更加陡峭. 随着电流增大, 气泡的生长速率增大, 时间系数降低得越快. 电流为0.06 mA时的气泡直径与光电解水实验中电流为0.1 mA 的气泡直径能较好吻合. 这是因为生长的气泡对光的散射会导致气泡底部电流密度的降低.Abstract: In order to enhance the efficiency of large-scale water decomposition, it is important to understand the oxygen bubble evolution on the electrode surface. In this work, a numerical model for the growth of oxygen bubbles on the electrode surface is proposed based on the dissolved oxygen flux at the bubble boundary, and the mechanisms of the reaction area and current during the bubble growth are investigated. The results show that the bubble diameters calculated from the oxygen flux at the bubble boundary are in good agreement with the diameters of the bubbles growing in the control phase of the chemical reaction. As the reaction region increases, the transition time from the diffusion-controlled stage to the chemical reaction-controlled stage becomes longer during the bubble growth. The concentration maximum value on the microelectrode surface is significantly higher than that on the large electrode surface, which leads to a steeper concentration gradient between the microelectrode surface and the bubble surface. As the current increases, the bubble growth rate increases and the time coefficient decreases faster. The bubble diameter at a current of 0.06 mA accords well with the bubble diameter at a current of 0.1 mA in the photoelectrochemical water splitting experiments. This is because the scattering of light by the growing bubbles leads to a decrease in the current density at the bottom of the bubble.
-
-
图 1 几何模型和模拟设置的示意图
Figure 1. Schematic diagram of the geometry and simulation settings.
图 3 四组网格计算得到的出口处的流速的r方向分量
Figure 3. The r-direction component of the flow velocity at the outlet calculated by the four sets of grids.
图 4 模拟得到的气泡生长直径和快照
Figure 4. Bubble growth diameter and snapshot obtained through simulation.
图 5 不同反应区域时气泡的生长直径 (a)气泡的直径随时间的变化; (b) 30 s时的直径
Figure 5. Growth diameter of the bubble at different reaction regions: (a) Diameter of the bubble as a function of time; (b) the diameter at 30 s.
图 6 不同反应区域下生长的气泡的时间系数
Figure 6. Time coefficient of bubbles growing in different reaction regions.
图 7 不同反应区域的气泡边界的溶解氧通量
Figure 7. Flux of dissolved oxygen at bubble boundaries in different reaction regions.
图 8 电极表面浓度随时间变化 (a)光斑直径1.8 mm; (b)光斑直径0.1 mm
Figure 8. Electrode surface concentration varies with time: (a) Laser diameter of 1.8 mm; (b) laser diameter of 0.1 mm.
图 10 光电极表面析气反应区域的示意图 (a)小气泡; (b)大气泡
Figure 10. Schematic diagram of the gas evolution reaction area on the photoelectrode surface: (a) Small bubble; (b) large bubble.
图 11 不同电流气泡边界的溶解氧通量
Figure 11. Flux of dissolved oxygen at bubble boundaries for different currents.
图 12 不同电流下气泡生长的时间系数 (a)气泡生长时的时间系数; (b)生长时间为0—3 s
Figure 12. Time coefficients of bubble growth at different currents: (a) Time coefficient when the bubble grows; (b) growth time from 0 to 3 s.
表 1 沸腾气泡与光解气泡的异同
Table 1. Similarities and differences between boiling bubble and photolysis bubble.
沸腾气泡 光解气泡 生长过程 成核、生长和脱离 成核、生长和脱离 相间作用 异相成核 异相成核 驱动力 过饱和温度 过饱和浓度 气泡成分 水蒸气 氢气/氧气 能质传输 涉及热能与物质的传递 涉及热能、化学能、光能及物质的传递 生长规律 生长速率受热传导和蒸气压支配, 快速膨胀后脱离 生长受限于光强、反应速率及气体扩散, 可能持续缓慢生长 稳定性 上升时可能因冷却而凝结 化学性质稳定, 不易再溶解 气泡尺寸/m 10–3—10–2 10–9—10–4 生长时间/s 10–2—10–1 10–3—102 
下载: 导出CSV
表 2 模拟参数
Table 2. Parameters used in simulation.
参数 值 表面张力 σ/(mN·m–1) 70 电流 I/mA 0.03—0.12 光斑半径 rlaser/mm 0.05—0.9 转移电子数 z 4 氧气摩尔质量 $M_{\rm O_2} $ /(g·mol–1)32 氧气扩散系数 $D_{\rm O_2} $ /(m2·s–1)2.1×10–9 气泡初始半径 rb/μm 15 参考压力 pref/kPa 101.325 浓度建立时间 twait/s 1.2×10–5
下载: 导出CSV
-
[1] Zhang S, Chen W 2022 Nat. Commun. 13 87 doi: 10.1038/s41467-021-27671-0 [2] Angulo A, Linde P van der, Gardeniers H, Modestino M, Fernández Rivas D 2020 Joule 4 555 doi: 10.1016/j.joule.2020.01.005 [3] Iwata R, Zhang L, Wilke K L, Gong S, He M, Gallant B M, Wang E N 2021 Joule 5 887 doi: 10.1016/j.joule.2021.02.015 [4] Chen J, Guo L, Hu X, Cao Z, Wang Y 2018 Electrochim. Acta 274 57 doi: 10.1016/j.electacta.2018.04.051 [5] Andaveh R, Darband G B, Maleki M, Rouhaghdam A S 2022 J. Mater. Chem. A 10 5147 doi: 10.1039/D1TA10519A [6] Zhan S, Yuan R, Huang Y, Zhang W, Li B, Wang Z, Wang J 2022 Phys. Fluids 34 112120 doi: 10.1063/5.0127299 [7] 郭烈锦, 曹振山, 王晔春, 张博, 冯雨杨, 徐强 2023 西安交通大学学报 57 1 doi: 10.7652/xjtuxb202303001 Guo L J, Cao Z S, Wang Y C, Zhang B, Feng Y Y, Xu Q 2023 J. Xi'an Jiaotong Univ. 57 1 doi: 10.7652/xjtuxb202303001 [8] Peñas P, Moreno Soto Á, Lohse D, Lajoinie G, van der Meer D 2021 Int. J. Heat Mass Transfer 174 121069 doi: 10.1016/j.ijheatmasstransfer.2021.121069 [9] Luo X Y, Xu Q, Ye X M, Wang M S, Guo L J 2024 Int. J. Hydrogen Energy 61 859 doi: 10.1016/j.ijhydene.2024.02.306 [10] Luo X Y, Xu Q, Nie T F, She Y L, Ye X M, Guo L J 2023 Phys. Chem. Chem. Phys. 25 16086 doi: 10.1039/D3CP01269G [11] Park S, Liu L, Demirkır Ç, Van Der Heijden O, Lohse D, Krug D, Koper M T M 2023 Nat. Chem. 15 1532 doi: 10.1038/s41557-023-01294-y [12] Da Silva J, Nobrega E, Staciaki F, Almeida F R, Wosiak G, Gutierrez A, Bruno O, Lopes M C, Pereira E 2024 Chemical Engineering Journal 494 152943 doi: 10.1016/j.cej.2024.152943 [13] Xu Q, Tao L Q, Nie T F, Liang L, She Y L, Wang M S 2024 J. Electrochem. Soc. 171 016501 doi: 10.1149/1945-7111/ad1c18 [14] Bashkatov A, Park S, Demirkır Ç, Wood J A, Koper M T M, Lohse D, Krug D 2024 J. Am. Chem. Soc. 146 10177 [15] Zhang B, Wang Y C, Feng Y Y, Zhen C H, Liu M M, Cao Z S, Zhao Q Y, Guo L J 2024 Cell Rep. Phys. Sci. 5 101837 doi: 10.1016/j.xcrp.2024.101837 [16] Liu H, Pan L M, Wen J 2016 Can. J. Chem. Eng. 94 192 doi: 10.1002/cjce.22378 [17] Meulenbroek A M, Vreman A W, Deen N G 2021 Electrochim. Acta 385 138298 doi: 10.1016/j.electacta.2021.138298 [18] Zhan S Q, Yuan R, Wang X H, Zhang W, Yu K, Li B, Wang Z T, Wang J F 2023 Phys. Fluids 35 032111 doi: 10.1063/5.0141648 [19] Raman A, Porto C C D S, Gardeniers H, Soares C, Fernández Rivas D, Padoin N 2023 Chem. Eng. J. 477 147012 doi: 10.1016/j.cej.2023.147012 [20] Meulenbroek A M, Deen N G, Vreman A W 2024 Electrochim. Acta 497 144510 doi: 10.1016/j.electacta.2024.144510 [21] Suen N T, Hung S F, Quan Q, Zhang N, Xu Y J, Chen H M 2017 Chem. Soc. Rev. 46 337 doi: 10.1039/C6CS00328A [22] Chen J W, Guo L J 2019 Appl. Phys. Lett. 114 231604 doi: 10.1063/1.5095194 [23] Obata K F, Abdi F 2021 Sustain. Energ. Fuels 5 3791 doi: 10.1039/D1SE00679G [24] Matsushima H, Kiuchi D, Fukunaka Y, Kuribayashi K 2009 Electrochem. Commun. 11 1721 doi: 10.1016/j.elecom.2009.07.009 [25] Cao Z S, Wang Y C, Xu Q, Feng Y Y, Hu X W, Guo L J 2020 Electrochimica Acta 347 136230 doi: 10.1016/j.electacta.2020.136230 [26] Fernández D, Maurer P, Martine M, Coey J M D, Möbius M E 2014 Langmuir 30 13065 doi: 10.1021/la500234r [27] Yang X, Karnbach F, Uhlemann M, Odenbach S, Eckert K 2015 Langmuir 31 8184 doi: 10.1021/acs.langmuir.5b01825 [28] Xu Q, Tao L Q, She Y L, Ye X M, Wang M S, Nie T F 2023 J. Electroanal. Chem. 935 117324 doi: 10.1016/j.jelechem.2023.117324 [29] Lu X, Nie T, Li X, Jing L, Zhang Y, Ma L, Jing D 2023 Physics of Fluids 35 103314 doi: 10.1063/5.0171694 [30] Nie T F, Li Z, Luo X Y, She Y L, Liang L, Xu Q, Guo L J 2022 Electrochimica Acta 436 141394 doi: 10.1016/j.electacta.2022.141394 [31] Dorfi A E, West A C, Esposito D V 2017 J. Phys. Chem. C 121 26587 doi: 10.1021/acs.jpcc.7b06536 [32] Holmes-Gentle I, Bedoya-Lora F, Alhersh F, Hellgardt K 2019 J. Phys. Chem. C 123 17 doi: 10.1021/acs.jpcc.8b07732 -
计量
- 文章访问数: 27
- HTML全文浏览数: 27
- PDF下载数: 0
- 施引文献: 0