-
1957年, Bardeen, Cooper与Schrieffer(BCS)提出声子介导费米面上
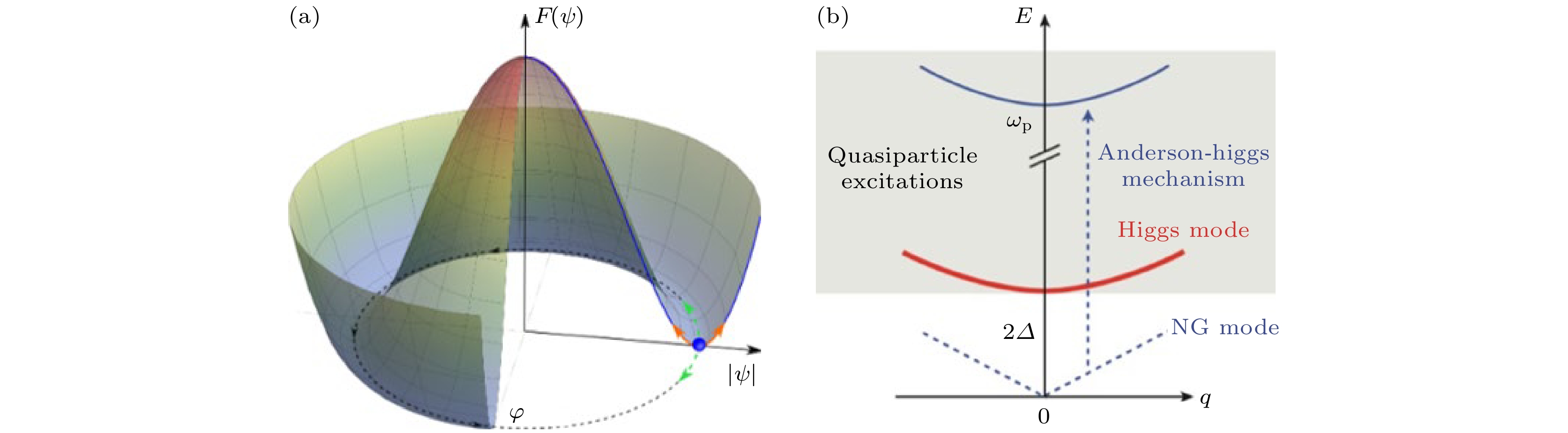
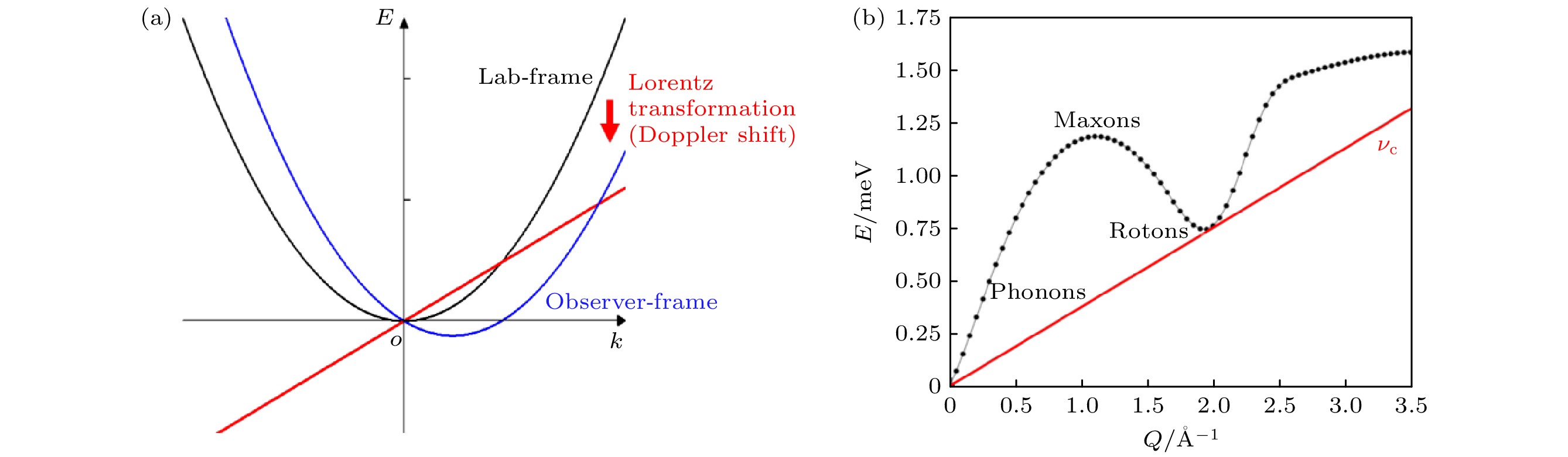
$ {\boldsymbol{k}}_{\uparrow } $ 态与$ {-\boldsymbol{k}}_{\downarrow } $ 态电子配对, 形成能量更低的束缚态(即库珀对), 为常规超导现象奠定了微观机理[1,2]. BCS理论在往后半个多世纪获得了巨大成功: 对于各类常规超导体的超导转变温度(Tc)、常规超导体的最高理论Tc 都做出了精准预言或验证[3]. 然而, BCS理论的巨大成功、伴随长期以来高温超导配对机制的悬而未解, 使得超导研究主要关注各类体系中电子配对的机制, 而忽略一个重要事实: 电子配对并不一定产生超流. 在解释超流液氦为什么存在临界速度$ {\boldsymbol{v}}_{{\mathrm{c}}} $ (即当超流液氦以大于$ {\boldsymbol{v}}_{{\mathrm{c}}} $ 的速度流动时会失去超流特性)时, Landau[4]指出玻色子之间的相互作用使单粒子激发行为演变为集体激发行为, 是超流无损耗输运的关键. 举例而言, 试想许多原子形成玻色凝聚, 玻色凝聚体中的每个原子处于其能量基态. 以实验室为参照系, 假设整个凝聚体以速度$ \boldsymbol{v} $ 沿容器壁匀速运动, 若以凝聚体自身为参照系做洛伦兹转换, 则凝聚体的能谱发生多普勒位移. 当$ \boldsymbol{v} $ 足够大、多普勒效应促使原子激发态的能量趋向于零时, 来自于容器或流体内部的热涨落会使凝聚体中的原子自发产生激发、破坏玻色凝聚、失去超流特征. 具体而言, 无相互作用的玻色子展现自由粒子的色散, 这种粒子构成的凝聚体无法维持任何$ {\boldsymbol{v}}_{{\mathrm{c}}} > 0 $ 的超流(图1(a))[5]. 唯有当粒子之间存在相互作用, 使玻色凝聚整体呈现出非自由粒子的色散关系时, 该凝聚体才有可能展现出$ {\boldsymbol{v}}_{{\mathrm{c}}} > 0 $ 的超流特性. 在液氦中, 氦原子之间的相互作用使液氦展现出类似声子的振荡模式, 因此,$ {\boldsymbol{v}}_{{\mathrm{c}}} $ 等于超流液氦自发产生roton的相速度(能量与波矢量的斜率)(图1(b)). 在超导体中, 临界电流$ {I}_{{\mathrm{c}}} $ 同样对应库珀对运动速度接近$ {\boldsymbol{v}}_{{\mathrm{c}}} $ 时, 多普勒效应使库珀对凝聚自发产生激发, 进而失超. 因此, 为进一步理解、提高各类材料、器件的超导物性, 关于超导体的集体动力学(即集体模式)研究至关重要.为进一步讨论超导体的集体模式, 我们首先指出超导相变破缺局域U(1) 规范对称. 这里的局域U(1) 规范对称指在Tc以上, 超导体的自由能关于序参量
$ \psi \left(x\right)=\left|\psi \left(x\right)\right|{{\mathrm{e}}}^{{\mathrm{i}}\phi \left(x\right)} $ 的相位$ \phi \left(x\right)\in [0, 2{\mathrm{\pi }}] $ 在局域(以及全局)上展现连续旋转不变性, 因此可以把$ \phi \left(x\right) $ 看作一个冗余自由度, 该冗余自由度对应的正是电磁相互作用中的规范自由, 下文会对此作进一步阐释. 库珀对在凝聚过程中会自发形成全局统一的相位(即宏观超导波函数的相位), 这使得原本在 [0, 2π] 范围内完全等价的序参量相位在局域上不再具有变换自由, 这一点与自由能表达式((1)式)中的梯度算符项($ K\nabla {\psi }^{*}\nabla \psi $ )呼应, 表明宏观超导态形成后局域上的相位扭曲、涨落需损耗能量. 需要注意的是, 超导体仍然保持全局U(1) 规范对称: 同时、按相同幅度旋转各个区域的超导序参量相位并不增加超导体的自由能、诱导任何可观测物理量的变化. Nambu-Goldstone理论指出: 连续对称破缺会使体系产生零能模. 在超导相变过程中, 该零能模对应超导序参量在长波极限下的相位涨落. 如图2(a)所示, 在Tc以下超导自由能与序参量呈墨西哥帽状依赖关系. 超导相位涨落对应序参量沿势能面周向的运动; 与其正交、沿径向的运动对应序参量的振幅涨落, 即库珀对束缚能的涨落. 由于势能面沿径向存在曲率, 后者具有非零频率, 需到达一定能量阈值才能激发. 这两个模式的色散关系如图2(b)所示[6].基于图2(b)中相位模式的色散关系, 超导体临界电流
$ {I}_{{\mathrm{c}}} $ 对应的超流临界速度$ {\boldsymbol{v}}_{{\mathrm{c}}} $ 是否由相位模式的斜率所决定呢? 1962年, Anderson[7]指出库珀对之间的电磁相互作用使得该零能模跃迁至等离子体频率, 并且使介导电磁相互作用的光子获得质量. 因此, 相位模式的色散并不是约束$ {I}_{{\mathrm{c}}} $ 大小的决定性因素. 我们可以从朗道相变理论((1)式), 即超导自由能的角度来理解Anderson提出的这套机制. 首先, 我们需引入超导序参量的局域振幅涨落与相位涨落:$ {\psi }_{0}\to \left|{\psi }_{0}+\delta \psi \left(\boldsymbol{x}\right)\right|{{\mathrm{e}}}^{{\mathrm{i}}({\phi }_{0}+\delta \phi (\boldsymbol{x}\left)\right)} $ ,$ \left|{\psi }_{0}\right| $ 与$ {\phi }_{0} $ 分别代表序参量振幅与相位在全局空间上的平均值,$ \delta \psi \left(\boldsymbol{x}\right) $ 与$ \delta \phi \left(\boldsymbol{x}\right) $ 分别代表局域振幅与相位涨落. 将其代入(1)式并化简、保留最低阶的涨落项, 可以得到:其中,
$ {F}_{0} $ 代表不含涨落的固定项. 从(2)式很容易看出包含振幅涨落$ \delta \psi \left(\boldsymbol{x}\right) $ 的两项对应的是有质量粒子的运动方程(譬如对比Dirac方程),$ \sqrt{2\left|a\right|} $ 对应粒子的质量. 而包含相位涨落$ \delta \phi \left(\boldsymbol{x}\right) $ 的表达式对应的则是无质量粒子或零能模的运动方程. 在这一步, 我们引入库仑相互作用: 利用最简耦合(minimal coupling), 即假设电磁场仅作用于库珀对的电荷并赋予其动量, 则自由能表达式中的梯度算符$ \nabla $ 应替换为库珀对在电磁场下的正则动量算符$ -{\mathrm{i}}\hslash \nabla +2{\mathrm{e}}\boldsymbol{A} $ . 将其代入(1)式、添加电磁场的空间能量密度后, 可得这里的关键一步是: 把超导序参量的局域相位涨落
$ \delta \phi \left(\boldsymbol{x}\right) $ 作为电磁场的规范, 吸纳到电磁矢势中去(上文曾提到: 超导序参量的冗余局域相位自由度对应电磁作用中的规范自由),利用新定义的电磁矢势
$ \boldsymbol{A}' $ , (3)式可化简为对比(2)式可以清晰发现: 超导序参量的局域相位涨落表面上从自由能的表达式中消失, 取而代之的是具有质量的电磁矢势的表达式. 这一过程的物理含义可以解读为超导序参量的局域相位涨落被电磁场吸收, 取而代之的
$ \boldsymbol{A}' $ 可看作是局域相位涨落与电磁场的杂化. 因此,$ \boldsymbol{A}' $ 既代表具有质量的电磁场/光子, 又代表非零能的超导相位模式.$ \sqrt{{4{e}^{2}K\left|{\psi }_{0}\right|}^{2}} $ 对应$ \boldsymbol{A}' $ 的质量, 这意味着在平均场超导体(绝大多数BCS超导体)中, 相位模式在长波极限下的能量阈值(即超流体等离子频率$ {\omega }_{{\mathrm{p}}} $ ) 与超流密度($ {n}_{{\mathrm{s}}}={\left|{\psi }_{0}\right|}^{2} $ )也息息相关. 在BCS超导体中两者是互相定义的$ {\omega }_{{\mathrm{p}}}\equiv \sqrt{{n}_{{\mathrm{s}}}} $ [8]. 实验上, 在常规超导体中, 超流密度往往是通过相位刚性(phase rigidity/phase stiffness)的测量来获取, 而后者可以通过伦敦穿透深度(London penetration depth)的测量来获取. 另外需要指出的是: 在真空中电磁相互作用是长程的; 在超导体中, 由于介导电磁作用的光子产生质量, 电磁相互作用变为短程相互作用, 具体体现为电磁场强度随距离呈指数衰减. 因此Anderson机制为迈森纳效应(完全抗磁效应)也提供了微观物理解释.最后, 我们简单讨论Anderson机制和Higgs机制的对应[9-11]. 在电弱理论中W±, Z玻色子介导电弱相互作用, 对应光子介导电磁相互作用; 同时, Higgs场对应超导序参量. Higgs场具有SU(2) 局域规范对称, 由4个自由度共同描述. 其中3个自由度的局域涨落可以当作W±, Z的规范被完全吸收, 使W±, Z玻色子获得质量(对应超导序参量的局域相位涨落被电磁场的规范吸收, 使光子产生质量); Higgs场剩余一个自由度的涨落产生标量激发(对应超导序参量的振幅模式), 被称为Higgs boson. 后者是Higgs场4个自由度中唯一一个独立存在、有可能被实验捕获的粒子激发, 因此在理论预期的参数范围内探测到Higgs boson便可以证实Higgs场的存在以及Higgs机制的真实合理性. 另外值得一提的是: 在粒子物理标准模型中Higgs场也与其他无质量粒子场(如夸克、轻子)发生Yukawa相互作用、使它们获得质量. 该机制不同于上述Anderson-Higgs机制. 从这些论述可以看出, Higgs场对于粒子物理标准模型的重要性. 在超导体中, Higgs模式同样有可能与其他自由度、集体模式发生相互作用, 影响其动力学行为以及材料物性. 由于以上这些共通性, 超导体也成为联系凝聚态物理与粒子物理的固体体系之一, Nambu-Goldstone理论和Anderson-Higgs机制在这两个领域都有着深远的意义.
-
不同于Higgs机制, Anderson机制的合理性不需要从实验上进行证明(譬如迈森纳效应已经可以作为Anderson机制的证据). 尽管如此, 在谱学实验中捕捉到超导Higgs模式仍是一项有意义的探索. 然而, 如同Higgs boson, 超导Higgs模式的探索一样面临不小的挑战. 这是由于Higgs模式对应
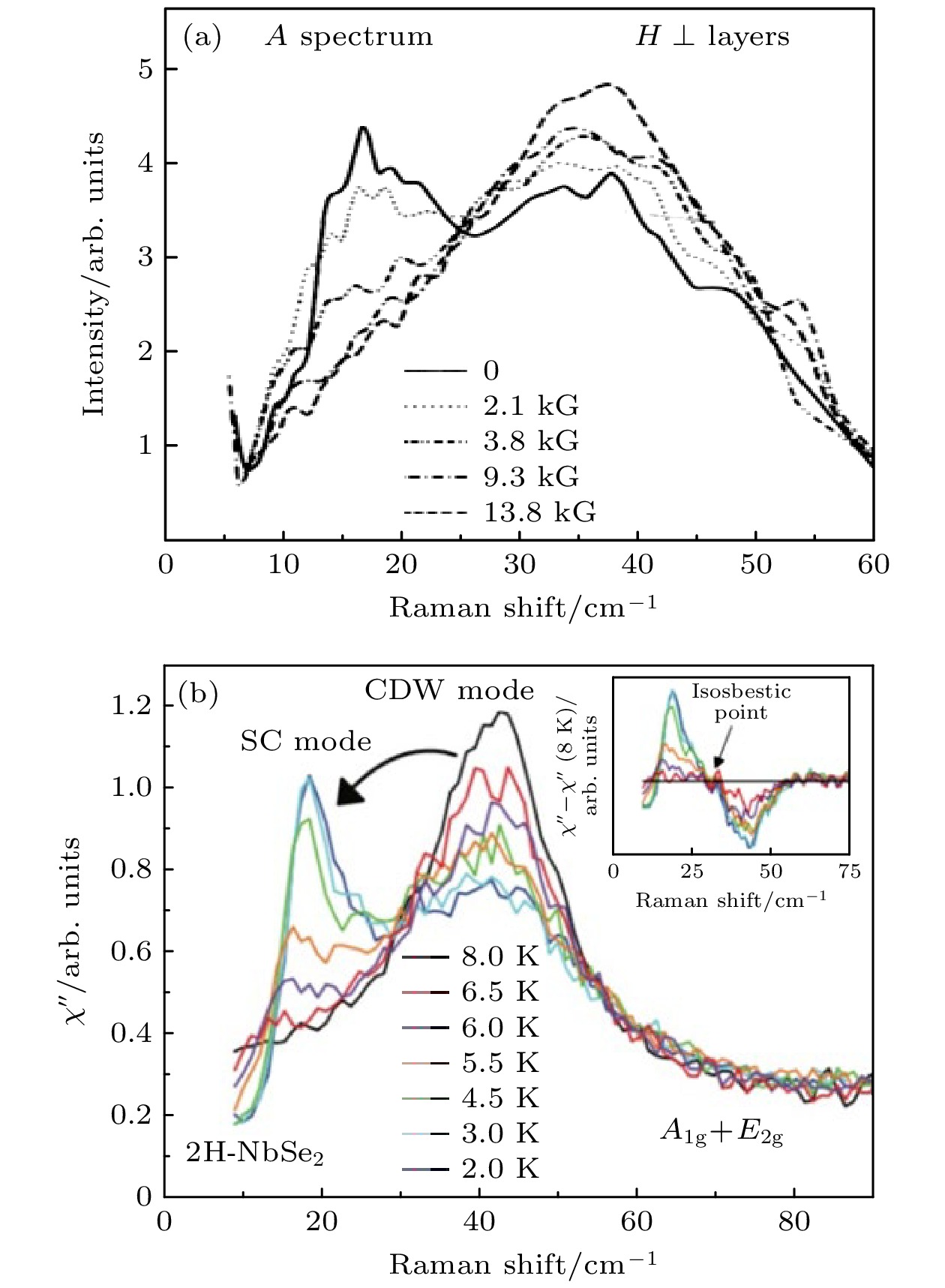
$ ({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow }) $ 电子对束缚能的涨落, 只具有拉曼活性(即中心反演对称), 因此无法与光电场线性耦合; 更重要的是Higgs模式与电子对束缚能(2Δ)简并[12], 因此有限波矢q 的Higgs模式激发有可能迅速衰变为费米面附近的准粒子(quasiparticle)激发, 导致该模式极短的寿命[13,14]. 虽然在超导体的谱学实验(如拉曼散射)中时常能观测到2Δ能量附近的非弹性散射信号, 长久以来我们认为: 这部分信号大多由库珀对拆对(pair-breaking)产生的准粒子激发所贡献, 而非库珀对的集体振荡所贡献. 另外, 一些理论工作也对Higgs模式与相位模式是否完全正交进行讨论, 质疑后者会影响Higgs模式在谱学实验中的观测[15,16]. 介于上述种种原因, 在Anderson机制被提出后的近20年间, 超导体的Higgs模式一直未被谱学实验观测到.1980年, Sooryakumar和Klein[17,18]报道了超导-电荷密度波材料2H-NbSe2在低温及磁场下的拉曼散射信号. 在降温过程中, 他们分别观测到上述两个物相对应的集体模式产生. 有趣的是, 在超导-电荷密度波共存温度 2 K附近, 通过施加磁场抑制超导态, 超导集体模式的拉曼信号减弱、伴随电荷密度波集体模式的拉曼信号增强, 暗示两者之间的耦合(图3(a)). 次年, Littlewood与Varma[19,20]提出, 该实验观测到的超导集体模式正是长久以来谱学实验未见的Higgs模式. 具体而言, 在2H-NbSe2中由于超导序与电荷密度波序之间存在相互作用, Higgs模式与电荷密度波振幅模式发生杂化, 前者的能量被重整至电子配对能2Δ以下, 因此无法衰变为准粒子激发, 从而保证了其较长的激发寿命. 另外, 由于电荷密度波的振幅模式本质上对应声学声子在布里渊区的折叠, Higgs模式与其杂化后获得声子的拉曼散射截面, 因此在拉曼散射实验中得以更加明显地体现出来.
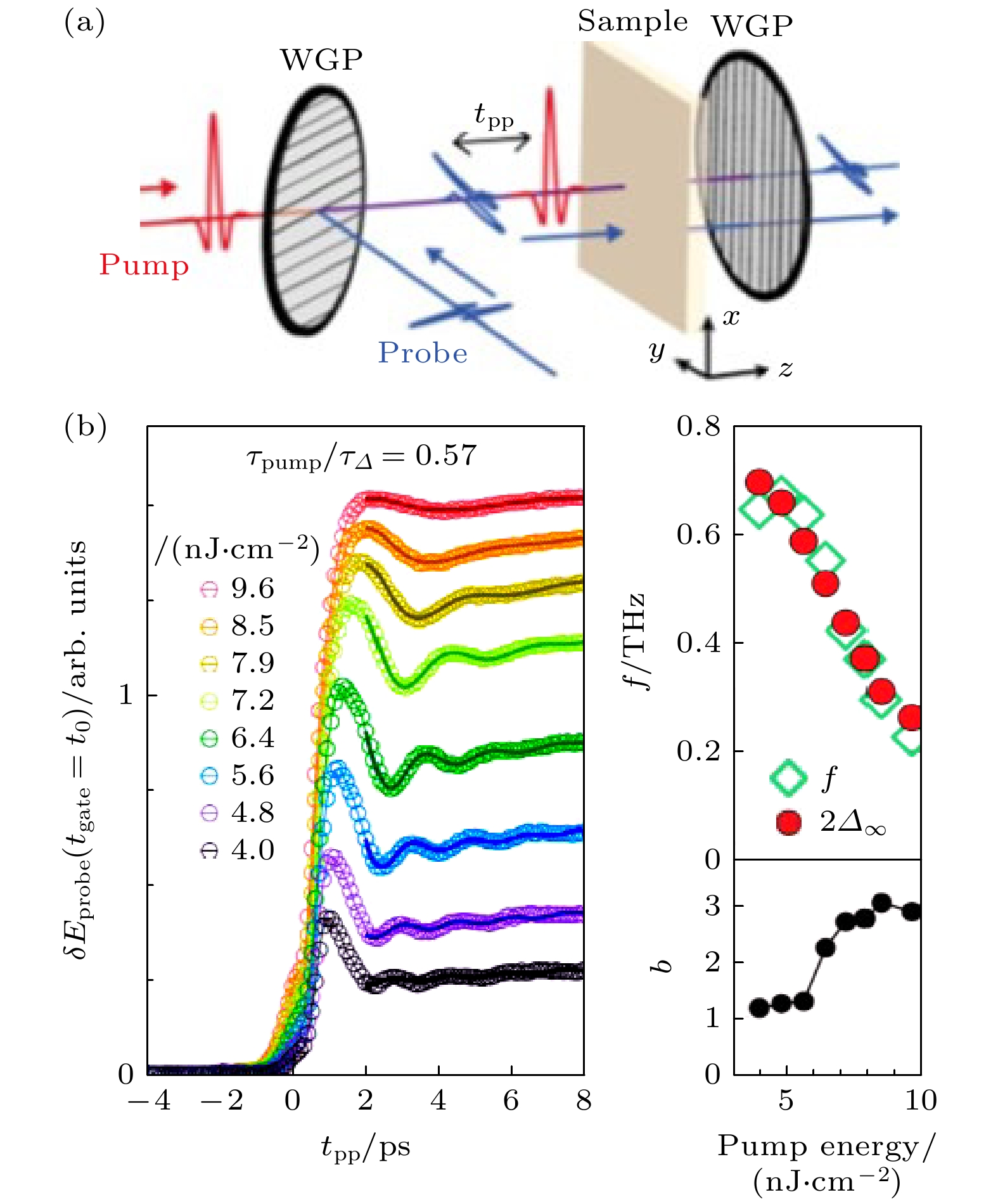
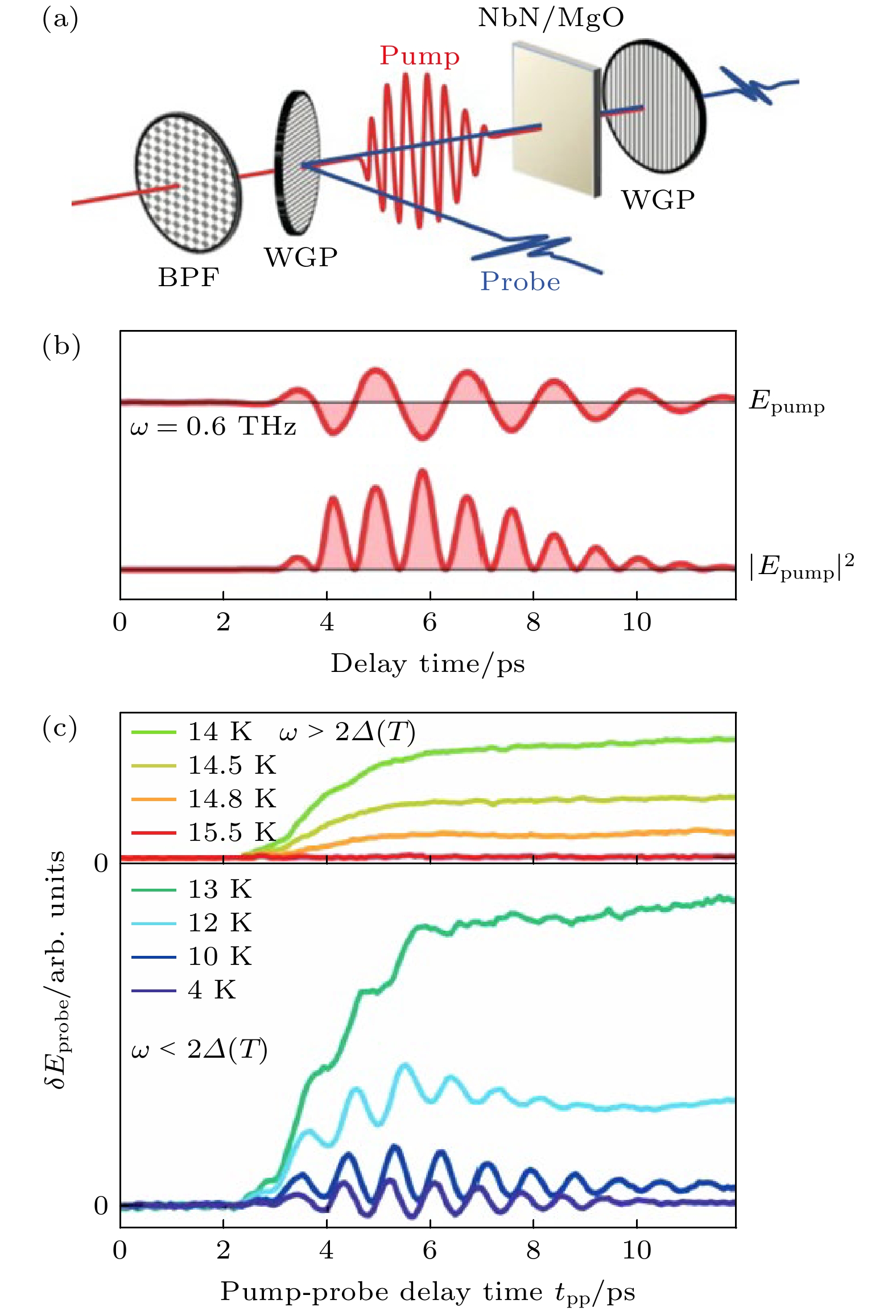
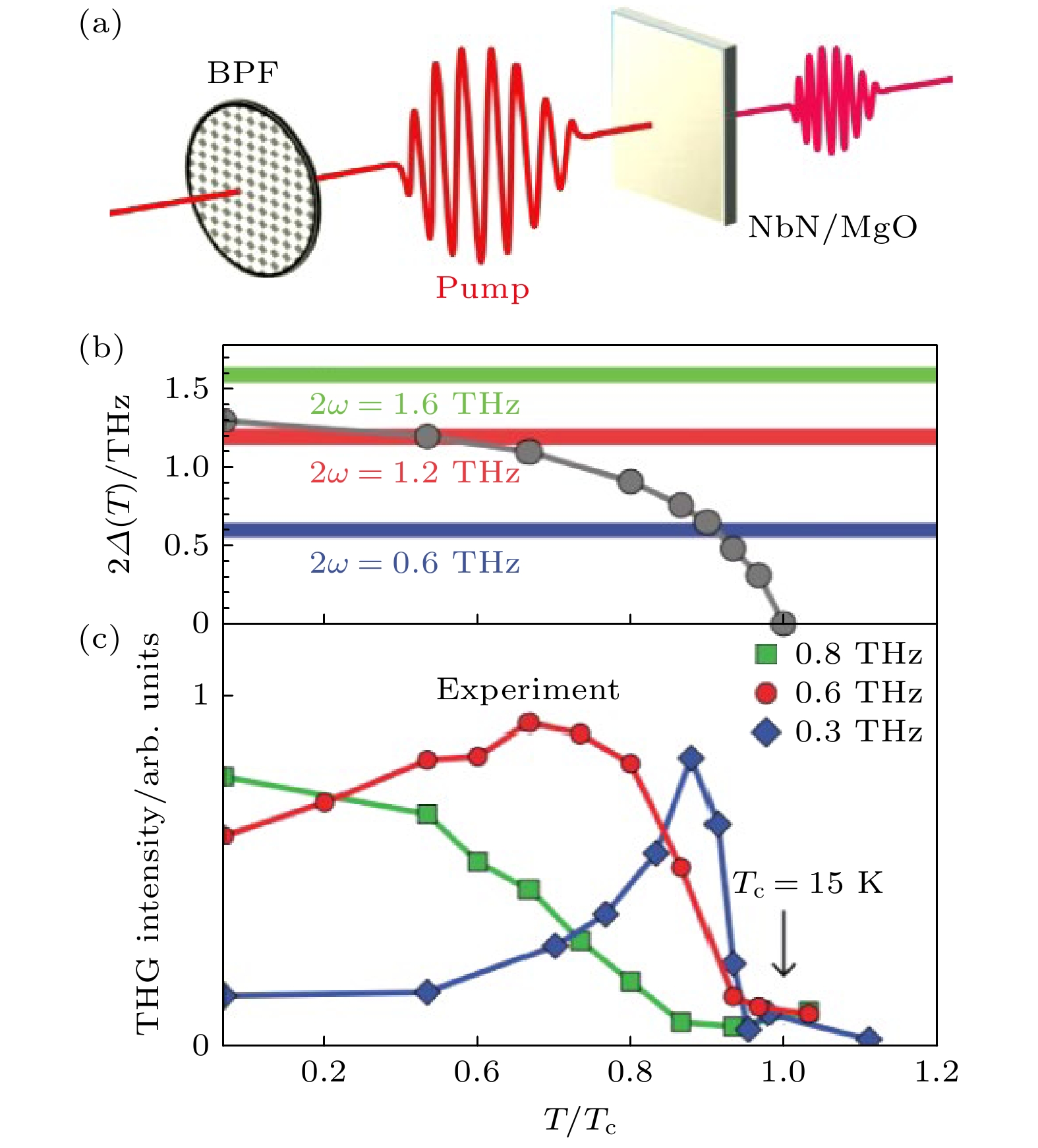
虽然2H-NbSe2展示了谱学实验探索Higgs模式的先例, 然而在此后的30多年间, Higgs模式的实验探索再次陷入停滞, 未再有实验报道其他超导体中的Higgs模式. 直到2013年, Matsunaga等[21]采用太赫兹脉冲在Nb1–xTixN超导薄膜中进行泵浦-探测实验, 才首次在时域上观测到Higgs模式的自由振荡. 在该实验中, 他们利用LiNbO3晶体产生的强场单周期太赫兹脉冲作为泵浦, 对样品的超导基态进行扰动; 同时利用另一束较弱、时间延迟的太赫兹脉冲对样品的透射率进行探测. 通过扫描泵浦光与探测光之间的延时, 可以获得样品透射率在飞秒尺度的时间演化. 在实验中, 他们观测到在泵浦光扰动超导基态后, 样品的太赫兹透射率随时间呈现周期振荡, 且振荡频率约等于2Δ, 符合Higgs模式的特征(图4). 2014年, 他们采用多周期(频率为ω)太赫兹脉冲对NbN超导薄膜进行驱动, 同时利用另一束单周期太赫兹脉冲探测样品的透射率演化, 发现在Tc以下透射率随时间呈2ω频率的振荡[22] (图5). 由于超导凝聚体的集体响应与光电场的最低阶耦合为二次(见(5)式), 该2ω 频率的振荡可以解读为超流体在周期驱动下的受驱振荡. 随后, 他们遮挡住探测光, 仅让泵浦光从样品穿透, 分析透射部分的频谱, 可以发现在Tc以下透射光包含明显的三次谐波(third Harmonic generation, THG)成分(图6). 当改变温度T使2Δ(T) 满足2Δ = 2ω时, Higgs模式的受驱振荡与太赫兹驱动场发生共振、使三次谐波信号在该温度展现共振峰.
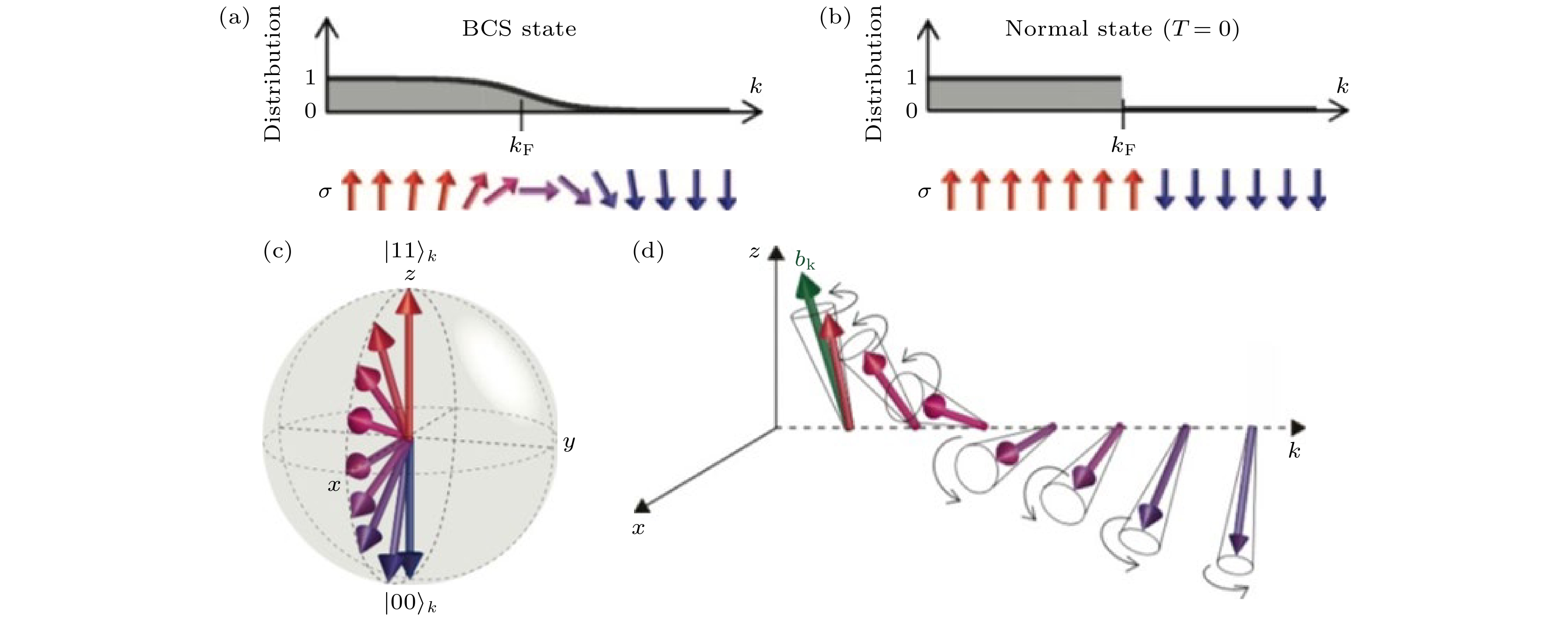
在上述实验中, 超导序参量在多周期太赫兹光电场驱动下的动力学过程可以通过Anderson pseudospin模型来描述[22-24] (图7). Anderson pseudospin描述一对波矢相反、自旋相反的电子态
$ ({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow }) $ 的占据状态: pseudospin =1/2 代表电子对处于被占据状态、pseudospin = –1/2 代表电子对处于空态. 不同能量的电子对的占据态因此可以投射为Anderson Bloch sphere(布洛赫球)上pseudospin的指向. 由于库珀对由费米面附近的$ {({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow }}) $ 电子对与$ {({\boldsymbol{k}}_{\downarrow }, -\boldsymbol{k}_{\uparrow })} $ 空穴对相干叠加形成, 因此BCS基态可以由费米面附近pseudospin = 1/2态与pseudospin = –1/2 态的相干叠加描述: 即pseudospin指向Anderson布洛赫球赤道面内. Tsuji和Aoki[22]模拟了多周期太赫兹泵浦光作用下, Anderson pseudospin在布洛赫球上以2ω为频率的进动过程, 并得出进动过程中太赫兹电场诱导的3ω电流响应, 解释了实验中观测到的2ω透射率振荡以及三次谐波辐射的起源. 值得一提的是, 2013年一项关于铜基高温超导体La2–xSrxCuO4 的近红外(1.55 eV)泵浦-宽谱可见光(1.6—3.2 eV)探测实验发现, 1.55 eV泵浦光诱导库珀拆对而产生的准粒子激发引动了更高能量尺度(2 eV)的反射率振荡, 且振荡频率与该材料的库珀对束缚能2Δ一致[25]. 这项工作同样以Anderson pseudospin为模型描述费米面附近的准粒子动力学过程. 如今看来, 我们不能排除这项工作中观测到的准粒子动力学行为正是La2–xSrxCuO4中Higgs模式自由振荡体现的可能性.除借助Anderson pseudospin模型帮助理解超导体集体激发的动力学过程, 太赫兹光电场驱 动下的非线性光学过程也可以从拉曼散射的微 观电动力学角度来直观理解, 这一点对于理解时域 太赫兹非线性谱学为何能有效探测Higgs模式、甚至其他凝聚相的低能集体模式尤为重要. 如上 文所述, 固体中的电子在电磁场作用下的动能为
$ [\boldsymbol{p}+ e\boldsymbol{A}]^{2}/\left(2 m\right) $ , 展开后可得两项含电磁矢势的表达式:$ [\boldsymbol{A}\cdot \boldsymbol{A}]\cdot {e}^{2}/\left(2 m\right) $ 与$ [\boldsymbol{p}\cdot \boldsymbol{A}+\boldsymbol{A}\cdot \boldsymbol{p}]\cdot e/\left(2 m\right) $ , 它们分别代表光电场与固体中电子的两种散射机制. 假设材料的宏观电子态在散射前后的状态分别为$ |I\rangle $ 和$ |F\rangle $ (注:$ |I\rangle $ 和$ |F\rangle $ 不一定对应材料哈密顿量的本征态$ |\alpha \rangle $ ,$ |\beta \rangle $ , …), 通过二次量子化1 , 光与电子的有效相互作用算符$ M $ 可表达为[26]:式中等号右边第1项中
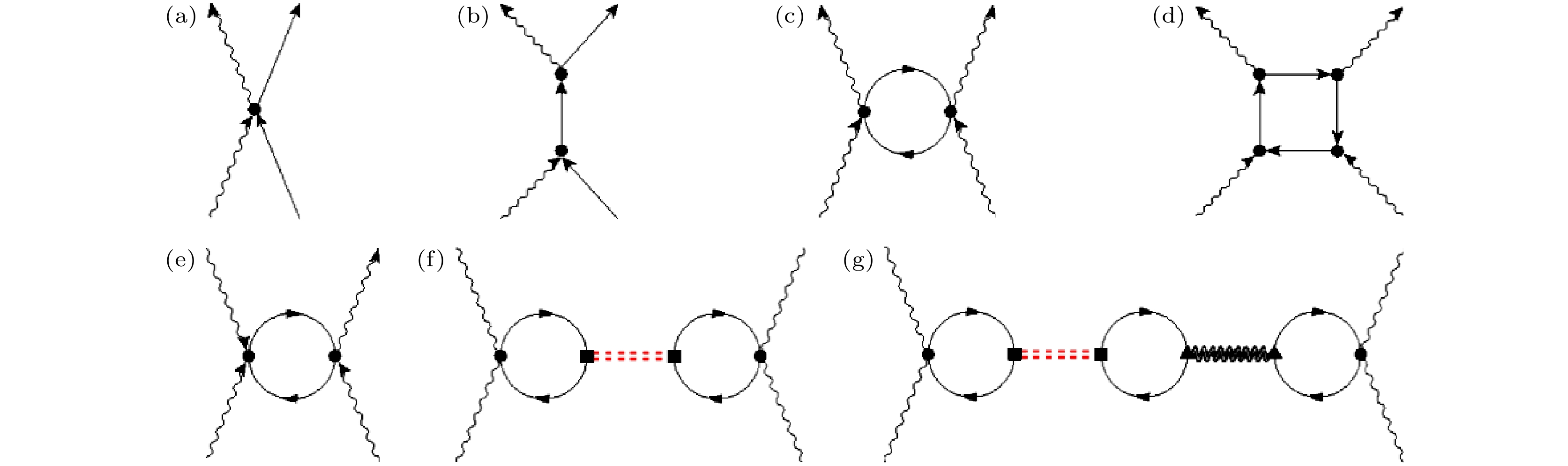
$ {\rho }_{\alpha , \beta }\left(\boldsymbol{q}\right)\equiv \langle \alpha |{{\mathrm{e}}}^{{\mathrm{i}}\boldsymbol{q}\cdot \boldsymbol{r}}|\beta \rangle = \displaystyle \int {{\mathrm{d}}}^{3}r{\varphi }_{\alpha }^{*}\left(\boldsymbol{r}\right){{\mathrm{e}}}^{{\mathrm{i}}\boldsymbol{q}\cdot \boldsymbol{r}}{\varphi }_{\beta }\left(\boldsymbol{r}\right) $ 是哈密顿量本征态之间的单粒子密度涨落(single-particle density fluctuations)矩阵元, 描述光子与电子发生非弹性散射 、交换部分能量与动量、使初态$ |I\rangle $ 跃迁至末态$ |F\rangle $ 的概率振幅(图8(a)); 第2项中$ {p}_{\alpha , {\alpha }'}\left({\boldsymbol{q}}_{{\mathrm{i}}}\right)\equiv \langle \alpha |\boldsymbol{p}\cdot {\boldsymbol{e}}_{{\mathrm{i}}}{{\mathrm{e}}}^{{\mathrm{i}}{\boldsymbol{q}}_{{\mathrm{i}}}\cdot \boldsymbol{r}}|{\alpha }'\rangle $ 是动量密度矩阵(momentum density matrix)元, 描述光子被共振吸收、使初态$ |I\rangle $ 跃迁至中间态$ |v\rangle $ 的概率振幅; 而后, 中间态$ |v\rangle $ 再通过共轭(时间反演)过程—辐射出光子—达到末态$ |F\rangle $ (图8(b)), 这个过程的概率振幅由$ {p}_{\beta , {\beta }'}\left({\boldsymbol{q}}_{{\mathrm{s}}}\right) $ 矩阵元描述.不难看出,
$ M $ 的第1项对应光电相互作用展开后的$ [\boldsymbol{A}\cdot \boldsymbol{A}]\cdot {e}^{2}/\left(2 m\right) $ 项,$ M $ 的第2项对应光电相互作用展开后的$ [\boldsymbol{p}\cdot \boldsymbol{A}+\boldsymbol{A}\cdot \boldsymbol{p}]\cdot e/\left(2 m\right) $ 项.$ M $ 描述的是散射振幅, 光与材料的散射截面(即实验所测得的拉曼散射强度)正比于$ {\left|M\right|}^{2} $ . 这意味着上述两种散射机制的全过程由图8(a), (b)乘以它们的时间反演来描述(图8(c), (d)). 可以看出, 这两种散射过程都涉及两个入射光子和两个出射光子. 当我们把图8(c)中的一束出射光变为入射光时(图8(e)), 得到的正是太赫兹三次谐波的微观过程. 这里需要特别指出, 当采用更高能量的中红外、近红外光对半导体材料进行三次谐波实验时, 若光子可以共振激发带间电子跃迁, 则该三次谐波生成的微观过程类似于图8(d), 与这里讨论的太 赫兹三次谐波的微观过程有所不同. 读者可能发现, 到目前我们描述的散射过程是弹性(Rayleigh)散射过程. 我们可以在上述过程中, 插入电子/空穴与材料中玻色子/集体模式的散射(图8(f)), 从而得到非弹性拉曼散射的散射截面. 以此类推, 图8(c), (d)可以分别演变为非共振和共振拉曼散射过程, 因此太赫兹三次谐波技术实际测量的正是材料的非共振拉曼散射响应.此处我们再具体描述超导体中太赫兹三次谐波散射过程(图8(f)). 由于太赫兹光子能量远小于带间电子跃迁所需能量, 无法被电子共振吸收, 只能与电子发生非弹性散射. 该过程(散射截面)等同于一对低能量光子(假设光子能量为ω)通过双光子吸收激发系统中的电子空穴对涨落; 后者湮灭并产生能量为2ω的Higgs涨落, Higgs涨落湮灭并再产生电子空穴对涨落, 最后能量为ωprobe的探针光子入射并吸收电子空穴湮灭时产生的能量、发生anti-Stokes散射, 产生能量为ωprobe + 2ω的出射光. 这一微观过程可以广泛解释图5和图6中的实验结果, 以及太赫兹泵浦-可见光探测的实验结果[27,28]. 在太赫兹三次谐波实验中, 虽然实验仅仅使用单束太赫兹脉冲, 而非泵浦-探测实验常见的两束脉冲, 多周期太赫兹光既起到泵浦的作用, 又起到探针作用, 因此也可以看作广义泵浦-探测实验手段的一种.
-
在Matsunaga与Shimano的开创性工作之后, 利用太赫兹泵浦诱导Higgs模式的受驱振荡、再使用光学探针进行超快时间分辨探测成为研究Higgs模式的主要手段之一. 然而, 对于这类实验普遍观测到的三阶非线性信号
$ {{\mathrm{\chi }}}^{\left(3\right)}({\omega }_{{\mathrm{p}}{\mathrm{r}}{\mathrm{o}}{\mathrm{b}}{\mathrm{e}}}+2{\omega }_{{\mathrm{T}}{\mathrm{H}}{\mathrm{z}}}, {\omega }_{{\mathrm{p}}{\mathrm{r}}{\mathrm{o}}{\mathrm{b}}{\mathrm{e}}}, {\omega }_{{\mathrm{T}}{\mathrm{H}}{\mathrm{z}}}, {\omega }_{{\mathrm{T}}{\mathrm{H}}{\mathrm{z}}}) $ 是否代表超导体的Higgs响应, Cea等[29]提出了不同看法. 尤其针对超导体的太赫兹三次谐波响应(即$ {{\mathrm{\chi }}}^{\left(3\right)} $ 中设$ {\omega }_{{\mathrm{p}}{\mathrm{r}}{\mathrm{o}}{\mathrm{b}}{\mathrm{e}}}={\omega }_{{\mathrm{T}}{\mathrm{H}}{\mathrm{z}}} $ ), 他们提出由电子空穴对涨落自身介导的散射过程(图8(e))比由Higgs涨落介导的散射过程(图8(f))贡献更主要的三次谐波信号. 同时, 前者贡献的三次谐波信号会展现出与晶格一致的各向异性, 而后者贡献的三次谐波信号则展现出各向同性. Matsunaga等[30]随后检验了NbN中三次谐波的偏振依赖, 发现明显的各向同性特征, 符合Higgs模式的贡献. Tsuji等[31]也指出, 对于干净极限(clean limit)的BCS超导体而言, 电子空穴对涨落确实会贡献更强的三次谐波信号, 然而大多数BCS超导体处于脏极限(dirty limit), 在这类体系中声子延迟(phonon retardation)效应会使得Higgs涨落仍然贡献最主要的三次谐波信号. 对此, Cea等[32,33]指出, 太赫兹脉冲时间展宽、体系中多能带的电荷激发、材料的无序(disorder)都有可能抹消来自电子空穴对涨落的三次谐波信号的各向异性. Tsuji和Nomura [34]同样考虑了多带模型在干净极限与脏极限下三次谐波的不同来源, 通过BCS自洽玻恩近似(Born approximation), 发现电子空穴对涨落介导的三次谐波仍然应具有明显的各向异性. 此外, Gabriele等[35]指出超导相位涨落(Josephson fluctuations, 也称作约瑟夫森涨落)也会贡献太赫兹三次谐波信号, 并且该过程(以及上述电子空穴对涨落)会在2Δ(T) = 2$ \omega $ 条件下产生共振, 因此仅仅从三次谐波的温度依赖难以判断其背后的微观机制. 值得注意的是, 以上理论研究普遍建立在平均场/BCS超导体的假设下, 对于强关联/高温超导体是否适用值得讨论. 譬如, 在BCS超导体中, Higgs模式往往被简并的准粒子激发迅速湮灭(除了2H-NbSe2), 而Lorenzana和Seibold[36]在近期的研究中发现, 强关联作用同样会使Higgs模式下降到准粒子激发阈值以下, 因此会展现出较长的寿命. 由此我们可以联想到: 在高温超导体的谱学实验中, Higgs模式的谱学响应有望与库珀拆对的准粒子谱学响应分离开来. 并且, 前者应当展现各向同性、后者应当展现各向异性; 前者是一个相干过程, 而后者理应是非相干过程. 文献[25]报道的光学激发下La2–xSrxCuO4样品的2Δ相干振荡或许正是强关联作用下Higgs模式重整至准粒子激发阈值以下的实验证据. 这些理论和实验依据将协助我们判断高温超导样品中三次谐波信号背后的微观动力学过程.在理论上厘清太赫兹三阶非线性信号来源的同时, Kemper等[37]预言如何使用时间分辨角分辨光电子能谱(ARPES)手段捕获常规超导体的Higgs模式谱学信号. Krull等[38]考虑了多带超导体(如MgB2)在非平衡状态下Higgs模式与Legget模式的耦合. Moor等[39]提出, 在超导电流流动情况下Higgs模式将获得红外活性, 这一预言也被Nakamura等在实验上展示[40]. Barlas和Varma[41]预言d波超导体会呈现多种不同对称性的Higgs模式, 这一观点在 Schwarz等[42]的工作中得到进一步细化: 在不同对称性的扰动下, s波、 d波、g波序参量会相应展现出不同数量、不同对称性的振荡模式, 因此实验上可以通过探测和罗列不同对称性的Higgs模式, 来判断新型超导体的配对对称性. Yang和Wu[43]发展了规范不变的微观超导运动理论, 用于处理超导体对光电场的响应, 并将该理论运用于计算超导相位模式与Higgs模式的光电场响应[44]. 此外, Murakami等[45,46]研究了声子与Higgs模式之间的耦合, 发现新的杂化模式以及Higgs模式衰变受到的影响.
实验上, 2015年, Sherman等[47]利用扫描隧道显微镜对比太赫兹谱学测量, 展示了无序NbN超导体中的单粒子激发与Higgs集体激发的迥异. 2018年Katsumi等[27]利用单周期太赫兹脉冲作为泵浦、800 nm飞秒脉冲作为探针, 研究了高温超导材料Bi2Sr2CaCu2O8+x中的Higgs响应, 其信号具体表现为800 nm波长的反射率随时间t展现出太赫兹驱动电场E(t) 模平方
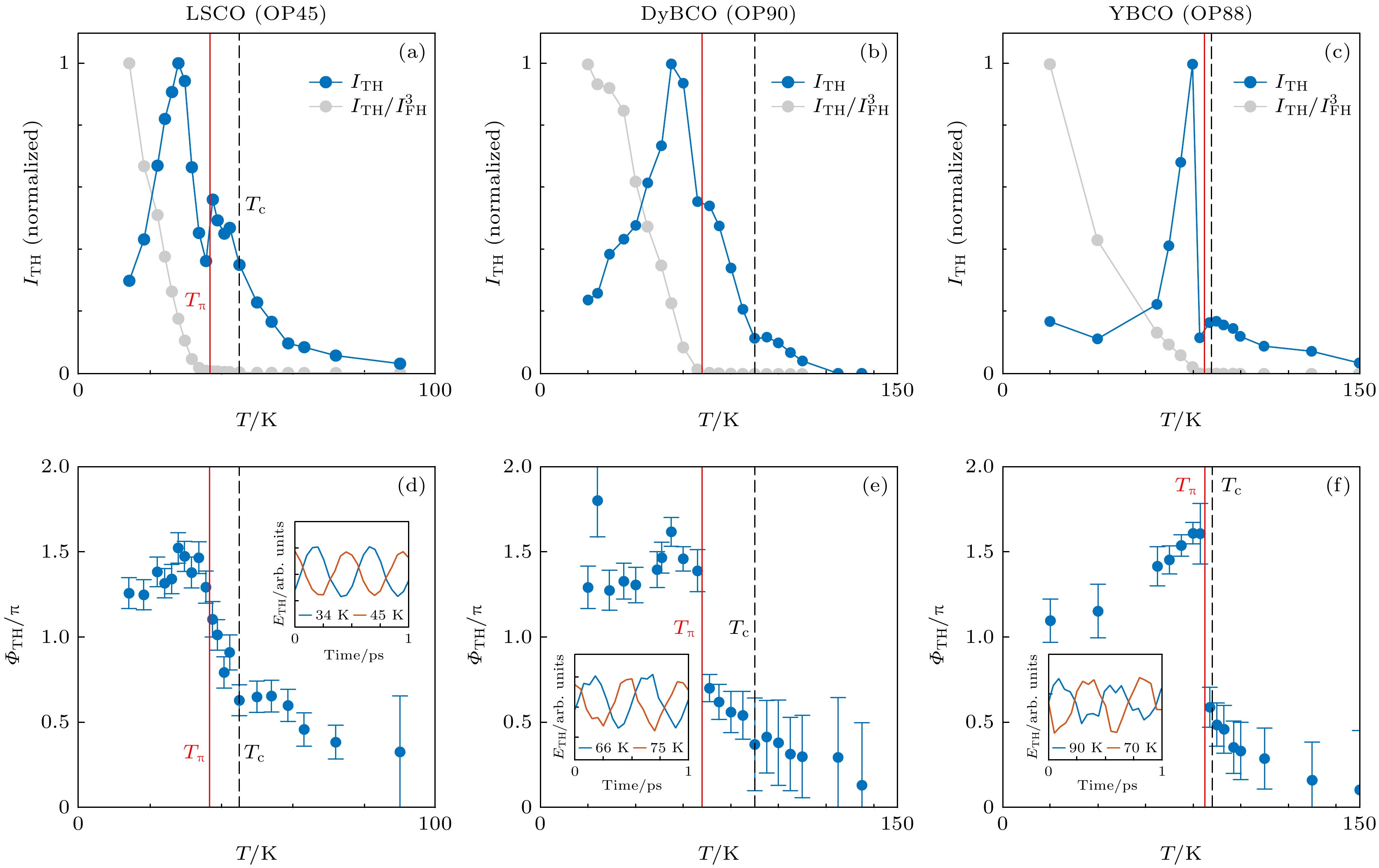
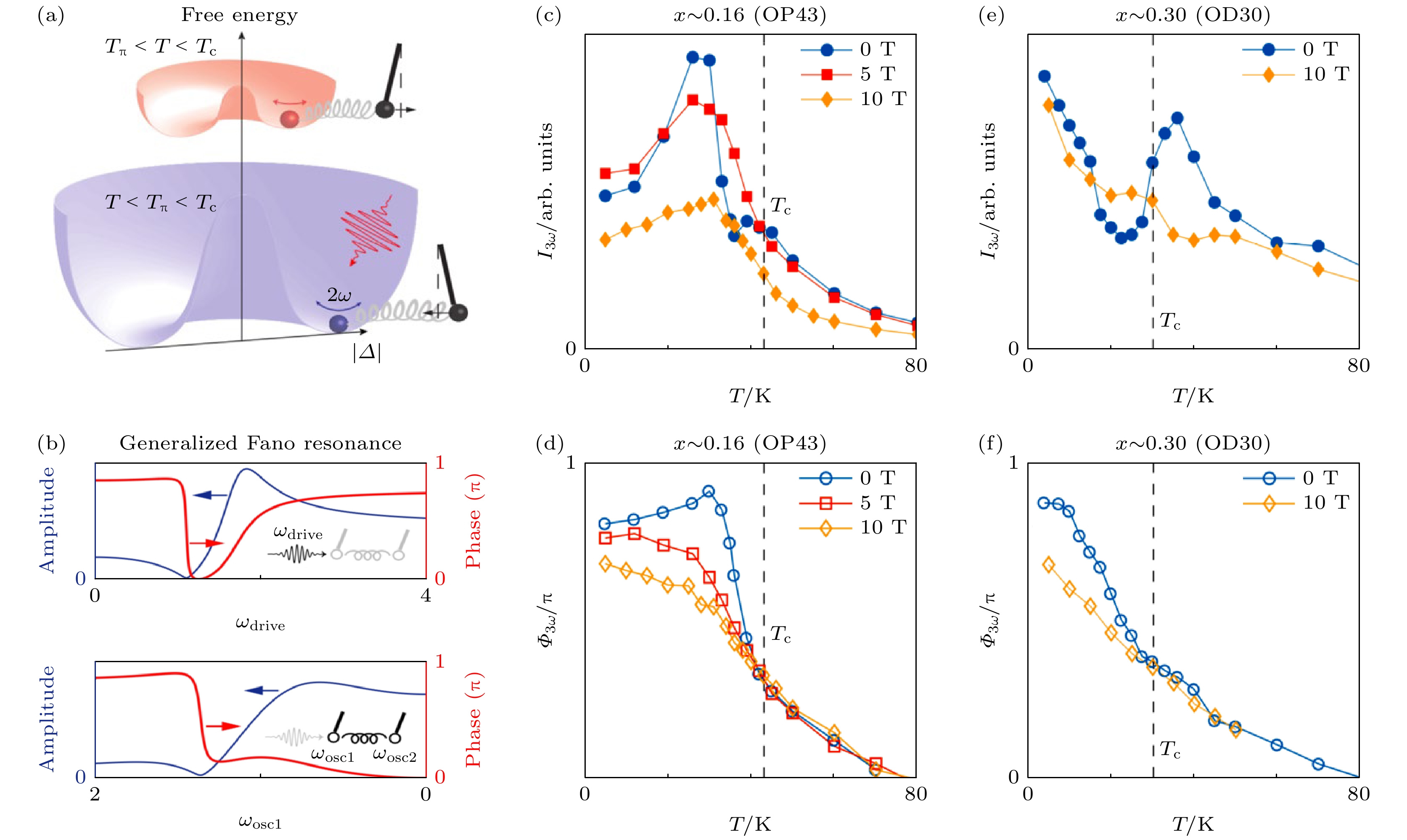
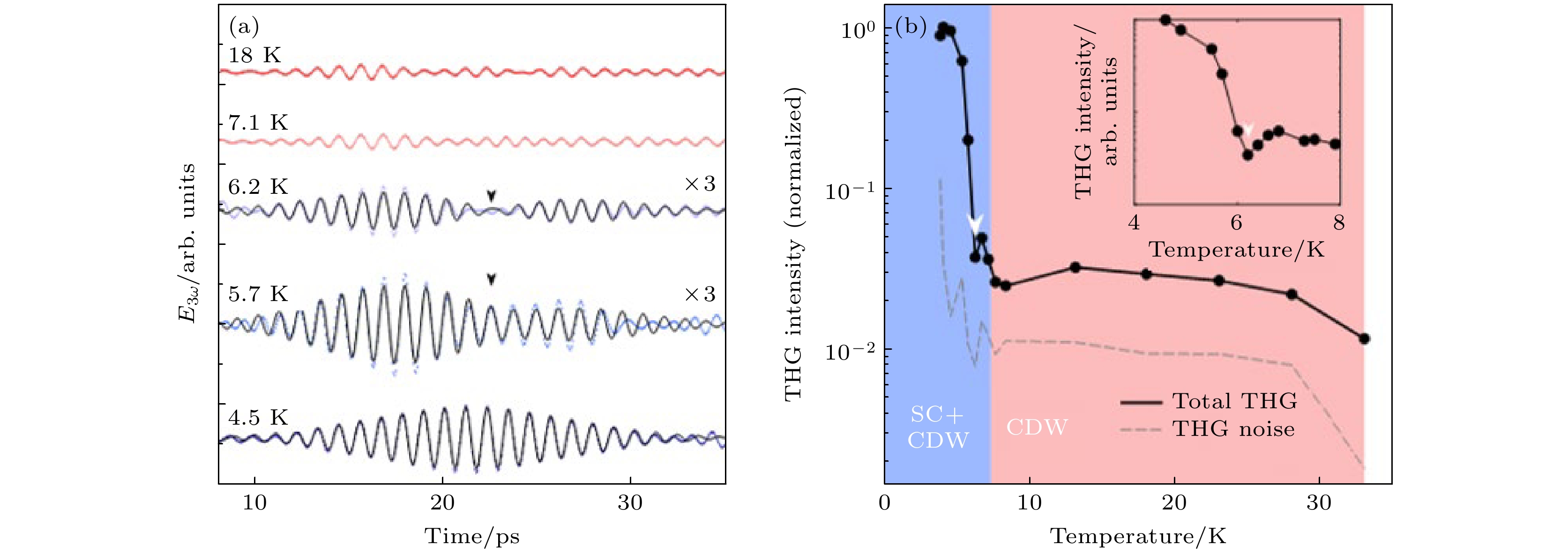
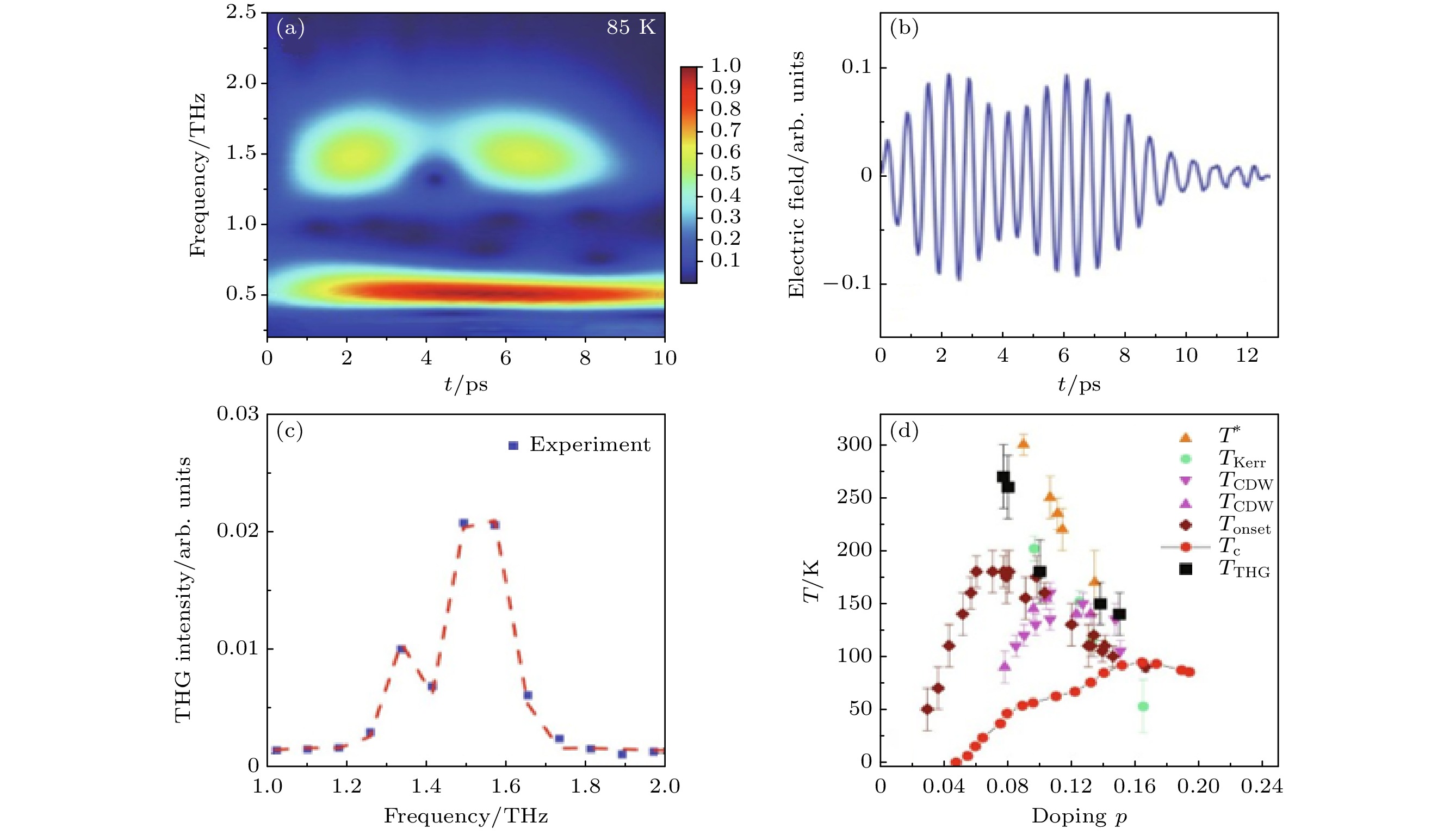
$ {\left|E\left(t\right)\right|}^{2} $ 形的振荡, 符合超流整体与光电场的二次耦合关系. 另外, 当改变太赫兹电场偏振与探测光偏振之间的夹角时, 超快反射率中的$ {\left|E\left(t\right)\right|}^{2} $ 响应主要呈各向同性; 少量的各向异性成分具有B1g对称性, 说明电子空穴对涨落贡献次要的三阶非线性光学信号. 在典型多带超导体MgB2 中, Kovalev等[48]利用太赫兹三次谐波手段寻找两个超导序参量各自的Higgs响应, 但是只观测到较大超导序参量的Higgs模式的信号特征. 在NbN 超导体中, Wang等[49]利用不同时间窗口的小波分析, 研究了材料在多周期太赫兹场驱动下的非线性响应, 发现了三次谐波以外的瞬态Higgs振荡.2020年, Chu等 [50]报道了铜基高温超导体的太赫兹三次谐波响应. 在这项工作中, 他们提取了三次谐波振荡关于太赫兹驱动场的相对相位(Φ3ω), 发现Φ3ω随温度改变展现出急剧的负π跳跃(图9). 通过对比受驱耦合谐振子模型的相位响应, 他们 认为这是过阻尼的Higgs模式与系统中另一欠 阻尼的集体模式发生耦合而产生反共振(anti- resonance)的谱学迹象. 随后, 利用法诺共振(欠阻尼激发态与过阻尼激发态/连续背景之间的干涉)模型来描述这一现象, 他们系统性地表征了La2–xSrxCuO4薄膜在不同空穴掺杂浓度与磁场环境下, Φ3ω随温度的跳跃行为. 他们观察到Φ3ω(T) 中的法诺共振 (反共振)现象被过掺杂以及磁场抑制, 由此推论: 与Higgs模式耦合的集体模式为电荷密度波/电荷序涨落[28] (图10). Schwarz等[51]参考2H-NbSe2的拉曼散射理论[52], 考虑Higgs涨落与电荷密度波涨落的耦合, 发现太赫兹三次谐波随温度确实会展现出反共振/法诺共振的谱学特征. 为进一步证实这个可能性, Feng等[53]利用太赫兹三次谐波手段表征了2H-NbSe2薄膜(图11), 发现在TCDW ~ 33 K和Tc ~ 8 K以下确实会分别产生新的三次谐波来源, 并且这两部分三次谐波信号在6 K附近产生非常明显的干涉, 与该样品中的拉曼实验结果相符(图3(b)). 同期, Yuan等[54]也在双层铜基高温超导体YBa2Cu3O7–x中观测到两部分三次谐波信号在Tc附近拍频的现象, 其中一部分信号诞生于Tc, 另一部分信号诞生于赝能隙温度
$T^* $ (图12), 推测后者可能是赝能隙集体模式贡献的动力学信号. 值得一提的是: 铜基高温超导体的库珀对束缚能2Δ一般在20—40 meV (即 5—10 THz)区间, 为满足2Δ(T) = 2ω的共振条件, 实验应当采用ω = 2.5—5 THz的驱动频率, 这超出了基于LiNbO3晶体的常见桌面太赫兹光源的频谱范围(下文会对此作进一步讨论). 然而, 由于铜基超导体的电子配对呈d波对称性, 这意味着配对能2Δ沿费米面不同方向呈现连续、周期演变. 因此, 相较于s波超导体, d波超导体的Higgs模式展现出更宽的谱宽, 在低至2ω = 0.1×2Δ(T) 的驱动频率以下仍预期具有较强的谱学响应[42]. 这解释了上述太赫兹实验中, 为何0.3—0.7 THz的太赫兹驱动会诱导明显的Higgs响应, 以及为什么我们可以为把d波超导体的Higgs模式看作法诺共振中的连续激发态.在非线性太赫兹谱学技术广泛运用于Higgs模式研究之际, 传统共振拉曼散射技术也在Higgs模式研究中取得重要进展. 利用该技术, Méasson等[55-57]系统性地研究了2H-NbSe2, 2H-NbS2, 2H-TaS2等层状材料中Higgs模式与电荷密度波模式在不同温度、压强下的演化. Glier等[58]则利用光学泵浦-拉曼散射探测技术研究了Bi2Sr2CaCu2O8+δ (Bi-2212) 高温超导体在共振激发后Higgs模式贡献的anti-Stokes拉曼信号, 进一步证实了Puviani与Manske等的理论预言: Higgs模式会贡献相当一部分2Δ能量尺度的拉曼散射信号, 因此长久以来认为2Δ能量附近的拉曼散射信号完全来自于库珀拆对的观点需要修正[59].
-
在过往十年间, 非线性太赫兹技术与共振拉曼散射技术大力推进了各类超导体中的Higgs模式研究, 涵盖了传统BCS超导体、铜基高温超导体、铁基高温超导体、二维超导材料. 微扰区间下Higgs模式的动力学研究有望为平衡态超导研究带来全新的认知, 特别是在高温超导领域, 有可能为赝能隙、电荷序背后的微观机制、电荷密度波与超导态之间的竞争/协作关系提供新颖的视角和信息. 针对非常规超导体中的交织序, 过往的研究往往依赖于对于各个序在不同物理条件(如温度、磁场)下静态、平衡态物理性质(如相变温度、关联长度)的测量. 譬如, 通过施加磁场抑制超导序、观测电 荷序关联长度的增长、相变温度的提高, 可以得出两个序之间相互竞争的结论. 利用耦合序参量朗道模型:
或等价的耦合谐振子模型来描述这类平衡态实验策略 (即通过改变静态物理条件来诱导平衡态下两个序参量的大小变化), 就如同拉拽耦合谐振子中的一个使之发生位移, 与之耦合的另一个谐振子的平衡态位置也会相应发生变化(图13(a)). 通过观察两个谐振子的静态位移, 我们可获悉它们之间存在相互作用, 却对该相互作用的能量尺度及微观机制无从了解. 唯有当我们动态扰动这两个谐振子, 才有可能从它们的协同运动过程中获知耦合弹簧的微观信息(图13(b)). 这正是Higgs模式研究(以及电荷序动力学研究)所能提供的独到视角.
另一方面, 上文曾提到在粒子物理标准模型中, Higgs场不仅通过Higgs机制为W±, Z玻色子带来质量, 其自身的自发对称破缺也通过Yukawa耦合(如
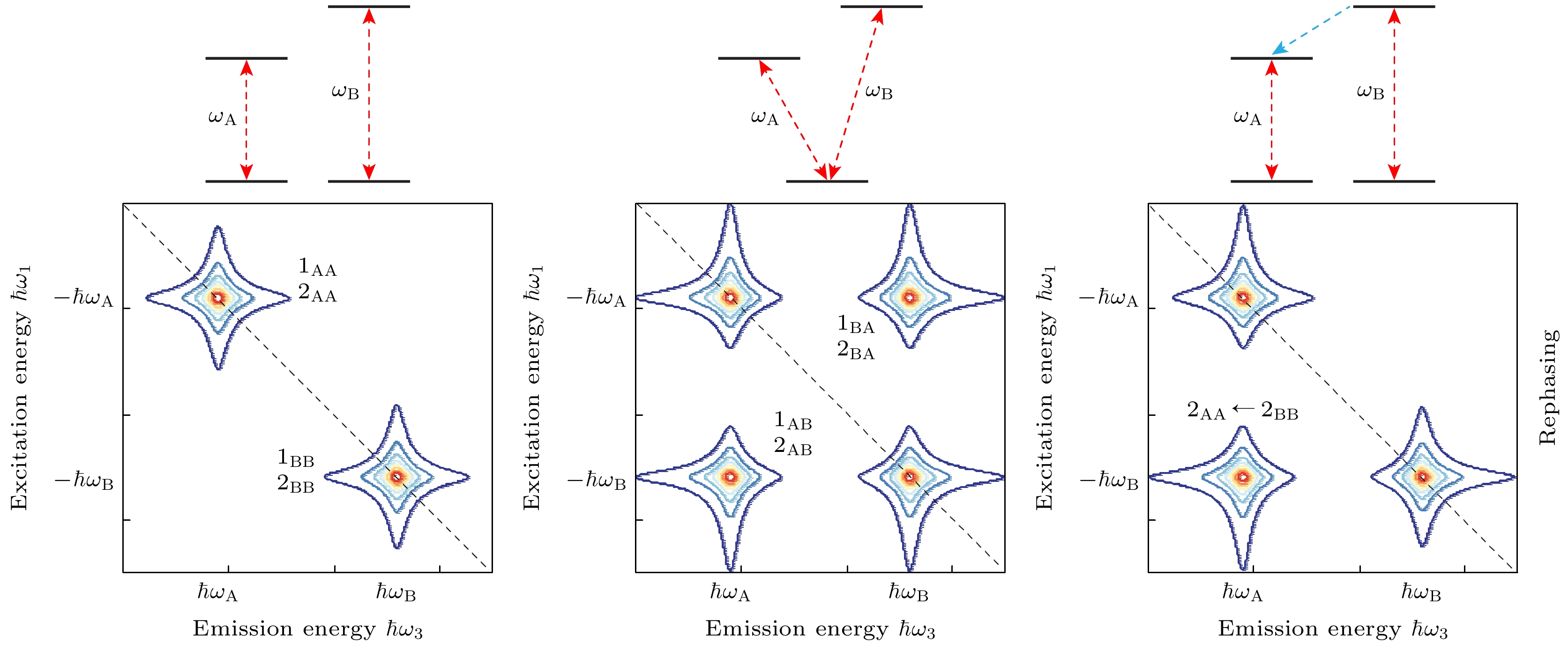
$ g{\psi }^{*}\phi \psi $ 形式)使一系列费米子产生或重整质量. 类似的相互作用机制是否也存在于超导体中值得思考: 在固体中, 按照不同不可约表示(irreducible representation)变换的序参量之间可以存在非biquadratic形式的耦合(即不同于(7)式中$ {\lambda \left|{\psi }_{{\mathrm{S}}{\mathrm{C}}}\right|}^{2}{\left|{\phi }_{{\mathrm{C}}{\mathrm{D}}{\mathrm{W}}}\right|}^{2} $ 形式的耦合). 在重费米子超导体URu2Si2[60]、自旋液体材料Cd2Re2O7[61]、铁基超导体[62]等体系中, 在极为临近的热力学空间范围内, 各类迥异的对称破缺相(反铁磁序、自旋密度波、向列序、隐藏序等)相继产生, 原因可能是不同序参量之间存在耦合, 且耦合形式不拘于biquadratic形式. 值得注意的是, 耦合的具体形式可能会影响到: 耦合序的相变类别(一阶非连续相变或二阶连续相变), 哪一个序参量/自由度是对称破缺的主要或次要诱因, 对称破缺的具体形式和类别. 在传统平衡态实验中, 推测不同序参量之间的耦合形式依赖于输运、谱学信号的对称性分析: 归纳不同序参量各自的不可约表示, 排除对称性所不允许的耦合形式; 然后参考不同序参量关于环境变量的依赖(其中展现出的指数、幂律依赖), 进而判断不同序参量之间的主次关系、耦合阶数[61,62]. 本文指出序参量的动力学研究, 是解析序参量耦合机制的另一种方法. 该方法的精髓如同高能物理实验中对撞不同类型粒子, 通过它们对撞散射的产物, 来解析它们相互作用的具体形式. 文献[28,53,54]报道的Higgs模式与电荷密度波涨落/赝能隙集体模式的动态相互作用研究, 初步展示了这一方法学的可行性. 未来, 我们期待在更多的材料体系中看到这套方法的运用, 补充、验证平衡态实验手段关于序参量耦合形式的推论.沿这一思路, 更加新颖的非线性太赫兹谱学技术有望为Higgs模式研究带来更多助力. 其中太赫兹二维光谱技术有望更加直观地揭示不同集体模式、自由度之间的相互作用(图14)[63]. 二维相干光谱技术在可见、红外波段已有广泛运用, 尤其是在半导体激子研究、生物/化学分子动力学研究领域. 在太赫兹波段以及凝聚态物理领域, 这项技术近年来正在迅速拓展. 利用该技术, Vaswani等 [64]研究了铁基超导体中不同超导能隙产生的Higgs杂化模式. 随后, Luo等 [65]又进一步详细区分了铁基超导体中不同的高阶非线性光学信号来源, 包括Higgs模式, bi-Higgs模式等. Katsumi, Armitage与合作者利用类似技术研究了NbN超导体中的
$ {{\mathrm{\chi }}}^{\left(3\right)}(\omega , \omega , -\omega , \omega ) $ 与$ {{\mathrm{\chi }}}^{\left(3\right)}(3\omega , \omega , \omega , \omega ) $ 响应(三阶线性响应与三次谐波响应), 发现前者相较于后者更能直接地体现Higgs模式的谱学响应[66]. Kim等 [67]采用光学泵浦-太赫兹三次谐波手段, 研究了铜基超导体在1.55 eV泵浦激发后不同延时下的Higgs模式动力学响应, 进一步讨论如何区分电子空穴对涨落(准粒子激发)与Higgs模式贡献的三次谐波响应. 二维光谱技术的核心在于其谱宽能有效覆盖多个激发态, 通过激发脉冲的相干性、使激发态之间产生相干性, 再通过第二、三束脉冲操控该相干态的演化、获得不同激发态的耦合、退相干物理信息, 揭示不同自由度之间的相互作用. 未来, 进一步 拓展单周期太赫兹脉冲的谱宽、使频谱能有效覆 盖更多自由度/序参量的激发, 是太赫兹二维光谱技术发展的关键. 目前, 实验室强场太赫兹脉冲一般采用LiNbO3晶体产生, 中心频率在1 THz以下. 对于高温超导体而言, 其库珀对束缚能2Δ在 20—40 meV (即 5—10 THz)区间, 而与超导相密切相关的自旋涨落、电荷序涨落、顶角氧声子等集体模式也大多分布在该能量区间, 因此将桌面太赫兹光源进一步拓展至更宽的频域是太赫兹二维光谱技术发展的重点. 目前可行的方案包括使用两束波长相近的近红外脉冲在有机非线性晶体中通过差频生成(different frequency generation, DFG)直接产生多周期太赫兹光电场(5—15 THz), 或利用 < 20 fs的800 nm脉冲在GaSe与GaP等晶体中产生超宽谱(1—10 THz)单周期太赫兹脉冲. 对于这类高频太赫兹脉冲的时域探测, 可以通过更薄的ZnTe晶体(< 100 μm)或GaSe晶体获得更宽频域的相位匹配. 这些较为成熟的太赫兹技术表明, 时域非线性太赫兹谱学仍然存在较大的技术发展空间来进一步支持Higgs模式研究的拓展.配合上述动力学方法论及谱学技术的拓展, 更多样化的超导样品、器件也将进一步丰富和开拓Higgs模式研究. 一方面, 通过剥离、分子外延生长技术制备层数精确可控的超薄样品, 有望推动Higgs模式研究与二维(超导)相变研究产生交集. 这项探索的意义在于: 根据Mermin-Wagner理论, 具有连续对称的二维体系在零以上温度无法产生长程对称破缺, 其根本原因在于连续对称破缺所产生的零能或低能集体激发, 其态密度/谱权重被低维度“放大”, 阻碍长程关联的保持. 因此, 低维度体系的集体模式动力学是影响/控制其相变的关键因素: Higgs模式研究有望为二维(超导)相变研究带来极为重要的动力学信息, 为Berezinskii-Kosterlitz-Thouless/BKT理论提供丰富的实验证据. 另外, 利用分子外延生长或脉冲激光沉积手段, 可以连续、精准地调控薄膜样品中的空穴/电子浓度, 实现超导序与电荷序、赝能隙、条纹序之间相互作用的精准调控. 在这些样品中, 系统性地进行Higgs模式谱学研究具有重要意义. 我们可以借鉴二十年前角分辨光电子能谱技术在高温超导体中捕捉到电子色散的扭折(kink)现象并深入挖掘其背后的电声子耦合, 来类比这项工作的科学价值. 由于这项系统性工程需结合样品生长、谱学测量、谱学技术发展、理论验证, 因此迫切需要超导、超快谱学领域不同实验、理论团队的广泛合作.
除此之外, 微观尺度及纳米器件中的Higgs模式研究也是目前另一个巨大空白. 2024年, Du等[68]首次报道了微米尺度、双层NbSe2薄膜中Higgs模式随温度以及磁场的演变, 探究了Higgs模式谱学特征与输运测量中观察到的异常金属(anomalous metal)相的联系. 这项研究首次展示了在超导研究中, Higgs谱学技术与输运技术如何相互补充、丰富我们对于新奇物相的全面认知. 未来, 我们设想类似的研究可以进一步拓展至转角石墨烯中的非常规超导相、过渡金属二硫属化物(transition metal dichalcogenide)在磁场环境中产生的非零动量超导(Fulde-Ferrell-Larkin-Ovchinnikov, FFLO)态、 超导约瑟夫森结. 这些体系的研究目前主要依赖电输运技术, 表征的是材料的基态; 若能进一步获得激发态谱学信息、尤其是Higgs模式谱学信息, 将为上述新奇超导态(异常金属态、FFLO态、魔角超导态)提供更加完整的物理图像.
最后值得一提的是, Higgs模式研究也有望为非平衡态超导研究、光致超导研究提供全新的观测视角. 近期, 利用Higgs模式的非线性太赫兹响应作为宏观超导态的判据, Isoyama等[69,70]研究了铁基、铜基超导体分别在1.55 eV与中红外脉冲泵浦下展现的类似光致超导增强现象. Collado等[71]对于周期驱动下的超导体的动力学进行研究, 发现其中会实现准粒子布局数反转, 诞生Rabi-Higgs杂化模式; 当引入耗散后, 根据驱动强度、频率、体系耗散之间的关系, 超导体会呈现包括混沌、时间晶体等不同的动态相[72,73]. Fan等[74]对周期驱动下超导体内时间晶体相的空间分布也进行了探索. 如果这些理论预言在未来的强场/非微扰太赫兹实验中得以验证, 我们将获得更丰富的手段调控、操控超导态, 实现微至电子器件层面、广至电气输送层面的超导技术. 可以预见, Higgs模式谱学研究所启发的非平衡态超导研究, 无论是微扰区间还是非微扰区间, 都将为凝聚态物理研究定义全新的实验和理论框架. 不仅帮助我们更好地理解平衡态超导机理, 也将帮助我们认识和创造平衡态以外的新物性、新物相, 让我们拭目以待这一切!
超导体的Higgs物理
Higgs physics in superconductors
-
摘要: Nambu-Goldstone理论指出: 连续对称的破缺会产生零能的玻色激发. 在超导相变中, 连续的局域U(1) 规范对称发生破缺, 理应产生零能的集体模式(即超导相位模式). 1962年, Philip Anderson指出: 库珀对(Cooper pairs)之间的库仑相互作用使该零能模跃迁至等离子体频率. 因此超流体在库珀对配对能量(2Δ)以内不存在玻色激发, 这套机制还导致介导电磁相互作用的光子获得质量. Anderson机制为超导体保持零损耗电流、展现完全抗磁效应提供了微观解释. 1964年, 为解释介导电弱相互作用的W±, Z玻色子为何具有质量, Peter Higgs, François Englert, Tom Kibble等分别提出自然界中存在(现称作)Higgs场的假设: 该物质场与零质量的W±, Z玻色子耦合, 使它们产生质量. 这套机制与超导体中光子产生质量的机制相似, 被统称为Anderson-Higgs机制. 2013年, 欧洲大型强子对撞机捕捉到Higgs场的标量激发(即Higgs boson)的实验证据, 证实了半个世纪以来关于Higgs场的猜想. 与Higgs boson对应的超导振幅模式因此被称作超导Higgs模式. 近半个世纪以来, 在众多超导材料的谱学研究中, 该模式同样难寻踪迹. 近年来, 超快/非线性谱学技术的发展与运用使谱学实验可以更加有效地捕获Higgs模式的踪迹. 本文将介绍超导Higgs模式的历史背景与最新研究进展, 讨论Higgs模式可能为高温超导研究带来的崭新视角、机遇与挑战.Abstract: As pointed out by Nambu-Goldstone theorem, the breaking of continuous symmetry gives rise to massless or gapless bosonic excitations. In superconductors, continuous local U(1) gauge symmetry is broken. The gapless excitation thus created is the collective phase mode of the superconducting order parameter. In 1962, Philip Anderson pointed out that the Coulomb interaction between Cooper pairs lifts this gapless mode to the superconducting plasma frequency. Therefore, in a superconducting fluid there are no bosonic excitations below the binding energy of the Cooper pairs (2Δ). Anderson’s mechanism also implies that the massless photon, which mediates electromagnetic interaction, becomes massive in a superconductor. This mechanism provides a microscopic theory for the dissipationless charge transport (in conjunction with Landau’s criterion for superfluidity) as well as the Meissner effect inside a superconductor. Jumping into particle physics, in 1964 in order to explain why the gauge bosons for electroweak interaction, namely the W±, Z bosons, are massive, Peter Higgs, François Englert, Tom Kibble and colleagues proposed the existence of a field (presently referred to as the Higgs field) in nature. This matter field couples to the massless W±, Z bosons and generates mass via the Higgs mechanism. Due to their conceptual similarities, these two mechanisms are collectively referred to as the Anderson-Higgs mechanism nowadays. In 2013, the scalar excitation of the Higgs field, namely the Higgs boson, was detected at the Large Hadron Collider, providing the final proof for the Higgs hypothesis nearly 50 years after its proposal. The amplitude mode of the superconducting order parameter, which corresponds to the Higgs boson through the above analogy, is referred to as the Higgs mode of a superconductor. Its spectroscopic detection has also remained elusive for nearly half a century. In recent years, the development of ultrafast and nonlinear spectroscopic techniques enabled an effective approach for investigating the Higgs mode of superconductors. In this paper, we will introduce the historical background of the Higgs mode and review the recent developments in its spectroscopy study. We will also discuss the novel perspectives and insights that may be learnt from these studies for future high-temperature superconductivity research.
-

-
图 1 朗道超流判据 (a) 无相互作用粒子的能量-动量色散关系, 当粒子以速度
$ \boldsymbol{v} $ (红色实线斜率)关于环境(如容器壁、晶格)匀速运动时, 粒子的能谱(黑色实线)发生多普勒位移(蓝色实线), 与$ \boldsymbol{v} $ 同方向的激发态发生红移, 与$ \boldsymbol{v} $ 反方向的激发态发生蓝移; 当某个态的能量红移至0时(严格来说0 + kBT 范围内), 环境与粒子之间的热涨落会使粒子自发产生该状态激发, 粒子因此不再处于基态, 玻色凝聚以及超流因此遭到破坏; (b) 氦原子间的范德瓦耳斯作用力使液氦展现出集体振荡模式, 在长波极限(Q → 0)下, 其色散呈线性关系, 保证超流液氦以该斜率以下的速度匀速运动时不会自发产生声子激发, 超流液氦的临界速度$ {\boldsymbol{v}}_{{\mathrm{c}}} $ 实际对应的是系统自发产生更高波矢量的roton激发的相速度[5]Figure 1. Landau criteria for superfluidity: (a) Energy-momentum dispersion relation of a non-interacting particle. When a particle travels at a velocity
$ \boldsymbol{v} $ (corresponding to the gradient of the red solid line) with respect to its environment (e.g. container, lattice), its excitation spectrum (black solid line) is Doppler-shifted (i.e. to the blue solid line): excitations with wavevectors parallel to$ \boldsymbol{v} $ are red-shifted while excitations with wavevectors anti-parallel to$ \boldsymbol{v} $ are blue-shifted. When a state is red-shifted to 0 energy (strictly speaking kBT from 0), thermal fluctuations between the environment and the particle in consideration may cause the particle to be spontaneously excited to that state. The particle no longer remains in its ground state, therefore the Bose-Einstein condensation and the superfluidity will be destroyed along the way. (b) The van der Waals interaction between helium atoms causes liquid helium to exhibit collective excitations. In the long-wavelength limit (Q → 0), these collective modes exhibit a linear dispersion. As long as superfluid helium flows at a speed smaller than the gradient of such acoustic mode, phonons will not be spontaneously excited. The critical velocity of superfluid helium corresponds to the phase velocity of the roton excitations[5].图 2 超导体的集体模式 (a) 超导转变温度(Tc)以下, 超导序的自由能
$ F $ 关于序参量$ \psi =\left|\psi \right|{{\mathrm{e}}}^{{\mathrm{i}}\phi } $ 展现墨西哥帽状的势能面; 在平衡态下, 序参量自发破缺周向的连续U(1) 对称; 序参量沿周向的运动对应超导相位$ \phi $ 的涨落, 沿径向的运动对应超导振幅$ \left|\psi \right| $ 的涨落, 这两个模式的能量分别为零和大于零, 因此可以看作无质量和有质量的准粒子激发; (b) 超导相位模式和振幅模式的色散关系[6], 其中零质量的相位模式(蓝色虚线)通过Anderson机制获得质量, 其能量提升至超导等离子体频率($ {\omega }_{{\mathrm{p}}} $ ); 有质量的振幅模式 (红色实线)在长波极限下展现出2Δ的能隙Figure 2. Collective modes of a superconductor: (a) Below the superconducting transition temperature (Tc), the free energy of a superconductor exhibits a Mexican hat-like potential surface with respect to the superconducting order parameter
$ \psi=\left|\psi\right|\mathrm{e}^{\mathrm{i}\phi} $ . In thermal equilibrium, the continuous U(1) symmetry in the order parameter phase$ \phi $ is spontaneously broken. The collective motion of the order parameter along the circumferential direction corresponds to fluctuations in the order parameter phase; the collective motion along the radial direction corresponds to fluctuations in the order parameter amplitude$ \left|\psi \right| $ . The energy of these two modes are zero and non-zero respectively. They can be described as massless and massive quasiparticles. (b) Dispersions of the phase mode and the amplitude mode of the superconducting order parameter[6]. Here, the massless phase mode (blue dotted line) becomes massive due to the Anderson mechanism. Its frequency is lifted to the superconducting plasma frequency ($ {\omega }_{{\mathrm{p}}} $ ). The massive amplitude mode (red solid line) is gapped with an energy of 2Δ图 3 2H-NbSe2的拉曼散射实验 (a) 在Sooryakumar和Klein的实验中[17], 通过施加外界磁场抑制超导态, 超导集体模式(~20 cm–1)与电荷密度波集体模式(~40 cm–1)的拉曼散射谱权重发生交换; (b) Méasson等[55]通过改变温度, 同样观测到超导集体模式与电荷密度波集体模式的拉曼散射谱权重发生交换, 在6 K附近, 两者的谱权重大致相等
Figure 3. Raman scattering experiments on 2H-NbSe2: (a) In the experiment by Sooryakumar and Klein[17], the superconductor collective mode (~20 cm–1) and the charge-density-wave collective mode (~40 cm–1) exchange spectral weight under the application of an external magnetic field that suppresses superconductivity. (b) By varying temperature, Méasson et al. [55] also observe an spectral weight transfer between the superconductor collective mode and the charge-density-wave collective mode. Around 6 K, the two modes have approximately equal spectral weight.
图 4 Higgs模式的时域自由振荡[21] (a) Matsunaga等[21]采用单周期太赫兹泵浦 - 单周期太赫兹探测手段测量了Nb1–xTixN超导薄膜的超快透射率; (b) 在单周期太赫兹脉冲对超导基态进行扰动后, 样品的太赫兹透射率呈现频率f~2Δ的自由振荡, 通过增大泵浦光的能量密度, 振荡频率 f 逐步降低、并伴随自由振荡的阻尼系数b逐步增强
Figure 4. Time-domain free oscillations of the Higgs mode[21]: (a) Using single-cycle terahertz pump – single-cycle terahertz probe technique, Matsunaga et al. [21] studied the ultrafast terahertz transmission of Nb1–xTixN superconducting thin films. (b) After the superconducting ground state is perturbed by the single-cycle pump pulse, the terahertz transmissivity of the sample is probed and is found to exhibit a free oscillation with a frequency f ~2Δ, with increasing pump pulse energy density, the oscillation frequency f decreases, accompanied also by an increase in the damping constant b.
图 5 多周期太赫兹光电场驱动的Higgs振荡[22] (a) Matsunaga等[22]利用太赫兹带通滤片过滤单周期太赫兹脉冲, 产生窄带多周期太赫兹光电场, 作为泵浦驱动NbN超导薄膜; 另一束单周期太赫兹脉冲作为探针测量样品的透射率; (b) 多周期太赫兹泵浦的波形及其模平方波形; (c) 在多周期太赫兹泵浦驱动下, 样品在Tc以上及以下的太赫兹透射率演化: 在Tc以上, 太赫兹泵浦仅诱导系统热化、带来透射率的单调变化; 而在Tc以下, 太赫兹泵浦诱导超流体展现出二倍驱动频的相干振荡, 起源于Higgs模式的受驱振荡
Figure 5. Higgs oscillations driven by multi-cycle terahertz pulses[22]: (a) Matsunaga et al. [22] pump the NbN superconducting films using multi-cycle terahertz pulses filtered from the single-cycle terahertz pulses (i.e. by using bandpass filters), and probe the transmissivity of the sample using another single-cycle terahertz pulse. (b) The waveform of the multi-cycle terahertz pulse and its modulus square. (c) Under the drive of the multi-cycle terahertz pulses, the terahertz transmissivity of the sample exhibits characteristic time-evolutions above and below Tc. Above Tc, the terahertz pump induces only thermal heating of the sample, manifested as a monotonic time-evolution of the terahertz transmissivity; below Tc, the terahertz pump induces a coherent oscillation of the superfluid at twice the driving frequency, originating from the driven Higgs oscillation.
图 6 NbN超导体的太赫兹三次谐波响应[22] (a) Matsunaga等[22]使用多周期太赫兹驱动光入射在NbN超导薄膜上, 从样品透射的太赫兹光谱中可以观测到明显的三次谐波响应; (b) 超导序参量2Δ的温度依赖以及两倍驱动频率 (ω = 0.3, 0.5, 0.7 THz) 的对比; (c) 不同频率的太赫兹场驱动下三次谐波强度的温度依赖, 可以看出当满足2Δ(T) = 2ω条件时, Higgs模式的受驱振荡与驱动场发生共振, 导致三次谐波信号的发散
Figure 6. Terahertz third harmonic generation (THG) response of NbN superconductors[22]: (a) Using multi-cycle terahertz pulses to drive the NbN superconducting thin film, Matsunaga et al. [22] observe a clear terahertz THG response from the sample below Tc. (b) The temperature-dependent superconducting order parameter 2Δ compared to twice the terahertz driving frequency (ω = 0.3, 0.5, 0.7 THz). (c) The temperature dependence of the THG intensity under different terahertz driving frequencies. At temperatures that satisfy 2Δ(T) = 2ω, the driven Higgs oscillation becomes resonant with the driving field, leading to a divergence of the THG signal.
图 7 多周期太赫兹电场驱动Anderson pseudospin的进动过程[22] (a), (c) BCS超导态下, 费米面附近的
$ ({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow})$ 电子对与$({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow})$ 空穴对相干叠加形成库珀对, 用pseudospin = 1/2 (–1/2)来定义该电子对的占据态(空态), 则BCS超导态可以表示为这两个pseudospin态的相干叠加. 投影到这两个pseudospin态定义的Bloch 球上, BCS基态对应Anderson pseudospin指向xy平面内; (b)对于半填充的金属而言, 费米面附近的$ ({\boldsymbol{k}}_{\uparrow}, -\boldsymbol{k}_{\downarrow}) $ 电子对与$({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow }) $ 空穴对无相干配对, 费米面由pseudospin = 1/2 态直接过渡到pseudospin = –1/2 态; (d) 在周期太赫兹场驱动下, Anderson pseudospin发生进动行为, 意味超导序参量发生涨落Figure 7. Precession of the Anderson pseudospin under a multi-cycle terahertz drive[22]: (a), (c) In the BCS state, pairs of electrons at
$ ({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow }) $ and pairs of holes at$ ({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow})$ are coherently superposed to form Cooper pairs. The occupancy of the pair of states at$ ({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow }) $ can be used to define a pseudospin = 1/2 state (occupied state) and a pseudospin = –1/2 state (empty state). Thus, the BCS state can be expressed as a superposition of the two pseudospin states. When projected to the Bloch sphere defined by the two states, the BCS state corresponds to Anderson pseudopsin pointing in the xy-plane. (b) In the normal metallic state, there is no coherence between the electrons at$({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow}) $ and the holes at$ ({\boldsymbol{k}}_{\uparrow }, -\boldsymbol{k}_{\downarrow }) $ . Therefore, the Fermi surface represents a disrupt transition from the pseudospin = 1/2 state to the pseudospin = –1/2 state. (d) Under the periodic drive of a terahertz pulse, the Anderson pseudospin undergoes a precession, signifying collective fluctuations in the superconducting order parameter.图 8 拉曼散射的微观机制 (a) 非共振光子-电子散射(也称作双光子散射、带内散射、diamagnetic scattering)诱导电子-空穴对密度涨落, 散射前后光子、电子的能量、动量均发生变化; (b) 共振光子-电子散射(也称作带间散射、paramagnetic scattering)过程中光子被电子完全吸收、产生电流、再辐射出; (c) 非共振弹性(Rayleigh)散射过程; (d) 共振弹性(Rayleigh)散射过程; (e) 太赫兹三次谐波生成过程; (f) 非共振拉曼/太赫兹三次谐波散射过程; (g) 两种玻色子共同参与的非共振拉曼/太赫兹三次谐波散射过程; 这里波浪线为光子传播子, 实线为电子传播子, 红色双虚线和黑色双波浪线为玻色子传播子
Figure 8. Microscopic mechanisms for Raman scattering in solids. (a) Non-resonant photon-electron scattering (also known as two-photon scattering, intraband scattering, diamagnetic scattering) induces electron-hole density fluctuations. During the scattering, the energy and momentum of the photon and the electron both change. (b) In the resonant photon-electron scattering process (also known as interband scattering, paramagnetic scattering), a photon is absorbed by an electron and generates a current, which later re-radiates out a photon. (c) Microscopic process for non-resonant elastic (Rayleigh) scattering. (d) Microscopic process for resonant elastic (Rayleigh) scattering. (e) Microscopic process for terahertz third harmonic generation (THG). (f) Microscopic process for non-resonant Raman scattering/terahertz THG. (g) Microscopic process for non-resonant Raman scattering/terahertz THG involving two different bosons. Here wavy lines represent photon propagators, solid lines represent electron propagators, red double dotted lines and black double wavy lines represent boson propagators.
图 9 铜基高温超导体的太赫兹三次谐波响应[50] (a)—(c) 最佳掺杂La2–xSrxCuO4, DyBa2Cu3O7–x, YBa2Cu3O7–x中太赫兹三次谐波强度的温度依赖; (d)—(f) 这3个样品中太赫兹三次谐波相位的温度依赖, 黑色虚线表示Tc, 红色实线表示三次谐波相位发生 –π跳跃的温度(Tπ), 与(a)—(c)中振幅响应的局域最低点重合, 对应耦合双谐振子模型中的反共振(anti-resonance)或法诺共振(Fano resonance)现象, 插图为Tπ 温度以上及以下两组三次谐波时域信号的对比
Figure 9. Terahertz THG response of cuprate high-temperature superconductors[50]: (a)–(c) Temperature dependence of the terahertz THG intensity from optimally-doped La2–xSrxCuO4, DyBa2Cu3O7–x, YBa2Cu3O7–x thin films. (d)–(f) Temperature dependence of the terahertz THG phase from the three samples. Black dotted line denotes Tc. Red solid line marks the temperature (Tπ) at which the THG phase shows an abrupt jump of –π, which coincides with the local minimum in the THG amplitude response in (a)–(c). These features are well-described by the anti-resonance of a coupled oscillators model or the Fano resonance. Insets show the comparison of two representative time-domain THG responses below and above Tπ.
图 10 铜基高温超导体太赫兹三次谐波响应的磁场依赖[28] (a) 超导体Higgs模式与另一集体模式耦合示意图, 在Tπ温度以下(以上)两者的受驱振荡展现出相同(相反)相位, 该相位翻转符合离散模式与连续激发态之间的法诺共振特征; (b) 一般谱学实验观测到的法诺共振体现在激发态关于不同驱动频率/探测波长(ωdrive)的非对称振幅/相位响应; 在太赫兹三次谐波实验中, 集体模式的共振频(ωosc1)随温度发生变化, 而太赫兹驱动频率保持不变, 因此法诺共振体现在集体模的振幅/相位式关于ωosc1 (或超导体温度)的非对称响应; (c), (e) 最佳掺杂及过掺杂La2–xSrxCuO4样品在不同磁场环境下的太赫兹三次谐波强度的温度依赖; (d), (f) 相应的太赫兹三次谐波相位的磁场及温度依赖; 该实验中磁场平行于样品的c轴, 可以看出, 沿c轴方向的磁场抑制了三次谐波信号随温度展现出的法诺共振现象
Figure 10. Magnetic field dependence of the terahertz THG response of cuprate high-temperature superconductors[28]. (a) Illustration for the coupling of the Higgs mode to another collective mode. Below (above) Tπ the driven motions of the two oscillators are in-phase (out-of-phase), consistent with the phase evolution of the Fano resonance between an underdamped mode and a continuous background. (b) In typical spectroscopy manifestations, Fano resonance manifests as an asymmetric profile in the amplitude and phase response of an oscillator as a function of the driving frequency (ωdrive) or probing wavelength. In the terahertz THG experiment, the resonance frequency (ωosc1) of the collective mode is varied by varying temperature while the driving frequency is kept constant. In this case, the Fano resonance is manifested in the characteristic evolution of the amplitude and phase response of the collective mode as function of ωosc1 or temperature. (c), (e) Temperature-dependent THG intensity from an optimally-doped and overdoped La2–xSrxCuO4 thin film under different magnetic field strengths. (d), (f) Temperature-dependent THG phase of the two samples under different magnetic field strengths. The magnetic field is applied along the c-axis of the sample. It is clear that the c-axis magnetic field suppresses the Fano resonance manifested in the THG response as a function of temperature.
图 11 2H-NbSe2的太赫兹三次谐波响应[53] (a) 超导及电荷密度波温区内的太赫兹三次谐波时域响应, 黑色箭头标注两个不同来源的三次谐波响应之间的干涉; (b) 太赫兹三次谐波强度的温度依赖, 在6 K附近, 可以看到两个不同来源的三次谐波响应之间的相消干涉导致三次谐波整体强度呈现局域最低点
Figure 11. Terahertz THG response of 2H-NbSe2[53]: (a) Time-domain terahertz THG response of the sample throughout the superconducting and the charge-density-wave temperature range. Black arrow marks the interference between two distinct sources of THG. (b) Temperature dependence of the total terahertz THG intensity. Near 6 K, the destructive interference between the two sources of THG leads to a suppression of the total THG intensity. This in turn leads to a local minimum in the temperature dependence of the total THG intensity.
图 12 YBa2Cu3O7–x的太赫兹三次谐波响应[54] (a) 最佳掺杂样品(Tc = 87.4 K)在85 K的太赫兹透射小波分析, 实验采用的驱动频率为0.5 THz, 从时域响应可以看出三次谐波(1.5 THz)响应展现出一前一后两个波包; (b) 样品在该温度下的三次谐波波形, 更加清晰地展示两部分波包; (c) 傅里叶分析显示频率相近的两个不同三次谐波信号成分; (d) 太赫兹三次谐波信号启始温度(TTHG)在YBa2Cu3O7–x相图中的分布; T*为赝能隙启始温度, TKerr表示光学克尔实验报道的时间反演对称破缺温度, Tonset表示c轴红外光谱实验探测到的超导涨落启始温度
Figure 12. Terahertz THG response of YBa2Cu3O7–x[54]. (a) The moving-wavelet Fourier analysis of the terahertz transmission of an optimally-doped sample (Tc = 87.4 K) under 0.5 THz periodic drive at 85 K. The time-domain THG response exhibits two individual wavelets separated in time. (b) The time-domain THG waveform. (c) Fourier analysis of the time-domain waveform shows two distinct components at the THG frequency. (d) The onset temperature for the terahertz THG response (TTHG) in the YBa2Cu3O7–x phase diagram. T* denotes the onset temperature for the pseudogap. TKerr denotes the onset temperature for time-reversal symmetry breaking as reported by optical Kerr measurements. Tonset denotes the onset temperature for superconducting fluctuations as determined by c-axis infrared ellipsometry measurements.
图 13 交织序的研究策略: 平衡态与非平衡态 (a)对于交织序(如超导与电荷密度波), 过往研究往往依赖于平衡态物性表征: 譬如, 通过施加外界磁场、应力场抑制超导态, 再利用X射线衍射观察电荷密度波的关联长度、临界温度, 从而得出两个序参量之间相互独立、竞争或协作的结论; 除了提供相互作用以及其类型(吸引、排斥)的实验证据, 该手段无法提供更加具体、微观的耦合信息; 这类平衡态研究策略可以类比为拉动耦合双谐振子中的一个, 由于耦合弹簧的存在, 另一个谐振子也相应发生位移; 通过观察两个谐振子的静态位移, 可以获知两个谐振子之间存在耦合, 却无法得知耦合的具体形式、能量尺度等物理信息. (b) 当我们动态驱动这两个耦合谐振子中的一个时, 两个谐振子之间的能量、动量传递随弹簧系数的变化, 展现不同的动力学过程; 因此通过观察两个谐振子的运动, 可以获取耦合弹簧的具体参数信息; 同理对于交织序, 通过动态观测耦合序参量的动力学过程, 我们有望得出更加微观和具象的耦合机制、能量尺度等物理信息
Figure 13. Experimental approaches for investigating intertwined orders: equilibrium versus non-equilibrium. (a) For investigating the relationship between intertwined orders (e.g. superconductivity and charge-density-wave), past studies have focused on their equilibrium manifestations. For example, by applying an external magnetic field or a strain field to suppress superconductivity, one may study the resulting changes to the charge-density-wave correlation length or ordering temperature using X-ray diffraction. While such an approach provides evidence for the coupling between the two orders and the type of such interactions (i.e. competing or co-operative), it does not provide further microscopic information about the interaction mechanism. Such an equilibrium strategy can be compared to displacing a coupled harmonic oscillator. Due to the presence of the coupling spring, the other oscillator is also displaced. By observing the static displacements of the two oscillators, one may infer that they are coupled. However, no more details about the coupling spring can be learnt using this approach. (b) When we dynamically drive one of the coupled oscillators, the energy and momentum transfer between the two oscillators depends sensitively on the coupling spring constant. Therefore, by studying the dynamics of both oscillators, we may obtain precise knowledge about the coupling spring constant. In a similar spirit, by studying the dynamics of the individual orders that are intertwined, we may obtain microscopic information about the energy-scale and the mechanism
图 14 二维光谱技术, 对于存在多自由度的物理体系而言, 不同自由度(包括它们的激发态)之间是否存在耦合, 是理解这类体系物性、相变的关键信息; 传统线性谱学技术(如吸收谱、反射谱、拉曼散射等)对于表征不同自由度的激发态已较为成熟, 然而这类谱学技术对于表征、验证不同自由度之间的相互作用却难以提供有效数据; 在这方面, 二维光谱技术具有巨大潜力, 该技术采用多束宽谱脉冲, 对样品中不同自由度的动力学过程进行探测; 第1束脉冲同时产生多个激发态: (中图)如果这些激发态源自同一个基态(同一个自由度), 或者(右图)这些激发态源自不同自由度但是它们之间存在耦合, 则这些激发态之间会产生相干性; 在一定时间延时τ后, 第2束以及第3束脉冲照射在样品上, 诱导该相干态的演化(rephasing或non-rephasing); 最后, 该相干态通过辐射, 使各自由度回落到基态. 通过采集不同延时τ下的辐射光谱, 并将其对τ做傅里叶变化, 可以获得以上示意的二维光谱信息, 二维光谱对角线上的峰对应各激发态的能量, 非对角线上的峰表示两个激发态之间的相干性(具体可以解读为源自同一基态或者存在能量弛豫通道等), 相较于线性谱学技术, 二维光谱可以提供更加直观、具体的耦合信息[63]
Figure 14. 2D spectroscopy, for systems exhibiting many different degrees of freedom (DOFs), the coupling between these DOFs (including their excitations) is often the key to understanding the physical properties or phase transitions of these systems. While conventional linear spectroscopy techniques (e.g. absorption, reflection, Raman scattering) are good at capturing the excitations of different types of DOFs, evidencing or characterizing the interactions between different DOFs proves to be difficult with current techniques. In this regard, 2D spectroscopy has demonstrated significant potential. 2D spectroscopy uses several broadband pulses to study the dynamics of multiple DOFs. The first pulse induces multiple excitations: (middle panel) if the excitations derive from the same ground state (i.e. the same DOF), or (right panel) if they derive from different DOFs but there is a coupling in-between, then a coherence between these excitations will be established. After a variable time-delay τ, the second and the third pulse interact with the sample, inducing an evolution of the coherent state (e.g. rephasing or non-rephasing). Finally, the coherent state radiates and the system falls back to the ground state. By sampling the radiation spectrum at each τ, and Fourier transforming these results with respect to τ, one obtains a 2D spectrum as illustrated above. The peaks lying on the diagonal of the 2D spectrum represents individual excitations. The peaks lying on the off-diagonal represents coherence between two excitations (they encode information such as a common ground-state for the two excitations or a relaxation channel between the two excitations). Compared to traditional linear spectroscopy techniques, 2D spectroscopy provides more direct and detailed information about the interaction between different DOFs[63].
-
[1] Bardeen J, Cooper L N, Schrieffer J R 1957 Phys. Rev. 106 162 doi: 10.1103/PhysRev.106.162 [2] Bardeen J, Cooper L N, Schrieffer J R 1957 Phys. Rev. 108 1175 doi: 10.1103/PhysRev.108.1175 [3] McMillan W L 1968 Phys. Rev. 167 331 doi: 10.1103/PhysRev.167.331 [4] Landau L 1941 Phys. Rev. 60 356 doi: 10.1103/PhysRev.60.356 [5] Yarnell J L, Arnold G P, Bendt P J, Kerr E C 1958 Phys. Rev. Lett. 1 9 doi: 10.1103/PhysRevLett.1.9 [6] Shimano R, Tsuji N 2020 Annu. Rev. Condens. Matter Phys. 11 103 doi: 10.1146/annurev-conmatphys-031119-050813 [7] Anderson P W 1963 Phys. Rev. 130 439 doi: 10.1103/PhysRev.130.439 [8] Basov D N, Woods S I, Katz A S, Singley E J, Dynes R C, Xu M, Hinks D G, Homes C C, Strongin M 1999 Science 283 49 doi: 10.1126/science.283.5398.49 [9] Higgs P W 1964 Phys. Rev. Lett. 13 508 doi: 10.1103/PhysRevLett.13.508 [10] Englert F, Brout R 1964 Phys. Rev. Lett. 13 321 doi: 10.1103/PhysRevLett.13.321 [11] Guralnik G S, Hagen C R, Kibble T W B 1964 Phys. Rev. Lett. 13 585 doi: 10.1103/PhysRevLett.13.585 [12] Volkov A F, Kogan S M 1973 J. Exp. Theor. Phys. 65 2038 [13] Peronaci F, Schiró M, Capone M 2015 Phys. Rev. Lett. 115 257001 doi: 10.1103/PhysRevLett.115.257001 [14] Pekker D, Varma C M 2015 Annu. Rev. Condens. Matter Phys. 6 269 doi: 10.1146/annurev-conmatphys-031214-014350 [15] Podolsky D, Auerbach A, Arovas D P 2011 Phys. Rev. B 84 174522 doi: 10.1103/PhysRevB.84.174522 [16] Cea T, Castellani C, Seibold G, Benfatto L 2015 Phys. Rev. Lett. 115 157002 doi: 10.1103/PhysRevLett.115.157002 [17] Sooryakumar R, Klein M V 1980 Phys. Rev. Lett. 45 660 doi: 10.1103/PhysRevLett.45.660 [18] Sooryakumar R, Klein M V 1981 Phys. Rev. B 23 3213 doi: 10.1103/PhysRevB.23.3213 [19] Littlewood P B, Varma C M 1981 Phys. Rev. Lett. 47 811 doi: 10.1103/PhysRevLett.47.811 [20] Littlewood P B, Varma C M 1982 Phys. Rev. B 26 4883 doi: 10.1103/PhysRevB.26.4883 [21] Matsunaga R, Hamada Y I, Makise K, Uzawa Y, Terai H, Wang Z, Shimano R 2013 Phys. Rev. Lett. 111 057002 doi: 10.1103/PhysRevLett.111.057002 [22] Matsunaga R, Tsuji N, Fujita H, Sugioka A, Makise K, Uzawa Y, Terai H, Wang Z, Aoki H, Shimano R 2014 Science 345 1145 doi: 10.1126/science.1254697 [23] Anderson P W 1958 Phys. Rev. 112 1900 doi: 10.1103/PhysRev.112.1900 [24] Tsuji N, Aoki H 2015 Phys. Rev. B 92 064508 doi: 10.1103/PhysRevB.92.064508 [25] Mansart B, Lorenzana J, Mann A, Odeh A, Scarongella M, Chergui M, Carbone F 2013 Proc. Natl. Acad. Sci. U. S. A. 110 4539 doi: 10.1073/pnas.1218742110 [26] Devereaux T P, Hackl R 2007 Rev. Mod. Phys. 79 175 doi: 10.1103/RevModPhys.79.175 [27] Katsumi K, Tsuji N, Hamada Y I, Matsunaga R, Schneeloch J, Zhong R D, Gu G D, Aoki H, Gallais Y, Shimano R 2018 Phys. Rev. Lett. 120 117001 doi: 10.1103/PhysRevLett.120.117001 [28] Chu H, Kovalev S, Wang Z X, Schwarz L, Dong T, Feng L, Haenel R, Kim M-J, Shabestari P, Hoang L P, Honasoge K, Dawson R D, Putzky D, Kim G, Puviani M, Chen M, Awari N, Ponomaryov A N, Ilyakov I, Bluschke M, Boschini F, Zonno M, Zhdanovich S, Na M, Christiani G, Logvenov G, Jones D J, Damascelli A, Minola M, Keimer B, Manske D, Wang N, Deinert J C, Kaiser S 2023 Nat. Commun. 14 1343 doi: 10.1038/s41467-023-36787-4 [29] Cea T, Castellani C, Benfatto L 2016 Phys. Rev. B 93 180507 doi: 10.1103/PhysRevB.93.180507 [30] Matsunaga R, Tsuji N, Makise K, Terai H, Aoki H, Shimano R 2017 Phys. Rev. B 96 020505 doi: 10.1103/PhysRevB.96.020505 [31] Tsuji N, Murakami Y, Aoki H 2016 Phys. Rev. B 94 224519 doi: 10.1103/PhysRevB.94.224519 [32] Cea T, Barone P, Castellani C, Benfatto L 2018 Phys. Rev. B 97 094516 doi: 10.1103/PhysRevB.97.094516 [33] Seibold G, Udina M, Castellani C, Benfatto L 2021 Phys. Rev. B 103 014512 doi: 10.1103/PhysRevB.103.014512 [34] Tsuji N, Nomura Y 2020 Phys. Rev. Res. 2 043029 doi: 10.1103/PhysRevResearch.2.043029 [35] Gabriele F, Udina M, Benfatto L 2021 Nat. Commun. 12 752 doi: 10.1038/s41467-021-21041-6 [36] Lorenzana J, Seibold G 2024 Phys. Rev. Lett. 132 026501 doi: 10.1103/PhysRevLett.132.026501 [37] Kemper A F, Sentef M A, Moritz B, Freericks J K, Devereaux T P 2015 Phys. Rev. B 92 224517 doi: 10.1103/PhysRevB.92.224517 [38] Krull H, Bittner N, Uhrig G S, Manske D, Schnyder A P 2016 Nat. Commun. 7 11921 doi: 10.1038/ncomms11921 [39] Moor A, Volkov A F, Efetov K B 2017 Phys. Rev. Lett. 118 047001 doi: 10.1103/PhysRevLett.118.047001 [40] Nakamura S, Iida Y, Murotani Y, Matsunaga R, Terai H, Shimano R 2019 Phys. Rev. Lett. 122 257001 doi: 10.1103/PhysRevLett.122.257001 [41] Barlas Y, Varma C M 2013 Phys. Rev. B 87 054503 doi: 10.1103/PhysRevB.87.054503 [42] Schwarz L, Fauseweh B, Tsuji N, Cheng N, Bittner N, Krull H, Berciu M, Uhrig G S, Schnyder A P, Kaiser S, Manske D 2020 Nat. Commun. 11 287 doi: 10.1038/s41467-019-13763-5 [43] Yang F, Wu M W 2018 Phys. Rev. B 98 094507 doi: 10.1103/PhysRevB.98.094507 [44] Yang F, Wu M W 2019 Phys. Rev. B 100 104513 doi: 10.1103/PhysRevB.100.104513 [45] Murakami Y, Werner P, Tsuji N, Aoki H 2016 Phys. Rev. B 93 094509 doi: 10.1103/PhysRevB.93.094509 [46] Murakami Y, Werner P, Tsuji N, Aoki H 2016 Phys. Rev. B 94 115126 doi: 10.1103/PhysRevB.94.115126 [47] Sherman D, Pracht U S, Gorshunov B, Poran S, Jesudasan J, Chand M, Raychaudhuri P, Swanson M, Trivedi N, Auerbach A, Scheffler M, Frydman A, Dressel M 2015 Nat. Phys. 11 188 doi: 10.1038/nphys3227 [48] Kovalev S, Dong T, Shi L Y, Reinhoffer C, Xu T Q, Wang H Z, Wang Y, Gan Z-Z, Germanskiy S, Deinert J C, Ilyakov I, van Loosdrecht P H M, Wu D, Wang N L, Demsar J, Wang Z 2021 Phys. Rev. B 104 L140505 doi: 10.1103/PhysRevB.104.L140505 [49] Wang Z X, Xue J R, Shi H K, Jia X Q, Lin T, Shi L Y, Dong T, Wang F, Wang N L 2022 Phys. Rev. B 105 L100508 doi: 10.1103/PhysRevB.105.L100508 [50] Chu H, Kim M J, Katsumi K, Kovalev S, Dawson R D, Schwarz L, Yoshikawa N, Kim G, Putzky D, Li Z Z, Raffy H, Germanskiy S, Deinert J C, Awari N, Ilyakov I, Green B, Chen M, Bawatna M, Cristiani G, Logvenov G, Gallais Y, Boris A V, Keimer B, Schnyder A P, Manske D, Gensch M, Wang Z, Shimano R, Kaiser S 2020 Nat. Commun. 11 1793 doi: 10.1038/s41467-020-15613-1 [51] Schwarz L, Haenel R, Manske D 2021 Phys. Rev. B 104 174508 doi: 10.1103/PhysRevB.104.174508 [52] Cea T, Benfatto L 2014 Phys. Rev. B 90 224515 doi: 10.1103/PhysRevB.90.224515 [53] Feng L W, Cao J Y, Priessnitz T, Dai Y Y, de Oliveira T, Yuan J Y, Oka R, Kim M J, Chen M, Ponomaryov A N, Ilyakov I, Zhang H T, Lv Y B, Mazzotti V, Kim G, Christiani G, Logvenov G, Wu D, Huang Y, Deinert J C, Kovalev S, Kaiser S, Dong T, Wang N L, Chu H 2023 Phys. Rev. B 108 L100504 doi: 10.1103/PhysRevB.108.L100504 [54] Yuan J Y, Shi L Y, Yue L, Li B H, Wang Z X, Xu S X, Xu T X, Wang Y, Gan Z H, Chen F C, Lin Z F, Wang X, Jin K, Wang X B, Luo J L, Zhang S J, Wu Q, Liu Q M, Hu T C, Li R S, Zhou X Y, Wu D, Dong T, Wang N L 2024 Sci. Adv. 10 eadg9211 doi: 10.1126/sciadv.adg9211 [55] Méasson M A, Gallais Y, Cazayous M, Clair B, Rodière P, Cario L, Sacuto A 2014 Phys. Rev. B 89 060503 doi: 10.1103/PhysRevB.89.060503 [56] Grasset R, Cea T, Gallais Y, Cazayous M, Sacuto A, Cario L, Benfatto L, Méasson M-A 2018 Phys. Rev. B 97 094502 doi: 10.1103/PhysRevB.97.094502 [57] Grasset R, Gallais Y, Sacuto A, Cazayous M, Mañas-Valero S, Coronado E, Méasson M-A 2019 Phys. Rev. Lett. 122 127001 doi: 10.1103/PhysRevLett.122.127001 [58] Glier T E, Tian S, Rerrer M, Westphal L, Lüllau G, Feng L, Dolgner J, Haenel R, Zonno M, Eisaki H, Greven M, Damascelli A, Kaiser S, Manske D, Rübhausen M 2024 arXiv: 2310.08162 [59] Puviani M, Baum A, Ono S, Ando Y, Hackl R, Manske D 2021 Phys. Rev. Lett. 127 197001 doi: 10.1103/PhysRevLett.127.197001 [60] Mineev V P, Zhitomirsky M E 2005 Phys. Rev. B 72 014432 doi: 10.1103/PhysRevB.72.014432 [61] Harter J W, Zhao Z Y, Yan J Q, Mandrus D G, Hsieh D 2017 Science 356 295 doi: 10.1126/science.aad1188 [62] Chu J H, Kuo H H, Analytis J G, Fisher I R 2012 Science 337 710 doi: 10.1126/science.1221713 [63] Moody G, Cundiff S T 2017 Advances in Physics: X 2 641 doi: 10.1080/23746149.2017.1346482 [64] Vaswani C, Kang J H, Mootz M, Luo L, Yang X, Sundahl C, Cheng D, Huang C, Kim R H J, Liu Z, Collantes Y G, Hellstrom E E, Perakis I E, Eom C B, Wang J 2021 Nat. Commun. 12 258 doi: 10.1038/s41467-020-20350-6 [65] Luo L, Mootz M, Kang J H, Huang C, Eom K, Lee J W, Vaswani C, Collantes Y G, Hellstrom E E, Perakis I E, Eom C B, Wang J 2023 Nat. Phys. 19 201 doi: 10.1038/s41567-022-01827-1 [66] Katsumi K, Fiore J, Udina M, Romero R, Barbalas D, Jesudasan J, Raychaudhuri P, Seibold G, Benfatto L, Armitage N P 2024 Phys. Rev. Lett. 132 256903 doi: 10.1103/PhysRevLett.132.256903 [67] Kim M J, Kovalev S, Udina M, Haenel R, Kim G, Puviani M, Cristiani G, Ilyakov I, de Oliveira T V A G, Ponomaryov A, Deinert J C, Logvenov G, Keimer B, Manske D, Benfatto L, Kaiser S 2024 Sci. Adv. 10 eadi7598 doi: 10.1126/sciadv.adi7598 [68] Du Y, Liu G, Ruan W, Fang Z, Watanabe K, Taniguchi T, Liu R H, Li J X, Xi X 2025 Phys. Rev. Lett. 134 066002 doi: 10.1103/PhysRevLett.134.066002 [69] Isoyama K, Yoshikawa N, Katsumi K, Wong J, Shikama N, Sakishita Y, Nabeshima F, Maeda A, Shimano R 2021 Commun. Phys. 4 1 doi: 10.1038/s42005-020-00504-0 [70] Katsumi K, Nishida M, Kaiser S, Miyasaka S, Tajima S, Shimano R 2023 Phys. Rev. B 107 214506 doi: 10.1103/PhysRevB.107.214506 [71] Collado H P O, Lorenzana J, Usaj G, Balseiro C A 2018 Phys. Rev. B 98 214519 doi: 10.1103/PhysRevB.98.214519 [72] Collado H P O, Usaj G, Balseiro C A, Zanette D H, Lorenzana J 2021 Phys. Rev. Res. 3 L042023 doi: 10.1103/PhysRevResearch.3.L042023 [73] Collado H P O, Usaj G, Balseiro C A, Zanette D H, Lorenzana J 2023 Phys. Rev. Res. 5 023014 doi: 10.1103/PhysRevResearch.5.023014 [74] Fan B, Cai Z, García-García A M 2024 Phys. Rev. B 110 134307 doi: 10.1103/PhysRevB.110.134307 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: