高级搜索

钕-150同位素三步选择性光电离理论研究

,  , 

downloadPDF

上一篇

下一篇

王立德, 张钧尧, 卢肖勇. 钕-150同位素三步选择性光电离理论研究[J]. 物理学报, 2025, 74(11): 113201-1. doi: 10.7498/aps.74.20250262
引用本文: 王立德, 张钧尧, 卢肖勇. 钕-150同位素三步选择性光电离理论研究[J]. 物理学报, 2025, 74(11): 113201-1. doi: 10.7498/aps.74.20250262
shu
Lide WANG, Junyao ZHANG, Xiaoyong LU. Numerical studies of three-step selective photoionization of neodymium-150 isotope[J]. Acta Physica Sinica, 2025, 74(11): 113201-1. doi: 10.7498/aps.74.20250262
Citation: Lide WANG, Junyao ZHANG, Xiaoyong LU. Numerical studies of three-step selective photoionization of neodymium-150 isotope[J]. Acta Physica Sinica, 2025, 74(11): 113201-1. doi: 10.7498/aps.74.20250262
shu

钕-150同位素三步选择性光电离理论研究

  • 1.

    粒子输运与富集技术全国重点实验室, 天津　300180

  • 2.

    核工业理化工程研究院, 天津　300180

    • 通讯作者: E-mail: wld15@tsinghua.org.cn.; 

  • 中图分类号: 32.10.Fn, 32.80.-t

Numerical studies of three-step selective photoionization of neodymium-150 isotope

  • 1.

    National Key Laboratory of Particle Transport and Separation Technology, Tianjin 300180, China

  • 2.

    Research Institute of Physical and Chemical Engineering of Nuclear Industry, Tianjin 300180, China

    • Corresponding author: E-mail: wld15@tsinghua.org.cn.; 

  • MSC: 32.10.Fn, 32.80.-t

  • 摘要: 富集钕-150同位素在核工业、科学研究等领域具有重要应用. 基于高效高选择性多步电离路径, 原子蒸气激光同位素分离法能够实现钕同位素分离, 但现用路径第2步跃迁的同位素位移(isotope shift, IS)几乎为零, 导致产品中Nd-150丰度偏低. 本文基于密度矩阵理论建立了通用的三步电离路径选择性光电离模型, 模型中综合考虑了同位素位移、超精细结构等原子参数和频率、功率、线宽、偏振等激光参数, 可在磁子能级级别计算原子与激光的相互作用过程. 基于上述模型, 通过与文献数据对比获得了现用路径分支比的最优拟合值, 评估了现用路径在不同线宽下的Nd-150丰度水平; 在仅改变第2步跃迁的前提下构造假定电离路径, 开展所有钕同位素的电离率计算, 评估不同同位素位移、超精细结构下的Nd-150丰度, 指导后续原子光谱实验. 数值计算发现第二激发态角动量J3 = 6, 同位素位移IS23,148 ≥ 300 MHz时, 在b12 ≤ 0.5 GHz, b23 ≤ 1.0 GHz, 平行线偏振的典型激光参数下可实现与电磁法相当的Nd-150丰度(> 95%). 在此基础上压窄激光线宽, 能够在保持电离率的同时获得超过电磁法的Nd-150产品. 后续原子光谱实验应着重寻找IS23,148 ≥ 300 MHz, J3 = 6的第2步跃迁, 第2步跃迁的约化电偶极矩达到现用路径的30%即可满足丰度要求.
    Abstract: The enriched neodymium-150 (Nd-150) isotope has important applications in fields such as nuclear industry and basic scientific research. The Nd isotope separation can be conducted by atomic vapor laser isotope separation (AVLIS), where the target isotope is selectively ionized through the λ1 = 596 nm → λ2 = 579 nm → λ3 = 640 nm photoionization scheme, and non-target isotopes remain neutral due to the frequency-detuned excitation. Subsequently, an external electric field is applied to extract the ions from the laser-produced plasma. The Nd-150 abundance in the product cannot meet the requirement of the application, attributed to the nearly negligible isotope shift of the λ2 = 579 nm transition, thus resulting in the excess ionization of non-target isotopes. A new high-selectivity photoionization scheme is desirable to address this limitation, and its expected parameter values can be determined through numerical calculations prior to the time-consuming atomic spectroscopy experiments. In this study, a three-step selective photoionization model is established based on the density matrix theory, with the consideration of the hyperfine structures and magnetic sublevels. This model allows the flexible adjustments of atomic parameters (e.g. branching ratio, isotope shift, hyperfine constant) and laser parameters (e.g. frequency, power density, bandwidth, polarization), while the ionization probabilities of magnetic sublevel transitions can be quantitatively predicted. For the existing schemes, the branching ratios are determined by comparing literature data with numerical results, and the Nd-150 abundance values under different laser bandwidths are evaluated. Further, an alternative scheme is numerically explored on the assumption that the first transition remains unchanged and the second transition has a more significant isotope shift and a smaller branching ratio, and the Nd-150 abundance values under different combinations of isotope shifts, hyperfine structures, and laser bandwidths are evaluated, with all the natural Nd isotopes included. From the numerical results, a scheme with the angular momentum of the second excited state J3 = 6, the isotope shift between Nd-148 and Nd-150 IS23,148 ≥ 300 MHz, and a lower reduced dipole matrix element of the second transition reaching approximately 30% of that of λ2 = 579 nm, can produce the high-abundance Nd-150 (>95%, equivalent to that of the electromagnetic separation method) under the bandwidths: b12 ≤ 0.5 GHz and b23 ≤ 1.0 GHz, and parallel linear-polarized lasers. Using the lasers with narrower bandwidth can achieve higher abundance, which is superior to the electromagnetic separation method. The expected high-abundance Nd-150 can be attributed to the combined effects of multi-factors: the larger isotope shift between Nd-150 and Nd-148 than that between other adjacent isotope pairs, the insignificant hyperfine splitting of odd isotopes, and the match between narrow-bandwidth lasers and Nd I spectroscopic parameters. These parameter values can serve as benchmarks helpful for experimental parameter selection in the forthcoming high-precision spectroscopy experiments.
  • 加载中

  • 图 1  三步电离路径示意图　(a) In = 0; (b) In ≠ 0

    Figure 1.  The three-step photoionization scheme: (a) In = 0; (b) In ≠ 0.

    下载: 全尺寸图片 幻灯片

    图 2  第2步饱和功率曲线实验值[11]

    Figure 2.  The experimental saturated power density curve of the second transition[11].

    下载: 全尺寸图片 幻灯片

    图 3  b23 = 0.1 GHz时, 不同β12, β23下的第2步饱和功率曲线计算值　(a) β12 = 0.05; (b) β12 = 0.1; (c) β12 = 0.15; (d) β12 = 0.2

    Figure 3.  The numerical saturated power density curve of the second transition under b23 = 0.1 GHz and different combinations of β12, β23: (a) β12 = 0.05; (b) β12 = 0.1; (c) β12 = 0.15; (d) β12 = 0.2.

    下载: 全尺寸图片 幻灯片

    图 4  b23 = 1.5 GHz时, 不同β12, β23下的第2步饱和功率曲线计算值　(a) β12 = 0.05; (b) β12 = 0.1; (c) β12 = 0.15; (d) β12 = 0.2

    Figure 4.  The numerical saturated power density curve of the second transition under b23 = 1.5 GHz and different combinations of β12, β23: (a) β12 = 0.05; (b) β12 = 0.1; (c) β12 = 0.15; (d) β12 = 0.2.

    下载: 全尺寸图片 幻灯片

    图 5  第2步饱和功率曲线的归一化Nd-150电离率计算值与实验值对比　(a) b23 = 0.1 GHz; (b) b23 = 1.5 GHz; (c) b23 = 1.5 GHz, 纵轴[0.9, 1]的局部放大图

    Figure 5.  The numerical and experimental saturated power density curve of the second transition (shown as normalized ionization probability of Nd-150): (a) b23 = 0.1 GHz; (b) b23 = 1.5 GHz; (c) b23 = 1.5 GHz, the partial enlarged view of the vertical axis in the range of [0.9, 1].

    下载: 全尺寸图片 幻灯片

    图 6  偏振、J3对第1步饱和功率曲线的影响

    Figure 6.  The influences of laser polarization and the angular momentum of the second excited state J3 on the saturated power density curve of the first transition.

    下载: 全尺寸图片 幻灯片

    图 7  偏振、J3对第2步饱和功率曲线的影响

    Figure 7.  The influences of laser polarization and the angular momentum of the second excited state J3 on the saturated power density curve of the second transition.

    下载: 全尺寸图片 幻灯片

    图 8  偏振对超精细跃迁通道相对跃迁强度的影响　(a) J1 = 4 → J2 = 5; (b) J2 = 5 → J3 = 4; (c) J2 = 5 → J3 = 5; (d) J2 = 5 → J3 = 6　　　　

    Figure 8.  The influences of laser polarization on the relative strengths of the hyperfine transition paths: (a) J1 = 4 → J2 = 5; (b) J2 = 5 → J3 = 4; (c) J2 = 5 → J3 = 5; (d) J2 = 5 → J3 = 6.

    下载: 全尺寸图片 幻灯片

    图 9  第二激发态超精细常数A3,145对钕奇同位素第2步跃迁超精细结构的影响, 以B3,145 = 0 MHz, IS23,148 = 0 GHz为示例　(a) Nd-145, A3,145 = 0 MHz, –20 MHz, –40 MHz, –60 MHz; (b) Nd-145, A3,145 = –80 MHz, –100 MHz, –120 MHz, –140 MHz; (c) Nd-143, A3, 143 = 1.6A3,145, A3,145 = 0 MHz, –20 MHz, –40 MHz, –60 MHz; (d) Nd-143, A3,143 = 1.6A3,145, A3,145 = –80 MHz, –100 MHz, –120 MHz, –140 MHz

    Figure 9.  The influences of the second excited state’s hyperfine constant A3,145 on the hyperfine structure of the second transition of Nd odd isotopes, taking B3,145 = 0 MHz, IS23,148 = 0 GHz as an example: (a) Nd-145, A3,145 = 0 MHz, –20 MHz, –40 MHz, –60 MHz; (b) Nd-145, A3,145 = –80 MHz, –100 MHz, –120 MHz, –140 MHz; (c) Nd-143, A3,143 = 1.6A3,145, A3,145 = 0 MHz, –20 MHz, –40 MHz, –60 MHz; (d) Nd-143, A3, 143 = 1.6A3,145, A3,145 = –80 MHz, –100 MHz, –120 MHz, –140 MHz.

    下载: 全尺寸图片 幻灯片

    图 10  不同第2步跃迁同位素位移、第二激发态超精细结构下的钕同位素选择性光电离效果　(a) IS23,148 = –1500 MHz; (b) IS23,148 = –1000 MHz; (c) IS23,148 = –500 MHz; (d) IS23,148 = –300 MHz; (e) IS23,148 = 0.0 MHz; (f) IS23,148 = 300 MHz; (g) IS23,148 = 500 MHz; (h) IS23,148 = 1000 MHz; (i) IS23,148 = 1500 MHz

    Figure 10.  The selective photoionization effects of Nd isotopes under different combinations of the second transition’s isotope shifts and the second excited state’s hyperfine structures: (a) IS23,148 = –1500 MHz; (b) IS23,148 = –1000 MHz; (c) IS23,148 = –500 MHz; (d) IS23,148 = –300 MHz; (e) IS23,148 = 0.0 MHz; (f) IS23,148 = 300 MHz; (g) IS23,148 = 500 MHz; (h) IS23,148 = 1000 MHz; (i) IS23,148 = 1500 MHz.

    下载: 全尺寸图片 幻灯片

    图 11  钕奇同位素超精细跃迁通道　(a) 路径一λ1, Nd-145; (b) 假定λ2, Nd-145; (c) Nd-145第2步谱线和λ1+λ2双光子跃迁; (d) 路径一λ1, Nd-143; (e) 假定λ2, Nd-143; (f) Nd-143第2步谱线和λ1+λ2双光子跃迁

    Figure 11.  The hyperfine transition paths of Nd odd isotopes: (a) λ1 of Scheme No. 1, Nd-145; (b) the imagined λ2, Nd-145; (c) the second spectral line and λ1+λ2 two-photon transition of Nd-145; (d) λ1 of Scheme No. 1, Nd-143; (e) the imagined λ2, Nd-143; (f) the second spectral line and λ1+λ2 two-photon transition of Nd-143.

    下载: 全尺寸图片 幻灯片

    图 12  钕奇同位素第二激发态布居率随作用时间的变化图　(a) Nd-145; (b) Nd-145, 纵轴[0, 2×10–4]的局部放大图; (c) Nd-143; (d) Nd-143, 纵轴[0, 6×10–5]的局部放大图

    Figure 12.  The population of the second excited state of Nd odd isotopes versus time: (a) Nd-145; (b) Nd-145, the partial enlarged view of the vertical axis in the range of [0, 2×10–4]; (c) Nd-143; (d) Nd-143, the partial enlarged view of the vertical axis in the range of [0, 6×10–5].

    下载: 全尺寸图片 幻灯片

    表 1  钕天然同位素

    Table 1.  Natural Nd isotopes.

    钕同位素 Nd-150 Nd-148 Nd-146 Nd-145 Nd-144 Nd-143 Nd-142
    天然丰度c0/% 5.62 5.73 17.22 8.30 23.85 12.17 27.11
    核自旋In 0 0 0 7/2 0 7/2 0
    衰变 2νββ 或 0νββ→Sm-150 — — — α → Ce-140 — —
    下载: 导出CSV

    表 2  钕同位素三步电离路径

    Table 2.  The three-step photoionization scheme of Nd isotopes.

    电离路径λ1/nmλ2/nmλ3/nm
    路径一[10,11]596579640
    路径二[16]588597597
    路径三[17]628560597
    路径四[17]562627597
    下载: 导出CSV

    表 3  数值计算中的激光参数取值

    Table 3.  The laser parameters adopted in the numerical calculation.

    参数第1束激光第2束激光第3束激光
    时域线型高斯线型
    脉宽30 ns (FWHM)
    时序关系峰值时刻同步
    频域线型修正的洛伦兹线型—
    截止系数κ12 = κ23 = 0.2—
    频率与Nd-150共振, f12 = f23 = 0—
    偏振平行线偏振0:1:00:1:0—
    混合偏振1/3:1/3:1/31/3:1/3:1/3—
    正交线偏振0:1:01/2:0:1/2—
    下载: 导出CSV

    表 4  路径一的能级参数

    Table 4.  The energy parameters of scheme No. 1.

    能级E/cm–1JA145/MHzA143/A145B145/MHzB143/B145τ/ns
    路径一E10 [13]4[29]–121.628[29]1.60860[29]64.634[29]1.897[29]∞
    路径一E216757.037 [13]5[15]–129.594[15]1.6099[15]90.6[15]1.91[15]600*
    路径一E334011.04 [11]6[30]0*0*0*0*100*
    注: “*”表示假定值.
    下载: 导出CSV

    表 5  路径一的同位素位移

    Table 5.  The isotope shifts of scheme No. 1.

    跃迁IS148/MHzIS146/IS148IS145/IS148IS144/IS148IS143/IS148IS142/IS148
    路径一λ11126.9[15]1.78[15]2.20[15]2.51[15]2.93[15]3.28[15]
    路径一λ20*—————
    注: “*”表示假定值.
    下载: 导出CSV

    表 6  路径一选择性光电离效果

    Table 6.  The selective photoionization effects of scheme No. 1.

    线宽/GHz1.0, 1.00.5, 1.00.3, 1.01.0, 0.51.0, 0.30.5, 0.50.3, 0.3
    C150/%49.8654.8155.8054.6458.8668.3561.00
    ρion,1500.38390.40710.41580.38480.38490.41440.4073
    下载: 导出CSV

    表 7  钕同位素假定电离路径的能级参数

    Table 7.  The energy parameters of the imagined photoionization scheme of Nd isotope.

    能级 E/cm–1 J A145/MHz A143/A145 B145/MHz B143/B145 τ/ns
    路径一E1 0 [13] 4[29] –121.628[29] 1.60860[29] 64.634[29] 1.897[29] ∞
    路径一E2 16757.037 [13] 5[15] –129.594[15] 1.6099[15] 90.6[15] 1.91[15] 600*
    假定E3 34011.04* 可选 † 可调 ‡ 1.6* 0* 1.9* 100*
    注: “*”表示假定值, “†”表示在4, 5, 6范围内可选, “‡”表示在(–∞, 0] MHz范围内可调, 根据低能级超精细常数数值, 本文选取的范围为[–140, 0] MHz.
    下载: 导出CSV

    表 8  钕同位素假定电离路径的跃迁参数

    Table 8.  The transition parameters of the imagined photoionization scheme of Nd isotope.

    跃迁 IS148/MHz IS146/IS148 IS145/IS148 IS144/IS148 IS143/IS148 IS142/IS148 β $ \langle J_m | d_{mn}| J_n \rangle $/(×10–30 C·m)
    路径一λ1 1126.9[15] 1.78[15] 2.20[15] 2.51[15] 2.93[15] 3.28[15] 0.15† 4.5535
    假定λ2 可调 ‡ 1.66* 2* 2.32* 2.66* 3* 0.05* 6.7004
    注: “*”表示假定值, “†”表示由理论模型得到的拟合值, “‡”表示在(–∞, ∞) GHz范围内可调, 根据第1步跃迁同位素位移数值, 本文选取的范围为[–1.5, 1.5] GHz.
    下载: 导出CSV

    表 9  第二激发态超精细常数B3,145对钕奇同位素第2步跃迁谱线分裂程度的影响

    Table 9.  The influences of the second excited state’s hyperfine constant B3,145 on the hyperfine splitting degree of the second transition of Nd odd isotopes.

    同位素 超精细常数 Nd-145超精细常数取值A'/MHz
    0 –20 –40 –60 –80 –100 –120 –140
    谱线分裂程度max(ν23, A, B) – min(ν23, A, B)/GHz
    Nd-145 B = –0.3A, A = A' 5.006 4.456 3.906 3.356 2.806 2.268 2.160 2.520
    B = –0.5A, A = A' 5.006 4.452 3.898 3.345 2.791 2.254 2.143 2.500
    B = –0.7A, A = A' 5.006 4.450 3.893 3.337 2.781 2.245 2.131 2.487
    B = –1.0A, A = A' 5.006 4.447 3.888 3.330 2.771 2.236 2.120 2.473
    Nd-143 B = –0.3A, A = 1.6A' 8.064 7.184 6.304 5.424 4.544 3.676 3.456 4.032
    B = –0.5A, A = 1.6A' 8.064 7.178 6.292 5.406 4.520 3.654 3.429 4.000
    B = –0.7A, A=1.6A' 8.064 7.174 6.284 5.394 4.504 3.639 3.410 3.979
    B= –1.0A, A=1.6A' 8.064 7.170 6.276 5.382 4.488 3.625 3.392 3.957
    下载: 导出CSV

    表 10  第二激发态超精细常数B3,145对钕奇同位素第2步跃迁超精细跃迁通道共振位置的影响

    Table 10.  The influences of the second excited state’s hyperfine constant B3,145 on the resonance frequencies of hyperfine transition paths of Nd odd isotopes’ the second transition.

    同位素 超精细常数 Nd-145超精细常数取值A'/MHz
    0 –20 –40 –60 –80 –100 –120 –140
    共振位置最大差异值max(|ν23, A, B – ν23, A, 0|)/MHz
    Nd-145 B = –0.3A, A = A' 0 2.4 4.8 7.2 9.6 11.9 14.3 16.7
    B = –0.5A, A = A' 0 4.0 8.0 11.9 15.9 19.9 23.9 27.8
    B = –0.7A, A = A' 0 5.6 11.1 16.7 22.3 27.8 33.4 39.0
    B = –1.0A, A = A' 0 8.0 15.9 23.9 31.8 39.2 47.7 55.7
    Nd-143 B = –0.3A, A = 1.6A' 0 3.8 7.6 11.5 15.3 19.1 22.9 26.7
    B = –0.5A, A =1.6A' 0 6.4 12.7 19.1 25.5 31.8 38.2 44.6
    B = –0.7A, A=1.6A' 0 8.9 17.8 26.7 35.6 44.6 53.5 62.4
    B = –1.0A, A = 1.6A' 0 12.7 25.5 38.2 50.9 63.6 76.4 89.1
    下载: 导出CSV

    表 11  Nd-150丰度最低时的钕同位素选择性光电离效果

    Table 11.  The selective photoionization effects of Nd isotopes in the case of the lowest Nd-150 abundance.

    线宽/GHz 丰度/%
    Nd-150 Nd-148 Nd-146 Nd-145 Nd-144 Nd-143 Nd-142
    1.0, 1.0 47.45 24.25 2.66 6.69 0.54 18.26 0.14
    0.5, 1.0 52.04 20.13 1.76 5.41 0.39 20.17 0.11
    0.3, 1.0 53.16 19.23 1.64 5.20 0.37 20.30 0.10
    1.0, 0.5 51.22 20.98 1.80 5.42 0.40 20.08 0.11
    1.0, 0.3 52.23 20.14 1.69 5.21 0.38 20.24 0.10
    0.3, 0.3 64.99 6.85 0.71 3.01 0.22 24.14 0.08
    0.5, 0.5 60.70 11.03 0.93 3.60* 0.26 23.39† 0.08
    注: 表中工况如图10(b)中的青色标记所示, f12 = f23 = 0, IS23,148 = –1000 MHz, A3,145 = –100 MHz; “*”, “†”对应的奇同位素第二激发态布居率随时间的变化曲线分别与图12(a), (b)相对应.
    下载: 导出CSV

    表 12  钕偶同位素共振位置

    Table 12.  The resonance frequency of Nd even isotopes.

    共振位置 Nd-150 Nd-148 Nd-146 Nd-144 Nd-142
    ν12/MHz 0 1126.9 2009.2 2827.7 3700
    ν23/MHz 0 –1000 –1660 –2320 –3000
    ν12+ν23/MHz 0 126.9 349.2 507.7 700
    注: 表中工况如图10(b)中的青色标记所示, IS23,148 = –1000 MHz, A3,145 = –100 MHz.
    下载: 导出CSV
  • [1] Akhmedzhanov R A, Gushchin L A, Nizov N A, Nizov V A, Sobgayda D A, Zelensky I V 2024 JETP Lett. 119 834 doi: 10.1134/S0021364024601167
    [2] Liang P J, Liu X, Li P Y, Zhou Z Q, Li C F, Guo G C 2020 J. Opt. Soc. Am. B 37 1653 doi: 10.1364/JOSAB.388740
    [3] Broderick K, Lusk R, Hinderer J, Griswold J, Boll R, Garland M, Heilbronn L, Mirzadeh S 2019 Appl. Radiat. Isot. 144 54 doi: 10.1016/j.apradiso.2018.10.025
    [4] Hu F, Cutler C S, Hoffman T, Sieckman G, Volkert W A, Jurisson S S 2002 Nucl. Med. Biol. 29 423 doi: 10.1016/S0969-8051(02)00290-1
    [5] Committee A 2015 Standard Practice for Analysis of Spent Nuclear Fuel to Determine Selected Isotopes and Estimate Fuel Burnup
    [6] Suryanarayana M V 2022 Sci. Rep. 12 11471 doi: 10.1038/s41598-022-15597-6
    [7] Barabash A S, Belli P, Bernabei R, Boiko R S, Cappella F, Caracciolo V, Cerulli R, Danevich F A, Fang D L, Ferella F, Incicchitti A, Kobychev V V, Konovalov S I, Laubenstein M, Leoncini A, Merlo V, Nisi S, Niţescu O, Poda D V, Polischuk O G, Shcherbakov I B K, Šimkovic F, Timonina A, Tinkova V S, Tretyak V I, Umatov V I 2025 Eur. Phys. J. C 85 174 doi: 10.1140/epjc/s10052-025-13901-y
    [8] https://www.isotopes.gov/products/neodymium
    [9] Letokhov V, Ryabov E (Trigg G L ed) 2004 Encyclopedia of Applied Physics (New York: Wiley) pp1015–1028
    [10] Babichev A P, Grigoriev I S, Grigoriev A I, Dorovskii A P, D'Yachkov A B, Kovalevich S K, Kochetov V A, Kuznetsov V A, Labozin V P, Matrakhov A V, Mironov S M, Nikulin S A, Pesnya A V, Timofeev N I, Firsov V A, Tsvetkov G O, Shatalova G G 2005 Quantum Electron. 35 879 doi: 10.1070/QE2005v035n10ABEH006601
    [11] Grigoriev I, Diachkov A, Kovalevich S, Labosin V, Mironov S, Nikulin S, Pesnia A, Firsov V, Shatalova G, Tsvetkov G 2003 Proc. SPIE Int. Soc. Opt. Eng. 5121 406
    [12] D'Yachkov A B, Kovalevich S K, Labozin V P, Mironov S M, Panchenko V Y, Firsov V A, Tsvetkov G O, Shatalova G G 2012 Quantum Electron. 42 953 doi: 10.1070/QE2012v042n10ABEH014929
    [13] Kramida A, Ralchenko Y, Reader J, (NIST ASD Team) 2024 NIST Atomic Spectra Database (Gaithersburg, MD: National Institute of Standards and Technology
    [14] Miyabe M, Iwata Y, Tomita H, Morita M, Sakamoto T 2024 Spectrochim. Acta Part B At. Spectrosc. 221 107036 doi: 10.1016/j.sab.2024.107036
    [15] van Leeuwen K A H, Eliel E R, Post B H, Hogervorst W 1981 Z. Phys. A 301 95 doi: 10.1007/BF01419237
    [16] Zyuzikov A D, Mishin V I, Fedoseev V N 1988 Opt. Spectrosc. 64 287
    [17] D'Yachkov A B, Gorkunov A A, Labozin A V, Mironov S M, Panchenko V Y, Firsov V A, Tsvetkov G O 2018 Quantum Electron. 48 75 doi: 10.1070/QEL16493
    [18] 张钧尧, 熊静逸, 魏少强, 李云飞, 卢肖勇 2023 物理学报 72 193203 doi: 10.7498/aps.72.20230978 Zhang J Y, Xiong J Y, Wei S Q, Li Y F, Lu X Y 2023 Acta Phys. Sin. 72 193203 doi: 10.7498/aps.72.20230978
    [19] Campbell P, Moore I D, Pearson M R 2016 Prog. Part. Nucl. Phys. 86 127 doi: 10.1016/j.ppnp.2015.09.003
    [20] Yang X F, Wang S J, Wilkins S G, Ruiz R F G 2023 Prog. Part. Nucl. Phys. 129 104005 doi: 10.1016/j.ppnp.2022.104005
    [21] Lu X Y, Wang L D 2023 Chin. Phys. B 32 53204 doi: 10.1088/1674-1056/ac9b2f
    [22] Lu X Y, Wang L D 2024 Appl. Radiat. Isot. 210 111334 doi: 10.1016/j.apradiso.2024.111334
    [23] Demtröder W 2008 Laser Spectroscopy: Vol. 1 Basic Principles (Berlin: Springer) pp5–60
    [24] Greenland P T 1990 Contemp. Phys. 31 405 doi: 10.1080/00107519008213790
    [25] Axner O, Gustafsson J, Omenetto N, Winefordner J D 2004 Spectrochim. Acta Part B At. Spectrosc. 59 1 doi: 10.1016/j.sab.2003.10.002
    [26] Agarwal G S 1970 Phys. Rev. A 1 1445 doi: 10.1103/PhysRevA.1.1445
    [27] Lambropoulos P, Lyras A 1989 Phys. Rev. A 40 2199 doi: 10.1103/PhysRevA.40.2199
    [28] Blagoev K B, Komarovskii V A 1994 At. Data Nucl. Data Tables 56 1 doi: 10.1006/adnd.1994.1001
    [29] Childs W J, Goodman L S 1972 Phys. Rev. A 6 1772 doi: 10.1103/PhysRevA.6.1772
    [30] Shen X P, Wang W L, Zhai L H, Deng H, Xu J, Yuan X L, Wei G Y, Wang W, Fang S, Su Y Y, Li Z M 2018 Spectrochim. Acta Part B At. Spectrosc. 145 96 doi: 10.1016/j.sab.2018.04.012
    [31] Lu X Y, Wang L D 2025 J. Phys. B: At. Mol. Opt. Phys. 58 025001 doi: 10.1088/1361-6455/ad978d
    [32] Wakasugi M, Horiguchi T, Guo Jin W, Sakata H, Yoshizawa Y 1990 J. Phys. Soc. Jpn. 59 2700 doi: 10.1143/JPSJ.59.2700
  • 加载中
图( 12) 表( 12)
计量
  • 文章访问数:  31
  • HTML全文浏览数:  31
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-02
  • 刊出日期:  2025-06-05

钕-150同位素三步选择性光电离理论研究

    通讯作者: E-mail: wld15@tsinghua.org.cn.; 
  • 1. 粒子输运与富集技术全国重点实验室, 天津　300180
  • 2. 核工业理化工程研究院, 天津　300180
  • 收稿日期:  2025-03-02

摘要: 富集钕-150同位素在核工业、科学研究等领域具有重要应用. 基于高效高选择性多步电离路径, 原子蒸气激光同位素分离法能够实现钕同位素分离, 但现用路径第2步跃迁的同位素位移(isotope shift, IS)几乎为零, 导致产品中Nd-150丰度偏低. 本文基于密度矩阵理论建立了通用的三步电离路径选择性光电离模型, 模型中综合考虑了同位素位移、超精细结构等原子参数和频率、功率、线宽、偏振等激光参数, 可在磁子能级级别计算原子与激光的相互作用过程. 基于上述模型, 通过与文献数据对比获得了现用路径分支比的最优拟合值, 评估了现用路径在不同线宽下的Nd-150丰度水平; 在仅改变第2步跃迁的前提下构造假定电离路径, 开展所有钕同位素的电离率计算, 评估不同同位素位移、超精细结构下的Nd-150丰度, 指导后续原子光谱实验. 数值计算发现第二激发态角动量J3 = 6, 同位素位移IS23,148 ≥ 300 MHz时, 在b12 ≤ 0.5 GHz, b23 ≤ 1.0 GHz, 平行线偏振的典型激光参数下可实现与电磁法相当的Nd-150丰度(> 95%). 在此基础上压窄激光线宽, 能够在保持电离率的同时获得超过电磁法的Nd-150产品. 后续原子光谱实验应着重寻找IS23,148 ≥ 300 MHz, J3 = 6的第2步跃迁, 第2步跃迁的约化电偶极矩达到现用路径的30%即可满足丰度要求.

English Abstract

    全文HTML

    1.   引　言

    • 钕(Nd)元素有7种天然同位素, 如表1所示. 富集钕同位素可应用于量子材料、特种能源、医学等多个领域, 具有很高的经济价值, 如高丰度Nd-142或Nd-143同位素可掺杂进晶体中以制备固态量子存储材料[1,2], 高丰度Nd-146靶材经反应堆辐照后可生产用于放射性同位素电源的Pm-147[3], 高丰度Nd-148靶材经反应堆辐照后可生产医用治疗同位素Pm-149[4]. 钕天然同位素中, 高丰度Nd-150同位素因在核工业、科学研究领域均具有重要应用, 因此在同位素分离过程中最受关注. 在核工业领域, Nd-148法是分析乏燃料燃耗水平的主流标准方法, 而Nd-150可用作同位素稀释剂补偿质谱仪的质量歧视效应[5]. 在科学研究领域, Nd-150是极少数可发生双中微子双β衰变的同位素之一, 其衰变能Q0νββ仅次于Ca-48 [6], 因此可用于开展粒子物理的无中微子双β衰变研究, 目前实验所用的同位素体量已达到千克级[7].

      钕元素所在的镧系元素普遍没有稳定的常温气态化合物, 不能采用气体动力学方法分离同位素. 电磁法虽然能够分离钕同位素, 并可达到68%—97%丰度水平[8], 但能耗高、经济性差, 难以大规模生产. 原子蒸气激光同位素法(atomic vapor laser isotope separation, AVLIS)[9]基于多步电离路径实现原子蒸气中目标同位素的选择性光电离, 非目标同位素则尽可能保持中性, 对光致等离子体施加外电场将离子引出, 从而获得高丰度的目标同位素产品, 非常适用于Nd-150同位素分离. 俄罗斯库尔恰托夫研究院采用λ1 = 596 nm → λ2 = 579 nm → λ3 = 640 nm的三步电离路径(即表2路径一)[10,11], 首次实现了Nd-150同位素的分离, 产率达到40 mg/h, 但产品丰度仅为60% [12], 与电磁法相比仍有一定差距.

      高效高选择性的光电离路径是激光法的核心, 决定了分离过程核心指标——目标同位素的电离率和相对于非目标同位素的选择性, 前者与产量相关, 后者则决定了产品中目标同位素的丰度. 确定光电离路径需要丰富的原子精细和超精细结构层次的基础信息, 但钕原子结构文献资料有限, 特别是高激发态的同位素位移(isotope shift, IS)、超精细结构数据严重缺失[6]. 钕原子的第一电离限仅为5.525 eV[13], 可通过λ1 = 434 nm → λ2 = 458 nm或λ1 = 430 nm → λ2 = 449 nm等双步电离路径电离, 虽然上述路径的电离截面较高, 但同位素位移几乎为零, 难以获得高选择性[14]; 三步电离路径可大幅提高选择性, 是钕同位素分离的首选方案, 表2为早期研究建立的钕同位素三步电离路径, 其中路径一是Nd-150分离的现用路径, 其他路径的分离效果尚未有文献报道. 值得注意的是, 路径一λ1 = 596 nm在550—650 nm波段内的钕原子第1步跃迁中拥有最大的同位素位移, Nd-148相对Nd-150的同位素位移达到IS12, 148 = 1126.9 MHz [15]; 而路径一λ2 = 579 nm则几乎没有同位素位移, 其具体数值尚未有文献报道.

      光电离路径的电离率和选择性一般通过激光共振电离质谱(resonance ionization mass spectrometry, RIMS)实验获得, 这也是获取原子激发态结构参数(如能级位置、角动量、能级寿命、同位素位移、超精细结构)的可行方法[18–20], 但先于实验开展光电离理论计算, 评估不同原子参数、激光参数下的选择性光电离效果, 明确Nd-150丰度满足要求时电离路径的同位素位移、超精细结构等参数水平, 对于后续原子光谱实验有着重要的指导意义. Suryanarayana[6]在只考虑偶同位素, 并忽略第2步跃迁同位素位移的前提下, 粗略评估了表2路径四的光电离效果, 认为在100 MHz的激光线宽条件下, 能够以600 mg/h的产率生产丰度达到66%的Nd-150同位素[6], 但这对激光参数要求过高, 难以实现大规模工程化应用. 近年来, 我们发展了基于密度矩阵理论的选择性光电离模型, 能够计算不同同位素在多步电离过程中的电离率等参数, 并开展了Yb-176 [21], Lu-176 [22]等多种同位素的理论计算, 理论结果与文献数据半定量一致.

      本文在简述选择性光电离理论模型后, 以路径一为钕同位素电离路径的基准, 通过理论模型获得路径一的分支比等关键参数; 在此基础上优化电离路径, 考虑到路径一λ1 = 596 nm拥有最大的同位素位移, 因此第1步跃迁沿用λ1 = 596 nm, 假定第3步跃迁电离截面与路径一相当, 仅改变第2步跃迁, 通过改变第二激发态角动量、同位素位移、超精细结构等参数构造假定电离路径, 通过理论模型开展所有钕同位素的电离率计算, 评估相应的选择性光电离效果能否满足应用要求, 为后续原子光谱实验提供方向性指导.

    2.   选择性光电离模型

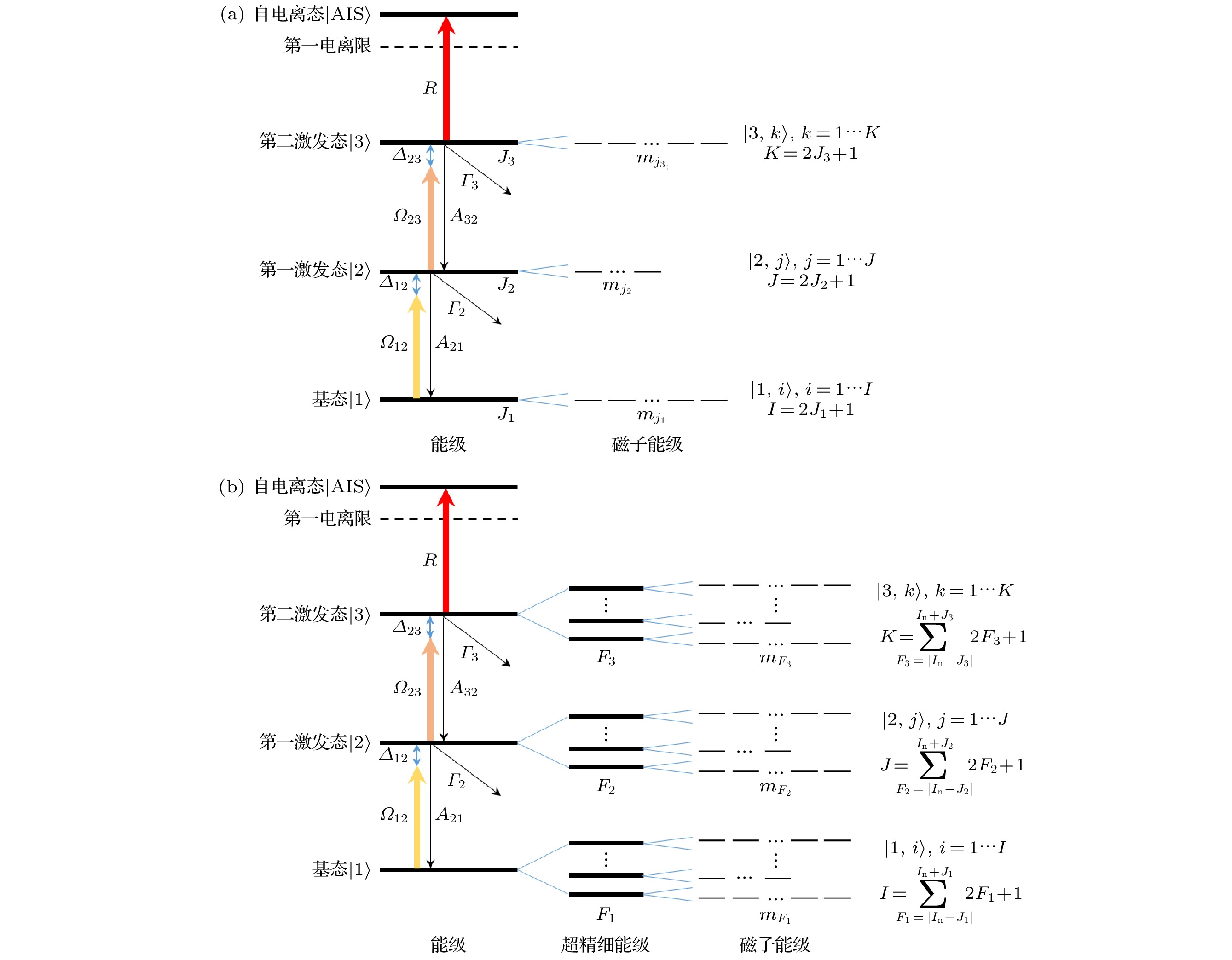
    • 考虑超精细结构和能级简并的三步电离路径如图1所示, 其中$ \left| 1 \right\rangle $, $ \left| 2 \right\rangle $, $ \left| 3 \right\rangle $分别为基态、第一激发态、第二激发态, $ \left| {1, i} \right\rangle $, $ \left| {2, j} \right\rangle $, $ \left| {3, k} \right\rangle $分别为对应的磁子能级, i, j, k分别表示对应的磁量子数, 磁子能级总数量分别为I, J, K, $ \left| {{\text{AIS}}} \right\rangle $为自电离态. 当核自旋In不为零时, 能级存在超精细分裂.

      在三步电离路径下, 原子共振吸收第1束激光后由基态跃迁至第一激发态, 再吸收第2束激光后跃迁至第二激发态, 继而吸收第3束激光跃迁至自电离态, 并快速弛豫产生离子. 该过程可通过半经典的密度矩阵理论描述. 考虑超精细结构和能级简并后, 原子波函数可表示为各能级本征态的线性叠加:

      其中Φ1(i), Φ2(j), Φ3(k)分别为$ \left| {1, i} \right\rangle $, $ \left| {2, j} \right\rangle $, $ \left| {3, k} \right\rangle $的本征波函数, a1(i), a2(j), a3(k)分别为$ \left| {1, i} \right\rangle $, $ \left| {2, j} \right\rangle $, $ \left| {3, k} \right\rangle $的概率振幅.

      在多束激光作用下, 原子波函数的时间演化满足Schrödinger方程, 将激光场视为微扰, 在电偶极近似、旋转波近似、绝热近似等近似条件下, 通过定义失谐量Δ、Rabi频率Ω, 可以得到(2)式所示的概率振幅时间演化方程组:

      密度矩阵矩阵元定义为

      其时间演化方程为

      将(2)式代入, 通过唯像方式引入上能级向 体系内部下能级的弛豫速率A、上能级向体系外 部低能级的弛豫速率Γ和第二激发态向自电离态的跃迁速率R, 通过相扩散模型引入激光线宽b, 可得到(3)式—(9)式所示的密度矩阵方程组分量形式:

      式中i为虚数单位, 上角标“*”表示复共轭. 第m步跃迁$ \left| {m, m'} \right\rangle \to \left| {n, n'} \right\rangle $(m = 1, 2; n = m+1)的失谐量为Δmn(m', n') = fmn – νmn(m', n'), fmn为第m束激光频率, νmn为第m步跃迁的共振位置. 对于不存在超精细结构的同位素, 同一能级不同磁子能级的角动量相同, 能级|m, m'$\rangle $的J值仅与m相关, 因此νmn与m', n'无关; 而对于存在超精细结构的同位素, 能级分裂为若干超精细能级, 同一能级不同磁子能级的原子总角动量及其沿量子化轴投影存在差异, 能级$ \left| {m, m'} \right\rangle $的F值, mF值与m, m'相关, 因此νmn与m', n'相关.

      不同核自旋In时, 磁子能级跃迁通道的Rabi频率可统一表示

      其中ħ为约化Planck常数; $E_{mn} = \sqrt {{{2{P_{mn}}} {/ } {\left( {c{\varepsilon _0}} \right)}}} $为第m束激光的电场振幅, Pmn为第m束激光功率, c为真空中光速, ε0为真空介电常数; $ \left\langle {{J_m}} \right.\left| {{d_{mn}}} \right|\left. {{J_n}} \right\rangle $为第m步跃迁的约化电偶极矩, 其计算公式为[23]

      式中, gn = 2Jn+1为上能级的统计权重, λ为跃迁波长, Anm = βmn/τn为Einstein A系数, βmn为跃迁分支比, τn为上能级寿命. 值得注意的是, 对于同一跃迁, 不同同位素的约化电偶极矩相同[24].

      对于In ≠ 0同位素, 磁子能级跃迁通道的系数如(12)式所示[25]:

      其中$\{ \} , ()$分别为Wigner 6j, 3j符号, q表示激光偏振性, 对于单步跃迁, q = –1, 0, 1分别表示左旋圆偏振光、线偏振光、右旋圆偏振光激发. 对于In = 0同位素, 上述系数可简化为

      因此上述模型能够在磁子能级级别计算原子与激光的相互作用过程.

      第二激发态向自电离态的跃迁速率R如(14)式所示:

      其中σion为电离截面, $ {\phi _{{\text{3A}}}} $为第3束激光的光子数.

      上述模型中, 基于相扩散模型[26,27]引入第m束激光的线宽项$ 2{b_{mn}}\dfrac{{\kappa _{mn}^2 b_{mn}^2}}{{\varDelta _{mn}^2 + \kappa _{mn}^2 b_{mn}^2}} $, bmn为线宽(半高全宽, FWHM), κmn为截止系数. 引入的频域线型为修正的洛伦兹线型, 近共振时|Δmn| < κmnbmn, 频域线型为洛伦兹线型; 远失谐时|Δmn|$ \gg $ κmnbmn, 频域线型近似于单色激光场. 通过改变κmn取值, 可以调整相扩散模型引入的激光频谱. 值得注意的是, 共振激发时Δmn = 0, κmn的取值不影响光与原子的相互作用过程.

      在上述分量形式的基础上, 构造广义向量ρ, 可得到如(15)式所示的密矩阵度方程组矩阵形式:

      其中Q为系数矩阵, 广义向量ρ的分量分别有I 2, J 2, K 2, 1, IJ, IK, JK项. 数值计算中, 假设初始时刻原子均处于基态, 求解(15)式所示的常微分方程组即可得到原子与激光作用后的电离率ρion.

      通过给定同位素位移、超精细结构等参数, 上述通用理论模型可适用于不同同位素. 对于目标同位素nt, 其光电离后的丰度如(16)式所示:

      其中c0,n, ρion,n分别为同位素 n 的天然丰度和电 离率.

    3.   计算结果

    • 根据目前的文献报道, 仅有表2中的路径一实现了工程化应用, 可选为钕同位素电离路径的基准. 首先通过理论模型获得路径一的分支比等关键参数, 在此基础上构造假定电离路径, 通过理论模型评估相应的选择性光电离效果, 给出Nd-150丰度满足应用要求时假定电离路径所需具备的参数水平, 指导后续的原子光谱实验. 考虑到路径一λ1 = 596 nm拥有最大的同位素位移, 因此第1步跃迁沿用λ1 = 596 nm, 假定第3步跃迁的电离截面与路径一相当, 仅改变第2步跃迁, 通过改变第二激发态角动量、超精细结构以及第2步跃迁同位素位移等参数构造假定电离路径.

      考虑到Nd-150为目标同位素, 选取其前两步跃迁共振位置为ν12,150 = ν23,150 = 0, 若无特殊说明, 其他钕同位素的共振位置均为该同位素相对Nd-150的共振位置. 数值计算中激光参数取值如表3所示, 计算过程中未考虑Doppler效应、Stark效应等导致的原子共振频率移动, 因此激光频率f12 = 0 (f23 = 0)表示第1束(第2束)激光频率与Nd-150共振; 激光功率、线宽、偏振等其他参数取值见文中说明. 数值计算中采用4阶固定步长显式Runge-Kutta算法, 总模拟时长90 ns, 步长0.01 ns.

      • 3.1.   路径一的性质

    • 路径一的能级参数、跃迁参数分别如表4和表5所示. 其中钕同位素第2步跃迁的同位素位移IS23以及奇同位素第二激发态的超精细常数A23, B23尚未有文献报道, 假定可忽略不计; 能级寿命同样未有报道, 由于第一激发态属于未知组态[13], 参考附近同属未知组态的16979.35 cm–1能级[13,28], 第一激发态能级寿命τ2假定为典型值600 ns[28]; 第二激发态能级寿命τ3过低(如小于激光脉宽)会导致第2束激光功率吸收不完全以及吸收后的自发辐射损失过多, τ3过高(如接近μs量级)则会降低第2步跃迁强度, 不利于后续的第3步跃迁, 因此τ3根据激光脉宽选取了典型值100 ns; 参考表2中路径三[17], 第3步跃迁的电离截面假定为相同量级的σion = 6 × 10–16 cm2.

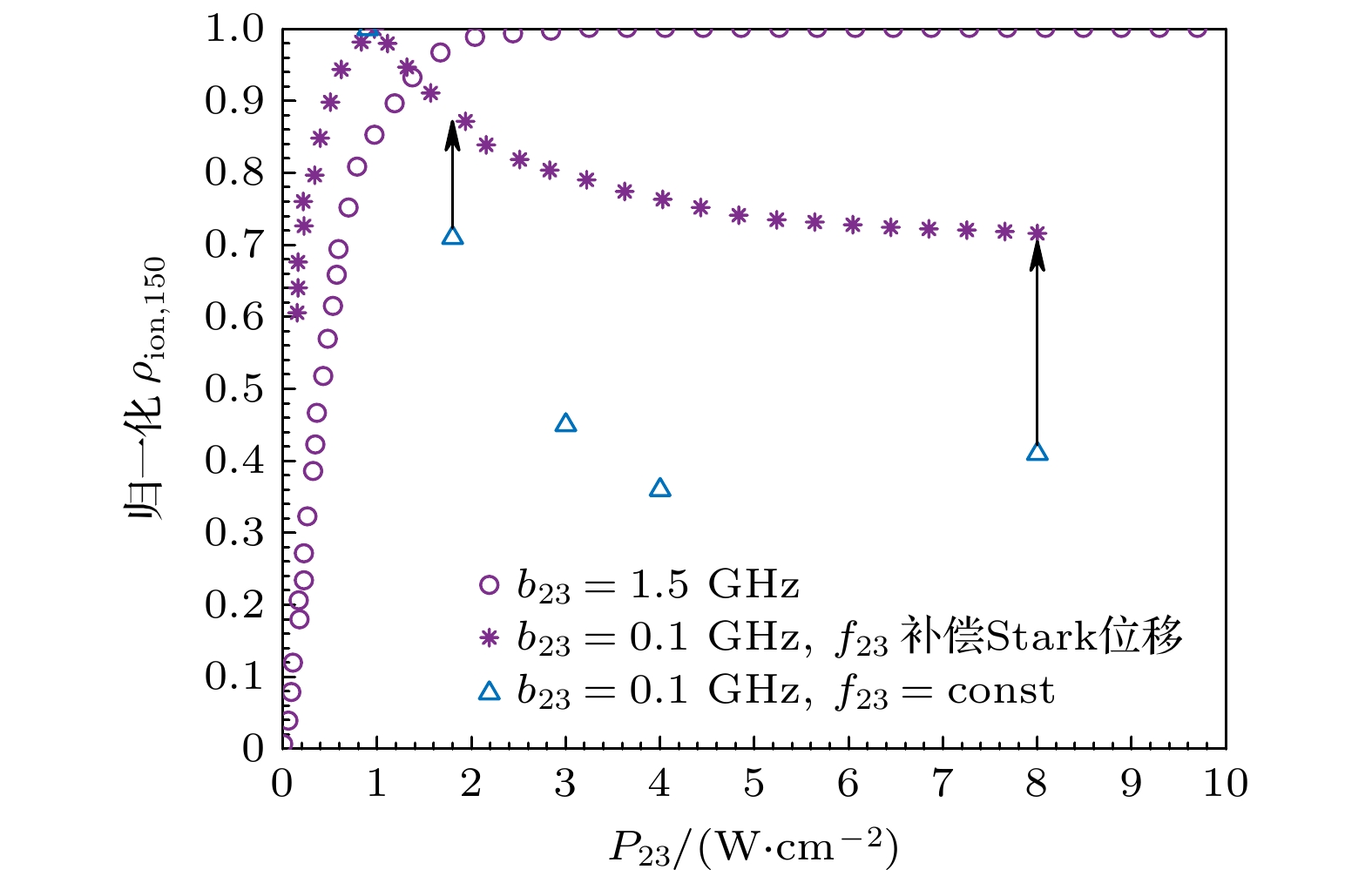
      分支比β是电离路径的重要参数, 在理论模 型中可以通过保持上能级寿命、角动量和跃迁波 长不变、仅调整分支比的方式改变跃迁电偶极矩, 从而改变饱和功率曲线的相对线型, 通过与实验测量的饱和功率曲线进行对比可确定分支比的取值. Grigoriev等[11]基于共振电离质谱装置开展了不同线宽下第2步饱和功率曲线测量. 实验中, 各束激光与Nd-150共振, 第1束激光线宽b12 = 0.1 GHz, 第1, 3束激光功率密度分别为P12 = 2 W/cm2, P3A = 13 W/cm2. 如图2所示, 第2束激光线宽为窄线宽(b23 = 0.1 GHz)时, 第2步饱和功率曲线先上升后下降; 为宽线宽(b23 = 1.5 GHz)时, 第2步饱和功率曲线呈现出正常的先上升后逐渐饱和的趋势. 值得注意的是, 实验中b23 = 0.1 GHz时出现了显著的Stark位移, 若第2束激光频率保持不变(如蓝色三角所示), 第2步饱和功率曲线在高功率处(P23 = 8 W/cm2)的信号强度约为最大强度的40%; 若功率增大过程中调整第2束激光频率对Stark位移进行补偿(如紫色星号所示), 上述比例约为70%. 推测是第2步饱和功率曲线实验值同时受单步跃迁和近共振2λ双光子跃迁等两方面影响, 由于能级位置的Stark位移与激光功率正相关, 前者的跃迁概率随激光功率增大而减小; 后者则随激光功率增大而增大. 考虑到基态钕原子吸收2λ2光子的激发位置34508.006 cm–1与34509.603 cm–1(J = 4)能级[30]接近, 且角动量满足双光子跃迁选择定则, 推测钕原子可能存在较强的近共振2λ2双光子跃迁, 从而能够在一定程度上抑制Nd-150电离率的降低, 甚至在更高功率下能够提升电离率.

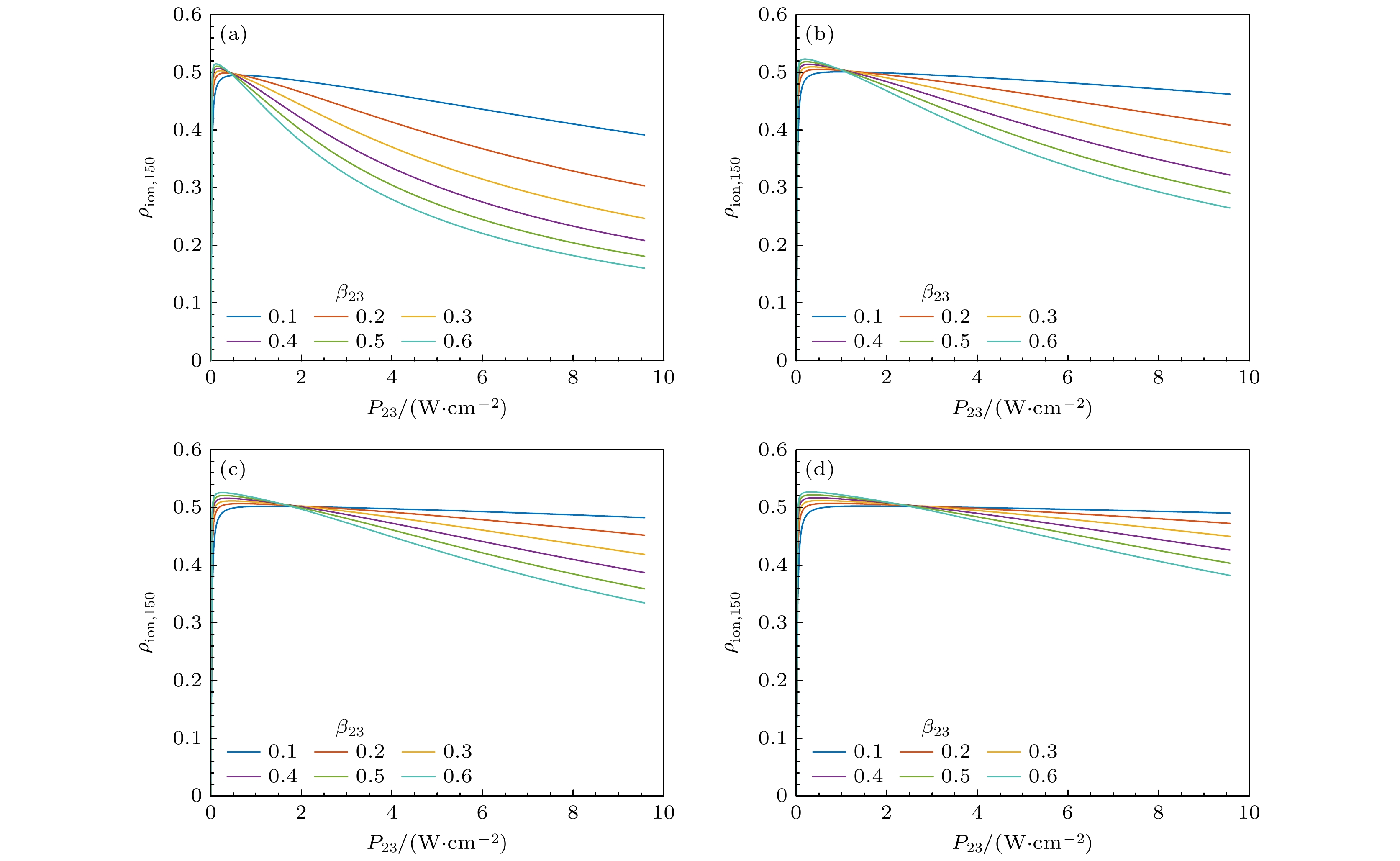
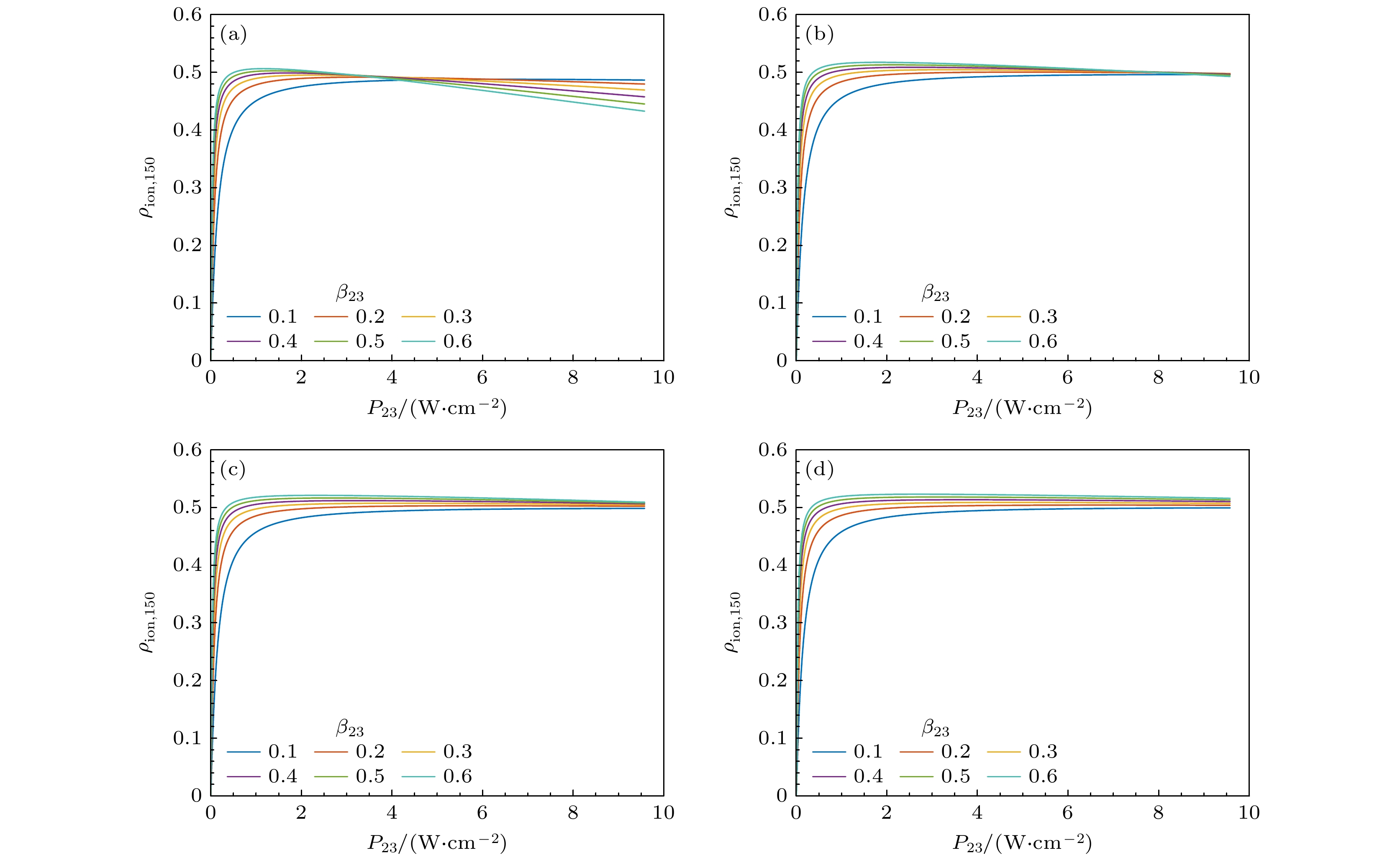
      在激光频率与Nd-150共振f12 = f23 = 0、平行线偏振以及上述线宽、功率条件下, 调整前两步跃迁分支比组合, 对第2步饱和功率曲线进行理论计算. 不同线宽下的第2步饱和功率曲线计算值分别如图3和图4所示, 每张子图代表某一第1步跃迁分支比β12和一组第2步跃迁分支比β23下的第2步饱和功率曲线. 如图3所示, b23 = 0.1 GHz时, 随着第2束激光功率增大, 理论曲线先上升后下降, 高功率区间的电离率下降程度与分支比组合相关. 如图4所示, b23 = 1.5 GHz时, 除β12 = 0.05, β23 = 0.4, 0.5, 0.6等少数曲线在高功率区间呈现明显的下降趋势外, 其他曲线均为正常的饱和功率曲线线型, 高功率区间的电离率基本保持不变或者下降程度可忽略. 可见, 前两步饱和功率曲线的计算值与实验值在定性上一致.

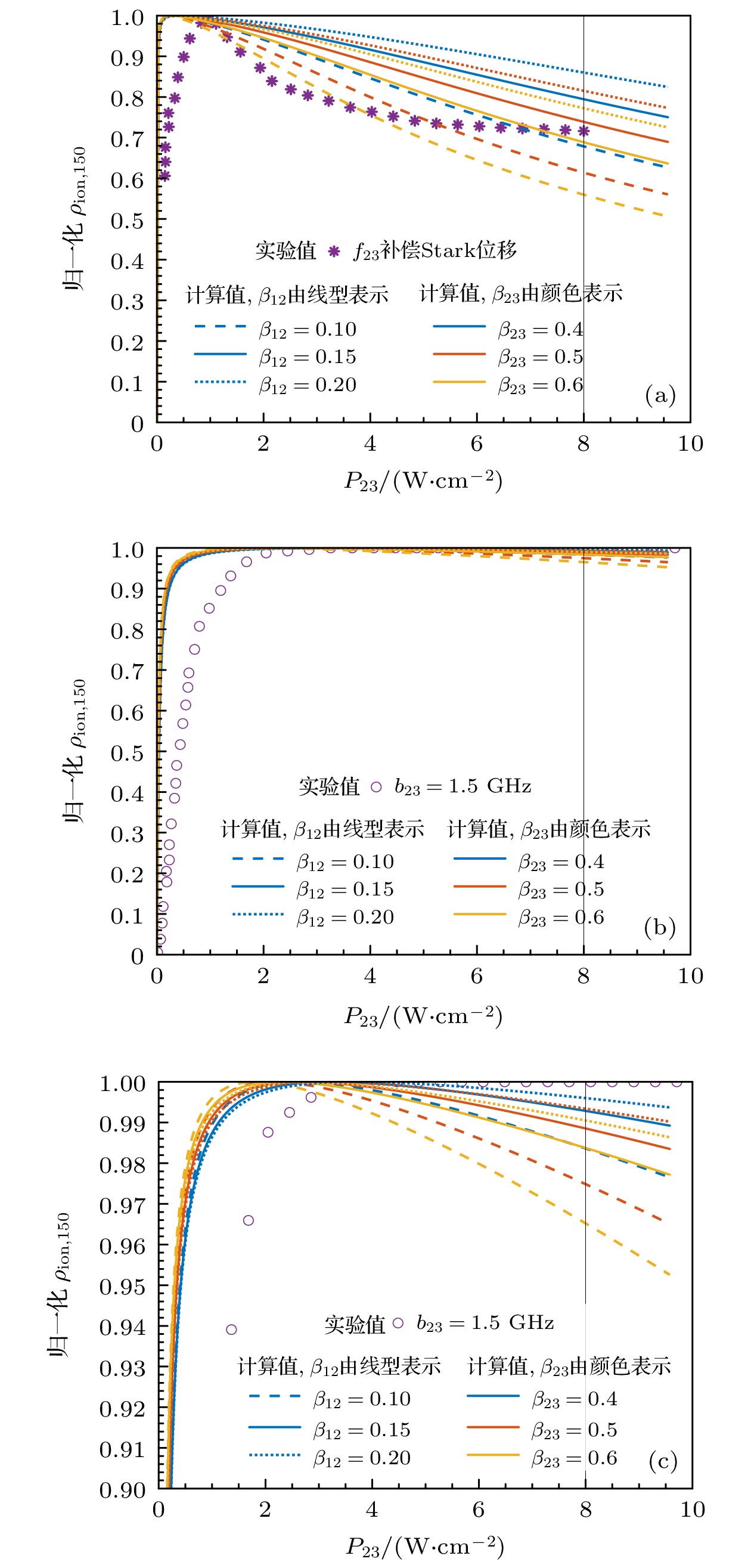
      由于Nd-150电离率理论计算时激光失谐量为Δ12 = Δ23 = 0, 因此激光频率始终与Nd-150共振, Nd-150电离率理论结果应与f23补偿Stark位移的实验结果对比. 为确定最优的跃迁分支比组合, 根据理论曲线在b23 = 0.1 GHz, P23 = 8 W/cm2的归一化电离率ρion,150定性判断理论曲线与实验值的符合程度. 第2步饱和功率曲线的归一化计算值与实验值如图5所示, 其中图5(a), (b)分别为窄线宽、宽线宽激发时的饱和功率曲线, 图5(c)为图5(b)纵轴[0.9, 1]的局部放大图, 紫色星号为窄线宽时补偿Stark位移后的实验值, 紫色圆圈为宽线宽时的实验值, 曲线为计算值, 曲线的线型(实线、虚线、点线)表示β12, 曲线的颜色表示β23.

      根据图5(a), 前两步跃迁分支比组合为β12 = 0.15, β23 = 0.5时, P23 = 8 W/cm2的归一化ρion,150计算值与实验值最为接近, 因此选取上述参数为路径一的最优分支比组合, 对应的约化电偶极矩分别为4.5535×10–30 C·m, 2.1188×10–29 C·m. 总体而言, 如图5橙色实线所示的第2步饱和功率曲线计算值与实验值的定性趋势一致. 图5中理论曲线与实验结果存在一定差异: 1)理论曲线在更低功率处(P23 = 0.5 W/cm2)达到电离率最大值或者饱和值, 可能的原因是实验所用激光频谱的线型及纵模分布与理论模型所采用的相扩散模型存在差异[31]. 2)理论曲线在高功率区间(P23 = 5—10 W/cm2)的下降趋势更加显著, 而实验值则快速趋于平缓, 推测是实验中钕原子近共振2λ2双光子跃迁补偿了Stark位移导致的电离率下降, 而本文模型仅考虑λ1或λ2单步跃迁、近共振λ1+λ2双光子跃迁等两种情况, 未考虑近共振2λ双光子跃迁等其他非线性效应.

      确定路径一的分支比后, 在饱和激发(P12 = P23 = 2 W/cm2)的条件下, 评估路径一的选择性光电离效果, 包括Nd-150电离率和Nd-150丰度. 计算过程中考虑所有钕同位素, 并忽略了奇同位素第二激发态的超精细分裂. 计算结果如表6所示, 可见在典型激光线宽下, 路径一的Nd-150丰度难以超过70%, 不能满足核工业、科学研究等领域对于富集Nd-150同位素的需求.

      • 3.2.   假定电离路径的性质

    • 如上所述, 路径一仅有第1步跃迁λ1 = 596 nm具备可观的同位素位移, 第2步跃迁λ2 = 579 nm则几乎没有同位素位移, 使得分离后的Nd-150丰度不能满足应用需求, 需要开展原子光谱实验寻找新电离路径以提高选择性. 考虑到原子光谱实验周期较长, 因此基于理论模型在假定路径参数的条件下开展电离率的数值计算, 评估假定电离路径的选择性光电离效果, 根据Nd-150丰度判断假定电离路径所需具备的参数水平, 这对于实验扫描有着重要指导意义.

      考虑到钕原子第一激发态研究较为充分, 第二激发态及自电离态数据缺失严重, 且路径一λ1 = 596 nm拥有最大的同位素位移, 因此电离路径的优化方案确定为: 第1步跃迁沿用λ1 = 596 nm, 在此基础上扫描第二激发态及自电离态, 寻找高效高选择性的光电离路径. 相应的数值计算中, 不改变第1步跃迁, 且假定第3步跃迁的电离截面与路径一相当, 仅改变第2步跃迁, 通过改变第二激发态角动量、超精细结构以及第2步跃迁同位素位移等参数构造假定电离路径. 计算时选取的能级参数、跃迁参数分别如表7和表8所示, 计算参数在多方面进行合理假设: 1)第二激发态能级位置、寿命假定不变, 通过调整角动量、分支比改变第2步跃迁的约化电偶极矩, 并调整第2步跃迁同位素位移、第二激发态的超精细结构, 以构造不同跃迁强度、跃迁共振位置的假定电离路径; 2)考虑到IS23一般小于IS12, 第2步跃迁的同位素位移比值假定在第1步跃迁的基础上有所降低, 因此选择性光电离效果评估相对偏保守; 3)考虑到同一跃迁难以兼具大同位素位移、大约化电偶极矩的性质, 为寻找高选择性电离路径需要增大IS23, 因此将分支比β23在路径一的基础上降低1个量级, 对应的约化电偶极矩$ \left\langle {{J_2}} \right.\left| {{d_{23}}} \right|\left. {{J_3}} \right\rangle $大约相当于路径一的30%.

      • 3.2.1.   偏振、第二激发态角动量对饱和功率曲线的影响

    • 如(11)式所示, 跃迁的约化电偶极矩与上能级角动量直接相关; 如(12)式和(13)式所示, 磁子能级间跃迁通道的电偶极矩通过Wigner 3j符号与激光偏振直接相关. 因此应首先优选偏振、第二激发态角动量J3取值, 针对最优参数值开展后续的选择性光电离效果理论评估.

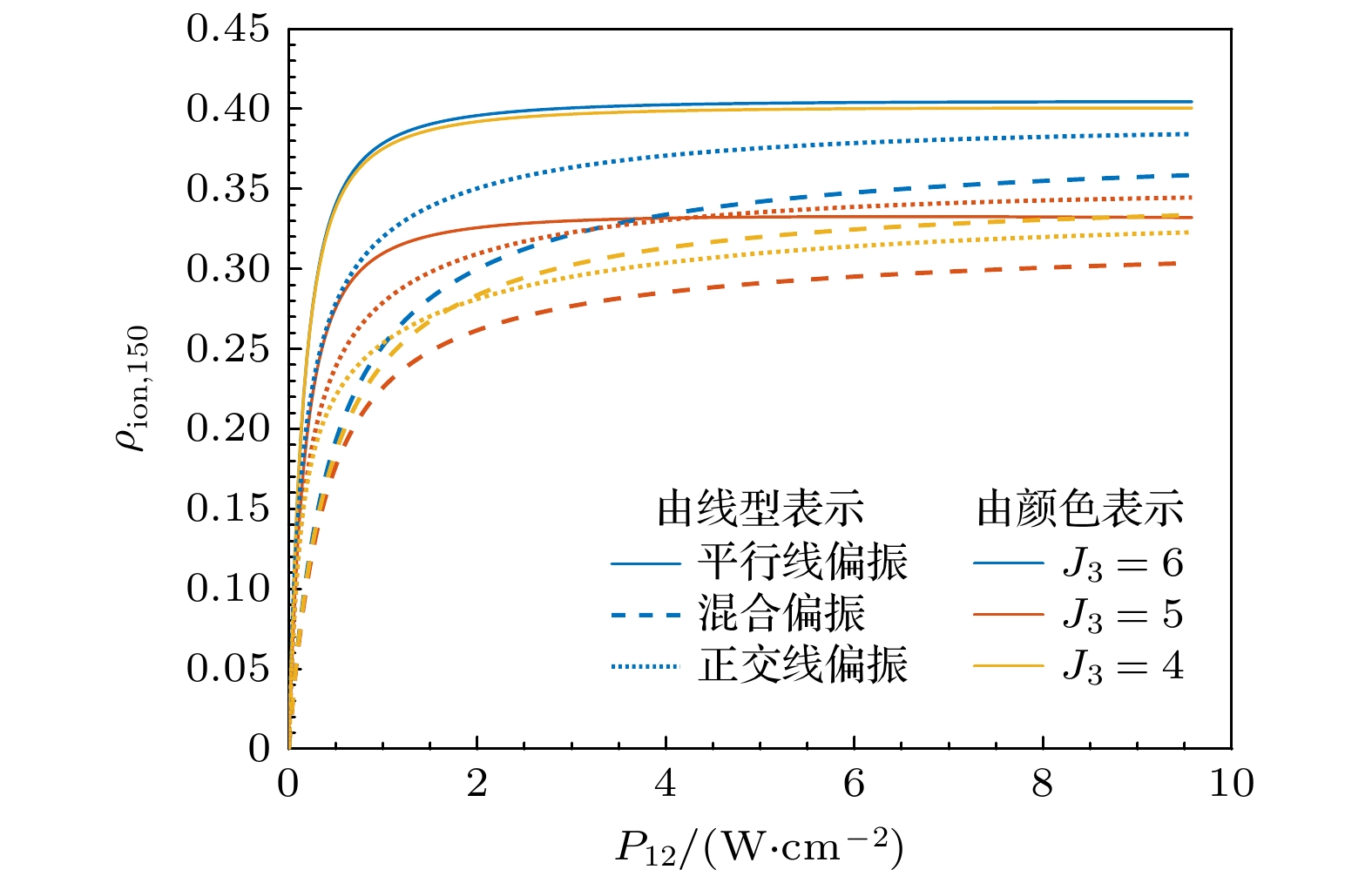
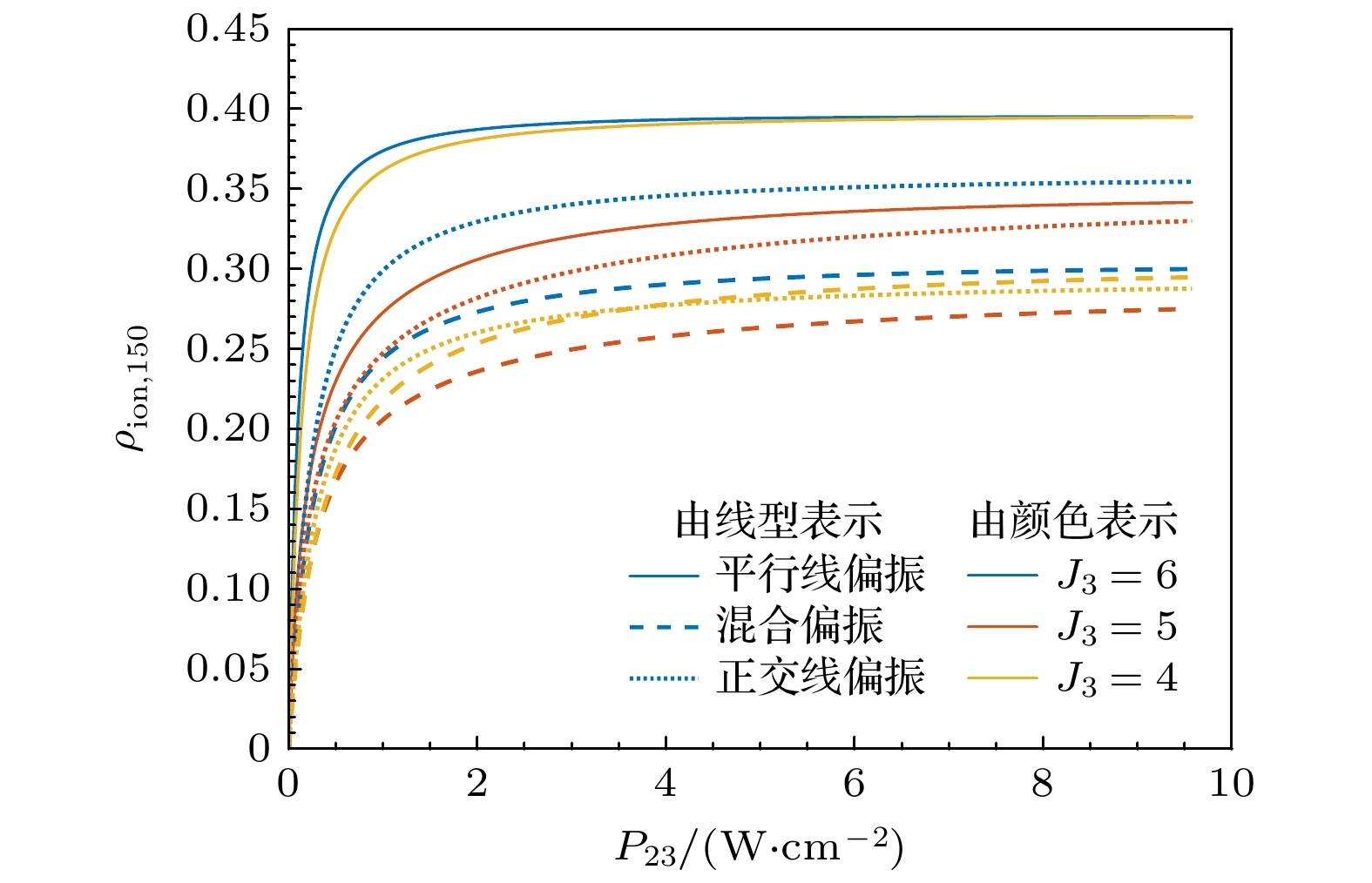
      在典型线宽b12 = b23 = 0.5 GHz, 频率与Nd-150共振的条件下, 开展假定电离路径的饱和功率曲线计算, 给出电离率最高的偏振、J3的参数组合. 第1步和第2步饱和功率曲线分别如图6和图7所示, 激光参数: f12 = f23 =0, P3A = 13 W/cm2, b12 = 0.5 GHz, b23 = 0.5 GHz, 偏振见图例, 图6为P12扫描, P23 = 2 W/cm2, 图7为P12 = 2 W/cm2, P23扫描. 其中曲线线型(实线、虚线、点线)表示如表3所示的激光偏振, 由于工程中难以实现高纯圆偏振光的高功率输出, 本节计算中仅考虑了线偏振和混合偏振等典型值; 曲线颜色表示J3取值. 可见, 现象一: 图6和图7相同颜色的不同线型曲线中, 实线最快达到饱和, 即相同J3取值时, 平行线偏振的饱和功率最低. 这是由于磁子能级相干布居囚禁效应, 该效应能够降低磁子能级跃迁通道的电离率, 而平行线偏振能够解除(对应In = 0, J1 = 0 → J2 = 1 → J3 = 2以及In = 0, J1 = 2 → J2 = 1 → J3 = 0等两种电离路径)或抑制(对应除前两者之外的其他电离路径)该效应, 相比其他激光偏振更能够有效激发下能级原子. 现象二: 图6相同颜色的不同线型曲线中, 橙色曲线中点线在高功率区间(P12 > 5 W/cm2)的电离率最高, 黄色、蓝色曲线中实线的电离率最高, 即对于高功率区间的第1步饱和功率曲线, J3 = 5时正交线偏振的电离率最高, J3 = 4, 6时平行线偏振的电离率最高. 现象三: 图6和图7所有工况中, 蓝色实线的饱和电离率最高, 即平行线偏振、J3 = 6为Nd-150电离率最高时的参数取值. 值得注意的是, 上述参数取值下, 即使β23 = 0.05相比路径一降低了1个量级, P12 = P23 = 2 W/cm2仍能够实现Nd-150的饱和电离.

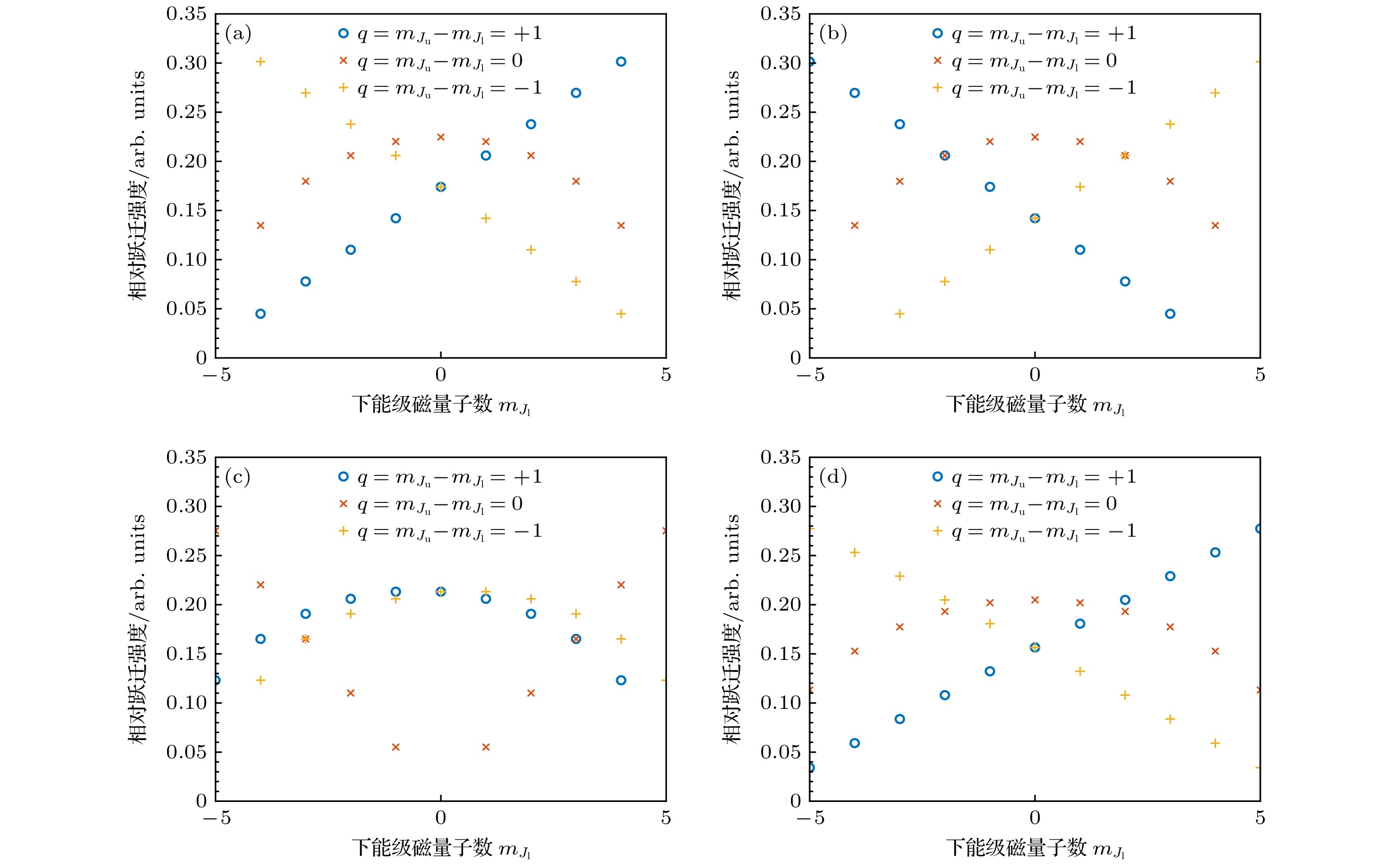
      上述现象二可通过图8定性解释, 其中图8(a)为第1步跃迁J1 = 4 → J2 = 5的磁子能级跃迁通道相对跃迁强度, 图8(b)—(d)分别为第2步跃迁J2 = 5 → J3 = 4, 5, 6的相对跃迁强度, 子图中蓝色圆圈、橙色叉号、黄色加号分别表示q = +1, 0, –1的相对跃迁强度. 可见, ΔJ = 0跃迁的超精细跃迁通道相对跃迁强度随下能级磁量子数增大的定性规律与ΔJ = ±1跃迁存在显著差异, ΔJ = 0时的q = 0相对跃迁强度关于mJ = 0呈对称发散状, q = ±1相对跃迁强度关于mJ = 0呈对称弧状; 而ΔJ = ±1时的q = 0超精细跃迁通道则关于mJ = 0呈对称弧状, q = ±1超精细跃迁通道则随着mJ值线性变化. 特别地, 由于跃迁定则, J2 = 5 → J3= 5的mJ2 = 0 → mJ3 = 0为禁戒跃迁. 对于第1步跃迁, 在线偏振激发下, 第一激发态原子主要布居在低磁量子数磁子能级(|mJ2| ≤ 2). 在平行线偏振下, 第2步跃迁发生q = 0跃迁, J3 = 6时|mJ2| ≤ 2磁子能级的相对跃迁强度与J3 = 4相当, 且显著高于J3 = 5, 因此J3 = 6的饱和电离率更高; 在正交线偏振下, 第2步跃迁发生q = ±1跃迁, J3 = 5时|mJ2| ≤ 2磁子能级的相对跃迁强度高于J3 = 4, 6, 因此J3 = 5的饱和电离率更高.

      • 3.2.2.   假定电离路径的选择性光电离效果

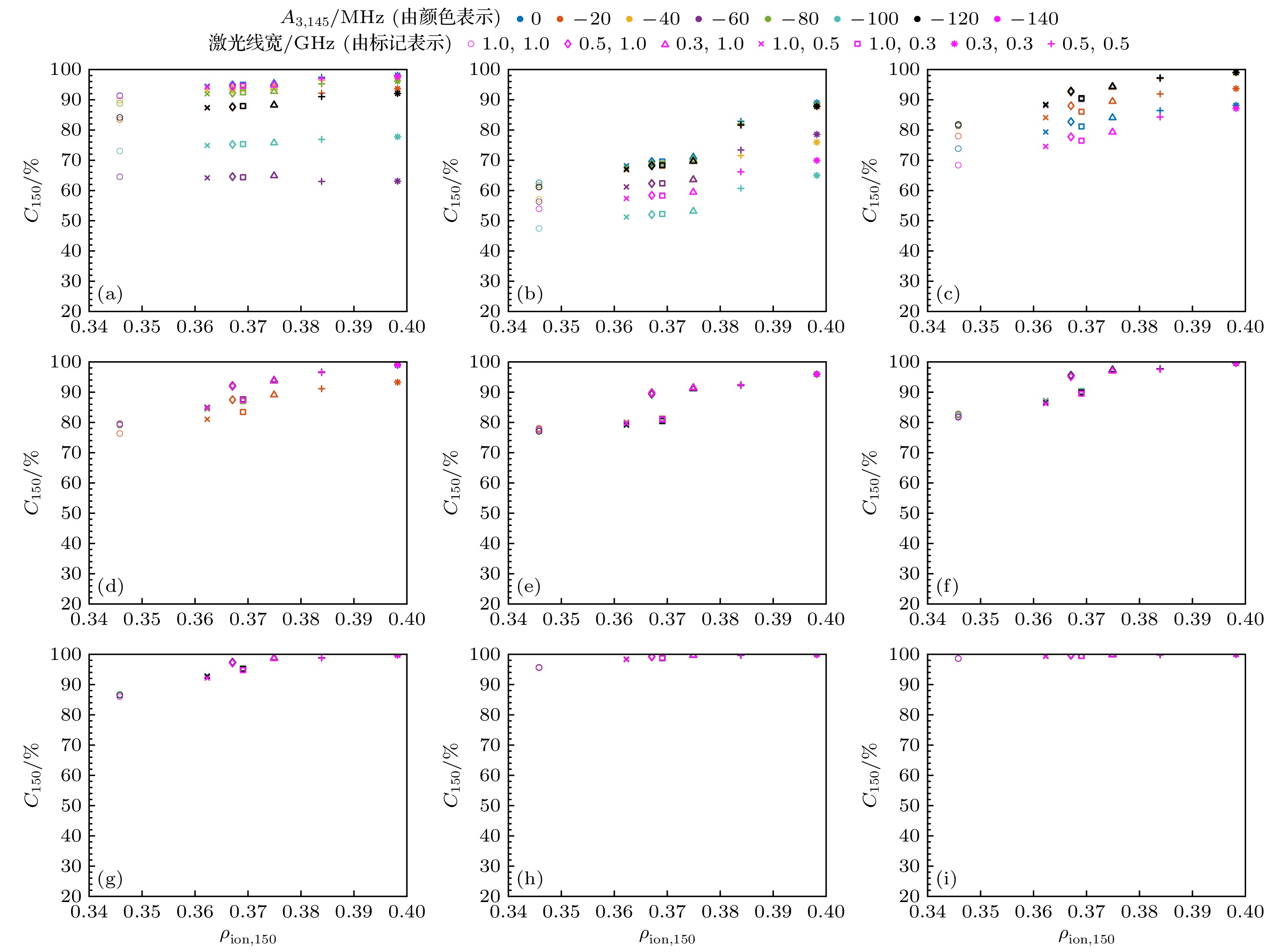
    • 基于以上讨论, 综合考虑工程实现难度与电离效果, 选取平行线偏振、J3 = 6开展假定电离路径在不同同位素位移、超精细结构下的选择性光电离效果评估. 文献[6]中忽略了钕奇同位素对Nd-150选择性光电离的影响, 而本文将所有钕同位素均考虑在内. 评估过程中, 给定Nd-148相对Nd-150的第2步跃迁同位素位移IS23,148, 按照表8所示的比例给出其他钕同位素相对Nd-150的同位素位移, 从而改变所有钕同位素的IS23; 以及给定Nd-145第二激发态的超精细常数A3,145, B3,145, 按照表7所示的比例给出Nd-143的超精细常数A3,143, B3,143, 从而改变钕奇同位素的超精细分裂. 钕奇同位素超精细结构的共振位置由超精细常数、重心相对Nd-150的同位素位移共同决定.

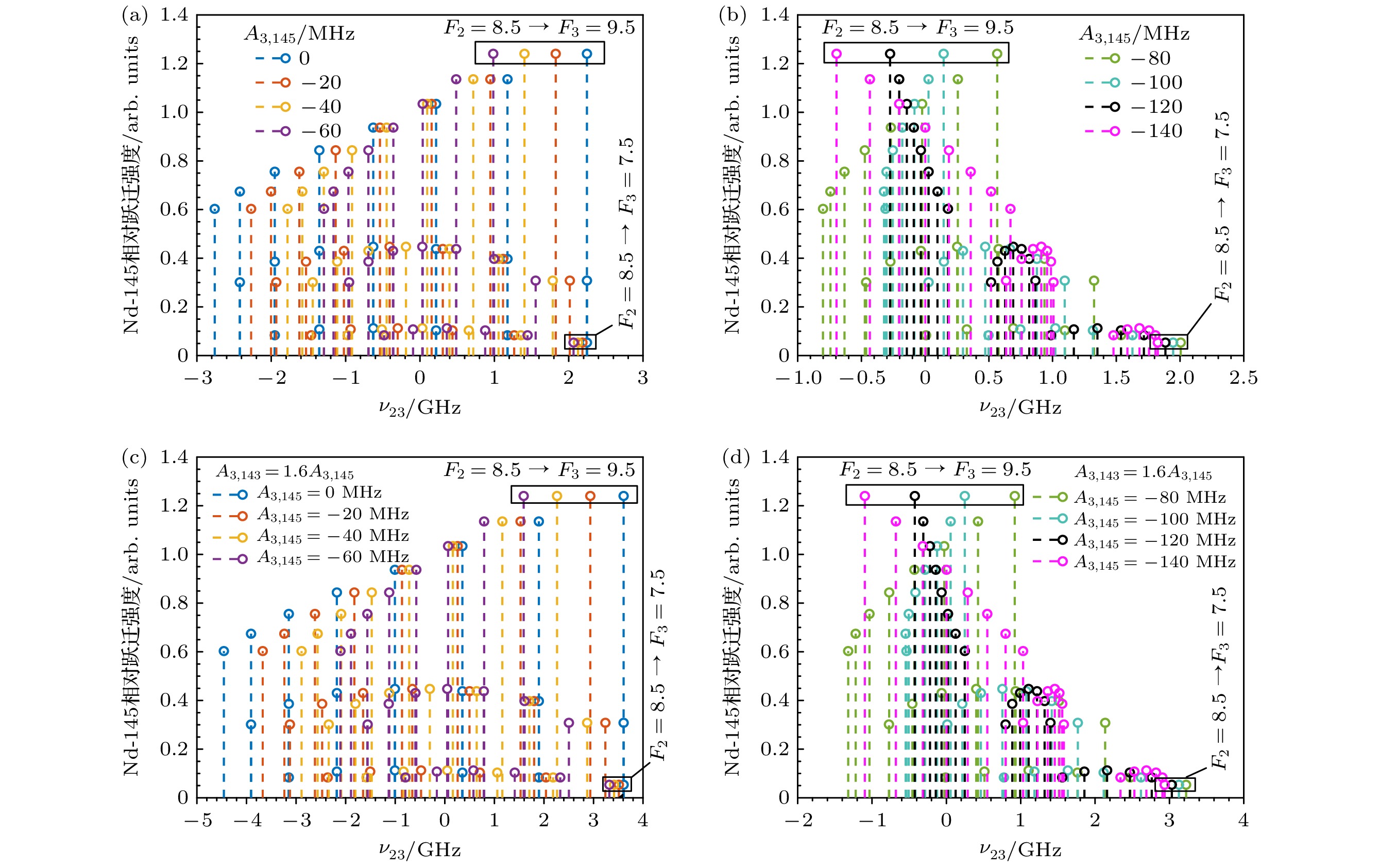
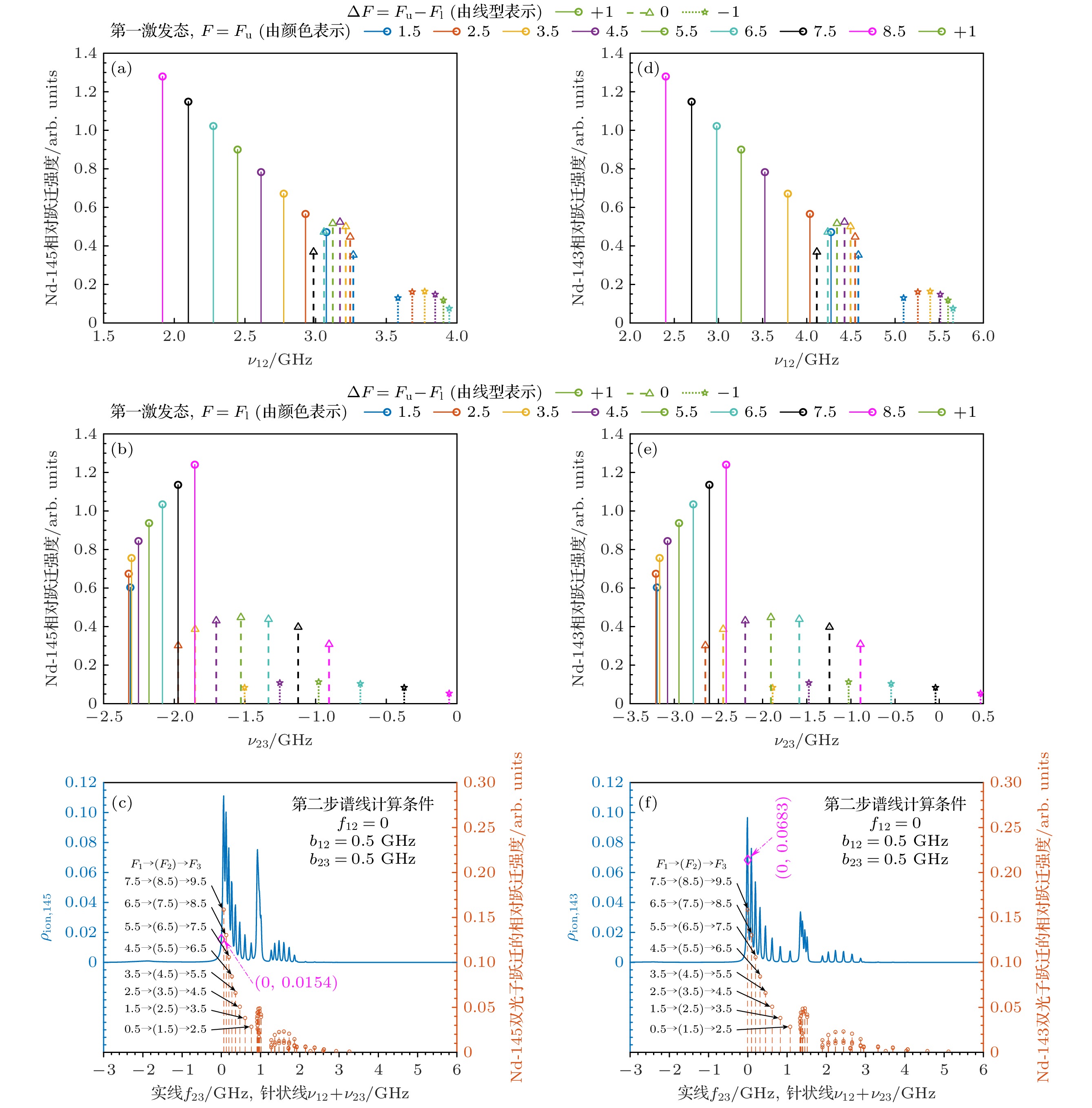
      在开展不同参数取值时各同位素电离率计算前, 首先评估超精细常数对钕奇同位素共振位置的影响. 第二激发态超精细常数A3,145对钕奇同位素第2步跃迁超精细结构的影响如图9所示, 以B3,145 = 0 MHz, IS23,148 = 0 GHz为示例. 其中图9(a), (b)为Nd-145的超精细结构共振位置, 图9(c), (d)为Nd-143的超精细结构共振位置, 图9子图的横轴ν23为超精细跃迁通道的共振位置, 纵轴为其相对跃迁强度, 针状线的颜色表示不同A3,145取值时的超精细结构, 跃迁强度最高的F2 = 8.5 → F3 = 9.5和跃迁强度最低的F2 = 8.5 → F3 = 7.5已用矩形框出. 可见, 在A3,145 = 0—140 MHz范围内, 随着A3,145逐渐偏离0 MHz, F2 = 8.5 → F3 = 9.5的共振位置由谱线的高频侧(如A3,145 = 0所示)逐渐移向中心(如A3,145 = –80 MHz, –100 MHz所示), 再逐渐移向低频侧(如A3,145 = –140 MHz所示), 而F2 = 8.5 → F3 = 7.5则均出现在谱线的高频侧. 由于Nd-143与Nd-145核自旋均为7/2, Nd-143超精细结构与Nd-145定性一致, 区别在于前者的分裂程度更大, 以及同位素位移所导致的超精细结构重心存在差异.

      第二激发态超精细常数B3,145对钕奇同位素第2步跃迁谱线分裂程度、共振位置的影响分别如表9和表10所示, 其中ν23, A, B为超精细常数分别取值为A, B时的第2步跃迁超精细跃迁通道共振位置, max(ν23, A, B), min(ν23, A, B)分别为共振位置的最大值、最小值, 二者的差值为谱线分裂程度, max(|ν23, A, B – ν23, A, 0|)为考虑B常数与不考虑B常数时的共振位置最大差异值. 可见, 第2步跃迁的谱线分裂程度在A3,145 = 0时最大, 随着A3,145逐渐偏离0 MHz分裂程度逐渐降低, 在A3,145 = –120 MHz时达到最小值, 后稍有增大. 综合图9、表9、表10, 钕奇同位素超精细结构主要由A常数决定, 其相对Nd-150的位置同时受IS23,148取值的影响; B常数对钕奇同位素共振位置的影响至多为数十MHz量级, 而谱线分裂程度在数GHz量级. 因此B常数对后续激发、电离的影响可忽略, 计算钕奇同位素电离率时仅考虑A常数导致的超精细分裂.

      在忽略B常数对超精细结构影响的前提下, 选取假定电离路径的Nd-148第2步跃迁同位素位移IS23,148, Nd-145第二激发态超精细常数A3,145典型值, 基于典型值调整所有同位素的同位素位移和奇同位素的超精细结构, 开展所有钕同位素电离率的计算, 评估相应的Nd-150选择性光电离效果. 如图10所示, 激光参数: f12 = f23 = 0, P12 = 2 W/cm2, P23 = 2 W/cm2, P3A = 13 W/cm2, 其中每张子图表示特定IS23,148取值下, 不同超精细结构、激光线宽时的选择性光电离效果, 横轴为Nd-150电离率, 纵轴为Nd-150丰度, 位于子图右上部分的选择性光电离效果较好; 奇同位素超精细结构由标记的颜色表示, 且与图9中针状线的颜色对应, 激光线宽由标记的样式(圆圈、菱形、三角、叉号、方形、星号、加号)表示. 可见, 在本文的假定电离路径下, 同位素位移、超精细结构对Nd-150选择性光电离影响的基本规律如下: 1)正向IS23(IS23 = ν23 – ν23, 150, 即其他钕同位素第2步跃迁共振位置与Nd-150的差值)的光电离效果优于负向IS23; 2)钕奇同位素超精细结构对光电离效果的影响在负向IS23时更为显著, 在正向IS23时不同超精细结构的影响没有明显差异; 3)压窄线宽能够提高Nd-150电离率和丰度, 负向IS23时压窄线宽对丰度的提升效果更为显著. 这是由于IS12 > 0, 正向IS23与IS12相互叠加, 在f12 = f23 =0激发下, 其他钕同位素的谱线相比IS23 = 0时更加偏离Nd-150共振位置, 从而抑制非目标同位素的激发电离, 提高Nd-150选择性; 而负向IS23会与IS12相互抵消, 在f12 = f23 = 0激发下, 奇同位素的一些超精细跃迁通道或者偶同位素的跃迁通道与Nd-150共振位置更为接近, 继而以近共振λ1 + λ2双光子电离的方式产生杂质离子, 降低Nd-150选择性.

      如图10(b)中青色标记所示, f12 = f23 = 0, IS23,148 = –1000 MHz, A3,145 = –100 MHz时Nd-150丰度最低. 下面以该组工况为例, 分析第2步跃迁同位素位移、第二激发态超精细结构对钕同位素选择性光电离过程的影响, 阐述近共振λ1+λ2双光子跃迁对钕同位素激发电离所产生的影响. 该组工况中, 光电离后的各同位素丰度如表11所示, 可见主要杂质同位素为Nd-148, Nd-143, Nd-145. 钕偶同位素的共振位置如表12所示, 其中ν12, ν23, ν12+ν23分别为J1 → J2第1步跃迁、J2 → J3第2步跃迁、J1 → (J2) → J3 λ1+λ2双光子跃迁的共振峰位. 可见, 激光频率与Nd-150共振时, Nd-148虽然由于J1 → J2 → J3双步跃迁的失谐量较大而跃迁概率偏低, 但仍可通过近共振λ1+λ2双光子跃迁的方式电离; 其他钕偶同位素相对Nd-150的同位素位移更大, 双步跃迁、双光子跃迁的概率均低于Nd-148, 且随着双光子跃迁失谐量的增大, 电离后的同位素丰度显著降低.

      钕奇同位素丰度高的原因可通过图11定性解释, 其中图11(a), (b)横轴ν12(ν23)分别为Nd-145第1步(第2步)超精细跃迁通道共振位置, 第一激发态F值由针状线的颜色表示, 相同颜色的针状线表示两步超精细跃迁通道F1 → F2 → F3, 跃迁类型ΔF由针状线线型(实线圆圈、虚线三角、点线五星)表示; 相应见图11(d), (e)的Nd-143超精细跃迁通道; 在图11(c)中, 蓝色实线为Nd-145第2步谱线, 计算条件为f12 = 0, b12 = b23 = 0.5 GHz, 对应横轴f23为第2束激光频率, 左纵轴为电离率, 橙色针状线为Nd-145 λ1+λ2双光子跃迁F1 → (F2) → F3, 对应横轴ν12+ν23为λ1+λ2双光子跃迁的共振位置, 右纵轴为双光子跃迁的相对强度, 当f12+f23位于共振位置附近时即可发生近共振λ1+λ2双光子跃迁, f12 = f23 = 0时的电离率如品红色菱形所示; 相应图11(f)为Nd-143的第2步谱线和λ1+λ2双光子跃迁. 从图11(c), (f)可看出, 第1束激光频率与Nd-150共振时, 钕奇同位素的第2步谱线峰位置与λ1+λ2双光子跃迁的共振位置一致, 第2步谱线主要由λ1+λ2双光子跃迁决定.

      具体到图10(b)青色标记的选择性光电离效果, 该组工况的计算条件为f12 = f23 = 0, IS23,148 = –1000 MHz, A3,145 = –100 MHz. Nd-145主要按照图11(a), (b)中品红色实线所示的F1 = 7.5 → (F2 = 8.5) → F3 = 9.5、黑色实线所示的F1 = 6.5 → (F2 = 7.5) → F3 = 8.5、青色实线所示的F1 = 5.5 → (F2 = 6.5) → F3 = 7.5等跃迁通道发生近共振λ1+λ2双光子跃迁, 相应的Nd-143 λ1+λ2双光子跃迁通道则如图11(c), (d)所示, 上述通道 恰好为跃迁强度靠前的超精细跃迁通道, 因此该组工况下, 激光频率与Nd-150共振时, 钕奇同位素电离率较大, 成为主要的杂质同位素.

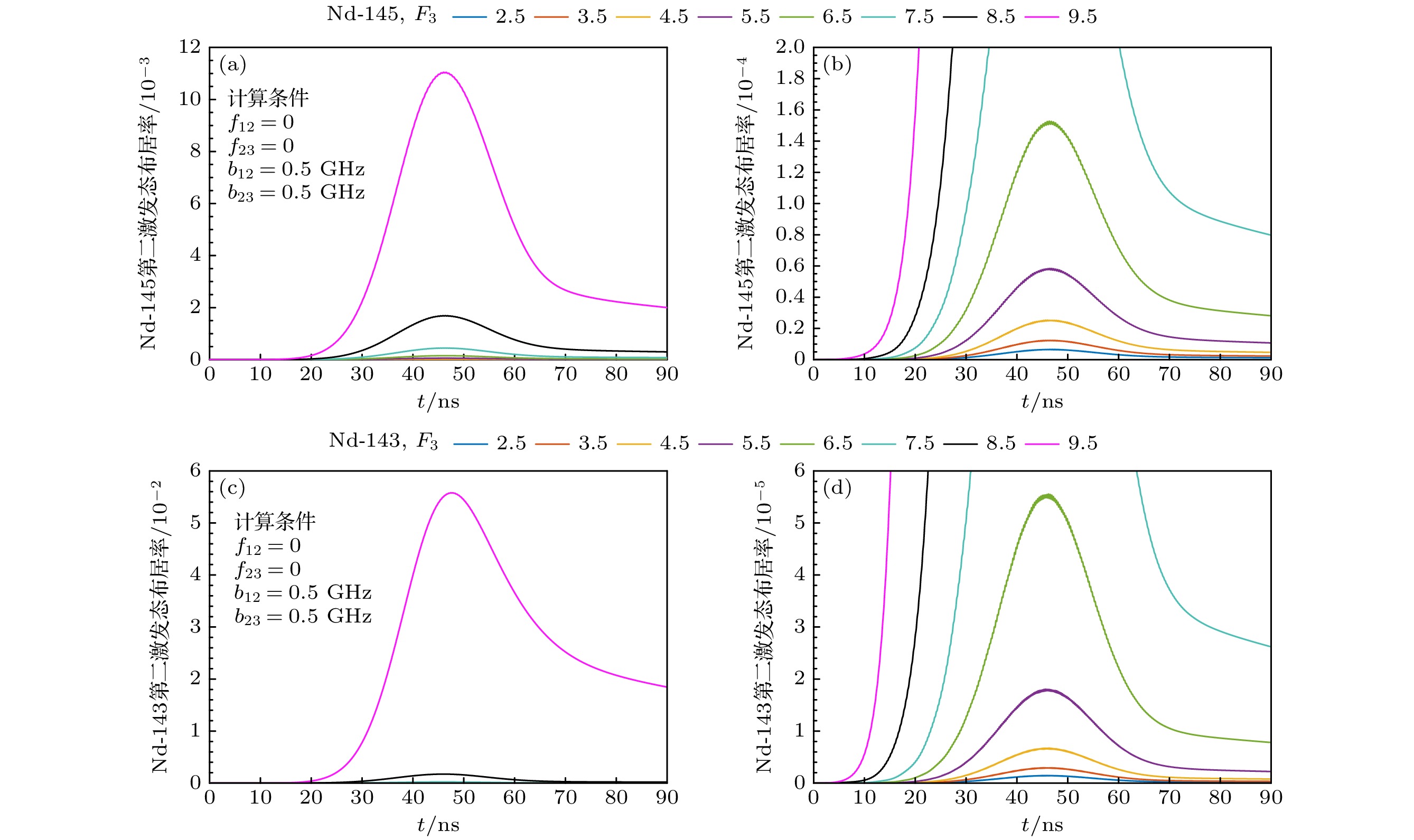
      另外, IS23,148 = –1000 MHz, A3,145 = –100 MHz, f12 = f23 = 0, b12 = b23 = 0.5 GHz时钕奇同位素第二激发态布居率随时间的变化图如图12所示, 其中Nd-145布居率和纵轴局部放大图分别如 图12(a), (b)所示, Nd-143布居率和纵轴局部放大图分别如图12(c), (d)所示, 图12中实线的颜色表示第二激发态能级的F值. 图12(a), (b)分别与表11“*”, “†”的工况相对应, f12 = f23 = 0在第2步谱线的位置如图11(c), (f)中的品红色菱形所示. 可见, 布居率按照F3由大至小的顺序依次降低, 该顺序与上述的λ1+λ2双光子跃迁强度顺序相对应.

      根据图10可知, 当IS23,148 ≥ 300 MHz时, 在b12 ≤ 0.5 GHz, b23 ≤ 1.0 GHz, 平行线偏振的典型激光参数下可实现Nd-150丰度大于95%, 与电磁法产品丰度相当, 并且此时钕奇同位素的超精细结构对Nd-150电离的影响较小. 在此基础上压窄激光线宽, 能够在保持电离率的同时下进一步提升Nd-150丰度, 超过电磁法产品丰度. 综上所述, 后续原子光谱实验应着重寻找同位素位移IS23,148 ≥ 300 MHz、第二激发态角动量J3 = 6的第2步跃迁, 第2步跃迁的约化电偶极矩达到路径一的30%即可满足丰度要求. 基于激光法可获得高丰度Nd-150同位素主要归因于以下3点的综合作用: 1) Nd-148, Nd-150间的同位素位移相较于其他同位素对更为显著, 这是由于Nd-148, Nd-150间的均方根核电荷半径差异约是其他同位素对的1.5倍[32]; 2)钕奇同位素超精细分裂程度相对较小, 对Nd-150电离的影响较低; 3)线宽等激光参数与钕原子光谱参数之间的相互匹配, 窄线宽激光的使用降低了其他杂质同位素的电离率.

    4.   结　论

    • 富集钕–150同位素在核工业、科学研究等领域有着重要应用. 基于高效高选择性多步电离路径, 原子蒸气激光同位素分离法能够实现钕同位素分离, 但现用路径第2步跃迁的同位素位移几乎为零, 导致产品中Nd-150丰度偏低. 为提高Nd-150选择性, 在假定电离路径参数取值的条件下开展钕同位素选择性光电离理论计算, 评估丰度满足要求时电离路径的同位素位移、超精细结构等参数水平, 指导后续原子光谱实验.

      本文基于考虑超精细结构和能级简并的三步电离模型, 通过与文献数据对比获得了现用路径分支比的最优拟合值β12 = 0.15, β23 = 0.5, 评估了现用路径在不同线宽下的Nd-150丰度水平; 为优化电离路径, 在沿用第1步跃迁, 采用跃迁强度更弱的第2步跃迁等前提下构造假定电离路径, 开展所有钕同位素的电离率计算, 评估不同同位素位移、超精细结构下的Nd-150丰度. 数值计算发现IS23,148 ≥ 300 MHz时, 在b12 ≤ 0.5 GHz, b23 ≤ 1.0 GHz, 平行线偏振的典型激光参数下可实现与电磁法相当的Nd-150丰度(> 95%). 在此基础上压窄激光线宽, 能够在保持电离率的同时获得超过电磁法的Nd-150产品. 后续原子光谱实验应着重寻找同位素位移IS23,148 ≥ 300 MHz、第二激发态角动量J3 = 6的第2步跃迁, 第2步跃迁的约化电偶极矩达到现用路径的30%即可满足丰度要求.

    参考文献 (32)

目录

/

返回文章
返回