高级搜索

基于物理信息神经网络的绝热捷径动力学分析

,  , 

downloadPDF

上一篇

下一篇

刘明, 张斯淇, 李宏. 基于物理信息神经网络的绝热捷径动力学分析[J]. 物理学报, 2025, 74(11): 114204-1. doi: 10.7498/aps.74.20250147
引用本文: 刘明, 张斯淇, 李宏. 基于物理信息神经网络的绝热捷径动力学分析[J]. 物理学报, 2025, 74(11): 114204-1. doi: 10.7498/aps.74.20250147
shu
Ming LIU, Siqi ZHANG, Hong LI. Dynamic analysis of shortcut to adiabaticity based on physical information neural network[J]. Acta Physica Sinica, 2025, 74(11): 114204-1. doi: 10.7498/aps.74.20250147
Citation: Ming LIU, Siqi ZHANG, Hong LI. Dynamic analysis of shortcut to adiabaticity based on physical information neural network[J]. Acta Physica Sinica, 2025, 74(11): 114204-1. doi: 10.7498/aps.74.20250147
shu

基于物理信息神经网络的绝热捷径动力学分析

  • 1.

    吉林工程技术师范学院数据科学与人工智能学院, 长春　130052

  • 2.

    吉林工程技术师范学院, 吉林省量子信息技术工程实验室, 长春　130052

    • 通讯作者: E-mail: lihong@jlenu.edu.cn.

  • 中图分类号: 42.50.–p, 03.67.-a, 07.05.Mh, 02.60.Cb

Dynamic analysis of shortcut to adiabaticity based on physical information neural network

  • 1.

    School of Data Science and Artificial Intelligence , Jilin Engineering Normal University, Changchun 130052, China

  • 2.

    Jilin Engineering Laboratory for Quantum Information Technology, Jilin Engineering Normal University, Changchun 130052, China

    • Corresponding author: E-mail: lihong@jlenu.edu.cn.

  • MSC: 42.50.–p, 03.67.-a, 07.05.Mh, 02.60.Cb

  • 摘要: 本文提出一种基于物理信息神经网络的量子绝热捷径方案. 与传统的绝热捷径技术相比, 创新性地引入机器学习技术, 利用参数化的物理信息神经网络解含参数的微分方程, 将神经网络作为量子绝热演化过程的逼近函数, 并将含参数的微分方程和微分方程的各种物理约束条件作为参数化的神经网络的损失函数, 训练神经网络, 拟合量子系统演化过程, 获得布居反转的驱动控制函数. 数值实验表明, 量子系统可以在短时间内实现布居反转, 并且具有很高的保真度、很强的鲁棒性. 神经网络具有很强的计算能力, 适合复杂系统的驱动控制函数的生成. 与传统的绝热捷径技术相比, 具有更好的效果和更强的实用性.
    Abstract: A quantum shortcut to adiabaticity scheme based on physics-informed neural networks is proposed in this work. Compared with traditional shortcut to adiabaticity technology, our method innovatively integrates machine learning methods by employing parameterized physics-informed neural networks to solve parameterized differential equations. The neural networks serve as an approximating function for quantum adiabatic evolution processes, while incorporating parameter-dependent differential equations and various physical constraints as components of the loss function. Through networks training, we effectively simulate quantum system dynamics and derive the driving control field for population inversion. Numerical simulations show that the quantum system can achieve rapid population inversion within significantly reduced time while maintaining high fidelity and exceptional robustness against parameter fluctuations. The neural networks exhibit remarkable computational capabilities, particularly suitable for generating control functions in complex quantum systems. Compared with conventional counter-diabatic driving and transitionless quantum driving methods, this PINN-based framework not only achieves better control performance but also provides the improved practicality for experimental implementations. The success of this method demonstrates its promising applications in quantum control tasks, including but not limited to quantum state preparation, quantum gate optimization, and adiabatic quantum computing acceleration.
  • 加载中

  • 图 1  STAPINN原理设计图

    Figure 1.  STAPINN principle design diagram.

    下载: 全尺寸图片 幻灯片

    图 2  PINN方法仿真和Mathematica软件仿真无驱动布居转移情况对比图　(a) PINN仿真无驱动布居转移; (b) Mathematica软件中无驱动布居转移的仿真. 参数选取为: $ {t_0} = $$ 5 \times {10^{ - 12}} {\text{ s}}, \;{t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}}, \;{\varOmega _0} = 10 {\text{ MHz}}, \;\delta = 600 {\text{ }} {\text{MHz}} $

    Figure 2.  Comparison between PINN method simulation and Mathematica software simulation of undriven population transfer: (a) PINN simulated undriven population transfer; (b) simulation of undriven population transfer in Mathematica software. The parameters are selected as: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}}, \;{t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}}, \;{\varOmega _0} = 10 {\text{ MHz}}, \;\delta = 600 {\text{ MHz}} $.

    下载: 全尺寸图片 幻灯片

    图 3  不同训练次数下的损失函数曲线图. 参数选取为$ {t_0} = 5 \times {10^{ - 12}} {\text{ s}}$, $ {t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, $ {\varOmega _0} = 10 {\text{ MHz}}$, $\delta = $$ 600 {\text{ MHz}} $

    Figure 3.  Loss function curves under different training times. The parameters are selected as: $ {t_0} = 5 \times {10^{ - 12}} {\text{ s}}, \;{t_{\text{f}}} = 2 \times $$ {10^{ - 10}} {\text{ s}}$, $ {\varOmega _0} = 10 {\text{ MHz}}, \;\delta = 600 {\text{ MHz}} $.

    下载: 全尺寸图片 幻灯片

    图 4  STAPINN方法和Mathematica软件仿真加驱动的布居转移情况对比　(a) STAPINN仿真加驱动的布居转移情况; (b) Mathematica仿真加驱动的布居转移情况. 参数选取为: ${t_0} = 5 \times {10^{ - 12}} {\text{ s}} $, $ {t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600 {\text{ MHz}} $

    Figure 4.  Comparison of driver population transfer after STAPINN method and Mathematica software simulation and optimization: (a) STAPINN simulation optimization drives population transfer; (b) population transfer driven by Mathematica simulation optimization. The parameters are selected as: $ {t_0} = 5 \times {10^{ - 12}} {\text{ s}}$, ${t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = $$ 10 {\text{ MHz}}$, $\delta = 600 {\text{ MHz}} $.

    下载: 全尺寸图片 幻灯片

    图 5  (a)多项式展开的驱动函数和傅里叶级数展开的驱动函数对比图; (b)利用Mathematica软件模拟此驱动下的布居转移情况, 蓝色和褐色实线为傅里叶级数展开的驱动函数对应的布居数反转曲线, 红色和绿色虚线为多项式展开的驱动函数对应的布居反转曲线. 参数选取为: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}} $, ${t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600 {\text{ MHz}} $

    Figure 5.  (a) Comparison between the driver function of polynomial expansion and the driver function of Fourier series expansion; (b) using Mathematica software to simulate the population transfer under this drive, the blue and brown solid lines are the population inversion curves corresponding to the driver function of Fourier series expansion, and the red and green dashed lines are the population inversion curves corresponding to the driver function of polynomial expansion. The parameters are selected as: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}} $, ${t_{\text{f}}} = 2 \times $$ {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600 {\text{ MHz}} $.

    下载: 全尺寸图片 幻灯片

    图 6  (a)不同训练次数下的驱动曲线图; (b)不同训练次数下的驱动实现的布居转移情况对比图. 参数选取为: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}}$, ${t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600 {\text{ MHz}} $

    Figure 6.  (a) Drive curves under different training times; (b) comparison diagram of population transfer of the drive under different training times. Set the parameter to: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}}$, ${t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600{\text{ }} {\text{ MHz}} $

    下载: 全尺寸图片 幻灯片

    图 7  保真度随参数$ {\varOmega _0} $和$ \delta $的变化

    Figure 7.  Variation of fidelity with parameter $ {\varOmega _0} $and $ \delta $.

    下载: 全尺寸图片 幻灯片
  • [1] Vitanov N V, Halfmann T, Shore B W 2001 Annu Rev. Phys. Chem. 52 763 doi: 10.1146/annurev.physchem.52.1.763
    [2] Law C K, Eberly J H 1996 Phys. Rev. Lett. 76 1055 doi: 10.1103/PhysRevLett.76.1055
    [3] Kuhn A, Hennrich M, Bondo T 1999 Appl Phys. B 69 373 doi: 10.1007/s003400050822
    [4] Torosov B T, Guérin S, Vitanov N V 2011 Phys. Rev. Lett. 106 233001 doi: 10.1103/PhysRevLett.106.233001
    [5] Brif C, Chakrabarti R, Rabitz H 2010 New J. Phys. 12 075008 doi: 10.1088/1367-2630/12/7/075008
    [6] Demirplak M, Rice S A 2002 J. Chem. Phys. 116 8028 doi: 10.1063/1.1467896
    [7] del Campo A 2011 Phys. Rev. A 84 031606 doi: 10.1103/PhysRevA.84.031606
    [8] del Campo A 2013 Phys. Rev. Lett. 111 100502 doi: 10.1103/PhysRevLett.111.100502
    [9] Tian L 2012 Phys. Rev. Lett. 108 153604 doi: 10.1103/PhysRevLett.108.153604
    [10] Berry M V 2009 J. Phys. A: Math. Theor. 42 365303 doi: 10.1088/1751-8113/42/36/365303
    [11] Ibáñez S, Li Y C, Chen X 2015 Phys. Rev. A 92 062136 doi: 10.1103/PhysRevA.92.062136
    [12] Song X K, Ai Q, Qiu J 2016 Phys. Rev. A 93 052324 doi: 10.1103/PhysRevA.93.052324
    [13] Liu S, Chen Y H, Wang Y 2022 Phys. Rev. A 106 042430 doi: 10.1103/PhysRevA.106.042430
    [14] Masuda S, Nakamura K 2008 Phys. Rev. A 78 062108 doi: 10.1103/PhysRevA.78.062108
    [15] Masuda S, Nakamura K 2011 Phys. Rev. A 84 043434 doi: 10.1103/PhysRevA.84.043434
    [16] Zhu J J, Chen X 2021 Phys. Rev. A 103 023307 doi: 10.1103/PhysRevA.103.023307
    [17] Luo D W, Pyshkin P, Lam C H 2015 Phys. Rev. A 92 062127 doi: 10.1103/PhysRevA.92.062127
    [18] Kang Y H, Chen Y H, Huang B H 2017 Ann. Phys. 529 1700004 doi: 10.1002/andp.201700004
    [19] Torrontegui E, Martínez-Garaot S, Muga J 2014 Phys. Rev. A 89 043408 doi: 10.1103/PhysRevA.89.043408
    [20] Güngördü U, Wan Y, FasihiM A 2012 Phys. Rev. A 86 062312 doi: 10.1103/PhysRevA.86.062312
    [21] 张瑶, 张云波, 陈立 2021 物理学报 70 168702 doi: 10.7498/aps.70.20210403 Zhang Y, Zhang Y B, Chen L 2021 Acta Phys. Sin. 70 168702 doi: 10.7498/aps.70.20210403
    [22] 田十方, 李彪 2023 物理学报 72 100202 doi: 10.7498/aps.72.20222381 Tian S F, Li B 2023 Acta Phys. Sin. 72 100202 doi: 10.7498/aps.72.20222381
    [23] 方波浪, 王建国, 冯国斌 2022 物理学报 71 200601 doi: 10.7498/aps.71.20220670 Fang B L, Wang J G, Feng G B 2022 Acta Phys. Sin. 71 200601 doi: 10.7498/aps.71.20220670
    [24] Cai Y H, He Y L, Lang S N, Cui X B, Zhang X Q, Yao Z J 2025 Comput. Geosci. 196 105857 doi: 10.1016/j.cageo.2025.105857
    [25] Nursyiva I, Maharani A B, Fatimah N H, Sugiyarto S, Danang A P 2025 Results Appl. Math. 25 100539 doi: 10.1016/j.rinam.2025.100539
    [26] Ko T, Kim D, Park J, Lee S H 2025 Appl. Energy 382 125318 doi: 10.1016/j.apenergy.2025.125318
    [27] Zheng J C, Yang Y L 2024 Appl. Soft Comput. 167 112370 doi: 10.1016/j.asoc.2024.112370
    [28] Chen X, Peng W Q 2025 Commun. Theor. Phys. 77 025002 doi: 10.1088/1572-9494/ad75f7
    [29] Roy A, Chatterjee T, Adhikari S 2024 Probab. Eng. Mech. 78 103701 doi: 10.1016/j.probengmech.2024.103701
    [30] Han J, Jentzen A, Weinan E 2018 Proc. Natl. Acad. Sci. U. S. A 115 8505 doi: 10.1073/pnas.1718942115
    [31] Rudy H S, Brunton L S, Proctor L J, Kutz N 2017 Sci. Adv. 3 e1602614 doi: 10.1126/sciadv.1602614
    [32] Raissi M, Karniadakis G E 2018 J. Comput. Phys. 357 125 doi: 10.1016/j.jcp.2017.11.039
    [33] Li J, Chen Y 2021 Commun. Theor. Phys. 73 015001 doi: 10.1088/1572-9494/abc3ad
    [34] Pu J C, Li J, Chen Y 2021 Nonlinear Dyn. 105 1723
    [35] Pu J C, Chen Y 2022 Chaos, Solitons Fractals 160 112182 doi: 10.1016/j.chaos.2022.112182
    [36] Lin S N, Chen Y 2022 J. Comput. Phys. 457 111053 doi: 10.1016/j.jcp.2022.111053
    [37] Ding Y C, Ban Y, Martín J, Solano E, Casanova J, Chen X 2021 Phys. Rev. A 103 L040401 doi: 10.1103/PhysRevA.103.L040401
    [38] Norambuena A, Mattheakis M, González F, Coto R 2024 Phys. Rev. Lett 132 010801 doi: 10.1103/PhysRevLett.132.010801
  • 加载中
图( 7)
计量
  • 文章访问数:  34
  • HTML全文浏览数:  34
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-02-07
  • 刊出日期:  2025-06-05

基于物理信息神经网络的绝热捷径动力学分析

    通讯作者: E-mail: lihong@jlenu.edu.cn.
  • 1. 吉林工程技术师范学院数据科学与人工智能学院, 长春　130052
  • 2. 吉林工程技术师范学院, 吉林省量子信息技术工程实验室, 长春　130052
  • 收稿日期:  2025-02-07

摘要: 本文提出一种基于物理信息神经网络的量子绝热捷径方案. 与传统的绝热捷径技术相比, 创新性地引入机器学习技术, 利用参数化的物理信息神经网络解含参数的微分方程, 将神经网络作为量子绝热演化过程的逼近函数, 并将含参数的微分方程和微分方程的各种物理约束条件作为参数化的神经网络的损失函数, 训练神经网络, 拟合量子系统演化过程, 获得布居反转的驱动控制函数. 数值实验表明, 量子系统可以在短时间内实现布居反转, 并且具有很高的保真度、很强的鲁棒性. 神经网络具有很强的计算能力, 适合复杂系统的驱动控制函数的生成. 与传统的绝热捷径技术相比, 具有更好的效果和更强的实用性.

English Abstract

    全文HTML

    1.   引　言

    • 量子态的快速、精确操控是原子和分子物理学中的一项基本操作, 在激光控制的化学反应、计量学、干涉测量、核磁共振和量子信息处理[1–3]等领域有着广泛的应用. 在各种实现量子态操控的方法中[4,5], 量子绝热过程是一种较为普遍适用的方法[6–9]. 目前已经提出了许多基于不同理论的绝热捷径技术(shortcuts to adiabaticity, STA), 包括无跃迁量子驱动[10–13]、Fast-Forward方法[14–16]、基于LR不变量的反控制法[17–20]等, 绝热过程的鲁棒性和近乎完美的保真度在这些绝热捷径方法中都能够得以保留. 量子绝热捷径技术需要求解微分方程, 微分方程的精确求解往往需要用到数值解法, 包括欧拉法、有限元法等. 这些方法在求解过程中普遍面临着微分方程约束条件和求解精度及算法复杂度等问题.

      随着计算科学的快速发展, 深度学习在许多领域取得了巨大成功, 包括计算机视觉(CV)、自然语言处理(NLP)、模式识别和蛋白质结构预测等[21–24]. 在这些领域中的成功应用证明了神经网络模型能够很好地逼近复杂函数. 微分方程的数值解一直是数学物理领域的一个热门话题. 具有通用近似计算能力的神经网络常用于代替传统方法求解微分方程. 物理信息神经网络(physics-informed neural networks, PINN)[25–29]被提出后, 其相关模型一直被应用于求解数学和物理领域的各种微分方程, 如微分方程未知解的函数逼近[30]和数据驱动等问题[31,32]. 诸多学者在此领域做了大量有意义的工作, 利用神经网络的这一特性, Raissi和Karniadakis[32]提出的PINN模型以其高预测精度和良好的泛化能力而被广泛认可. 该模型将物理模型编码为损失函数, 并通过不断地减小损失函数大小, 使之逐渐趋近于0, 在使其受到微分方程和边界条件的约束下, 完成方程解的近似. Chen和他的团队[33–35]对一些经典的数学物理方程进行了研究, 如Sine-Gordon方程、线性薛定谔方程和非线性薛定谔方程, 得到了这些方程的解; 并且在PINN模型的基础上, 提出了一种两阶段PINN[36], 对一类物理方程进行了模拟, 获得了这些方程的局域解. Ding等[37]提出了一种结合绝热捷径与深度强化学习的量子控制方法, 设计出了快速、抗干扰的控制脉冲. 相较于深度强化学习, PINNs模型结构紧凑, 逻辑清晰, 充分利用了神经网络的函数逼近能力和优化能力, 更加适合具有解析表达式的动力学过程的拟合和优化. Norambuena等[38]使用马尔可夫主方程作为物理约束去训练PINN, 从而实现量子系统的最优化控制.

      在上述研究中, 缺乏绝热捷径技术与PINN方法的有机融合, 本文重点关注利用物理信息神经网络方法解决量子系统的绝热捷径动力学问题, 即绝热捷径物理信息神经网络(shortcuts to adiabaticity physics-informed neural networks, STAPINN). 通过薛定谔方程推导出含参的微分方程, 根据微分方程提出了一种参数化的PINN模型, 并将模型应用于绝热捷径的动力学演化过程. 通过训练神经网络, 拟合量子系统演化过程, 获得布居反转的驱动控制函数, 实现量子系统布居反转.

      本文的结构如下: 第1节为引言; 第2节对PINN和STAPINN两种方法进行了详细的介绍; 第3节进行了数值分析模拟, 通过STAPINN方法找到了优化后的数值型驱动函数, 实现了布居反转, 为验证结果正确性, 把数值型驱动函数拟合成解析函数形式, 用此解析式同样实现了布居反转, 进而讨论了系统参数对保真度的影响; 第4节为结论.

    2.   深度学习方法

      2.1.   PINN方法

    • 微分方程的精确求解往往基于网格的方法, 例如有限差分法和有限元法, 它们是求解微分方程的传统方法. 这些方法在求解过程中普遍面临着微分方程约束条件的问题, 同时求解方程的精度受限于网格划分的精细程度. 近年来, 具有通用近似能力的神经网络常用于代替传统方法求解微分方程. 基于神经网络求解微分方程是一种无网格的方法, 在求解的过程中不需要网格划分, 同样能够较高精度地处理复杂的物理和数学等领域有关的微分方程的求解问题.

      PINN是一种结合深度学习与物理定律的数值方法, 用于求解微分方程. 它通过将微分方程的约束条件直接嵌入到神经网络的损失函数中, 利用自动微分技术来训练网络, 从而逼近微分方程的解.

      PINN模型通常由一个深度神经网络构成. 深度神经网络的损失函数中加入了物理信息项, 深度神经网络所代表的函数遵循物理定律. PINN通过最小化神经网络的损失函数来近似微分方程的解. 其中, 神经网络的损失函数由初始条件的损失项、边界条件的损失项以及微分方程约束的损失项等构成. PINN经过训练后, 可以获得微分方程的数值解. 模型训练时, 不仅要最小化数据误差, 还要最小化物理信息误差, 确保拟合的结果符合物理定律.

      设计PINN时, 先将待解的微分方程转化为一个优化问题, 将微分方程的约束条件编码到神经网络的损失函数中. 通过训练, 最小化损失函数, 使神经网络的输出逼近微分方程的真实解. 在训练过程中, 利用深度学习框架PyTorch中的自动微分模块, 计算神经网络输出值的各阶导数, 从而实现微分方程的约束条件. 通过神经网络的反向传播算法优化神经网络的参数, 以最小化损失函数. 不断更新网络权重值和偏置值, 直到损失函数满足收敛条件或达到预设的训练轮次. 本文将具有约束的常微分方程描述如下:

      其中$ {\varOmega _{{\mathrm{a}}}} $是控制参数; $ T $是时间域; $ c(t) $为方程的解, 是时间$ t $的函数; $ C $为解空间; $ B $为约束. STAPINN模型通常由一个深度神经网络构成, 在损失函数$ {\mathrm{Loss}} $中加入了物理信息项, 并将微分方程的约束条件直接嵌入到损失函数中, 神经网络的损失函数由初始条件的损失项、边界条件的损失项以及微分方程等约束条件构成. 神经网所代表的函数遵循物理定律. PINN通过最小化神经网络的损失函数来近似微分方程的解$ c(t) $. 在训练过程中, 利用深度学习框架PyTorch中的自动微分模块, 计算神经网络输出值的各阶导数, 从而实现微分方程的约束条件. 通过反向传播算法优化神经网络的参数, 以最小化损失函数.

      • 2.2.   STAPINN

    • 本文用PINN优化绝热捷径中的驱动项. 选取两能级哈密顿量系统, 其动力学方程描述为

      其中$ {c_1} $, $ {c_{2}} $为裸态$ \left| {1} \right\rangle $和$ \left| {2} \right\rangle $的振幅; $ {\varOmega _{\mathrm{R}}}\left( t \right) $为Rabi频率; $ \varDelta \left( t \right) $为失谐量; $ {\varOmega _{\mathrm{a}}}\left( t \right) $为驱动控制函数. 进一步化简得到两个含时演化微分方程:

      用抽象函数描述如下:

      其中$ {\varOmega _{{\mathrm{a}}}} $是驱动项, 视作微分方程的参数, 它也是时间$ t $的函数, 记作$ {\varOmega _{{\mathrm{a}}}}(t) $. $ {\boldsymbol{c}}(t) $代表在某一时刻系统所处的状态, 用布居数描述, 是时间的函数, 同时也是微分方程的解函数. $ \dot {\boldsymbol{c}} $是$ {\boldsymbol{c}}(t) $的导数. 微分方程是一个含参数项$ {\varOmega _{{\mathrm{a}}}}(t) $的微分方程. 本文的任务是找到能够满足约束条件的微分方程的解$ {\boldsymbol{c}}(t) $, 并找到在该解下能满足一定条件的恰当的驱动项$ {\varOmega _{{\mathrm{a}}}}(t) $. 本文通过参数化的PINN生成满足微分方程的驱动项$ {\varOmega _{{\mathrm{a}}}}(t) $.

      绝热捷径的目的是要克服绝热控制中系统态演化缓慢的问题, 通过参数控制, 快速模拟绝热过程, 因此微分方程在$ {t_0} $和$ {t_{\text{f}}} $时刻需要满足一定约束条件. 实现布居反转的一个关键因素是不同时刻采用合适的驱动值. 也就是说需要通过一定的方式找到满足一定条件的驱动项$ {\varOmega _{{\mathrm{a}}}}(t) $, 它能够使得系统沿着一条符合布居反转约束的轨迹演化. 这个演化过程很难直接通过计算得到, 且不具有唯一性. 它可能不是一个最优解, 但它能使布居反转. 这个过程可以描述为寻找微分方程的参变函数的过程. 利用传统的解析算法对于多能级复杂系统很难找到这个关于时间$ t $的函数, 本文通过构造含参的PINN可以找到, 并实现量子绝热捷径. 这个PINN称为绝热捷径物理信息神经网络, 称为STAPINN (shortcuts to adiabaticity PINN).

      • 2.3.   STAPINN设计

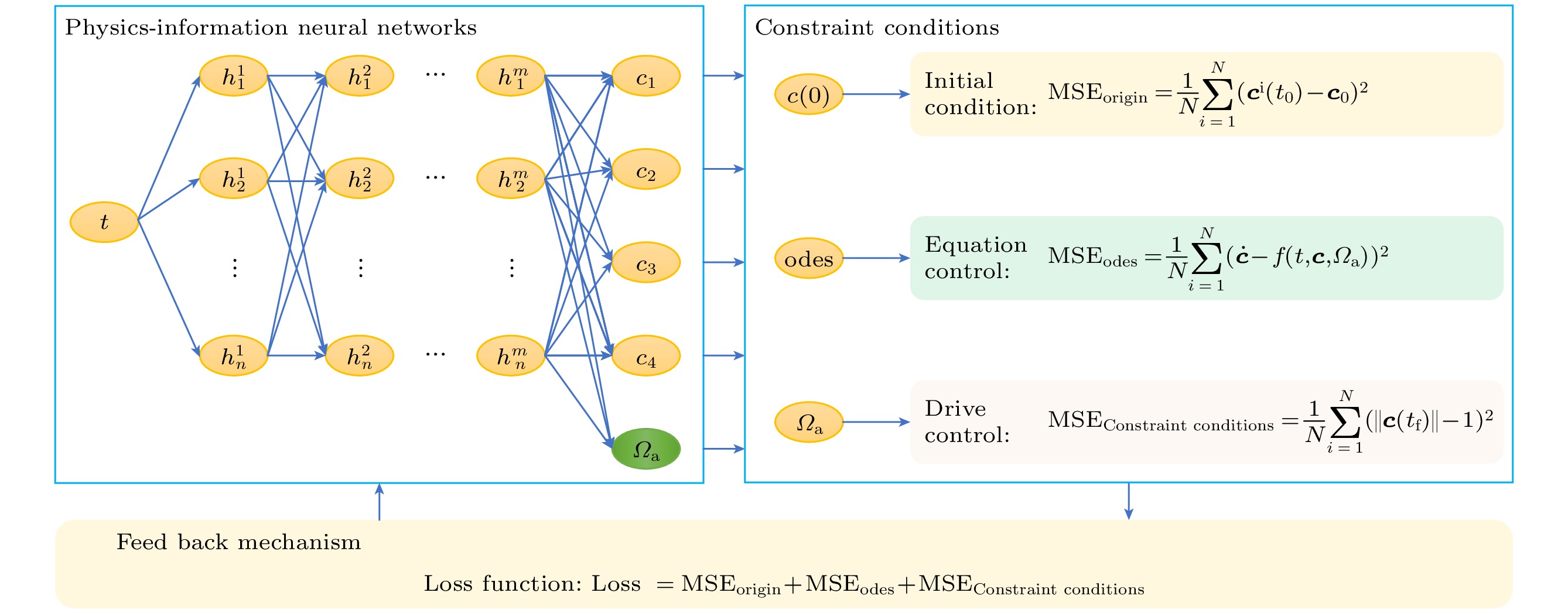
    • STAPINN原理图如图1所示. 时间$ t $作为神经网络的唯一输入值, 微分方程中的状态函数值作为输出, 二能级系统中共两个状态. 状态值是复数, 将状态拆分成实部和虚部, 分别作处理, 需要4个输出节点. 驱动值不仅要参与损失函数的计算过程, 在系统训练结束后, 需要输出随时间变化的驱动值. 驱动值也作为一个输出节点, 整个网络共有5个输出节点.

      当$ {\varOmega _{\text{a}}}(t) = 0 $或$ {\varOmega _{\text{a}}}(t) = C $, C为常数, 微分方程和神经网有确定的对应关系, 微分方程在约束条件下如果有确定解时, 神经网络会唯一地收敛到确切的状态. 含驱动控制参数的微分方程没有唯一解, 神经网络和微分方程也不具有完全确定的对应关系, 但通过这个网络可以找到一个符合条件的驱动$ {\varOmega _{\text{a}}}(t) $. 神经网络和带驱动项的含参微分方程对应. 根据绝热捷径布居反转的要求, 微分方程可能有最优解, 也可能没有最优解, 但可以找到满足条件的解, 解并不唯一. 对应的神经网络训练时会随机收敛到不同的状态, 微分方程可能沿着不同的路径演化, 但都可以实现布居数反转. 微分方程演化过程看成两个子系统的演化, 一个代表量子系统状态演化, 即布居反转过程. 另一个是含时的驱动子系统的演化. STAPINN实现微分方程时, 驱动项需要添加到损失函数中, 和微分方程一起作为约束条件, 限制系统演化方向, 它和微分方程相互作用, 相互制约, 协调演化, 最终实现布居反转. 之所以将驱动项作为神经网络的一个输出项, 目的是当神经网络收敛到我们想要的结果, 就能够明确地输出驱动随时间变化的值. 一个神经网络实际上实现了两个函数:

      整个神经网络用函数描述如下:

      其中

      上述公式中, (6)式是微分方程的解函数, (7)式是微分方程的关于时间的参数函数. 解函数和参数函数在神经网络中担负的任务不同, 适合采用多任务神经网络. 将神经网络分成两个子网络, 一个是解函数子网络, 一个是参数子网络, 使神经网络参数化. 与之对应, 数据处理过程形成两个通道, 一个是解通道, 另一个是参数通道, 对于不同的通道采取不同的约束条件. 当参数比较复杂时能够提高整个神经网络对于更复杂系统演化过程的拟合能力. 这种参数化的神经网络模型更加适合含时的量子演化动力学过程, 具有普适性. 为实现上述算法, 构造的神经网络结构如下: 神经网络采用全连接的6层BP神经网络, 含有4个隐藏层, 一个输入层, 一个输出层. 输入层只有一个节点, 时间$ t $作为神经网络的输入数据. 隐藏层每层包含100个节点, 输出层节点数为5, 包含4个状态值和1个驱动项. 驱动项也是时间的函数. 本文的目的也恰恰是要优化含时参数, 得到一个能够满足方程和初值约束的关于驱动值的时间函数. 用神经网络解微分方程的过程可以看作是用神经网络拟合含参微分方程的解的过程. 其中的关键是将微分方程和相应的初值等约束条件作为损失函数训练神经网络. 本文为实现两能级量子系统的布居反转, 构造损失函数如下:

      其中, $ {\text{MS}}{{\text{E}}_{{\mathrm{origin}}}} $是实现初值约束的损失函数; $ {\text{MS}}{{\text{E}}_{{\mathrm{odes}}}} $是微分方程控制项, 训练产生的结果中驱动项是时间的一元函数, 需要满足布居反转约束; $ {\text{MS}}{{\text{E}}_{{\mathrm{controlconstraint}}}} $是实现布居反转的损失函数, 是有关驱动控制约束条件. 该约束不是硬约束, 在该约束下, 微分方程没有唯一解. 在实现布居反转的前提下, 可能得到不同的驱动函数. 用上述损失函数训练的神经网络, 不仅可以找到驱动控制函数, 还可以仿真布居反转.

      时间$ t $的取值范围在$ 1 \times {10^{ - 10}}~ {\text{s}} $的量级上, 直接用作神经网络输入会使损失函数的值同样处在更低的量级上. 由于计算机数值计算本身有精度局限, 使损失函数严重失真, 甚至失效. 根据绝热演化微分方程的特点, 神经网输入值需要在满足物理微分方程的前提下做正则化处理, 使神经网输入值有效的同时, 保证微分方程的解不变.

    3.   数值模拟分析

    • 本文选取Allen-Eberly(AE)模型, 形式如下:

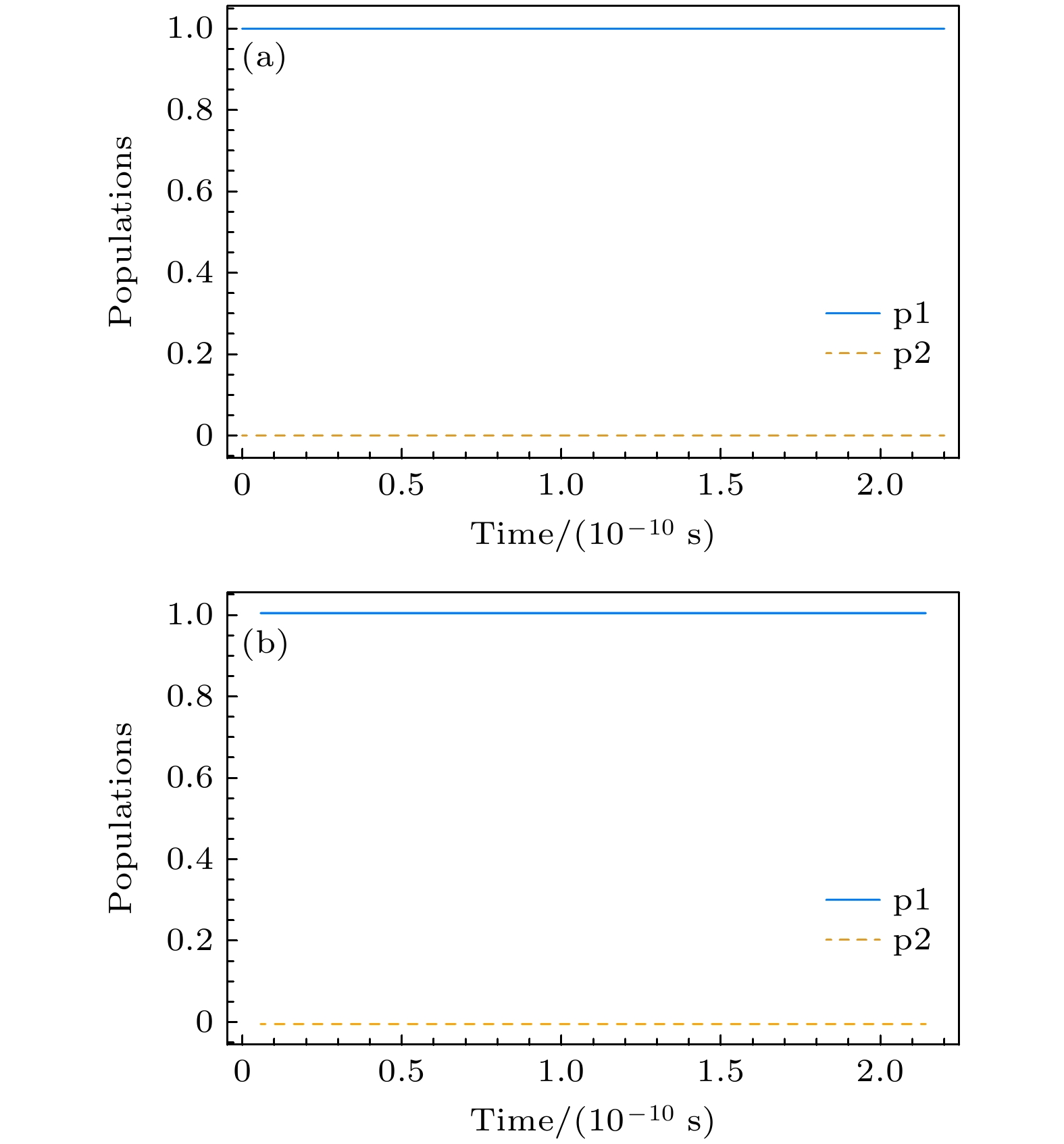
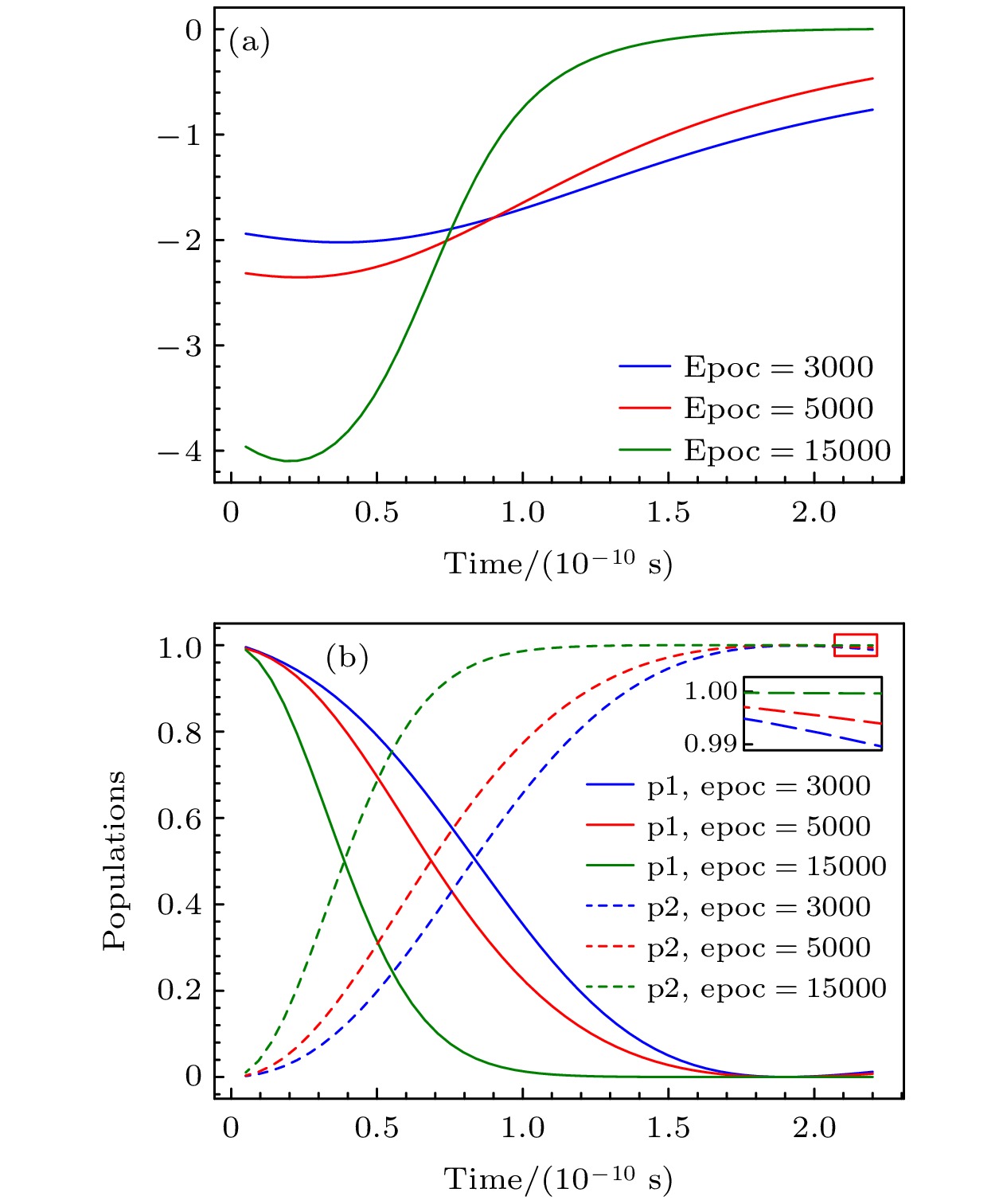
      其中$ {\varOmega _{0}} , {\delta _{0}} , {t_0} $为参数; $ {t_{\text{f}}} $为系统最终演化时间. 用pytorch中的nn.Module定义上述STAPINN模型, 使用pytorch中的均方差函数torch.nn.MSELoss 计算误差, 误差值大小为: $ {\text{Loss}} = \displaystyle\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{(L({c_i};c, t))}^2}} $. 采用pyTorch中的Adam作为优化器, 优化梯度下降算法. Adam是一种自适应学习率优化算法, 在深度学习中广泛使用. 训练时, 令学习率$ \eta = 1 \times {10^{ - 4}} $, 输入值为时间$ t $, 样本点$ t $值来自于采样的结果, 在系统演化的初始时刻$ {t_0} $和系统演化的结束时刻$ {t_{\text{f}}} $区间进行采样. 令初值$ {t_0} = 0.0{0}5 {\text{ ns}} $, 结束时刻$ {t_{\text{f}}} = {0}.2 {\text{ ns}} $, 采样数$ N = 50 $. 每轮训练固定将这50个样本值批量送入输入层节点. 输出值为系统演化过程中的布居数$ {c_i} $. 利用之前定义的损失函数训练神经网络. 训练好的网络可以看作一个拟合函数, 逼近了微分方程的解, 模拟了无驱动的绝热演化过程.

      本文首先模拟了无额外驱动的布居转移情况, 如图2(a)所示, 为神经网络训练$ {\text{epoc}} = 15000 $次后的结果, p1和p2分别代表激发态和基态的布居数. 为了验证结果的正确有效行性, 采用Mathematica数学软件解该微分方程, 结果如图2(b)所示. 从图2中可以看出, 在没有额外驱动的前提下, PINN方法和Mathematica数学软件仿真所得系统的状态演化曲线是一致的, 并且在整个演化时间周期内系统布居并未发生改变, 说明了利用STAPINN实现两能级量子系统演化数值模拟的可行性.

      在损失函数中加入驱动项$ {\varOmega _{\text{a}}}(t) $, 并在整个时间演化周期内若干次对演化过程施加控制, 限制布居转移过程. 将控制过程作为演化的约束条件, 加入到损失函数中. 损失函数定义为: $ {\text{Loss}} = {\text{MS}}{{\text{E}}_{{\mathrm{origin}}}} + {\text{MS}}{{\text{E}}_{{\mathrm{odes}}}} + {\text{MS}}{{\text{E}}_{{\mathrm{controlconditions}}}} $, 通过在不同时间节点控制布居数, 实现布居反转. 在训练过程中会出现很多驱动函数$ {\varOmega _{\text{a}}}(t) $. 利用不同的驱动函数$ {\varOmega _{\text{a}}}(t) $驱动系统演化, 会导致不同的演化过程, 形成一族系统演化路径, 目的就是要在其中找到实现布居反转的优化后的演化路径. 驱动函数$ {\varOmega _{\text{a}}}(t) $可以看作是微分方程的参数, 不同的参数会使得微分方程有不同的解. 将微分方程以及实现布居反转的控制过程作为约束条件, 将约束条件编码到神经网络的损失函数, 通过损失函数训练神经网络和优化网络. 训练后的神经网络不仅逼近了绝热演化过程, 还得到了一个满足布居反转条件的驱动函数.

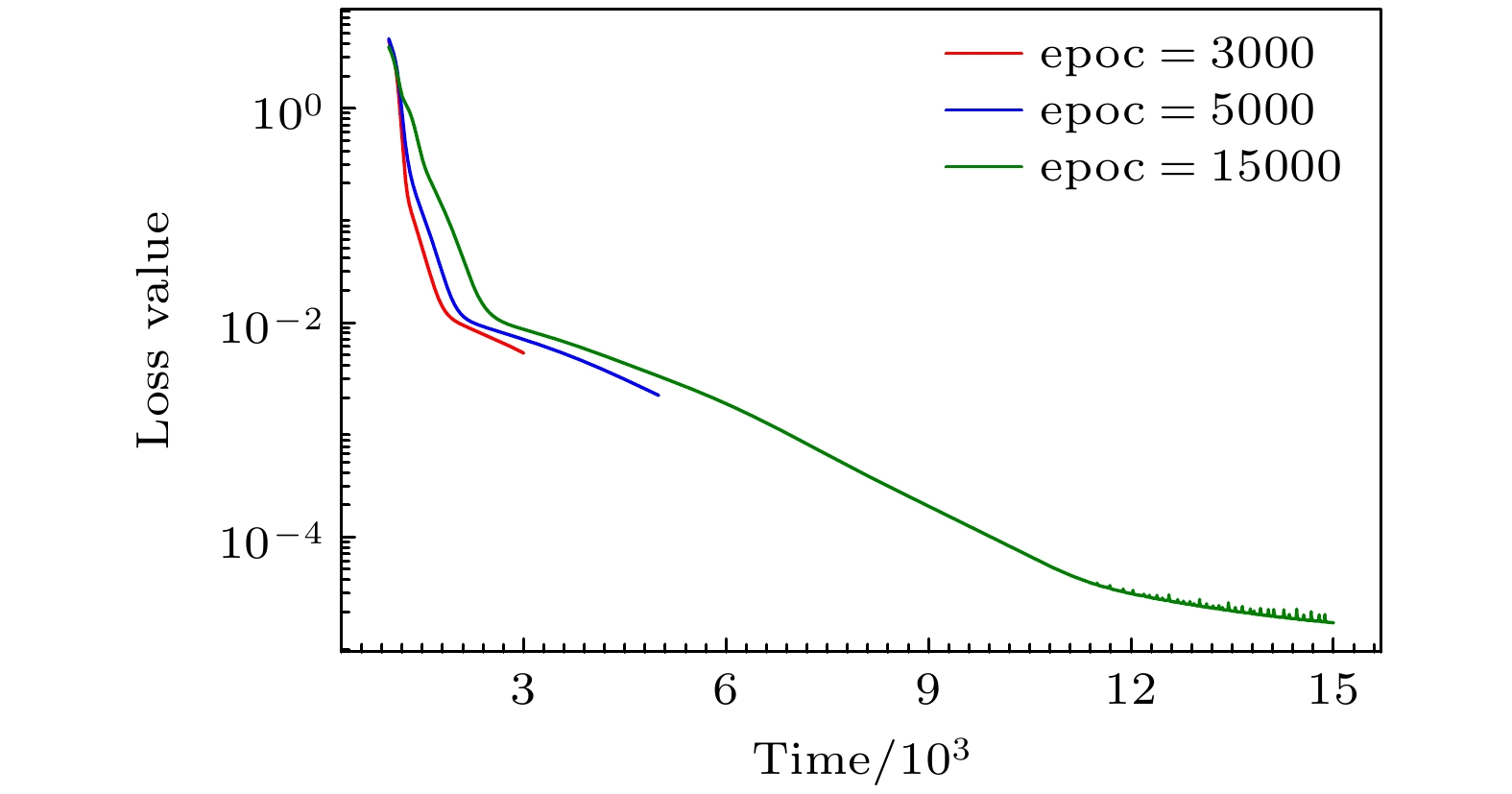
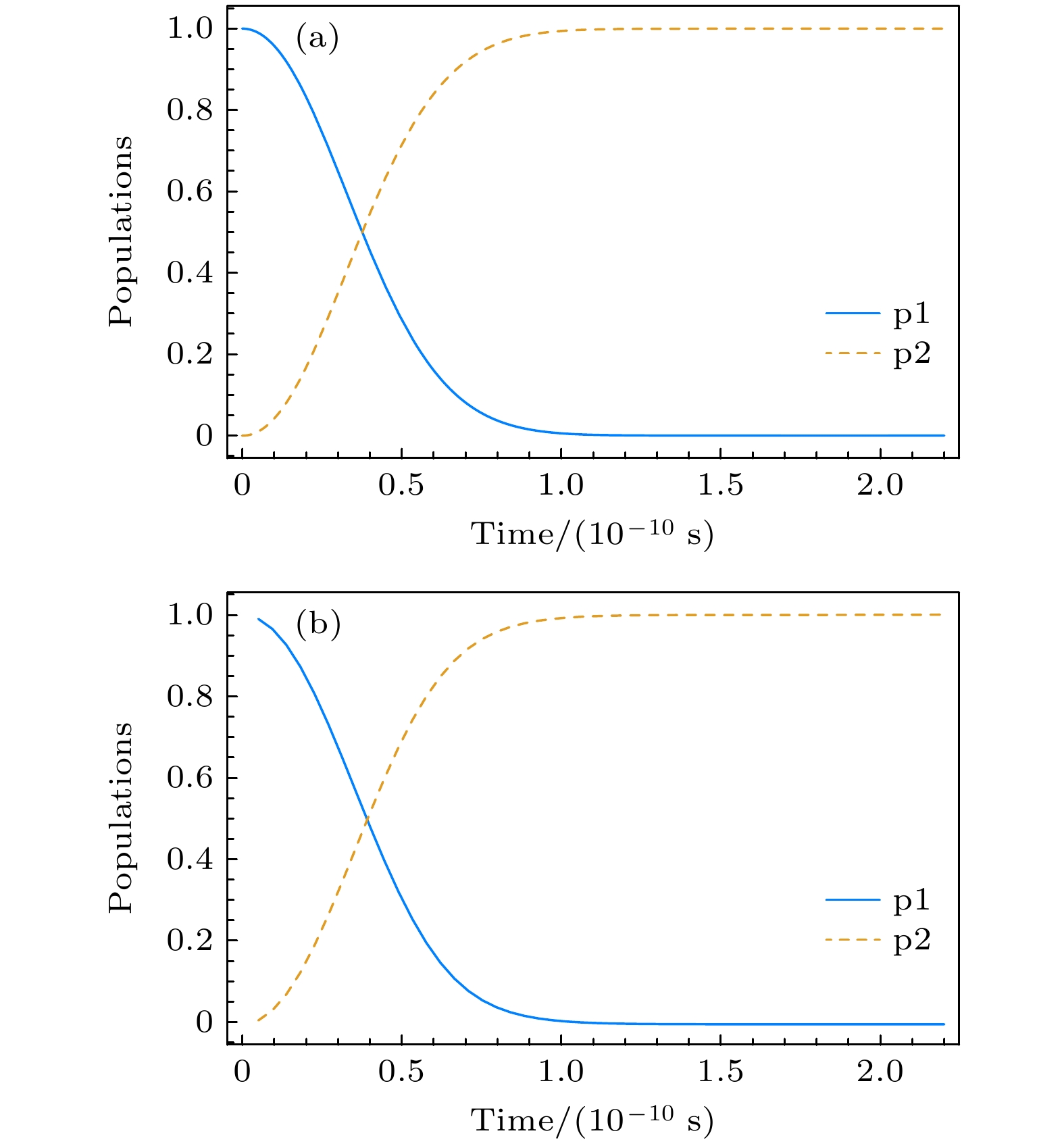
      神经网的训练次数为$ {\text{epoc}} = 15000 $. 训练过程中, 随着训练次数的增加, 损失函数的误差值减少. 最后误差逐步稳定在$ 1 \times {10^{ - 5}} $的数量范围. 损失函数变化趋势如图3所示. 从图3中可以看出, 在训练过程中损失函数具有较好的收敛性. 训练好的STAPINN就可以拟合系统演化过程. 从图4(a)中可以看出, 在时间$ t = {1} \times {10^{ - 10}} {\text{ s}} $时, 便实现了布居反转, 直到事先预定的演化过程的末端时刻$ t = {2} \times {10^{ - 10}} {\text{ s}} $, 演化过程一直处于稳定的布居反转状态. 选取同样的参数, 用Mathematica软件对系统演化进行模拟, 便得到了如图4(b)所示的演化曲线图, 发现二者一致, 证明了PINN方法仿真的正确性和有效性.

      通过STAPINN得到的$ {\varOmega _{{\mathrm{a}}}}(t) $是一个离散值函数. 本文将神经网中得到的离散的驱动函数用傅里叶级数和多项式两种方式展开. 将$ {\varOmega _{\text{a}}}(t) $展开成傅里叶级数, 生成由基本三角函数构成的脉冲函数. 傅里叶级数公式如下:

      其中傅里叶系数为

      经计算得到$ {a_n} $和$ {b_n} $的值:

      将$ {\varOmega _{\text{a}}}(t) $展开成多项式函数公式如下:

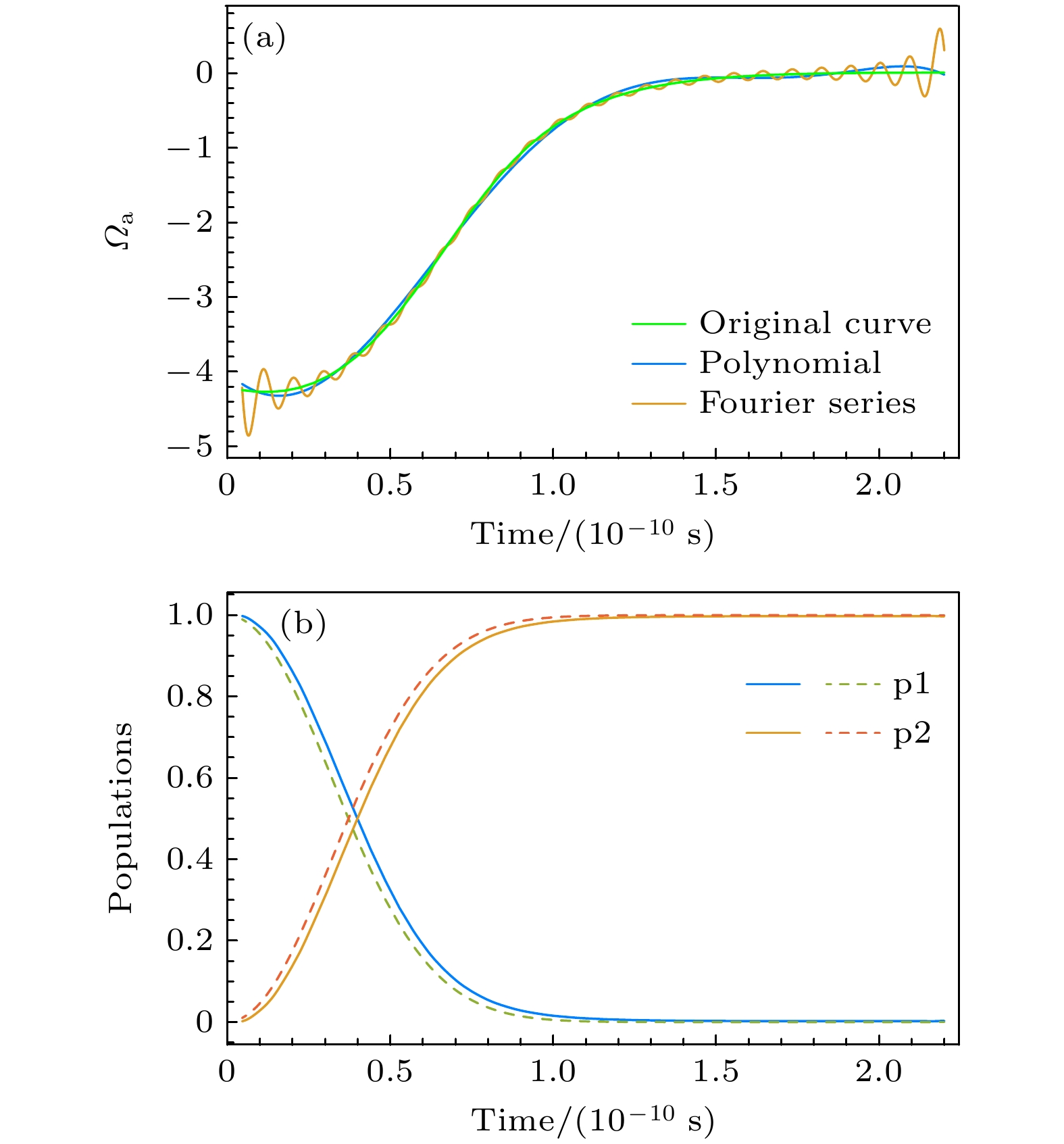
      其中$ {d_n} $的值分别为

      驱动曲线如图5(a)所示, 从图中可以看出, 利用现有的算法将数值函数拟合成多项式或者傅里叶级数的解析函数都有一定的偏差. 将两种展开的解析函数$ {\varOmega _{\text{a}}}(t) $代入原微分方程, 这时原微分方程由一个含参方程变为一个确定的方程. 将这个方程输入到Mathematica软件中, 用该软件解方程, 得到的演化过程如图5(b), 与图4的演化过程相比具有高度的一致性, 都实现了布居反转. 这进一步验证了找到的驱动函数是正确有效的.

      接下来采用不同的训练次数训练神经网络. 训练次数分别为$ \text{epoc}=3000, 5000, 15000 $. 训练结果如图6所示. 从图6中可以看到, 随着训练次数的增加, 系统实现布居数上升和下降交叉点的时刻前移, 保真度提高, 且更稳定. 这也能说明, 能够使布居反转的驱动函数$ {\varOmega _{\text{a}}}(t) $不具有唯一性, 同时随着训练轮数增加, 损失函数误差减小的过程中, 能够得到更好的驱动函数$ {\varOmega _{\text{a}}}(t) $. 这个函数和所期望的最优驱动函数更加接近.

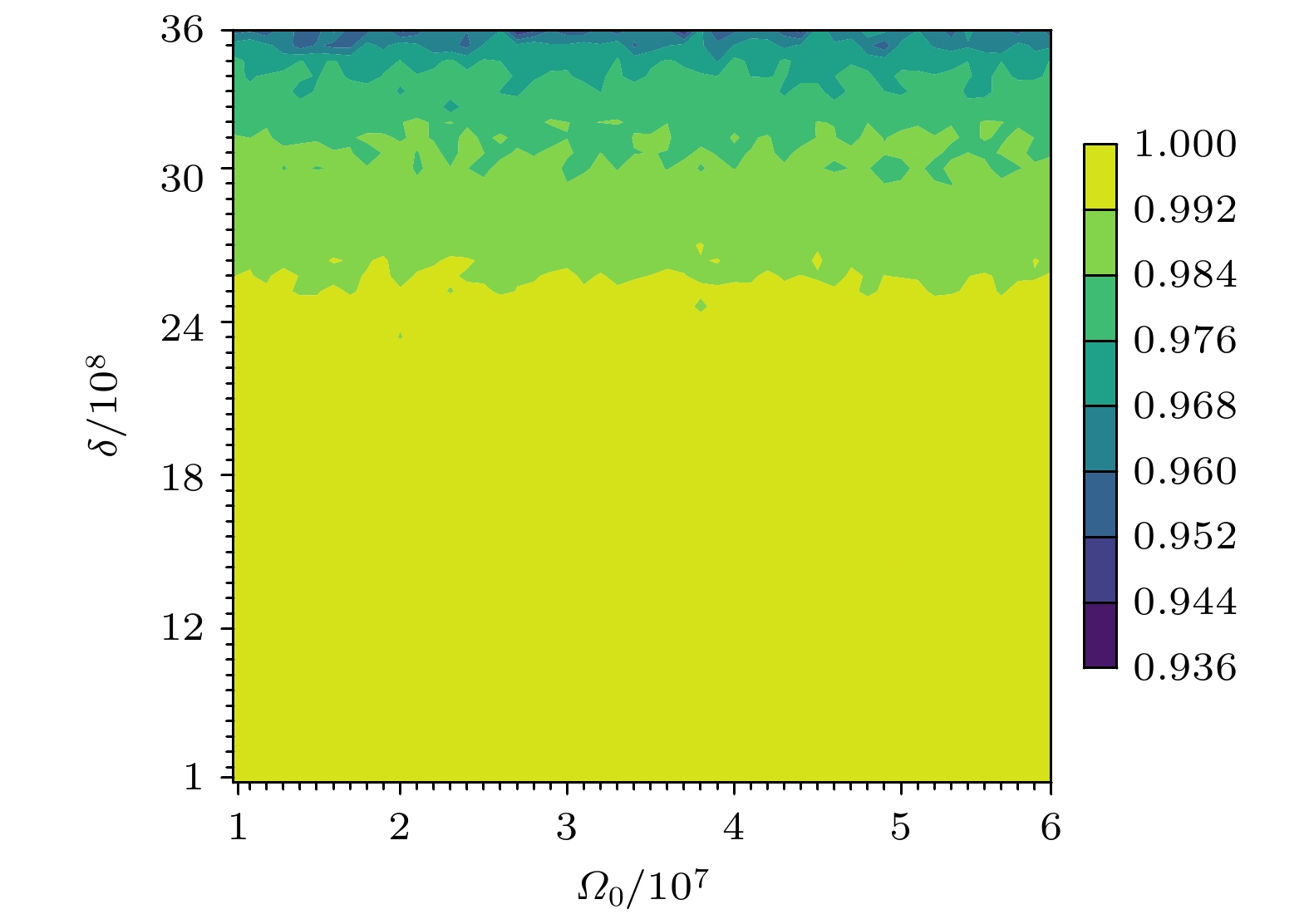
      接下来改变参数$ {\varOmega _0} $和$ \delta $的值. 针对不同的参数训练神经网络, 训练结果中保真度和参数的关系如图7所示. 当$ {\varOmega _0} = {10} {\text{ MHz}} $, $ \delta = {600} {\text{ MHz}} $时, 保真度的值为0.9999, 随着$ \delta $的增大而减小; 当$ {\varOmega _0} $和$ \delta $分别增加到原值的20倍时, 保真度最低; 当$ \delta $增加10倍时, 还能保持0.999以上的保真度, 说明本算法具有较强的鲁棒性.

      实验表明, 可以将神经网络看作一个函数逼近器, 逼近任意函数. 将微分方程作为约束条件, 神经网络等价于微分方程的解的拟合函数. 它不仅能找到普通微分方程的解函数, 还能够解含有参数的微分方程, 并通过一定的约束条件, 得到关于微分方程的含时参数. 它可能不是最优解, 也可能不是唯一解, 但它是有效解. 这为人们提供了一种灵活的优化算法, 通过该算法可以找到有效的驱动函数.

    4.   结　论

    • 本文提出一种基于物理信息神经网络的绝热捷径方案, 将绝热捷径实现方法变为解含有参数的微分方程. 通过参数化的物理神经网络求解含参数的微分方程, 拟合布居转移过程. 数值实验表明, 物理神经网络能够很好地拟合量子绝热演化过程, 并能够生成稳定的驱动函数, 保真度可以达到0.9999以上, 对于不同的参数具有很好的鲁棒性. 与传统量子绝热捷径相比, 具有保真度高和外场驱动选取灵活的特点. 通过神经网络的参数化, 增强了神经网络的拟合能力, 使系统能够适应更加复杂的量子绝热演化过程, 为量子绝热演化的进一步应用打开了一条新的通道.

    参考文献 (38)

目录

/

返回文章
返回