稠密等离子体焦点(DPF)装置是一种快脉冲(μs量级)、大电流(数百kA到数MA)的等离子体放电装置, 能够以简单高效的放电形式产生高温(~10⁷ K)、高速(10⁵—10⁶ m/s)和高密度(10²³—10²⁶ m^–3)的等离子体^[1,2]. 稠密等离子体焦点不仅可用于工业和科技领域中改善材料表面、制备纳米材料^[3–10], 还可作为关键装置应用于国防领域, 例如粒子加速器^[11]、空间推进^[12,13]、脉冲中子源^[14,15]等.

DPF最早是20世纪60年代由苏联的Fillpov^[1]和美国的Mather^[2]独立提出的. 基于探索受控核聚变的需求, 70—90年代欧洲和美国建立了一系列大型MA量级的DPF装置, 如美国的DPF-6装置^[16]、法国的Liemeil装置^[17]、德国的POSEIDON^[18]和SPEED装置^[19]、意大利的Frascati装置^[20]、波兰的PF-1000装置^[21]等, 其D-D中子产额均达到了10¹¹—10¹²/脉冲(D-T中子产额超过10¹³/脉冲). 近年来, 在国防尖端领域的需求牵引下, 美国进一步建立了一系列短脉冲、高产额的DPF装置(如Gemini、MJOLNIR、Sodium等). 国内最早开展DPF研究的单位是中国科学院原子能研究所浓密等离子体焦点研究小组. 1975年该小组建立了我国首个DPF装置(储能40 kJ), 平均中子产额为1.0×10⁹/脉冲^[22]. 90年代以后, 清华大学^[23–25]、西北核技术研究院^[26]、中国工程物理研究院流体物理研究所^[27,28]、核物理与化学研究所^[29–31]和电子工程研究所^[32]也相继建立了稠密等离子体焦点DPF装置.

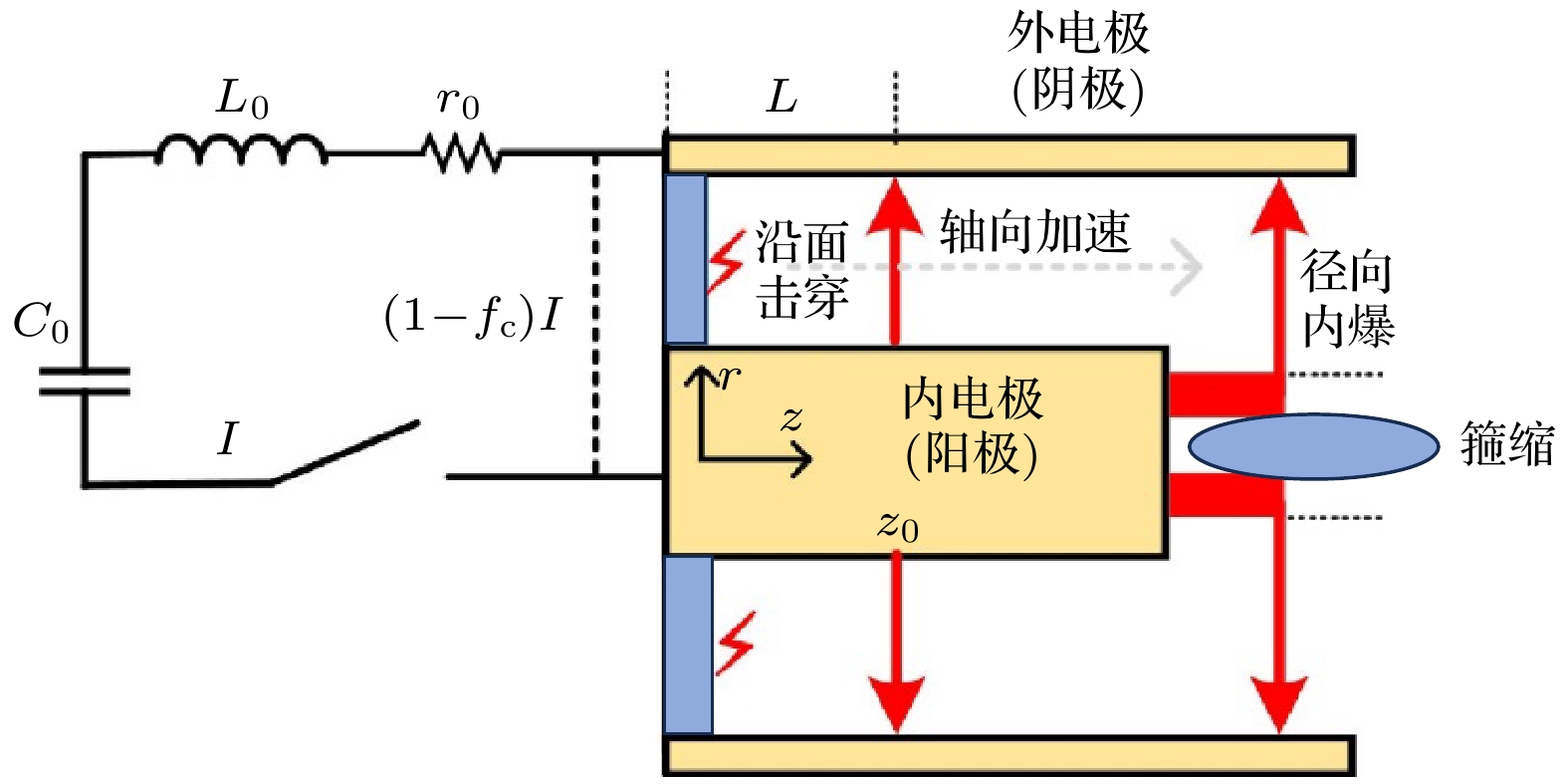
广义上稠密等离子体焦点(DPF)属于Z箍缩(Z-pinch)的一种, 其中DPF焦点形成阶段即为Z箍缩过程^[33]. DPF基本结构包括一对同轴型的电极, 电极一端采用绝缘子隔开, 电极间充满气体. 典型的DPF物理过程包括沿面击穿(gas breakdown)、轴向加速(run down)、径向内爆(run in)和箍缩(pinch)过程, 如图1所示. DPF装置的预充电(几十kV)高压电容器通过电感(几十nH)、触发开关对放电室放电, 工作电流峰值为10² kA—MA, 脉宽为数μs. 触发开关导通后, 绝缘子沿面击穿形成等离体鞘, 而后洛伦兹力推动等离子体鞘, 使其以超音速沿管道轴向加速. 到达内电极末端后部分等离子体沿径向向内压缩, 最终一个超密集、超热的等离子体柱被挤压到轴上.

DPF的理论模型可以分为雪耙模型、磁流体模型和粒子(PIC)模型3种^[34]. 雪耙模型认为当放电气体经历击穿过程后, 将形成等离子体鞘层结构, 该结构在电磁场洛伦兹力驱动下呈现类活塞式或雪耙状构型, 沿放电通道轴向持续推进, 将所遇到的中性气体电离为等离子体, 并堆积在鞘层里面, 同鞘层一起向前运动. 雪耙模型将等离子体电流鞘近似为一个均匀的薄层, 并使用动量守恒方程描述等离子体的轴向运动, 能近似地估算等离子体鞘的轴向运动速度和时间^[35]. Lee模型在雪耙模型基础上, 进一步考虑了DPF的径向内爆、箍缩、膨胀等过程, 并将所有阶段都与外电路进行了耦合, 以使能量和电荷保持一致^[36]. Lee模型由于其计算方便并且与实验拟合效果较好, 因此也被广泛用于许多DPF 装置的优化设计. 但Lee模型本质上是一个半经验模型, 需要调整模型参数, 将计算得到的总电流波形与实测波形进行拟合.

除Lee模型外, 磁流体模型和粒子PIC方法也被广泛用于DPF的研究. Potter等^[37]于1971年基于显式Lax-Wendroff方法, 建立了第一个自洽的二维磁流体(MHD)程序. Garanin等^[38]建立了隐式差分的二维MHD模型, 该模型可以消除磁声速对计算时间步长的限制, 并显著减小虚拟真空密度对等离子体动力学的影响. Meehan等^[39]使用ALEGRA MHD代码, 展示了DPF全三维数值模拟预测结果, 与二维轴对称相比, 全三维模型更准确地预测了DPF轴向阶段持续时间. 2012年以来, 美国的Schmidt等^[40–42]利用粒子模拟程序Chicago对DPF等离子体的动力学行为进行了深入探索. 粒子模拟可以细致考虑DPF等离子体箍缩过程中高能离子加速及中子产生过程, 但由于计算效率的限制, 目前主要针对箍缩阶段的高密度等离子体区域(百纳秒时间尺度)进行局部研究.

总体而言, 目前Lee模型在国内外DPF研究中应用最为广泛, 但是其假设等离子体层为无限电导率的平面薄层, 仅能对等离子体层的位置和运动速度进行简单的描述, 无法得到等离子体层在整个运动过程中的形态变化. 粒子模拟得到的物理图像最为细致, 但是只能针对箍缩阶段的高密度等离子体区域进行局部研究. 与上述两种模型相比, 磁流体模型一方面可以研究DPF等离子体鞘层运动、电流分布、流体不稳定性等宏观物理图像及演化过程, 另一方面可以评估参数(如电极几何、气压、驱动电流波形)对DPF整体性能的影响. 虽然在箍缩阶段, 磁流体模型无法自洽地计算DPF高能粒子束及中子产生等粒子动力学行为, 但是在不需要定量研究中子产额的场景下, 采用磁流体模型研究DPF宏观物理过程仍然具有显著意义. 因此, 本文主要基于双温磁流体动力学模型, 并耦合外电路来研究DPF轴向加速和径向内爆过程, 同时探索DPF 装置参数对等离子体运动的影响规律, 最后为DPF装置优化提供理论建议. 本文第2节详细介绍了我们使用的物理模型; 第3节对计算结果进行分析与讨论; 第4节是总结与展望.

在欧拉框架下, 单温理想磁流体方程组(不考虑任何耗散过程)的守恒形式如下^[43]:

方程(1)—(4)分别为连续性方程、动量方程、能量方程和磁场方程. 其中$ \rho $为等离子体密度, $ \boldsymbol{u} $为速度, $ B $为磁场. $ \varepsilon =\rho \dfrac{{\boldsymbol{u}}^{2}}{2} + E_{\rm t} +\dfrac{{B}^{2}}{{2\mu }_{0}} $为等离子体的总能, 包括了等离子体的动能$ \rho ({{\boldsymbol{u}}^{2}}/{2}) $、内能$ E_{\rm t} $和磁能$ {{B}^{2}}/({{2\mu }_{0}}) $; $ {P}_{{\mathrm{t}}{\mathrm{o}}{\mathrm{t}}}=P + {{B}^{2}}/({{2\mu }_{0}}) $为等离子体的总压, 包括了等离子体压力$ P $和磁压$ {{B}^{2}}/({{2\mu }_{0}}) $.

在理想磁流体方程中, 流体中没有任何耗散过程, 即忽略了等离子体的黏性和热传导, 且假定等离子体的电导率无穷大. 然而, 实际情况中等离子体系统是必然存在耗散过程的, 因此需要进一步考虑黏性、热传导以及电阻项, 进而建立非理想磁流体动力学模型. 此外, 在DPF物理过程中通常处于非局域热力学平衡, 还需要考虑电子温度和离子温度, 即双温磁流体. 基于DPF物理过程, 通过引入电子温度以及耗散过程, 构建了双温非理想MHD模型^[37].

连续性方程:

动量方程:

总能方程:

磁场方程:

电子能量方程:

欧姆定律:

其中$ \bar{\bar{\tau }}_{{\mathrm{i}}} $为离子黏性应力, $ {\lambda }_{{\mathrm{i}}} $, $ {\lambda }_{{\mathrm{e}}} $分别为离子和电子热导率, $ \sigma $为电导率, $ \boldsymbol{E} $为电场, $ j $为电流密度, $ \dfrac{1}{{\mu }_{0}}\boldsymbol{E}\times \boldsymbol{B} $表示电磁能量流密度向量. 总能$ \varepsilon= \rho({\boldsymbol{u}^2}/{2}) + E_{\rm i} + E_{\rm e} + {B^2}/({2\mu_0}) $包括了离子内能E_i和电子内能E_e, 总压$ {P}_{{\mathrm{t}}{\mathrm{o}}{\mathrm{t}}}={P}_{{\mathrm{i}}}+{P}_{{\mathrm{e}}} + {{B}^{2}}/({{2\mu }_{0}}) $包含电子压力$ {P}_{{\mathrm{e}}} $.

DPF等离子体物性参数采用经典的Braginskii系数^[44]. 其电子和离子热导率为

其中, 当$ {Z}_{{\mathrm{i}}}=1 $时$ {c}_{1}=3.16 $; 当$ {Z}_{{\mathrm{i}}}=2 $时$ {c}_{1}=4.9 $; 当$ {Z}_{{\mathrm{i}}}=3 $时$ {c}_{1}=6.1 $. $ {n}_{{\mathrm{e}}} $和$ {n}_{{\mathrm{i}}} $分别为电子密度和离子密度, $ {T}_{{\mathrm{e}}} $和$ {T}_{{\mathrm{i}}} $分别为电子温度和离子温度, 物理量$ {\tau }_{{\mathrm{e}}} $和$ {\tau }_{{\mathrm{i}}} $分别是电子和离子的碰撞时间:

其中 $ {\varepsilon }_{0} $ 是真空介电常数, $ {Z}_{{\mathrm{i}}} $为离子电荷数, $ {\mathrm{l}}{\mathrm{n}}\varLambda $为库仑对数.

离子的黏性系数如下:

电导率表达式如下:

其中c₂ 是依赖于离子电荷数$ {Z}_{{\mathrm{i}}} $的常数. 对于$ {Z}_{{\mathrm{i}}}= 1 $, c₂ = 1.96; 对于$ {Z}_{{\mathrm{i}}}=2, $ c₂ = 2.27; 对于$ {Z}_{{\mathrm{i}}}=3 $, c₂ = 2.5.

DPF系统外电路为典型的R-L-C串联电路, 电路方程如下^[36]:

式中, $ {V}_{0} $为电路初始电压, $ {C}_{0} $为电路电容, $ {L}_{0} $为电路电感, $ {r}_{0} $为电路电阻, 这些参数直接由实验给定(对于UNU装置, $ {V}_{0}=15\;{\mathrm{kV}} $, $ {C}_{0}=30\;{\text{μF}} $, $ {L}_{0}= 110\;{\mathrm{n}}{\mathrm{H}} $, $ {r}_{0}=12\;{\mathrm{m}}{{\Omega }} $). $ {U}_{{\mathrm{P}}{\mathrm{F}}} $为DPF系统的电压, 需要由MHD模拟结果自洽确定. 对于DPF放电系统, 其电压的计算方式如下:

其中$ \varPhi $为DPF系统的磁通量.

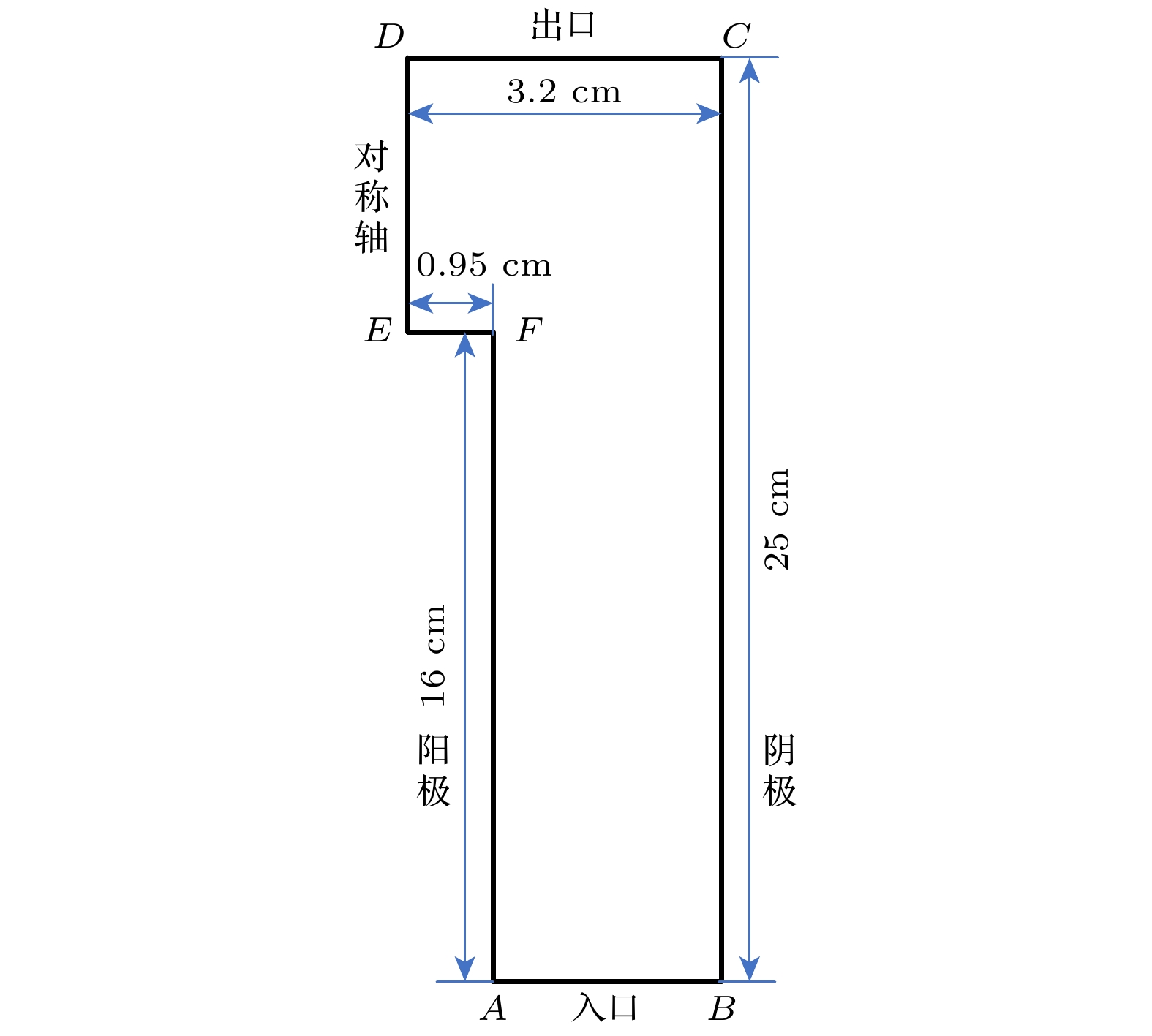
图2所示为DPF装置的计算域示意图(UNU装置^[36]). UNU型DPF装置的阳极半径为 a = 0.95 cm , 阴极半径为 b = 3.2 cm , 阴阳极间隙为 2.25 cm. DPF阳极长度为 16 cm, 阴极长度为 25 cm. 本数值模型构建中排除电极固体区域, 并基于DPF装置的轴对称几何特征, 采用二维轴对称模型进行数值模拟以提高计算效率.

具体边界条件如下. 电极表面(AF, EF和BC)使用导体壁面确定磁场边界, 使用滑移边界和绝热边界确定速度和温度:

入口(AB)设置为低速低密度, 磁场边界的磁感应强度为

首先需要根据外电路来计算电流, 然后根据电流计算入口(AB)处的磁场边界, 因此整个DPF系统还需要耦合外电路模型(方程(15)). 出口(CD)设置为超音速出口边界; 对称轴(DE)设置为轴对称边界.

最后, 模型假定初始等离子体完全电离, 这样的考虑主要出于以下两个方面: 一方面DPF在初始击穿后, 等离子体鞘在洛伦兹力作用下很快被加速并达到10—100 eV以上的高温高速状态, 此时被等离子体鞘扫过的中性气体均处于完全电离状态; 另一方面如果考虑中性气体, 则需要进一步建立多流体模型来进行自洽计算, 会显著增加模拟复杂度及计算量. 因此, 从简化模型角度出发, 本文假设等离子体处于完全电离状态, 并且存在一定合理性.

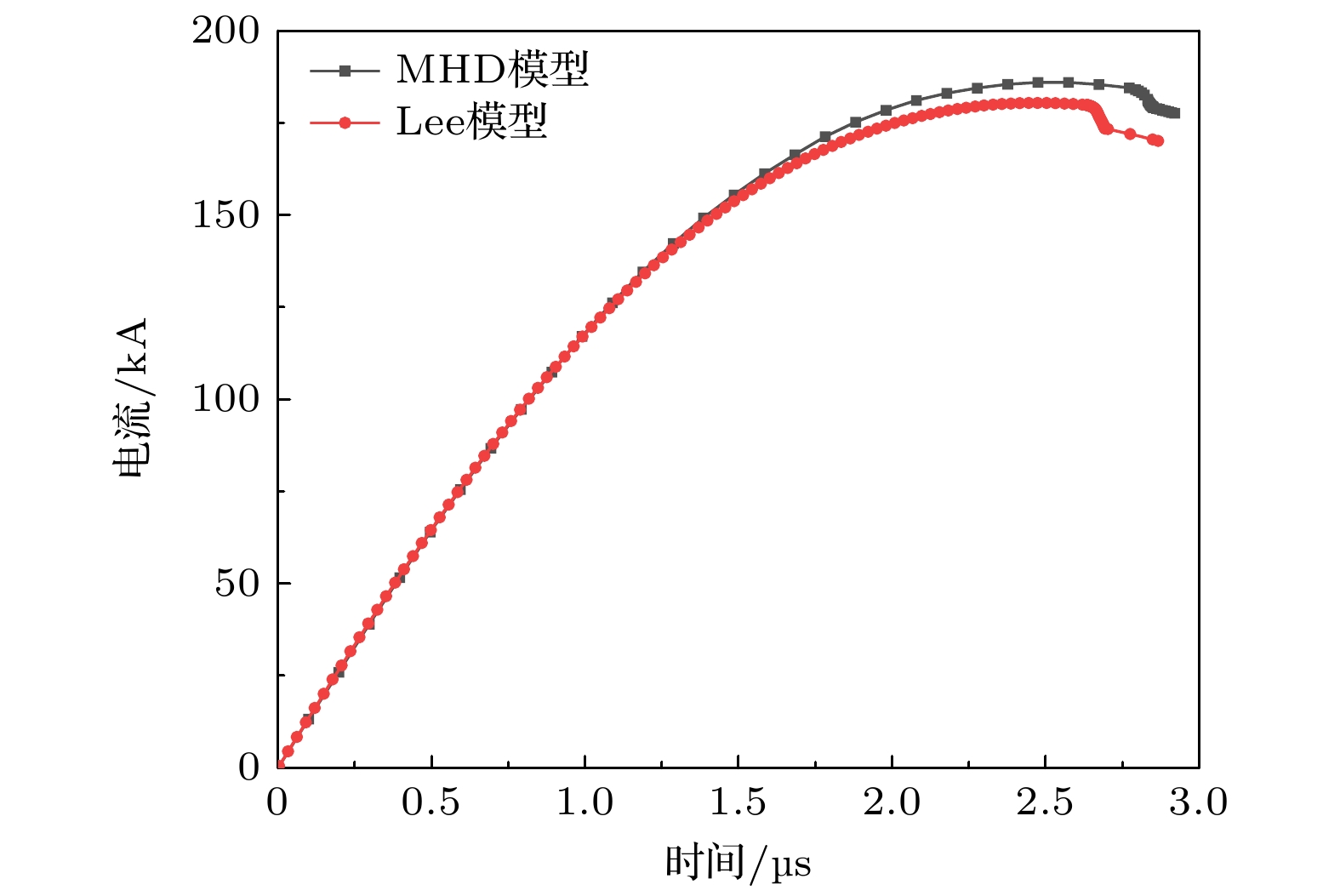
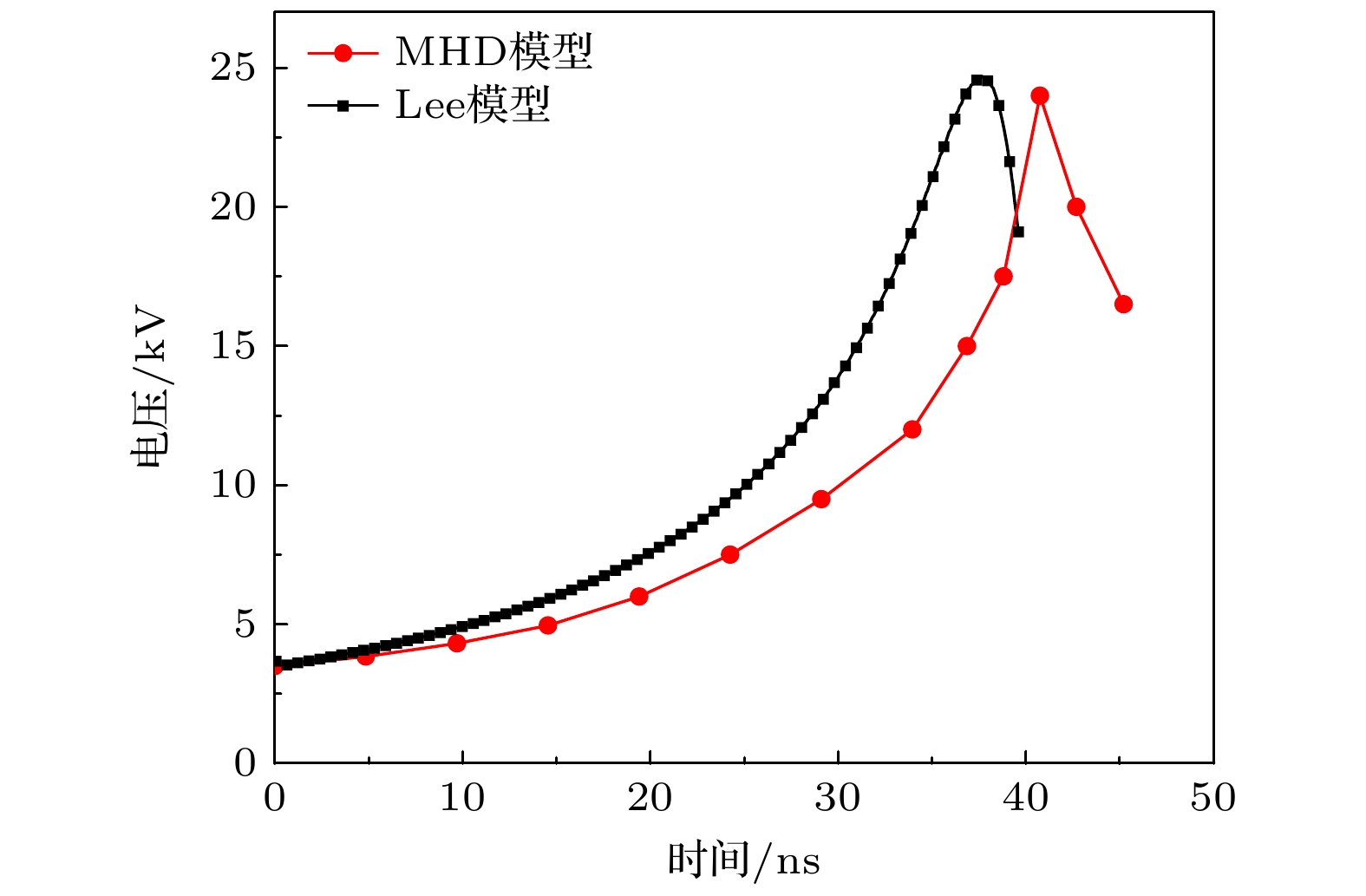
首先, 针对双温MHD模型进行验证与对比. 图3和图4对比了双温MHD模型和Lee模型计算得到的UNU装置的电流和电压^[36]. 需要注意的是, Lee模型在UNU装置上通过调整模型输入参数, 已经与实验进行了良好的拟合, 因此这里也可以看作与实验的电流与电压值进行对比. 对比结果表明MHD模型计算的DPF电流和电压值比较准确, 而且由于DPF电流与等离子体运动情况以及电磁场变化都密切相关, 也能进一步体现双温MHD模型关于磁场和等离子体模拟的准确性.

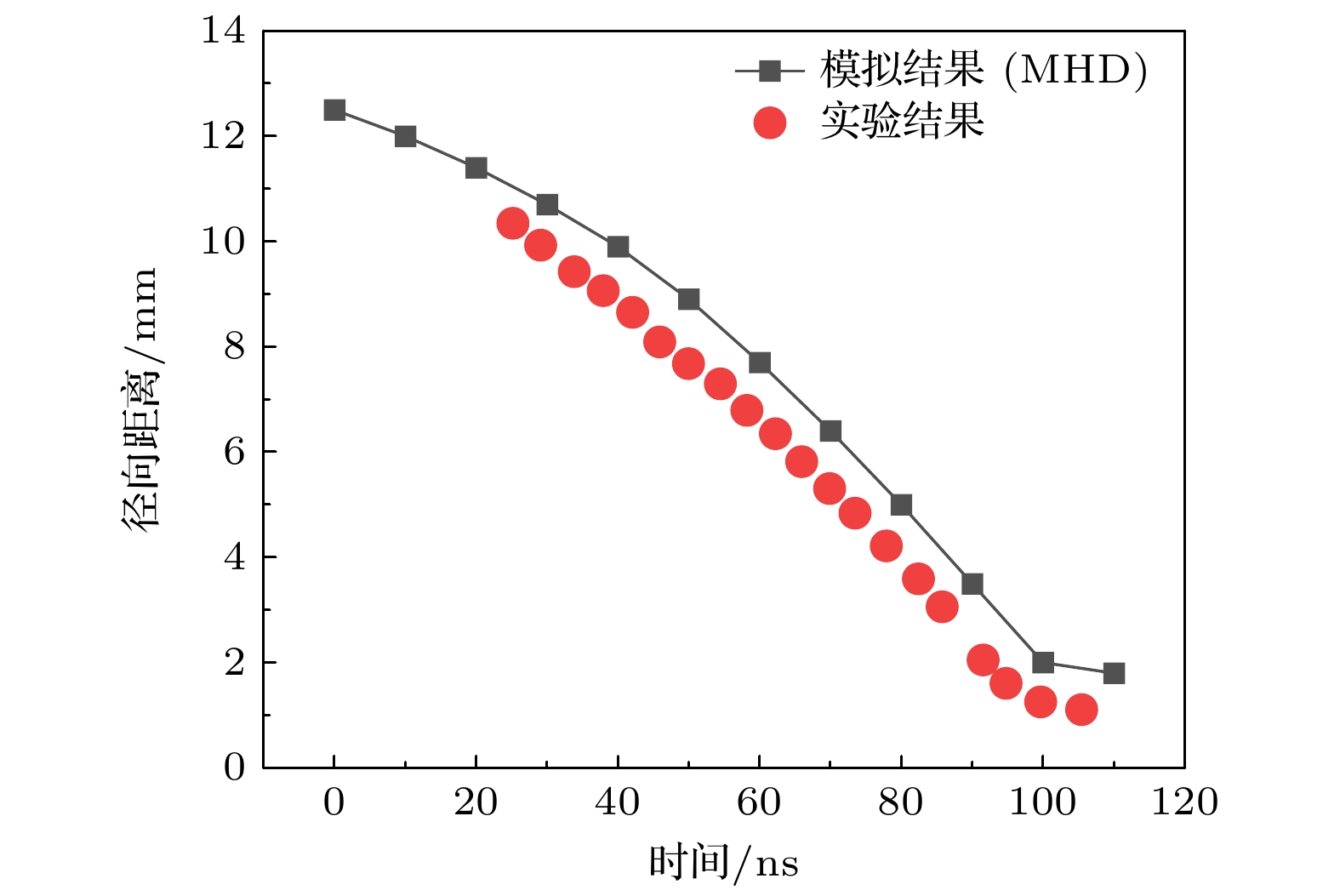
进一步与UDMPF1装置^[45]进行对比. 图5所示为双温MHD模拟的径向阶段轨迹与实验的对比情况. 可以发现计算得到的径向阶段等离子体运动情况与实验测量结果符合较好. 总体而言, 通过与UNU装置和UDMPF1装置的实验结果对比, 能够验证双温MHD模型在计算DPF轴向加速、径向内爆及外电路等方面的准确性.

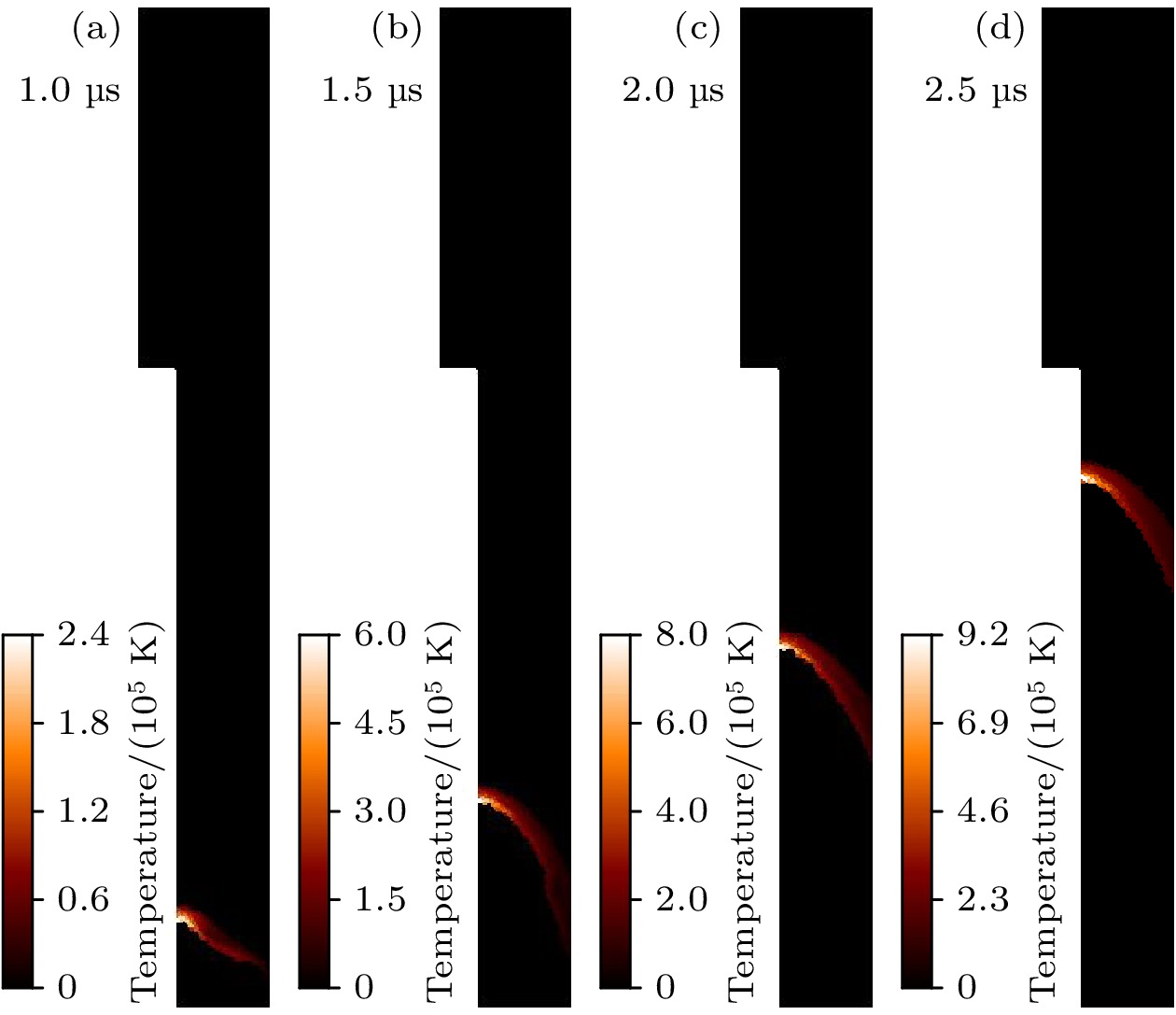
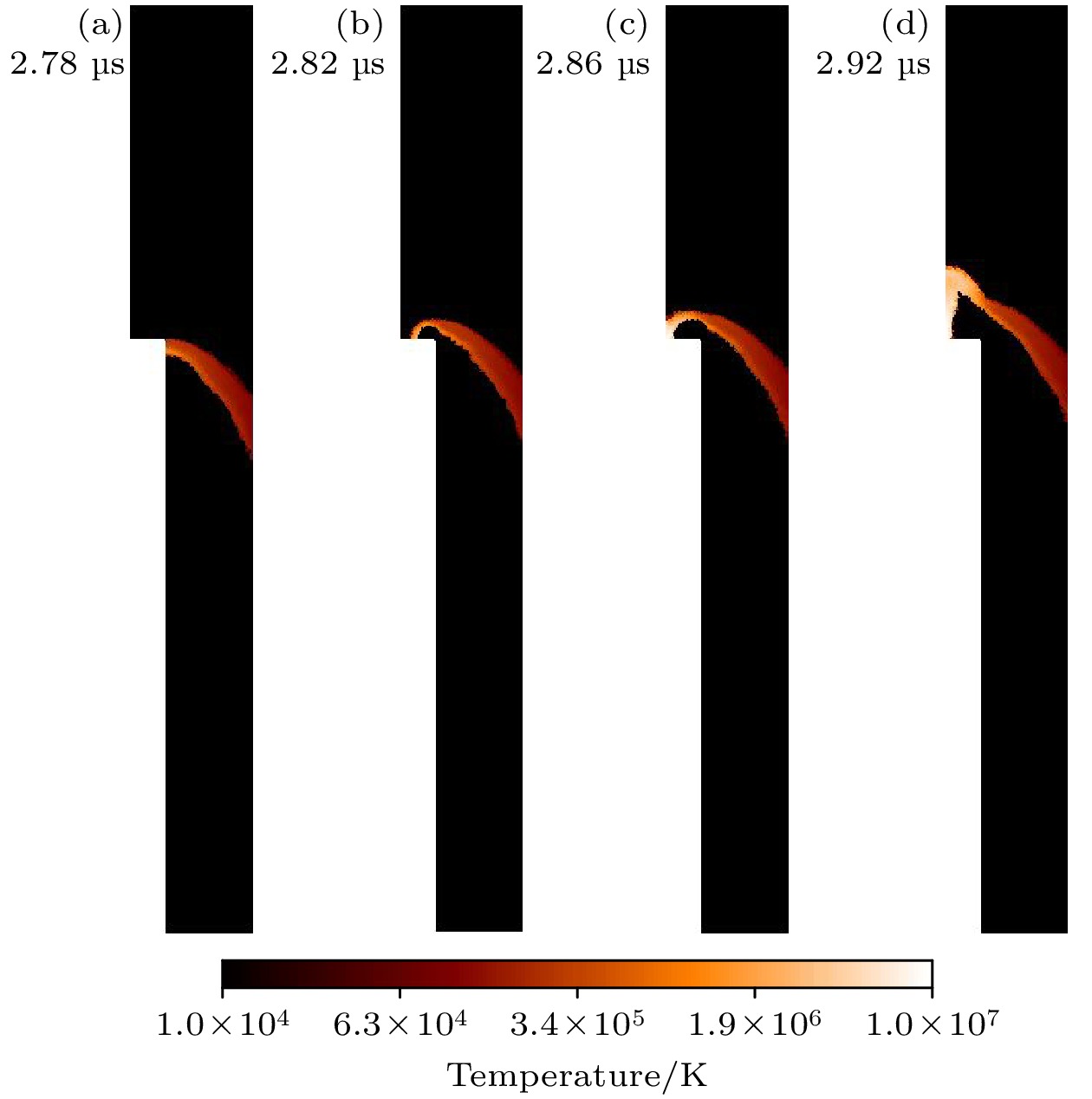
进一步研究DPF(UNU装置)轴向加速、径向内爆及箍缩等物理过程和规律. 假定等离子体完全电离, 背景D等离子体密度$ {n}_{0} $ = $ {2.4\times {10}^{23}\;{\mathrm{m}}}^{-3} $(对应的背景气压约为3.5 Torr (1 Torr =1.33×10² Pa)), 温度1 eV. 在入口处给定一个平均密度在4n₀左右的等离子体薄层(即等离子体鞘), 温度2 eV左右.

图6和图7所示为不同时刻DPF装置内等离子体的温度分布. 从图中可以看出, 等离子体鞘在洛伦兹力加速下沿轴向不断加速, 此时等离子体鞘的温度也不断升高. 内电极附近的等离子体鞘运动快于外电极, 这是因为磁场近似与半径成反比, 进而导致外电极附近等离子体受到的洛伦兹力远小于内电极. 当等离子体鞘运动到内电极末端后, 会沿径向向内弯曲, 最后被压缩在对称轴上形成高温高密的等离子体. 箍缩时刻大概在2.8 μs, 箍缩时刻温度上升2个量级左右. 需特别指出, 在0—2.5 μs阶段(图6), DPF等离子体呈现轴向运动特征, 与外电路电流上升期(图3)同步演化. 此阶段阴阳极间磁感应强度随电流增强呈单调递增的趋势, 致使洛伦兹力不断增大. 在洛伦兹力驱动下, 等离子体持续获得轴向加速并伴随温度上升. 而在2.78—2.90 μs阶段(图7), DPF系统主要为径向内爆模式, 此时电流变化显著趋缓(图3). 由于同轴电极系统磁场分布特征, 磁感应强度与等离子体鞘层径向位置呈近似反比, 伴随内爆进程推进, 鞘层-阳极间距持续压缩, 导致磁感应强度不断增强. 该机制促使洛伦兹力呈指数增长态势, 最终引发等离子体内爆速度及温度梯度陡升现象.

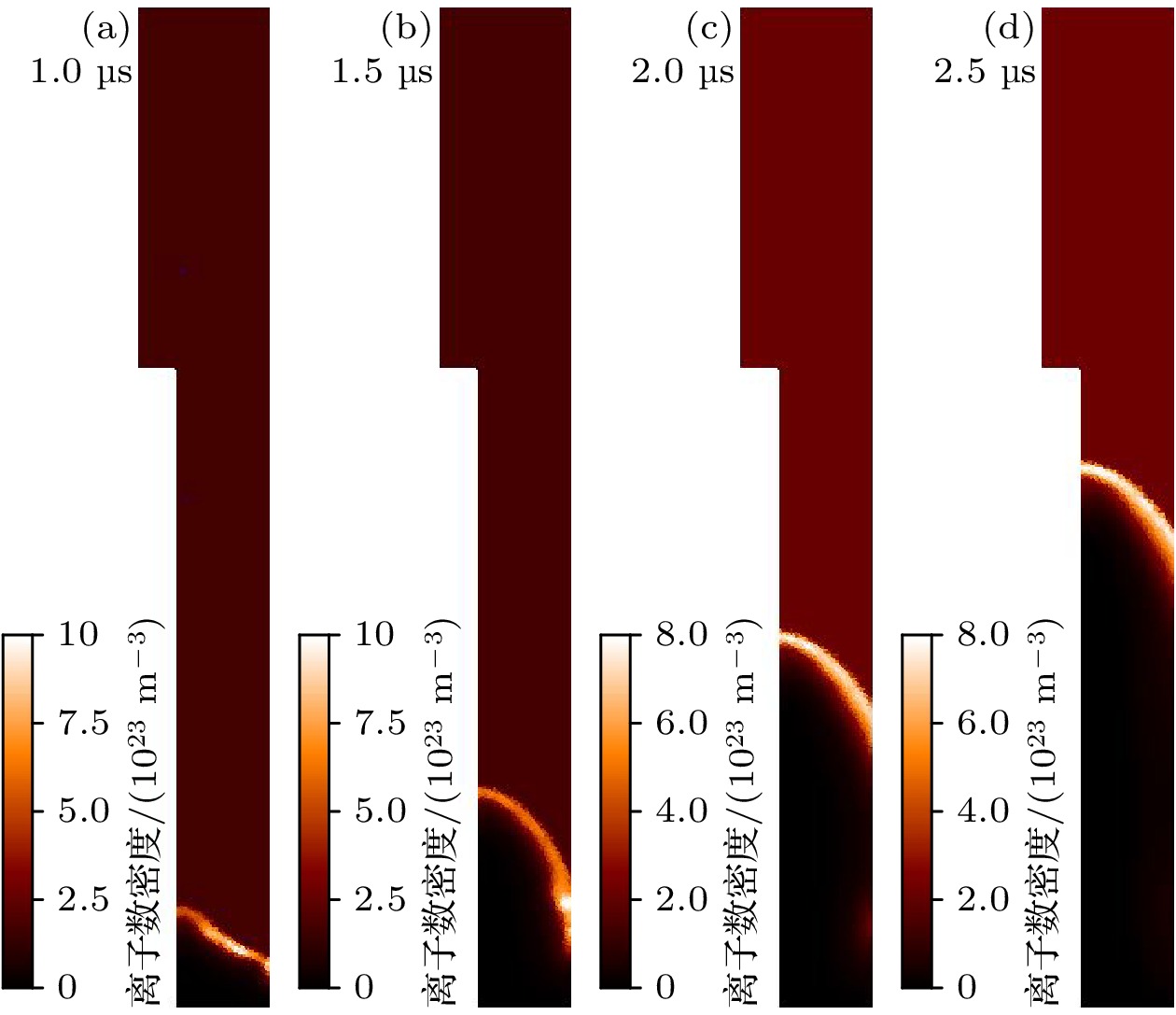
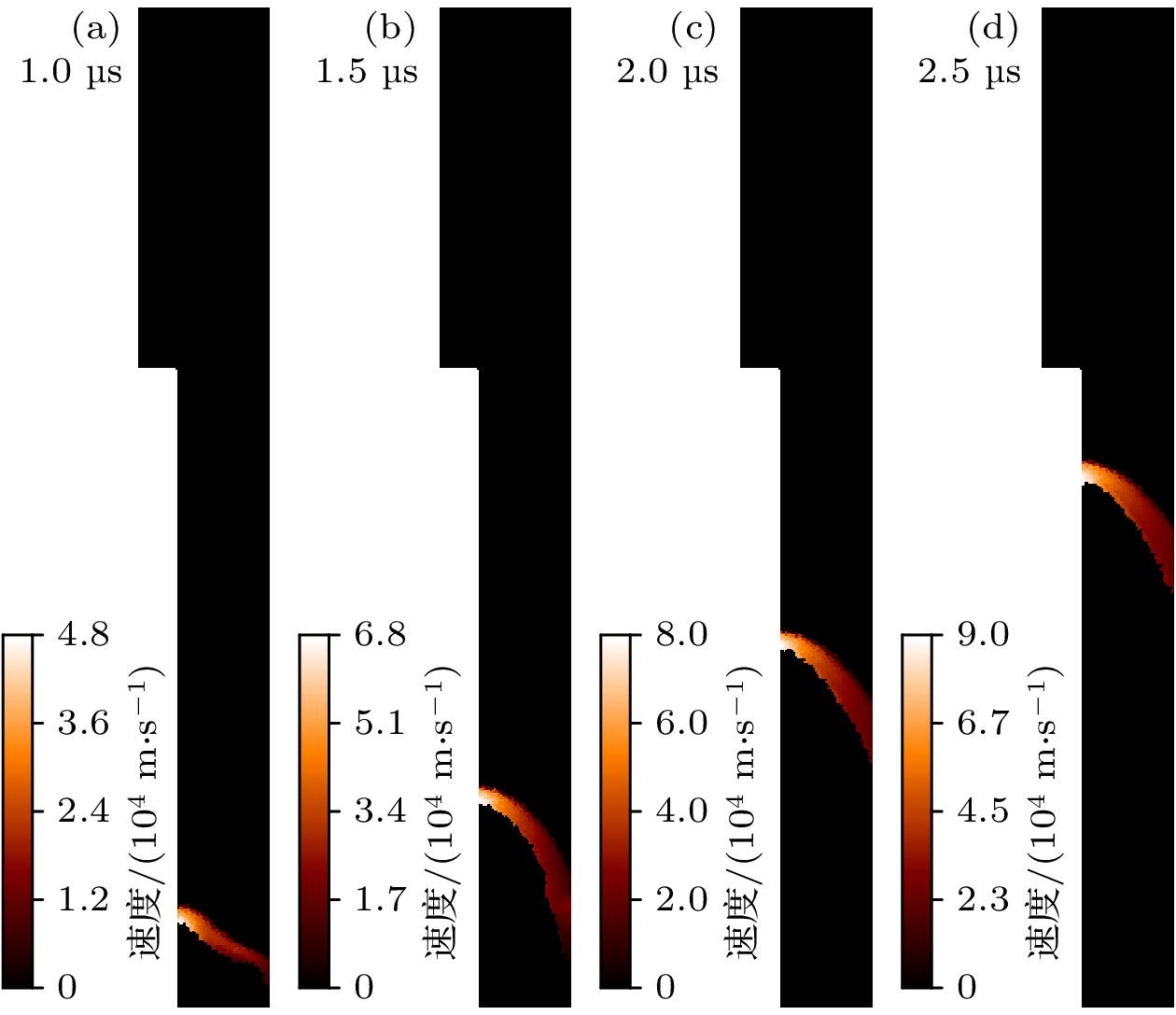
不同时刻的离子密度和速度分布如图8和图9所示. 从图中可以发现, 在洛伦兹力作用下, 等离子体鞘会不断加速. 同时由于等离子体鞘在运动过程中, 将其经过区域的气体不断扫入等离子体鞘内, 会导致等离子体质量不断增大, 因此等离子体鞘的厚度是一直在增大, 如图8所示. 等离子体鞘的密度分布与温度分布大体一致, 这表明等离子体鞘一直维持着高温高密度的一个状态, 这也会导致等离子体鞘经过区域的气体被迅速电离. 从图9可以看出, 在轴向阶段等离子体鞘的最高运动速度大约在9×10⁴ m/s, 与Lee模型符合较好. 轴向阶段的运动可看作一个简单的雪耙过程. 由于雪耙经过的区域, 等离子体质量不断增大, 因此加速效果会越来越差. 这也是实验中等离子体轴向速度的上限在10×10⁴ m/s左右的主要原因.

DPF物理过程中轴向阶段主要决定电流上升时间, 需要与电路进行匹配. 根据轴向运动和外电路的匹配原则, 轴向运动末期需要接近放电的1/4周期, 此时电流能够达到峰值, 进而将更多的系统能量传递到箍缩等离子体中. 径向内爆阶段决定了箍缩时的密度、温度和体积. 箍缩阶段则决定了不稳定性过程和束靶产生中子过程.

下面主要研究DPF参数对这些过程的影响作用. DPF的参数主要包括放电参数(电压$ {V}_{0} $、电容$ {C}_{0} $、电感$ {L}_{0} $和杂散电阻$ {R}_{0} $)和结构参数(阳极半径a、阴阳极半径比c = b/a).

首先, 对于电路参数, 主要关注$ {C}_{0} $和$ {L}_{0} $, 电阻$ {R}_{0} $与前两者相比作用几乎可以忽略. 在不考虑DPF负载情况下, 电路最大电流$ {I}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}={V}_{0}\sqrt{{{C}_{0}}/{{L}_{0}}} $, 因此通常比较直观地提升电流方法为增大线路电容$ {C}_{0} $、减小线路电感$ {L}_{0} $. 但是实际情况下, 对于MA级别的DPF装置, 继续增大$ {C}_{0} $和减小电感$ {L}_{0} $, 电路电流(尤其是pinch电流)通常会达到饱和. 因此, 针对外电路电流的饱和效应进行理论推导.

对于大型DPF装置, DPF腔室电感$ {L}_{{\mathrm{f}}} $远大于线路电感$ {L}_{0} $($ {L}_{{\mathrm{f}}}\gg {L}_{0} $), 电流幅值是由腔室电感决定, 而不由电容器组的电感决定.

此时, 最大电流近似为

其中$ {E}_{0}={{V}_{0}}^{2}{C}_{0} $表示DPF系统存储的能量. 而轴向匹配时间近似为

(21)式表示电路的1/4周期与DPF轴向运动时间相匹配, 这里近似认为DPF轴向阶段很快达到恒定轴向速度$ {v}_{z} $. DPF轴向电感为

最后, 可以推导得到:

式中, $ {v}_{z} $表示轴向速度, R为外径, r为内径. 可以发现对于MA级别的DPF装置, 继续增大$ {C}_{0} $和减小电感$ {L}_{0} $, 对于最大电流提升效果基本可以忽略(即电流容易达到饱和), 此时增大电路电压$ {V}_{0} $对电流提升比较显著.

对于结构参数, 主要是关注阳极半径a, 以及阴阳极半径之比c = b/a. 对于阳极半径a, 大量已有研究均发现等离子体层轴向运动速度的变化与阳极半径的尺寸成反比. 由(19)式可知, 在相同的电流条件下, 增大阳极半径会减弱阴阳极之间的磁感应强度, 导致等离子层所受到的洛伦兹力减小. 因此, 这里主要关注阴阳极半径之比c的影响.

对于大型DPF装置, DPF腔室电感$ {L}_{{\mathrm{f}}} $是一个至关重要的参数(此时线路电感可忽略). 主要体现在以下两点:

1) 尽量减小轴向阶段的电感和动态电阻, 进而提升电流峰值;

2) 径向阶段的电感和动态电阻尽量小, 从而显著提升箍缩电流.

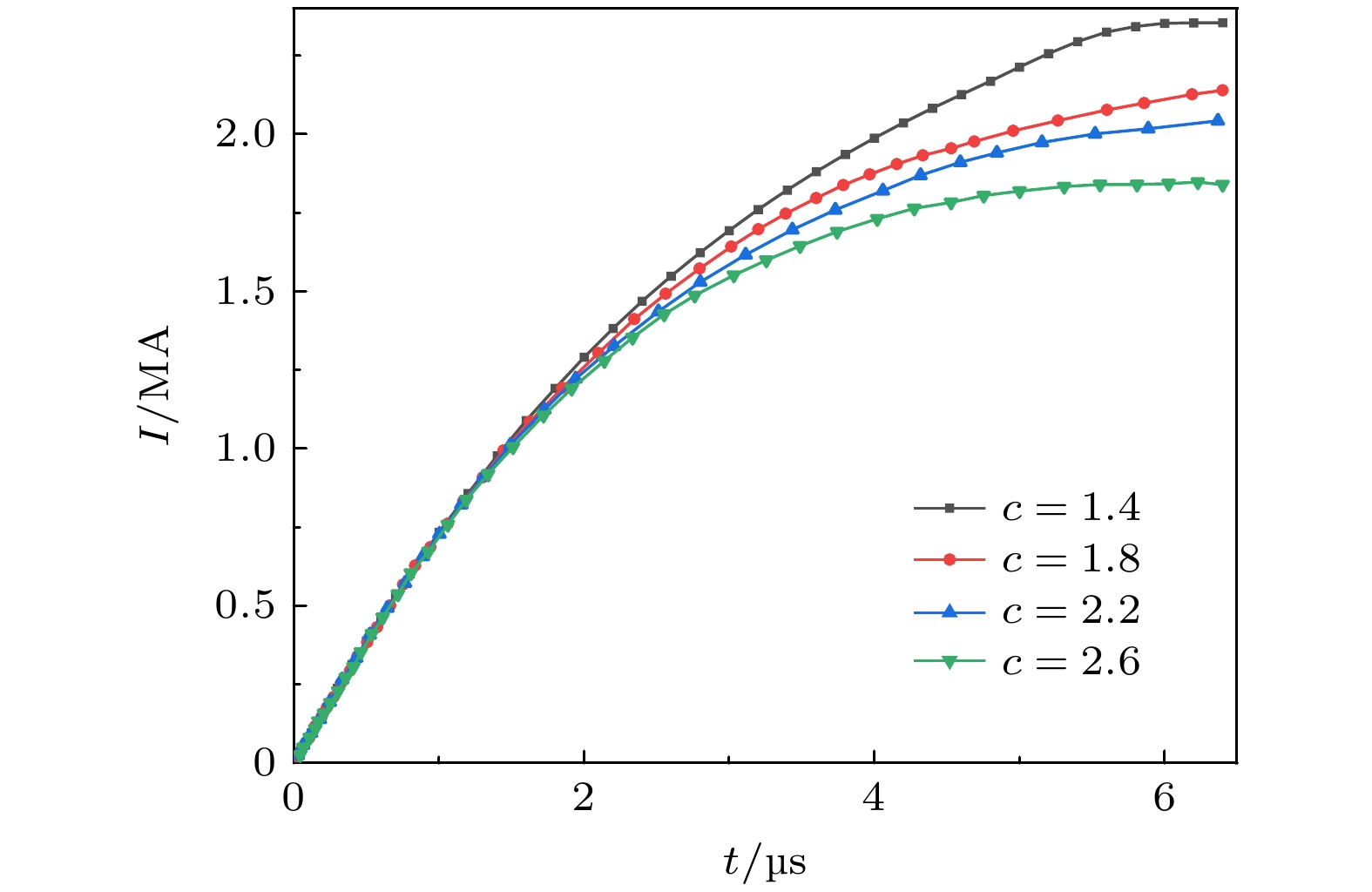
这里轴向电感为$ \dfrac{\mu }{2{\mathrm{\pi }}}\left({\mathrm{l}}{\mathrm{n}}c\right)z $, 轴向动态电阻为 $ \dfrac{\mu }{2{\mathrm{\pi }}}\left({\mathrm{l}}{\mathrm{n}}c\right)\dfrac{{\mathrm{d}}z}{{\mathrm{d}}t} $. 研究表明, 当参数c由3.0衰减至1.5时, 等效电感与动态阻抗呈现约2.7倍的衰减; 当参数c由2.0降至1.3时, 等效电感与动态阻抗呈现约2.6倍的衰减. 因此, MA级DPF装置需要实现参数c的最小化设计(在工程设计上确保不发生绝缘击穿的情况下). 这能在其他参数不变的情况下, 尽可能提升DPF的电流峰值和箍缩电流.

下面针对大型DPF装置(PF-1000装置^[21])进行双温MHD数值模拟. 图10所示为模拟得到的轴向阶段电流变化, 其他参数不变, 只改变外径b. 双温MHD计算结果表明, 同等参数条件下, c越小, DPF电流越高. 可以发现降低c能够明显提升电流. 从物理机制上可进行如下解释: 其他参数不变的情况下, c越小, DPF体积越小, 这样DPF系统消耗的磁能也越小, 电流才会越大. 因此, 可以预期DPF小型化之后应该能够提升系统电流, 这对于高DD产额装置比较关键.

本文建立了耦合外电路的双温MHD模型, 研究了DPF轴向加速和径向内爆过程. 首先通过与UNU装置和UDMPF1装置的实验结果对比, 验证了双温MHD模型的准确性. 然后进一步研究了DPF物理过程及规律.

1) DPF等离子体鞘在洛伦兹力加速下沿轴向不断加速, 此时等离子体鞘的温度也不断升高. 运动到内电极末端后, 等离子体鞘会沿径向向内弯曲, 最终被压缩在轴上形成高温高密等离子体, 密度上升1个量级, 温度上升2个量级左右.

2) 放电参数研究结果表明, 对于大型DPF装置(MA量级), 降低电感、提升电容, 电路电流容易达到饱和; 而增大电路电压对电流提升效果则比较显著.

3) 结构参数研究结果则表明, 对于DPF装置(尤其是MA量级), 阴阳极半径之比c需要尽可能小, 这能在其他参数不变的情况下, 尽可能提升DPF的峰值电流和箍缩电流.