高级搜索

HL-3装置中性粒子与碳杂质影响偏滤器脱靶的模拟研究

,  ,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

周雨林, 吴雪科, 徐欣亮, 肖国梁, 龙婷, 高金明, 范冬梅, 孟晗琪, 赵真, 王占辉. HL-3装置中性粒子与碳杂质影响偏滤器脱靶的模拟研究[J]. 物理学报, 2025, 74(11): 115203-1. doi: 10.7498/aps.74.20250065
引用本文: 周雨林, 吴雪科, 徐欣亮, 肖国梁, 龙婷, 高金明, 范冬梅, 孟晗琪, 赵真, 王占辉. HL-3装置中性粒子与碳杂质影响偏滤器脱靶的模拟研究[J]. 物理学报, 2025, 74(11): 115203-1. doi: 10.7498/aps.74.20250065
shu
Yulin ZHOU, Xueke WU, Xinliang XU, Guoliang XIAO, Ting LONG, Jinming GAO, Dongmei FAN, Hanqi MENG, Zhen ZHAO, Zhanhui WANG. Simulation research on effect of neutrals and carbon impurities on divertor detachment in HL-3 tokamak[J]. Acta Physica Sinica, 2025, 74(11): 115203-1. doi: 10.7498/aps.74.20250065
Citation: Yulin ZHOU, Xueke WU, Xinliang XU, Guoliang XIAO, Ting LONG, Jinming GAO, Dongmei FAN, Hanqi MENG, Zhen ZHAO, Zhanhui WANG. Simulation research on effect of neutrals and carbon impurities on divertor detachment in HL-3 tokamak[J]. Acta Physica Sinica, 2025, 74(11): 115203-1. doi: 10.7498/aps.74.20250065
shu

HL-3装置中性粒子与碳杂质影响偏滤器脱靶的模拟研究

  • 核工业西南物理研究院聚变研究所, 成都　610225

    • 作者简介: 周雨林.E-mail: zhouyl@swip.ac.cn .
    通讯作者: E-mail: xuxinliang@swip.ac.cn.; 

  • 中图分类号: 52.55.Fa, 52.55.Rk, 52.20.Hv, 52.65.-y

Simulation research on effect of neutrals and carbon impurities on divertor detachment in HL-3 tokamak

  • Southwestern Institute of Physics, Chengdu 610225, China

    • Corresponding author: E-mail: xuxinliang@swip.ac.cn.; 

  • MSC: 52.55.Fa, 52.55.Rk, 52.20.Hv, 52.65.-y

  • 摘要: 偏滤器脱靶是中国环流三号装置(HL-3)偏滤器热负载的主要控制手段. 然而目前的脱靶工作缺少对刮削层-偏滤器区域内复杂多成分粒子问题的研究, 如氢同位素(如氘)、外部注入杂质(如氖杂质)、内部固有杂质(如碳杂质)的碰撞、辐射等过程. 本工作使用新开发的刮削层-偏滤器多成分粒子输运程序SD1D, 研究了碳杂质和中性粒子对中国环流三号上抬升等离子体密度和偏滤器氖气注入两种脱靶方式的影响. 研究发现, 偏滤器产生的碳杂质对于抬升密度的脱靶方式具有促进作用, 但是对注入氖气实现脱靶的过程影响较小. 此外, 本工作还发现中性粒子(氘原子与氘分子)在这两种脱靶过程中的重要性也有很大的差别: 抬升等离子体密度可以促进偏滤器内再循环过程产生大量中性粒子, 等离子体与中性粒子反应导致的能量与动量损失是实现脱靶的关键因素; 向偏滤器内注入氖气直接降低了靶板上饱和电流, 抑制了再循环过程, 中性粒子的重要性也随之降低.
    Abstract: Divertor detachment is a critical technique for managing the thermal load on the divertor of the HL-3 tokamak, an important device in magnetic confinement fusion research. However, existing studies on detachment have largely overlooked the complex multi-species particle dynamics in the scrape-off layer (SOL) and divertor regions, particularly the interactions involving hydrogen isotopes (e.g, deuterium), externally injected impurities (e.g, neon), and intrinsic impurities (e.g, carbon). This study aims to address this problem by employing the newly developed multi-species particle transport code SD1D to investigate the effects of carbon impurities and neutral particles on two detachment scenarios in HL-3: plasma density ramp-up and neon injection into the divertor.The SD1D code models the transport, collision, and radiation processes of various particles, including deuterium ions, atoms, and molecules, as well as carbon and neon impurities, along the magnetic field lines from the SOL upstream to the divertor target. The study focuses on understanding how carbon impurities and neutral particles affect the detachment mechanisms under different conditions.The results reveal that carbon impurities generated in the divertor significantly enhance the detachment in the density ramp-up scenario by increasing the density of deuterium atoms, molecules, and ions near the target plate, thereby increasing the total radiation power. This effect lowers the density threshold required for detachment and reduces the peak current on the target plate. However, carbon impurities have a minimal influence on detachment achieved through neon injection, as they do not significantly change the density of deuterium species or the total radiation power in this scenario.Furthermore, this study highlights the distinct roles of neutral particles in the two detachment mechanisms. In the density ramp-up scenario, the increased plasma density promotes the recycling process in the divertor, generating a substantial population of neutral particles. The energy loss and momentum loss resulting from plasma-neutral interactions are crucial for achieving detachment. In contrast, neon injection directly reduces the saturation current on the target plate, suppressing the recycling process and diminishing the importance of neutral particles.In conclusion, this work demonstrates that carbon impurities play a significant role in facilitating detachment during plasma density ramp-up but have limited influence on detachment via neon injection. The findings underscore the importance of considering multi-species particle dynamics, including neutral particles and impurities, in understanding and optimizing divertor detachment strategies. Future work will involve validating the SD1D model based on experimental data from HL-3 to further refine its predictiveness.
  • 加载中

  • 图 1  托卡马克磁约束聚变装置截面结构

    Figure 1.  Power exhaust on tokamak plasma cross-section.

    下载: 全尺寸图片 幻灯片

    图 2  刮削层-偏滤器区域等离子体热流通道(沿磁力线方向)与主要反应

    Figure 2.  Heat flux flowing along the field line and the main reactions in scrape-off layer (SOL) and divertor region.

    下载: 全尺寸图片 幻灯片

    图 3  氖气注入偏滤器在沿磁力线方向形成的源剖面 $ {S}_{{{\mathrm{N}}{\mathrm{e}}}^{0}} $

    Figure 3.  The source profile $ {S}_{{{\mathrm{N}}{\mathrm{e}}}^{0}} $ of neon injection into divertor

    下载: 全尺寸图片 幻灯片

    图 4  刮削层-偏滤器碳杂质含量的影响　(a)抬升上游等离子体密度触发偏滤器脱靶; (b)氖杂质注入偏滤器脱靶. 蓝色曲线表示靶板上电流$ {J}_{{\mathrm{s}}{\mathrm{a}}{\mathrm{t}}, {\mathrm{t}}{\mathrm{a}}{\mathrm{r}}{\mathrm{g}}{\mathrm{e}}{\mathrm{t}}} $, 红色曲线表示靶板上电子温度, 碳杂质含量$ {f}_{{\mathrm{C}}} $分别为0, 1%和3%

    Figure 4.  The effect of carbon concentration in SOL and divertor region on two different divertor detachment regimes: (a) Density ramp induced detachment; (b) neon injection induced detachment. The blue curves and red curves represent the current and the electron temperature on the divertor target (three carbon concentrations used in simulations are 0, 1%, and 3%).

    下载: 全尺寸图片 幻灯片

    图 5  刮削层-偏滤器碳杂质含量($ {f}_{{\mathrm{C}}}=0, {\mathrm{ }}1{\mathrm{{\text{%}}}}{\mathrm{ }}, 3{\mathrm{{\text{%}}}} $)对平行方向上密度(氘分子、电离态氘分子、氘原子与氘离子)以及对辐射功率的影响 (a), (c)上游等离子体密度抬升至$ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}={0.11\times 10}^{20}\;{{\mathrm{m}}}^{-3} $时的剖面; (b), (d) 氖杂质注入通量为$ {6.7\times 10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}{\mathrm{s}}/{\mathrm{s}} $时的剖面, 靶板位于45 m处(由于氘粒子和碳杂质主要分布在靠近靶板的区域, 因此图中只给出了靠近靶板的平行剖面, 即42—45 m)

    Figure 5.  The effect of carbon concentration (0, 1%, and 3%) on the parallel density and radiation profiles in two detachment regimes: (a), (c) The density and radiation in density ramp induced detachment ($ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}={0.11\times 10}^{20}\;{{\mathrm{m}}}^{-3} $); (b), (d) the density and radiation in neon injection induced detachment (neon injection flux equal to $ {6.7\times 10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}{\mathrm{s}}/{\mathrm{s}} $). The parallel profile is 42–45 m (the target located at 45 m).

    下载: 全尺寸图片 幻灯片

    图 6  抬升密度和偏滤器氖杂质注入两种脱靶过程中的平行方向上密度(氘分子、电离态氘分子、氘原子与氘离子)以及辐射功率(氘与碳) (a), (c)刮削层上游电子密度在脱靶前$ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}={0.08\times 10}^{20}\;{{\mathrm{m}}}^{-3} $、脱靶开始$ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}={0.10\times 10}^{20}\;{{\mathrm{m}}}^{-3} $与脱靶后$ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}=0.145\times $$ 10^{20}\;{{\mathrm{m}}}^{-3} $时的剖面; (b), (d)氖杂质注入前, 以及杂质注入通量为$ {3.0\times 10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}{\mathrm{s}}/{\mathrm{s}} $, $ {12.5\times 10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}{\mathrm{s}}/{\mathrm{s}} $时的剖面, 图中碳杂质含量都为3%, 靶板位于45 m处 (由于氘粒子和碳杂质主要分布在靠近靶板的区域, 图中只给出了靠近靶板的剖面, 即42—45 m)

    Figure 6.  Comparison of the parallel density and radiation profiles in two detachment regimes: (a), (c) The density and radiation in density ramp induced detachment ($ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}={0.08\times 10}^{20}\;{{\mathrm{m}}}^{-3} $, $ {0.10\times 10}^{20}\;{{\mathrm{m}}}^{-3}, $ and $ {0.145\times 10}^{20}\;{{\mathrm{m}}}^{-3} $); (b), (d) the density and radiation in neon injection induced detachment (neon injection flux equal to $ \text{0 parts/s} $, $ {3.0\times 10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}{\mathrm{s}}/{\mathrm{s}}, $ and $ {12.5\times 10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}{\mathrm{s}}/{\mathrm{s}} $), carbon concentration equal to 3%; the parallel profile is 42–45 m (the target located at 45 m).

    下载: 全尺寸图片 幻灯片

    图 8  (a)上游密度抬升与(b)偏滤器注氖气两种脱靶过程中, 氘原子、氘分子、电离态氘分子与等离子体相互作用造成的等离子体动量损失与上游等离子体动量的比值, 即等离子体动量损失因子; (c)上游密度抬升与(d)偏滤器注氖气两种脱靶中, 氘粒子、碳杂质与氖杂质辐射造成的等离子体能量损失与上游等离子体能量的比值, 即等离子体能量损失因子, 碳含量为3%

    Figure 8.  Momentum loss factor caused by different types of collisional reactions during (a) density ramp induced detachment and (b) neon injection induced detachment; heat loss factor caused by radiations of different particle species during (c) density ramp induced detachment and (d) neon injection induced detachment (carbon concentration equal to 3%).

    下载: 全尺寸图片 幻灯片

    图 7  平行方向上从刮削层(0—24 m), 通过X点(24 m)氘靶板(45 m)的氖杂质密度和辐射功率(氖杂质注入通量为$ {3.0\times 10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}{\mathrm{s}}/{\mathrm{s}} $, 上游电子密度$ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}=0.08\times 10^{20}\;{{\mathrm{m}}}^{-3} $, 碳杂质含量为3%)

    Figure 7.  Neon density and radiation profile along the parallel direction from SOL to the target (neon injection flux equal to $ {3.0\times 10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}{\mathrm{s}}/{\mathrm{s}} $, $ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}={0.08\times 10}^{20}\;{{\mathrm{m}}}^{-3} $, carbon concentration equal to 3%).

    下载: 全尺寸图片 幻灯片

    表 1  氘原子、氘分子的碰撞反应

    Table 1.  Collisional reactions of D and D2.

    反应名称
    $ {\mathrm{e}}+{\mathrm{D}}\to 2{\mathrm{e}}+{{\mathrm{D}}}^{+} $电离
    $ {{\mathrm{D}}}^{+}+{\mathrm{D}}\to {\mathrm{D}}+{{\mathrm{D}}}^{+} $电荷交换
    $ {{\mathrm{D}}}^{+}+{\mathrm{e}}\to {\mathrm{D}} $复合
    $ {\mathrm{e}}+{{\mathrm{D}}}_{2}\to 2{\mathrm{e}}+{{\mathrm{D}}}_{2}^{+} $分子电离
    $ {\mathrm{e}}+{{\mathrm{D}}}_{2}\to {\mathrm{e}}+{\mathrm{D}}+{\mathrm{D}} $分解
    $ {{\mathrm{D}}}^{+}+{{\mathrm{D}}}_{2}\to {{\mathrm{D}}}_{2}^{+}+{\mathrm{D}} $分子电荷交换
    $ {\mathrm{e}}+{{\mathrm{D}}}_{2}^{+}\to {\mathrm{e}}+{{\mathrm{D}}}^{+} $+ $ {\mathrm{D}} $分解激发
    $ {\mathrm{e}}+{{\mathrm{D}}}_{2}^{+}\to 2{\mathrm{e}}+{{\mathrm{D}}}^{+} $+ $ {{\mathrm{D}}}^{+} $分解电离
    $ {\mathrm{e}}+{{\mathrm{D}}}_{2}^{+}\to $ $ {\mathrm{D}}+{\mathrm{D}} $分解复合
    下载: 导出CSV

    表 2  氖杂质的碰撞反应

    Table 2.  Collisional reaction of neon impurities.

    反应 名称
    $ {{\mathrm{N}}{\mathrm{e}}}^{{{Z}}+}+{\mathrm{e}}\to {{\mathrm{N}}{\mathrm{e}}}^{Z+1}+2{\mathrm{e}} $ 电离 ($ Z $ = 0—9)
    $ {{\mathrm{N}}{\mathrm{e}}}^{{{Z}}+}+{\mathrm{e}}\to {{\mathrm{N}}{\mathrm{e}}}^{Z-1} $ 复合 ($ Z $ = 1—10)
    $ {{\mathrm{N}}{\mathrm{e}}}^{{{Z}}+}+{\mathrm{D}}\to {{\mathrm{N}}{\mathrm{e}}}^{Z-1}+{{\mathrm{D}}}^{+} $ 电荷交换 ($ Z $ = 1—10)
    下载: 导出CSV

    表 3  SD1D主要输入参数

    Table 3.  The input parameters of SD1D.

    $ {n}_{\rm e,up}/({10}^{20}~{\rm m}^{-3})$ 氖气注入通量/(1020 part·s–1) Qheat,up/(MW·m–2) 总连接长度/m X点到靶板连接长度/m
    密度抬升脱靶 0.08—0.22 无 7.2 45 21
    氖杂质注入脱靶 0.8 0—15.0 7.2 45 21
    下载: 导出CSV
  • [1] Stangeby P C 2000 The Plasma Boundary of Magnetic Fusion Devices (CRC Press
    [2] Kallenbach A, Bernert M, Dux R, Reimold F, Wischmeier M, ASDEX Upgrade Team 2016 Plasma Phys. Contr. Fusion 58 045013 doi: 10.1088/0741-3335/58/4/045013
    [3] Stangeby P C 2018 Plasma Phys. Contr. Fusion 60 044022 doi: 10.1088/1361-6587/aaacf6
    [4] Verhaegh K, Lipschultz B, Bowman C, Duval B P, Fantz U, Fil A, Harrison J R, Moulton D, Myatra O, Wünderlich D, Federici F 2021 Plasma Phys. Contr. Fusion 63 035018 doi: 10.1088/1361-6587/abd4c0
    [5] Kunze H J 2009 Springer Science & Business Media 56 34
    [6] Bernert M, Wischmeier M, Huber A, Reimold F, Lipschultz B, Lowry C, Brezinsek S, Dux R, Eich T, Kallenbach A, Lebschy A 2017 Nucl. Mater. Energy 12 111 doi: 10.1016/j.nme.2016.12.029
    [7] Wu T, Nie L, Yu Y, Gao J M, Li J Y, Ma H C, Wen J, Ke R, Wu N, Huang Z H, Liu L, Zheng D L, Yi K Y, Gao X Y, Wang W C, Cheng J, Yan L W, Cai L Z, Wang Z H, Xu M 2023 Plasma Sci. Tech. 25 015102 doi: 10.1088/2058-6272/ac82df
    [8] Zhou Y, Dudson B, Militello F, Verhaegh K, Myatra O 2022 Plasma Phys. Contr. Fusion 64 065006. doi: 10.1088/1361-6587/ac6827
    [9] Boedo J, Gray D, Chousal L, Conn R, Hiller B, Finken K. H 1998 Rev. Sci. Instrum. 69 2663 doi: 10.1063/1.1148995
    [10] Boedo J A, Crocker N, Chousal L, Hernandez R, Chalfant J, Kugel H, Roney P, Wertenbaker J, NSTX Team 2009 Rev. Sci. Instrum. 80 123506 doi: 10.1063/1.3266065
    [11] Clark J G, Bowden M D, Scannell R 2021 Rev. Sci. Instrum. 92 043545 doi: 10.1063/5.0043813
    [12] Makarov S O, Coster D P, Kaveeva E G, Rozhansky V A, Senichenkov I Y, Veselova I Y, Voskoboynikov S P, Stepanenko A A, Bonnin X, Pitts R A 2023 Nucl. Fusion 63 026014. doi: 10.1088/1741-4326/acab76
    [13] Mailloux J, Abid N, Abraham K, Abreu P, Adabonyan O, Adrich P, Afanasev V, Afzal M, Ahlgren T, Aho-Mantila L, Aiba N 2022 Nucl. Fusion 62 042026 doi: 10.1088/1741-4326/ac47b4
    [14] Fil A, Lipschultz B, Moulton D, Thornton A, Dudson B D, Myatra O, Verhaegh K, EUROfusion MST1 Team 2022 Nucl. Fusion 62 096026 doi: 10.1088/1741-4326/ac81d8
    [15] Myatra O, Moulton D, Dudson B, Lipschultz B, Newton S, Verhaegh K, Fil A 2023 Nucl. Fusion 63 076030 doi: 10.1088/1741-4326/acd9da
    [16] Verhaegh K, Lipschultz B, Duval B P, Harrison J R, Reimerdes H, Theiler C, Labit B, Maurizio R, Marini C, Nespoli F, Sheikh U 2017 Nucl. Mater. Energy 12 1112. doi: 10.1016/j.nme.2017.01.004
    [17] Gao J M, Cai L Z, Cao C Z, Ma H C, Ke R, Wu N, Hu Y, Gao X Y, Cui C H, Huang Z H, Nie L 2023 Nucl. Fusion 63 036006 doi: 10.1088/1741-4326/acaf2f
    [18] 龙婷, 柯锐, 吴婷, 高金明, 才来中, 王占辉, 许敏 2024 . 物理学报 73 088901 doi: 10.7498/aps.73.20231749 Long T, Ke R, Wu T, Gao J M, Cai L Z, Wang Z H, Xu M, 2024 Acta Phys. Sin. 73 088901 doi: 10.7498/aps.73.20231749
    [19] Wu N, Cheng J, Yi K Y, Wang R, Han M K, Huang Z H, Wang W C, He Y, Yan L W, Du H L, Gao J M 2024 Nucl. Fusion 64 096007 doi: 10.1088/1741-4326/ad5e96
    [20] Liu J B, Wang L, Guo H Y, Wang H Q, Xu G S, Ding F, Xu J C, Liu X J, Yuan Q P, Wu K, Liu S C 2019 Nucl. Fusion 59 126046 doi: 10.1088/1741-4326/ab4639
    [21] Dudson B. D, Allen J, Body T, Chapman B, Lau C, Townley L, Moulton D, Harrison J, Lipschultz B 2019 Plasma Phys. Contr. Fusion 61 065008 doi: 10.1088/1361-6587/ab1321
    [22] Kallenbach A, Bernert M, Dux R, Eich T, Henderson S S, Pütterich T, Reimold F, Rohde V, Sun H J, ASDEX Upgrade Team 2019 Nucl. Mater. Energy 18 166 doi: 10.1016/j.nme.2018.12.021
    [23] Zhou Y, Dudson B, Wu T, Wang Z, Xia T, Zhong C, Gao J, Du H, Fan D 2024 Plasma Phys. Contr. Fusion 66 055005 doi: 10.1088/1361-6587/ad30fc
  • 加载中
图( 8) 表( 3)
计量
  • 文章访问数:  22
  • HTML全文浏览数:  22
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-01-16
  • 刊出日期:  2025-06-05

HL-3装置中性粒子与碳杂质影响偏滤器脱靶的模拟研究

    通讯作者: E-mail: xuxinliang@swip.ac.cn.; 
    作者简介: 周雨林.E-mail: zhouyl@swip.ac.cn
  • 核工业西南物理研究院聚变研究所, 成都　610225
  • 收稿日期:  2025-01-16

摘要: 偏滤器脱靶是中国环流三号装置(HL-3)偏滤器热负载的主要控制手段. 然而目前的脱靶工作缺少对刮削层-偏滤器区域内复杂多成分粒子问题的研究, 如氢同位素(如氘)、外部注入杂质(如氖杂质)、内部固有杂质(如碳杂质)的碰撞、辐射等过程. 本工作使用新开发的刮削层-偏滤器多成分粒子输运程序SD1D, 研究了碳杂质和中性粒子对中国环流三号上抬升等离子体密度和偏滤器氖气注入两种脱靶方式的影响. 研究发现, 偏滤器产生的碳杂质对于抬升密度的脱靶方式具有促进作用, 但是对注入氖气实现脱靶的过程影响较小. 此外, 本工作还发现中性粒子(氘原子与氘分子)在这两种脱靶过程中的重要性也有很大的差别: 抬升等离子体密度可以促进偏滤器内再循环过程产生大量中性粒子, 等离子体与中性粒子反应导致的能量与动量损失是实现脱靶的关键因素; 向偏滤器内注入氖气直接降低了靶板上饱和电流, 抑制了再循环过程, 中性粒子的重要性也随之降低.

English Abstract

    全文HTML

    1.   引　言

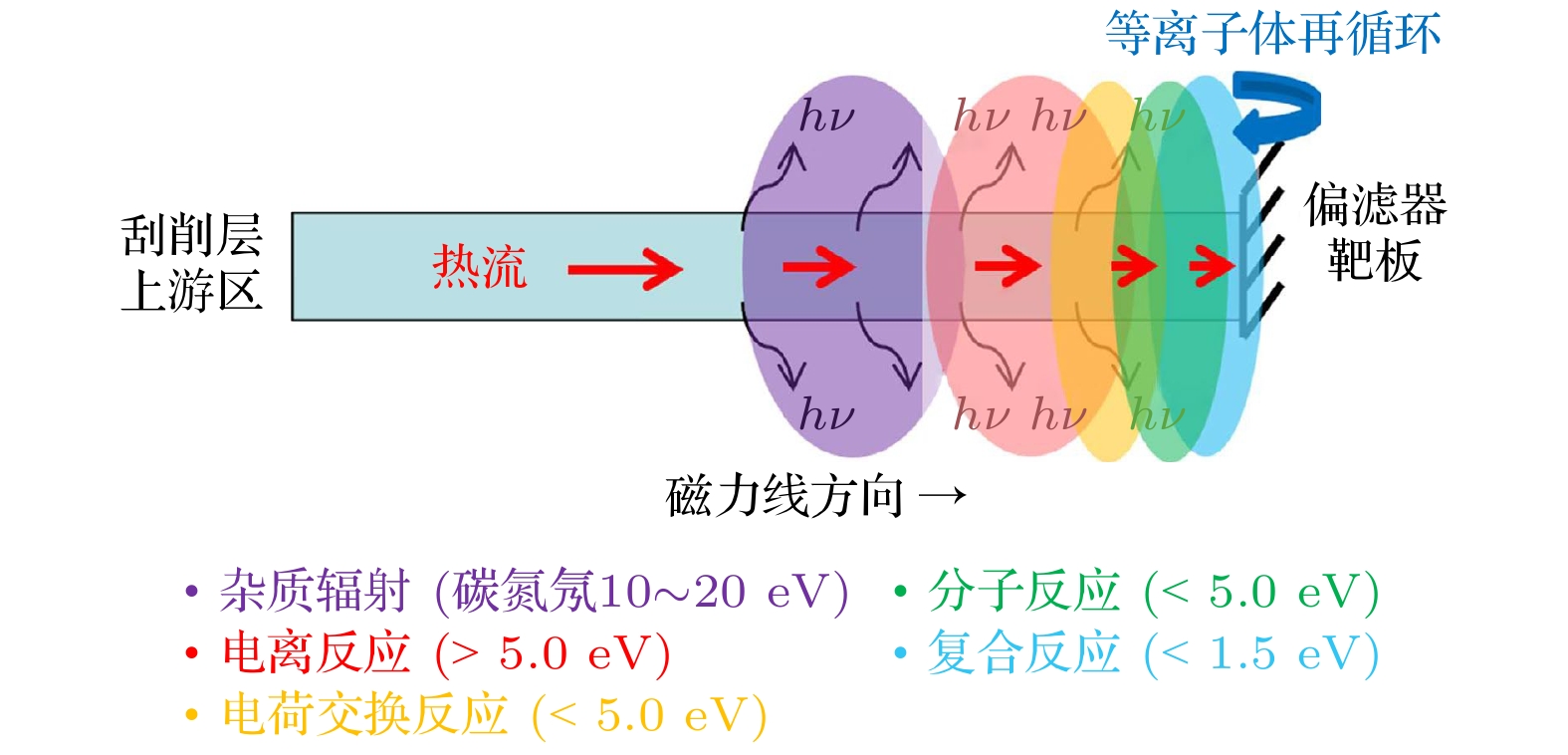
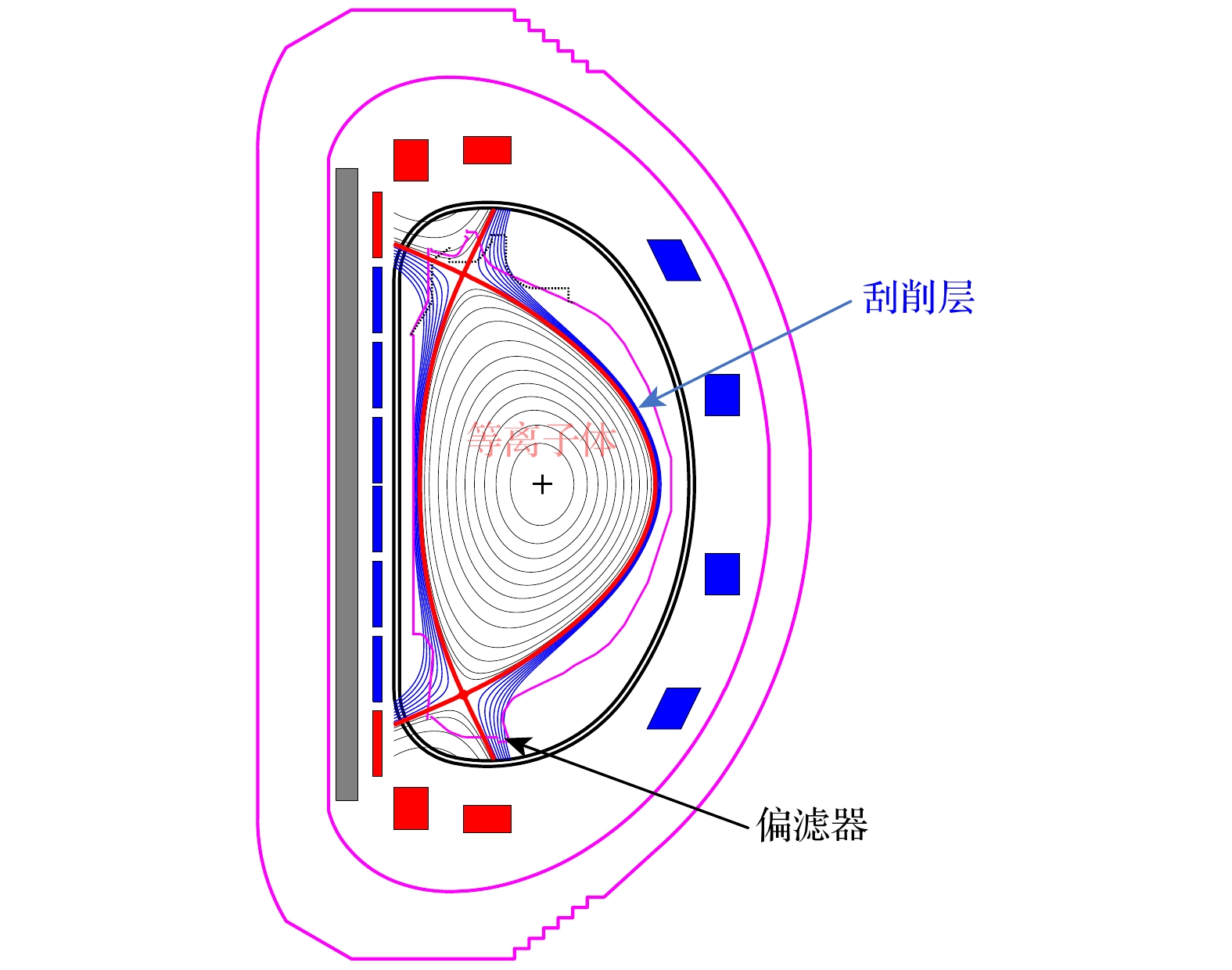
    • 实现核聚变要求等离子体温度达到上亿摄氏度, 尽管托卡马克(tokamak)磁约束装置在等离子体约束方面具备显著优势, 但由于等离子体边界不稳定性以及装置约束性能的局限性, 部分等离子体仍会从约束区域逃逸, 并进入刮削层(scrape-off layer, SOL), 如图1所示. 这些逃逸出来的等离子体大部分通过刮削层流入偏滤器(divertor), 并最终击打在偏滤器靶板上[1], 这一现象已成为当前磁约束聚变研究领域中亟待解决的关键排热问题[2,3]. 偏滤器靶板一般是由耐高温材料制成(例如耐高温碳材料或钨金属材料), 可以承受低参数条件下的热负载, 然而大型装置高参数实验条件下, 偏滤器的热负载将超出工程限制. 为了避免偏滤器在高参数条件下受到严重损坏, 目前大型托卡马克装置上通过实现偏滤器脱靶来控制偏滤器中的热流[3–6]. 常用的两种实现偏滤器脱靶方式如下[7,8].

      1) 通过向等离子体中加料提升刮削层上游等离子体密度, 增大流入偏滤器的等离子体通量, 促进偏滤器内再循环过程产生大量中性粒子与等离子体反应(图2), 从而有效降低偏滤器靶板上的等离子体温度和电流, 实现脱靶.

      2)向偏滤器内通入杂质气体(如氖气Ne)可以大幅增大偏滤器内的辐射功率, 从而耗散偏滤器内的等离子体能量, 实现脱靶.

      为了解决ITER及未来聚变堆的排热问题, 目前在世界上很多大型磁约束聚变装置上都积极开展了偏滤器脱靶控制热负载实验[9–11]. 因此, 偏滤器脱靶也成为了近几年托卡马克聚变研究的热点问题之一. 欧洲联合环状反应堆(the joint European torus, JET)开展了氘氚聚变实验, 模拟和实验研究验证了偏滤器脱靶是未来聚变堆装置高参数放电下可靠的热流控制手段[12,13]. 英国在MAST大型球形托卡马克装置基础上升级建造了MAST-U (mega ampere spherical tokamak upgrade), 主要升级的部分在于偏滤器采用了长腿偏滤器位形(能够兼容Super-X先进偏滤器磁位形)[14]. 长腿位形通过延长偏滤器里的空间, 增大了等离子体与偏滤器靶板的接触面积, 同时也增大了杂质辐射以及中性粒子与等离子体相互作用的空间. 研究发现长腿偏滤器位形可以更容易实现脱靶, 从而更加有效地降低靶板上的热负载[15]. 在TCV(tokamakà configuration variable)托卡马克封闭偏滤器位形的实验中, 研究人员通过在上游区域进行等离子体加料增大主等离子体密度以及向偏滤器内注入杂质两种手段也成功实现了脱靶, 降低了偏滤器热流 [16]. TCV研究表明, 相比于开放偏滤器位形, 封闭式偏滤器位形能更好地将中性粒子以及注入到偏滤器中的杂质约束在偏滤器中, 从而能更加有效地降低偏滤器中等离子体的动量与能量[16].

      我国磁约束聚变装置中国环流二号(HL-2A)及先进实验超导托卡马克EAST (experimental advanced superconducting tokamak)装置中, 都成功开展了注入杂质控制偏滤器热流的实验 [7,17,18]. 在HL-2A上, 通过向其封闭偏滤器中注入氮杂质成功将偏滤器靶板温度降到5 eV以下, 实现完全脱靶[7,17,19]. 针对国际热核聚变实验堆ITER的设计, EAST安装了钨材偏滤器, 并成功实现脱靶, 有效降低了偏滤器上的热流. 研究发现, 虽然注入氖杂质可以降低实现脱靶的等离子体密度条件, 但是注入氖杂质同时会破坏装置的等离子体约束性能[20].

      综上所述, 在国内外大型托卡马克聚变装置上已开展的偏滤器脱靶工作中, 主要研究了脱靶过程中的边界等离子体宏观输运、热流变化、能量约束、偏滤器位形等宏观问题, 缺少对刮削层-偏滤器中复杂多成分粒子的碰撞辐射反应等微观过程的研究工作, 特别是缺少中性粒子对脱靶影响的研究. 在中国环流三号HL-3装置中, 第一壁和偏滤器由碳材料构成, 因此碳杂质会不可避免地存在于等离子体中, 特别是刮削层-偏滤器中碳杂质含量较高, 会对实验造成很大影响. 因此, 开展碳杂质、中性粒子等不同种类粒子影响偏滤器脱靶的模拟研究对于理解HL-3的实验现象以及探索降低偏滤器热负载的有效方案具有重要价值, 也为未来HL-3装置燃烧等离子体实验下的偏滤器热流控制提供依据.

      本工作介绍了一个新升级开发的刮削层-偏滤器多成分粒子含时输运程序SD1D, 包括了氘、碳杂质、氖杂质等种类粒子沿磁力线从刮削层上游区域(SOL upstream)到偏滤器靶板(divertor target)的输运、碰撞、辐射等过程. 该程序可以快速模拟不同托卡马克装置上的偏滤器脱靶过程. 本文结构安排如下: 第2节介绍了程序的物理模型; 第3节基于HL-3装置实验参数模拟研究了不同碳杂质含量对脱靶的影响, 对比了刮削层-偏滤器区域中不同种类粒子与等离子体相互作用所造成的等离子体动量损失以及能量损失, 分析了不同脱靶机制下触发脱靶的主要因素; 第4节总结了文章的研究工作, 阐述了下一步研究计划.

    2.   SD1D程序物理模型

    • SD1D是近期升级开发的刮削层-偏滤器一维含时流体模拟程序[21], 包含了氘离子($ {{\mathrm{D}}}^{+} $)、氘原子($ {\mathrm{D}} $)、氘分子($ {{\mathrm{D}}}_{2} $)、电离态氘分子($ {{\mathrm{D}}}_{2}^{+} $)、碳杂质($ {\mathrm{C}} $)、氖杂质($ {\mathrm{N}}{\mathrm{e}} $)等粒子的碰撞、辐射模型, 可用于模拟刮削层-偏滤器沿磁力线方向的粒子输运过程、偏滤器脱靶控制热流过程等托卡马克边界物理问题.

      • 2.1.   氘等离子体、氘原子、氘分子及碳杂质物理模型

    • SD1D物理模型包括了等离子体密度方程(方程1(a))、内能方程(方程1(b)), 以及动量方程(方程1(c)). 其中, 内能方程计算的是等离子体静压强(static pressure), 即 $ p={p}_{{{\mathrm{D}}}^{+}}+{p}_{{\mathrm{e}}}={n}_{{{\mathrm{D}}}^{+}}{T}_{{{\mathrm{D}}}^{+}}+ {n}_{{\mathrm{e}}}{T}_{{\mathrm{e}}}: $

      方程中$ {\partial }_{/ / }=\boldsymbol{b}\cdot \nabla $ 表示沿磁力线方向的方向导数, 热通量$ \boldsymbol{q}={5}/{2}p\boldsymbol{b}{v}_{/ / , {{\mathrm{D}}}^{+}}-{\kappa }_{/ / }{\partial }_{/ / }{T}_{{\mathrm{e}}} $, 热传导系数$ \kappa = {\kappa }_{0}{{T}_{{\mathrm{e}}}}^{5/2} $, $ {\kappa }_{0}=2293.8\;{\mathrm{M}}{\mathrm{W}}\cdot{{\mathrm{m}}}^{-2}\cdot{{\mathrm{e}}{\mathrm{V}}}^{-5/2} $. $ {S}_{{\mathrm{n}}} $和$ {S}_{{\mathrm{E}}} $是从约束区输运到刮削层的等离子体源项和能量源项, $ S $和$ E $表示由碰撞反应过程引起的源项, R表示由辐射引起的能量损失, F表示作用在主等离子体上的力[8]. 模型假设等离子体是电中性的, 电子密度是所有带电离子电荷数总和(方程(1d)), 并且假设主离子(D+)和电子温度相等($ {T}_{{\mathrm{e}}}={T}_{{{\mathrm{D}}}^{+}} $). 氘原子、分子与等离子体反应详见表1.

      氘原子$ {\mathrm{D}} $、氘分子$ {{\mathrm{D}}}_{2} $以及电离态氘分子$ {{\mathrm{D}}}_{2}^{+} $的输运方程与等离子体方程类似(如方程(1a)—(1c))[8]. 区别在于, 方程中的密度源项、能量源项和作用力是由不同的碰撞与辐射反应过程决定的. 由于磁场不能限制中性粒子沿着磁力线运动, 跨磁场的输运过程对中性粒子非常重要. 在SD1D物理模型中, 为了研究中性粒子垂直方向运动的影响, 使用碰撞模型和绝热条件将中性粒子的垂直方向速度投影到平行方向上, 可得中性粒子在平行方向上总速度为$ {v}_{{\mathrm{D}}}={v}_{/ / , {\mathrm{D}}}-{\Big(\dfrac{{B}_{{\mathrm{\phi }}}}{{B}_{{\mathrm{\theta }}}}\Big)}^{2}\dfrac{{\partial }_{/ / }{p}_{{\mathrm{D}}}}{v} $[21], 其中$ {\mathrm{\nu }} $是原子与其他粒子碰撞反应的总碰撞频率, $ {({{B}_{{\mathrm{\phi }}}}/{{B}_{{\mathrm{\theta }}}})}^{2} = 10 $. 其他中性粒子的速度也使用相同的假设.

      本工作使用Bohm边界条件来处理偏滤器靶板上的$ {{\mathrm{D}}}^{+} $与$ {{\mathrm{D}}}_{2}^{+} $离子速度: 假设靶板上平行方向上离子速度大于等于声速, 如$ {v}_{/ / , {{\mathrm{D}}}^{+}}\geqslant {c}_{{\mathrm{s}}, {{\mathrm{D}}}^{+}} $和$ {v}_{/ / {, {\mathrm{D}}}_{2}^{+}}\geqslant {c}_{{\mathrm{s}}, {{\mathrm{D}}}_{2}^{+}} $, 其中, $ {c}_{{\mathrm{s}}, {{\mathrm{D}}}^{+}} = \sqrt{\dfrac{2\cdot {T}_{{{\mathrm{D}}}^{+}}}{{m}_{{{\mathrm{D}}}^{+}}}} $, $ {c}_{{\mathrm{s}}, {{\mathrm{D}}}^{+}} = \sqrt{\dfrac{2\cdot {T}_{{{\mathrm{D}}}_{2}^{+}}}{{m}_{{{\mathrm{D}}}_{2}^{+}}}} $. 本工作假设在鞘层入口处的$ {{\mathrm{D}}}^{+} $与$ {{\mathrm{D}}}_{2}^{+} $离子温度梯度为0, 并且设定鞘层热输运系数$ \gamma $= 6, 等离子体热通量表示为$ {q}_{{{\mathrm{D}}}^{+}}=\gamma {n}_{{{\mathrm{D}}}^{+}}{T}_{{{\mathrm{D}}}^{+}}{c}_{{\mathrm{s}}, {{\mathrm{D}}}^{+}} $以及$ {q}_{{{\mathrm{D}}}_{2}^{+}}= {\mathrm{\gamma }}{n}_{{{\mathrm{D}}}_{2}^{+}}{T}_{{{\mathrm{D}}}_{2}^{+}}{c}_{{\mathrm{s}}, {{\mathrm{D}}}_{2}^{+}} $. 在靶板上, 考虑再循环产生氘分 子过程, 再循环率为$ {f}_{{{\mathrm{D}}}_{2}, {\mathrm{ }}{\mathrm{r}}{\mathrm{e}}{\mathrm{c}}{\mathrm{l}}} = {{\varGamma }_{{{\mathrm{D}}}_{2}, {\mathrm{recl}}}}/{{\varGamma }_{{{\mathrm{D}}}^{+}}^{{\mathrm{t}}}}=0.99 $, 即再循环分子通量与打到靶板上的离子体通量的比值.

      近期工作中, 杂质辐射模块Atomic++coronal已经被耦合到SD1D程序中[8,21]. 该模块可以从ADAS数据库读取碳杂质的碰撞与辐射数据, 并将SD1D模拟的碳杂质总密度、电子温度数据输入Atomic++coronal, 通过日冕模型(coronal model)计算出碳在不同电离态的密度和碳杂质辐射功率. 其中碳杂质总密度由电子密度$ {n}_{{\mathrm{e}}} $乘以碳杂质含量系数$ {f}_{{\mathrm{C}}} = {{n}_{{\mathrm{C}}, {\mathrm{t}}{\mathrm{o}}{\mathrm{t}}{\mathrm{a}}{\mathrm{l}}}}/{{n}_{{\mathrm{e}}}} $得到. 该模块为SD1D模拟分析刮削层-偏滤器复杂的多成分原子分子过程提供强有力的支撑.

      虽然模拟中常使用日冕模型来计算辐射功率, 可是该模型在高等离子体密度条件下误差较大. 因此模拟中还需要其他模型来计算辐射功率, 比如Kallenbach使用非日冕模型来计算辐射系数, 该模型与实验中的到的辐射功率结果相符[22]. SD1D也将在未来工作中进行升级, 将碳原子以及不同碳离子的粒子、内能和动量方程加入到模型中, 独立计算不同碳杂质粒子产生的辐射功率.

      • 2.2.   氖杂质物理模型

    • 本工作将氖杂质输运、碰撞、辐射模型加入到了SD1D程序物理模型中, 包括了所有电离态的氖杂质$ {{\mathrm{N}}{\mathrm{e}}}^{Z+} $(Z =0—10). 与2.1节中的氘等离子体模型类似, 每种电离态的氖杂质都有自己的密度、内能和动量方程((2a)式、(2b)式 和(2c)式):

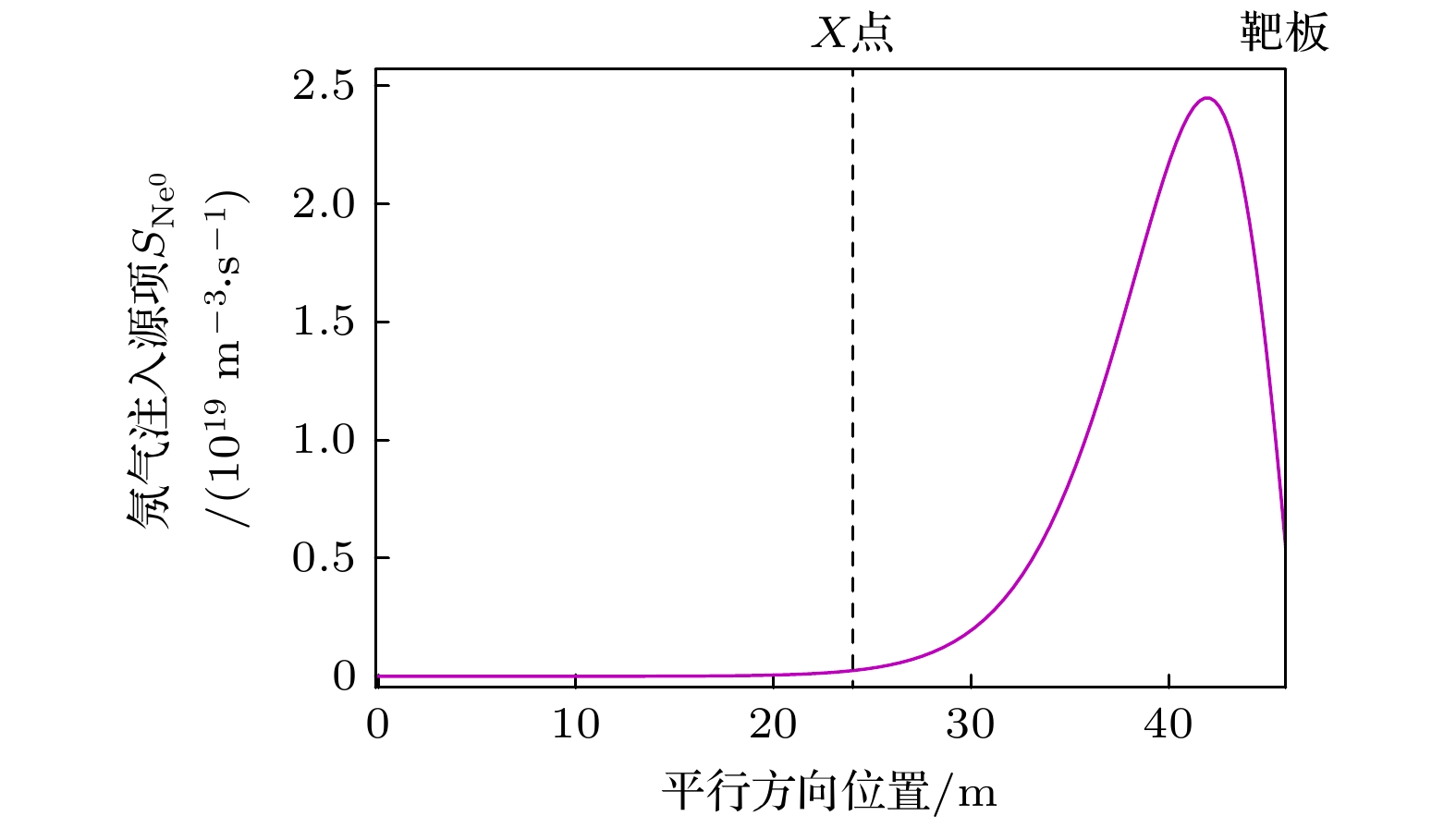
      密度和压强方程中的源项$ {S}_{{{\mathrm{N}}{\mathrm{e}}}^{{\mathrm{Z}}+}} $ 和 $ {E}_{{{\mathrm{N}}{\mathrm{e}}}^{{\mathrm{Z}}+}} $来自注入偏滤器的氖杂质、靶板上的再循环、碰撞与辐射反应. 动量方程中的作用力$ {F}_{{{\mathrm{N}}{\mathrm{e}}}^{{\mathrm{Z}}+}} $主要是由氖杂质的碰撞反应(见表2)和等离子体温度梯度等因素产生 [23]. $ {\boldsymbol{q}}_{{{\mathrm{N}}{\mathrm{e}}}^{Z+}} $表示氖杂质导致的平行能量热流. 在HL-3上的氖杂质触发脱靶实验中, 氖气常常被注入到偏滤器靶板附近. SD1D是在偏滤器内给定一个源项来模拟氖杂质注入的[23]. 如图3所示, 氖气注入偏滤器内的通量为$ 3.0\times {10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}/{\mathrm{s}} $. 本工作通过改变$ {S}_{{{\mathrm{N}}{\mathrm{e}}}^{0}} $峰值, 开展了氖杂质注入通量扫描(详见第3.1节).

      本工作使用SD1D程序中的杂质辐射模块Atomic++coronal来计算氖杂质的辐射功率 [23]. 该模块从ADAS数据库读取氖杂质的碰撞与辐射数据, 并将SD1D模拟的所有电离态下的氖杂质密度、电子温度、电子密度作为输入量, 计算出的氖杂质的辐射功率, 再反馈给SD1D程序模拟.

      对于氖杂质输运过程, SD1D使用了与2.1节氘模型相同的边界条件. 氖离子在偏滤器靶板上也会通过再循环变为氖原子, SD1D中给定氖离子的再循环率为$ {f}_{{{\mathrm{N}}{\mathrm{e}}}^{0}, {\mathrm{ }}{\mathrm{r}}{\mathrm{e}}{\mathrm{c}}{\mathrm{l}}} = {{\varGamma }_{{{\mathrm{N}}{\mathrm{e}}}^{0}, {\mathrm{r}}{\mathrm{e}}{\mathrm{c}}{\mathrm{l}}}}\big/{{\varGamma }_{{{\mathrm{N}}{\mathrm{e}}}^{{\mathrm{Z}}+}}^{{\mathrm{t}}{\mathrm{a}}{\mathrm{r}}{\mathrm{g}}{\mathrm{e}}{\mathrm{t}}}} $, 即靶板上再循环氖原子通量与靶板上氖离子通量的比值. 模拟中设定$ {f}_{{{\mathrm{N}}{\mathrm{e}}}^{0}, {\mathrm{ }}{\mathrm{r}}{\mathrm{e}}{\mathrm{c}}{\mathrm{l}}}=0.5 $. 氖离子$ {{\mathrm{N}}{\mathrm{e}}}^{{\mathrm{Z}}+} $与氘离子一样, 靶板上速度也采用Bohm边界条件处理. 在鞘层入口处的$ {\mathrm{氖}} $离子温度梯度为0, 氖离子热通量表示为$ {q}_{{{\mathrm{N}}{\mathrm{e}}}^{Z+}}= \gamma {n}_{{{\mathrm{N}}{\mathrm{e}}}^{Z+}}{T}_{{{\mathrm{N}}{\mathrm{e}}}^{Z+}}{c}_{{\mathrm{s}}, {{\mathrm{N}}{\mathrm{e}}}^{Z+}} $, 其中鞘层热输运系数$ \gamma $=6.

      升级后的SD1D模型已用于MAST-U, HL-3, HL-2A等国内外装置的偏滤器脱靶工作中. SD1D模拟速度快, 可以很好地模拟脱靶的关键物理量随时间的变化, 其与HL-2A脱靶实验对照结果非常理想[23]. SD1D作为一个一维含时刮削层-偏滤器输运模型, 没有包括跨磁场的二维输运过程. 虽然SD1D的模拟结果在开放或长腿位形条件下非常可靠, 但是在更加复杂的偏滤器位形或跨磁场输运较强的条件下, SD1D模型会产生较大误差, 只能进行定性上的研究.

    3.   HL-3装置偏滤器脱靶模拟研究

      3.1.   HL-3装置偏滤器脱靶模拟输入参数

    • 本节工作基于中国环流三号HL-3装置典型脱靶实验参数(第6270炮放电), 使用刮削层-偏滤器多成分粒子含时输运程序SD1D, 模拟研究不同碳杂质含量对偏滤器脱靶的影响, 并且对比了刮削层-偏滤器区域中不同种类粒子与等离子体相互作用所造成的等离子体动量损失以及能量损失, 分析了不同脱靶机制下触发脱靶的主要因素.

      SD1D的主要输入参数如表3所示. 针对密度抬升触发脱靶(第1种)和氖杂质注入偏滤器触发脱靶(第2种)两种方式, 本工作分别对上游电子密度$ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}} $($0.08 \times {10}^{20}\;{{\mathrm{m}}}^{-3} $—$ 0.22\times {10}^{20}\;{{\mathrm{m}}}^{-3} $的范围内)和氖气注入通量(最高至$ 15.0\times {10}^{20}\;{\mathrm{p}}{\mathrm{a}}{\mathrm{r}}{\mathrm{t}}/{\mathrm{s}} $)这两个参数进行扫描. 在模拟中上游等离子体热流通量($ {Q}_{{\mathrm{h}}{\mathrm{e}}{\mathrm{a}}{\mathrm{t}}, {\mathrm{u}}{\mathrm{p}}}=7.2\;{\mathrm{M}}{\mathrm{W}}/{{\mathrm{m}}}^{2} $)和总连接长度(刮削层上游到靶板为45 m)都保持一致. 此外, 3.2节对比了不同碳杂质含量系数($ {f}_{{\mathrm{C}}} = {{n}_{{\mathrm{C}}, {\mathrm{t}}{\mathrm{o}}{\mathrm{t}}{\mathrm{a}}{\mathrm{l}}}}/{{n}_{{\mathrm{e}}}} $)条件下的脱靶过程. $ {f}_{{\mathrm{C}}} $分别为0, 1%和3%.

      • 3.2.   碳杂质含量对偏滤器脱靶的影响

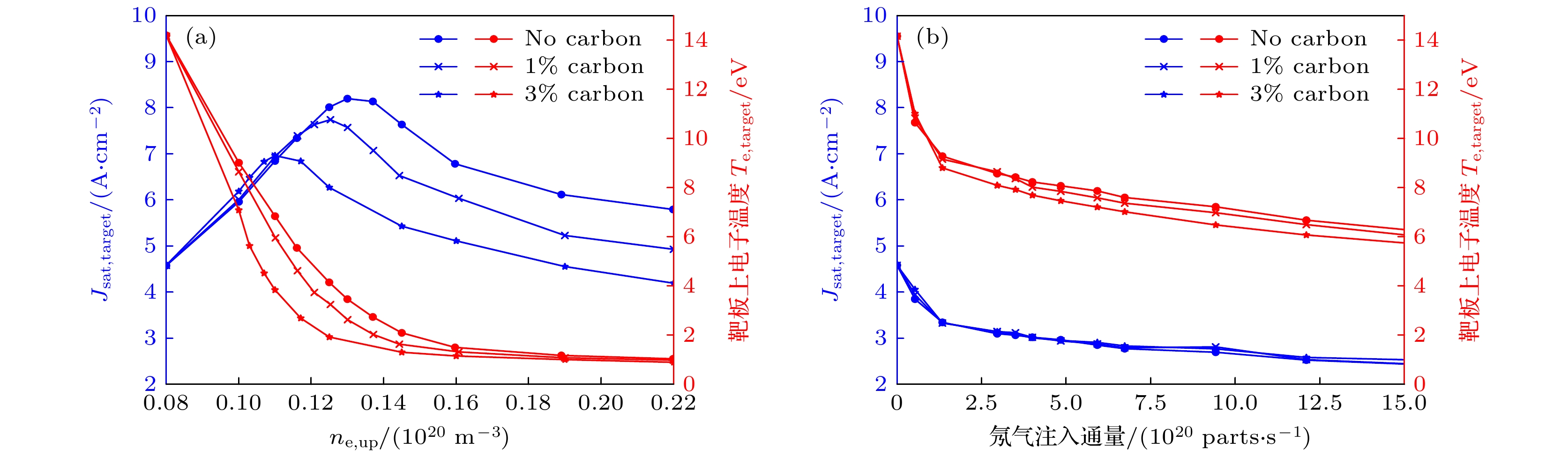
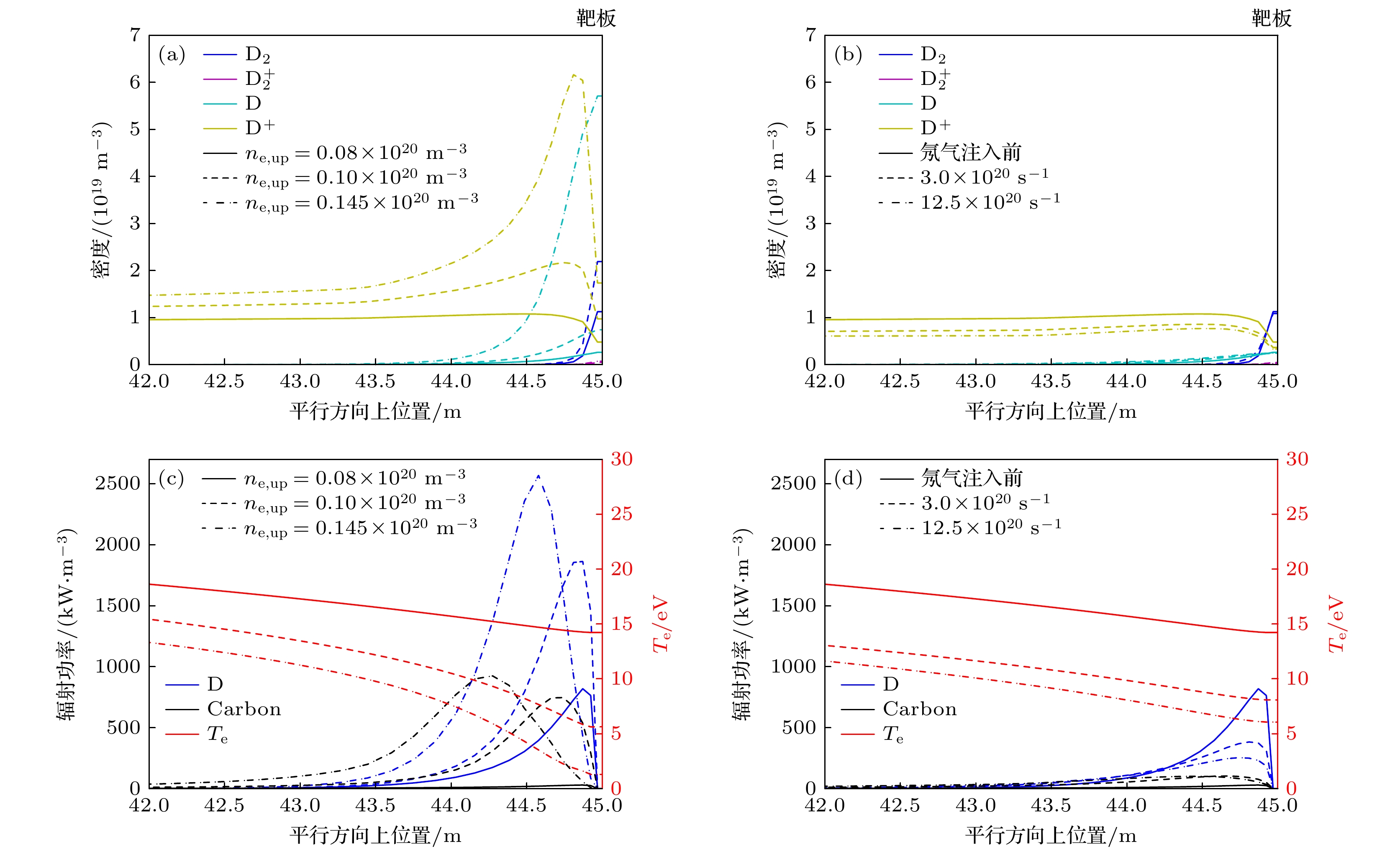
    • 通过对3.1节所述两种脱靶过程的模拟, 发现随着上游等离子体密度$ {n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}} $增大, 靶板上电子温度$ {T}_{{\mathrm{e}}, {\mathrm{t}}{\mathrm{a}}{\mathrm{r}}{\mathrm{g}}{\mathrm{e}}{\mathrm{t}}} $在不同碳杂质含量条件下都会快速降低, 模拟结果如图4(a)所示. 靶板上电流 $ {J}_{{\mathrm{s}}{\mathrm{a}}{\mathrm{t}}, {\mathrm{t}}{\mathrm{a}}{\mathrm{r}}{\mathrm{g}}{\mathrm{e}}{\mathrm{t}}} $ 分别在$ {{n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}=0.11\times 10}^{20}\;{{\mathrm{m}}}^{-3} $, $ {{n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}=0.125\times 10}^{20}\;{{\mathrm{m}}}^{-3} $ 以及 $ {{n}_{{\mathrm{e}}, {\mathrm{u}}{\mathrm{p}}}=0.135\times 10}^{20}\;{{\mathrm{m}}}^{-3} $ 处翻转(rollover), 即抬升密度实现偏滤器脱靶的标志[1]. 并且, $ {J}_{{\mathrm{s}}{\mathrm{a}}{\mathrm{t}}, {\mathrm{t}}{\mathrm{a}}{\mathrm{r}}{\mathrm{g}}{\mathrm{e}}{\mathrm{t}}} $ 在翻转处峰值随着碳杂质含量增大而降低. 研究结果表明, 适当提升偏滤器碳杂质含量有助于降低实现脱靶的密度阈值和降低靶板上电流峰值. 可是如图4(b)所示, 增大碳杂质含量对第2种脱靶方式(向偏滤器注入氖杂质)的影响很小, 只能小幅度降低靶板上电子温度, 对靶板上电流影响很小.

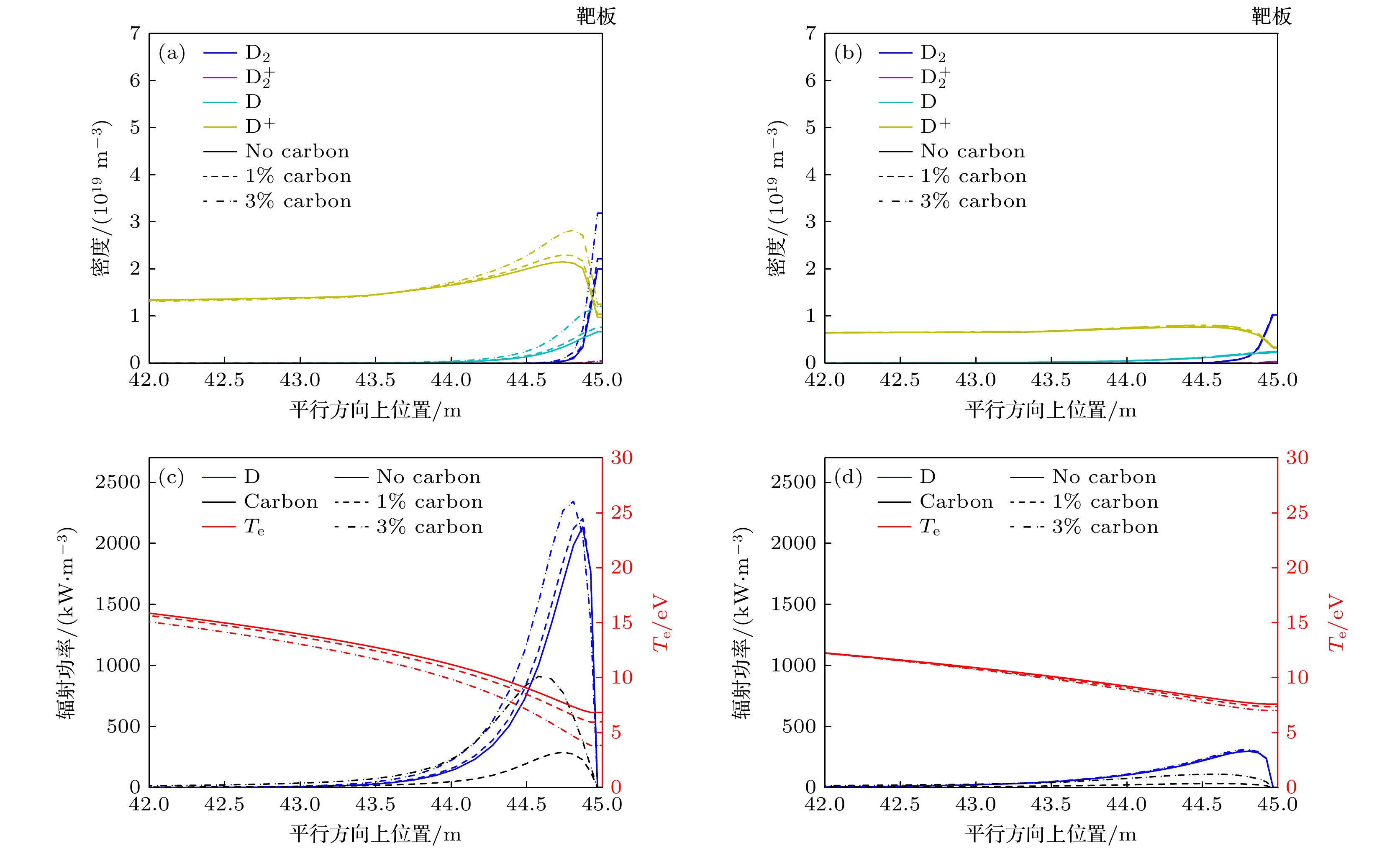
      碳杂质含量对两种脱靶影响有巨大差别的原因主要是: 如图5(a), (c)所示, 在抬升密度实现脱靶过程中, 增大碳杂质含量可以促使靶板附近碳杂质密度以及氘原子($ {\mathrm{D}} $)、氘分子($ {{\mathrm{D}}}_{2} $)、氘离子($ {{\mathrm{D}}}^{+} $)密度增大, 从而总辐射功率也随之增大, 使得偏滤器更加容易实现脱靶; 如图5(b), (d)所示, 在氖气注入实现脱靶过程中, 增大碳杂质含量不能有效提高偏滤器内氘原子、氘分子和氘离子的密度, 从而在固定氖注入通量条件下总辐射功率没有明显提高, 对脱靶影响很小.

      • 3.3.   两种偏滤器脱靶过程的对比

    • 为了进一步分析碳杂质在两种脱靶方式种的不同作用, 对比了两种脱靶过程中平行方向上的粒子密度和辐射变化.

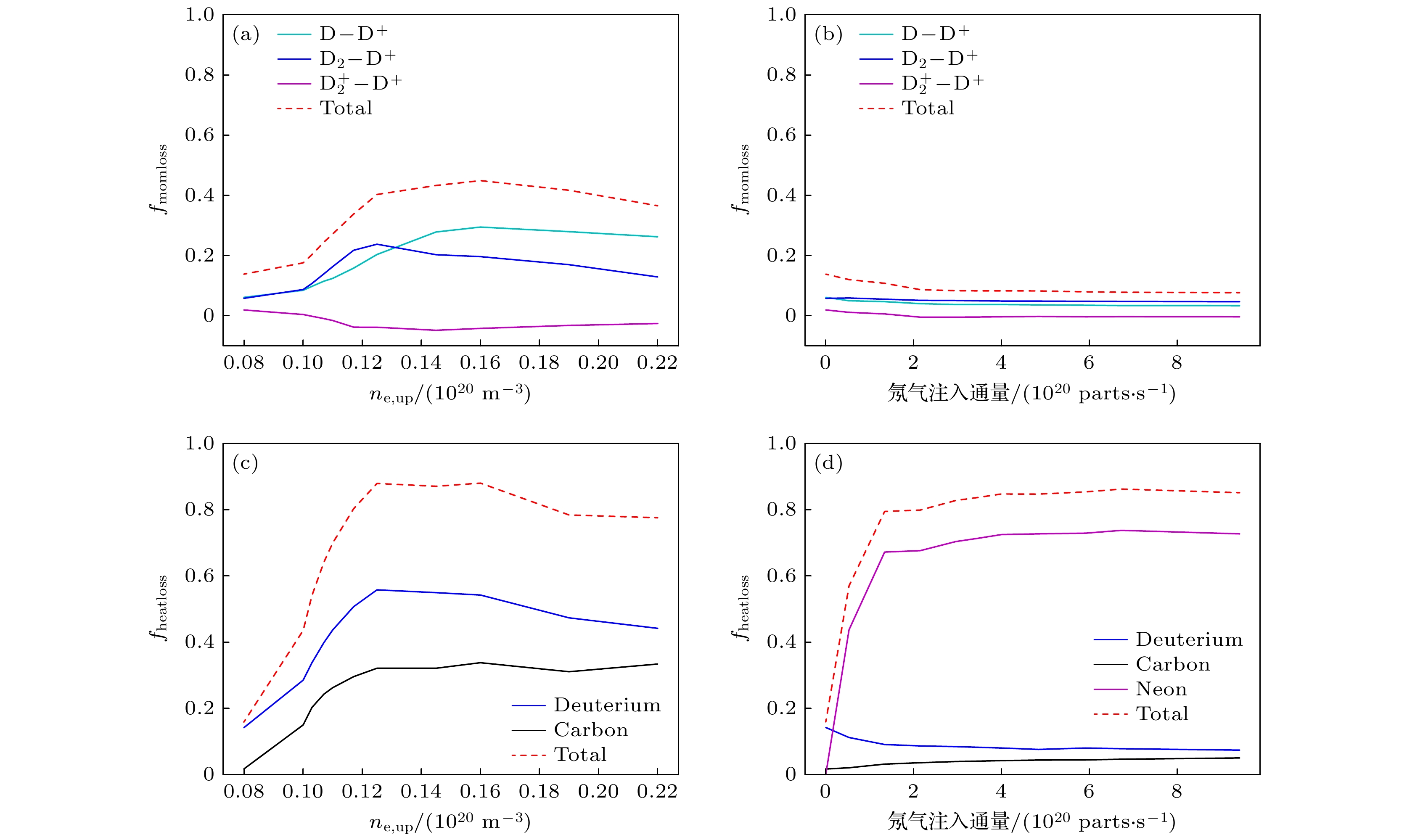
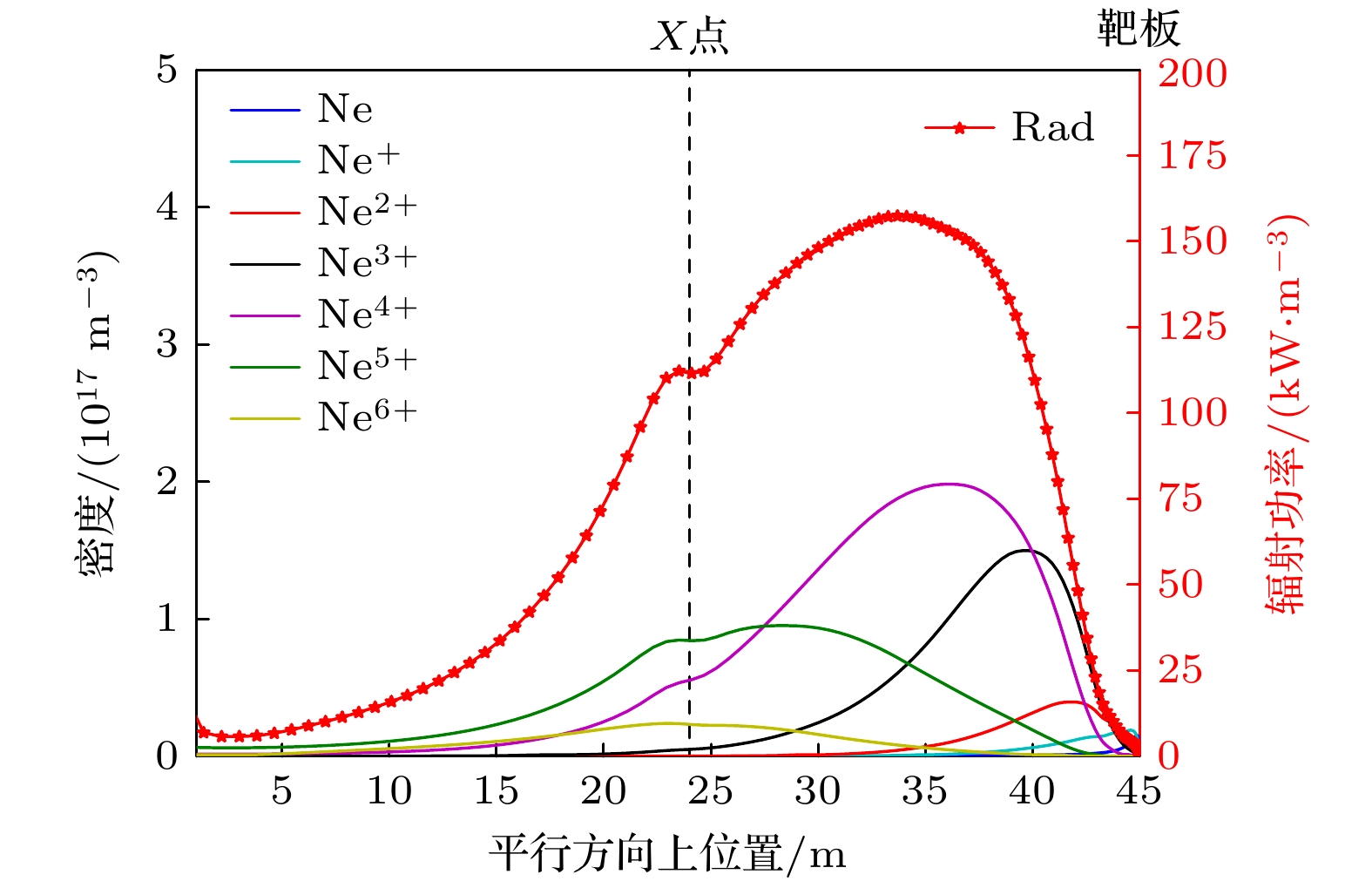
      2.1节介绍了偏滤器靶板上再循环率定义为再循环产生的中性粒子通量(如氘原子$ {{\mathrm{D}}}_{2}{\mathrm{或}} $氘分子$ {{\mathrm{D}}}_{2} $)与到达靶板的氘离子通量的之比, 即$ {f}_{{{\mathrm{D}}/{\mathrm{D}}}_{2}, {\mathrm{ }}{\mathrm{r}}{\mathrm{e}}{\mathrm{c}}{\mathrm{l}}}= {{\varGamma }_{{\mathrm{D}}/{{\mathrm{D}}}_{2}, {\mathrm{r}}{\mathrm{e}}{\mathrm{c}}{\mathrm{l}}}}\big/{{\varGamma }_{{{\mathrm{D}}}^{+}}^{{\mathrm{t}}}} $. 抬升上游氘离子密度可以增大到达靶板上的氘离子通量$ {\varGamma }_{{{\mathrm{D}}}^{+}}^{{\mathrm{t}}} $, 从而在$ {f}_{{{\mathrm{D}}/{\mathrm{D}}}_{2}, {\mathrm{ }}{\mathrm{r}}{\mathrm{e}}{\mathrm{c}}{\mathrm{l}}} $不变的情况下, 提升再循环产生的中性粒子通量$ {\varGamma }_{{\mathrm{D}}/{{\mathrm{D}}}_{2}, {\mathrm{r}}{\mathrm{e}}{\mathrm{c}}{\mathrm{l}}} $, 从而增大靶板附近的中性粒子密度, 增强其与 等离子体相互作用强度. 如图6(a), (c)所示, 随 着上游等离子体密度的抬升, 氘原子($ {\mathrm{D}} $)与氘 分子($ {{\mathrm{D}}}_{2} $)在靶板附近密度快速增大. 氘粒子和 碳杂质的辐射功率也随之猛增, 使偏滤器内电子 温度快速降低. 脱靶阶段, 氘原子、氘分子与等 离子体相互作用最多减小了超过40%的等离子体动量, 氘粒子与碳杂质辐射耗散了超过80%的 等离子体能量(如图8(a), (c)所示). 因此, 除了氘原子核氘分子, 碳杂质在此脱靶过程中也发挥了重要作用.

      而第2种脱靶是通过向偏滤器内注入少量氖杂质(氖杂质源剖面如图3所示), 利用氖杂质辐射耗散等离子体能量实现脱靶. 如图7所示, 氖杂质分布在刮削层-偏滤器中较广的区域里, 相比第1种脱靶方式可以在更宽的区域里辐射掉等离子体能量. 随着氖杂质注入通量增大, 靶板上电流将变小(图4(b)). 由于靶板上再循环强度与击打在靶板上电流成正比, 所以增大氖杂质注入通量会抑制靶板上再循环产生中性粒子(图6(b)), 因此氘原子、氘分子与等离子体相互作用强度随之降低(图8(b)). 相应地, 氘辐射耗散的等离子体能量也随之减小(图8(d)).

      此外, 还需要注意的是: 由于氘原子在极低电子温度条件下仍可以通过电离和辐射反应有效地耗散等离子体能量, 靠近靶板附近电子温度可以降到1 eV左右; 而氖杂质最佳的辐射温度区间是10 eV左右, 所以当偏滤器电子温度下降到10 eV以下时, 其辐射效率快速降低[23], 在HL-3实验条件下仅向偏滤器注入氖杂质很难将靶板电子温度降到5 eV以下.

    4.   结　论

    • 偏滤器脱靶是HL-3装置偏滤器热流控制的主要途径.

      本工作基于HL-3装置典型脱靶实验参数(第6270炮放电), 使用刮削层-偏滤器多成分粒子含时输运程序SD1D, 首先模拟了在不同碳杂质含量条件下的偏滤器脱靶过程. 研究发现: 在抬升等离子体密度脱靶过程中, 适当增大偏滤器内的碳杂质含量可以有效降低实现脱靶的密度阈值, 同时也能降低脱靶前靶板上的电流峰值; 但是改变碳杂质含量对偏滤器注入氖气实现脱靶过程影响较小.

      接着, 本工作对比了抬升上游等离子体密度和偏滤器内注入氖气两种脱靶途径, 分析了这两种脱靶机制下触发脱靶的主要因素: 抬升上游等离子体密度可以促进偏滤器再循环产生大量中性粒子, 其与等离子体碰撞反应能有效降低偏滤器内等离子体动量, 氘粒子与碳杂质辐射反应能有效耗散等离子体能量, 从而实现脱靶; 向偏滤器中注入氖杂质能快速增大偏滤器内的辐射功率, 可以有效耗散等离子体能量, 从而实现脱靶. 不同于密度抬升触发脱靶方式, 注入氖气会抑制偏滤器内再循环产生中性粒子, 氘原子、分子与等离子体反应强度也会因此降低.

      未来计划开展SD1D程序模拟与HL-3脱靶实验的对照工作, 将SD1D模拟得到的靶板上电流、温度、$ {{\mathrm{D}}}_{{\mathrm{\alpha }}} $辐射强度等物理量与HL-3装置偏滤器内诊断测量的数据进行对比, 进一步验证SD1D物理模型的可靠性.

      感谢核工业西南物理研究院吴婷副研究员和吴娜副研究员的讨论.

    参考文献 (23)

目录

/

返回文章
返回