高级搜索

Quincke活性胶体体系中吸引力对集体行为的影响

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

杜海婷, 周晓怡, 倪琦英, 陈康, 田文得, 张天辉. Quincke活性胶体体系中吸引力对集体行为的影响[J]. 物理学报, 2025, 74(11): 116401-1. doi: 10.7498/aps.74.20250292
引用本文: 杜海婷, 周晓怡, 倪琦英, 陈康, 田文得, 张天辉. Quincke活性胶体体系中吸引力对集体行为的影响[J]. 物理学报, 2025, 74(11): 116401-1. doi: 10.7498/aps.74.20250292
shu
Haiting DU, Xiaoyi ZHOU, Qiying NI, Kang CHEN, Wende TIAN, Tianhui ZHANG. Influence of attractive interactions on collective behavior in Quincke active colloidal systems[J]. Acta Physica Sinica, 2025, 74(11): 116401-1. doi: 10.7498/aps.74.20250292
Citation: Haiting DU, Xiaoyi ZHOU, Qiying NI, Kang CHEN, Wende TIAN, Tianhui ZHANG. Influence of attractive interactions on collective behavior in Quincke active colloidal systems[J]. Acta Physica Sinica, 2025, 74(11): 116401-1. doi: 10.7498/aps.74.20250292
shu

Quincke活性胶体体系中吸引力对集体行为的影响

Influence of attractive interactions on collective behavior in Quincke active colloidal systems

  • 摘要: 活性物质中的集体行为已被广泛研究. 然而, 活性个体间的吸引力对集体运动模式的影响还没有相关研究. 本研究发现, 在Quincke活性胶体体系, 通过增强电液流(EHD)效应诱导的长程吸引力, 速度对齐效应得到增强, 并在极性流体内部诱发密度相分离, 形成极性团簇, 破坏极性有序相的空间均匀性. 这是已有的实验观测中没有的. 而在排斥主导的活性体系, 极性流体空间均匀分布. 我们的研究结果表明活性个体间的吸引力会显著改变活性体系的微观和宏观动力学行为.
    Abstract: Active matter can form various collective motions. In dry and repulsive systems, a uniform polar fluid emerges in the presence of an aligning mechanism. Theoretical studies have shown that in active systems with attractive interactions, particles can achieve spontaneous velocity alignment and form clusters through the synergistic effect of self-propulsion and attraction. However, so far, the influence of attractions on collective behavior has not been well addressed experimentally. In this work, an electric-field driven Quincke system, where an electrohydrodynamic (EHD) long-range attraction is present, is used to investigate the influence of attraction on the collective behavior. It is found that the long-range attraction can significantly increase the interaction time during collision, thereby enhancing velocity alignment. The aligned particles can form dynamic polar clusters. Moreover, in the presence of a long-range attraction, a uniform polar fluid is unstable: density fluctuation leads to denser polar clusters which share the same direction of collective motion with the polar fluid. Our findings show that the attraction between active individuals can significantly change the microscopic and macroscopic dynamics of active systems and provide insights into understanding chemotactic attraction phenomena in biological systems.
  • 加载中

  • 图 1  两粒子(P1, P2)的碰撞过程($ E = 1.20{E_{\text{c}}} $)　(a) 实验装置及原理图; (b) 湿AOT导电溶液中粒子碰撞过程; (c)干AOT导电溶液中粒子碰撞过程. (b), (c)顶部: 粒子之间的距离随时间的变化. 插图: 对齐过程中的轨迹与速度变化. 中间: 两个粒子速度方向之间的角度随时间的变化. 底部: 两粒子速度变化

    Figure 1.  Collision dynamics between two particles ($ E = 1.20{E_{\text{c}}} $): (a) Schematic of the experimental setup and Quincke rolling; (b) particle collision process in wet AOT conductive solution; (c) particle collision process in dry AOT conductive solution. (b), (c) Top: Distance between the particles as a function of time. Inset: Speed and trajectories in an aligning process. Middle: The angle between the two orientations as a function of time. Bottom: Speed evolution in pair aligning.

    下载: 全尺寸图片 幻灯片

    图 2  (a) 排斥力占主导时的无序气体 ($ E = 1.20{E_{\text{c}}} $); (b)—(d) 吸引力主导下形成的团簇及其消散过程($ E = 1.20{E_{\text{c}}} $); (e)—(h)对应于图(a)—(d)的速度方向着色图, 左下角圆盘为方向色标

    Figure 2.  (a) Repulsion-dominated disordered gas state ($ E = 1.20{E_{\text{c}}} $); (b)–(d) attraction-driven cluster formation and subsequent dissipation ($ E = 1.20{E_{\text{c}}} $); (e)–(h) velocity direction color maps corresponding to panels (a)–(d). The direction color key is shown in the lower-left disk.

    下载: 全尺寸图片 幻灯片

    图 3  吸引Quincke体系的亚临界行为　(a) $ E = 0.9{E_{\text{c}}} $时的实验原图; (b)对应于图(a)的速度彩图, 图中白色粒子为静止不动的粒子, 右侧为速度大小色标. 图中标尺为$100{\text{ μm}}$

    Figure 3.  Subcritical behavior of the attraction-driven Quincke system: (a) Raw experimental image at $ E = 0.9{E_{\text{c}}} $; (b) velocity color map corresponding to Figure (a), white particles denote stationary colloids, and the velocity color scale is shown on the right. Scale bar: $100{\text{ μm}}$.

    下载: 全尺寸图片 幻灯片

    图 4  集体运动　(a) 排斥力占主导时的极性流体($ E = $$ 1.30{E_{\text{c}}} $); (b) EHD吸引力占主导时的极性团簇 ($ E = 1.30{E_{\text{c}}} $); (c), (d)对应于图(a)和图(b)的速度方向着色图, 左下角圆盘为方向色标. 图中标尺为$100{\text{ μm}}$

    Figure 4.  Collective motion: (a) Repulsion-dominated polar fluid ($ E = 1.30{E_{\text{c}}} $); (b) EHD attraction-driven polar cluster ($ E = $$ 1.30{E_{\text{c}}} $); (c), (d) velocity direction color maps corresponding to Figure (a) and Figure (b). The directional color key is shown in the lower-left disk. Scale bar: $100{\text{ μm}}$.

    下载: 全尺寸图片 幻灯片
  • [1] Das M, Schmidt C F, Murrell M 2020 Soft Matter 16 7185 doi: 10.1039/D0SM90137G
    [2] Vicsek T, Zafeiris A 2012 Phys. Rep. 517 71 doi: 10.1016/j.physrep.2012.03.004
    [3] Deutsch A, Friedl P, Preziosi L, Theraulaz G 2020 Philos. Trans. R. Soc. London, Ser. B 375 20190377 doi: 10.1098/rstb.2019.0377
    [4] Dombrowski C, Cisneros L, Chatkaew S, Goldstein R E, Kessler J O 2004 Phys. Rev. Lett. 93 098103 doi: 10.1103/PhysRevLett.93.098103
    [5] Zhang H P, Be'er A, Florin E L, Swinney H L 2010 Proc. Natl. Acad. Sci. U. S. A. 107 13626 doi: 10.1073/pnas.1001651107
    [6] Chen X, Yang X, Yang M C, Zhang H P 2015 Europhys. Lett. 111 54002 doi: 10.1209/0295-5075/111/54002
    [7] Cavagna A, Giardina I 2014 Annu. Rev. Condens. Matter Phys. 5 183 doi: 10.1146/annurev-conmatphys-031113-133834
    [8] Cavagna A, Cimarelli A, Giardina I, Parisi G, Santagati R, Stefanini F, Viale M 2010 Proc. Natl. Acad. Sci. U. S. A. 107 11865 doi: 10.1073/pnas.1005766107
    [9] Katz Y, Tunstrom K, Ioannou C C, Huepe C, Couzin I D 2011 Proc. Natl. Acad. Sci. U. S. A. 108 18720 doi: 10.1073/pnas.1107583108
    [10] Shimoyama N, Sugawara K, Mizuguchi T, Hayakawa Y, Sano M 1996 Phys. Rev. Lett. 76 3870 doi: 10.1103/PhysRevLett.76.3870
    [11] Baglietto G, Albano E V 2009 Comput. Phys. Commun. 180 527 doi: 10.1016/j.cpc.2008.12.026
    [12] Vicsek T, Czirok A, Ben-Jacob E, Cohen I I, Shochet O 1995 Phys. Rev. Lett. 75 1226 doi: 10.1103/PhysRevLett.75.1226
    [13] Cates M E, Tailleur J 2015 Annu. Rev. Condens. Matter Phys. 6 219 doi: 10.1146/annurev-conmatphys-031214-014710
    [14] Buttinoni I, Bialké J, Kümmel F, Löwen H, Bechinger C, Speck T 2013 Phys. Rev. Lett. 110 238301 doi: 10.1103/PhysRevLett.110.238301
    [15] Blair D L, Neicu T, Kudrolli A 2003 Phys. Rev. E 67 031303 doi: 10.1103/PhysRevE.67.031303
    [16] Deseigne J, Dauchot O, Chaté H 2010 Phys. Rev. Lett. 105 098001 doi: 10.1103/PhysRevLett.105.098001
    [17] 陈健丽, 李佳健, 艾保全 2025 物理学报 74 060501 doi: 10.7498/aps.74.20241746 Chen J L, Li J J, Ai B Q 2025 Acta Phys. Sin. 74 060501 doi: 10.7498/aps.74.20241746
    [18] Bricard A, Caussin J B, Desreumaux N, Dauchot O, Bartolo D 2013 Nature 503 95 doi: 10.1038/nature12673
    [19] Karani H, Pradillo G E, Vlahovska P M 2019 Phys. Rev. Lett. 123 208002 doi: 10.1103/PhysRevLett.123.208002
    [20] Lu S Q, Zhang B Y, Zhang Z C, Shi Y, Zhang T H 2018 Soft Matter 14 5092 doi: 10.1039/C8SM00371H
    [21] Pradillo G E, Karani H, Vlahovska P M 2019 Soft Matter 15 6564 doi: 10.1039/C9SM01163C
    [22] Bricard A, Caussin J B, Das D, Savoie C, Chikkadi V, Shitara K, Chepizhko O, Peruani F, Saintillan D, Bartolo D 2015 Nat. Commun. 6 7470 doi: 10.1038/ncomms8470
    [23] Mauleon-Amieva A, Mosayebi M, Hallett J E, Turci F, Liverpool T B, van Duijneveldt J S, Royall C P 2020 Phys. Rev. E 102 032609
    [24] Boymelgreen A, Schiffbauer J, Khusid B, Yossifon G 2022 Curr. Opin. Colloid Interface Sci. 60 101603 doi: 10.1016/j.cocis.2022.101603
    [25] Das D, Saintillan D 2013 Phys. Rev. E 87 043014 doi: 10.1103/PhysRevE.87.043014
    [26] Ristenpart W D, Aksay I A, Saville D A 2007 Langmuir 23 4071 doi: 10.1021/la062870l
    [27] Liu Z T, Shi Y, Zhao Y, Chate H, Shi X Q, Zhang T H 2021 Proc. Natl. Acad. Sci. U. S. A. 118 e2104724118 doi: 10.1073/pnas.2104724118
    [28] Michor F, Iwasa Y, Nowak M A 2004 Nat. Rev. Cancer 4 197 doi: 10.1038/nrc1295
    [29] Vishwakarma M, Thurakkal B, Spatz J P, Das T 2020 Philos. Trans. R. Soc. London, Ser. B 375 20190391 doi: 10.1098/rstb.2019.0391
    [30] Haga H, Irahara C, Kobayashi R, Nakagaki T, Kawabata K 2005 Biophys. J. 88 2250 doi: 10.1529/biophysj.104.047654
    [31] Hsu M F, Dufresne E R, Weitz D A 2005 Langmuir 21 4881 doi: 10.1021/la046751m
  • 加载中
图( 4)
计量
  • 文章访问数:  19
  • HTML全文浏览数:  19
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-07
  • 刊出日期:  2025-06-05

Quincke活性胶体体系中吸引力对集体行为的影响

  • 收稿日期:  2025-03-07

摘要: 活性物质中的集体行为已被广泛研究. 然而, 活性个体间的吸引力对集体运动模式的影响还没有相关研究. 本研究发现, 在Quincke活性胶体体系, 通过增强电液流(EHD)效应诱导的长程吸引力, 速度对齐效应得到增强, 并在极性流体内部诱发密度相分离, 形成极性团簇, 破坏极性有序相的空间均匀性. 这是已有的实验观测中没有的. 而在排斥主导的活性体系, 极性流体空间均匀分布. 我们的研究结果表明活性个体间的吸引力会显著改变活性体系的微观和宏观动力学行为.

English Abstract

    全文HTML

    1.   引　言

    • 活性物质由大量具有自驱动能力的个体构成, 个体(如鸟、细胞、分子机器等)通过消耗自身或环境储备的自由能实现自驱动[1]. 运动的活性个体通过相互作用可形成一致的运动速度和运动或转动方向, 形成集体运动[2]. 集体运动广泛存在于多尺度生命体系中: 微观层面可见于神经嵴细胞的定 向迁移[3]与细菌群落的协调运动[4–6], 而宏观尺度则体现为鸟群[7,8]、鱼群[9]等生物群体的复杂集群行为.

      为深入探究集体运动的物理机制, 科研人员已开展了大量相关研究[10,11]. 其中, Vicsek模型是解释活性体系中集体运动涌现的经典模型之一[12]. 在该模型中, 活性个体间的相互作用被简化为速度对齐机制. 在速度对齐机制的作用下, 体系超过一定密度时会发生无序到有序的转变, 形成集体运动.

      排斥力主导的活性体系(如振动颗粒、排斥性胶体等)为理解无序-有序相变提供了重要模型. 实验与理论研究表明, 在无速度对齐的纯排斥体系中, 粒子相互碰撞减速, 当体系密度达到一定程度时会产生运动诱导相分离 (motility-induced phase separation, MIPS)[13,14]. 这类体系通过引入速度对齐机制可自发形成涡旋、动态团簇等集体运动现象. 速度对齐机制可来源于粒子的几何外形[15]、粒子内置的极性不对称[16]等等. 然而, 现有实验观 测多集中于纯排斥系统或忽略流体相互作用的“干燥”活性体系, 吸引力在集体运动中的作用常常 被忽略. 值得注意的是, 具有吸引性相互作用的活性布朗粒子系统可以通过自推进与吸引作用的 协同效应实现自发速度对齐, 并形成团簇结构[17]. 但吸引力对集体行为的影响尚未在实验中得到充分验证.

      近年来, 基于Quincke旋转效应的胶体系统因其独特的电驱动力学特性, 被广泛应用于集体行为的研究[18–24]. Quincke粒子在临界电场以上可发生持续旋转[25], 其运动模式高度依赖于介电环境与流体力学的耦合. 不同于传统排斥性活性体系, Quincke系统存在长程电流体动力吸引相互作用[26]. 并已被证明该吸引相互作用在亚临界场形成凝聚结构中起关键作用[27]. 然而, 吸引力对集体行为的影响到目前为止还没有得到很好的研究.

      在生物体系中, 趋化吸引现象十分普遍[3]. 在动物群体的迁徙、细胞迁移、细菌群落生长等过程中, 运动个体之间通过趋化吸引形成集体运动. 例如神经嵴细胞的集体迁移、胚胎发育以及癌细胞转移[28]、伤口愈合[29,30]等等. 因此, 理解活性体系中吸引力对集体行为的影响是至关重要的.

      本研究以电场驱动的Quincke体系为实验模型, 研究了吸引力对Quincke活性胶体动力学行为的影响. 研究发现, 吸引力的引入会显著地增强速度对齐效应, 并诱发极性流体的密度分离, 形成极性凝聚相, 破坏极性有序相的空间均匀性. 这是已有的实验观测中没有的. 而在排斥主导的活性体系, 极性流体空间均匀分布. 我们的研究结果表明, 活性个体间的吸引力会显著地改变活性体系的微观和宏观动力学行为, 为探索更丰富的集体现象提供了新途径.

    2.   实验方法

    • 根据Bricard等[18]的研究, 我们制备了二维的Quincke胶体颗粒体系. 实验中, 将直径为10.1 μm的聚苯乙烯小球(thermo scientific G1000)分散在0.12 mol/L的AOT溶液/正十六烷中(sodium di-2-ethylhexylsulfosuccinate, 二–2-乙基己基磺基琥珀酸钠, AOT), 并将悬浮液密封在由两块ITO导电玻璃(indium tin oxide, 氧化铟锡, ITO)构成的微腔中, 两块玻璃之间用绝缘双面胶带隔开. 当施加垂直于极板的直流外电场$ E $(图1(a)), 胶体粒子获得反平行于电场的电偶. 由于溶液中存在热扰动, 粒子电偶不再反平行于电场, 从而出现电偶分量(垂直于电场), 然后产生电偶扭矩${\boldsymbol{P}} \times{\boldsymbol{ E}}$. 当电场强度超过临界电场强度${E_{\mathrm{c}}}$时, 这个扭矩就会克服溶液的黏性扭矩, 推动小球旋转. 小球在固体表面上, 转动将转化为沿固体表面的平移运动. 在平行于电场方向观察, 胶体颗粒在ITO导电玻璃表面做二维平动.

      AOT溶液是一种极易吸水的溶液. 含水量的多少不仅会影响溶液的导电率, 还会影响体系内电液流(electrohydrodynamic flow, EHD flow)诱导的长程吸引力[26,31](EHD吸引力)的强弱, 进而影响Quincke粒子的动力学行为. 本实验中的AOT溶液由多库酯钠固体与正十六烷溶剂按一定配比混合得到的. 由于多库酯钠具有很强吸湿性, 本实验通过真空冷冻干燥预处理多库酯钠固体, 与正十六烷混合制得基础溶液. 将配制好的基础溶液放置在恒温恒湿箱中处理, 控制温度和湿度及放置时间, 使得导电溶液的含水量不同. 本研究中使用的AOT导电溶液为两种, 分别为含水量少的干AOT (电导率$\sigma = 2.0 \times {10^{ - 8}}{\text{ S}} \cdot {{\text{m}}^{ - 1}}$)以及含水量多的湿AOT (电导率$\sigma = 3 \times {10^{ - 7}}{\text{ S}} \cdot {{\text{m}}^{ - 1}}$).

      我们使用光学显微镜对实验现象进行观测, 并使用高速成像相机(CMOS, 拍摄速率1000帧/秒)记录实验过程. 拍摄的图像经过处理后利用IDL, Matlab等程序软件得到粒子的实时位置、速度等关键实验数据. 我们使用的是直流外电场, 实验中主要控制的参数为电场强度和导电溶液的电导率.

    3.   实验结果

      3.1.   单粒子碰撞

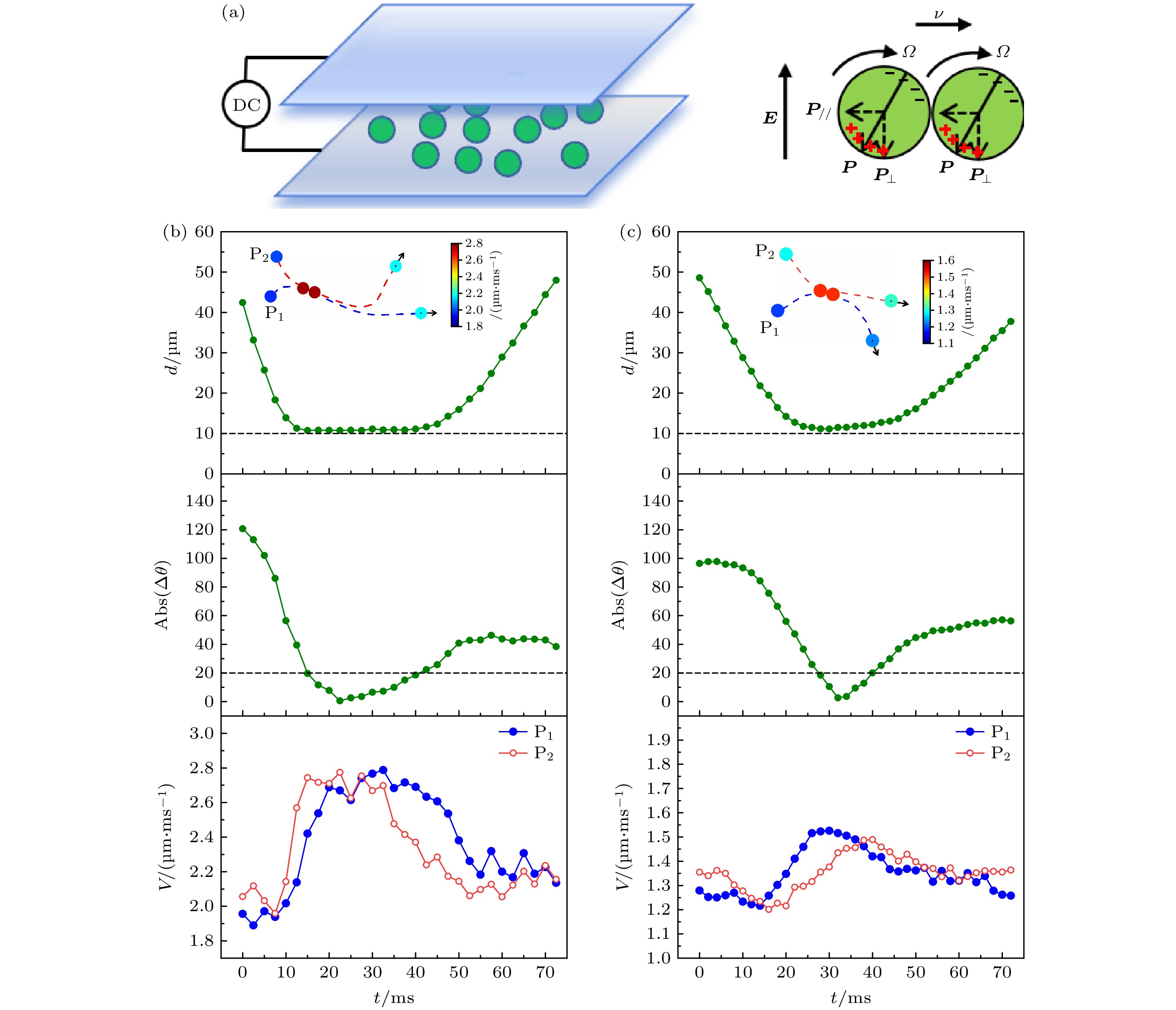
    • 在临界电场以上, 我们分别观察了干、湿两种AOT导电溶液中粒子的碰撞对齐过程(图1(b), (c)). 两个粒子均以一定的初始速度方向角度差靠近. 在粒子靠近过程中, 粒子均经历了伴随着$\left| {\Delta \theta } \right|$大幅度减少, 速度同步提高的过程. 这表明在这两种导电溶液中, 粒子碰撞过程中都发生了速度对齐. 这种速度对齐机制在之前的研究中也有相关的报道[20]. 但因导电溶液差异, 粒子速度对齐过程略有不同.

      在湿AOT导电溶液中(图1(b)), 当t = 5 ms时, 两粒子的$\left| {\Delta \theta } \right|$开始大幅度减少, 表明发生了对齐. 伴随着对齐, 粒子的速度开始同步提高. 在5—20 ms时间内, 粒子速度由约$2.0{\text{ }}{{{\text{μm}}} {/ } {{\text{ms}}}}$提升至约$2.7{\text{ }}{{{\text{μm}}} {/ } {{\text{ms}}}}$, 且在20 ms时粒子速度开始趋于稳定. 在20—40 ms时间内, 粒子间的距离保持在约$11{\text{ μm}}$, 且粒子间的速度方向角度差$\left| {\Delta \theta } \right|$均小于${20^ \circ }$, 粒子速度稳定在约$2.7{{{\text{ μm}}} {/ } {{\text{ms}}}}$, 表明粒子间形成了稳定的对齐. 随后, 当$\left| {\Delta \theta } \right|$大于${20^ \circ }$时, 对齐开始不稳定, 粒子间距离开始增大, 粒子速度也开始降低.

      干AOT体系(图1(c))呈现不同的动力学特征, 当t = 15 ms时, 两粒子的$\left| {\Delta \theta } \right|$开始大幅度减少, 表明发生了对齐. 在15—40 ms时间内, 速度由约$1.2{{{\text{ μm}}} {/ } {{\text{ms}}}}$提升至约$1.5{{{\text{ μm}}} {/ } {{\text{ms}}}}$. 在此期间, 当$\left| {\Delta \theta } \right|$小于${20^ \circ }$时, 粒子间距离约为$12{\text{ μm}}$. 随后, 当t = 40 ms时, 对齐开始不稳定, 粒子间距离开始增大, 粒子速度也随之降低.

      在湿AOT溶液中, 粒子形成速度对齐, 粒子速度增幅约$0.7{\text{ }}{{{\text{μm}}} {/ } {{\text{ms}}}}$, 粒子间最近距离保持在约$11{\text{ μm}}$. 对齐过程从开始到结束持续约35 ms (5—40 ms时间段内). 而在干的AOT溶液中, 粒子速度增幅约$0.3{\text{ }}{{{\text{μm}}} {/ } {{\text{ms}}}}$. 粒子间最近距离保持在约$12{\text{ μm}}$. 对齐过程从开始到结束持续约25 ms (15—40 ms 时间段内), 相较于干AOT溶液中的粒子对齐过程, 在湿AOT溶液中, 粒子靠得更近, 对齐时间更长, 速度增幅也较大, 对速度的提升效果更加明显. 在这里, 粒子所处的电场强度是相同的, 唯一不同的是粒子所处的导电溶液. 由此可以认为, 在湿AOT溶液中, 由于EHD吸引力的存在, 粒子在对齐过程中更加稳定, 对速度的提升效果也更加明显. 也就是说EHD吸引力能够有效地促进粒子间的速度对齐, 并延缓粒子的分离.

      同时我们也注意到, 在同一电场强度下的不同导电溶液中, 粒子速度差异较大, 这是因为在湿AOT导电溶液中, 由于含水量更多, 溶液的电导率更高, 由此造成溶液中的自由电荷更多, 粒子的旋转扭矩更大, 因此粒子的速度也就更大.

      • 3.2.   动态团簇

    • 上述单粒子碰撞对齐实验表明, 吸引力能显著改变粒子的微观动力学行为. 增强吸引力能够有效促进粒子间的速度对齐, 并延缓粒子的分离. 那么在多粒子体系中, 吸引力又会产生怎样的影响呢?

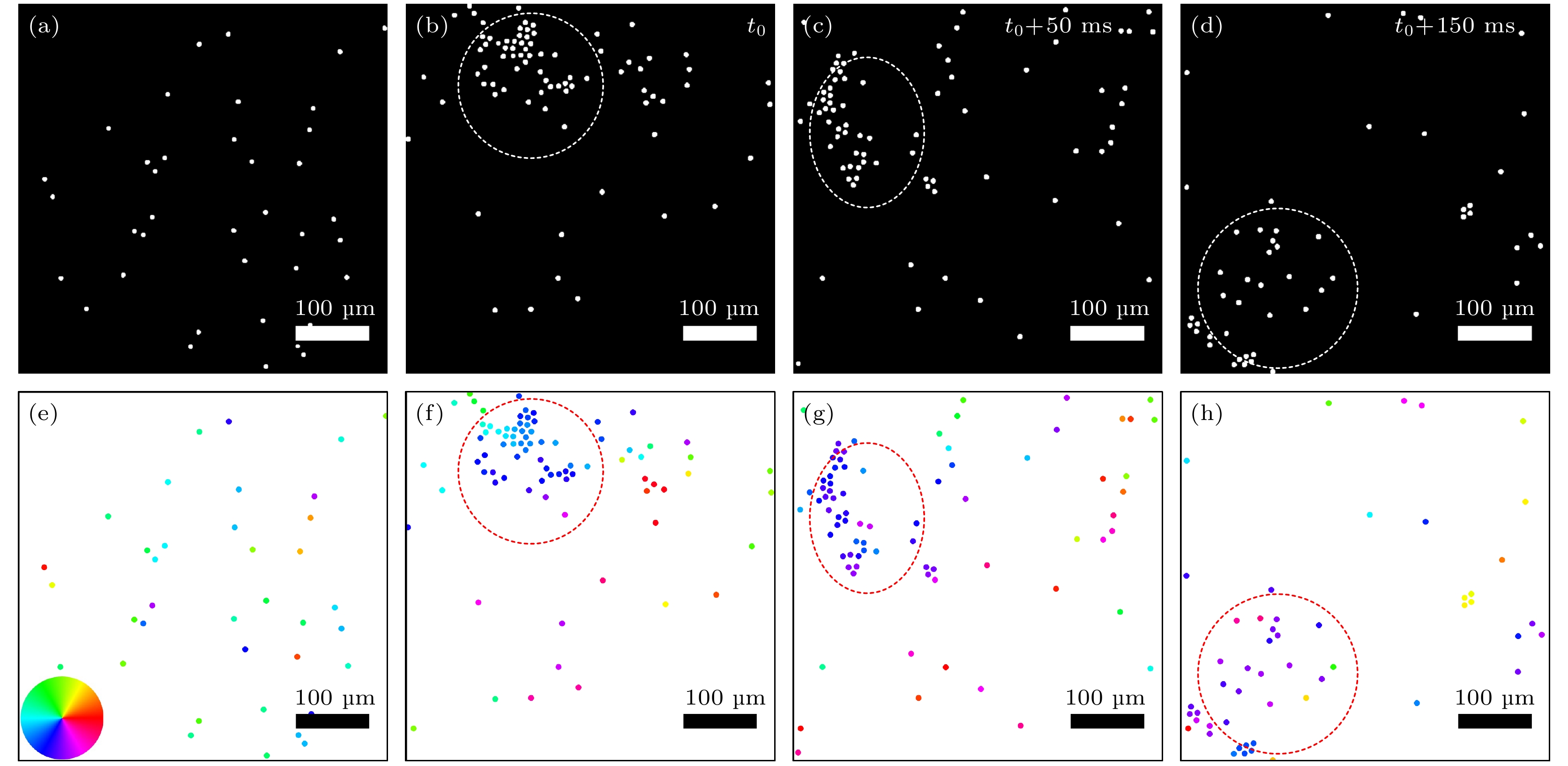
      当体系内EHD吸引力可忽略时, 体系为无序气体(图2(a), (e)). 当体系内EHD吸引力占主导时, 实验中观察到粒子聚集形成团簇(图2(b)). 从对应的速度方向着色图(图2(f))则可以看到, 团簇内粒子颜色着色大致相同, 这表明团簇内粒子具有相同的运动方向. 然而, 粒子聚集形成的团簇并不是稳定不变的, 而是在动态变化. 如图所示(图2(b)—(d)、图2(f)—(h))为团簇随时间演化最后消失的过程. 团簇在运动过程中, 会有粒子进入或者离开团簇. 当离开团簇的粒子多于进入团簇的粒子, 团簇则会消失.

      这种动态团簇与MIPS形成的团簇是不同的. MIPS通常是由活性粒子碰撞减速导致的聚集高密相. MIPS中的高密相是准静态的, 没有定向运动或转动. 本研究中, 团簇的形成源于EHD吸引力的聚集效应. 在高于临界电场的弱电场下, Quincke粒子活性不强, 电偶排斥力也不强, 粒子碰撞后在相对较强的EHD吸引力作用下能形成聚集态. 聚集后的粒子在速度对齐机制下, 形成集体定向运动. 而且Quincke体系的聚集态能提升粒子活性. 这些特点是典型MIPS形成的聚集态所没有的.

      粒子聚集形成团簇不仅与EHD吸引力有关, 同时还受到电场强度的调控. 当电场强度增大到一定程度时, 便无法观察到团簇. 这是因为当电场强度较低时, EHD吸引力能够平衡粒子间的电偶排斥相互作用, 使得粒子可能发生聚集. 随着电场强度的逐渐增大, 粒子间的电偶排斥相互作用在逐渐增大, EHD吸引力无法平衡粒子间的电偶排斥相互作用. 此外, 随着电场强度的增大, 粒子的运动速度也在相应的提高, EHD吸引力无法约束高速运动的粒子, 粒子就很难发生聚集.

      • 3.3.   亚临界行为

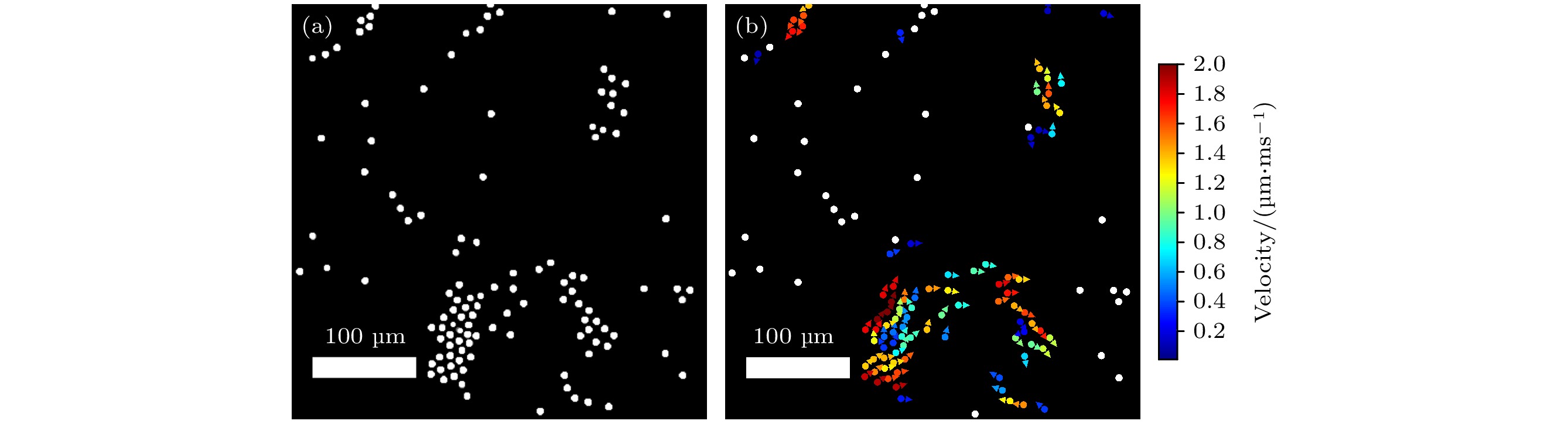
    • 当电场强度处于临界电场以下($E \approx 0.9{E_{\text{c}}}$), 在EHD吸引力作用下, 粒子也会发生明显的聚集, 如图所示(图3(a)). 而从对应的速度彩图(图3(b))则可以发现, 聚集的粒子是在运动的, 孤立的粒子则保持静止. 这因为当粒子处于孤立状态时, 在临界电场以下, 单个粒子的电偶扭矩不足以克服溶 液中黏滞阻力的力矩, 因此粒子处于静止状态. 而当粒子在EHD吸引力作用下发生聚集时, 近邻粒子间面内电偶的相互增强效应显著, 从而激活粒子的Quincke转动. 这种近邻粒子在亚临界电场下相互作用而运动的现象在已有的研究中有相关的报道[27].

      • 3.4.   集体运动

    • 通过前面研究我们发现, EHD吸引力能够使得粒子聚集形成团簇, 并产生特有的亚临界现象. 那么在集体运动中, 吸引力又会产生怎样的影响呢?

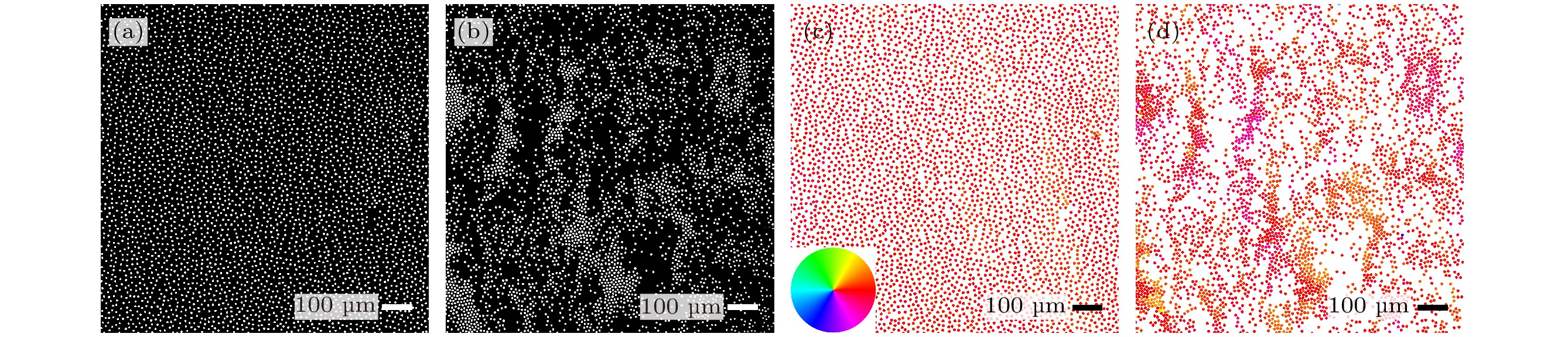
      当Quincke体系中的吸引力可以忽略, 静电排斥力占主导时, 体系会通过相分离形成定向运动的极性流体, 如图所示(图4(a), (c)). 极性流体的形成源于粒子间的速度对齐机制以及流体相互作用. 这种排斥力占主导下形成的极性流体在之前的研究中也有相关的报道[22].

      当体系内吸引力占据主导地位时, 情况会有所不同. 在EHD吸引力的作用下, 体系内不再是密度分布均匀的极性流体, 集体运动内部密度分布变得不均匀, 粒子出现明显聚集, 形成高密团簇(图4(b)). 从相应的速度方向着色图则可以发现(图4(d)), 粒子速度方向颜色着色基本一致, 这表明高密团簇与低密区粒子运动方向一致, 具有相同的极性序. 因此, 我们称其为极性团簇. 极性团簇是在集体运动(极性流体)内部, 由强吸引力导致的极性有序相内部的密度涨落. 极性团簇和周围的极性流体具有相同的极向序, 即相同的运动方向. 极性团簇和极性流体中的所有活性粒子的运动是持续定向的.

      在已有的研究中, 团簇的出现通常伴随着高密相和低密相的相分离过程. 高密相为团簇, 低密相为无序气体. 团簇内部粒子运动方向可以是无序的[14], 也可以是有序的[19]. 然而在这里, 团簇出现在集体运动内部, 高密团簇与低密区粒子具有相同的极性序(图4(d)). 这是已有研究中没有观察到的.

    4.   结　论

    • 本研究以二维Quincke胶体体系为实验模型, 揭示了吸引力对Quincke活性胶体动力学行为的影响. 实验表明, 吸引力的引入显著增强了粒子间的速度对齐效应, 延长了碰撞对齐的持续时间. 在多粒子体系中, EHD吸引力通过平衡电偶排斥作用, 驱动动态凝聚相的形成与演化, 产生特有的亚临界行为. 尤为重要的是, 在集体运动层面, 吸引力促使极性流体自发发生密度分离, 形成具有极性序的团簇结构——这一现象揭示了吸引与对齐机制耦合下的新型有序态. 本研究不仅为吸引力对活性物质的影响提供了实验依据, 也有助于模拟生物体系中的趋化集体行为.

    参考文献 (31)

目录

/

返回文章
返回