2018年, 扭角双层石墨烯系统中关联绝缘体和超导电性的发现标志着在研究非常规超导体的物理机制过程中又有了新的突破, 该发现进一步激发了人们对非常规超导体的研究兴趣, 开启了人们研究扭角系统的大门^[1,2]. 它与铜基和铁基超导体相似, 也是典型的强关联系统, 未掺杂时表现出莫特关联绝缘体的特征, 通过掺杂则会在半填充的莫特关联绝缘体两侧出现两个明显的拱形超导电性区域, 并且该区域电导表现出V型变化趋势^[3]和小相干长度^[1,4]. 另外, 还存在奇异金属^[5,6]以及量子反常霍尔效应^[7]等特性. 扭角双层石墨烯更为 独特之处在于随着扭转角度的改变在实空间内会形成不同原胞大小的莫尔纹. 狄拉克费米子的费米速度随着扭转角度的不同而不同, 靠近每一单层 石墨烯的每一个波谷的电子态和另一层对应的电子态杂化, 当扭转角度接近1.1°时电子结构会呈 现出平带的性质. 载流子浓度的增加使得系统的化学势位于平带附近, 从而电子之间的关联效应显著 增强^[8–10]. 扭角双层石墨烯的最大优势在于掺杂时不会引起无序以及具有可调控的载流子浓度, 因而被认为是研究非常规超导电性微观机理的理想 系统.

针对扭角双层石墨烯系统这些新奇的关联态, Lu等^[4]利用四端法测量扭转角度接近1.1°的双层石墨烯系统得到了更为详细的相图, 结果显示在莫尔原胞内含有整数个电子或者空穴, 即所有非零整数莫尔带填充下的$ (v = \pm1,\; \pm2, \;\pm3) $电阻具有明显的峰值. 通过细致分析电导和温度的关系, 发现电导表现出的一系列峰值表明该系统此时处于关联绝缘体态. 此外根据电阻阻值的测量还可以绘制出更为详细的物理相图, 相图中除了关联绝缘体态外, 最为显著的是关联态临界超导态区域, 对于不同的掺杂区域和不同的温度, 这些关联态也会呈现出不同的状态. 为了对扭角双层石墨烯系统的超导特性和关联态有更为全面的了解, Cao等^[11]实验上成功制备了各种扭转角度的双层石墨烯系统, 实验结果显示, 除了扭转角度为1.08°的扭角双层石墨烯系统呈现出超导电性外, 其他小扭转角度的双层石墨烯系统也存在超导电性. 观察在最佳掺杂下超导临界转变温度和扭转角度的关系, 实验上发现扭转角度接近1.08°的扭角双层石墨烯的超导临界转变温度较高, 这说明不同的扭转角度对超导临界转变温度具有较大的影响.

理论上研究扭角双层石墨烯系统的超导电性遇到的第一个问题就是扭角双层石墨烯对称性所带来的原胞中原子数急剧增大问题. 不同于高度有序的单层石墨烯结构(单层石墨烯满足$ C_{6} $对称性), 扭角双层石墨烯的层间耦合随着扭转角度的变化而变化, 从而导致层间对称性也会不断变化. 最显著的特点是当两层石墨烯发生扭转时上层石墨烯和下层石墨烯晶格不再重合, 随着扭转角度越来越小原胞逐渐扩大. 以扭转角度$ \theta = 1.08^{\circ} $的扭角双层石墨烯晶格为例, 此时原胞内包含的原子多达11164个^[12]. 考虑理论结果的可靠性, 数值模拟应在包含多个原胞的超胞中进行, 然而任何理论方法都无法模拟该系统对应的真实模型. 因此解决该问题的关键是在清楚地了解扭角双层石墨烯能带结构的基础上构建有效的理论模型. 针对扭角双层石墨烯的能带结构, 注意到极小的扭转角度将会使晶格发生位错而出现具有局域周期的莫尔条纹, 可以预见在莫尔条纹中两层原子彼此相对将形成很窄的平带^[13]. 这样的平带特点也被第一性原理研究的结果所证实, Lucignano等^[14]构建了扭转角度为1.08°的扭角双层石墨烯结构, 利用密度泛函理论模拟了该系统的能带结构, 优化后的扭角双层石墨烯能带结构在费米面E = 0.0 meV附近形成一个极窄的平面, 相应的能带宽度大约为12 meV, 该结果和实验测得的能带宽度比较一致. 最近基于扭角双层石墨烯的瓦尼尔轨道对称性分析, Yuan和Fu^[15,16]的研究工作证实蜂巢晶格中有效两轨道哈伯德模型可以反映出扭角双层石墨烯系统的电子结构和库仑相互作用效应等基本物理性质. 这个模型为研究扭角双层石墨烯中扭转角度和电荷载流子浓度对狄拉克费米子的重构提供了有用的理论依据.

其次, 关于扭角双层石墨烯超导体的电子配对形式也存在争议, 前期的研究同时考虑平带结构和排斥电子相互作用预测了半满状态下是莫特绝缘体, 而电子掺杂下可能是拓扑超导态^[17]. 更细致的理论研究预测扭角双层石墨烯的电子配对形式可能是手性$ {\mathrm{d}}+{\mathrm{id}} $波^[18–22], 也可能是扩展的s波和p波以及f波^[23–29], 更多的共识认为其最有可能是手性$ {\mathrm{d}}+{\mathrm{id}} $波配对形式^[30]. 除先前这些重要的研究结果之外, 越来越多的研究工作认为电声子相互作用对扭角双层石墨烯系统的超导电性具有重要作用^[31–38]. 例如, Chen等^[31]使用微米分辨率的角分辨光电子能谱来观察处在超导态下的扭角双层石墨烯中的平带结构, 这些平带结构有均匀的能带间距, 大小约为150 meV, 而系统在非超导态时则不存在这种行为, 这表明系统存在较强的电声子耦合. 同时还确定了超导态下的扭角双层石墨烯平带结构的形成源于石墨烯K点的横向光学声子模式与电子的强耦合.

受上述一系列研究工作的启发, 本文利用大尺度无偏差的约束路径量子蒙特卡罗方法研究有效两轨道哈伯德模型的扭角双层石墨烯系统中的磁性和超导电性的内在关联, 从电声子耦合的层面讨论晶格中近邻吸引库仑相互作用对超导电性的调控效应以及磁性对超导电性的影响. 结果显示电声子耦合会强烈地增强系统的超导电性, 从更深层的角度分析出反铁磁序的增强是调控超导电性的先决条件. 另一方面, 通过构建不同的扭角双层石墨烯有效两轨道哈伯德模型, 来讨论扭转角度对超导电性的调控效应以及磁性和超导电性之间的关联, 结果表明更小的扭转角度有利于增强系统的超导电性, 并再次证实了反铁磁序和超导电性之间存在协调效应.

该工作使用文献[15,16,39]提出的描述扭角双层石墨烯结构的有效两轨道哈伯德模型. 该模型包括动能部分$ \hat{H}_{{\mathrm{t}}} $和相互作用部分$ \hat{H}_{{\mathrm{int}}} $, 哈密顿量$ \hat{H}_{{\mathrm{t}}} $包括轨道内的$ \hat{H}_{0} $、对称性破缺项$ \hat{H}_{1} $和$ \hat{H}_{2} $, 其中引入的两个对称性破缺项分别打破了$ {SU}(4) $和$ {U}(1) $对称性. 哈密顿量$ \hat{H}_{{\mathrm{t}}} $描述如下:

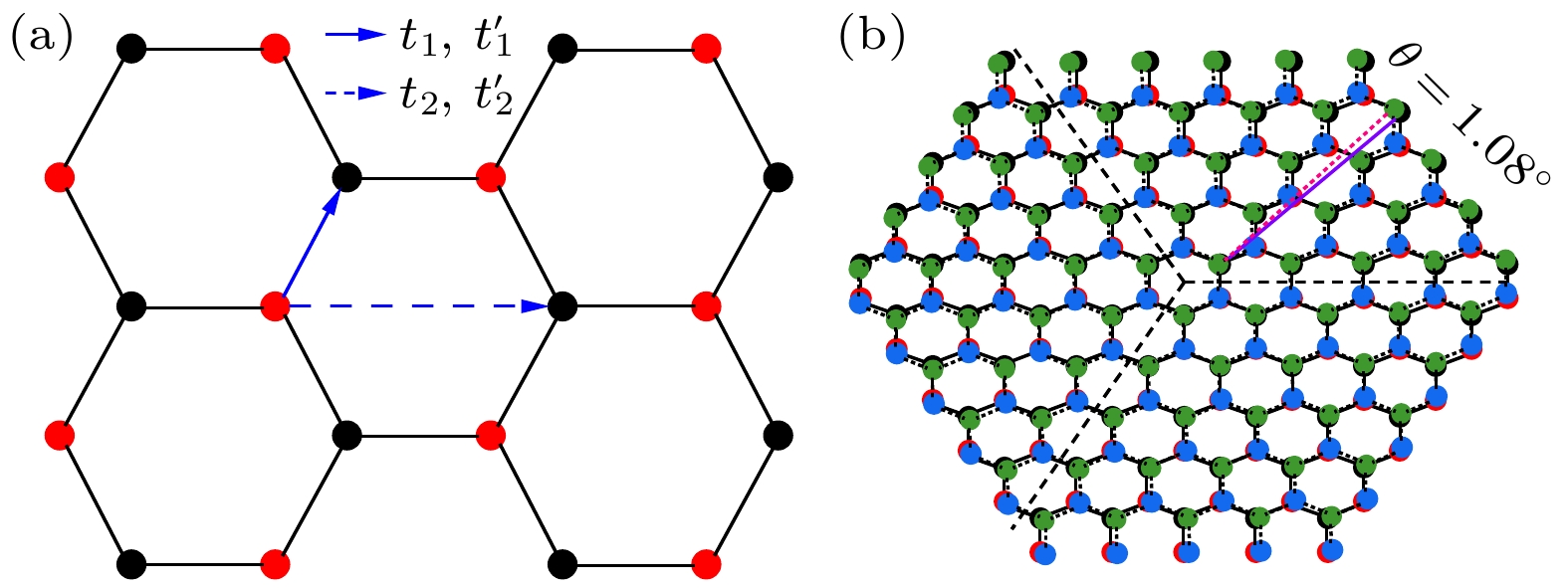
式中, $ \hat{c}_{i, \sigma} = (\hat{c}_{i, x, \sigma}, \hat{c}_{i, y, \sigma})^{{\mathrm{T}}} $, 算符$ \hat{c}_{i, x(y), \sigma} (\hat{c}^{\dagger}_{i, x(y), \sigma}) $表示湮灭(产生)一个位于i位置自旋为$ \sigma(\sigma = \uparrow, \downarrow) $的$ p_{x(y)} $电子. 如图1(a)所示, $ t_{1} $和$ t_{2} $分别表示轨道内最近邻和第五近邻的电子跳跃积分强度. $ \hat{c}_{\pm, \sigma} = (\hat{c}_{x, \sigma}\pm {\mathrm{i}}\hat{c}_{y, \sigma})/\sqrt{2} $的具体形式为$ p_{x, \sigma}\pm {\mathrm{i}}p_{y, \sigma} $, 并遵守手性基本法则. 式中$ \hat{H}_{1} $打破${SU}(4) $对称性从而分解为${U}(1)\times {SU}(2) $对称性. 这里${U}(1) $对称性指的是轨道手性守恒, ${SU}(2) $对称性指的是自旋旋转对称性. 哈密顿量$ \hat{H}_{2} $项中的$ {\boldsymbol e}^{{/ /}, \perp}_{ij} $表示与最近邻连接的平行和垂直单位矢量. 哈密顿量$ \hat{H}_{2} $项沿着最近邻格点连接的三个方向具体的动能表达式分别为$ \hat{c}^{\dagger}_{ix}\hat{c}_{jx}-\hat{c}^{\dagger}_{iy}\hat{c}_{jy} $, $ -\dfrac{1}{2}(\hat{c}^{\dagger}_{ix}\hat{c}_{jx}-\hat{c}^{\dagger}_{iy}\hat{c}_{jy})- \dfrac{\sqrt{3}}{2}(\hat{c}^{\dagger}_{ix}\hat{c}_{jy} + \hat{c}^{\dagger}_{iy}\hat{c}_{jx}) $, 以及$ -\dfrac{1}{2}(\hat{c}^{\dagger}_{ix}\hat{c}_{jx}- \hat{c}^{\dagger}_{iy} \hat{c}_{jy}) + \dfrac{\sqrt{3}}{2} \times (\hat{c}^{\dagger}_{ix} \hat{c}_{jy} + \hat{c}^{\dagger}_{iy}\hat{c}_{jx}) $. 这里$ \hat{H}_{2} $进一步破缺了$ {U}(1) $对称性. 需要指出的是本文的跳跃参数和文献[15,16] 选取的参数不相同. 本文以跳跃振幅$ t_{1} $为单位能量, 其他跳跃参数分别设置为$ t_{2} = 0.025 $以及$ t_{1}' = t_{2}' = 0.1 $.

相互作用部分包括在位库仑排斥相互作用项$ \hat{H}_{U} $和轨道内最近邻库仑相互作用项$ \hat{H}_{V} $, 该部分的哈密顿量$ \hat{H}_{{\mathrm{int}}} $描述如下:

式中β表示$ {p}_{x(y)} $轨道, $ \langle i,j\rangle $表示最近邻格点. U表示在位库仑排斥相互作用强度, V表示轨道内最近邻库仑相互作用强度.

在讨论计算方法和结果之前需要说明的是, 本文的数值模拟是在周期性的六角晶格中进行的. 如图1(b)所示, 该图代表边长为L = 5, 扭转角度为1.08°的扭角双层石墨烯模型, 该模型包含$ 4\times3 L^{2} $个原子. 为了求解这类含有多原子的哈伯德模型, 使用能够精确求解关联电子系统基态信息的大尺度无偏差约束路径量子蒙特卡罗方法. 该方法的基本策略是在斯莱特行列式空间中通过多分支随机游走投影一个初始波函数$ |\varPsi_{{\mathrm{T}}}\rangle $得到关联电子系统的基态波函数$ |\varPsi_{{\mathrm{g}}}\rangle $, 投影方程可以描述为

其中$ \hat{H} $表示系统的哈密顿量, τ是实数且大于$ 0 $. 数值上该投影方程可以通过迭代的方式来实现, 即

初次迭代时$ |\varPsi^{(0)}\rangle = |\varPsi_{{\mathrm{T}}}\rangle $, 对于很小的$ \Delta\tau $可以使用Trotter-Suzuki (TS)分解^[40,41], 在忽略高阶近似的情况下将(4)式改写为

式中$ \hat{H}_{{\mathrm{t}}} $是二次型的费米算符, 其以指数形式作用在初始波函数上, 就是简单的将波函数对应的斯莱特行列式转换成另一个斯莱特行列式. 对于四次算符形式的$ \hat{H}_{{\mathrm{int}}} $费米算符, 则需要通过利用离散的Hubbard-Stratonovich (HS)变换将算符$ {\mathrm{e}}^{-\Delta\tau\hat{H}_{{\mathrm{int}}}} $转换成二次算符形式, 具体的变换形式可参考文献[42].

最终通过TS分解和HS变换迭代方程(4)表示为

至此, 投影算符$ {\mathrm{e}}^{-\Delta\tau \hat{H}} $变成了一个复杂的二次算符形式, 虽然该算符复杂, 但优势在于克服了无法求解四算符的困难. 经过上述处理, 方程(6)可以视为多辅助场的求和, 相应的表达式为

式中

代表概率密度函数, $ \hat{B}^{\sigma}(x) = \hat{B}^{\sigma}_{{\mathrm{K}}}\hat{B}^{\sigma}_{\mathrm{{I}}} $ ($ \sigma = \uparrow, \downarrow $)代表$ {\mathrm{HS}} $变换的辅助场传播因子, $ \hat{B}^{\sigma}_{{\mathrm{K}}} $为动能部分的传播因子, $ \hat{B}^{\sigma}_{{\mathrm{I}}}(x) $为势能部分的传播因子. 蒙特卡罗方法是对辅助场$ x_{i} $的多维求和, 当波函数达到收敛后, 相应的系统中物理量$ \mathcal{O} $的期望值通常基于回传^[43]技术求得, 即

其中$l_{\rm BP} $为回传步数, 数值模拟过程中设置$ l_{\rm BP}=40$.

通过上述介绍可以了解到, 初始波函数的选择将是影响数值模拟结果准确性的关键因素, 约束路径量子蒙特卡罗方法的优势在于无论是以自由电子波函数为初始波函数还是以其他类型的波函数(如非限制Hartree-Fork波函数)为初始波函数得到的统计误差和结果一致^[44–46]. 从模拟技术上来说, 蒙特卡罗方法是在斯莱特行列式空间中随机多分支游走产生抽样样本, 即波函数写为$ |\varPsi^{(n)}\rangle = \displaystyle\sum\nolimits_{k}\chi_{k}|\phi^{n}_{k}\rangle $. 同时考虑到费米子基态波函数需要满足反对称性, 对于表示基态波函数的斯莱特行列式的集合$ \{|\phi\rangle\} $, 反对称性意味着斯莱特行列式还存在另外一个集合$ \{-|\phi\rangle\} $也可以正确表示基态波函数. 随着抽样次数的增多必然导致蒙特卡罗方法在进行数值模拟时出现符号问题. 约束路径量子蒙特卡罗方法的核心思想和优势是通过合理定义一个界面${\rm N}'$将抽样样本局限在一个样本空间, 数值计算中该方法要求样本$ |\phi^{(n)}_{k}\rangle $和试探波函数$ |\varPsi_{{\mathrm{T}}}\rangle $有正的交叠积分$ \langle\varPsi_{{\mathrm{T}}}|\phi_{k}^{(n)}\rangle > 0 $, 这就是所谓的约束路径近似, 也正是这种近似保证了结果的快速收敛和准确性.

为了全面理解扭角双层石墨烯中的超导特性, 计算了各种配对形式的轨道内电子配对关联函数, 配对关联函数的定义如下:

式中的$ \varDelta_{\alpha}^{\dagger}({\boldsymbol{i}}) $ ($ \varDelta_{\alpha}({\boldsymbol{i}}) $)是配对对称性为α的电子配对产生(湮灭)算符. 单态和三态的产生算符可以写为

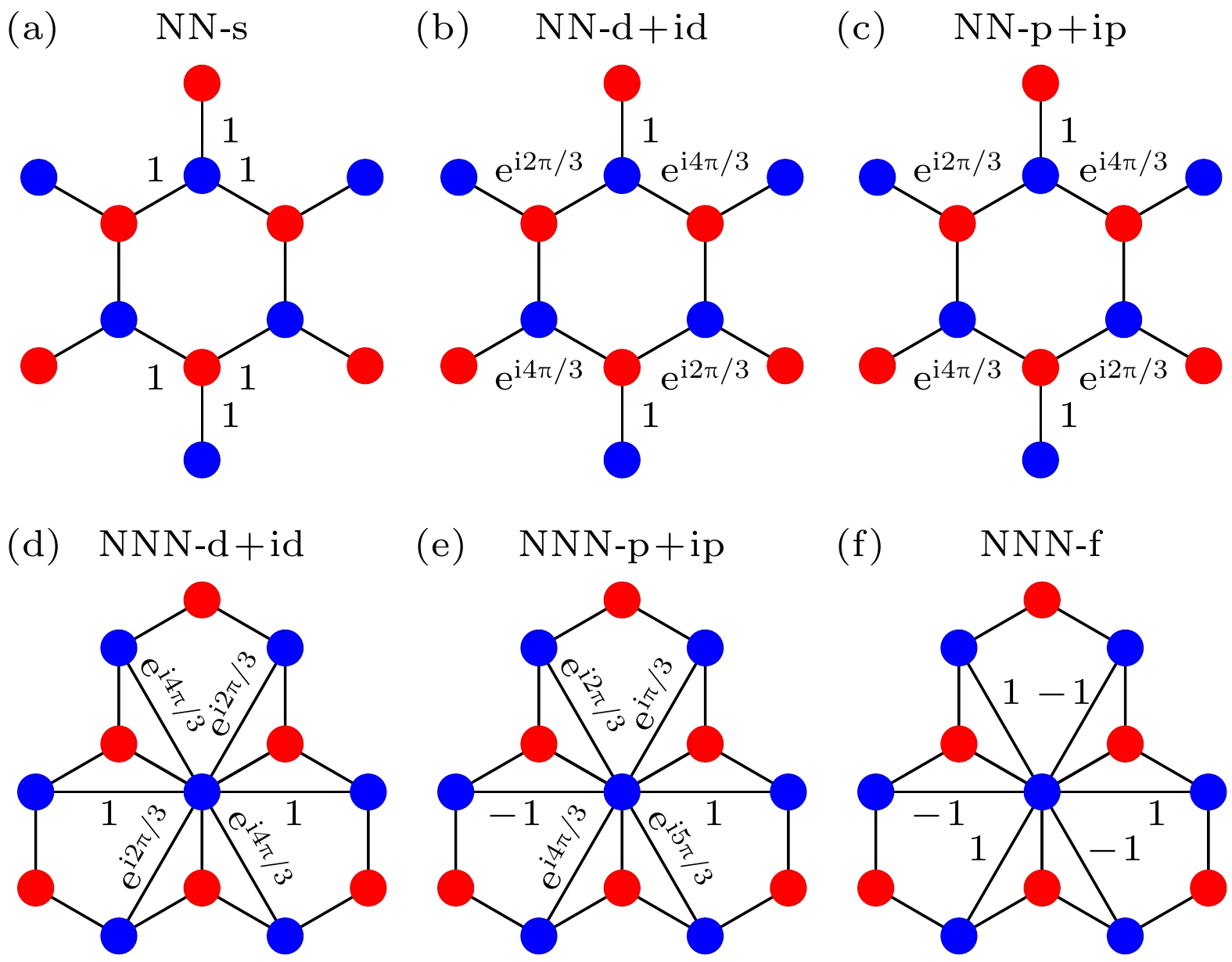
式中$ f_{\alpha}({\boldsymbol \delta}_{{l}}) $是形状因子用于区别不同类型的配对方式. $ -(+) $对应单态(三态)配对. 取决于不同类型的配对方式, 矢量$ {\boldsymbol \delta}_{{l}} $表示最近邻或次近邻同类格子的连接. $ {N}_{\alpha} $是归一化系数, 对于最近邻配对${N}_{\alpha} = 3 $, 次近邻配对$ {N}_{\alpha} = 6 $. 文中考虑了所有可能的近邻和次近邻配对, 这些配对方式有NN-$ {\mathrm{s}} $对称性波, NN-$ {\mathrm{d}}+{\mathrm{id}} $对称性波, NN-$ {\mathrm{p}}+{\mathrm{ip}} $对称性波, NNN-$ {\mathrm{d}}+{\mathrm{id}} $对称性波, NNN-${\mathrm{p}}+{\mathrm{ip}} $对称性波, NNN-$ {\mathrm{f}} $对称性波^[47,48]. 这些配对对称性的形状因子$ f_{\alpha}({\boldsymbol \delta}_{{l}}) $如图2所示, 其具体的定义为

方程(11)中, 矢量$ {{\boldsymbol \delta}_{{l}}} $ ($ {{l}} = 1, 2, 3 $) 代表最近邻晶格的方向, $ {{\boldsymbol \delta}_{{{l}}{'}}} $($ {{{l}}{'}} = 1, 2, 3, 4, 5, 6 $)代表次近邻格点的方向.

考虑到电子配对关联函数可能容易受到哈密顿量中的非相互作用部分的强烈影响^[48–50], 本文还计算了有效配对关联函数, 其定义为

其中$ \tilde{P_{\alpha}}({R}) $是非关联的单粒子贡献, 可以通过将$ \langle \hat{c}^{\dagger}_{i\downarrow}\hat{c}_{j\downarrow}\hat{c}^{\dagger}_{k\uparrow}\hat{c}_{l\uparrow}\rangle $解耦为$ \langle \hat{c}^{\dagger}_{i\downarrow}\hat{c}_{j\downarrow}\rangle \langle \hat{c}^{\dagger}_{k\uparrow}\hat{c}_{l\uparrow} \rangle $获得. 可以通过这个有效配对关联函数的增强(压制)趋势来确定体系主导的配对形式. 为了能够反映相互作用部分对电子配对对称性长程序的影响, 长程平均有效配对关联函数可以表示为

式中R表示格点之间的距离, $ N_{1} $表示电子配对距离$ R\geqslant3 $的格点配对数.

在对各类超导体物理性质的研究中, 普遍认为磁性与超导电性密切相关, 因此本文也计算了扭角双层石墨烯中的磁序, 在波矢空间中自旋结构因子$ S(q) $的定义为

式中$ \hat{S}_{i, d} = \hat{n}_{i, d, \uparrow}-\hat{n}_{i, d, \downarrow} $; $ d = d{'} $情况下, $ \epsilon_{d, d{'}} = 1 $; $ d \ne d{'} $情况下, $ \epsilon_{dd'} = -1 $. 最后, 针对此扭角双层石墨烯模型我们使用约束路径量子蒙特卡罗方法进行数值模拟, 选择电子闭壳层填充以及自由电子波函数为初始波函数, 模拟中的主要参数为: 随机游走数9000, 投影步长$ \varDelta =0.04 $. 在测量物理量之前进行1280步的蒙卡抽样, 测量物理量时设置为320步的蒙卡抽样, 40次独立测试确保统计的独立性, 当模拟达到平衡时, 物理量的期望值可以基于回传技术进行求解.

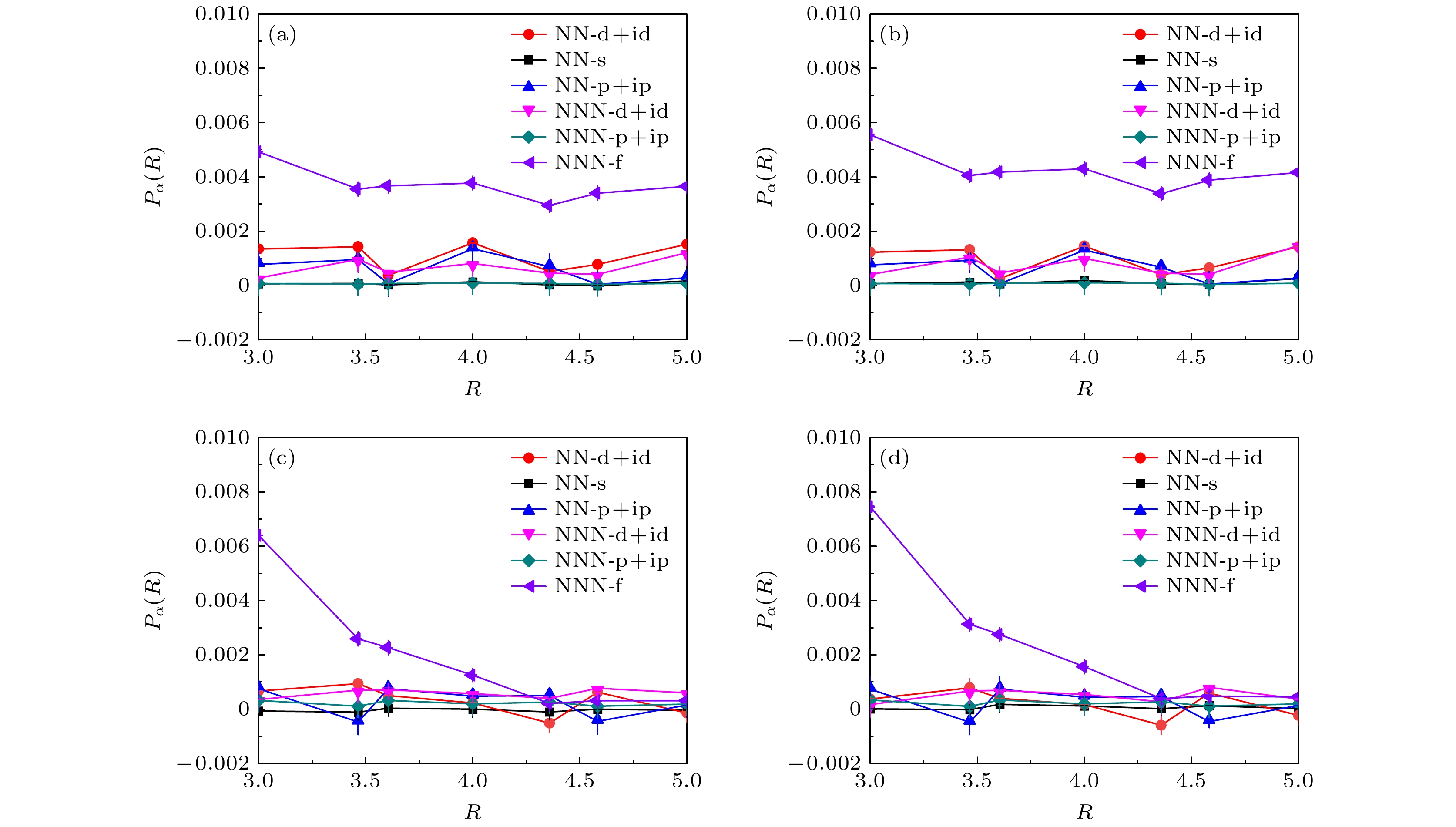
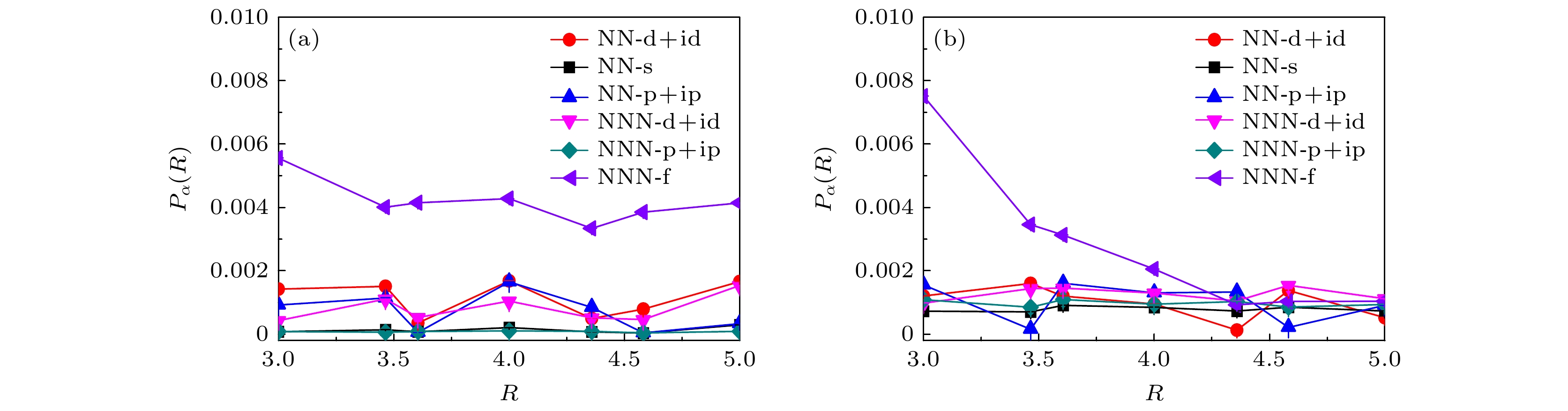
该小节着重分析近邻库仑相互作用强度对扭角双层石墨烯系统的超导配对对称性的影响, 图3展示了不同库仑相互作用强度下晶格大小为$ L = 5 $的各类电子配对对称性的配对关联函数在配对距离$ R \geqslant 3 $上的演化曲线. 图3(a)和图3(b)分别对应电子填充浓度$ \langle n \rangle = 0.933 $下$ U = 2.0, V = 0.0 $和$ U = 0.0, V = -0.3 $的情况, 图3(c)和图3(d)则分别对应电子填充浓度$ \langle n \rangle = 0.893 $下$ U = 2.0,V = 0.0 $和$ U = 0.0, V = -0.3 $的情况. 从图中可以清楚地观察到, 对于只有在位库仑相互作用强度$ U = 2.0 $(图3(a)和图3(c))或者近邻吸引库仑相互作用强度$ V = -0.3 $(图3(b)和图3(d))的情况, 整个长程距离$ R\geqslant3.0 $上三重态NNN-f波配对对称性的强度始终处于最高位置, 基于当前的数值模拟结果在扭角双层石墨烯系统中似乎支持电子的配对对称性是三重态的NNN-f波配对对称性. 然而一个重要的问题是先前的量子蒙特卡罗方法研究石墨烯系统中的超导特性指出, 电子的配对对称性容易受到哈密顿量中非相互作用部分的强烈影响^[48–50], 故从配对关联函数得出的结论并不十分可信.

为了进一步证实哈密顿量中的无相互作用部分对电子配对对称性是否有强烈影响, 图4(a)和图4(b)展示了无相互作用时各类电子配对对称性随配对距离R的演化曲线. 图中的数值模拟结果表明电子填充浓度$ \langle n \rangle = 0.933 $和$ \langle n \rangle = 0.893 $两种情况下三重态NNN-f波的配对强度依然大于其他类型的电子配对对称性强度. 通过对比图3和图4的结果可以发现, 各种配对形式的关联函数随长程距离R的变化趋势完全一致, 从而无法分析相互作用部分对电子配对对称性的影响. 基于此结果, 从关联函数出发得到三重态NNN-f波配对对称性为主导的配对形式应该是无相互作用部分电子结构造成的. 所以无相互作用部分掩盖了相互作用部分对电子配对对称性的有效信息, 即从关联函数无法准确分析扭角双层石墨烯的电子配对对称性.

基于前面的讨论, 考虑到无相互作用部分对电子配对对称性的影响, 接下来重点基于有效配对关联函数来分析电子的配对对称性. 近期角分辨光电子能谱揭示了一维铜基超导体中空穴和自旋能带随掺杂浓度的变化, 发现一个明显的空穴折叠分支, 文献[51]指出该分支来源于电声子耦合引起的近邻吸引库仑相互作用. 另外, 理论采用变分非高斯精确对角化方法在模拟一维哈伯德模型中得出的结果与上述实验结果进行定量比较, 在合理的电声子耦合范围内得到相邻电子之间的吸引相互作用强度与实验观测结果符合^[52]. 其次, 利用量子蒙特卡罗方法研究棋盘状四方晶格的数值结果揭示了近邻吸引库仑相互作用强烈地增强d波超导态^[53]. 故电声子耦合的具体表现可视为近邻电子之间的吸引相互作用, 其对理解非常规超导体机理可能扮演着重要角色, 受这一系列工作的启发, 本文通过系统地研究近邻吸引库仑相互作用对扭角双层石墨烯系统超导电性的调控来说明电声子耦合是如何影响超导电性的. 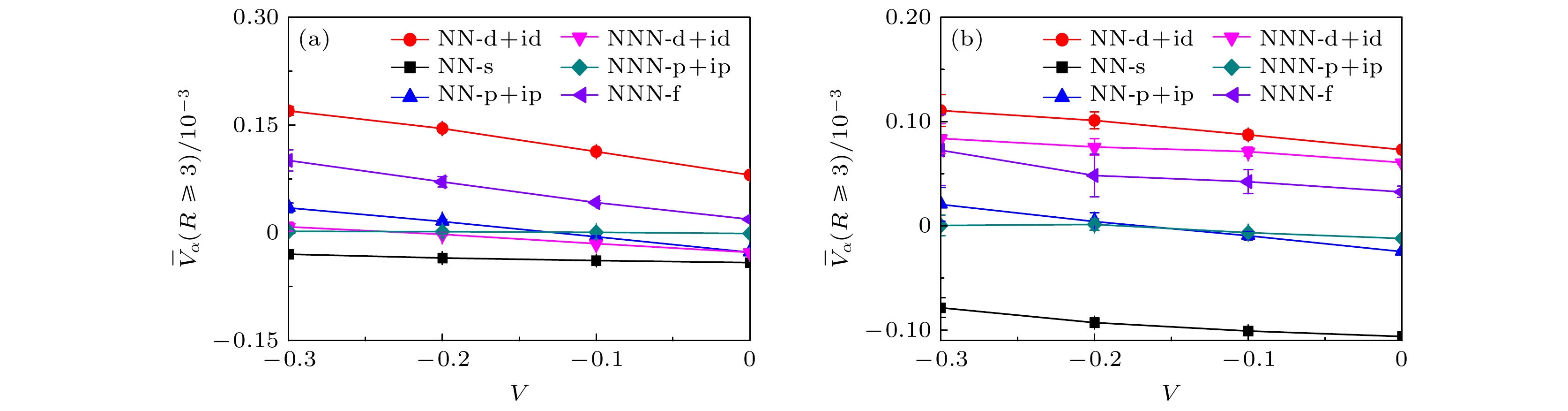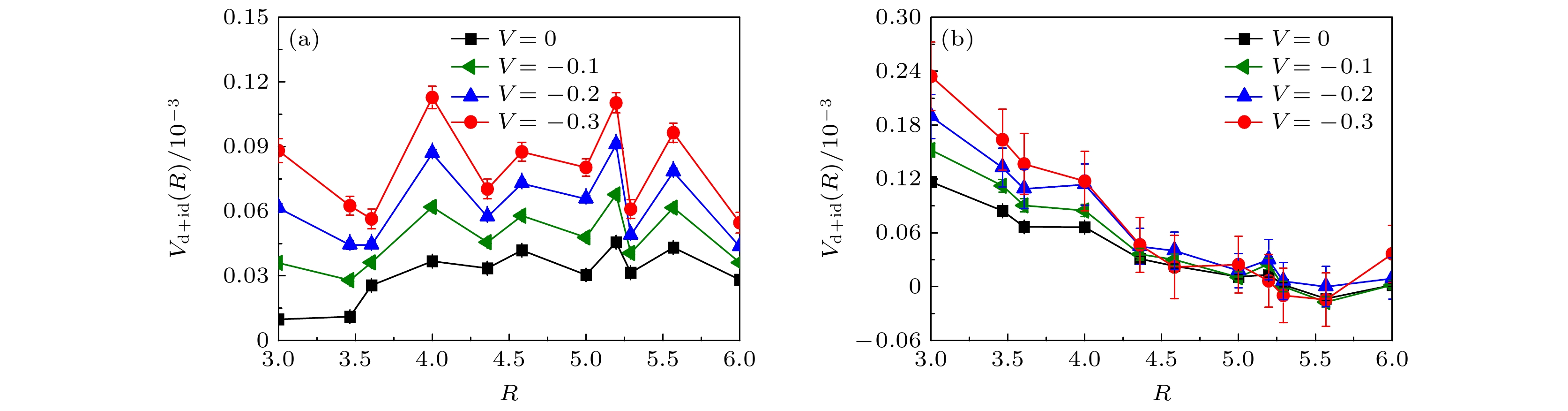图5展示了各种配对形式的平均有效配对关联函数$ \overline{V}_{\alpha}(R\geqslant3) $关于近邻吸引库仑相互作用强度V的函数关系. 图5(a)和图5(b)的数值结果也是在晶格大小为$ L = 5 $的尺寸下模拟获得的, 选择的电子填充浓度同样分别为$ \langle n \rangle = 0.933 $和$ \langle n \rangle = 0.893 $. 首先, 在近邻库仑相互作用强度$ V = 0.0 $情况下可以轻易地观察到, 手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波对应的平均有效配对关联强度明显大于其他电子配对形式, 此结果显然和图3基于配对关联函数出发得到的三重态NNN-f波是主导的配对形式完全不同, 这不仅证实了无相互作用部分确实会对电子配对对称性有强烈影响, 还表明扭角双层石墨烯系统中电子的配对形式为手性NN-${\mathrm{d}}+{\mathrm{id}} $波配对对称性. 其次, 图5的数值模拟结果还说明随着近邻吸引库仑相互作用强度的增加, 所有类型的电子配对形式的平均有效配对关联函数都增加. 更为重要的是, 手性NN-$ \mathrm{d} +{\mathrm{id}} $波电子配对对称性始终处于主导地位并且具有最大增幅, 需要指出的是, 相比于近邻库仑相互作用强度$ V = 0.0 $时的手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波配对对称性的平均有效配对关联强度, 当存在吸引库仑相互作用且强度增加到$ V = -0.3 $情况时, 对于电子填充浓度$ \langle n \rangle = 0.933 $的情况, 手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波的配对强度增加了2.106倍; 电子填充浓度$ \langle n \rangle = 0.893 $的情况, 手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波的配对强度增加了1.514倍, 该结果充分表明近邻吸引库仑相互作用强度可以剧烈地增强手性NN-$ {\mathrm{d}}+{\mathrm{id}} $超导态.

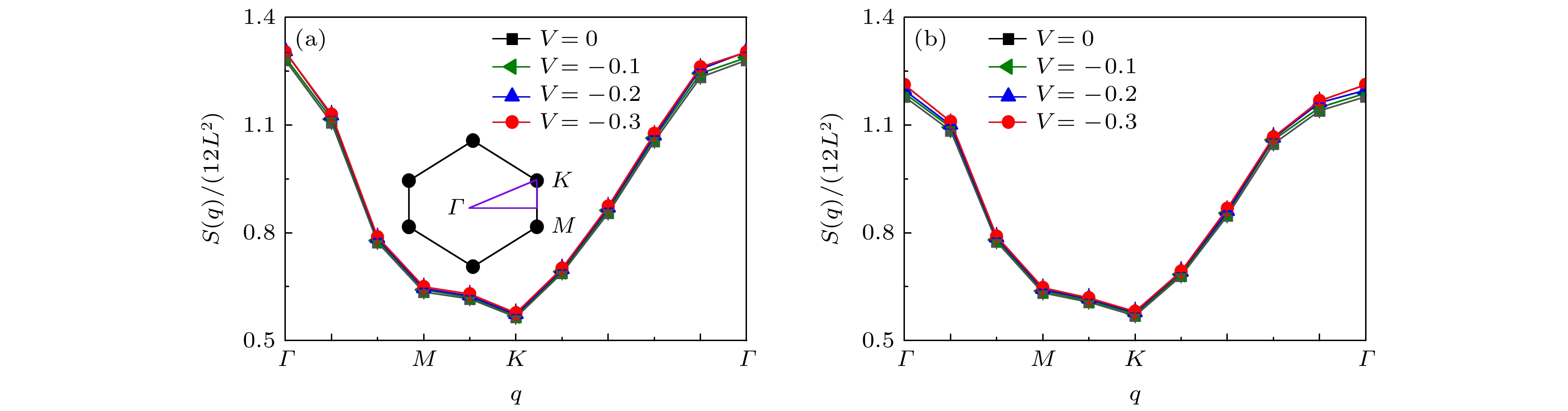
考虑到晶格尺寸效应, 本文在更大的晶格尺度上进行数值模拟, 以晶格大小$ L = 6 $为例, 图6(a)和图6(b)展示了在位库仑相互作用强度$ U = 2.0 $情况下, 手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波配对对称性的有效配对关联函数在长程距离$ R\geqslant3 $上的函数曲线, 这里选择的电子填充浓度$ \langle n \rangle = 0.954 $(图6(a))和电子填充浓度$ \langle n \rangle = 0.926 $(图6(b)). 基于该图的数据结果可以观察到, 随着近邻吸引库仑相互作用强度V的增加, 手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波配对对称性的有效配对关联函数在整个长程距离上都呈现增强的趋势, 尤其靠近半满电子填充浓度$ \langle n \rangle = 0.954 $时手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波的变化最显著. 图5和图6的结果一致性表明, 近邻吸引库仑相互作用强度V有效地增强了手性NN-$ {\mathrm{d}}+{\mathrm{id}} $超导态.

非常规超导态中的研究广泛认为磁性和超导电性密切关联, 以典型的高温铜氧化物超导体^[54–57]和铁基超导体^[58–61]为例, 反铁磁涨落在调制超导电性中扮演着重要角色. 基于扭角双层石墨烯的能带结构发现, 每一个轨道波谷上的电子和另一个轨道上的电子杂化以及未填充时表现出莫特绝缘体特性, 说明了该系统和铜基超导体以及铁基超导体类似, 也是典型的强关联电子系统, 故可以预见在此系统中磁性对超导电性也具有重要的影响. 考虑到磁性和超导电性的关联, 图7展示了自旋结构因子$ S(q) $沿着第一布里渊区高对称线方向的演化关系, 该图的数据模拟是在在位库仑相互作用强度$ U = 2.0 $, 晶格大小为$ L = 5 $中进行, 选择的电子填充浓度分别为$ \langle n \rangle = 0.933 $(图7(a)), $ \langle n \rangle = 0.893 $(图7(b)). 从图7可以清楚地观察到, 随着近邻吸引库仑相互作用强度V的增强, 自旋结构因子$ S(q) $在Γ点表现出明显的增强趋势, 这说明电子呈现反铁磁排布以及系统是稳健的反铁磁态. 因此, 该结果表明了反铁磁序的调制是增强手性NN-${\mathrm{d}}+{\mathrm{id}} $超导态的重要原因.

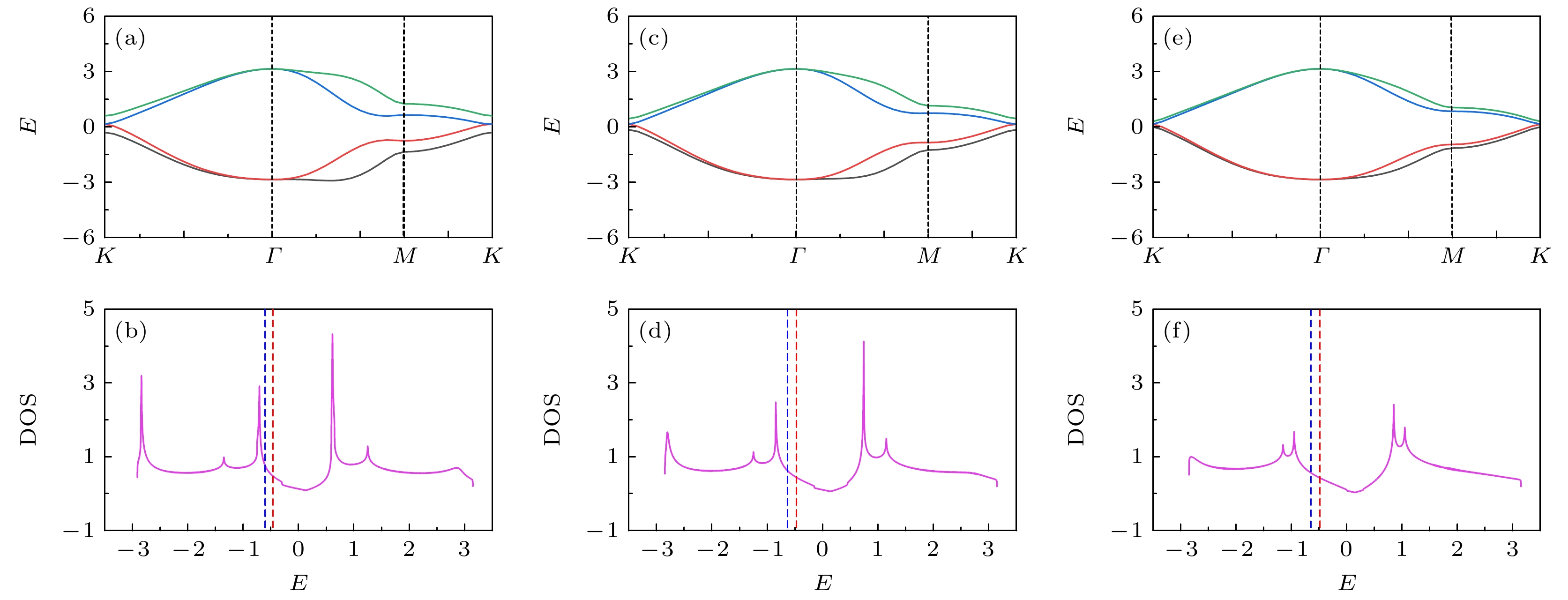
除了讨论近邻吸引库仑相互作用对扭角双层石墨烯超导态的影响, 本文还重点研究了1.08°附近不同扭转角度的双层石墨烯的超导电性. 实验^[8,9,62]和理论^[14,63–65]结果指出, 扭角双层石墨烯最重要的特征是当扭转角度逐渐靠近1.08°时, 随着扭转角度的减小能带结构在费米能级附近呈现出较平坦的趋势, 这表明扭转角度和能带结构存在直接关联. 受此启发, 我们可以通过调节扭角双层石墨烯有效两轨道哈密顿量破缺项中的电子跳跃强度来构建不同类型的平带结构以研究扭转角度对超导电性的影响, 不同类型的平带结构可以通过同步调节方程(1)中的$ t_{1}' $和$ t_{2}' $的强度来构建. 图8所示为扭角双层石墨烯无相互作用哈密顿量的能带结构和态密度. 图8(a)、图8(c)、图8(e)代表能带结构沿着第一布里渊区高对称线方向的演化曲线, 这里构建能带结构的方法为固定$ t_{1} = 1.0 $, $ t_{2} = 0.025 $, 同步调节$ t_{1}' $和$ t_{2}' $, 图8(a)、图8(c)、图8(e)对应的电子跳跃参数为$ t_ {1}' = t_{2}' = 0.15 $, $ t_{1}' = t_{2}' = 0.10 $,$ t_{1}' = t_{2}' = 0.05 $. 对比三个子图中的能带结构可以发现, 同步减小$ t_{1}'$和$ t_{2}' $的电子跳跃强度, 能带结构在第一布里渊区$ \varGamma \to M $区间高对称线上的能带宽度逐渐减小, 即平带趋势越来越显著. 结合第一性原理计算的结果以及扭角双层石墨烯有效两轨道哈伯德模型^[14–16], 说明$ t_{1}' = t_{2}' = 0.10 $对应扭转角度为1.08°的扭角双层石墨烯能带特征, $ t_{1}' = t_{2}' = 0.15 $对应扭转角度大于1.08°的扭角双层石墨烯能带特征, $ t_{1}' = t_{2}' = 0.05 $对应扭转角度小于$ 1.08^{\circ} $的扭角双层石墨烯能带特征. 同时, 对于不同扭转角度的能带结构, 图8(b)、图8(d)、图8(f)展示了状态数关于能量的函数关系. 这些子图中的红色虚线和蓝色虚线分别标注电子填充浓度为$ \langle n \rangle = 0.933 $和$ \langle n \rangle = 0.893 $的费米能级位置.

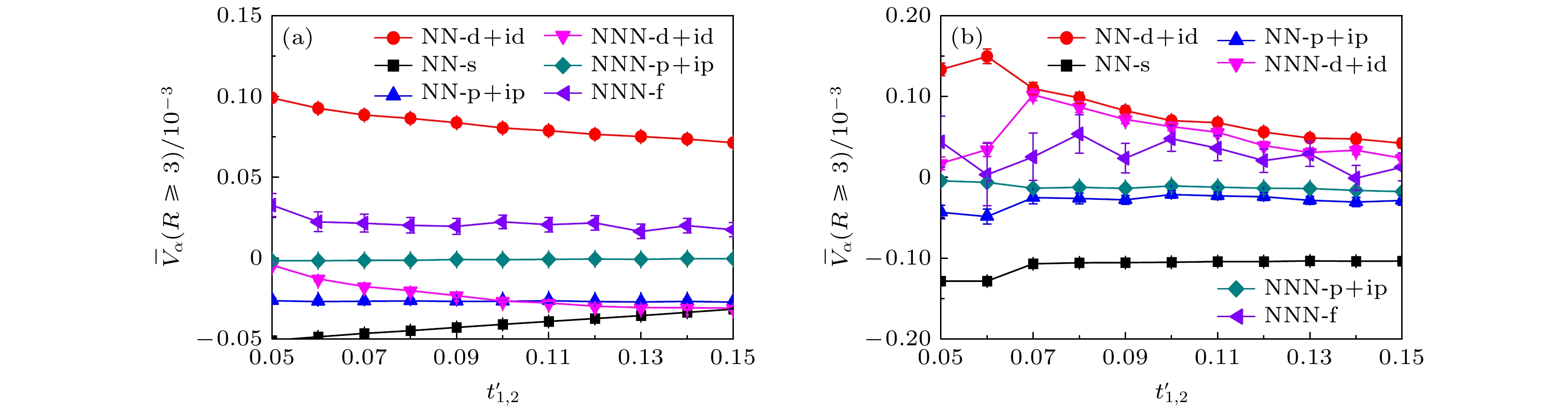
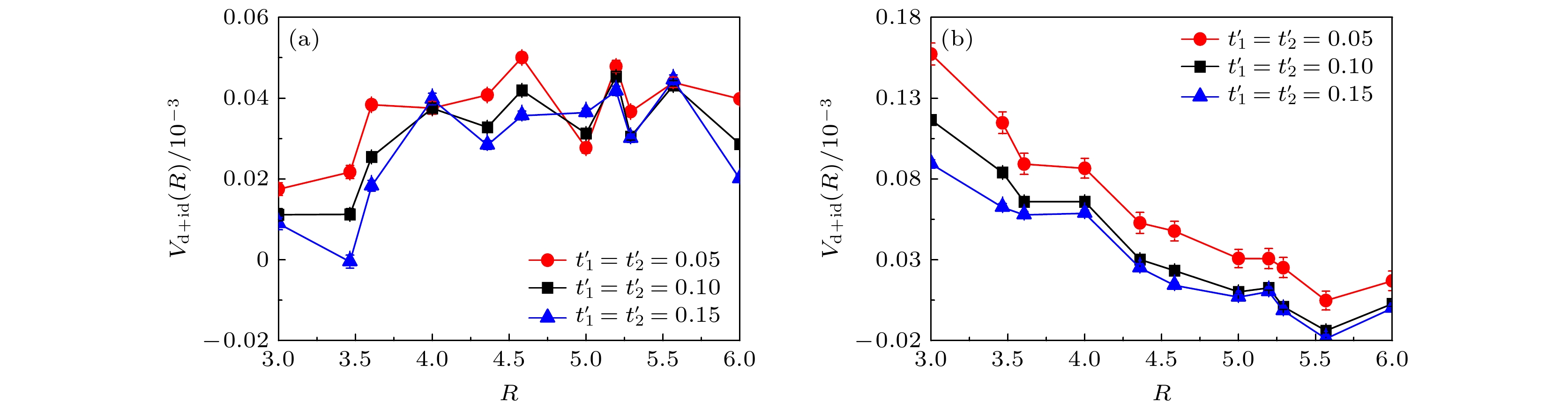
依据上述的讨论, 接下来以构建的不同类型扭角双层石墨烯的平带结构来讨论扭转角度对超导态的影响. 图9的数值模拟结果为各种类型的电子配对对称性的平均有效配对关联函数$ \overline{V}_{\alpha}(R\geqslant3) $关于电子跳跃破缺项$ t_{1, 2}' $的函数曲线, 数值模拟的晶格大小为$ L = 5 $, 在位库仑相互作用强度$ U = 2.0 $及近邻库仑相互作用强度$ V = 0.0 $, 选择的电子填充浓度同样为$ \langle n \rangle = 0.933 $和$ \langle n \rangle = 0.893 $. 从图9可以清楚地观察到, 随着电子跳跃破缺项$ t_{1, 2}' $强度同步减小, 对于电子填充浓度$ \langle n \rangle = 0.933 $的情况除了三重态手性NN-$ {\mathrm{p}}+{\mathrm{ip}} $和NNN-$ {\mathrm{p}}+{\mathrm{ip}} $波配对对称性的平均有效配对关联函数强度无明显变化以及单重态NN-${\mathrm{s}} $波表现出较微弱的减小外, 单重态手性NN-$ {\mathrm{d}}+{\mathrm{id}} $和NNN-$ {\mathrm{d}}+{\mathrm{id}} $以及三重态NNN-$ {\mathrm{f}} $波配对对称性的平均有效配对关联函数都表现出增强趋势并且单重态的手性NN-${\mathrm{d}}+{\mathrm{id}} $波配对对称性始终处于主导地位. 另外, 对于手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波平均有效配对关联函数的具体增幅以$ t_{1}' = t_{2}' = 0.10 $时的平均有效配对关联函数强度为基准, $ t_{1}' = t_{2}' = 0.05 $时平均有效配对关联函数强度增加了23.15%, $ t_{1}' = t_{2}' = 0.15 $时平均有效配对关联函数强度减小了11.22%. 对于电子填充浓度为$ \langle n \rangle = 0.893 $的情况, 不同之处是单重态NN-$ {\mathrm{s}} $波配对对称性的平均有效配对关联函数强度无明显变化, 以及由于计算误差的影响单重态NNN-$ {\mathrm{d}}+{\mathrm{id}} $波强度甚至出现减弱的情况. 相同之处是其他类型的电子配对对称性的变化趋势几乎一致, 且单重态手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波依然占据优势地位. 同样地, 以$ t_{1}' = t_{2}' = 0.10 $时的平均有效配对关联函数强度为基准, $ t_{1}' = t_{2}' = 0.05 $时单重态的手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波的平均有效配对关联函数强度增加了18.99%; $ t_{1}' = t_{2}' = 0.15 $时平均有效配对关联函数强度减小了93.98%. 通过以上分析, 首先可以预见扭转角度在1.08°附近且逐渐减小时扭角双层石墨烯的超导临界转变温度会有明显的提高, 即更小扭转角度下该系统将会有更稳健的超导电性. 其次, 高电子填充浓度$ \langle n \rangle = 0.933 $下扭转角度大于1.08°时, 该系统仍具有稳健的超导电性; 而对于低电子填充浓度$ \langle n \rangle = 0.893 $下扭转角度大于1.08°时, 由于手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波平均有效配对关联函数强度的急剧减小, 该系统呈现的超导状态将会被破坏.

为进一步验证上述计算结果的可靠性, 将数值模拟进一步扩展到$ L = 6 $的晶格尺度上, 图10展示了平带结构调控下的手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波配对对称性的有效配对关联函数在长程距离$ R\geqslant3 $上的演化曲线. 该图选择的计算参数设置为近邻库仑相互作用强度$ V = 0.0 $, 在位库仑相互作用强度以及电子填充浓度与图6一致. 如图10所示, 两种电子填充浓度下都可以观察到, 通过调节电子跳跃破缺项使能带呈现更为窄而平坦的结构时, 整个长程距离上手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波配对对称性的有效配对关联函数强度明显增强. 此外还注意到, 通过调节电子跳跃破缺项使能带结构呈现较为宽而凸的结构时, 整个长程距离上手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波配对对称性的有效配对关联函数强度呈现减弱趋势. 故该结果证实, 当扭转角度偏离1.08°时, 扭转角度进一步减小有利于超导电性的增强, 而扭转角度的增大会抑制系统的超导电性.

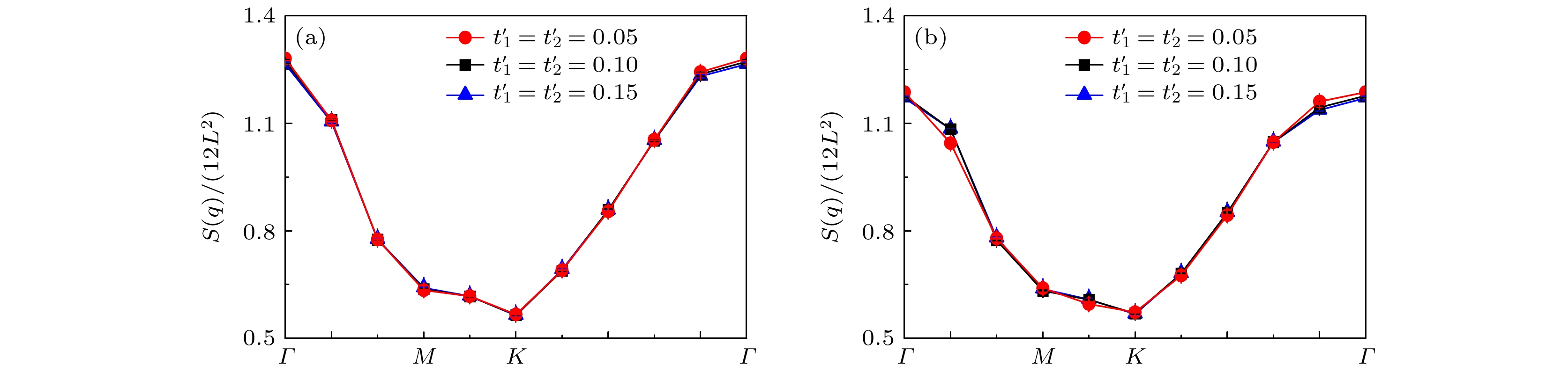
前面的讨论中提到磁性和超导电性密切相关, 接下来重点分析平带调控下磁性和超导电性的关系. 图11显示了自旋结构因子$ S(q) $沿着第一布里渊区高对称线$ \varGamma \to M \to K \to \varGamma $方向的变化曲线. 该图选择的计算参数除了固定近邻库仑相互作用强度$ V = 0.0 $外, 其余的参数与图7一致. 首先基于此结果可以清楚地观察到, 自旋结构因子在Γ点附近具有最大的数值, 这表明系统呈现稳健的反铁磁序, 间接说明扭角双层石墨烯超导体的电子配对形式是单重态的手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波配对对称性. 其次通过调节电子跳跃破缺项来调控扭角双层石墨烯的平带结构过程中, 当电子跳跃破缺项$ t_{1}' = t_{2}' = 0.05 $时, 窄而平坦的能带结构将会诱发自旋结构因子在Γ点附近呈现出增强趋势; 而当电子跳跃破缺项$ t_ {1}' = t_{2}' = 0.15 $时, 宽而凸的能带结构将会导致自旋结构因子在Γ点附近呈现出减弱趋势, 这进一步说明, 平带结构的调控使得系统表现出稳健的反铁磁序是形成手性NN-$ {\mathrm{d}}+{\mathrm{id}} $超导态的一个重要条件.

本文使用量子蒙特卡罗方法研究了扭角双层石墨烯有效两轨道哈伯德模型中的磁性和超导电性的内在关联, 皆是通过数值模拟探究提高扭角双层石墨烯系统超导临界转变温度的方法. 首先, 研究近邻吸引库仑相互作用对超导电性的调控, 来说明电声子耦合对扭角双层石墨烯系统具有重要影响. 数值结果不仅说明扭角双层石墨烯系统的超导态是手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波主导的电子配对形式, 还说明近邻吸引库仑相互作用会极大地诱发手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波的有效配对关联函数在整个长程距离上的增加. 至此证实了近邻吸引库仑相互作用对于提高系统的超导电性具有积极效应.

其次, 研究了扭转角度对超导态的影响, 基于电子跳跃破缺项构建的平带结构来反映不同的扭转角度. 数值模拟结果显示, 扭转角度偏离1.08°且逐渐减小时, 手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波的有效配对关联函数具有较大的增幅, 而扭转角度增大时, 手性NN-${\mathrm{d}}+{\mathrm{id}} $波的有效配对关联函数强度会有减小趋势. 该结果预言了扭角双层石墨烯系统的扭转角度进一步减小时可能具有更高的超导临界转变温度.

最后, 从磁性的角度分析近邻吸引库仑相互作用以及平带结构调控超导电性的原因. 基于自旋结构因子在布里渊区Γ点附近的增强, 说明了反铁磁序的增强是提高体系超导临界转变温度的先决条件, 同时也是形成手性NN-$ {\mathrm{d}}+{\mathrm{id}} $波的有利条件. 通过这一系列的研究, 所得结果不仅有助于更全面地理解扭角双层石墨烯这类强关联系统, 还为寻找更高超导临界转变温度的扭角系统提供了研究方向.

感谢西北师范大学张彦教授和湖北第二师范学院杨辉博士的积极讨论.