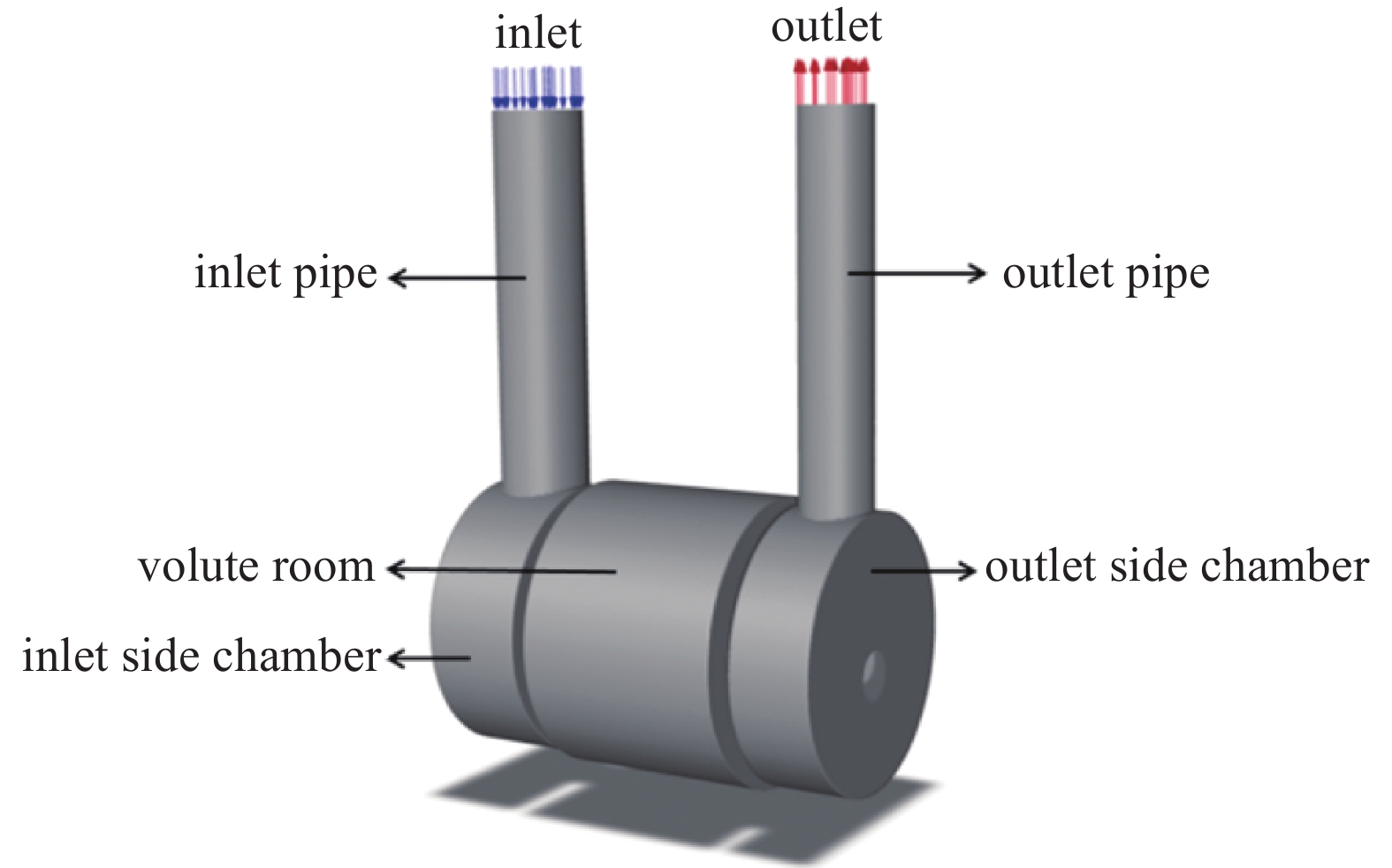
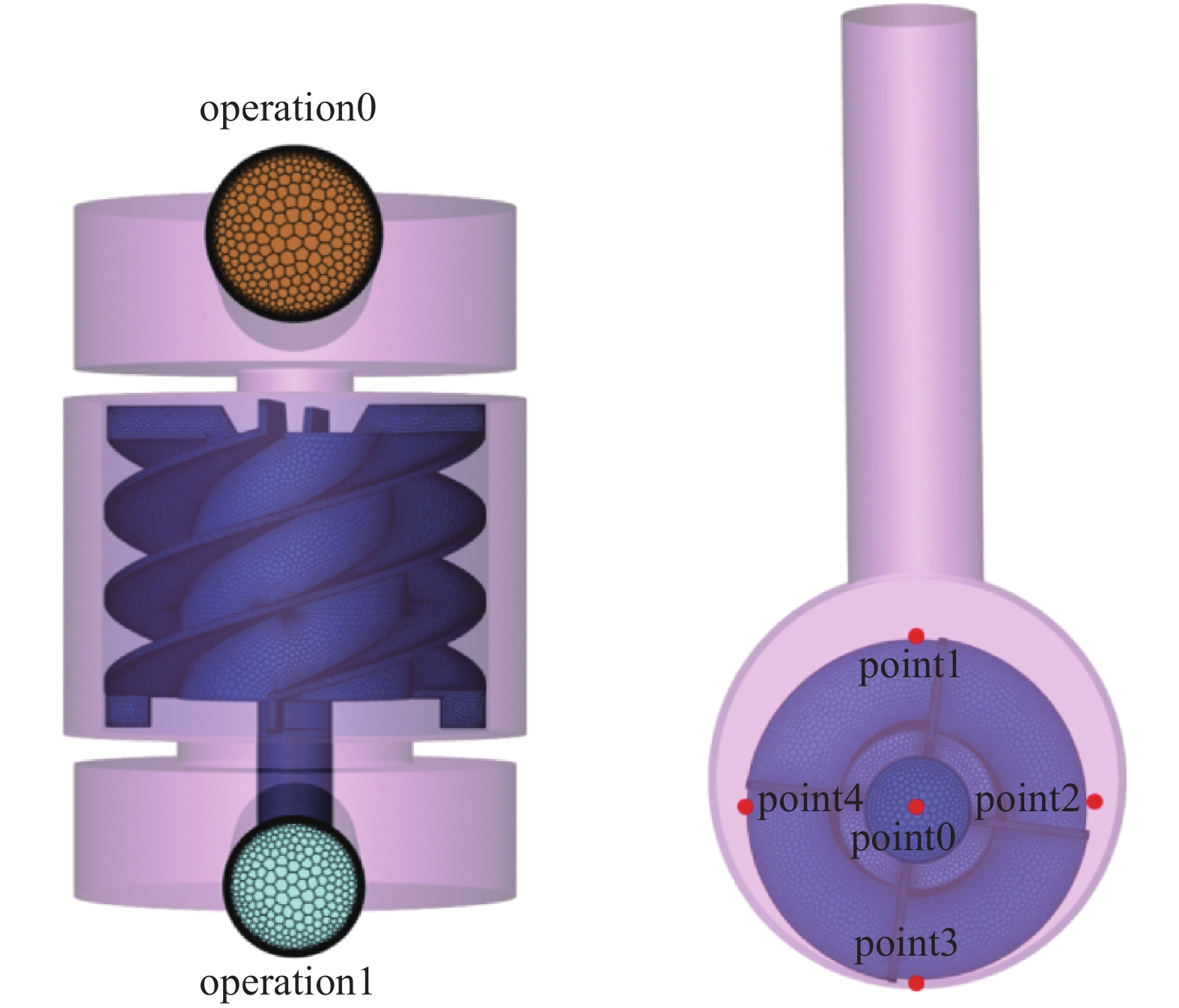
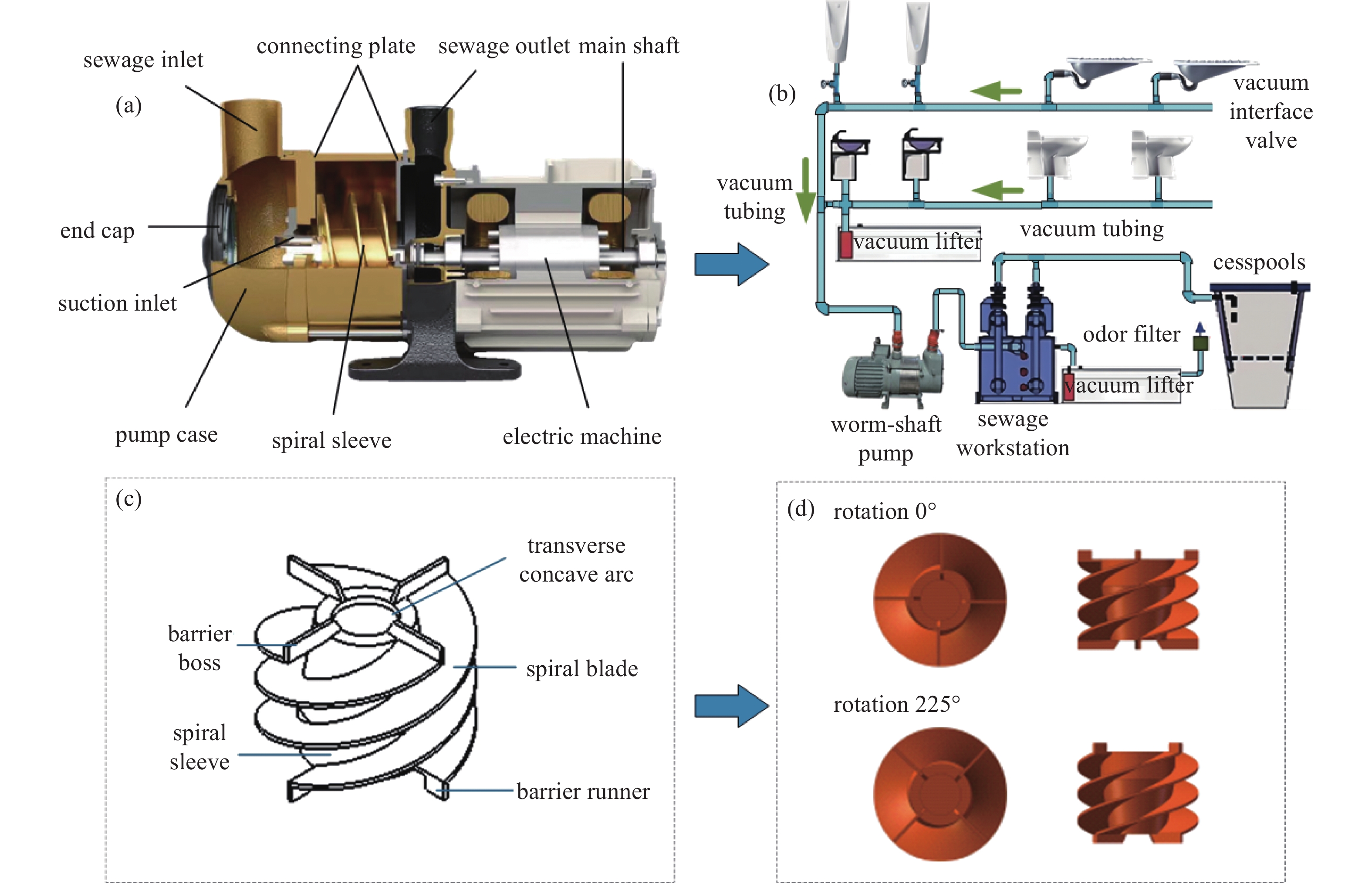
蜗轴泵在船舶真空排污系统中发挥着至关重要的作用。通过操作蜗轴泵，可以在真空管道系统中创建一个低压区域，从而迅速将空气和废水吸入管道。图1（b）中所示的蜗轴泵连接到真空管道和接口阀，能够高效地从多个真空厕所或污水设备中抽取废水。由于航行过程中存在重力和船体倾斜等复杂因素，传统的基于重力的排污系统往往无法满足要求。然而，结合真空排污系统，蜗轴泵能够在负压环境中有效地输送废水，且不受重力影响，从而确保船舶排污系统的稳定运行。其主要过程如下：废水通过真空接口阀进入管道，并在蜗轴泵产生的负压作用下迅速被吸入管道。废水经过真空和除臭过滤器后，进入排污工作站。蜗轴泵的功能模块主要由两部分组成：提供动力的电动机和泵体。电动机包括轴、电机控制器及其他部件，而泵体由叶轮、泵壳、进出口、端盖等部分组成。转子是完成真空抽吸的关键零件部件，其设计包括螺旋叶片、隔板、隔流通道等元件，具体如图1所示。

本文使用的蜗轴泵工作原理为泵轴带动偏心布置的转子旋转，受离心力作用在泵腔内形成与主轴同心的水环。由于转子与泵腔存在偏心距，水环、转子及主轴共同构成周期性变化的密闭容腔。随着转子持续转动，吸气口的空气被叶片逐渐卷入容腔，在螺旋推进作用下沿轴向压缩并输送至排气口，从而实现气体的连续抽吸过程。蜗轴泵的参数流量为12±6 m³/h，转速为2200~3000 r/min，参数如表1所示。

降阶模型旨在将高维复杂系统转化为低维近似系统，在保证近似模型与原始系统之间的误差保持在可接受范围内的前提下，显著降低计算时间和存储空间需求。降阶模型的输入参数为实数标量，可包括材料特性、边界条件或形状参数等物理属性。在实验设计阶段确定输入参数，以便在模拟过程中对参数进行有效的参数化，从而生成稳态模拟结果。此外，为确保各实验点的拓扑结构一致，在处理形状参数时，必须利用变形工具保持数据拓扑结构的等价性，以保证数据一致性与可比性。

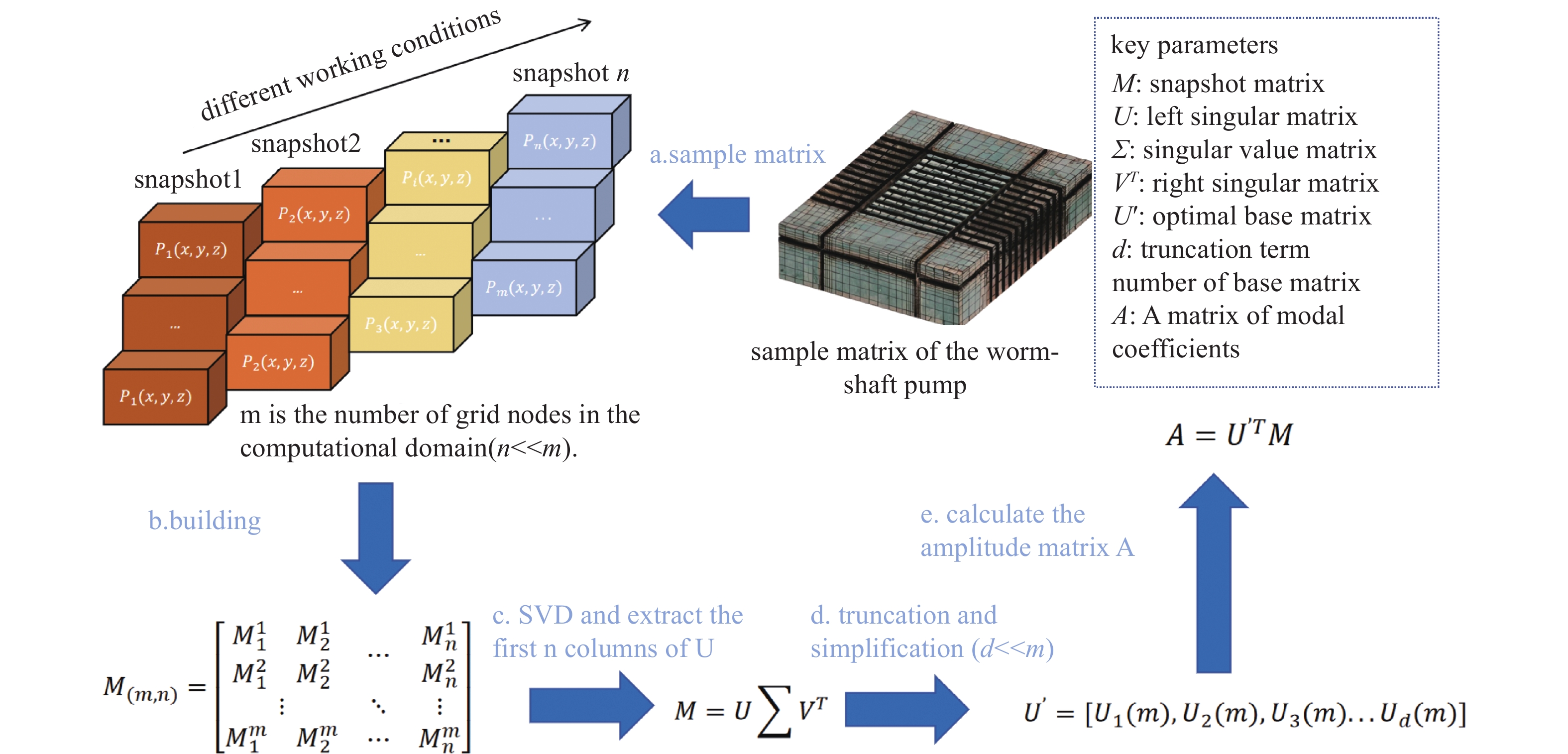
在降阶模型中，传统的POD方法是一种基于物理场的有效降阶方法，通过奇异值分解（SVD）从大量数据中提取主要特征模式，构建正交基，仅需选取所占比重较大的几组特征向量，便可将全样本空间中的数据信息最大程度上还原。因此，POD方法能够在大幅简化计算的同时保留模型的关键特征和准确性。

对原始样本矩阵$ M $进行奇异值分解，如下公式（1）。

$ U $是POD的正交基构$ m \times n $成的矩阵，每一列是一个空间模态，$ V $是参数相关系数矩阵；$ \sum $是一个由矩阵的奇异值组成的对角线矩阵，一般有$ m > n $，所以只有$ n $个非零奇异值。由矩阵运算法则可知，正交基底矩阵$ U $和$ V $中的列向量分别是矩阵$ M{M^T} $和$ {M^T}M $的特征向量，矩阵$ M{M^T} $和$ {M^T}M $的特征值都是矩阵的奇异值的平方，其特征向量反映样本数据$ M $所代表物理场信息量（流场压力和速度）。

通过模型降阶，截断$ U $，保留前$ d $个模态基，形成降维后的响应矩阵$ U' \in {R^{m \times d}} $，再计算模态系数矩阵$ A $，表示每个模态基在不同工况下的权重，矩阵的参数是不同工况下的模态系数$ \alpha $，可以通过公式（2）获得。

获得模态系数后以用更少的基向量来重构流场，降维后的响应如下式（3）所示：

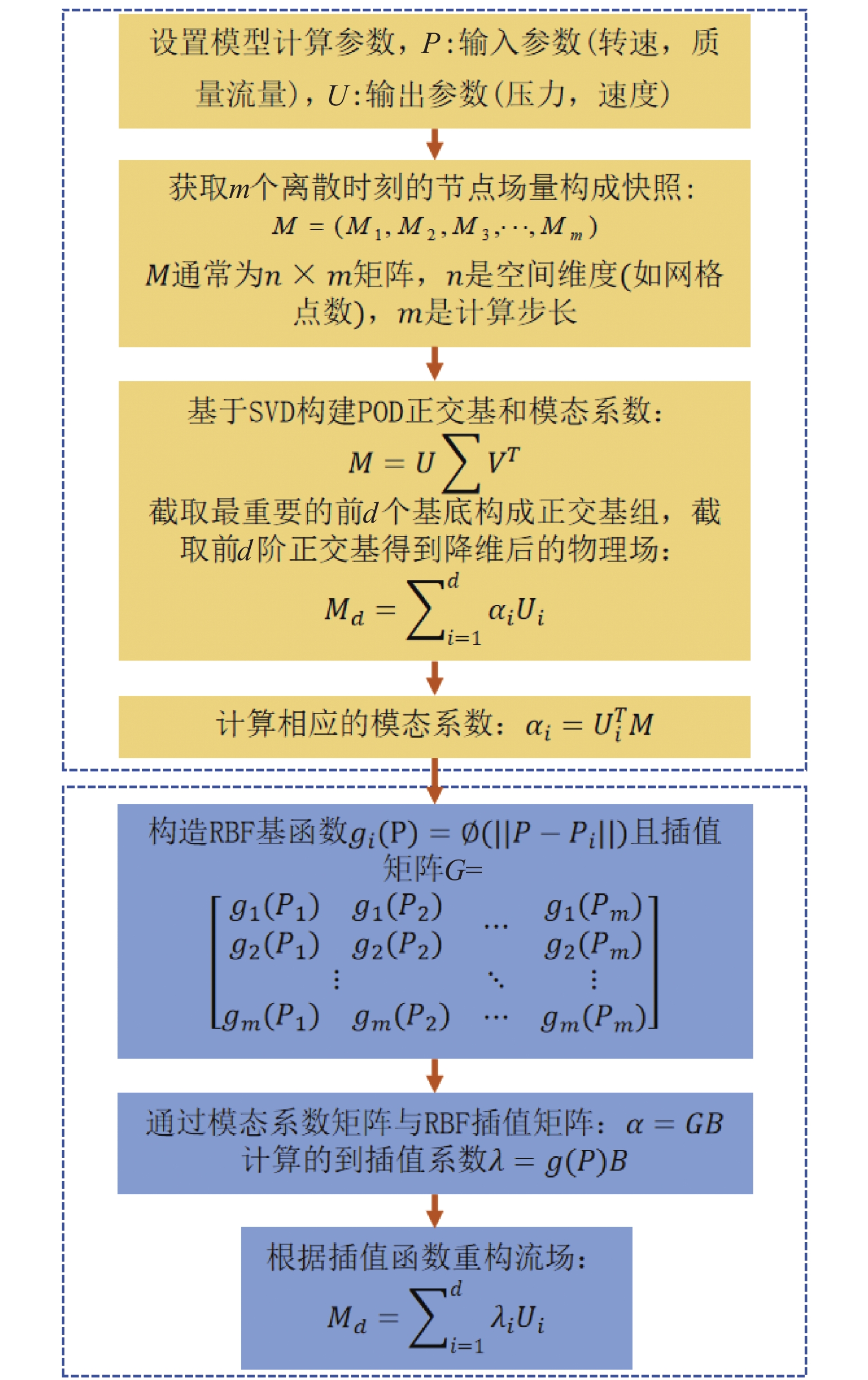
其中，$ {M_d} $是空间位置的流场（例如速度或压力），$ {U_i} $为降阶模态，表示空间上的正交基函数。算法降阶的原理如下图2所示。

POD能够重构降维流场，但是不同工况下的流场还是需要重新计算再降维。为了大幅降低计算开销，预测不同工况下的流场。本文提出一种基于径向基函数插值法（RBF）和POD法相结合的蜗轴泵降阶模型，在处理多维数据时表现出较高的计算效率，在POD降阶的基础上完成流场预测^[25]。

在RBF插值法中，响应面模型可以表示为样本点的加权求和形式，如下公式（4）所示。

其中，$ {\lambda _i} $为待求的插值系数，在降阶模型中是模态系数用于构建预测流场，$ \phi $是径向基函数，本文采用的方式是高斯函数，$ P $是待预测工况的参数，$ {P_i} $为已知样本工况参数。$ ||P - {P_i}|| $表示各样本点到参考点的欧氏距离，$ {g_i} $是RBF插值核函数，插值矩阵$ G $为$ {g_i} $组成的矩阵。

为求解模态系数$ {\lambda _i} $，需要满足插值条件，即在样本点$ {P_i} $处，响应面模型的值与真实函数值一致，如下式（5）所示。

将插值函数$ \lambda $代入条件，和POD正交基预测重构流场，如下式（6）所示。

综上，基于TB-RBF的降阶模型建立流程如图3所示。通过求解线性方程组，方程组$ A $的系数矩阵由径向基函数计算得到。有了预测的模态系数可以通过线性组合POD模态来重构流场^[26]。

TB-RBF与传统POD方法得到的降阶模型不同之处在于，该方法具有高保真度的流场预测功能，通过径向插值法求得插值系数，取代原函数的模态系数计算求解即可求得未出现工况的流场降阶模型^[27]。

本文是基于$ \kappa - \omega $湍流模型来实现稳态仿真，它是基于纳维-斯托克斯（Navier-Stokes)）方程，用于封闭雷诺应力项。附加了描述湍流的湍动能$ \mathrm{\kappa } $和比耗散率$ \omega $的传输方程，在稳态条件下，减去其时间相关项动量方程和湍流模型方程如式（7）所示。

转速$ N $对应的雷诺数$ {R_e} $如式（8）所示：

其中，$ \rho $是流体密度，$ D $是泵的特征长度，$ \mu $是流体动力粘度。转速$ N $的变化影响流场结构，进而影响POD模态分解结果。

通过改变泵的转速$ N $，可以控制雷诺数，从而改变流场的流动特性。这在仿真中是非常重要的，因为不同的雷诺数会影响流场的速度分布、压力分布以及湍流结构。在使用POD降阶模型分析流场快照时，雷诺数影响流场的主要模态特征。不同雷诺数下的流场快照矩阵会有不同的特征模态。这可以通过分析不同雷诺数下的POD模态来展示。

通过降阶后的流场变量，简化$ \kappa - \omega $湍流模型方程的求解。例如，在降阶空间中，速度向量可以表示式（9）所示。

其中，$ {\phi _i}(x) $即降阶基函数。

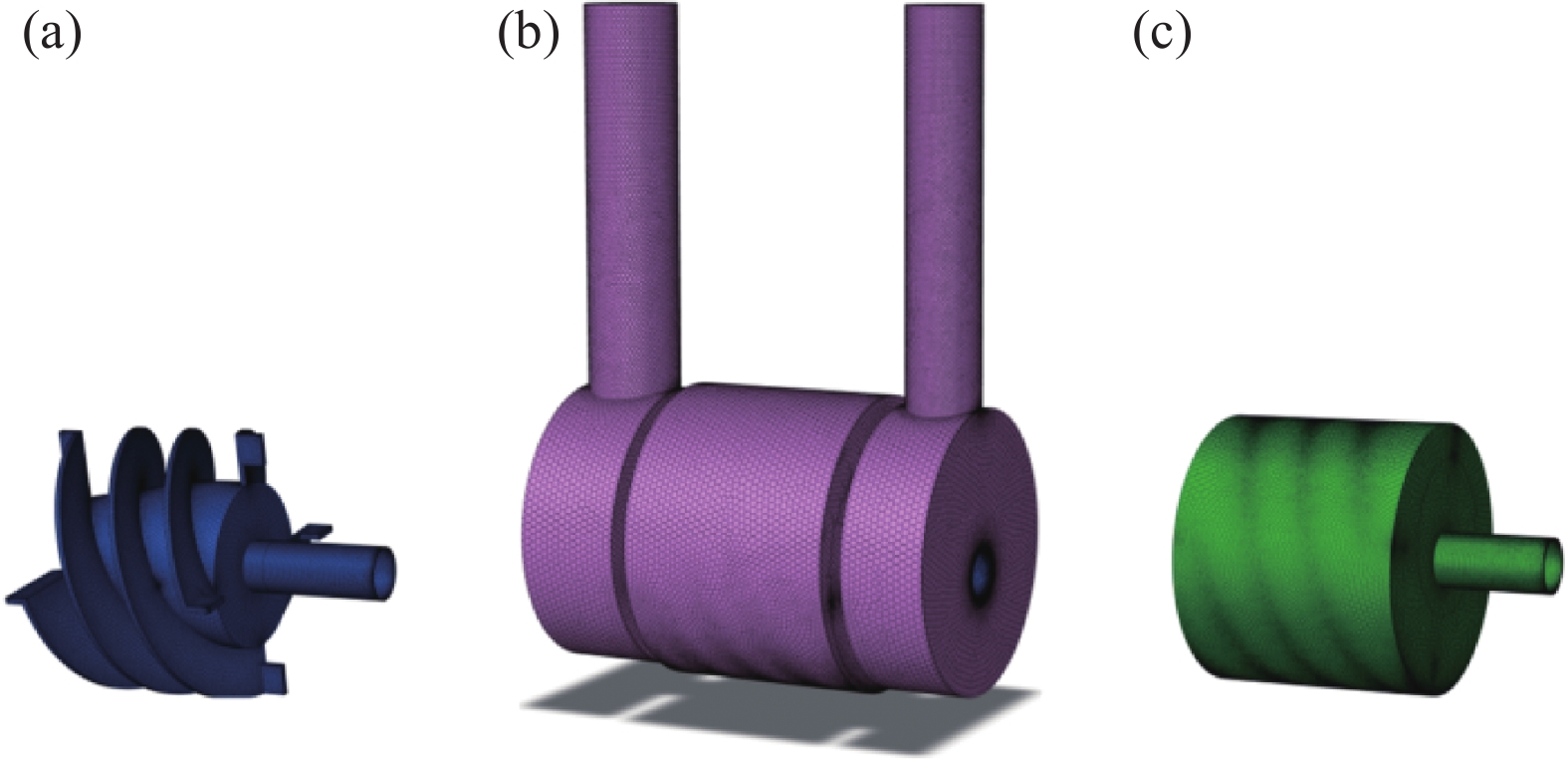
为了验证本文提出的降阶计算方法的有效性，以蜗轴泵水力模型为研究对象。使用图4数值域进行实际流动模拟。根据蜗轴泵的水力模型图，建立反映流道、叶轮等实体边界区域的三维水力模型。基于该三维水力模型，对全流道进行数值模拟。蜗轴泵的主要区域包括进口导向管区、进气侧室、转子蜗壳、出气侧室、出口导向管区组成。

本模型采用了六面体网格，分别对转子、蜗壳和流体域3部分计算域进行网格划分，如图5，总共有147万个单元。由于蜗轴泵等流体机械问题同时涉及运动部件和静止部件，通常将模型划分为多个计算区域，并用一个子接口来关联和分离各个部分，即MRF计算方法。计算采用标准的$ k - \omega $湍流模型，选择质量流量流入口，初始表压为0。湍流规范方法设置为强度和黏度比分别为5%和10。求解方法选择压力−速度耦合的SIMPLEC格式，在空间离散上采用基于最小二乘网格的梯度、二阶压力、二阶迎风动量、比耗散率和湍动能。

模型精度验证后，在Twin Builder中封装使用，本文实验在降阶模型中插入监测点，如图6所示，来获取仿真时蜗轴泵内流特性信息，监测速度和压力数据，用于后续分析。

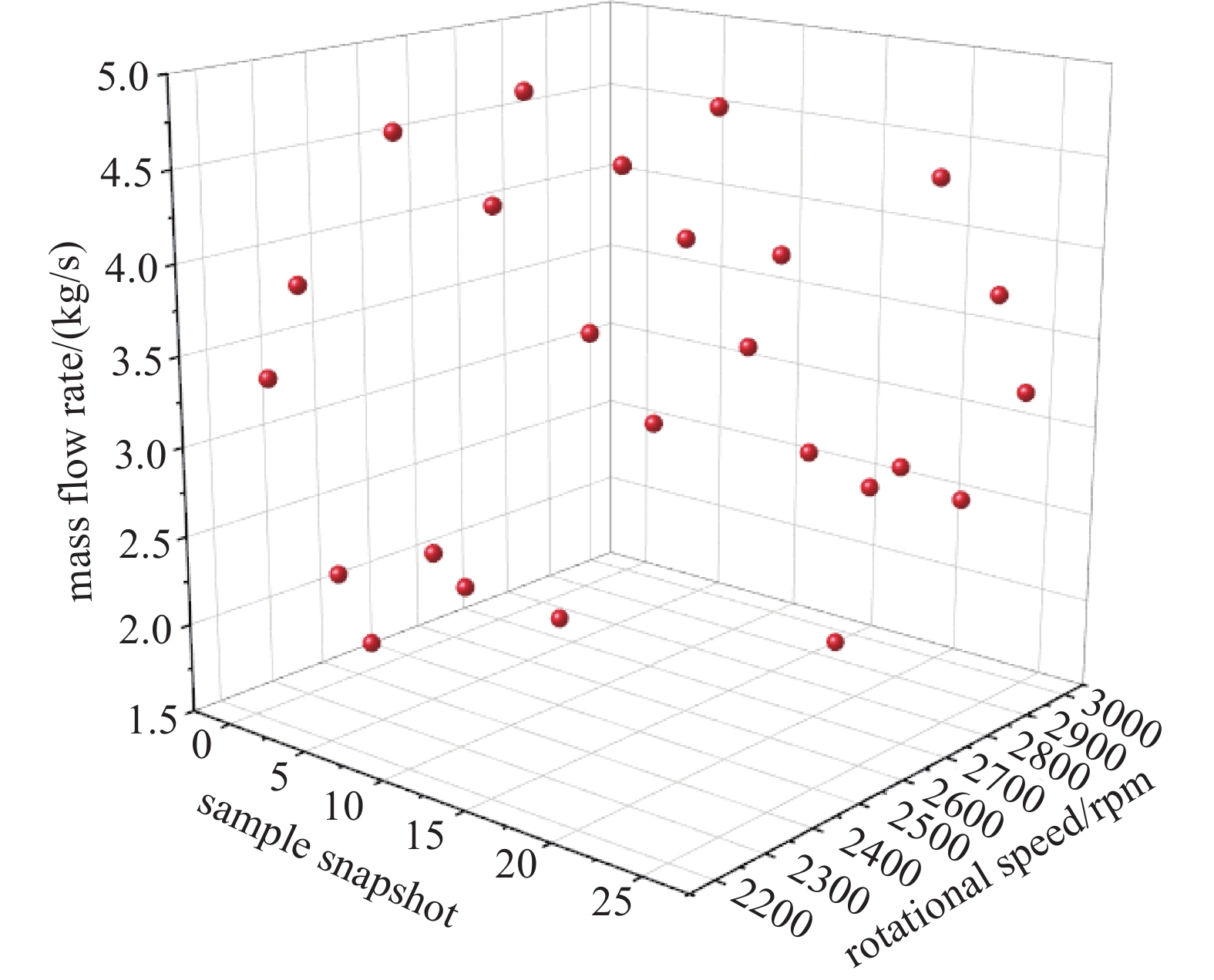
本文以工况转速和进口质量流量速率为输入参数，以设备各部件压力和速度场为输出参数组成多组工况条件下的样本空间集。采用拉丁超立方抽样方法在蜗轴泵额定工况中抽取25组样本点作为输入数据，保证样本点在每个维度上均匀分布，提高样本的代表性。抽取的实验样本设计点如图7所示。

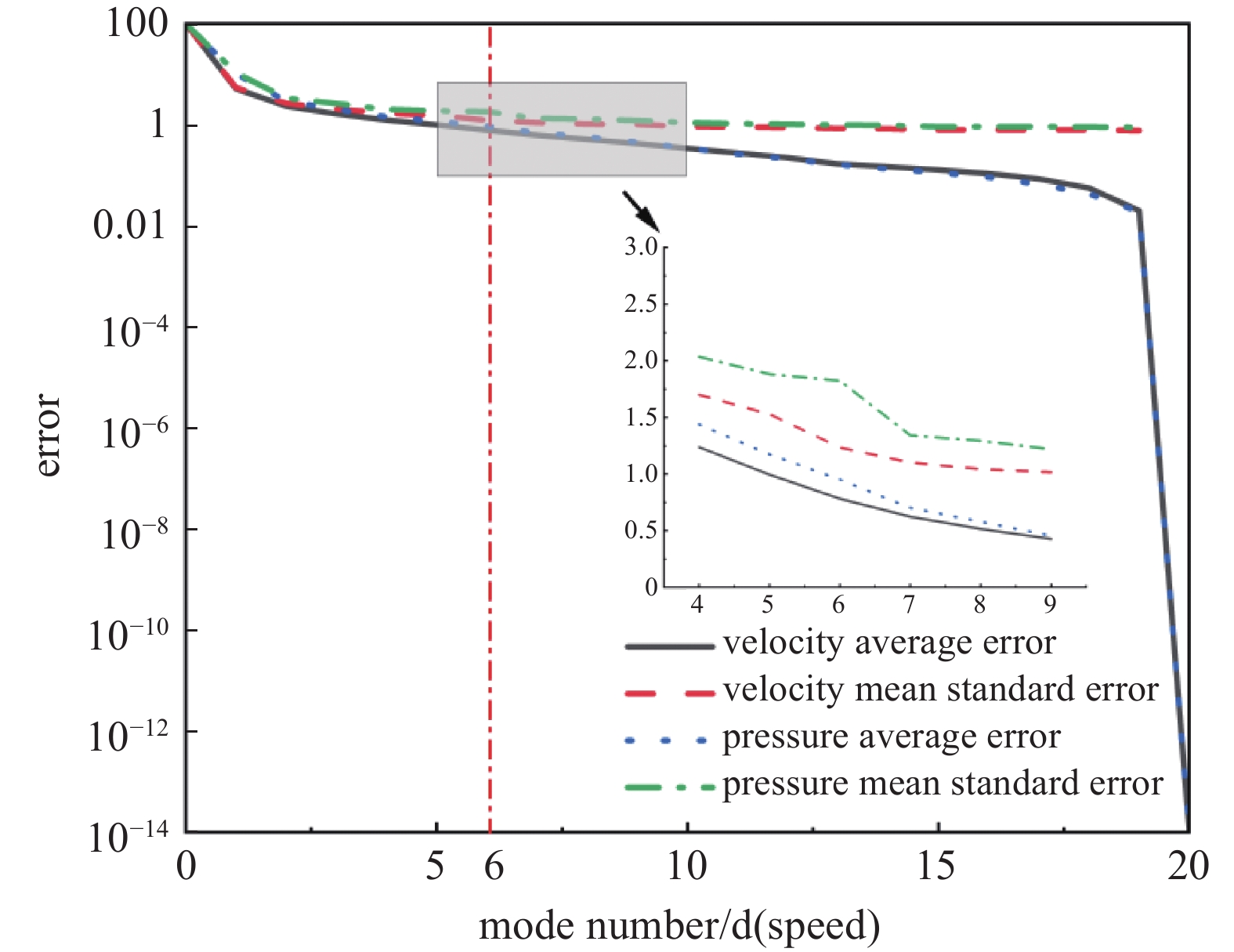
根据上图25组样本工况使用Fluent仿真得到流场模型数据库，随机选取其中80%工况数据采用POD方法构建速度场和压力场降阶模型，剩余的20%用于验证。对于较小的模式数，投影误差基本稳定，表明主要模式已有效捕捉流场的主导特征，既能准确表示学习集，又具备较强的泛化能力。当模式数增加，学习集与外部快照的误差差值逐渐扩大，新增高阶模式更倾向于拟合学习集的局部特征而非全局特性。通过选取误差差值显著增大的分离点作为最优模式数，可在保证精度的同时避免过拟合，蜗轴泵的最优模式数基于此方法确定。

通过Twin Builder ROM工具来帮助选择最佳模式数，如图8所示，当阶数为6时，降阶模型平均投影误差已降至0.782%，平均标准投影误差也已经趋近收敛，因此该模式数满足构建POD降阶模型的误差要求，在此POD基础上在再进行RBF插值，完成TB-RBF降阶模型的构建。

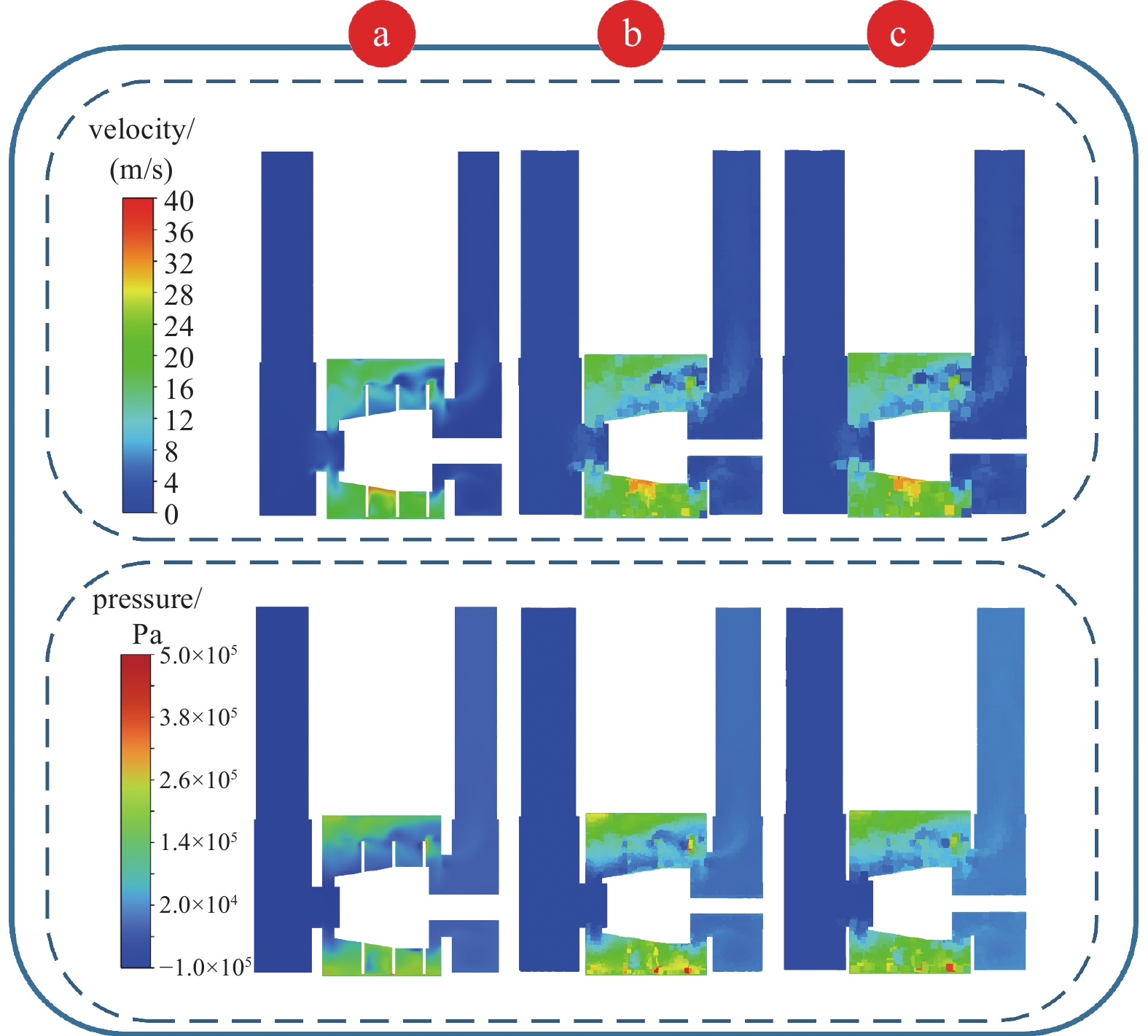
相同工况下CFD全阶模型、POD法、TB-RBF法三者云图呈现出相似的流场特性。速度场分布方面，CFD全阶模型能够清晰地展示流场的细节特征，如蜗轴泵工作高速区域和涡流结构。POD模型在整体趋势上与CFD结果较为一致，但局部细节的分辨率有所降低。相比之下，TB-RBF模型的结果更为平滑，部分细节进一步简化，但仍然能保持整体流场分布的准确性。在压力场分布方面，CFD在高压和低压区域的分布上有很高的精度。POD模型在捕捉压力场整体变化趋势方面表现良好，但在高梯度区域细节的保留能力有所下降。TB-RBF模型则表现出更明显的平滑化效果，对高梯度区域的复杂分布有所弱化。三者流场对比如下图所示9所示。

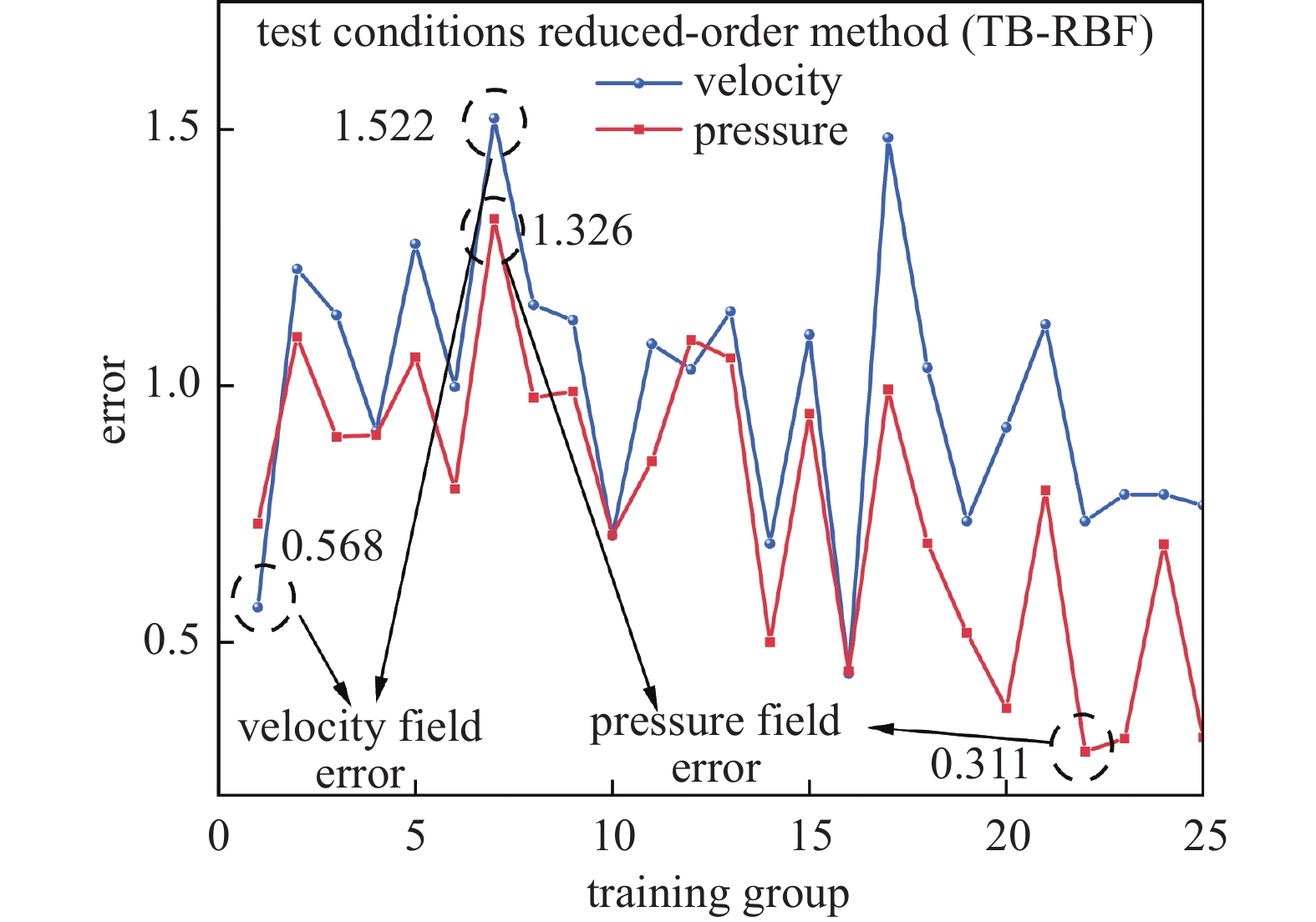
降阶模型的误差来源已经在上文讨论过。本文通过计算25组训练工况生成的降阶模型测试结果的速度场误差和压力场误差。如图10所示为TB-RBF方法重构的压力场和速度场精度表现，六阶模式系数下重建的流场中速度场最大误差为1.36%，压力场最大误差为1.64%，同时随着训练组数的增加平均误差也开始相应的减少，证实了TB-RBF法构建降阶模型的的可靠性。

图11展示蜗轴泵中间段速度场和压力场在POD降阶模型与TB-RBF降阶模型下的流场表现，以及两者之间的相对误差分布。选取误差最小和最大的工况进行验证，其中压力场误差最小的工况为进口流量3.75 kg/s、转速2940 r/min，误差最大的工况为2.6 kg/s、转速2915 r/min；速度场误差最小的工况为4.5 kg/s、转速2560 r/min，误差最大的工况同样为2.6 kg/s、转速2915 r/min。压力场的预测精度整体高于速度场，其误差主要集中于转子下方流线密集区域。相比之下，速度场的误差在复杂流动区域（如涡流和剪切层）表现更为显著，表明速度场包含更多高频特征，对降阶模型的要求更高。总体而言，降阶模型在接近设计工况下表现最佳，而在低流量、高复杂度的非设计工况下误差显著增加。

TB-RBF降阶模型在计算效率上显著优于全阶模型，可有效满足数字孪生应用中对流场实时仿真的需求，仿真时间对比如表2所示，使用Fluent进行一个工况全阶模型仿真需要4673 s，使用TB-RBF降阶模型仅需0.7 s，计算时间缩短了6676倍。基于该降阶模型构建的仿真工具，可进一步发展为在线部署的数字孪生系统，用于实时流场预测与监控。

综上，TB-RBF降阶方法在蜗轴泵性能预测中不同阶段具有不同的优势：设计阶段时间充裕，模型可深入分析各工况下的流场特性，为优化设计提供支持；而在实时性能预测中，则需在快速计算与精度之间取得平衡，以确保准确捕捉流场动态特性并及时预测其发展趋势。这种灵活的适应性使降阶模型成为数字孪生技术中流体仿真的重要工具。

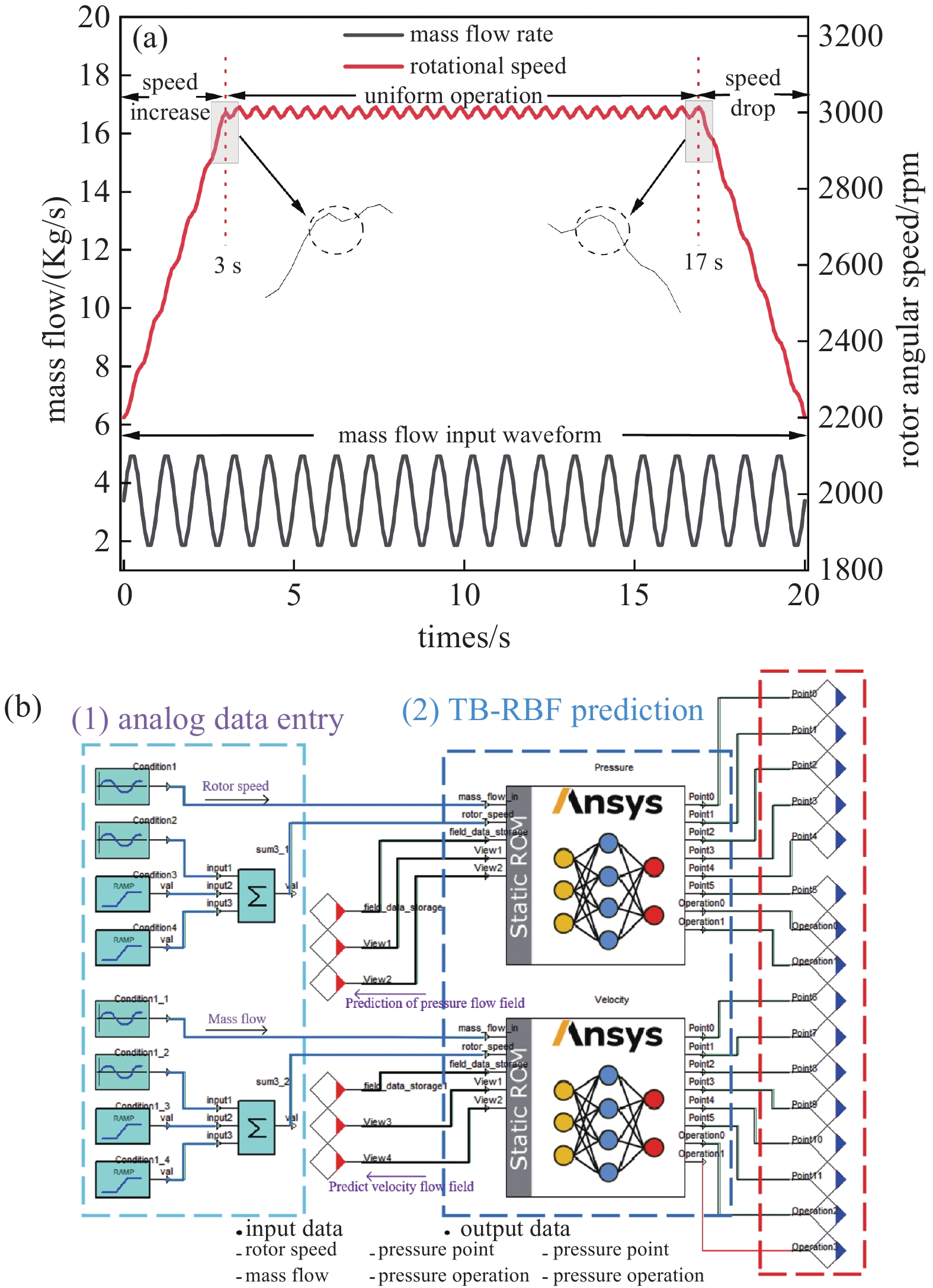
本文数字孪生仿真系统采用TB-RBF法构建的降阶模型封装，在离线模型中输入仿真工况来验证该仿真系统。采用余弦函数模拟质量流量输入，使其在1.6 kg/s−5 kg/s波动，采用转速调节方式模拟转速输入，使转速从2200 r/min上升至3000 r/min后平稳运行一段时间再降至2200 r/min。具体模拟输入工况如下图12（a）所示，该配置便于向降阶模型提供工况信息。此外，系统配置还包括创建压力和速度流场云图，以及输出特定监测点的压力和速度运行状况。该综合仿真系统如图12（b）所示。

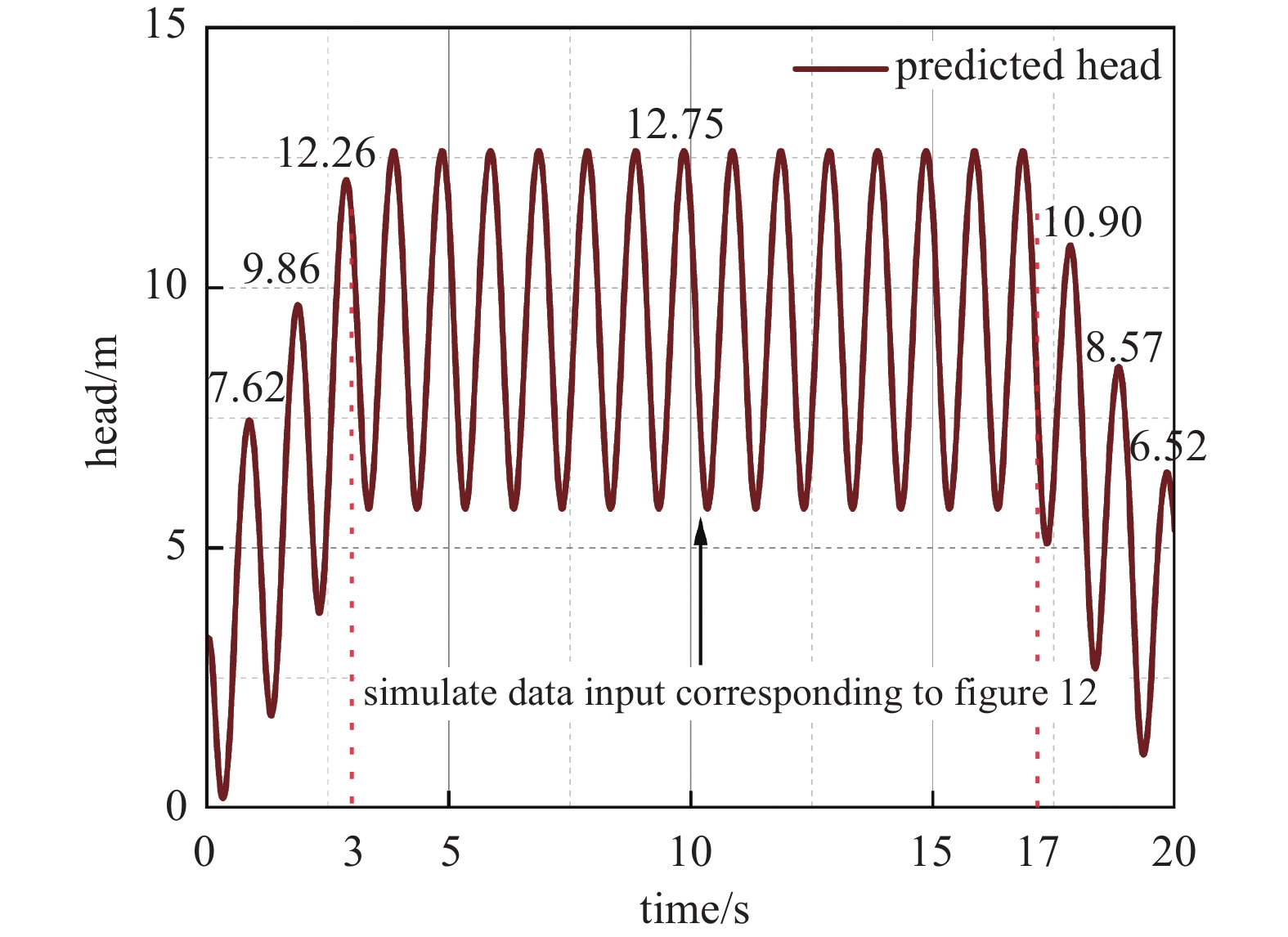
结果显示，蜗轴泵的扬程与进出口压力有关，其性能可以由扬程曲线显示，如图13所示，在第1 s到第3 s和第17 s到第20 s出现显著波动，这些波动幅度与系统输入运行工况的变化高度相关。

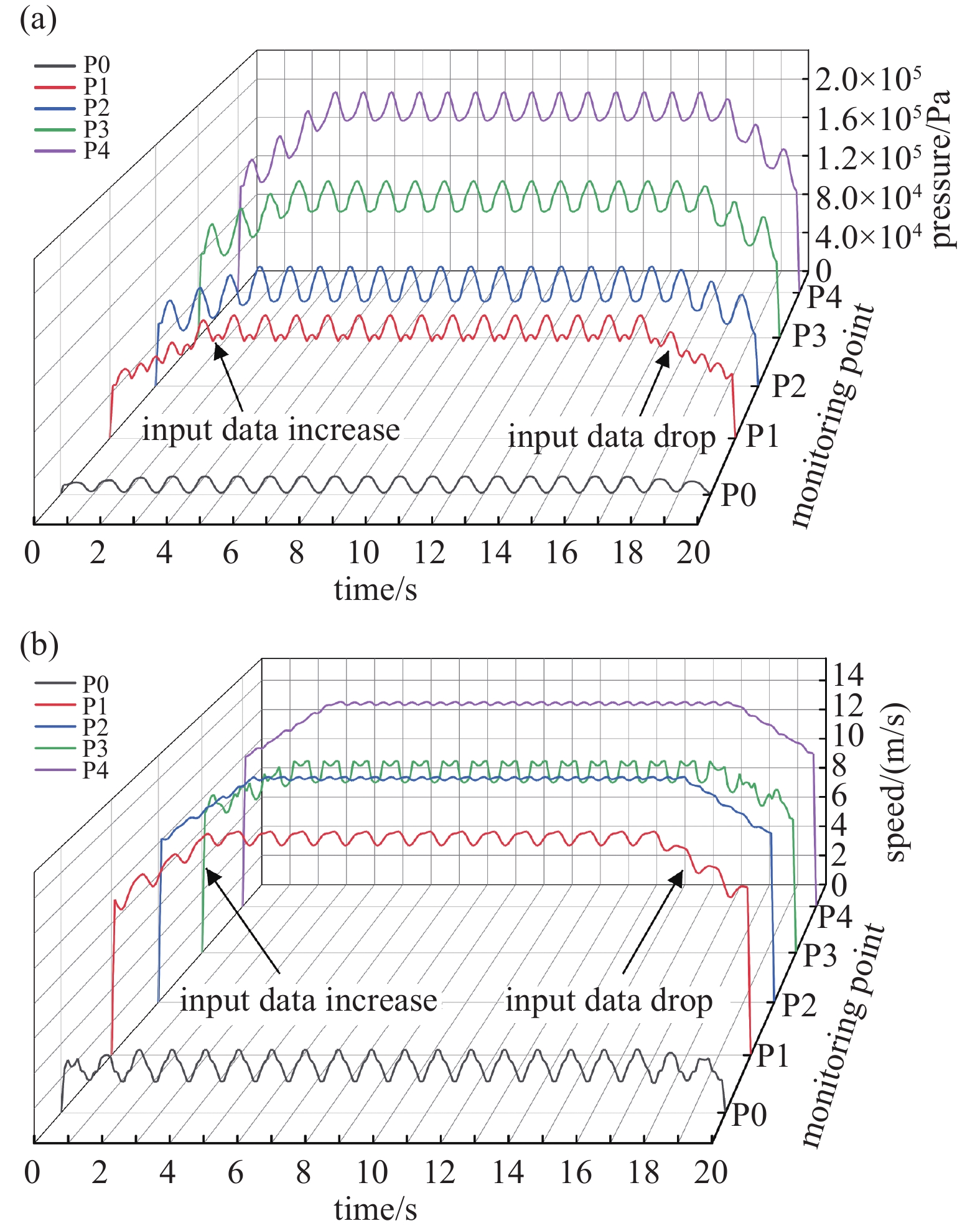
监测蜗壳内压力的时域变化，如图14（a）所示，可以观察到压力波动与叶轮转动呈现一致的周期性变化。沿P0到P4方向，平均压力逐渐升高，反映出压力沿流动方向的积累规律。在偏心位置处，压力达到最大值（约1.5×10⁵ Pa），该区域因流体动压转化为静压而产生了显著的压力提升。说明本文蜗轴泵设计在流体压力调节中具有明确的空间分布特性。

在流速变化的时域分布中，如图14（b）所示，转子区域的流体速度显著高于进出口区域，其中主要监测点的流速平均约为11.9 m/s，次监测点约为2.6 m/s。转子区域的高流速反映了其能量集中的特点。尽管选定监测点未处于速度峰值区域，但能够较好地反映流场内的速度分布趋势，验证了仿真模型与实际预期的一致性。

这些结果表明，蜗轴泵的流体动力特性在空间和时间分布上均符合设计要求，但部分非稳态现象仍需进一步优化。

总的来说，蜗轴泵内压力随位置呈递增趋势，偏心区域压力最高；扬程在特定时刻出现显著波动，反映了蜗轴泵运行特性；转子区域流体速度显著高于其他区域，符合预期的设计要求。

为了增加本文方法的应用价值，对蜗轴泵扬程预测实验，基于蜗轴泵船用生活污水真空收集系统试验台进行测试，试验台由控制箱、蜗轴泵、真空罐、流量计、压力计等组成。实验装置如下图15所示。

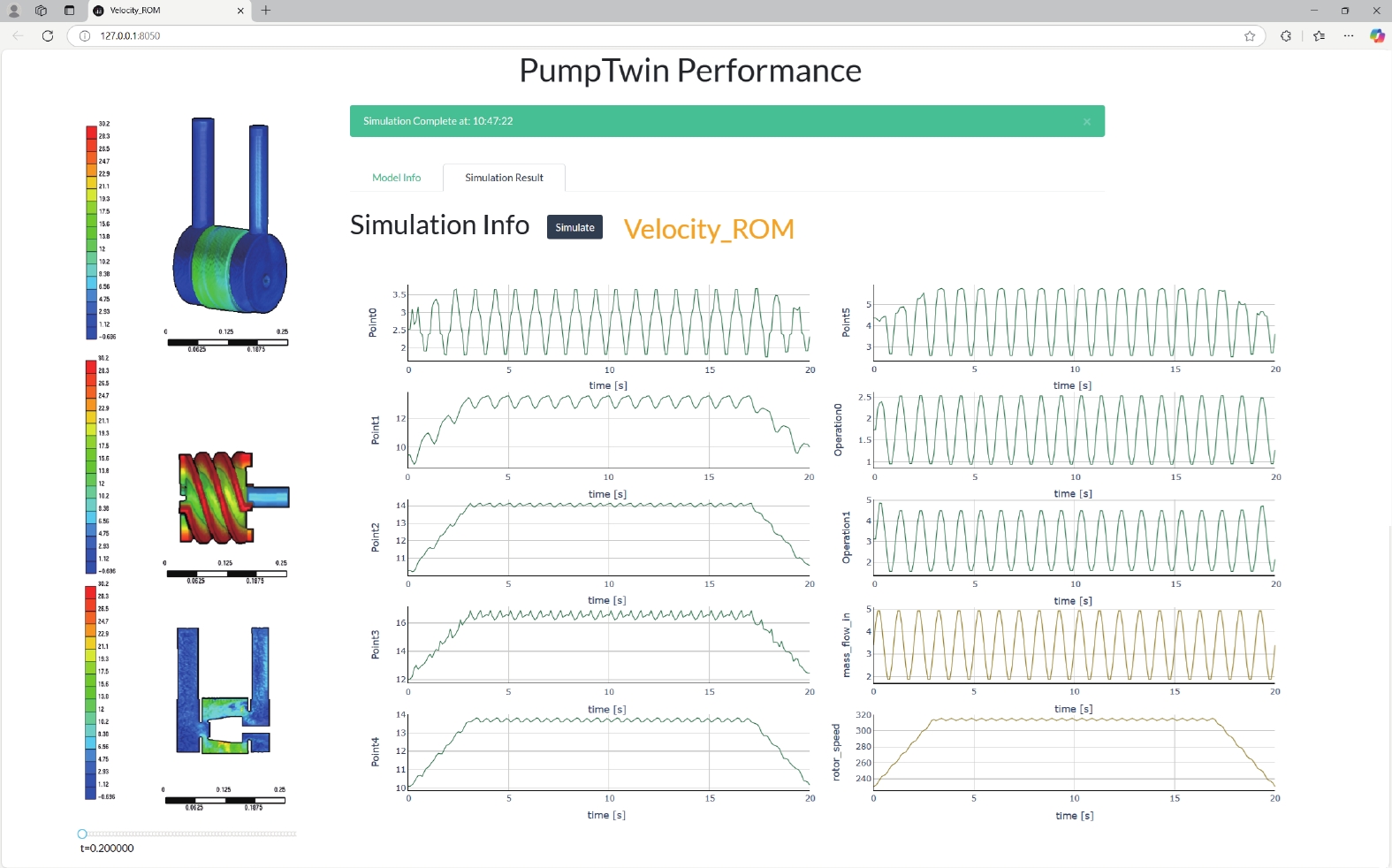
在数字孪生系统应用实验中将TB-RBF模型封装为在线模型，输入试验台实际蜗轴泵流量、转速工况参数后，系统依托降阶算法快速解算，以动态曲线直观呈现监测点压力、速度等数据，同时通过流场云图可视化展示内部流场压力分布、流速变化，实现多物理场参数的实时映射，对蜗轴泵进行高效的性能预测，图16为蜗轴泵数字孪生应用界面。

本文选取实验台3组共27个实际运行工况，通过CFD软件的实际数值模拟结果与TB-RBF降阶模型的扬程计算结果进行对比，并通过误差验证降阶模型的准确性和可用性。主要得到的结果是通过流量扬程外特性曲线来表明误差。表3为预测的CFD数值模拟蜗轴泵扬程与降阶模型计算的工况点，包含了不同质量流率和速度的变化。

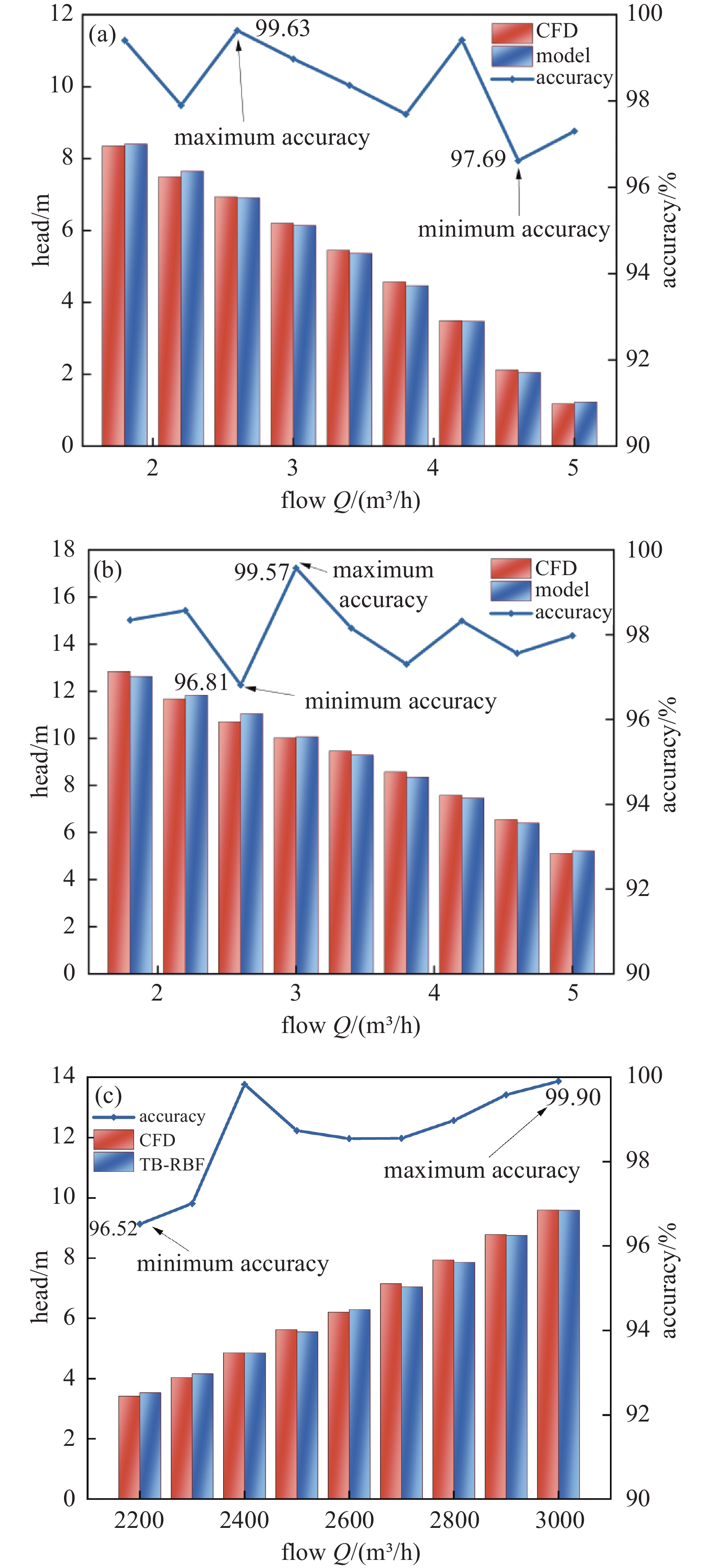
从图17中可以看出，降阶模型预测值和CFD仿真值均符合如下规律：旋转速度保持不变，质量流量提升，出口流量变大，会导致扬程降低；质量流率保持不变，转子旋转速度增大，会导致泵扬程上升。在三个测试组中，降阶模型的准确率最低分别出现在工况：质量流量4.6 kg/s，转速2500 r/min；质量流量2.6 kg/s，转速3000 r/min；质量流量3.3 kg/s，转速2200 r/min。准确率最高出现在工况：质量流量2.6 kg/s，转速2500 r/min；质量流量3 kg/s，转速3000 r/min；质量流量3.3 kg/s，转速2400 r/min。其余各工况的降阶模型准确率均不低于96.5%。由此，可说明本文所提降阶算法具有准确的预测能力。

为实现蜗轴泵内流场的快速计算，本文将Twin Builder降阶模型与径向插值法相结合，构建了一种高保真度流体装备预测模型，旨在支持数字孪生应用。具体结论如下：

（1）本文提出的TB-RBF孪生模型成功地将Twin Builder降阶模型与径向插值法（RBF）相结合，创建了一种新的高保真度的蜗轴泵性能预测方式。该模型能够准确地预测未知工况的数据值，与传统POD法相比流场表现出更明显的平滑化效果。

（2）本研究所提出的降阶模型在计算效率上有了显著提升，每个测试工况的生成时间缩短至仅0.7 s，同时保持了高精度。此外，通过与全阶模型以及传统POD法的对比，进一步证明了本研究方法在计算效率和预测准确性方面的优越性。

（3）搭建基于数字孪生的蜗轴泵性能预测平台，实现了快速性能预测和流场云图可视化，与全阶模型的仿真结果高度一致，在27组验证工况下的准确率均超过了96.5%。本研究已封装为在线预测平台，可直接集成至船舶真空排污系统控制终端，实现扬程与流场的实时监控，为故障预警与能效优化提供支持。