-
离子与物质相互作用的电荷转移过程是原子物理学的重要基础课题, 影响离子的电荷态演化[1–3]和能量损失[4–6], 相关研究在加速器技术、天体物理、材料科学和生物医学等领域具有重要的应用价值. 在重离子加速器装置中, 通常利用离子束穿过气体或固体靶产生高电荷态离子, 提高离子束的加速效率[7]. 离子-原子碰撞中的电荷交换过程是许多天体环境中X射线发射的重要机制, 对于解释天文观测谱[8], 反推日球层边界的结构和太阳风动态[9], 揭示恒星演化、行星大气逃逸及宇宙线传播机制至关重要. 同时, 离子在物质中的电荷态是决定离子能量弛豫过程的关键参数(
$ - \dfrac{{{\text{d}}E}}{{{\text{d}}x}} \propto \dfrac{{Z_{{\text{eff}}}^{2}}}{{{v^2}}} \times L $ ), 与离子束驱动产生高能量密度物质、离子束精准放射治疗、材料辐照损伤及抗辐照加固研究息息相关[10–14].过去的几十年里国内外发展了诸多理论模型或程序来预测离子在物质中的电荷态演化. 当入射离子速度远高于靶电子运动速度时, 直接电离机制起主导作用, 玻尔剥离准则[15]和大量半经验模 型[16–25]预测的离子有效电荷态呈现良好的一致性. 这些半经验模型可以快速估算离子的平均电荷态, 在预测离子与物质相互作用中的电荷态演化及能量沉积等方面发挥着重要作用. 然而, 当离子能量降至百keV/u量级(对应入射离子速度接近电子速度), 电子俘获、辐射退激或俄歇退激以及靶原子直接电离等多通道竞争效应显著增强, 导致现有理论模型对有效电荷态的预测偏离实验观测值[26,27], 亟需高精度实验数据, 为相关理论模型提供检验.
1950年, Lassen[28]首次观察到离子与固体碳箔作用后的出射电荷明显高于从气体靶中出射的离子电荷. Bohr和Lindhard[29]对此现象进行了解释: 当离子穿过固体靶时, 高电子密度和频繁碰撞使得离子碰撞时间尺度超过离子激发态寿命, 电子激发态退激前即被剥离, 电子俘获速率降低、库仑电离速率升高, 最终导致离子电荷态升高; 而在低密度的气体物质中, 入射离子电子壳层的碰撞激发会因自发辐射跃迁迅速衰减至基态, 电离过程主要从基态发生, 产生的离子电荷态较低, 即靶密度效应[30,31]. 这一解释后来在GSI加速器装置上得到了验证[7]. 但是, 该实验主要针对高能离子, 而靶密度效应与离子速度、靶原子序数以及靶密度密切相关, 针对低能区离子在介质中的靶密度效应和电荷交换研究仍未得到充分的实验验证. 目前离子在物质中的电荷交换实验和理论研究主要集中于固体靶和气体靶, 针对泡沫材料的相关研究比较少, 确定低能离子在泡沫中的电荷演化实验数据更是缺乏. 自1931年Kistler[32]用硅酸钠(sodium silicate)制成气凝胶以来, 这种凝胶类或泡沫状物质已经有了很大的发展. 该泡沫材料可以在百摄氏度下保持稳定, 被加热时也主要在孔隙内部发生膨胀, 对靶的整体结构影响较小, 已被广泛应用于激光等离子体实验[33–36].
本文基于星光III强激光装置开展了激光加速中低能(1.5—4.5 MeV)碳离子在醋酸三纤维素(tri-cellulose acetate, TCA) C9H16O8泡沫中的平衡电荷态分布实验测量. 理论上基于半经验公式和求解速率方程, 考虑了电离、俘获、激发和退激等电荷交换过程, 获得了离子的平均平衡电荷态. 实验结果与理论对比发现, 只有同时考虑了电离、俘获、激发和退激等过程的速率方程结果与实验符合较好. 采用气体靶截面数据求解速率方程的理论值低估了实验值, 原因在于泡沫靶中固态纤维丝引起的靶密度效应导致离子电荷态升高. 当离子能量高于3 MeV时, 实验值与采用了固态靶截面数据的速率方程理论预期一致; 但在低能区出现明显偏差, 原因在于当入射能量小于3 MeV时, 离子激发态寿命小于碰撞时间尺度, 激发态电子在发生第2次碰撞之前退激发回到基态, 靶密度效应减弱, 平均电荷态降低.
-
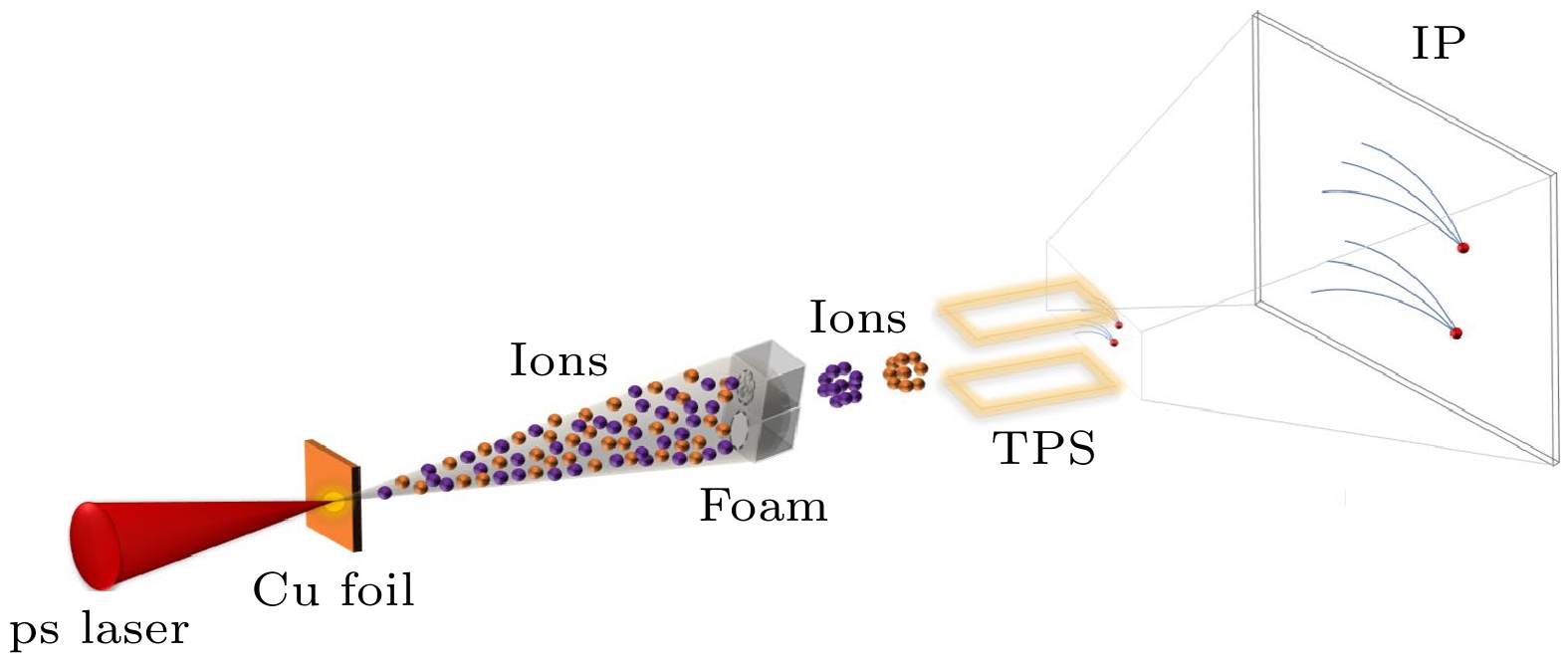
基于中国工程物理研究院激光聚变研究中心的星光III强激光装置, 开展电荷交换实验的实验装置布局如图1所示. 皮秒激光脉冲(能量130 J, 脉宽843 fs)作用在10 μm厚的平面铜箔上, 由于铜箔表面通常附有碳氢化合物和水蒸气组成的纳米厚污染层, 激光与铜箔作用时, 激光在靶前表面产生的大量高能电子穿过靶后时形成鞘层场, 将污染层中的碳氢原子电离并加速, 即靶法向鞘场加速(target normal sheath acceleration, TNSA), 从而获得能量范围较宽的质子束和碳离子束[37–41], 本文仅讨论碳离子. 碳离子束经过1.15 cm后与泡沫靶发生相互作用, 离子能谱由汤姆孙谱仪(Thomson parabola spectrometer, TPS)结合Fuji成像板(image plate, IP)测量.
实验中使用上下对称的双孔靶设计, 上孔为泡沫靶, 下孔为空通孔, 汤姆孙谱仪为双通道的汤姆孙谱仪, 激光加速碳离子同时穿过泡沫靶和空靶, 进入双通道汤姆孙谱仪. 这种方式可以单发同步测得激光加速离子束与泡沫靶作用前后的能谱分布. 实验中的泡沫靶由体密度为2 mg/cm3, 厚度为1 mm的C9H16O8泡沫组成, 该泡沫具有多孔结构, 孔径直径大多数小于2 μm, 纤维丝半径大多在10—50 nm之间. 这种泡沫材料和靶的设计已经在质子能量损失[34]、实验室天体物理[35]和离子在等离子体中的电荷交换[42]等实验中广泛使用. 该实验设计方案已经成功应用于5—10 MeV碳离子在泡沫中的靶密度效应研究[43], 本文只讨论低能区的平均电荷态结果.
-
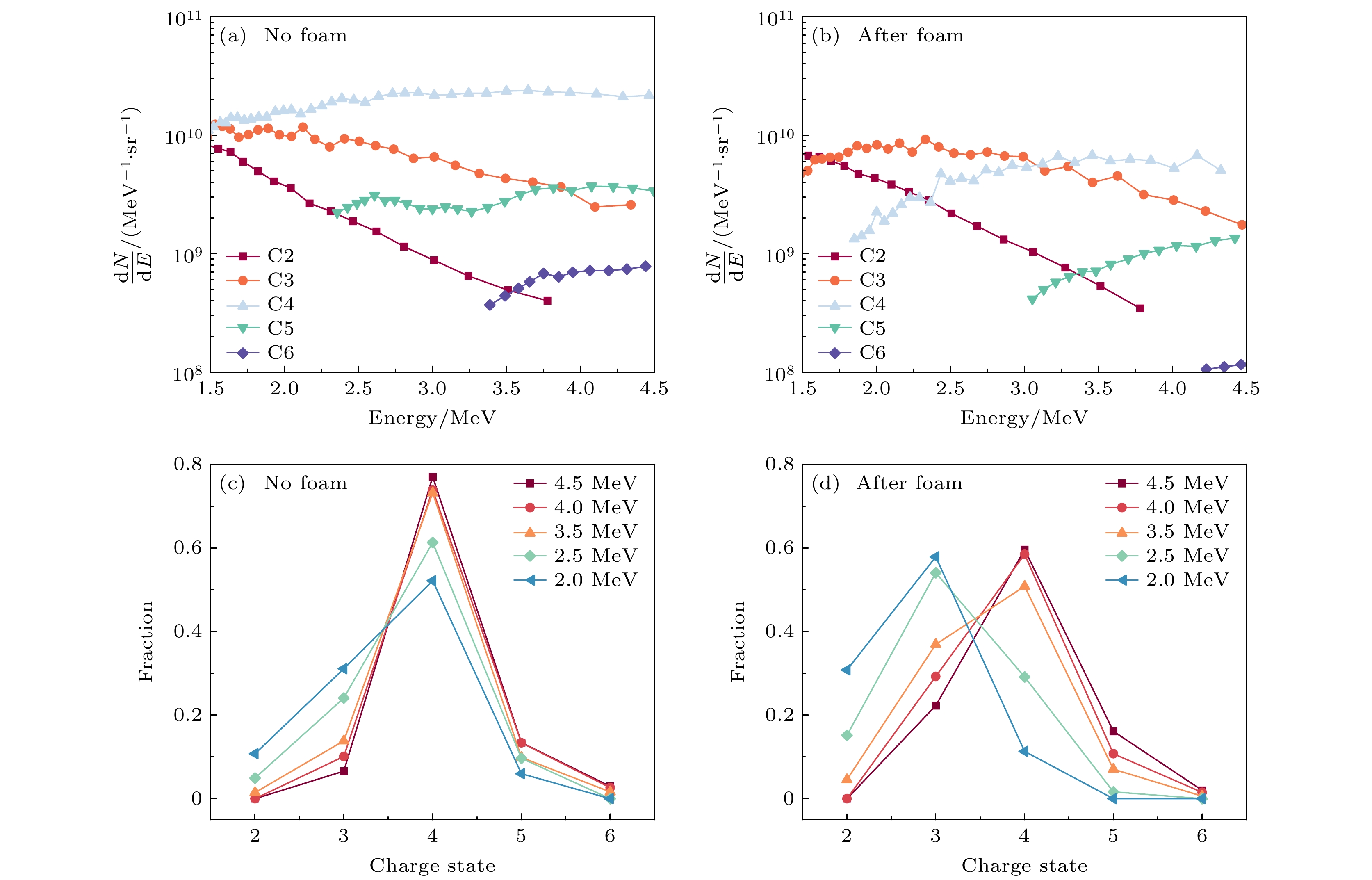
碳离子束穿过空靶和泡沫靶后测得的能谱分布如图2(a), (b)所示, 穿过空靶后的碳离子, 即激光加速产生的初始碳离子包含C6+, C5+, C4+, C3+, C2+多种类离子, 其中C4+离子数目最多. 穿过泡沫靶后的碳离子数目整体降低, 能谱发生明显移动. 离子束穿过空靶和泡沫靶后的电荷分布如图2(c), (d)所示, 其中, 激光TNSA机制加速的碳离子初始电荷态分布主要集中在C4+价态, 激光直接加速出的碳离子在C5+, C2+和C3+离子的占比较小. 在穿过泡沫靶后, 由于靶中原子与碳离子发生复杂的库仑碰撞电离和电子俘获等相互作用, 碳离子的电荷态分布发生明显变化, 主要表现为初始比例最高的C4+离子数目显著减少, 同时更低电荷态的离子(C2+和C3+)占比明显增大, 且离子能量越低, 这种趋势越明显, 原因在于随着离子能量降低, 电子俘获概率增大, 电离概率降低.
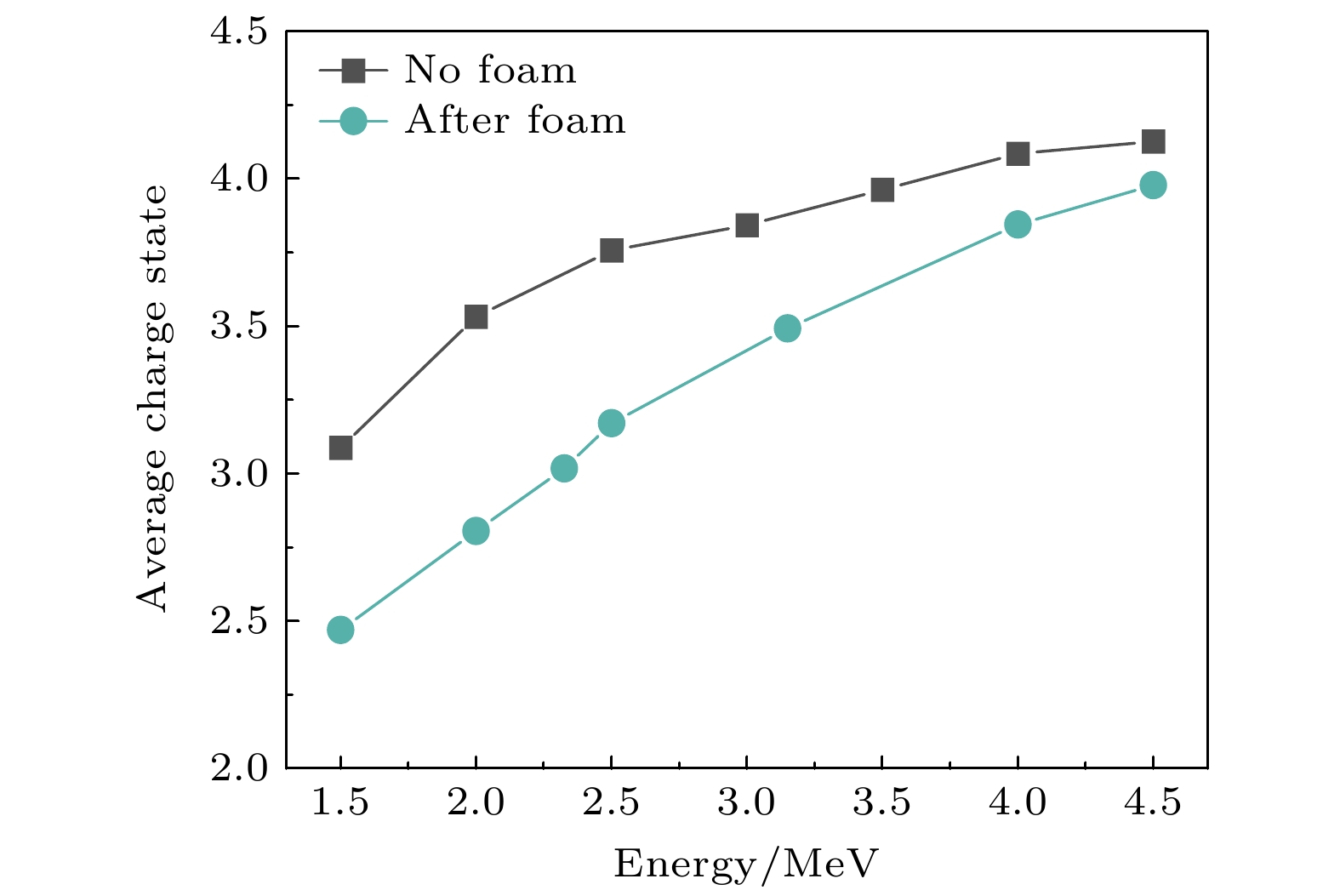
离子在穿过靶物质时的平衡长度一般与离子速度、靶物质密度、离子电荷态等参数有关. 在固体靶中, 离子达到平衡电荷状态所需的长度(或时间)主要是入射离子速度(或能量)的函数. Hattass等[44]实验证明, 离子在固体中的平衡长度约nm量级, 平衡时间在fs量级. 因此, 本文实验测量到的平均电荷态可以合理地认为是出射碳离子的平衡电荷态. 根据碳离子的能谱分布, 图3给出了碳离子穿过空靶和泡沫靶后的平均电荷态
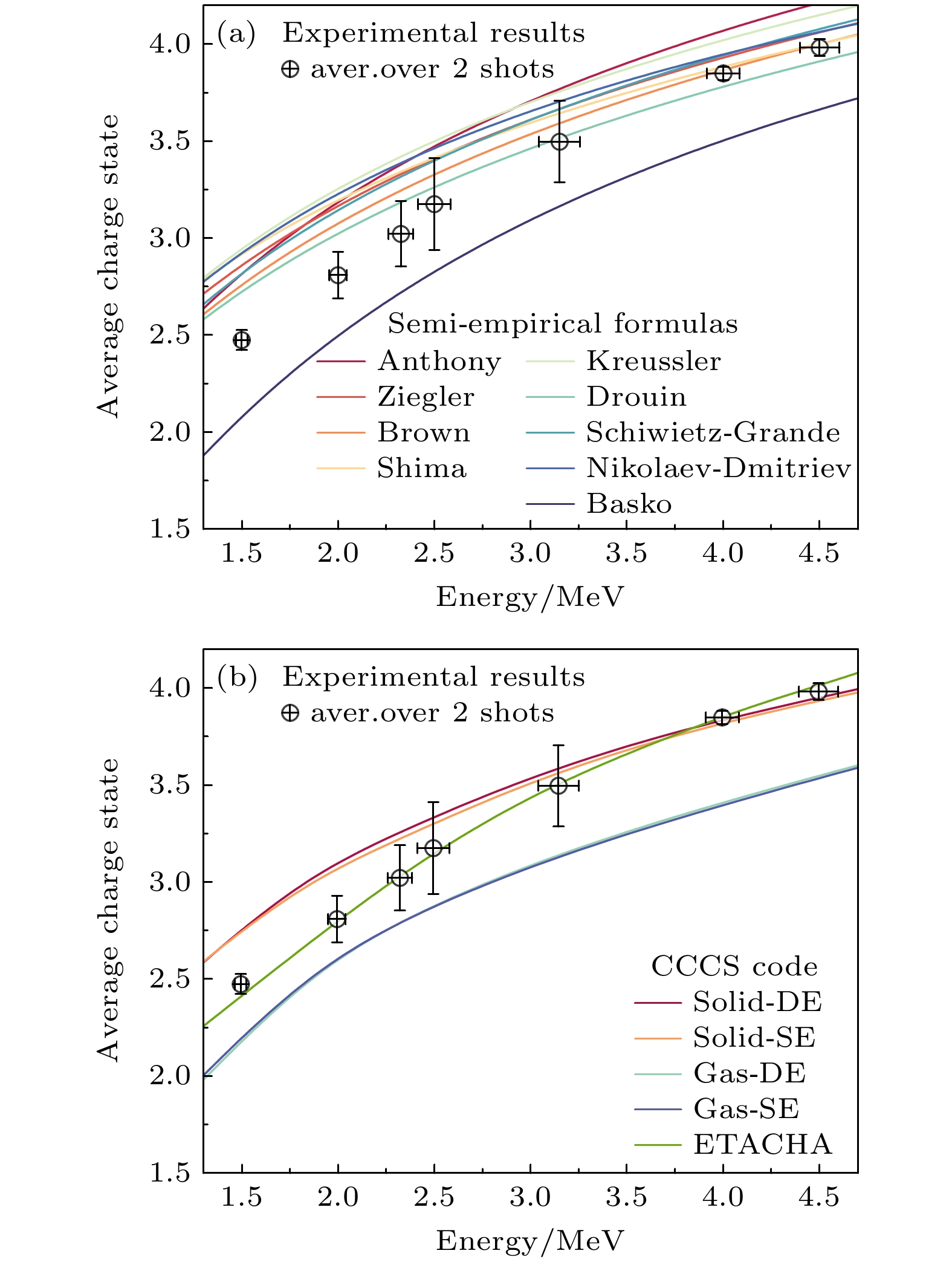
$\overline Q = \displaystyle\sum\nolimits_q {q{F_q}\left( E \right)} $ , 其中Fq(E)表示电荷量为q、能量为E的碳离子数占比. 结果显示, 碳离子在与泡沫靶相互作用后, 平均电荷态有所降低. 例如, 对于动能为2 MeV的碳离子, 平均电荷态从3.5减小到2.8, 降幅约25%.碳离子束穿过泡沫靶后的平均平衡电荷态实验测量值与基于玻尔剥离准则[15]和Northcliffe公式[25]对比如图4(a)所示. 其中, Basko公式[24]预测值远低于实验值, 该公式更适用原子序数Z大于20的离子; Anthony经验公式[16]适用于入射离子原子序数6 ≤ Zp ≤ 53、靶物质6 ≤ Zt ≤ 79的数据拟合; Ziegler 公式[17]在Northcliffe公式[25]基础上考虑了靶内电子运动对入射离子有效电荷的影响; Kreussler模型[18]在不考虑热速度而考虑离子与靶电子间的相对速度时也可用于冷物质中的电荷计算; Nikolaev和Dmitriev半经验公式[19]用于拟合部分原子序数大于20的实验数据. 上述模型预测值整体高估了实验值. Brown 公式[20]基于重离子在薄靶中的数据; Shima半经验公式[21]拟合入射离子原子序数大于8、能量小于6 MeV/u以及靶物质4 ≤ Zt ≤ 79的实验数据; Drouin经验公式[22]基于部分重离子在固体靶中的实验数据; Schiwietz和Grande拟合公式[23]适用于入射离子原子序数1 ≤ Zp ≤ 92、靶物质4 ≤ Zt ≤ 83的实验数据. 这些经验公式在能量大于3 MeV时能较好地预测电荷态, 在能量小于3 MeV时明显高于实验值.
为了对离子与泡沫相互作用中的具体电荷交换过程进行解析, 需要计算电离和俘获截面以及求解速率方程. 当离子与物质相互作用时, 其电荷分布通过求解速率方程得到:
其中, σi, k (Zt, E)为电荷转移截面; i, k分别表示离子碰撞前后的状态; F表示各价态碳离子数占比. 碳离子在气体密度和固体密度介质中的单电子(single electron, SE)和双电子(double electron, DE)过程的电荷转移截面由电荷变化截面程序(charge changing cross sections code, CCCS code)[45,46]计算得到. 该程序可以给出能量0.001—50 MeV/u、原子序数5—54的入射离子在气体和固体介质中的电荷转移截面. 将该截面数据代入速率方程, 求解后获得各价态离子的占比, 进而得到碳离子在介质中的平均平衡电荷态
${\overline q _{{\text{eq}}}} = \displaystyle\sum\nolimits_k {k{F_k}\left( E \right)} $ . 图4(b)对比了碳离子束穿过泡沫靶后的平均平衡电荷态实验测量值与速率方程理论预期. 结果表明, 双电子过程的加入对电荷态的影响可以忽略, 这是因为激光直接加速出的碳离子平均电荷态约为4, 同时电离失去两个电子或俘获两个电子的概率很小, 单电子过程为主要过程. 采用气体靶截面数据求解速率方程获得的平衡电荷态远远低估了实验值, 原因在于泡沫靶是由纤维丝和孔隙结构组成, 碳离子穿过该结构靶中的固态纤维丝引起的靶密度效应导致离子电荷态升高.在求解速率方程过程中采用固体截面数据时, 可以较好地预测离子能量高于3 MeV的实验值, 在低于3 MeV区间内出现明显偏差, 理论高估了实验值. 离子在介质中的电荷转移靶密度效应的内在物理原因在于离子激发态寿命与离子-原子碰撞时间尺度之间的竞争关系, 与靶密度、离子速度、离子原子序数息息相关. 只有当激发态寿命大于碰撞时间尺度时, 离子激发态在未退激发回到基态发生二次碰撞, 处于高激发态的电子极易被碰撞电离, 最终造成电离截面增大而俘获截面减小, 离子电荷态升高.
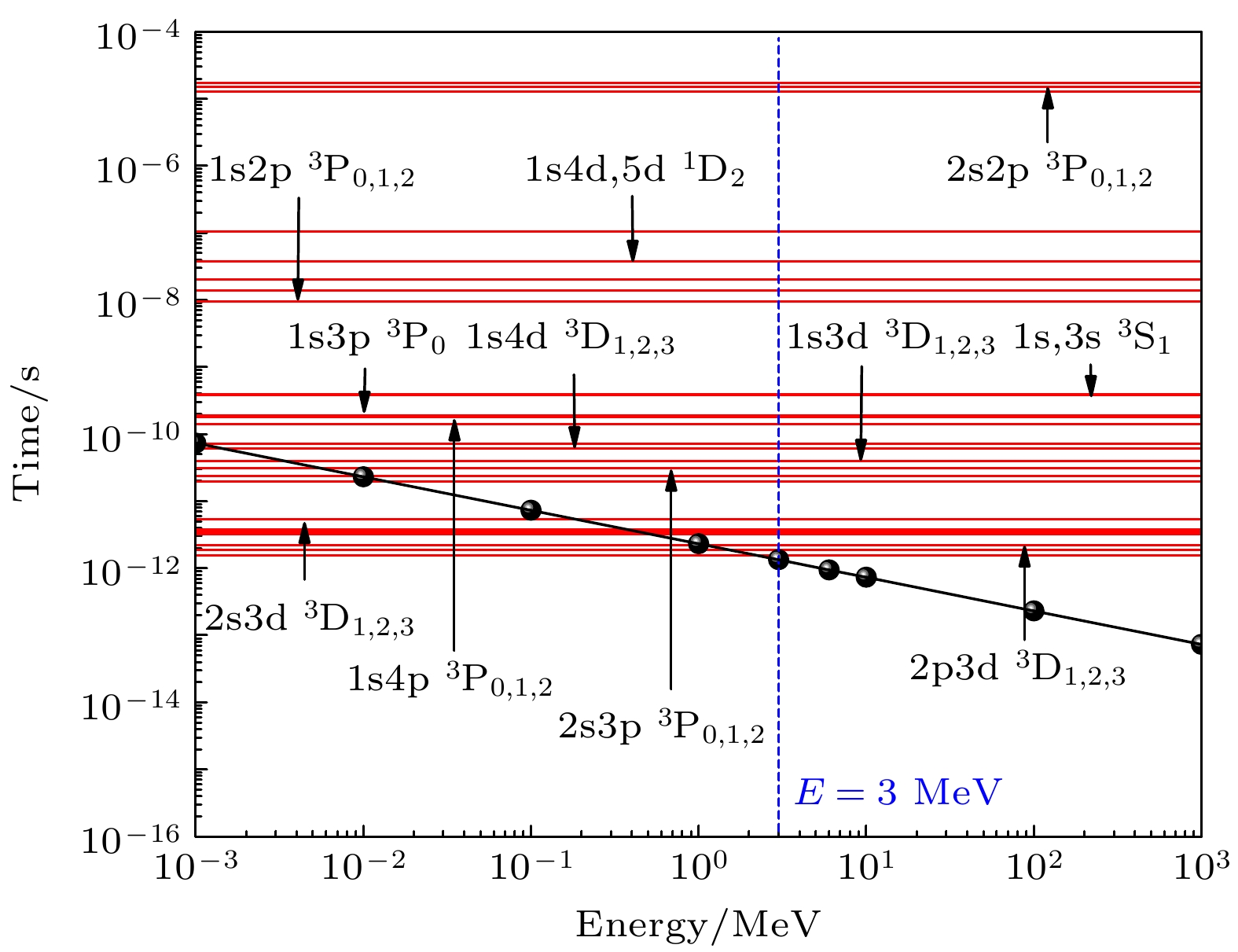
对于本实验当前的碰撞系统, 不同能量C4+离子的激发态寿命和碰撞时间尺度的对比如图5所示, 当入射离子能量大于3 MeV时, 碳离子激发态寿命大于相邻碰撞时间尺度, 靶密度效应起重要作用, 故实验测得的离子平均平衡电荷态与基于固体截面的速率方程解符合较好. 当入射离子能量小于3 MeV时, 碳离子激发态寿命小于相邻碰撞时间尺度, 靶密度效应减弱, 离子电荷降低. 碳离子束穿过泡沫靶后的平均平衡电荷态实验测量值与ETACHA代码[47–49]对比如图4(b)所示, 理论与实验结果整体符合很好, 原因在于该程序对能量大于0.1 MeV/u的入射离子, 充分考虑了离子-原子碰撞中的俘获、电离、激发以及辐射和俄歇退激过程, 进一步验证了激发态对离子电荷交换过程的重要贡献及其与离子能量的依赖关系.
-
本文基于绵阳激光聚变中心星光III装置, 开展了1.5—4.5 MeV碳离子在CHO泡沫靶中的电荷转移过程实验研究及相应的理论分析. 结果表明, 泡沫结构靶中存在明显的靶密度效应, 即离子激发态在未退激发回到基态发生二次碰撞被电离, 造成电离截面增大而俘获截面减小, 离子电荷态升高现象. 这种靶密度效应与靶密度和离子能量密切相关, 在本文碰撞系统中, 离子能量高于3 MeV时, 靶密度效应作用显著, 低于3 MeV时, 靶密度效应减弱. 只有详细考虑了电离、俘获、激发和退激等过程的ETACHA程序可以较好地预测实验结果.
激光加速低能碳离子束在CHO泡沫中的电荷转移过程
Charge transfer process of laser-accelerated low-energy carbon ion beams in porous CHO foams
-
摘要: 离子与物质相互作用中的电荷转移过程研究对于离子束驱动高能量密度物理、材料离子辐照损伤、离子束电荷剥离技术等领域至关重要. 本文利用激光驱动靶背鞘层场加速机制产生了能量在数MeV量级的碳离子束, 测量了碳离子束穿过具有孔状结构的C9H16O8泡沫靶后的电荷态分布. 实验结果与理论对比发现, 只有同时考虑了电离、俘获、激发和退激等过程的速率方程结果与实验符合很好. 采用气体靶截面数据求解速率方程获得的平衡电荷态低估了实验值, 原因在于泡沫结构靶中固态纤维丝引起的靶密度效应导致离子电荷态升高. 当离子能量高于3 MeV以上时, 实验值与采用了固态靶截面数据的速率方程理论预期一致; 但在低能区出现明显偏差, 原因在于当入射能量小于3 MeV时, 离子激发态寿命小于碰撞时间尺度, 激发态电子在发生第二次碰撞之前退激发回到基态, 靶密度效应减弱, 平均电荷态降低, 实验结果与详细考虑了激发和退激过程的ETACHA程序预期吻合. 该工作为理解离子束与物质相互作用微观机制以及电荷转移模型检验提供了数据和参考.Abstract: Charge transfer processes in ion-matter interactions are crucial for ion beam-driven high-energy density physics, material irradiation damage, and charge state stripping in accelerator techniques. Here we generate carbon ion beams in the MeV energy range through target normal sheath acceleration (TNSA) mechanism, and measure the average charge state of 1.5–4.5 MeV carbon ion beams passing through porous C9H16O8 foam with a volume density of 2 mg/cm3. The measured average charge states are compared with the average equilibrium charge-states predicted by semi-empirical formula and rate equation. The results show that the predictions from the rate equation that fully considers the ionization, capture, excitation, and de-excitation processes are in good agreement with experimental results. The prediction from the rate equation by using gas target cross-section data underestimates the experimental data, because the target density effect caused by the solid fiber filaments in the foam-structured target increases the ionization probability through frequent collisions, reduces the electron capture probability, and thus leads to an enhancement of ion charge states. In the projectile energy range above 3 MeV, the experimental data agree with the predictions from the rate equation using solid-target cross-section data. However, a significant deviation emerges in the energy region below 3 MeV due to the fact that in this energy range, the lifetime of ion excited states is shorter than the collisional time scale. In this case, excited electrons have time to de-excite the ground state before the second collision occurs. Consequently, the target density effects are weakened, and the charge states are reduced. The experimental results agree well with predictions from the ETACHA code that considers excitation and de-excitation processes in detail. This work provides the data and references for better understanding ion-matter interactions and distinguishing various charge exchange models.
-
Key words:
- laser acceleration /
- carbon ion beam /
- charge transfer /
- target density effects .
-

-
图 1 皮秒激光聚焦在铜箔上, 通过TNSA机制产生强流碳离子束. 使用与IP耦合的双通道TPS记录穿过泡沫靶和空靶的碳离子能谱
Figure 1. Experimental setup. A picosecond laser is focused onto a copper foil, generating an intense carbon ion beam through the TNSA mechanism. The energy spectra of carbon ions passing through the foam target and the empty hole are measured with a dual-channel TPS coupled to the IP.
图 2 激光加速的碳离子分布 (a) 穿过空靶的能谱分布; (b) 穿过泡沫靶的能谱分布; (c) 穿过空靶的电荷分布; (d) 穿过泡沫靶的电荷分布
Figure 2. Carbon ions distribution of laser-accelerated: (a) The energy spectra of passing through without target; (b) the energy spectra of passing through foam target; (c) charge state distribution of passing through without foam; (d) charge state distribution of passing through foam target.
图 4 测量的平均电荷态与理论预测值的比较 (a)与半经验模型比较; (b)与通过求解速率方程得出的预测值的比较. 实验数据是两发次的平均值, 其中能量误差为TPS对各电荷态碳离子能量分辨的最小值, 电荷态误差源于实验统计误差和发次抖动误差
Figure 4. Comparison of measured average charge states with theoretical predictions: (a) The comparison with semiempirical models; (b) the comparison with predictions through solving rate equations. The experimental data are averaged over two shots, the error bars of energy represent the energy resolution of the TPS for the ion species that has the lowest resolution, the error bars of the average charge state originate from the statistical errors and shot-to-shot fluctuations
-
[1] Shima K, Kuno N, Yamanouchi M 1989 Phys. Rev. A 40 3557 doi: 10.1103/PhysRevA.40.3557 [2] Zhao Y T, Zhang Y N, Cheng R, He B, Liu C L, Zhou X M, Lei Y, Wang Y Y, Ren J R, Wang X, Chen Y H, Xiao G Q, Savin S M, Gavrilin R, Golubev A A, Hoffmann D H H 2021 Phys. Rev. Lett. 126 115001 doi: 10.1103/PhysRevLett.126.115001 [3] Rothard H, Grandin J P, Jung M, Clouvas A, Rozet J P, Wünsch R 1997 Nucl. Instrum. Methods Phys. Res. Sect. B 132 359 doi: 10.1016/S0168-583X(97)00439-4 [4] Betz H D 1972 Rev. Mod. Phys. 44 465 doi: 10.1103/RevModPhys.44.465 [5] Deutsch C, Maynard G 2016 Matter Radiat. Extremes 1 277 doi: 10.1016/j.mre.2016.11.004 [6] Gao J, Hu Z, Wu Y, Wang J, Sisourat N, Dubois A 2021 Matter Radiat. Extremes 6 014404 doi: 10.1063/5.0025623 [7] Erb W 1978 GSI Report GSI-P-78 (Darmstadt [8] Ali R, Beiersdorfer P, Harris C L, Neill P A 2016 Phys. Rev. A 93 012711 doi: 10.1103/PhysRevA.93.012711 [9] Ma X W, Zhang S F, Wen W Q, Huang Z K, Hu Z M, Guo D L, Gao J W, Najjari B, Xu S Y, Yan S C, Yao K, Zhang R T, Gao Y, Zhu X L 2022 Chin. Phys. B 31 093401 doi: 10.1088/1674-1056/ac8736 [10] Kawata S, Karino T, Ogoyski A I 2016 Matter Radiat. Extremes 1 89 doi: 10.1016/j.mre.2016.03.003 [11] Hofmann I 2018 Matter Radiat. Extremes 3 1 doi: 10.1016/j.mre.2017.12.001 [12] Zhao Q, Cao S C, Liu M, Sheng X K, Wang Y R, Zong Y, Zhang X M, Jing Y, Cheng R, Zhao Y T, Zhang Z M, Du Y C, Gai W 2016 Nucl. Instrum. Methods Phys. Res. Sect. A 832 144 doi: 10.1016/j.nima.2016.06.103 [13] Zhao Y, Zhang Z, Gai W, Du Y, Cao S, Qiu J, Zhao Q, Cheng R, Zhou X, Ren J, Huang W, Tang C, Xu H, Zhan W 2016 Laser Part. Beams 34 338 doi: 10.1017/S0263034616000124 [14] Zhao Y T, Cheng R, Wang Y Y, Zhou X M, Lei Y, Sun Y B, Xu G, Ren J R, Sheng L N, Zhang Z M, Xiao G Q 2014 High Power Laser Science and Engineering. 2 e39 doi: 10.1017/hpl.2014.44 [15] Bohr N 1941 Phys. Rev. 59 270 doi: 10.1103/PhysRev.59.270 [16] Anthony J M, Lanford W A 1892 Phys. Rev. A 25 1868 doi: 10.1103/PhysRevA.25.1868 [17] Ziegler J F, Biersack J P 1985 Treatise on Heavy-Ion Science 6 93 doi: 10.1007/978-1-4615-8103-1_3 [18] Kreussler S, Varelas C, Brandt W 1981 Phys. Rev. B 23 82 doi: 10.1103/PhysRevB.23.82 [19] Nikolaev V S, Dmitriev I S 1968 Phys. Lett. A 28 277 doi: 10.1016/0375-9601(68)90282-X [20] Brown M D, Moak C D 1972 Phys. Rev. B 6 90 doi: 10.1103/PhysRevB.6.90 [21] Shima K, Ishihara T, Mikumo T 1982 Nucl. Instrum. Methods Phys. Res. 200 605 doi: 10.1016/0167-5087(82)90493-8 [22] To K X, Drouin R 1976 Phys. Scr. 14 277 doi: 10.1088/0031-8949/14/6/006 [23] Schiwietz G, Grande P L 2001 Nucl. Instrum. Methods Phys. Res. Sect. B 175 125 [24] Basko M M 1984 Sov. J. Plasma Phys. 10 689 [25] Northcliffe L C 1960 Phys. Rev. 120 1744 doi: 10.1103/PhysRev.120.1744 [26] Gauthier M, Chen S N, Levy A, Audebert P, Blancard C, Ceccotti T, Cerchez M, Doria D, Floquet V, Lamour E, Peth C, Romagnani L, Rozet J P, Scheinder M, Shepherd R, Toncian T, Vernhet D, Willi O, Borghesi M, Faussurier G, Fuchs J 2013 Phys. Rev. Lett. 110 135003 doi: 10.1103/PhysRevLett.110.135003 [27] Tolstikhina I Y, Shevelko V P 2018 Phys.-Usp. 61 247 doi: 10.3367/UFNe.2017.02.038071 [28] Lassen N O 1950 Phys. Rev. 79 1016 doi: 10.1103/PhysRev.79.1016.2 [29] Bohr N, Lindhard J 1954 Dan. Mat. Fys. Medd. 28 1 doi: 10.1016/s1876-0503(08)70178-6 [30] Shevelko V P, Rosmej O, Tawara H, Tolstikhina I Y 2004 J. Phys. B: At. Mol. Opt. Phys. 37 201 doi: 10.1088/0953-4075/37/1/012 [31] Shevelko V P, Tawara H, Ivanov O V, Miyoshi T, Noda K, Sato Y, Subbotin A V, Tolstikhina I Y 2005 J. Phys. B: At. Mol. Opt. Phys. 38 2675 doi: 10.1088/0953-4075/38/15/008 [32] Kistler S S 1931 Nature 127 741 doi: 10.1038/127741a0 [33] Rosmej O N, Suslov N, Martsovenko D, Vergunova G, Borisenko N, Orlov N, Rienecker T, Klir D, Rezack K, Orekhov A, Borisenko L, Krousky E, Pfeifer M, Dudzak R, Maeder R, Schaechinger M, Schoenlein A, Zaehter S, Jacoby J, Limpouch J, Ullschmied J, Zhidkov N 2015 Plasma Phys. Control. Fusion 57 094001 doi: 10.1088/0741-3335/57/9/094001 [34] Ren J R, Deng Z G, Qi W, Chen B Z, Ma B B, Wang X, Yin S, Feng J H, Liu W, Xu Z F, Hoffmann D H H, Wang S Y, Fan Q P, Cui B, He S K, Cao Z R, Zhao Z Q, Cao L F, Gu Y Q, Zhu S P, Cheng R, Zhou X M, Xiao G Q, H W, Zhang Y H, Zhang Z, Li Y T, Wu D, Zhou W M, Zhao Y T 2020 Nat. Commu. 11 5157 doi: 10.1038/s41467-020-18986-5 [35] Ma B B, Ren J R, Wang S Y, Hoffmann D H H, Deng Z G, Qi W, Wang X, Yin S, Feng J H, Fan Q P, Liu W, Xu Z F, Chen Y, Cui B, He S K, Cao Z R, Zhao Z Q, Gu Y Q, Zhu S P, Cheng R, Zhou X M, Xiao G Q, Zhao H W, Zhang Y H, Zhang Z, Li Y T, Xu X, Wei W Q, Chen B Z, Zhang S Z, Hu Z M, Liu L R, Li F F, Xu H, Zhou W M, Cao L F, Zhao Y T 2021 Astrophys. J. 920 106 doi: 10.3847/1538-4357/ac18c3 [36] Renner O, Klimo O, Krus K, Nicolaï P, Poletaeva A, Bukharskii N, Tikhonchuk V T 2025 Matter Radiat. Extremes 10 037403 doi: 10.1063/5.0246250 [37] Braenzel J, Andreev A A, Platonov K, Klingsporn K, Ehrentraut L, Sandner W, Schnürer M 2015 Phys. Rev. Lett. 114 124801 doi: 10.1103/PhysRevLett.114.124801 [38] Henig A, Steinke S, Schnürer M, Sokollik T, Hörlein R, Kiefer D, Jung D, Schreiber J, Hegelich B M, Yan X Q, Meyerter V J, Tajima T, Nickles P V, Sandner W, Habs D 2009 Phys. Rev. Lett. 103 245003 doi: 10.1103/PhysRevLett.103.245003 [39] Braenzel J, Barriga-Carrasco M D, Morales R, Schnürer M 2018 Phys. Rev. Lett. 120 184801 doi: 10.1103/PhysRevLett.120.184801 [40] 朱军高, 卢海洋, 赵媛, 赖美福, 古永力, 徐世祥, 周沧涛 2022 物理学报 71 194102 doi: 10.7498/aps.71.20220599 Zhu J G, Lu H Y, Zhao Y, Lai M F, Gu Y L, Xu S X, Zhou C T 2022 Acta Phys. Sin. 71 194102 doi: 10.7498/aps.71.20220599 [41] Zhao S A, Lin C, Chen J E, Ma W J, Wang J J, Yan X Q 2016 Chin. Phys. Lett. 33 035202 doi: 10.1088/0256-307X/33/3/035202 [42] Ren J R, Ma B B, Liu L R, et al. 2023 Phys. Rev. Lett. 130 095101 doi: 10.1103/PhysRevLett.130.095101 [43] Ma B B, Ren J R, Liu L R, Wei W Q, Chen B Z, Zhang S Z, Xu H, Hu Z M, Li F F, Wang X, Li W X, Li Q Y, Yin S, Feng J H, Zhou X M, Gao Y F, Li Y, Shi X H, Li J X, Ren X G, Xu Z F, Deng Z G, Qi W, Wang S Y, Fan Q P, Cui B, Wang W W, Yuan Z Q, Teng J, Wu Y C, Cao Z R, Zhao Z Q, Gu Y Q, Cao L F, Zhu S P, Cheng R, Lei Y, Wang Z, Zhou Z X, Xiao G Q, Zhao H W, Hoffmann D H H, Zhou W M, Zhao Y T 2024 Phys. Rev. A 109 042810 doi: 10.1103/PhysRevA.109.042810 [44] Hattass M, Schenkel T, Hamza A V, Barnes A V, Newman M W, McDonald J W, Niedermayr T R, Machicoane G A, Schneider D H 1999 Phys. Rev. Lett. 82 4795 doi: 10.1103/PhysRevLett.82.4795 [45] Charge changing cross sections code, Novikov N V http://cdfe.sinp.msu.ru/services/cccc/htm/ [2024-7-28] [46] Novikov N V, Teplova Y A 2014 Phys. Lett. A 378 1286 doi: 10.1016/j.physleta.2014.03.004 [47] Rozet J P, Stephan C, Vemhet D 1996 Nucl. Instrum. Methods Phys. Res. Sect. B 107 67 doi: 10.1016/0168-583X(95)00800-4 [48] Tarasov O B, Bazin D 2008 Nucl. Instrum. Methods Phys. Res. Sect. B 266 4657 doi: 10.1016/j.nimb.2008.05.110 [49] Lamour E, Fainstein P D, Galassi M, Prigent C, Ramirez C A, Rivarola R D, Rozet J P, Trassinelli M, Vernhet D 2015 Phys. Rev. A 92 042703 doi: 10.1103/PhysRevA.92.042703 [50] Manai S, Salhi D E, Nasr S B, Jelassi H 2022 Res. Phys. 37 105487 doi: 10.1016/j.rinp.2022.105487 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: