-
在磁约束聚变实验装置中, 等离子体电磁涨落对等离子体约束和输运具有重要的影响[1,2]. 高频磁探针是一种非常重要的测量等离子体电磁涨落的诊断, 对研究高频电磁涨落(通常其频率在几十至几百kHz), 如高能粒子激发的阿尔芬Alfven不稳定性涨落[3–6]以及等离子体不均匀性激发的电磁湍流涨落[7–12]等, 起到非常重要的作用. 因此很多磁约束聚变实验装置, 如SUNIST[13,14], J-TEXT[15,16], KTX[17], HL-2 A[18], EAST[19–21], NCST[22], DIII-D[23], JET[24,25], MAST[26], WEST[27], JT-60 SA[28]等托卡马克, 以及H-1 NF[29], LHD[30], W7-X[31], TJ-II[32]等仿星器, 根据其自身的特点和研究目标, 均建有高频磁探针阵列诊断.
西南交通大学正在建设中国首台准环对称仿星器(Chinese First Quasi-axisymmetric Stellarator, CFQS), 该装置大半径R = 1 m, 平均小半径a = 0.25 m, 设计中心磁场强度
$ {B_{{\mathrm{T0}}}} = 1{\text{ T}} $ , 环向周期数n = 2, 其是国际上一台优化了新经典输运的具有准环对称磁位形的先进仿星器[33–39]. CFQS装置的建设得到了日本核融合科学研究所及核工业西南物理研究院等多家单位的支持和帮助. CFQS装置实验运行分为两个阶段, 第1阶段(也称为CFQS-T准环对称仿星器, 时间从2024年8月—2025年5月)在$ {B_{{\text{T0}}}} = 0.1{\text{ T}} $ 条件下验证准环对称磁位形, 并随后进行低磁场强度($ {B_{{\text{T0}}}} \leqslant 0.1{\text{ T}} $ )及低加热功率(30 kW)的等离子体物理实验, 实现全局准环对称磁位形等离子体放电与芯部准环对称磁位形加边界磁岛偏滤器位形等离子体放电, 目标等离子体电子密度在${10^{17}}\;{{\text{m}}^{ - 3}}$ 量级, 电子温度在10—50 eV范围, 验证该实验条件下等离子体新经典输运水平相较于传统仿星器得到优化; 第2阶段(2026年底及以后)在$ {B_{{\text{T0}}}} = 1{\text{ T}} $ 条件下实现准环对称磁位形, 并随后开展高磁场强度($ {B_{{\text{T0}}}} \leqslant 1{\text{ T}} $ )及高加热功率(500 kW)的等离子体物理实验, 目标等离子体电子密度在1018—1019 m–3量级, 芯部电子温度超过500 eV, 在该参数条件下实验验证准环对称仿星器具有低新经典输运损失的理论预言, 系统研究优化磁位形下湍流输运和磁流体不稳定性的特征及相应的抑制手段, 为全面提高仿星器的约束性能提供科学依据. 目前, CFQS仿星器实验运行的第1阶段工程目标已经成功完成[40], 正在进行实验数据的分析整理, 与此同时, CFQS装置正在为第2阶段实验运行进行升级.针对CFQS仿星器实验运行的第1阶段(也称为CFQS-T准环对称仿星器, 下同)的物理研究目标, 除了需要为CFQS-T研制用于测量磁场和低频磁涨落(
$f \leqslant 50{\text{ kHz}}$ )的低频磁探针阵列(low-frequency magnetic probe array, LFMPA)诊断[41], 也需要为CFQS-T研制专门用于测量磁涨落(包括低频和高频磁涨落)的高频磁探针阵列(high-frequency magnetic probe array, HFMPA)诊断. LFMPA和HFMPA诊断也将用于CFQS第2阶段物理实验, 因此在设计时, 需要同时仔细考虑CFQS两个阶段的实验参数特征. CFQS-T高频磁探针阵列诊断共包括8个独立的三维磁探针, 每个磁探针可以同时测量极向、环向及径向的磁涨落信息, 综合考虑传输线及磁探针本身绕线等的影响, 最终设计出的高频磁探针共振频率高于400 kHz, 满足对50—300 kHz的高频磁涨落的测量需求, 通过优化高频磁探针空间位置的布局, 可以方便研究磁涨落的极向和环向传播特征. 相比低频磁探针阵列最高能分辨环向模数$n = \pm 6$ , 高频磁探针阵列将环向模数分辨能力提升至$n = \pm 16$ .本文主要介绍CFQS-T准环对称仿星器上新研制的高频磁探针阵列诊断及其在实验分析中的初步应用, 报道了CFQS-T仿星器中高频磁涨落的初步测量结果. 本文第2节主要对CFQS-T高频磁探针阵列诊断的各主要子系统进行简要介绍, 并介绍高频磁探针阵列的有效面积及原位频率响应标定的结果; 第3节介绍CFQS-T高频磁探针阵列在低频及高频磁涨落测量分析中的初步应用; 第4节是对本文工作的总结及未来工作的展望.
-
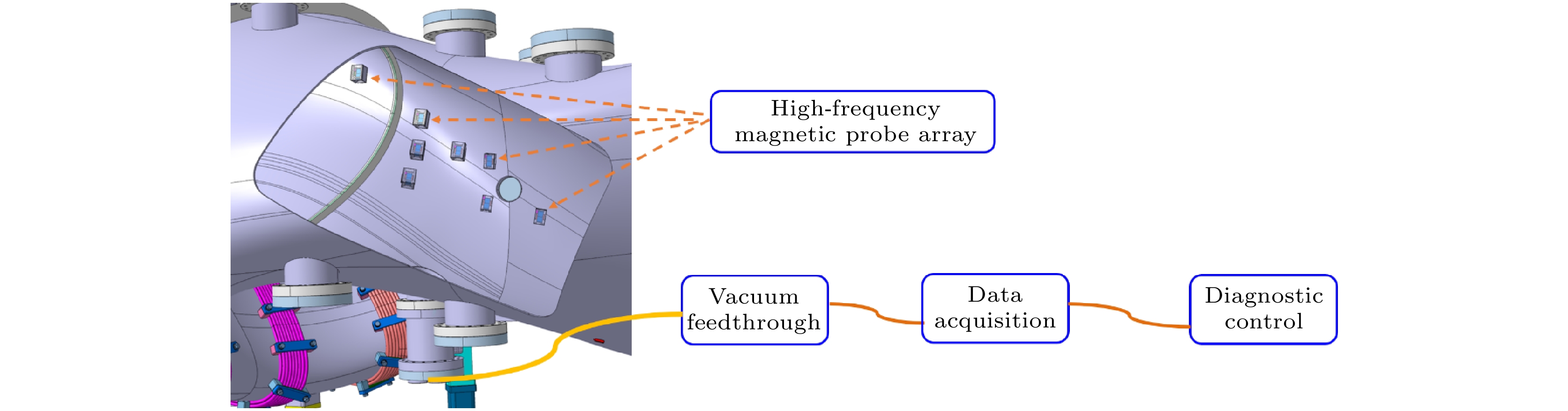
CFQS-T准环对称仿星器上高频磁探针阵列(HFMPA)诊断主要由安装在真空室内壁的分立的高频磁探针及相应的机械支撑保护部件、真空穿墙插座、真空室外的信号传输线以及采集和控制单元等组成, 其示意图如图1所示. 在本节中将分别简要介绍这些子系统、诊断的标定以及在诊断研发中克服的挑战和创新.
-
HFMPA诊断的机械系统主要包括诊断核心的三维高频磁探针, 其相应的机械支撑和保护部件, 以及安装在真空室上定制的法兰等部件. 仿星器上的高频磁探针设计需要考虑可安装空间、待测磁扰动的幅度和频率特征、真空环境要求、热负荷及辐射环境, 以及信号传输线长度等因素. CFQS-T准环对称仿星器上的高频磁探针计划安装在装置特征磁位形之一的三角形磁位形区域, 因为这里同时也安装有低频磁探针阵列(LFMPA)诊断[41], 便于高频磁探针和低频磁探针信号间的比较与相关物理研究. 由于CFQS-T没有安装用于保护真空室内壁附近部件的限制器, 设计的磁探针径向高度应参考并小于装置设计的最外闭合磁面与该区域真空室内壁的距离, 并做好磁探针的保护. 增大磁探针有效面积(如提高绕线匝数等)可以提高磁探针测量信号的输出幅度, 但会降低磁探针共振频率, 进而影响对高频磁信号的探测, 因此需要平衡磁探针有效面积大小和共振频率之间的关系, 对于CFQS-T仿星器, 要求高频磁探针能够测量最高频率为300 kHz的等离子体磁扰动. CFQS-T仿星器实验运行要求真空度维持在
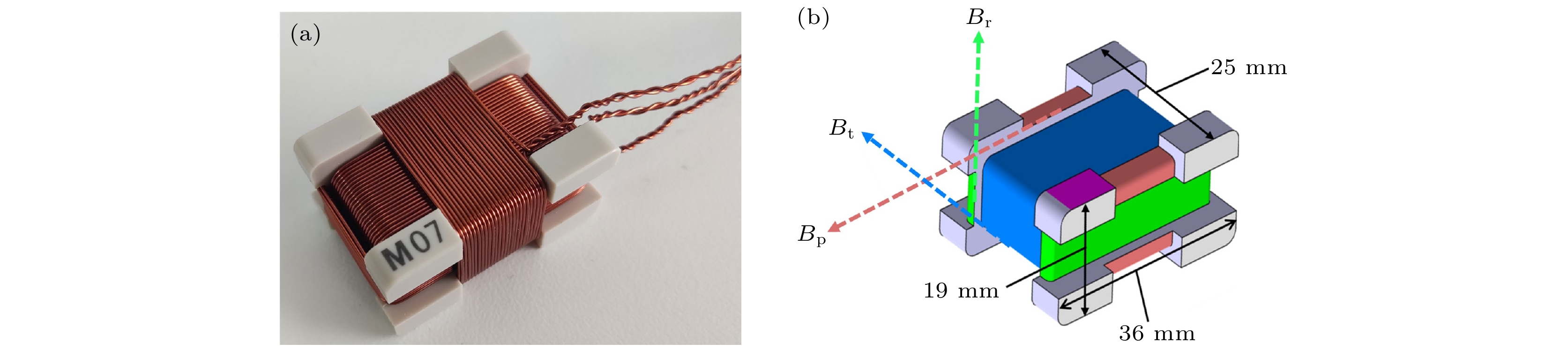
${10^{ - 5}}{\text{ Pa}}$ 量级, 磁探针绕线需选用适用于高真空环境的低出气率材料. 由于没有保护限制器, 在CFQS-T等离子体放电期间(一次等离子体放电通常小于10 s), 磁探针将更加容易受到边缘等离子体轰击, 所带来的大的热负荷要求磁探针保护壳和磁探针本身的绕线能够承受放电过程中的间歇性高温. 此外, 等离子体放电期间会产生软X射线等, 需要对磁探针做相应的保护. 根据实验室现场环境和要求, 高频磁探针的信号传输线将达到30 m. 在综合考虑了上述因素后, 设计了CFQS-T高频磁探针, 如图2所示, 其绕线选用了直径为0.5 mm的低出气率耐高温漆包线, 绕线骨架选择聚醚醚酮(PEEK)材料, 其短时间能耐受300 ℃高温, 与西班牙TJ-II仿星器的新型螺旋磁探针阵列的绕线骨架为同种材料[32], 沿绕线骨架3个方向正交绕线, 最内层绕 制2层线圈, 每层26匝, 用于测量环向磁扰动 (如图2(b)中蓝色箭头所示); 中间层绕制2层 线圈, 每层16匝, 用于测量径向磁扰动(如图2(b)中绿色箭头所示); 最外层绕制2层线圈, 每层26匝, 用于测量极向磁扰动(如图2(b)中粉红色箭头所示).高频磁探针阵列的最终空间布置如图3所示, 这样布置的目的在于利用有限的磁探针实现对高频磁涨落的极向与环向传播特征进行有效测量. 图3中标号HM2—HM8的高频磁探针均通过激光跟踪仪精确定位, HM1由于很难通过激光跟踪仪定位, 通过人工用卷尺测量与其他高频磁探针的相对位置来定位, 所以其位置的精度要低一些. HM5与HM2环向角相差约11.14°, 理论上最高能测量环向模数
$n = \pm 16$ . 相比于低频磁探针阵列环向模数最高可测$n = \pm 6$ , 高频磁探针阵列测量磁涨落环向模数的能力有了大幅提升.CFQS-T准环对称仿星器高频磁探针的机械支撑和保护部件也经过专门设计, 考虑了可安装空间大小以及对磁探针热负荷和辐射的防护. 为CFQS-T的高频磁探针设计了两种机械保护部件, 如图4(a)所示, 左边的机械保护壳厚度为0.5 mm, 里面还有一个框架, 其既可以用于固定磁探针又可以用于使磁探针与保护壳间增加一定的距离, 更有利于降低从保护壳传递到磁探针上的热负荷, 左边的机械保护壳外还有一个带孔的小块, 专门用于定位保护壳中的磁探针; 右边的机械保护壳厚度为1 mm, 设计成刚好可以放进高频磁探针的尺寸, 更加简洁. 两种机械保护壳的一面均开有狭缝, 用于信号线的引出, 两种保护壳及内部框架的材料均为316 L无磁不锈钢, 如图4(b)所示, 其中编号HM1—HM5的高频磁探针的用图4(a)左边的保护壳, 编号HM6—HM8的高频磁探针用右边的保护壳. 为了便于第3节讨论分析, 图4(c)还展示了CFQS-T上的低频磁探针阵列及其支撑保护部件的模型, 其用编号M1—M13表示. 材料的电磁屏蔽性能与材料本身的相对磁导率、相对电导率、材料厚度, 以及电磁波的频率有关[42,43]. CFQS-T高频磁探针保护壳选用金属材料, 这是托卡马克和仿星器装置上磁探针常用的材料, 其能有效地防护等离子体热与粒子轰击以及软X射线等辐射, 低的出气率也有助于实验前的装置真空抽气. 金属材料对电磁波具有一定的屏蔽能力, 金属壳厚度的增大将降低电磁波穿过金属壳到达磁探针的信号幅度, 这还与电磁波的频率有关. 在设计CFQS-T高频磁探针金属保护壳时, 在其中的一个面开有狭缝, 除了便于信号线引出, 也有助于降低保护壳的屏蔽能力; 此外, 在安装CFQS-T高频磁探针金属保护壳时, 也在保护壳与真空室壁之间留有狭缝, 也是为了降低金属保护壳的电磁屏蔽能力. 非导电的陶瓷也常用作磁探针的保护壳, 其相比于同样尺寸的金属保护壳, 电磁屏蔽能力更弱, 更有利于电磁波传播至其内部的磁探针; 但陶瓷保护壳在等离子体粒子和热的轰击下, 相比于金属保护壳, 其更容易被破坏, 进而产生杂质影响等离子体放电, 此外陶瓷材料更加容易吸附气体, 增加装置真空抽气的难度. 因此在设计磁探针机械保护壳时, 需要根据磁探针测量目标, 平衡各种需求, 设计出适应于所在装置本身实验运行条件的机械保护壳.
-
CFQS-T准环对称仿星器高频磁探针的信号传输线的选择需要考虑物理研究目标和实验室现场环境要求. 对于真空室内每个高频磁探针的信号线尽量保证以相同长度双绞后引至装置下窗口特定的真空穿墙插座上; 真空室外, 选用定制的相同长度同轴线从真空穿墙插座引至高频磁探针专用的采集机柜. 不同位置的高频磁探针尽量采用相同长度的信号传输线, 目的是避免计算不同高频磁探针间测得信号的相位差时, 引入因传输线不同带来的非物理的相位差. 根据实验室管理要求, 磁测量采集机柜不能就近在装置二层平台布置, 需要集中在一个远离装置的指定区域布置, 因此增大了信号传输线的长度, 根据现场情况, CFQS-T高频磁探针在真空室外信号传输线长度定为30 m. 真空室外信号传输线选用同轴线而非双绞线的原因在于, 同轴线的外层金属网对电磁波能量具有屏蔽作用, 有利于降低辐射损耗, 在这一方面优于双绞线[44,45]. 在设计高频磁探针时已经考虑了信号传输线长度对磁探针频率响应的影响. 根据模拟计算, 仍满足对测量频率的要求, 在2.5节将介绍对安装后的高频磁探针的原位频率响应标定的结果.
-
CFQS-T准环对称仿星器高频磁探针阵列诊断的采集系统硬件主要由3个BNC信号转接盒(型号BNC-2090 A或BNC-2090)、1个PXIe-1062Q机箱、1个PXIe-8842控制器以及2张PXIe-6358数据采集卡组成. 从真空穿墙插座引来的信号线通过BNC信号转接盒与数据采集卡连接. PXIe-6358数据采集卡最大采样率达1.25 (MS/s)/通道, 满足实验测量的要求. 实验中采集到的数据通过连在控制器上的千兆网线传至CFQS-T数据存储服务器. 高频磁探针阵列诊断的控制系统通过设置不同的触发时间, 可以灵活控制数据开始采集的时刻, 也可以灵活设置一炮放电中采集的时长和采样频率(最高1.25 (MS/s)/通道), 这样可以根据实验的不同目标进行灵活设置和数据采集, 有利于节省数据存储空间, 和根据需要进行诊断问题排查.
-
准确标定磁探针的有效面积有利于计算实验中测得的磁涨落的绝对扰动幅度, 对深入开展相关物理研究具有重要意义. 对于磁探针的有效面积标定, 比较成熟的方法是相对标定法, 其已经用于DIII-D托卡马克[23]、HL-3托卡马克[46]及EAST托卡马克[20,21,47] 等装置上的磁探针有效面积标定. CFQS-T高频磁探针的有效面积标定采用相对标定法, 并借用核工业西南物理研究院的通电螺线管、高精度信号源(型号: 福禄克5502A)、标准磁探针、高精度数字万用表(型号: 福禄克8845A)及示波器等设备进行了具体的标定工作. 在标定过程中, 标准磁探针和待测高频磁探针放置在螺线管中心, 注意高频磁探针待测线圈与标准磁探针的线圈平行; 高精度信号源设置输出电流为10 A、频率为100 Hz, 为螺线管通电, 使其在螺线管中心产生均匀的磁场, 并垂直于标准磁探针和待测高频磁探针的线圈所在的平面; 用示波器采集标准磁探针和待测高频磁探针的输出信号, 判断待测高频磁探针绕线正负有无标记准确, 用高精度数字万用表测量标准磁探针输出信号
${\varepsilon _0}$ 和待测高频磁探针的输出信号$\varepsilon $ . 因为感应电动势$ \varepsilon=-NS\dfrac{\text{d}B}{\text{d}t} $ , 通电螺线管中标准磁探针和待测高频磁探针的线圈中感受的磁场变化$\dfrac{{{\text{d}}B}}{{{\text{d}}t}}$ 近乎相同, 因此$ \dfrac{\varepsilon_0}{\varepsilon}=\dfrac{N_0S_0}{NS} $ , 其中$ N_0S_{\text{0}} $ 为已知的标准磁探针的有效面积, 而$ NS_{ } $ 为高频磁探针待测方向的线圈的有效面积, 进而可以计算得到$ NS_{ }=N_0S_0\dfrac{\varepsilon}{\varepsilon_0} $ . 因为标准磁探针和待测高频磁探针的信号引出线约为5 m, 尽管标准磁探针和待测高频磁探针的共振频率不同, 但两磁探针共振频率均远高于100 Hz, 因此本标定实验设置仍可用于标定高频磁探针的有效面积$ NS_{ } $ . 对所有高频磁探针3个测量方向线圈的有效面积的标定结果如表1所列. 可以看到, 测量环向和径向磁扰动的线圈有效面积接近, 并大于测量极向磁扰动的线圈有效面积, 它们的大小在0.02 m2 附近, 标定误差在0.1%左右. -
由于磁探针本身及其信号传输线具有阻抗, 磁探针诊断最终的输出信号
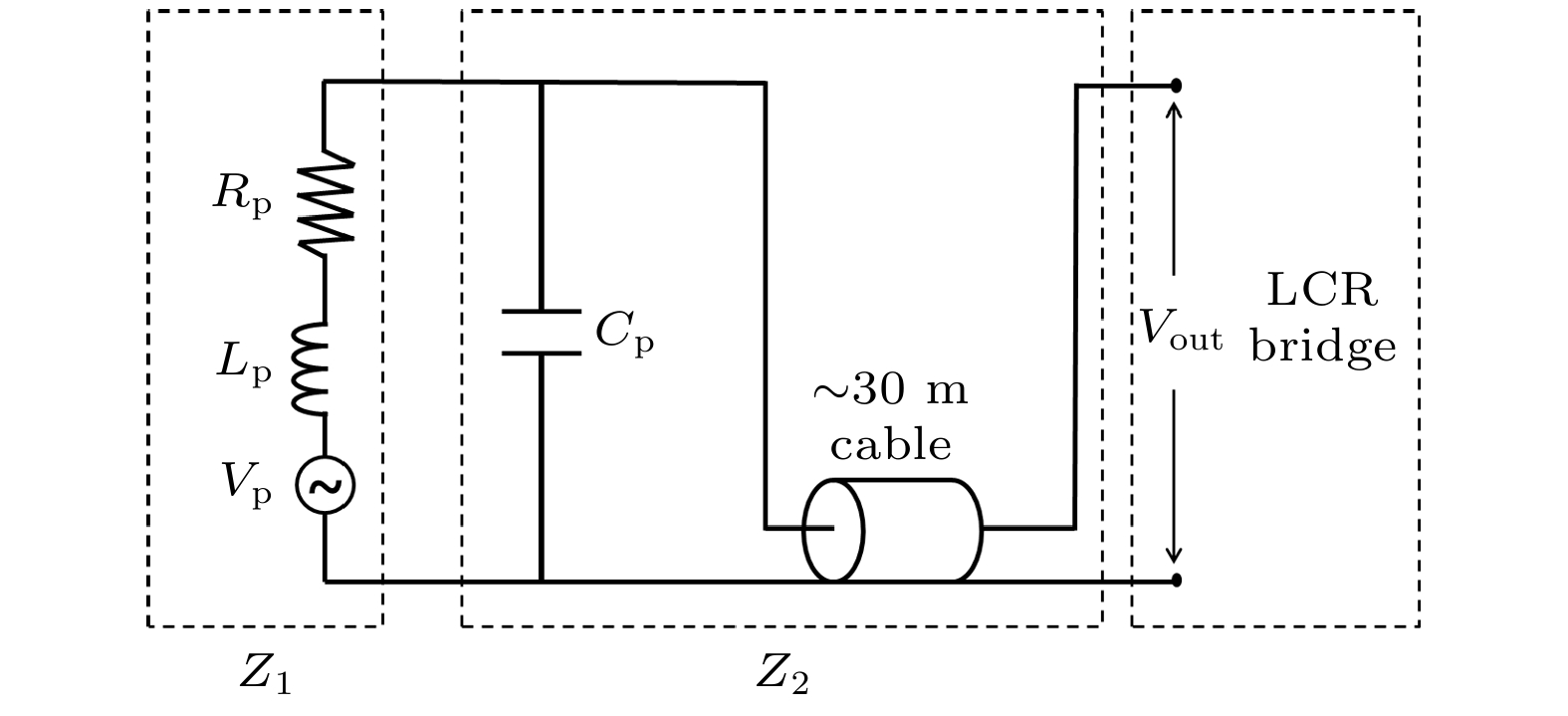
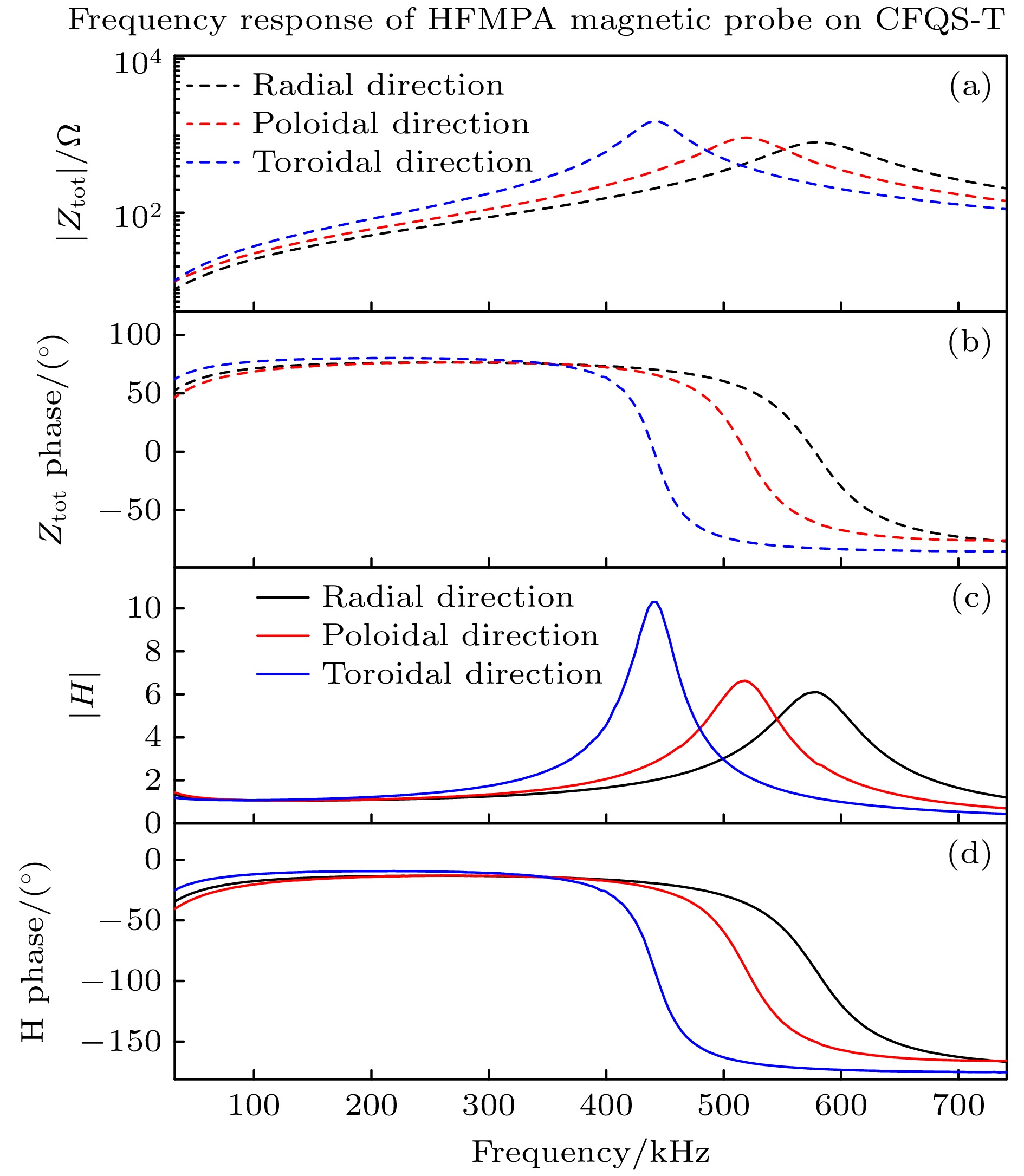
${V_{{\text{out}}}}$ 的幅度和相位与磁探针本身初始感应到的信号${V_{\text{p}}}$ 不同, 并与频率有关. 为了获得等离子体放电中磁探针附近的真实磁扰动信号的幅度和相位信息, 并了解所设计的磁探针对磁扰动频率的测量能力, 有必要对磁探针进行频率响应标定. 本研究基于具有高工作频率的阻抗分析仪(型号: GWINSTEK LCR-8210)对CFQS-T高频磁探针阵列(HFMPA)进行原位频率响应标定. 该方法也曾应用于SUNIST球形托卡马克[13,14]及EAST托卡马克[21]等装置上的磁探针频率响应研究. 图5所示为CFQS-T高频磁探针进行频率响应标定时的电路示意图, 在高频磁探针30 m信号传输线的末端没有接BNC信号转接盒, 而是接了阻抗分析仪, 图中虚线框${Z_1}$ 表示高频磁探针的电阻(${R_{\text{p}}}$ )和电感(${L_{\text{p}}}$ )的总阻抗, 即${Z_1} = {R_{\text{p}}} +{\text{i}}\omega {L_{\text{p}}}$ , 其中$\omega $ 表示角频率; 虚线框${Z_2}$ 表示高频磁探针的电容(${C_{\text{p}}}$ )和信号传输线的总阻抗, 因此总的电路输出阻抗${Z_{{\text{tot}}}}$ 满足关系式$\dfrac{1}{{{Z_{{\text{tot}}}}}} =\dfrac{1}{{{Z_1}}} + \dfrac{1}{{{Z_2}}}$ , 或写作${Z_{{\text{tot}}}} = \dfrac{{{Z_1}{Z_2}}}{{{Z_1} + {Z_2}}}$ . 标定过程中, 通过设置阻抗分析仪的扫频范围(如设置1 kHz—1 MHz)可以快速得到总的电路输出阻抗${Z_{{\text{tot}}}}$ 的幅度-频率响应和相位-频率响应特征, 分别如图6(a), (b)所示. 对于图5所示的磁探针电路, 其传递函数$H = \dfrac{{{V_{{\text{out}}}}}}{{{V_{\text{p}}}}} = \dfrac{{{Z_2}}}{{{Z_1} + {Z_2}}}$ , 由于高频磁探针的电阻(${R_{\text{p}}}$ )和电感(${L_{\text{p}}}$ )可以提前在实验室测得, 因此磁探针总的电路的传递函数$H$ 可以通过已知的${Z_1}$ 和测得的$ {\mathrm{Z}}_{\mathrm{t}\mathrm{o}\mathrm{t}} $ 导出, 其幅度-频率响应与相位-频率响应曲线分别如图6(c), (d)所示. 由于CFQS-T的8个高频磁探针的频率响应类似, 因此本节只展示了一个高频磁探针的频率响应特征, 可以看到高频磁探针3个测量方向的频率响应有所不同, 其中测量极向磁扰动的线圈的共振频率在~518 kHz, 测量环向磁扰动的线圈的共振频率~443 kHz, 测量径向磁扰动的线圈的共振频率~580 kHz, 3个测量方向共振频率均高于400 kHz, 满足对相关物理研究的需求. -
高频磁探针阵列(HFMPA)诊断已在CFQS-T准环对称仿星器上研制成功, 本节将介绍高频磁探针阵列诊断在CFQS-T上的初步应用. 首先将介绍高频磁探针阵列诊断在低频磁涨落测量分析中的应用, 通过与低频磁探针阵列(LFMPA)诊断测量结果的比较, 以证明高频磁探针阵列已经正常工作; 接着将介绍高频磁探针阵列诊断在CFQS-T高频磁涨落分析中的应用.
-
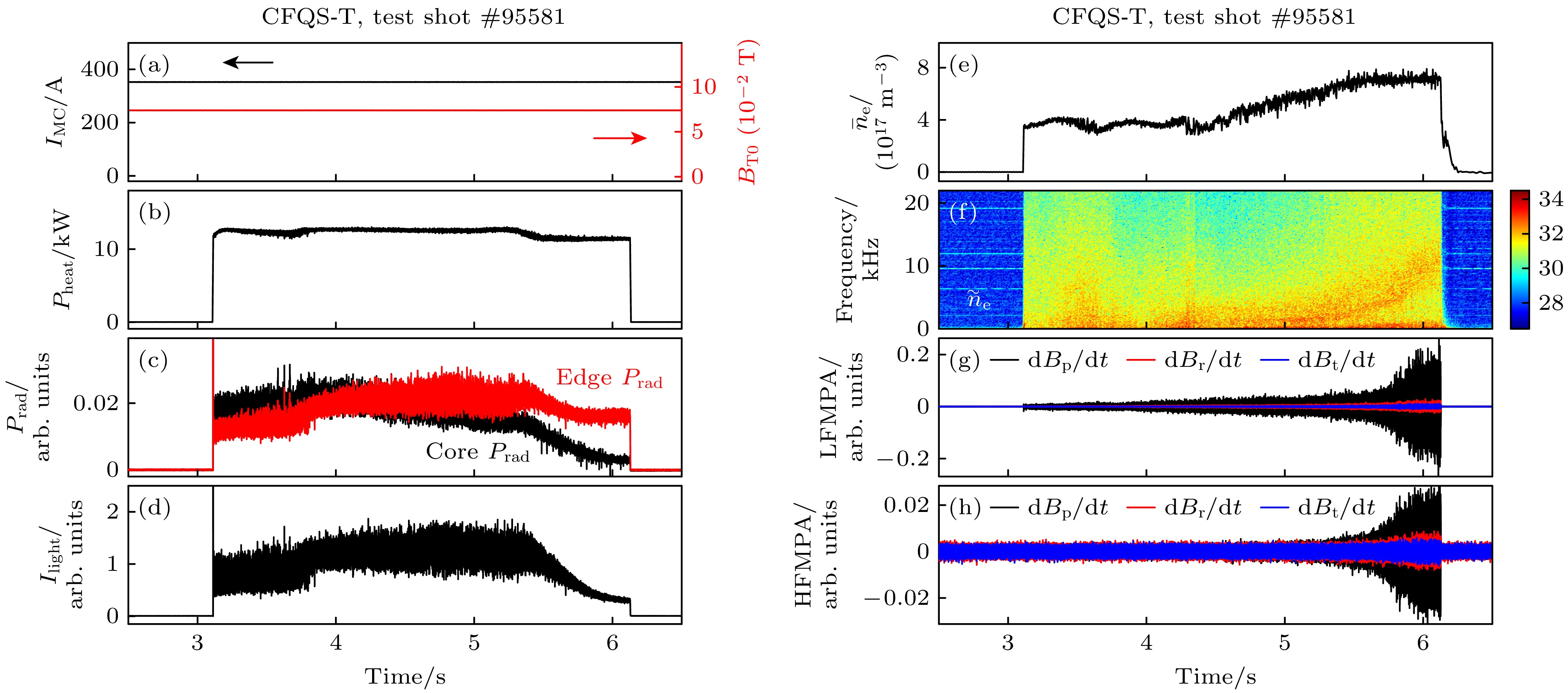
等离子体磁涨落对等离子体约束和输运具有重要的影响, 因此有必要仔细分析实验中的磁涨落特征. 本节以一炮典型放电实验为例介绍在CFQS-T等离子体中, 观察到一支低频准相干磁涨落模式, 其与等离子体参数的变化密切相关, 本节还将介绍基于高频磁探针阵列(HFMPA)诊断对其进行的初步测量分析以及与低频磁探针阵列(LFMPA)诊断对比分析的结果. 图7所示为这一典型放电(#95581)的基本参数随时间演化信息, 这是一炮氦等离子体放电, 模块化磁体线圈电流(
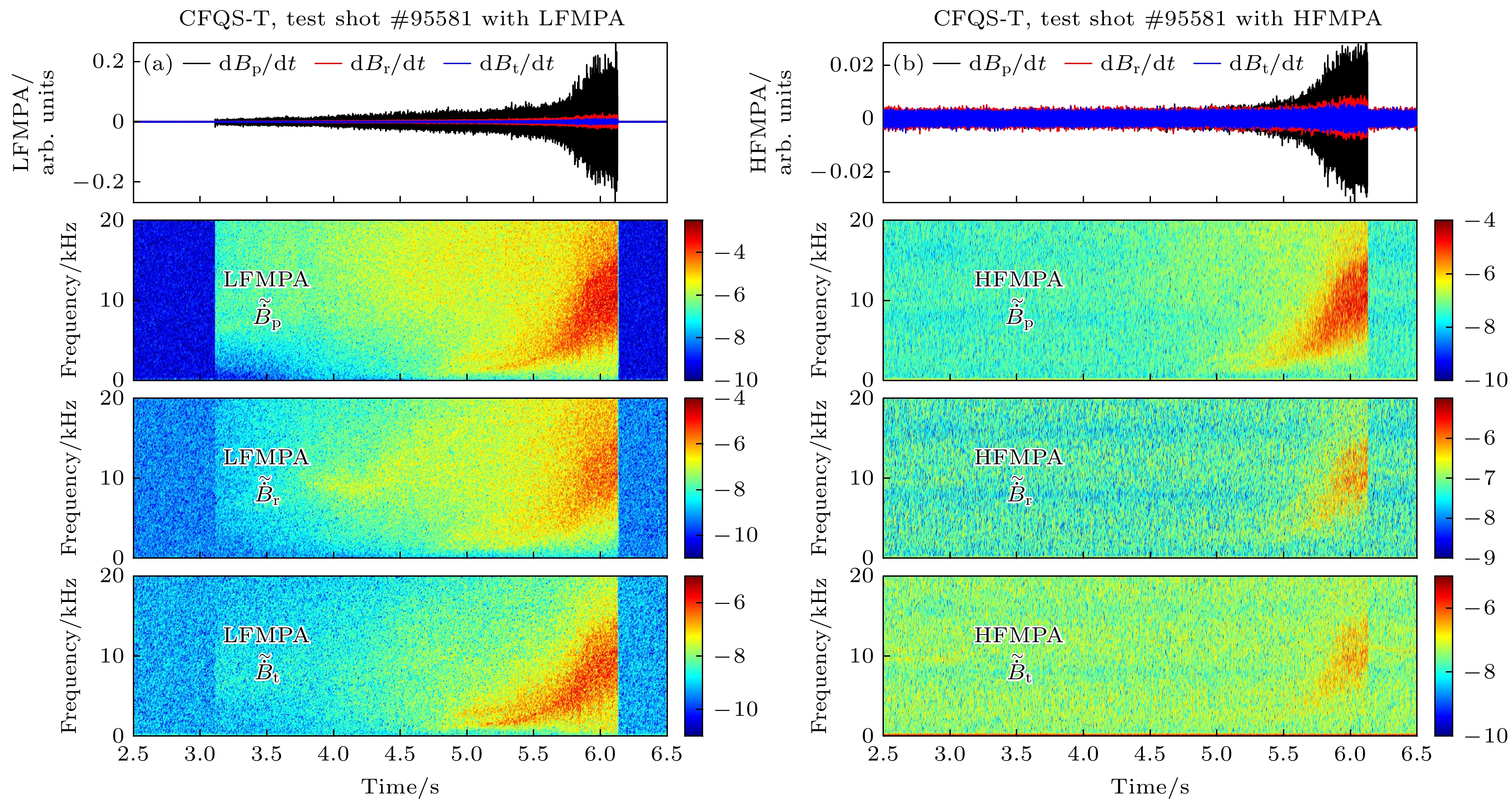
${I_{{\text{MC}}}}$ )为357 A(如图7(a)中黑线所示), 其使得在CFQS-T仿星器中产生中心平衡磁场${B_{{\text{T0}}}}$ 约为0.0749 T(见图7(a)中红线所示)的准环对称磁位形, 这里${B_{{\text{T0}}}}$ 是在理论模拟分析基础上, 根据定标公式${B_{{\text{T0}}}} = \dfrac{{0.0875}}{{417}}{I_{{\text{MC}}}}$ 计算得到, 其中${I_{{\text{MC}}}}$ 的单位为安培A, 求得的${B_{{\text{T0}}}}$ 单位为特斯拉T; 如图7(b)所示, 本次放电的射频波加热入射功率约为12 kW, 其由2.45 GHz的磁控管产生, 微波干涉诊断测得放电中等离子体电子弦平均密度从3.7 × 1017 m–3逐渐增至7.2 × 1017 m–3 (见图7(e)), 等离子体辐射功率测量(图7(c))和可见光谱测量(没有加滤光片, 图7(d))显示在5.4 s左右边界和芯部等离子体辐射与可见光谱强度均开始显著降低; 与此同时, 如图7(f)所示, 微波干涉诊断测得的等离子体密度涨落出现一支准相干模, 在时间t = 5.50—6.05 s, 频率从 3 kHz增至7—13 kHz, 在t = 5.5 s之后LFMPA磁探针和HFMPA磁探针测得的三维磁扰动分量也均有显著增大, 分别如图7(g), (h)所示, 这说明放电中等离子体涨落与等离子体状态变化有密切的关系. 图8(a), (b)分别给出本次放电中LFMPA磁探针与HFMPA磁探针测得的三维磁涨落(极向磁涨落$ {\tilde {\dot B}_{\text{p}}} $ 、径向磁涨落$ {\tilde {\dot B}_{\text{r}}} $ 以及环向磁涨落$ {\tilde {\dot B}_{\text{t}}} $ )的时频谱信息, 可以看到在5 s附近低频模涨落已经出现(频率约1.5 kHz), 但在5.5 s左右其幅度和频率开始有明显增强, 在6 s左右其频率增至3—16 kHz. 图7和图8中用到的LFMPA磁探针和HFMPA磁探针编号分别为M7和HM4, 如图4(c)所示. 微波干涉诊断与磁探针诊断均观察到低频准相干模, 尽管两者分别测量涨落的静电分量和磁分量, 频率有所不同, 但比较接近, 还是可以说明实验中观察到低频准相干模具有电磁物理属性, 且具有三维磁扰动分量.基于高频磁探针阵列(HFMPA)和低频磁探针阵列(LFMPA)诊断进一步分析该低频电磁涨落模式的传播特征. 选取
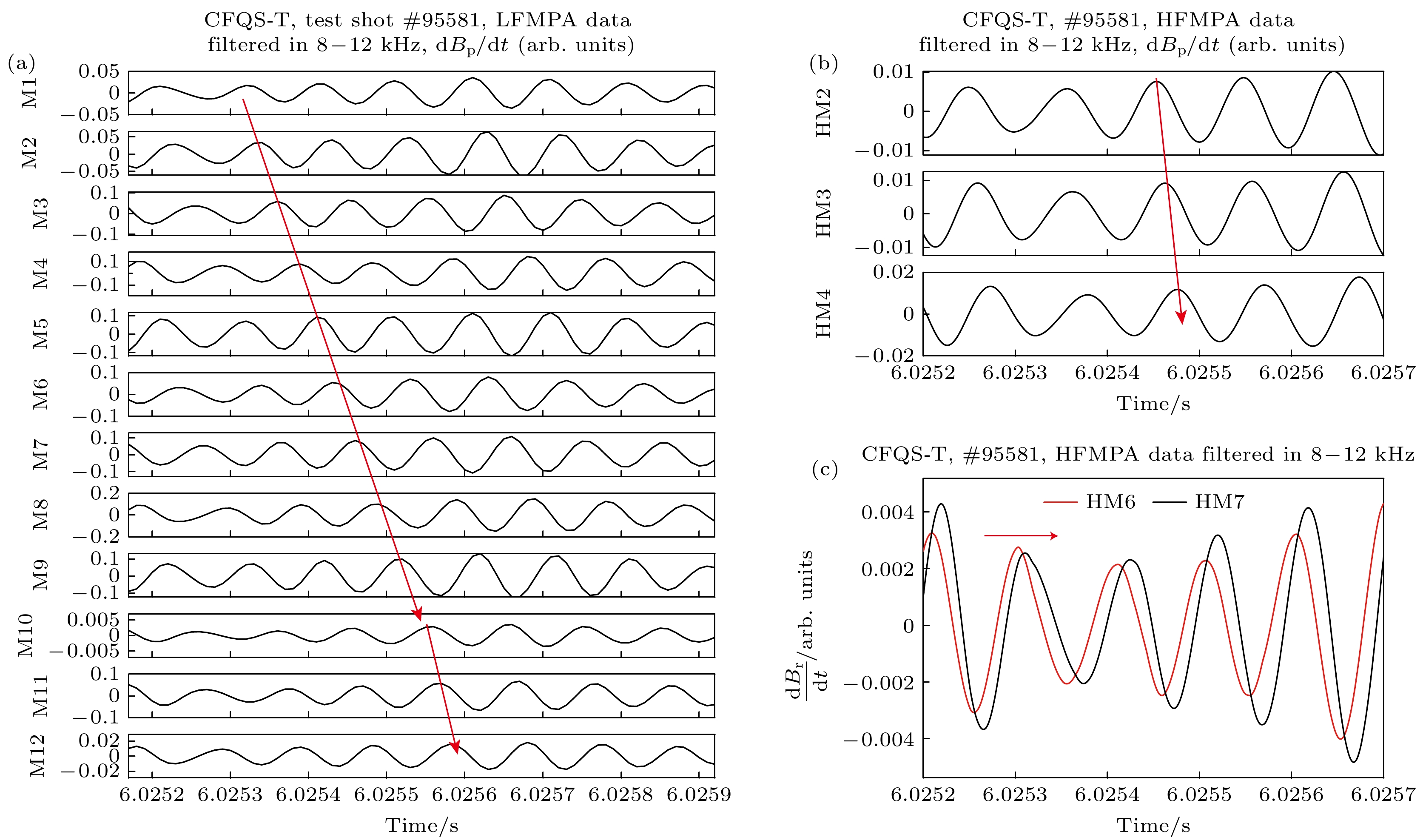
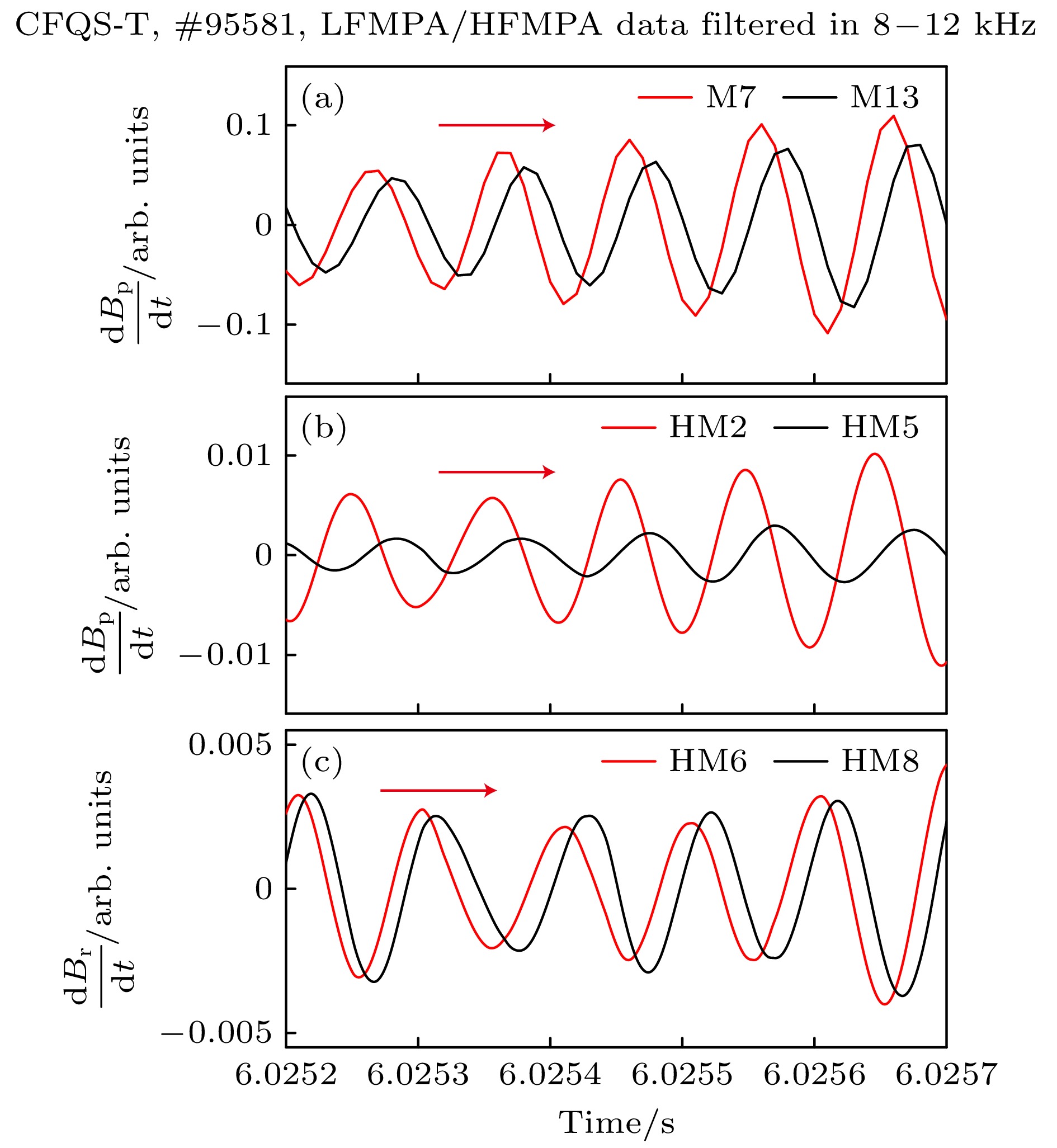
$t = 6{\text{ s}}$ 附近的一段短时间片($t = 6.0252—6.0257{\text{ s}}$ )的磁探针数据进行分析, 对磁探针数据均进行频率$f = 8—12{\text{ kHz}}$ 的带通滤波, 基于滤波后的磁探针数据分析低频准相干电磁涨落模式在$t = 6{\text{ s}}$ 附近的极向传播和环向传播特征, 分别如图9和图10所示. 图9(a)所示为各LFMPA磁探针测得的极向磁涨落数据经过带通滤波后的时间演化信息, 每个编号的LFMPA磁探针对应的空间位置如图4(c)所示, 可以看到低频准相干电磁涨落模式沿极向按LFMPA磁探针编号顺序从M1传播至M2, 再传播至M3, 最终传播至M12, 如图中红线箭头所示. 图9(b)所示为分布在不同极向位置的3个HFMPA磁探针(HM2, HM3 和HM4)测得的极向磁涨落数据经过带通滤波后的时间演化信息, 图9(c)所示为分布在不同极向位置的两个HFMPA磁探针(HM6和HM7)测得的径向磁涨落数据经过带通滤波后的时间演化信息, 每个编号的HFMPA磁探针对应的空间位置也可在图4(c)找到, 可以看出HFMPA磁探针测得的低频准相干电磁涨落模式的极向传播方向与LFMPA磁探针测得的极向传播方向相同, 均传播在顺时针方向, 说明HFMPA磁探针也同样适用于研究磁涨落的极向传播特征. 从LFMPA诊断测得的低频磁涨落的极向传播特征(图9(a)所示)看出, 磁涨落特定频段的波形沿极向方向传播近似经过了3个周期, 因此其极向模数m近似可得m = 3. 如2.1节所述, 因为编号HM1—HM5的高频磁探针用的机械保护壳与编号HM6—HM8的高频磁探针用的机械保护壳不同, 两种保护壳对磁涨落传播至其内部的磁探针后引起的相位改变不同, 因此暂不便通过分析带不同保护壳的磁探针之间的相位差研究磁涨落的传播.基于高频磁探针阵列(HFMPA)与低频磁探针阵列(LFMPA)诊断, 对放电(#95581)中的低频电磁涨落的环向传播特征进行分析. 图10所示为带通滤波后的分布在不同环向位置的低频或高频磁探针测得的磁涨落数据的时间演化, 每个编号的磁探针位置同样可在图4(c)中找到, 如图10中红线箭头所示, 图10(a)显示低频准相干电磁涨落模式从M7传播至M13, 图10(b)显示低频准相干磁涨落模式从HM2传播至HM5, 图10(c)显示低频准相干磁涨落模式从HM6传播至HM8, 可以看出HFMPA测得的低频准相干磁涨落的环向传播方向与LFMPA测得的环向传播方向相同, 均为逆时针方向, 说明高频磁探针也同样适用于研究磁涨落的环向传播特征. HFMPA诊断的磁探针HM6和HM8环向间距
$\Delta {\phi _{\text{g}}} \approx {14.15^\circ }$ , 由HFMPA测得的低频电磁涨落(f = 8—12 kHz)从HM6传播到HM8的相位差$\Delta {\phi _m}$ 在$ {28.19^\circ }—{36.26^\circ } $ 范围, 初步估算环向模数的数值范围$n = \dfrac{{\Delta {\phi _m}}}{{\Delta {\phi _{\text{g}}}}} \approx 1.99—2.56$ , 更精确的环向模数计算还有待后期进一步分析确定. -
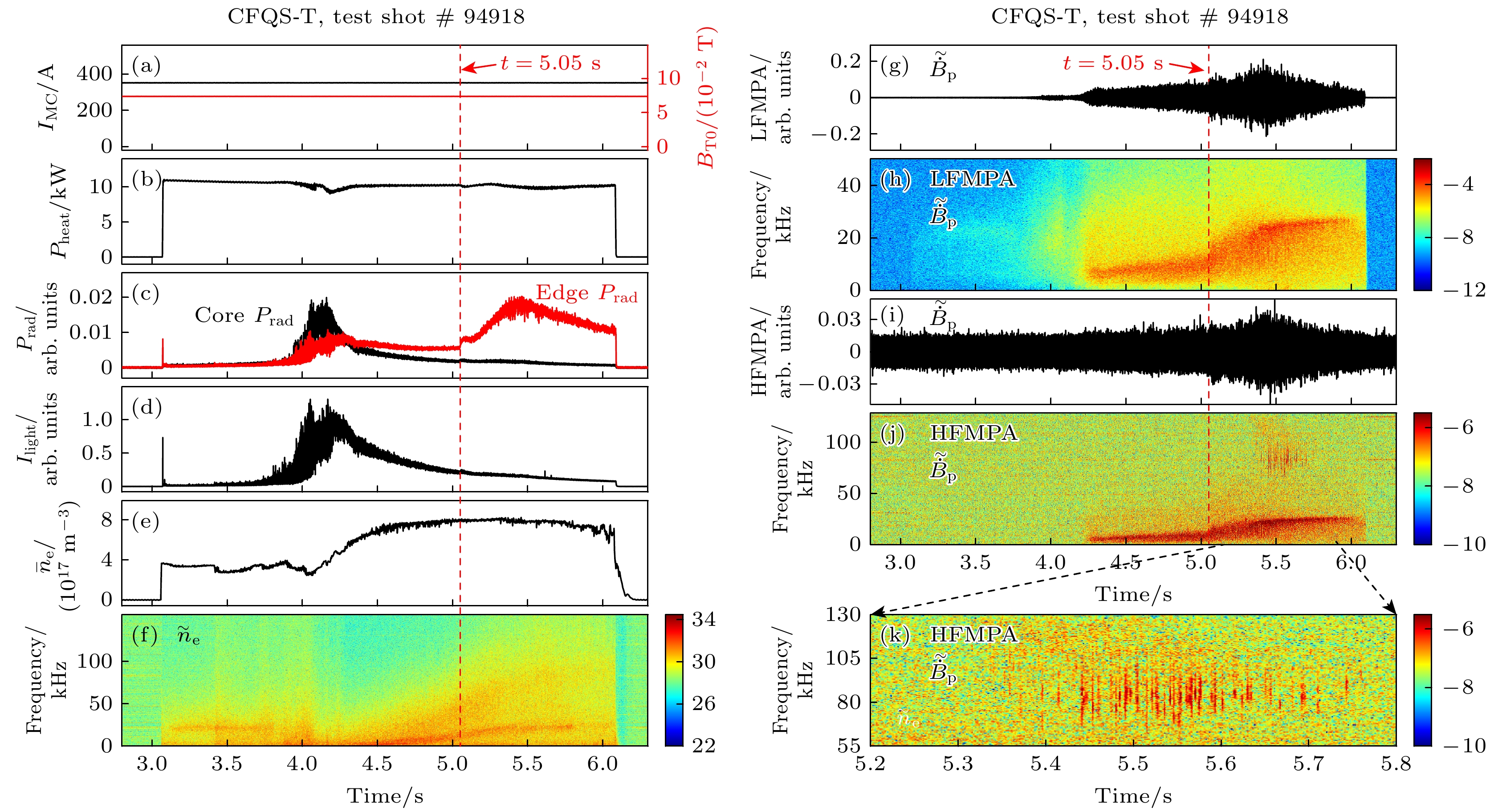
虽然CFQS-T准环对称仿星器目前的放电等离子体参数不高, 但在一些特定实验参数条件下, 也能在等离子体放电中观察到高频磁涨落. 高频磁探针阵列诊断作为目前CFQS-T上唯一能够测量频率大于50 kHz的磁涨落的诊断, 对相关物理实验研究起非常重要的作用. 图11所示为CFQS-T典型的一炮等离子体出现的高频磁涨落的放电参数演化信息, 这一炮是氢等离子体放电, 模块化磁体线圈电流同样也是357 A (见图11(a)中黑线), 对应的仿星器中心平衡磁场
${B_{{\text{T0}}}}$ 约为0.0749 T(见图11(a)中红线), 对于本次放电, 如图11(b)所示, 射频波加热的入射功率约为10.5 kW, 加热时间从3.06—6.08 s, 图11(c)—(e)所示分别为放电中等离子体辐射功率、可见光谱强度(没有加滤光片)及弦平均密度的随时间演化信息, 在时间$t = 5.05{\text{ s}}$ 左右, 等离子体边界辐射再次增强, 伴随等离子体涨落幅度也随之增强, 如图11(f)—(k)所示. 其中, 图11(f)是微波干涉诊断测得的等离子体密度涨落的时频谱, 可以看到在t = 5.05—5.90 s的时间内, 低频准相干密度涨落的频率由13 kHz增至 28 kHz, 与此同时, 20—100 kHz的宽谱密度涨落幅度也有所增强; 图11(g), (h)分别所示为LFMPA磁探针(M7, 见图4(c))测得的极向磁涨落信号的时间演化及其对应的时频谱, LFMPA也观察到了微波干涉诊断测得的低频准相干模, 说明该涨落模式具有电磁物理属性; 图11(i), (j)分别所示为HFMPA磁探针(HM4, 见图4(c))测得的极向磁涨落信号的时间演化及其对应的时频谱, 可以看到HFMPA不仅测得了低频准相干模, 还测得了频率在65—105 kHz的高频阵发性磁涨落, 如图11(j), (k)所示, 该高频磁涨落与微波干涉诊断测得的高频宽谱密度涨落有明显差别, 说明该高频阵发性涨落的静电分量很弱, 主要以磁扰动分量为主. 如图11(c)所示, 在等离子体放电早期t = 4 s附近, 辐射诊断测得的等离子体芯部辐射(图中黑线)高于边界辐射(图中红线), 而在放电后期(如t = 5.05 s以后), 边界等离子体辐射显著高于芯部辐射, 在t = 5.35 s左右, 高频磁涨落出现, 说明边界等离子体辐射增强与高频磁涨落出现有较强的相关性.基于高频磁探针阵列(HFMPA)诊断, 可以方便研究图11(k)中所示的高频磁涨落的传播特征. 选取
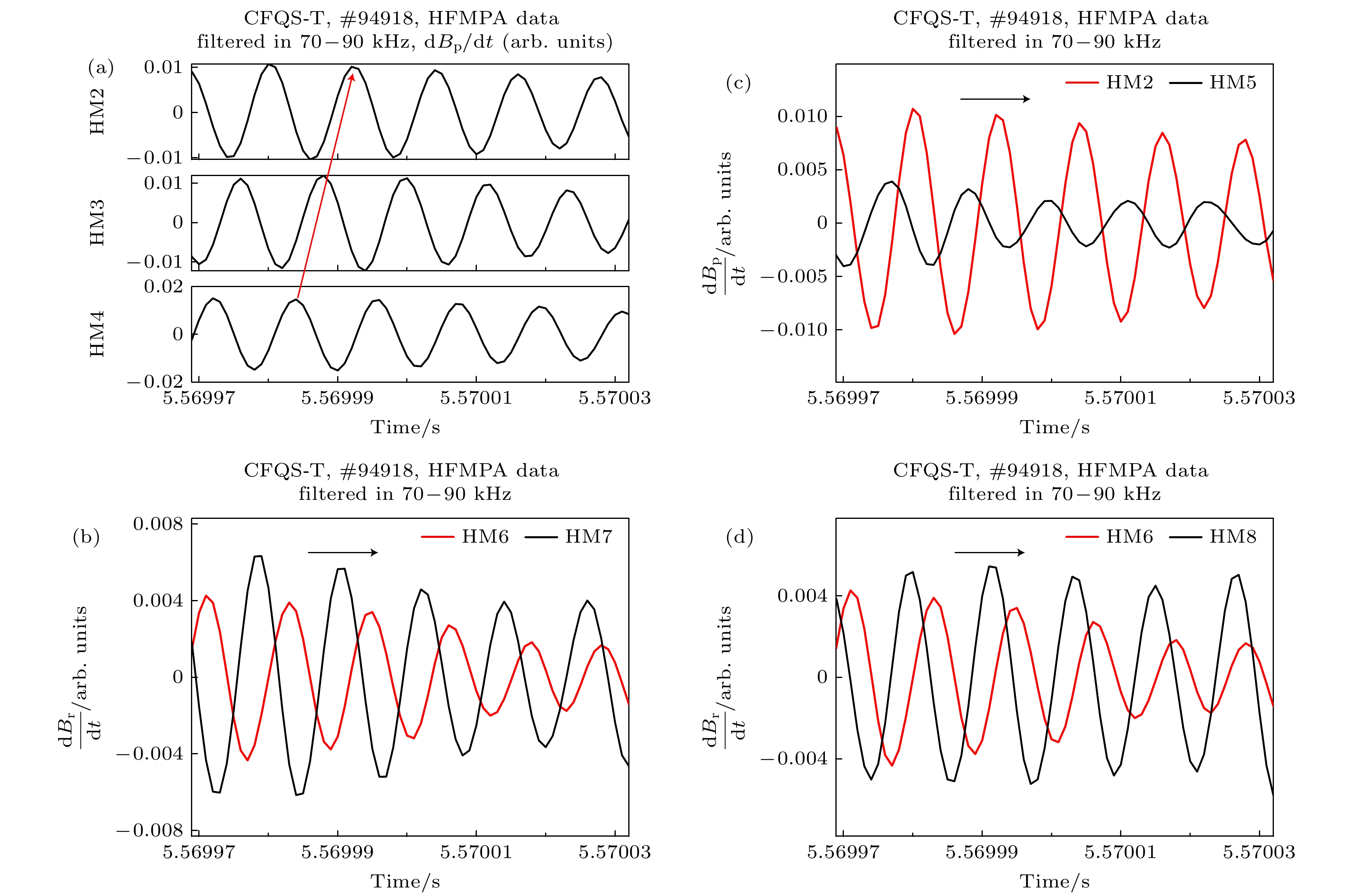
$t = 5.56{\text{ s}}$ 附近的一段短时间片($t = 5.56997— 5.57003{\text{ s}}$ )的高频磁探针数据进行频率$f = 70— 90{\text{ kHz}}$ 的带通滤波, 基于滤波后的HFMPA磁探针数据分析高频磁涨落模式在$t = 5.56{\text{ s}}$ 附近的极向传播和环向传播特征, 如图12所示. 图12(a), (b)所示分别为带不同保护壳的布置在不同极向位置的HFMPA磁探针测得的磁信号经过带通滤波后的时间演化信息, 它们的编号代表的位置信息如图4所示, 如图12(a), (b)中箭头所示, 可以看到$f = 70—90{\text{ kHz}}$ 的高频磁涨落模式的极向传播是从HM4经HM3传播至HM2(见图12(a)), 或从HM7传播至HM6(见图12(b)), 均反映在极向上传播在逆时针方向. 由于CFQS-T不同极向位置磁场曲率不同, 对扰动模结构影响较大, HFMPA在极向上布置的磁探针数量非常有限(一个环向位置沿极向最多只布置了3个磁探针), 因此, HFMPA在计算磁涨落极向模数时误差比较大, 很难准确给出高频磁涨落的极向模数. 图12(c), (d)所示分别为带不同保护壳的布置在不同环向位置的HFMPA磁探针测得的磁信号经过带通滤波后的时间演化信息, 如图中箭头所示, 可以看到$f = 70—90{\text{ kHz}}$ 的高频磁涨落模式环向传播从HM5传播至HM2(见图12(c)), 或从HM8传播至HM6(见图12(d)), 均反映在环向传播在顺时针方向. 同样基于HFMPA的编号为HM6和HM8的磁探针(环向间距$\Delta {\phi _{\text{g}}} \approx {1}{4.15^\circ }$ )估算高频磁涨落的环向模数, 由于HFMPA测得的高频磁涨落(f = 70—90 kHz)从HM8传播到HM6的相位差$\Delta {\phi _m}$ 在${4.37^\circ }—{36.23^\circ }$ 范围, 初步估算环向模数的数值范围$n = \dfrac{{\Delta {\phi _m}}}{{\Delta {\phi _{\text{g}}}}} \approx 0.31—2.56$ , 更精确的环向模数计算还有待后期进一步分析确定. -
本文报道了在CFQS-T准环对称仿星器中新研制的高频磁探针阵列诊断及其在等离子体放电分析中的初步应用. 所报道的高频磁探针阵列诊断是CFQS-T仿星器上首个可以测量分析高频磁涨落的诊断. 高频磁探针阵列诊断共由8个相同的高频磁探针组成, 高频磁探针绕线骨架经过精心设计, 绕线也选用满足CFQS-T实验条件的线材, 每个高频磁探针可以同时测量极向、环向及径向磁涨落; 高频磁探针在真空室内壁不同极向和环向位置布置, 可用于研究磁涨落在极向和环向的传播特征; 相比于低频磁探针阵列最高可以分辨环向模数
$n = \pm 6$ , 高频磁探针阵列最高可以分辨环向模数$n = \pm 16$ , 具有研究更高环向模数的磁涨落的潜力. 每个高频磁探针的有效面积均已经标定, 其原位频率响应标定也已经完成, 分析显示高频磁探针3个测量方向的共振频率均高于400 kHz, 满足对300 kHz及以下磁涨落的测量需求.高频磁探针阵列诊断在CFQS-T等离子体放电中的初步应用显示, 高频磁探针阵列诊断在测量三维低频磁涨落及其极向和环向传播方向时与CFQS-T低频磁探针阵列测量结果相似, 说明高频磁探针阵列已正常工作. 本文首次报道了在CFQS-T上观察到等离子体放电中出现高频磁涨落(频率在
$f = 65—105{\text{ kHz}}$ ), 通过高频磁探针阵列测量得其极向和环向传播特征, 这为后续深入研究该高频磁涨落的物理性质奠定了基础.后续将基于高频磁探针阵列及CFQS-T其他诊断测得的实验数据, 编写更多实验数据分析程序, 并结合理论模拟程序, 深入开展CFQS-T低频和高频磁涨落的模结构特征分析及其与等离子体参数演化关系的物理研究. 基于目前高频磁探针阵列的研制经验, 计划在未来CFQS仿星器上增加更多的高频磁探针, 助力CFQS仿星器开展相关物理实验研究.
感谢西南交通大学聚变科学研究团队、核工业西南物理研究院, 以及合肥科烨电物理设备制造有限公司的相关老师和同学对高频磁探针阵列诊断研制过程中的帮助.
CFQS-T准环对称仿星器高频磁探针阵列诊断的研制及初步应用
Development and preliminary application of high-frequency magnetic probe array on quasi-axisymmetric stellarator CFQS-T
-
摘要: 对于磁约束聚变实验装置, 磁探针诊断是一种基础又非常重要的研究等离子体磁涨落的诊断. 中国首台准环对称仿星器(Chinese First Quasi-axisymmetric Stellarator, CFQS)实验运行的第1阶段(也称为CFQS-T准环对称仿星器)的物理实验研究需要磁探针诊断提供相应的等离子体磁涨落测量. 本文报道了在CFQS-T准环对称仿星器上新研制的高频磁探针阵列诊断, 其由8个相同的三维高频磁探针组成, 每个高频磁探针可以同时测量极向、径向及环向3个方向的磁涨落信号; 优化的空间布置使得高频磁探针阵列可以用于研究磁涨落的极向和环向传播特征, 其最高环向模数分辨相比于低频磁探针阵列的n = ±6提高至n = ±16. 本文将简要介绍高频磁探针阵列诊断的机械系统、信号传输线、采集与控制系统等主要子系统及在研制各系统过程中克服的挑战, 以及对高频磁探针的有效面积标定和原位频率响应标定的研究结果, CFQS-T高频磁探针每个测量方向的共振频率均大于400 kHz, 满足测量50—300 kHz高频磁涨落的设计需求. 初步的应用研究显示高频磁探针阵列诊断可用于低频和高频磁涨落的时频谱、极向和环向传播分析, 值得注意的是, 本文首次报道了对CFQS-T上高频磁涨落的测量分析结果. 高频磁探针阵列诊断的成功研制有助于CFQS-T深入开展等离子体电磁涨落的相关研究.
-
关键词:
- CFQS-T准环对称仿星器 /
- 高频磁探针阵列 /
- 系统设置与标定 /
- 初步应用
Abstract: For magnetic confined fusion devices, magnetic probe diagnostic is a basic but very important diagnostic tool for studying plasma magnetic fluctuations. The first experimental phase of the Chinese First Quasi-axisymmetric Stellarator (CFQS), which is also called CFQS-T, needs magnetic probe diagnostics to provide plasma magnetic fluctuation measurements, especially the high-frequency ($50 \leqslant f \leqslant 300$ kHz) magnetic fluctuation measurements. In this paper, a newly developed high-frequency magnetic probe array (HFMPA) diagnostic on the CFQS-T is reported. This array consists of 8 identical three-dimensional high-frequency magnetic probes, each of which can simultaneously measure magnetic fluctuations in the poloidal, radial and toroidal directions. The HFMPA magnetic probes are carefully mounted on the inner vacuum vessel wall of the CFQS-T, and their positions are precisely measured by the laser tracker system. The HFMPA can be used to study the poloidal and toroidal propagation characteristics of magnetic fluctuations due to the optimized spatial arrangement, and its maximum toroidal mode number resolution is improved to n = ±16 compared with n = ±6 of the low-frequency magnetic probe array (LFMPA, used for the $f \leqslant 50$ kHz magnetic fluctuation measurements). The main subsystems of the HFMPA diagnostic, such as the mechanical system, signal transmission lines, acquisition and control systems, and the challenges overcome in the development of each subsystem, will be briefly introduced in this paper. The effective areas of the HFMPA magnetic probes are calibrated by the relative calibration method, which shows that their areas are all around 0.02 m2. The in-situ frequency response of the HFMPA magnetic probes is calibrated with an LCR digital bridge with a maximum working frequency of 10 MHz. The resonance frequency of the HFMPA magnetic probe in each measurement direction is greater than 400 kHz, which meets the design requirements for measuring 50–300 kHz high-frequency magnetic fluctuations in CFQS-T. Preliminary applications of the HFMPA diagnostic in studying the low-frequency (1.5–16.0 kHz) magnetic fluctuations and high-frequency (65–105 kHz) magnetic fluctuations in CFQS-T are briefly introduced, which shows that the HFMPA diagnostic works well for providing the spectrogram, poloidal, and toroidal propagation information of low-frequency and high-frequency magnetic fluctuations. It is worth noting that the measurement and analysis results of high-frequency (65–105 kHz) magnetic fluctuations in CFQS-T are reported for the first time in this paper. The successful development of the HFMPA diagnostic will help to carry out in-depth research on plasma magnetic fluctuations in CFQS-T stellarator. -

-
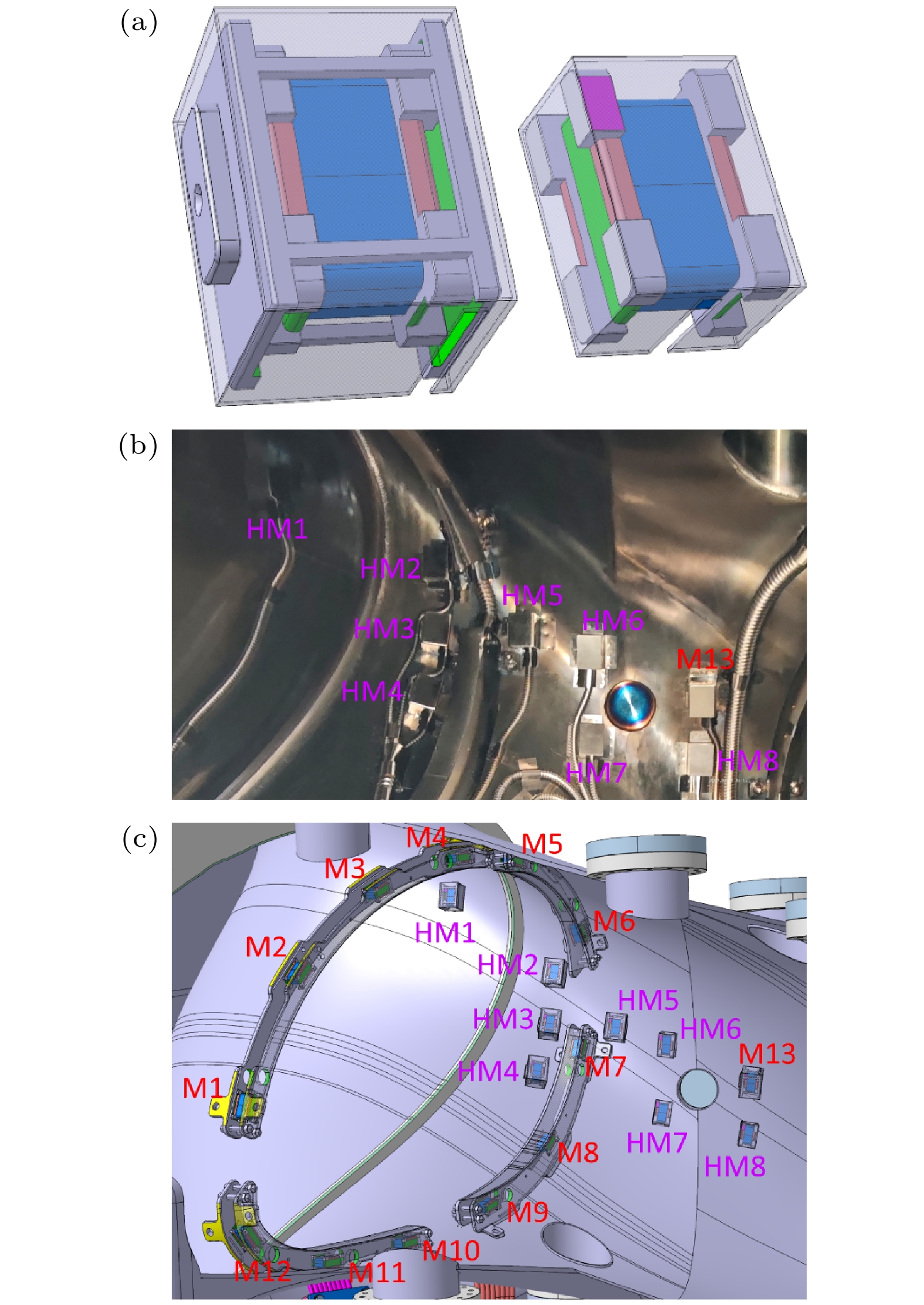
图 4 (a) CFQS-T准环对称仿星器上的高频磁探针及其机械保护部件的模型; (b) CFQS-T准环对称仿星器上的高频磁探针的实物照片; (c) 包含低频磁探针阵列(M1—M13)和高频磁探针阵列(HM1—HM8)的模型
Figure 4. (a) Models of the high-frequency magnetic probes and their metal protective cases; (b) photo of the high-frequency magnetic probe array on CFQS-T; (c) model of the low-frequency (M1–M13) and high-frequency (HM1–HM8) magnetic probe arrays on CFQS-T.
图 6 CFQS-T仿星器上三维高频磁探针的原位频率响应标定结果 (a), (b) 高频磁探针总的线路输出阻抗的幅度和相位频率响应; (c), (d) 高频磁探针总的线路传递函数的幅度和相位频率响应
Figure 6. Results of in-situ frequency response calibration of the HFMPA 3D magnetic probe on CFQS-T: (a), (b) Frequency responses of amplitude and phase of the total output impedance respectively; (c), (d) frequency responses of the amplitude and phase of the transfer function, respectively.
图 7 CFQS-T一炮氦等离子体放电(#95581)随时间演化信息 (a) 模块化线圈的电流(黑线)和根据定标公式计算的中心平衡磁场强度(红线); (b) 加热入射功率; (c) 等离子体芯部辐射功率(黑线)与边界辐射功率(红线); (d) 可见光谱强度; (e) 弦平均电子密度; (f) 微波干涉诊断测得的电子密度的时频谱; (g) 低频磁探针(选用M7, 见图4)测得的三维磁扰动; (h) 高频磁探针(选用HM4, 见图4)测得的三维磁扰动
Figure 7. Time history of a helium discharge #95581 on CFQS-T: (a) Electric current through a modular coil (black color), corresponding equilibrium magnetic field in the plasma center calculated with a scaling equation (red color); (b) injecting power of the plasma heating system; (c) core plasma radiation power (black color) and edge plasma radiation power (red color); (d) intensity of the visible light measured by a spectrometer; (e) line-averaged electron density measured by a microwave interferometer; (f) spectrogram of the plasma electron density measured by the microwave interferometer; (g) three-dimensional magnetic fluctuations measured by a low-frequency magnetic probe (M7, see Fig. 4); (h) three-dimensional magnetic fluctuations measured by a high-frequency magnetic probe (HM4, see Fig.4).
图 8 CFQS-T仿星器一炮放电(#95581)的时间演化信息 (a) 一个低频磁探针(M7, 见图4)测得的三维磁涨落信号及其对应的极向、径向及环向的磁涨落时频谱; (b) 一个高频磁探针(HM4, 见图4)测得的三维磁涨落信号及其对应的极向、径向及环向的磁涨落时频谱
Figure 8. Time evolutions of three-dimensional magnetic signals and their spectrograms in the discharge #95581 on CFQS-T: (a) A low-frequency magnetic probe (M7, see Fig. 4); (b) a high-frequency magnetic probe (HM4, see Fig. 4).
图 9 CFQS-T仿星器一炮放电中(#95581)的磁信号随时间演化信息 (a) 不同极向位置的低频磁探针测得的极向磁涨落信号经过8—12 kHz带通滤波后的演化信息; (b) 高频磁探针(HM2, HM3和HM4)测得的极向磁涨落信号经过8—12 kHz带通滤波后的演化信息; (c) 高频磁探针(HM6和HM7)测得的径向磁涨落信号经过8—12 kHz带通滤波后的演化信息; M1, HM2等标签表示不同的磁探针, 在图4中标出了这些磁探针的位置, 红色箭头表示8—12 kHz的磁涨落沿极向的传播方向
Figure 9. Time evolution of the magnetic signals in the discharge #95581 on CFQS-T: (a) Poloidal magnetic signals of the LFMPA magnetic probes; (b) poloidal magnetic signals of the HFMPA magnetic probes (HM2, HM3, and HM4); (c) radial magnetic signals of the HFMPA magnetic probes (HM6 and HM7), in different poloidal positions and filtered in the frequency band of 8–12 kHz; the labels M1, HM2, etc. represent different magnetic probes as shown in Fig. 4, the red arrows indicate the poloidal propagating direction of the magnetic fluctuations in the frequency range of 8–12 kHz.
图 10 CFQS-T仿星器一炮放电中(#95581)的磁信号随时间演化信息 不同环向位置的(a)低频磁探针(M7和M13)测得的极向磁涨落信号经过8—12 kHz带通滤波后的演化信息; (b) 高频磁探针(HM2和HM5)测得的极向磁涨落信号经过8—12 kHz带通滤波后的演化信息; (c) 高频磁探针(HM6和HM8)测得的径向磁涨落信号经过8—12 kHz带通滤波后的演化信息; 图中标签M7, HM2等表示不同的磁探针, 在图4中已经标记出来, 红色箭头显示了8—12 kHz的磁涨落沿环向的传播方向
Figure 10. Time evolution of the magnetic signal in the discharge #95581 on CFQS-T: (a) Poloidal magnetic signals of two LFMPA magnetic probes (M7 and M13); (b) poloidal magnetic signals of two HFMPA magnetic probes (HM2 and HM5); (c) radial magnetic signals of two HFMPA magnetic probes (HM6 and HM8), in different toroidal positions and filtered in the frequency band of 8–12 kHz; the labels M7 and HM2, etc. represent different magnetic probes as shown in Fig. 4, the red arrows indicate the toroidal propagating direction of the magnetic fluctuations in the frequency range of 8–12 kHz.
图 11 CFQS-T一炮氢等离子体放电(#94918) 随时间演化信息 (a) 模块化线圈的电流(黑线)以及根据定标公式计算的中心平衡磁场强度(红线所示); (b) 加热入射功率; (c) 等离子体芯部辐射功率(黑线所示)与边界辐射功率(红线所示); (d) 可见光谱强度; (e) 弦平均电子密度; (f) 微波干涉诊断测得的电子密度的时频谱; (g) 低频磁探针(选用M7, 见图4)测得的极向磁扰动信号及其(h) 时频谱; (i) 高频磁探针(选用HM4, 见图4)测得的极向磁扰动信号及其(j) 时频谱; (k)是图 (j)在5.2—5.8 s放大图
Figure 11. Time history of the hydrogen discharge #94918 on CFQS-T: (a) Electric current through a modular coil (black color) and corresponding equilibrium magnetic field in the plasma center calculated with a scaling equation (red color); (b) injecting power of the plasma heating system; (c) core plasma radiation power (black color) and edge plasma radiation power (red color); (d) intensity of the visible light measured by a spectrometer; (e) line-averaged electron density measured by a microwave interferometer; (f) spectrogram of the plasma electron density measured by the microwave interferometer; (g) poloidal magnetic signal measured by a low-frequency magnetic probe (M7, see Fig. 4) and its (h) spectrogram; (i) poloidal magnetic signals measured by a high-frequency magnetic probe (HM4, see Fig. 4) and its (j) spectrogram; (k) is the zoomed-in plot of Fig. (j).
图 12 CFQS-T仿星器一炮放电中(#94918)磁信号随时间演化信息 (a) 不同极向位置的高频磁探针(HM2, HM3及HM4)测得的极向磁涨落信号经过70—90 kHz带通滤波后的演化信息; (b) 不同极向位置的高频磁探针(HM6和HM7)测得的径向磁涨落信号经过70—90 kHz带通滤波后的演化信息; (c) 不同环向位置的高频磁探针(HM2和HM5)测得的极向磁涨落信号经过70—90 kHz带通滤波后的演化信息; (d) 不同环向位置的高频磁探针(HM6和HM8)测得的径向磁涨落信号经过70—90 kHz带通滤波后的演化信息; 标签HM2, HM5 和 MH8 等表示不同位置的高频磁探针, 见图4标记; (a), (b)中箭头显示了70—90 kHz的磁涨落沿极向的传播方向, (c), (d)中箭头显示了70—90 kHz的磁涨落沿环向的传播方向
Figure 12. Time evolution of the magnetic signals in the discharge #94918 on CFQS-T: (a) Poloidal magnetic signals of three poloidally separated HFMPA magnetic probes (HM2, HM3, and HM4), filtered in the frequency band of 70–90 kHz; (b) radial magnetic signals of two poloidally separated HFMPA magnetic probes (HM6 and HM7), filtered in the frequency band of 70–90 kHz; (c) poloidal magnetic signals of two toroidally separated HFMPA magnetic probes (HM2 and HM5), filtered in the frequency band of 70–90 kHz; (d) radial magnetic signals of two toroidally separated HFMPA magnetic probes (HM6 and HM8), filtered in the frequency band of 70–90 kHz; the labels HM2, HM5, and MH8, etc. represent the high-frequency magnetic probes in different positions as shown in Fig. 4, the arrows in (a), (b) indicate the poloidal propagating direction of the magnetic fluctuations in the frequency range of 70–90 kHz, while the arrows in (c), (d) indicate the toroidal propagating direction and of the magnetic fluctuations in the frequency range of 70–90 kHz.
表 1 CFQS-T仿星器高频磁探针标定后的有效面积(
$ NS $ )Table 1. Calibrated effective areas (
$ NS $ ) of HFMPA magnetic probes on CFQS-T.HFMPA
magnetic
probe
number$ NS $ in toroidal
direction/m2$ NS_{ } $ in radial
direction/m2$NS$ in poloidal
direction/m21 0.02003 0.02025 0.01756 2 0.02038 0.02030 0.01802 3 0.01999 0.02037 0.01729 4 0.02049 0.02095 0.01758 5 0.02040 0.02100 0.01797 6 0.01998 0.02022 0.01791 7 0.02040 0.02033 0.01721 8 0.01961 0.02097 0.01797 -
[1] Gates D A, Anderson D, Anderson S, Zarnstorff M, Spong D A, Weitzner H, Neilson G H, Ruzic D, Andruczyk D, Harris J H, Mynick H, Hegna C C, Schmitz O, Talmadge J N, Curreli D, Maurer D, Boozer A H, Knowlton S, Allain J P, Ennis D, Wurden G, Reiman A, Lore J D, Landreman M, Freidberg J P, Hudson S R, Porkolab M, Demers D, Terry J, Edlund E, Lazerson S A, Pablant N, Fonck R, Volpe F, Canik J, Granetz R, Ware A, Hanson J D, Kumar S, Deng C, Likin K, Cerfon A, Ram A, Hassam A, Prager S, Paz-Soldan C, Pueschel M J, Joseph I, Glasser A H 2018 J. Fusion Energ. 37 51 doi: 10.1007/s10894-018-0152-7 [2] Yoshida M, McDermott R M, Angioni C, Camenen Y, Citrin J, Jakubowski M, Hughes J W, Idomura Y, Mantica P, Mariani A, Mordijck S, Paul E J, Tala T, Verdoolaege G, Zocco A, Casson F J, Dif-Pradalier G, Duval B, Grierson B A, Kaye S M, Manas P, Maslov M, Odstrcil T, Rice J E, Schmitz L, Sciortino F, Solano E R, Staebler G, Valovič M, Wolfrum E, Snipes J A 2025 Nucl. Fusion 65 033001 doi: 10.1088/1741-4326/ad8ced [3] Toi K, Ogawa K, Isobe M, Osakabe M, Spong D A, Todo Y 2011 Plasma Phys. Contr. Fusion 53 024008 doi: 10.1088/0741-3335/53/2/024008 [4] Chen L, Zonca F 2016 Rev. Mod. Phys. 88 015008 doi: 10.1103/RevModPhys.88.015008 [5] Rahbarnia K, Thomsen H, Schilling J, vaz Mendes S, Endler M, Kleiber R, Könies A, Borchardt M, Slaby C, Bluhm T, Zilker M, Carvalho B B 2021 Plasma Phys. Contr. Fusion 63 015005 doi: 10.1088/1361-6587/abc395 [6] Salewski M, Spong D A, Aleynikov P, Bilato R, Breizman B N, Briguglio S, Cai H, Chen L, Chen W, Duarte V N, Dumont R J, Falessi M V, Fitzgerald M, Fredrickson E D, García-Muñoz M, Gorelenkov N N, Hayward-Schneider T, Heidbrink W W, Hole M J, Kazakov Y O, Kiptily V G, Könies A, Kurki-Suonio T, Lauber P, Lazerson S A, Lin Z, Mishchenko A, Moseev D, Muscatello C M, Nocente M, Podestà M, Polevoi A, Schneider M, Sharapov S E, Snicker A, Todo Y, Qiu Z, Vlad G, Wang X, Zarzoso D, Van Zeeland M A, Zonca F, Pinches S D 2025 Nucl. Fusion 65 043002 doi: 10.1088/1741-4326/adb763 [7] Xanthopoulos P, Mynick H E, Helander P, Turkin Y, Plunk G G, Jenko F, Gorler T, Told D, Bird T, Proll J H 2014 Phys. Rev. Lett. 113 155001 doi: 10.1103/PhysRevLett.113.155001 [8] Zhong W L, Zhao K J, Zou X L, Dong J Q 2020 Rev. Mod. Plasma Phys. 4 11 doi: 10.1007/s41614-020-00047-5 [9] Diallo A, Laggner F M 2021 Plasma Phys. Contr. Fusion 63 013001 doi: 10.1088/1361-6587/abbf85 [10] Fujisawa A 2021 Proc. Jpn. Acad Ser. B Phys. Biol. Sci. 97 103 doi: 10.2183/pjab.97.006 [11] Nespoli F, Masuzaki S, Tanaka K, Ashikawa N, Shoji M, Gilson E P, Lunsford R, Oishi T, Ida K, Yoshinuma M, Takemura Y, Kinoshita T, Motojima G, Kenmochi N, Kawamura G, Suzuki C, Nagy A, Bortolon A, Pablant N A, Mollen A, Tamura N, Gates D A, Morisaki T 2022 Nat. Phys. 18 350 doi: 10.1038/s41567-021-01460-4 [12] Sánchez E, Bañón Navarro A, Wilms F, Borchardt M, Kleiber R, Jenko F 2023 Nucl. Fusion 63 046013 doi: 10.1088/1741-4326/acb44e [13] Liu Y Q, Tan Y, Pan O, Ke R, Wang W H, Gao Z 2014 Rev. Sci. Instrum. 85 11E802 doi: 10.1063/1.4886423 [14] Cheng Z B, Tan Y, Gao Z, Wang S Z, Wang B B, Liu W B 2021 Rev. Sci. Instrum. 92 053518 doi: 10.1063/5.0043631 [15] Guo D J, Hu Q M, Li D, Shen C S, Wang N C, Huang Z, Huang M X, Ding Y H, Xu G, Yu Q Q, Tang Y J, Zhuang G 2017 Rev. Sci. Instrum. 88 123502 doi: 10.1063/1.4996360 [16] Han D L, Shen C S, Wang N C, Li D, Mao F Y, Ren Z K, Ding Y H, the J-TEXT Team 2021 Plasma Sci. Tech. 23 055104 doi: 10.1088/2058-6272/abeeda [17] Tu C, Liu A D, Li Z C, Tan M S, Luo B, You W, Li C G, Bai W, Fu C S, Huang F C, Xiao B J, Shen B, Shi T H, Chen D L, Mao W Z, Li H, Xie J L, Lan T, Ding W X, Xiao C J, Liu W D 2017 Rev. Sci. Instrum. 88 093513 doi: 10.1063/1.5003039 [18] Liang S Y, Ji X Q, Sun T F, Xu Y, Lu J, Yuan B S, Ren L L, Yang Q W 2017 AIP Adv. 7 125004 doi: 10.1063/1.5000268 [19] Chen D L, Shen B, Shi T H, Guo B H, Li T Y, Chen L X, Xue M M, Chu N 2023 Plasma Sci. Tech. 25 125102 doi: 10.1088/2058-6272/ace87d [20] Lan H, Shi T H, Yan N, Li X Q, Li S, Chen R, Duan M Y, Hu G H, Liu L N, Zhang W, Chen M, Zheng Y Y, Yuan Z, Wang Y, Xu Z H, Xu L Q, Zi P F, Chen L, Liu S C, Wu D G, Ding G F, Meng L Y, Wang Z C, Zang Q, Wu M Q, Zhu X, Hao B L, Lin X D, Gao X, Wang L, Xu G S 2023 Plasma Sci. Tech. 25 075105 doi: 10.1088/2058-6272/acbef5 [21] Lan H, Shi T H, Yan N, Li X Q, Li S, Chen R, Duan M Y, Liu L N, Chen M, Chen L X, Chen D L, Shen B, Wang Y, Xu Z H, Lu Z K, Shao L M, Zheng Y Y, Yuan Z, Xu L Q, Hu G H, Chen L, Liu S C, Zi P F, Wang P, Wu D G, Ding G F, Meng L Y, Shen J F, Yang S, Shao J R, Zang Q, Wang L, Xu G S 2024 Fusion Eng. Des. 207 114636 doi: 10.1016/j.fusengdes.2024.114636 [22] Ouyang T B, Qian Y Z, Liu S Q, Yang X S, Chen X C 2022 AIP Adv. 12 015314 doi: 10.1063/5.0074127 [23] Strait E J 2006 Rev. Sci. Instrum. 77 023502 doi: 10.1063/1.2166493 [24] Heeter R F, Fasoli A F, Ali-Arshad S, Moret J M 2000 Rev. Sci. Instrum. 71 4092 doi: 10.1063/1.1313797 [25] Artaserse G, Baruzzo M, Henriques R B, Gerasimov S, Lam N, Tsalas M 2019 Fusion Eng. Des. 146 2781 doi: 10.1016/j.fusengdes.2019.05.032 [26] Hole M J, Appel L C, Martin R 2009 Rev. Sci. Instrum. 80 123507 doi: 10.1063/1.3272713 [27] Moreau P, Le-Luyer A, Spuig P, Malard P, Saint-Laurent F, Artaud J F, Morales J, Faugeras B, Heumann H, Cantone B, Moreau M, Brun C, Nouailletas R, Nardon E, Santraine B, Berne A, Kumari P, Belsare S, Team W 2018 Rev. Sci. Instrum. 89 10J109 doi: 10.1063/1.5036537 [28] Takechi M, Matsunaga G, Sakurai S, Sasajima T, Yagyu J, Hoshi R, Kawamata Y, Kurihara K, Nishikawa T, Ryo T, Kagamihara S, Nakamura K 2015 Fusion Eng. Des. 96-97 985 [29] Haskey S R, Blackwell B D, Seiwald B, Hole M J, Pretty D G, Howard J, Wach J 2013 Rev. Sci. Instrum. 84 093501 doi: 10.1063/1.4819250 [30] Sakakibara S, Yamada H 2010 Fusion Sci. Tech. 58 471 doi: 10.13182/FST10-A10833 [31] Endler M, Brucker B, Bykov V, Cardella A, Carls A, Dobmeier F, Dudek A, Fellinger J, Geiger J, Grosser K, Grulke O, Hartmann D, Hathiramani D, Höchel K, Köppen M, Laube R, Neuner U, Peng X, Rahbarnia K, Rummel K, Sieber T, Thiel S, Vorköper A, Werner A, Windisch T, Ye M Y 2015 Fusion Eng. Des. 100 468 doi: 10.1016/j.fusengdes.2015.07.020 [32] Ascasibar E, Lapayese F, Soleto A, Jimenez-Denche A, Cappa A, Pons-Villalonga P, Portas A B, Martin G, Barcala J M, Garcia-Gomez R, Chamorro M, Cebrian L, Anton R, Bueno L, Reynoso C, Guisse V, Lopez-Fraguas A 2022 Rev. Sci. Instrum. 93 093508 doi: 10.1063/5.0102037 [33] Liu H F, Shimizu A, Xu Y H, Okamura S, Kinoshita S, Isobe M, Li Y B, Xiong G, Wang X Q, Huang J, Cheng J, Liu H, Zhang X, Yin D P, Wang Y, Murase T, Nakagawa S, Tang C J 2021 Nucl. Fusion 61 016014 doi: 10.1088/1741-4326/abbc85 [34] Shimizu A, Kinoshita S, Isobe M, Okamura S, Ogawa K, Nakata M, Yoshimura Y, Suzuki C, Osakabe M, Murase T, Nakagawa S, Tanoue H, Xu Y, Liu H F, Liu H, Huang J, Wang X, Cheng J, Xiong G, Tang C, Yin D, Wan Y 2022 Nucl. Fusion 62 016010 doi: 10.1088/1741-4326/ac369a [35] Wang X Q, Xu Y, Shimizu A, Isobe M, Okamura S, Todo Y, Wang H, Liu H F, Huang J, Zhang X, Liu H, Cheng J, Tang C J 2021 Nucl. Fusion 61 036021 doi: 10.1088/1741-4326/abd3ec [36] 黄捷, 李沫杉, 覃程, 王先驱 2022 物理学报 71 185202 doi: 10.7498/aps.71.20220729 Huang J, Li M S, Qin C, Wang X Q 2022 Acta Phys. Sin. 71 185202 doi: 10.7498/aps.71.20220729 [37] Liu H F, Zhang J, Xu Y H, Shimizu A, Cooper W A, Okamura S, Isobe M, Wang X Q, Huang J, Cheng J, Liu H, Zhang X, Tang C J 2023 Nucl. Fusion 63 026018 doi: 10.1088/1741-4326/acadef [38] 苏祥, 王先驱, 符添, 许宇鸿 2023 物理学报 72 215205 doi: 10.7498/aps.72.20230546 Su X, Wang X Q, Fu T, Xu Y H 2023 Acta Phys. Sin. 72 215205 doi: 10.7498/aps.72.20230546 [39] 李丹, 刘海峰 2025 物理学报 74 055203 doi: 10.7498/aps.74.20241606 Li D, Liu H F 2025 Acta Phys. Sin. 74 055203 doi: 10.7498/aps.74.20241606 [40] Cheng J, et al. Construction progress of the Chinese First Quasi-axisymmetric Stellarator (CFQS) and preliminary experimental results on CFQS-Test device Plasma Phys. Control. Fusion (PPCF-105174 [41] Lan H, et al. Development of a low-frequency magnetic probe array for the quasi-axisymmetric stellarator CFQS-T Fusion Engineering and Design (FUSENGDES-D-25-00438 [42] 黄晓莉 2009 博士学位论文(哈尔滨: 哈尔滨工业大学) Huang X L 2009 Ph. D. Dissertation (Harbin: Harbin Institute of Technology [43] 许亚东2019 博士学位论文(太原: 中北大学) Xu Y D 2019 Ph. D. Dissertation (Taiyuan: North University of China [44] 胡庆, 刘文晶, 赖小龙, 张德民 2021 电信传输原理、系统及工程(西安: 西安电子科技大学出版社) 第26页 Hu Q, Liu W J, Lai X L, Zhang D M 2021 Telecommunication Transmission Principles, Systems and Engineering (Xi'an: Xidian University Press) p26 [45] 陈力行, 陈大龙, 沈飊, 钱金平, 陈明 2024 核聚变与等离子体物理 44 105 Chen L X, Chen D L, Shen B, Qian J P, Chen M 2024 Nucl. Fusion Plasma Phys. 44 105 [46] Zhang J Z, Ji X Q, Sun T F, Liang S Y, Wang A, Wang J, Li J X, Liu J, Yang Q W 2021 ucl. Fusion Plasma Phys. 41 585 [张均钊, 季小全, 孙腾飞, 梁绍勇, 王傲, 王金, 李佳鲜, 刘健, 杨青巍 2021 核聚变与等离子体物理 41 585] Zhang J Z, Ji X Q, Sun T F, Liang S Y, Wang A, Wang J, Li J X, Liu J, Yang Q W 2021 ucl. Fusion Plasma Phys. 41 585 [47] Shen B 2016 Fusion Eng. Des. 112 969 doi: 10.1016/j.fusengdes.2016.02.051 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: