随着超声技术的发展, 弯曲振动超声换能器的应用越来越广泛^[1]. 其中夹心式弯曲振动换能器由于具有结构简单, 负载能力强, 易于加工以及功率容量大等优势, 被应用于超声焊接^[2,3]、超声加工^[4,5]、超声振动车削^[6,7]以及超声电机^[8–10]等领域.

声黑洞现象在1988年被Mironov^[11]发现, 即弯曲波在几何结构呈二次及以上幂率变化的截面中传播时, 其波速将随截断高度的减小而减小, 当截断高度减小至零时, 弯曲波波速会减小至零. 这种声波阻滞结构^[12]被称为声黑洞结构. 随后声黑洞结构作为一种新型的弯曲波调控技术被广泛运用于减振^[13]、降噪^[14]、波动调控^[15]以及能量回收^[16]等领域. 同时在功率超声器件性能提升方面, 刘洋等^[17]提出一种声黑洞结构径向夹心式径-弯复合换能器, 利用声黑洞结构实现振动模式之间的转换以及换能器辐射性能的提升. 王怡等^[18]设计出一种新型声黑洞楔形结构模式转换超声换能器, 利用声黑洞结构的能量聚焦能力实现多功能梯度声场的构造. Remillieux等^[19]将声黑洞运用到叠片式换能器设计中来增强超声辐射的性能. Chen等^[20]提出了一种声黑洞结构浸入式声化学反应器, 通过改变探头的对称结构, 引入纵弯耦合振动, 并结合声学黑洞探头的设计, 显著增强其侧向辐射能力, 从而实现高效的声空化处理. Wen等^[21]提出了一种基于声黑洞结构的纵弯复合振动斧型超声换能器, 通过斧柄的纵向振动激发斧头的二阶弯曲振动, 利用声黑洞的能量聚焦效应, 使能量集中于斧头的尖端, 形成高能区域, 实现了口罩的焊接工作. 上述研究表明, 声学黑洞结构在提升超声器件性能方面具有重要的应用价值和潜力.

基于此, 本文提出了一种声黑洞夹心式弯曲振动换能器, 该换能器由夹心式弯曲振动换能器与声黑洞探头组成. 利用Timoshenko梁理论, 通过传输矩阵法建立了换能器弯曲振动的理论模型求出了共振频率的解析解, 并将其与有限元仿真所得出的数值解进行对比分析. 通过有限元法对换能器电阻抗频率响应特性、振动模态、辐射声场和振动位移进行详细讨论, 并与悬链线型换能器的各项结果进行对比分析. 最后, 加工出该换能器样机, 对其电阻抗特性和振动模态进行实验测量, 并将实验结果与仿真结果进行对比验证, 以此验证声黑洞结构在位移放大及辐射增强方面的优势. 该研究弥补了其他反应器侧向辐射能力薄弱的缺点, 为小型浸入式声化学反应器的设计提供了新思路.

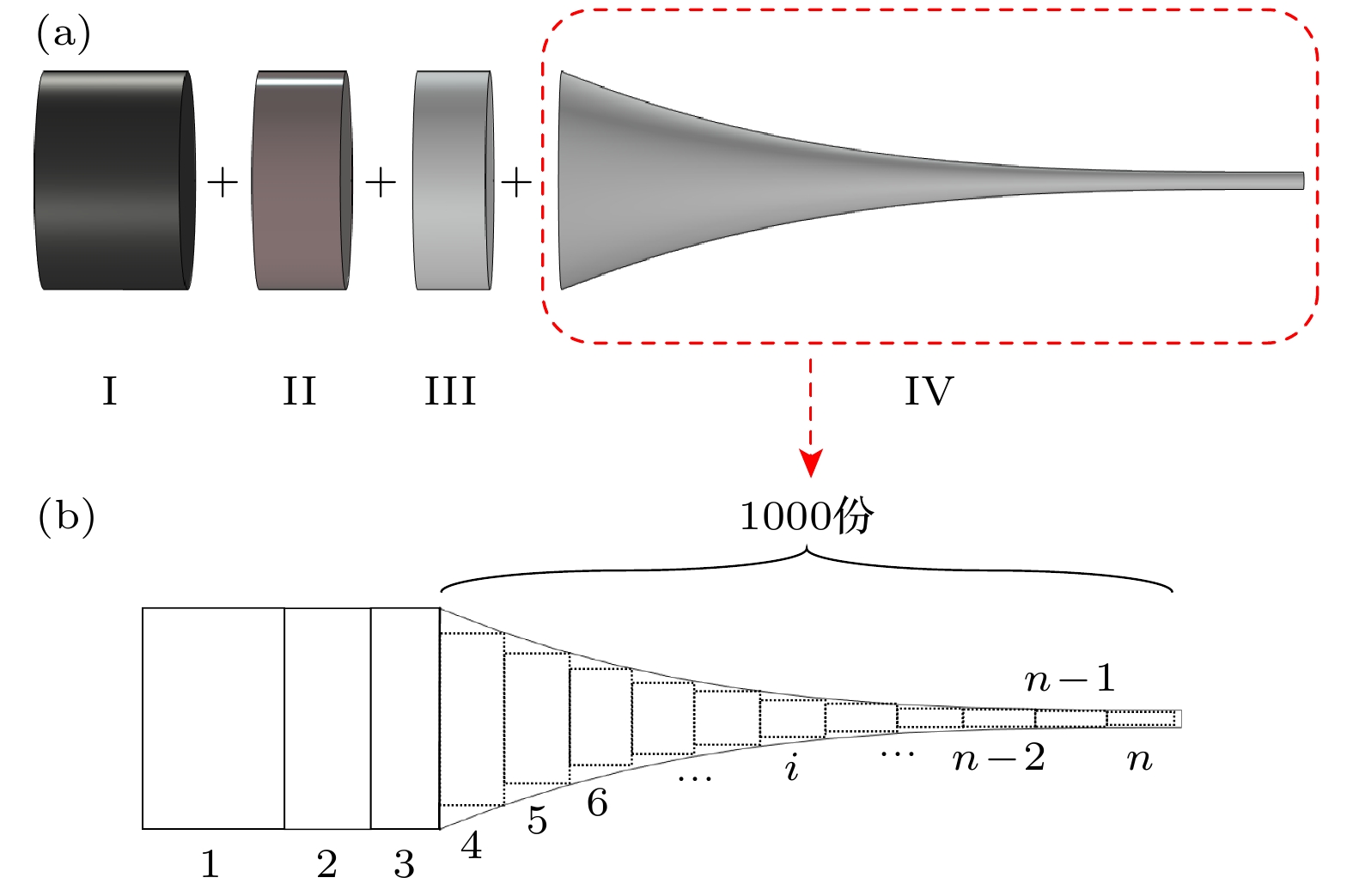
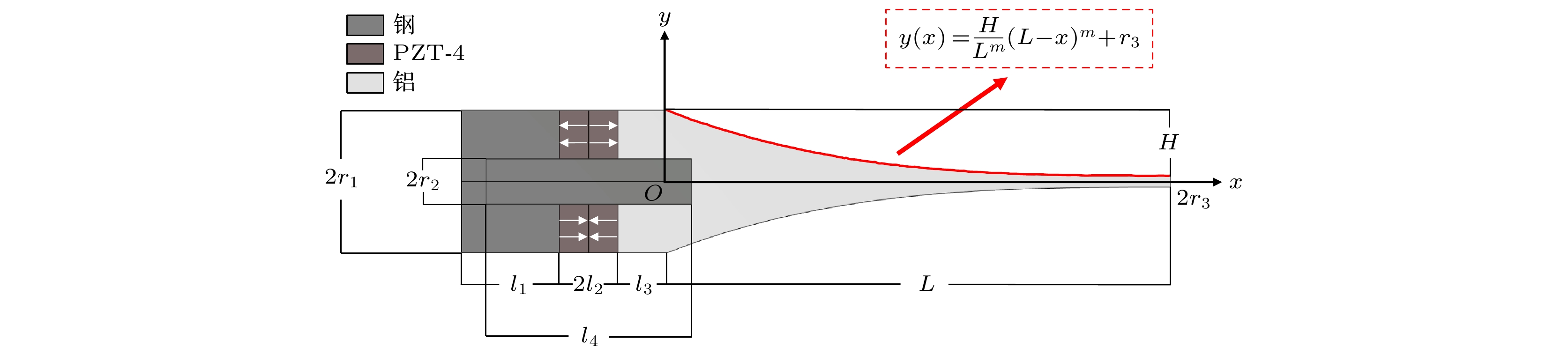
本文所提出的基于声黑洞结构的夹心式弯曲振动换能器的结构如图1所示. 图中黑色部分为钢制后盖板与螺栓, 灰色部分为铝制声黑洞探头, 棕色部分为4片厚度极化的半圆环状压电陶瓷晶片, 白色箭头为压电陶瓷片的极化方向, 其中L为探头长度, $l_1$为后盖板厚度, $l_2 $为压电陶瓷片厚度, $l_3 $为前盖板厚度, $l_4$为螺栓长度, m为声黑洞函数的指数项, r₂为螺栓半径, r₃为声黑洞探头的尖端半径, H为声黑洞轮廓曲线的高度, 其大小等于总半径r₁ (压电片半径)与探头尖端半径r₃之差. 该换能器中相邻两片压电陶瓷晶片的极化方向相反, 4片半圆环状的陶瓷片通过双头螺栓固定于前后盖板之间. 当压电陶瓷片受到电信号激励时, 4片半圆片压电陶瓷中的上部相邻两片将产生膨胀, 下部相邻两片则产生收缩, 进而形成弯曲力矩并激发整个结构产生弯曲振动.

探头尖端半径r₃应尽可能地小, 但考虑实际加工难度过大的问题, 取值为1 mm. 本文所选用的压电陶瓷片规格为25 mm × 8 mm × 6 mm, 故声黑洞轮廓线高度H取值为11.5 mm. 为确定声黑洞函数指数m的取值, 计算了m从1.8—3的一至六阶共振频率(见表1), 以及第六阶弯曲振动时探头尖端处的最大声压, 分别是3.4 × 10⁴(悬链线), 1.6 × 10⁴ (m = 1.8), 3.6 × 10⁴ (m =2.1), 8.6 × 10⁴ (m = 2.4), 2.0 × 10⁵ (m = 2.7), 4.5 × 10⁵ (m = 3). 结果发现, m的取值越大, 第六阶弯曲振动时探头尖端处的最大声压越高, 但随着m取值的增大, 声黑洞探头的加工精度要求越高, 加工难度越大, 应力显著集中, 故将m的取值确定为3. 在确定声黑洞探头长度L时, 考虑到实验中常见的试管和烧杯深度一般在10 cm左右, 且为了保证其在液体负载中仍能在大于20 kHz的超声频率下工作, 选取声黑洞探头长度L为103 mm.

对于声黑洞结构, 当其轮廓按照幂函数变化, 即满足方程:$h(x) = \varepsilon {x^n}\left( {n \geqslant 2} \right)$时, 有关系式^[11]:

此时在该结构中弯曲波的波数k趋近于无穷大, 即:

且相速度${c_{\text{p}}}$与群速度${c_{\text{g}}}$趋近于0, 振幅$A$也趋近于无穷大, 即:

这里x为坐标, $\rho $为材料密度, $E$为材料杨氏模量, $\omega $为角频率, ε为比例常数, $h_0$为声黑洞区域外部的均匀厚度.

为实现对换能器模态以及工作频率的快速运算与优化设计, 通过基于Timoshenko梁理论的传输矩阵方法, 得出该换能器弯曲振动的解析模型.

在建立该理论模型时, 忽略了用于固定前后盖板与压电陶瓷片的螺栓结构, 并将压电陶瓷晶堆看成弹性体, 则该换能器的结构可以简化为如图2(a)所示的Ⅰ, Ⅱ, Ⅲ, Ⅳ四个部分, 对于Ⅳ部分又可等间距的分为1000段等截面单元梁.

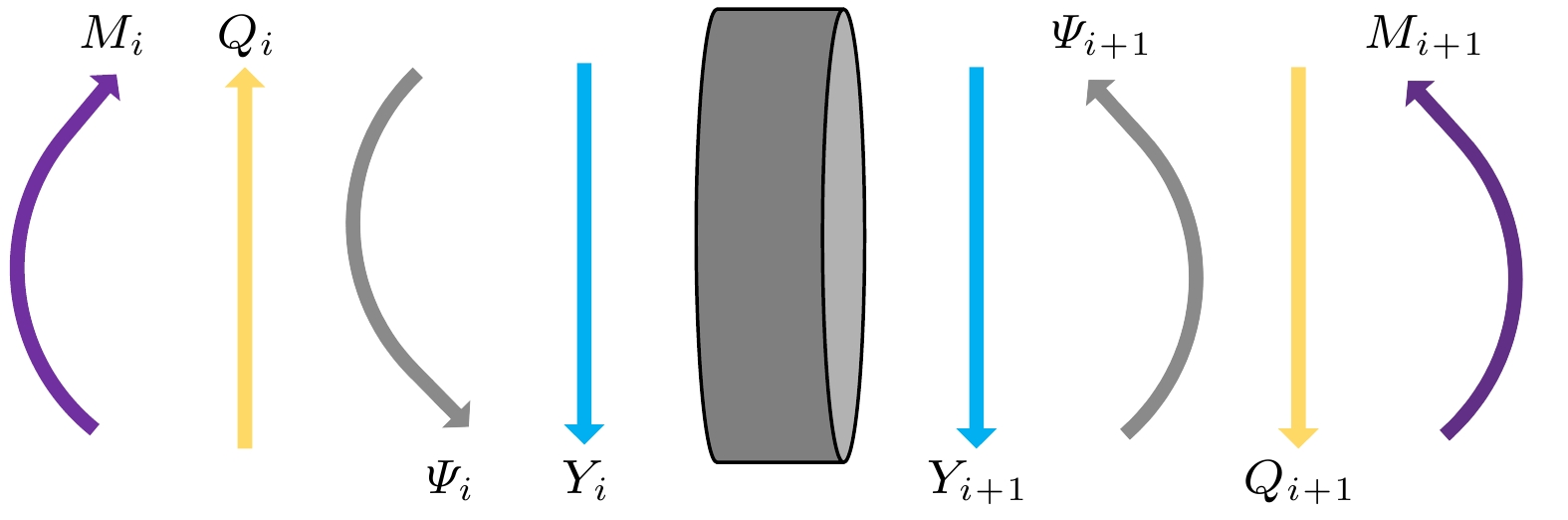
如图2(b)所示, 根据Timoshenko梁理论, 在考虑剪应力与转动惯性后, 第i个弯曲振动的等截面梁, 其弯曲位移${Y_{\text{b}}}$与剪切位移${Y_{\text{s}}}$表示为^[22]

其中,

这里$E$为材料的杨氏模量, $G$为剪切模量, $\rho $为材料的密度, $I$为截面的惯性矩, ${A_0}$为横截面积, $K'$为剪切系数, ${C_{\text{O}}}$为纵波波速, ${C_{\text{S}}}$为横波波速, $\omega $为角频率, f为振动频率, ch为双曲余弦函数, sh为双曲正弦函数. C₁, C₂, D₁, D₂为通过求解常微分方程得到弯曲位移${Y_{\text{b}}}$与剪切位移${Y_{\text{s}}}$表达式时引入的待定系数. 令$Y$, $\varPsi $, $M$, $Q$分别为该等截面梁在弯曲振动时的总横向位移、转角、弯矩、剪力, 其中,

将(1)式和(2)式代入(3)式, 可得总横向位移Y的表达式

将(1)式代入(3)式, 可得转角$\varPsi $的表达式:

将(1)式代入(3)式, 可得弯矩M的表达式:

将(2)式代入(3)式中, 可得剪力Q的表达式:

如图3所示, 设该等截面梁左右两个端面的振动参量分别用${Y_i}$, ${\varPsi _i}$, ${M_i}$, ${Q_i}$和${Y_{i + 1}}$, ${\varPsi _{i + 1}}$, ${M_{i + 1}}$, ${Q_{i + 1}}$表示, 上述参量间的关系可以表示为

并令:

矩阵${{\boldsymbol{a}}^i}$为第i个做弯曲振动的等截面单元的4 × 4矩阵, 其中的各矩阵元素与材料参数、振动频率、几何尺寸有关. 矩阵中各元素的表达式见附录A.

通过以上分析可知任一等截面梁两端的振动参量关系, 且有在公共边界处位移和转角的连续条件以及弯矩和剪力的平衡条件, 则该换能器在做弯曲振动时Ⅰ, Ⅱ, Ⅲ, Ⅳ四个部分总共n段梁两端的弯曲振动参量${Y_1}$, ${\varPsi _1}$, ${M_1}$, ${Q_1}$和${Y_{n + 1}}$, ${\varPsi _{n + 1}}$, ${M_{n + 1}}$, ${Q_{n + 1}}$之间的关系可以表示为

矩阵A是换能器的总矩阵, 等于所有做弯曲振动的等截面单元的4 × 4矩阵的乘积.

因该换能器两端自由, 则其两端满足弯矩$M$和剪力$Q$为零的条件, 即:

代入可得

(12)式所示的行列式方程是换能器的共振频率方程. 在材料参数、几何尺寸和边界条件确定的情况下, 通过求解该方程可得到对应的共振频率.

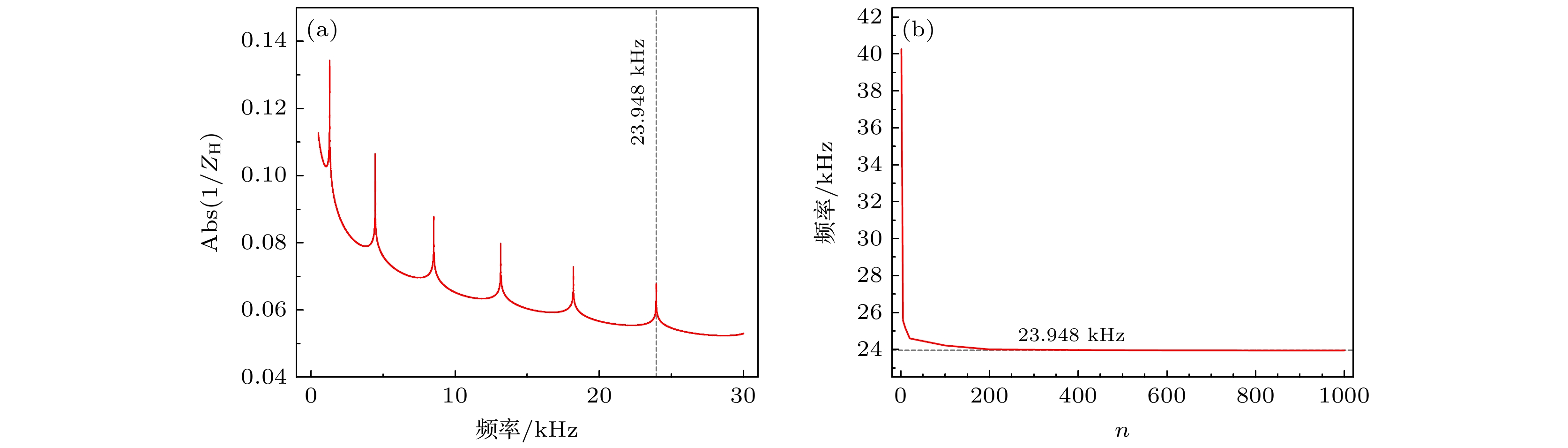
基于商用有限元仿真软件COMSOL Multiphysics中的固体力学、静电、压力声学模块, 建立了与理论模型尺寸一致的三维仿真模型, 具体尺寸参数$l_1 $—$l_4$分别为20 mm, 6 mm, 10 mm, 42 mm; r₁—r₃分别为12.5 mm, 3 mm, 1 mm; L为103 mm; m为3 mm; H为11.5 mm. 在仿真软件中将后盖板与螺栓材料设置为钢, 压电陶瓷材料设置为PZT-4且相邻压电陶瓷半圆环之间的极化方向相反, 声黑洞探头材料设置为铝, 具体材料参数值见表2, 并设置压电陶瓷晶堆两端接地, 两层压电陶瓷之间添加1 V的激励电压, 网格大小设置为波长的1/5. 在设置完各项参数后便对该仿真模型的弯曲振动频率进行求解, 结果如图4(a)所示, 随后将该数值解与使用MATLAB数学软件求解出的解析解进行比较, 最后对n取其他值时理论求解所得出频率的收敛性做出验证, 验证结果如图4(b)所示, 其中${Z_{\text{H}}} = {\lg ^{({A_{31}}{A_{42}} - {A_{32}}{A_{41}})}}$.

表3为有限元仿真与理论计算得出的换能器前六阶弯曲振动频率结果对比. ${f_{\text{T}}}$为利用传输矩阵法所得出的解析解, ${f_{\text{F}}}$为利用有限元仿真法所得出的数值解, $\varDelta $为相对误差, 其计算方法为

结果显示误差均不超过2%, 说明理论解析结果与有限元仿真结果吻合较好, 表明理论模型具有较好的精确性, 主要误差来源于在建立理论模型时忽略了连接螺栓的影响.

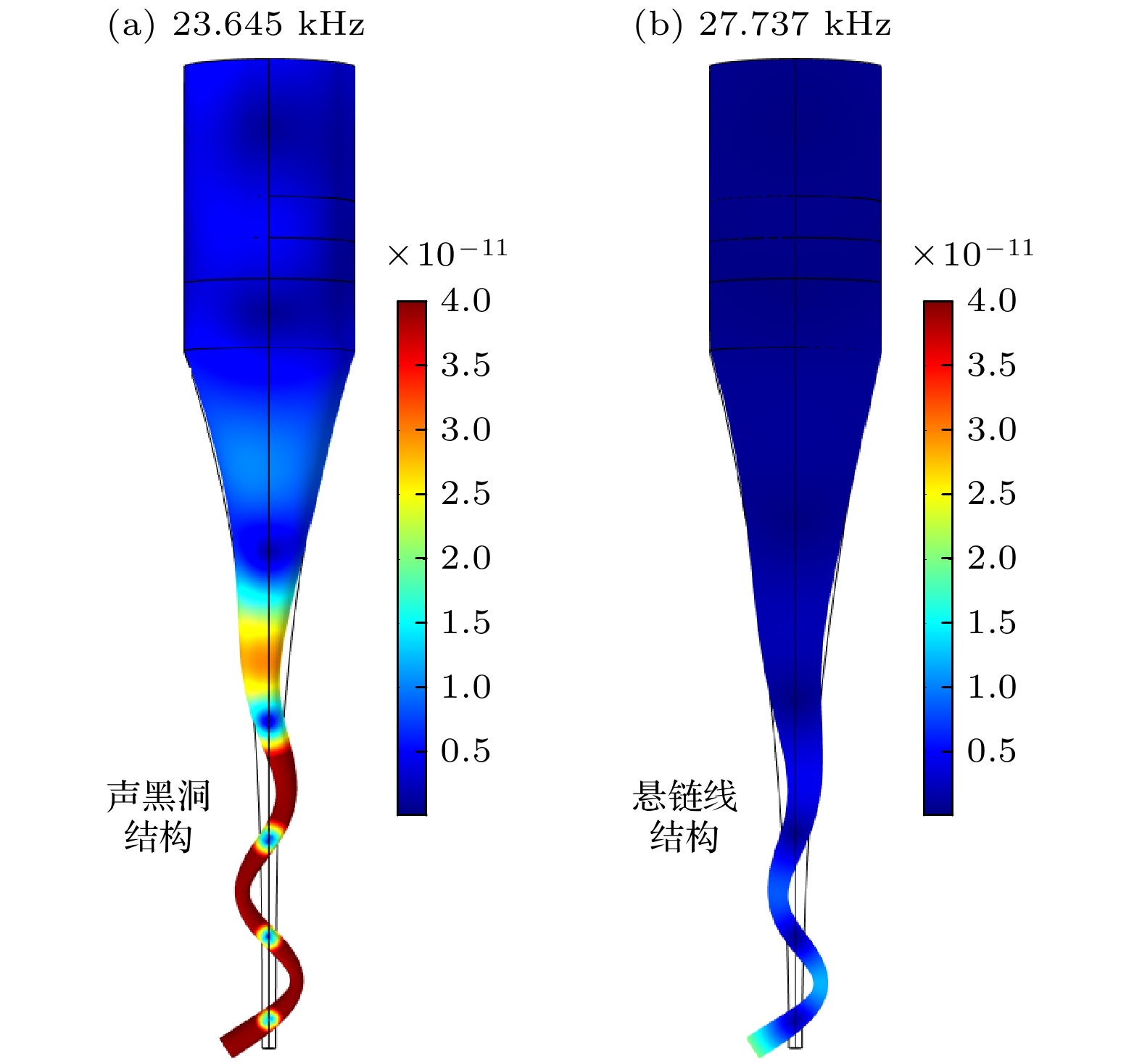
根据表3, 选用振动频率大于20 kHz的第六阶弯曲振动模态, 在此模态下对该换能器进行振动与声场分析. 同时, 为验证声黑洞结构在辐射增强与位移放大方面的优势, 本文设计了另一种夹心式弯曲振动换能器作为对照组, 其探头采用悬链线型轮廓. 利用有限元仿真软件COMSOL Multiphysics对声黑洞型与悬链线型夹心式弯曲振动换能器进行有限元仿真建模, 并设置该悬链线曲线方程为

其中${L_1} = 21.18{\text{ mm}}$, ${L_2} = 20.18{\text{ mm}}$, 材料参数与2.2节相同, 并添加1 V的激励电压, 通过仿真得出如图5所示的换能器振动模态.

同时为研究换能器水中声场, 在COMSOL软件中使用压力声学模块, 添加半径40 mm、高110 mm的圆柱体作为水域, 设置声黑洞探头入水深度为50 mm, 并在圆柱水域外表面添加一厚度为10 mm的完美匹配层, 将完美匹配层划分为5层网格, 以保证声波被充分吸收, 压力声学模块设置为包括完美匹配层在内的整个部分, 并将声压级参考声压设置为$1 {\text{ μPa}}$, 且将探头与水的接触面选取为声-结构边界.

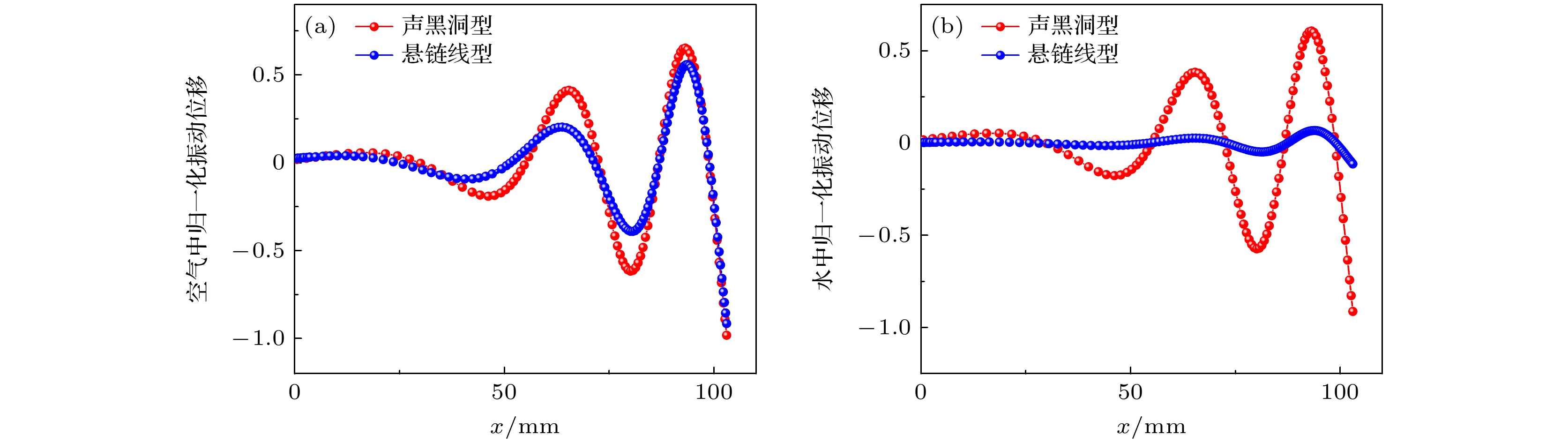
通过仿真计算换能器探头中心轴线上的位移分布, 得出如图6(a)所示的空气中位移分布, 可以看出, 声黑洞结构的振动位移较悬链线型结构的振动位移提升较为显著. 同时通过仿真得出换能器探头入水后中心轴线上的位移分布, 如图6(b)所示, 由于水的阻尼作用导致两种结构在水中的振动位移小于在空气中的振动位移, 但声黑洞结构在水和空气两种介质中的振动位移均大于悬链线型结构. 验证了声黑洞结构对弯曲波位移振幅增强方面的优势.

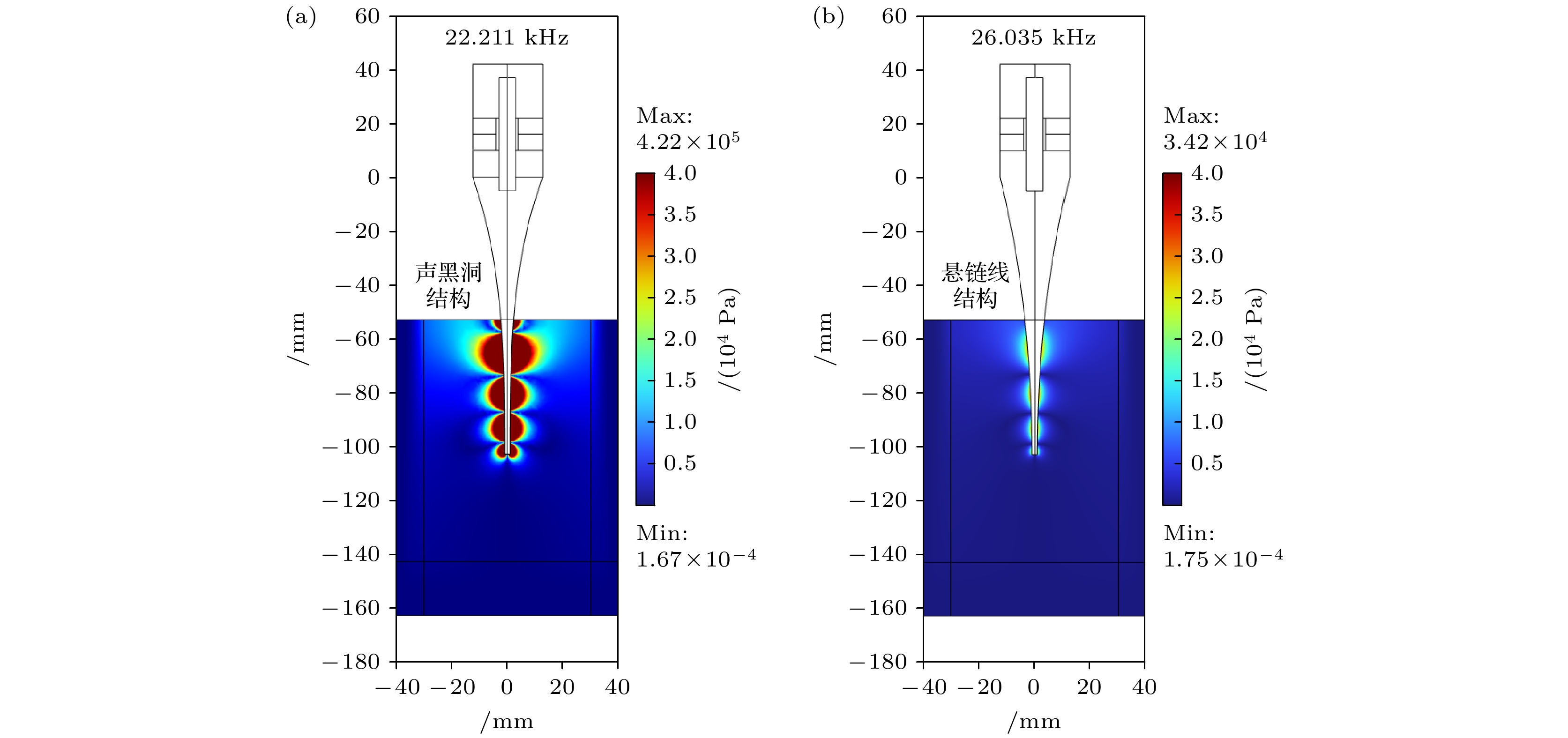
通过仿真得到声黑洞型结构与悬链线型结构的水中声压, 如图7所示, 且在考虑水载荷对探头的影响下重新计算了两种结构的第六阶弯曲振动频率. 将结果进行对比分析发现, 在水中声黑洞结构的最大声压为$4.22 \times {10^5}{\text{ Pa}}$, 悬链线结构的最大声压为$3.42 \times {10^4}{\text{ Pa}}$, 说明声黑洞结构的最大声压较悬链线结构的最大声压提升效果显著. 在声黑洞探头附近的高压条件能够有效促进声空化气泡的形成, 从而加快化学反应速度, 提高反应效率. 使得该换能器可以作为小型声化学反应器来促进化学反应的进行.

此外还选取入水深度为25 mm和75 mm来对入水深度的影响进行分析讨论, 仿真结果如表4所列, 由于受到负载的影响, 入水深度越深负载越大, 导致共振频率降低. 虽然当入水深度从25 mm增至50 mm时声黑洞探头产生的最大声压下降了约50%, 但悬链线探头产生的最大声压下降了1个数量级, 说明声黑洞结构相较于悬链线结构在提升探头处最大声压方面的优势更加显著.

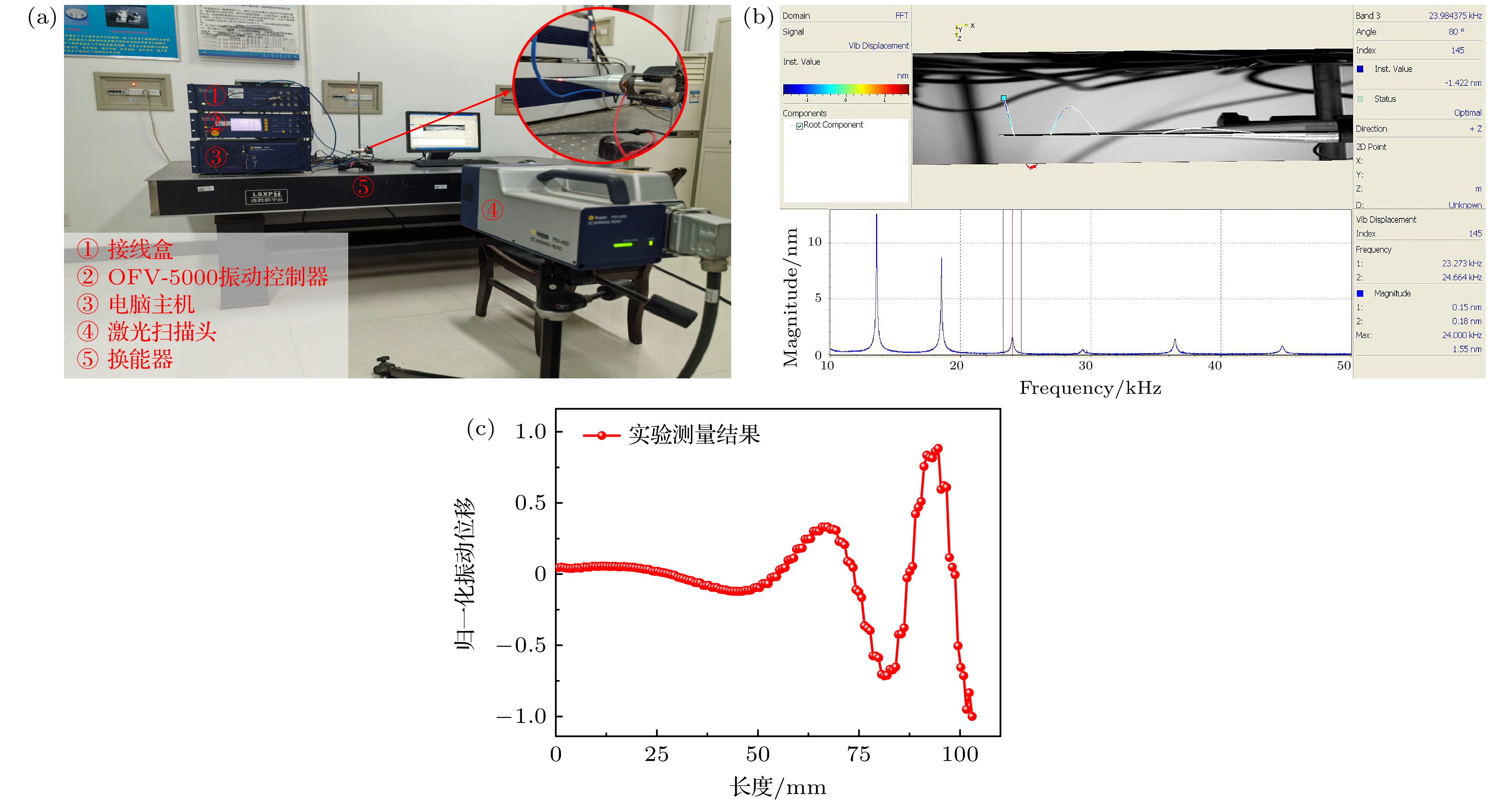
为验证该声黑洞夹心式弯曲振动换能器设计的可行性, 加工制作了如图8所示的换能器样机, 其后盖板材料为钢, 压电材料为厚度极化的PZT-4, 声黑洞探头材料为铝. 利用阻抗分析仪和激光振动测量系统对该换能器样机的电阻抗频率响应以及弯曲振动模态进行实验分析.

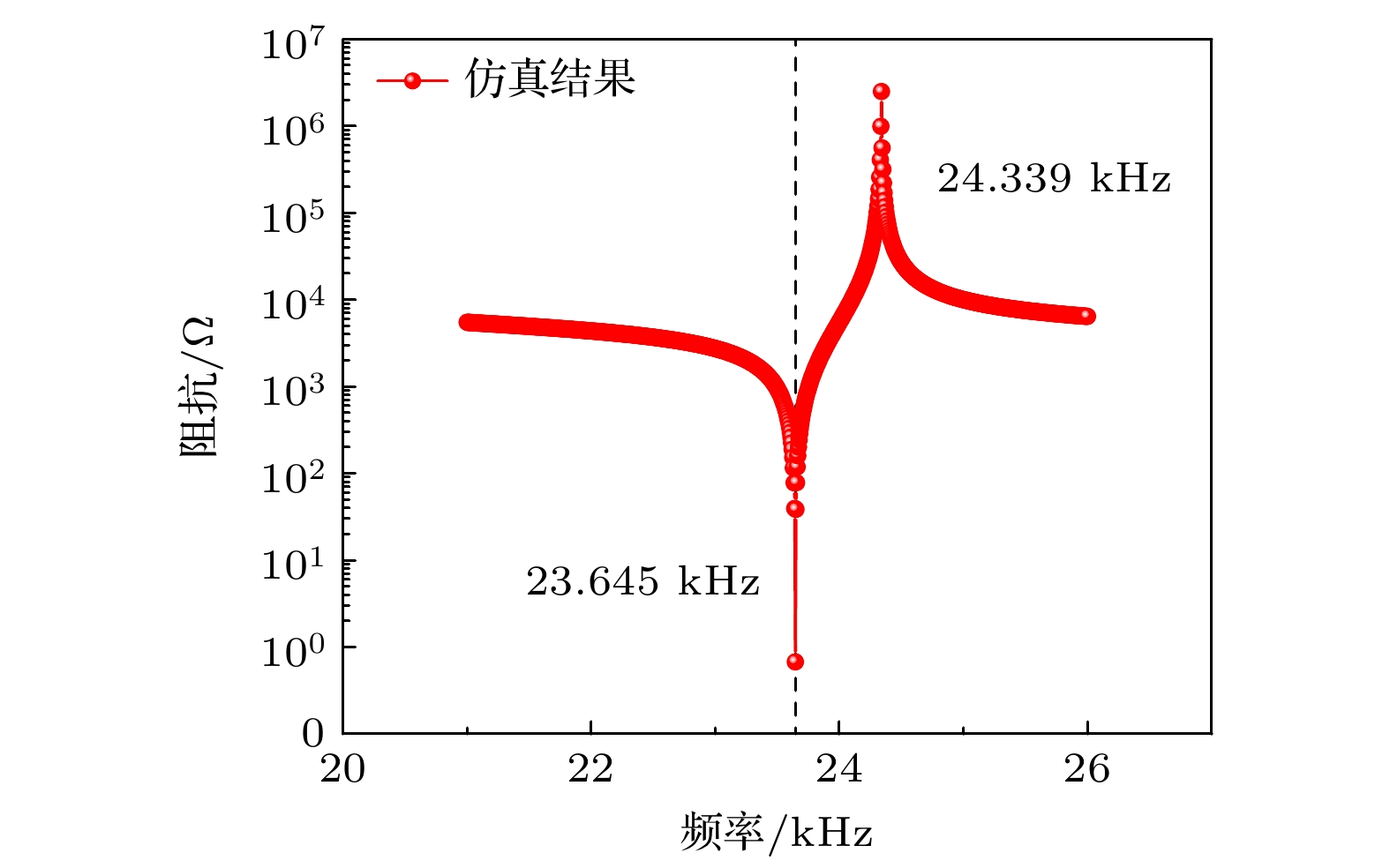
图9为通过有限元仿真所得到的换能器电阻抗频率响应曲线图. 由图9可知换能器仿真所得谐振频率为23.645 kHz.

换能器的有效机电耦合系数定义为

其中, f_m和f_n分别为换能器的最小阻抗频率和最大阻抗频率, 即电流最小时的频率与电流最大时换能器的谐振频率, 将图9中频率代入公式计算得出此时的有效机电耦合系数约为0.237.

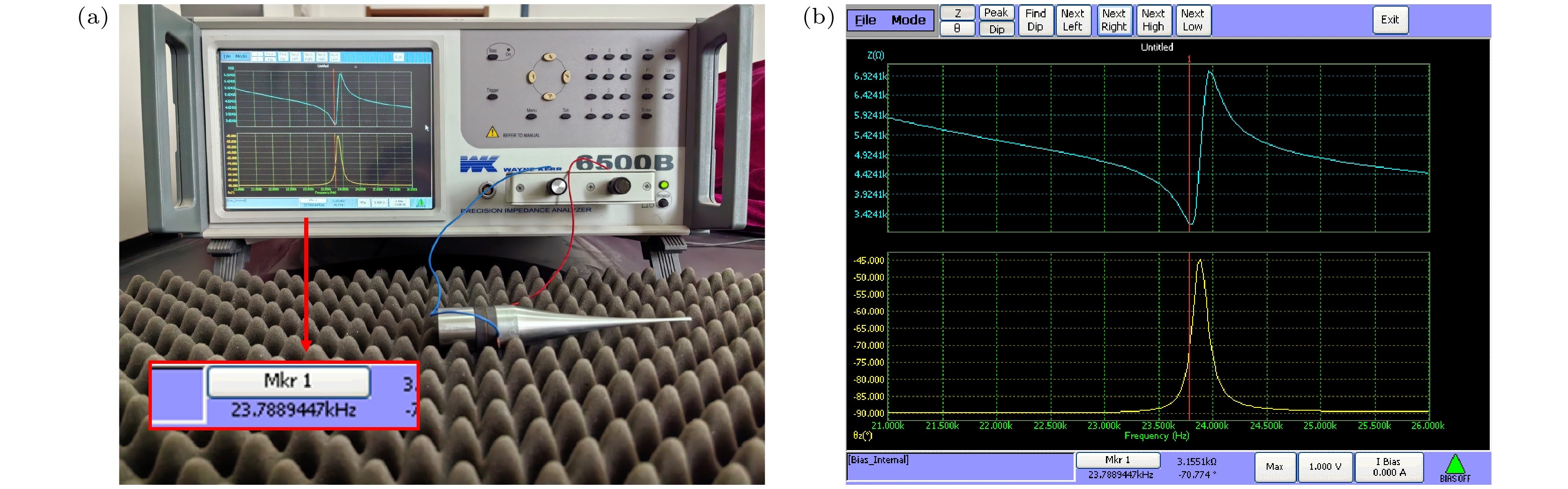
为验证仿真结果的准确性, 采用WK6500B精密阻抗分析仪对换能器的阻抗进行测量. 从图10所示的实验测量结果可以看出, 换能器样机的谐振频率${f_{\text{E}}}$为23.789 kHz, 仿真模拟与实验测量之间的误差为

其中误差的主要来源有以下3点:

1)样机加工所使用材料的参数与仿真软件中所使用材料的参数之间存在一定偏差;

2)样机加工机床精度有限, 且在样机装配过程中存在误差;

3)有限元仿真忽略了实际测量时存在的机械损耗与介电损耗.

为验证有限元仿真得出的振动模态结果, 使用图11(a)的Polytec PSV-400全场扫描式激光振动测量系统对换能器的弯曲振动模态进行测量, 并设置激励电压为1 V, 扫频范围为10—50 kHz. 图11(b)所示为模态测量结果, 振动位移分布测量结果如图11(c)所示. 可以看出, 实验测量结果与有限元仿真得到的结果相吻合, 说明该弯曲振动模态能够被有效激励, 验证了设计的可行性, 同时探头尖端处的振幅十分显著, 与声黑洞结构的功能一致.

本文基于声黑洞结构设计了一种新型声黑洞夹心式弯曲振动换能器, 基于Timoshenko梁理论, 利用传输矩阵法建立了该声黑洞换能器的理论模型, 计算所得误差最大不超过2%, 说明该理论模型可以高效、准确地计算任意变截面换能器弯曲振动的频率. 利用有限元方法分析了悬链线型换能器与声黑洞型换能器的电阻抗频率响应和振动模态, 比较了辐射声场与振动位移, 发现声黑洞型换能器的最大声压与振动位移均优于悬链线型换能器, 说明声黑洞结构在弯曲波调控方面独特的优势. 加工出换能器样机并进行实验测量, 测得的电阻抗频率响应以及弯曲振动模态与有限元方法得出结果吻合较好. 研究表明通过引入声黑洞结构可以有效提升最大声压与振动位移, 这将加强其作为小型浸入式声化学反应器的空化能力, 有望应用于生物细胞破碎、超声乳化、有机合成和固体材料的粉碎与分散等领域中.

(8)式矩阵中各矩阵元素的表达式为