量子控制分子转动是原子分子物理与光学领域的重要研究方向, 在物理学^[1-4]、化学^[5-9]及量子信息科学^[10-12]中具有基础性意义. 例如, 在立体化学反应中, 通过控制反应物分子取向, 可以调控化学反应的选择性^[13-15]; 在量子信息领域, 利用分子取向作为量子比特的载体, 通过脉冲操控实现量子态编码^[16,17]; 在分子成像中, 周期性取向的分子阵列可发射相干的太赫兹波, 用于成像或通信^[18-20]. 最早的纯静电场产生分子取向方法^[21-23]由于对实验温度、电场强度和被操控分子大偶极矩的要求很严格, 理论和实验研究开始探索使用脉冲场诱导场后分子取向^[24-26]. 场后分子取向指脉冲结束后, 分子转动波包因量子相位演化产生周期性“复苏”现象, 表现为取向度的振荡衰减^[27-29]. 根据激光中心频率与分子跃迁频率的关系和电偶极作用机制, 脉冲场诱导分子取向的方法可分为共振激发方案^[30-33]、非共振激发方案^[34-39]和杂化激发方案^[40-43]. 非共振激发方案主要通过脉冲场与分子的极化率和超极化率相互作用, 通过调节基频脉冲和倍频脉冲场的相位、振幅和延迟时间, 调控分子转动态产生分子取向^[44-49]. 然而, 该方案需要使用强超短脉冲, 这不可避免地引发强场现象, 如显著的电离以及电子或振动态激发. 在杂化控制方案中, 非共振激光首先激发分子的偶数转动态实现预准直, 随后通过共振激光与电偶极矩作用使其向奇数转动态跃迁^[50-52], 该过程中非共振激发阶段对强激光的需求同样无法避免. 相比之下, 共振激发方案采用短脉宽、低场强且中心频率与分子跃迁频率相近的激光脉冲, 激发产生分子的奇数和偶数转动态叠加, 可以有效避免强场效应, 越来越引起理论实验的兴趣^[53-56].

实验上基于共振激发方案, Nelson及其同事^[31]首次在常温条件下利用强单周期太赫兹脉冲实现了太赫兹诱导的分子取向, Kitano 等^[53]通过库仑爆炸成像技术, 探测和分析太赫兹脉冲激发的分子取向变化. 然而, 由于太赫兹脉冲强度和频率的限制, 这种方法在布居高度激发转动态方面面临挑战. 理论研究表明, 通过对转动叠加态的精确量子控制, 可以实现目标分子取向^[57-62]. 对于超冷线性或对称顶极性分子, 通过在最低两个、三个、四个和五个转动态之间构建相干叠加态, 并利用解析设计的微波脉冲序列或强超短激光脉冲, 分别可以实现0.577, 0.775, 0.861和0.906的最大取向度^[63-69]. 最近, 我们提出了一种多能级脉冲面积定理框架, 能够有效控制选定的一组转动态, 并生成特定相干叠加态以实现期望的分子场后取向^[70]. 通过设计15个具有优化振幅、相位和延迟的微波脉冲, 在理论上实现了最低16个转动态的期望叠加态, 从而在超冷双原子分子中实现了期望值$ |\langle \cos\theta \rangle|_{\rm max}> 0.99 $的最大取向度, 其中θ表示分子轴与微波脉冲场的偏振方向之间的夹角. 由于解析设计的挑战性, 多个脉冲序列的使用极大地延长了操控时间, 不利于克服分子退相干效应的影响. 设计更短脉冲场, 实现高的场后分子取向度仍然是一个长期存在的挑战.

量子最优控制理论为设计整形脉冲激光场提供了有效途径^[71-77]. 然而, 传统的量子最优控制方法往往忽视了实验约束条件, 导致优化后的脉冲场在理论上虽能达到最优控制效果, 但其复杂的时频特性却难以在实验中实现, 且不利于深入理解其物理机制. 此外, 为获得高精度的分子取向度, 理论计算需要涵盖较大的转动空间, 这不仅要考虑众多转动态的贡献, 还需计及振转耦合效应的影响, 这进一步增加了理论计算的复杂性和脉冲场的复杂度. 为此, 本文提出多目标多约束量子最优控制算法, 寻找满足脉冲面积及能量约束的控制场. 探索在超冷极性分子中基于共振激发方案, 操控目标转动态空间有限个转动态布居和相位分布, 形成相应最大的场后分子取向. 通过对优化脉冲场进行时频分析, 结合含时取向度的傅里叶变换谱计算, 揭示产生最大分子取向的内在激发机制.

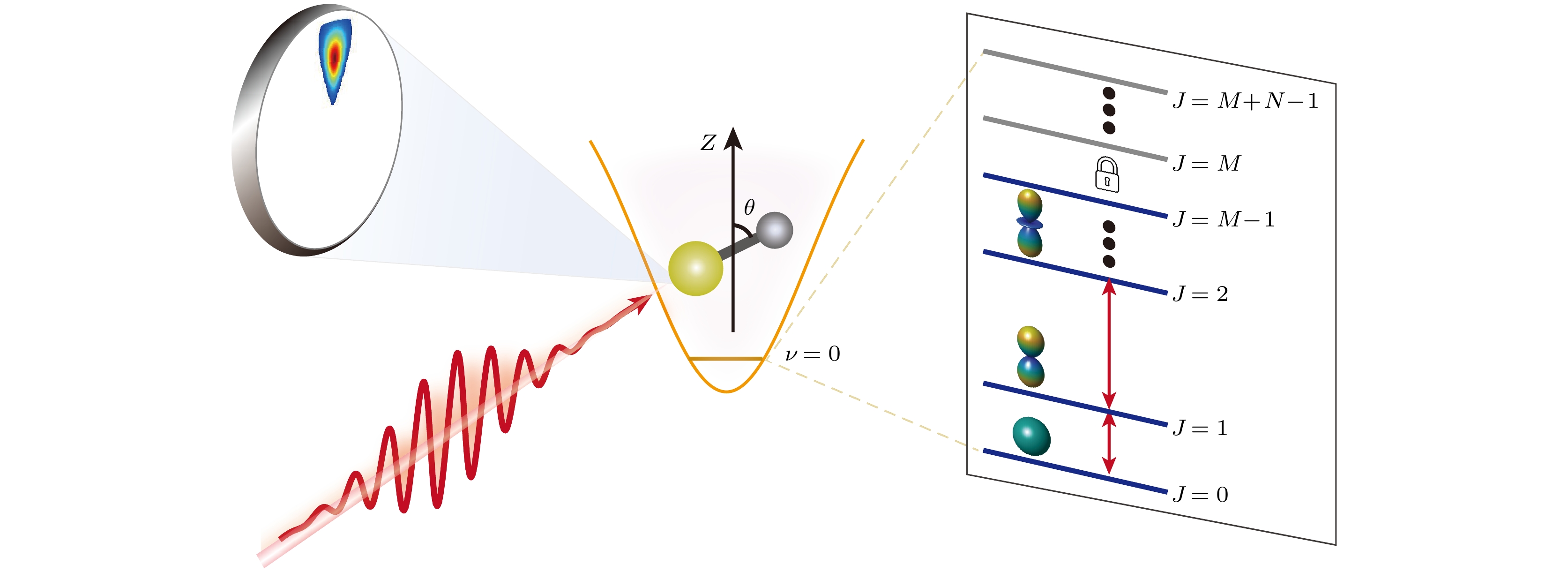
为了解释本文的理论方法, 图1示意性展示了如何使用共振激发方案在超冷双原子分子基电子态的基振动态制备转动相干叠加态, 从而获得有效的场后分子取向. 基于刚性转子近似, 并且设置普朗克常数$ \hbar = 1 $, 分子的自由哈密顿量可以写为

其中, $ \hat{J} $为角动量算符, B为转动常数, 对应的本征能量为$ E_{J}=BJ(J+1) $, 本征函数为球谐函数. 由于考虑分子初始在转动基态, 并且使用线偏振脉冲场激发, 因而在激发过程中磁量子数恒等于0, 本文使用狄拉克符号$ |J\rangle $代表量子数为J的转动态. 为了便于后续分析, 将分子的最低M个转动态定义为目标子态空间, 而将其上方的N个转动态定义为非目标态子空间. 因此, 整个模型包含最低$ M+N $个转动态, 如图1所示. 脉冲场$ {\cal{E}}(t) $在$ t_{0} $时刻开启, 激发处于基转动态的分子, 并在$ t_{{\mathrm{f}}} $时刻关闭, 目标态子空间的所有转动态布居和相位分布被调制, 随后激发的转动相干叠加态自由演化, 产生场后分子取向. 通过这一设计, 旨在目标态子空间中生成一个期望的转动相干叠加态, 同时避免对非目标态子空间转动态的激发.

电偶极近似下, 分子与脉冲场的相互作用哈密顿量$ \hat{H}_{\mathrm{c}}(t) $可表示为

其中$ \hat{\mu} $为跃迁偶极算符, 其矩阵元可以表示为永久偶极矩$ \mu_0 $与跃迁矩阵元$ {\cal{M}}_{J, J+1}=\left \langle J+1 \right | \cos \theta \left | J \right \rangle = \sqrt{(J+1)^{2}/(2 J+3)(2 J+1)} $的乘积. 系统在相互作用绘景下从初始时刻$ t_{0} $到给定时刻t的演化可由时间演化算符$ \hat{U}(t, t_0) $描述, 其解为

其中, $\mathbb{I} $为单位矩阵, $ \hat{U} \left ( t_0, t_{0} \right ) $为单位算符, $ {\hat{H}_{{\mathrm{I}}}\left ( t \right ) } = \exp ( {\mathrm{i}}\hat{H}_{0}t ) [-\hat{\mu}\cdot {\pmb{\cal{E}}}(t)]\exp ( -{\mathrm{i}}\hat{H}_{0}t ) $. 对应的含时波函数可表示为

其中, 频率$ \omega_{J}=E_{J} $, 展开因子$ c_{J}(t)\exp({\mathrm{i}}\varphi_{J}) = \langle J | \hat{U}(t, t_{0})\left | 0 \right \rangle $.

为了方便设计约束脉冲场, 先定义目标函数. 在外场作用下, 含时间的分子取向度可以定义为^[70]

其中跃迁频率为$ \omega_{J+1, J}=E_{J+1}-E_{J} = 2(J+1)B $, 相对相位为$ \varphi_{J+1, J }=\varphi_{J+1}-\varphi_{J} $. 控制目标是在脉冲结束时使分子取向度达到最大, 即$ h_{1}=\langle \cos\theta\rangle (t_{{\mathrm{f}}}) $最大化. 当满足相位关系

场后取向度的最大值方向会周期性地复苏, 其复苏周期为分子的转动周期$ T= {2\pi/\omega_{1, 0}} $.

目标态子空间内的最大分子取向, 可以通过减少非目标子空间内的量子态布居来实现. 对应的拉格朗日乘子法可以表示为

其中, λ为拉格朗日乘子, $h_1 = \displaystyle\sum\limits_{J=0}^{J_{\max}-1} 2\mathcal{M}_{J,J+1} c_{J+1} c_{J} $, $ h_{2} = 1- \displaystyle\sum\limits_{J = 0}^{M-1}c_{J} ^{2} $为另一个控制目标. 令$ \nabla {\cal{L}} = 0 $, 得到

通过求解上述方程, 可以在N态最小布居的条件下, 获得达到最大取向度时M子空间内转动态的布居条件为^[70]

且理想条件下目标态的系数满足归一化条件$ \displaystyle\sum\nolimits_{J = 0}^{M-1}c_J^2 = 1 $, 意味着非目标态的影响最小.

为实现上述两个目标, 优化算法引入控制哑变量s, 用于记录控制场$ {\cal{E}}(t) $在控制空间中的变化轨迹. 这一多目标优化问题可以表示为

这两个不等式的物理意义在于, 通过在控制变量空间中迭代优化脉冲$ {\cal{E}}(s, t) $, 第一个控制目标(即分子取向度)单调递增, 而第二个控制目标(即非目标态总布居)单调递减.

为了保证优化的脉冲场满足麦克斯韦方程组且其能量不发散, 优化算法引入两个等式约束:

其中, 第一个约束条件$ h_{3}=\displaystyle\int_{t_{0}}^{t_{{\mathrm{f}}}}{\cal{E}}\left ( s, t \right ) {\mathrm{d}}t = 0 $表示脉冲面积约束, 确保优化场始终不含直流成分; 第二个约束条件$ h_{4}=\displaystyle\int_{t_{0}}^{t_{{\mathrm{f}}}}{\cal{E}}^{2} \left ( s, t \right ) {\mathrm{d}}t={\cal{F}} $表示优化场保持能量不变. 这两个约束条件共同保证了优化脉冲场的物理合理性和能量稳定性.

该优化算法的核心就是需要优化场$ {\cal{E}}(s, t) $的梯度变化$ \dfrac{{\partial {\cal{E}} \left( {s, t} \right)}}{{\partial s}} $同时满足方程(10)—(13)四个方程, 对应的充分不必要解为

其中, $ S\left( t \right) > 0 $是脉冲包络函数, $ {q_{\ell}}\left( {s, t} \right) $为

(14)式中$ {{\boldsymbol{\varGamma}} _{\ell\ell'}} $为$ 4 \times 4 $维矩阵, 对应的矩阵元为

根据以上目标和约束函数的定义, 对应的两个目标梯度$ g_{1} $和$ g_{2} $可以表示为

而两个约束梯度$ g_{3} $和$ g_{4} $可以表示为

和

将$ q_1(s, t) $$ q_2(s, t) $,$ q_3(s, t) $和$ q_4(s, t) $代入方程(16), 计算矩阵${\boldsymbol{\varGamma}} $及其逆矩阵 $ \boldsymbol\varGamma^{-1} $, 并将它们一起代入方程(14), 即可获得控制场的变化梯度. 在优化过程中, 采用一阶微分方程的数值解法(如一阶欧拉法)逐步更新脉冲场:

其中 $ {\text{δ}} s $为哑变量的离散步长, $ {\cal{E}}(s = 0, t) $为初始猜测场. 通过调整步长$ {\text{δ}} s $并迭代更新场, 可使控制目标单调收敛至期望的精度. 为进一步确保优化过程的稳定性与收敛性, 本文引入了适应性步长调整策略与严格的收敛判据. 具体而言, 若某一迭代中目标函数(即分子取向度)未能保持单调递增, 或非目标子空间中转动态的总布居超过设定阈值$ 1\times10^{-3} $, 则动态减小迭代步长${\text{δ}} s $, 以抑制非期望激发并提高数值稳定性, 当连续迭代中目标函数的增长量低于$ 1\times10^{-13} $时, 即可认为优化已收敛, 终止计算.

为了检验和展示该方法, 本文选择超冷分子 LiH作为研究对象, 其转动常数为$ B = 7.51\text{ cm}^{-1} $, 永久偶极矩为$ \mu_{0} = 5.88\; {\rm D}$^[78]. 计算中初始猜测脉冲设定为

式中, k 是调节初始脉冲能量的参数, 脉冲的初始时间设置为$ -2.5 T $, 脉冲的关闭时间设置为$ 2.5 T $, 其中$ T=\pi/B $为分子转动周期. 包络函数取为高斯函数, 其脉宽为$ \tau=\pi/\omega_{1, 0} $, 即一个光学周期. 模拟中强制包络函数在初始和末时刻为0, 以便严格保证脉冲在初始时刻$ t_0 $打开, 末时间$ t_{\mathrm{f}} $关闭. 时间空间被离散为$ N_{t} = 2\times10^{4} $份, 哑变量变化步长设置为$ {\text{δ}} s = 1\times10^{-9} $, 迭代次数记为$ N_{{\mathrm{s}}} $. 如果取向度目标未实现单调递增, 或者非目标子空间转动态总布居大于$ 1\times10^{-3} $, 则适应性调整迭代步长$ {\mathrm{d}}s $. 如果取向度目标随迭代的增长值小于$ 1\times10^{-13} $, 则认定优化结果收敛. 为了展示该优化算法的有效性和优越性, 本文先针对目标态空间包含少数(2个和3个)转动态进行研究, 在此基础上再研究包含多数(17个)转动态情形.

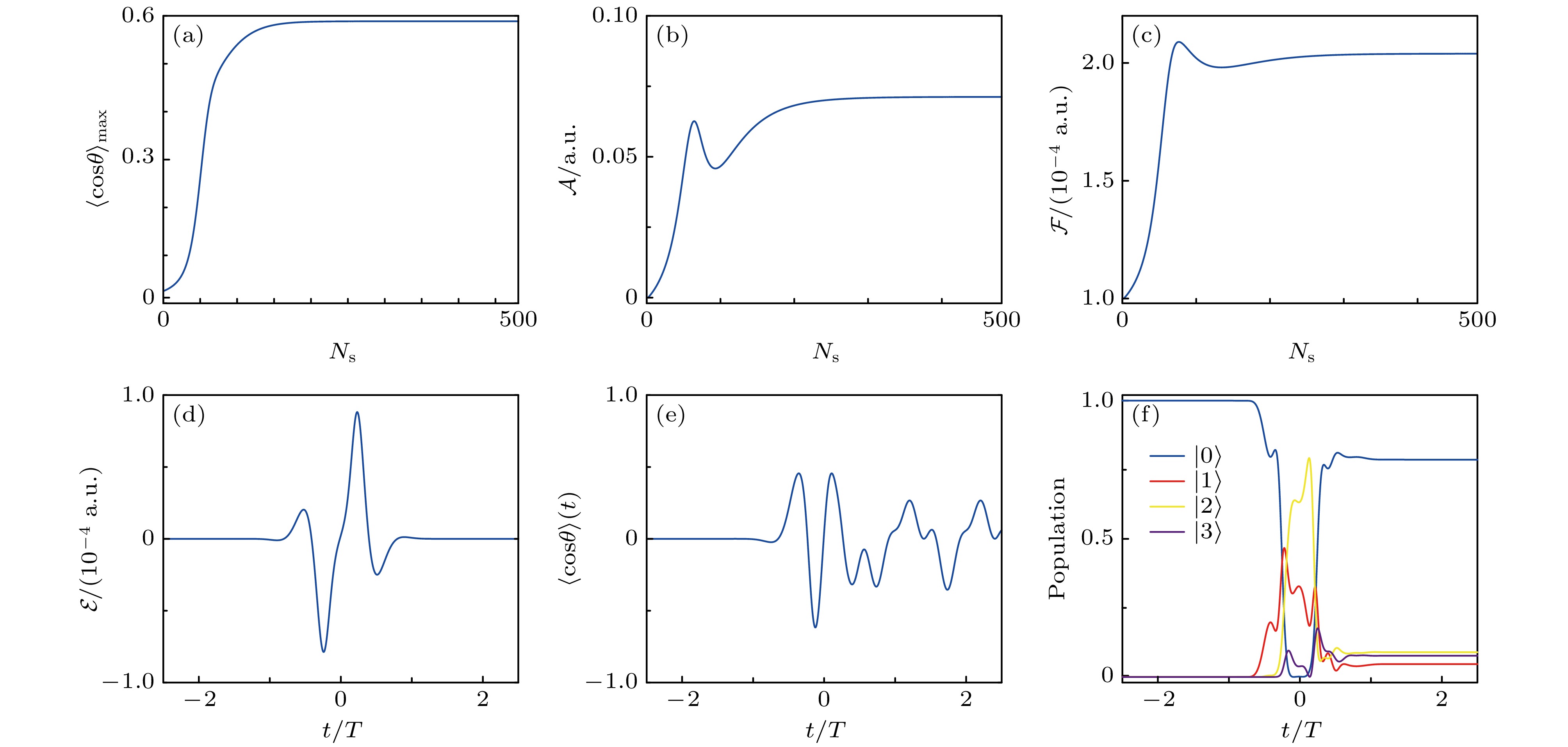
为了展示考虑非目标态子空间和约束的重要性, 本文先以调控目标态空间最低两个转动态($ M = 2 $)为例, 考虑忽略约束条件和非目标子空间($ N = 0 $)的情形. 图2(a)—(c)刻画了对应最大取向度$ \left \langle \cos\theta \right \rangle_{\text{max}} $、脉冲面积$ {\cal{A}} $以及能量$ {\cal{F}} $随迭代次数的变化. 最大取向度随迭代次数单调收敛至理论极限值0.577, 而脉冲面积与能量因未施加约束呈现持续增长趋势. 这一现象表明: 优化后脉冲场的直流分量显著增强; 最终脉冲能量明显高于初始猜测值. 为了检验优化脉冲的有效性, 将最终优化的脉冲用于一个4能级系统($ M = 2 $和$ N = 2 $), 也就是考虑两个邻近的非目标转动态影响. 图2(d)—(f)刻画了对应的含时脉冲场、取向度以及4个态的布居演化. 从图2(e)可见, 仅设置分子取向目标时, 脉冲结束时刻的分子取向度并非转动周期中的最大值, 与图2(a)中的最大期望值0.577存在显著偏差. 从图2(f)的布居演化可以看到, 优化的脉冲并不是只激发最低的两个转动态, 同时激发了非目标态空间的转动态. 这些结果证明: 要实现目标态空间内精准的布居分布及取向控制, 需要考虑非目标态子空间转动态的影响, 并引入适当的约束条件限制优化脉冲的成分和能量变化.

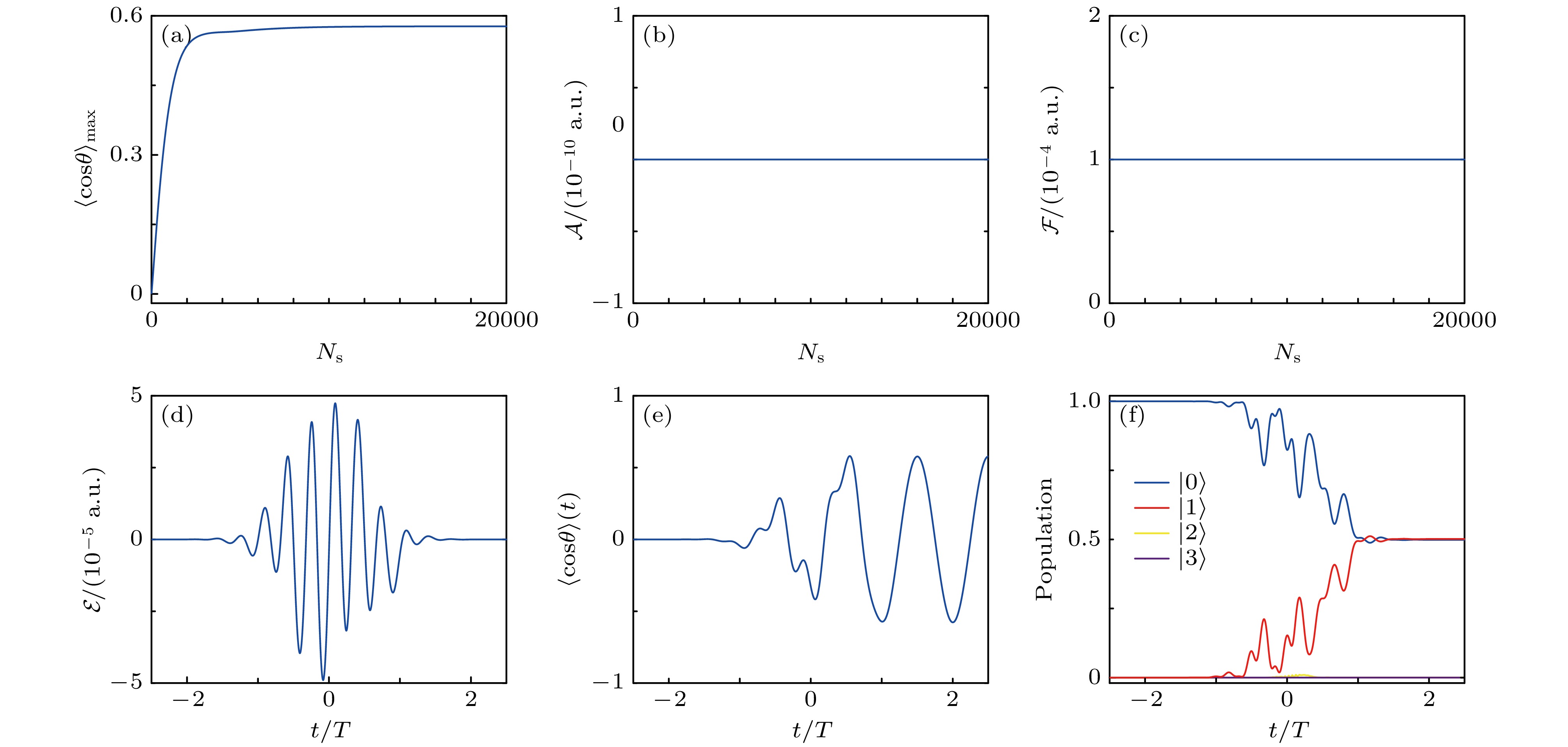
为此, 本文采用新发展的优化算法进行研究. 在保持初始脉冲不变的条件下, 考虑两个非目标态($ N = 2 $)并考虑脉冲面积及能量约束. 如图3(a)—(c)所示, 最大取向度、脉冲面积及脉冲能量随迭代次数的变化趋势表明: 新方法能单调递增分子最大取向度, 使其渐进逼近理论最大值0.577, 同时保持优化脉冲的能量和面积恒定. 图3(d)—(f)同时呈现了优化获得的时变脉冲场及其对应的取向度与转动态布居演化过程. 结果显示, 转动激发被有效约束在目标态空间内, 非目标态未出现激发现象. 这表明新算法能有效实现预期控制目标, 且优化场满足约束条件.

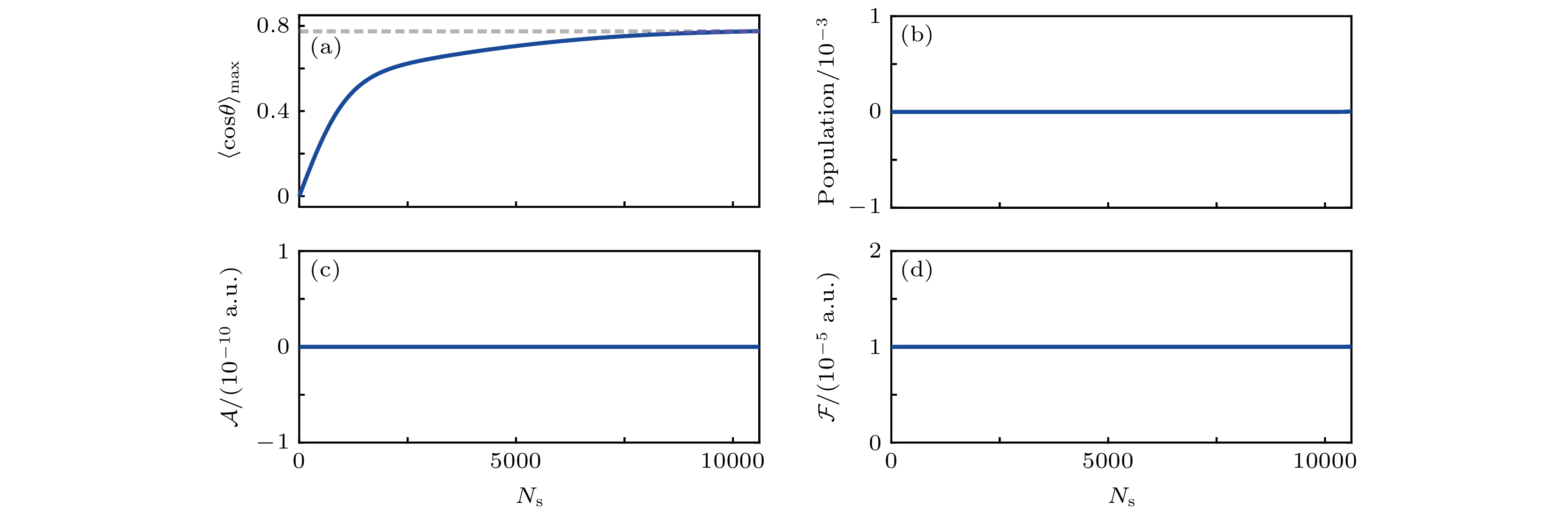
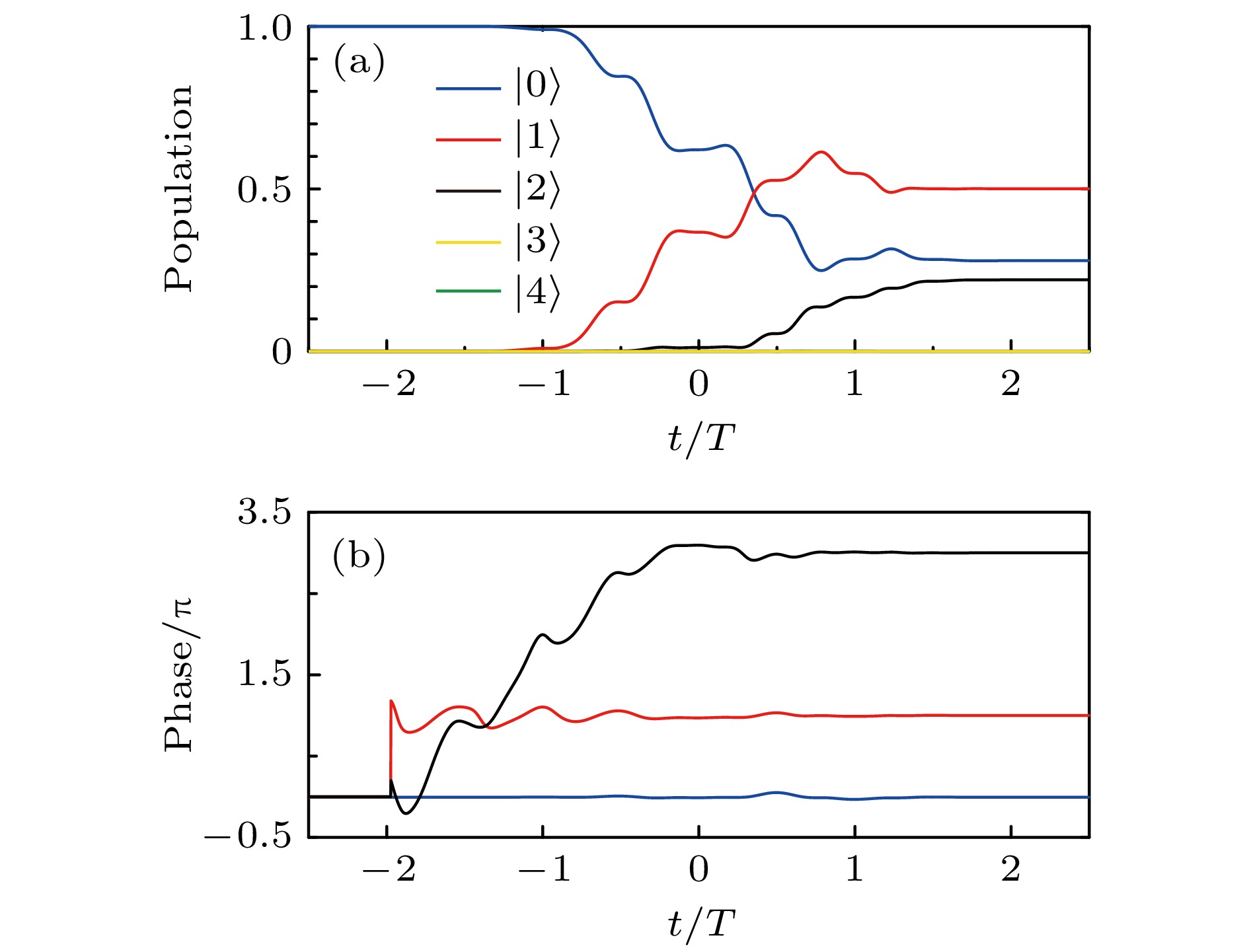
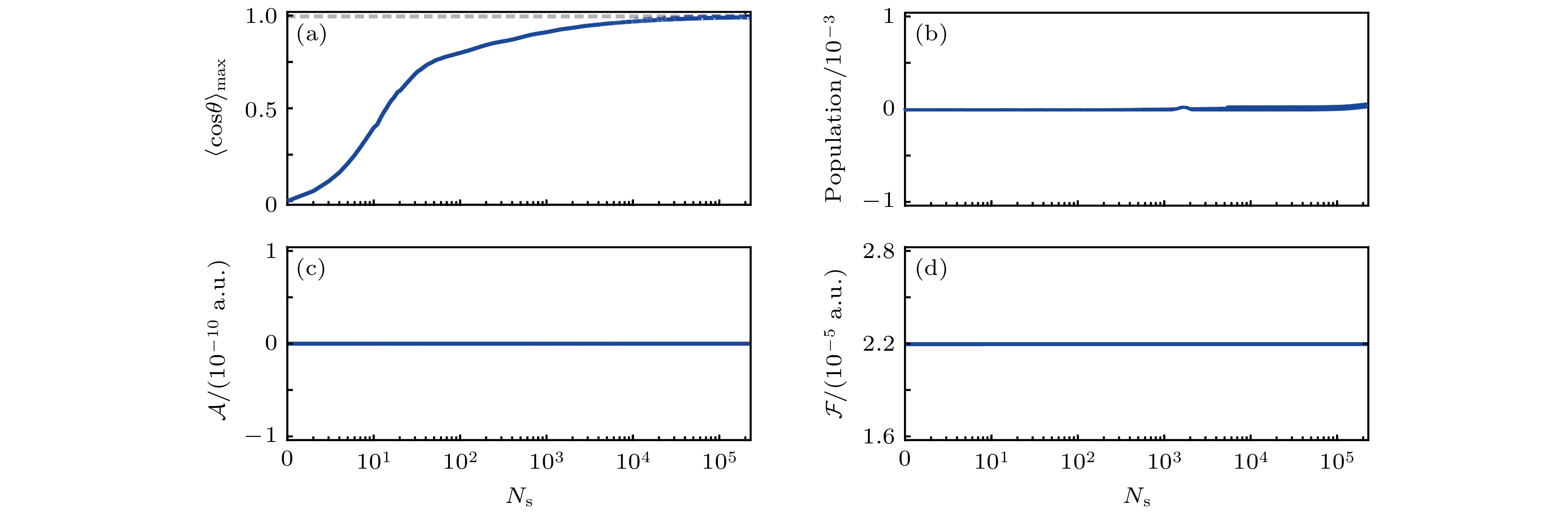
为深入验证该方法, 将最低三个转动态设为目标态情形, 探究最优脉冲实现分子最大取向的物理机制. 优化参数设置为: 目标态空间转动态数为$ M = 3 $, 非目标态空间转动态数为$ N = 2 $, 初始脉冲能量参数$ {\cal{F}} = 1 × 10^{-5} $. 图4绘制了最大分子取向度、非目标态总布居、脉冲面积以及脉冲能量随迭代次数的变化曲线. 从优化的结果可以发现, 分子的最大取向度被单调递增至理论最大值0.775, 且在迭代过程中, 非目标子空间量子态的总布居被控制在$ 1.0\times10^{-5} $以内, 脉冲面积数值上被限制在$ 1.0\times10^{-14} $以内, 脉冲能量变化与初始设定值比值小于$ 1.0\times10^{-5} $, 进一步表明新算法的有效性.

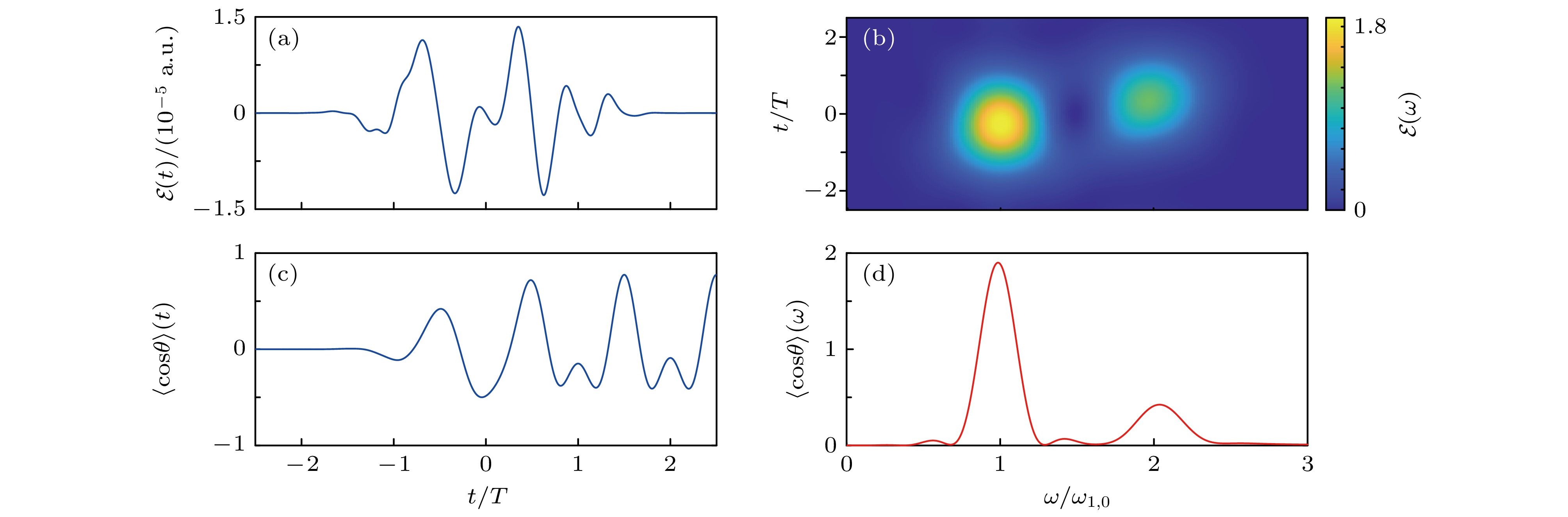
为揭示最优脉冲调控分子取向的物理机制, 图5和图6绘制了优化的含时脉冲场、分子取向度, 各转动态布居及其相位演化曲线. $ J = 1 $和$ J = 2 $态的初始相位设为零. 可以发现, 优化脉冲驱动分子在目标态空间演化, 脉冲结束时, 最低三个转动态的布居分别为$ {\cal{P}}_{0} = 0.2793 $, $ {\cal{P}}_{1} = 0.5003 $和$ {\cal{P}}_{2} = 0.2204 $, 与解析解((8)式)获得的理论值0.28, 0.5和0.22高度符合, 而非目标态($ J = 3 $和$ J = 4 $)布居总被限制在$ 7.0\times10^{-6} $以内. 此外, 脉冲结束时相邻转动态相位差满足$ \varphi_{1, 0} = \pi $和$ \varphi_{2, 1} = 2\pi $, 与解析条件((6)式)一致. 这一结果表明, 优化脉冲场通过调控转动态布居分布, 并控制三个态之间相位差, 制备了优化的相干叠加态, 从而获得期望的分子取向.

为了展示优化脉冲的激发机理, 对图6(a)中的脉冲进行了时频分析, 如图6(b)和图6(d)所示. 结果显示: 优化脉冲的频率中心主要为$ \omega_{1, 0} $和$ 2\omega_{1, 0} $处, 对应为$ \left | 0 \right \rangle $与$ \left | 1 \right \rangle $之间的跃迁频率, 以及$ \left | 1 \right \rangle $和$ \left | 2 \right \rangle $之间的跃迁频率. 从这两个频率出现的时间先后可以发现, 基频脉冲先打开, 激发处于$ \left | 0 \right \rangle $态分子 $ \omega_{1, 0} $向$ \left | 1 \right \rangle $跃迁, 随后打开的二倍频脉冲进一步将分子激发到$ \left | 2 \right \rangle $态, 这一激发机理可以从图5(b)中的转动态布居演化看出. 这个激发机理与通过解析设计脉冲序列调控三态最大分子取向的理论研究一致, 但优化方案避免了解析推导方式假设脉冲分开激发的限制^[70].

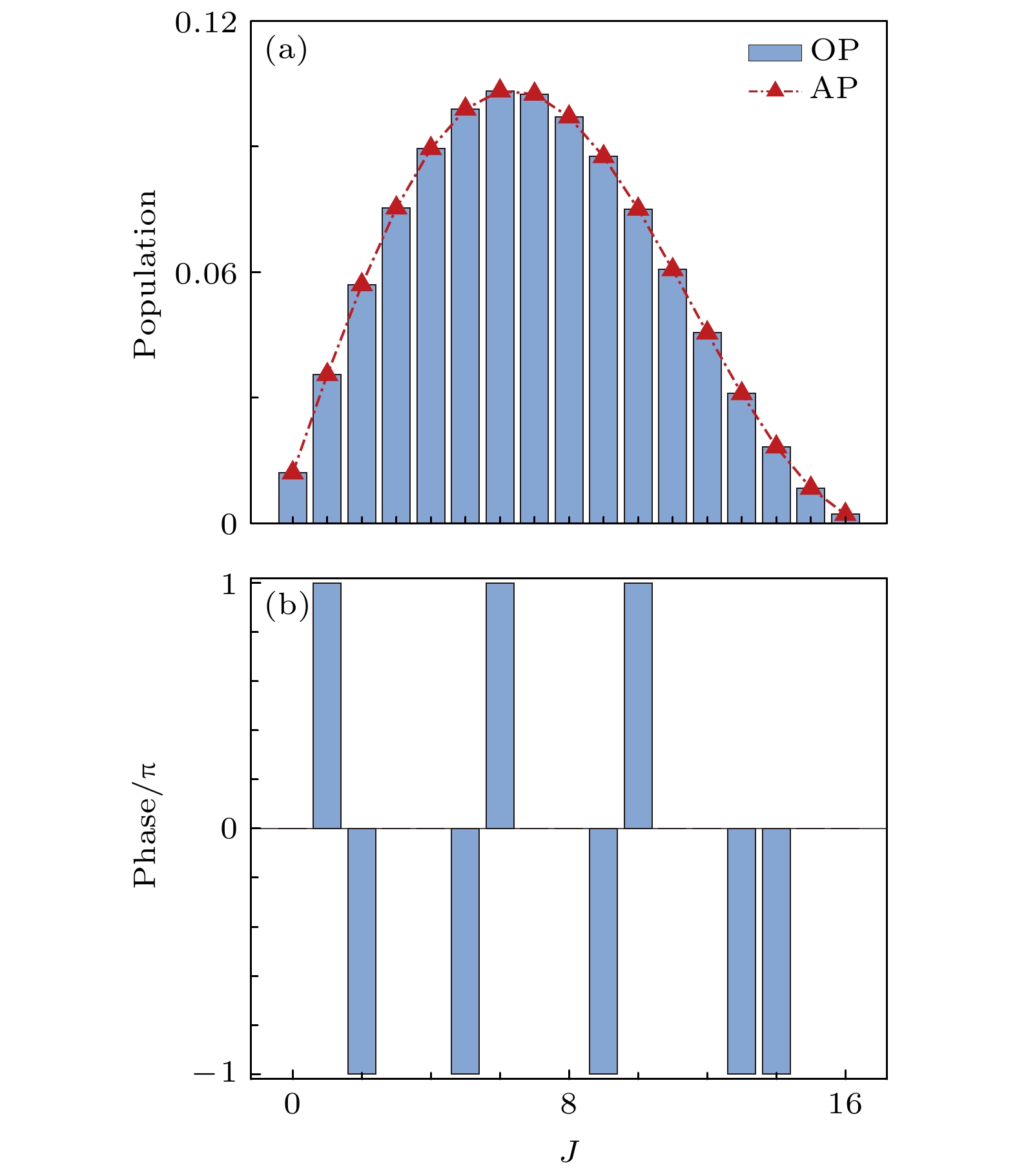
本文进一步将该方法应用于更多目标态系统, 以实现更高的分子取向度. 最近的研究成果表明, 通过优化超过16个最低转动态, 可以将分子的最大正取向度提高至0.99以上^[70]. 为此, 本节设定目标转动态数量为$ M = 17 $, 非目标转动态数量为$ N = 2 $, 初始猜测脉冲的能量为$ {\cal{F}} = 2.2 \times 10^{-3} $. 图7展示了最大取向度、非目标态总布居、脉冲面积和脉冲能量随迭代次数的变化曲线. 如图7(a)所示, 经过230000次迭代后, 取向度的最大值达到0.99055, 与理论最大值0.99057相差甚微. 由于进一步优化的增长非常缓慢, 且保真度已超过0.99997, 终止程序, 不再继续迭代. 进一步分析图7可以发现, 在迭代过程中, 非目标空间中的转动态布居始终保持在极低水平, 脉冲面积和能量在允许的波动范围内保持稳定. 本文也将该方法用于其他目标态系统, 结果一致性地展示方法在获得最大取向度、限制非目标态布居、脉冲面积和脉冲能量上的能力, 表明该优化算法的有效性和普适性.

从上面的研究发现, 分子最大取向度的获得源于目标空间转动态的相干叠加. 也就是优化脉冲场有效调控了目标空间的转动态分布以及各个转动之间的相位关系. 为此, 图8刻画了最优脉冲结束后, 目标空间转动态布居分布以及转动态相位. 可以发现, 优化的转动态布居分布与理论计算值一致, 且相邻态相位差为π的整数倍, 满足获得最大分子取向所需要的相位关系. 在先前的研究中, 我们通过解析计算15个脉冲序列的振幅、相位、中心频率、时延等参数, 获得了优化的脉冲序列, 从而获得了最低16个态的转动态最优分布以及需要的相位关系^[70]. 为获得解析的表达式, 我们在先前的推导过程中要求脉冲序列的每个子脉冲彼此分开. 这一假设对应的激发机理是, 每个脉冲选择激发邻近的两个转动态, 通过一系列阶梯式激发, 目标空间的转动态布居和相位被优化, 从而获得最大的分子取向.

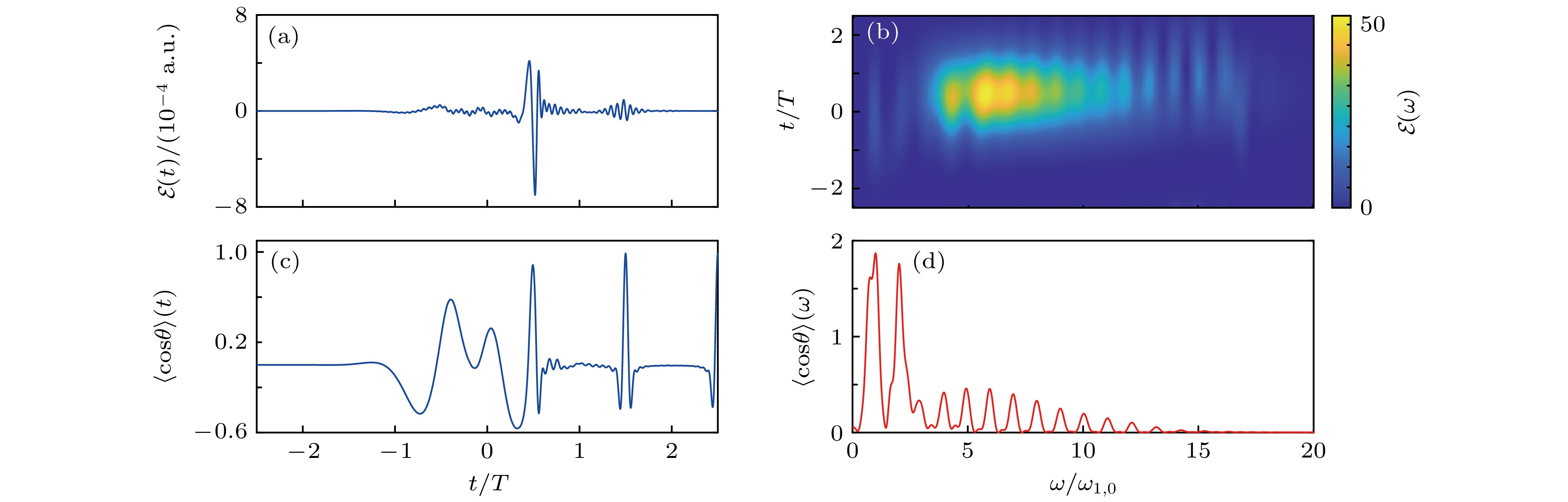
为了深入探究激发机制, 图9(a)和图9(b)展示了最终优化的含时脉冲场及其对应的时间-频率分布图. 时频图揭示了优化脉冲场包含16种不同的频率成分, 这些成分对应于16组相邻能级的跃迁频率, 且基频和低阶频率脉冲依次激活. 这表明直接相邻态之间的单光子跃迁在激发过程中起主导作用. 为了进一步揭示各个转动态对最大分子取向度的贡献, 图9(c)和图9(d)描绘了相应的含时取向度及其傅里叶变换谱. 从含时脉冲场到含时取向度的演化可以看出, 脉冲的初始阶段较弱, 分子取向度较低, 而在脉冲结束时, 最大取向度的变化也不大, 这表明转动激发主要集中在脉冲的中间阶段. 取向度的傅里叶谱图中主要包含13个显著的谱峰, 这意味着只有最低的14个态对取向度有显著贡献, 而高阶激发对取向度的贡献较小. 之前的研究表明, 激发最低的5个和16个转动态分别可以获得超过0.9和0.99的取向度^[70]. 然而, 引入更多高阶转动态通常需要更多的高频脉冲, 这不仅增加了系统的复杂度, 而且对提升最大取向度的贡献有限. 因此, 在实际应用中, 除非追求极高的取向度, 否则对于双原子分子系统, 仅激发少数低阶转动态即可实现较为理想的取向效果. 优化方法避免了引入离散脉冲序列, 大大减少了产生最优转动布居分布所需的时间, 这对于克服转动退相干的负面影响具有重要意义.

本文提出了一种多目标多约束量子最优控制算法, 旨在精确调控双原子LiH分子的有限转动态布居和相位分布, 以实现最大分子取向. 该算法的核心在于将分子转动态空间划分为目标态空间和非目标态空间, 通过优化算法将转动激发限制在目标态空间内, 同时最小化非目标态空间的影响. 在约束条件方面, 该算法不仅要求优化脉冲面积为零(以消除静电场成分), 还要求保持脉冲输入能量不变. 通过对两态和三态目标空间问题的研究, 研究发现该算法能够有效调控目标空间内的转动态布居和相位分布, 从而实现预期的最大分子取向. 进一步地, 本文将该算法应用于包含17个转动态的目标态空间问题, 成功获得了最大取向度为0.99055的结果. 为深入理解激发机理, 本文对优化脉冲进行了时频分析, 并计算了含时取向的傅里叶变换谱. 计算结果显示, 优化脉冲通过激发邻近转动态, 采用阶梯激发方式实现了优化的转动态布居和相位分布. 此外, 高阶转动激发对分子最大取向度的贡献较小. 与先前采用的解析设计脉冲序列方案相比, 优化脉冲方案在缩短激发时间方面展现出显著优势. 值得注意的是, 该最优脉冲在理论上表现出优异的控制效果, 其实验实现需要先进的微波或者太赫兹脉冲整形技术. 基于当前成熟的微波技术, 我们期望该工作可以引起实验学家的关注, 用于设计优化微波脉冲, 操控超冷分子的有限转动态, 从而实现高精度操控分子转动.