-
超导纳米线单光子探测器(superconducting nanowire single-photon detector, SNSPD)是当前最先进的单光子探测技术之一, 凭借其接近饱和的系统探测效率(>98%)[1]、亚纳秒级时间分辨率(~3 ps)[2]、极低的暗计数率(数Hz)[3]以及GHz量级的光子计数能力[4], 在量子密钥分发[5]、深空激光通信[6]和单光子激光雷达[7,8]等前沿领域展现出无可替代的性能优势. 该技术的物理机制可追溯至2001年Gol’tsman等[9]提出的开创性工作: 他们在蓝宝石衬底上沉积5 nm厚的氮化铌(NbN)薄膜, 构建微桥型纳米线结构, 首次实现了基于超导的热点效应单光子探测. SNSPD的工作原理[10]本质上是一个超导态-电阻态-超导态之间的动态量子相变过程. 当纳米线被偏置在临界电流(Ic)附近, 入射单光子会导致局域大量库珀对解离, 形成准粒子并产生非超导的“热点”区域. 在偏置电流贡献的焦耳热驱动下, 该区域进一步扩展, 最终在纳米线内形成贯通的电阻带, 从而在外部电路中激发出纳秒级的电压脉冲. 随后, 热点通过电子-电子相互作用以及电子-声子相互作用耗散能量, 纳米线重新恢复至超导态. 值得注意的是, 热点尺寸与器件性能密切相关: 较大的热点区域不仅降低了触发相变所需的偏置电流, 有助于抑制本征暗计数, 还能提升对低能(长波长)光子的响应能力, 从而拓展探测波段至中远红外区域[11,12]. 经过二十余年的技术演进, SNSPD的系统探测效率已从最初的1%提升至98%以上, 这一突破性进展得益于超导材料体系的持续优化与创新. 超导薄膜材料的超导物性参数与器件性能之间存在显著关联, 其临界温度不仅决定了器件的工作温度, 同时超导能隙Δ还直接影响光子响应阈值波长; 相干长度ξ不仅影响纳米线的非平衡动力学行为, 同时更长的ξ还可增强超导纳米线的鲁棒性, 降低微纳工艺缺陷对器件性能的影响; 正常态电子扩散系数
$ {D}_{\mathrm{e}} $ 直接影响准粒子的扩散过程, 间接决定了光子产生的热点的大小; 同时薄膜材料的均匀性还通过局部临界电流密度涨落影响探测器的本征探测效率[13]. 因此, 系统地研究超导薄膜材料的物理学性质对高性能SNSPD的研制至关重要.在早期研究中, 氮化铌(NbN)因其较高的超导转变温度、较大的临界电流密度以及快速响应能力, 成为SNSPD研制的主流材料[9]. 然而, 纳米尺度下NbN薄膜易形成颗粒结构并产生大量晶界缺陷, 显著限制了其探测性能. 为此, 研究人员曾通过选用晶格匹配的衬底(如MgO衬底)、引入缓冲层(如AlN缓冲层)以及优化薄膜沉积工艺以提升器件性能和系统探测效率[14–16]. 同时, 研究人员还进一步通过引入Ti元素形成的NbTiN合金降低NbN的结晶温度并细化晶粒, 从而降低器件的本征暗计数[17,18]. 为克服上述限制, 研究人员逐步转向非晶超导材料体系. 相比晶态颗粒超导薄膜材料, 非晶超导体是由不同类型完全随机分布的原子构成, 因而具有极佳的均匀性以及鲁棒的超导电性. 但非晶超导体通常具有更小的超导能隙和更低的临界电流密度, 在吸收单光子后可形成更大的热点区域, 同时对衬底材料要求较低, 适合研制大光敏面以及中远红外SNSPD[19–23]. 在2011年, Baek等[24]首次实现基于非晶硅化钨(WSi)材料的SNSPD, 器件面积达到16 μm×16 μm, 并在可见至1850 nm波长范围内实现饱和内量子效率. 随后Marsili等[19]率先利用WSi实现了系统探测效率达到93%的非晶SNSPD. 最近Wollman等[25]开发的直径达320 μm的64像素WSi阵列被成功应用于深空光通信领域. 相比WSi, MoSi材料具有更高的临界温度, 使得SNSPD可在更高的工作温度(2—3 K)下运行, 这将有效降低了对冷却系统的依赖[26–28]. Banerjee等[29]对MoSi的超导特性进行了系统研究, 证实其在较高温度下仍具有良好的单光子探测性能. Wollman等[30]设计的基于MoSi的紫外波段SNSPD可在4.2 K下工作, 在250—370 nm范围内实现70%—80%的探测效率与~0.25 counts/s的暗计数率. 除MoSi外, MoGe材料也显示出相近的超导性能. Verma等[21]基于MoGe开发的SNSPD同样展现高转变电流、高信噪比以及优异的时间分辨性能.
当前, 除WSi, MoSi和MoGe等非晶超导体, 探索可用于高性能SNSPD研制的新型非晶材料仍是研究的热点问题. 我们近期报道了一种新型非晶超导材料—锗化钨(WGe), 其超导性能与WSi相似, 同时展现出更长波长的响应范围与更大的制备尺寸潜力, 是中远红外SNSPD器件的理想候选材料[31,32]. 为系统研究WGe薄膜的超导物理特性, 并与现有非晶材料进行对比, 本文制备了不同厚度的WGe, WSi和MoGe薄膜样品. 通过测量不同磁场条件下的超导转变行为, 深入探讨其超导输运性质, 为理解新型非晶材料的微观参数与SNSPD器件性能之间的关系提供了重要的实验依据和数据支持.
-
非晶WGe, WSi和MoGe超导薄膜主要通过磁控共溅射技术沉积在直径2—4 in (1 in = 2.54 cm)的硅衬底晶圆上. 这些非晶超导薄膜皆是在室温下于3 mTorr (1 Torr = 1.33322 × 102 Pa)氩气(Ar)氛围中沉积. 其中, 金属元素Mo和W通过直流磁控溅射沉积, 非金属元素Si和Ge则通过射频磁控溅射沉积. 钼(Mo)和钨(W)靶材的纯度为99.95%, 硅(Si)和锗(Ge)靶材的纯度为99.999%. 为了精确地调控非晶WGe, WSi和MoGe超导薄膜的化学计量比, 并同时降低其他变量对材料组分的影响, 将Si靶与Ge靶的溅射功率固定在其最稳定的射频功率(50 W)下, 通过改变W靶与Mo靶的溅射功率(40—75 W)从而实现对薄膜材料组分的调控[33]. 薄膜材料的精确组分通过场发射扫描电子显微镜的能谱仪(Zeiss GeminiSEM 300)进行测量, 其加速电压设置为15 kV以确保每个元素的特征X射线都能被激发. 为实现具有高临界温度的非晶超导薄膜材料, 金属成分化学计量比一般控制在约80%(原子百分比), 非金属成分化学计量比约20%[34]. 在完成薄膜材料的组分调控后, 通过测量相应目标组分的沉积速率, 进而通过沉积时间控制薄膜材料的厚度. 为系统地研究非晶超导薄膜材料超导物理学性质随薄膜材料厚度的变化, 分别制备了一系列厚度范围(4—100 nm)的WGe, WSi和MoGe薄膜.
-
在完成不同厚度非晶超导薄膜材料沉积后, 利用划片机将薄膜材料晶圆切割为5 mm × 5 mm的正方形以用于超导电输运测试. 薄膜材料的薄层电阻的温度与磁场依赖性通过综合物性测量系统(physical property measurement system, PPMS)测量, 其电学连接采用标准的四线法, 利用绑线机将铝线绑定至被测样品上[35]. 通过不同厚度非晶超导薄膜材料在不同垂直磁场下的正常态-超导态转变, 系统研究非晶超导薄膜材料的相干长度、正常态电子扩散系数以及磁场穿透深度等物性参数.
-
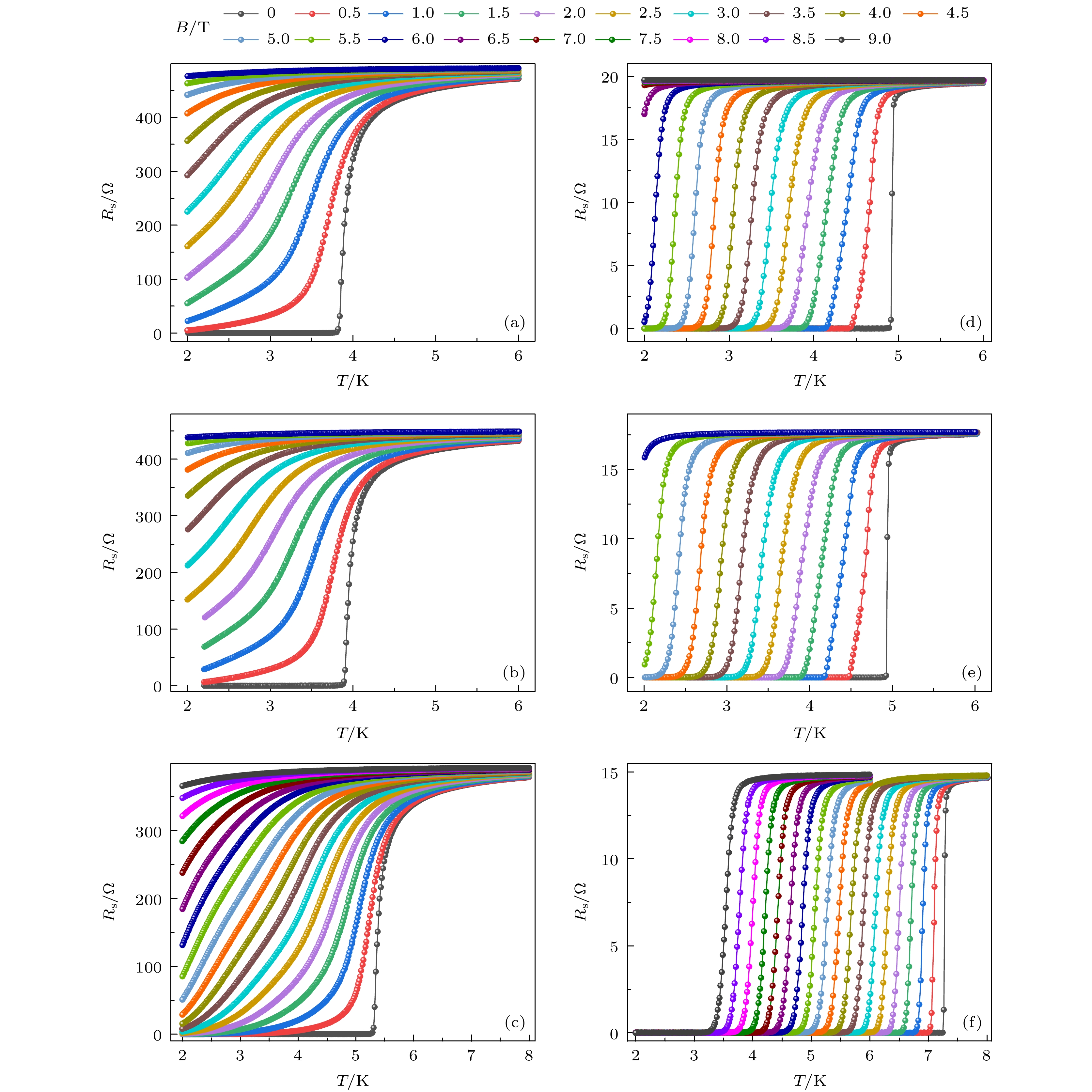
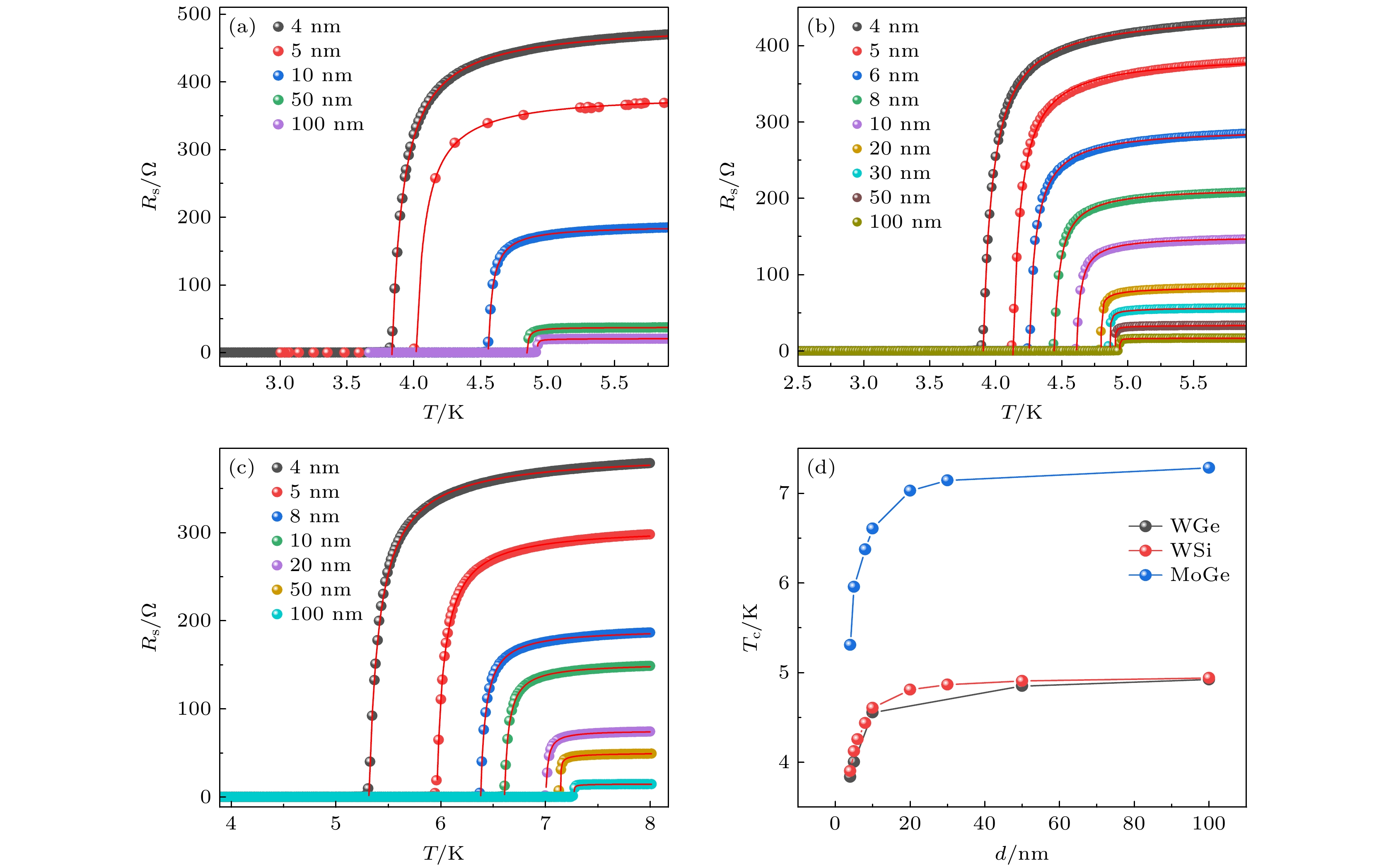
临界温度Tc是超导材料最基础的物理性质, 通常通过测量薄膜材料的薄层电阻的温度依赖性Rs(T )所确定. 图1(a)—(c)分别展示了零磁场下不同厚度WGe, WSi和MoGe薄膜材料的正常态-超导态转变. 在临界温度附近, 薄膜的薄层电阻Rs(T )随温度的降低而减小, 并在进入超导态时剧降到零. 根据非平衡准粒子的涨落效应, 超导临界温度附近准二维(≤10 nm)与三维(>10 nm)体材料薄膜的薄层电阻可以分别表达为[36]
其中,
$ {R}_{\mathrm{s}\mathrm{n}} $ 是正常态电阻; ħ是普朗克常数; e是元电荷; ξ(0)是相干长度; d是薄膜厚度;$ {A}_{2\mathrm{D}} $ 与$ {A}_{3\mathrm{D}} $ 分别为二维与三维涨落系数, 其综合考量了Aslamazov-Larkin(AL)涨落电导以及Maki-Thompson(MT)涨落电导[35]. 通过(1)式和(2)式拟合非晶超导薄膜的Rs(T), 分别得到了WGe, WSi和MoGe三种非晶薄膜材料的临界温度Tc随薄膜厚度的变化曲线, 见图1(d). 当薄膜材料厚度低于20 nm时, 薄膜材料的Tc随着厚度的减小而显著降低, 这主要是超导序参量空间涨落的影响. 而薄膜材料厚度超过20 nm时, 其Tc随薄膜厚度的增大不再显著提升. 此外, 非晶WGe和WSi的Rs与Tc非常接近, 且具有近乎一致的Tc(d )依赖性, 这意味着WGe可能与WSi超导物性相似, 可用于高性能SNSPD的研制.由于SNSPD的单光子响应性能以及暗计数率等关键性能参数都与超导薄膜材料的物理学参数(如相干长度ξ、磁场穿透深度λ与正常态电子扩散系数De)密切相关, 因此为进一步研究超导薄膜材料物理学参数, 系统测量了不同磁场下的超导薄膜材料的正常态-超导态转变. 通过分析薄膜材料上临界磁场的温度依赖性, 结合超导薄膜材料的正常态电阻率和超导能隙, 可计算超导薄膜材料物理学参数随薄膜材料厚度的变化[22]. 图2(a)—(c)分别展示了4 nm厚WGe, WSi和MoGe材料的超导相变曲线Rs(T, B), 而图2(d)—(f)则展示了100 nm厚WGe, WSi和MoGe体材料的正常态-超导态转变. 由于磁场对库珀对凝聚能的抑制, 薄膜临界温度Tc随磁场强度增大而逐渐降低. 其中4 nm厚WGe, WSi和MoGe材料的临界温度分别从3.84 K(0 T), 3.90 K(0 T)和5.31 K(0 T)下降至2.10 K(3 T), 2.02 K(3 T)和2.04 K(6.5 T), 而100 nm厚WGe, WSi和MoGe体材料的临界温度分别从4.92 K(0 T), 4.94 K(0 T)和7.28 K(0 T)下降至2.13 K(6 T), 2.16 K(5.5 T)和3.54 K(9 T). 同时在超薄非晶超导薄膜材料中, 由于其内部无涡旋钉扎中心, 因此在磁场下其更容易受到磁通涡旋的影响. 在超导临界温度Tc(B)附近, 薄层电阻呈现出了一定的翘曲, 并在更低的温度下方进入零电阻超导态.
-
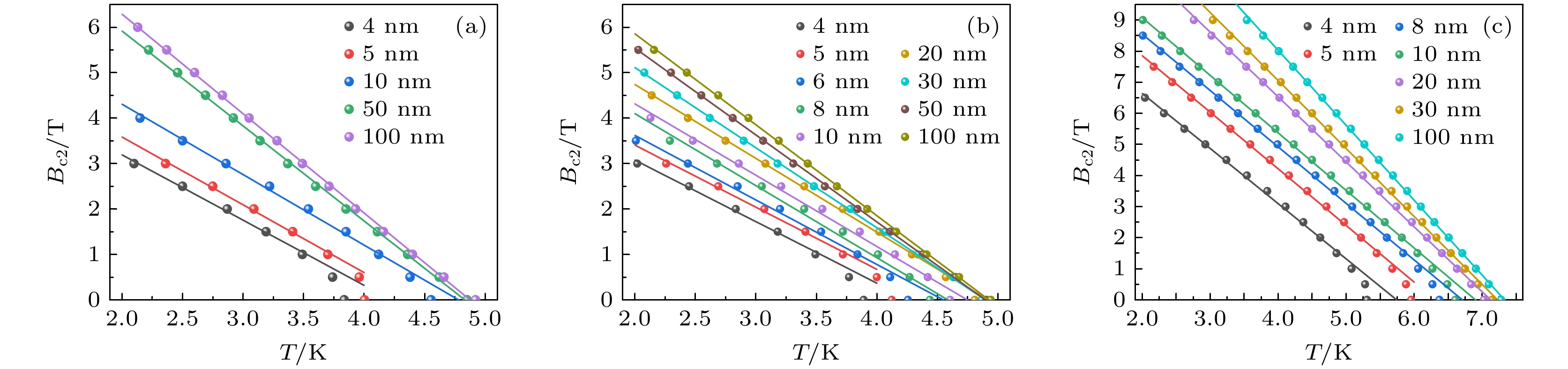
由于磁场下的超导转变曲线无相应的超导涨落理论描述, 因此使用最常用的Rsn/2判据标准(即将磁场下的临界温度定义为薄层电阻降低50%时所对应的温度)得到非晶超导薄膜材料在不同磁场下的临界温度Tc(B)[37]. 图3(a)—(c)分别展示了不同厚度WGe, WSi以及MoGe超导薄膜材料上临界磁场的温度依赖性. 根据金兹堡-朗道(Ginzburg-Landau, GL)理论, 当温度接近Tc(0)时, 上临界磁场的温度依赖性近似为线性关系. 通过线性拟合临界温度附近薄膜材料的上临界磁场即可得到薄膜材料的零温度上临界磁场Bc2(0)[38].
如图3所示, 在较厚的非晶超导薄膜材料中, 其Tc(0)附近的斜率更大, 同时上临界磁场更高. 然而在绝对零度附近, 由于量子涨落的影响, 实际超导薄膜材料的上临界磁场一般低于线性外插值. 尤其是对于无序度较高的“脏”超导体, 通过线性外插得到的Bc2(0)值通常高于实际临界磁场, 需乘以修正因子0.69才能获得合理值[39]. 根据GL理论, 绝对零度上临界磁场Bc2(0)与GL相干长度ξ具有如下关系[40]:
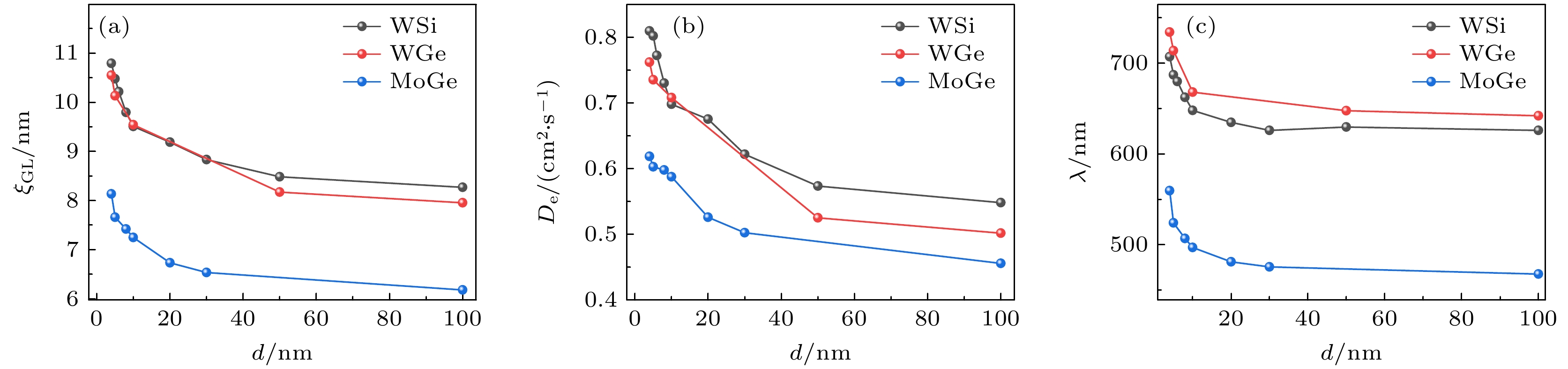
其中Φ0是磁通量子(Φ0 = ħ/(2e) = 2.07 × 10–15 V⋅s), GL相干长度ξ表征序参量在空间尺度上的变化范围. 计算得到的三类非晶超导薄膜材料的GL相干长度随厚度的变化如图4(a)所示. 随着薄膜厚度的减小, 这三类非晶超导薄膜材料的GL相干长度显著增大, WGe与WSi的相干长度相近, 较MoGe非晶超导薄膜材料高出近30%. 在具有较低维度的SNSPD中, 具有较高的ξ, SNSPD将能够更鲁棒地避免纳米线局域缺陷引起的超导序参量空间涨落, 从而降低微纳工艺缺陷对SNSPD临界电流的影响, 并降低探测器的本征暗计数率[19,22].
同时, 对于超导薄膜材料, 其正常态电子的扩散系数De可通过Tc(B)曲线在零磁场超导转变温度Tc(0)附近的斜率确定[22]:
其中kB是玻尔兹曼常数. 如图4(b)所示, 3种薄膜的正常态电子扩散系数De随薄膜厚度减小而增大. 其中4 nm厚WGe和WSi材料的De分别约为0.80和0.85 cm2/s, 比相同厚度MoGe材料更高(0.64 cm2/s). 因此, 入射光子诱导的正常态电子在WGe和WSi中的扩散距离更长, 形成更大的热点区域, 这意味着相同几何结构的WGe-或WSi-SNSPD可能具有更高的本征探测效率与更长的截止波长.
除超导相干长度与正常态电子扩散系数外, 另一与SNSPD光响应密切相关的超导薄膜物性 参数是磁场穿透深度, 其表征了外磁场能够影响 超导体物性的最大深度. 在足够低的磁场中, 超导体在临界温度 Tc 之下具有完全抗磁性, 表现为超导体的内部磁场为零[41]. 不过磁通量仍然会渗 透进入超导体的边缘, 并在空间中遵循指数衰减 规律[42]:
其中λL是伦敦磁穿透深度, 下标z表示磁场方向. 在非理想超导体中有效磁场穿透深度λ可以表达为伦敦磁场穿透深度λL, BCS (Bardeen-Cooper-Schrieffer) 相干长度ξ0和电子平均自由程l的乘积[43]:
BCS相干长度ξ0可通过费米速度vF和超导能隙Δ(0)表示为[44]
根据BCS理论
$ \varDelta \left( 0 \right)=\left( {\pi /{{\text{e}}^\gamma }} \right){k_{\text{B}}}{T_{\text{c}}} \left( {\gamma = 0.577} \right) $ , 计算出3种薄膜的超导能隙, 由此, 绝对零度下的磁场穿透深度可用如下公式表达:其中μ0为真空磁导率; ρn为薄膜的正常态电阻率, 其值与薄层电阻Rsn和薄膜厚度d的关系为ρn = Rsn×d. 本文研究的3种非晶薄膜材料WGe, WSi和MoGe, 其磁场穿透深度与薄膜厚度的依赖关系如图4(c)所示. 随着薄膜厚度的减小, 磁场穿透深度逐渐增大. 对于高度无序的非晶WGe和WSi材料, 其电子平均自由程l相对较小, 磁场穿透深度λ(0)则相对较大. 较高的磁场穿透深度可降低超导纳米线或微米线中偏置电流的非均匀分布, 这是因为SNSPD的几何线宽一般远小于其有效磁场穿透深度. 因此偏置电流在纳米线中的分布不再随纳米线的位置而变化, 这有效地降低了因偏置电流分布不均匀引起的本征暗计数. 此外, 由于磁场穿透深度的增大, 其将大幅降低涡旋进入纳米线或微米线的势垒, 无论是单个涡旋在纳米线边缘的成核势垒还是纳米线中涡旋-反涡旋对的成核势垒. 这将更有利于超导纳米线吸收光子后形成一条横跨纳米线的正常态阻带(hot belt), 进而提升SNSPD的本征光响应性能, 尤其是在线宽更宽的超导微米线中[45].
最后, 表1—表3分别列出了本文中所有计算得到的WGe, WSi, 以及MoGe的电输运参数.
-
本文系统地研究了3种非晶态超导材料WGe, WSi和MoGe在不同厚度范围(4—100 nm)内的超导物性变化规律. 首先, 利用磁控溅射技术分别沉积制备了4—100 nm厚WGe, WSi和MoGe非晶超导薄膜, 并通过电输运测试系统地研究了其超导物理学性质, 包括临界温度Tc、相干长度ξ(0)、正常态电子扩散系数De、磁穿透深度λ(0)以及超导能隙Δ(0). 研究结果表明, WGe与当前广泛用于SNSPD研制的WSi在多个超导物性参数上具有高度相似性, 包括相近的临界温度和相干长度, 稍低的正常态电子扩散系数及更高的磁穿透深度. 与另一种非晶材料MoGe相比, WGe和WSi均表现出更大的正常态电子扩散系数、更长的相干长度和更深的磁穿透深度. 从超导物理学参数上看, 相较于WSi超导薄膜材料, WGe-SNSPD的热点尺寸可能略小, 但其有效温度更高, 结合其更高的光子能量转化效率[31], WGe-SNSPD的本征探测效率可能更高, 即在更低的偏置电流下即可实现更灵敏的光子响应, 但其磁场穿透深度更大、磁通涡旋势垒更低, 因而可能具有更高的本征暗计数率. 但在超导微米线中, 此时热点尺寸一般远小于微米线线宽, WGe微米线中更低的涡旋-反涡旋对的势垒将使得其具有更好的单光子响应性能. 基于上述分析, 我们预期WGe与WSi类似, 均可应用于大光敏面高性能SNSPD的研制, 其在中远红外波段可能具有更高的单光子响应灵敏度.
面向超导纳米线单光子探测器研制的新型非晶超导薄膜材料的物性研究
Physical properties of novel amorphous superconducting thin film materials for superconducting nanowire single-photon detectors
-
摘要: 非晶超导薄膜材料具有超导电性均匀性高以及光响应灵敏度好等优势, 是研制大光敏面以及中远红外超导纳米线单光子探测器的理想超导薄膜材料. 本文系统研究了新型非晶锗化钨超导体的超导物性随薄膜材料厚度的变化. 对比硅化钨与锗化钼非晶超导薄膜, 研究发现锗化钨合金与硅化钨具有相似的超导物性, 包括相近的临界温度和相干长度, 稍低的正常态电子扩散系数和较高的磁穿透深度. 相较于锗化钼, 锗化钨合金与硅化钨的电子扩散系数和磁穿透深度均呈现不同程度的增大. 通过研究3种不同非晶薄膜的超导物性参数, 为大光敏面、高灵敏度超导纳米线单光子探测器的研发与性能优化提供了新的材料选择与实验依据.
-
关键词:
- 超导纳米线单光子探测器 /
- 非晶超导薄膜材料 /
- 锗化钨 /
- 超导物理学性质
Abstract: Amorphous superconducting thin film materials have the advantages of high superconducting uniformity and good optical response sensitivity, which make them ideal materials for fabricating large-area and mid-infrared superconducting nanowire single-photon detectors (SNSPD). In this paper, three series of different amorphous superconducting films are deposited on Si wafers by room-temperature magnetron co-sputtering. For these films, the dependence of their physical properties, i.e. critical temperature Tc, Ginzburg-Landau coherence length ξ(0), normal-state electron diffusion coefficient De, magnetic penetration depth λ(0), and superconducting energy gap Δ(0), on film thickness is systematically investigated. Compared with amorphous tungsten silicide (WSi) and molybdenum germanide (MoGe) superconducting thin films, WGe alloys and WSi have similar superconducting properties, including critical temperature and coherence length, slightly lower normal-state electron diffusion coefficient and higher magnetic penetration depth. Compared with MoGe, both WGe and WSi alloys exhibit larger normal-state electron diffusion coefficient and higher magnetic penetration depths. By studying the superconducting properties of three different amorphous thin films, this research provides new material choices and experimental evidence for developing and optimizing the performance of large-area, high-sensitivity superconducting nanowire single-photon detectors. -

-
图 1 零磁场下非晶薄膜WGe (a), WSi (b), MoGe (c)超导转变的厚度依赖关系; (d) WGe, WSi和MoGe薄膜的临界温度的厚度依赖性
Figure 1. Thickness dependence of normal to superconducting transition for amorphous WGe (a), WSi (b), MoGe (c) films in absence of magnetic field; (d) the critical temperatures as functions of the film thickness for WGe, WSi and MoGe.
图 3 不同厚度WGe (a), WSi (b)和MoGe (c)薄膜临界磁场的温度依赖曲线(通过对温度依赖曲线的线性拟合, 提取出绝对零度上临界磁场Bc2(0))
Figure 3. Critical magnetic field of WGe (a), WSi (b), MoGe (c) films (points) of different thickness as a function of temperature. Through linear fitting of these temperature dependence, the absolute zero critical magnetic field Bc2(0) are extracted.
图 4 (a) 绝对零度下的GL相干长度ξ(0)与薄膜厚度的函数关系; (b) 正常态电子扩散系数De与薄膜厚度的函数关系; (c) 磁场穿透深度λ与薄膜厚度的函数关系
Figure 4. (a) The GL coherence length at absolute zero temperature ξ(0) as a function of film thickness; (b) thickness dependence of the diffusion constant of the electrons in the normal-conducting state; (c) the magnetic penetration depth λ(0) as a function of film thickness.
表 1 不同厚度WGe薄膜材料的超导物性参数
Table 1. Superconducting physical property parameters of the WGe film with different thicknesses.
样品 d/nm Rsn/Ω Tc/K ξ(0)/nm De/(cm2·s–1) Δ(0)/meV λ(0)/nm WGe 4 471.25 3.84 10.55 0.76 0.58 734 5 371.80 4.00 10.13 0.74 0.61 714 10 185.30 4.55 9.54 0.71 0.69 668 50 37.09 4.85 8.17 0.53 0.74 647 100 18.49 4.92 7.95 0.50 0.75 642 表 2 不同厚度WSi薄膜材料的超导物性参数
Table 2. Superconducting physical property parameters of the WSi film with different thicknesses.
样品 d/nm Rsn/Ω Tc/K ξ(0)/nm De/(cm2·s–1) Δ(0)/meV λ(0)/nm WSi 4 444.65 3.90 10.79 0.81 0.59 707 5 354.90 4.12 10.48 0.80 0.63 687 6 298.85 4.26 10.22 0.77 0.65 680 8 221.84 4.44 9.80 0.73 0.67 662 10 176.25 4.61 9.51 0.70 0.70 648 20 88.31 4.81 9.19 0.68 0.73 635 30 57.95 4.87 8.83 0.62 0.74 626 50 35.47 4.91 8.48 0.57 0.75 630 100 17.65 4.94 8.27 0.55 0.75 626 表 3 不同厚度MoGe薄膜材料的超导物性参数
Table 3. Superconducting physical property parameters of the MoGe film with different thicknesses.
样品 d/nm Rsn/Ω Tc/K ξ(0)/nm De/(cm2·s–1) Δ(0)/meV λ(0)/nm MoGe 4 378.75 5.31 8.14 0.62 0.81 560 5 298.30 5.96 7.66 0.60 0.91 524 8 186.59 6.37 7.42 0.60 0.97 507 10 148.76 6.61 7.25 0.59 1.00 497 20 74.15 7.03 6.73 0.53 1.07 481 30 49.12 7.14 6.54 0.50 1.09 476 100 14.52 7.28 6.18 0.46 1.11 468 -
[1] Chang J, Los J W N, Tenorio-Pearl J O, Noordzij N, Gourgues R, Guardiani A, Zichi J R, Pereira S F, Urbach H P, Zwiller V, Dorenbos S N, Esmaeil Zadeh I 2021 APL Photonics 6 036114 doi: 10.1063/5.0039772 [2] Korzh B, Zhao Q Y, Allmaras J P, Frasca S, Autry T M, Bersin E A, Beyer A D, Briggs R M, Bumble B, Colangelo M, Crouch G M, Dane A E, Gerrits T, Lita A E, Marsili F, Moody G, Peña C, Ramirez E, Rezac J D, Sinclair N, Stevens M J, Velasco A E, Verma V B, Wollman E E, Xie S, Zhu D, Hale P D, Spiropulu M, Silverman K L, Mirin R P, Nam S W, Kozorezov A G, Shaw M D, Berggren K K 2020 Nat. Photonics 14 250 doi: 10.1038/s41566-020-0589-x [3] Shibata H, Fukao K, Kirigane N, Karimoto S, Yamamoto H 2017 IEEE Trans. Appl. Supercond. 27 2200504 doi: 10.1109/TASC.2016.2631947 [4] Zhang W J, Huang J, Zhang C J, You L X, Lv C L, Zhang L, Li H, Wang Z, Xie X M 2019 IEEE Trans. Appl. Supercond. 29 2200204 doi: 10.1109/TASC.2019.2895621 [5] Chen J P, Zhang C, Liu Y, Jiang C, Zhang W J, Han Z Y, Ma S Z, Hu X L, Li Y H, Liu H, Zhou F, Jiang H F, Chen T Y, Li H, You L X, Wang Z, Wang X B, Zhang Q, Pan J W 2021 Nat. Photonics 15 570 doi: 10.1038/s41566-021-00828-5 [6] Khatri F I, Robinson B S, Semprucci M D, Boroson D M 2015 Acta Astronaut. 111 77 doi: 10.1016/j.actaastro.2015.01.023 [7] Zhang B, Guan Y Q, Xia L H, Dong D X, Chen Q, Xu C, Wu C, Huang H X, Zhang L B, Kang L, Chen J, Wu P H 2021 Supercond. Sci. Technol. 34 034005 doi: 10.1088/1361-6668/abd576 [8] Taylor G G, Morozov D, Gemmell N R, Erotokritou K, Miki S, Terai H, Hadfield R H 2019 Opt. Express 27 38147 doi: 10.1364/OE.27.038147 [9] Gol'tsman G N, Okunev O, Chulkova G, Lipatov A, Semenov A, Smirnov K, Voronov B, Dzardanov A, Williams C, Sobolewski R 2001 Appl. Phys. Lett. 79 705 doi: 10.1063/1.1388868 [10] 张彪, 陈奇, 管焰秋, 靳飞飞, 王昊, 张蜡宝, 涂学凑, 赵清源, 贾小氢, 康琳, 陈健, 吴培亨 2021 物理学报 70 198501 doi: 10.7498/aps.70.20210652 Zhang B, Chen Q, Guan Y Q, Jin F F, Wang H, Zhang L B, Tu X C, Zhao Q Y, Jia X Q, Kang L, Chen J, Wu P H 2021 Acta Phys. Sin. 70 198501 doi: 10.7498/aps.70.20210652 [11] Verma V B, Korzh B, Walter A B, Lita A E, Briggs R M, Colangelo M, Zhai Y, Wollman E E, Beyer A D, Allmaras J P, Vora H, Zhu D, Schmidt E, Kozorezov A G, Berggren K K, Mirin R P, Nam S W, Shaw M D 2021 APL Photonics 6 056101 doi: 10.1063/5.0048049 [12] Chen L, Schwarzer D, Lau J A, Verma V B, Stevens M J, Marsili F, Mirin R P, Nam S W, Wodtke A M 2018 Opt. Express 26 14859 doi: 10.1364/OE.26.014859 [13] 尤立星 2018 红外与激光工程 47 1202001 doi: 10.3788/IRLA201847.1202001 You L X 2018 Infrared Laser Eng. 47 1202001 doi: 10.3788/IRLA201847.1202001 [14] Miki S, Takeda M, Fujiwara M, Sasaki M, Otomo A, Wang Z 2009 Appl. Phys. Lett. 2 075002 doi: 10.1143/APEX.2.075002 [15] Sun R, Makise K, Zhang L, Terai H, Wang Z 2016 AIP Adv. 6 065119 doi: 10.1063/1.4954743 [16] Cheng R S, Wang S H, Tang H X 2019 Appl. Phys. Lett. 115 241101 doi: 10.1063/1.5131664 [17] Tanner M G, Natarajan C M, Pottapenjara V K, O'Connor J A, Warburton R J, Hadfield R H, Baek B, Nam S, Dorenbos S N, Ureña E B, Zijlstra T, Klapwijk T M, Zwiller V 2010 Appl. Phys. Lett. 96 221109 doi: 10.1063/1.3428960 [18] Dorenbos S N, Reiger E M, Perinetti U, Zwiller V, Zijlstra T, Klapwijk T M 2008 Appl. Phys. Lett. 93 131101 doi: 10.1063/1.2990646 [19] Marsili F, Verma V B, Stern J A, Harrington S, Lita A E, Gerrits T, Vayshenker I, Baek B, Shaw M D, Mirin R P, Nam S W 2013 Nat. Photonics 7 210 doi: 10.1038/nphoton.2013.13 [20] Verma V B, Marsili F, Harrington S, Lita A E, Mirin R P, Nam S W 2012 Appl. Phys. Lett. 101 251114 doi: 10.1063/1.4768788 [21] Verma V B, Lita A E, Vissers M R, Marsili F, Pappas D P, Mirin R P, Nam S W 2014 Appl. Phys. Lett. 105 022602 doi: 10.1063/1.4890277 [22] Zhang X, Engel A, Wang Q, Schilling A, Semenov A, Sidorova M, Hübers H W, Charaev I, Ilin K, Siegel M 2016 Phys. Rev. B 94 174509 doi: 10.1103/PhysRevB.94.174509 [23] Häussler M, Mikhailov M Y, Wolff M A, Schuck C 2020 APL Photonics 5 076106 doi: 10.1063/5.0004677 [24] Baek B, Lita A E, Verma V, Nam S W 2011 Appl. Phys. Lett. 98 251105 doi: 10.1063/1.3600793 [25] Wollman E E, Allmaras J P, Beyer A D, Korzh B, Runyan M C, Narváez L, Farr W H, Marsili F, Briggs R M, Miles G J, Shaw M D 2024 Opt. Express 32 48185 doi: 10.1364/OE.541425 [26] Verma V B, Korzh B, Bussières F, Horansky R D, Dyer S D, Lita A E, Vayshenker I, Marsili F, Shaw M D, Zbinden H, Mirin R P, Nam S W 2015 Opt. Express 23 33792 doi: 10.1364/OE.23.033792 [27] Zhang X F, Ma R Y, Guo Z M, Zhang C J, Chen D, Huan Q C, Huang J, Zhang X Y, Xiao Y, Yu H Q, Liu X Y, Li H, Wang Z, Xie X M, You L X 2023 Opt. Express 31 30650 doi: 10.1364/OE.501552 [28] Ma R, Guo Z, Chen D, Dai X, Xiao Y, Zhang C, Xiong J, Huang J, Zhang X, Liu X, Rong L, Li H, Zhang X, You L 2025 Adv. Photonics Nexus 4 026003 doi: 10.1117/1.APN.4.2.026003 [29] Banerjee A, Baker L J, Doye A, Nord M, Heath R M, Erotokritou K, Bosworth D, Barber Z H, MacLaren I, Hadfield R H 2017 Supercond. Sci. Technol. 30 084010 doi: 10.1088/1361-6668/aa76d8 [30] Wollman E E, Verma V B, Beyer A D, Briggs R M, Korzh B, Allmaras J P, Marsili F, Lita A E, Mirin R P, Nam S W, Shaw M D 2017 Opt. Express 25 26792 doi: 10.1364/OE.25.026792 [31] Ercolano P, Zhang X, Pepe G P, You L 2025 Supercond. Sci. Technol. 38 015011 doi: 10.1088/1361-6668/ad9996 [32] Yang S J, Chen Y, Sun L M, Zhou H, Li Y M, Huang J, Zheng X Q, Ma R Y, Xiong J M, Wan Z, Liu X Y, Li H, Zheng J H, Peng W, Zhang X F, You L X 2025 Appl. Phys. Lett. 126 162601 doi: 10.1063/5.0264958 [33] Zhang X F, Charaev I, Liu H L, Zhou T, Zhu D, Berggren K K, Schilling A 2021 Supercond. Sci. Technol. 34 095003 doi: 10.1088/1361-6668/ac1524 [34] Johnson W L, Tsuei C C, Raider S I, Laibowitz R B 1979 J. Appl. Phys. 50 4240 doi: 10.1063/1.326456 [35] Zhang X, Lita A E, Sidorova M, Verma V B, Wang Q, Nam S W, Semenov A, Schilling A 2018 Phys. Rev. B 97 174502 doi: 10.1103/PhysRevB.97.174502 [36] Skocpol W J, Tinkham M 1975 Rep. Prog. Phys. 38 1049 doi: 10.1088/0034-4885/38/9/001 [37] Zhang X F, Lita A E, Smirnov K, Liu H, Zhu D, Verma V B, Nam S W, Schilling A 2020 Phys. Rev. B 101 060508 doi: 10.1103/PhysRevB.101.060508 [38] Zhang X F, Shu R, Liu H L, Elsukova A, Persson P O A, Schilling A, Von Rohr F O, Eklund P 2022 Commun. Phys. 5 282 doi: 10.1038/s42005-022-01059-y [39] Helfand E, Werthamer N R 1966 Phys. Rev. 147 288 doi: 10.1103/PhysRev.147.288 [40] Zhang X F, Huan Q C, Ma R Y, Zhang X Y, Huang J, Liu X Y, Peng W, Li H, Wang Z, Xie X M, You L X 2024 Adv. Quantum Technol. 7 2300378 doi: 10.1002/qute.202300378 [41] Meissner W, Ochsenfeld R 1933 Naturwissenschaften 21 787 doi: 10.1007/BF01504252 [42] London H, London F 1935 Proc. R. Soc. London, Ser. A 149 71 doi: 10.1098/rspa.1935.0048 [43] Tinkham M, Emery V 1996 Phys. Today 49 74 doi: 10.1063/1.2807811 [44] Bardeen J, Cooper L N, Schrieffer J R 1957 Phys. Rev. 108 1175 doi: 10.1103/PhysRev.108.1175 [45] Zotova A N, Vodolazov D Y 2012 Phys. Rev. B 85 024509 doi: 10.1103/PhysRevB.85.024509 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: