-
偏微分方程(PDEs)在物理学和金融数学中具有极为重要的作用和意义, 是描述物理现象和金融模型的核心工具, 广泛应用于流体力学、量化金融和量子力学等多个领域. 例如, 流体力学中的Navier-Stokes方程用于分析流体运动, 为航空航天和船舶设计提供了理论支持[1]; Black-Scholes方程描述了金融衍生品价格的动态变化过程, 为风险管理和投资决策提供了指导[2]; Schrödinger方程揭示了微观粒子的概率分布规律, 奠定了半导体物理和凝聚态物理的基础[3]. PDEs的研究价值不仅在于其对物理和金融现象的精确描述, 还在于其为相关理论的深化与发展提供了强大的数学支持[4]. 通过对PDEs的研究, 可以发现新的物理现象和规律, 例如孤立子理论的诞生. 然而, 只有少数PDEs具有解析解[5]. 因此, 建立合适且高效的数值算法以近似求解PDEs显得尤为重要. 这不仅为复杂物理系统的模拟提供了有力支持, 还降低了实验成本, 提高了研究效率. 传统的数值算法包括有限元法(FEM)、有限差分法(FDM)和有限体积法(FVM). 这些非学习类的数值迭代方法[6-8]通常要求将求解域离散化为一系列网格, 而网格划分的方式及尺寸大小对求解精度与效率有显著影响. 不当的网格选择可能导致数值解难以稳定收敛[9]. 此外, 针对网格外的数据点, 还需借助额外的插值方法进行修正[10].
近年来, 人工智能(AI)技术迅猛发展, 并广泛渗透并深度赋能各个研究领域, 尤其在与传统科学深度融合方面(AI for Science[11]). 众多非线性动力学模型的建模工作借助于基于数据驱动的深度学习方法, 例如对于孤子动力学研究, Si等[12]和Fang等[13]采用循环神经网络(RNN)及其变体(如双向长短期记忆网络、BiLSTM)来处理孤子动力学问题, 并着重强调了注意力机制在提升预测精度方面的关键作用. 同时, Li等[14]展示了傅里叶神经算子(FNO)在高维孤子问题中的应用潜力. 通过利用傅里叶变换捕捉全局变化, FNO有效避免了传统数值方法的复杂性. 在PDEs算子学习(DeepONet)方面, Mouton等[15]提出了一种量子加速的DeepONet方法, 借助量子计算降低了输入维度的计算复杂度. Fourier-DeepONet通过引入傅里叶变换增强了DeepONet的特征表达能力, 并在复杂的地震波传播问题中展现了出色的预测性能[16]. 这些研究均验证了深度学习模型的预测结果与实验数据或精确解的一致性, 充分展示了深度学习在超快光学和非线性动力学领域的应用潜力. 计算力学领域也因此受AI for Science启发, 二者融合主要体现在两个方面. 一方面, 通过深度学习方法, 利用真实的实验数据或可靠的数值结果, 构建基于神经网络的推理模型[17]. 这种方法属于隐式编程, 即通过输入数据, 借助人工智能算法卓越的非线性拟合能力, 输出由神经网络参数组成的程序, 从而避免了为解决特定问题而显式编写程序模式[18]. 通过数据驱动方式构建端到端的推理模型, 其核心在于利用神经网络对数据间抽象关系进行建模. 如果训练成功且测试集与训练集在数据分布上保持一致, 则该模型通常能够在测试集上表现出较高的计算效率和推理准确性. 然而, 这种数据驱动方法也存在一些限制. 首先, 它依赖于大量高质量数据, 数据质量和数量直接决定模型预测质量. 此外, 由于缺乏物理约束, 模型可解释性欠缺, 导致难以进一步提升模型预测性能. 另一方面, 将物理定律嵌入神经网络训练的损失函数中, 构成了物理信息机器学习(PIML[19])的核心内容. 其中, 最具代表性且在多个学科中展现出广泛应用潜力[20-22]的方法是Raissi等[23]提出的物理信息神经网络(PINNs). 其核心思想是利用连续可微的多层感知器(MLPs)作为通用逼近函数[24], 并通过自动微分技术[25]将PDEs的算子和边界约束编码到神经网络损失函数中, 通过网络训练来优化其参数以逼近PDEs目标场函数.
基于PINNs建模思想, 众多学者从细化网络架构、优化目标及损失策略等方面入手, 在该领域开展了大量富有成效的改进工作, 以期提升其鲁棒性并优化性能[26,27]. 在网络架构优化上, Ren等[28]专注于卷积核与微分算子之间的内在关联, 开发出更适用于PINNs的卷积结构, 专门用于提取离散化数据分布中的分辨率特征. Lei等[29]则考虑到诸多真实物理系统的时间相关性, 即系统未来状态依赖于过往状态, 由此融合长短期记忆网络(LSTM), 强化了模型对时序相关特征的挖掘能力. 不过, 该方法的损失函数在多目标优化进程中仍存在平衡性不足. f-PICNN[30]采用堆叠非线性卷积网络(CNN)以增强对关联特征的捕捉能力, 但该模型欠缺聚焦与捕获隐藏特征中的关键特征. KINN[31]采用Kolmogorov-Arnold网络(KAN)[32]完全替代PINNs中MLPs, 这一改进思路具有一定参考价值. 该思路借助了KAN有效学习非线性激活函数的线性组合, 进而提升非线性拟合性能. 然而KINN在训练优化过程中易受到惩罚因子不受控而导致模型训练寻优效率欠佳. 针对优化目标, Jahani-Nasab等[33]提出一种带有两阶段训练的增强型PINNs. 即先利用边界条件对部分网络权重进行训练, 随后训练算子约束的权重并更新已训练的边界权重, 以此加速模型收敛. 然而, 该方法未能充分兼顾多约束优化之间的整体平衡. 梯度增强法通过引入PDEs的高阶导数作为正则化项来强化PINNs训练, 在许多高维场景下表现较好[34]. 深度Ritz方法(DRM)则另辟蹊径, 采用PDEs的变分形式作为新的目标函数, 从而规避高阶导数计算[35]. 在损失策略层面, 由于PDEs描述的物理系统通常需同时满足多个约束条件, 仅依赖PINNs的二次惩罚函数直接优化, 必然会导致不同约束条件下收敛速度不匹配的问题. Yang等[36]基于Hirota线性方法得到的孤子解, 对PINNs进行了扩展, 并结合损失函数权重衰减策略, 实现了孤子正问题中的传输预测以及逆问题中的参数识别. Li等[37]提出一种基于隐式多步法和龙格-库塔方法的时间迭代训练方法, 以此补充PINNs的残差项. Wang等[18]则提出一种自适应学习率的退火算法, 借助模型训练过程中梯度统计信息, 平衡损失函数中不同残差项的相互作用. 进一步地, 基于神经切线核(NTK)理论, Wang等证实PINNs存在频谱偏差, 这使得它们难以收敛到高频分量, 因此Jacot等[38]提出一种基于NTK的学习率退火方案. 然而, 该方法需额外计算特征值, 从而显著增加了计算成本. 此外, 从多目标优化视角出发, 部分研究人员还提出运用最大似然估计学习模型训练中的高斯噪声, 进而自适应调整不同约束项权重[39].
上述工作针对网络结构改进的PINNs[28-31]在模型训练过程中寻优能力不足, 而对于优化策略改进的PINNs[37-39]则存在关联特征提取与关键特征聚焦能力欠缺的局限. 本文注意到, 在信息表征方面, 传统PINNs仅采用单向信息传递的MLPs作为逼近函数, 难以捕捉序列间的关联特征[40], 且缺乏对关键特征的识别能力. 同时, 传统注意力机制依赖于softmax函数, 其动态加权计算成本较高[41]. 在损失优化方面, PINNs的损失函数为嵌入物理约束的二次罚函数, 若惩罚因子未施加约束, 易导致模型训练寻优效率不佳. 为应对上述挑战, 本文提出一种基于信息表征-损失优化的改进PINNs—allaPINNs, 旨在增强模型的关键特征提取能力和训练寻优能力, 提升其求解PDEs数值解的准确性和泛化能力. 具体而言, allaPINNs首先使用门控循环单元(GRU[42])来捕获输入序列之间的关联特征. 其次, 引入线性注意力(LA)来解耦传统注意力计算中的softmax函数, 增强模型关键特征识别能力, 同时降低权重动态加权的计算复杂度. 最后, 通过MLPs将其映射为目标输出序列. 此外, allaPINNs引入增广拉格朗日(AL)函数重构目标损失函数, 利用可学习的拉格朗日乘子和惩罚因子有效调控各损失残差项的相互作用, 使得模型训练具备更精确的寻优能力.
本文结构安排如下: 第2节首先介绍了PINNs模型, 并详细阐述所提出的allaPINNs模型网络架构, 包括线性注意力计算过程; 同时, 分析PINNs损失函数存在的局限, 并引入增广拉格朗日函数重构其损失函数. 随后, 第3节使用四个基准方程对allaPINNs与当前先进PINNs模型进行对比评估, 以及通过消融实验来验证allaPINNs改进的网络结构和损失函数性能. 最后, 第4节给出本文总结和未来研究方向.
-
通过PINNs[23]求解包含边界约束和初始条件的PDEs定义如下:
其中,
$ {\cal{D}} $ 表示PDEs的线性或非线性算子;$ {\cal{B}} $ 表示边界条件算子(如Dirichlet或Neumann边界条件);$ u_{0} $ 表示初始条件;$ \varOmega $ 表示空间变量x的定义域;$ \partial\varOmega $ 表示空间域$ \varOmega $ 的边界; 时间变量t的定义域为$ (0, T) $ ;$ (x, t) $ 共同构成了PDEs的时空坐标;$ f, g $ 表示外源项;$ u(x, t) $ 表示场函数在时空点$ (t, x) $ 处的物理量. 方程(1)通常称为泛定方程, 而方程(2)和(3)则分别称为边界条件和初始条件, 二者共同构成了PDE的定解条件[43]. 引入连续可微权函数$ w(x, t) $ , 将上述PDE转换为加权残差形式, 具体如下:由于神经网络的训练本质上是在一个高维参数空间中的非凸优化问题, PINNs将权函数
$ w(x, t) $ 定义为其加权的残差形式, 从而构造出如下嵌入物理信息约束的损失函数$ {\cal{L}} $ :其中,
$ \hat{u}(\cdot;\theta) $ 为具体的神经网络模型, 其代表场函数u的逼近函数, PINNs采用传统MLPs[44]; θ表示神经网络在参数空间中的可学习参数;$ \lambda_{\rm{d}},\; \lambda_{\rm{b}},\; \lambda_{\rm{i}} $ 为超参数, 分别用于控制微分方程残差项、边界条件残差项和初始条件残差项的惩罚系数;$ N_{\rm{d}},\; N_{\rm{b}}, N_{\rm{i}} $ 分别表示从微分方程、边界条件和初始条件中随机采样的训练数据点的数量.从方程(7)可以看到, PINNs将PDEs的物理约束整合到损失函数中, 将PDEs求解问题转化为一个无约束优化的半监督学习问题. 尽管通用逼近定理[24]表明, 在给定足够数量的隐藏神经元和适当的权重配置下, 前馈神经网络能够以任意精度逼近任何连续可测函数, 但其在处理输入序列的时序关联特征时表现欠佳, 尤其缺乏关键特征的识别能力. 此外, 方程(7)本质上是一个二次罚函数, 将惩罚因子作为固定超参数存在模型训练寻优局限, 其不受约束易引发优化过程中的病态失衡问题[45].
-
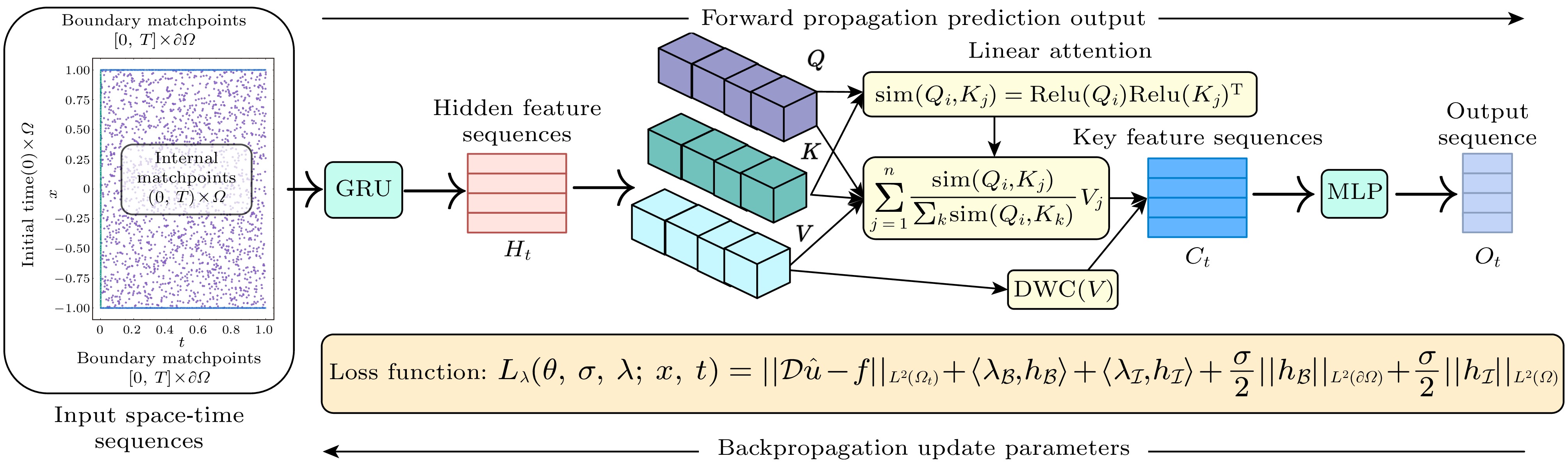
本文从提升关联特征表征与关键特征识别(网络结构)和优化损失策略(损失函数)两个关键层面改进PINNs, 提出如图1所示的allaPINNs模型, 旨在提高求解PDEs数值解的准确性和泛化能力. 本节着重阐述allaPINNs的网络架构, 其损失函数设计则在第2.3节予以详细介绍.
传统PINNs网络架构采用单向信息传递机制的MLPs, 这种设计虽然简化了训练过程, 但也限制了对序列关联关系的表征能力, 并容易表现出频率偏差的学习偏好[46]. 对于复杂的PDEs动力系统, 其输出不仅依赖于当前时刻的输入, 还与过去或近期的输出状态密切相关. 相比之下, 具有反馈结构的RNNs因其对动力系统的一致逼近性质, 能够有效近似任意非线性动力系统[47]. 然而, RNNs在训练过程中容易受梯度爆炸和梯度消失问题影响, 简单的梯度截断方法难以有效解决长程依赖问题. 为解决这一挑战, 引入门控机制成为一种有效的解决方案, 通过有选择地加入新信息和遗忘旧信息来控制信息的积累速度. 基于此, 本文首先采用GRU[42]来代替PINNs的MLPs, 以增强对输入序列关联特征的挖掘能力.
GRU通过引入门控机制动态控制信息流的更新方式, 包括决定何时更新隐状态以及何时重置隐状态, 这些机制均通过训练过程自动学习得到. 其核心设计包括重置门和更新门: 重置门用于捕捉序列中的短期依赖关系, 而更新门则用于捕捉序列长期依赖关系, 且无需额外引入记忆单元. 具体而言, 重置门被构造为区间
$ (0, 1) $ 内的向量, 通过对历史信息和当前输入进行凸组合, 控制模型保留过去状态信息的量. 更新门则决定新状态中应包含多少旧状态的副本信息, 从而实现信息动态更新. GRU中每个时间步的输入由当前时间步的输入和前一个时间步的隐状态共同决定. 对于时间步t, 假设输入序列为小批量数据$ X_t \in \mathbb{R}^{n\times r} $ (其中n为样本数, r为样本维度), 前一个时间步的隐状态为$ H_{t-1} \in \mathbb{R}^{n\times h} $ (其中h为隐藏单元数), 则重置门$ R_t\in\mathbb{R}^{n\times h} $ 、更新门$ Z_t\in\mathbb{R}^{n\times h} $ 和候选隐状态$ {\widetilde{H}}_t \in \mathbb{R}^{n\times h} $ 的相关计算如下:其中,
$ W_{xr},\; W_{xz},\; W_{xh} \in \mathbb{R}^{r\times h} $ 和$ W_{hr},\; W_{hz},\; W_{hh} \in \mathbb{R}^{h\times h} $ 是可学习权重参数;$ b_r,\; b_z,\; b_h \in \mathbb{R}^{1\times h} $ 是可学习偏置参数; ω表示GELU函数; 符号$ \odot $ 表示哈达玛积运算符, 即按元素乘积运算. 隐状态序列$ H_{t} $ 通过$ Z_t $ 在$ H_{t-1} $ 和$ {\widetilde{H}}_t $ 之间进行按元素的凸组合实现更新, 即显然, 当
$ Z_t $ 接近于1时, 模型倾向于保留旧隐状态, 同时忽略新候选隐状态; 而当$ Z_t $ 接近于0时, 新隐状态则完全由候选隐状态决定, 旧隐状态的累计信息被忽略. 这样的凸组合能够更精确地捕捉长时间步序列中的依赖关系.其次, 考虑到不同隐藏特征对模型输出贡献程度存在差异, 本文融合了注意力机制[48], 通过提高对隐藏特征序列进行注意力分布加权聚合的计算效率, 从而提取出关键特征序列. 具体而言, 将方程(11)中的隐状态特征序列
$ H_{t} $ 作为键值对输入, 并将GRU隐藏层传递到最后一层的隐状态向量$ h_n \in \mathbb{R}^{n\times h} $ 作为查询向量输入, 得到如下$ Q, K, V \in \mathbb{R}^{n \times h} $ :其中,
$ W_{Q},\; W_{K},\; W_{V} $ 分别将输入投影到查询、键和值的张量表示. 传统注意力机制首先通过softmax函数计算查询项$ Q_{i} $ 与键$ K_{j} $ 之间的成对相似性, 再将其作用于值$ V_{j} $ 加权得到输出, 即其中,
$ \mathrm{Sim}(\cdot) $ 表示相似性函数, 传统注意力机制[41]使用如下点积形式:由(13)式和(14)式易知, 传统注意力机制需要先完成指数函数中的
$ QK^{{\mathrm{T}}} $ 计算, 导致计算复杂度与查询和键的数量n呈二次关系, 即$ {\cal{O}} (n^{2}h) $ , 显著增加了计算成本. 为此, 本文引入线性注意力, 旨在通过建立适当的近似函数来解耦softmax函数, 以先计算$ K^{{\mathrm{T}}}V $ 来改变传统注意力的计算顺序, 从而降低其计算成本. 具体而言,$ \mathrm{Sim}(\cdot) $ 被重新定义为如下形式:其中, 通过
$ \mathrm{Relu} $ 函数将Q和K从(14)式转化为简单的线性关系, 从而使得(13)式可以优先解耦出计算$ K^{{\mathrm{T}}}V $ , 进而将计算复杂度降低为$ {\cal{O}} (nh^{2}) $ , 即查询和键的数量不再呈二次关系而是线性关系. 关于传统注意力和LA的时间复杂度详细分析由附录C提供. 至此, 得到隐藏特征聚合加权后的关键特征序列$ C_{t} \in \mathbb{R}^{n\times h} $ , 即其中,
$ \mathrm{DWC}(\cdot) $ 表示深度可分离卷积运算[49]. 最后由MLPs将$ C_{t} $ 映射为目标输出序列$ O_{t} $ , 即 -
分析发现, PINNs框架中二次罚函数的病态优化问题源于其未对惩罚因子实施有效约束. 具体而言, 方程(1)—(3)可表示为如下形式的等式约束优化问题:
其中,
$ h_{{\cal{B}}} $ 和$ h_{\cal{I}} $ 分别表示满足PDEs边界条件和初始条件约束的连续函数. PINNs通过引入二次罚函数, 将上述约束优化问题转化为如下形式的无约束优化问题:其中, σ为正实数惩罚因子, 用于量化违反约束的程度;
$ L^{2}(\cdot) $ 表示$ L_{2} $ 范数的平方. 设$ \theta^\ast $ 表示方程(21)的最优解, ξ为约束条件的指标集, 则方程(18)的Karush-Kuhn-Tucker(KKT)[50]条件可表示为其中,
$ \lambda_i^\ast $ 表示相应条件约束项的最优乘子. 此外, 方程(21)的KKT条件为当方程(22)和方程(24)收敛到同一临界点时(
$ \theta = \theta^\ast $ ), 通过比较二者的梯度可得其中, 由于
$ \lambda_i^\ast $ 为确定值. 为确保满足方程(18)—(20)中规定的所有约束条件, 惩罚因子σ在优化过程中将逐步增大并趋于无穷. 此外, 考虑二次罚函数$ L_{\sigma} $ 的Hessian矩阵, 其形式如下:其中, L为
$ L_\sigma $ 的拉格朗日函数. 可以观察到,$ \nabla_{\theta\theta}^2 L_\sigma $ 可近似分解为一个定值矩阵和一个最大特征值趋于正无穷的矩阵之和. 该结构导致$ \nabla_{\theta\theta}^2 L_\sigma $ 的条件数急剧增大, 从而显著增加了原问题的求解成本. 综合以上分析, 无论是从KKT条件的角度, 还是从Hessian矩阵条件数的角度分析, 这些不稳定因素均限制了PINNs训练的寻优效率. 为此, 本文引入一种基于增广拉格朗日函数的目标损失函数重构方法, 以进一步提升模型训练的寻优能力, 具体形式如下:其中,
$ \lambda_{\cal{B}}, \lambda_\mathcal{I} \in \mathbb{R}^{n_{\mathrm{b}}} $ 分别表示PDEs边界条件和初始条件的拉格朗日乘子,$ n_{\mathrm{b}} $ 为满足相应约束条件的训练样本数量;$ \left\langle \cdot \right\rangle $ 表示向量的内积运算. 与$ L_{\sigma} $ 相比,$ L_{\lambda} $ 具有更稳定的寻优能力[51]. 首先, 相较于二次罚函数, 增广拉格朗日方法通过显式引入并动态更新拉格朗日乘子, 规避了因惩罚因子趋于无穷所引发的数值病态与收敛困难. 具体而言, AL仅需有限罚因子即可令约束违反度以$ {\cal{O}}\left({1}/{\sigma}\right) $ 的速率下降; 而二次罚函数必须令$ \sigma \to \infty $ 方可保证可行性, 致使优化问题的条件数急剧增大[52]. 其次, AL借助可学习的拉格朗日乘子有效抑制Hessian矩阵条件数的增长, 为数值优化提供了更强的稳定性; 相比之下, 二次罚函数缺乏乘子修正机制, 只能单调提升σ, 极易导致优化病态[53]. 最后, 在满足线性无关约束规范(LICQ)与二阶充分条件的局部极小点邻域内, 存在有限阈值$ \sigma^{*} $ , 使得AL能够转化为精确罚函数[54], 即求解方程组(18)—(20)与求解方程(27)完全等价. 因此, 本文采用方程(27)作为2.2节所提网络模型的损失函数, 对惩罚因子施加有效的约束. 在该框架下, 拉格朗日乘子λ和惩罚因子σ均被视为模型的可训练参数, 并通过反向传播算法[55]迭代更新, 具体更新规则如下:其中,
$ \alpha_\lambda $ 和$ \alpha_\sigma $ 分别为λ和σ的学习率. 需要注意的是, 它们与模型参数θ的优化相互独立. 至此, allaPINNs的训练过程可归纳为如下步骤:第1步: 由Kaiming方法[56]初始化网络模型参数, 包括GRU, LA和MLP. 初始化损失函数中的拉格朗日乘子λ设置为零向量, 惩罚因子σ设置为1. 由拉丁超立方抽样方法(LHS[57])随机生成PDEs时空域中的输入序列
$ X_{t} $ , 开始模型的迭代训练;第2步: 由所提模型的前向计算过程通过(11)式、(19)式和(20)式分别计算得到
$ H_{t}, C_{t}, O_{t} $ ;第3步: 由自动微分方法动态计算方程(27)所重构的损失函数, 并通过AdamW优化方法[58]反向更新训练参数
$ \theta, \lambda, \sigma $ .第2步和第3步循环迭代直到模型训练周期结束.
-
本节详细说明数值实验的相关设置、预测结果和优化性能, 旨在证明allaPINNs的准确性和泛化性. 首先, 将训练完成的allaPINNs预测解与相应解析解或传统数值解进行比较, 并展示allaPINNs与当前先进PINNs模型的绝对误差和相对误差的对比结果. 其次, 提供了allaPINNs训练过程中的拉格朗日乘子和惩罚因子的收敛结果, 以及其在验证集上的泛化误差收敛情况, 进一步验证模型优化性能. 本节选取了四个复杂程度各异的PDEs作为基准方程, 以共同验证allaPINNs的有效性. 相关模型代码已发布于GitHub
1 , 便于研究者复现与对比. 所有计算均在配备16 GB内存的单个Nvidia RTX 3060 Ti GPU上完成.实验设置 本文以Helmhlotz, Black-Scholes, Burgers和非线性Schrödinger方程四个PDEs作为所提模型待求解的基准方程, 这些基准方程及其损失函数的详细信息见附录A. 参与无监督学习(满足算子约束)的采样规模设置nd为2048, 而参与有监督学习(满足初始和边界条件约束)的采样规模nb仅为256. 显然, 对于有监督学习而言这是一种小样本学习策略[59], 降低了模型对边界数据的依赖性. 所提模型和对比模型的超参数选择和求解时间消耗由附录B展示. 最后, 采用
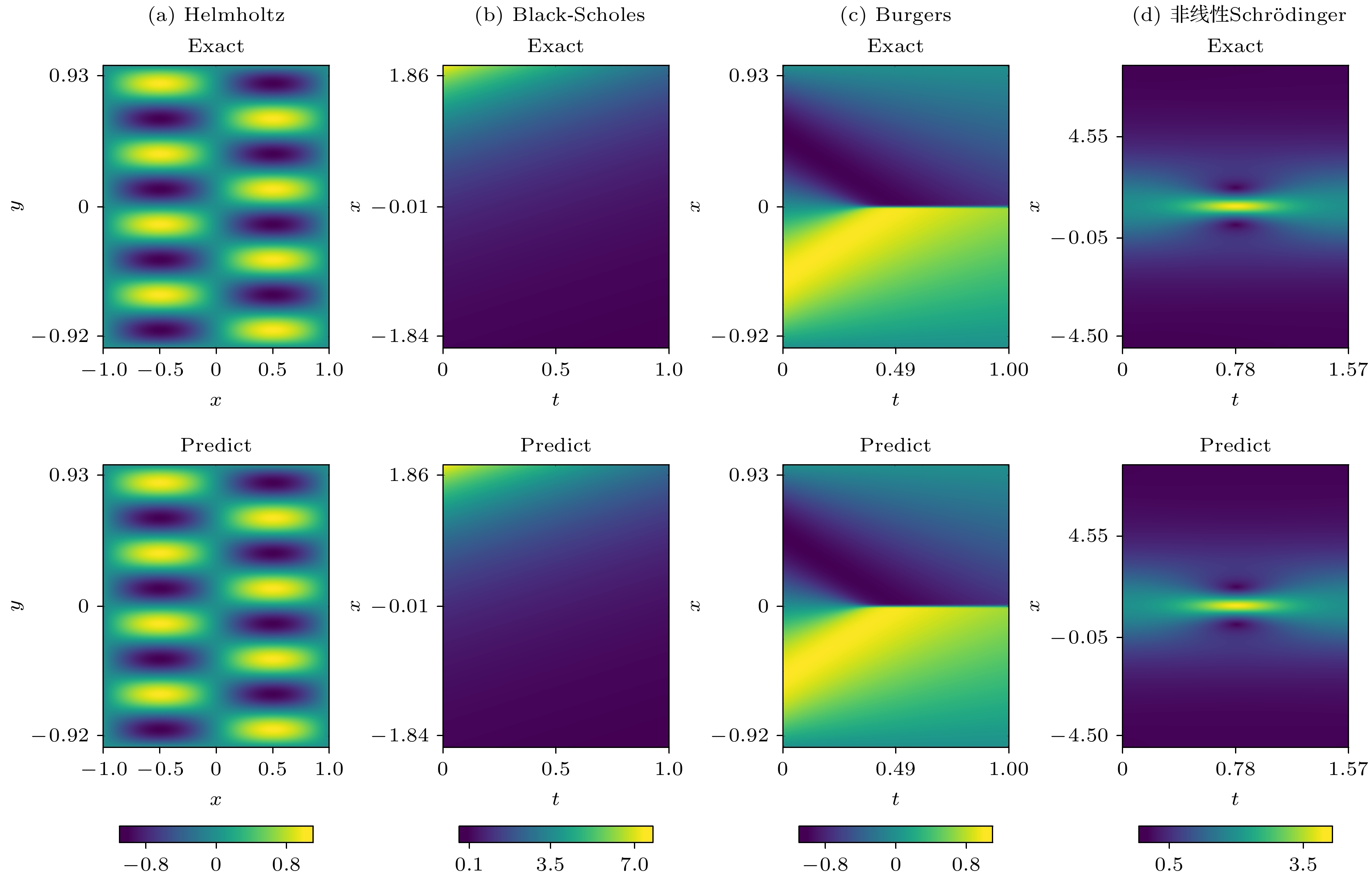
$ L^{2} $ 相对误差指标($ ||\hat{y}-y||_{L^{2}} / ||y||_{L^{2}} $ )评估模型求解误差. 其中$ \hat{y} $ 表示模型的预测解, y表示其对应的解析解或传统数值解. 值得注意的是, y并不参与模型的任何训练, 仅用作评估模型泛化误差.实验结果 图2直观地展示了allaPINNs在求解四个基准方程中预测解与精确解的对比结果. 其中, 图2(a)和图2(b)所示的场函数呈现出周期和光滑的特征, 而图2(c)所示的场函数在
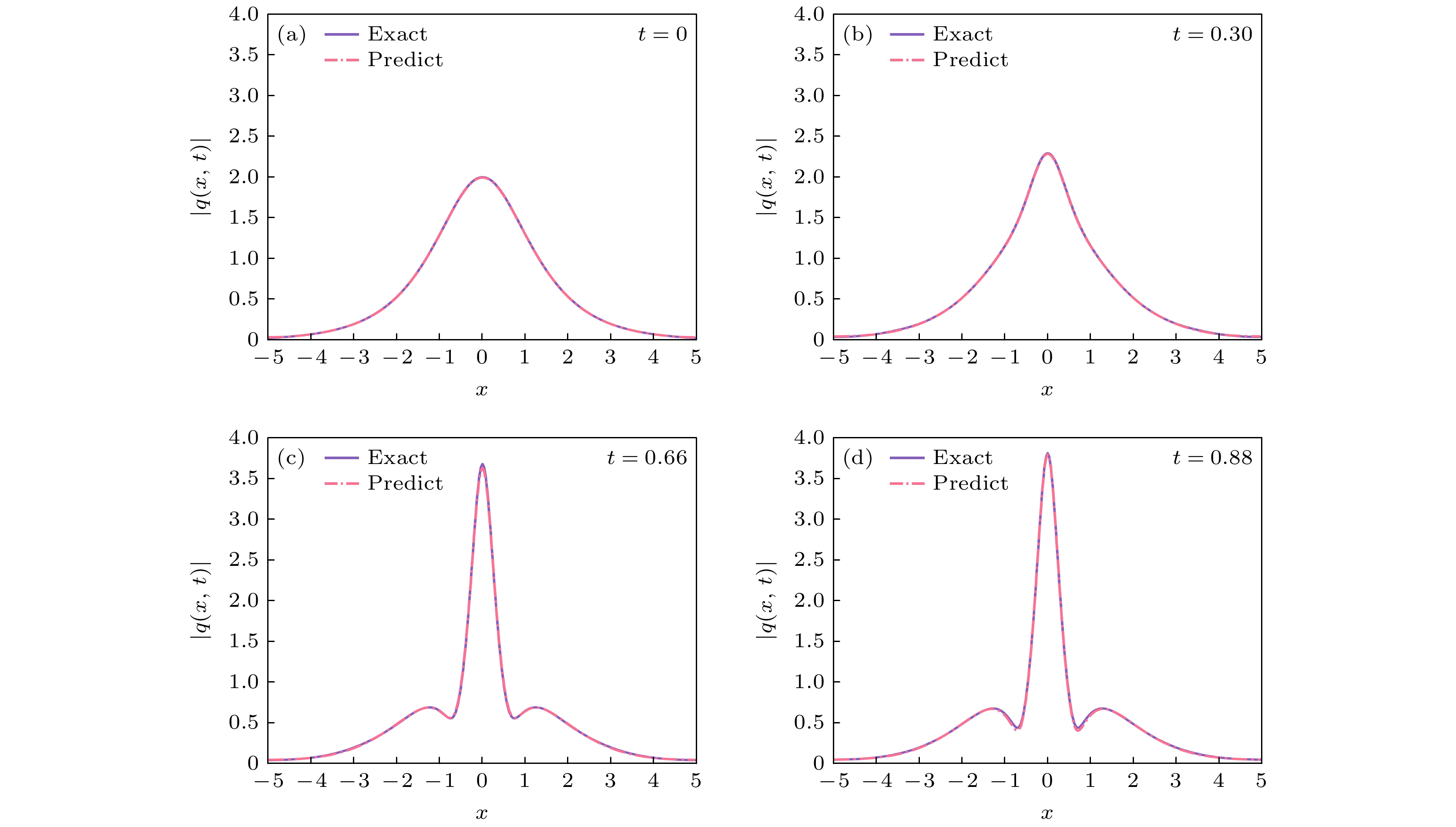
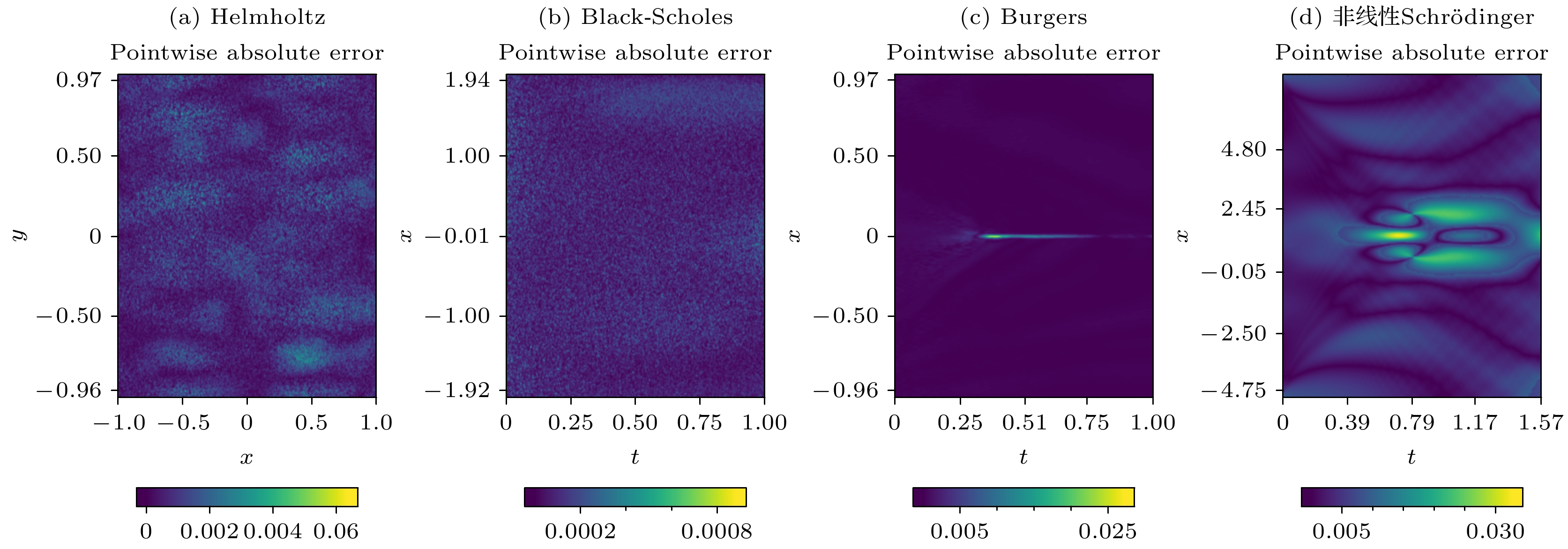
$ x = 0 $ 处表现出急剧的过渡行为. 此外, 为进一步验证allaPINNs在复杂多输出物理量场景中的有效性, 本文还将其应用于非线性Schrödinger方程的数值求解, 该方程用于描述怪波现象. 该现象通常具有不稳定性, 且其峰值振幅往往超过背景波的两倍以上, 而非线性Schrödinger方程作为量子力学的基石, 在定量描述原子尺度非相对论性问题方面发挥着关键作用[3,37,60]. 值得强调的是, 非线性Schrödinger方程的场函数是由实部和虚部组成的复值函数. 因此, allaPINNs需要同时预测同一时空坐标下的实部u和虚部v, 并计算其模长$ |q(x, t)| = \sqrt{(u(x, t))^2+(v(x, t))^2} $ 作为相应数值解. 图2(d)展示出$ |q(x, t)| $ 的全局振幅演化, 其在$ t = 0,\; 0.3,\; 0.66,\; 0.88 $ 这四个时刻的振幅快照由图3呈现. 可以直观地看出, 畸形波解的振幅在极短时间内发生剧烈变化, 而allaPINNs能够准确地捕捉到这一行为. 与专门用于求解非线性Schrödinger方程的模型相比[3], allaPINNs作为一种从信息汇聚和损失优化两方面改进PINNs的通用求解器, 展现出了不逊于前者的预测性能. 在相同的网络层数和神经元数量条件下, allaPINNs的泛化误差为6.71 × 10–4, 而专业模型为6.79 × 10–4. 上述预测结果表明, 在全局时空域尺度上, 无论对于连续平滑的场函数, 还是具有急剧冲击行为的场函数, allaPINNs都能够细致地捕捉到这些周期性和局部剧烈变化的特征, 从而有效地预测对应场函数的实际演化分布, 其变化趋势与精确解高度符合. 同时, allaPINNs在多输出物理量场景中也表现出良好的适用性. 图4进一步展示了allaPINNs的预测解与精确解逐点之间的绝对误差分布, 反映了在相同时空点上, 精确场函数与预测场函数之间的绝对误差距离. 在逐点绝对误差尺度上, 模型预测解与精确解之间的误差精度均维持在1 × 10–3—1 × 10–4的水平, 且误差分布较为均匀, 未出现异常突变. 这一结果表明, 通过融合线性注意力能够有效提取出高维隐特征中的关键特征, 使得模型聚焦这些关键信息来提升学习场函数的演化行为, 并实现相对平稳的误差分布.表1总结了allaPINNs与当前先进PINNs模型在四个基准方程上的
$ L^{2} $ 相对误差对比结果. 实验结果显示, allaPINNs在求解PDEs数值解的相对误差方面表现最佳, 相较于其他基准方法, 预测精度平均提升了一至两个数量级. 传统PINNs[23]仅采用单向信息传递的MLPs结构, 难以捕获输入序列之间的关联关系和关键特征. 尽管AL-PINNs[61]也采用拉格朗日函数来重构损失函数, 却将惩罚因子σ固定为超参数. 如(27)式所示, 损失函数的惩罚约束项由λ和σ共同控制. 当λ收敛时, σ被限制在一个相对有界的范围内, 从而避免了二次惩罚函数中σ无限膨胀的影响. 如果σ保持为固定超参数, 则难以通过λ的学习来对其调节以实现最优平衡, 进而影响模型的预测精度. 此外, f-PICNN[30]和KINN[31]由于缺少对隐藏特征进行相应注意力分布计算的能力, 难以聚焦关键特征, 从而影响其预测准确性. 表2消融实验分别列出allaPINNs在不同网络结构及损失函数条件下的$ L^{2} $ 平均相对误差对比结果. 对比发现, 融合注意力机制的LA在网络结构改进层面展现出卓越性能, 而在损失优化改进层面, 通过增广拉格朗日函数重构的损失函数同样呈现出最佳表现. 这些结果均表明: allaPINNs通过线性注意力有助于模型聚焦关键特征; 同时引入可学习的惩罚因子和拉格朗日乘子的增广拉格朗日函数重构了损失函数, 进而有效提高了模型训练的寻优能力, 使得模型在求解PDEs数值解方面展现出显著优势和卓越的泛化能力. 这不仅提高了模型的准确性和鲁棒性, 也凸显在PINNs中探索融合注意力机制和优化损失策略的重要性.图5展示了allaPINNs在训练过程中达到最佳泛化误差时所学习到的最优拉格朗日乘子序列
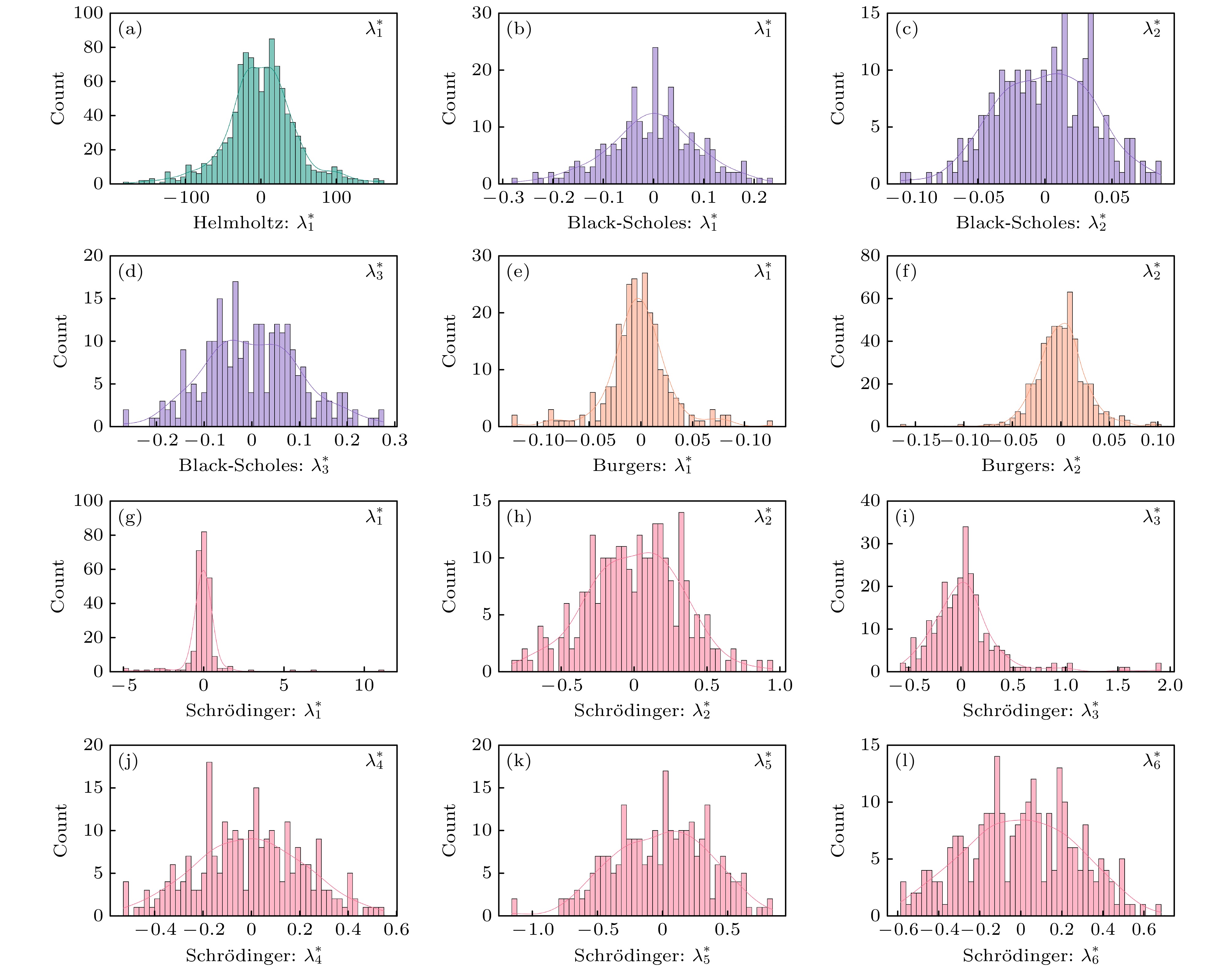
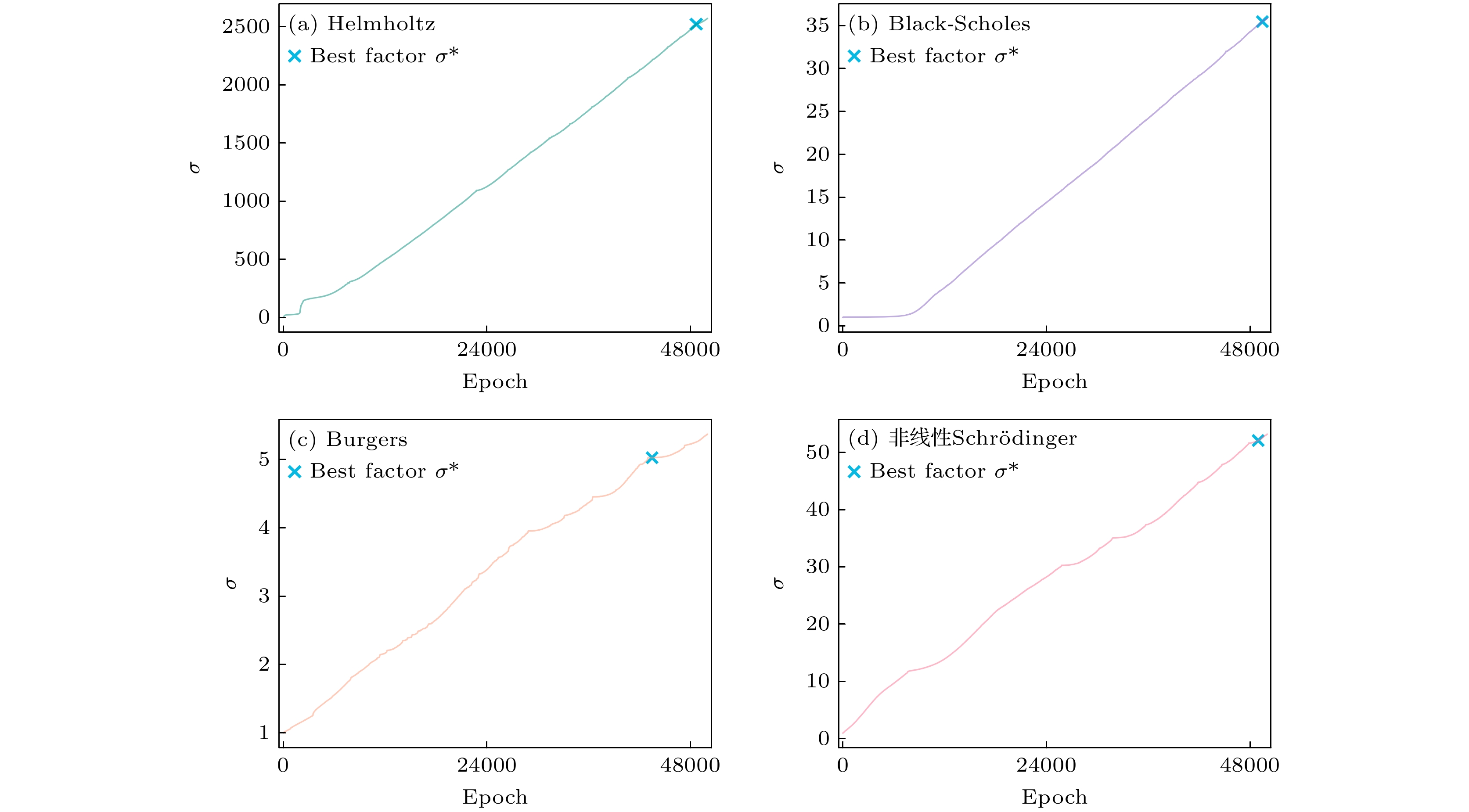
$ \lambda^{*} $ 的频率直方图. 在训练开始之前, λ的初始值被设置为全零序列, 并应用于PDEs的不同约束条件, 即假设损失函数中的各惩罚项均满足约束条件. 在训练过程中, λ作为可学习参数与模型参数同步更新, 并逐渐收敛为图5所示的近似正态分布. 分布中的数值大小反映了约束条件的违反程度. 可以观察到, 几乎所有的λ在零点附近呈现出大致的中心对称特性, 这表明拉格朗日乘子能够在模型学习过程中有效调控模型参数的更新, 防止其破坏对应的约束条件. 此外, 根据(21)式和(27)式, 当它们都收敛到相同的最优参数$ \theta^{*} $ 时, 为保证最优解的一致性,$ \lambda^{*} $ 满足:$ \lambda^{*} \gets \lambda + \sigma h(\theta^{*};x) $ . 当模型训练趋于稳定, 即$ h(\theta^{*};x) $ 趋于零时,$ \lambda^{*} $ 也收敛到一个有界序列. 这表明模型能够通过λ的学习有效地调整不同惩罚约束之间的平衡, 从而确保模型在满足约束条件的同时达到最优性能. 另一方面, 惩罚因子σ是allaPINNs的可学习参数之一, 图6分别展示了其在求解四个基准方程训练过程中的变化曲线. 可以观察到, 随着训练次数的增加, σ在整个训练过程中基本呈现递增趋势, 这与经典离散数值迭代方法中σ的更新规则一致. 此外, 图6还记录了模型训练过程中使当前泛化误差达到最小的σ, 并将其定义为最优惩罚因子$ \sigma^{*} $ . 结果显示,$ \sigma^{*} $ 正向增长且相对有界, 进一步证明了可学习的λ能够有效约束σ的膨胀影响, 从而有助于提升模型的泛化能力.图7展示了allaPINNs求解所有基准方程的训练过程中, 其在验证集上的
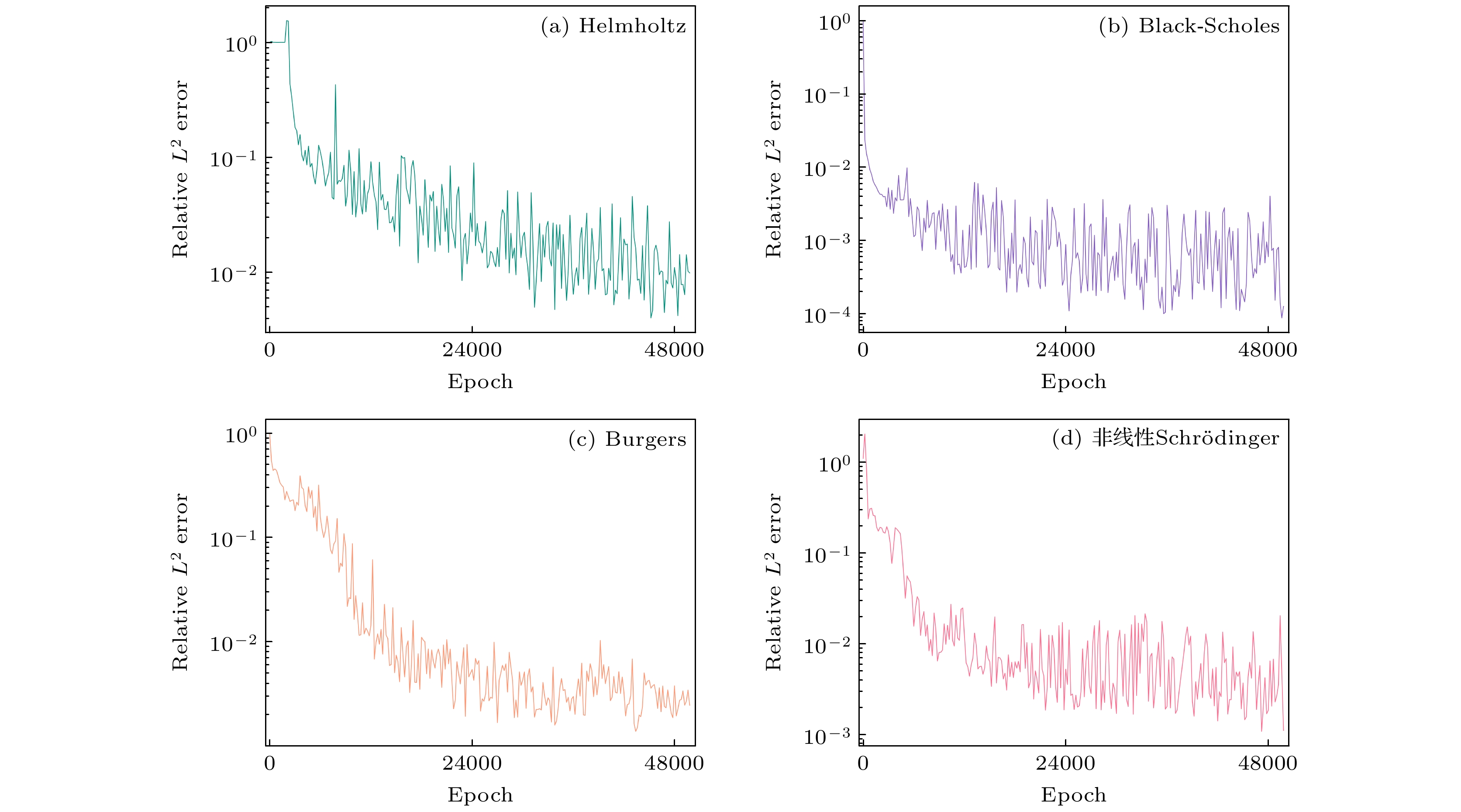
$ L^{2} $ 相对泛化误差收敛结果. 其中, 纵坐标已调整为对数尺度. 结果显示, 模型在训练初期处于拟合阶段, 相对误差显著下降; 训练中后期进入扩散阶段, 信噪比呈随机状态, 模型逐渐稳定收敛至局部极小值. 这表明通过增广拉格朗日函数重构的损失函数在训练过程中可具有比PINNs更精确的寻优能力, 其可学习的拉格朗日乘子有助于提升模型的泛化能力. -
本文通过引入线性注意力与增广拉格朗日函数优化PINNs求解PDEs, 提出一种基于信息表征-损失优化改进的PINNs—allaPINNs, 旨在提升求解PDEs数值解精度和泛化能力. 以Helmholtz, Black-Scholes和Burgers方程验证所提模型的有效性. 实验结果显示, allaPINNs能够有效求解不同类型的PDEs, 并展现出卓越的数值解预测精度与泛化能力. 相比当前先进PINNs模型, 其预测精度提升一至两个数量级. 此外, 通过不同网络结构和损失策略的消融实验, 验证了LA在聚焦关键特征识别能力以及增广拉格朗日函数在重构损失函数优化方面, 对PINNs预测性能的改进效果最为显著.
尽管本文研究取得一定进展, 但针对PINNs的物理可解释性与优化理论探究仍属起步阶段, 诸多问题亟待深入剖析. 其一, 基于PINNs的改进模型在底层结构设计中仍采用仿射结构的神经元, 且其非线性依赖于全局定义的激活函数. 然而, 这种设计缺乏足够的物理可解释性. 因此, 未来可探索将传统数值方法与神经网络相结合, 为神经元赋予参数化的基函数结构, 从而增强模型在物理层面进行非线性拟合的可解释性. 其二, 当前基于PINNs的优化主要依赖一阶与二阶优化方法交替应用. 然而, 在处理高维非线性及非凸损失面时, 这些优化器常陷入局部极小值或鞍点困境. 因此, 开发更高效的拟牛顿优化方案也是未来研究的重要方向.
-
四个基准方程和其各自重构的损失函数如下.
Helmholtz方程
本文选取的第1个基准方程为如下形式的二维Helmholtz方程[62]:
其中,
$ k = 1,\; a_{1} = 1,\; a_{2} = 4 $ . 其损失函数被重构为Black-Scholes方程
本文选取的第2个基准方程是转化为非退化前向时间形式的Black-Scholes方程[2]:
其边界条件为
其损失函数被重构为
Burgers方程
本文选取的第3个基准方程为如下形式的黏性Burgers方程[62]:
其中,
$ v = {1}/({100 \pi}) $ . 其损失函数被重构为非线性Schrödinger方程
本文选取的第4个基准方程为如下包含狄利克雷和诺伊曼边界条件的非线性Schrödinger方程[3,37]:
其中,
$ \mathrm{i} = \sqrt{-1} $ 表示虚数单位,$ q(x, t) = u(x, t)+\mathrm{i}v(x, t) $ 是关于$ t, x $ 的复值函数, 由实部u和虚部v组成. 因此, 所提模型的输出可表示为$ [u(t, x), v(t, x)] $ , 并满足$ |q(x, t)| = \sqrt{(u(x, t))^2+(v(x, t))^2} $ , 则方程(A8)可转化为其损失函数被重构为
-
本节详细列出了数值实验部分中所有基准实验的超参数配置, 以及本文所提算法与其他对比方法求解所有基准方程的时间消耗. 表B1汇总了表1中不同神经求解模型共有的超参数选择, 包括网络层数、神经元数量、参数学习率、训练完成后求解所有基准方程的时间消耗. 在所有基准实验中, 求解方程的时空配点序列均通过LHS随机生成, 其中内部配点规模为2048, 边界配点规模为256. 模型训练的迭代次数设置为50000轮, 优化器采用AdamW算法, 所有计算均在单个Nvidia RTX 3060 Ti GPU上完成. 结果表明, 本文提出的模型能够在使用较少网络层数和神经元数量的情况下, 实现更高的预测精度. 与此同时, 各算法训练完成后在推断阶段的时间消耗并无显著差异. 这一结果进一步验证了通过LA注意力汇聚和AL损失重构在优化PINNs方面的显著优势及其应用潜力.
-
本节详细分析传统注意力计算和线性注意力计算的时间复杂度. 定义输入
$ x \in \mathbb{R}^{n \times h} $ , 其中n表示序列长度, h表示隐藏特征维度, 通常$ n > h $ (例如本文中设置$ n = 1024, h = 64 $ ). 投影矩阵定义为$ W_{Q},\; W_{K},\; W_{V} \in \mathbb{R}^{h \times h} $ , 显然,$ Q, K,\;V $ 的时间复杂度为$ {\cal{O}}(3 nh^{2}) $ .传统注意力的时间复杂度
首先, 计算如下注意力分数:
(C1)式是一个作用在非线性指数函数上的两两相似性计算, 其时间复杂度为
$ {\cal{O}}(n^{2}h) $ . 其次, 进行如下归一化操作:(C2)式计算的时间复杂度为
$ {\cal{O}}(n^{2}) $ . 最后, 进行如下加权 求和:(C3)式计算的时间复杂度为
$ {\cal{O}}(n^{2}h) $ . 可得传统注意力的总时间复杂度为$ {\cal{O}}(3 nh^{2}) + {\cal{O}}(n^{2}h) + {\cal{O}}(n^{2}) + {\cal{O}}(n^{2}h) \sim {\cal{O}}(n^{2}h) $ .线性注意力的时间复杂度
同理, 计算如下注意力分数:
由于
$ \mathrm{Relu}(\cdot) $ 是逐元素操作, 故(C4)式计算的时间复杂度为$ {\cal{O}}(nh) $ . 其次, 进行如下归一化操作:(C5)式计算的时间复杂度为
$ {\cal{O}}(n) $ . 最后, 进行如下加权 求和:其中, 深度可分离卷积
$ \mathrm{DWC}(\cdot) $ 的时间复杂度为$ {\cal{O}}(nh) $ , 故(C6)式计算的时间复杂度为$ {\cal{O}}(nh) $ . 则可得线性注意力的总时间复杂度为$ {\cal{O}}(3 nh^{2}) + {\cal{O}}(nh) + {\cal{O}}(n) + {\cal{O}}(nh) \sim {\cal{O}}(nh^{2}) $ .综上分析, LA通过引入线性操作来解耦传统注意力的计算顺序, 从而将时间复杂度由
$ {\cal{O}}(n^{2}h) $ 降低到$ {\cal{O}}(nh^{2}) $ .
信息表征-损失优化改进的物理信息神经网络求解偏微分方程
allaPINNs: A physics-informed neural network with improvement of information representation and loss optimization for solving partial differential equations
-
摘要: 物理信息神经网络(PINNs)作为人工智能助力科学研究(AI for Science)求解偏微分方程(PDEs)的一种无网格化求解框架, 近年来受到广泛关注. 然而, 传统PINNs存在局限性: 一方面, PINNs网络结构使用单向信息传递的多层感知机(MLPs), 难以有效聚焦序列数据中蕴含的关键特征, 信息表征能力弱; 另一方面, PINNs的损失函数为嵌入物理约束的二次罚函数, 其未受约束而无限膨胀的惩罚因子影响模型训练寻优效率. 为应对上述挑战, 本文提出一种基于信息表征-损失优化改进的PINNs—allaPINNs, 旨在增强模型关键特征提取和训练寻优能力, 提升其求解PDEs数值解的准确性和泛化能力. 在信息表征方面, allaPINNs引入高效线性注意力(LA)增强模型关键特征识别能力, 同时降低权重动态加权的计算复杂度. 在损失优化方面, allaPINNs通过引入增广拉格朗日(AL)函数重构目标损失函数, 利用可学习的拉格朗日乘子和惩罚因子有效调控各损失残差项的相互作用. 由Helmholtz, Black-Scholes, Burgers和非线性Schrödinger四个基准方程验证allaPINNs的有效性. 结果表明, allaPINNs能够有效求解不同类型PDEs, 并展现出卓越的数值解预测精度与泛化能力. 相较于当前先进PINNs, 其预测精度提升一至两个数量级.Abstract: Physics-informed neural networks (PINNs) have recently garnered significant attention as a meshless solution framework for solving partial differential equations (PDEs) in the context of AI-assisted scientific research (AI for Science). However, traditional PINNs exhibit certain limitations. On one hand, their network architecture, typically multilayer perceptrons (MLPs) with unidirectional information transfer, struggles to effectively capture key features embedded in sequential data, resulting in weak information characterization. On the other hand, the loss function of PINNs, a quadratic penalty function embedded with physical constraints, has an unconstrained and infinitely inflated penalty factor that affects the efficiency of the model’s training optimization search. To address these challenges, this paper proposes an improved PINN based on information representation and loss optimization, termed allaPINNs, which aims to enhance the model’s key feature extraction capability and training optimization search ability, thereby improving its accuracy and generalization for solving numerical solutions of PDEs. In terms of information characterization, allaPINNs introduces efficient linear attention (LA) to enhance the model’s ability to identify key features while reducing the computational complexity of dynamic weighting. In terms of loss optimization, allaPINNs reconstructs the objective loss function by introducing the augmented Lagrangian (AL) function, utilizing learnable Lagrangian multipliers and penalty factors to efficiently regulate the interaction of each loss residual term. The feasibility of allaPINNs is validated through four benchmark equations: Helmholtz, Black-Scholes, Burgers, and nonlinear Schrödinger. The results demonstrate that allaPINNs can effectively solve various PDEs of different complexities and exhibit excellent numerical solution prediction accuracy and generalization ability. Compared to the current state-of-the-art PINNs, the predictive accuracy is improved by one to two orders of magnitude.
-

-
图 5 最优拉格朗日乘子
$ \lambda_{*} $ 的频率直方图, 其中Helmholtz方程包含$ \lambda_{1}^{*} $ , Black-Scholes方程包含$ \lambda_{1}^{*}{\text{—}}\lambda_{3}^{*} $ , Burgers方程包含$ \lambda_{1}^{*} $ 和$ \lambda_{2}^{*} $ , 非线性Schrödinger方程包含$ \lambda_{1}^{*}{\text{—}}\lambda_{6}^{*} $ Figure 5. Frequency histogram of the optimal Lagrangian multipliers
$ \lambda^{*} $ , where the Helmholtz equation contains$ \lambda_{1}^{*} $ , the Black-Scholes equation contains$ \lambda_{1}^{*}-\lambda_{3}^{*} $ , the Burgers equation contains$ \lambda_{1}^{*}, \;\lambda_{2}^{*} $ , and nonlinear Schrödinger equation contains$ \lambda_{1}^{*}-\lambda_{6}^{*} $ .图 6 惩罚因子σ的学习过程, 其中(a), (b), (c), (d)中的
$ \sigma^{*} $ 分别位于第48665, 49420, 43467和48933轮迭代, 对应的数值分别为2517.21, 35.45, 5.02和52.08Figure 6. Learning process of the penalty factor σ, where
$ \sigma^{*} $ for (a), (b), (c), (d) are located at rounds 48665, 49420, 43467, and 48933, corresponding to values of 2517.21, 35.45, 5.02, and 52.08, respectively.表 1 allaPINNs模型和当前先进PINNs模型求解四个基准方程实验的
$ L^{2} $ 相对误差对比结果Table 1. Comparison of
$ L^{2} $ relative errors between allaPINNs model and current state-of-the-art PINNs model for solving the four benchmark equations.物理信息神经求解器 求解方程 PINNs[23] AL-PINNs[61] f-PICNN[30] KINN[31] allaPINNs (本文) Helmholtz 5.63 × 10–2 1.82 × 10–3 2.51 × 10–3 1.08 × 10–3 8.06 × 10–4 Black-Scholes 7.18 × 10–2 7.41 × 10–3 5.24 × 10–3 4.35 × 10–3 3.48 × 10–4 Burgers 7.04 × 10–2 3.39 × 10–3 2.49 × 10–3 3.02 × 10–3 8.31 × 10–4 非线性Schrödinger 2.09 × 10–2 1.55 × 10–3 4.18 × 10–3 1.37 × 10–3 6.71 × 10–4 表 2 allaPINNs模型在不同网络结构和损失函数条件下的平均
$ L^{2} $ 相对误差对比结果Table 2. Comparison of mean
$ L^{2} $ relative errors of allaPINNs model with different network structure and loss function conditions.网络结构 基准方程平均 $ L^{2} $ 相对误差损失函数 基准方程平均 $ L^{2} $ 相对误差MLPs 7.26 × 10–2 罚函数 8.55 × 10–3 CNN 3.09 × 10–3 罚函数 (高斯噪声) 1.63 × 10–3 LA 6.61 × 10–4 AL 6.61 × 10–4 表 B1 各对比模型中超参数配置和求解基准方程时间消耗
Table B1. Hyperparameter configuration and time consumption for solving the benchmark equations in each comparison model.
物理信息神经求解器 对比指标 PINNs[23] AL-PINNs[61] f-PICNN[30] KINN[31] allaPINNs (本文) 网络层数 8 8 6 5 5 神经元数量 200 256 128 80 64 参数学习率 1 × 10–3 1 × 10–4 1 × 10–4 1 × 10–4 1 × 10–3 求解Helmholtz时间消耗/s 1476 1520 1529 1606 1513 求解Black-Scholes时间消耗/s 1538 1585 1604 1714 1624 求解Burgers时间消耗/s 1519 1574 1593 1636 1588 求解非线性Schrödinger时间消耗/s 1545 1628 1650 1745 1661 -
[1] Jin X, Cai S, Li H, Karniadakis G E 2021 J. Comput. Phys. 426 109951 doi: 10.1016/j.jcp.2020.109951 [2] Roul P, Goura V P 2020 J. Comput. Appl. Math. 363 464 doi: 10.1016/j.cam.2019.06.015 [3] Pu J C, Li J, Chen Y 2021 Chin. Phys. B 30 60202 doi: 10.1088/1674-1056/abd7e3 [4] Cuomo S, Di Cola V S, Giampaolo F, Rozza G, Raissi M, Piccialli F 2022 J. Sci. Comput. 92 88 doi: 10.1007/s10915-022-01939-z [5] Samaniego E, Anitescu C, Goswami S, Nguyen-Thanh V M, Guo H, Hamdia K, Zhuang X, Rabczuk T 2020 Comput. Methods Appl. Mech. Eng. 362 112790 doi: 10.1016/j.cma.2019.112790 [6] Taylor C A, Hughes T J, Zarins C K 1998 Comput. Methods Appl. Mech. Eng. 158 155 doi: 10.1016/S0045-7825(98)80008-X [7] Zhang Y 2009 Appl. Math. Comput. 215 524 doi: 10.1016/j.amc.2009.05.018 [8] Van Hoecke L, Boeye D, Gonzalez-Quiroga A, Patience G S, Perreault P 2023 Can. J. Chem. Eng. 101 545 doi: 10.1002/cjce.24571 [9] Hasan F, Ali H, Arief H A 2025 Int. J. Appl. Comput. Math. 11 1 doi: 10.1007/s40819-024-01814-5 [10] Choo Y S, Choi N, Lee B C 2010 Appl. Math. Modell. 34 14 doi: 10.1016/j.apm.2009.03.022 [11] Lawrence N D, Montgomery J 2024 R. Soc. Open Sci. 11 231130 doi: 10.1098/rsos.231130 [12] Si Z Z, Wang D L, Zhu B W, Ju Z T, Wang X P, Liu W, Malomed B A, Wang Y Y, Dai C Q 2024 Laser Photonics Rev. 18 2400097 doi: 10.1002/lpor.202400097 [13] Fang Y, Han H B, Bo W B, Liu W, Wang B H, Wang Y Y, Dai C Q 2023 Opt. Lett. 48 779 doi: 10.1364/OL.482946 [14] Li N, Xu S, Sun Y, Chen Q 2025 Nonlinear Dyn. 113 767 doi: 10.1007/s11071-024-10243-4 [15] Mouton L, Reiter F, Chen Y, Rebentrost P 2024 Phys. Rev. A 110 022612 doi: 10.1103/PhysRevA.110.022612 [16] Zhu M, Feng S, Lin Y, Lu L 2023 Comput. Methods Appl. Mech. Eng. 416 116300 doi: 10.1016/j.cma.2023.116300 [17] Li X, Liu Z, Cui S, Luo C, Li C, Zhuang Z 2019 Comput. Methods Appl. Mech. Eng. 347 735 doi: 10.1016/j.cma.2019.01.005 [18] Wang S, Teng Y, Perdikaris P 2021 SIAM J. Sci. Comput. 43 A3055 doi: 10.1137/20M1318043 [19] Chew A W Z, He R, Zhang L 2025 Arch. Comput. Methods Eng. 32 399 doi: 10.1007/s11831-024-10145-z [20] Bai J, Rabczuk T, Gupta A, Alzubaidi L, Gu Y 2023 Comput. Mech. 71 543 doi: 10.1007/s00466-022-02252-0 [21] Son S, Lee H, Jeong D, Oh K Y, Sun K H 2023 Adv. Eng. Inf. 57 102035 doi: 10.1016/j.aei.2023.102035 [22] 方泽, 潘泳全, 戴栋, 张俊勃 2024 物理学报 73 145201 doi: 10.7498/aps.73.20240343 Fang Z, Pan Y Q, Dai D, Zhang J B 2024 Acta Phys. Sin. 73 145201 doi: 10.7498/aps.73.20240343 [23] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686 doi: 10.1016/j.jcp.2018.10.045 [24] Hornik K 1991 Neural Networks 4 251 doi: 10.1016/0893-6080(91)90009-T [25] Baydin A G, Pearlmutter B A, Radul A A, Siskind J M 2018 J. Mach. Learn. Res. 18 1 [26] De Ryck T, Mishra S 2024 Acta Numer. 33 633 doi: 10.1017/S0962492923000089 [27] Karniadakis G E, Kevrekidis I G, Lu L, Perdikaris P, Wang S, Yang L 2021 Nat. Rev. Phys. 3 422 doi: 10.1038/s42254-021-00314-5 [28] Ren P, Rao C, Liu Y, Wang J X, Sun H 2022 Comput. Methods Appl. Mech. Eng. 389 114399 doi: 10.1016/j.cma.2021.114399 [29] Lei L, He Y, Xing Z, Li Z, Zhou Y 2025 IEEE Trans. Ind. Inf. 21 5411 doi: 10.1109/TII.2025.3555981 [30] Yuan B, Wang H, Heitor A, Chen X 2024 J. Comput. Phys. 515 113284 doi: 10.1016/j.jcp.2024.113284 [31] Wang Y, Sun J, Bai J, Anitescu C, Eshaghi M S, Zhuang X, Rabczuk T, Liu Y 2025 Comput. Methods Appl. Mech. Eng. 433 117518 doi: 10.1016/j.cma.2024.117518 [32] Li L L, Zhang Y P, Wang G H, Xia K L 2025 Nat. Mach. Intell. 7 1346 doi: 10.1038/s42256-025-01087-7 [33] Jahani-Nasab M, Bijarchi M A 2024 Sci. Rep. 14 23836 doi: 10.1038/s41598-024-74711-y [34] Yu J, Lu L, Meng X, Karniadakis G E 2022 Comput. Methods Appl. Mech. Eng. 393 114823 doi: 10.1016/j.cma.2022.114823 [35] Jiao Y, Lai Y, Lo Y, Wang Y, Yang Y 2024 Anal. Appl. 22 57 doi: 10.1142/S021953052350015X [36] Yang A, Xu S, Liu H, Li N, Sun Y 2025 Nonlinear Dyn. 113 1523 doi: 10.1007/s11071-024-10235-4 [37] Li Y, Zhou Z, Ying S 2022 J. Comput. Phys. 451 110884 doi: 10.1016/j.jcp.2021.110884 [38] Jacot A, Gabriel F, Hongler C 2018 32nd Conference on Neural Information Processing Systems (NIPS 2018) Montreal, Canada, December 3–8, 2018 p8570 [39] Xiang Z, Peng W, Liu X, Yao W 2022 Neurocomputing 496 11 doi: 10.1016/j.neucom.2022.05.015 [40] Tancik M, Srinivasan P, Mildenhall B, Fridovich-Keil S, Raghavan N, Singhal U, Ramamoorthi R, Barron J, Ng R 2020 34th Conference on Neural Information Processing Systems (NeurIPS 2020) Vancouver, Canada, December 6–12, 2020 p7537 [41] Zhang Z, Wang Y, Tan S, Xia B, Luo Y 2025 Neurocomputing 625 129429 doi: 10.1016/j.neucom.2025.129429 [42] Zhang W, Li H, Tang L, Gu X, Wang L, Wang L 2022 Acta Geotech. 17 1367 doi: 10.1007/s11440-022-01495-8 [43] Zhang Z, Wang Q, Zhang Y, Shen T, Zhang W 2025 Sci. Rep. 15 10523 doi: 10.1038/s41598-025-92900-1 [44] Cybenko G 1989 Math. Control Signals Syst. 2 303 doi: 10.1007/BF02551274 [45] Wang C, Ma C, Zhou J 2014 J. Global Optim. 58 51 doi: 10.1007/s10898-013-0111-9 [46] Yi K, Zhang Q, Fan W, Wang S, Wang P, He H, An N, Lian D, Cao L, Niu Z 2023 Adv. Neural Inf. Process. Syst. 36 76656 doi: 10.5555/3666122.3669471 [47] Durstewitz D, Koppe G, Thurm M I 2023 Nat. Rev. Neurosci. 24 693 doi: 10.1038/s41583-023-00740-7 [48] Chang G, Hu S, Huang H 2023 J. Supercomput. 79 6991 doi: 10.1007/s11227-022-04950-1 [49] Ocal H 2025 Arabian J. Sci. Eng. 50 1097 doi: 10.1007/s13369-024-09131-1 [50] Wu H C 2009 Eur. J. Oper. Res. 196 49 doi: 10.1016/j.ejor.2008.03.012 [51] Curtis F E, Jiang H, Robinson D P 2015 Math. Program. 152 201 doi: 10.1007/s10107-014-0784-y [52] Sun D, Sun J, Zhang L 2008 Math. Program. 114 349 doi: 10.1007/s10107-007-0105-9 [53] Kanzow C, Steck D 2019 Math. Program. 177 425 doi: 10.1007/s10107-018-1261-9 [54] Rockafellar R T 2023 Math. Program. 198 159 doi: 10.1007/s10107-022-01768-w [55] Dampfhoffer M, Mesquida T, Valentian A, Anghel L 2023 IEEE Trans. Neural Networks Learn. Syst. 35 11906 doi: 10.1109/TNNLS.2023.3263008 [56] Humbird K D, Peterson J L, McClarren R G 2018 IEEE Trans. Neural Networks Learn. Syst. 30 1286 doi: 10.1109/TNNLS.2018.2869694 [57] Zhang Z, Wang Q, Zhang Y, Shen T 2025 Digital Signal Process. 156 104766 doi: 10.1016/j.dsp.2024.104766 [58] Zhou P, Xie X, Lin Z, Yan S 2024 IEEE Trans. Pattern Anal. Mach. Intell. 46 6486 doi: 10.1109/TPAMI.2024.3382294 [59] Rather I H, Kumar S, Gandomi A H 2024 Artif. Intell. Rev. 57 226 doi: 10.1007/s10462-024-10859-3 [60] Thulasidharan K, Priya N V, Monisha S, Senthilvelan M 2024 Phys. Lett. A 511 129551 doi: 10.1016/j.physleta.2024.129551 [61] Son H, Cho S W, Hwang H J 2023 Neurocomputing 548 126424 doi: 10.1016/j.neucom.2023.126424 [62] Song Y, Wang H, Yang H, Taccari M L, Chen X 2024 J. Comput. Phys. 501 112781 doi: 10.1016/j.jcp.2024.112781 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: