近年来，建立三维PIC-MCC模型和分析等离子体行为的方法被应用于霍尔等离子体加速器的研究。采用数值模拟的方法研究了放电特性^[13]、离子行为^[14]和放电稳定性^[15]。特别是对于带电粒子非轴对称分布的研究^[16]，这种研究方法有其自身的优势。由于MSS与霍尔等离子体加速器具有相似的放电机理，因此采用类似的研究方法模拟了MSS中的氩气辉光放电。随着高功率脉冲磁控溅射（High Power Impulse Magnetron Sputtering，HiPIMS）成为近年来的研究热点^[17-21]，该模型也可以用于模拟HiPIMS的放电过程。

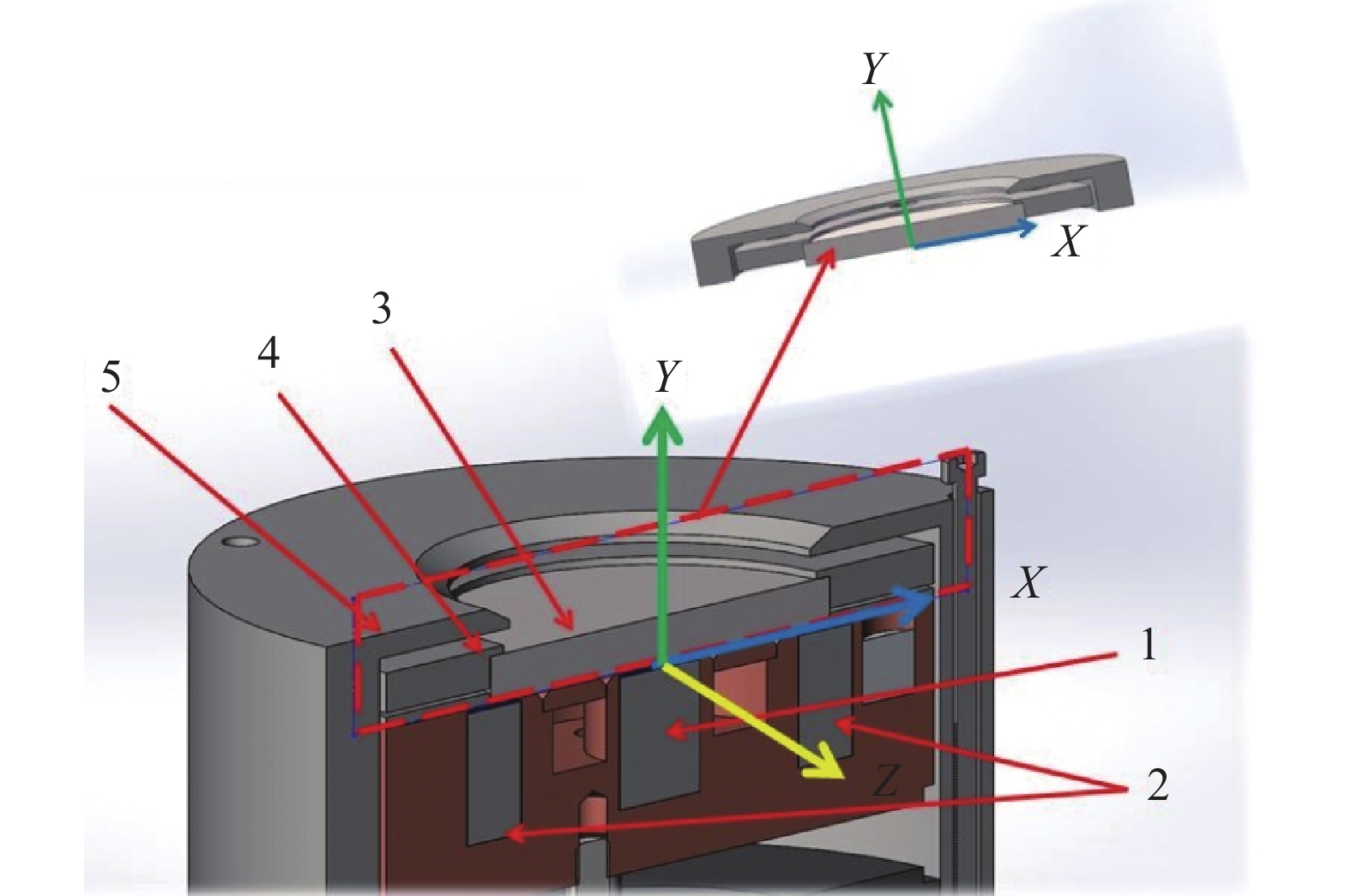
以AJA公司物理V气相沉积（Physical Vapor Deposition, PVD）系统中的2英寸MSS结构为基础，利用Tech-X公司的VORPAL软件^[22]建立了三维PIC-MCC模型，如图1所示。三维模型的仿真区域尺寸为100 mm×20 mm×100 mm （图1中红色虚线包围），考虑到计算效率，网格尺寸设置为2 mm×2 mm×2 mm。在每个网格中，宏粒子的数量设为5，模型中考虑的宏粒子总数为2.5×10⁵。为了避免网格尺寸大于德拜长度（Debye length）所导致的“网格加热效应”（一种在模拟中会导致等离子体密度高得多的数值不稳定性）^[23]，模型采用了粒子电荷和电流的高阶插值，有效地保证计算精度。

仿真区域外的其余固体部分不影响磁控溅射源放电，考虑到计算效率，将其省略。仿真区域的实体部件如图1的右上角所示。

在放电初始阶段，认为中性氩气均匀分布在6个模拟区域内。靶和压环具有给定的负电势，模拟区域内其余部分的电势设为0 V。通过求解泊松方程，可以计算出放电过程中每个时间步长的电场：

式中，$ \phi $为电势，e为基本电荷，$ {\varepsilon _0} $为真空介电常数（8. 85×10⁻¹² F/m）， $n \mathrm{_i}$和$ n_{\mathrm{e}} $分别为离子和电子的密度。

初始阶段，模拟区域内静态均匀分布着近4×10³的电子宏粒子，此电子被称为“种子电子”，用于启动放电。在电磁场的作用下，这些“种子电子”在靶材表面附近开始振荡。等离子体是由少数“种子电子”与中性氩粒子之间的碰撞电离碰撞产生的^[15]。整个模型采用吸收边界。一旦粒子到达模拟区域边界，该粒子将被消除，其跟踪也将停止。在洛伦兹力的作用下，带电粒子的运动可以表示为：

式中m为粒子质量，v为粒子速度，t为时间，q为粒子电荷，E为电场强度，B为磁场强度，r为粒子位置。利用上述运动方程，可以对带电粒子进行跟踪，并得到它们的运动轨迹。

对于粒子间的相互作用，模型考虑了五种碰撞过程。对于电子和中性粒子，考虑了电离、激发和弹性碰撞；对于离子和中性粒子，动量和电荷交换过程被考虑在内。这些碰撞可以表示为：

对于弹性碰撞，应用动量守恒定律计算粒子碰撞后的速度；但对于非弹性碰撞（激发和电离），能量和动量守恒不再适用。因此，引入电子速度减小因子^[24]，可描述为：

式中： $ \Delta \varepsilon $为电子碰撞后的能量损失，$ {\raise0.7ex\hbox{${m{v^2}}$} \mathord{\left/ {\vphantom {{m{v^2}} 2}}\right.} \lower0.7ex\hbox{$2$}} $为电子碰撞前的动能。

对于离子与中性粒子之间的动量交换，取随机数R计算粒子碰撞后的速度：

式中$ {E_i} $和$ {E'_i} $分别为碰撞前后的离子动能，$ \theta $为碰撞前的轴向角，R为0~1之间的随机数。

离子和中性粒子之间的电荷交换是一个比较简单的例子。所需要做的就是在碰撞后在两个粒子之间交换信息。

对于模型中所有类型的碰撞，将需要在0到1之间的另一个随机数$ {R_\psi } $来获得碰撞后的轴向角$ \chi $和方位角$ \psi $。

对于碰撞后的粒子速度$ ({v_x},{v_y},{v_{\textit{z}}}) $，应用经典欧拉变换：

式中v、$ \theta $、$ \varphi $为碰撞前粒子的速度大小、轴向角和方位角。

根据MSS的常用操作参数，氩气压力设为0。5 Pa，放电电压（靶材电位幅度）在260~340 V范围内调节。

磁场数据由数值计算软件编制，并导入三维模型。磁通密度数据采用有限元法得到。数据由每个网格节点上的磁通密度B分量Bx、By和Bz组成。在模拟区域的其他空间点上，通过线性插值计算B。在MSS放电过程中，离子向靶材移动，形成垂直于靶材表面的离子流。根据麦克斯韦方程组，电流对磁通密度的影响可表示为：

式中$ {\mu _0} $为真空导率（$4\text{π} $×10⁻⁷ H/m）， $ {\boldsymbol{J}} $为表面电流密度（A/m²）。因为$ {\varepsilon _0}{\mu _0} $相当一个较小常数和$ {\boldsymbol{E}} $的时间变化也小，方程中$ {\varepsilon _0}{\mu _0}\dfrac{{\partial {\boldsymbol{E}}}}{{\partial t}} $可以忽略。通常情况下，MSS表面电流密度$ {\boldsymbol{J}} $小于250 A/m²，导致磁通密度小于3 G的方位偏差。由于$ {\boldsymbol{B}} $的量级为数百G，因此偏差很小，也可以忽略。也就是说，可以忽略离子电流对磁场的影响，将静态磁场数据导入三维模型。

然而，对于HiPIMS，表面电流密度J通常比直流MSS器件高两个数量级。在这种情况下，必须考虑到离子电流对磁场的影响，在每个时间步长都要更新电磁场数据。电磁场数据的更新基于电磁感应法拉第定律和安培定律，可以表示为：

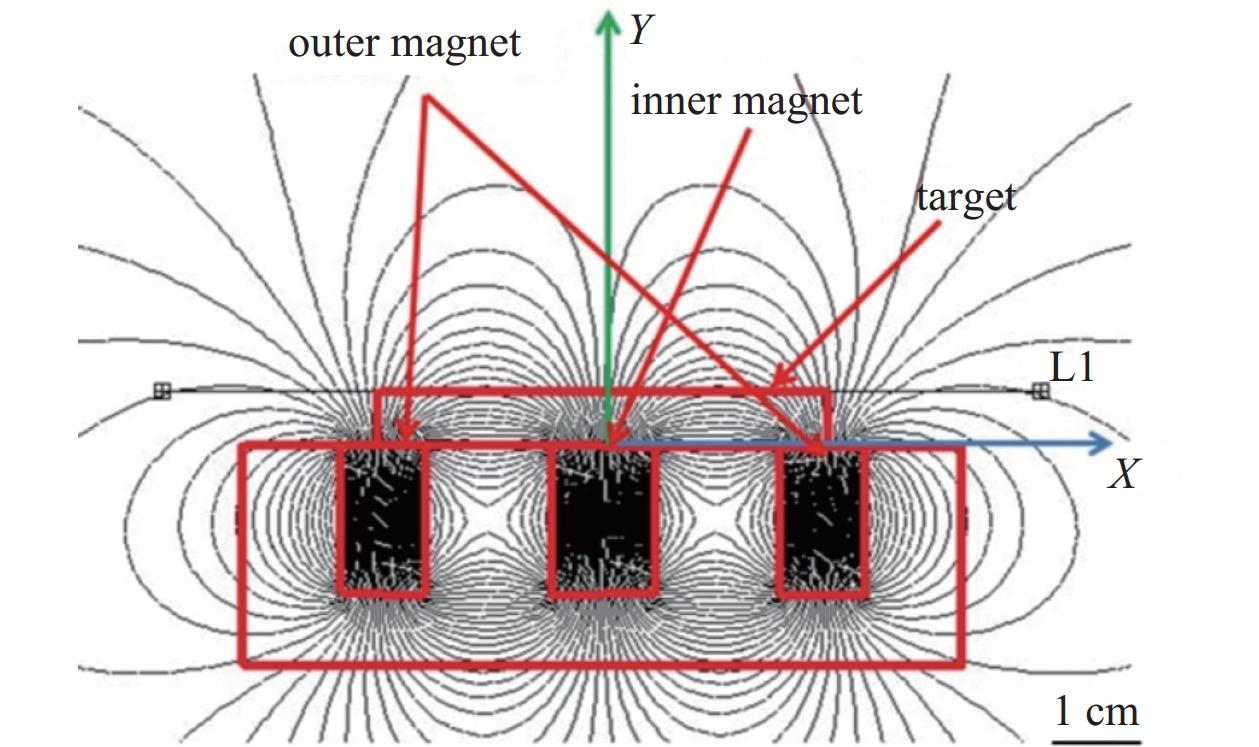
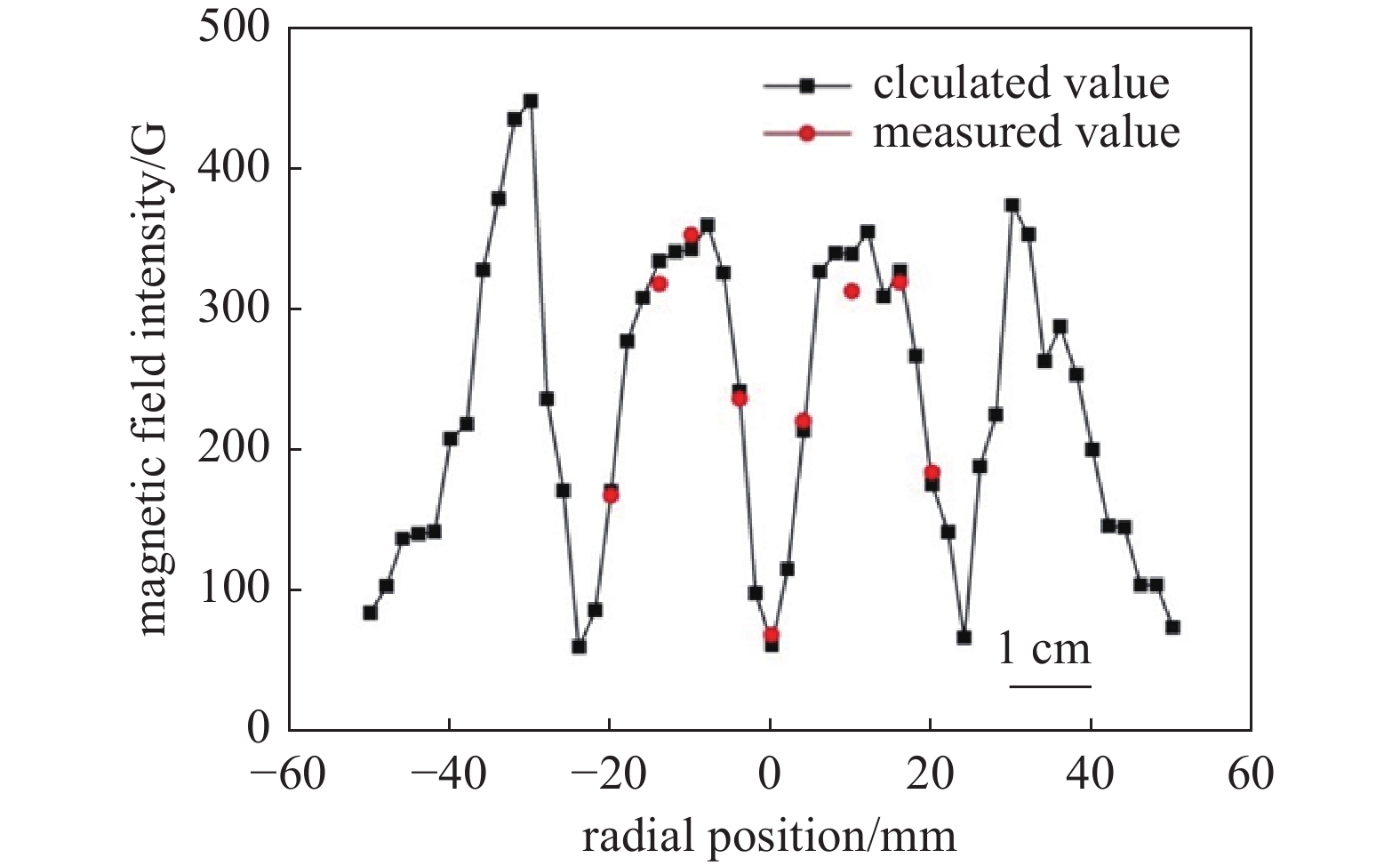
式中$ {{\boldsymbol{B}}_{n + 1}} $为时间步长n+1时的磁场强度，$ {{\boldsymbol{B}}_n} $为时间步长n时的磁场强度，$ \Delta t $为时间步长，$ {{\boldsymbol{E}}_{n + \frac{1}{2}}} $为时间步长$ n + \dfrac{1}{2} $时的电场强度，$ {{\boldsymbol{E}}_{n - \frac{1}{2}}} $为时间步长$ n - \dfrac{1}{2} $时的电场强度。

如图2所示，磁场具有平行于靶材表面和垂直于靶材表面的分量。在磁控溅射源放电中，电子主要被平行磁场限制在靶材附近，使得电子中性碰撞概率增大^[25]，等离子体能在较低的气体压力条件下产生和维持。对于MSS放电，溅射效率取决于平行磁场分量。模型的可靠性还取决于输入数据与实际磁场值的一致性。因此，将计算值与靶材表面（图2中的L1）上的实测值进行比较。如图3所示，计算值和实测值都在50~400 G的范围内，两者之间存在约15%的偏差。由于小表面积的位置测量偏差可能导致较大的测量误差，因此模拟可以接受磁场数据的相对误差为15%。从而证实了磁场数据的可靠性。

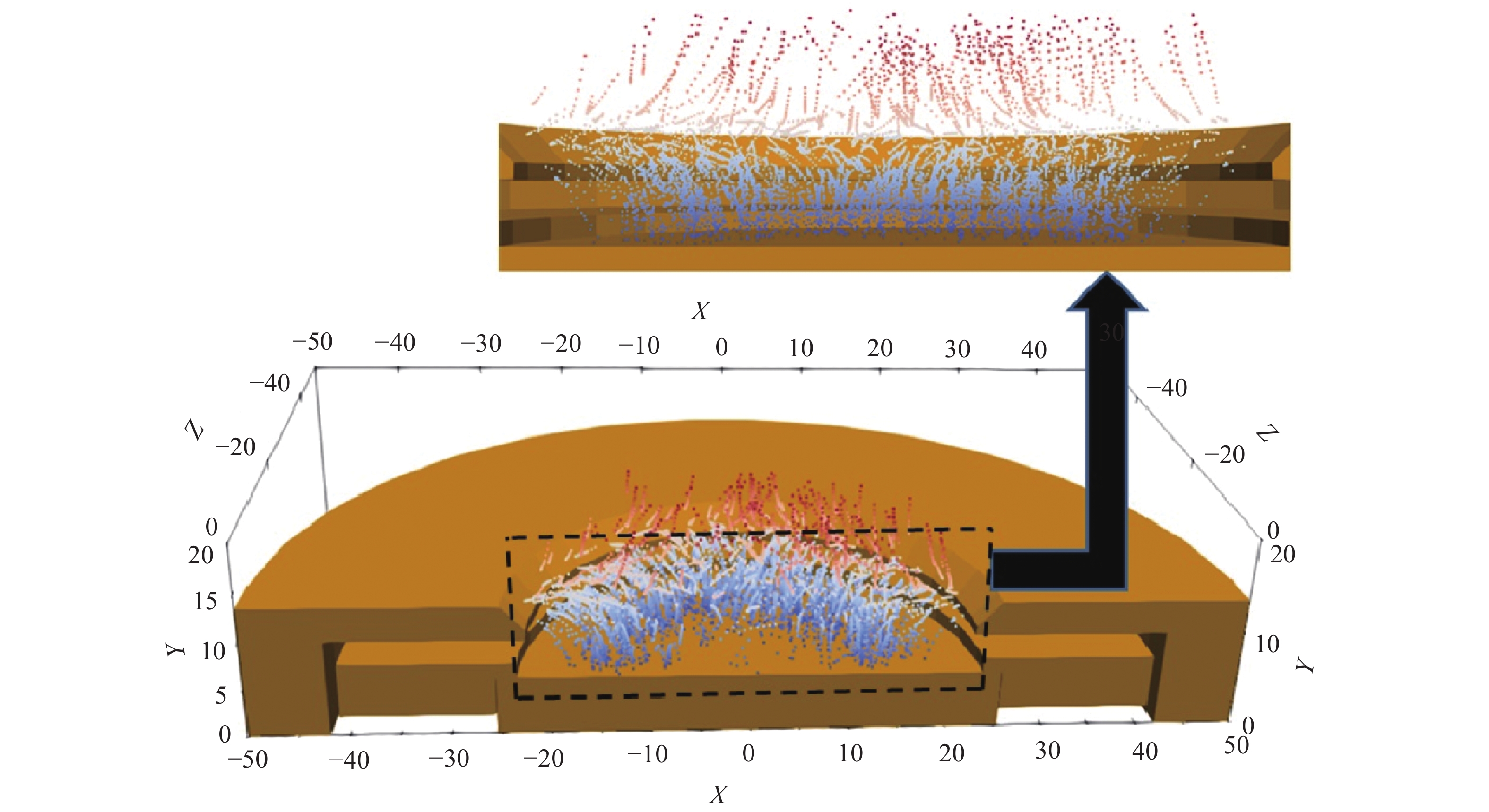
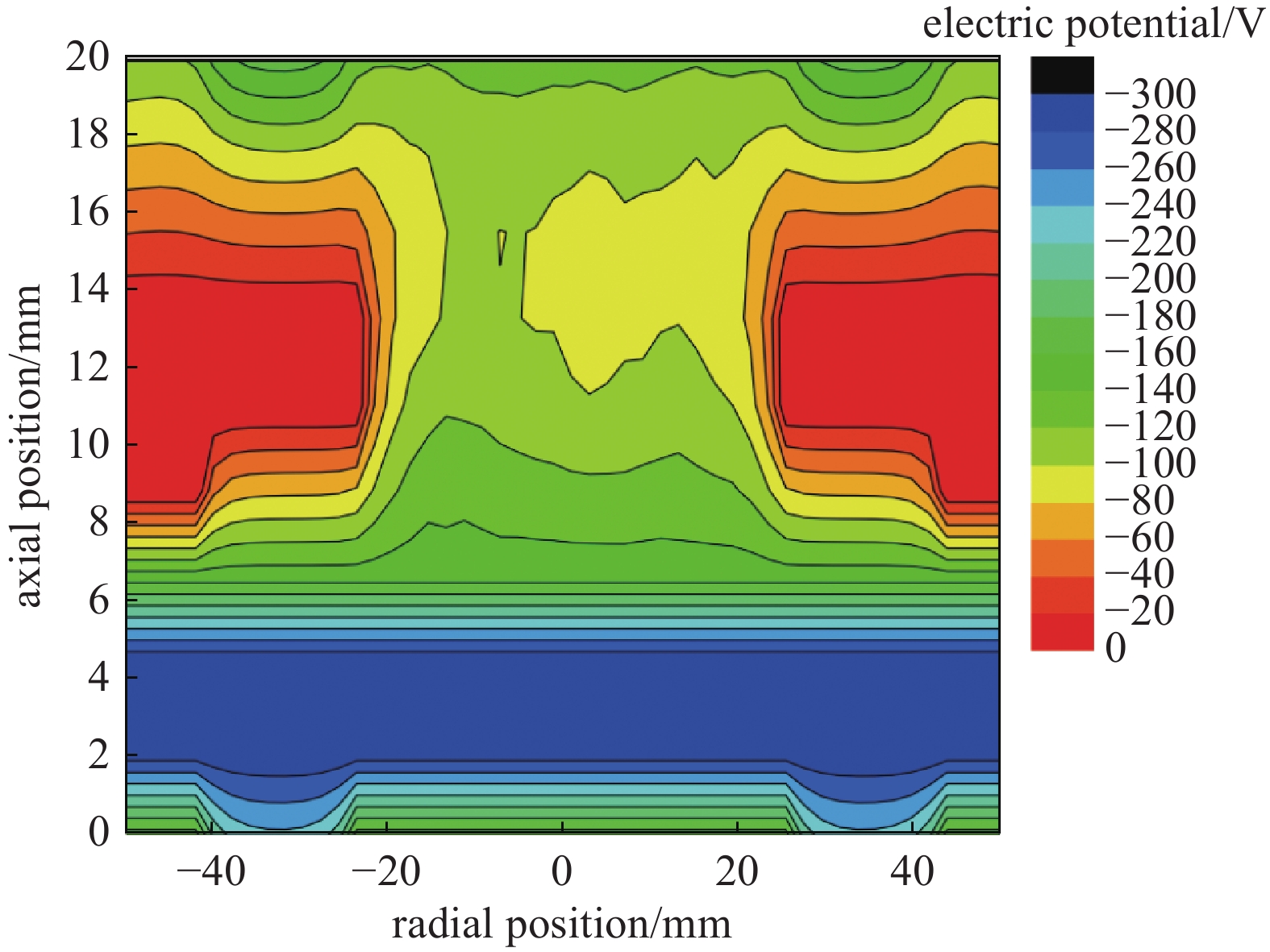
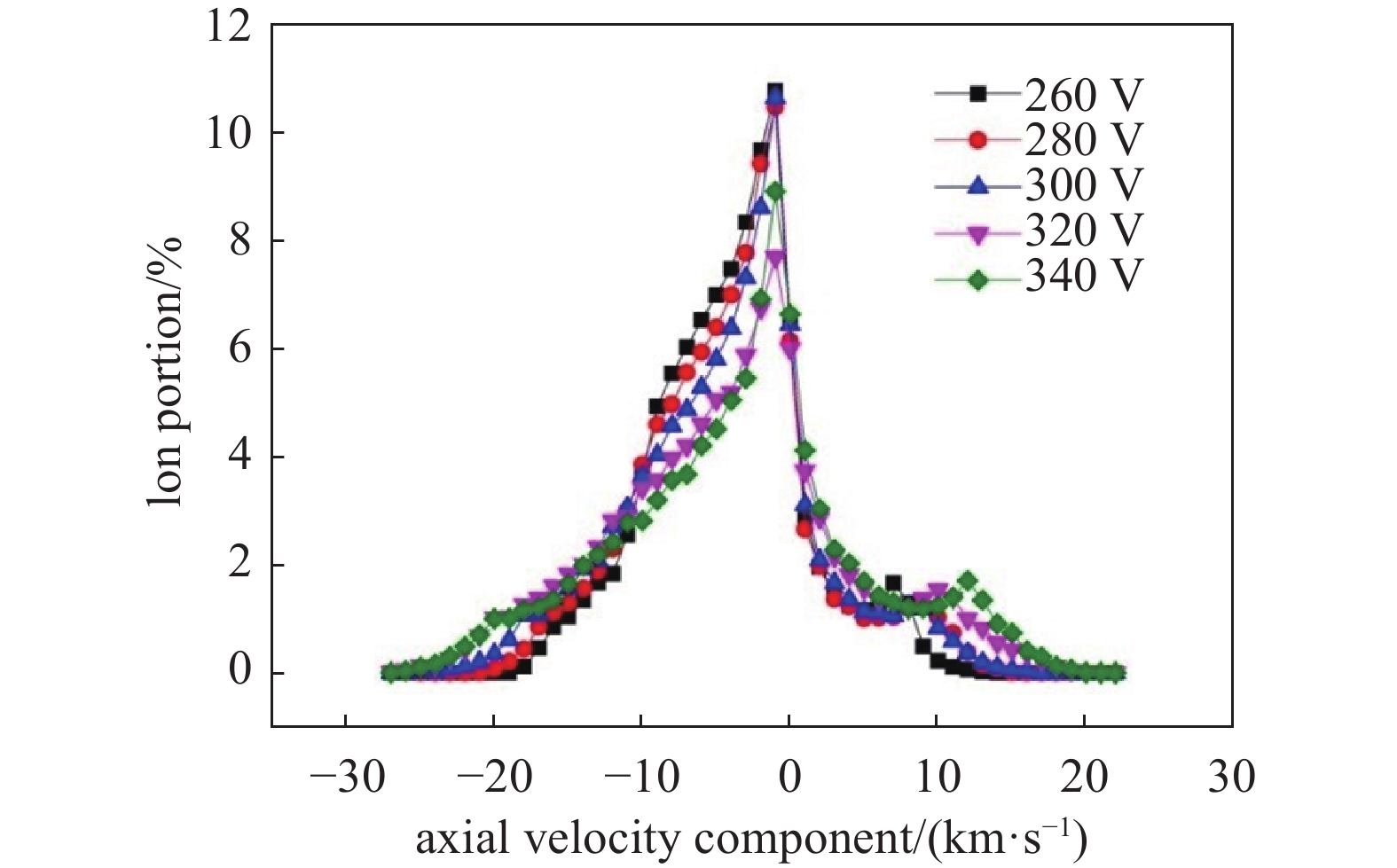
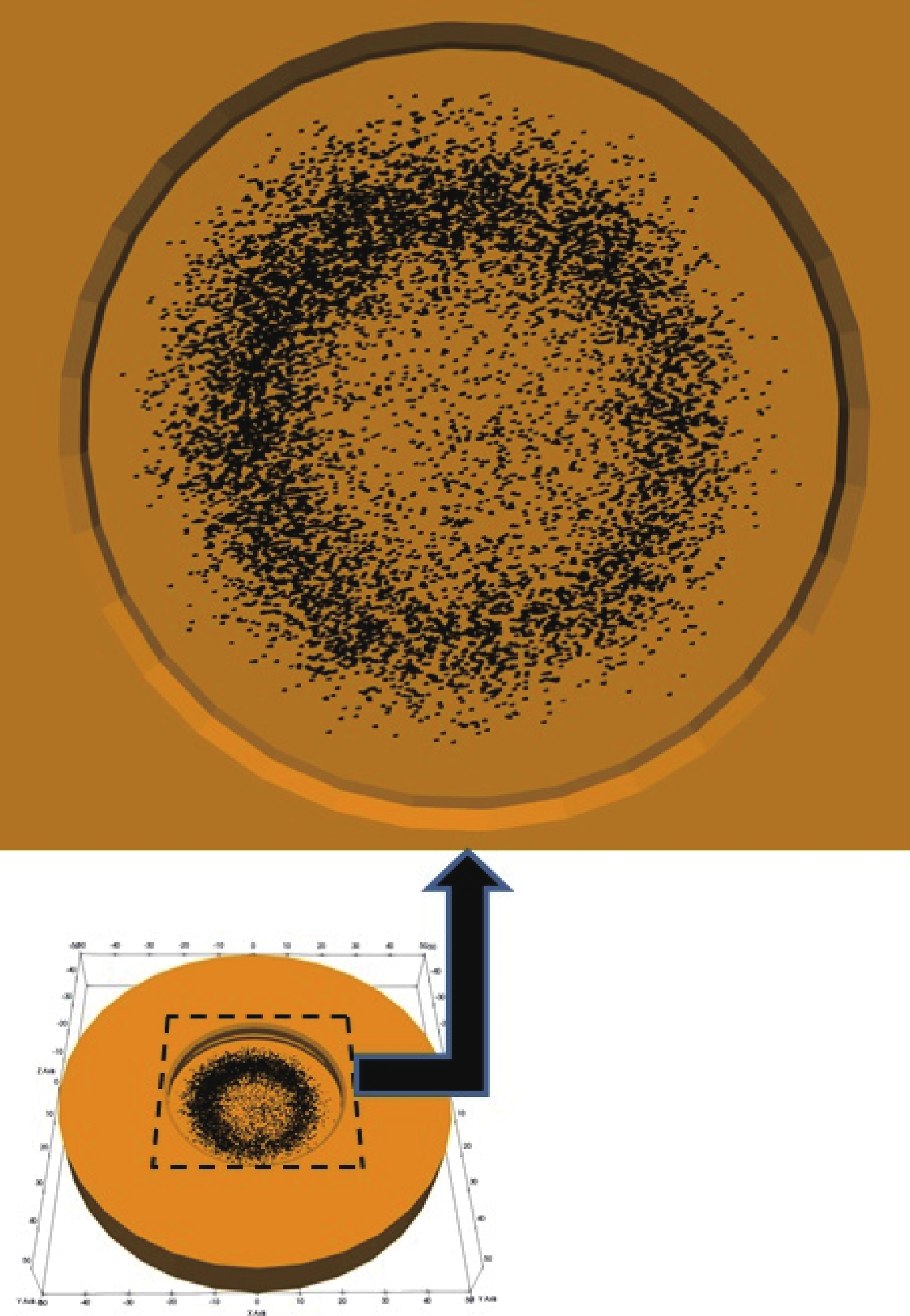
在模拟过程中，记录了所有氩离子和电子的空间坐标（x, y, z）和速度（$ {{{\boldsymbol{v}}}}_{{x}} $,$ {{{\boldsymbol{v}}}_{{y}}} $,$ {{{\boldsymbol{v}}}_{{{\textit{z}}}}} $）。通过跟踪离子在相邻时间节点上的空间位置得到离子的轨迹，如图4所示。由于离子具有不同的非零水平速度分量$ {{{\boldsymbol{v}}}}_{\parallel}={{{\boldsymbol{v}}}_{{x}}}+{{{\boldsymbol{v}}}_{{{\textit{z}}}}} $，它们与靶材表面的入射角不同。在图4中可以观察到另一种现象。如图4中不同颜色的轨迹所示，并不是所有的离子都能到达靶材表面，部分离子（红色轨迹）只是移动，最终从靶材表面“逃逸”。这种离子行为是图5中电势分布的结果。由于正电荷离子的存在，轴向位置12~16 mm区域（图5黄色区域）的电势高于其他区域。因此，无论离子向靶区移动还是远离靶区移动，由于电势的空间分布（由高电势区向低电势区），离子总是会加速。

在图6中，每条单线在10 km/s离子轴向速度值附近都有另一个峰值。随着放电电压的增大，各峰值对应的速度幅度也增大，是由于逃逸离子受到电势的作用而得到加速的证据。

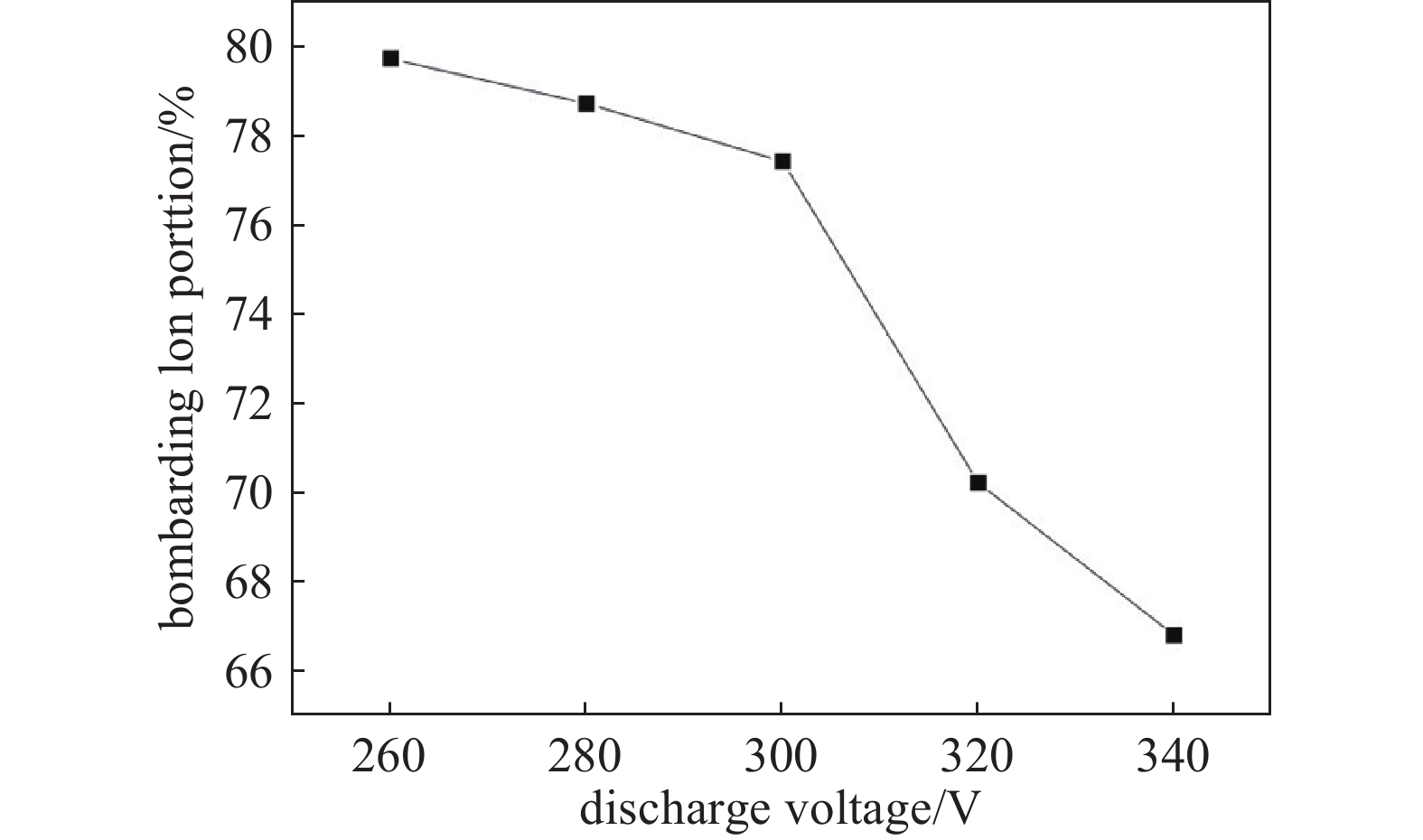
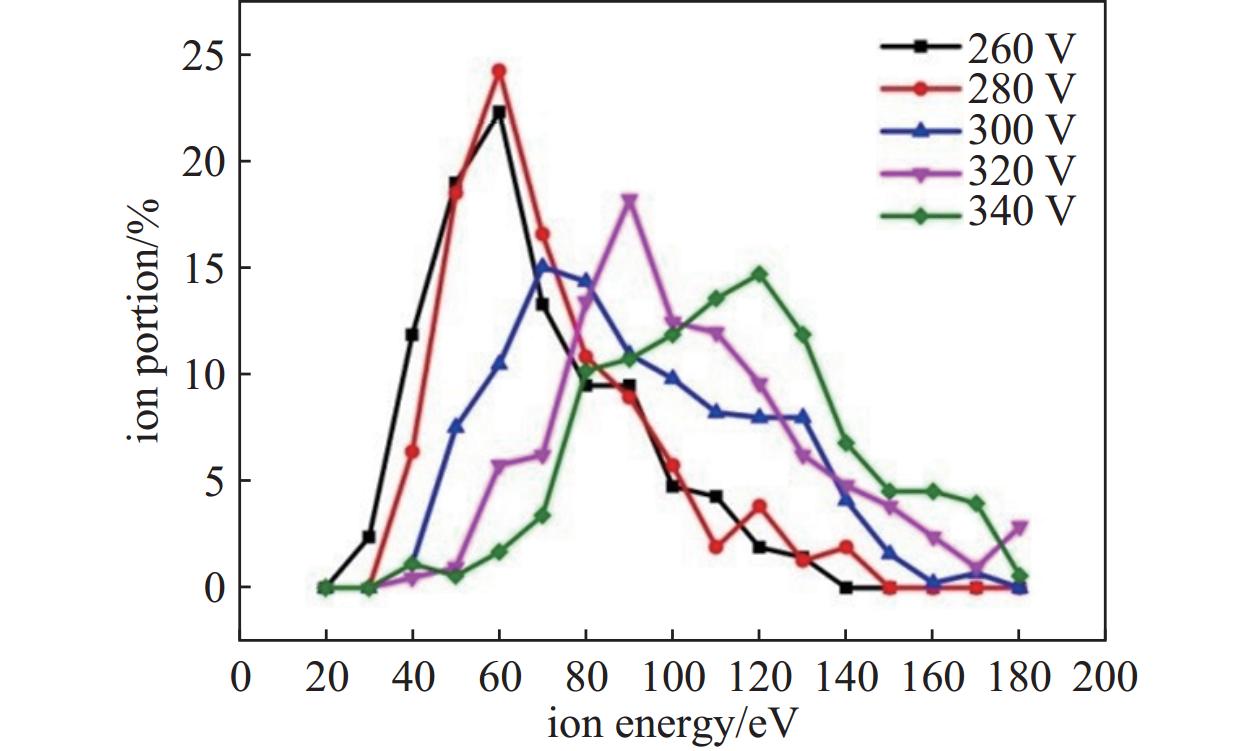
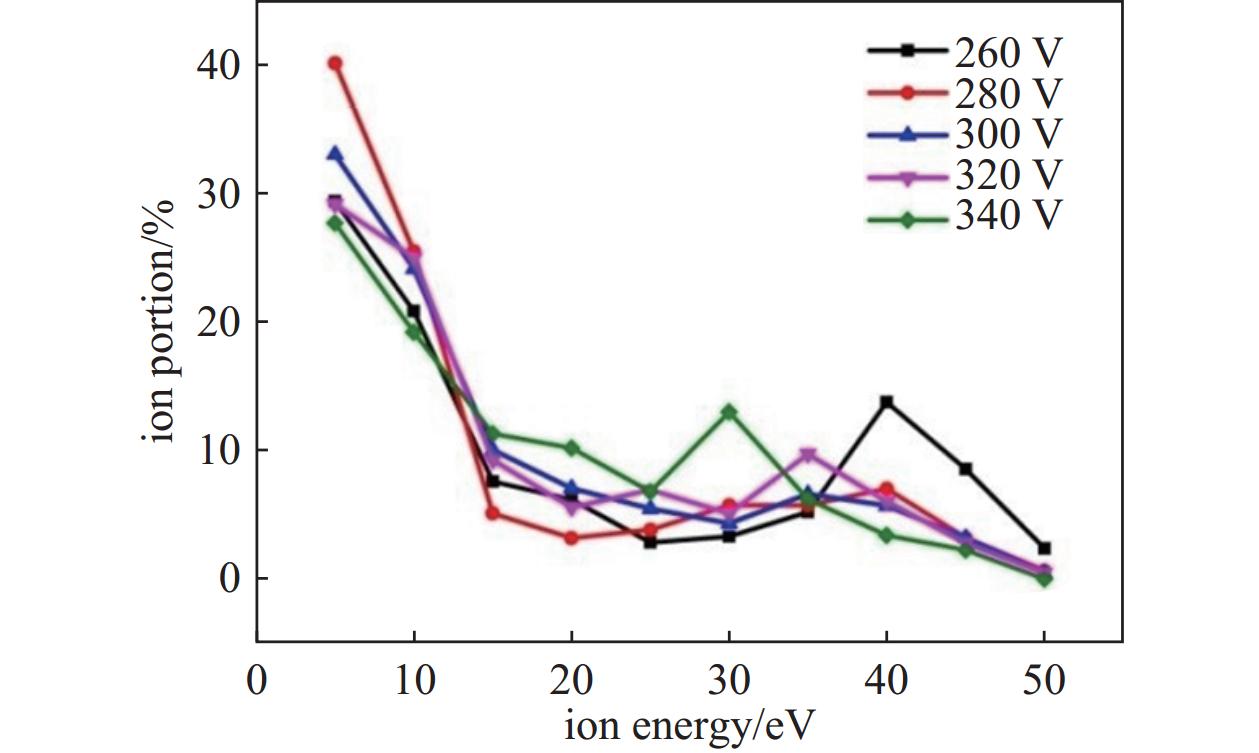
由于离子总是受到电势的加速作用，因此离子的初始轴向速度分量将决定它们是否能够撞击靶材而引起溅射。根据该推论，离子的分布与能量利用率（电源输出功率的利用效率）有关。换句话说，负$ {{\boldsymbol{v}}_{y}} $值的比例越大，轰击离子的比例就越高，从而使得能量利用率越高。图6显示了离子轴向速度分量$ {{\boldsymbol{v}}_{y}} $的分布，负$ {{\boldsymbol{v}}_{y}} $值表示离子向靶材移动。从图6中可以看出，放电电压的变化对离子轴向速度分量的分布趋势没有影响，总体上有20%以上的离子从靶中逸出。但是，通过进一步分析离子轴向速度分量$ {{\boldsymbol{v}}_{y}} $的数据，可以得出放电电压对轰击离子比例的影响，如图7所示。通过计算具有负$ {{\boldsymbol{v}}_{y}} $值的离子的比例，可以得到轰击离子的比例。从图7中可以清楚地看出，轰击离子量随着放电电压的增加而减小。这是因为，增加放电电压固然可以产生更多的氩离子，但由于密度较大的离子之间的相互作用，离子从靶体逸出的概率也增加了。结果，有效轰击离子比例降低。从这个角度来看，过高的放电电压可能会降低能量利用率。

影响MSS能量利用率的另一个因素是溅射效率。能否产生溅射粒子取决于轰击离子的入射能量和入射角^[26-27]。基于以上考虑，采用统计方法计算出离子入射能量和入射角分布，如图8和图9所示。

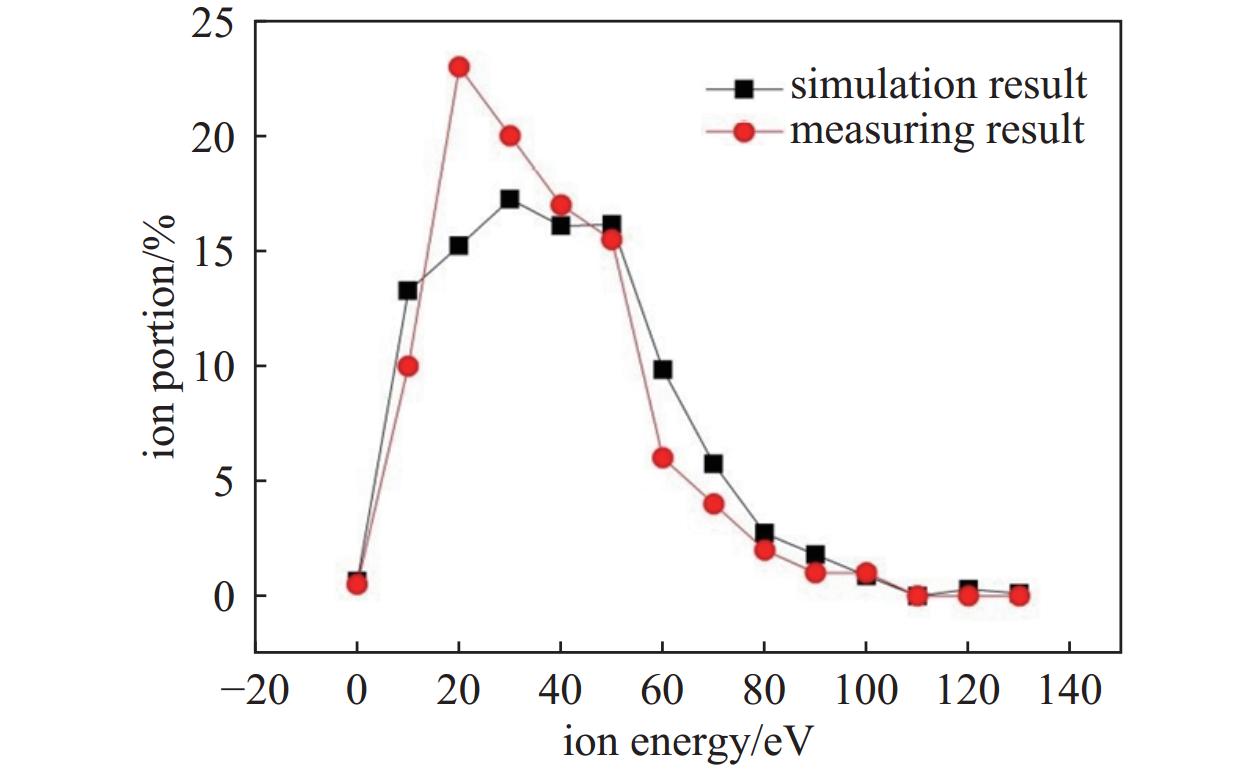
由于模型具有吸收边界，离子一旦到达靶材表面就会从模拟区域中被移除。图8和图9的结果是根据靶材表面附近1 mm范围内的离子数据得出的。大多数离子的入射能量在40 eV~160 eV之间，平均入射能量随放电电压的增加而增加。模拟结果与相关文献中的测量结果吻合较好^[28]。用自制的栅格离子能量分析仪（又称减速场能量分析仪，RFEA ）进行了验证试验。四网格探针位于距靶材表面15 mm处（模拟区域上边界），面向靶材表面，可获得距靶材表面15 mm处的离子能量分布。试验中，工作气体压力0.5 Pa，放电电压300 V，电源输出功率100 W。通过图10的测量和仿真结果对比，证实了建模的有效性。

对于入射角，超过60%的离子入射角在1°~10°范围内，这表明这些离子很难产生有效的溅射（窄入射角对应的溅射良率16相当低），器件本身还需要进一步优化以获得更好的性能^[26]。从图9也可以看出，放电电压对离子入射角分布没有明显影响。综上所述，提高放电电压有利于离子以更高的入射能量撞击靶材，有利于提高溅射成品率。

通过以上分析，可以得出MSS的放电电压是一个至关重要的工作参数。一方面，增加放电电压会减少轰击离子部分，似乎不利于提高能量利用率。另一方面，增大放电电压，离子的平均入射能量增大，有利于提高溅射成品率。因此，在兼顾溅射成品率和能量利用率的前提下，根据工作压力选择合适的放电电压是MSS参数优化的关键。

本文讨论了能量利用率的影响因素，并对靶材利用效率问题进行了探讨。虽然根据以上模拟结果，有效溅射部分相对较低，但靶表面的蚀刻轮廓仍然与轰击离子沉积位置密切相关。原因是离子溅射只发生在轰击离子沉积区，离子溅射会在靶表面形成蚀刻槽。靶材利用率随刻蚀槽宽度和深度的增加而增加。因此，可以基于轰击离子沉积位置的分布来分析靶材利用效率。

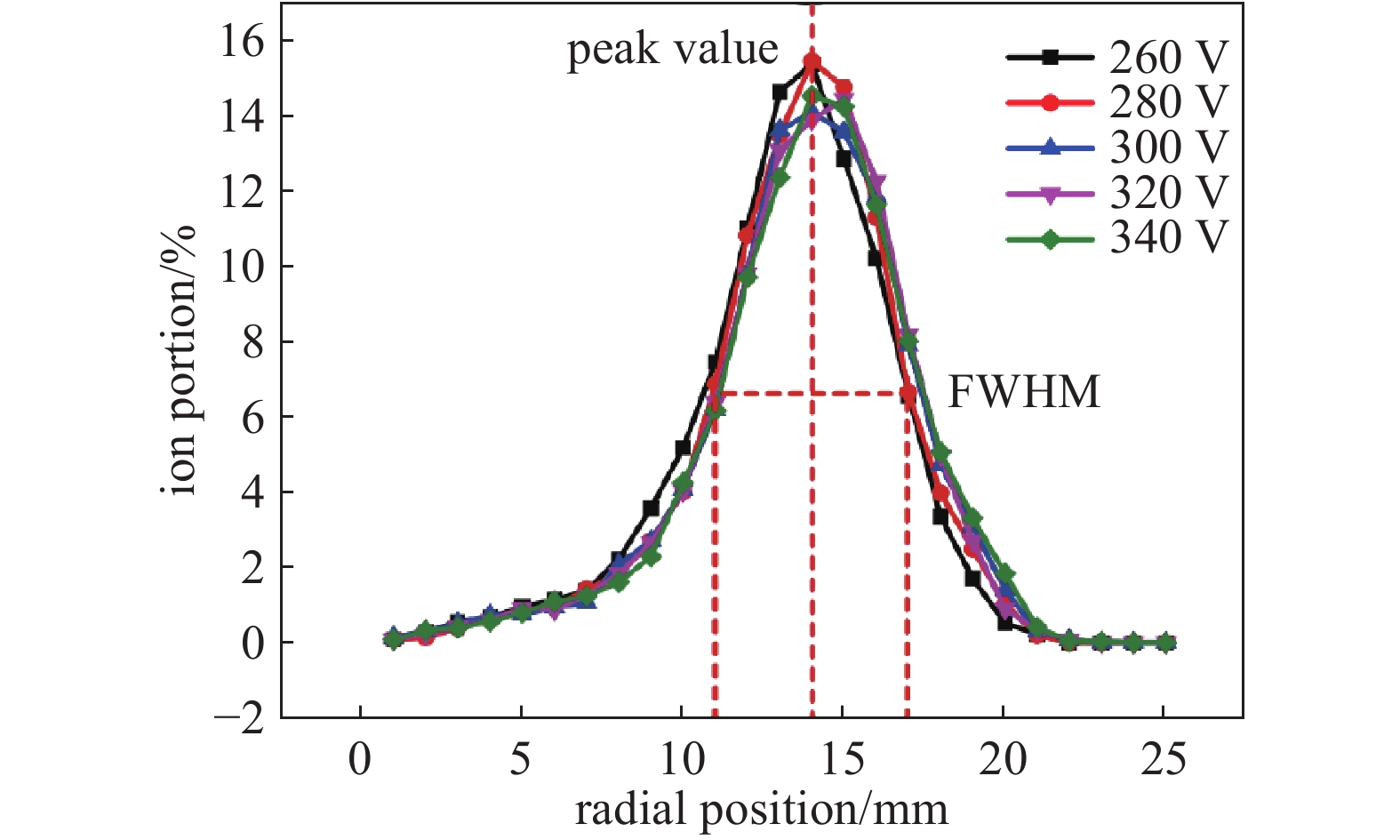
从图11和图12可以清楚地看出，放电电压对轰击离子在靶上的沉积位置分布没有影响。在靶表面，65%以上的轰击离子沉积在一个宽度为6 mm的环空区域（FWHM见图12），平均半径约为14 mm（峰值见图12），该区域也是侵蚀槽所在的区域。根据侵蚀面积比例，可以推断出靶材利用效率约为30%。轰击离子部分的最大值出现在14 mm~15 mm径向位置，说明侵蚀槽深度也应在该区域达到峰值。并通过实际靶材的侵蚀剖面测量结果验证了仿真结果。

由于工作功率低（≤100 W），对靶材的平均侵蚀速率很低（~20 nm/min），需要长时间工作（≥1000 h）才能出现明显的靶材侵蚀轮廓。因此，通过侵蚀新靶材来验证模型的有效性并不是一种经济可行的方法。然而，由上述结果可知，离子轰击位置分布与放电电压（或电源输入功率）无关，因此，在不同工作功率条件下，累积侵蚀的靶材可以作为离子轰击位置分布结果建模有效性的证明。图13显示了不同材料的侵蚀靶材。所有靶材的侵蚀深度在径向位置达到峰值，约为14.5 mm，在21 mm半径的圆形区域内存在侵蚀现象。回顾图12中虚线包围的区域，可以得出仿真和测量结果非常吻合的结论。

基于2英寸MSS结构，建立了三维粒子数值模拟模型，研究了决定MSS性能的离子行为。仿真结果与实测结果吻合较好，验证了仿真的可靠性。MSS优化既需要提高靶材利用率，也需要提高能量利用率。通过离子行为的模拟结果，可以得出以下结论：

（1） MSS的能量利用率和放电电压是相互矛盾的。从以上模拟结果可以看出，由于离子的空间分布，生成离子的密度越大，轰击离子的比例就越小。为了提高能量利用率，必须牺牲一部分由高放电电压带来的高溅射产额和沉积速率的有益效果。

（2）轰击离子沉积位置的分布与MSS的结构设计密切相关。为提高靶材的利用效率，应优化磁场分布，特别是使水平B分量分布更均匀。根据一些相关的研究工作，通过使用更小的磁体或增加磁靴来增加磁环数是值得尝试的方法。

此外，通过优化MSS的结构，提高离子的产生速率和平均能量等努力仍然值得尝试。数值模拟模型和分析方法为MSS性能优化的进一步研究提供了理论依据。