-
原子尺度的精准表征与调控是材料科学发展的核心驱动力。随着纳米材料制备技术的突破,研究范式正从宏观体系向原子级精准操纵转变[1]。以石墨烯为代表的二维材料体系的崛起[2],验证了原子级结构构筑对材料性能的决定性作用。在此背景下,基于超高真空环境的原子尺度表征技术成为关键研究手段。扫描隧道显微镜(STM)作为表面科学领域的革命性工具,其核心原理基于量子隧穿效应。当导电探针与样品间距缩小至纳米量级时,隧穿电流呈现指数型距离依赖性(I∝e−ks)[3],通过反馈机制实现表面形貌的高精度探测[4]。在恒定电流模式下,STM可达到原子级分辨率,为表面电子态密度(LDOS)的实空间成像提供了技术基础[5]。此外,STM衍生的针尖操控技术[6]能够实现单原子或分子的精确调控,在纳米结构构建[7]以及分子吸附位点调控[8]等领域展现出独特优势。
然而,STM测量过程易受多种因素干扰,包括仪器噪声[9]、机械震动[10]、针尖状态[11]、样品表面杂质[12]等,这些因素可能降低成像精度并影响后续分析。由于STM输出以图像形式呈现,图像修复技术已经被应用于复原原子尺度表征信号。该技术通过信号处理去除图像退化和噪声[13],已成功应用于医学成像[14]、卫星图像处理[15]以及日常图像优化[16]等领域。将图像修复技术引入STM成像,可有效解决噪声问题,提升成像质量,恢复物质表面原始信息,为精确表征材料表面、研究物理化学性质及开发新型材料提供了重要技术支持。
传统扫描隧道显微镜(STM)成像质量退化通常归因于探针针尖退化与系统噪声引起的图像破损。早期研究认为针尖形状畸变是导致图像退化的主因,传统修复方法主要依赖针尖盲重构算法通过盲解卷积实现形貌复原[17-19]。针对外加噪声引起的破损问题,传统修复技术可分为两类:基于结构信息的方法通过偏微分方程建模局部梯度与边缘特征,对破损区域进行扩散填充修复[20];基于纹理信息的方法则采用模式匹配算法实现待修复区域与完好区域的自适应拼接[21]。然而,传统方法在亚纳米尺度细节复原中存在显著局限性。盲解卷积算法对针尖先验模型依赖性强,易导致边缘伪影和结构失真;结构导向修复易出现边缘断裂,而纹理匹配修复在处理复杂晶格结构时可能出现周期性失配。此外,现有方法通常需要针对特定样品表面特性调整算法参数,缺乏跨平台适用性,限制了其在多尺度材料表征中的普适应用。
随着人工智能技术的发展,基于深度学习的图像修复方法在多个领域展现出显著优势,但其在扫描隧道显微镜(STM)成像中的应用受到成像机制特殊性的限制。STM成像基于隧道电流的物理机制以及独特的外加噪声特性,使得传统深度学习模型在STM图像修复中的效果受限。针对这一问题,已有研究提出多种解决方案。例如,Joucken F等[22]开发了一种基于卷积神经网络(CNN)的去噪方法,通过紧束缚电子结构模型生成模拟图像进行训练,实现了优于传统滤波器的去噪效果。然而,STM模拟图像的真实性问题仍需解决,因针尖状态的影响使得纯净无噪声图像难以反映实际观测条件。为克服模拟图像真实性不足的问题,Xie J等[23]提出了一种物理增强的深度学习方法,利用物理模型生成模拟数据,并结合对抗域适应(PDA-Net)框架实现无监督去噪,避免了对参考图像的依赖。同时,Oliveira J P等[24]开发了一种基于稀疏编码的去噪算法,通过学习字典表示图像的稀疏线性组合,将伪影视作缺失数据进行修复,同样无需依赖参考图像。
尽管上述方法在STM图像修复中取得了一定进展,但现有算法多基于模拟数据或未充分考虑人类视觉系统的需求。为此,本文提出了一种基于多尺度特征提取与注意力机制的编码−解码原子尺度结构修复网络(MAED-CNN),通过人工修复的图像数据进行训练,优化了修复结果的可视化效果,使其更符合人类研究员的观察需求。实验表明,该方法在性能上优于经典深度学习模型,为STM原子尺度表征的图像修复提供了创新性解决方案。
-
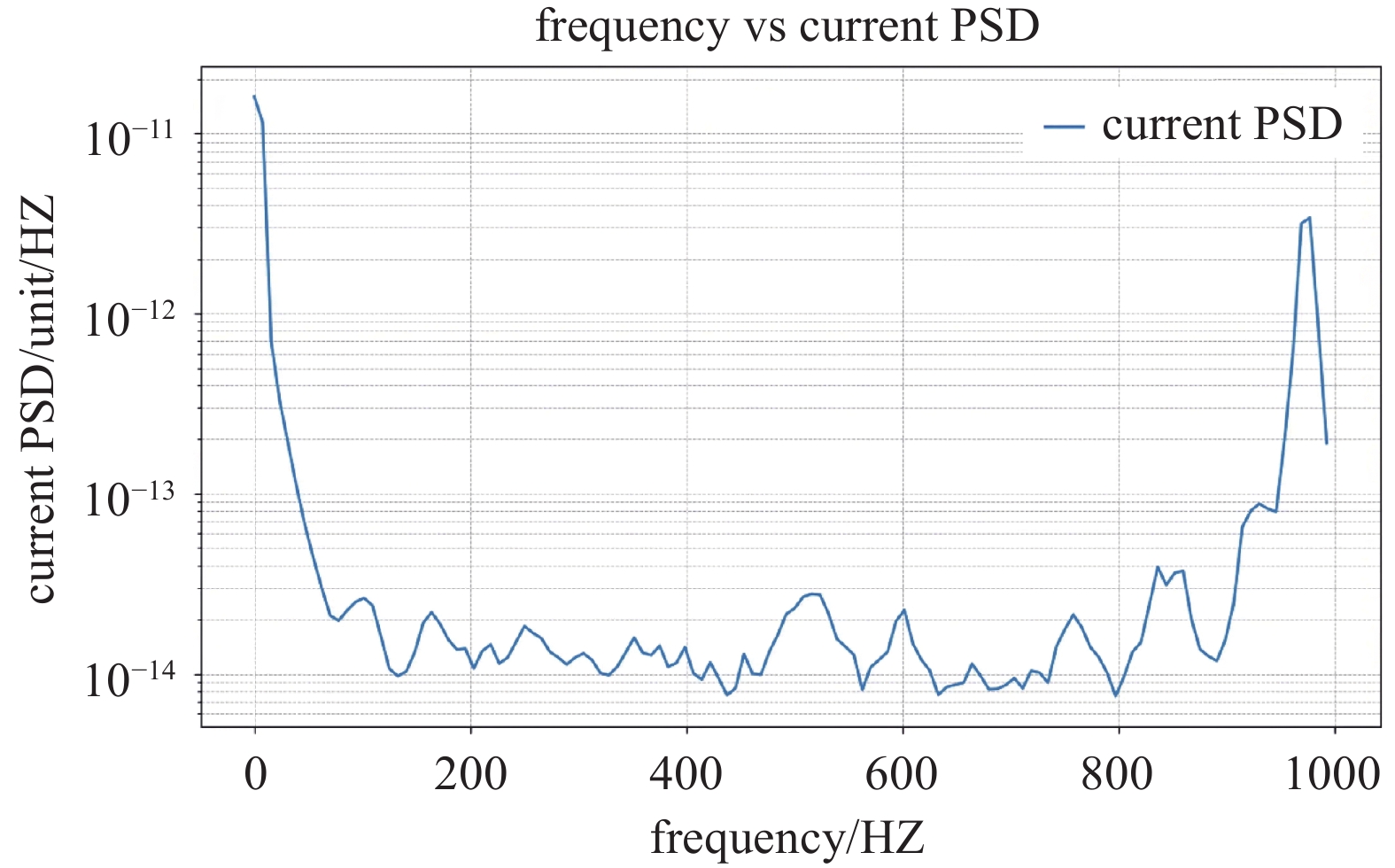
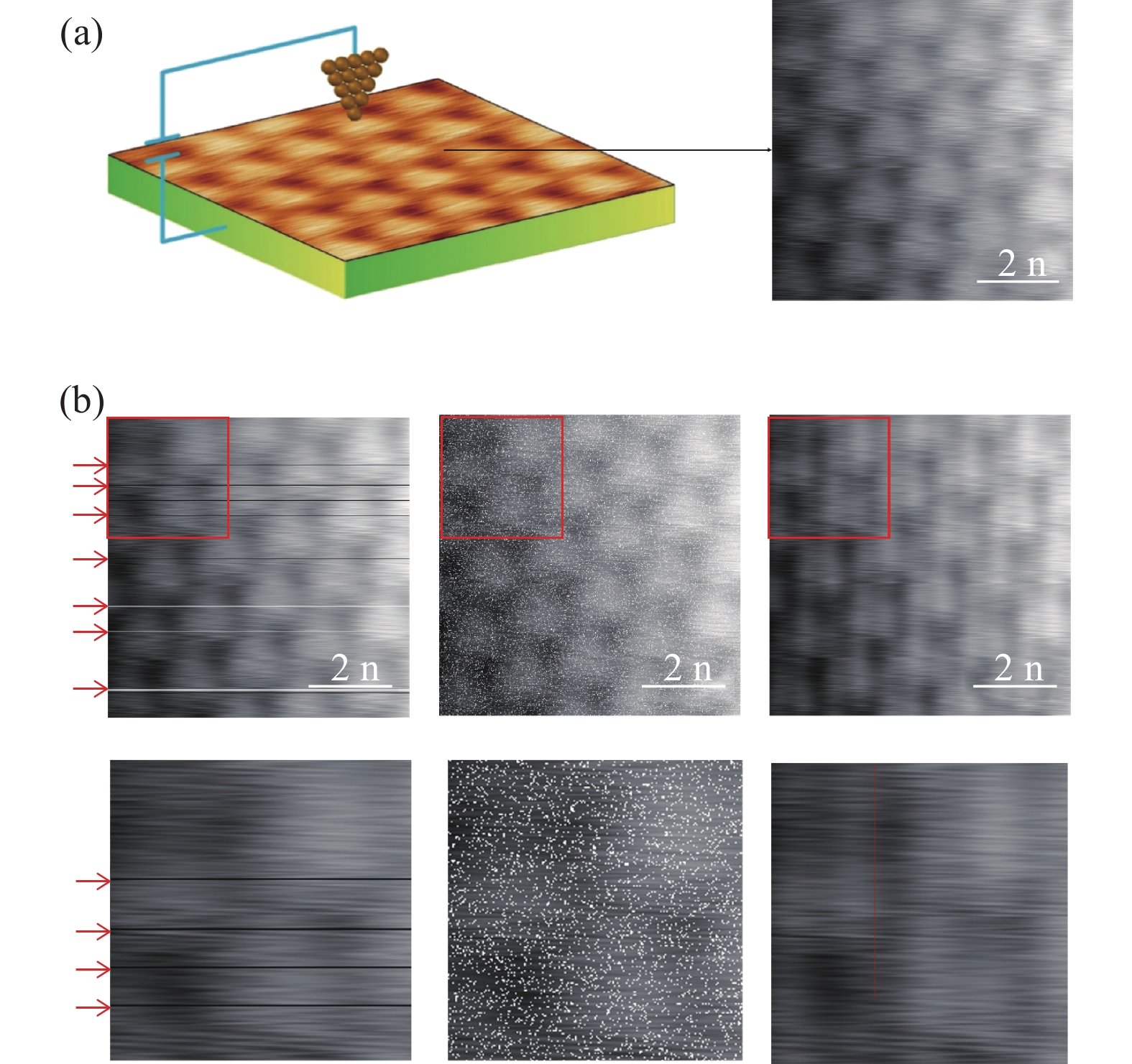
本文研究采用Tl掺杂TaSe2体系作为实验样品,所有数据均在5 K温度下通过扫描隧道显微镜(STM)获取。由于STM对针尖与样品间距的高度敏感性[25-26],取得的图像通常是带有比较复杂的噪声的。如图1(a)所示,长周期扫描受温漂影响的条纹状干扰,可认为是低频噪声,对应图2中较大的电流功率谱密度。此外,高频段(500−1000 Hz)同波动一般被认为是电子元器件产生的噪声。
为提高数据质量,采用空间域滤波[27-28]和频域变换[29]技术对原始图像进行预处理,获得干净的参考图像。
为进一步增强模型的泛化能力,基于文献[9]、[10]、[31]中对STM噪声来源的分析,人工添加了三种典型噪声(图1(b)):扫描噪声(源于电气波动[30])、高斯噪声(源于电子元件热波动[31])和周期噪声(源于机械震动[9])。这些噪声类型的选择基于其与真实STM噪声的统计一致性,并参考了Sun L S等的研究[32]。通过将这三种噪声随机组合并作用于原始图像,实现了数据增广,涵盖了更广泛的噪声类型,从而为模型训练提供了更具代表性的样本。
-
本文设计的深度学习模型基于Python语言开发,采用Pytorch框架作为后端支持。近年来,卷积神经网络(CNN)在图像降噪领域取得了显著进展[33],其核心优势在于能够通过多层卷积操作学习图像的复杂特征表示[34-35],包括噪声特征,并实现盲图像去噪[36-39]。在此基础上,研究者进一步引入感知损失[40-42]、注意力机制[43-44]和多尺度学习[45-47]等多技术,显著提升了CNN的图像修复能力。本文提出的多尺度注意力编码−解码卷积神经网络(MAED-CNN)整体工作流程如图3所示。首先,从STM仪器获取原始图像数据;其次,利用图1(b)所示的数据增强技术对图像进行预处理,通过添加扫描噪声、高斯噪声和周期噪声实现数据集扩展;最后,将增强后的图像输入MAED-CNN模型进行训练。模型以人工修复的干净图像作为参考,采用均方误差(MSE)作为损失函数,其表达式如公式(1)所示。
其中,
$ {N} $ 表示样本数量,$ \widehat {{{y}_{i}}} $ 表示生成图像,$ {{y}_{i}} $ 表示参考图像。MSE损失函数对异常值较为敏感,平方计算会放大噪声点对损失的贡献,因此特别适合用于修复噪声图像。其计算简单且为平滑函数,有助于算法的收敛。通过MAED-CNN处理后,最终输出的图像清晰度显著改善。为量化评估修复效果,本文采用峰值信噪比(PSNR)、结构相似性指数(SSIM)和 普遍图像质量指标(UQI)三项指标结合FFT对称性指标对修复质量进行评价。实验结果表明,MAED-CNN在去除噪声的同时有效保留了图像的关键结构信息,为STM图像修复提供了高效解决方案。
-
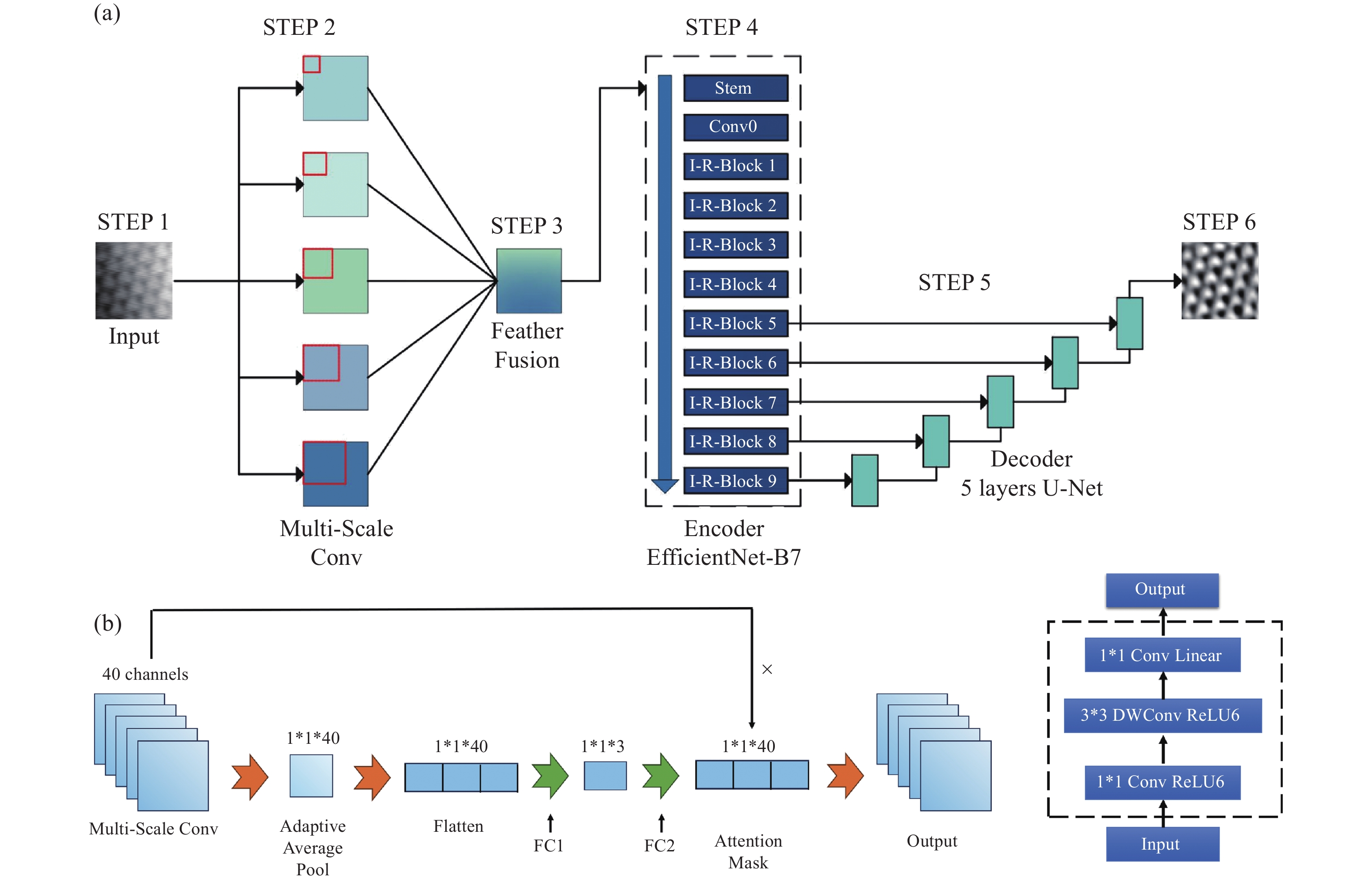
本文设计的MAED-CNN整体结构如图4(a)所示。该网络以带噪声的STM图像为输入(STEP 1),通过多尺度卷积核提取不同尺度的图像特征,以增强对噪声图像的大尺度结构和细节特征的同时感知能力(STEP 2)。具体而言,模型采用1×1、3×3、5×5、7×7和9×9五种不同尺寸的卷积核,针对不同类型的噪声进行特征提取。小尺度卷积核(如1×1、3×3)更适合捕捉高斯噪声和针尖震动等局部噪声的分布特征,而大尺度卷积核(如7×7、9×9)则在学习扫描噪声和周期噪声等宽作用域噪声的分布上更具优势。这种多尺度特征提取策略借鉴了Lu L P等[48]提出的MixDehazeNet,通过并行多尺度卷积有效提升了特征表达的多样性。之后,作者也对所设计的多尺度卷积模块的计算复杂度进行了详细测试与分析。该模块包含1000个参数,浮点运算次数(FLOPs)为44.16 M,内存占用为48.37 MB。在处理512×512×1尺寸的图像时,平均吞吐量达到731.82张图片/秒。这些结果表明,该多尺度卷积模块具有较低的计算复杂度和较高的推理速度,在实际应用中表现出优异的运行效率。这种高效性使其能够在保证修复质量的同时,满足实时处理的需求,为STM图像修复提供了高效的技术支持。
在特征融合阶段,将提取到的5个尺度共计40个通道的特征图像,送入特征融合模块进行处理,以实现特征的归纳与融合,并对每个通道分配相应的权重,从而增强对任务相关特征的关注(STEP 3)。特征融合模块基于SE(Squeeze-and-Excitation)通道注意力机制[49],其架构如图4(b)所示。先通过全局平均池化压缩图像至1×1大小,并保持通道数不变,然后将1×1大小的40个通道展平为40维向量,输入到全连接层FC1,将通道压缩到3个,FC1的目的是为了提取通道之间的高级特征表示,增强全局感受野,同时也减少计算量。再通过全连接层FC2恢复到40通道,生成注意力掩码,此时是结合FC1提取的通道之间高级特征以及图像特征给每个通道分配权重,捕捉通道之间的相关性。最后将输入的40个通道的特征图像与注意力掩码相乘,得到归纳总结后的特征图像,使得后续任务中可以更关注对当前任务有更大贡献的通道。
U-Net编码器在图像修复中至关重要,负责从原始特征中提取高级特征。对于STM图像修复,保留噪声下的电子态细节和原子缺陷信息是关键。本文选取EfficientNet-B7[50]作为U-Net图像修复架构的编码器(STEP 4),在Hu G等[51]研究者的工作中,通过对铁道缺陷的识别任务,发现了Efficient-B7优越的特征提取与计算速度性能,并且对于裂纹
等小缺陷具有极高的灵敏度,这对于STM图像的缺陷细节保留是极具优势的。图像经过特征融合后输入EfficientNet-B7编码器。该编码器由输入部分Stem、初始卷积层Conv0及多个倒残差(I-R-Block)模块构成。倒残差模块通过如图4(c)所示的深度可分离卷积(DWConv)对各通道运用独立的卷积核计算[52],不跨通道操作,有效降低计算量,并保持高精度。EfficientNet-B7借此高效提取深层特征,且参数量与计算量较少[50]。
编码后的信息输入U-Net架构解码器,其最后五层与解码器的五层通过跳跃连接相连(STEP 5),保留低级特征,确保细节和边缘信息的保留[53]。如图4(a)STEP 5所示,U-Net的对称结构以及跳跃连接,可以保留相对低级的信息特征,有助于原始图像的细节与边缘信息的保留,原有细节的保留对于生成高质量的图像是极为重要的参考与评估指标,跳跃连接的U-Net结构有效缓解了模型在去除噪声分布的同时“误伤”原有的图像细节等问题。通过连续五层的U-Net结构,对编码信息进行逐步解码与生成,最后得到了输出的高质量STM图像(STEP 6)。
-
MAED-CNN使用Adam优化器,学习率为1×10−4,将原始数据集通过随机的方式将518张噪声图像划分为0.9比例的训练集与0.1比例的测试集,于GTX-3090-24G上训练完成。
数据集来源于课题组成员运用STM扫描的包括Tl参杂浓度为0.6、0.8、1.0的TaSe2体系,扫描参数覆盖了−3−3V,30 pA−230 pA的设定电流。
-
运用于图像修复的深度学习模型已经十分丰富,但是大多运用于医学成像、老照片修复、视频修复等方面,直接与STM图像修复相关的深度学习模型相对欠缺。STM图像具有其独特的成像体系,其图像的退化以及外加噪声也有其单独的特性,通用的图像修复模型不一定适用于STM图像体系。于是,本文选择了PDA-Net[9]、HCANet[54]、CBDNet[55]、DnCNN[56]、PMRID[57]、RIDNet[58]等图像修复深度学习模型作为对比,以探究开发STM原子尺度结构修复网络的必要性。如图5所示为不同的深度学习模型在同样的STM图像上的修复效果,除了HCANet以外的所有模型均训练到损失值完全收敛。从图5(a)中可以看出,所有的模型能够缓解条纹噪声对图像清晰度的影响,修复出来的图像边缘更加清晰,但CBDNet、DnCNN、PMRID以及RIDNet修复出的图像肉眼可见的较“脏”,说明对于STM条纹噪声即仪器机械震动所带来的低频噪声分布,这些通用的图像修复模型并不能很好的适应。PDA-Net作为专用于STM图像的修复模型,具有较好的修复效果,其分子结构清晰,但具有微小变形。为了维持前提条件的一致,此处的PDA-Net并没有通过模拟数据的训练,而是直接用真实数据训练的,从局部放大图来看,其相比于MAED-CNN的修复效果依然存在一定的差距,分子结构产生了一定的变形。HCANet的修复效果在肉眼上与MAED-CNN几乎一致,不仅去除了低频的条纹噪声,也保留了原有的细节。为了避免偶然性,测试了另一种偏压下具有不同形貌的TaSe2图像加入到对比测试中,也就是图5(b)的图像。在这个过程中发现原本效果与MAED-Net效果差不多的PDA-Net与HCANet在对于具有复杂细节的图像修复上出现了细节模糊、结构破碎的问题。HCANet虽在仅训练10个epoch后便取得较好效果,具备进一步提升性能的潜力,但其训练时间已接近其他模型从训练开始到损失收敛所需时间的三分之二。由于其基于复杂的Transformer架构,计算资源和训练成本显著高于其他方法,对于结构相对简单的STM图像修复任务而言,其高昂的开销在实际应用中难以接受。而PDA-Net在没有模拟数据预训练的情况下,同样表现出了相对较差的修复性能,在同样的训练成本上不如MAED-CNN的训练效果。综上,MAED-CNN在综合了训练成本与性能的性价比上,优于其他通用模型或复杂模型。
-
为了客观评价MAED-CNN的修复质量,本节计算了图5所示的六种深度学习模型其图像修复质量的数字化指标,如表1所示。PSNR表示峰值信噪比,衡量重建图像与原始图像之间信噪比,PSNR值越高表示图像质量越好;SSIM表示结构相似性指数,SSIM越接近于1表示图像的结构恢复越好;UQI表示通用质量指数,综合考量亮度、对比度以及结构信息,越接近于1说明图像质量越高。
三项数字化指标中的最优值均加粗标记,从表中可以看出在考虑训练成本的情况下MAED-CNN的PSNR、SSIM、UQI指标均高于其他模型,说明无论是在像素级别上或是结构级别以及整体质量上,MAED-CNN的结构修复质量优于其他模型。
-
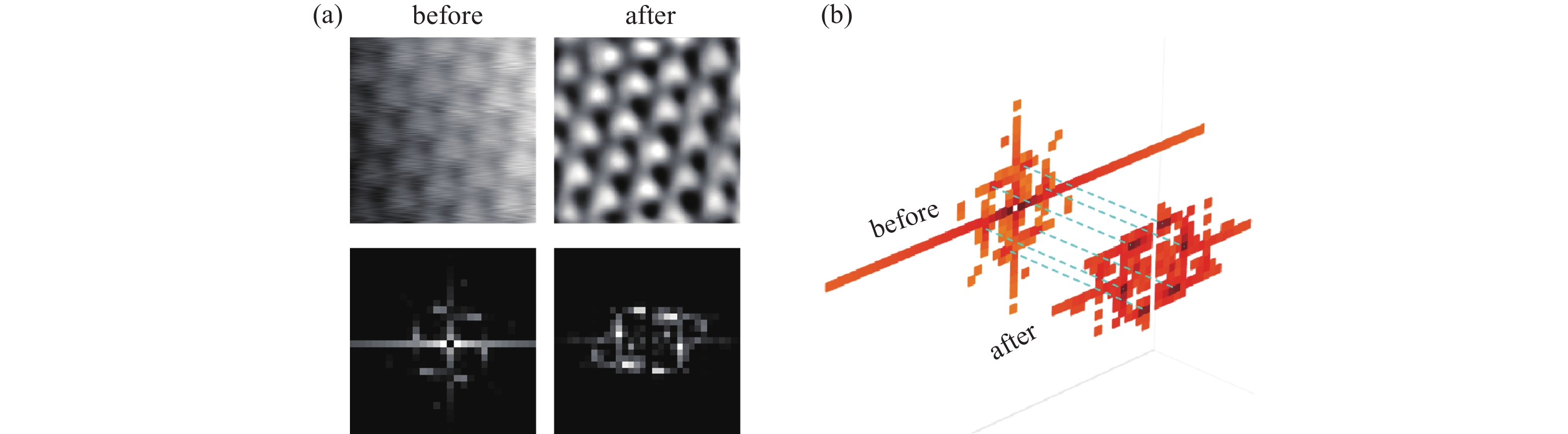
为了分析MAED-CNN深度学习模型的修复过程是否会导致图像部分失真,即导致晶体结构发生破坏,本文计算并对比了STM图像修复前后的快速傅里叶变换图像(FFT),如图6所示。从图6(a)中可以看出,修复前后的STM图像,其傅里叶图谱的六方晶格对称性仍然存在,即其晶格对称性并没有发生改变,原子位置几乎没有偏移。图6(b)的内容更好的说明了这一点,从图像中可以看到两者的六方晶格对称点几乎是重叠的。
-
综上所述,本文提出了一种适用于STM图像修复的深度学习模型,其运用人工修复的STM图像作为参考图像进行训练,通过多尺度特征提取模块获取了噪声图像的多尺度特征,结合SE注意力机制对图像进行特征融合,最后运用了U-Net结构并结合EfficientNet-B7作为编码器,作为高质量图像的生成部分。最后获取的高质量STM图像,将其与多种通用深度学习模型对比,证明了本文所提出的深度学习模型在STM图像修复上性能的优越性。STM图像质量的高低对研究工作的分析以及传播有着深远的影响,高质量的图像更便于分析与传播。
目前直接应用于STM图像修复的深度学习模型较少,且通用模型效果不佳,建设STM图像体系的深度学习环境十分重要,需要有更多的模型架构加入到STM的图像修复中,以适应更多不同的材料体系与仪器。此外,高质量的STM图像获取所花费的工作成本较高,通常需要多次调整扫描参数甚至是更新针尖状态才能得到清晰的STM图像,深度学习模型可以有效缓解这类问题,通过修复手段避免多次重复的扫描,从而提升研究员的工作效率。相信随着深度学习技术的进步,可以为STM的研究工作带来更加广阔的发展前景。
MAED-CNN:一种原子尺度图像降噪的深度学习模型
MAED-CNN: A Deep Learning Model for Atomic-Scale Image Denoising
-
摘要: 工作在超高真空环境下的扫描隧道显微镜(STM)具备原子级分辨率,广泛应用于材料表面结构的精细成像。然而,STM图像易受机械振动、电子噪声、环境扰动等多种因素影响,导致图像质量下降,严重制约其科学研究价值。为提升STM图像的可用性和精度,文章提出一种基于多尺度特征提取与注意力机制的深度学习图像修复模型——MAED-CNN。该模型采用U-Net编码−解码结构,融合多尺度卷积模块与通道注意力机制,并引入人工修复图像作为监督参考,有效增强对图像局部细节与全局结构的重构能力。在多个真实STM图像数据集上进行测试,MAED-CNN在PSNR、SSIM、UQI等评价指标上均优于现有主流图像修复模型,表现出更高的图像还原精度与稳定性。研究为STM图像智能修复提供了新思路,对提升纳米尺度成像技术的应用水平具有重要意义。Abstract: The Scanning Tunneling Microscope (STM), operating under ultra-high vacuum conditions, enables atomic-scale resolution imaging of material surfaces. However, STM images are often affected by various sources of noise, which degrades image quality. This paper proposes a deep learning model for STM image restoration, named MAED-CNN - Multi-scale Attention Encoder-Decoder Convolutional Neural Network. It uses artificially repaired STM images as references. The model leverages manually restored STM images as references and combines multi-scale convolution, attention modules, and an encoder-decoder U-Net architecture to transform noisy input images into high-quality, denoised outputs. Compared with several general deep learning models, the proposed model demonstrates superior performance in metrics such as PSNR, SSIM, and UQI. It effectively restores STM images and holds significant promise for advancing STM image restoration techniques and promoting research in imaging technologies.
-
Key words:
- Deep Learning /
- Image Restoration /
- Scanning Tunneling Microscope .
-

-
图 1 STM获取图像以及人工添加的常见噪声类型。(a)STM获取图像,扫描参数为:偏压4.5 V,设定电流230 pA,图像具有明显的低频条纹噪声。(b)用于数据增广的常见的噪声类型,从左至右分别为扫描噪声、高斯噪声、周期噪声
Figure 1. Images acquired by STM and common types of artificially added noise. (a) An STM-acquired image with scanning parameters of a bias voltage of 4.5 V and a set current of 230 pA, which has obvious low-frequency stripe noise. (b) Common types of noise used for data augmentation, from left to right are scan noise, Gaussian noise, and periodic noise
图 2 电流信号谱图,由图中可以看出,低频区间(0−100 Hz)PSD值较大,低频噪声对信号的影响较大;高频区间(500−1000 Hz)PSD值相对较小,但仍然存在波动,噪声依然存在影响
Figure 2. The current signal spectrum. It can be seen from the figure that the PSD values in the low-frequency range (0−100 Hz) are relatively large, indicating that low-frequency noise has a significant impact on the signal. In the high-frequency range (500−1000 Hz), although the PSD values are relatively smaller, there are still fluctuations, and the impact of noise cannot be ignored
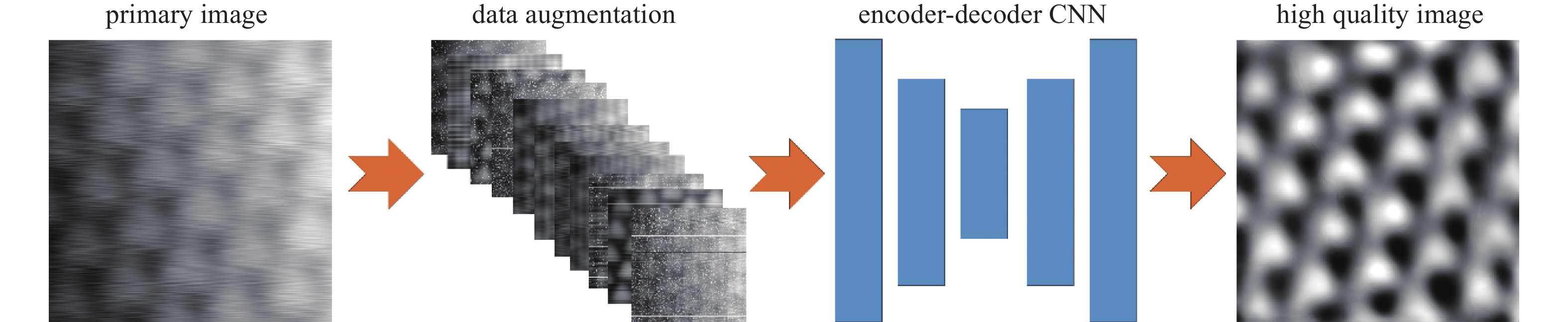
图 3 MAED-CNN整体流程图。原始图像先通过随机添加噪声的方式进行数据增广,然后送入一个带有编码器−解码器结构的卷积神经网络中处理,最后输出高质量图像
Figure 3. The overall flowchart of the MAED-CNN. The original image is first augmented by randomly adding noise, then it is fed into a convolutional neural network with an encoder-decoder architecture for processing, and finally, a high-quality image is output
图 4 MAED-CNN结构示意图。(a)为神经网络整体结构,输入图像经由5个不同大小的卷积核提取多尺度特征,并经过一个通道扩充层丰富特征数量,然后将所有特征图经由一个特征融合层归纳,之后由EfficientNet-B7作为编码器编码特征,由U-Net作为解码器生成最后的输出图像。(b)特征融合层的具体结构,运用SE通道注意力模块,通过两次全连接层,对40个通道的不同尺度特征分配权重,得到注意力掩码,然后与原始特征图像相乘,得到最后输出的特征图像。(c)为到残差模块示意图,由深度可分离卷积层结合1×1卷积层构成
Figure 4. The schematic diagram of the MAED-CNN structure. (a) Illustrates the overall structure of the neural network. The input image is processed through five convolutional kernels of different sizes to extract multi-scale features. These features are then enriched by a channel expansion layer. After that, all feature maps are integrated via a feature fusion layer. Subsequently, EfficientNet-B7 serves as the encoder to encode the features, and U-Net acts as the decoder to generate the final output image. (b) Details the specific structure of the feature fusion layer, which employs the SE (Squeeze-and-Excitation) channel attention module. Through two fully connected layers, it assigns weights to the multi-scale features of 40 channels, obtaining an attention mask. This mask is then multiplied with the original feature images to produce the final output feature images. (c) A residual module diagram, consisting of a combination of depthwise separable convolutional layers and 1×1 convolutional layers
图 5 不同深度学习模型的图像修复效果对比。包括了原始图像、MAED-CNN、PDA-Net、HCANet、CBDNet、DnCNN、PMRID以及RIDNet,红色矩形框表示在该图片的下方对该区域局部放大。(a)、(b)图展示了不同偏压下具有不同形貌的同一区域图像
Figure 5. Comparison of image restoration effects of different deep learning models. This includes the original image, MAED-CNN, PDA-Net, HCANet, CBDNet, DnCNN, PMRID, and RIDNet. The red rectangular boxes indicate local magnification of the corresponding regions below the images. Figures (a) and (b) show images of the same area with different morphologies under different biases
图 6 MAED-CNN修复过程对晶体对称性结构的影响分析示意图。(a)第一行为修复前后的图像,第二行为修复前后的STM图像的傅里叶变换图谱。(b)修复前后的STM图像的傅里叶图谱映射到三维空间中的对比
Figure 6. chematic diagram of the impact of the MAED-CNN restoration process on the symmetry structure of crystals.(a) The first row shows the images before and after restoration, and the second row shows the Fourier transform spectra of the STM images before and after restoration.(b) The Fourier spectra of the STM images before and after restoration are mapped into three-dimensional space for comparison
表 1 图像修复质量的数字化指标
Table 1. Digital Metrics for Image Restoration Quality
Evaluation MAED-CNN PDA-Net HCANet CBDNet DnCNN PMRID RIDNet PSNR 31.87 21.22 21.74 17.61 17.26 16.23 16.59 SSIM 0.8989 0.7753 0.8162 0.4286 0.4480 0.4394 0.4206 UQI 0.8982 0.8838 0.8327 0.4569 0.4735 0.4788 0.4494 -
[1] Zhang Q Z, Zhang Y, Hou Y H, et al. Nanoscale control of one-dimensional confined states in strongly correlated homojunctions[J]. Nano Letters, 2022, 22(3): 1190−1197 doi: 10.1021/acs.nanolett.1c04363 [2] Yang Y C, Gao Q F, Liang W B, et al. Enhanced stretchable 2D metal‐graphene membranes with superior mechanical properties for sieving lithium from brine (Small 15/2025)[J]. Small, 2025, 21(15): 2570118 doi: 10.1002/smll.202570118 [3] 李全锋. 扫描隧道显微镜[D]. 合肥: 中国科学技术大学, 2012 (in Chinese) Li Q F. Scanning tunneling microscope[D]. Hefei: University of Science and Technology of China, 2012 [4] Qiu X H, Bai C L. Scanning tunnelling microscopic investigation of organic molecular assembling systems[J]. Journal of the Graduate School of the Chinese Academy of Sciences, 2003, 20(1): 107−111 [5] Ren Y N, Ren H Y, Watanabe K, et al. Realizing one-dimensional moiré chains with strong electron localization in two-dimensional twisted bilayer WSe2[J]. Proceedings of the National Academy of Sciences of the United States of America, 2024, 121(45): e2405582121 [6] Wang D F, Bao D L, Zheng Q, et al. Twisted bilayer zigzag-graphene nanoribbon junctions with tunable edge states[J]. Nature Communications, 2023, 14(1): 1018 doi: 10.1038/s41467-023-36613-x [7] 王金刚, 汤儆, 陈招斌, 等. STM针尖诱导构筑-置换两步法制备Pt表面纳米结构[J]. 电化学, 2006, 12(4): 357−362 (in Chinese) doi: 10.3969/j.issn.1006-3471.2006.04.001 Wang J G, Tang J, Chen Z B, et al. STM tip-induced nanostructuring-replacement method to construct Pt surface nanostructures[J]. Journal of Electrochemistry, 2006, 12(4): 357−362 doi: 10.3969/j.issn.1006-3471.2006.04.001 [8] 施宏, 刘慧慧, 李喆, 等. 乙炔分子在TiO2(110)表面吸附的低温STM研究[J]. 中国化学会, 2021 (in Chinese) Shi H, Liu H H, Li Z, et al. Low-temperature STM study on the adsorption of acetylene molecules on the TiO2(110) Surface[J]. Chinese Chemical Society, 2021 [9] 江月山, 王晓光, 杨乃恒, 等. 压电陶瓷对STM图像的影响及计算机校正[J]. 真空科学与技术学报, 1997, 17(4): 264−268 (in Chinese) Jiang Y S, Wang X G, Yang N H, et al. Computer correction for distorted STM images caused by piezoceramics[J]. Vacuum Science and Technology, 1997, 17(4): 264−268 [10] 高论. 提高SPM检测表面形貌精度的研究[D]. 长春: 吉林大学, 2004 (in Chinese) Gao L. Research on improving precision of surface topography by SPM[D]. Changchun: Jilin University, 2004 [11] 宋永, 杨阔. STM探针形貌与图像质量的关系研究[J]. 湖北成人教育学院学报, 2013, 19(2): 82−83,79 (in Chinese) doi: 10.3969/j.issn.1673-3878.2013.02.028 Song Y, Yang K. Research on the relationship between STM probe morphology and image quality[J]. Journal of Hubei Adult Education Institute, 2013, 19(2): 82−83,79 doi: 10.3969/j.issn.1673-3878.2013.02.028 [12] 张颜萍. 怎样获得一幅效果良好的STM图像[J]. 甘肃高师学报, 2006, 11(5): 14−15 (in Chinese) doi: 10.3969/j.issn.1008-9020.2006.05.006 Zhang Y P. How to obtain a better STM picture[J]. Journal of Gansu Normal Colleges, 2006, 11(5): 14−15 doi: 10.3969/j.issn.1008-9020.2006.05.006 [13] 朱秀昌, 唐贵进. 现代数字图像处理[M]. 北京: 人民邮电出版社, 2020: 473 (in Chinese) Zhu X C, Tang G J. Advanced digital image processing[M]. Beijing: Posts & Telecom Press, 2020: 473 [14] Fan D, Yue T, Zhao X, et al. LIR: A Lightweight Baseline for Image Restoration[J]. arXiv preprint arXiv:2402.01368, 2024 [15] Toker A, Eisenberger M, Cremers D, et al. SatSynth: Augmenting image-mask pairs through diffusion models for aerial semantic segmentation[C]//2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle: IEEE, 2024: 27685−27695 [16] Xu X G, Kong S, Hu T, et al. Boosting image restoration via priors from pre-trained models[C]//2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle: IEEE, 2024: 2900−2909 [17] Bonnet N, Dongmo S, Vautrot P, et al. A mathematical morphology approach to image formation and image restoration in scanning tunnelling and atomic force microscopies[J]. Microscopy Microanalysis Microstructures, 1994, 5(4-6): 477−487 doi: 10.1051/mmm:0199400504-6047700 [18] Villarrubia J S. Morphological estimation of tip geometry for scanned probe microscopy[J]. Surface Science, 1994, 321(3): 287−300 doi: 10.1016/0039-6028(94)90194-5 [19] Williams P M, Shakesheff K M, Davies M C, et al. Blind reconstruction of scanning probe image data[J]. Journal of Vacuum Science & Technology B: Microelectronics and Nanometer Structures, 1996, 14(2): 1557−1562 [20] 李亮. 基于偏微分方程的图像修复算法研究[D]. 长春: 吉林大学, 2012 (in Chinese) Li L. Image inpainting algorithms based on partial differential equation[D]. Changchun: Jilin University, 2012 [21] 张燕. 数字图像修复技术研究[D]. 成都: 成都理工大学, 2008 (in Chinese) Zhang Y. Research of digital image inpainting technique[D]. Chengdu: Chengdu University of Technology, 2008 [22] Joucken F, Davenport J L, Ge Z H, et al. Denoising scanning tunneling microscopy images of graphene with supervised machine learning[J]. Physical Review Materials, 2022, 6(12): 123802 doi: 10.1103/PhysRevMaterials.6.123802 [23] Xie J, Ko W, Zhang R X, et al. Physics-augmented deep learning with adversarial domain adaptation: Applications to STM image denoising[J]. arXiv preprint arXiv:2409.05118, 2024 [24] Oliveira J P, Bragança A, Bioucas-Dias J, et al. Restoring STM images via Sparse Coding: noise and artifact removal[J]. arXiv preprint arXiv:1610.03437, 2016 [25] Hofer W A, Foster A S, Shluger A L. Theories of scanning probe microscopes at the atomic scale[J]. Reviews of Modern Physics, 2003, 75(4): 1287−1331 doi: 10.1103/RevModPhys.75.1287 [26] Rerkkumsup P, Aketagawa M, Takada K, et al. Highly stable atom-tracking scanning tunneling microscopy[J]. Review of Scientific Instruments, 2004, 75(4): 1061−1067 doi: 10.1063/1.1651637 [27] Kumar B K S. Image denoising based on Gaussian/bilateral filter and its method noise thresholding[J]. Signal, Image and Video Processing, 2013, 7(6): 1159−1172 doi: 10.1007/s11760-012-0372-7 [28] Wang Z, Tao J. A fast implementation of adaptive histogram equalization[C]//2006 8th international Conference on Signal Processing. IEEE, 2006, 2 [29] You N, Han L B, Zhu D M, et al. Research on image denoising in edge detection based on wavelet transform[J]. Applied Sciences, 2023, 13(3): 1837 doi: 10.3390/app13031837 [30] 于春伟. 电气设备噪声主动控制的研究及输出电路的设计[D]. 哈尔滨: 哈尔滨理工大学, 2008 (in Chinese) Yu C W. The study on active control of electrical equipment noice and design of output circuit[D]. Harbin: Harbin University of Science and Technology, 2008 [31] 陈华. 半导体纳米器件的噪声模型及其应用研究[D]. 西安: 西安电子科技大学, 2010 (in Chinese) Chen H. Research on noise models and their applications in Nano-scale semiconductor devices[D]. Xi’an: Xidian University, 2010 [32] 孙立书. 改进算法在混合噪声STM图像滤波中的应用[J]. 沈阳理工大学学报, 2011, 30(6): 86−91 (in Chinese) doi: 10.3969/j.issn.1003-1251.2011.06.020 Sun L S. Application of improved algorithm in filtering of STM images with mixed noise[J]. Journal of Shenyang Ligong University, 2011, 30(6): 86−91 doi: 10.3969/j.issn.1003-1251.2011.06.020 [33] LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278−2324 doi: 10.1109/5.726791 [34] Xie J X, Stavrakis S, Yao B. Automated identification of atrial fibrillation from single-lead ECGs using multi-branching ResNet[J]. Frontiers in Physiology, 2024, 15: 1362185 doi: 10.3389/fphys.2024.1362185 [35] Wang Z K, Stavrakis S, Yao B. Hierarchical deep learning with generative adversarial network for automatic cardiac diagnosis from ECG signals[J]. Computers in Biology and Medicine, 2023, 155: 106641 doi: 10.1016/j.compbiomed.2023.106641 [36] Zhang K H, Ren W Q, Luo W H, et al. Deep image deblurring: A survey[J]. International Journal of Computer Vision, 2022, 130(9): 2103−2130 doi: 10.1007/s11263-022-01633-5 [37] Min C, Wen G Q, Li B R, et al. Blind deblurring via a novel recursive deep CNN improved by wavelet transform[J]. IEEE Access, 2018, 6: 69242−69252 doi: 10.1109/ACCESS.2018.2880279 [38] Huang L Q, Xia Y S. Joint blur kernel estimation and CNN for blind image restoration[J]. Neurocomputing, 2020, 396: 324−345 doi: 10.1016/j.neucom.2018.12.083 [39] Shen Z Y, Lai W S, Xu T F, et al. Deep semantic face deblurring[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City: IEEE, 2018: 8260−8269 [40] Johnson J, Alahi A, Fei-Fei L. Perceptual losses for real-time style transfer and super-resolution[C]//14th European Conference on Computer Vision, Amsterdam: Springer, 2016: 694−711 [41] Lu B Y, Chen J C, Chellappa R. UID-GAN: unsupervised image deblurring via disentangled representations[J]. IEEE Transactions on Biometrics, Behavior, and Identity Science, 2020, 2(1): 26−39 doi: 10.1109/TBIOM.2019.2959133 [42] Zhang K H, Luo W H, Zhong Y R, et al. Deblurring by realistic blurring[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle: IEEE, 2020: 2734−2743 [43] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach: ACM, 2017: 6000−6010 [44] Zhang D Y, Liang Z W, Shao J. Joint image deblurring and super-resolution with attention dual supervised network[J]. Neurocomputing, 2020, 412: 187−196 doi: 10.1016/j.neucom.2020.05.069 [45] Nah S, Kim T H, Lee K M. Deep multi-scale convolutional neural network for dynamic scene deblurring[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu: IEEE, 2017: 257−265 [46] Kim K, Lee S, Cho S. MSSNet: multi-scale-stage network for single image deblurring[C]//European Conference on Computer Vision, Tel Aviv: Springer, 2023: 524−539 [47] Dong J X, Pan J S, Yang Z B, et al. Multi-scale residual low-pass filter network for image deblurring[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris: IEEE, 2023: 12311−12320 [48] Lu L P, Xiong Q, Xu B, et al. Mixdehazenet: Mix structure block for image dehazing network[C]//2024 International Joint Conference on Neural Networks (IJCNN). IEEE, 2024: 1−10 [49] Hu J, Shen L, Albanie S, et al. Squeeze-and-excitation networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(8): 2011−2023 doi: 10.1109/TPAMI.2019.2913372 [50] Tan M X, Le Q V. EfficientNet: Rethinking model scaling for convolutional neural networks[C]//Proceedings of the 36th International Conference on Machine Learning, Long Beach: ICML, 2019: 6105−6114 [51] Hu G X, Li J, Jing G Q, et al. Rail flaw B-scan image analysis using a hierarchical classification model[J]. International Journal of Steel Structures, 2025, 25(2): 389−401 doi: 10.1007/s13296-024-00927-3 [52] Sandler M, Howard A, Zhu M L, et al. MobileNetV2: inverted residuals and linear bottlenecks[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City: IEEE, 2018: 4510−4520 [53] Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation[C]//18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich: Springer, 2015: 234−241 [54] Hu S, Gao F, Zhou X W, et al. Hybrid convolutional and attention network for hyperspectral image denoising[J]. IEEE Geoscience and Remote Sensing Letters, 2024, 21: 5504005 [55] Guo J, Yan Z F, Zhang K, et al. Toward convolutional blind denoising of real photographs[C]//IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach: IEEE, 2019: 1712−1722 [56] Zhang K, Zuo W M, Chen Y J, et al. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142−3155 doi: 10.1109/TIP.2017.2662206 [57] Wang Y Z, Huang H B, Xu Q, et al. Practical deep raw image denoising on mobile devices[C]//16th European Conference on Computer Vision, Glasgow: Springer, 2020: 1−16 [58] Zhuo S K, Jin Z, Zou W B, et al. RIDNet: recursive information distillation network for color image denoising[C]//IEEE/CVF International Conference on Computer Vision Workshop, Seoul: IEEE, 2019: 3896−3903 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: