量子照明雷达是近年来快速发展的一种在高噪声环境下实现高灵敏探测的新型雷达技术. 其基本原理是利用量子纠缠光源产生强相关的信号光和参考光, 通过传输信号光照射目标并接收其回波, 然后与保留的参考光进行联合测量, 从而在高噪声环境下实现对目标的高灵敏探测. 量子照明雷达最初是在2008年由Lloyd^[1]在理论上提出. 2011年, Lanzagorta^[2]对量子雷达的研究状况进行了全面总结, 并从理论上将量子雷达的工作频段由光波扩展至微波、毫米波波段, 提出了量子雷达散射截面等概念. 在2013年, Lopaeva等^[3]完成了第1个量子照明雷达实验演示, 紧接着Shapiro等^[4]完成了基于量子照明的实验. 早期量子照明雷达主要集中在可见光波段, 使用连续变量纠缠高斯态. 目前这方面研究持续发展, 并积极开展大气对纠缠相干态量子雷达影响机理方面的研究^[5,6]. 2015年, Barzanjeh等^[7]提出了微波量子照明理论. 2019年苗强等^[8]对量子微波制备方法与实验研究进展进行了综述, 归纳、分析了微波单光子、纠缠微波光子以及压缩微波场和纠缠微波场的产生原理、方法和相关典型实验的进展. Barzanjeh等^[9]于2020年实现了室温下微波频段的量子照明实验, 证明其信噪比可超过传统相干雷达. 2022年Livreri等^[10]提出了一种基于约瑟夫森行波参量放大器(JTWPA)的微波量子雷达装置, 有效提高了带宽. 2023年Wei等^[11]对微波量子照明雷达的最大探测范围进行推导与分析, 同年, Borderieux等^[12]利用广义去极化量子信道研究了微波光子在大气中传播演化模型以及纠缠生存距离, 这些研究有力地促进了微波量子照明雷达的发展.

大气中微波量子照明雷达的研究, 需要分析各种大气气象环境对微波量子雷达信号传播的影响, 而对于不同大气环境(如: 降雨、沙尘、雾霾等), 其中悬浮粒子的吸收和散射引起信号的衰减需先考虑. 然而, 目前对微波量子照明雷达的研究中, 要么仅引入大气衰减常数, 要么直接忽略, 很少看到考虑不同大气气象环境对系统性能影响的研究. 例如, Lanzagorta^[13]的研究只考虑了衰减系数, 而没有考虑具体的大气条件; Borderieux等^[12]将大气看作广义去极化量子信道, 并将其与经典衰减联系起来, 但也没有考虑具体的大气环境. 为了使微波量子雷达能更有效地在不同大气环境中工作, 需开展各种大气环境对量子照明雷达性能影响的研究.

扬沙天气和沙尘暴是一种风沙灾害天气, 在干旱和半干旱的沙漠化地区常发生. 为了使量子照明雷达能几乎全天候的工作, 就需对不同能见度沙尘大气下中的带电和不带电的沙尘粒子对光子的吸收、散射进行细致研究, 以更好地开展沙尘大气对量子照明雷达性能影响的研究. 目前, 国内外关于不带电和带电沙尘大气中电磁波传播特性的研究已有不少. 相对早期, 以不带电沙尘大气中电磁波传播的研究较多^[14,15], 近年, 已逐步趋于成熟^[16,17]. 对于带电沙尘大气中的电磁波传播的研究, 近些年来还在持续增加^[18–20].

本文采用分光链路模型来描述实际大气环境, 基于Mie散射理论采用蒙特卡罗多重散射模拟方法, 对不同浓度、携带不同带电量沙尘粒子的沙尘大气对微波量子照明雷达性能的影响进行研究, 对检测误差概率、信噪比、最大探测距离等进行分析. 本研究可为微波量子照明雷达在大气中的工作状态优化提供方法和理论基础.

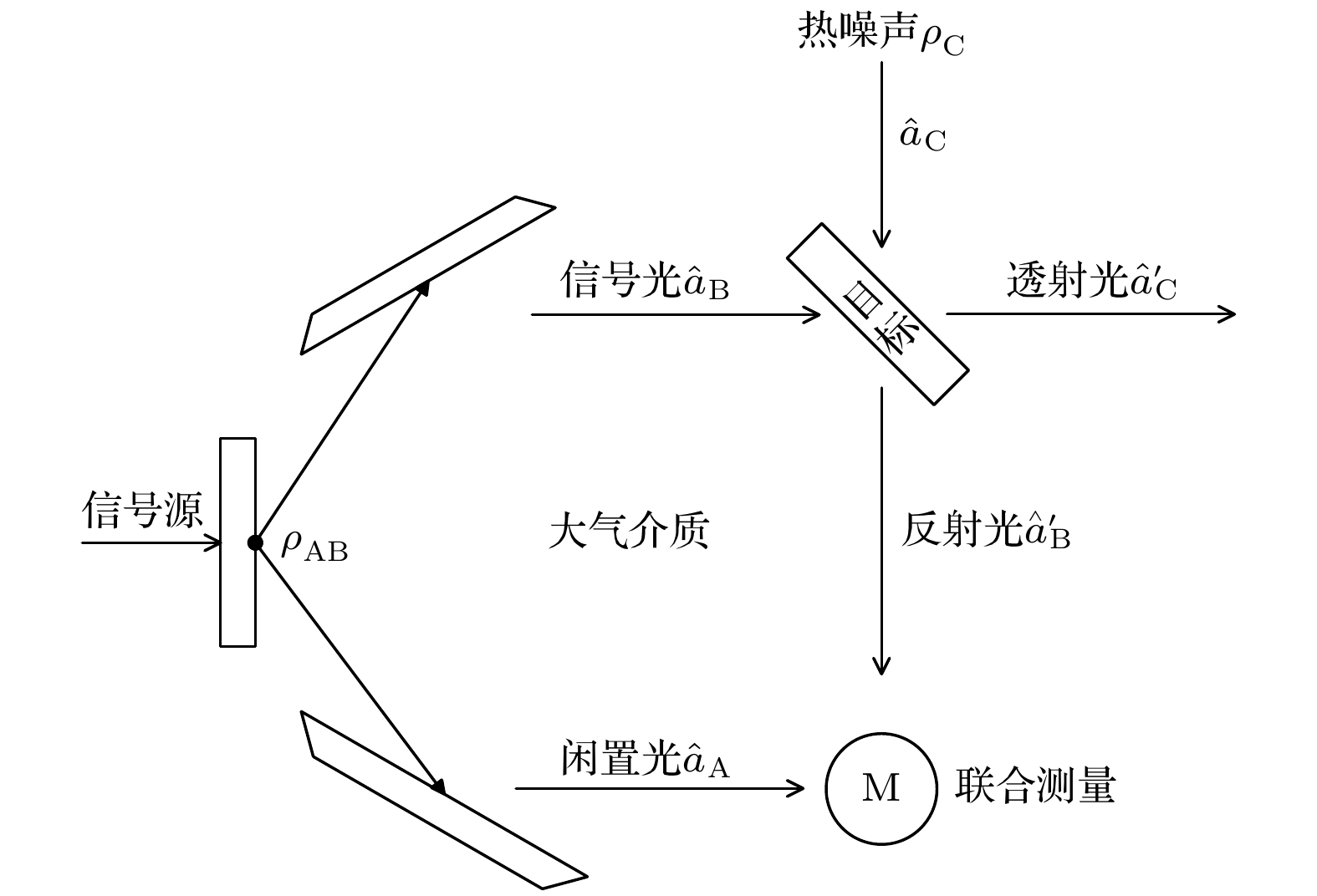
量子照明雷达系统的等效模型如图1所示, 其基本原理可以表述为: 系统发射机处的光源产生一对纠缠光子, 其密度矩阵为${{\mathbf{\rho }}_{{\text{AB}}}}$, 其中A模式为闲置光, B模式为信号光, 信号光用于探测目标物体, 若目标物体存在, 信号光会与热噪声对应的光场(密度矩阵为${{\mathbf{\rho }}_{\text{C}}}$, 平均光子数为${N_{{\text{th}}}}$)混合并与目标发生相互作用, 随后反射的光与闲置光会被进行联合测量, 若目标不存在, 则信号光丢失, 热光场与闲置光会被进行联合测量.

根据分束器理论和探测原理, 探测的目标可等效为一个分束器^[21,22], 分束器对混合光场的作用可以用分束器的幺正算符${U_{{\text{BS}}}}$来表示, 则与目标相互作用后目标处反射光的密度矩阵${\boldsymbol{\rho }}_{{\text{AB}}}^{\prime}$为

其中, ${\hat a_{\text{B}}}$和${\hat a_{\text{C}}}$分别是信号光和热光场的湮灭算符, $\xi = {\sin ^{ - 1}}\sqrt \eta $, $\eta $是目标物体的反射率.

根据量子照明雷达的原理, 在接收机处进行联合测量处可以得到两种可能的输出态${\rho _0}$和${\rho _1}$, 其表达式如下:

其中Tr是对密度矩阵求偏迹, 如果目标存在的, 在数值计算过程中需要将热噪声的平均光子数调整为$N_{{\text{th}}}^{\prime} = {N_{{\text{th}}}}/\left( {1 - R} \right)$, 以补偿混合过程中的损耗.

联合测量的目的是判断目标是否存在, 这一问题可以被等效为两个量子态${\rho _0}$和${\rho _1}$的辨识过程, 通常使用检测错误概率来评估. 最小检测错误概率可以由Helstrom极限给出^[23]:

其中$\left| {\left| \rho \right|} \right| = {\text{Tr}}\sqrt {{\rho ^\dagger }\rho } $代表着量子态$\rho $的迹范数, $N$为同时用于探测的纠缠光源拷贝数, $ {{\rho }_{0}}^{\otimes N} $表示密度矩阵$ {\boldsymbol{\rho }}_{0} $的N次张量积, 即 $ {\boldsymbol{\rho }}_{0}\otimes{\boldsymbol{\rho }}_{0} \dots \otimes {\boldsymbol{\rho }}_{0} $. 当$N$的数量较大时, 在数值计算过程中Helstrom 极限的计算复杂度呈指数上升, 为简化计算可以采用量子Chernoff边界(quantum Chernoff bound, QCB ), 又简称为QCB极限, 来衡量辨识错误概率, 它具有更松弛的上界, 但降低了计算复杂度, 其表达式如下^[24]:

其中$\mathop {{\text{min}}}\limits_{0 \leqslant t \leqslant 1} $意味着需要在0—1之间取得合适的t, 使得${\text{Tr}}\left[ {\rho _0^t\rho _1^{1 - t}} \right]$的值最小.

量子照明雷达发射的信号光子在大气中传输时, 大气环境不仅会使其产生退相干, 还会被大气中离散随机分布的粒子吸收和散射, 直接影响接收机的检测性能.

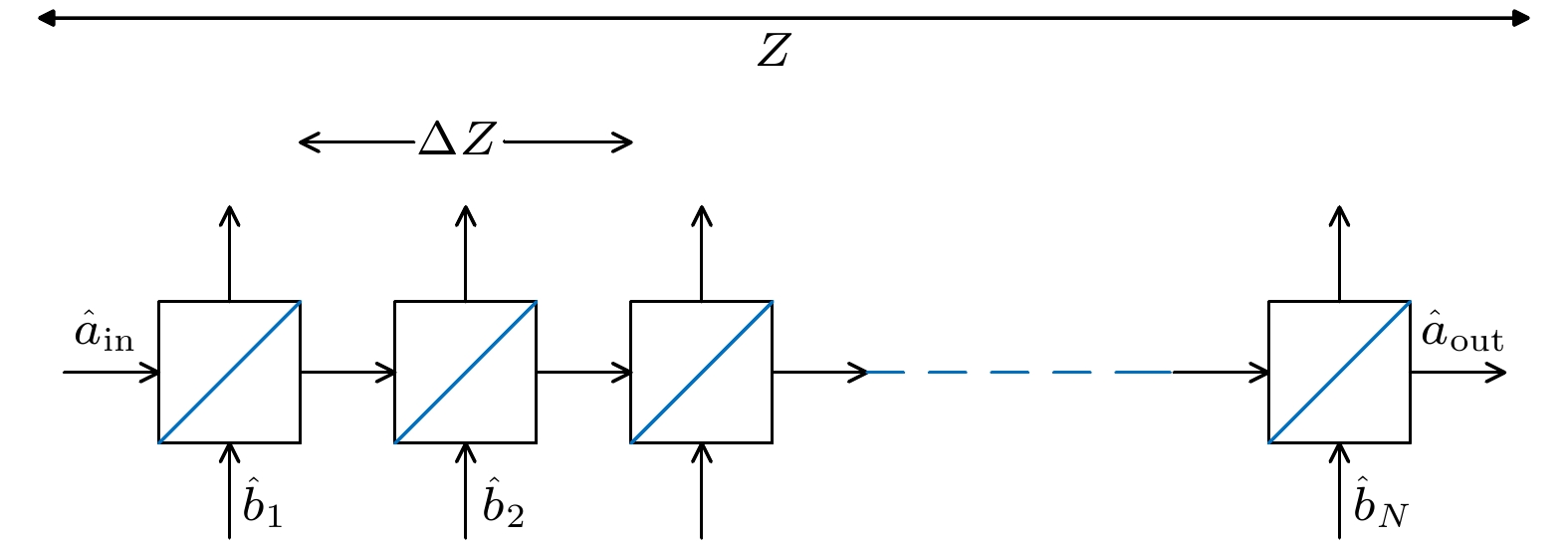
根据文献[13,25], 实际大气环境可以用分光链路来描述, 即可将其等价为连续分束器链, 如图2, 令$t = \sqrt T $, $r = \sqrt {1 - T} $, 其中$ T $为大气介质的透过率, 则通过分束器链后的湮灭算子${\hat a_{{\text{out}}}}$为

其中${\hat a_{{\text{in}}}}$为信号光对应的湮灭算子, $k$是波数, $z$是传输距离, ${b_n}\left( {n = 1, 2, \cdots , N} \right)$为热光场的湮灭算子, $N$为连续分束器的个数, $\exp ({\text{i}}k{{\Delta }}z)$为附加相位. 令$N \to \infty $, 则${{\Delta }}z \to 0$, 求极限可得

可近似写为

其中大气介质的衰减系数$X$的取值与大气离散介质的粒子尺度分布、折射率, 形状以及信号频率都有关. 在沙尘大气中微波量子照明雷达性能的研究中, 采用粒子散射Mie理论和蒙特卡罗多重散射模拟方法^[15], 计算不同能见度的带电和未带电的沙尘大气毫米波衰减系数, 并根据(9)式来分析光子传播通过不同情况下沙尘大气介质的湮灭算符变化.

信号光子遇到目标后反射回雷达接收机, 用$\eta $表示目标反射率, 考虑到大气环境的影响, 由(9)式和(10)式可求出返回接收机处的信号光子的湮灭算符表达式为

在经典雷达中雷达回波功率可表示为

其中P_t是发射功率, G_t和G_r分别是雷达发射天线和接收天线的方向性增益, $\sigma $是雷达散射截面, $\lambda $是波长, $z$是传播距离. 将发射功率用光子能量代替, 则回波功率可写为

其中${N_{\text{s}}}$是发射信号每个模式的平均光子数, $\omega $是发射信号的中心角频率, $\hbar $是约化普朗克常量, $W$是带宽, $\sigma $由经典雷达散射截面变为量子雷达散射截面.

为简化模型, 噪声源只考虑热光场产生的热噪声和量子噪声${N_{\text{q}}}$, 其中热光场每个模式的平均光子数表达式为

其中$k$为玻尔兹曼常数, $T$为温度. 则量子雷达信噪比可以写为

根据文献[10], 雷达接收机可以通过信号处理获得信噪比增益G_d, 如果将(16)式得到的信噪比称之为输入信噪比SNR_in, 那么经过信号处理得到的信噪比可以表示为输出信噪比SNR_out:

对于零均值双模高斯态, 或者说是双模压缩真空态(TMSV)信号源, 其G_d满足公式^[11]:

其中$M = W{T_{\text{d}}}$, 是信号的模式数, ${T_{\text{d}}}$是检测窗口的持续时间. 同样的对于具有相干态光源的经典TMN雷达(双模噪声雷达)^[11], 其结构与量子照明雷达相似, 两者都存在信号光与本地闲置光, 都会在接收机处对接收信号与本地闲置信号进行联合测量, 区别在于量子照明雷达会采用纠缠光子作为信号源, 而TMN雷达会采用经典的非纠缠光子作为信号源, 把(18)式中的${C_{\text{q}}}$用${C_{\text{c}}}$来替换, 且${C_{\text{c}}} = \sqrt \eta {N_{\text{S}}}$.

若雷达接收机输入的最小可检测信噪比用${\text{SN}}{{\text{R}}_{{\text{min}}}}$表示, 则根据(17)式可以得到量子照明雷达最大探测范围为^[10]

在考虑大气环境衰减时, 最大探测距离为

对于量子照明雷达, 其雷达的收机需满足以下两种条件之一就会达到最大探测范围: a)接收机达到最小可检测信噪比; b)在一个检测事件中至少可以检测到一个信号光子, 即$\eta MNS \geqslant 1$. 其中, $M = W{T_{\text{d}}}$为信号的模式数. 假设满足条件a)的最大探测范围为$z_{{\text{max}}}^{\text{a}}$, 满足条件b)的最大探测范围为$z_{{\text{max}}}^{\text{b}}$, 则最大探测范围应该取$z_{{\text{max}}}^{\text{a}}$和$z_{{\text{max}}}^{\text{b}}$中的最小值, 即${\text{min}}\left( {z_{{\text{max}}}^{\text{a}}, z_{{\text{max}}}^{\text{b}}} \right)$.

另外, 发射与接收天线的方向性增益都不能使回波信号功率大于发射信号的功率. 因此, 在讨论量子雷达方程时, 可以将雷达探测过程分为两个步骤, 其一是信号从发射机到目标的过程, 其二是信号从目标反射回接收机的过程^[11,12], 可得到如下表达式:

为了满足发射天线和接收天线的方向性增益都不能使回波信号功率大于发射信号的功率这一条件, ${\eta _1}$和${\eta _2}$需要满足${\eta _1} \leqslant 1$, ${\eta _2} \leqslant 1$. ${\eta _1} \leqslant 1$意味着$z \geqslant \displaystyle\sqrt {{{{G_{\text{t}}}\sigma \exp \left( { - Xz} \right)}}/{{\left({4{\text{π}}} \right)}}} $, 在满足这一条件的前提下如果同时满足条件a), 那么, 最大探测范围满足方程:

如果同时满足条件b), 那么, 最大探测范围满足方程:

若${\eta _1} \leqslant 1$的条件不满足, 为了保证天线方向增益不能增大信号功率, 则接收信号的最大功率被限制为${N_{\text{s}}}{G_{\text{r}}}{\lambda ^2}W\hbar \omega /\big[ {{{(4{\text{π}})}^2}{z^2}} \big]$, 若同时满足条件a), 那么, 最大探测范围满足方程:

若同时满足条件b), 那么, 最大探测范围满足方程:

综上, 量子照明雷达的最大探测范围为min{$z_{{\text{max}}}^{\left( {1} \right)}, z_{{\text{max}}}^{\left( 2 \right)}, z_{{\text{max}}}^{\left( 3 \right)}, z_{{\text{max}}}^{\left( 4 \right)}$}.

考虑到${\eta _2} \leqslant 1$, 意味着$z \geqslant \sqrt \dfrac{{{G_{\text{r}}}{\lambda ^2}\exp (-X \cdot z)}} {(4{\text{π}})}$, 按照参考文献[12], 探测范围有最小值${z_{{\text{min}}}} = {10\sqrt {{G_{\text{r}}}{\lambda ^2}\exp \left( { - X \cdot z} \right)}} /{( {{\text{4\pi }}} )}$, 只有在大于最小探 测范围时最大探测范围才有意义, 否则雷达无法 工作.

对于不同的大气气象环境(如: 沙尘、雾霾、降水), 在大气中离散随机的分布着不同尺度的粒子, 当介质的粒子浓度较低时, 可以基于Mie散射理论计算粒子的消光截面, 并根据粒子尺度分布计算电磁波在大气介质中传播的衰减. 当大气介质中粒子浓度较高时, 也就是大气能见度较低时, 光子与粒子之间会发生多次散射, 此时基于Mie理论的单次散射不能很好地反映实际多重散射情况, 就需采用蒙特卡罗(Monte Carlo, MC)模拟方法来模拟电波传播过程中粒子对光子的多次散射及对电磁波造成的衰减.

蒙特卡罗数值模拟方法是以概率和统计理论为指导的离散统计计算方法. MC方法将电磁波视为离散光子束. 光子与离散随机介质中的粒子相互作用, 要么被粒子散射, 要么被吸收, 要么从被检测介质区域中逃逸, 其中一些光子可能直接穿过介质到达接收器, 而有些光子需要经过多次散射后可能到达接收器. 对于散射光子, 在分析下一次散射时, 这种散射只与光子之前的散射状态有关, 可用马尔可夫过程来描述光子的多重散射历史状态和过程. 也就是说, 经过m次自由空间传播和被粒子散射后, 可用光子的状态序列可以构造一个样本空间, $\left\{ {{S_i}\left( {i = 1, 2, \cdots , m} \right)} \right\}$. 光子在离散随机介质中传播并被粒子散射后, 到达相空间状态点s, 该状态点由$m\left( {m = 0, 1, 2, \cdots, m} \right)$独立事件组成. 使用全概率公式, 该事件的概率可以写为

其中${P_m}$为光子在大气离散随机介质中传播或散射m次后到达相空间点s的概率. 由于光子在介质中的随机传播是一个马尔可夫过程:

(31)式中条件概率$P\left( {{s_i}/{s_{i - 1}}} \right)\left( {i = 1, 2, \cdots , n} \right)$表示光子相空间点${s_{i - 1}}$经过传播或被散射后到达相空间点${s_i}$的概率. 则估计函数可表示为

式中, $ {C}_{\text{ t}}=\rho \langle {\sigma }_{\text{ext}}\rangle $, $\left\langle {{\sigma _{{\text{ext}}}}} \right\rangle $是离散介质粒子的平均消光截面, $ \rho $是粒子数密度. 其中$\eta \left( x \right) = 1\;(x > 0)$, $\eta \left( x \right) = 0\;\left( {x \leqslant 0} \right)$. ${W_m}$为光子的生存概率权函数, 表示为

式中, ${\alpha _m}$是光子第m次散射方向与z轴的夹角, ${C_{\text{a}}} = \rho \left\langle {{\sigma _{\text{a}}}} \right\rangle $, 光子的初始权值${W_0} = 1$. 通过跟踪N个光子, 记录它们在介质中的散射路径、位置和方向, 筛选出能够到达接收面并存活下来的光子, 最终可以计算出电磁波束的透射率为

利用MC方法可以计算得到大气中的离散随机介质的透过率, 进而求得其对量子照明雷达性能的影响.

根据沙尘粒子尺度大小可将沙尘大气分为浮尘、扬尘、扬沙、及沙尘暴等. 实测表明, 大气中沙尘粒子的尺寸通常在1—300 μm之间, 对于某种类型的沙尘大气, 其中粒子尺寸的大小可用粒子尺寸分布函数来描述. 沙尘大气、颗粒之间由于互相摩擦作用通常会带电, 在不同地区、不同环境和气候条件下的沙尘天气, 沙尘粒子的带电量可有所不同, 通常沙尘粒子带电量的荷质比范围为0—300 μC/kg ^[26,27]. 本文将对35, 78和95 GHz频率的量子照明雷达在带电沙尘大气中受到的影响进行计算分析, 在不带电时沙尘粒子的复介电常数$\varepsilon $分别为: 4.0+1.3i, 3.52+0.052i, 3.69+0.053i^[28], 带电时沙尘粒子的等效复介电常数$\varepsilon '$满足$\varepsilon ' = \varepsilon - {{\text{i}}\sigma }/{\left( {\omega {\varepsilon _0}} \right)}$ ^[29], 其中$\sigma $是电导率, 电导率大小与带电量有关, $\omega $是电磁波频率, ${\varepsilon _0}$是自由空间介电常数.

描述沙尘大气中粒子尺度分布概率密度函数常有: 指数分布模型, 正态分布模型和对数正态分布模型等. 对于我国大部分沙漠地区沙尘天气的粒径分布常采用对数正态分布函数^[30], 其表达式为

其中$r$是粒子半径, $m$和$\sigma $是$ {\mathrm{ln}}(r) $的均值和标准方差, 文献[27]给出了不同类型沙尘大气的$m$和$\sigma $参数. 由于沙尘类型较多, 本文将针对扬沙大气开展研究, 其尺寸分布参数值为–7.68和0.89.

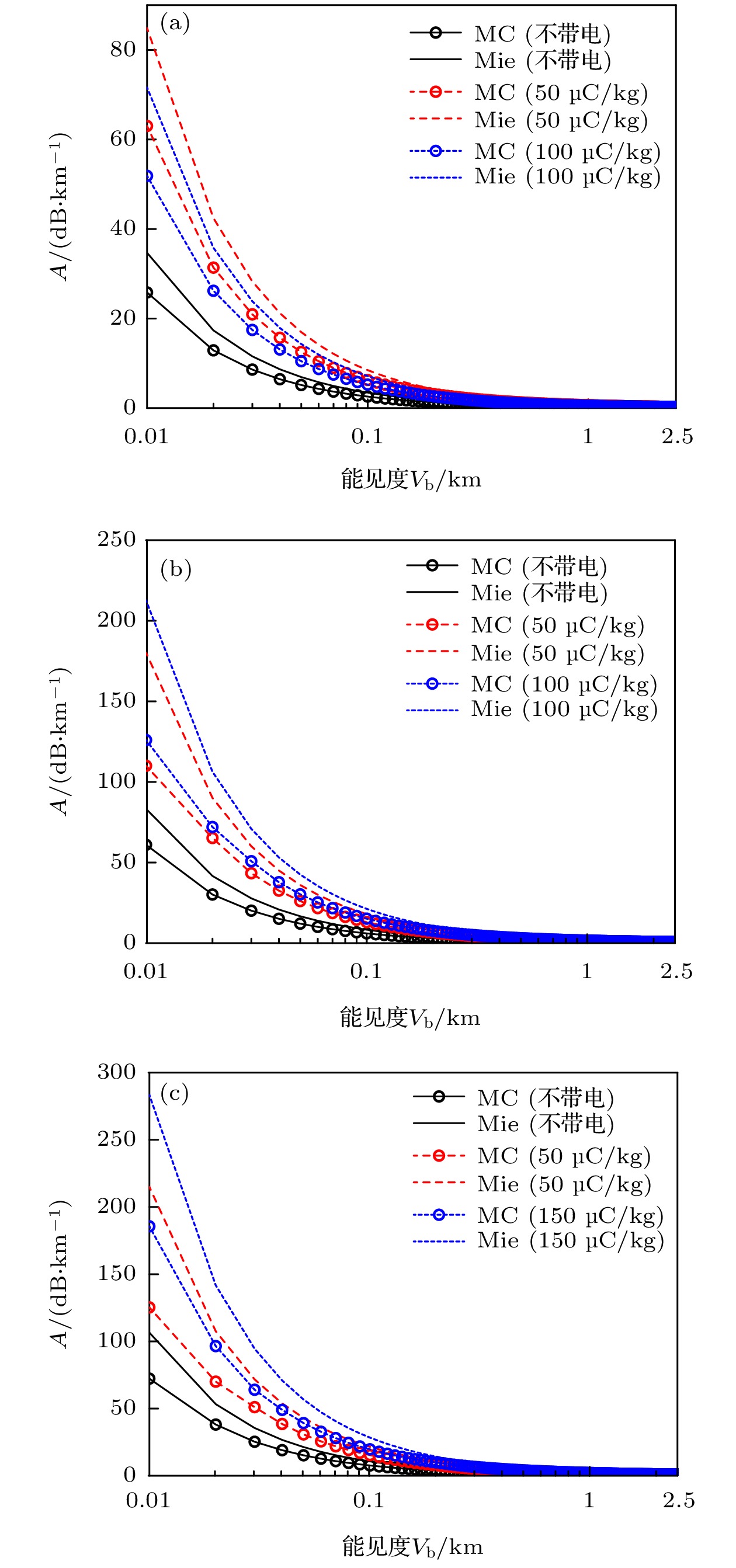
应用Mie散射理论和考虑多重散射的MC模拟方法, 分别对35, 78和95 GHz的毫米波在不同能见度和不同带电量的沙尘大气中传播的特征衰减进行计算, 如图3所示. 结果表明, 无论沙尘粒子是否带电, 通过MC模拟考虑多重散射时得到的特征衰减均比基于Mie理论得到的小, 大气能见度越小差别越大, 而随着大气能见度的增大两者差值逐渐减小. 这是由于当沙尘大气能见度较小时, 其中粒子数密度较大, 发生多次散射的概率较大; 而当能见度较大时, 粒子数密度降低, 粒子对电磁波散射的主要贡献为单次散射, 两者结果差别变小并趋于一致. 因此, 在沙尘大气能见度较小时需考虑多重散射对电磁波传播衰减的影响, 并随着频率的增大, 多重散射效应的影响越大. 对带电和不带电沙尘大气的传播衰减的比较可看出, 带电沙尘大气引起的衰减通常大于不带电沙尘大气的结果. 此外还可发现能见度和带电量相同的条件下频率越高特征衰减越大. 考虑多重散射的MC方法得到大气衰减系数更接近于实际情况.

零均值高斯态或者说是双模压缩真空态在光子数相同的情况下纠缠度较高, 且制备较容易, 因此本文选取TMSV态作为纠缠微波光源的光子态, 并与相干态(coherent state)微波光源进行对比, 双模压缩真空态在FOCK表象下的表达式如下:

其中$\lambda = \tan s$, $s$是压缩参数, 与平均光子数${N_{\text{S}}}$的关系如下:

对于相干态, 其量子态为$\left| a \right\rangle $, 在FOCK表象下的表达式如下:

相干态的平均光子数${N_{\text{S}}} = \left| {{\alpha ^2}} \right|$.

基于对带电扬沙大气环境下35, 78和95 GHz频段的毫米波衰减的计算结果, 开展带电沙尘大气对微波量子照明雷达的重要探测性能影响, 即检测错误概率, Helstrom 极限和量子Chernoff边界的分析研究, 所需参数如表1所示.

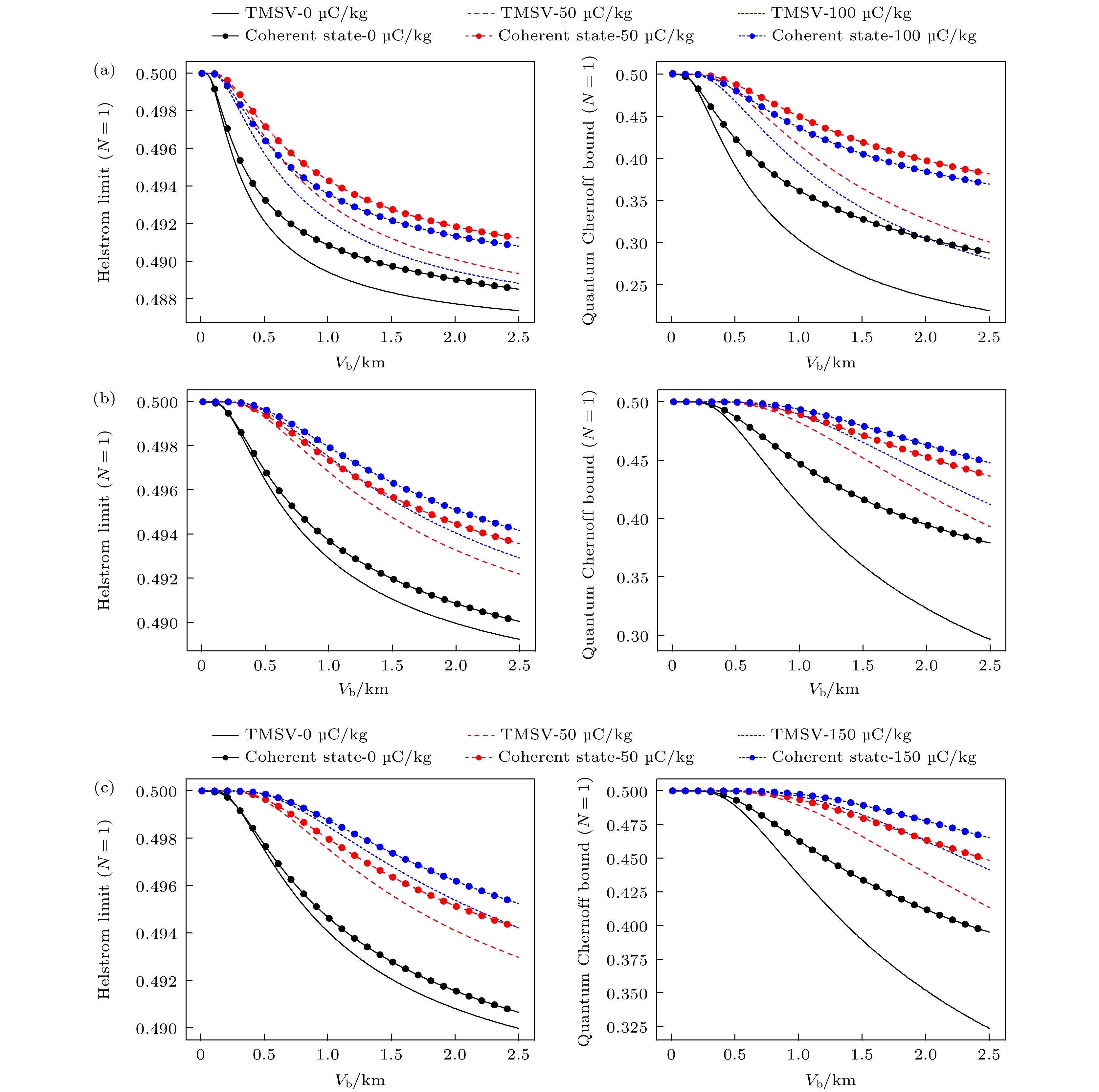
根据(5)式、(6)式及表1中仿真参数值, 可得到微波量子照明雷达在带电沙尘大气环境下最小检测错误概率以及量子Chernoff界, 即Helstrom极限和QCB (单位: ${10^{ - 3}} + 0.4995$), 其中最大截断维度${n_{{\text{max}}}}$是利用QuTip库在数值仿真过程中对量子态的截断维度, 结果如图4.

根据图4可得, 在相同条件下随着能见度的增大, Helstrom极限和QCB都呈现递减趋势, 这表明微波量子照明雷达的检测错误概率随着沙尘大气衰减系数的减小而不断减小. 能见度越大、衰减系数越小则对微波量子照明雷达的性能影响越小. 对比相同条件下Helstrom极限和QCB可以看出, 相同能见度下Helstrom极限小于QCB, 说明用Helstrom极限能更好地表征辨识误差概率.

通过对比不同荷质比的结果, 可以得出: 荷质比大小对应的沙尘大气衰减越大, 则对应的Helstrom极限和QCB也越大; 反之, 结果相反.

对比信号源光子态为双模压缩真空态与相干态的结果, 当沙尘荷质比相同且能见度相同时, TMSV光源得到的Helstrom极限和QCB极限明显小于相干态光源得到的检测错误概率. 这表明纠缠光子作为信号源性能更好, 体现出量子照明雷达的优势.

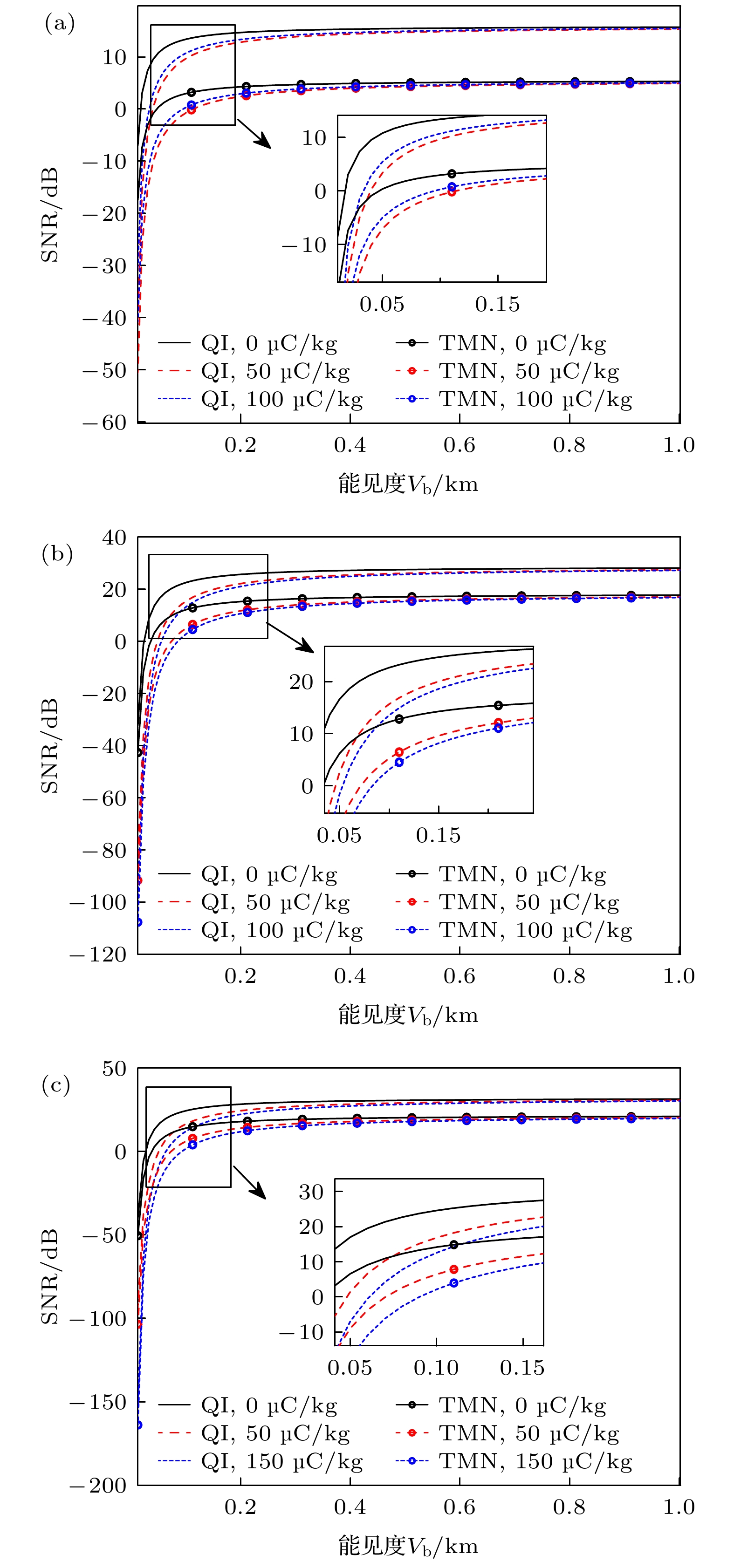
应用(17)式进行带电沙尘大气环境对量子照明雷达(QI)和经典双模噪声(TMN)雷达的输出信噪比的影响进行分析, 计算需参数见表2, 结果如图5所示. 从图5可看出, 随着能见度的不断增大, 两种雷达的输出信噪比不断增大, 并最终趋于一个稳定的值. 在相同条件下量子照明雷达的输出信噪比高于经典雷达, 这是因为在信号源每个模式的平均光子数为0.1的情况下, 量子照明雷达的信噪比增益要远大于经典TMN雷达.

对比不同频率下的信噪比, 可以看出在低能见度下35 ${\text{GHz}}$信号源的雷达信噪比最大, 95 ${\text{GHz}}$的最小, 随着能见度的增大, 35 ${\text{GHz}}$信号源的雷达信噪比反而变得最小, 而95 ${\text{GHz}}$的变得最大. 这一现象产生的原因是提高频率可以增强信噪比, 但也会导致带电沙尘大气环境的衰减加剧, 在低能见度下, 频率提升导致的特征衰减的增大超过了信噪比的提升, 因此, 高频率信号的信噪比反而较低; 相反, 在高能见度下, 频率提升带来的特征衰减的增大小于信噪比的提升, 这意味着高频率信号具有更高的信噪比. 对比沙尘不同带电量情况下信噪比的差异, 可以看出沙尘带电量对应的衰减效应越大则信噪比越小.

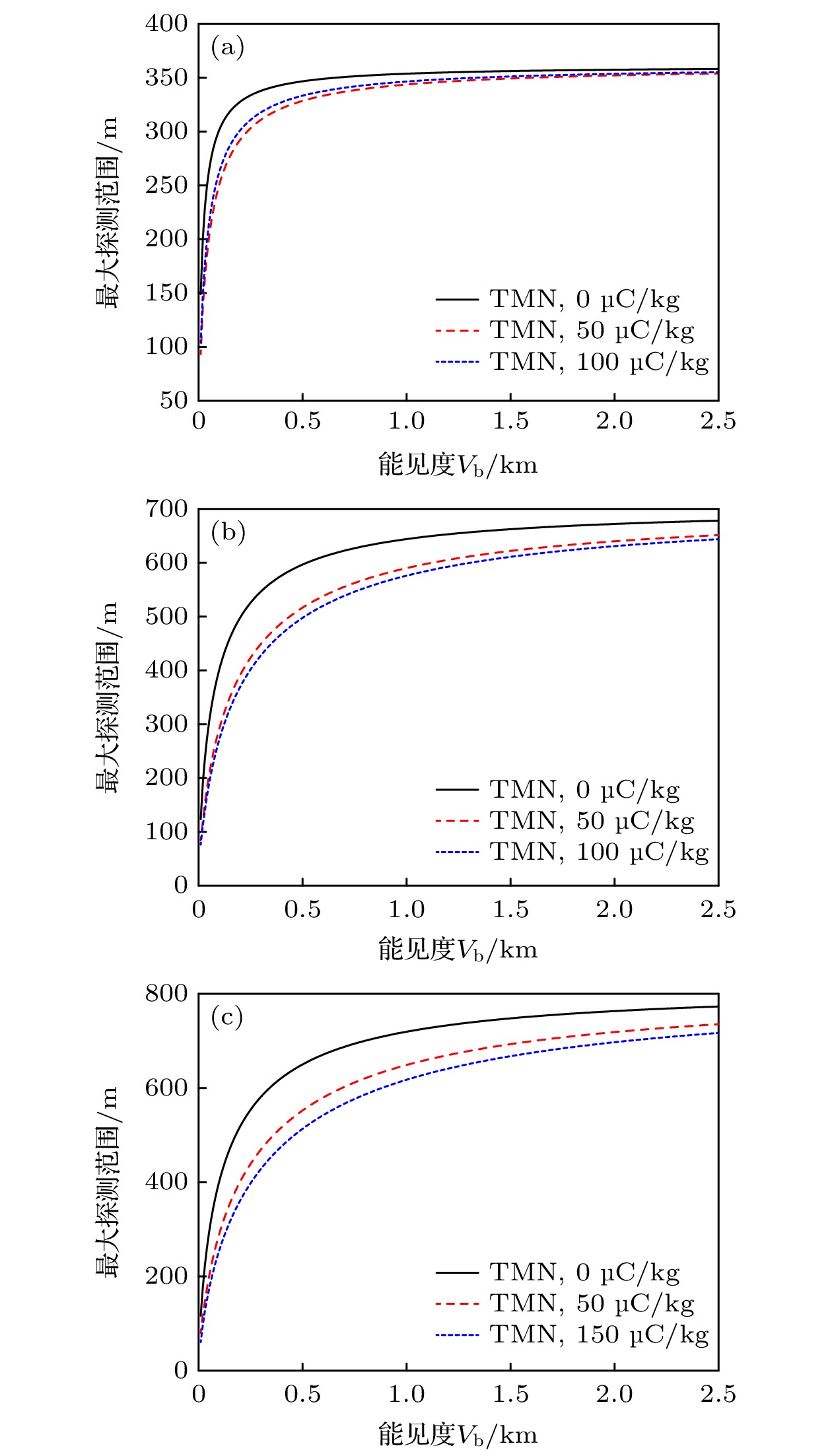
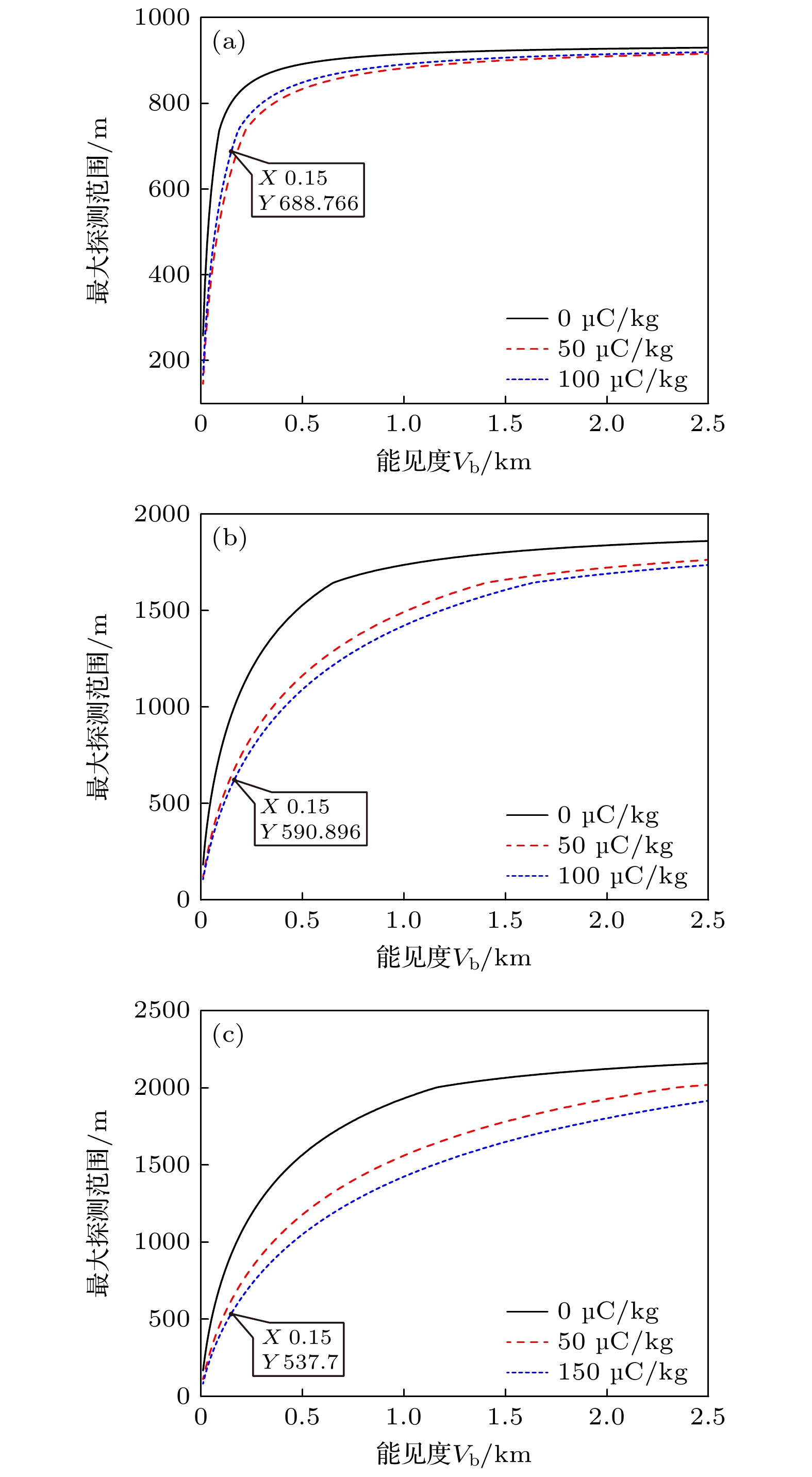
根据量子照明雷达最大探测范围理论, 对带电沙尘环境下的量子照明雷达的最大探测范围进行计算, 并以TMN雷达的性能进行比较分析. 设最小可检测信噪比${\text{SN}}{{\text{R}}_{{\text{min}}}} = 5 {\text{dB}}$, 其余参数如表2, 仿真计算结果如图6与图7所示.

从图6可看出, 随着沙尘大气能见度的增大, 量子照明雷达的最大探测范围不断增大, 最后趋向于某个值. 对于35 ${\text{GHz}}$的信号当带电量为0 ${\text{μC/kg}}$时最大探测范围最大, 50${\text{μC/kg}}$时最大探测范围最小, 78 ${\text{GHz}}$和95 ${\text{GHz}}$的信号随着带电量的增大最大探测范围不断减小, 这与沙尘衰减随带电量变化一致.

对于不同频率, 可看出能见度在2.5 km时, 频率越高的信号最大探测范围越大, 但当能见度较低时, 如0.15 km时35 GHz的信号源的最大探测范围最大, 95 GHz的信号源的最大探测范围最小, 这表明高能见度下提高频率可以显著提高最大探测范围, 但在低能见度下低频率信号的最大探测范围更大, 这是因为信号频率越高大气环境产生的衰减影响越大, 在低能见度下尤为明显, 这种衰减影响抵消掉频率提高带来的探测范围增大. 这表明需要合适选择参数来达到较优效果.

对于TMN雷达的探测范围的计算结果如图7所示, 其规律与图6的基本一致. 对比图6和图7, 可以看出相同条件下量子照明雷达的最大探测范围要明显优于TMN雷达的, 这体现出量子雷达的优势.

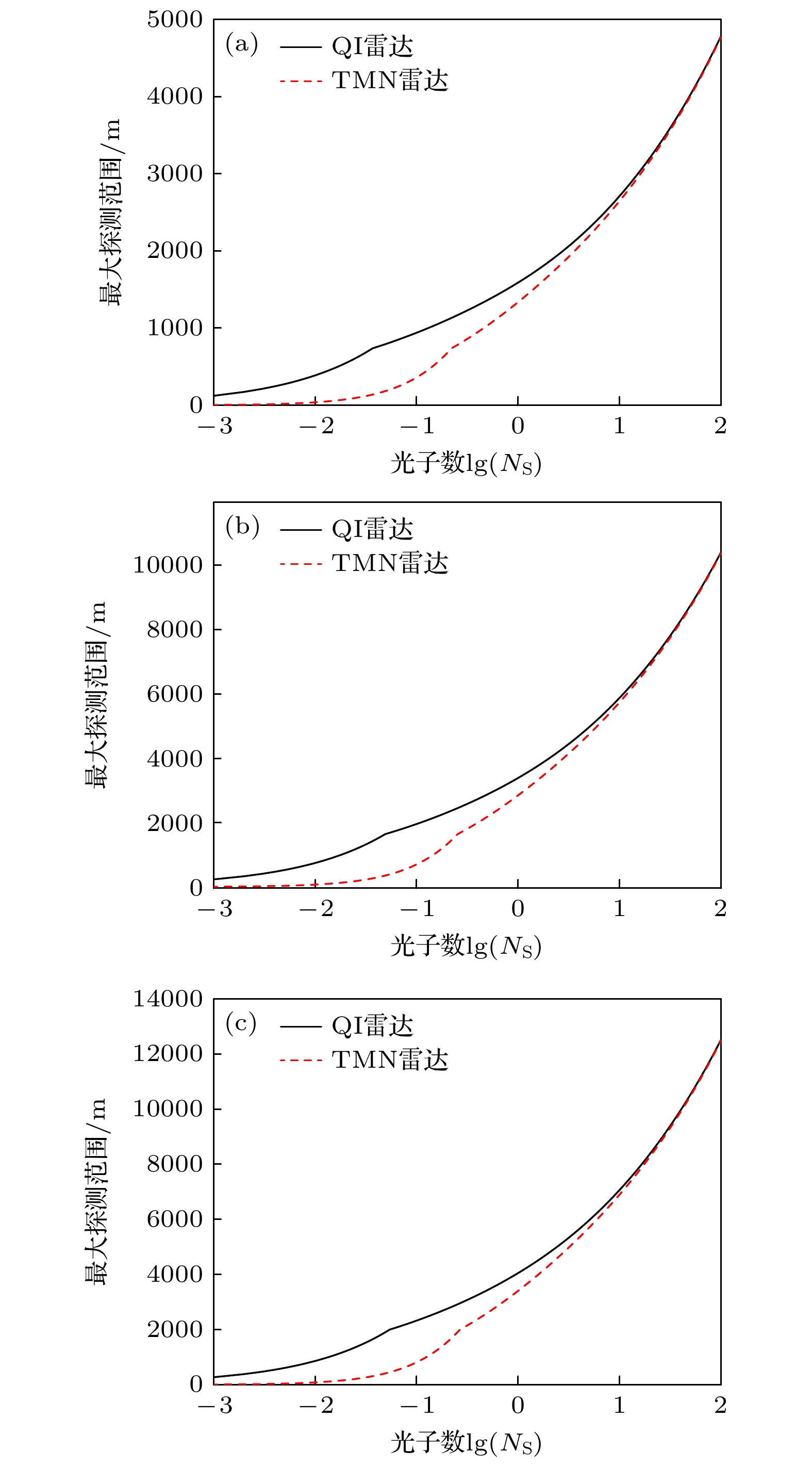
另外, 仿真研究了发射信号平均光子数对微波量子照明雷达和TMN雷达探测范围的影响, 计算结果如图8所示, 可以看出随着光子数的增大, 两种雷达的探测范围都逐渐增大, 在光子数较低时, 量子照明雷达的探测范围明显优于TMN雷达, 随着光子数增大, 两种雷达的最大探测范围逐渐一致, 这表明随着光子数增大量子照明雷达的优势逐渐消失, 该结论同样适用于信噪比和检测错误概率. 除此之外, 可看到TMN雷达在光子数较低时, 存在一段区域最大探测范围为几乎为0, 这是因为在这一段区域内最大探测范围已经小于雷达的最小探测范围, 所以TMN雷达已经不能正常工作.

为了使微波量子照明雷达在沙尘大气环境下能更好地发挥作用, 基于Mie散射理论和考虑多重散射的Mc方法模拟了35, 78和95${\text{GHz}}$信号沙尘大气衰减, 应用微波量子照明雷达的理论, 研究了不同能见度、不同带电量的沙尘大气对微波量子照明雷达探测性能的影响, 包括检测错误概率、信噪比和最大探测范围等性能指标参数, 并与TMN雷达性能进行对比分析. 结果表明: 在带电沙尘大气环境下, 即当能见度和带电量不变时, 适当改变量子照明雷达的部分参数, 可以使其达到更佳工作状态. 如果不考虑频率对雷达模式数的影响, 那么频率增大会因为衰减增大而使得量子照明雷达的性能降低. 如果考虑频率对模式数的影响, 即雷达接收机具有相对带宽, 那么在能见度较高时, 适当的提高信号频率可以通过增大模式数来提高量子照明雷达的性能. 当能见度极低时, 频率提高带来的增益会小于衰减增大带来的性能下降, 这种情况不宜增大频率. 此外, 适当的增大发射信号的平均光子数也可以提高量子照明雷达的性能, 但随着光子数的增大, 量子照明雷达相比经典雷达得到的增益会逐渐减小, 从而丧失纠缠信号带来的优势, 那么, 发射信号的平均光子数需要根据不同的大气气象环境做相应的选择, 因此, 对于不同大气气象条件对量子照明雷达影响的研究势在必行, 且需要更加广泛深入地开展.