非线性动力学领域的研究工作一直致力于从有限数据中提取复杂非线性系统的特征. 精确地表征不同系统的特征对于后续的识别、分类和检测工作至关重要^[1-4]. 传统的研究方案是通过单通道的一维数据对系统隐含的非线性动力学特性进行表征^[5-7]. 例如, 针对一个n维的复杂非线性系统, 利用相空间重构将一维的数据映射到高维. 在高维空间中, 观察吸引子结构, 分析相空间中轨线的运动规律, 计算该系统诸如李雅普诺夫指数、分形维数、熵等非线性特征量^[8]. 从而揭示出该系统隐含的非线性动力学特性. 可以看出, 传统的非线性动力学研究都是利用单变量的观测数据提取复杂系统的非线性动力学特征. 这种研究思路的优点在于对先验信息的要求较少. 但这种研究方法的缺点是无法完整、精确地描述系统的动力学特性.

相比于单通道数据, 利用多个传感器同时采集的多通道数据可以为非线性动力学系统的分析提供额外信息^[9,10]. 例如, 在水声信号处理领域, 阵列采集的多通道数据可提高特定方向上的信噪比^[11,12]. 从复杂系统的多通道数据中提取不同的特征向量, 可以有效地帮助神经网络、深度学习和支持向量机对不同的系统进行分类识别^[13,14]. 在非线性动力学研究领域中, 像李雅普诺夫指数、分形维数、熵等经典非线性特征量通常只适用于一维时间序列(单通道数据). 针对多通道数据, 也只能分别计算每一个通道对应的非线性特征量. 这样的处理方式忽略了通道之间的内在联系, 浪费了大量的有效信息.

作为一种经典的非线性特征量, 熵被广泛应用于机械故障诊断、水声信号分类识别、病理信号诊断等领域^[15-17]. 经过学者们的不断改进, 熵算法衍生出许多的分支. 如近似熵(approximate entropy, AE)^[18]、样本熵(sample entropy, SE)^[19]、排列熵(permutation entropy, PE)^[20]、多尺度样本熵(multiscale sample entropy, MSE)等^[21]. 熵算法具有适用性强、计算量相对较小等优点. 不同的熵算法从不同的角度对给定一维数据的复杂度进行了表征. 在实际应用中, 可以根据需要选取不同的熵算法提取目标信号的复杂度特征. 然而, 现有的熵算法都只能处理单通道数据, 无法直接用来提取多通道数据的复杂度信息.

近年来, Ahmed和Mandic^[22]将多尺度样本熵算法中的计算步骤进行了升维处理并提出了多通道多尺度样本熵算法(multivariate multiscale sample entropy, MMSE). 该算法可以直接处理多通道数据, 提取多通道数据的复杂度信息. 然而, 在将嵌入维数从m增加到$ m+1 $并重构出对应的$ (m+1) $维相空间时, Ahmed和Mandic发现MMSE算法无法在这一个计算步骤中得到一个确定的$ (m+1) $维相空间. 为此, Ahmed和Mandic提出了两种不同的多通道多尺度样本熵算法, 分别是朴素多通道多尺度样本熵算法(naive MMSE)和严格多通道多尺度样本熵算法(rigorous MMSE). 朴素多通道多尺度样本熵算法单独计算了每一种可能的$ (m+1) $维相空间中对应的概率, 并将所有可能出现的$ (m+1) $维相空间对应的概率求和取平均得到最终需要的概率. 而严格多通道多尺度样本熵算法将所有可能的$ (m+1) $维相空间合并, 在合并后的相空间中计算出最终需要的概率. 通过仿真研究, Ahmed和Mandic认为严格算法是优于朴素算法的. 因为严格算法可以提取不同通道之间的相关性信息. 需要注意的是, 采用严格多通道多尺度样本熵算法计算多通道数据的复杂度时, 隶属于不同通道的样本点之间的相似性也会对结果产生影响. 而不同通道间数据计算相似性对结果产生的影响是不确定的: 一方面, 在计算熵值时考虑不同通道的样本点之间的相似性可能给严格多通道多尺度样本熵算法带来了提取通道间的相关性信息的能力; 另一方面, 在实际应用中, 不同通道之间数据的相关性是无法确定的. 盲目地计算不同通道之间样本点的相似性可能使最终结果出现偏差. Ahmed和Mandic直观地认为在算法中考虑不同通道之间样本点的相似性可以提升算法的性能, 使算法可以提取通道间的相关性信息.

除此之外, 多通道多尺度样本熵算法的理论证明并不充分. 在将多尺度样本熵升维处理时, 事实上是有很多不同的升维策略的. 现有的研究中没有对所有的策略进行充分完整的讨论, 而是直接将多通道多尺度样本熵算法与其他诸如模态分解等技术结合并应用于故障诊断等领域^[23,24]. 因此, 有必要对可能的策略进行全面的分析和讨论, 使多通道熵算法的理论更加可靠和完整. 本文从单通道熵算法MSE的核心思想出发, 分析了MSE算法的升维过程. 通过理论研究, 证明了严格多通道多尺度样本熵和朴素多通道多尺度样本熵都不是MSE算法在多通道情况下的精确推广. 基于以上的理论分析, 提出了一种无偏差的多通道多尺度样本熵算法(UMMSE). 通过理论证明与仿真实验, 证明了计算不同通道间样本点的相似性不能给算法带来提取通道间相关性信息的能力. 也就是说, 使用严格算法将得到一个有偏差的熵结果.

本文后续的结构如下: 第2节介绍无偏差的多通道多尺度样本熵算法; 第3节对无偏差的多通道多尺度样本熵算法、naive MMSE以及rigorous MMSE算法升维过程中的策略进行分析讨论; 第4节利用不同的仿真实验证明改进后算法优于原始多通道多尺度样本熵算法; 最后第5节给出结论.

Ahmed和Mandic等^[22]于2011年提出MMSE算法. 该算法成功地将一种仅适用于一维数据的熵算法拓展到了多维情形. 虽然仿真实验和实际数据处理的结果证明了该算法是一种有效的复杂度度量方法, 并且可以有效地提取通道内和通道间的相关性信息. 但是, 至今没有学者对该算法进行严格的推导与证明. Ahmed和Mandic^[22]没有从根本上解决MMSE算法存在的问题, 而是提出了两种子算法(严格算法以及朴素算法)来弥补MMSE算法存在的缺陷.

针对MMSE算法存在的问题, 本文进行了改进并提出无偏差的多通道多尺度样本熵算法. 该算法由以下步骤组成.

1) 给定多通道数据$ \{x_{i, j}\}, 1 \leqslant i \leqslant N, 1 \leqslant j \leqslant p $. 其中, N表示每个通道内的样本点数, p表示通道数. 为了消除不同通道间的幅值差异对结果产生的影响, 对各个通道进行归一化处理.

2) 在归一化处理后, 利用下式将每一个通道分别进行粗粒化处理:

其中, n表示尺度因子, $ N_{n} = \left\lfloor {\dfrac{N}{n}} \right\rfloor $表示$ \dfrac{N}{n} $向下取整. 对于每一个通道来说, 粗粒化过程将原本的时间序列$ \{x_{i, j}\} $分割成了$ N_{n} $个子序列, 并将每一段子序列求和取平均得到新的序列$ \{y_{i, j}^{(n)}\} $. 注意当尺度因子$ n = 1 $时, $ \{y_{i, j}^{(n)}\} = \{x_{i, j}\} $.

步骤1) 和2) 与后续的熵算法相互独立, 因此在下文介绍改进多通道样本熵算法时, 省略了尺度因子角标n, 用$ \{y_{i, j}\} $表示经过粗粒化处理后的多通道数据.

3) 得到$ \{y_{i, j}\} $后, 进行相空间重构^[25-27]:

式中, i是M维相空间中各个向量的索引角标; $ {\boldsymbol{M}} = [m_1,\; m_2,\; \cdots, \;m_p]\in \mathbb{R}^{p} $表示嵌入维数向量; $ {\boldsymbol{\tau}} = [\tau_1, \;\tau_2, \;\cdots,\; \tau_p]\in \mathbb{R}^{p} $表示的是时间延迟向量; $ M = \displaystyle\sum\nolimits_{i = 1}^{p}m_{i} $. 在重构出的M维相空间中共有q个向量.

4) 在利用(2)式重构出M维相空间后, 计算出相空间中任意两个不同向量之间的切比雪夫距离. 计算$ r\cdot {\mathrm{tr}}({\boldsymbol{S}}) $作为阈值, 其中r是需要事先给定的系数, $ {\mathrm{tr}}({\boldsymbol{S}}) $是多通道数据协方差矩阵$ {\boldsymbol{S}} $的迹. 在定义好距离并设置好阈值后, 针对M维相空间中的任意一个向量$ {\boldsymbol{Y}}_{M}(i) $, 就可以统计出在M维相空间中与其距离小于给定阈值的向量个数, 记为$ C^{M}_{i}(r) $. 当两个向量之间的距离小于阈值时, 称这两个向量相似.

5) 根据下式计算出相应的$ B^{M}_{i}(r) $:

$ B^{M}_{i}(r) $表示的是M维相空间中的其余向量与向量$ {\boldsymbol{Y}}_{M}(i) $之间的距离小于阈值的概率.

6) 遍历相空间中的所有向量, 将对应的$ B^{M}_{i}(r) $求和取平均, 求出

7) 得到$ B^{M}(r) $后, 增加嵌入维数使其从$ {\boldsymbol{M}} = [m_1, m_2, \cdots, m_p] $变为$ {\boldsymbol{M}} + p = [m_{1}+1, m_{2}+1, \cdots, m_{p}+1] $. 根据新的嵌入维数, 重复步骤3)—6), 重构出对应的$ (M+p) $维相空间并计算出对应的$ C^{M+p}_{i}(r) $, $ B^{M+p}_{i}(r) $和$ B^{M+p}(r) $.

8) 最后, 求出无偏差的多通道多尺度样本熵结果:

无偏差的多通道多尺度样本熵算法实现了对多通道数据复杂度的估计. 一方面, 该算法是MSE算法在多维情况下的准确推广. 另一方面, 与MSE算法相比, 由于无偏差的多通道多尺度样本熵算法同时涉及了所有的通道, 因此也可以揭示不同通道之间的相关性信息.

为了更好地对不同算法进行对比, 本文在这里对Ahmed和Mandic^[22]提出的多通道多尺度样本熵算法进行介绍. 其中包含朴素和严格两种算法. 步骤1)—6)与无偏差的多通道多尺度样本熵算法相同. 为了与无偏差的多通道多尺度样本熵区分, MMSE的后续步骤编号会增加星号角标.

7^*) 在得到$ B^{M}(r) $后, 增加嵌入维数使嵌入维数向量各元素之和从M变为$ M+1 $. 当通道个 数为p时, 就会有p种可能的情况, 相应地可以重构出p种可能的$ (M+1) $维相空间. 由于生成的$ (M+ 1) $维相空间不唯一, 因此不能直接套用步骤4)—6)计算出相应的$ B^{M+1}(r) $. 下面将分别介绍朴素算法与严格算法.

朴素的多通道多尺度样本熵算法　针对每一个可能的$ (M+1) $维相空间, 重复步骤4)—6)计算出对应的概率, 在这里用$ B^{{M+1}_{i}}(r) $表示第i个通道的嵌入维数增加1后重构的$ (M+1) $维相空间对应的概率, 其中$ 1\leqslant i \leqslant p $. 对p个$ B^{{M+1}_{i}}(r) $求和取平均, 得到最终的$ B^{M+1}(r) $.

严格的多通道多尺度样本熵算法　现有p种可能的$ (M+1) $维相空间, 每一个相空间中有$ q' $个向量, 则共有$ pq' $个向量. 针对所有的向量, 重复步骤4)—6)计算得到最终的$ B^{M+1}(r) $.

则根据(6)式即可计算出朴素的和严格的多通道多尺度样本熵结果:

Ahmed和Mandic^[22]提出的多通道多尺度样本熵算法可以直接处理多通道数据, 对多通道数据的复杂度进行表征. 但是在对算法进行升维时, 由于没有合理地增加嵌入维数导致无法重构出一个确定的相空间. 因此, Ahmed和Mandic^[22]提出了朴素算法和严格算法. 经过分析发现, 不同通道之间数据点的相似性也会对严格算法的结果产生影响. 利用仿真实验对比不同方法的性能, Ahmed和Mandic发现严格算法可以提取多通道数据通道间的相关性信息. 因此他们得出结论, 认为严格算法是优于朴素算法的.

事实上, 不论是严格算法还是朴素算法都缺乏相应的理论支撑. 不同通道的数据之间计算相似性会使熵结果不稳定. 而算法提取通道间相关性信息的能力并不是由不同通道之间数据计算相似性带来的. 本文将从概率论的角度出发, 对无偏差的多通道多尺度样本熵算法、朴素算法和严格算法进行分析.

无论是Ahmed和Mandic^[22]提出的多通道多尺度样本熵算法还是本文提出的无偏差的多通道多尺度样本熵算法, 其本质上都是多尺度样本熵算法在多通道数据情况下的推广. 因此, 本文将先对算法中涉及的不同事件进行定义, 再依次分析多尺度样本熵、朴素算法、严格算法、及无偏差的多通道多尺度样本熵算法. 证明无偏差的多通道多尺度样本熵算法的优越性. 在算法分析与证明这一部分中, 以两通道数据为例分析多通道情况下的多通道多尺度样本熵算法和无偏差的多通道多尺度样本熵算法. 在分析单通道情况下的多尺度样本熵算法时, 使用第一个通道的数据进行分析(选择任意通道均不影响后续的分析与证明). 多尺度样本熵的其余计算参数也不需要专门进行设定, 使用多通道熵算法中参数的第一个分量即可. 由于粗粒化与归一化作为预处理步骤与后续的熵算法步骤独立, 因此在这里省略了步骤1)和2), 等效为仅讨论在尺度为1时的情况.

给定两通道数据$ \{x_{i, j}\},\; i = 1,\cdots, N; j = 1, 2 $. 每个通道内包含N个样本点. 嵌入维数与时间延迟分别为$ {\boldsymbol{M}} = [m_{1}, m_{2}] $和$ {\boldsymbol{\tau}} = [\tau_1, \tau_2] $. 表1列举了算法涉及的事件以及对应的表示符号.

在单通道情况下, 多尺度样本熵算法根据给定的嵌入维数$ m_1 $和时间延迟$ \tau_1 $可以重构出一个确定的$ m_1 $维相空间. 与无偏差的多通道多尺度样本熵算法类似, 在计算样本熵时, 需要先计算嵌入维数为$ m_1 $时对应的$ B^{m_1}(r) $, 再计算嵌入维数增加到$ m_1+1 $时对应的$ B^{m_1+1}(r) $. 在得到$ B^{m_1}(r) $与$ B^{m_1+1}(r) $后, 计算$ B^{m_1+1}(r)/B^{m_1}(r) $的负自然对数. 推广到多通道的情况, 在改变嵌入维数时每一个通道的嵌入维数增量应该保证不大于1. 根据最初给定的嵌入维数$ {\boldsymbol{M}} = [m_{1}, m_{2}] $可以重构出一个确定的M维相空间($ M = \displaystyle\sum\nolimits_{i = 1}^{p}m_{i} $), 并计算得到对应的$ B^{M}(r) $. 当增加嵌入维数时, 朴素算法与严格算法将嵌入维数之和从M增加到$ M+1 $. 而无偏差的多通道多尺度样本熵算法将嵌入维数之和从M增加到$ M+p $(在这里, $ p = 2 $). 对于不同的嵌入维数增加策略, 重构出对应的相空间并计算对应的$ B^{M+i}(r) $, $ i = 1,\; 2 $. 表2列出了不同的嵌入维数与$ B^{M+i}(r) $, $ i = 0,\; 1,\; 2 $所对应的事件.

在对本文涉及的所有熵算法中包含的事件进行定义后, 下面利用上述事件及其概率分别分析多尺度样本熵算法、朴素算法、严格算法、以及无偏差的多通道多尺度样本熵算法.

在多尺度样本熵算法中, 当嵌入维数为$ m_1 $时, 算法中的$ B^{m_1}(r) $可以等效为事件A的概率. 当嵌入维数增加到$ m_1+1 $时, 对应的$ B^{m_1+1}(r) $可以等效为事件A与事件C的联合概率. 因此, 最终的结果即可以用概率表示为$ P( {\rm{AC}} )/P( {\rm{A}} ) = P( {\rm{C}} | {\rm{A}} ) $. 可以看出, 多尺度样本熵本质上计算了在特定时间尺度下, 当一段长度为$ m_1 $的子序列在增加一个样本点后依然保持相似的条件概率的负自然对数.

接下来对Ahmed和Mandic^[22]提出的多通道多尺度样本熵算法进行分析. 由于在算法中使用的策略是将嵌入维数增加到$ M+1 $, 从表2 可以看到会有两种可能出现的嵌入维数结果. 这就是Ahmed和Mandic必须提出朴素算法与严格算法的原因. 因为没有一个适用的标准来选择一个确定的嵌入维数, 导致后续重构相空间时也会出现两种可能的$ (M+1) $维相空间.

朴素算法需要分别计算每一种可能的$ (M+1) $维相空间对应的$ B^{(M+1)_{i}} $. 例如, 当嵌入维数为$ [m_{1}+1, m_{2}] $时, 对应的$ B^{(M+1)_{1}} $即为事件ABC的联合概率. 本文使用$ B^{(M+1)_{i}} $来表示第i个通道的嵌入维数增加1以后计算得到的概率. 那么, 经过计算得到的最终的$ B^{M+1}(r) $即可以用概率表示为

结合(7)式与表2中的结果, 可以得到朴素算法的概率表示:

从概率论的角度对(8)式进行分析, 可以看出朴素算法本质上计算的依然是条件概率均值的负自然对数. 并且需要注意的是, (8)式中的条件概率, 分别只考虑了某一个特定的通道. 并没有出现类似于$ P( {\rm{CD}} | {\rm{AB}} ) $这样同时考虑所有通道的条件概率.

对于严格算法, 在计算最终的$ B^{M+1}(r) $时同时考虑了所有可能出现的$ (M+1) $维相空间. 为了便于理解, 这里对参数进行赋值. 给定每个通道的数据长度为$ N = 4 $, $ {\boldsymbol{M}} = [2, 2] $, $ {\boldsymbol{\tau}} = [1, 1] $, $ r = 0.15 $, 先重构出对应的M维相空间. 重构出的相空间如(9)式所示:

根据(9)式中的向量$ {\boldsymbol{X}}_{M}(i), 1\leqslant i\leqslant 3 $和系数r, 可以计算出对应的联合概率$ B^{M}(r) = P( {\rm{AB}} ) $. 当增加嵌入维数时, 会出现两种可能的结果. 分别是$ {\boldsymbol{M}}_{1} = [3, 2] $和$ {\boldsymbol{M}}_{2} = [2, 3] $. 相应地可以重构出两种不同的$ M+1 $维相空间. 这里使用$ \mathbb{V}_{1} $和$ \mathbb{V}_{2} $分别表示两种可能的$ (M+1) $维相空间. 严格算法将两种可能的相空间合并, 结果如(10)式所示:

其中, $ {\boldsymbol{X}}_{M}^{k}(i) $表示相空间$ \mathbb{V}_{k} $中的第i个向量, M是各通道嵌入维数之和. 根据严格算法的定义, 由$ \mathbb{V}' $计算得到的$ B^{M+1}(r) $可以写成(11)式中的概率形式:

式中, ABCD所代表的事件在表1中已经进行了说明. 需要注意的是, (11)式包含一个干扰事件T. 这里首先给出事件T的定义. T: 隶属于不同通道的样本点之间的距离小于给定阈值, 即属于不同通道的样本点相似. (10)式可以看到, 严格算法在增加嵌入维数后会出现计算不同通道样本点之间距离的情况. (12)式即为一个典型例子.

需要注意的是, (11)式中的事件T是事件T的子集. 在(12)式中, 计算了$ |x_{3, 1}-x_{2, 2}| $这两个分属于不同通道之间样本点的距离. 距离在广义上可以理解为相似性. 也就是说在对比某一个通道内样本点的相似性时, 严格算法混入了小部分其他通道的样本点数据.

(13)式给出了严格算法的概率表达:

Ahmed和Mandic^[22]认为是事件T使严格算法可以提取通道间的相关性信息. 然而对比(8)式和(13)式可以发现, 严格算法在条件概率中出现了不同通道之间的联合概率. 反观朴素算法, 则只有各个通道的条件概率($ P( {\rm{C}} | {\rm{AB}} ), P( {\rm{D}} | {\rm{AB}} ) $). 因此, 严格算法提取通道间相关性信息的能力可能并不是由事件T带来的. 相反, 这项能力可能是由不同通道之间联合的条件概率带来的.

对于无偏差的多通道多尺度样本熵算法来说, 当嵌入维数从M增加到$ M+2 $时. 由于约束条件的存在使得每一个通道的嵌入维数增量不能大于1. 因此可以生成一个确定的$ (M+2) $维相空间. 根据生成的$ (M+2) $维相空间, 可以计算得到对应的$ B^{M+2}(r) $, 如下式所示:

(14)式表明当嵌入维数增加到$ M+2 $时, $ B^{M+2}(r) $是事件$ {\mathrm{ABCD}} $的联合概率. (15)式给出了无偏差的多通道多尺度样本熵算法的概率表示方法:

对比(8)式, (13)式和(15)式可发现仅有严格算法包含了事件T的子事件T. 同时, 无偏差的多通道多尺度样本熵算法和严格算法均含有不同通道之间的联合条件概率. 本文认为, 事件T会使多通道熵算法的结果有偏. 而不同通道之间的联合条件概率使算法有能力提取通道间的相关性信息. 在后续的仿真实验中, 本文构造出特定的仿真信号, 对比不同算法之间性能的差异来证明本文的观点.

仿真实验主要分为以下几个部分: 首先, 研究数据长度、嵌入维数和阈值系数这3个参数对无偏差的多通道多尺度样本熵算法性能的影响, 并给出相应的参数选择范围. 在确定合适的参数后, 第一组仿真实验研究无偏差的多通道多尺度样本熵算法提取通道内相关性信息方面的能力; 第二组仿真实验则对比研究3种算法在提取通道间相关性信息方面的表现; 第三组仿真实验重点探究严格算法与无偏差算法之间的差异. 这里使用这两种算法计算了各通道间方差不同的高斯白噪声数据的熵值, 结果表明无偏差算法比严格算法更为稳定. 最后一组仿真实验比较了在相同参数条件下3种算法计算样本熵值所需的时间, 以研究不同多通道熵算法的计算效率. 需要说明的是, 除了第4组仿真实验外, 其余的仿真图均为误差条图. 绘制方法是: 独立重复多次进行仿真, 计算熵值的均值与方差. 根据计算得到的均值与方差, 绘制对应的误差条图.

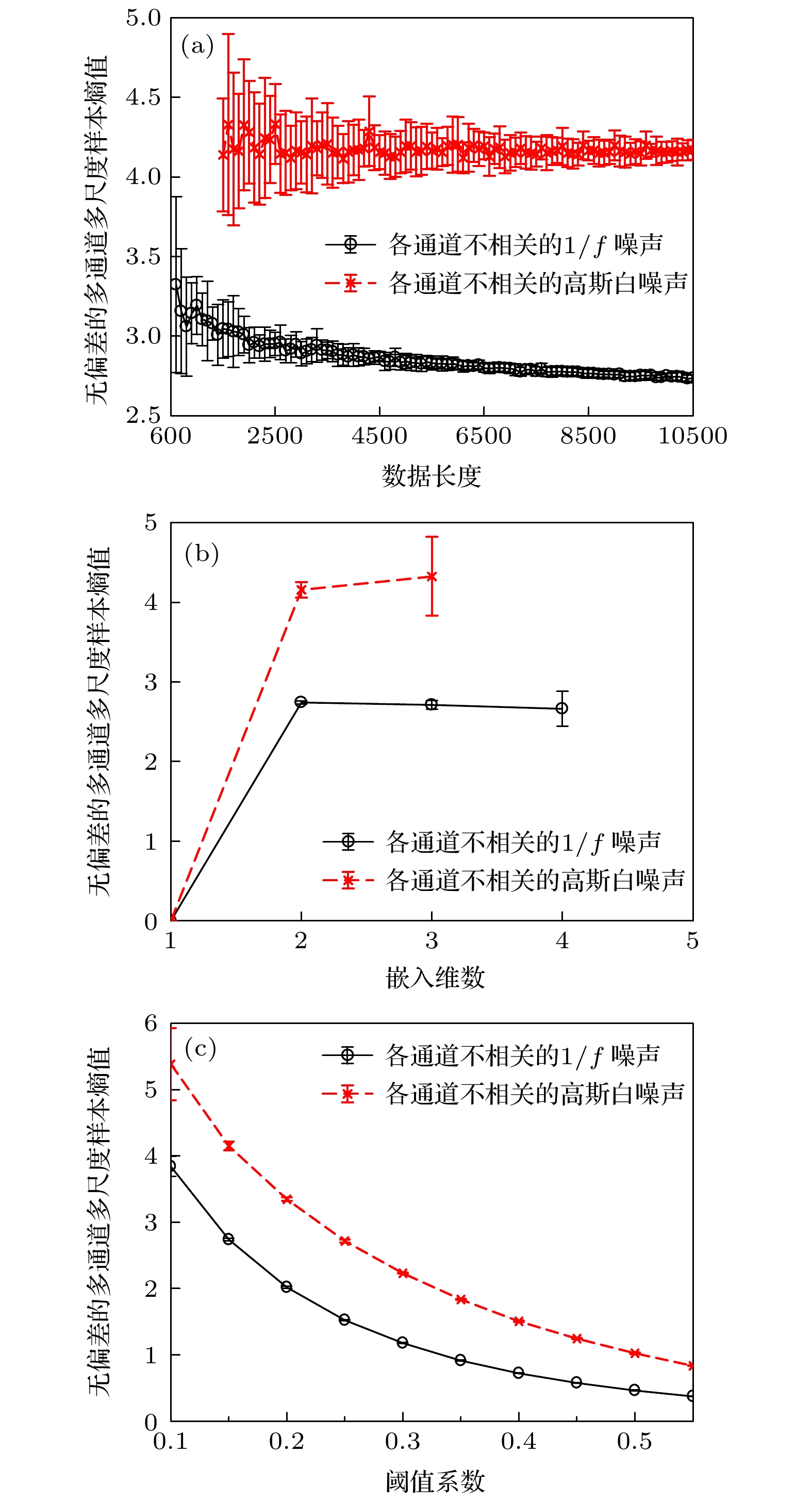
在无偏差的多通道多尺度样本熵算法中, 主要涉及的参数分别为数据长度、嵌入维数以及阈值系数. 在计算过程中采用控制变量法, 控制其余参数不变, 单独研究某一个特定参数对结果产生的影响. 参数设置为: 数据长度$ 10000 $, 嵌入维数$ {\boldsymbol{M}} = [2, 2, 2] $, 阈值系数为$ 0.15 $. 结果如图1所示.

在图1(a)中, 计算熵值时改变数据长度, 范围为$ [600, 10500] $, 其余参数不变. 结果可以看出当数据长度过短时, 由于数据量不足, 在计算过程中可能会出现$ B^{M}(r) $或$ B^{M+p}(r) $过小甚至等于0的情况, 从而使熵结果不稳定. 当数据长度小于$ 5000 $时, 数据长度的变化会对结果的稳定性产生较大影响. 当数据长度大于$ 5000 $时, 数据长度的变化对稳定性产生的影响较小. 无偏差的多通道多尺度样本熵值随着数据长度的增加逐渐稳定. 考虑到实际应用中数据长度的获取成本以及计算效率的问题, 通常将数据长度的范围设置为$ [5000, 10000] $. 图1(b)展示了选取不同的嵌入维数时, 无偏差的多通道多尺度样本熵结果. 从结果可以看出通常每个通道的嵌入维数均应设置为2. 最后, 图1(c)展示了阈值系数对无偏差的多通道多尺度样本熵结果的影响. 如果系数设置过小, 相空间中没有满足阈值条件的向量, $ B^{M}(r) $或$ B^{M+p}(r) $会出现过小甚至等于0的情况. 如果系数设置过大, 熵值结果会趋于稳定. 但是过于宽松的阈值会导致算法无法准确地提取数据的复杂度特征并对不同类型的信号进行区分. 结合仿真实验的结果, 本文认为应在大于$ 0.1 $的条件下选择尽可能小的阈值系数. 这样可以在保证算法稳定的条件下有效地对不同类型信号进行区分.

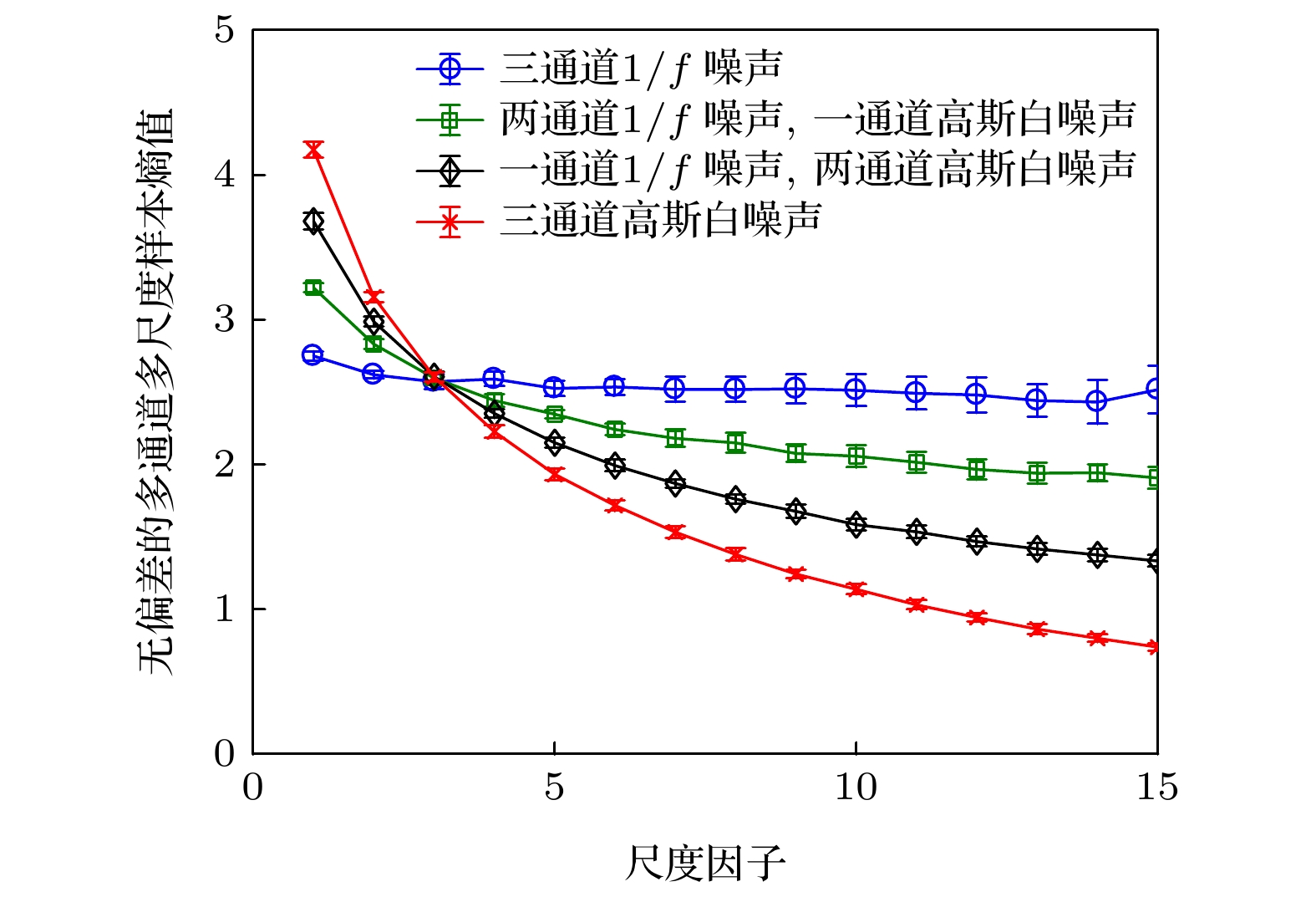
第一组仿真实验, 构造一组3通道的高斯白噪声. 各通道之间的噪声相互独立. 进一步地, 逐步将3个通道的高斯白噪声替换为独立的$ 1/f $噪声. 由于高斯白噪声和$ 1/f $噪声的通道内相关性不同. 改变通道中的噪声类型会逐步改变数据通道内的相关性. 参数设置为$ {\boldsymbol{M}} = [2, 2, 2] $, $ {\boldsymbol{\tau}} = [1, 1, 1] $和$ r = 0.15 $. 每个通道的数据长度为$ 10000 $.

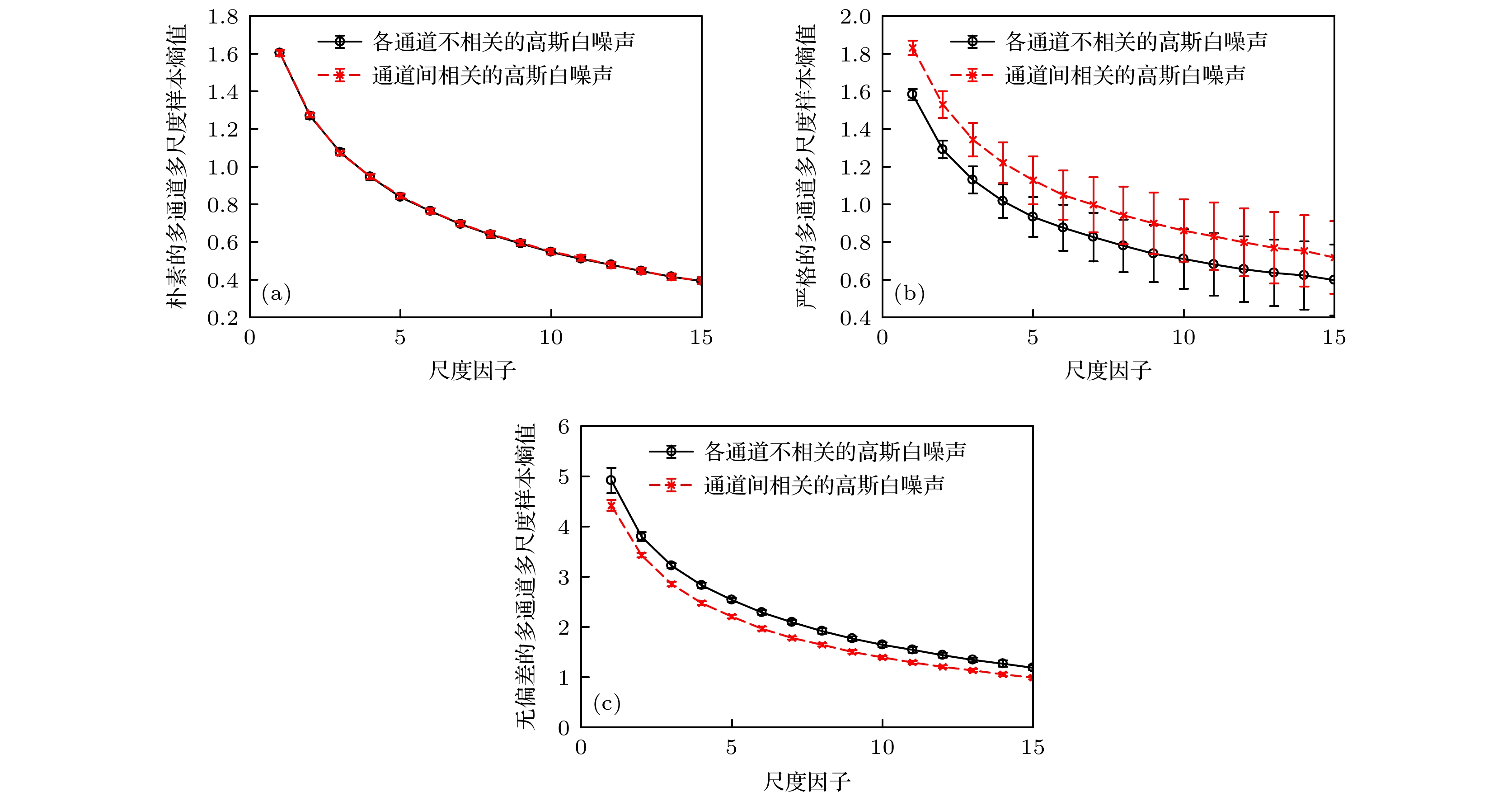
随着包含$ 1/f $噪声的通道数增加, 多通道数据的通道内相关性增强. 从图2可以看出, 改进的多通道多尺度样本熵算法可以有效地提取多通道数据通道内相关性信息.

第二组仿真实验, 构造两组3通道数据. 分别为通道间相关的高斯白噪声和通道间不相关的高斯白噪声. 分别计算其对应的朴素多通道多尺度样本熵结果、严格多通道多尺度样本熵结果和改进的多通道多尺度样本熵结果. 参数设置为$ {\boldsymbol{M}} = [2, 2, 2] $, $ {\boldsymbol{\tau}} = [1, 1, 1] $和$ r = 0.12 $. 每个通道的数据长度为$ 10000 $. 结果如图3所示.

从图3可以看出, 在不考虑稳定性的前提下严格算法和无偏差的多通道多尺度样本熵算法均可以区分相关和不相关的高斯白噪声. 但是考虑到严格算法的方差过大, 在实际应用中往往会使得对通道间相关性不同的信号出现误判. 而朴素多通道多尺度样本熵无法对两种不同的信号进行区分. 这证明了第3.5节（算法分析与证明）理论分析中的结论, 即事件T不能给多通道熵算法带来提取通道间相关性信息的能力. 而不同通道间的联合条件概率可以有效地提取通道间相关性信息. 同时, 这也说明了严格多通道多尺度样本熵算法事实上是有偏的, 在处理实际信号时会使结果不稳定.

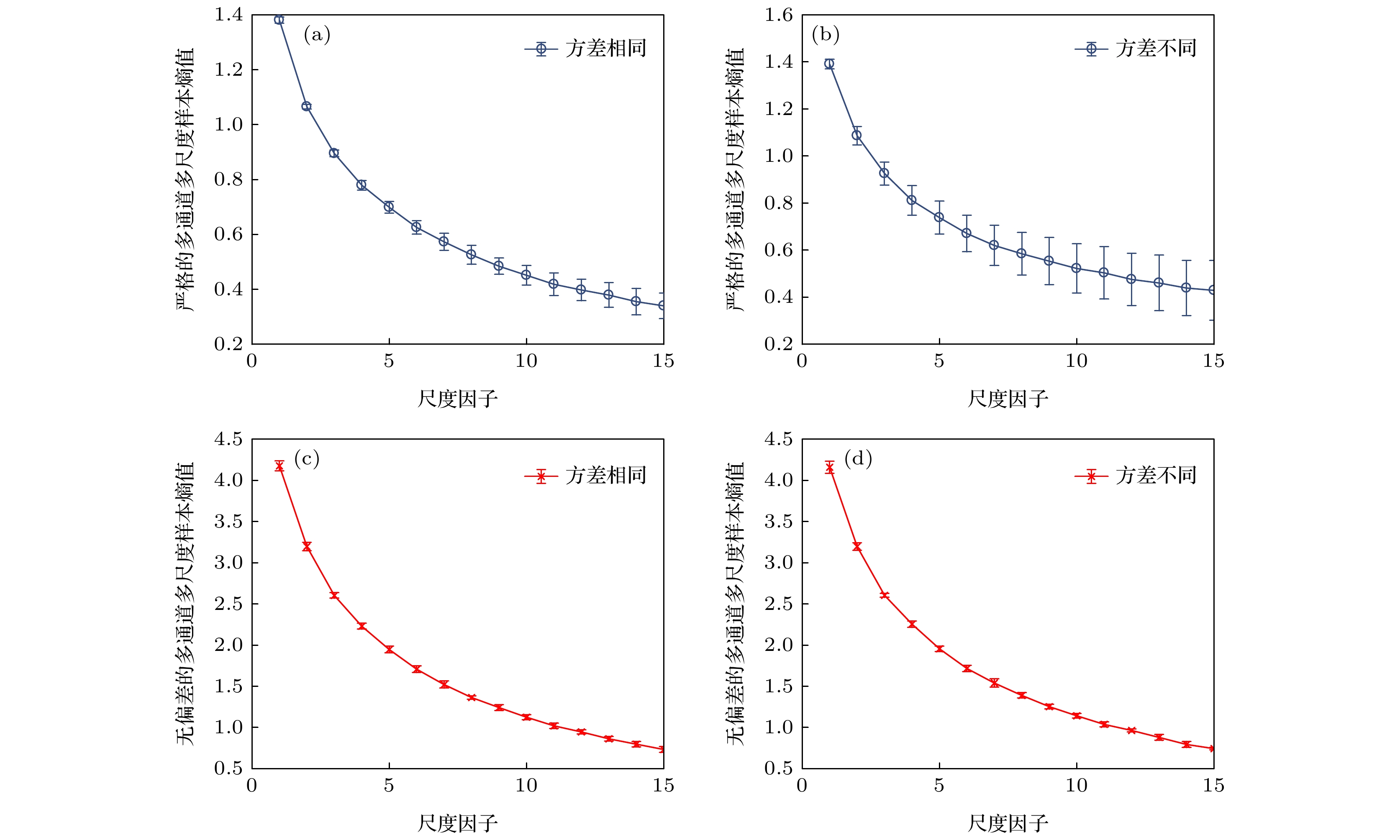
第三组仿真实验, 构造两组3通道的高斯白噪声数据. 两组多通道噪声数据中各个通道的方差分别为$ [1, 1, 1] $和$ [1, 5, 10] $. 分别使用严格算法和无偏差的多通道多尺度样本熵算法计算其熵值. 结果如图4所示.

由图4可以看出, 从整体上看, 严格算法的熵值方差比无偏差的多通道多尺度样本熵的熵值方差更大. 并且, 当通道间的方差区别较大时, 严格算法的方差出现了明显的增大. 这也说明了事件T在各通道之间方差较大时会使熵值结果不稳定.

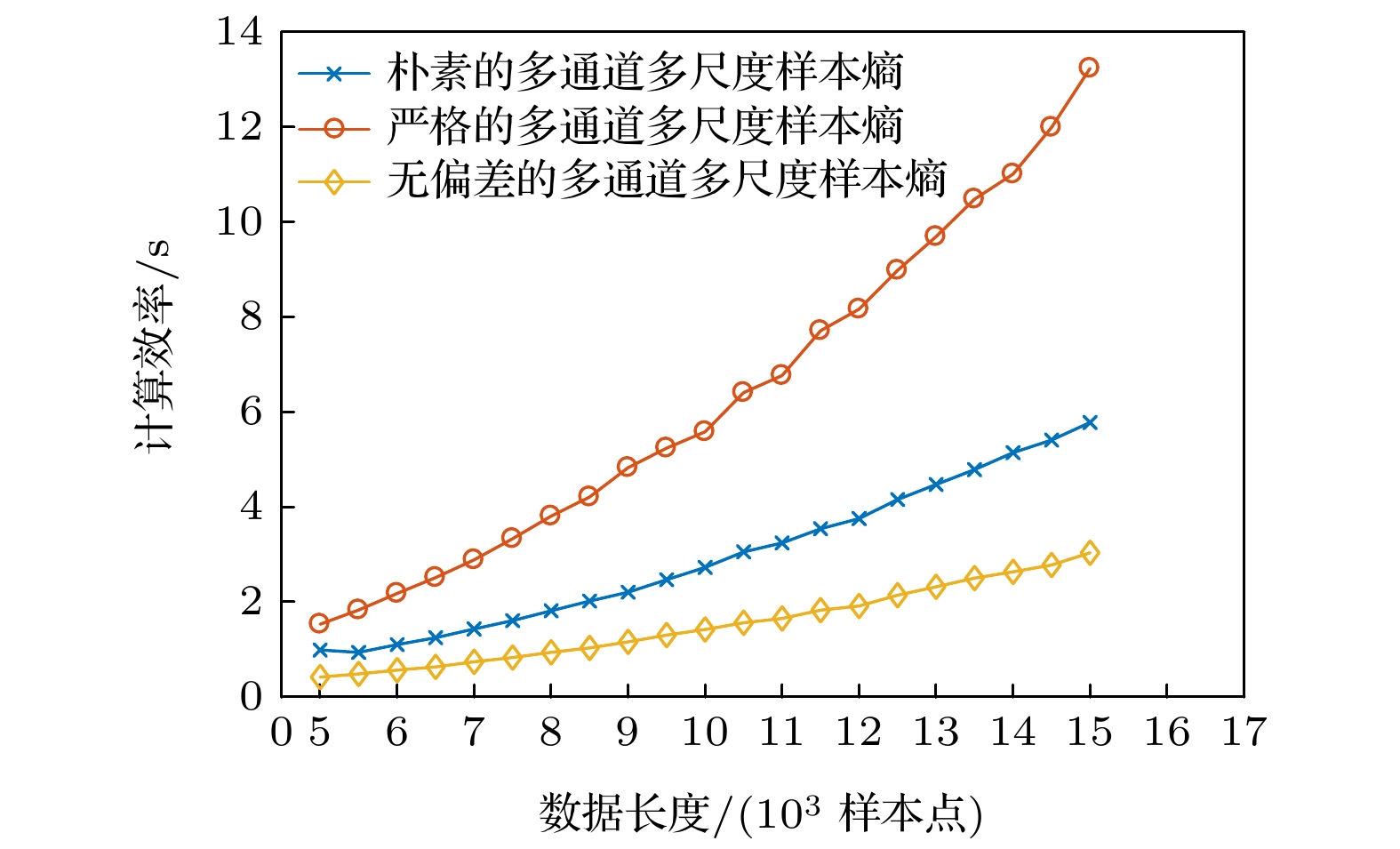
在最后一组仿真实验中, 本文对比研究了朴素算法、严格算法以及无偏差的多通道多尺度样本熵算法的计算效率. 这一组仿真实验所使用的仿真信号为3通道的高斯白噪声. 各通道之间相互独立. 嵌入维数和时间延迟分别为$ {\boldsymbol{M}} = [2, 2, 2] $以及$ {\boldsymbol{\tau}} = [1, 1, 1] $. 阈值系数为$ r = 0.15 $. 通过改变数据长度, 得到不同的熵算法计算所需的时间, 比较不同算法的计算效率. 结果如图5所示.

图5的横坐标是数据长度, 纵坐标为计算时长. 图5对比研究了数据长度不同时, 不同的多通道熵算法计算效率的变化趋势. 可以看出, 当数据长度较短时3种多通道熵算法计算所需的时间比较接近. 随着数据长度的增加, 严格算法的计算时长增速要远高于其余两种算法. 同时可以观察到, 三种算法中无偏差的多通道多尺度样本熵算法的计算时长受数据长度影响最小, 计算效率最高.

多通道多尺度样本熵(MMSE)作为近年来提出的一种新算法, 能够有效地表征多通道数据的复杂度. 然而, 现有的朴素算法和严格算法未能兼顾算法性能和稳定性. 为了解决这一问题, 本文提出了一种无偏差的多通道多尺度样本熵算法. 通过概率论的角度对多尺度样本熵、朴素算法、严格算法以及无偏差的多通道多尺度样本熵算法进行了深入分析. 理论分析结果显示, 朴素算法未包含不同通道事件的联合条件概率, 因此无法有效地提取多通道数据通道间的相关性信息. 而严格算法由于考虑了干扰事件, 导致计算结果有偏差且稳定性较差. 相比之下, 无偏差的多通道多尺度样本熵算法是多尺度样本熵在多通道情况下的准确推广. 本文通过仿真实验确定了一般条件下无偏差的多通道多尺度样本熵算法的参数范围: 计算无偏差多通道多尺度样本熵时的数据长度范围是$ [5000, 10000] $, 每个通道的嵌入维数为2. 阈值系数的范围应大于$ 0.1 $. 同时, 利用仿真实验证明了无偏差多通道多尺度样本熵算法能够有效地提取通道内和通道间的相关性信息. 此外, 还证明了多通道的联合条件概率有助于熵算法提取通道间相关性信息, 而干扰事件T则会导致结果有偏差且不稳定. 最后, 本文对比了不同多通道熵算法的计算效率, 结果表明无偏差的多通道多尺度样本熵算法具有最小的计算成本和最高的效率. 通过本文的理论推导与仿真实验分析, 完善了经典非线性特征量——熵的一般化理论. 证明了在增加嵌入维数时, 将嵌入维数从M变为$ M+p $是最优的策略. 这也为其他诸如排列熵、模糊熵等算法的一般化提供了理论支撑.

感谢卫卓君对本文的润色和语法检查.