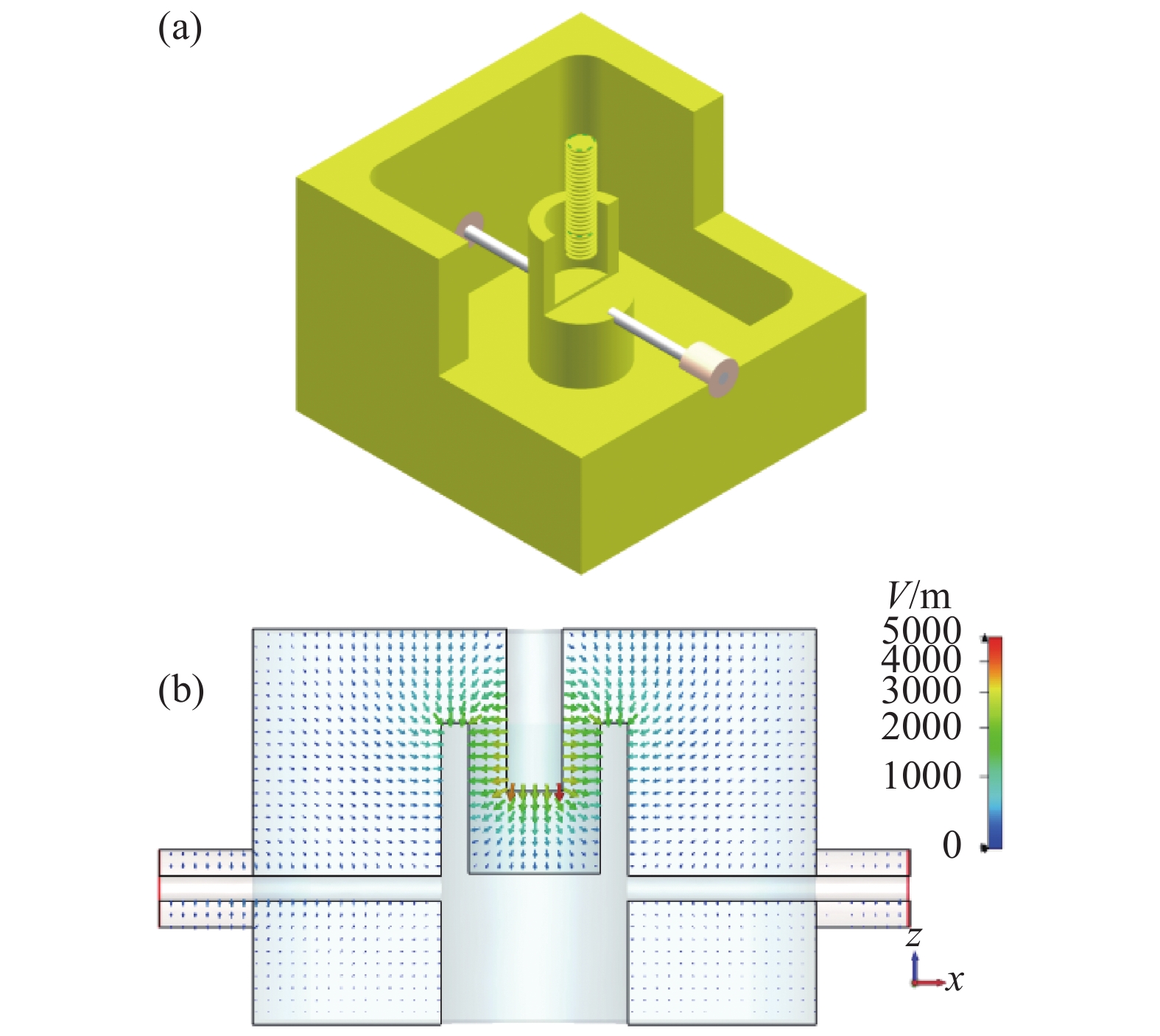
同轴腔体微波部件具备品质因子Q值高、功率容量大、成本低等优良特性，在移动和卫星通信系统得到广泛应用。本文选取常用的电容加载同轴谐振器结构进行部件设计，选用2A12型铝材，尺寸结构如图1（a）所示。同轴谐振器内部腔体尺寸为30 mm×30 mm×21 mm；腔体内部四个角进行圆倒角处理以减少边缘效应引起的局部场增强，倒角半径为3 mm；谐振柱的高度为16 mm，直径选取10 mm以提高谐振器的无载Q值。谐振柱中间向下开有深度为8 mm的凹槽，能够使得谐振器在腔体高度较小情况下实现更大的谐振频率调谐范围，有利于微波部件的小型化。通过改变调谐螺钉的高低进而控制谐振柱凹槽内的空气间隙可以实现中心频率的调谐。

图1（b）电场分布结果表明谐振柱与调谐螺钉之间电场分布均匀，且垂直于两个平行面，调谐螺钉底部电场强度最大，达到900.16 V/cm。故将该区域（图1 (b) 红圈部分）近似为平行平板结构，且作为微波击穿发生的初始位置对低气压放电初期的粒子碰撞进行动力学分析计算，进而可以利用蒙特卡罗方法对击穿功率阈值仿真模拟。

蒙特卡罗方法，也称为统计模拟方法，是一种以概率统计理论为指导的数值计算方法。它主要是在随机性过程中通过随机模拟和统计的方法进行真实有效物理过程的模拟^[12-13]。在微波击穿扩散理论中，碰撞电离是唯一的电子产生源。因此，在模拟过程中也主要是针对空间内电子的碰撞过程进行模拟分析进而判断击穿是否发生。

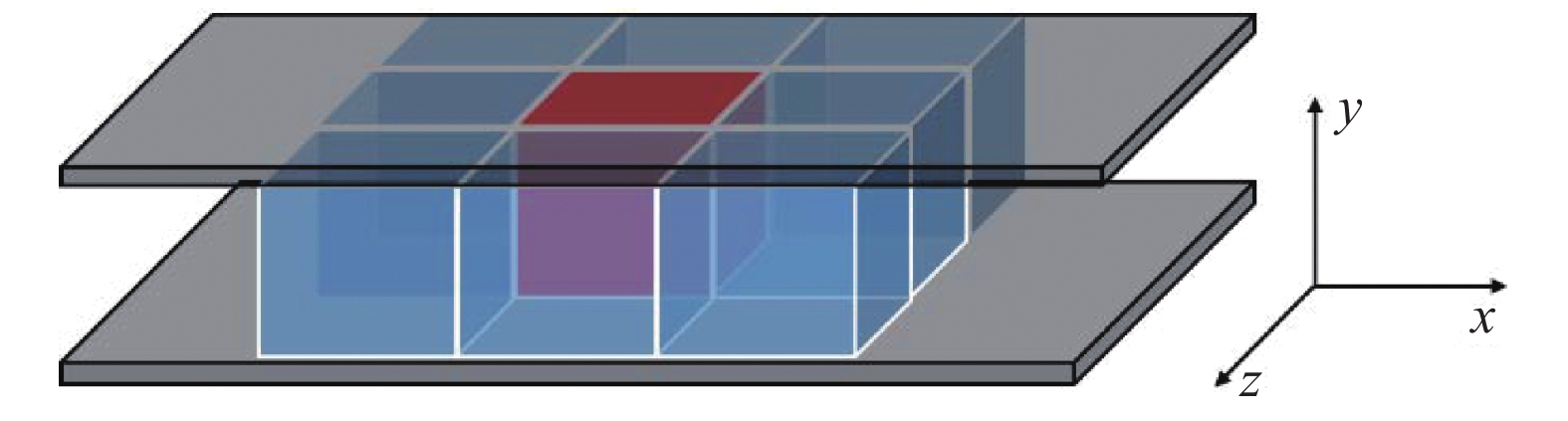
蒙特卡罗模拟采用平行平板结构，在理论研究过程中将金属板大小设置为无穷 ，微波电场在两平行平板间垂直且均匀的分布。空间内的自由电子在微波电场加速下会与气体分子发生碰撞电离，产生的等离子体则会形成干扰微波电场的空间电荷场，最终两者会达到动态平衡，形成稳定的等离子体。而当微波电场能量过大时，碰撞电离产生的新的高能带电粒子会在微波电场作用下继续加速，并与气体分子碰撞电离进而导致整个空间内带电粒子数雪崩式增长，致使气体放电也就是微波气体电离击穿。由此可见，对电子状态的追踪与模拟是方法准确与否的关键。

本文采用单粒子蒙特卡罗模拟方法^[8]，在模拟过程中对空间内所有电子的轨迹进行追踪，经历一定的时间间隔判断电子是否与器壁或者气体分子发生碰撞，同时进行相应的碰撞处理，到达预设的模拟时间后对电子数的涨落进行统计来确定特定气压、频率以及平板间隙下的微波击穿临界电场大小。模拟开始前先对微波电场、空气压强、种子电子数量、初始位置及初始速度等参数进行预设。该阶段微波电场不受空间电荷的干扰，在平板间均匀分布，可表示为：

式中，E_rms是平板间加载微波电场的均方根幅值/V·m⁻¹；ω是微波电场的角频率/rad·s⁻¹；φ为微波电场的初始相位/rad；e_y是y方向上的单位矢量。

种子电子数N₀设置在10³~10⁴，且分布在平行平板之间有效计算区域内（−a≤x≤a，0≤y≤d，−a≤z≤a），如图3所示。能量服从麦克斯韦分布，概率密度分布函数为：

式中，k为玻尔兹曼常数/J·K⁻¹；T为电子的温度/K。由此可推断出电子能量的概率分布函数：

考虑到F(ε)在[0,1]区间内均匀分布，故可通过概率密度函数变换法随机对种子电子的初始能量进行随机抽样。R为均匀分布在区间[0,1]内的一个随机数，令F(ε₀)=R就可以求解出种子电子的初始能量，并可以进一步确定其初始速度各分量：

式中，θ₀为极角/rad；φ₀为方位角/rad。它们大小均由随机数R确定：

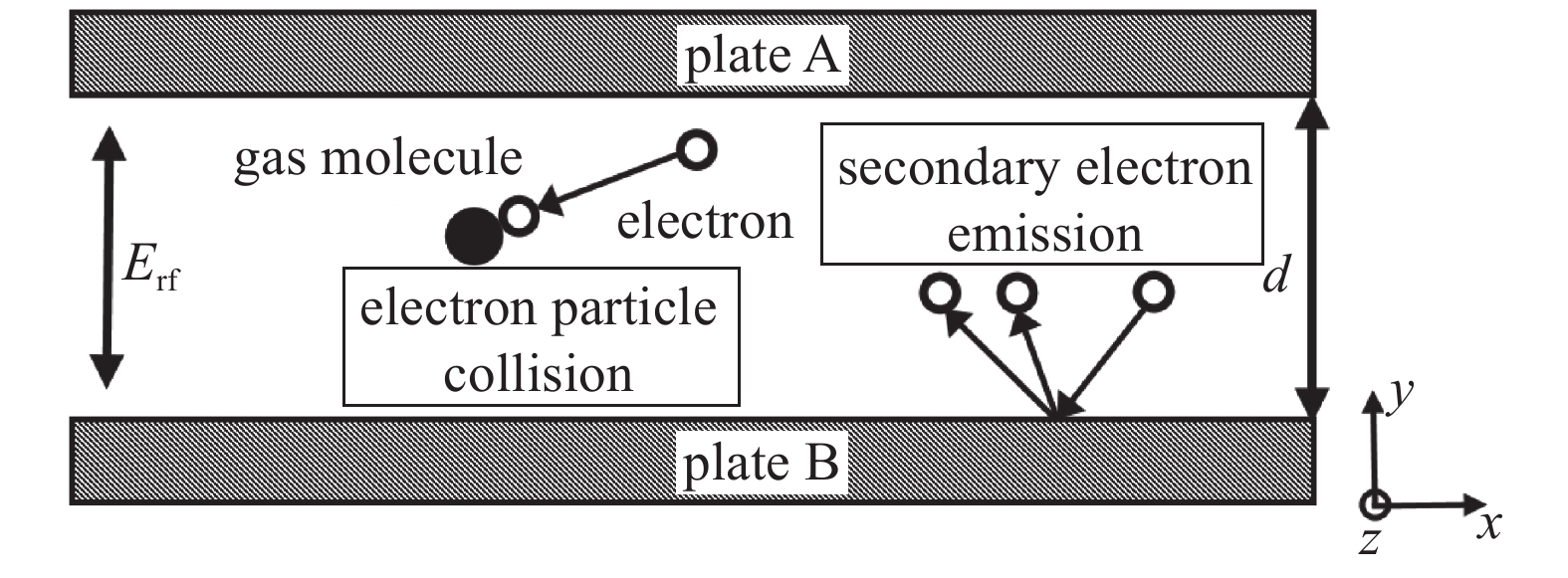
在图2所示的平行平板之间自由电子在微波电场的作用下做快速往返运动，其运动方程可以描述为：

故可以结合式（1）进行连续积分，得到各个方向上的速度分量：

继续对各方向上的速度分量式（10）~（12）积分可以得到电子所处位置：

式中，x₀、y₀、z₀为电子的初始位置/m。由此可以根据其位置判断是否与金属极板或分子发生碰撞。根据图3有效计算区域为−a≤x≤a，0≤y≤d，−a≤z≤a，若轨迹更新后电子位置满足y<0或y>d，则可以判断电子与极板发生碰撞，电子的入射能量和入射角度可以确定为：

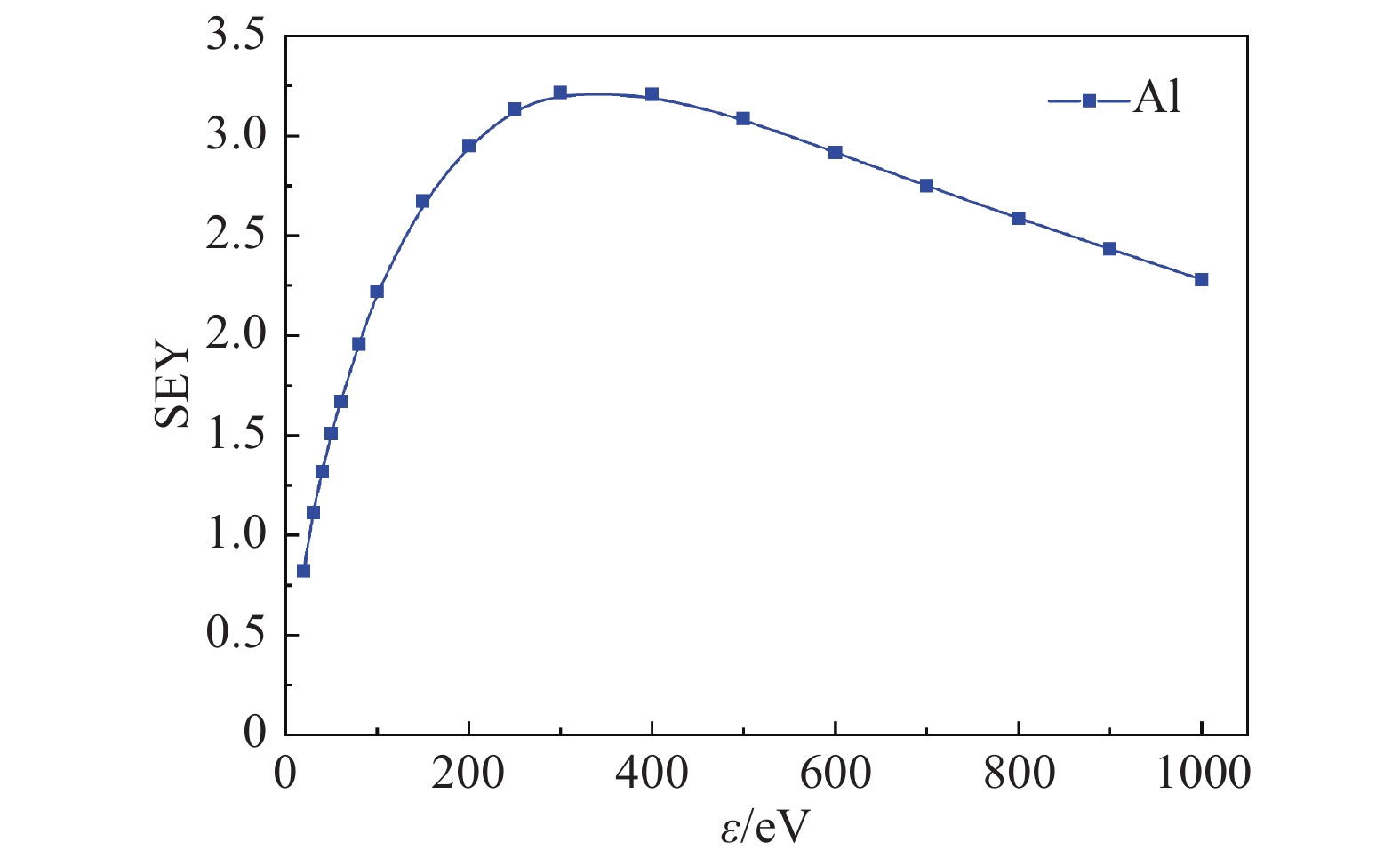
根据二次电子发射Furman模型确定出射二次电子的数量、出射能量以及角度等信息，使仿真模拟结果更符合实际的电子-材料表面互作用情形。谐振器腔体加工所用铝材SEE模型如下图4所示：

综上所述，随着仿真时间的推进可以获得一定微波电场强度条件下电子数随时间的演变情况，并由电子数的涨落特性确定临界击穿电场。在平板间电子会发生各种类型的碰撞，导致电子能量会被重新分配。随着时间推进电子能量在微波电场作用下会进入稳定振荡的阶段，若发生电离碰撞则会激发新的电子产生，电子数目增大，而发生吸附碰撞则会使得电子数目逐渐减少。当电场强度使得电子能量激发与吸附达到动态平衡时，即电子数净增长为零，那么对应的微波电场强度即为所求的临界击穿电场。

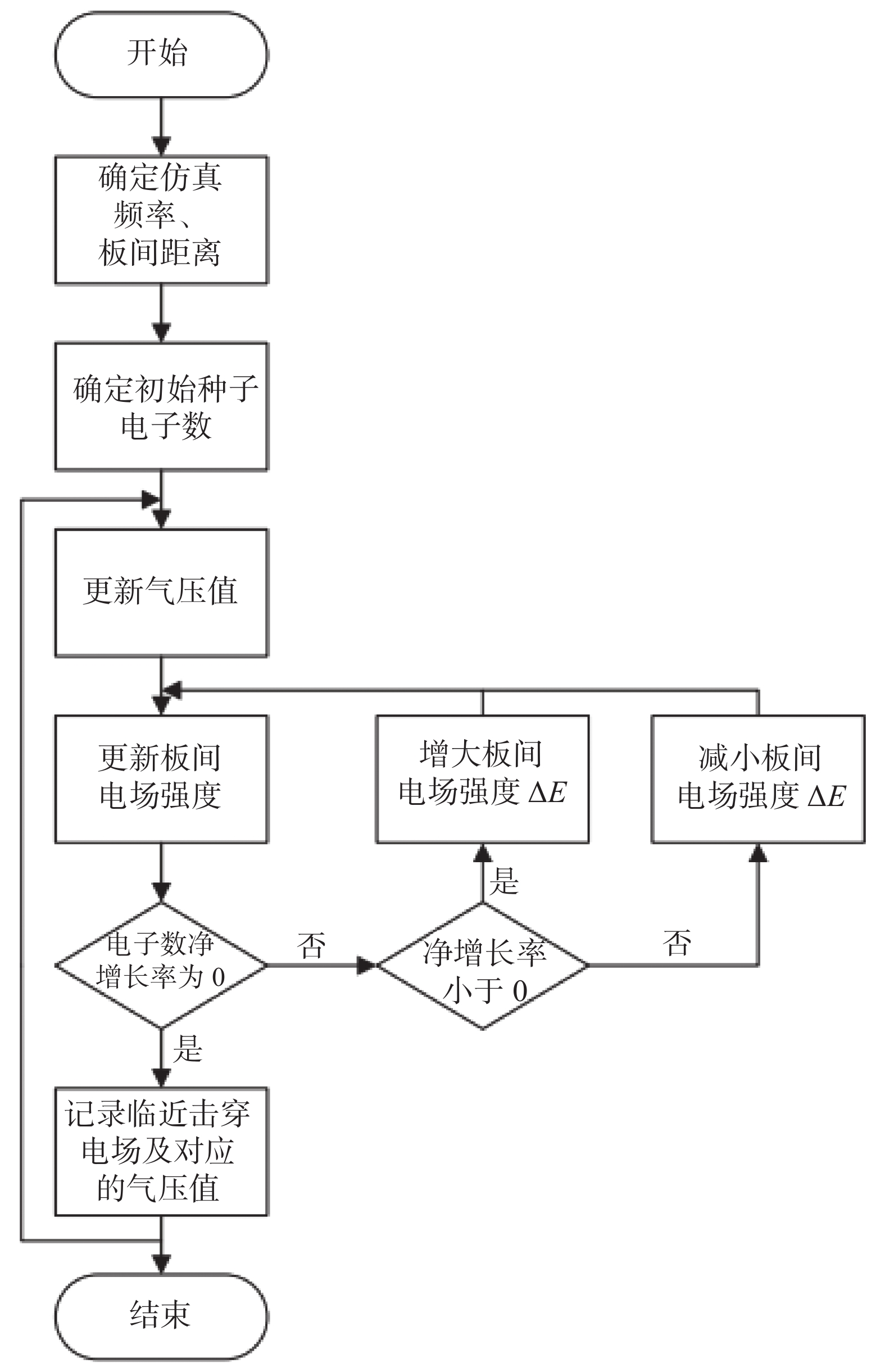
根据1中设计好的同轴谐振器，将谐振柱与腔体上壁之间近似等效为平行平板结构，利用单粒子蒙特卡罗模拟方法进行仿真模拟。气压值设定在100 Pa，谐振频率为2.6 GHz，平板间隔为4.38 mm。初始种子电子数设置为1000，能够在保证模拟结果精度的同时兼顾仿真的效率。蒙特卡罗模拟仿真流程图如图5所示：

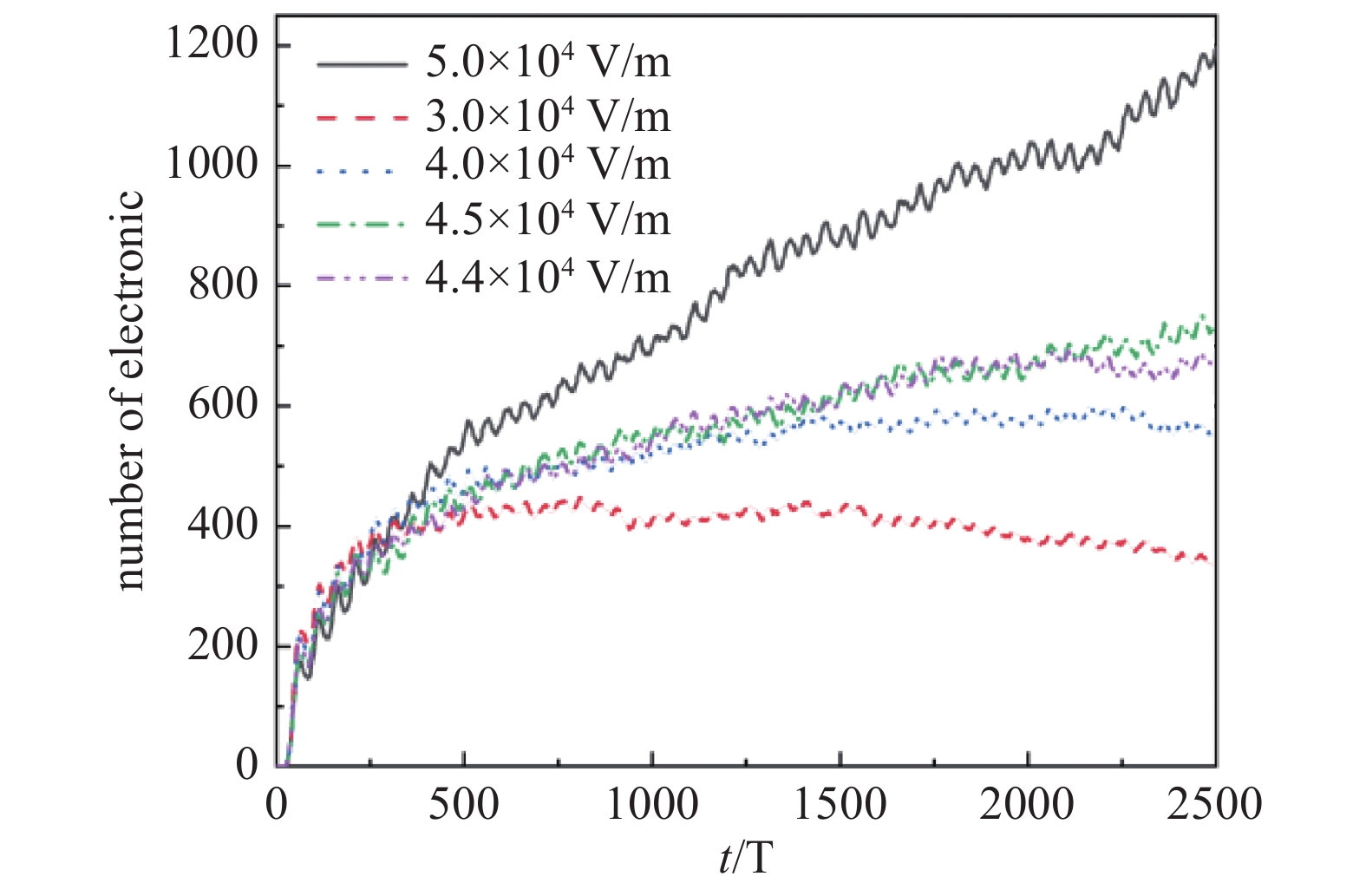
改变电场强度大小可以获得电子数的演变特性，如图6所示。横轴表示仿真时间的离散化，即1个微波周期T。当电场强度设置为4.4×10⁴ V/m时，随时间的推进电子数净增长率趋于零，即为临界击穿电场。

同理，可以确定100~1000 Pa气压范围内同轴谐振器的临界击穿电场。根据击穿功率阈值与临界击穿电场的平方成正比可得如下关系，并由此确定击穿功率随气压变化曲线。

其中，P₀是CST中端口默认的馈入功率（0.5 W），E_bd是蒙卡方法模拟出的临界击穿电场，E₀是CST中谐振器内部中心沿z轴方向上电场强度的均方根值。

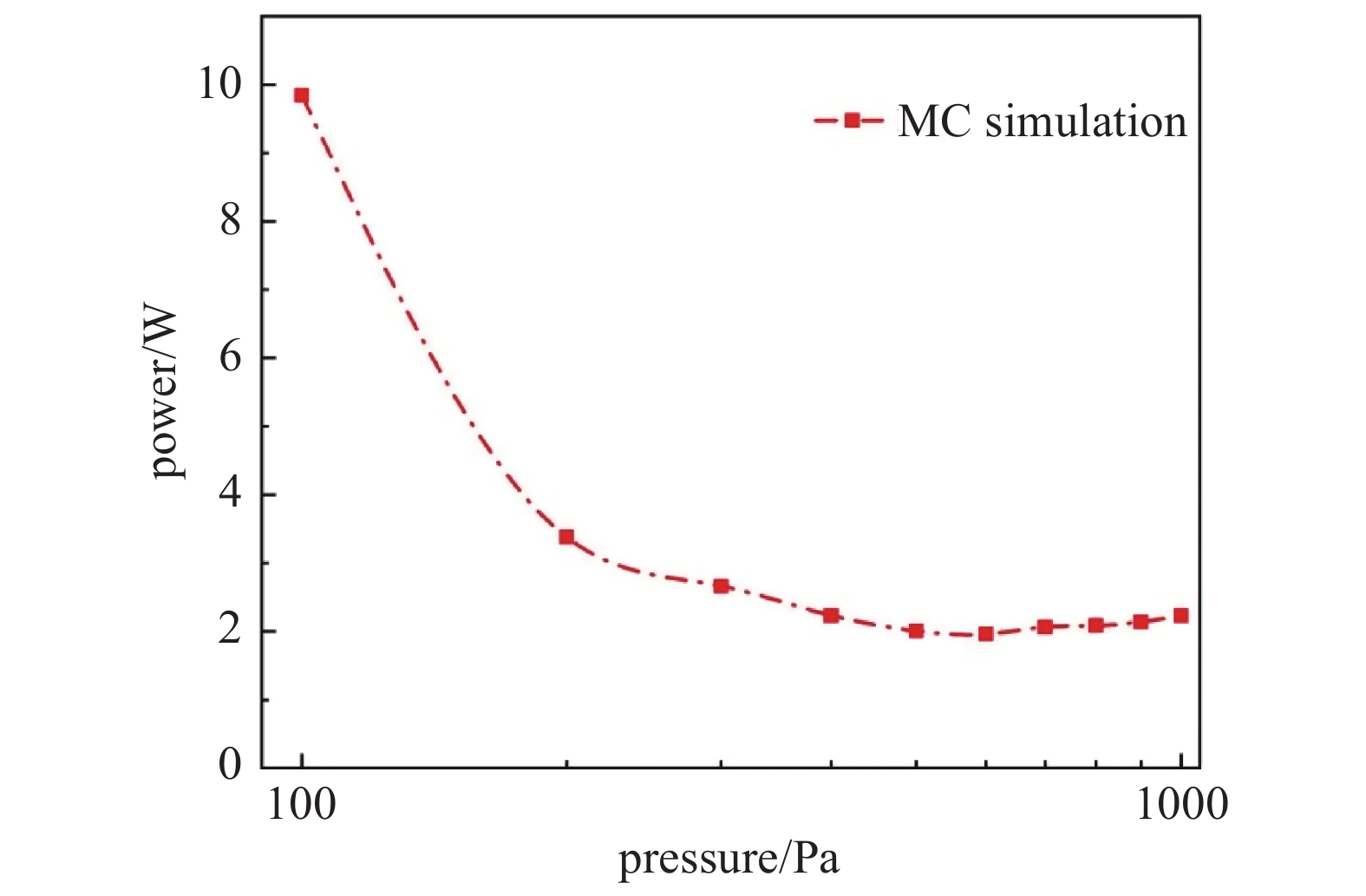
图7为蒙特卡罗模拟仿真数据，仿真结果表明谐振腔阈值电压随着气压升高先迅速下降后缓慢上升，在700 Pa时功率阈值达到最小1.894 W，为临界气压点。

低气压放电是指在较低气压环境中（1.333×10¹~1.333×10⁴ Pa），带电粒子在射频场作用下加速，一部分高能带电粒子与气体分子碰撞致使其电离产生新的带电粒子，并且这些新的带电粒子继续在射频场作用下与气体分子发生碰撞电离，导致空间内带电粒子数呈雪崩式增长的气体放电现象^[14-15]。

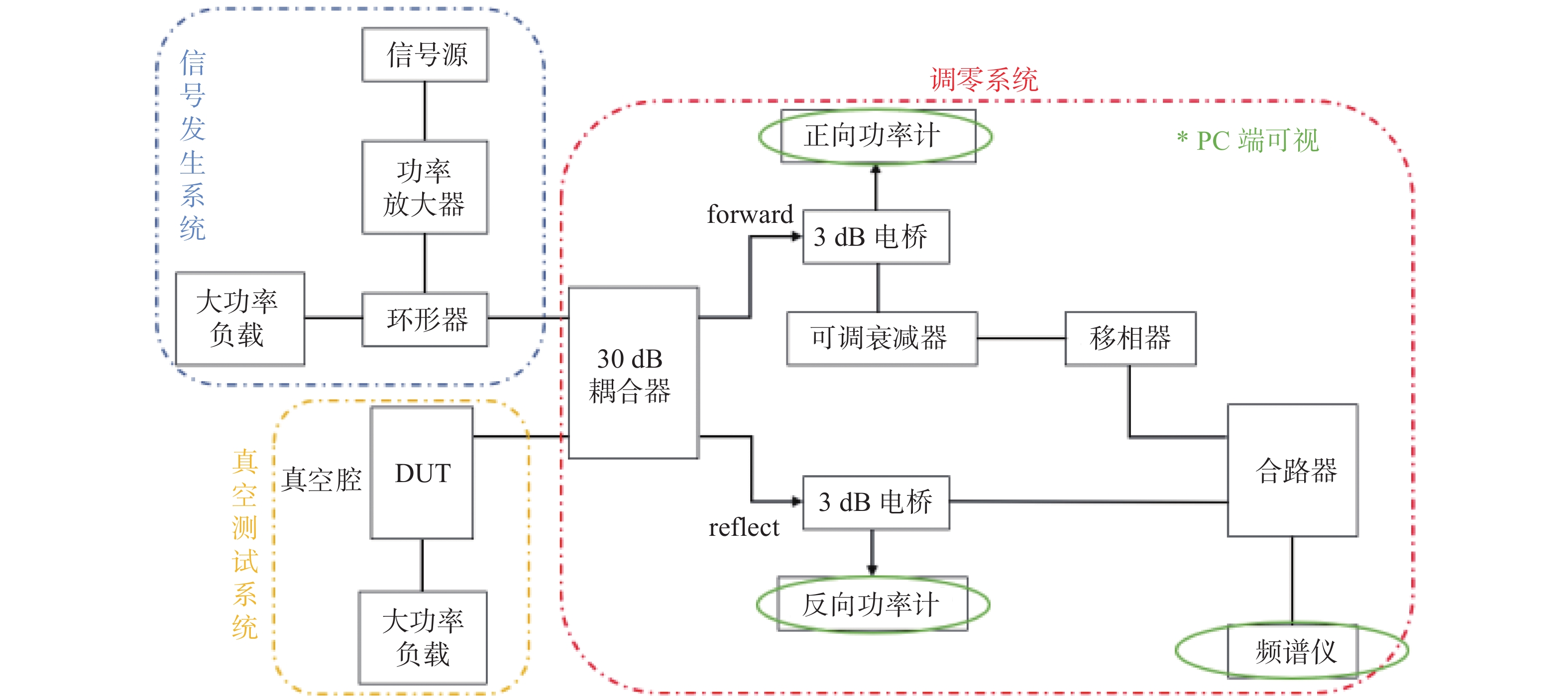
测试平台主要由信号发生系统、真空放电系统以及数据采集系统三个部分组成，系统框图如图8所示，平台实物如图9所示。

信号源在实验开始阶段输出2.6 GHz的小功率（25 dBm）连续正弦波信号，经功率放大器进行功率放大，放大后的信号通过环形器进入调零系统，利用环形器正向导通反向隔离的特性防止待测件在发生低气压放电时反射信号突然增大对功率放大器造成损坏。调零系统^[16-17]的输出接入真空腔内的待测微波部件，最终大功率信号被负载吸收。当真空腔中微波部件发生放电击穿时反向功率会增大，进而频谱仪中调零信号幅值会发生明显跳变，以此作为微波电离击穿发生的判据。

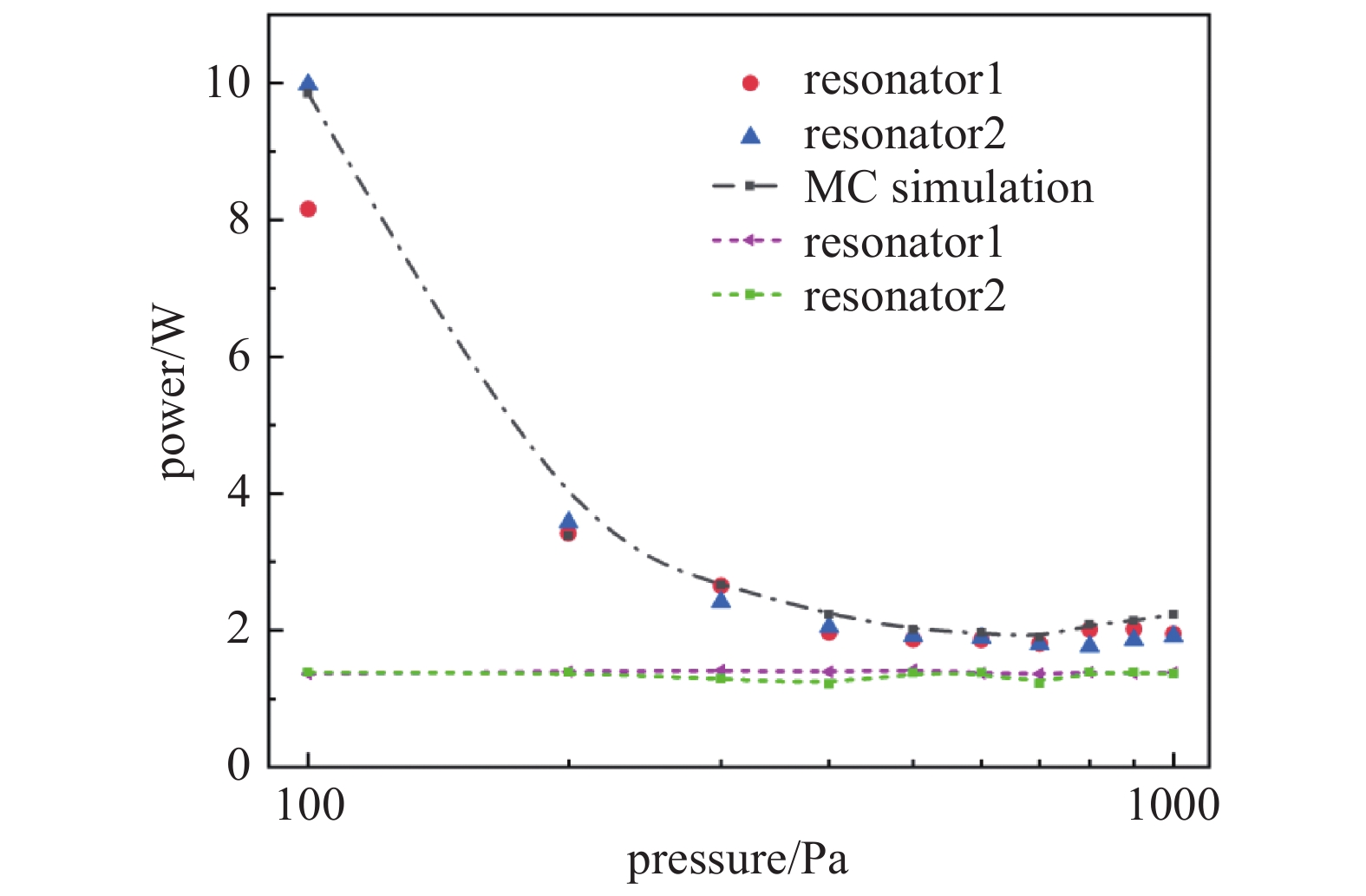
本文针对该同轴谐振器的低气压放电击穿功率进行研究，测试的气压范围为100~1000 Pa，真空腔中为空气气氛。微波电离击穿功率阈值为入射功率与击穿时的反向功率之差，因此在实验过程中记录调零信号跳变前的正向功率计示数以及跳变后的反向功率计示数。实验测试所得击穿功率阈值与气压的关系曲线如图10所示。

测试结果表明同轴谐振器低气压放电击穿功率阈值随气压的升高先减小后上升，在700 Pa附近处于临界气压点，此时击穿功率为最小值。谐振腔1号测试结果为700 Pa处1.807 W，谐振腔2号测试结果为800 Pa处1.768 W。但2号在700 Pa处功率阈值为1.795 W，两者数值大小上差别极小，且与蒙特卡罗模拟预测结果误差都在5.5 %以下。综合其他气压点处测试结果与蒙卡模拟预测值对比，验证了该模拟方法预测的准确性，整体误差都能保持在10 %以内。模拟结果与实测结果的差异来源主要为3个方面：（1）种子电子数N₀设置不够大。考虑到程序运行时间以及电脑的计算能力，种子电子数N₀的提升都会使得模拟时常成倍增加。因此为了兼顾模拟精度和效率做出折衷选择；（2）二次电子发射模型的选取。根据电子产生机制可以知道电子-分子碰撞界面数据会很影响临界击穿电场模拟结果。谐振器内壁材料二次电子发射特性数据的准确性将影响模拟结果精度，而内壁材料表面粗糙度会对SEY有较大影响——同一材料的表面粗糙度越大，相应的二次电子产额减小，导致相同材料SEY测试结果在数值上仍可能存在差异；（3）测试真空腔法兰处存在引线的泄露，气压在测试过程中会略有增加，同时连续测试也会导致谐振器温度升高，对模拟结果的精度造成影响。

整个过程变化的趋势与直流放电帕邢曲线相似。同时，击穿曲线存在拐点与Campbell等在研究具有微米气隙结构的同轴谐振器的微波击穿特性时的报道相符，归因于电子振荡幅度与气隙大小可比拟时急剧增大的壁损失^[18]。从电子与气体分子的碰撞过程考虑也可以进行解释：（1）在馈入功率一定的情况下，气压升高将导致真空腔内粒子数增多，那么分配到单个粒子上的能量将会减小；（2）气压升高，分子密度增大，电子自由程变短导致被微波电场加速度距离变短，电子能量下降进而使得电离效率降低。因此在碰撞概率和电子能量两个因素共同作用下：当气压很低时，虽然单个电子能量大，但分子总数少，碰撞概率很低导致击穿不易发生，此时击穿功率表现为高阈值；而当气压升高后，水分子数量增多，电子能量将减小难以电离，也会导致击穿难以发生，此时击穿功率也表现为高阈值。因此，击穿功率的阈值曲线呈现出“中间低两边高”，与帕邢曲线相似。此外，两个谐振腔的维持功率测试结果比较稳定，不随气压变化发生波动，基本保持在1.38 W左右，这表明该谐振腔结构尺寸以及工作频率确定后，维持功率也将随之确定。

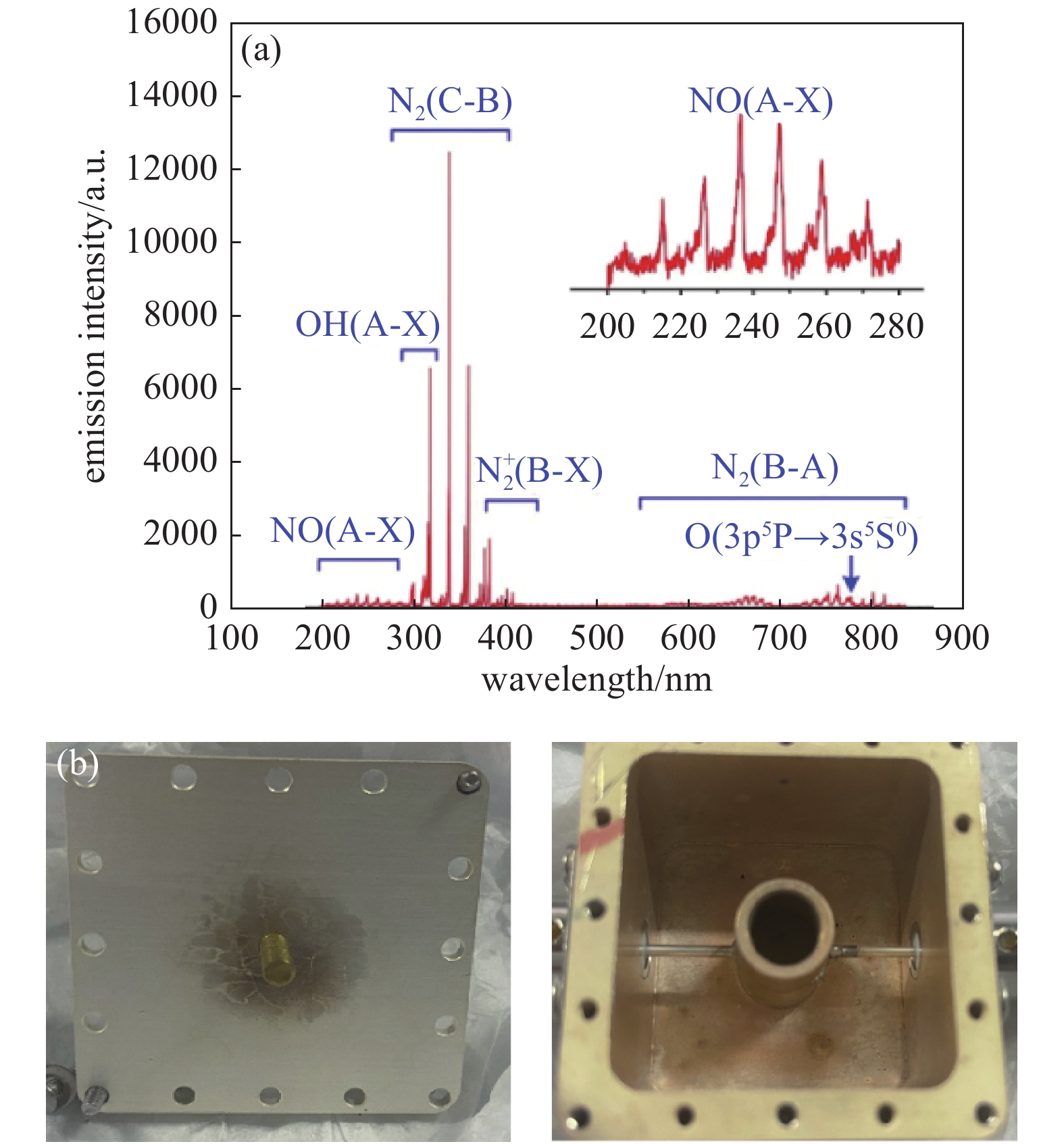
图11（a）展示了空气气氛下气压为500 Pa时谐振腔内放电产生的等离子体的发射光谱，检测结果显示发射光谱主要由氮、氧粒子组成，还包含相当数量的羟基（OH）粒子。这正是因为空气的主要成分为氮气和氧气，通过电子碰撞引起的电离、激发反应以及重粒子之间的反应生成各类产物。此外显著的OH发射谱线也说明等离子体中含有大量的OH粒子^[19-20]，进一步说明放电气体中存在水分子的掺杂。

图11（b）为放电后同轴谐振器腔体中心及盖板中心的破坏痕迹。在谐振柱凹槽内击穿最为严重，呈现出焦黑的颜色，符合CST中的电场分布。证明蒙特卡罗模拟仿真中对调谐螺钉位置处做平行平板结构等效的合理性。另外盖板也表明在调谐螺钉附近颜色最深，并且随着击穿所产生的等离子体逸散向外逐渐变浅。

本文在S波段进行同轴谐振器的设计，并利用单粒子蒙特卡罗模拟方法实现对其低气压放电击穿阈值的仿真预测，通过开展低气压放电实验进行验证，得出以下结论：（1）低气压空气气氛中同轴谐振器击穿功率随气压的升高先减小后增大，呈现中间低两边高的趋势，存在一个临界气压点700 Pa；（2）同轴谐振器维持功率基本不随气压变化，主要由结构尺寸以及工作频率决定；（3）单粒子蒙特卡罗模拟方法精度高，实验测得结果与仿真结果误差小于10%，表明该方法可以在设计阶段对微波部件功率容量进行有效预估。同时，本文也为更多以谐振器为基本单元的微波部件低气压放电研究提供有价值的参考。