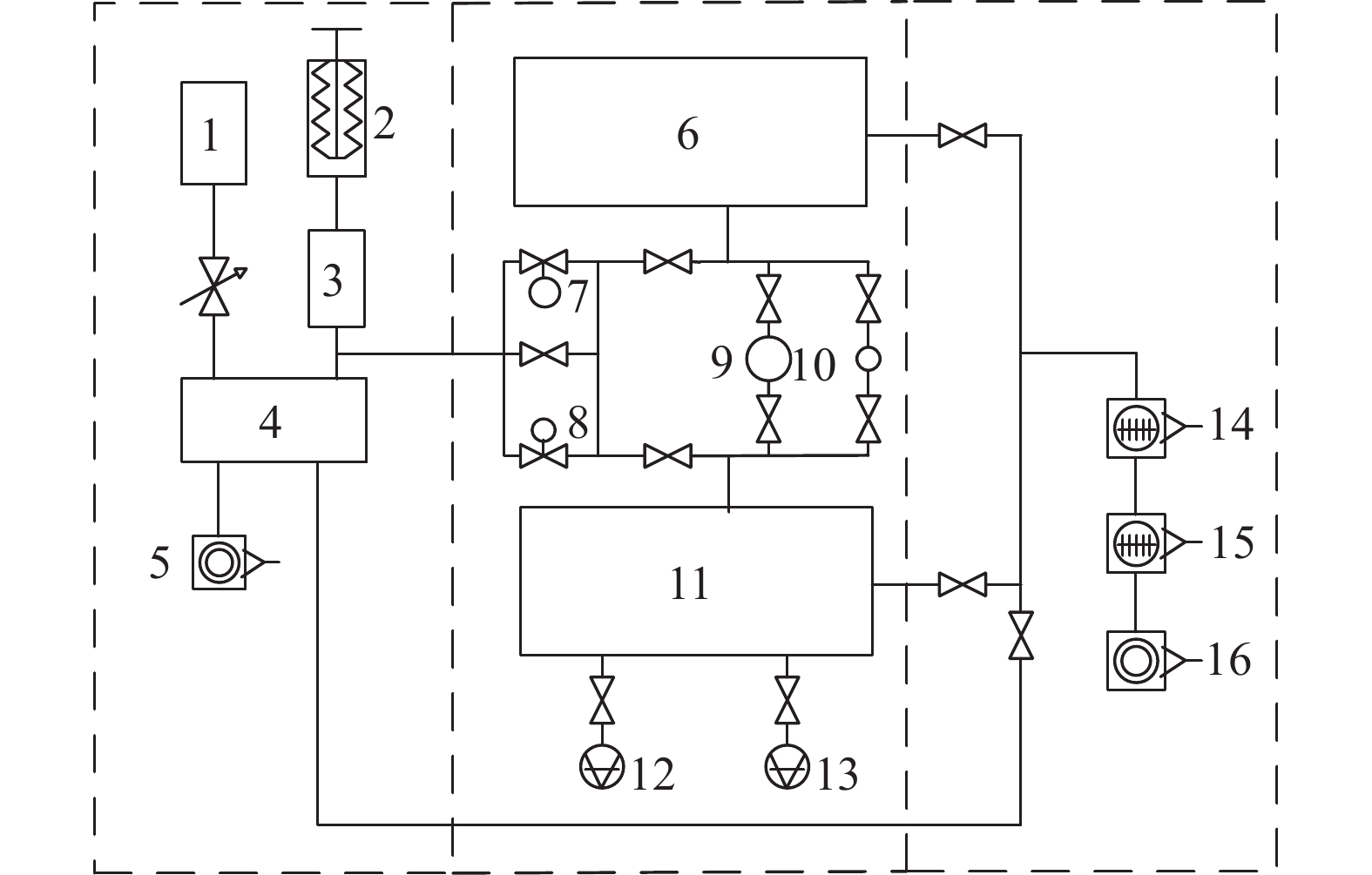
实验使用兰州空间技术物理研究所真空计量一级站的金属膨胀法真空标准装置进行气压值直接比对，得到电容薄膜真空计的原始气压测量值和所对应的气压标准值。该装置是中、低真空段的国防最高标准装置，其测量范围为10⁵ Pa～10⁻⁴ Pa，不准确度为0.01％～1.0％。金属膨胀法真空标准装置可以通过选择不同的膨胀路径来对取气前级中的气体进行相应倍数的膨胀，从而得到所需的标准气压^[7]。使用该装置采集电容薄膜真空计的气压测量数据保障了实验数据的准确可靠性，金属膨胀法真空标准装置的结构示意图如图1所示：

金属膨胀法真空标准装置根据取气前级所设置的气体压强（p_{前级取气压强}），通过所选择的膨胀倍数通道完成气体的膨胀。第一次膨胀后的气压标准值$ p_{L1} $（VL校准室中的气压）可通过式（1）计算得出：

式中：k为膨胀系数，其中k的计算公式（2）如下：

式中：V₁为校准室的体积，V₂为膨胀室的体积。

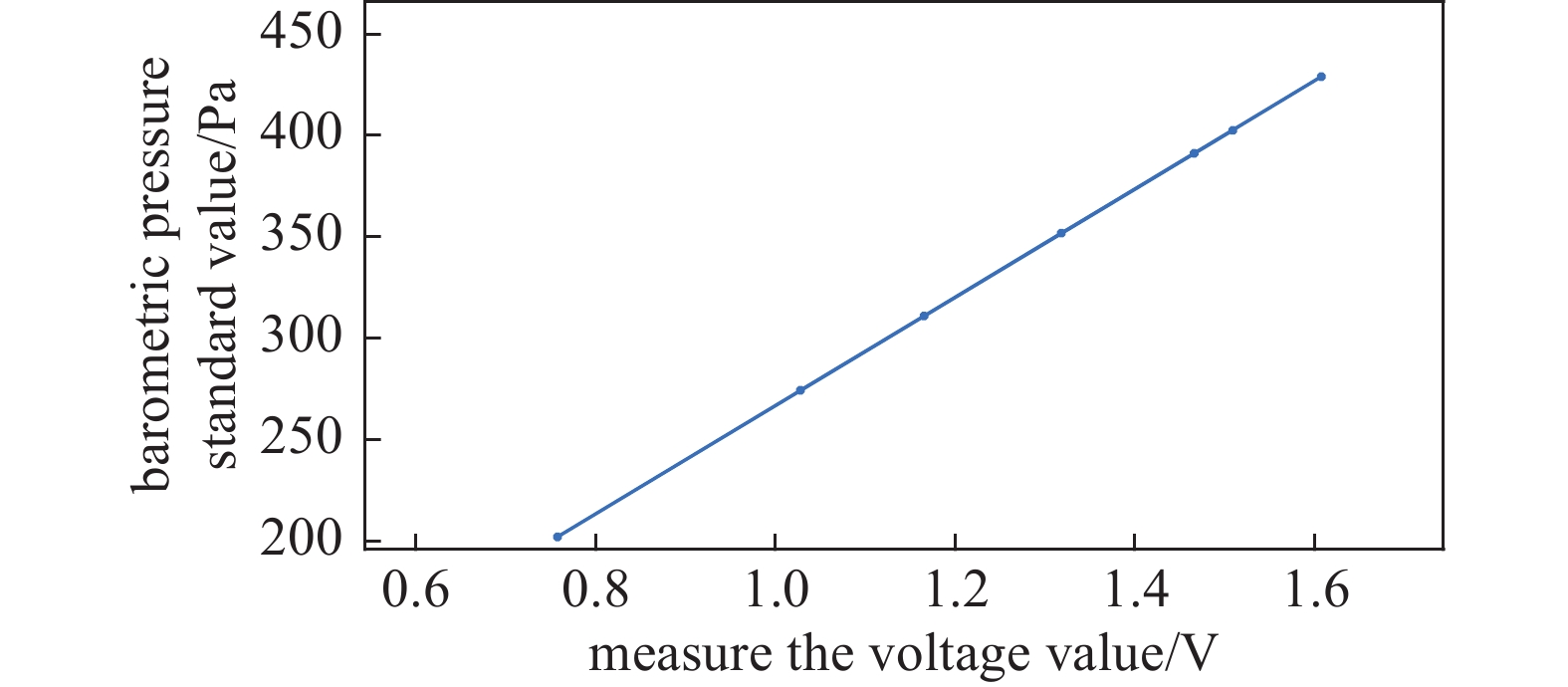
设第一次进气后校准室得到的膨胀气体压强为$ p_{L1} $，第$ n $次膨胀后校准室的气体压强为$ p_{Ln} $，前级取气的压强统一用p_{前级取气压强}表示，则第$ n $次膨胀后的校准室气体压强计算公式(3)为：

因为每次气体膨胀都会给校准室带入一定的误差，所以单次进气次数越多其带入的误差也就会越多。为了保证实验数据的准确性，本实验选择分为两个区段进行采集，分别为0 Pa～266 Pa （0 V～1 V）和266 Pa～2666 Pa （1 V～10 V）两个区段。并且在0.7 V～1.7 V区间上采集了多个数据点，由于电容薄膜真空计在此区段上数据线性度较好，所以可以使用这些数据点求出对应的一次线性插值函数，近似得出0.7 V～1.7 V数据段上所对应的气压标准值，如图2所示。

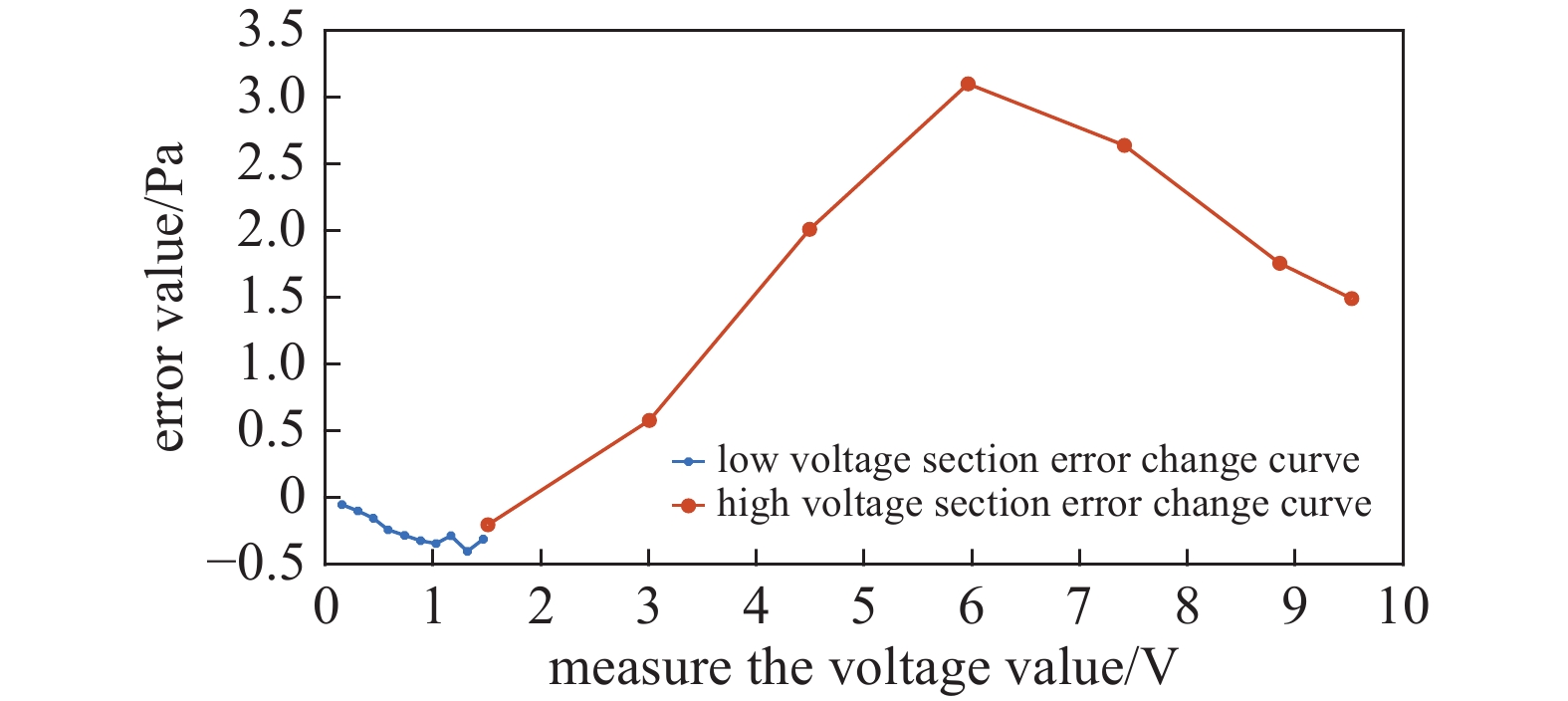
如图3可知，电容薄膜真空计在高、低压两个量程上的误差曲线具有不同的特性，误差曲线分段拟合修正方法的使用可以分别根据高、低压量程段上的误差曲线特性得到更加精确的误差数据拟合结果，从而更加准确的对各自分段上的数据进行修正。

通过计算可以得出电容薄膜真空计低压和高压部分测量数据的误差拟合曲线，再将与气压测量值相对应的电压值带入其中，来获得各个气压测量点的误差数据拟合值。然后，用电容薄膜真空计的原始气压值减去相应的误差拟合值来获得气压测量数据的修正值。

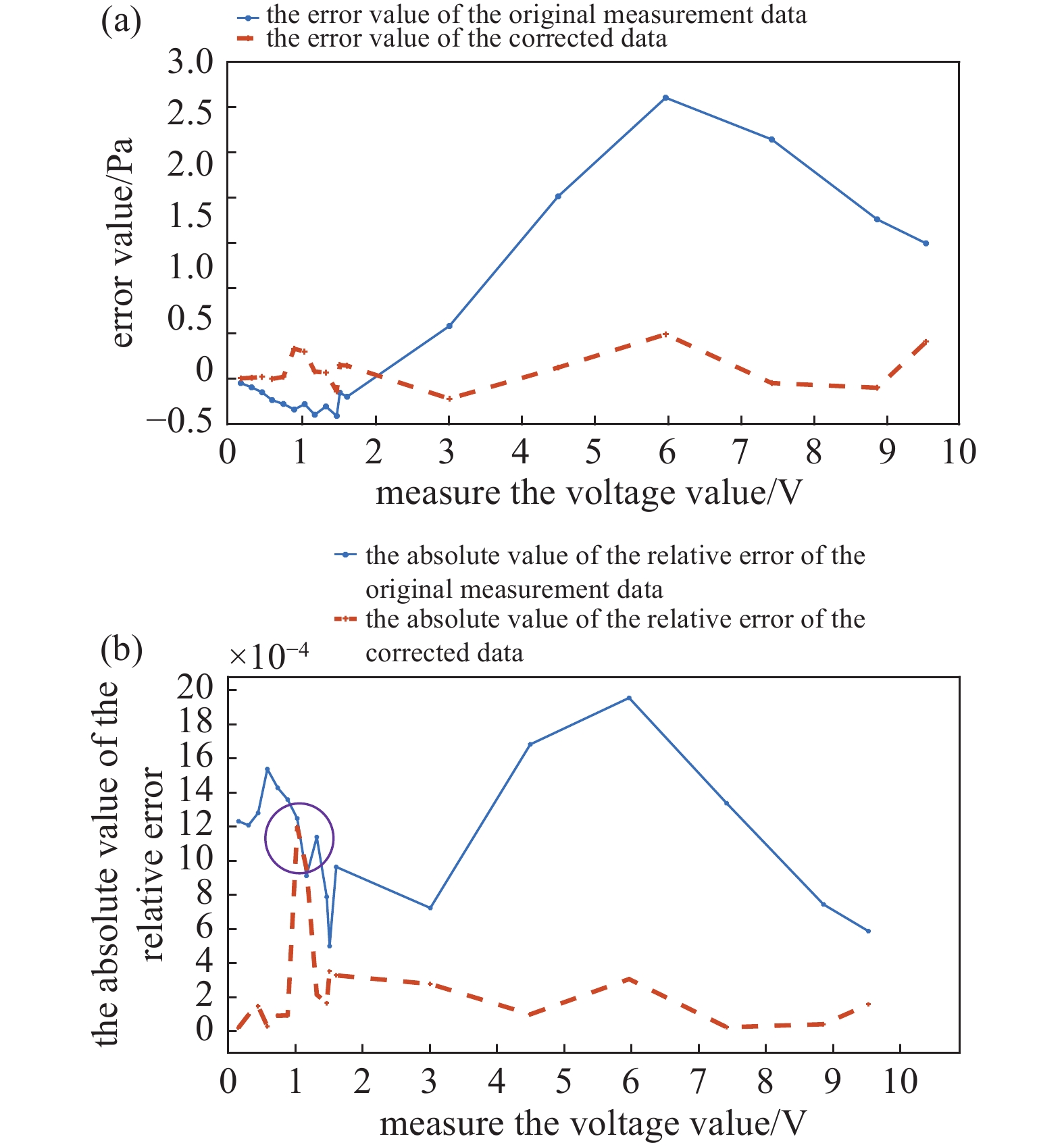
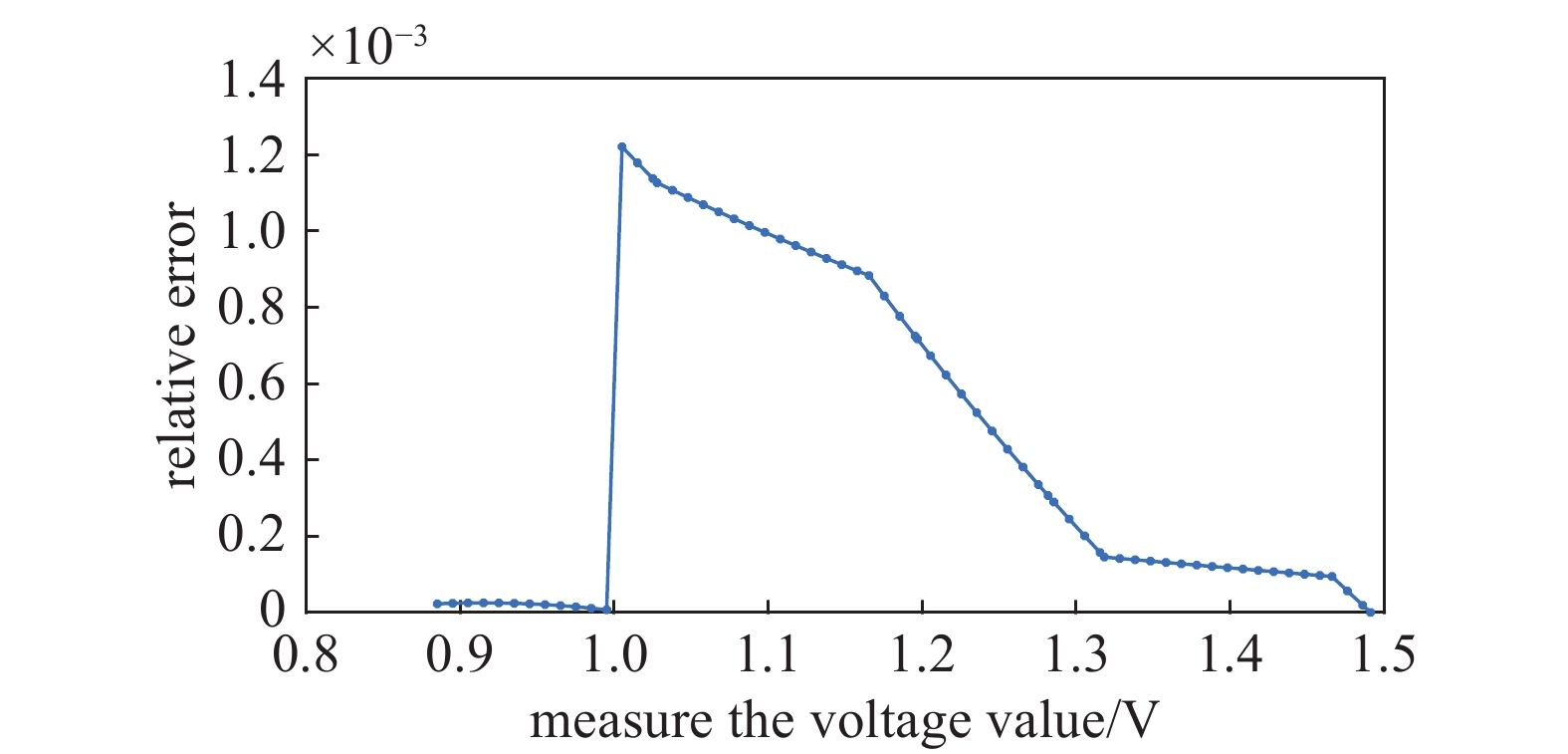
图4（a）可以看出经过分段误差拟合曲线的修正后各个数据点的误差都得到了一定的减小且都稳定在0值附近，而修正前的气压测量数据各点的误差值较大且变化幅度较大。图4（b）可以看出远离分界点的数据相对误差都得到了大幅的减小，但是分界点（1 V）附近数据的相对误差依然很大（紫色圆圈中的部分）。

虽然使用测量误差分段曲线拟合修正的方法取得了较好的数据修正效果，减小了大部分测量点上的误差，但是数据处理的过程中发现,在低压段与高压段数据分界点的地方，修正后的数据出现了数据曲线左右不连续的现象，如图5所示。

图6可以更加明显的看出分界点附近区域因为数据曲线跳跃间断而产生相对误差突然增大的现象。可以看出当电压值小于分界点（1 V）时，经过低压段测量误差数据拟合曲线的修正后，数据与标准值之间的相对误差基本小于0.025％。但是，在分界点（1 V）处的修正值产生的相对误差突变到了0.122％，并且后续相邻区间上的修正数据值也产生了较大的相对误差，随着电压值的增大，修正后数据点的相对误差才又慢慢减小，这种现象很大的影响了电容薄膜真空计在分界点附近测量数据的准确性和连续性。

本文总结归纳了实验所用电容薄膜真空计在跳跃间断区间上产生的系统误差及其变化规律，然后根据测量数据对模糊控制算法的隶属度函数和模糊规则进行多次调整，最终设计出合适的模糊控制数据处理算法。通过该算法，数据处理芯片可以根据测量数据实时计算出该点会产生的误差近似值，然后用测量值减去误差值，从而达到减小跳跃间断区间上测量数据误差的目标。

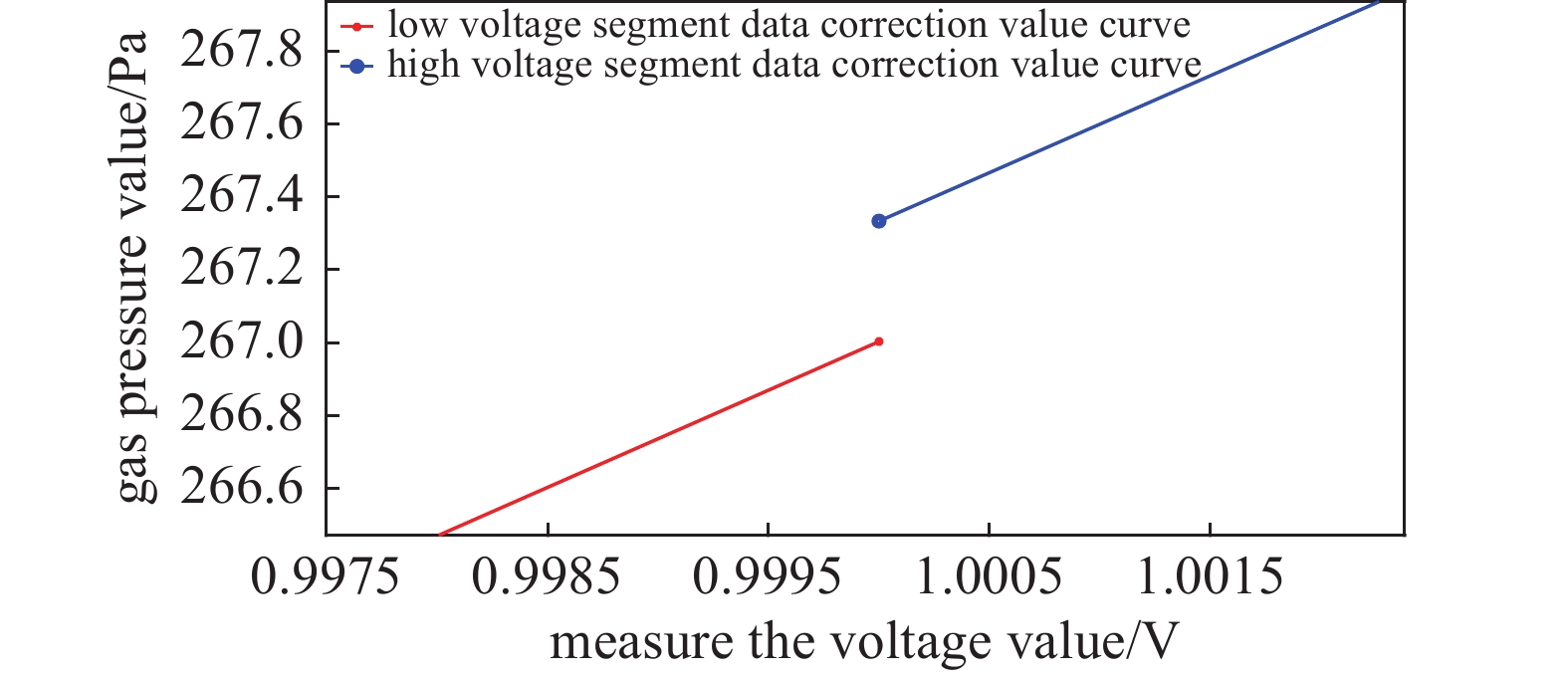
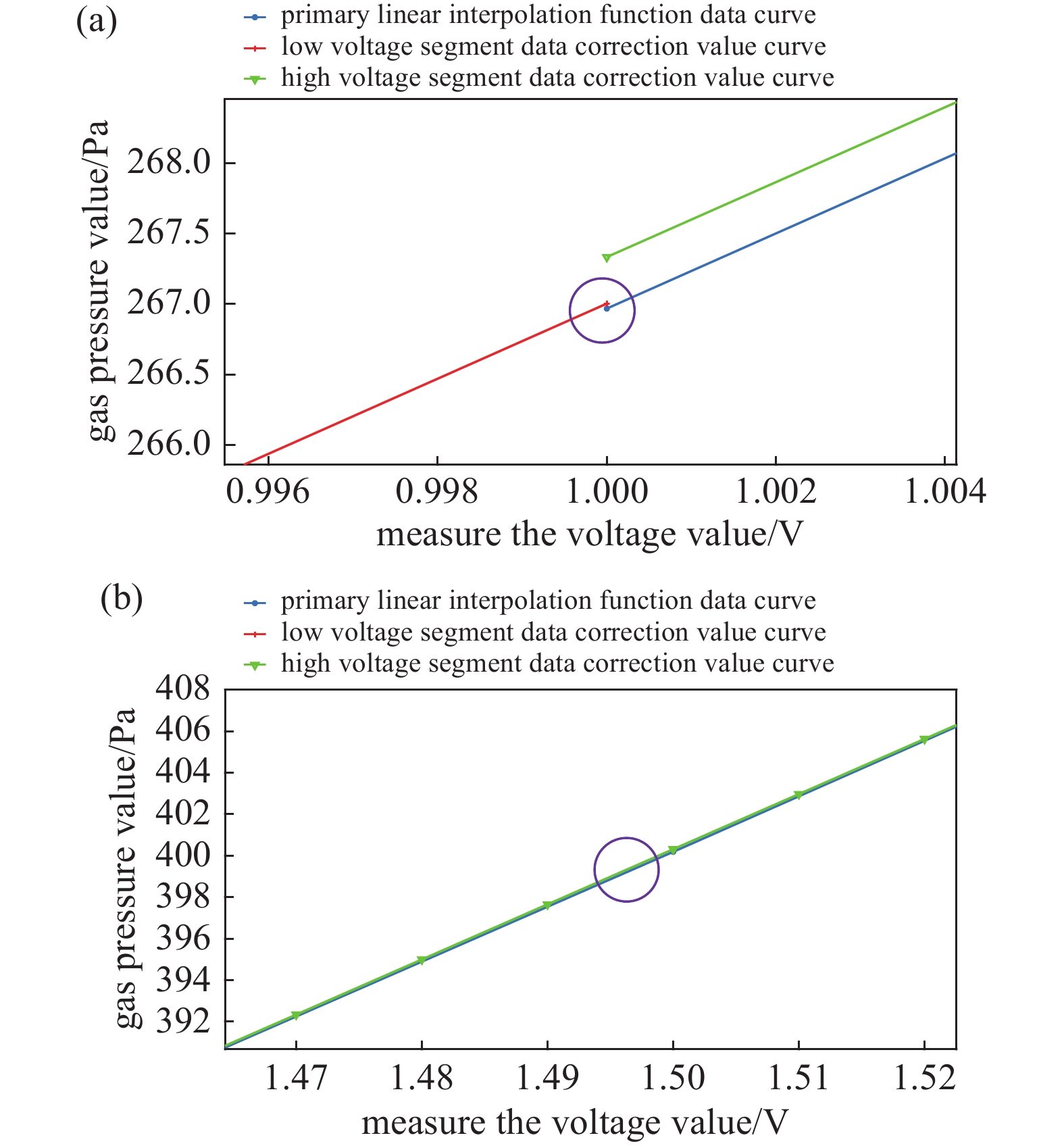
根据实验数据做出高、低压段修正数据曲线和一次线性插值函数的数据曲线图像，如图7（a）和图7（b）所示：

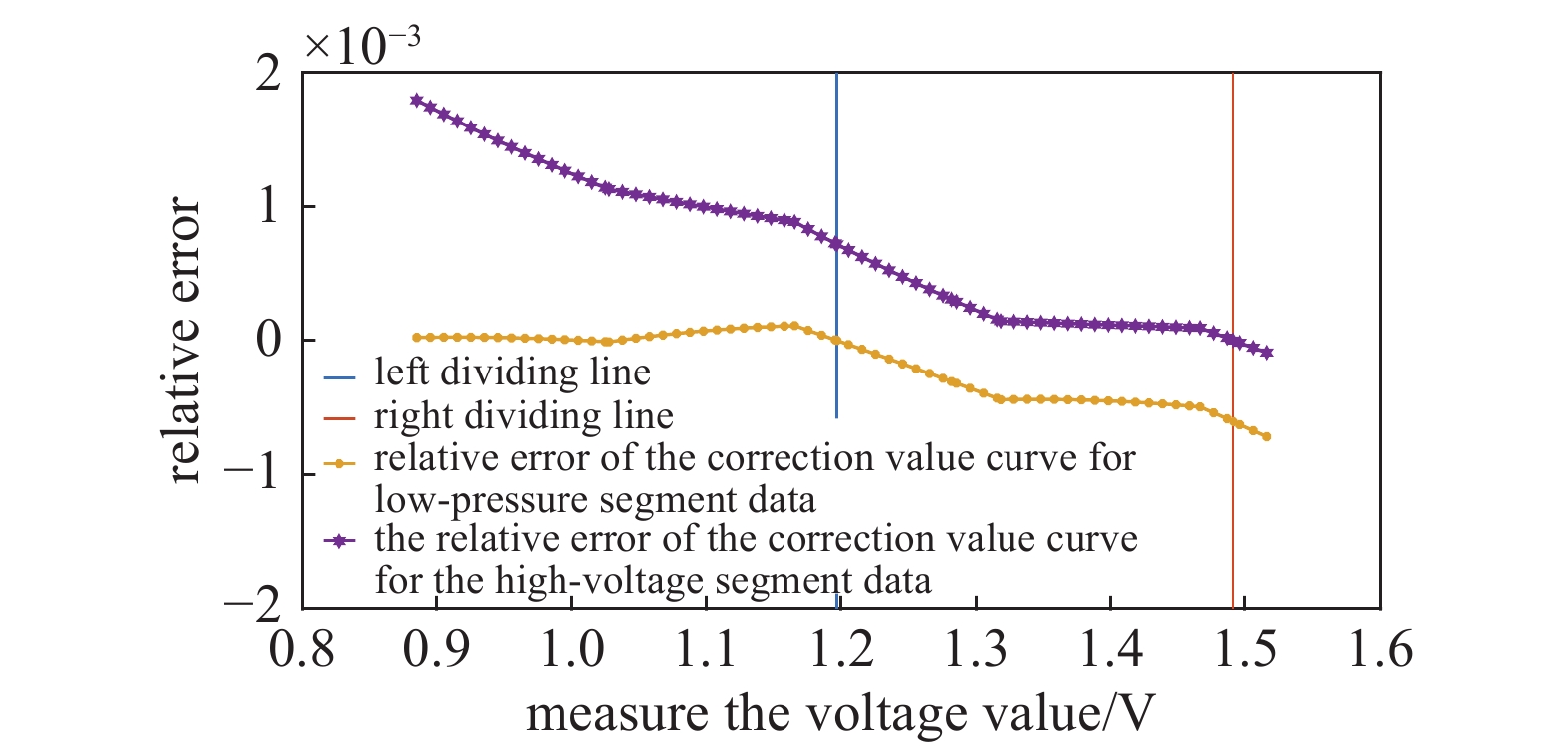
由图7（a）和图7（b）可知，插值函数的数据曲线在电压值1 V附近与低压段的修正数据曲线几乎重合，然后随着电压值的增大又慢慢的趋向于高压段的修正数据曲线。为了更加精确的分析插值函数曲线与高、低压段修正数据曲线的关系，以0.1 V为间隔从电压值1 V到1.52 V求出了对应电压值上的高、低压段气压数据修正值和气压标准值，然后根据高、低压段气压数据修正值的相对误差，画出了相对误差的变化曲线图，其结果如图8所示。

从图8中可以看出，在电压为1 V～1.2 V的数据区段上低压段的修正曲线与对应的标准值相对误差小于0.01％，所以可以在1 V～1.2 V区段上直接使用低压段的数据修正值。又因为在1.197 V数据点处的低压段气压修正值与标准值间的误差趋近于0，1.491 V数据点处的高压段压强修正值与该点标准值间的误差趋近于0。所以选择1.197 V和1.491 V两个数据点作为数据跳跃区间的左右端点。

设电容薄膜真空计的测量电压值为z，z在跳跃间断区间上的取值范围为[1.197 V，1.491 V]，根据图8可以看出高压段修正数据的相对误差随着z与1.197 V端点的距离增大而呈现逐渐减小的趋势，所以本算法选择z与1.197 V的差值作为输入量，用x表示。这里为了使跳跃间断区间的端点也能得到较好的处理，将x的取值范围适当扩大为[−0.1 V，0.3 V]。

由计算结果可知，高压区段的数据修正值与标准值间的相对误差范围为0％～0.0718％，为了提升模糊控制算法的处理效果，将高压区段的数据修正值与标准值间的相对误差值E扩大1000倍，将其定义为输出值u₂，即u₂的表达式（4）为：

模糊算法输出值u₂的基本论域为[0，0.718]，但是为了防止输出值的端点处得不到良好的控制导致算法输出失控，所以适当的扩大了u₂的基本论域，根据多次的实际处理结果，选择u₂的基本论域为[−0.1，1]。

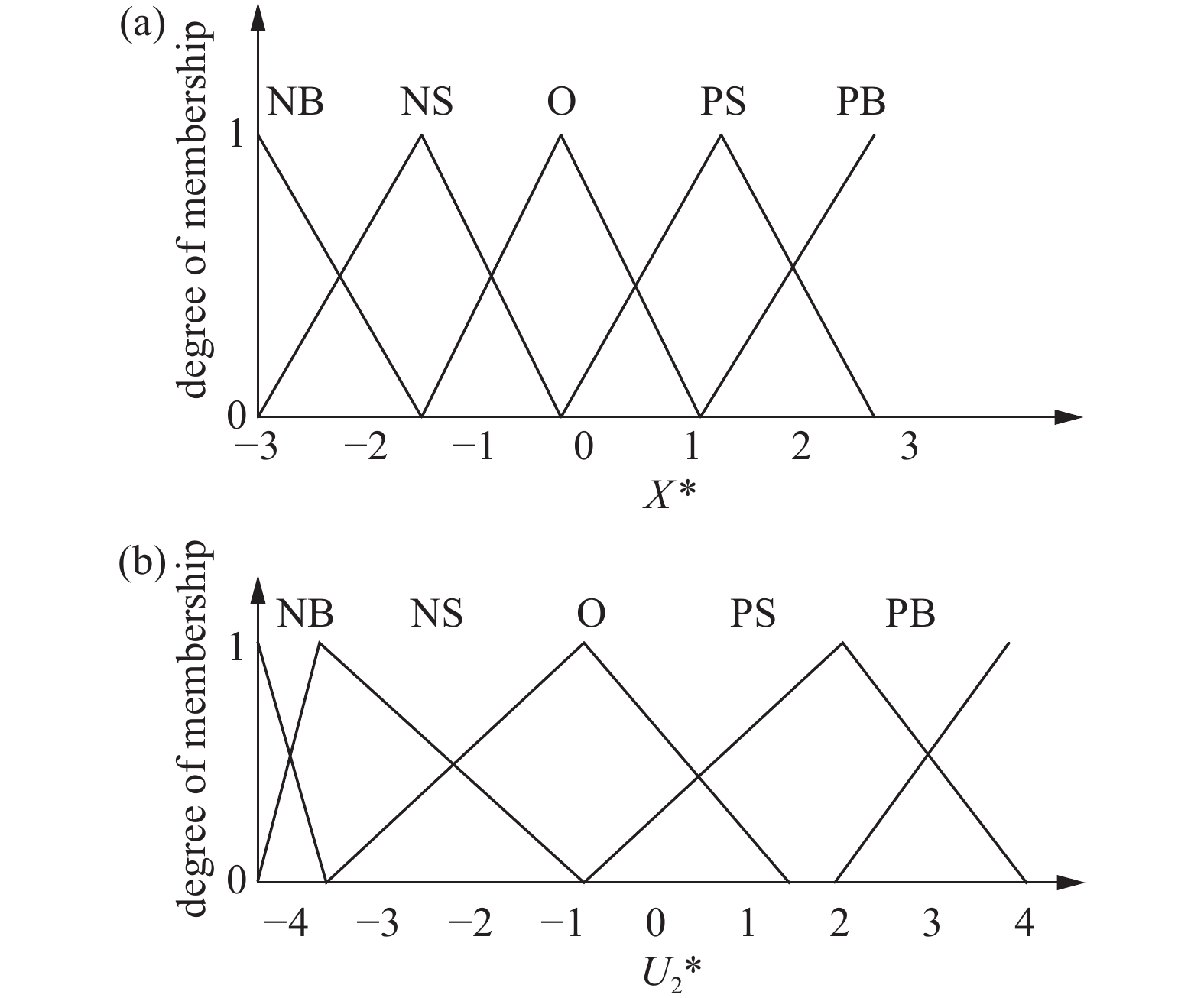
本文根据前面设定好的输入量x与输出量u₂的基本论域，初步选择它们的等级量论域分别为X=[−3，−2，−1，0，1，2，3]，U₂ =[−4，−3，−2，−1，0，1，2，3，4]。模糊控制算法的输入输出量都需要进行模糊化才能带入到算法中，选用线性变换公式（5）来对取值在[a，b]之间的连续量转换到[−n，n]之间,转换后的输入量用X*表示，转换后的输出量用U₂*来表示^[8]。

式中：y*为变换后的值，y为[a，b]之间的值。

最后将输入X*和输出U₂*的模糊控制论域语言表达变量设定为{NB，NS，O，PS，PB}，依次代表负大，负小，零，正小，正大^[9-13]。

选用三角隶属度函数作为基础函数，然后再根据输入量X*和输出量U₂*的几个关键值来对整个隶属度函数进行调整，使得其输出的结果更加符合预期。

输入量X*和输出量U₂*的隶属函数图像分别如图9（a）和图9（b）所示。

高压段的修正数据曲线与对应标准值的相对误差值u₂会随着电压值x（x∈[1.197 V,1.491 V]）的增大而呈现逐渐减小的趋势。所以该算法根据这一规律设定模糊规则如下表1所示。

其代表的含义为，当X*靠近跳跃间断区间左端点的时候，U₂*较大，当X*处于跳跃间断区间靠近中间部分时，U₂*为一个大概值，当X*靠近跳跃间断点右端点时，U₂*较小。

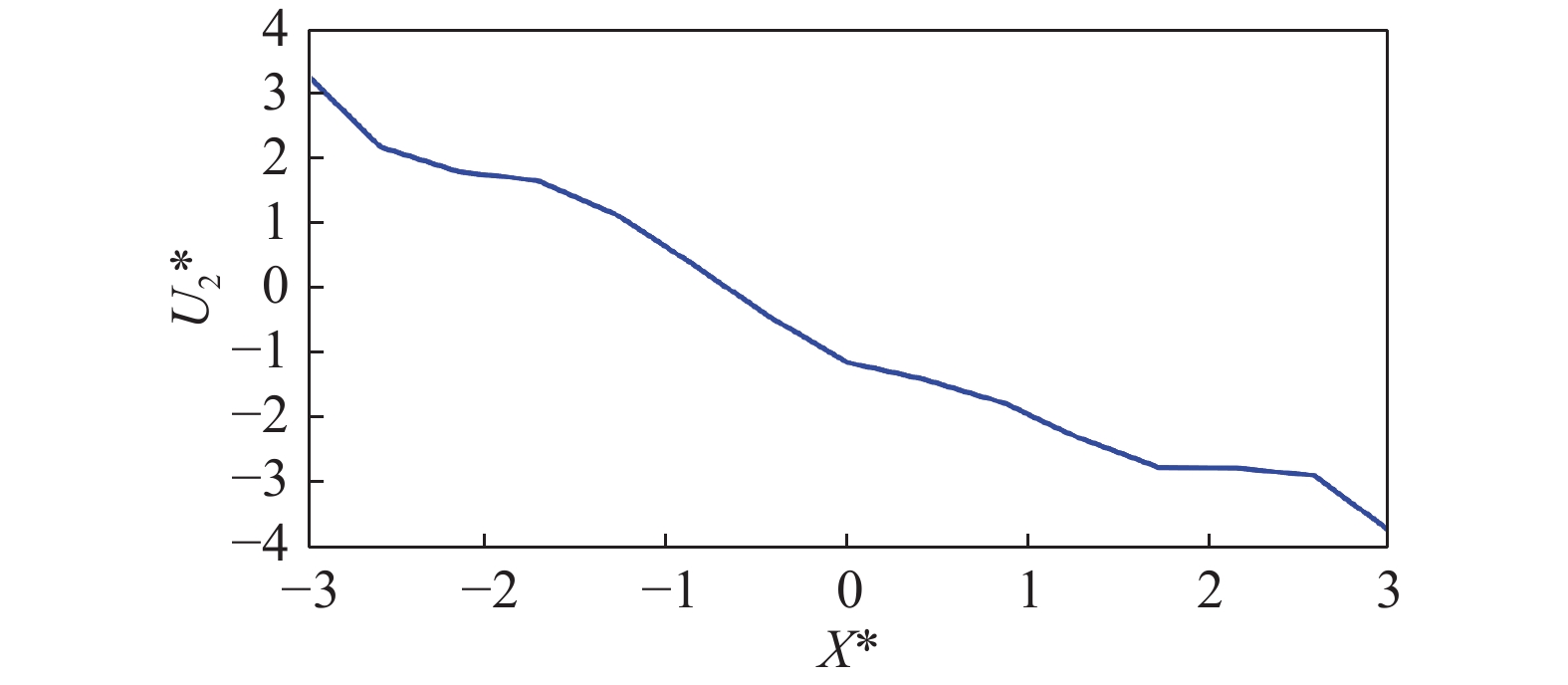
通过模糊推理得到的输出结果需要通过解模糊的过程才能转化为执行器可以执行的精确量，该算法采用重心法进行解模糊，重心法是目前比较常用的解模糊方法，它可以很好的兼顾多个部分对输出结果的控制，从而使输出值更加合理，重心法的计算公式如式（6）所示：

式中：$ \mu ({U_2}{*^ \bullet }) $为相应的模糊子集隶属函数的隶属度。

通过重心法解模糊后的输出值数据曲线如图10所示，可以看出模糊控制的输出值曲线符合所预期的输入输出量关系。

U₂*在得到解模糊化后需要通过线性变化公式（5）将U₂*的值重新转换为[-0.1,1]上的U₂值。在得出输入电压x值所对应的U₂值后，便可以用式（7）计算出此电压值点所对应的气体压强修正值p*。

式中：$p*$为经过模糊控制算法得出的对应于电压值x的气压修正值，p为电压值x所对应的高压段气压数据值。

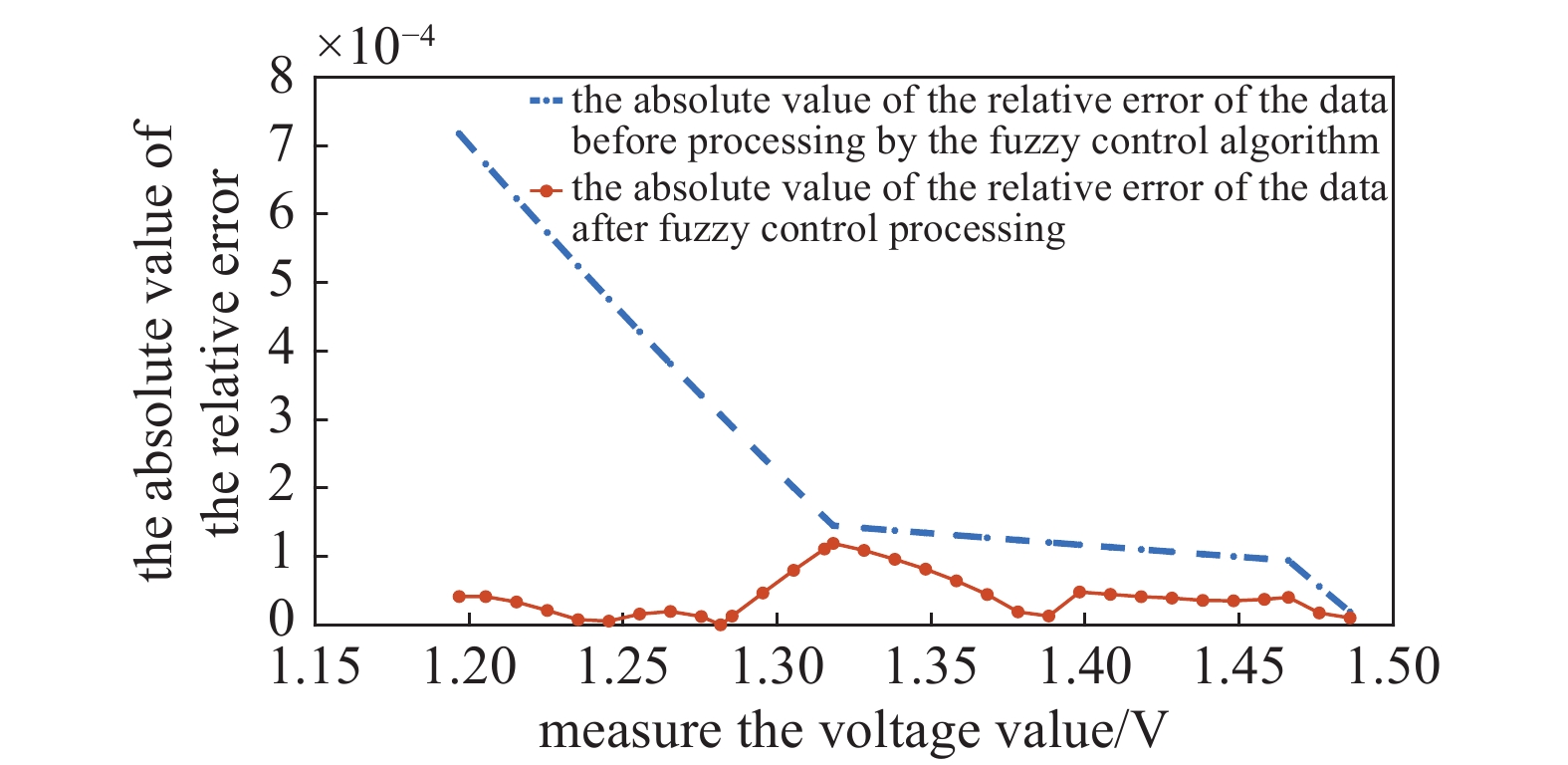
经过模糊控制算法的处理后，跳跃间断区间上气压数据的相对误差绝对值的变化如图11所示。

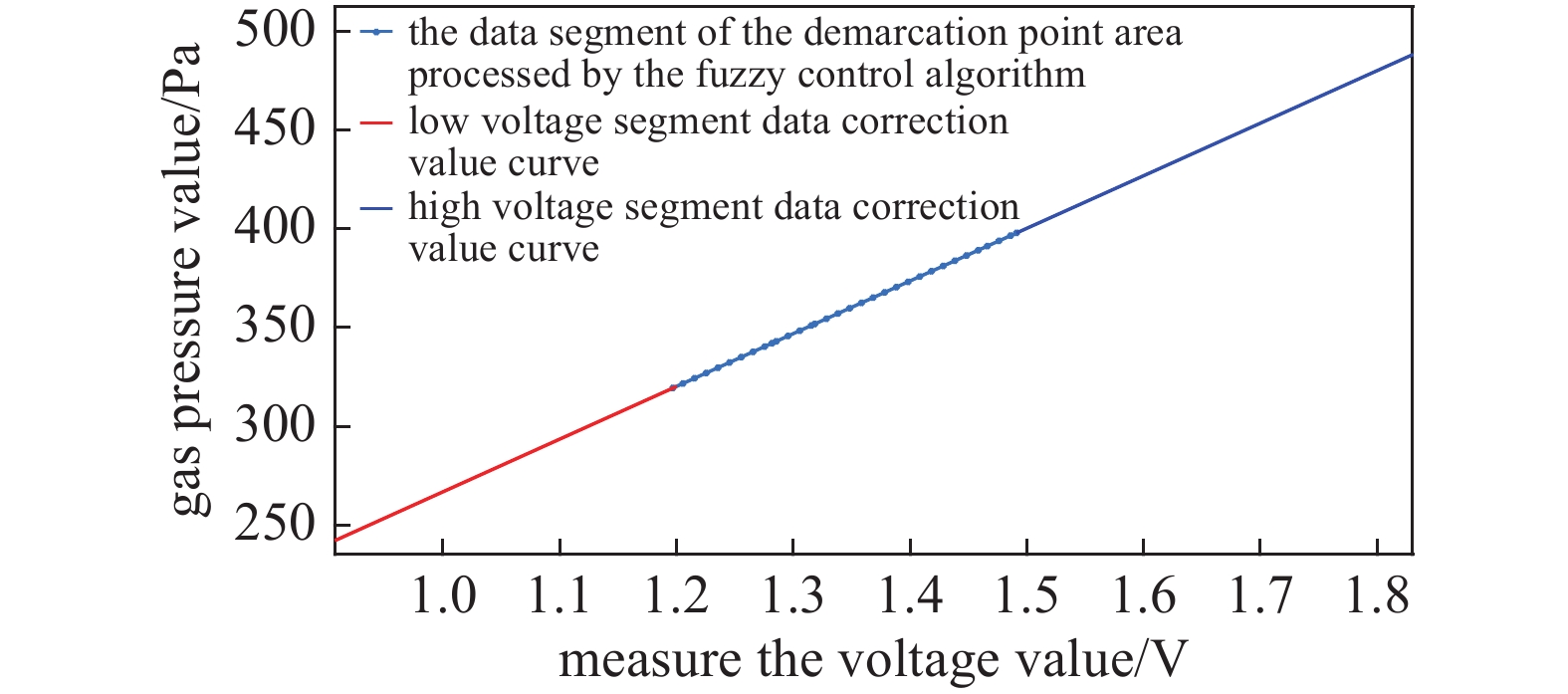
从图11中可以看出，通过数据模糊控制算法的处理后，跳跃间断区间上数据的相对误差绝对值都得到了减小，大部分数据的相对误差都减小为修正前的50％以下。如图12可以看出经过模糊控制算法处理后电容薄膜真空计的气压测量数据在全量程上为一条平滑连续的曲线，分界点处的跳跃间断现象得到了明显的减小。

为了在实际测量中验证该模糊控制算法对电容薄膜真空计的实际处理效果，将上述的误差曲线分段拟合修正算法和模糊控制算法写入到电容薄膜真空计的数据处理芯片中，然后在金属膨胀法标准装置上进行了两组全量程的测量实验，每次测量实验可以测得两个位于跳跃间断区间内的电容薄膜真空计气压测量值和其对应的气压标准值。这两组测量值通过数据算法处理后的结果如表2所示。

由表2可以看出，靠近分界点 1.197 V的数据点，在经过误差曲线拟合修正后，其相对误差变得比未修正前的数据相对误差还大，在经过了模糊控制数据处理算法的修正后其相对误差得到了减小，且小于原始测量数据的相对误差，提高了分界点附近数据的测量准确性，并且越靠近分界点的数据其修正效果越好。模糊控制数据处理算法的使用解决了分界点附近区间上数据出现跳跃间断的问题，使电容薄膜真空计在全量程上的测量数据曲线更加平滑连续，实际测试的结果验证了模糊控制数据处理算法的有效性。

使用误差曲线分段拟合的校准方法可以有效地降低电容薄膜真空计气压测量数据在各自分段区间内的误差。然而，在电容薄膜真空计的实际使用过程中，它会导致修正后的气压数据点在相邻段的分界点处产生跳跃和中断，导致边界点附近的气压值出现无法测量和误差较大的问题。模糊控制数据处理算法的加入，解决了测量数据在边界点附近出现间断跳跃的问题，使电容薄膜真空计的测量曲线更加平滑、更加连续，从而提高电容薄膜真空计的测量精度。

增加数据区间分割的数量可以在一定程度上提高电容薄膜真空计的测量精度，模糊控制数据处理算法的应用可以实现更多数据区间的划分，而不用担心各分段边界点出现跳跃间断的问题。

尽管数据处理算法可以在一定程度上弥补电容薄膜真空计在材料和加工技术方面的不足，但要实现更高的测量精度，电容薄膜真空计在材料结构和加工技术等方面仍需进一步改进，只有不断的提高电容薄膜真空计的测量稳定性和重复性，才能更好的发挥出数据处理算法的作用。