-
EAST作为中国研发的世界首个核聚变装置,通过磁约束进而实现受控核聚变[1]。EAST装置是中国核聚变能源研究的重要平台,通过对等离子体物理和工程技术的研究,为实验核聚变能源提供重要的数据来源以及技术支持。同时EAST装置也是中国与国际核聚变能源研究机构合作的重要坚实基础,为中国在国际核聚变能源研究领域的地位提升和影响力提供重要支持,推动了中国在核聚变能源领域的技术创新与发展,为中国在未来能源领域的发展提供重要技术支持。它可以有效保障高参数等离子体的运行,为聚变反应提供重要工程应用基础。然而,作为获取EAST装置真空环境的重要设备分子泵,难免在实验过程中会发生异物坠入或真空泄露等故障,使分子泵叶片变形甚至碎裂,给EAST装置带来次生危害[2]。所以,为了减少分子泵故障对EAST装置的损害,需要采取措施来预防和处理这些故障是非常有必要的。
故障诊断指通过测试、判断等手段,对设备、系统或工艺出现的故障进行分析和判断,发现问题,完善改进。通过有效的故障诊断策略,可以及时发现设备或者系统存在的潜在问题及安全隐患,采取措施避免事故发生,从而保障人员和设备安全。减少不必要的维修和更换成本,意义重大。故障诊断通过三个步骤实现。首先采集正常以及故障振动信号,然后对数据预处理,实现特征提取,最后构建故障诊断模型,进行测试集诊断。其中,数据的预处理以及模型的优劣直接决定故障诊断精度的高低。
目前信号处理和机器学习的特征提取方法已普遍用于振动信号分析。机器学习算法利用自主学习模式,挖掘数据间隐藏杂乱无章的规律,在使用机器学习模型训练过程中,由于模型参数较多,网络层次较深,导致训练时间变长。基于时域频域提取的特征可以节约时间,无需模型的反复训练,对于分子泵故障诊断非常有利。同时直接对原始数据处理,最大程度保留数据特征,所以本文提出基于时域频域方法对数据进行预处理。
目前,国内学者对故障诊断研究取得了一系列成果。黄竞楠等[3]针对故障轴承由于噪声及故障信息不易提取问题,提出BP神经网络融合奇异值分解与集合经验模式分解的轴承故障诊断策略,结果表明该方法可用于轴承故障诊断。熊剑等[4]针对滚动轴承信号不稳以及不易提取等问题,提出短时傅里叶结合改进残差网络方法,实现更高的准确率诊断。贾凯等[5]针对分子泵故障诊断率低问题,提出时域结合频域的数据处理方法,最后输送到改进LightGBM算法,有效实现分子泵高精度检测。慕晓冬等[6]针对航天器测控故障诊断率低问题,提出基于注意力残差网络(AM-ResNet)故障诊断策略,使得航天器测控系统故障检测率得到有效提高。Zhou等[7]提出了一种基于多模态特征融合的深度学习方法直接提取时域数据中涉及的异常特征的潜在频率,实现对旋转机械进行准确诊断。Shuai等[8]研究提出了一种结合形态学特征提取和支持向量的智能故障诊断策略回归(SVR)分类器,在不受噪声影响的情况下,该方法具有较高的精度。王骁贤等[9]提出通过多传感器信号深度特征融合的方法实现有效识别电机运行状态。
目前机器学习诊断算法,在数据集是平衡的情况下取得了较好(或很好)的成果。但面对工业实际运行状况,分子泵故障数据是极少的,数据集是不平衡的,导致机器学习算法故障诊断精度低以及模型过拟合问题。针对上述情况,本文提出一种基于时频域预处理与改进BP相结合的算法,实现分子泵故障诊断。
BP神经网络可以有效的解决非线性问题[10],是目前阶段比较成熟的神经网络。BP算法与其他机器学习算法最大的特点是信号传递方向与误差传递方向不一致。信号是向前传递的,而误差是向后传递的。当神经网络在传递过程中,出现输出结果与实际结果误差较大时,就会自主改变传播方向,不断调整权值和阈值,使误差最小。但在BP神经网络训练的过程中,往往存在陷入局部最优解的问题,不易训练出最优模型。
为了解决这个问题,提出在BP神经网络原始的基础上引入PSO算法,保障BP神经网络在计算过程中,可以很大程度上避免局部最优解,同时结合五折交叉验证算法避免模型过拟合,从而寻找最佳适应度值,得到最优参数,训练出最优神经网络模型,提高分子泵故障诊断的精度。
-
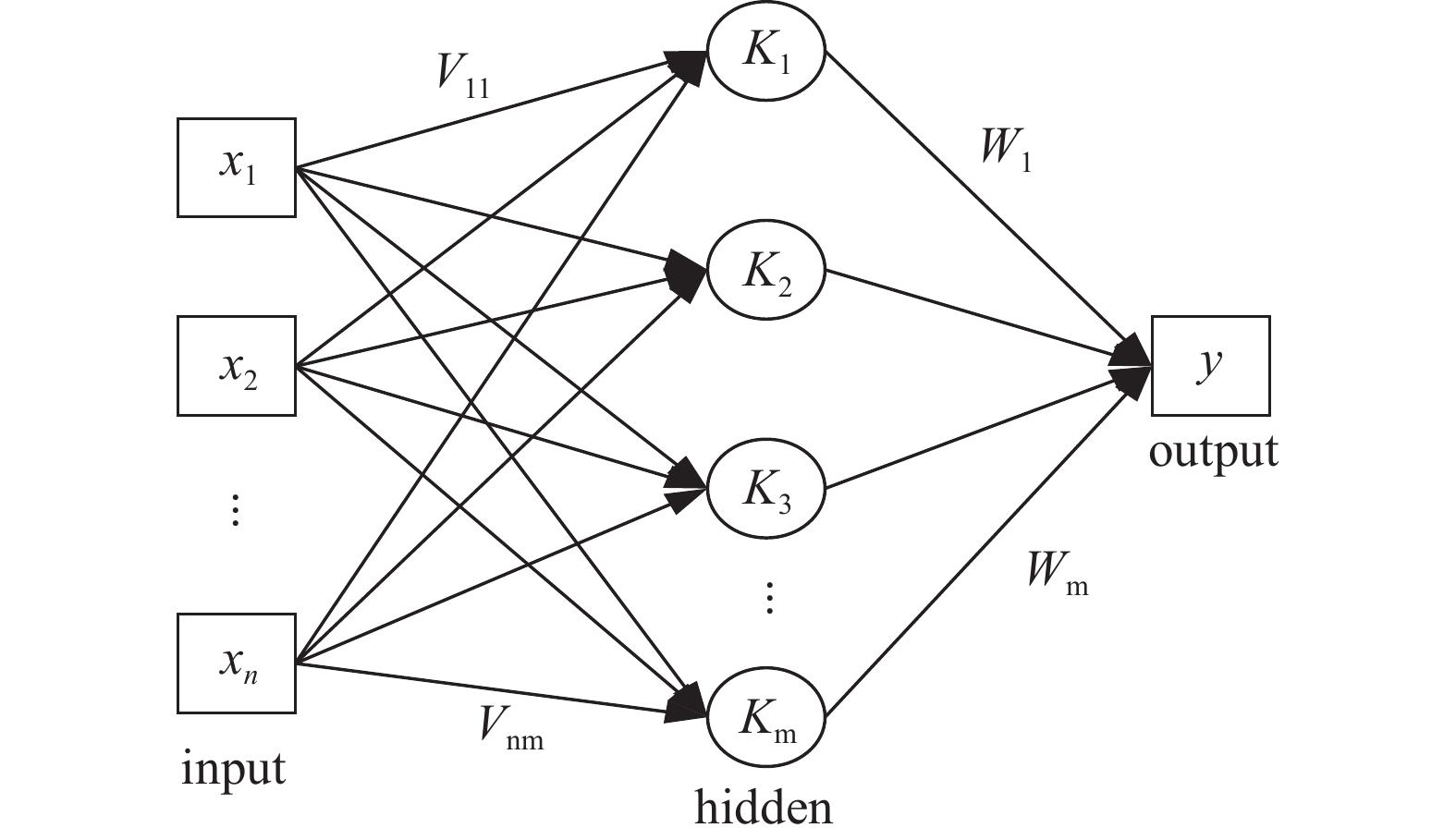
BP神经网络作为一种常见的人工神经网络,同时也作为一种监督学习方法,多用于训练神经网络以进行回归与分类任务[11]。图1为BP神经网络原理图,包括输入层、输出层和隐含层[12-13]。其中
$ x_{1}, x_{2}, \cdots ,x_{n} $ 为输入变量,$ y $ 为输出变量,$ k_{m} $ 为隐藏神经元的输出,存在$ f $ 为激活函数的映射关系。假设$ \boldsymbol{v}_{ {ij }} $ 为第$ i $ 个输入变量与第$ j $ 个隐藏层神经元的权重;$ \theta_{j}^{{k}} $ 为隐藏层$ k $ 第$ j $ 个神经元的阈值,即偏置项。可得$ k_{j} $ 表达式:假设
$ w_{j} $ 为第$ j $ 个神经元与$ y $ 连接的权重,$ \theta^{y} $ 为$ y $ 的偏置,存在$ f $ 为激活函数的映射关系。可得输出$ y $ 表达式为: -
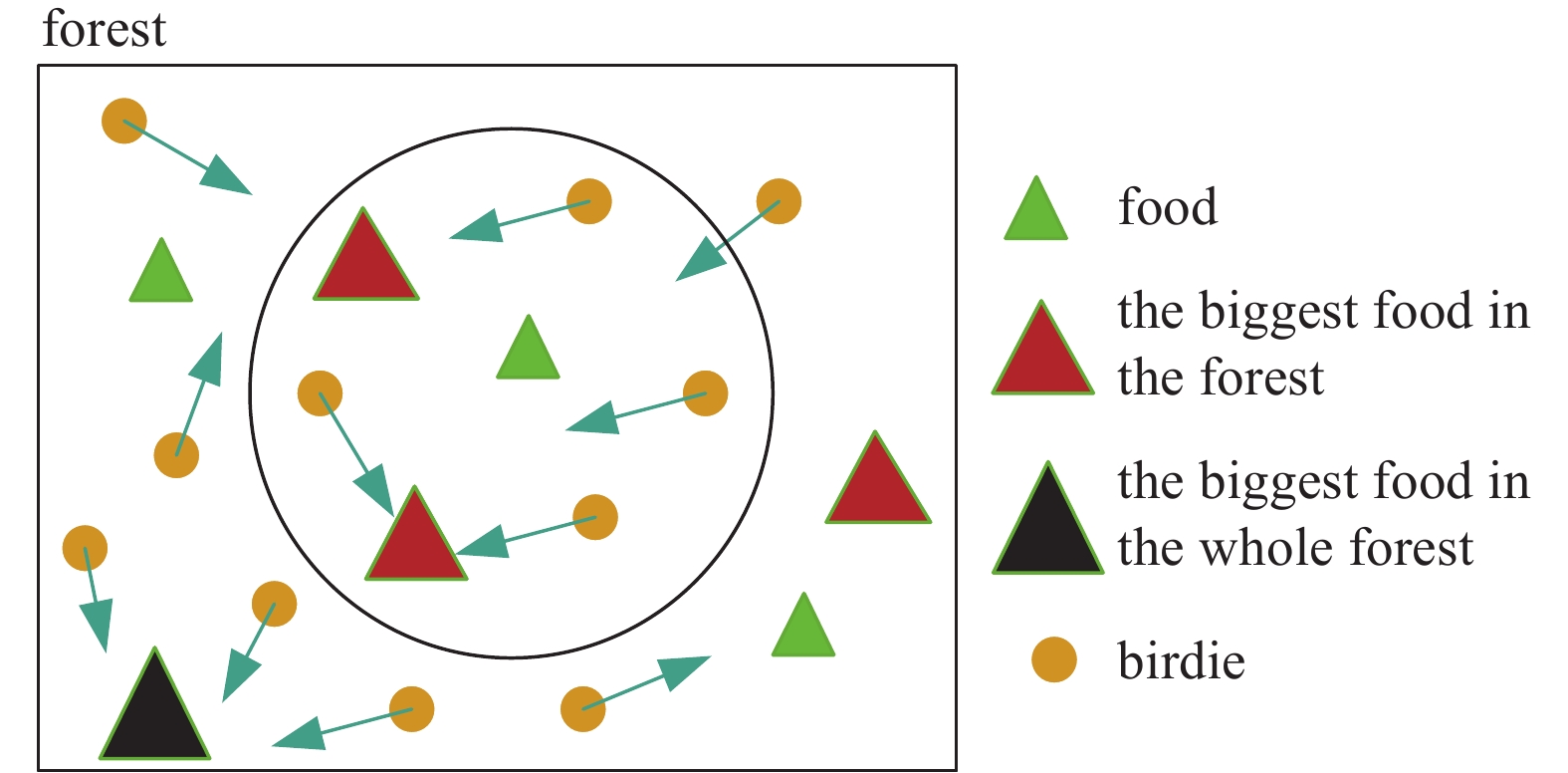
粒子群算法的思想就是类比鸟群通过集体的信息共享,从而求得问题的最优解[14-15]。粒子群算法具有优良的收敛速度和搜索效率[16]。原理如图2所示,鸟相当于粒子;森林相当于求解空间;食物的相当于适应度值;每只鸟所处的位置相当于空间中的一个解;食物量最多的位置相当于全局的最优解。
假设
$ D $ 维搜索空间中,单个群落包含$ N $ 个粒子,单个$ D $ 维向量由第$ i $ 个粒子表示,记为:单个
$ D $ 维的向量也可表示第$ i $ 个粒子的飞行速度,记为:个体极值定义为第
$ i $ 个粒子群搜索到的最优位置,记为:全局极值定义为整个粒子群检索到的最优位置为,记为:
在找到这两个最优值时,粒子需要根据如下公式来更新自己的速度和位置:
$ N $ 代表粒子群规模,$ i(i=1,2, \cdots N) $ 代表粒子序号;$ D $ 代表粒子维度;$ d(d=1,2, \cdots D) $ 代表粒子维度序号;$ t $ 代表迭代次数;$ \boldsymbol{w} $ 代表惯性权重;$ c_{1} $ 代表个体学习因子;$ C_{2} $ 代表群体学习因子;$ r_{1}, r_{2} $ 代表区间在$ [0,1] $ 内的随机数[17-18];$ v_{id}(t) $ 代表粒子$ i $ 在第$ t $ 次迭代中第$ d $ 维的速度向量;$ x_{i d}(t) $ 代表粒子$ i $ 在第$ t $ 次迭代中第$ d $ 维的位置向量;$ P_{ {beat }}(t) $ 代表粒子$ i $ 在第$ t $ 次迭代中第$ d $ 维的历史最优位置,$ P_{ {d,gbest }}(t) $ 代表粒子在第$ t $ 次迭代中第$ d $ 维的历史最优位置。通过粒子群算法较快的收敛速度以及高效的全局搜索能力,同时对于BP神经网络的初始化参数不敏感等优势,由助于提高BP神经网络的性能与泛化能力,从而更好的提升分子泵故障诊断的精度。 -
交叉验证是一种统计分析方法,将数据分成K组,按K-1与1的比例提取训练集与验证集,重复K次,获取K组训练模型状态,再利用相关评价指标,选定其中误差最小的一组来定义最优模型。本文实验选取五折交叉验证避免模型训练出现过拟合现象,来提高模型预测精度。
-
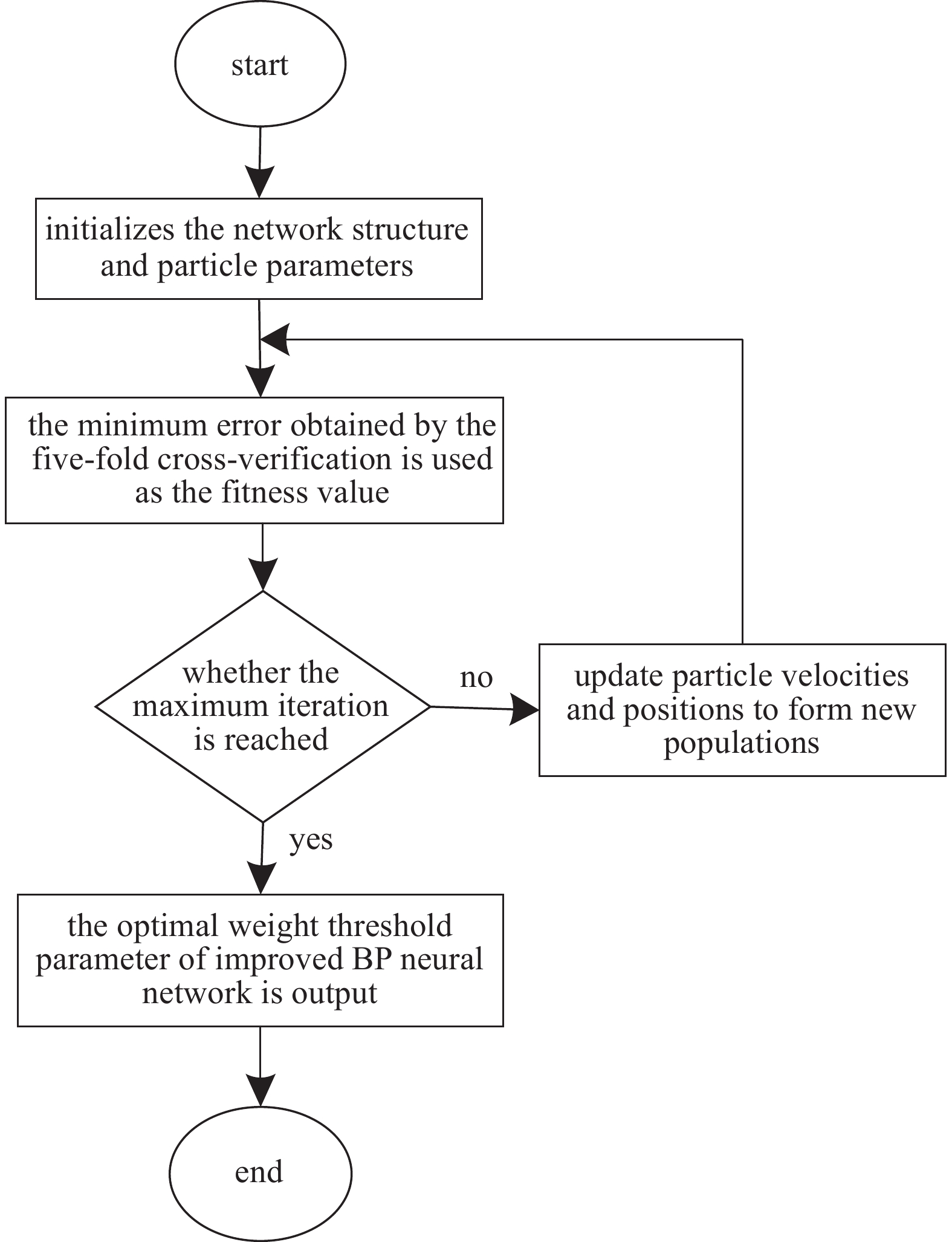
针对分子泵在不同故障类型状态下,由于数据集不均衡导致故障诊断精度低问题,提出在BP神经网络的基础上引入粒子群与五折交叉验证算法来优化诊断模型,提高分子泵故障诊断的精度。改进BP算法流程如图3所示。
首先,初始化BP神经网络结构和种群参数,通过五折交叉验证得到最小误差作为适应度值。在没有达到设定的最大迭代次数前,不断更新调整当前粒子的速度与位置,形成新的种群,并结合五折交叉验证计算最佳适应度值。直到迭代次数完成,输出改进BP算法的最优权值阈值参数,模型训练结束。
-
信号的分析主要可分为时域分析、频域分析和时频域分析[19]。基于传统的时频域特征提取方法,可以提取最直接的信号特征,是一种快速且高效的特征提取计算方法。时域特征统计表达式如表1所示,其中N代表一个周期内采样点数,X代表样本数据,
$ x_{i} $ 表示当前周期内第$ i $ 个数据样本。本文选取最大值、最小值、峰峰值等10种时域特征来描述振动信号状态信息,如表1所示。仅仅依据时域统计特征,很难完整反映分子泵振动信号的特征,所以结合频域分析,更好反映数据隐藏的特征。时域信号和频域信号参数通过快速傅里叶(FFT)相互转化, FFT的数学表达式如(9)所示:
其中
$ k=0,1, \cdots N-1 $ ,$ W_{N}=e^{-j \tfrac{2 \pi}{N}} $ 是旋转因子,$ X_{k} $ 为频域值,$ x(n) $ 为时域采样点,$ {n} $ 为时域采样点的序列索引,$ {k} $ 为频域值的索引,$ N $ 为转换的采样点数量。本文选用频率均值、频率重心、频率标准差三种状态频域特征描述分子泵振动状态信息,与时域特征结合,多层面反应信号特征,可以有效提高故障诊断的精度。具体表达式如表2,单个周期FFT变换频谱长度与基波对应频谱幅度分别由L和
$ f_{j} $ 代表。 -
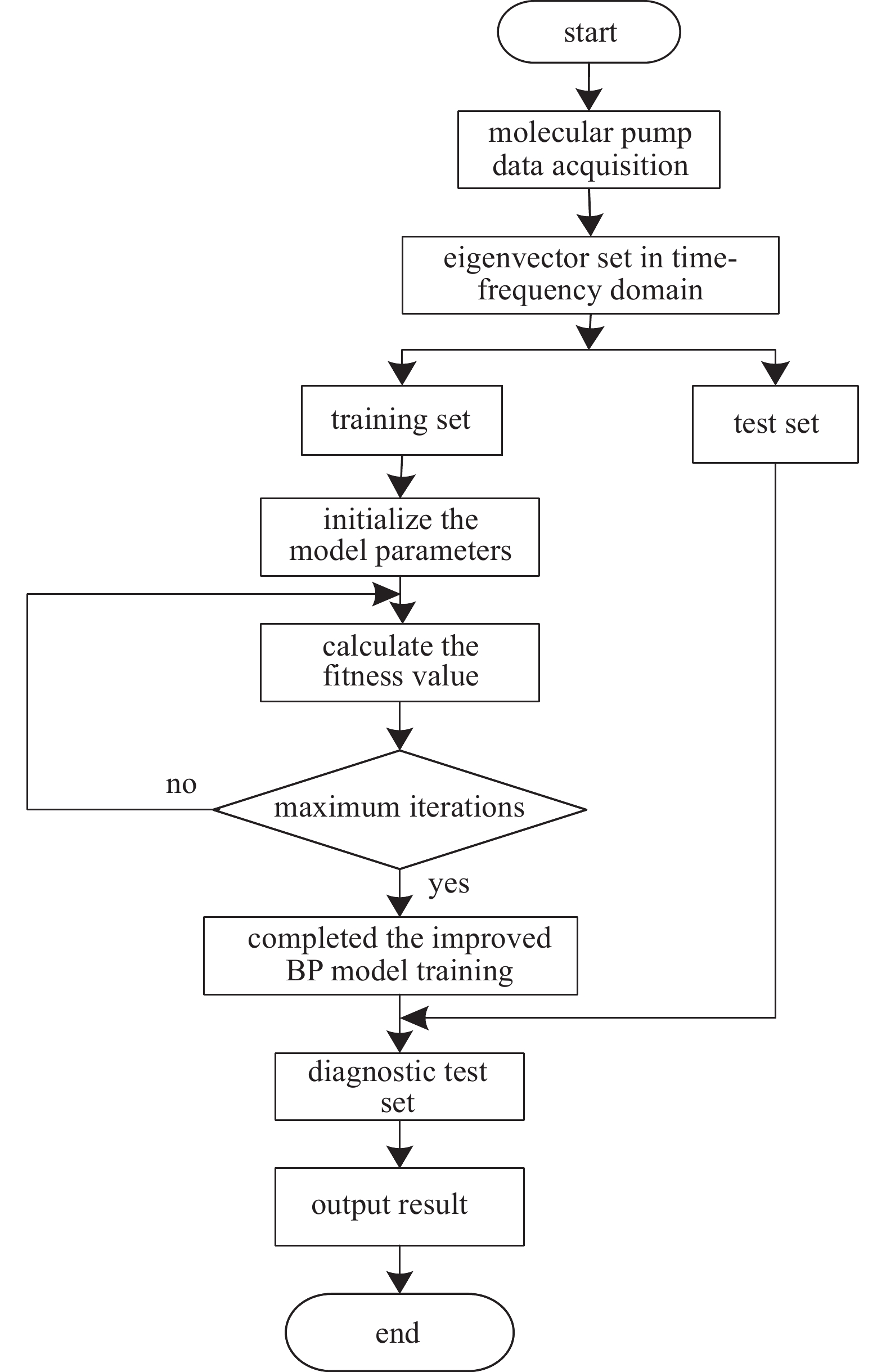
分子泵故障诊断流程如图4所示。首先,对实验平台采集的振动数据做预处理,提取时域频域特征,组成特征向量集,按一定比例提取测试集,输送到初始化状态的模型,通过五折交叉验证算法得到最小误差作为适应度值,根据是否达到最大迭代次数,不断更新粒子种群参数,并结合五折交叉验证计算最佳适应度值,完成模型训练;最后,将预处理好的测试特征向量集输入已经训练好的模型,通过相关评价指标判断模型诊断结果的好坏。
-
此实验在搭建的模拟分子泵破坏性测试平台上开展,为EAST装置的前期模拟试验阶段。在分子泵中,流动的气体分子与电机驱动的旋转叶片或者转子发生剧烈碰撞,导致泵内气体分子不断失去动能,最终被抽出真空室,从而为后期实验提供高真空的运行环境。为了保障分子泵电机的正常运转,机械泵需要提前启动,待工作一段时间,让装置获得一个较低的真空环境大概10 Pa左右,再打开分子泵继续抽真空,从而获得一个高真空运行环境。
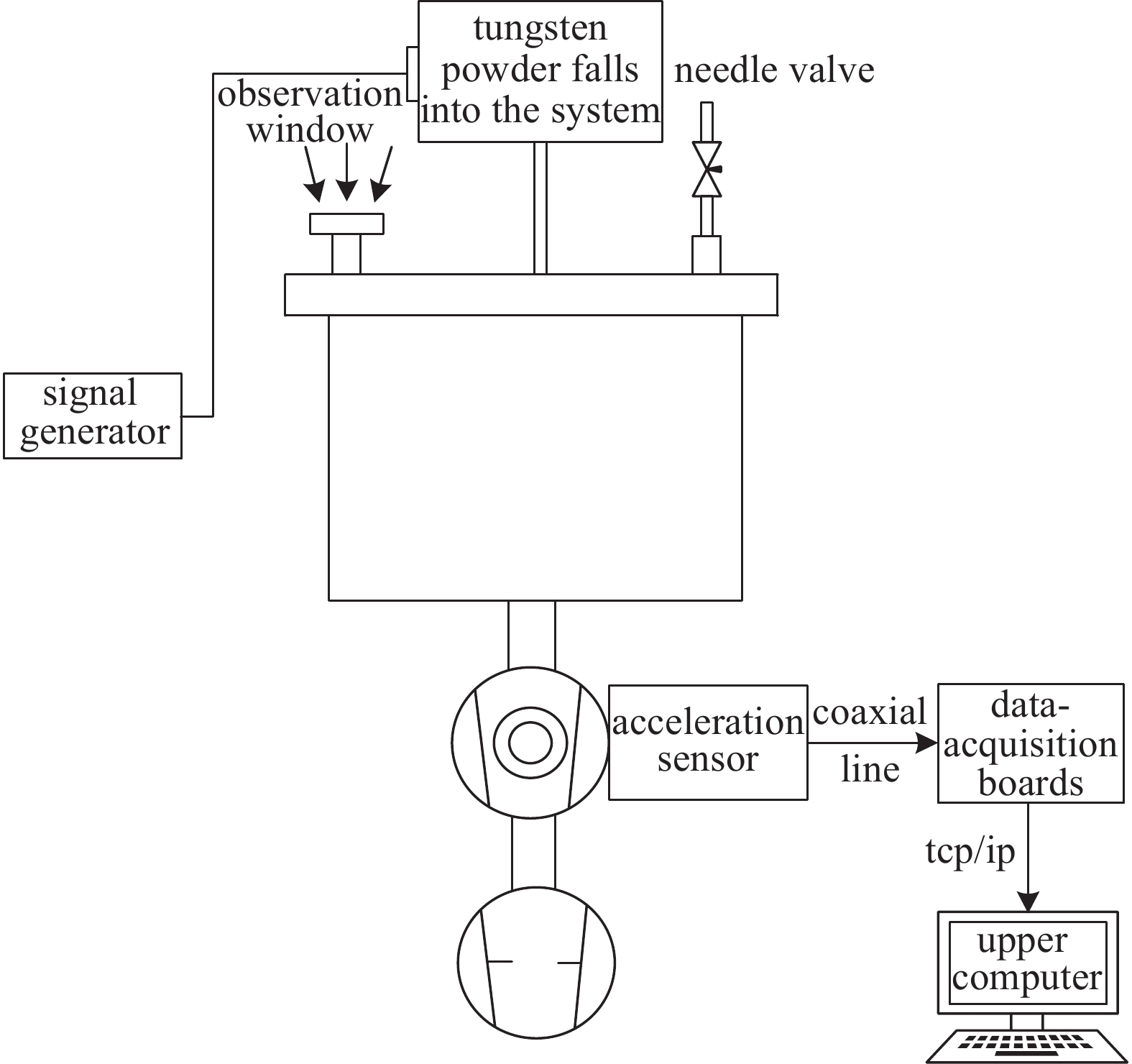
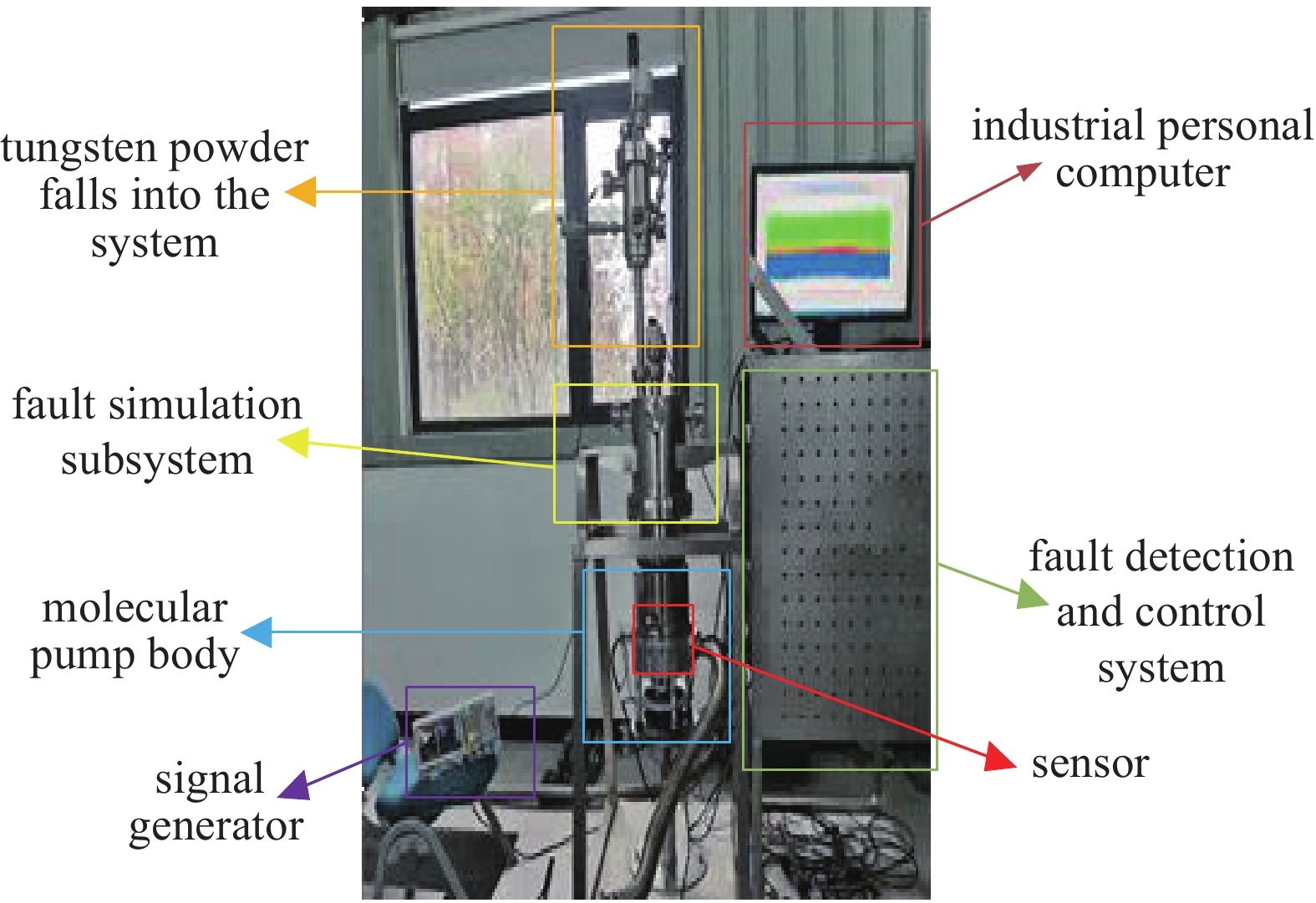
分子泵破坏性测试平台示意图如图5所示。该系统主要由抽气系统,真空腔体、针阀、传感器、信号发生器、钨粉坠入系统以及上位机组成。系统涉及仪器设备型号:久泰真空分子泵、久泰真空分子泵电源、普发真空计、NI-9232采集板卡、cDAQ-9189以太网机箱、加速度传感器、RIGOL信号发生器以及Windows 11 64位上位机系统环境,该系统有效的保障了故障诊断实验的顺利开展。
-
此实验采集3种分子泵运行状态的振动信号。(1)在分子泵处于正常状态运转时,采集分子泵正常振动信号;(2)在分子泵正常状态运行下,打开泄气阀,泄气至100 Pa,采集轻度真空泄漏故障振动信号;(3)在分子泵正常状态运行下,打开泄气阀,泄气至250 Pa,采集中度真空泄漏故障振动信号;(4)在分子泵正常状态运行下,采集钨粉坠入系统故障振动信号;
设置采样频率为1 KHz。在采集钨粉异物坠入实验时,信号发生器峰峰值设为15 V,频率设为2.25 KHz,手动触发信号,循环数设为9000,通过多次触发,对钨粉进行流量标定,计算得每触发一次流量为0.00618 g,本实验共触发352次,共坠入2.17536 g。
采集正常数据20000个,真空泄漏100 Pa故障数据8000个,真空泄漏250 Pa故障数据6000个,钨粉坠入故障数据4000个。经过时频域特征提取,得到2000组正常振动特征数据,800组轻度真空泄漏故障数据,600组中度真空泄漏故障振动特征数据,400组钨粉坠入故障振动特征数据,将训练集与测试集按8:2划分。实验平台如下图6所示。
-
改进BP神经网络参数设置如表3所示。13个特征作为输入,输入层节点数为13;隐藏层节点数设为6;输出为4分类,输出层节点数为4;学习率设为0.002;目标误差设为0.00001;最大训练次数设为500;最大迭代次数设为75;种群数量设为8。
-
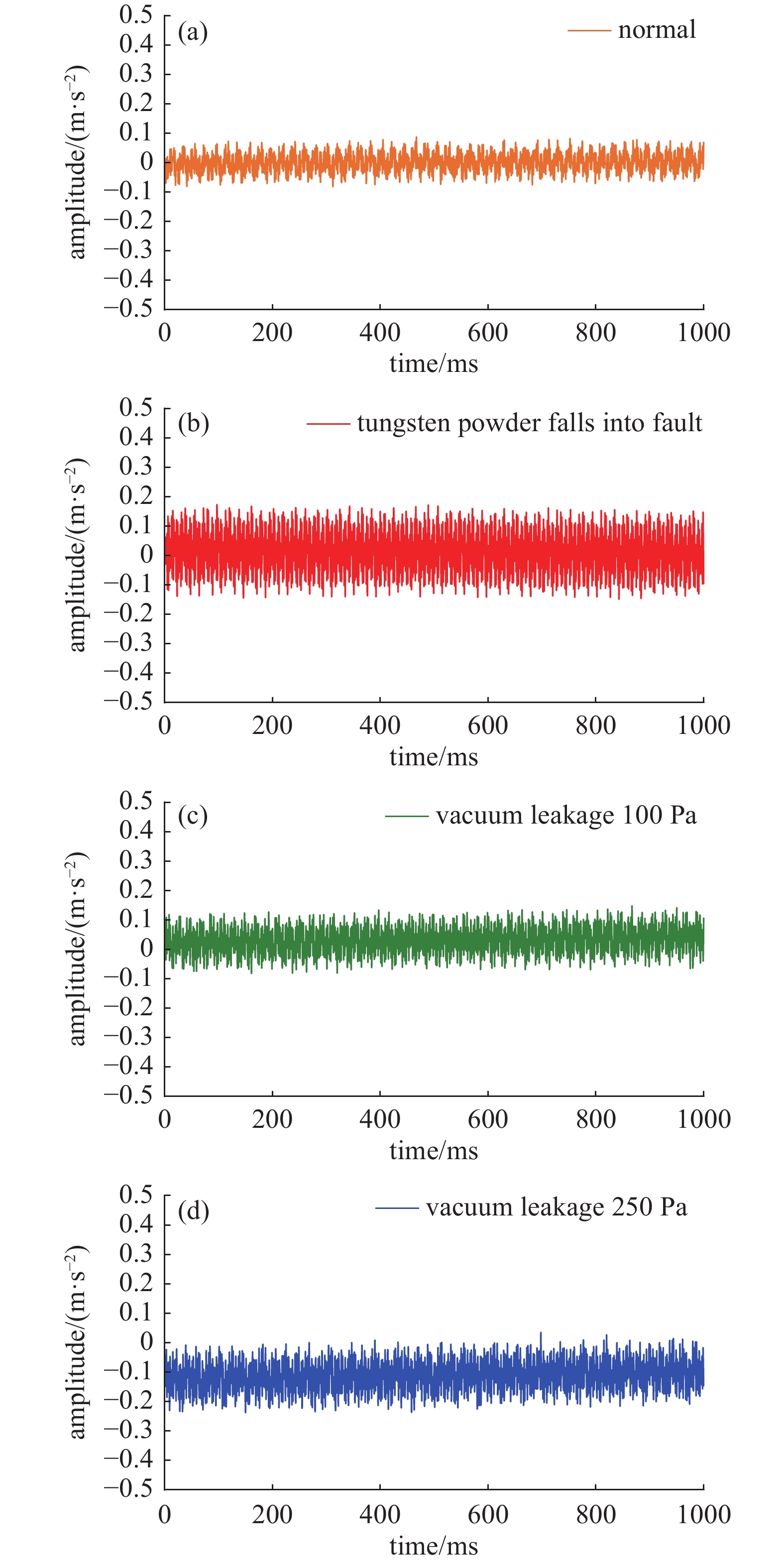
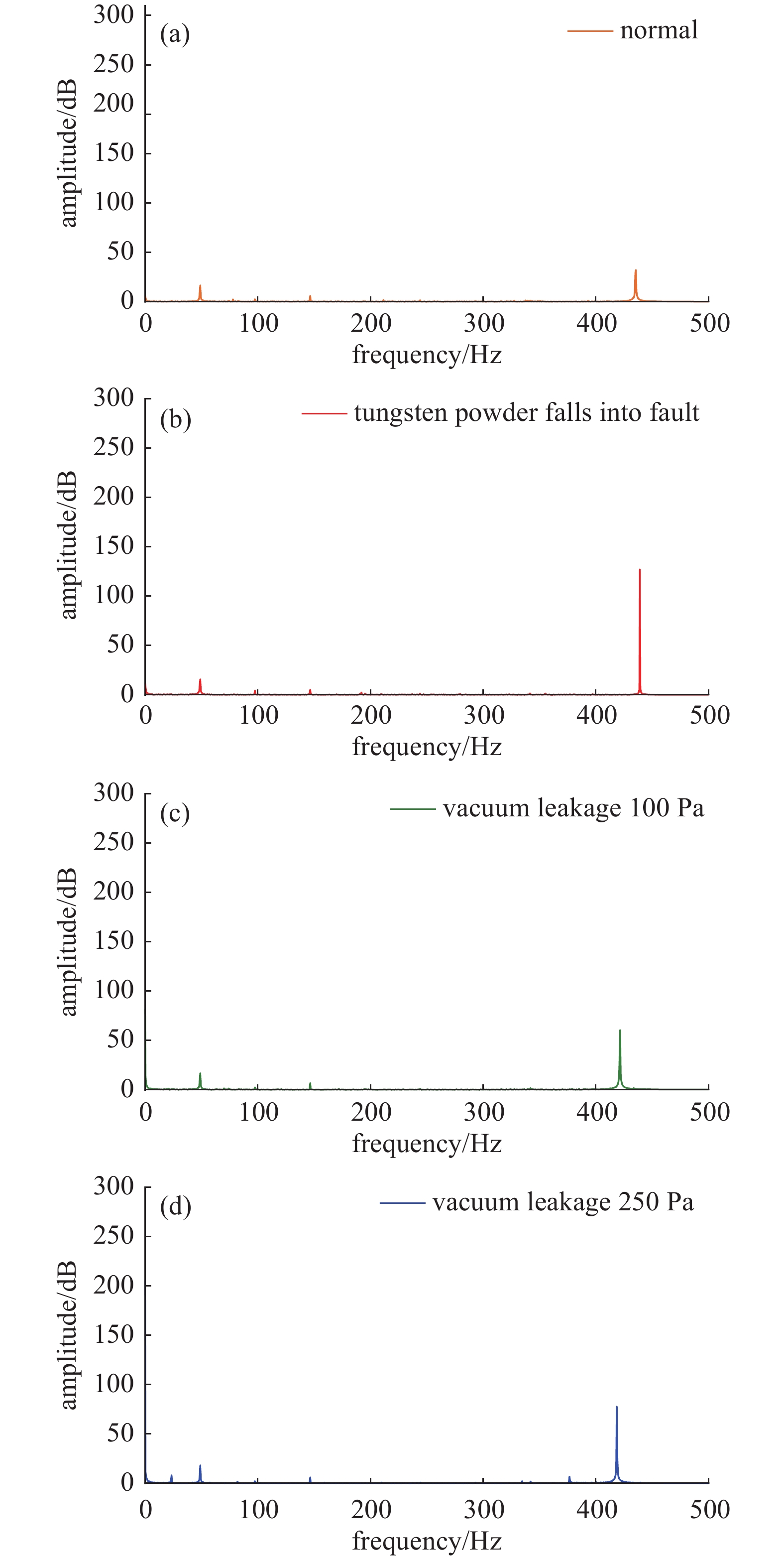
在分子泵主体外部安装加速度传感器,全方位(X轴、Y轴、Z轴)监测采集分子泵振动信号。如图7、图8所示,是分子泵在正常状态、钨粉坠入故障态以及真空泄漏故障态四种状态下运行的Y轴时域、频域图。时域图可以直观的显示信号的波形振幅等信息,观察信号的瞬时变化情况,由时域图7可知,分子泵在故障态下,电机负载运行,振动幅度明显高于正常状态且故障态振动信号毛刺明显增加。为了更好的分析振动信号的特征,通过引入频域图,如图8所示,可以更直观显示不同频率成分的贡献状况,相较于正常态,在故障态下固有频率处幅度发生变化。
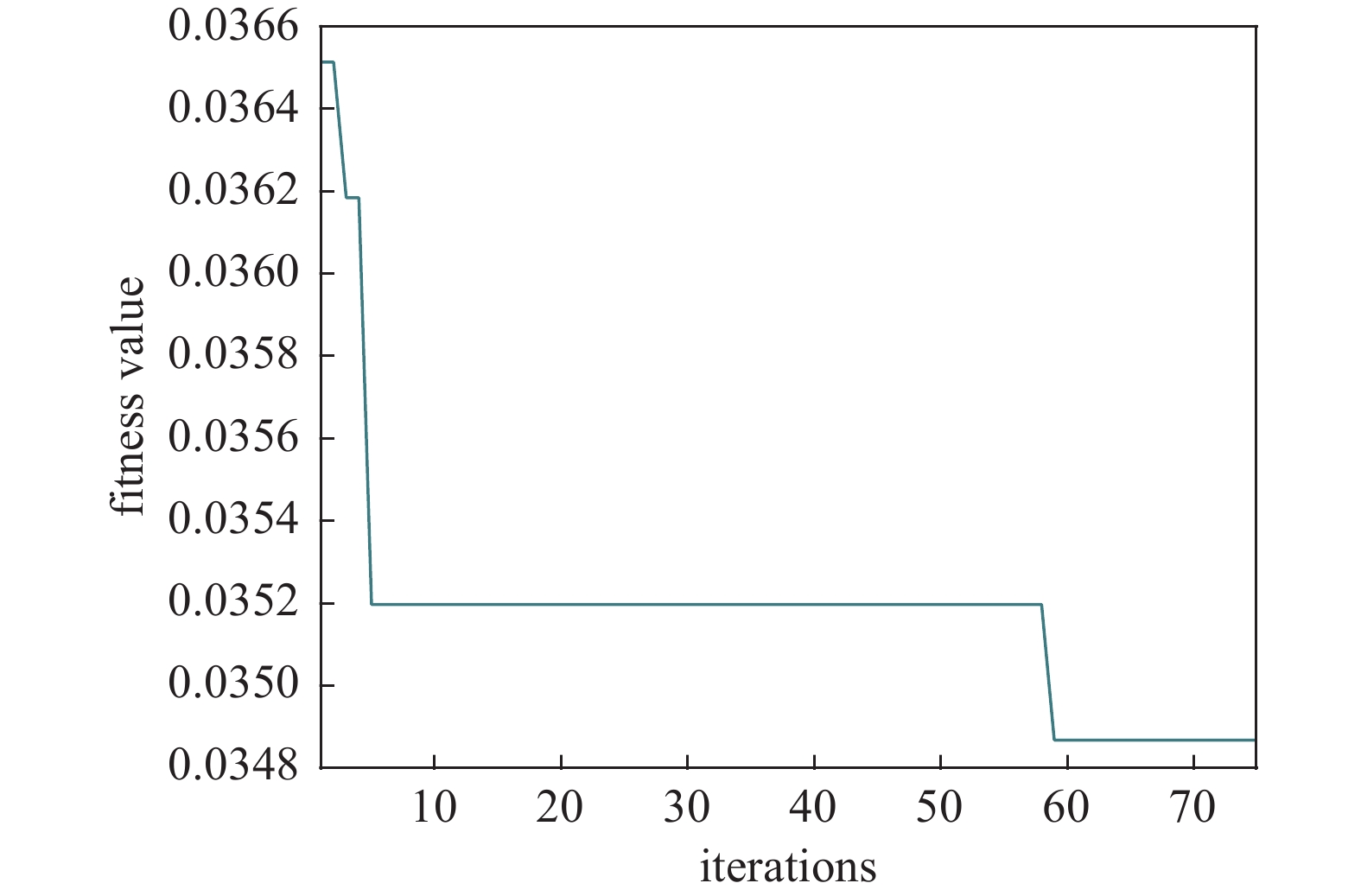
由图9分析可得,开始随着搜索的进行,惯性权重w线性地减小,在搜索过程中,粒子群算法能够在全局范围内寻找到较好的区域。在迭代的前期阶段,适应度曲线下滑较快,而在搜索后期,粒子群算法能够在极值点周围做精细的搜索,使得算法有较大的概率向全局最优解位置收敛,从而寻找到网络最佳的权值和阈值,训练出最优的模型。
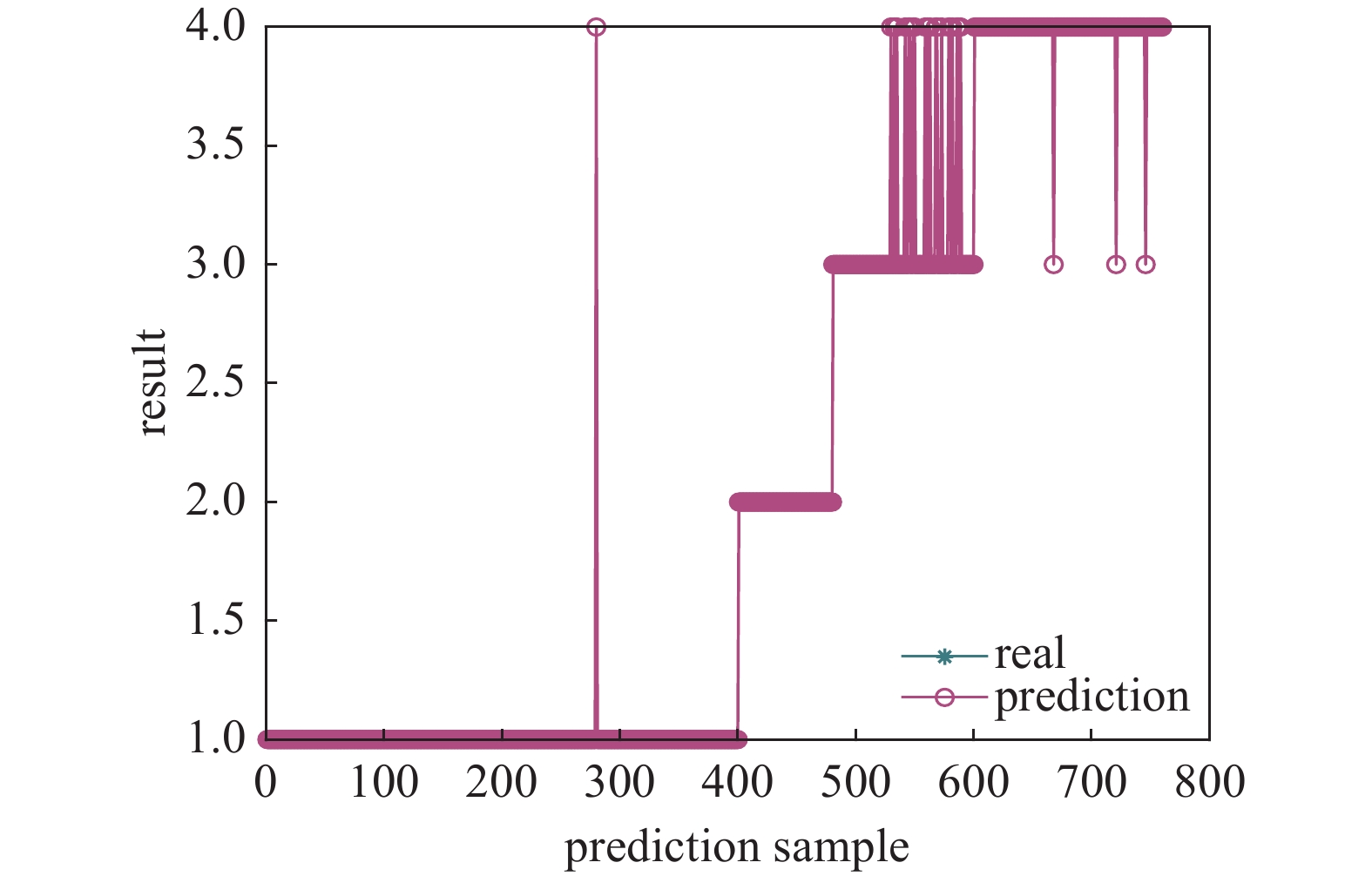
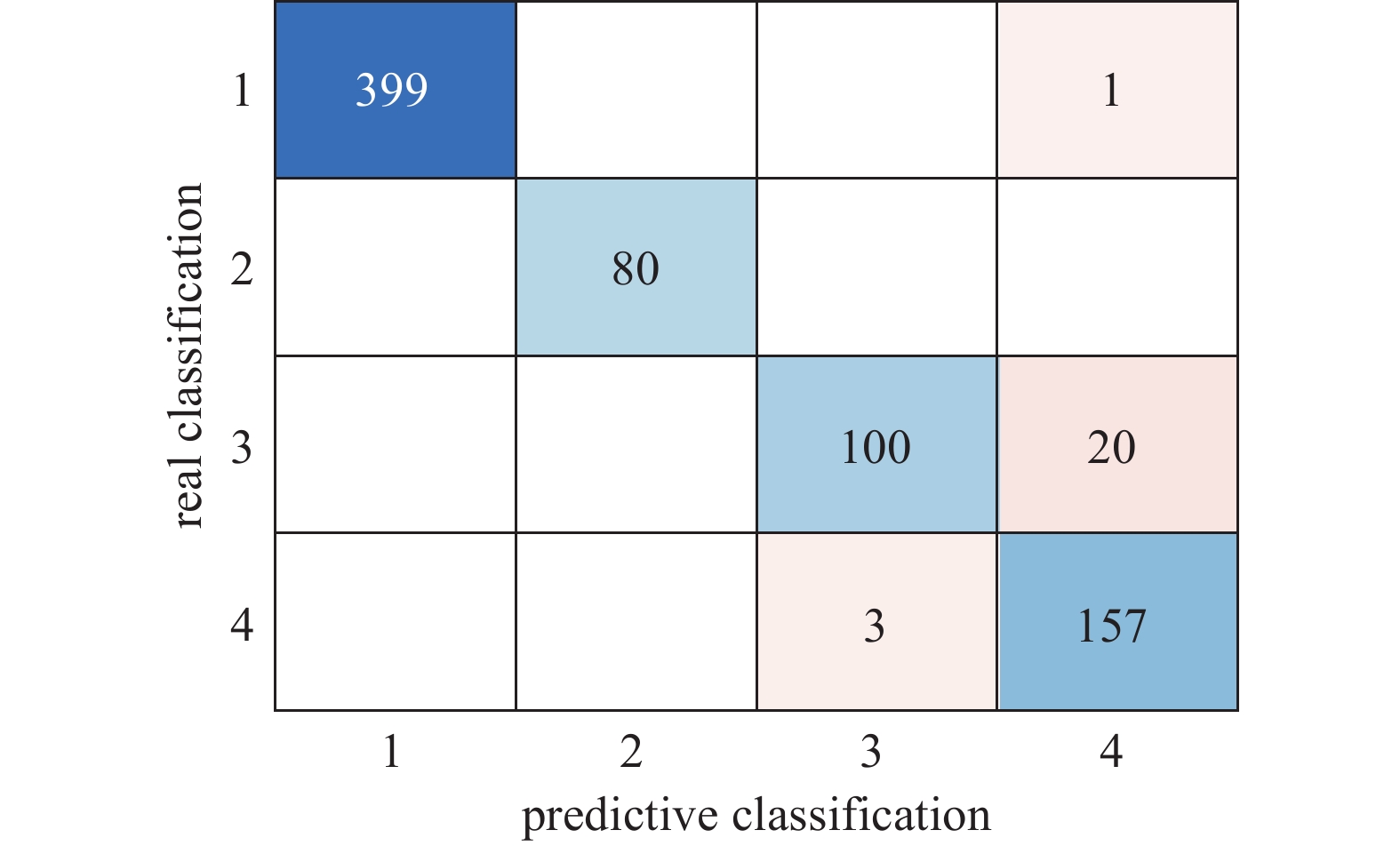
图10为4种分子泵状态分类可视化图,图11为4种分类的混淆矩阵。其中类别1代表分子泵正常状态;类别2代表分子泵钨粉坠入状态;类别3代表分子泵真空泄漏250 Pa状态,类别4代表分子泵真空泄漏100 Pa状态。由图可以分析出:类别1中1个识别为类别4;类别2实现全识别;类别3中20个识别为类别4;类别4中3个识别为类别3,整体诊断准确率达96.84%。实验结果表明,改进BP的神经网络模型,有效实现对分子泵故障的高准确分类。
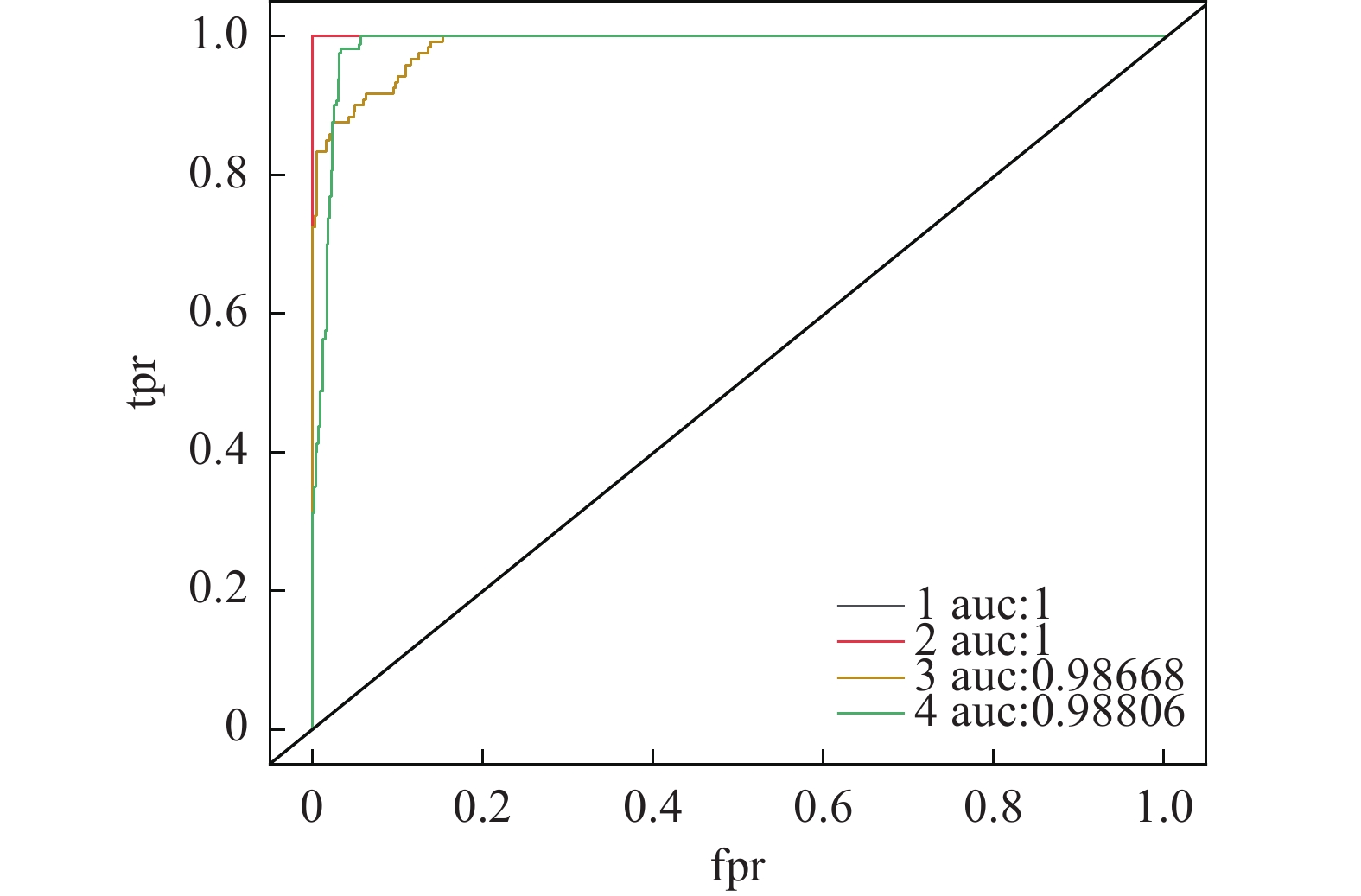
图12为4种类别的ROC曲线图,可以看出4种曲线都靠近左上角,且曲线下方所围面积AUC值都接近1,曲线1和曲线2的AUC值等于1,充分说明改进的BP神经网络分类器性能优越,可以实现对分子泵不同状态进行有效诊断。
-
为了更好的验证本文改进算法诊断的有效性,分别与SVM、KNN、BP算法进行对比。引入Accuracy (准确率),Recall (召回率),Precision (精确率)指标作为评价指标。
如表4所示,改进BP的神经网络算法在准确度上分别高于SVM、KNN、BP,3.37%,3.37%,0.82%;在类别1的召回率高KNN,0.26%;在类别3的召回率分别高SVM、KNN、BP,37.89%,16.56%,11.57%;在类别4召回率分别高KNN、BP,7.94%,0.65%。在类别1的精度上高SVM,2.55%;在类别2的精度上高BP,1.25%;在类别3的精度上分别高KNN、BP,14.10%,1.18%。在类别4的精度上分别高SVM、KNN、BP,13.09%,6.43%,2.33%。所以,可得改进的BP诊断算法相较于传统的算法有明显的优越性,更适用于分子泵故障诊断研究。
-
本文通过模拟分子泵破坏性实验平台,采集不同种类故障振动信号,模拟EAST分子泵故障类型。通过时频域数据预处理,并在BP神经网络模型的基础上引入粒子群算法与五折交叉验证来优化模型,从而实现对分子泵故障高准确诊断。
基于振动信号的传统时域频域特征提取方法,有效还原数据的真实原貌,而且提取效率高,适用于分子泵故障诊断研究。粒子群算法与五折交叉验证的引用,解决BP神经网络容易陷入局部最小值的问题,提高了诊断精度。同时,通过方法对比,本文所提基于改进BP的神经网络算法明显优于SVM、KNN以及BP算法。充分说明,本文算法更适用于分子泵故障诊断,为EAST探索一种新的诊断方式,为核聚变装置中稳定可靠的真空泵系统铺平了道路。
基于改进BP的分子泵故障诊断研究
Molecular Pump Fault Diagnosis Based on Improved BP
-
摘要: 分子泵为EAST装置提供洁净的真空环境,其运行状态影响EAST实验的顺利开展。由于在EAST实验运行过程中,分子泵设备可能会出现异物坠入或者真空泄漏故障,对装置造成次生危害。针对分子泵故障数据集不平衡导致故障诊断精度低以及模型过拟合问题,提出一种基于时域频域预处理与改进BP相结合的算法,实现分子泵故障诊断。通过在BP神经网络的基础上,引入粒子群算法(PSO)并结合五折交叉验证优化模型。首先在模拟分子泵故障的破坏性测试平台上,采集正常态、真空泄漏以及异物坠入故障振动信号,然后对数据进行时域频域特征提取融合,将得到的特征向量集作为优化算法的输入,对模型进行训练,实现分子泵故障诊断。经实验验证,所提出改进BP算法在诊断精确率上可以达到96.84%,优于支持向量机(SVM)、K近邻(KNN)和BP算法。Abstract: The molecular pump provides a clean vacuum environment for the EAST device, and its running state affects the smooth development of the EAST experiment. During the operation of the EAST experiment, the molecular pump equipment may suffer from foreign matter falling in or vacuum leakage, causing secondary hazards to the device. Aiming at the problem of low fault diagnosis accuracy and model over-fitting caused by the imbalance of molecular pump fault data set, an algorithm based on the combination of time and frequency domain preprocessing and improved BP was proposed to realize molecular pump fault diagnosis. On the basis of BP neural network, particle swarm optimization (PSO) is introduced and combined with five-fold cross-verification to optimize the model. Firstly, vibration signals of normal, vacuum leakage and foreign body falling faults are collected on a destructive test platform simulating molecular pump faults, and then the data are extracted and fused in the time domain and frequency domain. The obtained feature vector set is used as the input of the optimization algorithm to train the model and realize molecular pump fault diagnosis. The experimental results show that the diagnostic accuracy of the proposed improved BP algorithm can reach 96.84%, which is superior to support vector machine (SVM), K-nearest neighbor (KNN) and BP algorithm.
-

-
图 7 四种状态时域图。(a)正常状态时域图,(b)异物坠入状态时域图,(c)真空泄露100 Pa状态时域图,(d)真空泄露250 Pa状态时域图
Figure 7. Time domain diagram of four states. (a) Time domain diagram of normal state, (b) time domain diagram of foreign body fall state, (c) time domain diagram of vacuum leakage 100 Pa state, (d) time domain diagram of vacuum leakage 250 Pa state
图 8 四种状态频域图。(a)正常状态频域图,(b)异物坠入状态频域图,(c)真空泄露100 Pa状态频域图,(d)真空泄露250 Pa状态频域图
Figure 8. Frequency domain diagram of four states. (a) Frequency domain diagram of normal state, (b) frequency domain diagram of foreign body fall state, (c) frequency domain diagram of vacuum leakage 100 Pa state, (d) frequency domain diagram of vacuum leakage 250 Pa state
表 1 时域统计特征
Table 1. Time domain statistical features
时域特征参数 表达式 类别
最大值$ {X_{\max }} = \max \left( {{x_i}} \right) $
有量纲
最小值$ {X_{\min }} = \min \left( {{x_i}} \right) $
有量纲
峰峰值$ {X_{ff}} = {X_{\max }} - {X_{\min }} $
有量纲
平均值$ {X_{{\mathrm{mean}}}} = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{x_i}} $
有量纲
方差$ {{{X}}_{{{\mathrm{var}}} }} = \dfrac{1}{N}{\displaystyle\sum\limits_{i = 1}^N {\left( {{x_i} - {X_{{\mathrm{mean}}}}} \right)} ^2} $
有量纲
标准差$ {{{X}}_{{\mathrm{std}}}} = \sqrt {\dfrac{1}{N}{{\displaystyle\sum\limits_{i = 1}^N {\left( {{x_i} - {X_{{\mathrm{mean}}}}} \right)} }^2}} $
有量纲
均方根$ {{{X}}_{{{RMS}}}} = \sqrt {\dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{x_i}^2} } $
有量纲
波形因子$ {{{X}}_{ff}} = \dfrac{{{X_{RMS}}}}{{\overline {\left| X \right|} }} $
无量纲
峰值因子$ {{{X}}_{cf}} = \dfrac{{{X_{\max }}}}{{{X_{RMS}}}} $
无量纲
脉冲因子$ {{{X}}_{pf}} = \dfrac{{{X_{\max }}}}{{\overline {\left| X \right|} }} $
无量纲表 2 频域统计特征
Table 2. Frequency domain statistical features
频域特征参数 表达式
频谱均值$ {F_{{\mathrm{mean}}}} = \dfrac{1}{L}\displaystyle\sum\limits_{j = 1}^L {{f_j}} $
频谱重心$ {{{F}}_{fc}} = \frac{{\displaystyle\sum\limits_{j = 1}^L {\overline {{f_j}} {f_j}} }}{{2\pi \displaystyle\sum\limits_{j = 1}^L {{f_j}^2} }} $
频谱标准差$ {{{F}}_{{\mathrm{std}}}} = \sqrt {\dfrac{{\displaystyle\sum\limits_{j = 1}^L {{{\left( {{f_j} - {F_{{\mathrm{mean}}}}} \right)}^2}} }}{L}} $ 表 3 改进BP神经网络参数设置
Table 3. Parameter settings of improved BP neural network
参数 设置 参数 设置 输入层 13 目标误差 0.00001 隐藏层 6 最大训练次数 500 输出层 4 最大迭代次数 75 学习率 0.002 种群数量 8 表 4 诊断结果对比
Table 4. Comparison of diagnostic results
诊断方法 类别 Accuracy Recall Precision
SVM1
93.68%100.00% 97.51% 2 100.00% 100.00% 3 64.06% 100.00% 4 98.79% 77.99%
KNN1
93.68%99.49% 100.00% 2 100.00% 100.00% 3 75.78% 85.09% 4 90.91% 82.87%
BP1
96.05%99.75% 100.00% 2 100.00% 98.77% 3 79.17% 95.96% 4 97.5% 86.19%
改进的BP1
96.84%99.75% 100.00% 2 100.00% 100.00% 3 88.33% 97.09% 4 98.13% 88.20% -
[1] 李建刚. 托卡马克研究的现状及发展[J]. 物理,2016,45(2):88−97(in Chinese) Li Jiangang. The status and progress of tokamak research[J]. Physics,2016,45(2):88−97 [2] Yuan Xiaolin, Jia Kai, Chen Yue, et al. A support vector machine framework for fault detection in molecular pump[J]. Journal of Nuclear Science and Technology. 2022, 60:72−82 [3] 黄竞楠, 王少红, 马超. 基于SVD-EEMD和BP神经网络的滚动轴承故障诊断[J]. 北京信息科技大学学报(自然科学版),2019,34(02):69−74(in Chinese) Huang Jingnan, Wang Shaohong, Ma Chao. Fault diagnosis of rolling bearing based on SVD-EEMD and BP neural network[J]. Journal of Beijing Information Science& Technology University,2019,34(02):69−74 [4] 熊剑, 邓松, 时大方. 基于改进残差网络的滚动轴承故障诊断[J]. 轴承,2020(11):50−55(in Chinese) Xiong Jian, Deng Song, Shi Dafang. Fault diagnosis for rolling bearing based on improved residual network[J]. Bearing,2020(11):50−55 [5] 贾凯, 江明, 袁啸林, 等. 基于代价敏感型LightGBM的分子泵故障检测[J]. 电子测量与仪器学报,2022,36(10):55−64(in Chinese) Jia Kai, Jiang Ming, Yuan Xiaolin, et al. Fault detection of molecular pump based on cost-sensitive LightGBM[J]. Journal of Electronic Measurement and Instrumentation,2022,36(10):55−64 [6] 慕晓冬, 魏轩, 曾昭菊. 基于注意力残差网络的航天器测控系统故障诊断[J]. 仪器仪表学报,2022,43(9):81−87(in Chinese) Mu Xiaodong, Wei Xuan, Zeng Zhaoju. Fault diagnosis method of spacecraft tracking telemetry and control system based on the attention residual network[J]. Chinese Journal of Scientific Instrument,2022,43(9):81−87 [7] Zhou Funa, Hu Po, Yang Shuai, et al. A multimodal feature fusion-based deep learning method for online fault diagnosis of rotating machinery[J]. Sensors, 2018, 18(10):3521 [8] Shuai Jun, Shen Changqing, Zhu Zhongkui. Adaptive morphological feature extraction and support vector regressive classification for bearing fault diagnosis[J]. International Journal of Rotating Machinery, 2017, (2017):1−10 [9] 王骁贤, 陆思良, 何清波, 等. 变转速工况下基于多传感器信号深度特征融合的电机故障诊断研究[J]. 仪器仪表学报, 2022, 43(3):59−67(in Chinese) Wang Xiaoxian, Lu Siliang, He Qingbo, et al. Motor fault diagnosis based on deep feature funsion of multi-sensor data under variable speed condition[J]. Chinese Journal of Scientific Instrument, 2022, 43(3):59−67 [10] Li Qiang, Yu Jingyuan, Mu Baichun, et al. BP neural network prediction of the mechanical properties of porous NiTi shape memory alloy prepared by thermal explosion reaction[J]. Materials Science and Engineering:A,2006,419(1−2):214−217 doi: 10.1016/j.msea.2005.12.027 [11] 曹洁, 张玉林, 王进花, 等. 基于VMD和SVPSO-BP的滚动轴承故障诊断[J]. 太阳能学报, 2022, 43(09):294−301(in Chinese) Cao Jie, Zhang Yulin, Wang Jinhua, et al. Fault diagnosis of rolling bearing based on VMD and SVPSO-BP[J]. Acta Energiae Solaris Sinica, 2022, 43(09):294−301 [12] 董珍一, 林莉, 孙旭, 等. 基于BP神经网络的超声表面波定量表征金属表层裂纹深度研究[J]. 仪器仪表学报,2019,40(8):31−38(in Chinese) Dong Zhenyi, Lin Li, Sun Xu, et al. Study on the quantitative characterization of mental surface crack depth through BP neural network combined with SAW technique[J]. Chinese Journal of Scientific Instrument,2019,40(8):31−38 [13] 张越, 张峰, 张峰瑞, 等. 一种基于BP神经网络的轮胎磨损程度检测算法[J]. 电气自动化, 2023, 45(01):109−112(in Chinese) Zhang Yue, Zhang Feng, Zhang Fengrui, et al. A tire wear detection algorithm based on BP neural network[J]. Electrical Automation, 2023, 45(01):109−112 [14] 罗巍, 卢博, 陈菲, 等. 基于PSO-SVM及时序环节的数控刀架故障诊断方法[J]. 吉林大学学报(工学版), 2022, 52(02):392−399(in Chinese) Luo Wei, Lu Bo, Chen Fei, et al. Fault diagnosis method of NC turret based on PSO-SVM and time sequence[J]. Journal of Jilin University, 2022, 52(02):392−399 [15] 陶志勇, 于子佳, 林森. PSO_SVM算法在太阳能电池板裂缝缺陷检测研究[J]. 电子测量与仪器学报,2021,35(1):18−25(in Chinese) Tao Zhiyong, Yu Zijia, Lin Sen. Research on crack defect detection of solar cell based on PSO_SVM[J]. Journal of Electronic Measurement and Instrumentation,2021,35(1):18−25 [16] 王文杰, 韩振华, 黄从兵, 等. 基于PSO的水利蜗壳泵叶轮和导叶匹配设计[J]. 中南大学学报(自然科学版),2022,53(11):4282−4291(in Chinese) Wang Wenjie, Han Zhenhua, Huang Congbing, et al. Matching design of impeller and diffuser of hydraulic volute pump based on PSO[J]. Journal of Central South University(Science and Technology),2022,53(11):4282−4291 [17] 何存富, 王志, 刘秀成, 等. 基于GA-PSO混合算法的钢杆磁特性参数识别方法[J]. 仪器仪表学报,2017,38(4):838−843(in Chinese) He Cunfu, Wang Zhi, Liu Xiucheng, et al. Magnetic property parameter identification of steel pole based on GA-PSO hybird algorithm[J]. Chinese Journal of Scientific Instrument,2017,38(4):838−843 [18] 杨赫然, 孙兴伟, 戚朋, 等. 基于改进BP神经网络的螺杆转子铣削表面粗糙度预测[J]. 电子测量与仪器学报,2022,36(10):189−196(in Chinese) Yang Heran, Sun Xingwei, Qi Peng, et al. Roughness prediction of spiral surface milling based on improved BP neural network[J]. Chinese Journal of Scientific Instrument,2022,36(10):189−196 [19] 赵柄锡, 冀大伟, 袁奇, 等. 采用时域与时频域联合特征空间的转子系统碰磨故障诊断[J]. 西安交通大学学报,2020,54(01):75−84(in Chinese) doi: 10.7652/xjtuxb202001010 Zhao Bingxi, Ji Dawei, Yuan Qi, et al. Rubbing fault diagnosis of rotor system based on combined feature space in time and time-frequency domains[J]. Xi’an Jiaotong University Xuebao,2020,54(01):75−84 doi: 10.7652/xjtuxb202001010 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: