首页
登录
注册
-
涡轮分子泵 (Turbomolecular Pump, TMP)是产生和维持清洁高真空(Clean High Vacuum, CHV)环境的关键机械设备，广泛应用于半导体、托卡马克装置、空间环境模拟等领域[1]。得益于控制技术和加工技术的发展，TMP的转子叶片可以成型为更为复杂的结构以提高性能[2-3]，这为涡轮转子叶型的设计与仿真计算提供了新的机遇与挑战。日本学者Sawada[4-5]对TMP的性能计算理论和单级叶列性能测试做出了大量工作。Li等[6]使用3D直接模拟蒙特卡洛(Direct Simulation Monte Carlo, DSMC)方法模拟TMP性能，Sun等[7]基于试验粒子蒙特卡罗(Test Particle Monte Carlo, TPMC)方法，编写自定义程序计算TMP性能，但这些方法不具有模型普适性，对于特定结构的TMP需重新建模编程；Schneider[8]基于仿真结果总结推导出工程计算公式，但计算精度有待商榷。Tu等[9]基于质量守恒方法，研究了TMP涡轮叶列开口率、叶片长度等因素对组合叶列性能的影响，并推导出了性能计算公式。Katsimichas等[10]基于TPMC方法，使用三维模型对不同类型的叶列通道的性能进行了模拟计算。Li等[11-12]从TMP抽气的基本原理出发，推导出用于氦质谱检漏仪用的多口分子泵的性能计算方法，并使用DSMC方法模拟在不同压力下TMP涡轮叶列性能。目前，研究人员根据仿真数据建立数据回归模型[13]，进行插值计算，评价性能，预测偏于保守，计算效率低下。匡等[14-15]使用面积加权平均法计算涡轮叶列的抽气性能，增加了性能预测精度，并提出了一种曲面叶片模型，用于对分子泵涡轮叶列进行优化设计。
20世纪80年代兴起的反向传播神经网络（Back Propagation Neural Network, BPNN）能有效近似复杂系统模型，广泛应用于汽车、机械、传动等领域有高精度预测[16]。通过调整网络权重和偏差，BPNN能够有效学习和模拟复杂动态行为，TMP的抽气能力受多因素影响，且各参数间影响复杂，具有很强的非线性，适合使用BPNN解决其性能预测问题。
本文建立神经网络模型，根据TMP二维模型对应的无量纲数，对传输几率进行预测，将预测结果与其他模拟仿真得到的结果进行比较分析。同时对TMP的抽速进行实验测试，测试结果与仿真预测结果具有较好的一致性。此预测模型能够用于TMP结构设计中的性能评估。
在本文中，公式及图中相关字母符号及其意义见表1。
-
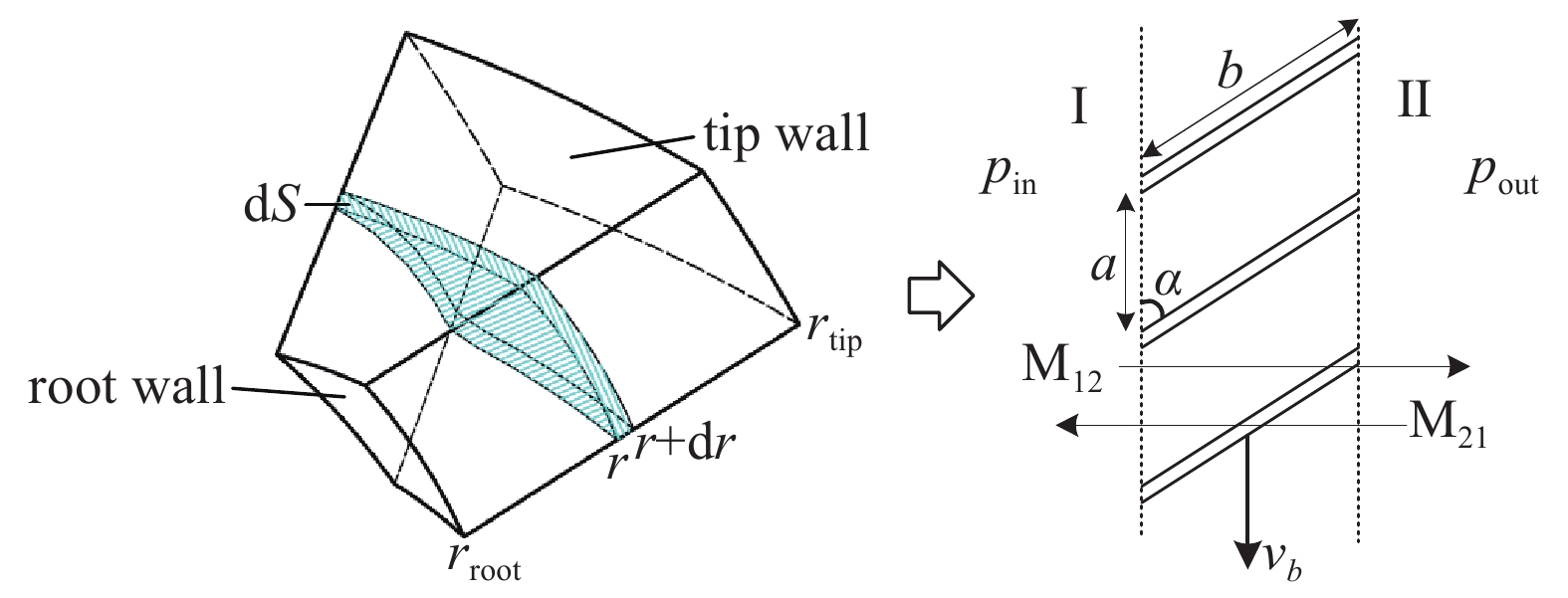
对于TMP的涡轮叶列，可以抽取单流道流域为研究对象，在不考虑叶顶间隙的情况下，边界分别为进口、出口、叶根壁面、叶顶壁面、两侧叶片壁面，其结构如图1所示。
在流道内截取半径方向上微元展开成为二维模型，与Kruger[17]提出的模型具有一致性。
在分子流下常使用触发式TPMC方法计算二维模型的正反向传输几率[9]。
式中，N12 为从入口到达出口的粒子数，N21为从出口到达入口的粒子数，N 为在边界释放的粒子数。
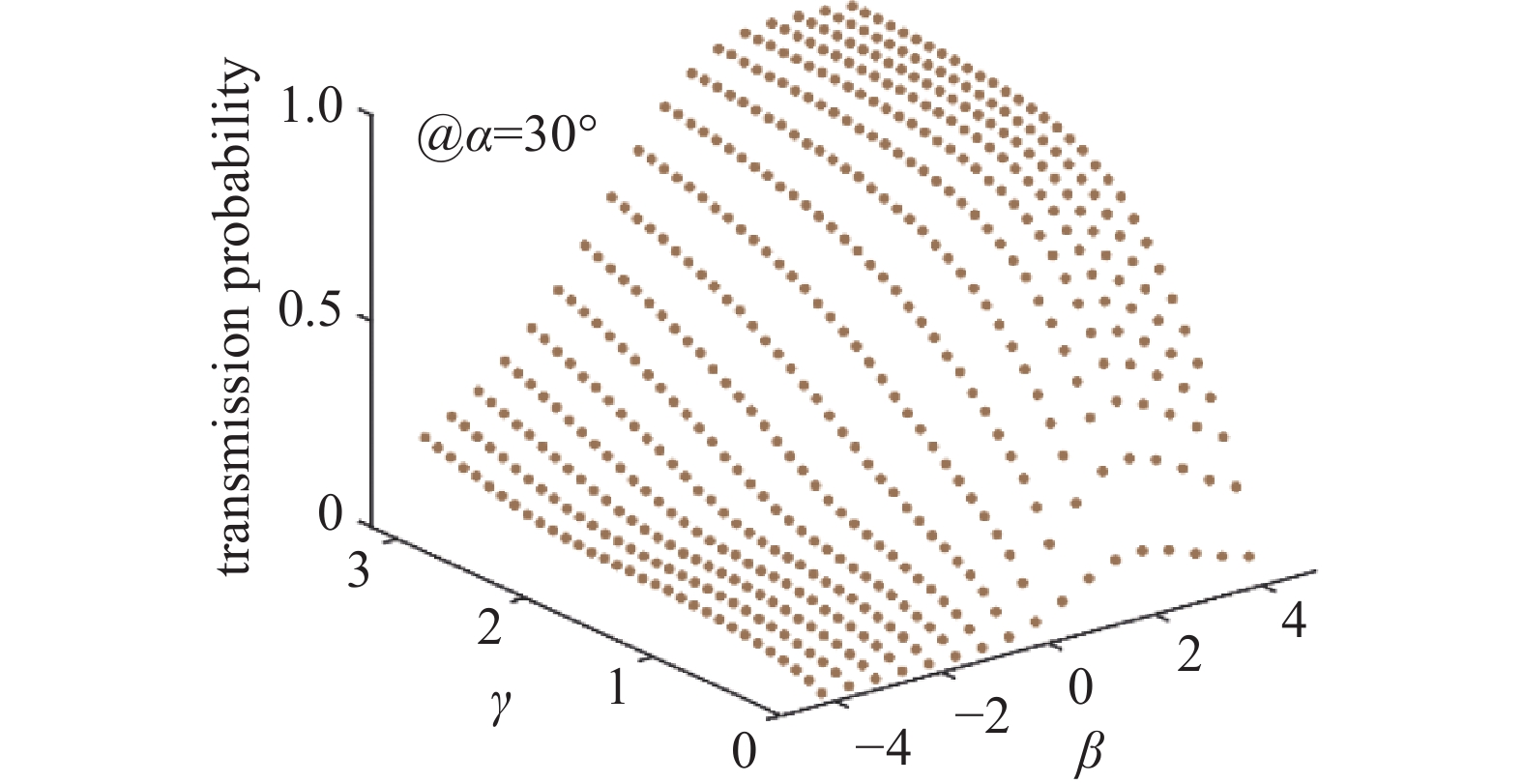
本研究中对常用的数值范围进行了原始数据的模拟，其中，叶片攻角α的取值范围是10°~72°，取值步长为2°；速度比β的取值范围是−4~4，取值步长为0.01；节弦比γ的取值范围是0.1~3，取值步长为0.1。如图2所示是α=30°时，传输几率随着β和γ变化的离散数据。
使用面积加权积分计算单通道的正反向传输几率[14]。
式中，
$ {r} $ 为叶片半径，$ {r}_{1} $ 为叶根半径，$ {r}_{2} $ 为叶顶半径，$ S $ 为抽气通道面积。组合叶列的正、反向传输几率为[18]
式中，
$ {P}_{n} $ 、${Q_n} $ 为前n级的正、反向传输几率，M12、M21为第n级的正反向传输几率。组合叶列的抽气能力为[19]
式中，R为气体状态常数，T为气体开氏温度，M为气体分子质量。
整个计算过程中，式(1)(2)是关键，使用TPMC方法计算具有高效性、适应性广等优点，但是TMP具有的结构参数变化范围广，不可能穷尽所有的结构参数，因此，在本研究中使用TPMC方法计算有限组具有代表性的数据，使用这些数据对神经网络模型进行训练，再使用训练后的模型对TMP的性能进行预测。
-
在神经网络模型中，将式(1)(2)转化为映射关系：
对于同一涡轮叶列，M12和M21随对应的自变量差别仅为速度比β的符号不同（β > 0时为M12；β < 0时为M21），将映射关系进一步变化为：
-
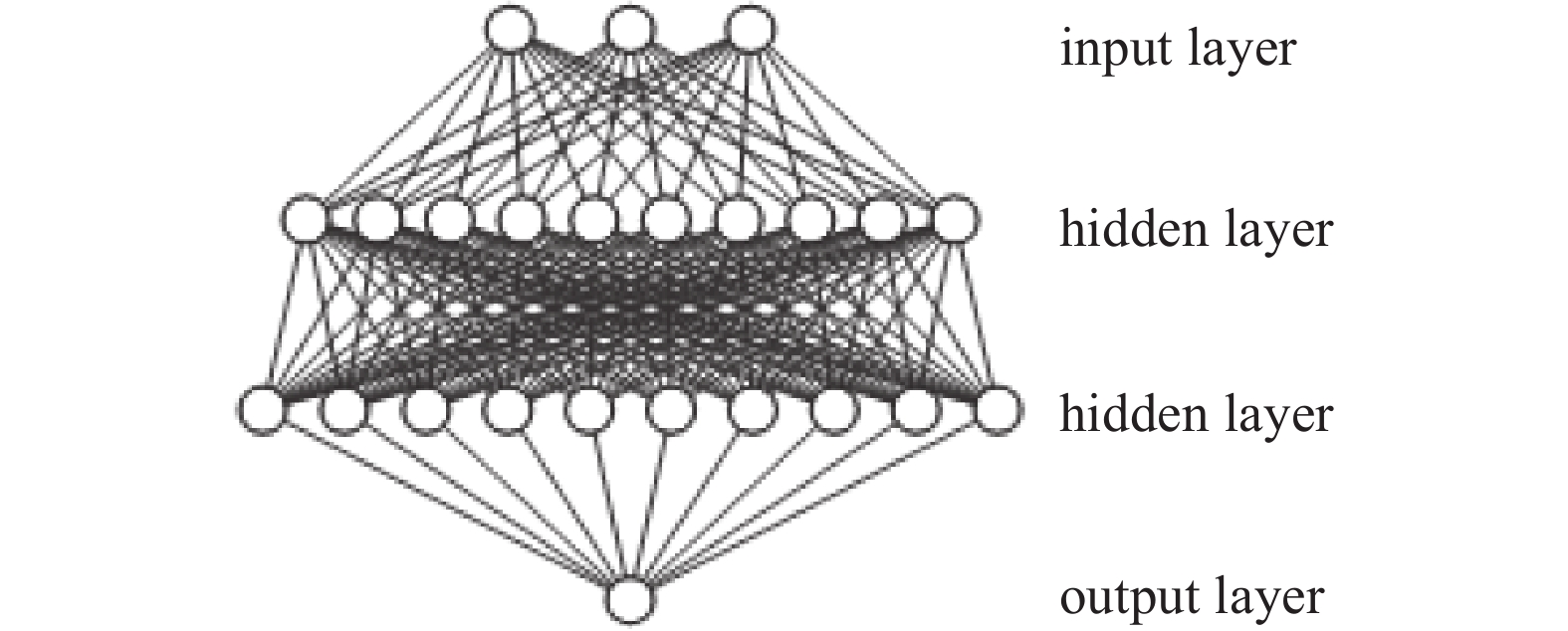
为提高预测精度，针对传输几率构建如图3所示神经网络模型，其实现的功能对应于式(9)，用于处理3个输入变量并预测1个输出变量，模型包括1个输入层、2个隐藏层（每个包含10个神经元）和1个输出层。双层全连接神经网络模型具有出色的非线性拟合能力，可以处理复杂的数据关系，同时也平衡了模型的高效性和准确性。
此模型预测过程为：
式中，x为输入量，g为输出量，σ为激活函数，w为权重矩阵，b为每层的阈值。
使用TMPC方法模拟得到的数据集对此模型进行训练，即可求得模型中权重矩阵和阈值。在此处使用BP算法对此网络进行训练。
-
在训练中，数据归一化是一项重要的预处理步骤，有助于加快优化算法的收敛速度，避免数值不稳定性，改善激活函数的表现，同时提高模型的泛化能力。在本研究中使用特征缩放（MinMax）将每个特征的范围转化到[−1, 1]区间内，再对网络进行训练。在使用此模型预测TMP性能时，需要将数据进行反归一化处理。
均方误差（Mean Squared Error，MSE）和相关系数R用于衡量训练过程中模型对数据的拟合程度：
式中，y为实际观测值；
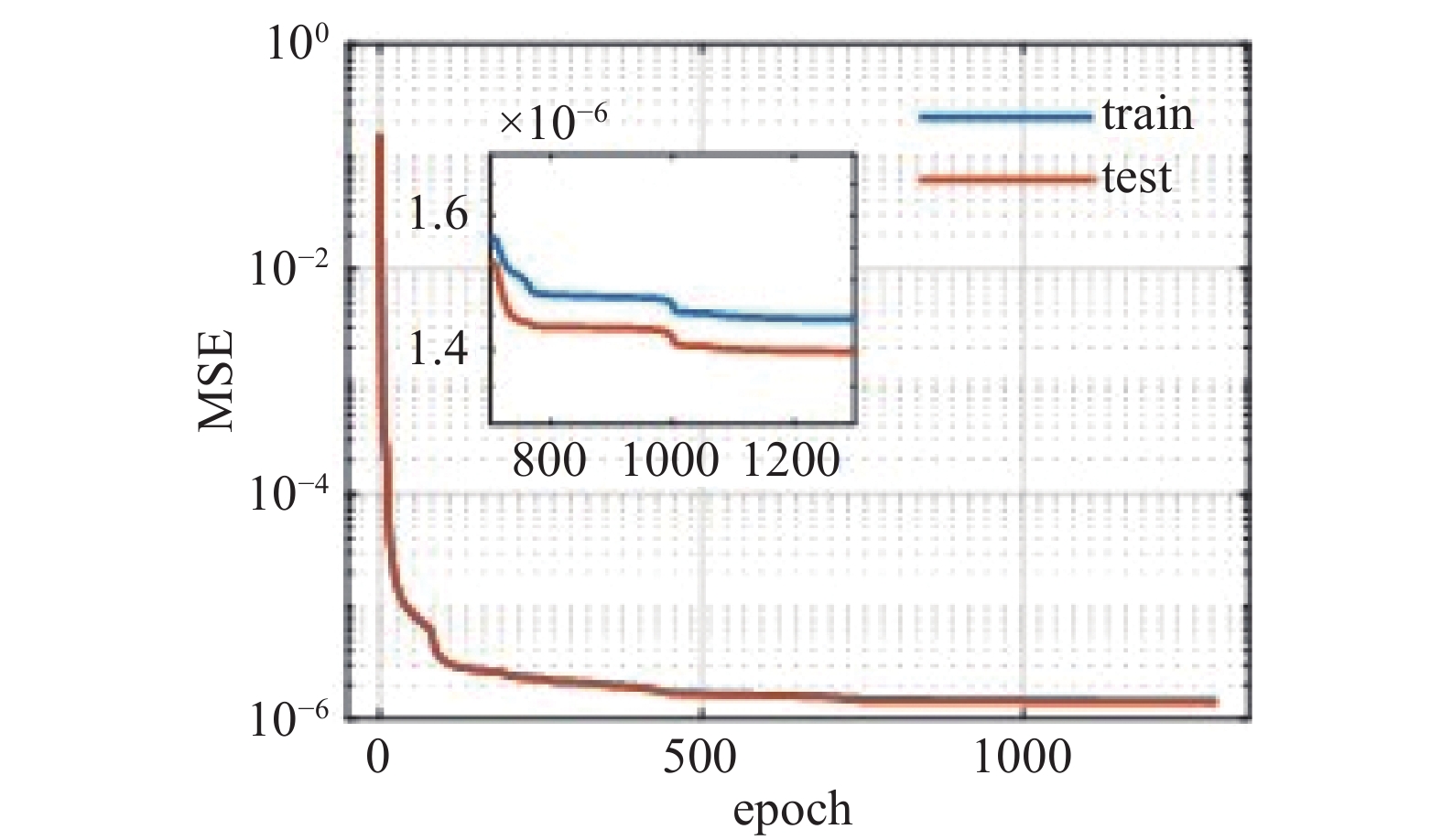
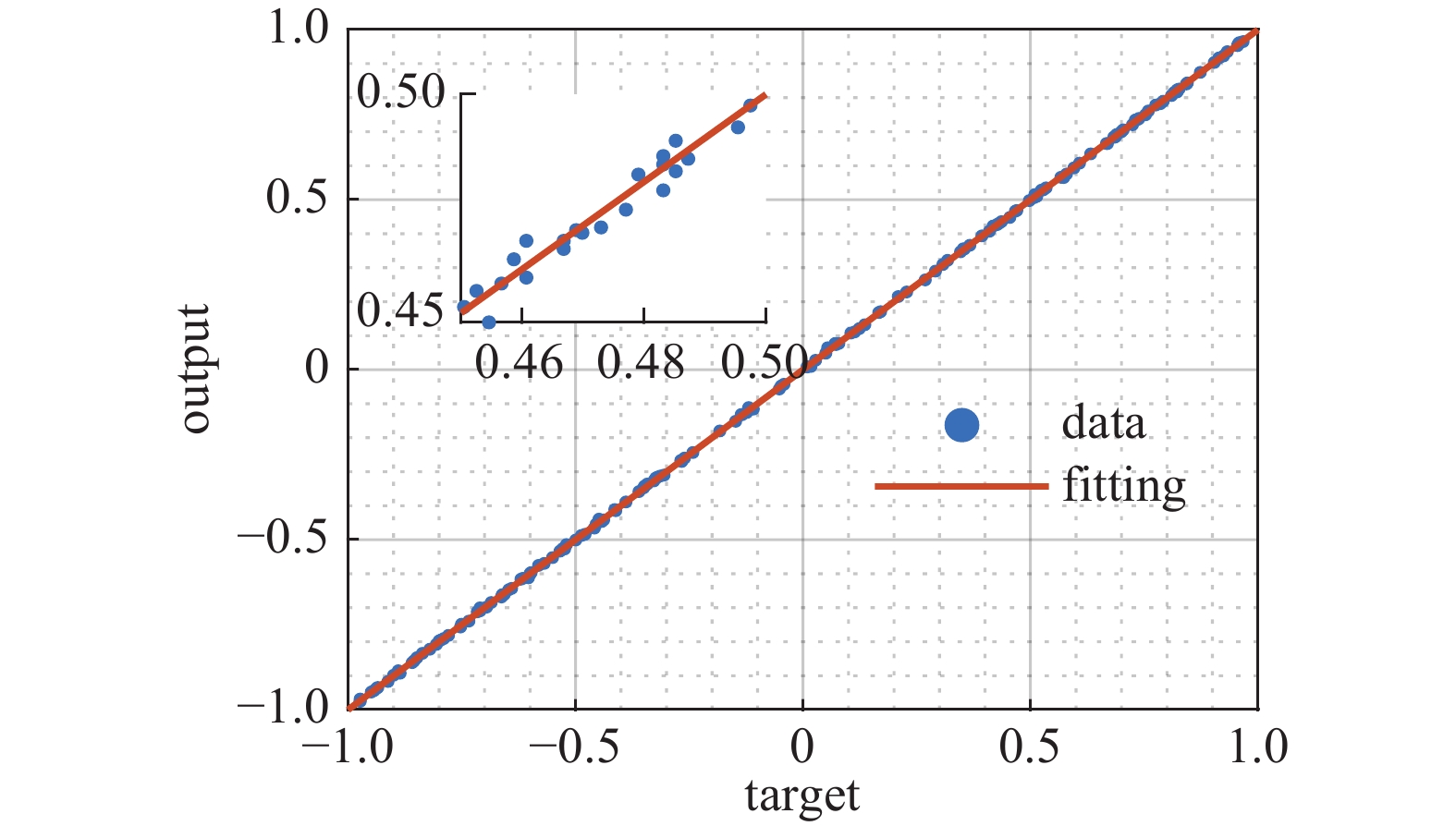
$ \hat{{y}} $ 为对应的预测值；SSres 表示残差平方和；SStotal 表示总平方和。如图4所示在训练过程中，训练集(train)和测试集(test)的MSE均随迭代次数增加而不断减小，且具有很高的一致性，最终均稳定在2×10−6 以下；如图5所示，完成训练后模型的预测试和目标值具有很强的一致性，两者的拟合关系式为：
拟合后的 R=0.99998，很好地反应了神经网络模型的预测精度。
-
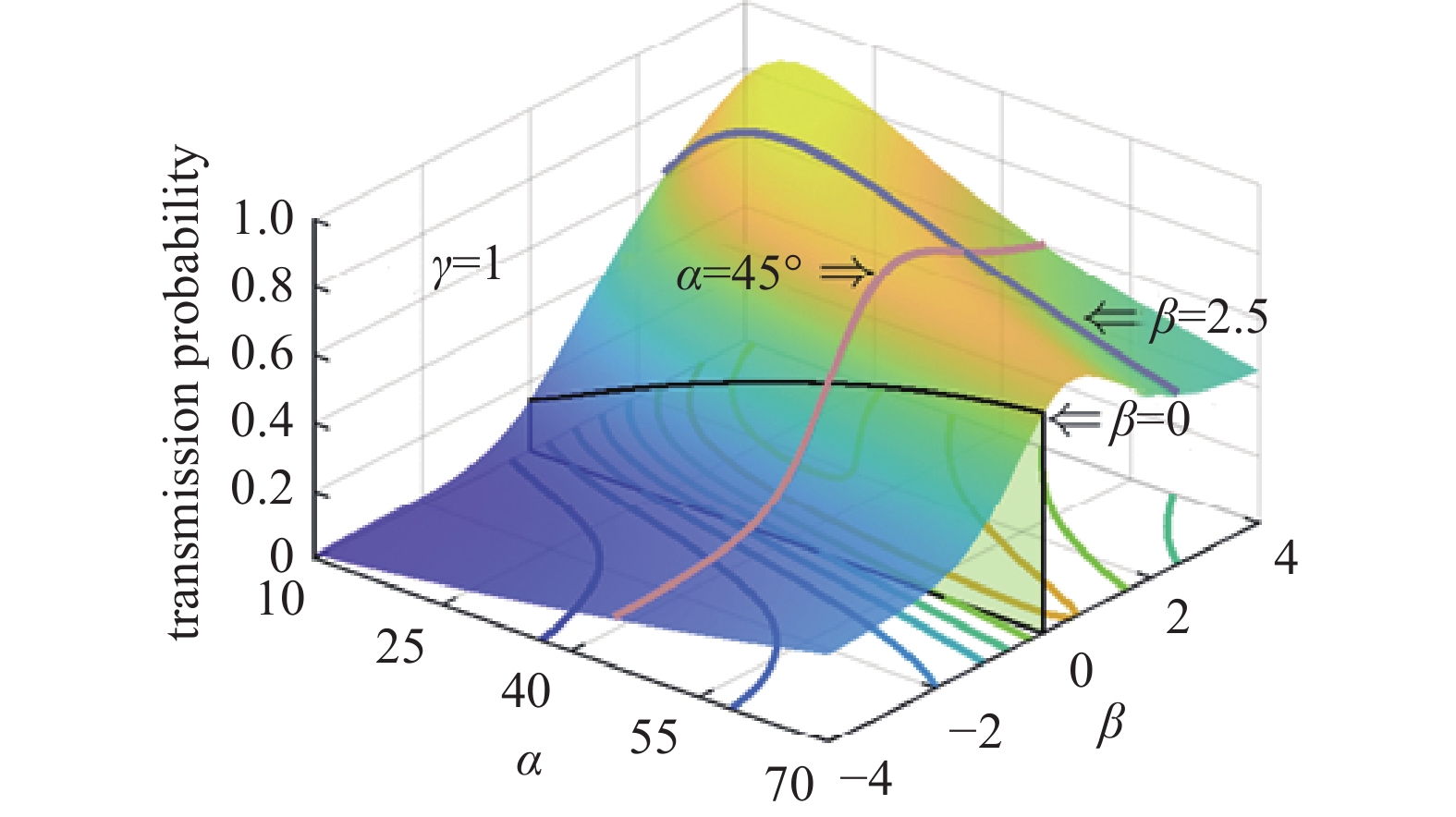
图6是在节弦比γ = 1时，叶列传输概率与叶片角度和速度比的相应曲面。在图中β < 0范围内是叶列的反向传输概率，β > 0范围内是叶列的正向传输概率，β = 0平面与曲面相交所得的曲线表示的是速度比为0时叶列的正反向传输概率，从中可以看出当速度比为0时，虽然在不同角度下宏观叶片的抽气能力均为0，但随着叶片的角度逐渐增大，正反向传输概率均是逐渐增大的。对于常见气体，尤其是对于速度比不大的气体（对于一般TMP，其叶片线速度与H2的最可几速率之比小于0.5），若是能在后级涡轮叶列中减少反向传输的粒子数，即减小角度对组合叶列的抽气量的提升也有促进作用。
在叶片角度α不变的情况下，如图中α = 45°所展示的曲线，随着速度比的增大，气体分粒子的传输概率先增大，在β = 1附近取极大值，随后随着速度比的增大而逐渐减小，并趋于稳定。这是因为在正向传输概率（β > 0）的情况下，当到速度比较小（0 < β < 1）时，叶片对气体正向传输的作用不是很明显，只有少部分分子受到了叶片的碰撞，得到的向下传递的动量，随着速度比的增大，更多的粒子得到了叶片传递的动量；当速度比更大（1 < β < 2）时，相当部分气体分子可能会与叶片壁面发生多次碰撞，导致整体的抽气模型不再符合Kruger提出的几何模型，多次与叶片相碰撞的粒子会损失之前已经获得的正向速度，因此传输概率会下降；而当速度比β > 2时，几乎所有的气体分子均会与叶片表面发生多次碰撞，叶列的传输概率会趋于稳定，收敛于某一数值。
固定叶片的速度比β和节弦比γ，如图所示的曲线中可以观察出传输概率随着叶片角度的变化。随着角度的逐渐增大，粒子的正向传输概率迅速增大，到达极大值后又逐渐减小，在25°左右取极大值。
-
在仿真中，使用前文训练完成的神经网络进行性能预测，耗费机时少，分别使用积分中值法[13]、线性插值法[14]、神经网络模型对型号为F400-3500 的TMP涡轮级[18]的抽气能力进行预测，记录程序耗时于表2之中。
通过对比，不难发现几何中值法耗费的机时最少，这是因为几何中值法仅选取了叶片中部截面的几何尺寸来代表整个单级涡轮叶列模型，计算量非常小。线性插值法耗费的机时是几何中值法的800多倍，因为插值法需要对叶片在径向进行离散，然后根据离散的几何结构在数据库中进行插值计算，计算其抽气参数，尽管其计算精度要优于几何中值法，但此方法需要占用大量的计算机内存及计算时间，仅适用于计算算例较少的场景。
神经网络模型模型因具有能高效预测组合涡轮叶列性能的特点，非常适合在对结构进行优化设计时使用。
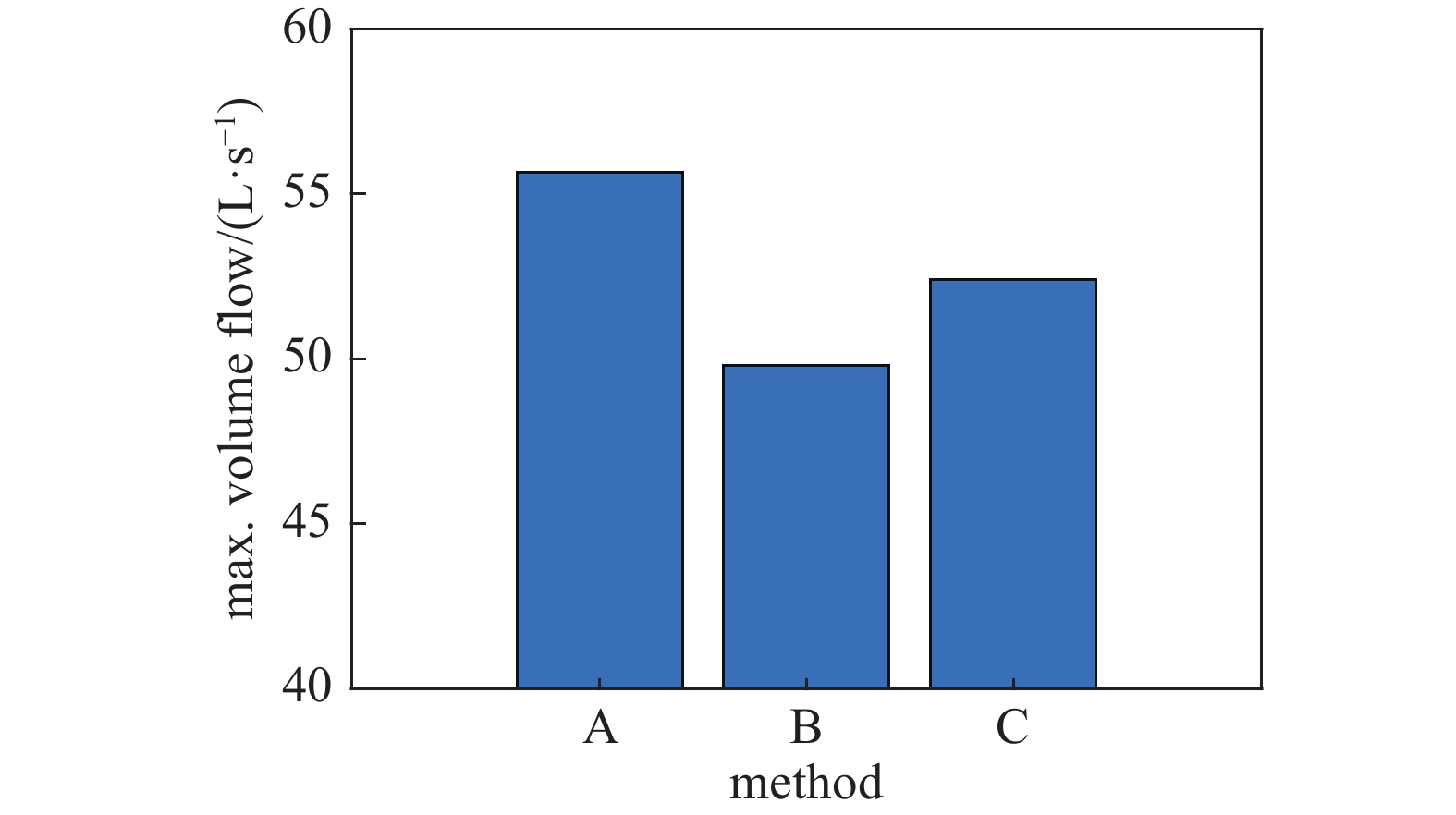
按照以上计算流程，使用神经网络预测模型对型号为F-63/55的TMP前四级结构的最大抽速进行了预测，计算结果如图7所示，A为线性插值方法计算出的预测结果[20]，B是实验测试[20]得到的计算结果，C是通过前文训练神经网络模型的预测结果。通过对比不难发现神经网络的预测结果优于插值算法，更接近于实测值，说明神经网络模型的预测结果具有更好的准确性。
-
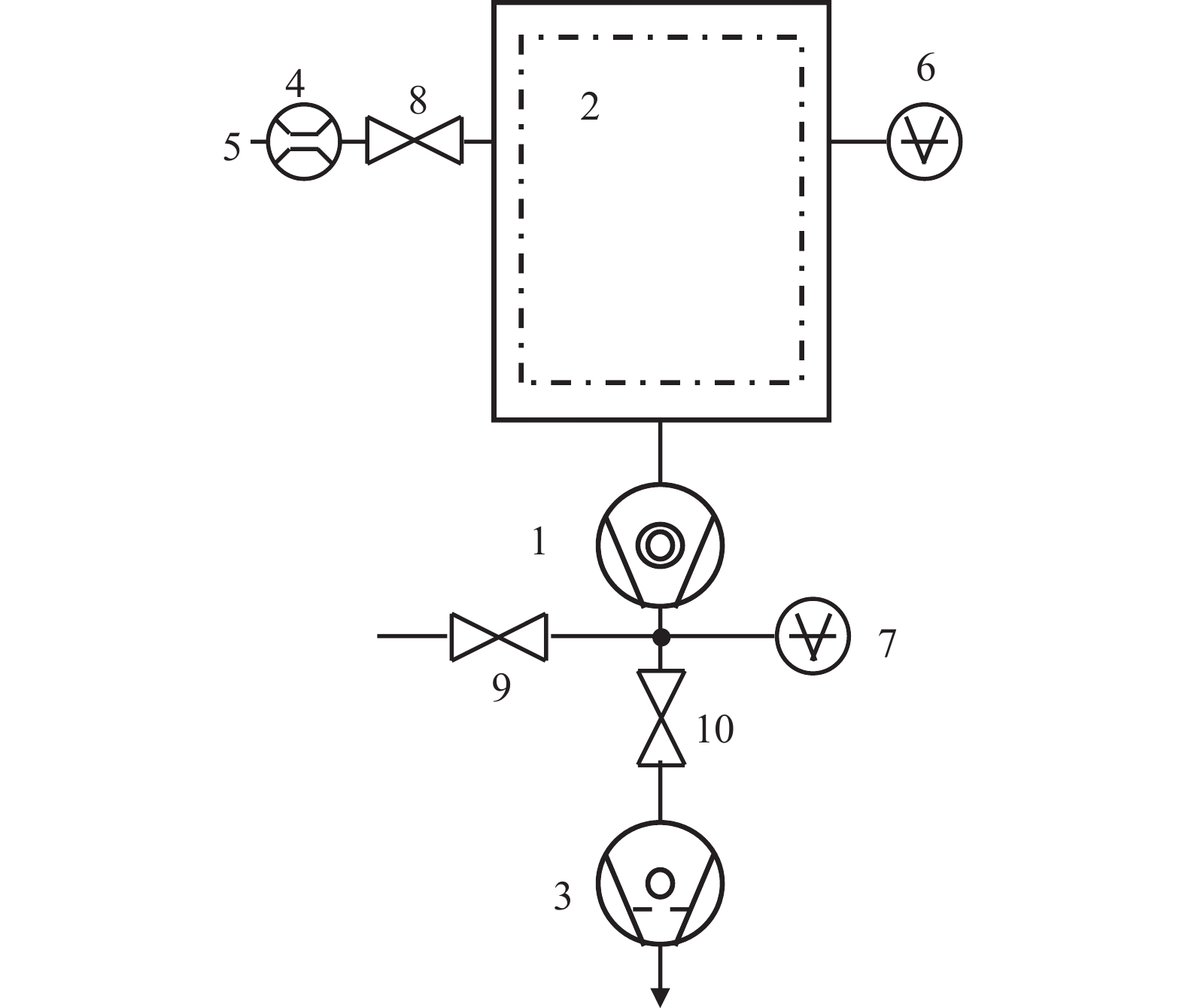
按照《真空技术 涡轮分子泵性能参数的测量》(ISO 5302:2003、GB/T 7774-2007)中的流量计法测试分子泵性能，图8是分子泵性能测试系统组成，各仪器编号及型号如表3所示。系统核心为被测TMP；测试罩用以模拟实际工作条件；前级干泵负责初始抽空及维持TMP前级真空；流量计组控制并测量进入系统的气体流量；气瓶用于提供高纯度测试气体(在本研究中使用N2)；真空计监测测试罩内压力、前级压力。
-
测试开始时，首先调整TMP转速，当转速稳定后开始测量TMP的极限真空度p1,0，由真空计6测得。在此之后调整系统进气量，由流量计4测量气流量Q，真空计6和真空计7分别测TMP入口压力p1和出口压力p2，当各仪表读数稳定时记录实际。
TMP抽速为
本研究中，在295 K温度下测试了TMP的4个工况：在TMP实际转速为额定转速的76.36%、83.64%、90.91%、100% 时，TMP抽速随入口压力的变化曲线。
-
在分析数据时，将TMP的抽速测试数据和仿真模拟数据除以抽速测试值的最大值进行无量纲化，数据缩放到[0,1]范围内。保留了数据之间的相对关系。
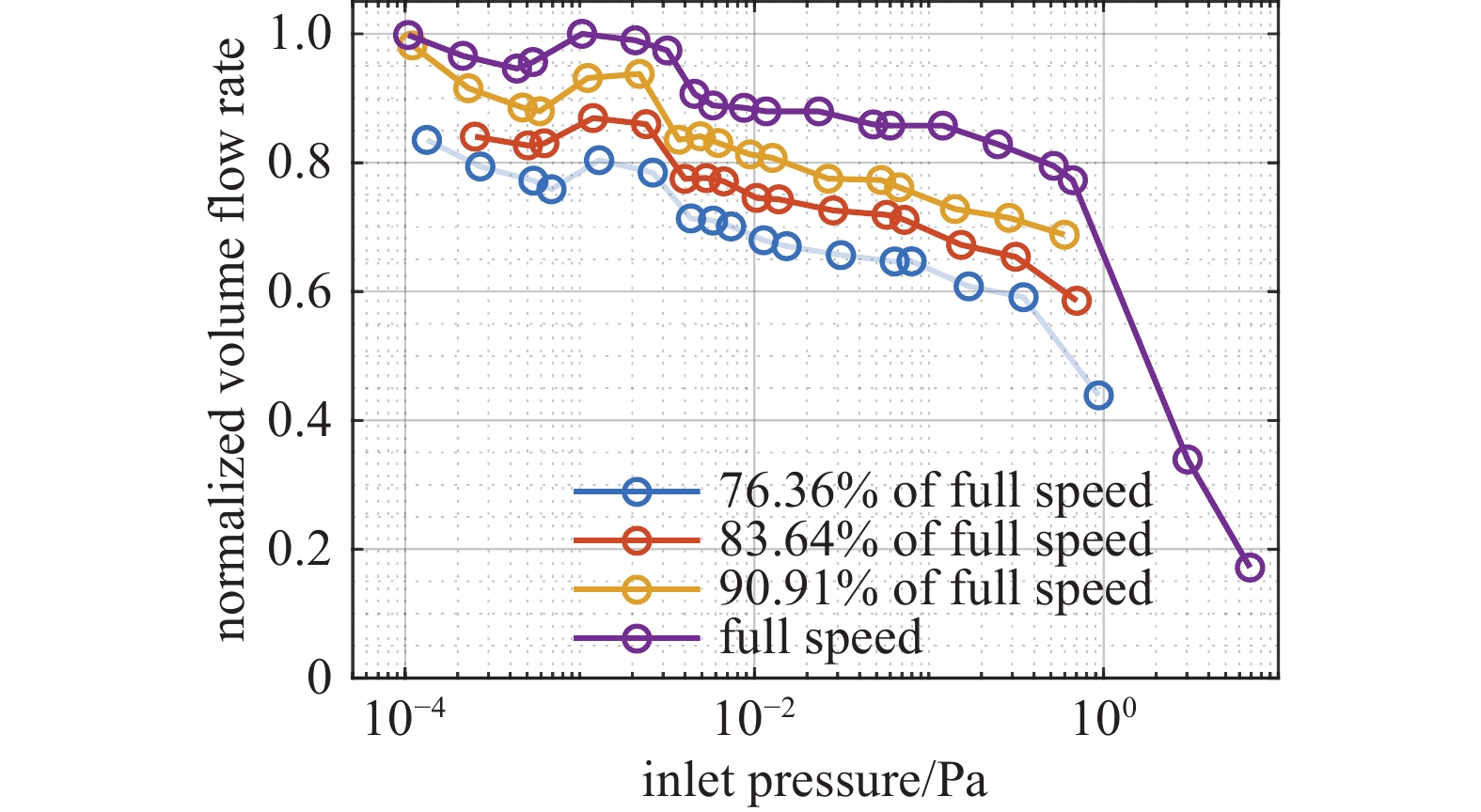
图9是不在不同转速下，TMP的抽速随入口压力变化的曲线。在低入口压力区域，各曲线均呈现出随着转速升高，抽速显著增加的趋势。该现象可归因于分子扩散主导的气体输送机制。转速提升会增大分子与叶片间的有效碰撞频率，进而提高气体分子从入口到出口的扩散效率，促使TMP抽速增大。这与文献[8]结论具有一致性：在叶片线速度与气体最可几速率之比的范围区间为[0,1]时，随着速度的增大，叶列的最大何氏系数（最大抽气系数）逐渐增大。随着TMP入口压力持续增高，抽速随转速的提升幅度逐渐减缓，各曲线趋于平缓。此时，叶轮抽气效率主要受几何结构和转速制约。升高转速虽能增强叶轮叶片与分子的碰撞，但其贡献逐渐被流体特性限制，导致抽速增幅减小。
随着入口压力的逐渐增大，TMP的抽速会逐渐减小，以满转速的情况为例，在入口压力为10−4 Pa ~ 0.8 Pa时，TMP的抽速随着入口压力升高缓慢降低，在0.8 Pa之后，TMP抽速下降趋势显著增大。在0.8 Pa时气体的流态发生的变化，逐渐从分子流态转化到过渡流态，气体分子之间的碰撞频率增大，导致抽速下降。因此，此TMP的适用工作环境应在真空度优于0.8 Pa的情况。TMP入口压力对其抽速影响显著，在实际的真空系统设计中，应选择与适应的TMP才能发挥其全部性能。
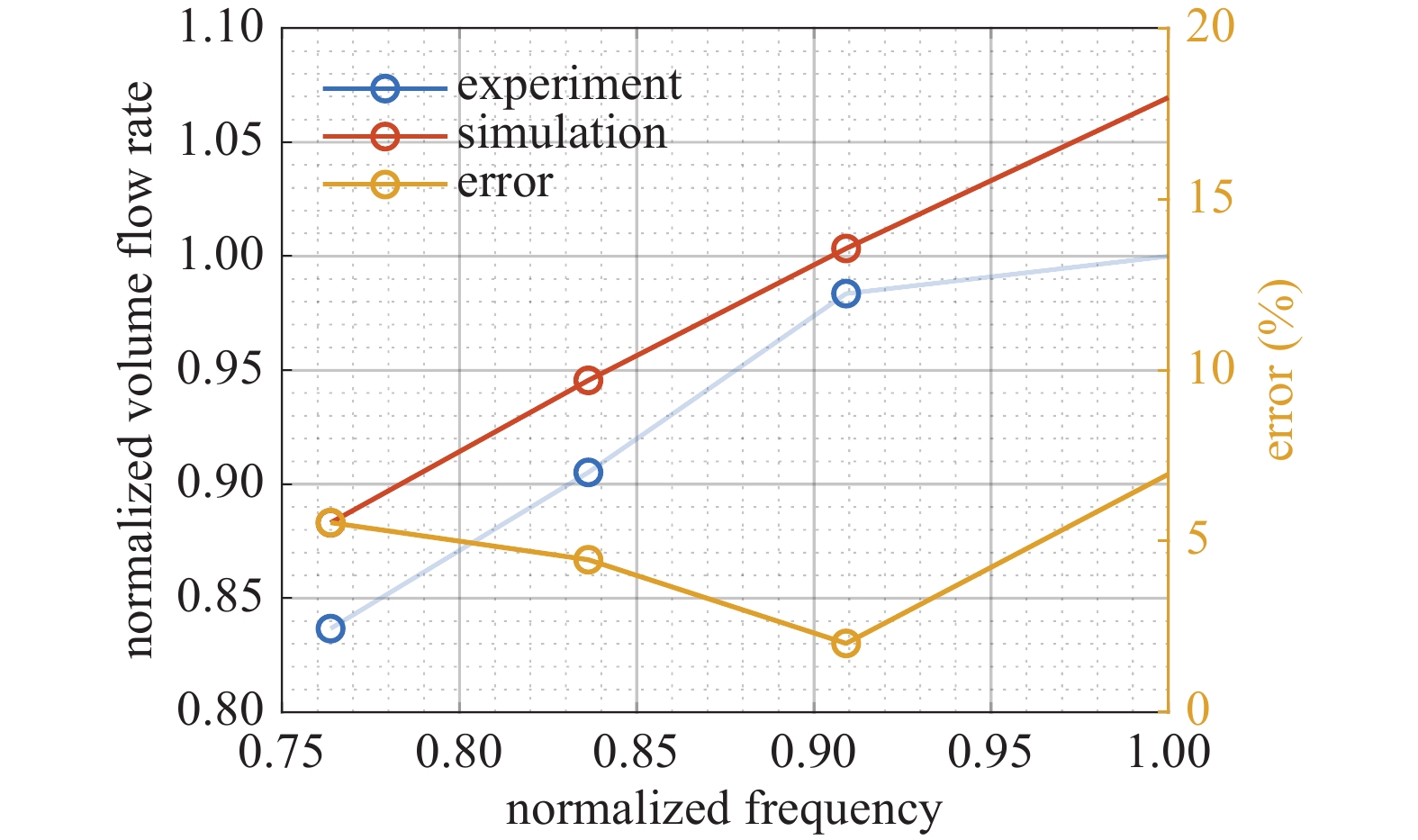
图10是针对TMP的抽速测试和抽速模拟预测对比结果，模拟预测的抽速和测试结果随转速的变化趋势具有一致性，两者之间的最大相对误差出现在满转速下，约为5%；模拟预测抽速整体略高于测试抽速，这是因为在模拟中未完全考虑分子泵的间隙泄漏、压差引起的反流等因素的影响。
TMP的转速从100% 降到90% 左右时，其最大抽速仅降低2%左右，降低幅度较为平缓，斜率约为0.18；而当转速降到额定转速的90% 以下时，抽速下降斜率约为1.01，说明在额定转速附近，由于气载等原因导致TMP转速降低时，对其抽速影响不是很明显；但当TMP转速降低到额定转速的90%以下时，其抽速与转速几乎是等比例下降，此时转速对TMP的抽速影响显著，同时也与图6中α=45°所对应的曲线在0 < β < 1范围的趋势一致。因此在实际的应用中，在TMP额定转速附近工作才能稳定发挥其抽气能力，维持较好的真空环境。
-
本文在大量仿真数据的基础上结合神经网络模型，提出了一种用于预测涡轮分子泵抽气能力的方法。通过深入的数据收集、神经网络模型的设计和训练，以及与数值模拟和实验测试的双重验证，此研究取得了一系列重要的发现和成果。首先，神经网络模型具有准确性和高效性，能够准确预测涡轮分子泵的抽气性能。有望帮助工程师和研究人员更好地优化和设计涡轮分子泵。其次，通过模型的应用，分析了影响涡轮分子泵抽气性能的多个因素，对于了解和改善涡轮分子泵的工作机制及机械结构非常重要。为涡轮分子泵的结构设计提供了有力的工具，有望提高其抽气效率和适用性。最后，由于试验粒子蒙特卡罗方法仅能模拟分子流下的抽气性能，具有一定局限性，下一步计划是使用直接模拟蒙特卡罗方法计算在过渡流态分子泵的抽气性能，拓展预测的压力范围。
基于神经网络的涡轮分子泵性能预测
Prediction of Turbomolecular Pump Performance Using Neural Networks
-
摘要: 涡轮分子泵作为维持洁净高真空环境的关键设备，广泛应用于半导体制造、空间模拟等诸多领域。然而，准确高效预测涡轮分子泵性能一直是亟待解决的难题，现有方法往往因模型缺乏通用性和计算效率不足而难以令人满意。文章聚焦于开发一种基于神经网络模型的涡轮分子泵抽气性能预测方法，旨在攻克上述挑战。提出了一种神经网络模型，该模型能够有效学习和模拟涡轮分子泵的复杂动态行为。模型训练数据涵盖数值模拟结果和实验测试数据，使其具备良好的泛化能力和预测精度。通过数值模拟和实验测试的双重验证，证明了神经网络模型能够准确预测涡轮分子泵抽气性能，并且根据实验测试结果综合分析了影响其抽气能力的诸多因素。结果表明，该模型可作为在分子流态下涡轮分子泵结构设计和性能评估的工具，能助力优化涡轮分子泵设计，进而提升其抽气效率和适用性。Abstract: Turbomolecular pumps, as critical equipment for maintaining a clean high-vacuum environment, are widely utilized in various fields such as semiconductor manufacturing and space simulation. However, accurately and efficiently predicting the performance of turbomolecular pumps has been a challenging issue. Existing methods often suffer from a lack of generality and computational efficiency, making them less than satisfactory. This study focuses on developing a performance prediction method for turbomolecular pumps based on a neural network model to address these challenges. A neural network model is proposed, which can effectively learn and simulate the complex dynamic behavior of turbomolecular pumps. The model is trained using a combination of numerical simulation results and experimental test data, endowing it with excellent generalization and predictive accuracy. Through dual verification via numerical simulation and experimental testing, it is demonstrated that the neural network model can accurately predict the pumping performance of turbomolecular pumps. Additionally, a comprehensive analysis of the factors influencing pumping capacity is performed based on experimental test results. The results indicate that this model can serve as a tool for evaluating the structural design and performance assessment of turbomolecular pumps, aiding in the optimization of their design to enhance pumping efficiency and applicability.
-
Key words:
- Turbomolecular pump /
- Neural network /
- Numerical calculations /
- Performance prediction .
-
-
图 2 传输几率的TPMC模拟结果@α=30°
Figure 2. The results of transmission probability by TPMC@α=30°
图 4 神经网络预测结果的MSE随训练过程变化
Figure 4. The change of MSE in neural network prediction results during training
图 7 对F-63/55的预测（A-插值预测 B-实验测试 C-神经网络预测）
Figure 7. Prediction of F-63/55 (A-interpolation prediction B-experimental test C-neural network prediction)
图 9 不同转速下TMP的体积流率随入口压力的变化
Figure 9. Variation of volume flow rate of TMP with inlet pressure at different rotational speeds
图 10 实验测试结果和仿真结果的对比
Figure 10. Comparison of experimental test results and simulation results
表 1 符号说明
Table 1. List of symbols
符号 意义 单位 符号 意义 单位 α 叶片攻角 ° M 气体分子的质量 g/mol β 叶片速度比β =vb/vp 1 Smax 最大抽速 m3/s γ 叶片节弦比 γ=a/b 1 Kmax 最大压缩比 1 a 叶片节长 mm σ 激活函数 b 叶片弦长 mm wi 第i层的权重矩阵 vb 叶片线速度 m/s bi 第i层的阈值 vp 气体的最可几速度 m/s MSE 均方误差 m12, m21 二维模型的正、反向传输几率 1 y 实际观测值 N 示踪粒子总数 1 $ \hat{y} $ 预测值 N12, N21 正、反向通过叶片通道的示踪粒子数 1 Ssres 残差平方和 M12, M21 三维模型的正、反向传输几率 1 Sstotal 总平方和 r1 , r2 抽气通道的内、外径 mm Q 气体流量 Pa·m3/s S 抽气通道面积 m2 p1 分子泵测试罩内压力 Pa Pn, Qn 前n级组合叶列的正、反向传输几率 1 p1,0 分子泵测试罩内初始压力 Pa R 气体状态常数；相关系数 1 p2 分子泵出口压力 Pa T 气体开氏温度 K pin, pout 叶片入、出口的压力 Pa 
下载: 导出CSV
表 2 单算例的计算耗时
Table 2. Time required for each case calculation
数值方法 耗时/s 几何中值法 0.0212 线性插值法 17.7861 神经网络模型 0.0312
下载: 导出CSV
表 3 实验所用仪器和设备
Table 3. Instruments and equipment used in experiment
编号 名称/型号 1 TMP 2 分子泵测试罩（可烘烤） 3 前级干泵 4 气体流量计组 5 气瓶（N2） 6 真空计BGP400 7 真空计GDC0250D 8、9、10 真空阀门
下载: 导出CSV
-
[1] Huang Z, Han B, Le Y. Multidisciplinary design strategies for turbomolecular pumps with ultrahigh vacuum performance[J]. IEEE Transactions on Industrial Electronics,2019,66(12):9549−9558 doi: 10.1109/TIE.2019.2891440 [2] Shams M, Sheykhzadeh H, Taghavi M. Mathematical simulation of free molecular flow in a three-dimensional turbomolecular pump with nonparallel blades[J]. Journal of Dispersion Science and Technology, 2010:299-306 [3] Sengil N. Performance increase in turbomolecular pumps with curved type blades[J]. Vacuum,2012,86(11):1764−1769 doi: 10.1016/j.vacuum.2011.12.018 [4] Sawada T, Murakami K. The axial flow molecular pump (I)[J]. Shinku,1971,14(2):33−41 doi: 10.3131/jvsj.14.33 [5] Sawada T, Murakami K. The axial flow molecular pump (2)[J]. Shinku,1971,14(3):75−82 doi: 10.3131/jvsj.14.75 [6] Li Y, Chen X, Guo W, et al. Accurate simulation of turbomolecular pumps with modified algorithm by 3D direct simulation Monte Carlo method[J]. Vacuum,2014,109:354−359 doi: 10.1016/j.vacuum.2014.03.023 [7] Sun K, Zhang S W, Han F, et al. A new modeling method to reveal pumping mechanism of turbomolecular pump[J]. Journal of Applied Fluid Mechanics,2020,14(1):165−173 [8] Schneider T N, Katsimichas S, De Oliveira C R E, et al. Empirical and numerical calculations in two dimensions for predicting the performance of a single stage turbomolecular pump[J]. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films,1998,16(1):175−180 [9] Tu J Y, Yang N H. Theoretical studies of the modern turbomolecular pump[J]. Vacuum,1987,37(11-12):831−837 doi: 10.1016/0042-207X(87)90183-7 [10] Katsimichas S, Goddard A J H, Lewington R, et al. General geometry calculations of one-stage molecular flow transmission probabilities for turbomolecular pumps[J]. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films,1995,13(6):2954−2961. [11] Wang M, Li Z. Simulations for gas flows in microgeometries using the direct simulation Monte Carlo method[J]. International Journal of Heat and Fluid Flow,2004,25(6):975−985 doi: 10.1016/j.ijheatfluidflow.2004.02.024 [12] 李博, 马兆俊, 王晓冬, 等. 基于DSMC方法的涡轮分子泵跨流态抽气性能研究[J]. 东北大学学报(自然科学版),2020,41(11):1623−1627+1632 (in Chinese) Li B, Ma Z J, Wang X D, et al. On the cross flow regime pumping performance of turbomolecular pumps based on DSMC method[J]. Journal of Northeastern University Natural Science,2020,41(11):1623−1627+1632 [13] 张鹏飞, 王晓冬, 张磊, 等. 复合分子泵抽气特性算法改进与结构优化[J]. 真空,2018,55(3):1−5 (in Chinese) Zhang P F, Wang X D, Zhang L, et al. Algorithm improvement for pumping characteristics and structure optimization of compound molecular pump[J]. Vacuum,2018,55(3):1−5 [14] 匡永麟, 王晓冬, 黄海龙, 等. 涡轮分子泵叶列抽气性能的计算方法改进[J]. 真空科学与技术学报,2022,42(01):26−30 (in Chinese) Kuang Y L, Wang X D, Zhang G Y, et al. Pumping characteristics of curved blades of turbomolecular pump[J]. Chinese Journal Vacuum Science and Technology,2022,42(01):26−30 [15] 匡永麟, 王晓冬, 张国玉, 等. 涡轮分子泵曲面叶片抽气特性研究[J]. 真空科学与技术学报,2022,42(10):731−736 (in Chinese) Kuang Y L, Wang X D, Huang H L, et al. Improvement of the calculation method of the pumping performance of the turbomolecular pump blade row[J]. Chinese Journal Vacuum Science and Technology,2022,42(10):731−736 [16] LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature,2015,521(7553):436−444 doi: 10.1038/nature14539 [17] Kruger C H. The axial-flow compressor in the free-molecule range[D]. Massachusetts Institute of Technology, 1960 [18] 匡永麟. 涡轮分子泵曲面叶片的抽气特性研究[D]. 沈阳:东北大学, 2023 (in Chinese) Kuang Y L. Study on the pumping characteristics of curved surface blades of turbomolecular pump[D]. Shenyang:Northeastern University, 2023 [19] 王晓冬, 巴德纯, 张世伟, 等. 真空技术[M]. 冶金工业出版社, 2021 (in Chinese) Wang X D, Ba D C, Zhang S W, et al. Vacuum technology[M]. Metallurgical Industry Press, 2021 [20] 王晓冬, 张磊, 巴德纯, 等. 涡轮分子泵抽气性能计算的误差分析[J]. 真空科学与技术学报,2016,36(4):432−435 (in Chinese) Wang X D, Zhang L, Ba D C, et al. Calculations of pumping behavior of turbo molecular pump and error analysis[J]. Chinese Journal Vacuum Science and Technology,2016,36(4):432−435 -
图( 10) 表( 3)
计量
- 文章访问数: 356
- HTML全文浏览数: 356
- PDF下载数: 2
- 施引文献: 0