高级搜索

用于分析单轴/双轴双各向异性媒质电磁特性的快速传输矩阵法

,  ,  , 

downloadPDF

上一篇

下一篇

樊久扬, 张玉贤, 冯晓丽, 黄志祥. 用于分析单轴/双轴双各向异性媒质电磁特性的快速传输矩阵法[J]. 物理学报, 2024, 73(24): 244101-1. doi: 10.7498/aps.73.20241346
引用本文: 樊久扬, 张玉贤, 冯晓丽, 黄志祥. 用于分析单轴/双轴双各向异性媒质电磁特性的快速传输矩阵法[J]. 物理学报, 2024, 73(24): 244101-1. doi: 10.7498/aps.73.20241346
shu
Jiu-Yang Fan, Yu-Xian Zhang, Xiao-Li Feng, Zhi-Xiang Huang. Rapid-transfer matrix method for analyzing electromagnetic properties of uniaxial/biaxial bianisotropic media[J]. Acta Physica Sinica, 2024, 73(24): 244101-1. doi: 10.7498/aps.73.20241346
Citation: Jiu-Yang Fan, Yu-Xian Zhang, Xiao-Li Feng, Zhi-Xiang Huang. Rapid-transfer matrix method for analyzing electromagnetic properties of uniaxial/biaxial bianisotropic media[J]. Acta Physica Sinica, 2024, 73(24): 244101-1. doi: 10.7498/aps.73.20241346
shu

用于分析单轴/双轴双各向异性媒质电磁特性的快速传输矩阵法

  • 1.

    安徽大学电子信息工程学院, 合肥　230601

  • 2.

    安徽大学, 信息材料与智能感知安徽省实验室, 合肥　230601

  • 3.

    安徽大学, 集成电路先进材料与技术产教研融合研究院, 合肥　230601

    • 通讯作者: E-mail: yxzhang_tute@126.com.; 

  • 中图分类号: 41.20.Jb, 42.25.Gy, 63.22.Np, 78.67.Pt

Rapid-transfer matrix method for analyzing electromagnetic properties of uniaxial/biaxial bianisotropic media

  • 1.

    School of Electronic and Engineering, Anhui University, Hefei 230601, China

  • 2.

    Information Materials and Intelligent Sensing Laboratory of Anhui Province, Anhui University, Hefei 230601, China

  • 3.

    Industry-Education-Research Institute of Advanced Materials and Technology for Integrated Circuits, Anhui University, Hefei 230601, China

    • Corresponding author: E-mail: yxzhang_tute@126.com.; 

  • MSC: 41.20.Jb, 42.25.Gy, 63.22.Np, 78.67.Pt

  • 摘要: 提出了一种高效分析单轴/双轴双各向异性媒质电磁特性的快速传输矩阵法(rapid-transfer matrix method, R-TMM). 该方法基于旋度麦克斯韦方程, 构造了关于电场的齐次微分方程, 并通过复杂的矩阵运算, 导出用于特征值求解的布克四次方程. 随后, 从特征方程中提取单轴/双轴双各向异性媒质的特征值. 在此基础之上, 通过对层状结构中电磁场在分界面处切向连续性的深入研究, 构建了适用于多层媒质中平面波传播的传输矩阵. 结合上下行波在不同区域的传播关系, 推导出单轴/双轴双各向异性传播系数的计算公式. 最后, 设计了单轴/双轴双各向异性材料模型, 并对R-TMM和传统传输矩阵法(conventional-transfer matrix method, C-TMM)的计算结果进行了分析. 数值实验表明, R-TMM不仅能够精确计算单轴/双轴双各向异性媒质的传输系数, 而且可以实现计算效率的大幅度提升. 该方法为科研人员开展单轴/双各向异性媒质电磁特性的研究提供了可靠且高效的计算策略.
    Abstract: Uniaxial/biaxial bianisotropic materials are widespreadly used in manufacturing optical devices , owing to their distinctive electromagnetic response characteristics. To effectively analyze the electromagnetic properties of uniaxial/biaxial bianisotropic materials, rapid-transfer matrix method (R-TMM) to investigate the propagation process of plane waves in the media is proposed. Starting from the Maxwell’s equations in the time domain, a homogeneous differential equation about the electric field is constructed by processing the matrix containing dielectric and magnetic conductivity, electric and magnetic loss, tellegen and chirality carrier parameters, and the complex matrix operation is applied to that equation to obtain the Booker quartic equation, and then the formulae method is utilized to obtain the eigenvalues in the uniaxial/biaxial bianisotropic media. Subsequently, the tangential continuity of layered media at the interface is employed to establish a transfer matrix for single-layered media. In the case of multi-layered media, the transfer matrix of plane waves propagating in multi-layered uniaxial/biaxial bianisotropic media can be obtained by means of a continuous iteration process based on the transfer matrix of single-layered media. The formula for calculating the propagation coefficients of uniaxial/biaxial bianisotropic materials can be derived based on the different upward and downward waves in the reflection/transmission region. Finally, the reliability and efficiency of R-TMM are verified from two numerical experiments with the plane waves incident at different angles on uniaxial/biaxial bianisotropic media. The first experiment is designed as a single-layered biaxial bianisotropic model with more general electromagnetic parameters, and the second experiment is designed as a double-layered uniaxial and biaxial bianisotropic model consisting of common optical materials, which are composed of two non-magnetic materials, lithium niobate (LiNbO3) and cadmium sulfide (CdS). The experimental results demonstrate that compared with the conventional conventional-transfer matrix method (C-TMM), the R-TMM reduces the computational memory and CPU time required for calculating the reflection and transmission coefficients of the uniaxial/biaxial bianisotropic model by over 98%, while maintaining the accuracy of the reflection and transmission coefficient calculations. Therefore, R-TMM provides an efficient and dependable approach for the designing complex optical devices and analyzing uniaxial/biaxial bianisotropic propagation characteristics.
  • 加载中

  • 图 1  平面波在单轴/双轴双各向异性媒质中的双折射现象

    Figure 1.  Birefringence phenomenon of plane waves in uniaxial/biaxial bianisotropic media.

    下载: 全尺寸图片 幻灯片

    图 2  平面波在层状单轴/双轴双各向异性媒质中传播

    Figure 2.  Propagation of plane waves in layered uniaxial/biaxial bianisotropic media.

    下载: 全尺寸图片 幻灯片

    图 3  单层媒质的模型图

    Figure 3.  Model diagram of single-layered medium.

    下载: 全尺寸图片 幻灯片

    图 4  TE模式下, 单层双轴双各向异性媒质传播系数的对比　(a)反射系数; (b)透射系数

    Figure 4.  Comparison of propagation coefficients for single-layered biaxial bianisotropic media in TE mode: (a) Reflection coefficient; (b) transmission coefficient.

    下载: 全尺寸图片 幻灯片

    图 5  TM模式下, 单层双轴双各向异性媒质传播系数的对比　(a)反射系数; (b)透射系数

    Figure 5.  Comparison of propagation coefficients for single-layered biaxial bianisotropic media in TM mode: (a) Reflection coefficient; (b) transmission coefficient.

    下载: 全尺寸图片 幻灯片

    图 6  多层光学材料模型图

    Figure 6.  Model diagram of multi-layered optical material.

    下载: 全尺寸图片 幻灯片

    图 7  TE模式下, 多层光学材料传播系数的对比　(a)反射系数; (b)透射系数

    Figure 7.  Comparison of propagation coefficients for multi-layered optical materials in TE mode: (a) Reflection coefficients; (b) transmission coefficients.

    下载: 全尺寸图片 幻灯片

    图 8  TM模式下, 多层光学材料传播系数的对比　(a)反射系数; (b)透射系数

    Figure 8.  Comparison of propagation coefficients for multi-layered optical materials in TM mode: (a) Reflection coefficients; (b) transmission coefficients.

    下载: 全尺寸图片 幻灯片

    表 1  单层双轴双各向异性的电磁参数

    Table 1.  Electromagnetic parameters of single-layered biaxial bianisotropic medium.

    $\boldsymbol\varepsilon_{\rm r}$ $\boldsymbol \mu_{\rm r} $ $\boldsymbol \sigma_{\rm e} $ $\boldsymbol \sigma_{\rm m} $
    $ \left[ {\begin{array}{*{20}{c}} {5.6}&0&0 \\ 0&{4.8}&0 \\ 0&0&{6.1} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {2.9}&0&0 \\ 0&{4.2}&0 \\ 0&0&{2.6} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {2.9}&0&0 \\ 0&{4.2}&0 \\ 0&0&{2.6} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {271}&0&0 \\ 0&{422}&0 \\ 0&0&{354} \end{array}} \right] $
    $\boldsymbol \xi $ $\boldsymbol \zeta $
    $ \left[ {\begin{array}{*{20}{c}} {3.9 + 0.01{\text{j}}}&0&0 \\ 0&{5.3 + 0.03{\text{j}}}&0 \\ 0&0&{4.3 + 0.06{\text{j}}} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {3.9 - 0.01{\text{j}}}&0&0 \\ 0&{5.3 - 0.03{\text{j}}}&0 \\ 0&0&{4.3 - 0.06{\text{j}}} \end{array}} \right] $
    下载: 导出CSV

    表 2  C-TMM和R-TMM计算单层媒质传播系数的效率比较

    Table 2.  Comparison of efficiency between C-TMM and R-TMM in calculating the propagation coefficients of single-layered medium.

    方法CPU核数内存/MBCPU时间/s

    TE
    TM
    C-TMM1729.49.254110.6075
    R-TMM15.30.13030.1521
    比率 (R-TMM / C-TMM)0.00730.014080.01434
    下载: 导出CSV

    表 3  两种光学材料的电磁参数

    Table 3.  Electromagnetic parameters of two optical materials.

    Media $\boldsymbol\varepsilon_{\rm r}$ $\boldsymbol\mu_{\rm r}$ $\boldsymbol\sigma_{\rm r}$ $\boldsymbol\sigma_{\rm r}$
    LiNbO3 $ \left[ {\begin{array}{*{20}{c}} {32.3}&0&0 \\ 0&{32.3}&0 \\ 0&0&{37.4} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {1.0}&0&0 \\ 0&{1.0}&0 \\ 0&0&{1.1} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {4.9}&0&0 \\ 0&{4.9}&0 \\ 0&0&{5.8} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {356}&0&0 \\ 0&{356}&0 \\ 0&0&{564} \end{array}} \right] $
    CdS $ \left[ {\begin{array}{*{20}{c}} {6.25}&0&0 \\ 0&{6.01}&0 \\ 0&0&{6.32} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {1.0}&0&0 \\ 0&{1.0}&0 \\ 0&0&{1.0} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {0.02}&0&0 \\ 0&{0.03}&0 \\ 0&0&{0.01} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} 0&0&0 \\ 0&0&0 \\ 0&0&0 \end{array}} \right] $
    Media $\boldsymbol\xi $ $\boldsymbol\zeta $
    LiNbO3 $ \left[ {\begin{array}{*{20}{c}} {0.02}&0&0 \\ 0&{0.02}&0 \\ 0&0&{0.01} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {0.02}&0&0 \\ 0&{0.02}&0 \\ 0&0&{0.01} \end{array}} \right] $
    CdS $ \left[ {\begin{array}{*{20}{c}} {4.5 + 0.01{\text{j}}}&0&0 \\ 0&{6.6 + 0.02{\text{j}}}&0 \\ 0&0&{3.9 + 0.01{\text{j}}} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {4.5 - 0.01{\text{j}}}&0&0 \\ 0&{6.6 - 0.02{\text{j}}}&0 \\ 0&0&{3.9 - 0.01{\text{j}}} \end{array}} \right] $
    下载: 导出CSV

    表 4  C-TMM和R-TMM在计算多层光学材料传播系数时的效率对比

    Table 4.  Comparison of efficiency between C-TMM and R-TMM in calculating the propagation coefficient of multilayer optical materials.

    方法 CPU核数 内存/MB CPU时间/s
    TE TM
    C-TMM 1 744.2 11.8062 11.8935
    R-TMM 1 7.6 0.1796 0.1851
    比率 (R-TMM/C-TMM) 0.0102 0.0152 0.0156
    下载: 导出CSV
  • [1] Chen Y X, Duan G Y, Xu C Y, Qin X F, Zhao Q, Zhou H Q, Wang B X 2024 Diam. Relat. Mater. 143 110939 doi: 10.1016/j.diamond.2024.110939
    [2] Hosseini K, Atlasbaf Z 2018 IEEE Trans. Antennas Propag. 66 7483 doi: 10.1109/TAP.2018.2866990
    [3] Ahmed F, Hassan T, Shoaib N 2020 IEEE Antennas Wirel. Propag. Lett. 19 1833 doi: 10.1109/LAWP.2020.3020949
    [4] Dong Z J, Feng X, Zhou H Q, Liu C, Zhang M H, Liang W J 2023 IEEE Trans. Geosci. Remote Sens. 61 4503120 doi: 10.1109/TGRS.2023.3286945
    [5] Kong J A 1972 Proc. IEEE 60 1036 doi: 10.1109/PROC.1972.8851
    [6] 王一平 2007 工程电动力学 (第二版) (西安: 西安电子科技大学出版社) 第23−24页 Wang Y P 2007 Engineering Electrodynamics (2rd Ed.) (Xi’ an: Xidian University Press) pp23–24
    [7] Zarifi D, Soleimani M, Abdolali A 2014 IEEE Trans. Antennas Propag. 62 1538 doi: 10.1109/TAP.2013.2297166
    [8] Dimitriadis A I, Kantartzis N V, Tsiboukis T D 2013 IEEE Trans. Magn. 49 1769 doi: 10.1109/TMAG.2013.2238517
    [9] Mousvai S M, Arand B A, Forooraghi K 2021 IEEE Access. 9 54241 doi: 10.1109/ACCESS.2021.3071112
    [10] Hasar U C, Ozturk G, Kaya Y, Barroso J J, Ertugrul M 2021 IEEE Trans. Antennas Propag. 69 7064 doi: 10.1109/TAP.2021.3098550
    [11] Karimi P, Rejaei B, Khavasi A 2023 IEEE Trans. Antennas Propag. 71 2507 doi: 10.1109/TAP.2023.3234826
    [12] 陈伟, 黄海, 杨利霞, 薄勇, 黄志祥 2023 物理学报 72 060201 doi: 10.7498/aps.72.20222113 Chen W, Huang H, Yang L X, Bo Y, Huang Z X 2023 Acta Phys. Sin. 72 060201 doi: 10.7498/aps.72.20222113
    [13] 谢国大, 侯桂林, 牛凯坤, 冯乃星, 方明, 李迎松, 黄志祥 2023 物理学报 72 150201 doi: 10.7498/aps.72.20230501 Xie G D, Hou G L, Niu K K, Feng N X, Fang M, Li Y S, Huang Z X 2023 Acta Phys. Sin. 72 150201 doi: 10.7498/aps.72.20230501
    [14] Demarest K 1987 IEEE Trans. Antennas Propag. 35 826 doi: 10.1109/TAP.1987.1144183
    [15] 葛德彪, 闫玉波 2005 电磁波时域有限差分方法 (第三版) (西安: 西安电子科技大学出版社) 第259—294页 Ge D B, Yan Y B 2005 Finite-Difference Time-Domain Method for Electromagnetic Waves (3rd Ed.) (Xi’an: Xidian University Press) pp259−294
    [16] 王飞, 葛德彪, 魏兵 2009 物理学报 58 6356 doi: 10.7498/aps.58.6356 Wang F, Ge D B, Wei B 2009 Acta Phys. Sin. 58 6356 doi: 10.7498/aps.58.6356
    [17] Greenwood A D, Jin J M 1999 IEEE Trans. Antennas Propag. 47 1260 doi: 10.1109/8.791941
    [18] 孙宏祥, 许伯强, 王纪俊, 徐桂东, 徐晨光, 王峰 2009 物理学报 58 6344 doi: 10.7498/aps.58.6344 Sun H X, Xu B Q, Wang J J, Xu G D, Xu C G, Wang F 2009 Acta Phys. Sin. 58 6344 doi: 10.7498/aps.58.6344
    [19] Hanninen I, Nikoskinen K 2008 IEEE Trans. Antennas Propag. 56 278 doi: 10.1109/TAP.2007.913171
    [20] 王哲, 王秉中 2014 物理学报 63 120202 doi: 10.7498/aps.63.120202 Wang Z, Wang B Z 2014 Acta Phys. Sin. 63 120202 doi: 10.7498/aps.63.120202
    [21] 葛德彪, 魏兵 2011 电磁波理论 (北京: 科学出版社) 第62—73页 Ge D B, Wei B 2011 Electromagnetic Waves Theory (Beijing: Science Press) pp62−73
    [22] Johnston T W 1969 Radio Sci. 4 729 doi: 10.1029/RS004i008p00729
    [23] Chen H C 1981 Radio Sci. 16 1213 doi: 10.1029/RS016i006p01213
    [24] Tan E L, Tan S Y 1999 IEEE Trans. Antennas Propag. 47 1820 doi: 10.1109/8.817658
    [25] 郑宏兴, 葛德彪 2000 物理学报 49 1702 doi: 10.7498/aps.49.1702 Zheng H X, Ge D B 2000 Acta Phys. Sin. 49 1702 doi: 10.7498/aps.49.1702
    [26] Jiang Y Y, Shi H Y, Zhang Y Q, Hou C F, Sun X D 2007 Chin. Phys. 16 1959 doi: 10.1088/1009-1963/16/7/026
    [27] Sarrafi P, Qian L 2012 IEEE J. Quantum Electron. 48 559 doi: 10.1109/JQE.2012.2183116
    [28] 王飞, 魏兵 2019 物理学报 68 244101 doi: 10.7498/aps.68.20190823 Wang F, Wei B 2019 Acta Phys. Sin. 68 244101 doi: 10.7498/aps.68.20190823
    [29] Zhang Y X, Feng N X, Wang G P, Zheng H X 2021 IEEE Trans. Antennas Propag. 69 4727 doi: 10.1109/TAP.2020.3044591
  • 加载中
图( 8) 表( 4)
计量
  • 文章访问数:  184
  • HTML全文浏览数:  184
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-24
  • 刊出日期:  2024-12-20

用于分析单轴/双轴双各向异性媒质电磁特性的快速传输矩阵法

    通讯作者: E-mail: yxzhang_tute@126.com.; 
  • 1. 安徽大学电子信息工程学院, 合肥　230601
  • 2. 安徽大学, 信息材料与智能感知安徽省实验室, 合肥　230601
  • 3. 安徽大学, 集成电路先进材料与技术产教研融合研究院, 合肥　230601
  • 收稿日期:  2024-09-24

摘要: 提出了一种高效分析单轴/双轴双各向异性媒质电磁特性的快速传输矩阵法(rapid-transfer matrix method, R-TMM). 该方法基于旋度麦克斯韦方程, 构造了关于电场的齐次微分方程, 并通过复杂的矩阵运算, 导出用于特征值求解的布克四次方程. 随后, 从特征方程中提取单轴/双轴双各向异性媒质的特征值. 在此基础之上, 通过对层状结构中电磁场在分界面处切向连续性的深入研究, 构建了适用于多层媒质中平面波传播的传输矩阵. 结合上下行波在不同区域的传播关系, 推导出单轴/双轴双各向异性传播系数的计算公式. 最后, 设计了单轴/双轴双各向异性材料模型, 并对R-TMM和传统传输矩阵法(conventional-transfer matrix method, C-TMM)的计算结果进行了分析. 数值实验表明, R-TMM不仅能够精确计算单轴/双轴双各向异性媒质的传输系数, 而且可以实现计算效率的大幅度提升. 该方法为科研人员开展单轴/双各向异性媒质电磁特性的研究提供了可靠且高效的计算策略.

English Abstract

    全文HTML

    1.   引　言

    • 在光学器件制造和材料科学发展的历史进程中, 新型复合材料的作用日益凸显[1]. 随着材料科学技术的快速发展, 电磁波与材料之间的相互作用变得日益复杂, 需要采用新型技术去探究波在媒质中的传播特性. 单轴/双轴双各向异性材料是一种特殊类型的双各向异性材料, 具有复杂的光学性质, 广泛应用于光学器件和通信等领域[2–4].

      关于单轴/双轴双各向异性媒质的研究可以追溯到1972年, 孔金瓯教授[5]在麦克斯韦方程组的基础上, 引入量子假设对双各向异性媒质中的电磁场进行量子化. 随后, 王一平教授[6]给出了双各向异性媒质本构关系的表示形式. 进入21世纪后, 计算机性能的显著提升为科研人员对双各向异性材料电磁特性的深入探索提供了条件. 2014年, Zarifi等[7]扩展了基于状态空间方法的电磁表征方法, 实现了双轴双向异性媒质的电磁表征. 之后, 科研人员开始将注意力转向双各向异性超表面[8,9]、超材料[10,11]等前沿领域, 并采用多种数值算法对材料的电磁特性给予测定. 利用电磁计算理论和方法模拟平面波在媒质中的传播, 探究其在媒质中的电磁特性, 是计算电磁学领域的热点议题[12,13]. 数值计算方法是计算电磁学研究各种电磁特性的重要工具, 主要包括时域有限差分法[14–16]、有限元法[17,18]、矩量法[19,20]和传输矩阵法[21]等. 传输矩阵法有效简化了平面波在介质中的传播过程, 从而在分析复杂电磁特性时显著提高了计算效率, 确立了其在快速计算领域内的优势地位. 在采用传输矩阵法对各类均匀分层媒质的电磁特性进行研究时, 特征方程和特征值的获取是该方法的核心问题. 早在1969年, Johnston[22]建立了用于分析特殊电/磁各向异性媒质的布克四次方程. 1981年, Chen[23]应用无坐标形式的色散方程和布克四次方程求解了各向异性媒质的波反射问题. 1999年, Tan等[24]从色散关系出发, 导出了互易和无损条件下多层双各向异性结构的布克四次方程. 2000年, 郑宏兴和葛德 彪[25]成功实现了分层各向异性媒质传输矩阵法的构建, 并据此推导出了媒质中反射系数和透射系数的计算公式. 然而, 他们的研究局限于单轴各向异性媒质, 且并未进行不同条件下数值结果的比较. 2007年, Jiang等[26]分析了双轴各向异性媒质中平面波的传播特性, 理论推导了平面波的存在条件. 2012年, Sarrafi和Qian[27]使用广义时域传输矩阵法对具有谐振非线性的层状结构中的脉冲传播进行建模, 相比于时域有限差分法, 该方法大幅度提高了计算效率. 2019年, 王飞和魏兵[28]建立了有耗分层媒质的传播矩阵模型, 计算了“无限薄”石墨烯层的反射系数和透射系数, 并讨论了含石墨烯涂层Si/SiO2周期结构的吸收率, 但其所使用的分层模型仍基于简单的各向同性, 尚未涉及复杂模型的计算与分析. 直到2021年, Zhang等[29]利用传输矩阵法计算了多层全各向异性媒质的传播系数, 并预测了平面波在媒质中能量的传输过程.

      在相关领域的探索中, 科研人员对双各向异性材料与传输矩阵法的应用进行了多元化的探讨. 然而, 迄今为止, 尚无成熟的方法能够对单轴/双轴双各向异性媒质的电磁特性做以高效的数值计算. 为此, 本文提出了一种新型快速传输矩阵法(rapid-transfer matrix method, R-TMM), 旨在有效攻克此技术瓶颈. 本文的主要创新点如下:

      1) 本文拓展了传输矩阵法在分层媒质中的应用范围, 并成功构建了平面波在单轴/双轴双各向异性媒质中传播的传输矩阵.

      2) 本文采用R-TMM实现了单轴/双轴双各向异性媒质反射系数和透射系数的精确计算. 相比于C-TMM, R-TMM节省了超过98%的内存和CPU时间.

      本文的结构安排如下: 第2节首先主要探讨如何获取空气以及单轴/双轴双各向异性媒质中的特征值, 然后聚焦于传输矩阵的构建及传播系数计算公式的推导. 在第3节, 设计了单轴/双轴双各向异性数值算例, 并将所得结果与传统传输矩阵法 (conventional-transfer matrix method, C-TMM) 进行对照, 从而验证了R-TMM的可靠性和高效性. 最后, 第4节中, 对全文的内容作以总结.

    2.   R-TMM的推导

      2.1.   特征值的计算

    • 单轴/双轴双各向异性的旋度麦克斯韦方程可以写成如下形式:

      式中, 关于时间t的偏导数$ \dfrac{\partial }{{\partial t}} = {\text{j}}\omega $, 3×3张量$\boldsymbol\sigma_{\rm e}$和$\boldsymbol\sigma_{\rm m} $分别是电损耗和磁损耗. 电通量D和磁通量B本构关系表示为

      式中, ε0和µ0是空气中的介电常数和磁导系数; εr和µr分别是相对介电常数和相对磁导系数; 张量$\boldsymbol \xi $和$\boldsymbol \zeta $可写为

      其中, 特勒根参数${\boldsymbol \varsigma } $和手性度承载参数${\boldsymbol \kappa} $都是无量纲参数. 通过将(3)式代入(1)式, (4)式代入(2)式, 可以得到

      式中, 张量${\boldsymbol \chi } $, γ, τ和υ分别可以表示为

      将(6)式代入(5)式中, 可以获得关于电场E的齐次微分方程:

      其中, ψ是一个复杂的微分矩阵, 表示电磁波在单层单轴/双轴双各向异性媒质中传播时的亥姆霍兹方程, I为3×3单位矩阵.

      平面波在空气中传播时, 波的时谐场形式可以表示为

      其中U可以代表电场E和磁通量B. 经过推导, 纵向矢量kz满足如下关系:

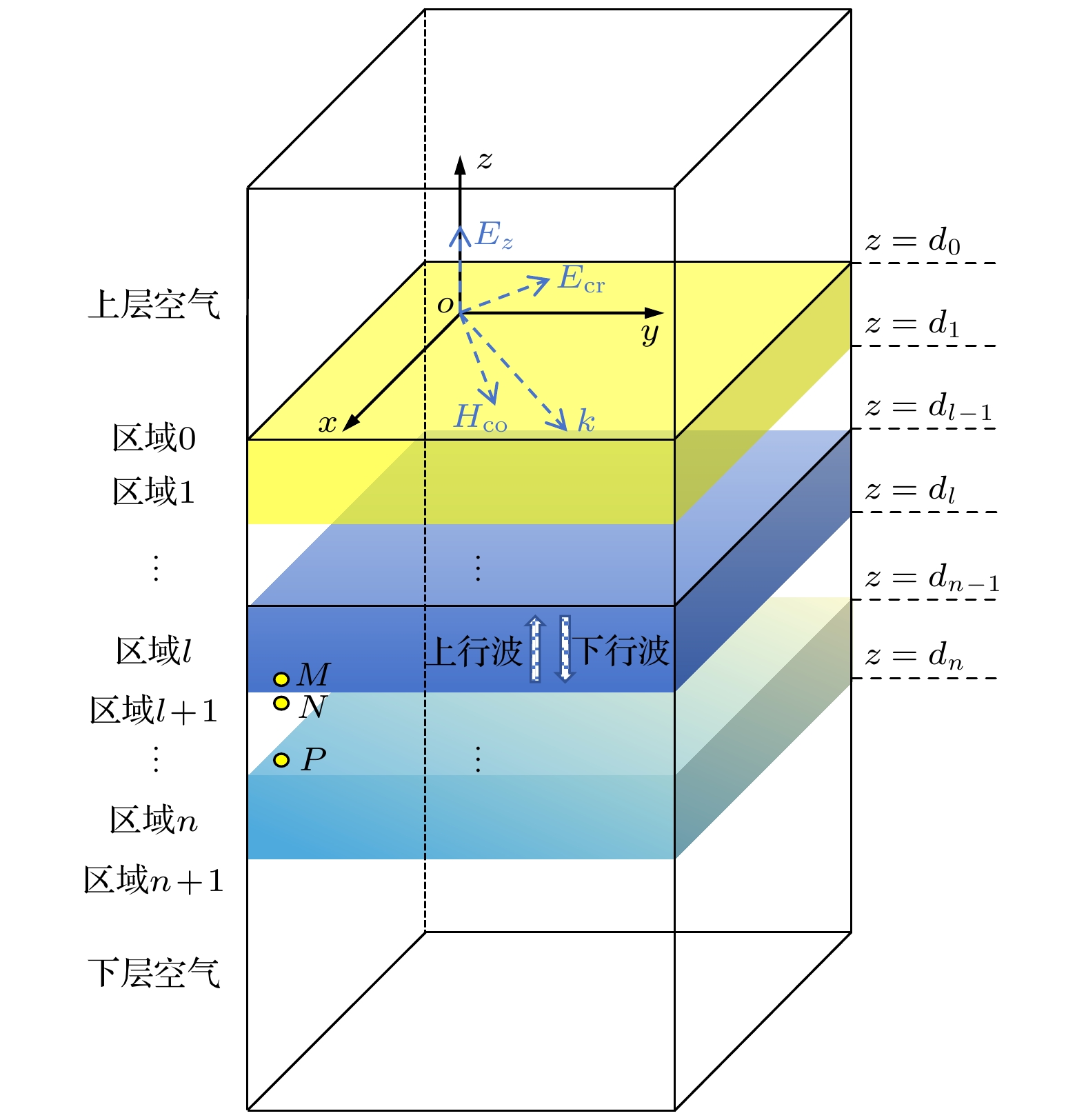
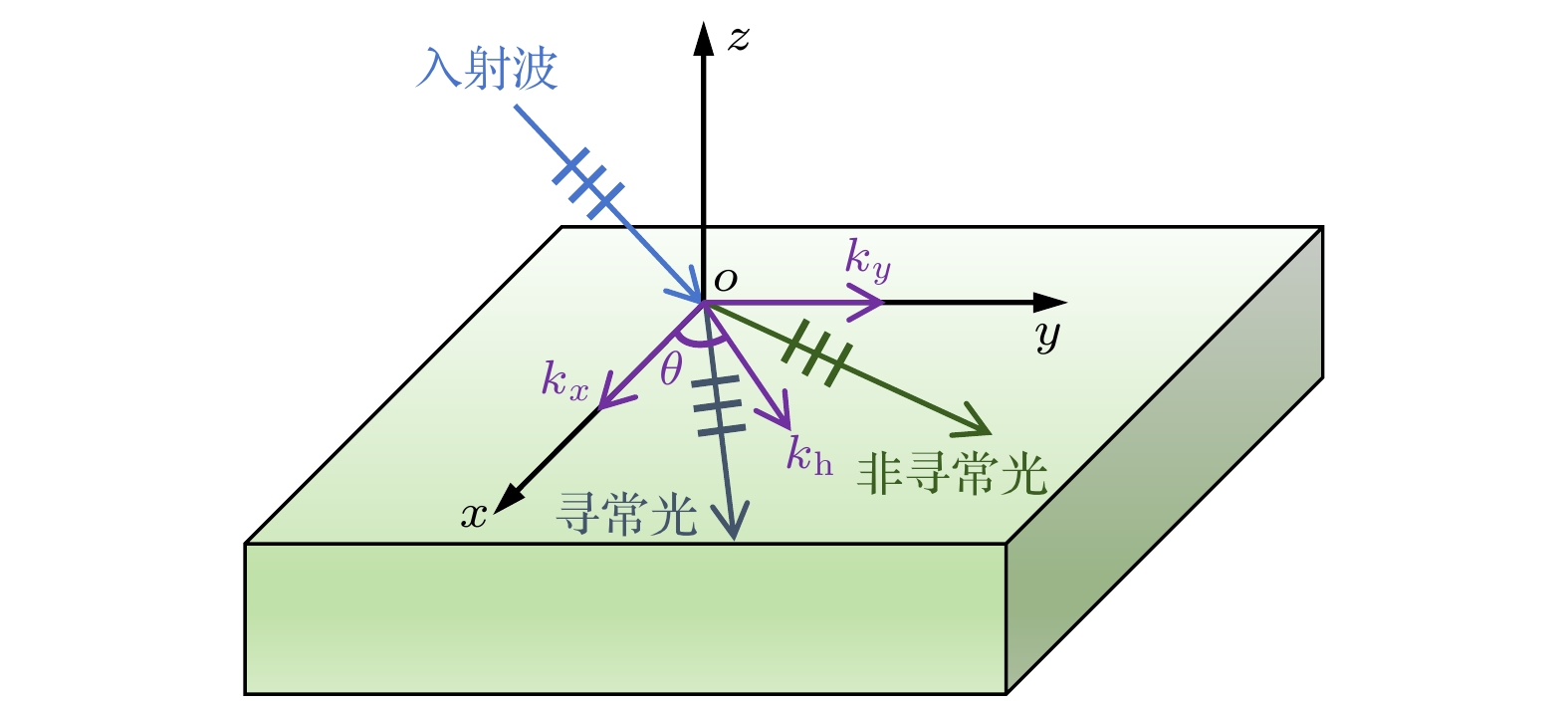
      如图1所示, 平面波从空气进入单层单轴/双轴双各向异性媒质时, 会发生双折射现象, 从而在媒质中产生两束透射光波, 分别为寻常光和非寻常光. 在xOy平面中, 入射波的横向波矢量(kx, ky)可以等效为kh. 在此基础上, 横向波矢量kx与kh之间的夹角被定义为横向角θ. 根据这一几何关系, 可以推导出横向波矢量(kx, ky)和kh之间的数值关系为

      由于平面波始终沿z方向传播, 且每层媒质的物理性质均匀, 不随空间位置而改变. 因此, 横向波矢量(kx, ky)在各层媒质中保持不变. 纵向矢量kz随频率的变化而变化, 决定了平面波在单轴/双轴双各向异性媒质中的传播特性.

      由此而见, 纵向矢量kz的计算是平面波在双轴各向异性媒质中传播的核心问题. 当平面波斜入射双轴各向异性媒质时, 通过对(7)式进行展开和简化, 推导出布克四次方程, 其具体形式如下:

      经过推导, 由于单轴/双轴双各向异性媒质电磁参数的特殊性, (11)式中关于纵向矢量kz的三次幂项为零. 其中, 由矩阵${\boldsymbol \chi } $, γ, τ和υ中的元素构成的系数α4, α3, α2和α1为

      (11)式中, 参数Λ可以表示电场强度E = (Ex, Ey, Ez)T. 若把(5)式代入(6)式, 也能导出关于磁场强度H的齐次微分方程. 观察(11)式可知, 由于表征电场强度E和磁场强度H的参数Λ不能为零, 为保证该方程有解, 所以参数Λ的系数项必须为零. 随后, 求解关于纵向矢量kz的布克四次方程, 其中间变量i, d, e, u, g和h分别为

      在(12c)式中, 由于变量d不能为零, 因此要依据(12b)式选择$\left| d \right|$达到最大值时所对应的i值. 因为(12f)式中的u也不能为零, 所以要根据(12d)式选出$\left| u \right|$取得最大值时所对应的d值. 由此, 可以确定在单频点下, 单层单轴/双轴双各向异性媒质中的4个特征值ρi = –jkz,i (i = 1, 2, 3, 4). 特征值的显式表达式如下:

      • 2.2.   单轴/双轴双各向异性媒质中的传输矩阵

    • 在一般情形下, 平面波的入射方式以斜入射为主. 众所周知, 当斜平面波在媒质中传播时, 可分为TE模式和TM模式. 以TE模式为例, 平面波在单轴/双轴双各向异性媒质中的传播过程如图2所示.

      在区域l中, 上行波和下行波同时存在, 电场强度E = (Ex, Ey, Ez)T和磁场强度H = (Hx, Hy, Hz) T可以表示为

      其中, A1,l , A2,l和 B1,l , B2,l分别代表区域l中的下行波和上行波的幅值; 变量$ {{\eta }_{{i}, { }{{E}_{y}}, {l}}} $和$ {{\eta }_{{i}, { }{{E}_{z}}, {l}}} $分别为

      在区域l和区域l + 1的分界面处, 电场和磁场切向分量连续的边界条件为

      把(15a)式—(15d)式转换成矩阵形式, M点到N点的传输关系为

      式中, 矩阵Vl 和Vl+1分别表示为

      其中, $ {{p}_{l}} $, $ {{q}_{l}} $和$ {{p}_{{l + }{1}}} $, $ {{q}_{{l + }{1}}} $的表达形式类似. 在此, 给出pl和ql的表达式:

      在区域l+1中, 平面波从N点到P点的传播过程可用矩阵的形式表示为

      (17)式为恒等式, 目的是引入传输矩阵VNP,l. 结合(17)式, 平面波从M点到P点的传播过程可用矩阵的形式表示为

      分层媒质传输矩阵的构建本质上是对单层媒质传输矩阵的迭代, 但需要注意的是, 其传输矩阵的末项表示的是平面波从区域n到区域n + 1的传播过程. 据此, 平面波从区域0到区域n + 1的传输矩阵为

      其中, 前向传输矩阵V0(n+1)描述的是平面波自上层空气进入媒质层后, 到达下层空气的传播过程. 若平面波的传播方向和上述情况相反, 则前向传输矩阵的逆矩阵定义为后向传输矩阵.

      鉴于区域0为反射区域, 其中不存在透射 波(下行波), 因此可以得到$ {{A}_{{\text{1,0}}}}\exp ({{\rho }_{1, {0}}}{{d}_0}) = {{A}_{{\text{2,0}}}} \times \exp ({{\rho }_{3, {0}}}{{d}_0}) = 0 $; 而区域$n+1$为透射区域, 则其中不存在反射波(上行波), 则由此可得

      在本文中, 假设初始入射场$ {\boldsymbol X} = {[1, 0]^{\text{T }}} $, 经过推导, 平面波在反射区域和透射区域分别有以下传输 关系:

      这里, v0(n+1)是指矩阵V0(n+1)的元素, 矩阵M和Y均是2×1的矩阵. 根据(20)式和(21)式, 单轴/双轴双各向异性媒质的反射系数和透射系数的幅值可以表示为

      这里, mxx和myx分别是矩阵M的第1行第1列和第2行第1列元素; yxx和yyx分别是矩阵Y的第1行第1列和第2行第1列元素. 上述的理论推导为在TE模式下, R-TMM计算单轴/双轴双各向异性媒质反射系数和透射系数的过程. 通过电磁对偶原理, 即可获得TM模式下反射系数和透射系数的计算公式.

    3.   数值计算

    • 为了验证R-TMM在分析单轴/双轴双各向异性媒质电磁特性方面的有效性, 本文对平面波在有耗单层/多层媒质中的传播过程进行了数值模拟. 此外, 将R-TMM与C-TMM的计算结果进行了对比, 用于体现R-TMM的准确性和高效性.

      • 3.1.   单层媒质传播系数

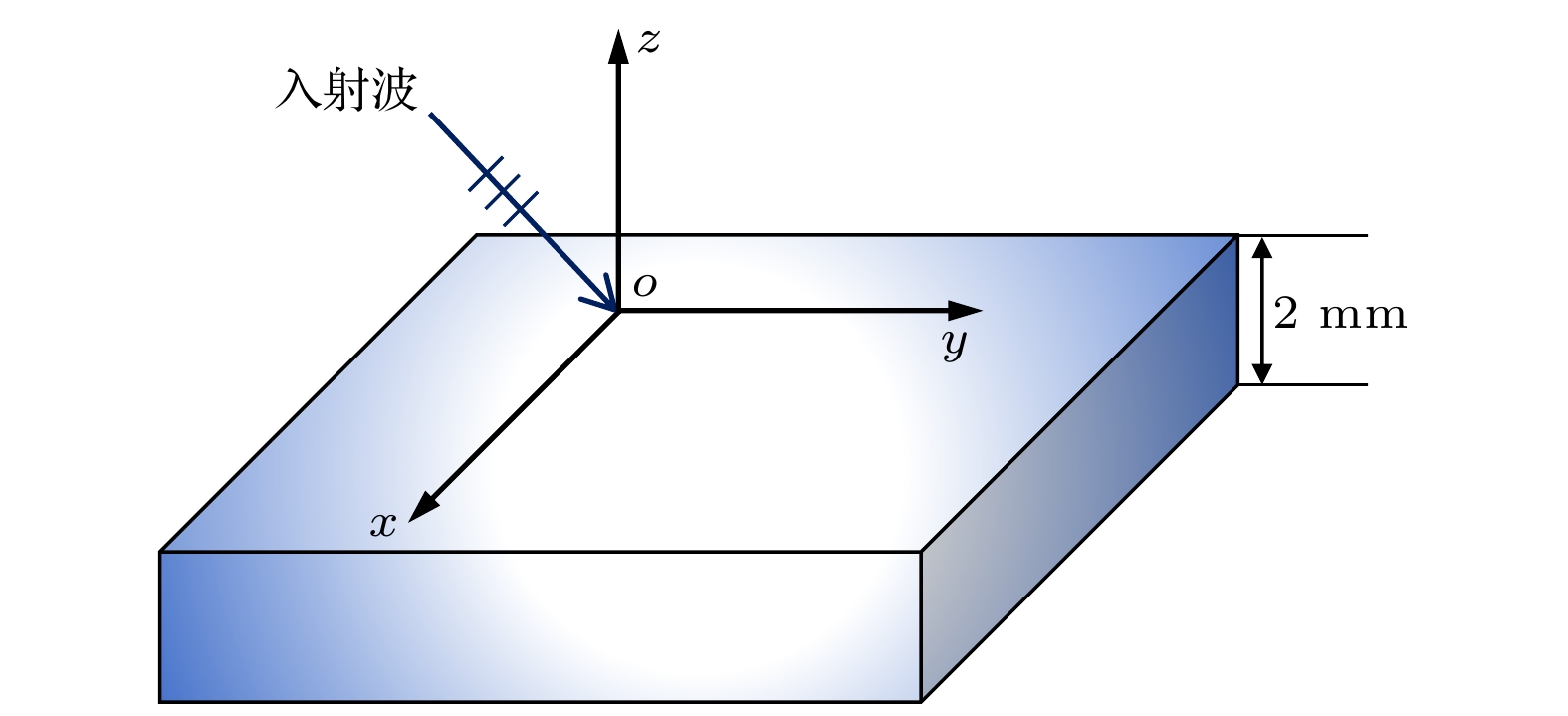
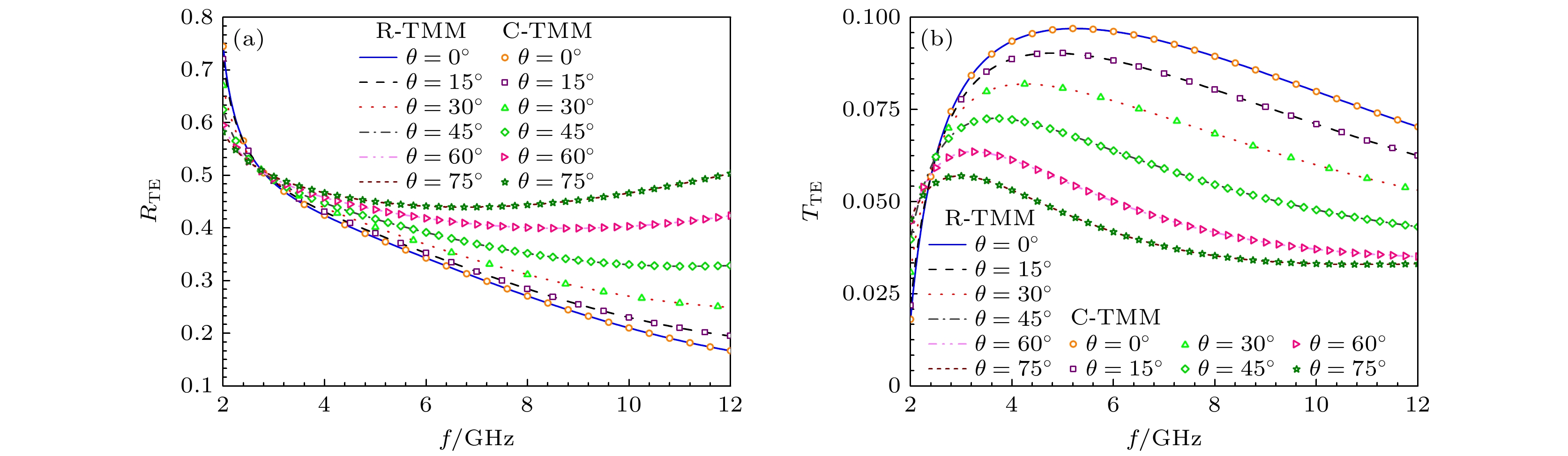
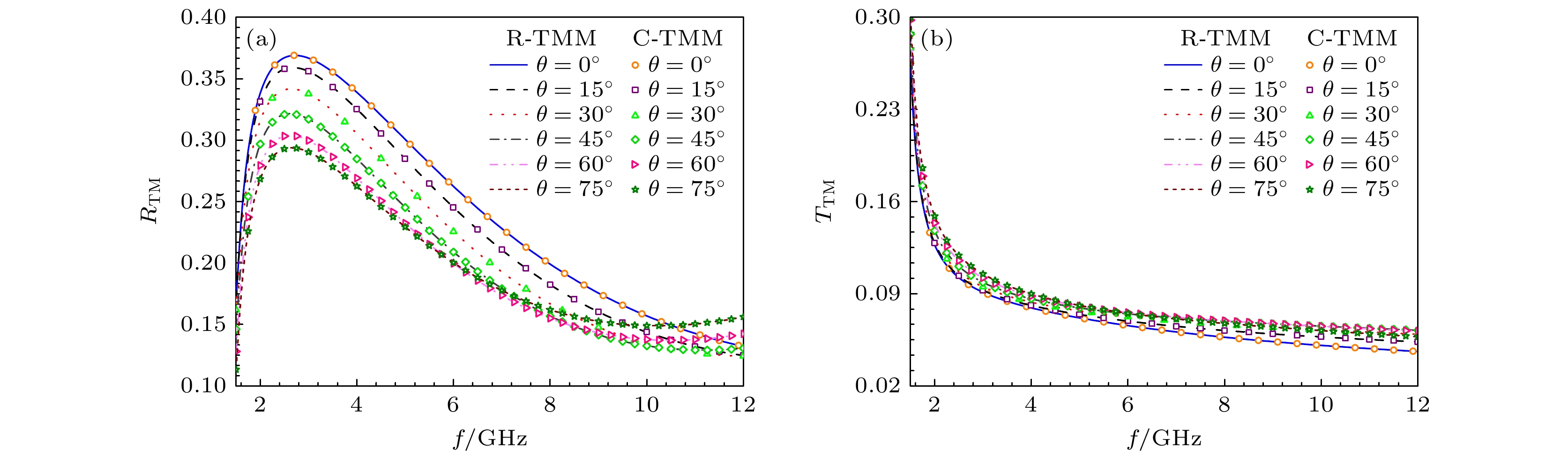
    • 图3为平面波斜入射单层双轴双各向异性媒质的模型, 媒质厚度设定为 2 mm, 具体的电磁参数如表1所列. 在TE模式下, 横向矢量kh 的大小设定为40, 频率f = [2,12] GHz. 当横向角θ = 0°, 15°, 30°, 45°, 60°和75°时, 分别计算不同角度下的传播系数, R-TMM和C-TMM反射系数和透射系数的比较结果如图4所示. 对于TM模式, 横向矢量kh 的取值为30, 设定频率f = [1.5, 12] GHz, 横向角θ的取值和TE模式下的情况相同, R-TMM和C-TMM的反射系数和透射系数曲线如图5所示. 图4和图5表明, R-TMM和C-TMM计算出的传播系数相吻合, 从而验证了R-TMM计算单层双轴双各向异性媒质传播系数时的准确性. 通过观察TE模式下的传播系数曲线, 发现当横向角θ为60°, 70°时, 随着频率的增大, 反射系数先下降后逐渐上升, 而其他角度下的反射系数持续下降; 透射系数在横向角θ = 70°时表现为先增大后减小, 随后略有增大, 而其他角度下的透射系数则表现为先增大后持续减小. 对于TM模式, 在横向角θ为60°, 70°时, 反射系数随频率的增大表现出先上升后下降, 再逐渐上升的趋势, 而其他角度下的反射系数先上升后下降; 透射系数在不同横向角下均随频率增大而不断减小. 由此可见, 不同情况下的反射系数和透射系数呈现出规律性的变化. 这种现象可为探究单层双轴双各向异性媒质的结构特性提供依据.

      双轴双各向异性媒质的传播系数计算效率受到多种因素的影响. 这些因素不仅包括所采用的计算方法, 还涵盖媒质的类型、模型的厚度、入射方式以及频点的数量. 在本实验中, 横向角θ的调整只会导致平面波入射条件的变化, 不会造成传播系数计算复杂性的增加. 因此, 横向角θ的变化对R-TMM和C-TMM的效率没有明显影响. 据此, 以横向角θ = 30°为具体案例, 本文比较了R-TMM与C-TMM在效率上的差异. 表2的数据显示, R-TMM显著提升了计算效率, 与C-TMM相比, 计算机内存的消耗减小了约99.27%. 此外, TM模式的CPU计算时间略高于TE模式, 这是由于TM模式下的频点数为211个, 而TE模式仅为201个. 在TE模式和TM模式下, CPU的计算时间分别节省了大约98.59%和98.57%. 计算效率的大幅度提高主要归功于以下两个原因: 1) 特征值求解以及传输矩阵构建过程的简化, 显著减少了矩阵的运算量. 2) 通过采用Fortran编程语言对R-TMM进行编译, 有效提升了计算效率.

      • 3.2.   多层光学材料的传播系数

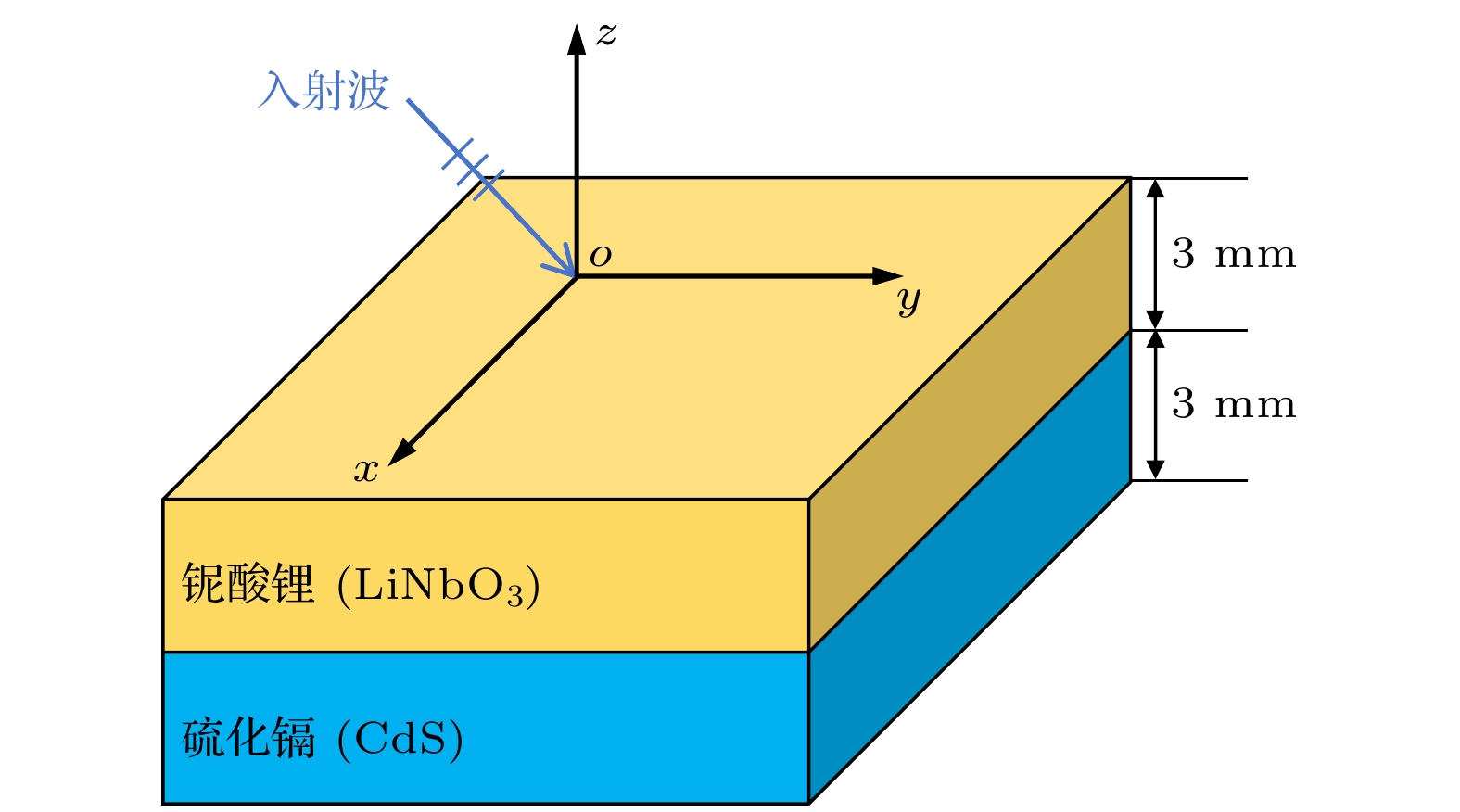
    • 单层双轴双各向异性媒质传播系数的准确性得到验证之后, 为进一步评估R-TMM在分析多层光学材料电磁特性时的性能, 本节设计了如图6所示的两层光学材料模型. 该模型由两种非磁性光学材料组成, 分别为具有单轴双各向异性的铌酸锂(LiNbO3)和呈现双轴双各向异性的硫化镉(CdS), 两种材料的厚度均为3 mm. 具体的电磁参数列于表3中.

      铌酸锂的特勒根参数与电光效应引起的折射率变化相关, 其变化范围一般在0.01—0.03之间. 由于铌酸锂材料本身不具有手性特性, 因此其手性度承载参数设定为零. 对于硫化镉, 其特勒根参数受晶体结构的影响, 作为一种广泛使用的半导体材料, 硫化镉的手性度承载参数通常变化幅度较小, 这是因为其主要展现的是光学各向异性, 而非显著的手性效应.

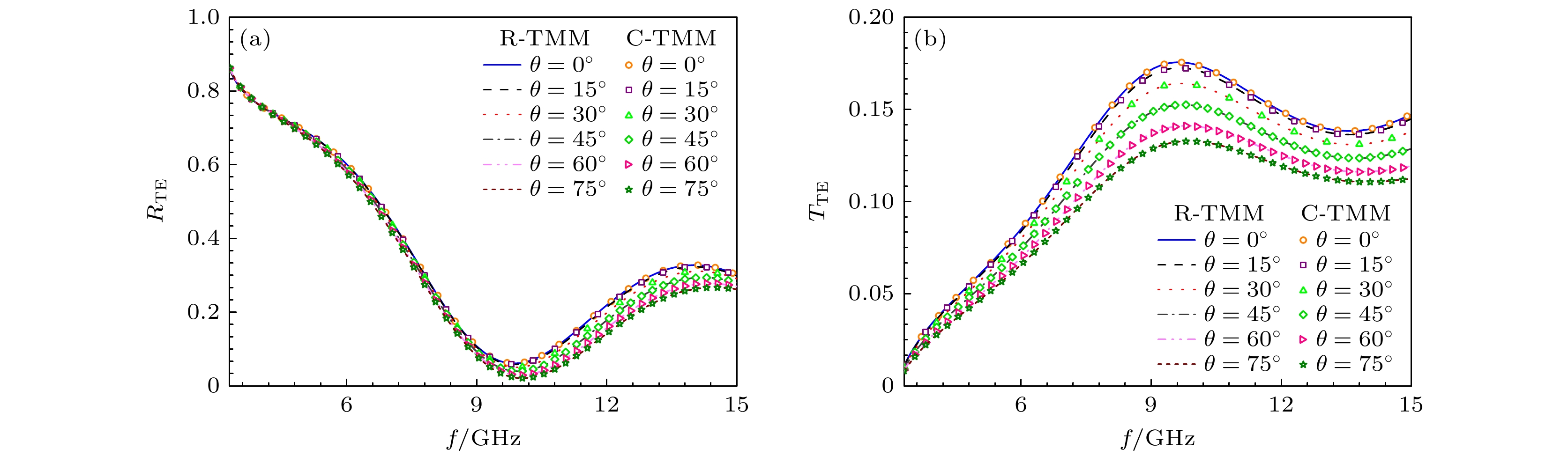
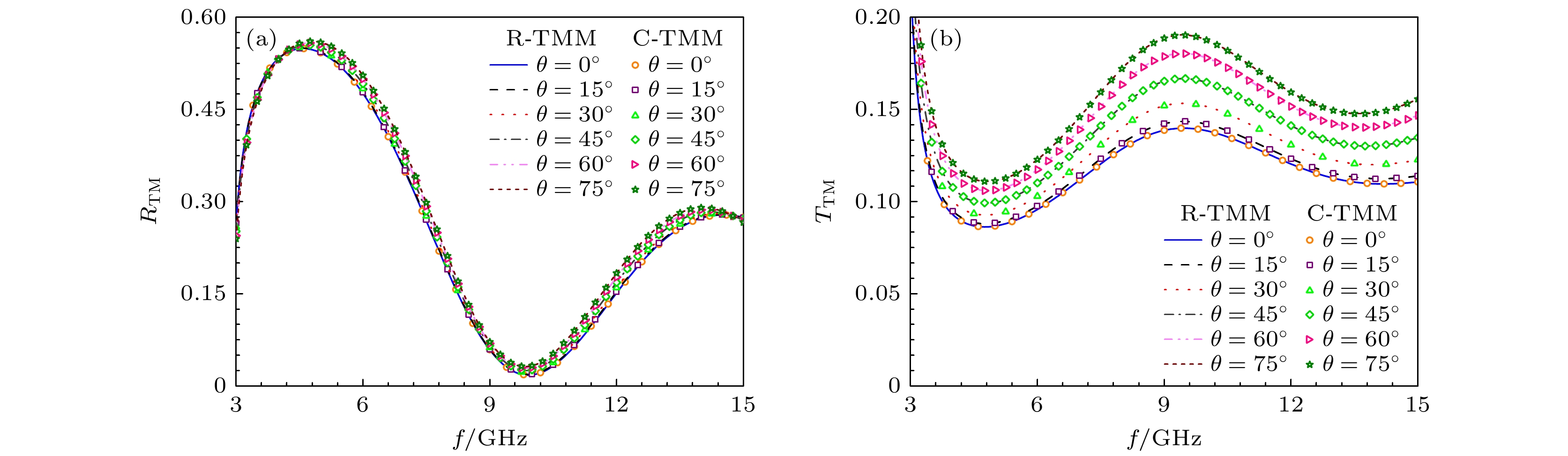
      当平面波从空气斜入射双层光学材料时, TE模式下的横向矢量kh设定为65, 频率f = [3.3, 15] GHz. 在该条件下, 实验验证了横向角θ分别为0°, 15°, 30°, 45°, 60°和75°时的传播系数. R-TMM和C-TMM的反射系数和透射系数曲线如图7所示. 在TM模式下, 设定横向矢量kh为60, 频率f = [3.0, 15] GHz, 横向角θ的取值和TE模式相同, R-TMM和C-TMM的反射系数和透射系数曲线如图8所示. 图7和图8表明, 在TE模式和TM模式下, R-TMM计算所得的反射系数和透射系数与C-TMM的结果展现出高度的一致, 这证实了R-TMM在计算多层光学材料传播系数时的可靠性.

      随着频率的不断增大, TE模式下的反射系数经历了先下降后上升, 随后略有下降的动态变化过程, 而透射系数则先上升后下降, 并最终呈现略有上升的趋势; 在TM模式下, 反射系数表现为先增大后减小, 随后增大并最终略微减小, 透射系数的变化趋势则与反射系数相反. 随着横向角θ的增大, TE模式下的反射系数在频率f = [4.0, 15] GHz内持续减小, 而透射系数在整个频域范围内不断下降; TM模式下的反射系数在频率f = [4.1, 15] GHz内持续上升, 透射系数在整个频域范围内不断增大. 在分析传播系数随不同横向角、频率和入射模式变化时, 发现双层光学材料模型在特定角度或频率下表现出显著的反射增强或透射增强, 这表明该材料模型具备一定的电磁屏蔽特性. 探究传播系数在不同条件下的变化, 有助于获取单轴/双轴双各向异性媒质的折射率和吸收特性等信息, 从而实现材料的精确表征和光学器件的性能优化.

      在本实验中, 横向角θ的变化仅作为调控平面波入射条件的手段, 而未增加额外的计算复杂度至传播系数的计算过程中. 因此, 横向角θ的变化对R-TMM和C-TMM的计算效率无显著影响. 以横向角θ = 45°为例, 表4中的数据表明, R-TMM在计算多层光学材料的传播系数时表现出极高的效率, 其计算所需内存相较于C-TMM降低了约98.98%. 鉴于TE模式下的频点总数为235个, 而TM模式下的频点总数则为241个, 因此, TM模式的CPU时间消耗相较于TE模式有所增加. 此外, R-TMM在TE模式和TM模式下分别实现了约98.48%和98.44%的CPU计算时间节省. 该方法所展现的高精度与高效性, 使其在光学器件设计领域具有独特的优势, 并为快速评估复杂材料的电磁特性提供了可靠的数值计算手段.

    4.   结　论

    • 本文提出了一种适用于计算单轴/双轴双各向异性媒质传播系数的R-TMM. 该方法基于单轴/双轴双各向异性媒质的旋度麦克斯韦方程组, 通过求解布克四次方程获得了媒质中的特征值, 进而构建用于计算反射系数和透射系数的传输矩阵. 为了评估R-TMM的准确性和高效性, 本文设计了单层双轴双各向异性媒质和多层光学材料的数值算例. 通过这两组数值实验, 成功验证了TE模式和TM模式在不同横向角下的反射系数和透射系数. 与C-TMM相比, R-TMM节省了98%以上的内存和CPU时间. 该项研究工作不仅扩展了传输矩阵法的应用范围, 还为单轴/双轴双各向异性媒质传播系数的快速验证以及光学器件的设计提供了坚实的理论基础.

    参考文献 (29)

目录

/

返回文章
返回