-
人工合成的多晶金刚石膜拥有媲美天然金刚石的热导率,其高热导率可以作为集成电路的散热衬底,高电阻率可作为绝缘层[1]。微波等离子体化学气相沉积(MPCVD)不使用金属电极放电,由微波能量维持等离子体,避免了沉积过程中因电极使用造成的污染[2]。另外,MPCVD放电区域比较集中,不但能产生高密度的等离子体活性基团,且放电过程即为稳定,也正因此,MPCVD一直是国内制备金刚石膜的首选方法[3-6]。在MPCVD沉积过程中由于设备内在高电场情况下钼板边缘处容易出现放电现象,导致等离子体在钼板中间分布稀疏、边缘电子密度聚集,从而导致薄膜生长不均匀,大大减小了金刚石的可用面积[7]。想要沉积出大面积高均匀性金刚石,需要对腔体等离子体分布状态分析并结合工艺改进。现有研究员通过设计新MPCVD设备,改变气体流动进出方式或通过改善基台结构来改善沉积均匀性,但以上方法成本高,周期长较为复杂[8-9]。对于MPCVD的仿真分析,德国科学家Füner M等[10]针对MPCVD提出了唯象线性模型,该模型对TM01比较适用,主要对电场强度以及电子密度简化计算。法国的Hassouni K等[11]在基于大量的粒子碰撞截面数据、化学反应相关的数据将等离子体中各种现象进行耦合,构建自洽耦合模型。金帅[12]建立了基于纯H2的多物理场耦合的二维模型,主要研究了沉积室中氢等离子特性,但电子碰撞仅仅考虑了电子和氢气高能反应,没有考虑电子与氢原子以及离子之间的碰撞。产思义等[13]了模拟不同基台高度对2英寸衬底表面电场均匀性影响,在实验中观测等离子球状态。上述学者对沉积过程中使用简化物理模型对氢等离子体特性进行研究,或使用单一物理场研究衬底表面均匀性。本论文在前人的研究基础上,通过电子漂移扩散近似的等离子体模拟方法建立了多物理场纯氢放电二维数值模型,探索了等离子体放电过程中输入特性,钼板高度以及钼环对沉积过程的电子密度分布与均匀性影响。
-
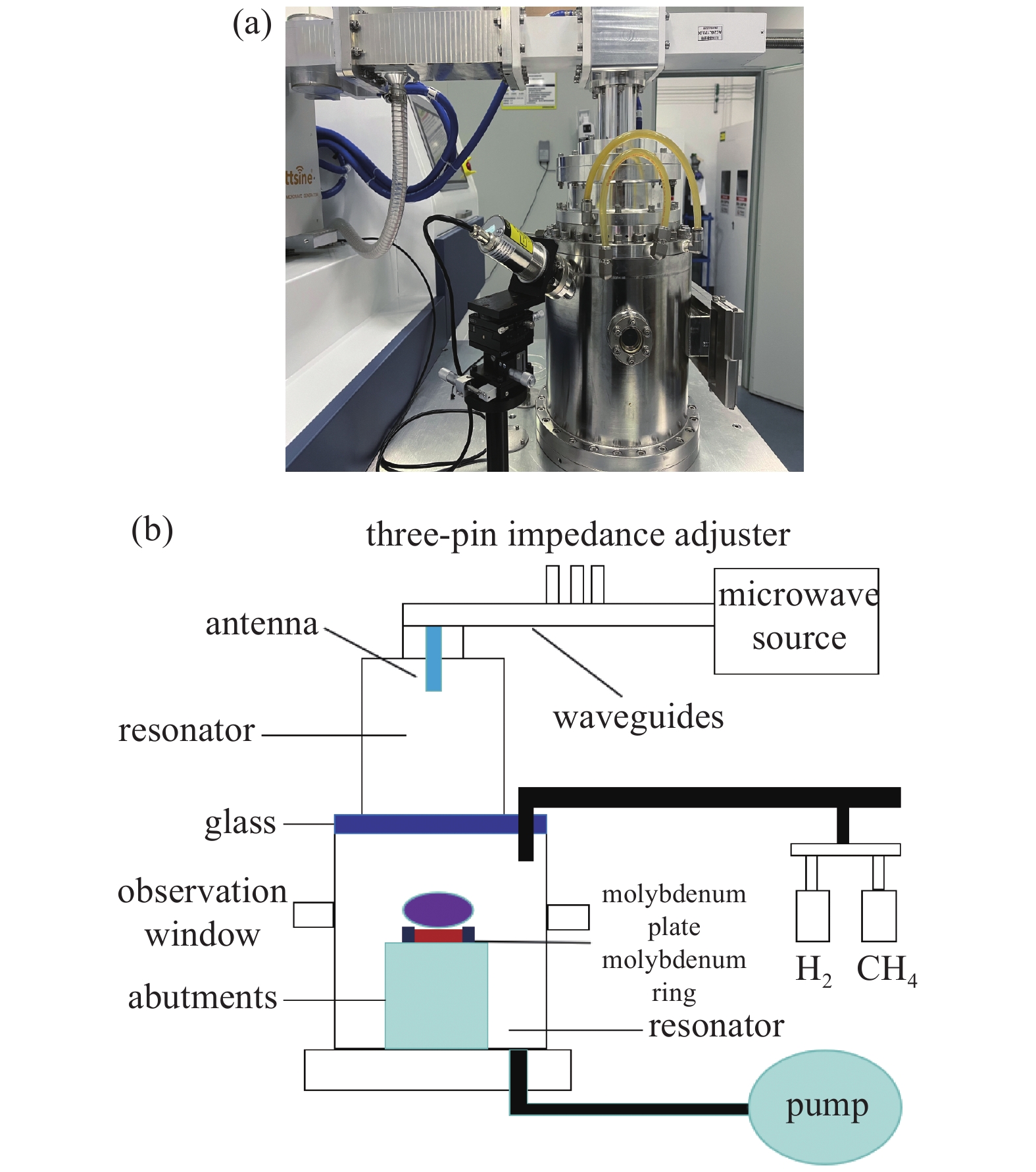
本文模拟的柱形腔MPCVD装置为自行研制的圆柱形谐振腔,腔体结构分为上下两个不同直径的圆柱腔,石英玻璃放置在两个圆柱体中间。设备频率为2.45 GHz,微波输出0.5−5 kW连续可调,腔体极限压力20 kPa,MPCVD设备实物图及示意图如下图1所示。该设备主要包括微波源、微波传输及耦合系统、等离子体反应装置、真空系统等。该腔体谐振腔模式设计为TM013,磁控管输出的微波经由矩形波导以主模TE波传输,通过天线模式转换成TM模在腔体平稳放电。
-
由于电场分布会直接影响等离子体的分布,所以第一步应该求解的是电磁场,计算电磁场的过程是在求解麦克斯韦方程组:
式中
$E$ 是电场,$\omega $ 和${k_0}$ 是电磁波的角频率和波数,$ {\varepsilon}_{0} $ 是真空介电常数,$ \mu\mathrm{_r} $ 、$ \varepsilon\mathrm{_r} $ 和$\sigma $ 分别是材料的相对磁导率、相对介电常数和电导率,${j}$ 为虚部单位。下腔体为电离区域,由于电离后形成等离子体会改变放电区域的介电性质,其电导率和等离子体的相对介电常数由下式给出:$ \omega\mathrm{_p} $ 的计算式为:式中
$ v\mathrm{_e} $ 代表电子与粒子之间的碰撞频率$q$ 和$ m\mathrm{_e} $ 分别是电子的电荷量与质量,电子密度为$ n\mathrm{_e} $ 。等离子体模拟较为复杂,漂移−扩散近似是一种较为准确的方法,它通过对等离子体宏观物理量的描述来简化计算过程,假设电子能量分布函数为麦克斯韦形式,可以推导出等离子体的漂移和扩散行为。下面给出了求解电子密度变化率,电子能密度变化率等控制方程:
式中
$ue$ 是电子迁移率,$De$ 是电子扩散率,$ n_{\text{ε}} $ 是电子能量密度,${Q_{{\mathrm{rh}}}}$ 为电子热源耦合,${\Gamma _{\mathrm{e}}}$ 是电子通量,${Re} $ 是电子的来源,$R\varepsilon $ 是由非弹性碰撞引起的能量变化。电子源定义为:
其中
$ {x_j} $ 是反应$j$ 的目标物质的摩尔分数,${k_j}$ 是反应$j$ 的速率系数,$ N_{\mathrm{n}} $ 是总中性数密度,电子能量损失是通过将所有反应的碰撞能量损失相加而获得的。制备金刚石主要的气体是氢气和甲烷(5%左右),现有研究在二维模型中考虑
${{\text{H}}_2}$ /${\text{C}}{{\text{H}}_4}$ 混合气体模拟[14],模拟结果表明${\text{C}}{{\text{H}}_4}$ 对等离子体的影响较小,因此模拟过程中可以忽略${\text{C}}{{\text{H}}_4}$ 的放电带带来的影响。本文中关于氢气的等离子体反应来自Hassouni K等[15]的工作,生成8种物质分别为$e$ ,${{\text{H}}_{\text{2}}},{\text{H}},{\text{H}}({{n = 2}}),{\text{H}}({{n = 3}}), {{\text{H}}^{\text{ + }}} {\text{H}}_{\text{2}}^{\text{ + }}, {\text{H}}_{\text{3}}^{\text{ + }}$ ,考虑了多种电子碰撞反应,相应的碰撞截面数据从LXCat数据库中获取,部分碰撞反应如下表1所示:气体温度分布在传热方程中忽略对流效应对于传热方程的影响,气体传热主要依靠氢气的热传导[15],具体公式如下:
式中
$k$ 是气体的热导率,$Q$ 为气体热源,$Tg$ 为气体温度。 -
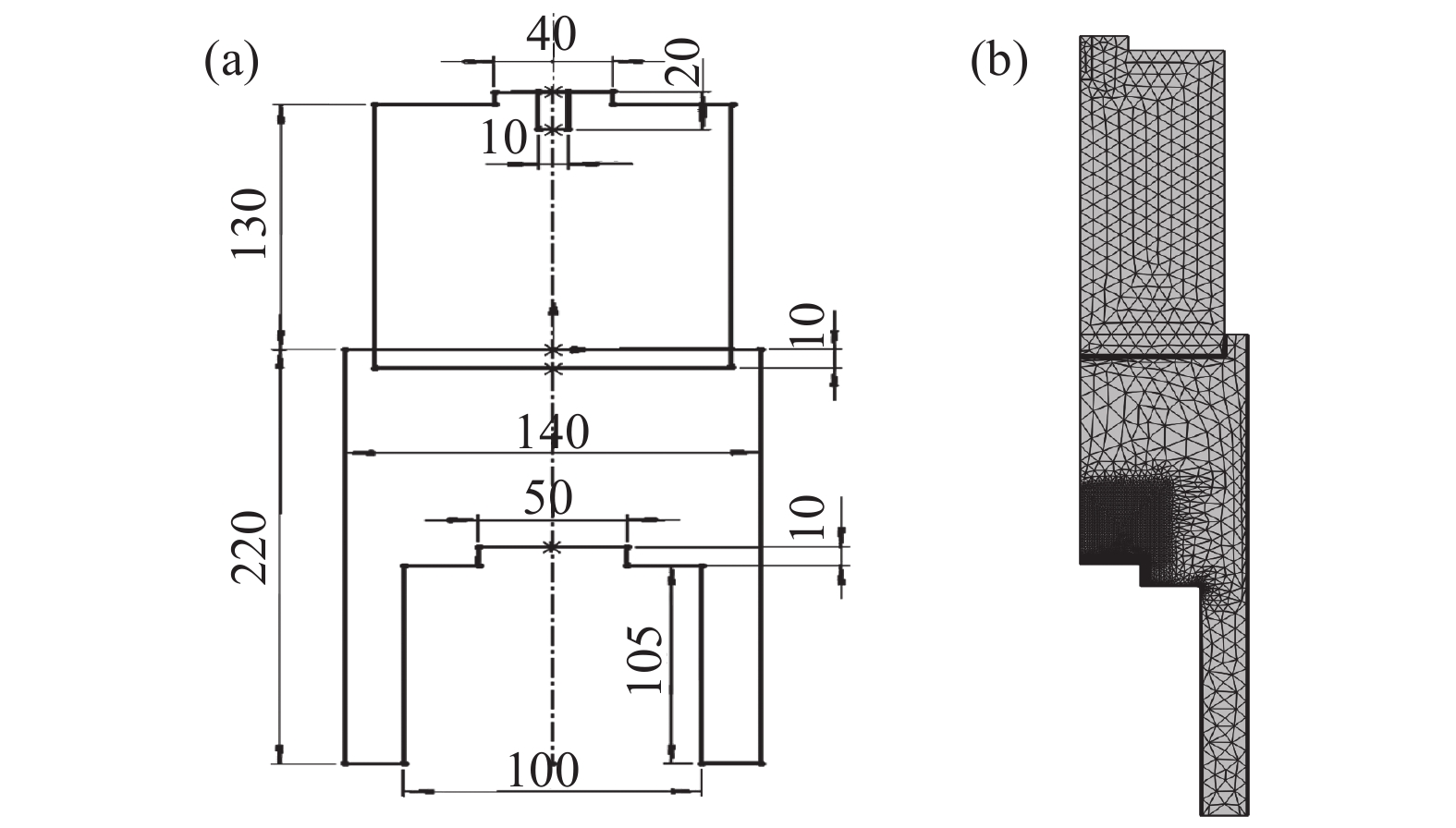
由于三维模型仿真MPCVD腔体计算量和复杂性比较大,本文使用 COMSOL Multiphysics 中构建的二维轴对称氢等离子通过配置多物理场接口(电子热源和等离子体电导耦合),模型尺寸及网格划分如图2所示,其中基台高度105 mm,钼板高10 mm,直径25 mm,钼环的直径设置为58 mm。使用更精细自由三角形进行划分,其中最小质量为 0.05 mm,平均质量为 0.862 mm。边界层属性包括拉伸因子为1.2的3个边界层,并对等离子体室边界也进行了细化。
计算域电场覆盖整个模型,端口处选择同轴输入,腔体内壁边界条件设置为理想电导体;等离子体的计算域是在石英玻璃下方腔体进行,在等离子体中下半腔体内壁设置为接地,初始电子密度为1×1013 1/m3,初始电子平均能量为2 V,粒子
${\text{H}}_2^ + ,{{\text{H}}^ + }$ 初始数密度设置为1×107 1/m3,${\text{H}}_{\text{3}}^{\text{ + }}$ 来自电中性约束,由于初始气体呈现电中性,所以${\text{H}}_{\text{3}}^{\text{ + }}$ 初始数密度与初始电子密度一致,${\text{H}}$ 初始摩尔分数1×10−5,${\text{H}}({{n = 2}})$ 为1×10−8,$ \text{H}(\mathit{{n}}=3) $ 为1×10−10,$ {{\text{H}}_{\text{2}}} $ 设置为来自质量约束[16-17]。 -
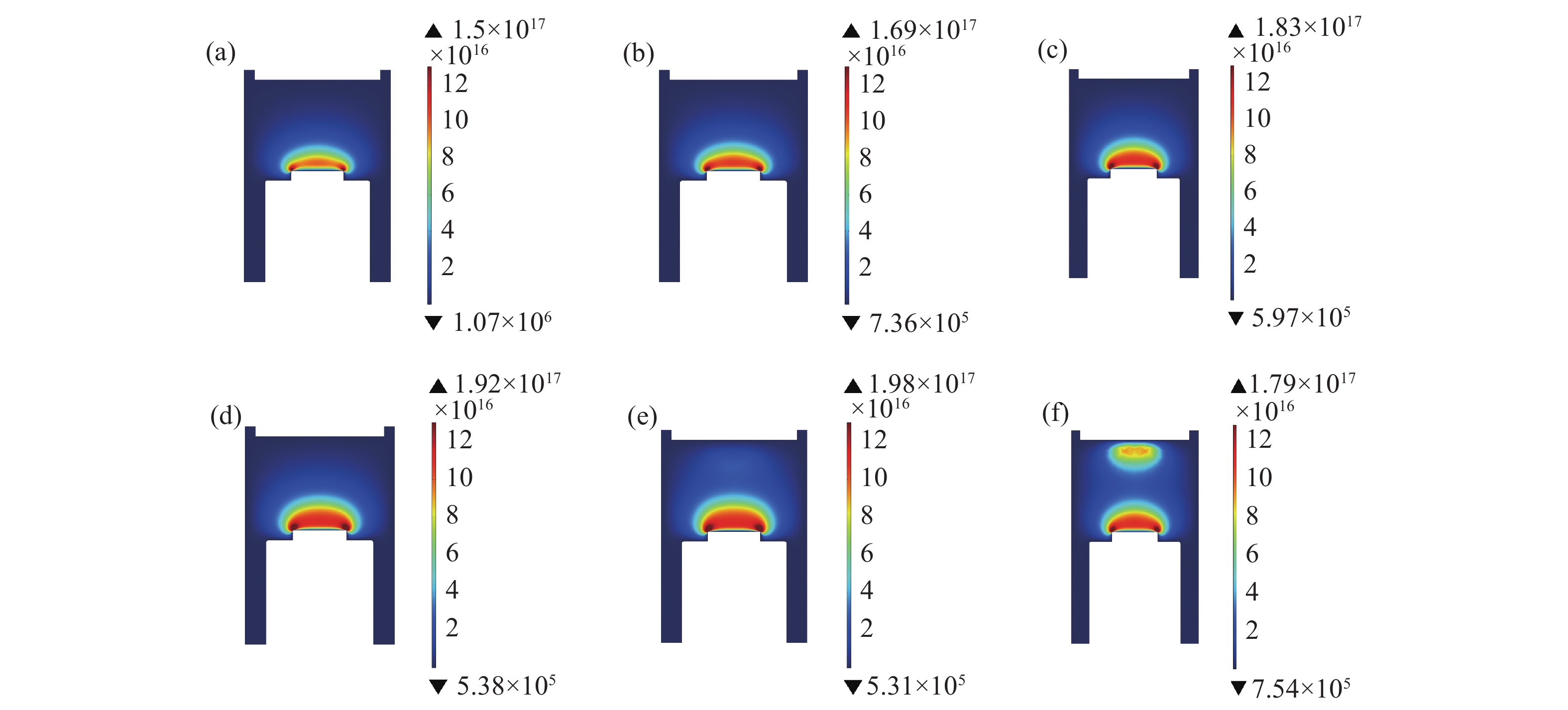
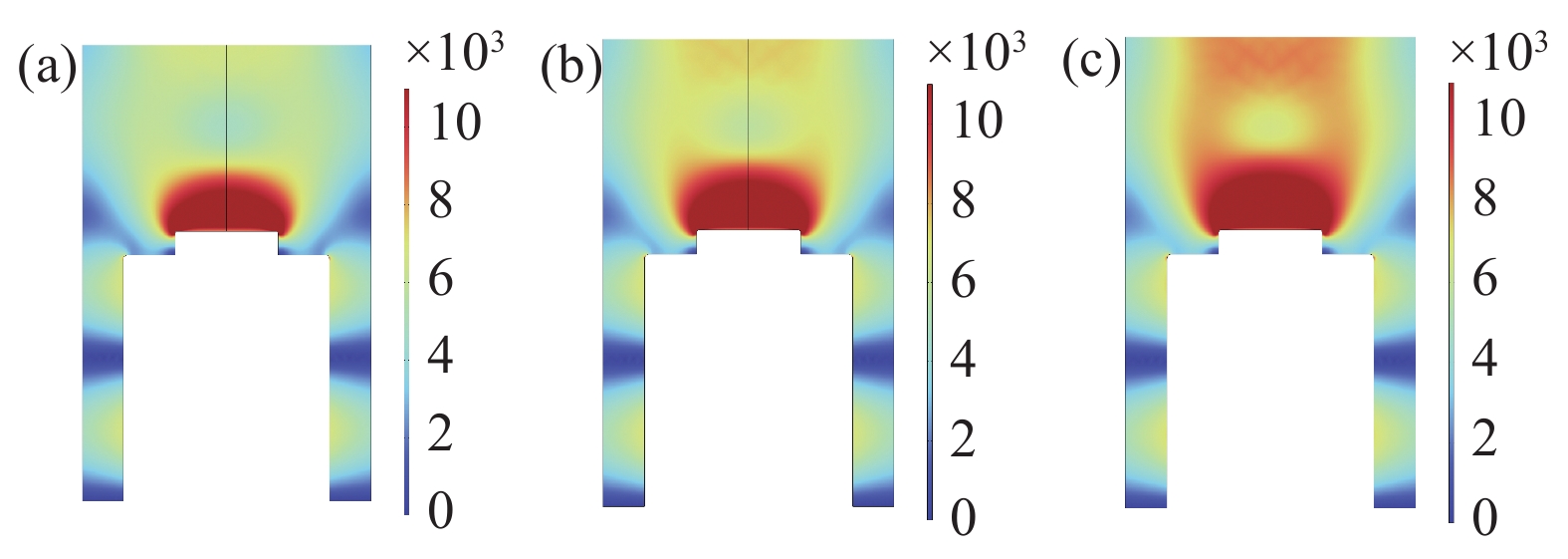
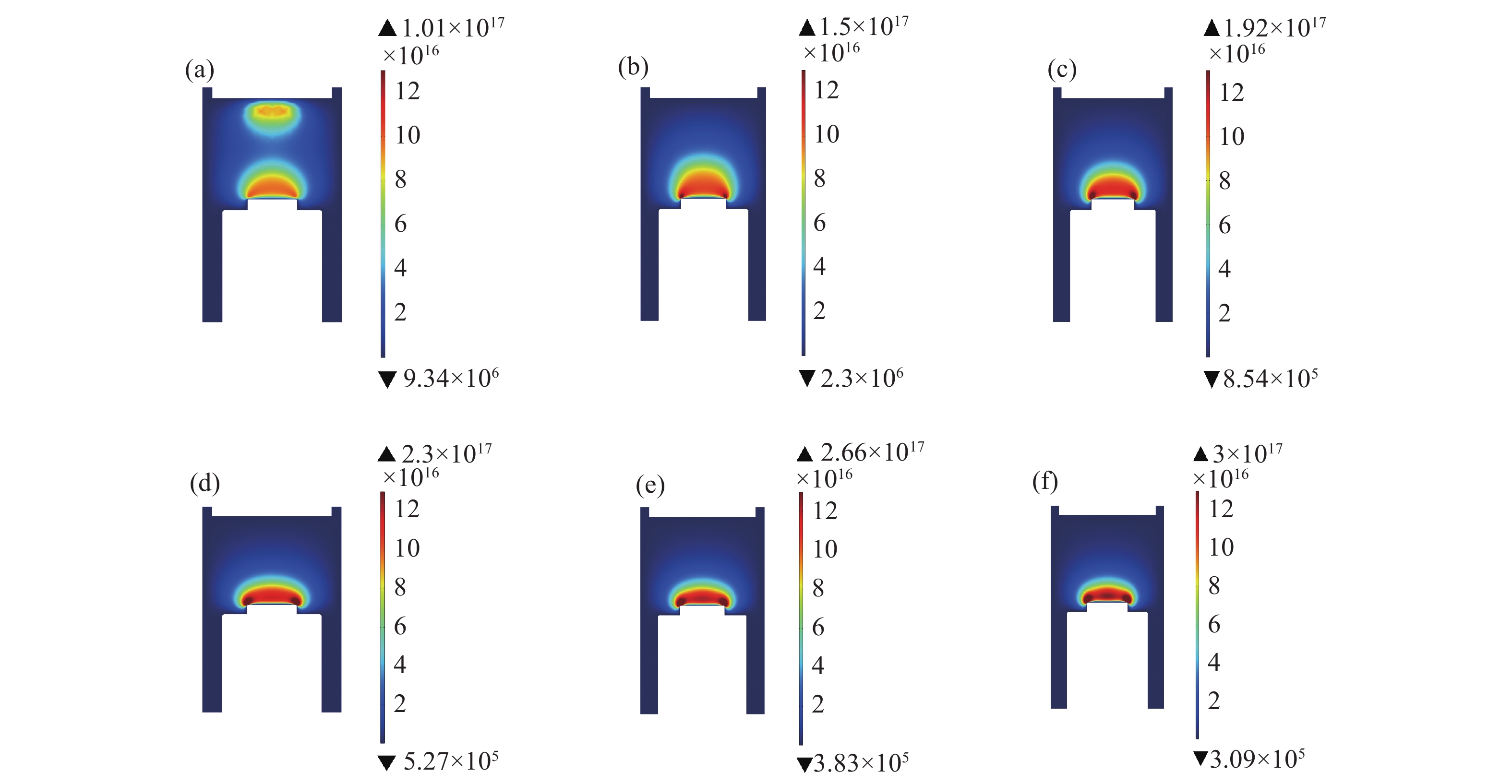
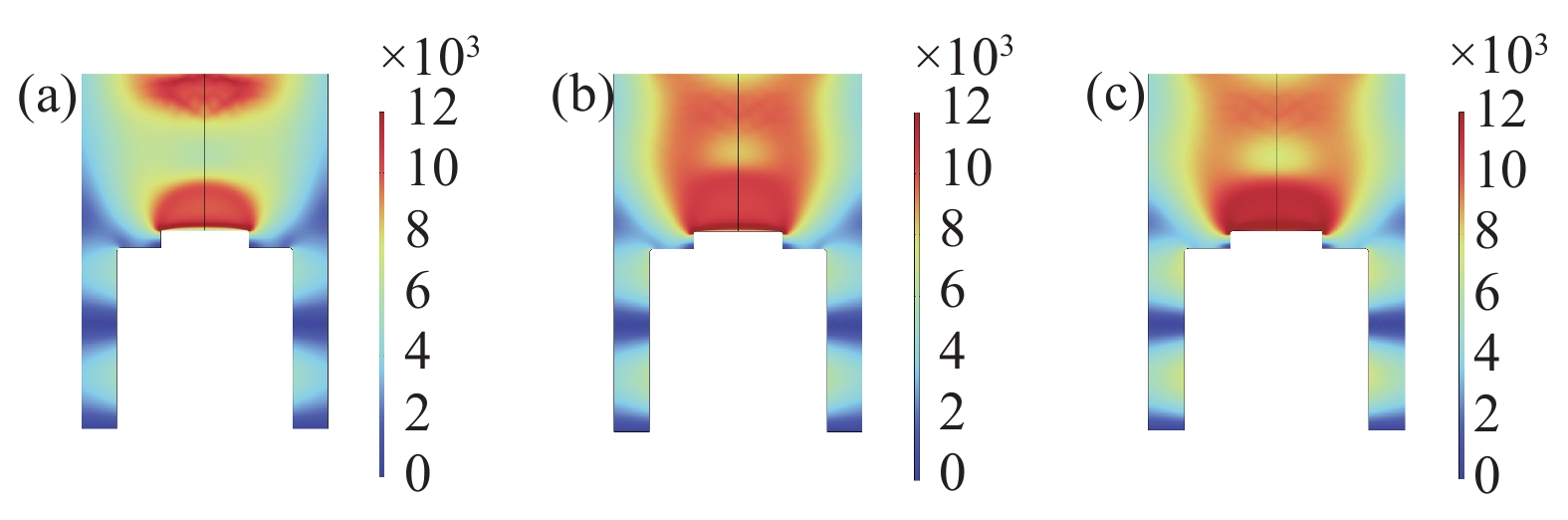
设置压强不变(5 kPa)功率分别设置了600 W−1600 W,随着功率增加,气体分子获得的能量也会增加,气体的电离程度加剧导致电子密度峰值增加,功率增加仿真结果如下图3所示,功率从600 W到1200 W工况中,腔体内等离子体球电子密度峰值和体积慢慢增大,在1400 W时,靠近石英玻璃处出现微弱的次生等离子体,随着功率进一步增大到1600 W时,次生等离子体越来越明显,腔体内的峰值也开始下降。由微波激发等离子体理论可知,只有当微波产生电场的均方根值大于反应气体的击穿场强时,才能使气体分子的核外电子脱离轨道,从而进一步形成等离子体[18]。也就是说要达到激发等离子体条件,微波产生的电场要能够与击穿场强相匹配,当压强较小而功率较大时,激发等离子体相对容易。当功率压强不匹配会出现跳模现象,氢气会刻蚀烧灼石英玻璃。为了更好看出等离子体球体积与电子密度变化,给出了600 W−1000 W电场分布图,从图4中可以看出电场变化趋势与电子密度变化趋势基本一致,随着功率增加衬底上方强电场区域逐渐增大。
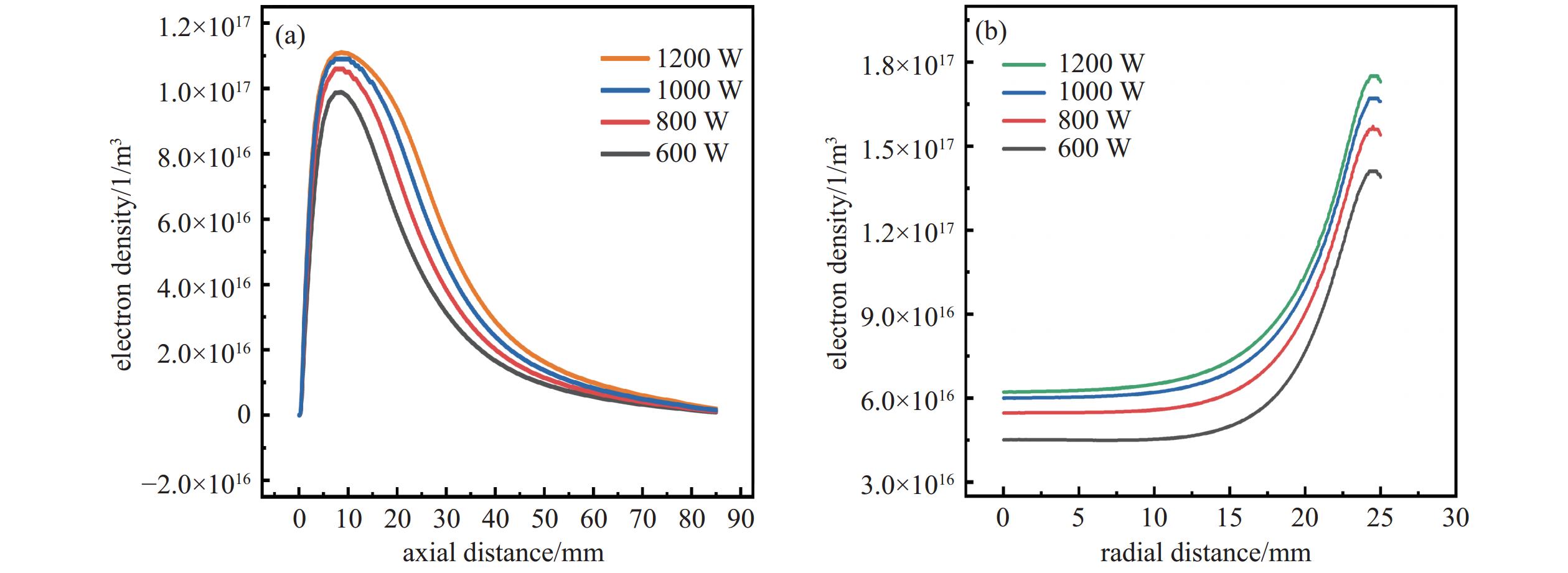
通过comsol后处理得到不同工况条件下钼板上方轴向及其径向方向处的电子密度,其中轴向起点为钼板正中心位置处,径向位置选取的是距离表面2 mm位置,后处理结果如下图5所示,600 W−1200 W轴向的电子密度先增大后减小,随着等离子体球的增大在轴向方向呈现先上升后下降趋势,变化不明显,说明增加功率对轴向方向的电子密度梯度影响较小。径向方向电子密度变化趋势基本一致,在r=0−20 mm位置上电子密度变动幅度不大,靠近边缘r=25 mm处出现较高电子密度是因为衬底边缘局部电场强度较大导致电子密度突增。
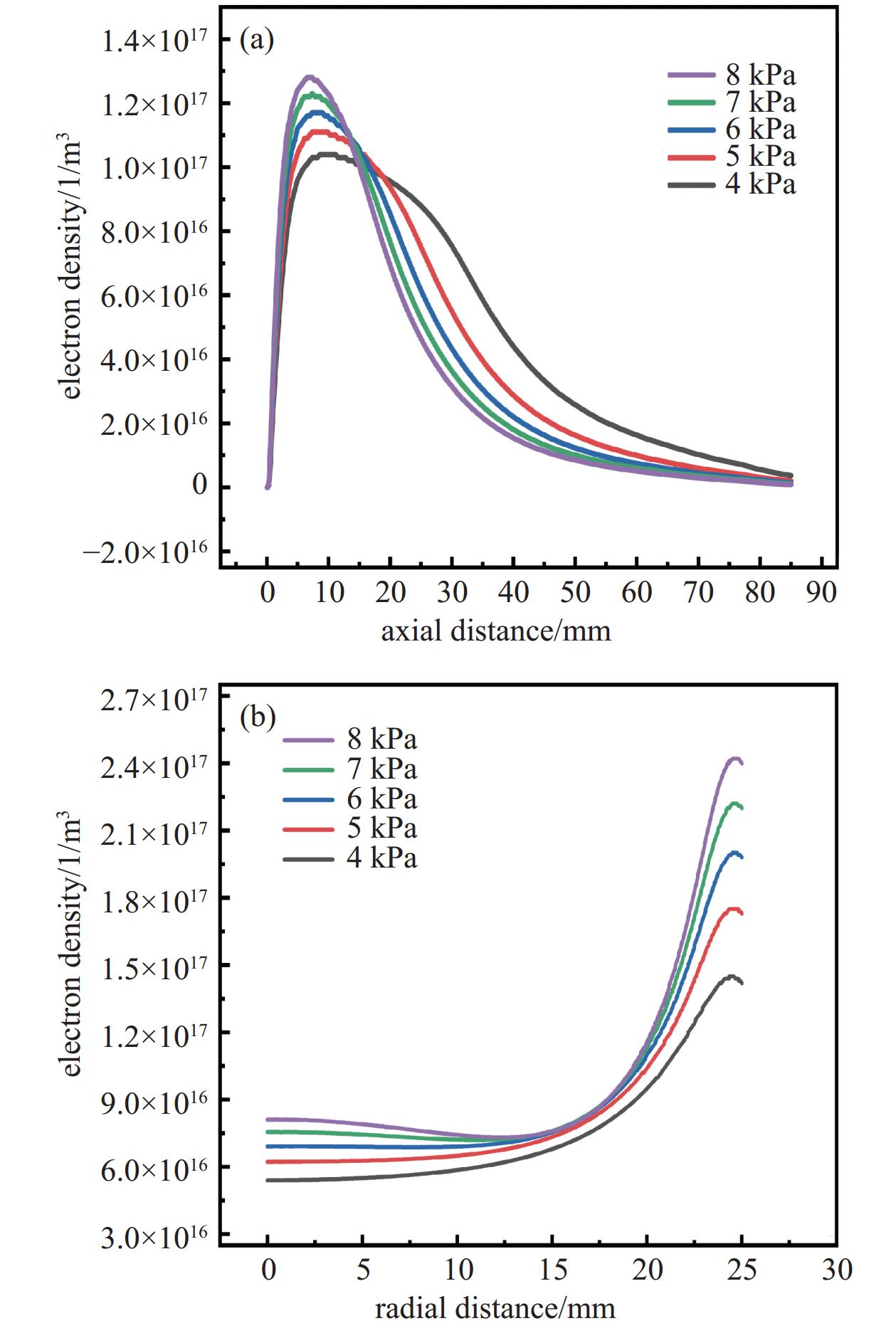
设置功率不变(1200 W),压强分别为3 kPa−8 kPa,功率恒定腔体内压强增大通常会导致腔体内气体分子密度的增加,进而增加电子与气体分子的碰撞频率,从而在一定程度上提高沉积速率。压强变化电子密度变化如图6所示,MPCVD装置在一定功率下运行时,气压需要升高并超过一定的值才能避免次生等离子体的出现[19],3 kPa工况下靠近石英玻璃的气体也被激发形成双等离子体球对沉积产生不利影响,下图7给出了3 kPa−5 kPa电场仿真图,从图中可以看出随着压强增大,次生电场与钼板表面电场差距逐渐增大,说明增加气压能够避免次生等离子体产生。从4 kPa提升至8 kPa过程中钼板上方等离子体球体积不断减小,对比4 kPa和8 kPa工况下发现等离子体球变得比较扁平。压强增大等离子体球体积减小但电子密度峰值不断增大,这也意味着等离子体内轴向电子密度梯度比较大,对均匀性有一定影响。
压强变化电子密度在轴向以及径向变化如下图8所示,轴向位置选取的是钼板中心,轴向电子密度同样先增大后减小,但是随着压强增大在轴向到达峰值位置开始下降的速度不断增大,压强越大轴向峰值下降越陡,其均匀性也相对下降;径向位置同样选取距离钼板表面2 mm位置,可以看到在边缘25 mm处也出现电子密度激升现象,随着压强不断增大,在径向r=15 mm位置处出现部分电子密度重叠,这说明压强增大对径向电子密度均匀性也有一定影响。
-
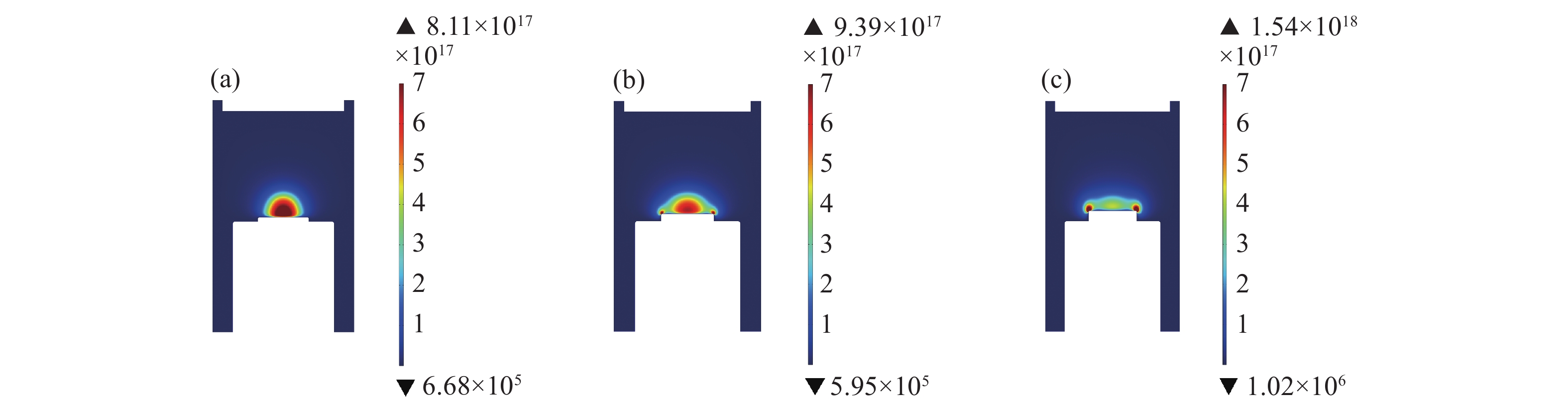
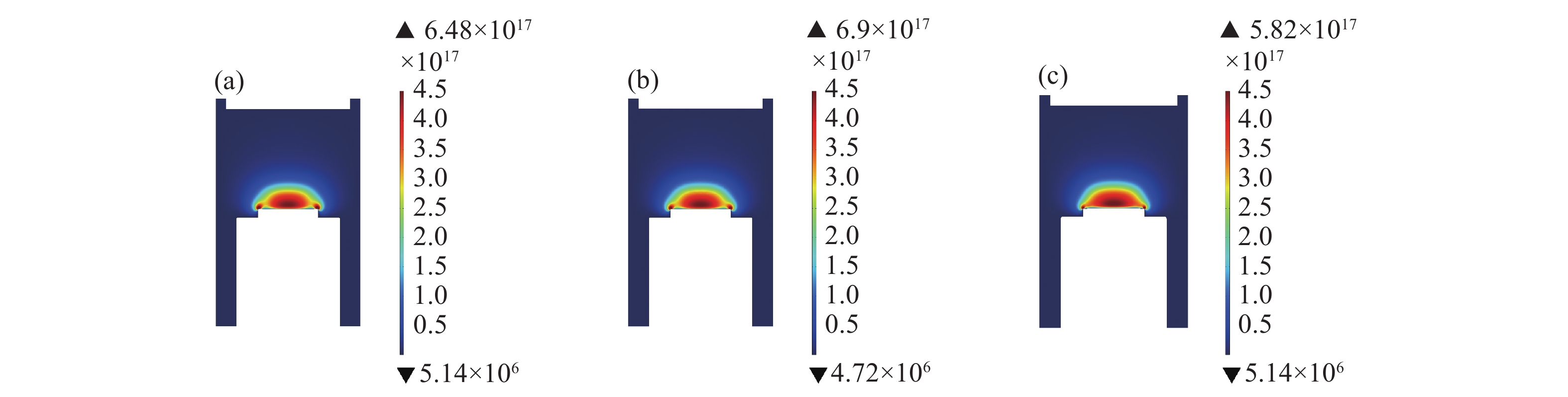
在3000 W,15 kPa的工况下研究不同钼板高度对其表面等离子体均匀性的影响,仿真过程中基台高度不变,钼板半径25 mm,厚度分别设置为H1=4 mm,H2=7 mm,H3=10 mm,电子密度变化如下图9所示。
对比三种不同高度钼板电子密度的仿真结果可以看出在高度为H1=4 mm时钼板过低没有出现边缘放电现象,但等离子体没有完全覆盖整个钼板。随着高度增加,钼板边缘开始逐渐有等离子体存在,在高度10 mm边缘放电最明显,同时腔体内电子密度极值也不断增大,极值主要分布在边缘处。为了更加直观的看出高度变化对表面均匀性的影响,后处理截取钼板中心轴向r=0,以及距离表面2 mm径向位置电子密度,变化如下图10所示。
从图中可以看到高度改变轴向电子密度变化趋势基本一致,表现为先上升后下降;径向方向在H1时发现从中心到边缘电子密度迅速下降,边缘电子密度接近0,在高度为H2和H3时可以直观看出峰值主要出现在边缘位置,且随着高度增加,边缘电子密度陡增现象越明显,其表面不平整性也越来越高。为了进一步定性研究钼板高度变化对径向等离子体分布均匀性的影响,通过采用变异系数计算方法对各组电子数密度的均匀性进行评价。变异系数是一组数据的标准差与其相应的均值之比,主要用于比较不同组别数据的离散程度[20],其计算公式为:
式中:
$ \mathrm{\mathit{C}}_{\mathrm{v}} $ 为变异系数,$ \mathrm{\sigma } $ 为标准差,$ \mathrm{\mu } $ 为平均值。通过计算得出不同钼板高度电子密度数据及其变异系数如下表2所示。
变异系数表示电子密度沿着平均值波动的幅度比例,表格数据显示钼板厚度较低或较高时变异系数较大,这表面径向电子密度分布不均匀,在高度为H2时虽然存在边缘电子密度较大现象,但相比较于H1和H3其均匀性适中。
-
在实际沉积薄膜时不好观测等离子体球放电状态,选择较高钼板高度虽然边缘放电但能保证等离子体完全覆盖钼板,所以有必要解决钼板高度较高工况表面均匀性问题。本文通过添加不同高度的钼环来调整相对位置,对3000 W,15 kPa钼板半径25 mm高度7 mm工况下表面电子密度进行分析,仿真过程中基台高度保持不变,钼环高度分别为6.8 mm、7 mm、7.2 mm ,钼环与钼板之间相对高度分别选取h1=−0.2 mm (凹) h2=0 (持平) h3=0.2 mm (凸)三种情况,H2即为钼板高度7 mm无钼环工况,仿真电子密度结果如下图11所示。
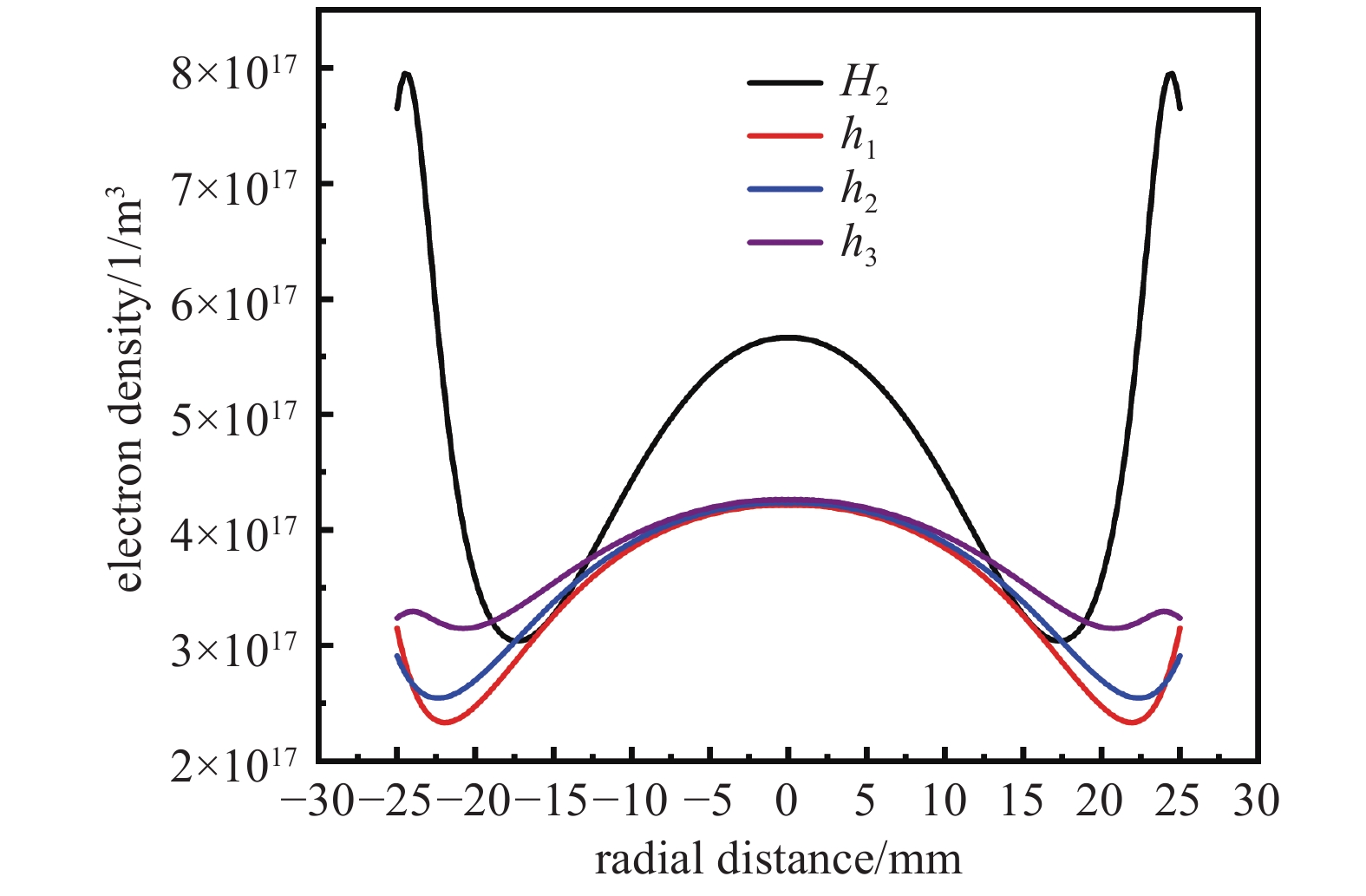
在3000 W 15 kPa三种不同高度钼环工况下,发现当钼板与钼环持平附近较强电子密度区域主要是集中在钼环边缘区域,对比H2工况下避免了钼板边缘放电现象,分布也比较均匀。后处理截取了距离表面2 mm,z=114的径向位置电子密度分布图,其结果如下图12所示。
从图中可以直观看添加钼环后钼板边缘电子密度大幅度下降,对比h1,h2,h3三种工况下发现从中心r=0到r=10 mm位置处均匀性基本一致,在r=10 mm往后h1和h2下降趋势增加且h3下降更快,这表明其径向均匀性相对较差。此外,电子密度原始数据及其变异系数如下表3所示。
由表格数据可以看出,在无钼环H2工况条件下变异系数为27.74%,添加钼环后变异系数有所下降,表明钼环的添加能够改善表面其表面径向电子密度的均匀性;在h1和h2工况下虽然能够一定程度改善表面电子密度均匀性,但其线平均值相比于其他高度都较小;相比较于前两种高度的钼环,在高度为h3时其表面的变异系数最低达到了最低11.15%,其表面均匀性达到最佳,线平均值最高。综合以上分析结果考虑,钼板和钼环高度在持平附近(−0.2 mm−0.2 mm)能够能够很好的改善电子密度的均匀性,解决其钼板边缘尖端放电情况,其中钼板高出钼环0.2 mm时径向均匀性最好。
-
针对自制的MPCVD柱形腔,采用数值模拟方法对腔体内氢等离子体的电子密度进行研究,在其他参数不变的情况下,研究了不同输入特性(功率 压强)其电子密度分布。在讨论功率以及压强工艺参数对电子密度均匀性带来影响时,仿真过程中发现钼板表面在径向位置边缘处呈现电子密度等激增现象,在培育多晶金刚石时会影响表面均匀性,探索钼板高度和钼环添加对钼板表面均匀性带来的影响,结果表明:
(1)输入特性(功率压强):功率增大(600 W−1200 W)等离子体球体积逐渐增大,压强增大(4 kPa−8 kPa)等离子体球的体积减小,因此要想在等离子体球体积保持不变前提下提高功率密度,需要功率压强同时调控;压强恒定(5 kPa),输入功率过高会导致石英玻璃出现次生等离子体导致生长无法继续,因此输入功率存在一个上限,不能单依靠提高功率来实现大面积多晶金刚石生长;功率压强增大腔体内电子密度峰值均相应增加,相比于增加功率,压强的增加会导致轴向电子密度梯度增加,对轴向电子密度均匀性影响较大。
(2)钼板高度:钼板高度改变会影响表面径向电子密度分布,钼板高度较低等离子体不能覆盖整个钼板,钼板高度较高电子密度主要集中在钼板边缘,选择合适钼板高度能提高表面径向均匀性。
(3)钼环的添加能够有效改善钼板表面径向电子密度,解决边缘尖端放电问题。计算钼板高出钼环0.2 mm时变异系数为11.15%,相比于无钼环工况下降低了16.59%,均匀性达到最佳。
MPCVD 柱形腔中电子密度分布特性数值模拟分析
Numerical Simulation Analysis of Electron Density Distribution Characteristics in MPCVD Cylindrical Cavity
-
摘要: 使用微波等离子体法沉积多晶金刚石薄膜过程中,工艺参数调整往往对等离子体球大小及均匀性影响较大。文章基于实验室自制的5 kW MPCVD柱形腔,通过耦合多物理场,在氢气放电环境下对不同工艺参数条件下钼板表面轴向及径向电子密度分布进行研究,并结合变异系数评价等离子体分布的均匀性。主要工艺参数包括输入特性(功率、压强),不同钼板高度以及不同高度钼环使用。仿真结果表明:等离子体球的体积随功率增加而增加,随着压强的增大而减小,相比较于功率,压强改变对离子体球轴向电子密度均匀性影响较大;钼板高度较低或较高均会影响表面径向均匀性,随着钼板高度增加边缘放电现象越明显;钼环的增加能够改善表面均匀性,钼板与钼环高度在持平附近径向均匀性较好,其中钼板高出钼环0.2 mm变异系数为11.1%,相比较于无钼环工况下径向均匀性提高了59.6%。
-
关键词:
- 微波等离子体化学气相沉积 /
- 氢等离子体 /
- 数值模拟 /
- 均匀性
Abstract: In the process of depositing polycrystalline diamond thin films by microwave plasma method, the adjustment of process parameters often has a greater impact on the size and uniformity of the plasma ball. Based on the 5 kW MPCVD cylindrical chamber made in the laboratory, this paper combines multiple physical fields to study the axial and radial electron density distribution on the surface of tungsten plate under hydrogen discharge conditions under different process parameter conditions, and evaluates the uniformity of the plasma distribution using the coefficient of variation. The main process parameters include input characteristics (power and pressure), different heights of tungsten plates, and the use of different height tungsten rings. The simulation results show that the volume of the plasma ball increases with the increase of power and decreases with the increase of pressure. Compared with power, pressure change has a greater impact on the axial uniformity of the plasma ball electron density. The surface radial uniformity of the tungsten plate will be affected by the height being too low or too high, and the more obvious edge discharge phenomenon will be observed as the height increases. The addition of tungsten rings can improve the surface uniformity, and the radial uniformity is better when the height of the tungsten plate and the tungsten ring is approximately the same, among which the coefficient of variation of the radial uniformity is 11.1% when the tungsten plate is 0.2 mm higher than the tungsten ring, an improvement of 59.6% compared with the condition without tungsten ring.-
Key words:
- Microwave Plasma Chemical Vapor Deposition /
- Hydrogen plasma /
- Numerical simulation /
- Uniformity .
-

-
表 1 电子碰撞部分反应
Table 1. Electrons collide with partial reactions
1 ${\text{e}} + {{\text{H}}_2} \to 2{\text{e}} + {\text{H}}_2^ + $ 电离 2 ${\text{e}} + {{\text{H}}_2} \to {\text{e}} + 2{\text{H}}$ 解离激发 3 ${\text{e}} + {{\text{H}}_2} \to {\text{e}} + {{\text{H}}_2}$ 弹性碰撞 4 ${\text{e}} + {\text{H}} \to 2{\text{e}} + {{\text{H}}^ + }$ 电离 5 $ {\mathrm{e}} + {{\text{H}}_2} \to {\mathrm{e}} + {\text{Hn}}2 $ 激发 6 ${\mathrm{e}} + {{\text{H}}_2} \to {\text{H}} + {\text{Hn3}}$ 复合 表 2 高度改变电子密度数据
Table 2. Height changes electron density data
高度 最大值 线平均值 标准差 变异系数 H1 7.94×1017 4.23×1017 2.65×1017 62.53% H2 7.95×1017 4.65×1017 1.29×1017 27.81% H3 1.04×1018 3.85×1017 2.12×1017 55.18% 表 3 原始数据和电子数密度的变异系数
Table 3. Coefficient of variation of raw data and electron number density
名称 最大值 线平均值 标准差 变异系数 H2 7.95×1017 4.65×1017 1.29×1017 27.74% h1 4.21×1017 3.42×1017 6.76×1016 19.76% h2 4.23×1017 3.52×1017 6.14×1016 17.44% h3 4.26×1017 3.73×1017 4.16×1016 11.15% -
[1] 张一卓. 新型MPCVD金刚石膜沉积装置模拟及实验研究[D]. 太原理工大学, 2022 (in Chinese) Zhang Y Z. Simulation and experimental study of new MPCVD diamond film deposition device[D]. Taiyuan University of Technology, 2022 [2] Zheng Y, Liu J, Wang J, et al. The direct-current characteristics and surface repairing of a hydrogen terminated free-standing polycrystalline diamond in aqueous solutions[J]. Journal of Physics and Chemistry of Solids, 2019, 130: 111−119 doi: 10.1016/j.jpcs.2019.02.022 [3] May P W. Diamond thin films: a 21st-century material[J]. Philosophical Transactions of the Royal Society of London series A: Mathematical, Physical and Engineering Sciences, 2000, 358(1766): 473−495 doi: 10.1098/rsta.2000.0542 [4] Kamo M, Sato Y, Matsumoto S, et al. Diamond synthesis from gas phase in microwave plasma[J]. Journal of Crystal Growth, 1983, 62(3): 642−644 doi: 10.1016/0022-0248(83)90411-6 [5] 吕反修, 唐伟忠, 李成明, 等. 大面积光学级金刚石自支撑膜研究进展[J]. 红外技术, 2003(4): 1−7 (in Chinese) Lv F X, Tang W Z, Li C M, et al. Research progress on large-area optical-grade diamond self-supporting films[J]. Infrared Technology, 2003(4): 1−7 [6] Messier R, Badzian A R, Badzian T, et al. From diamond-like carbon to diamond coatings[J]. Thin Solid Films, 1987, 153(1-3): 1−9 doi: 10.1016/0040-6090(87)90164-7 [7] Nad S, Gu Y, Asmussen J, et al. Growth strategies for large and high-quality single crystal diamond substrates[J]. Diamond and Related Materials, 2015, 60: 26−34 doi: 10.1016/j.diamond.2015.09.018 [8] Wang B, Weng J, Wang Z T, et al. Investigation on the influence of the gas flow mode around substrate on the deposition of diamond films in an overmoded MPCVD reactor chamber[J]. Vacuum, 2020, 182: 109659 doi: 10.1016/j.vacuum.2020.109659 [9] Li L, Zhao C C, Zhang S L, et al. Simulation of diamond synthesis by microwave plasma chemical vapor deposition with multiple substrates in a substrate holder[J]. Journal of Crystal Growth, 2022, 579: 126457 doi: 10.1016/j.jcrysgro.2021.126457 [10] Füner M, Wild C, Koidl P, et al. Numerical simulations of microwave plasma reactors for diamond CVD[J]. Surface and Coatings Technology, 74–75 (1995) 221–226 [11] Hassouni K, Grotjohn T, Gicquel A, et al. Self-consistent microwave field and plasma discharge simulations for a moderate pressure hydrogen discharge reactor[J]. Journal of Applied Physics, 1999, 86(1): 134−151 doi: 10.1063/1.370710 [12] 金帅. 微波化学气相沉积腔内等离子体特性及反应过程数值模拟[D]. 哈尔滨工业大学, 2020 (in Chinese) Jin S. Numerical simulation of plasma characteristics and reaction process in microwave chemical vapor deposition cavity[D]. Harbin Institute of Technology, 2020 [13] 产思义, 屠菊萍, 黄珂, 等. 2英寸MPCVD光学级均匀金刚石膜的制备研究[J]. 无机材料学报, 2023, 38: 1413−1419 (in Chinese) Chan S Y, Tu J P, Huang K, et al. Preparation of 2-inch MPCVD optical-grade homogeneous diamond film[J]. Journal of Inorganic Materials, 2023, 38: 1413−1419 [14] Shivkumar G, Tholeti S S. Analysis of hydrogen plasma in a microwave plasma chemical vapor deposition reactor[J]. Journal of Applied Physics, 2016, 119(11): 113301-1−113301-13 doi: 10.1063/1.4943025 [15] Hassouni K, Silva F, Gicquel A, et al. Modelling of diamond deposition microwave cavity generated plasmas[J]. Journal of Physics D: Applied Physics, 2010, 43(15): 153001(45pp) [16] Marques L, Jolly J, Alves L L, et al. Capacitively coupled radio-frequency hydrogen discharges: The role of kinetics[J]. Journal of Applied Physics, 2007, 102: 063305 doi: 10.1063/1.2779268 [17] Capitelli M, Ferreira C M, Gordiets B F, et al. Plasma kinetics in atmospheric gases[M]. Springer Science and Business Media, 2013 [18] 苏帆. CVD 金刚石膜可控性生长的研究[D]. 武汉工程大学, 2014 (in Chinese) Su F. Study on controllable growth of CVD diamond film[D]. Wuhan Institute of Technology, 2014 [19] Hagelaar G J M, Hassouni K, Gicquel A, et al. Interaction between the electromagnetic fields and the plasma in a microwave plasma reactor[J]. Journal of Applied Physics, 2004, 96(4): 1819−1828 doi: 10.1063/1.1769607 [20] 张斌华, 简小刚. MPCVD金刚石涂层均匀性生长的数值模拟与实验[J]. 金刚石与磨料磨具工程, 2024, 44(2): 161−168 (in Chinese) Zhang B H, Jian X G. Numerical simulation and experiment of uniform growth of MPCVD diamond coating[J]. Diamond and Abrasives Engineering, 2024, 44(2): 161−168 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: