首页
登录
注册
下载:
-
随着人工智能和电子技术的快速发展, 现代电子产品的集成度和复杂性显著提高, 电磁干扰(electromagnetic interference, EMI)问题日益严重[1,2], 尤其在高密度电路板和集成电路的设计中, 复杂的电磁环境可能导致信号完整性下降和系统可靠性降低[3,4]. 当前, 常用的辐射源识别方法包括全波仿真软件和实际的近场扫描(near-field scanning, NF)测量[5,6]. 全波仿真软件可以在已知结构的条件下快速确定辐射源, 但由于商业保密和复杂设计等限制, 实际电路板的详细结构通常难以获得. 而通过近场扫描直接获取辐射源位置虽然精确, 但实际测量时间过长. 为此, 源重构方法(source reconstruction method, SRM)[7]通过在被测器件(device under test, DUT)表面重建等效辐射源, 简化辐射源模型并降低计算复杂度, 为集成电路的EMI分析和优化提供了一种高效解决方案.
等效辐射源的常见模型主要是电磁电流模型和偶极子模型[8]. 电磁电流模型虽然可以提供全面的电磁场描述, 但其在复杂环境下的计算复杂度和资源消耗较高, 从而导致效率低下[9]. 相比之下, 偶极子在源重构技术运用更加广泛. 它是通过将辐射源简化为离散的偶极子, 然后通过转移系数矩阵计算出电磁场, 并在实际工程应用中实现较低的计算成本. 在传统的偶极子重构算法, 我们需要同时提供场的幅值和相位信息[10]. 然而相位在实际的近场扫描中很难测量, 所以绝大多数研究都是针对无相位辐射源重构[11].
偶极子无相位辐射源重构常用的方法包括迭代算法、插值方法、全局优化算法和神经网络算法[12]. 首先是全局优化算法, 其中包括如遗传算法[13], 差分进化方法[14]和粒子群优化算法[15]. 主要是通过优化搜索策略, 来解决源重构中非线性和多峰问题. 然而, 全局优化算法对初始参数的选择较为敏感, 可能会收敛到局部最优解. 神经网络算法[16]近年来逐渐被引入辐射源重构领域, 具备自适应学习能力. 然而, 其训练过程需要大量的数据和计算资源, 且模型的适配性相对单一. 插值方法[17]利用单层近场数据重构辐射源, 但在数据值差异较大时会导致结果不准确和产生较大误差. 与上述方法相比, 迭代算法[18]具有更高的精度和收敛能力. 通过反复更新辐射源的估计值, 迭代算法能够逐步接近真实辐射源的分布, 尤其在面对复杂问题时表现出显著优势, 尽管计算时间较长.
本文利用奇异值分解(singular value decomposition, SVD)正则化技术和快速迭代收缩阈值算法(fast iterative shrinkage-thresholding algorithm, FISTA), 对模型中的辐射源进行重构. SVD正则化[19]能够降低噪声影响, 提高重构的稳定性和精确度, 并保留关键的辐射特征. FISTA[20]擅长求解非平滑正则项的凸优化问题. 本文所提方法的优势在于将FISTA算法引入到SVD正则化中, 加速收敛过程, 显著地减少迭代次数达到稳定, 从而提高计算效率. 比传统的双层无相位迭代算法和单层无相位插值算法, 迭代时间更短, 重构精度更高.
本文的其余部分组织如下: 第2节详细阐述了该方法; 第3节对贴片天线的模型进行仿真分析, 验证该算法的有效性和准确性, 然后讨论正则化参数和噪声影响; 第4节, 通过芯片模型对该算法进行实验验证; 最后, 对本文进行总结.
-
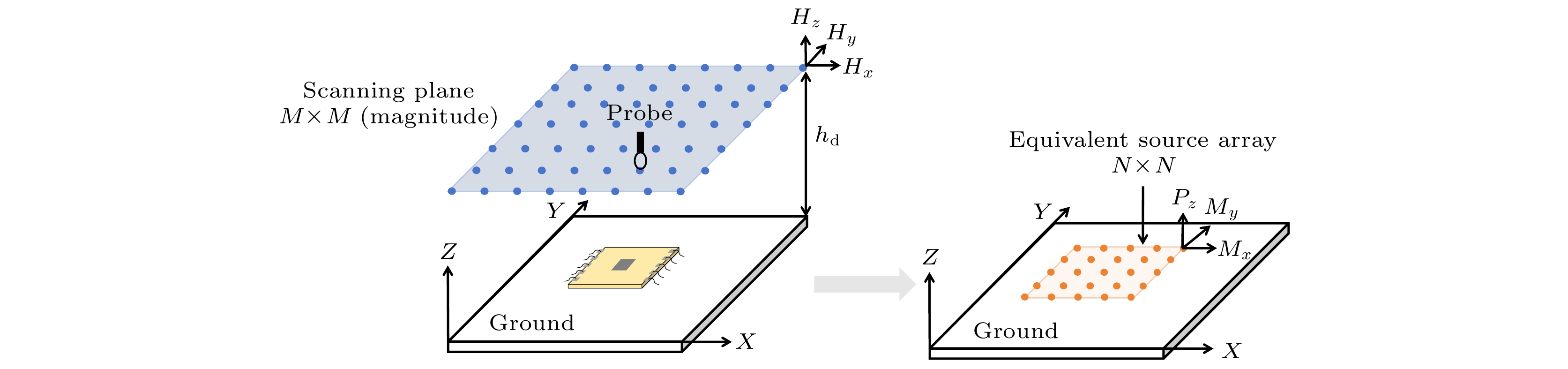
在集成电路设计中, 信号的传输主要依赖于微带线和垂直互连线. 当集成电路位于理想的地平面时, 内部的封装线和地之间形成回路造成磁场辐射. 为了简化这种辐射, 利用近场扫描得到数据建立等效偶极子模型. 本文方法预先设定了偶极子类型和偶极子阵列大小, 将传统模型中的6个偶极子简化为2个等效磁偶极矩和1个等效电偶极矩.
这一简化的主要依据在于电路板内部互连线形成的回路电流. 这些回路电流会产生磁场, 其分布特性与X, Y方向的磁偶极子产生的磁场非常相似. 因此, 采用等效磁偶极矩Mx, My来有效表征这些回路电流的磁场特性. 此外, 另一个重要的干扰源是接地平面与其上方电路板之间的电位差. 这种电位差会引发电磁场的变化, 其特性可以通过垂直于平面(Z方向)的电偶极矩Pz来等效建模. 本文定义了偶极矩Xi阵列.
其中(xi, yi)为第
$ i $ 个偶极子的位置; Re和Im为Mx, My和Pz的实部和虚部; T为阵列的转置; i为第i个偶极子.如图1所示, 扫描平面上的点(M×M)标记了磁场采样位置, 我们通过对这些位置的磁场(Hx, Hy和Hz)进行扫描来实现源重构. 在待测物上方, 构建了一个偶极子阵列, 其中每个点均由Mx, My和Pz三种偶极矩构成. DUT被放置在足够大的地平面上, 形成了一个等效的N×N偶极子阵列, 其覆盖范围包括整个DUT. 偶极矩X、转移系数阵列T和磁场幅值F之间的关系为[10]
其中Hx, Hy和Hz分别表示x, y和z方向的磁场分量. 近场扫描得到的一个大小为M 2×1的列向量, 偶极矩Mx, My和Pz的大小为N 2×1. 转移系数阵列T反映了偶极矩和磁场分量之间的关系. 例如, THxPz描述了所有Pz偶极矩(构成一个向量Pz)对扫描平面内所有Hx磁场分量幅值(构成一个向量Hx)的贡献. 这只是Pz部分,
$T_{H_xM_x}$ 和$T_{H_xM_y}$ 描述了Mx和My对Hx的贡献. 以此类推, 转移系数矩阵里其他符号的含义.为了简化算法的计算量, 统一对阵列进行归一化. 归一化操作如(5)式, 最后得到(6)式[17]:
其中Fn是归一化的F矩阵; Tn是归一化的转移系数矩阵; Xn是归一化的
$ \boldsymbol{X} $ 矩阵; k0是自由空间波数. -
通过以上公式计算出Xn, 才能够得到具体的偶极子阵列. 通常, 一个条件良好的运算可以直接使用最小二乘法求解. 然而, 对于大多数EMI问题, 转移系数阵列Tn往往是病态的. 先用吉洪诺夫正则化方法[15]求解. 公式可以定义为
其中α是一个约束参数. 其中,
$ {\boldsymbol{T}}_n' $ 是Tn的转置矩阵. 该公式的复杂度主要是来自于$ {\boldsymbol{T}}_n'{{\boldsymbol{T}}_n} + {\alpha ^2}{\boldsymbol{I}} $ 的逆运算. 为了减少阵列的计算时间, 利用SVD方法将矩阵Tn分解为三个矩阵. 最终, 公式可以表示为[17]其中Un是一个2MN维的酉矩阵,
$ {\boldsymbol{V}}_n' $ 是一个3MN维的酉矩阵($ {\boldsymbol{V}}_n' = {\boldsymbol{V}}_n^{ - 1} $ $ {\boldsymbol{V}}_{n}^{\prime} $ ), Sn是一个2mn×3mn的矩阵,$ {\zeta _i} ~( {i = 1, 2, \cdots , n} ) $ 是矩阵Tn的奇异值.FISTA算法是一种用于优化非平滑正则项凸问题的方法. 通过引入动量项tk, 该算法在保证较低相对误差的同时加速收敛速度, 缩短迭代时间. 在每次迭代中, 首先将当前解yk投影到约束集上, 以通过
获得新的解Xk [20]. 然后, 根据
更新动量项tk, 以计算下一个动量值tk+1. 接下来, 根据
使用当前解Xk、上一个解Xk–1和动量项tk更新下一个状态的解yk+1. 最后, 将用下一个状态的解yk+1替代当前解yk, 以此进行迭代.
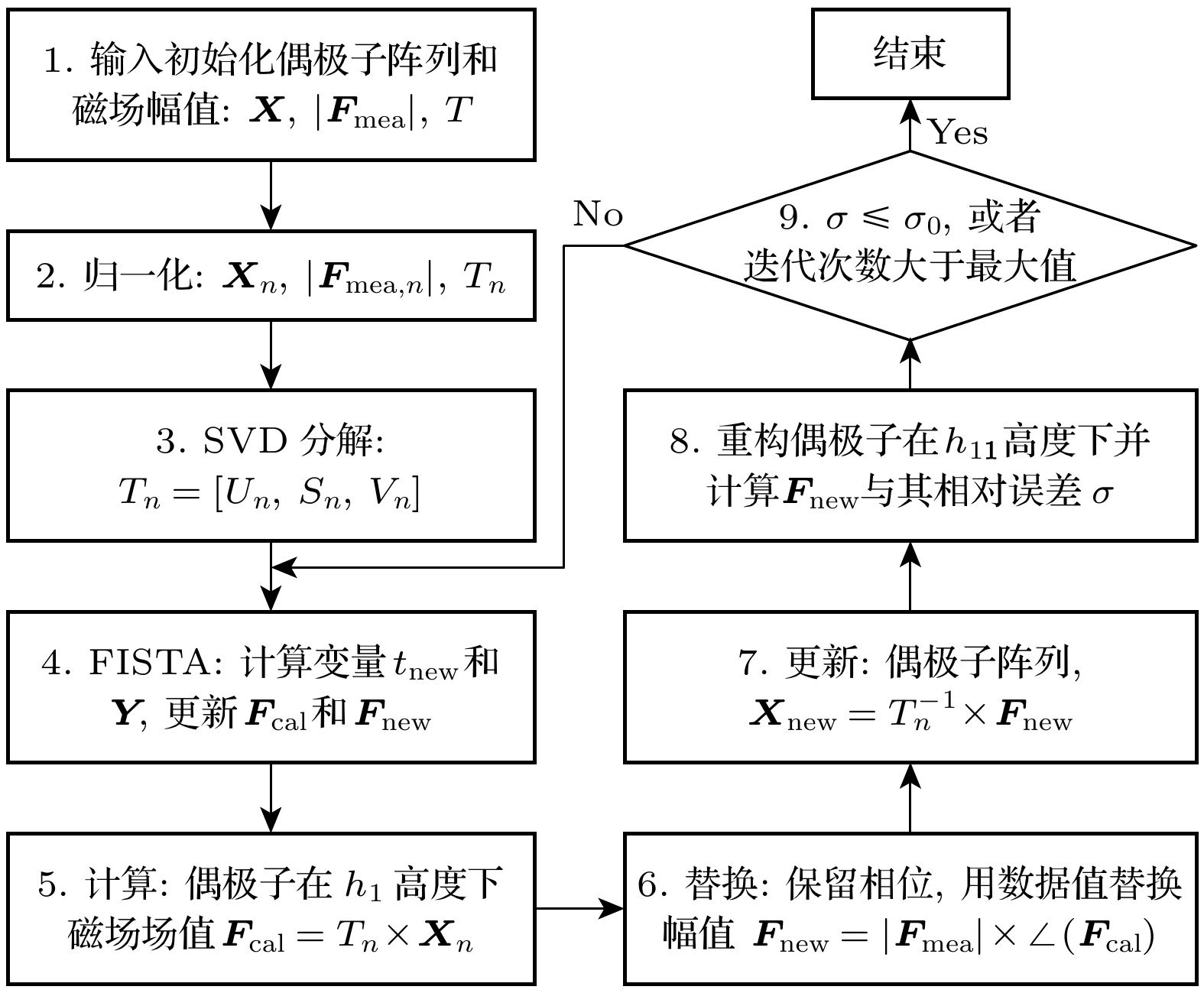
图2展示了所提方法的完整流程, 分为准备阶段和迭代阶段两个部分. 准备阶段包括步骤1至步骤3. 首先, 初始化偶极矩阵列X (幅值为1, 初始相位为0)、近场磁场数据
$ \left| {{F_{{\text{mea}}}}} \right| $ 和转移系数矩阵T, 并对这些数据进行归一化处理以提高计算的速率. 随后, 通过SVD对转移系数矩阵T进行矩阵分解, 为后续更新提供支持.迭代阶段则包括步骤4至步骤9. 在该阶段, 采用FISTA加速计算过程, 更新变量t和Y, 并计算磁场值|Fcal|. 最新的解Y将赋值给偶极矩X. 在保持磁场相位不变的基础上, 调整幅值以与测量 数据一致, 并通过矩阵反演更新偶极子分布Xnew. 最后, 利用误差公式
评估重构磁场分布与测量数据之间的相对误差, 为下一次迭代做准备.
该方法的计算复杂度可分为准备阶段和迭代阶段. 在准备阶段, 最复杂的操作是对转移系数矩阵T进行SVD分解, 计算复杂度为O(MN 2). 迭代阶段的计算复杂度为O(MN 2), 主要由矩阵乘法和FISTA更新步骤组成. 与仅使用 SVD 分解的传统算法相比, 尽管每次迭代的计算复杂度相同, 但引入FISTA后, 能够加速收敛, 减少迭代次数, 从而有效降低总体计算时间.
本文所提方法的优势在于将FISTA算法与SVD算法相结合, 有效地解决了大规模矩阵求解和无相位辐射源重构问题中的数值不稳定性与收敛速度问题. 与传统方法相比, 该方法在处理逆问题时表现出更大的优势. 通过引入FISTA算法, 可以根据相对误差调整迭代次数, 从而提高计算效率, 节省计算资源和时间.
-
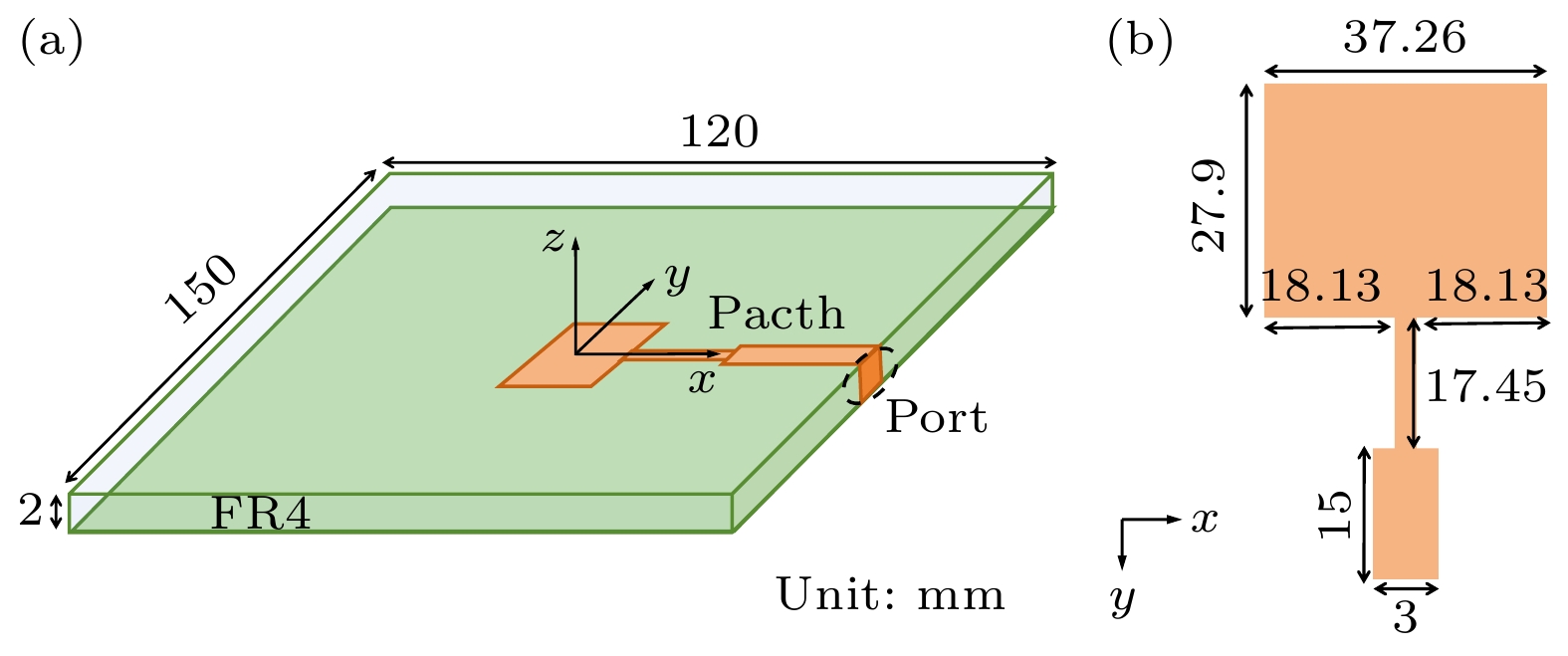
本节利用贴片天线模型验证所提出的无相位辐射源重构方法的准确性. 贴片天线的尺寸为37.26 mm×27.9 mm, 具体参数如图3所示. 下方为一块尺寸为150 mm×120 mm×2 mm的FR4基板, 介电常数为4.4, 正切损耗为0.02. 地平面设置为150 mm×120 mm, 位于FR4基板的下方, 并位于z = 0 mm的XY平面. 天线的集总端口通过端口激励输入1 V信号, 工作频率为3.4 GHz. 考虑到实际应用中电磁干扰源通常表现为宽带辐射源, 选择2.5 GHz作为仿真频率, 远离工作频率, 以便更全面地模拟实际电磁干扰情况. 该模型在全波仿真软件ANSYS HFSS中构建, 并获取了相应的近场扫描数据, 供后续分析使用.
近场扫描平面高度h1设置为z = 7 mm(天线上方5 mm, λ/24), 尺寸为120 mm×120 mm, XY方向上的间隔都为3 mm (
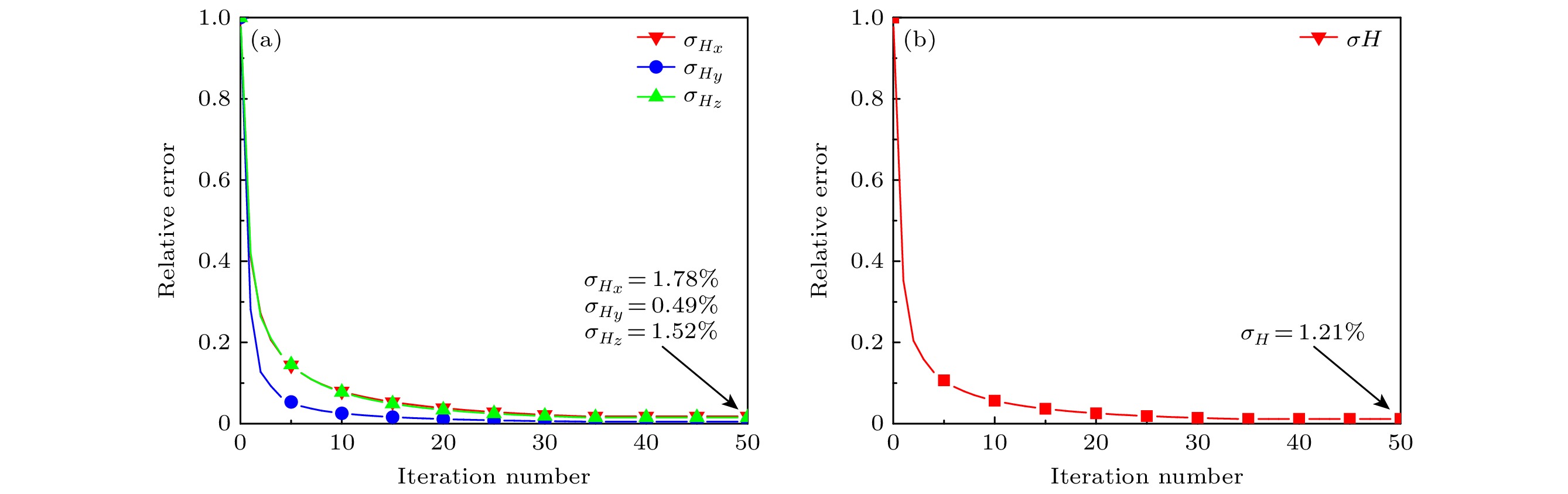
$ \Delta x = \Delta y = 3{\text{ mm}} $ , λ/40), 因此总共有1681个采样点(41×41). 获得验证平面高度为h2, 位置在z = 12 mm (天线上方10 mm, λ/12), f = 2.5 GHz时的磁场分量幅值数据, 如图4(a)所示.由于辐射源位置未知, 因此在z = 2.1 mm处设置了一个10 × 10偶极子阵列. 初始化的偶极矩阵列X是相位为0幅值为1的单位矩阵. 通过将h1得到的近场数据输入到算法中, 经过迭代算法计算出偶极矩X. 然后根据新的转移系数矩阵, 计算出验证平面h2的磁场幅值分量, 源重构分布如图4(b)所示. 此外, 图5显示了Hx, Hy和Hz磁场分量的相对误差图, 以及总相对误差. 从第35次迭代开始, 磁场分量相对误差
$\sigma_{H_x}, ~\sigma_{H_y}和\sigma_{H_z}$ . 分别稳定在1.78%, 0.49%和1.52%, 总相对误差σH收敛到1.21%. -
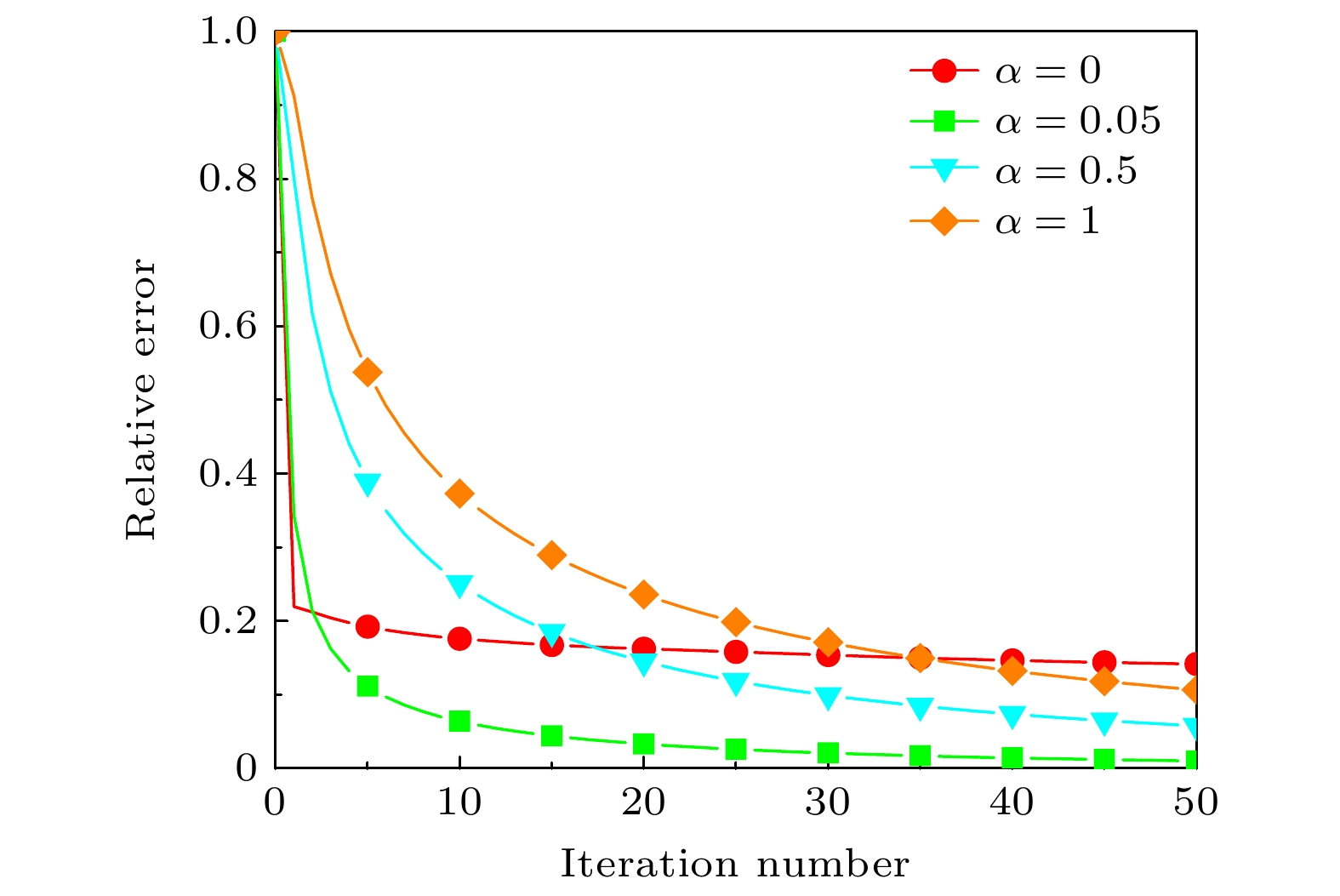
在SVD正则化算法中, 正则化参数α起着至关重要的作用. 它主要用于控制阵列解的稳定性和平滑性, 尤其在处理非线性阵列解时更为显著. 在奇异值分解及求逆过程中, 微小的噪声波动可能会被放大, 从而影响重构结果. 因此, 正则化参数α通过约束解的过程, 确保了主要信息的保留. 通常, α的取值范围在[0, 1]之间. 为了分析不同正则化参数的影响, 我们选取了α = 0, 0.05, 0.5, 1四个值作为参考, 进行重构结果的对比.
如图6所示, 不同正则化参数的选择会导致结果存在显著差异. 实验结果表明, 当α = 0.05时, 相对误差为1.21%, 而当α = 0.5时, 相对误差升高至5.2%. 对于α = 0和α = 1的情况, 相对误差均高于其他两点. 这是因为过大的α会导致解的边缘模糊, 而过小的α会引起稀疏分布, 二者均会导致较大的相对误差. 综合对比后, 我们发现α = 0.05是最为合适的选择.
-
为了验证该方法的鲁棒性, 在得到的仿真数据中加入高斯白噪声, 来模拟测量噪声. 然后再将其输入到迭代算法中, 进行辐射源重构. 在扫描平面z = 12 mm, f = 2.5 GHz处的磁场幅值分别加入不同功率的高斯白噪声. 以下仿真的前提是α = 0.05. 噪声功率可以定义为
其中Pnoise代表噪声功率; Psignal表示为信号功率; M×M表示为采样点数.
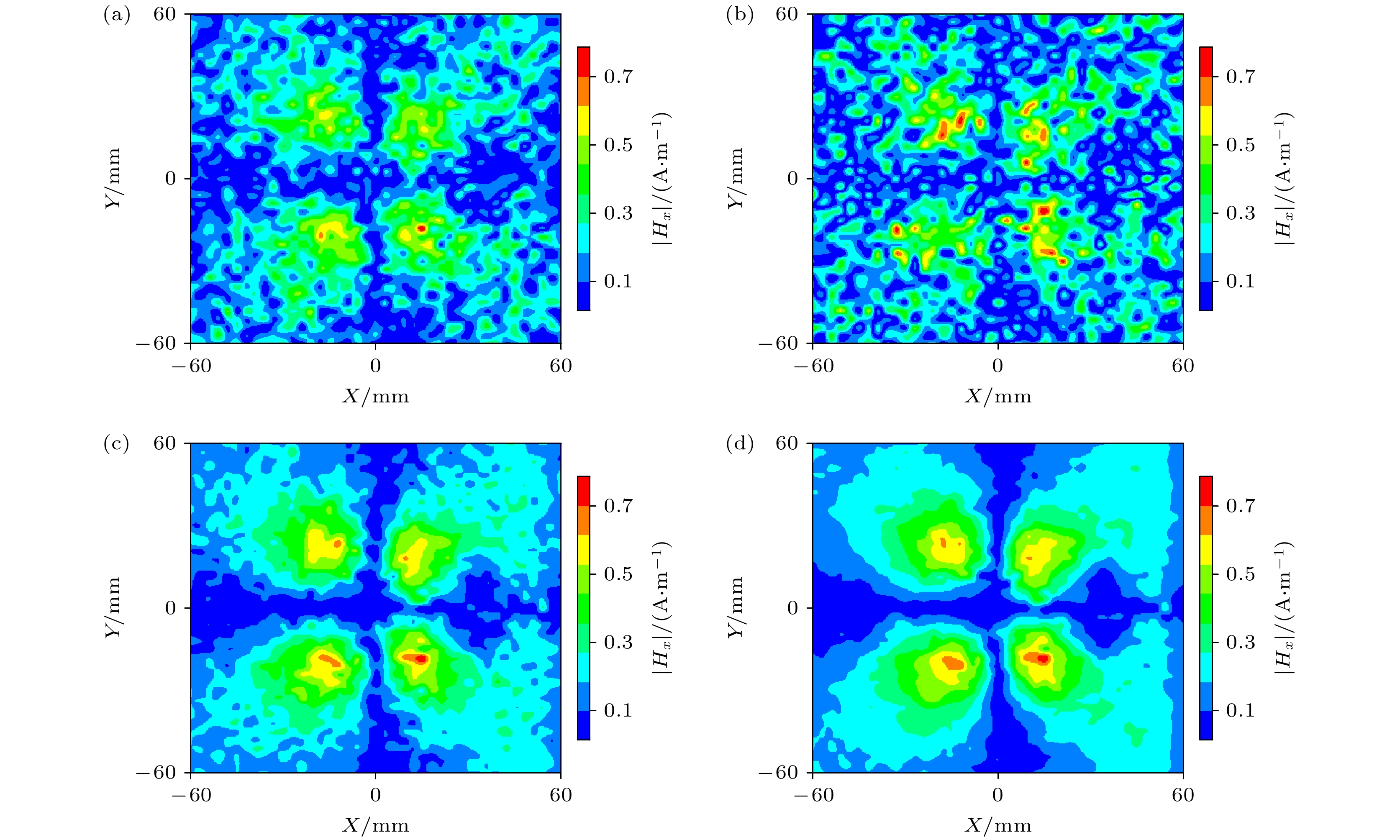
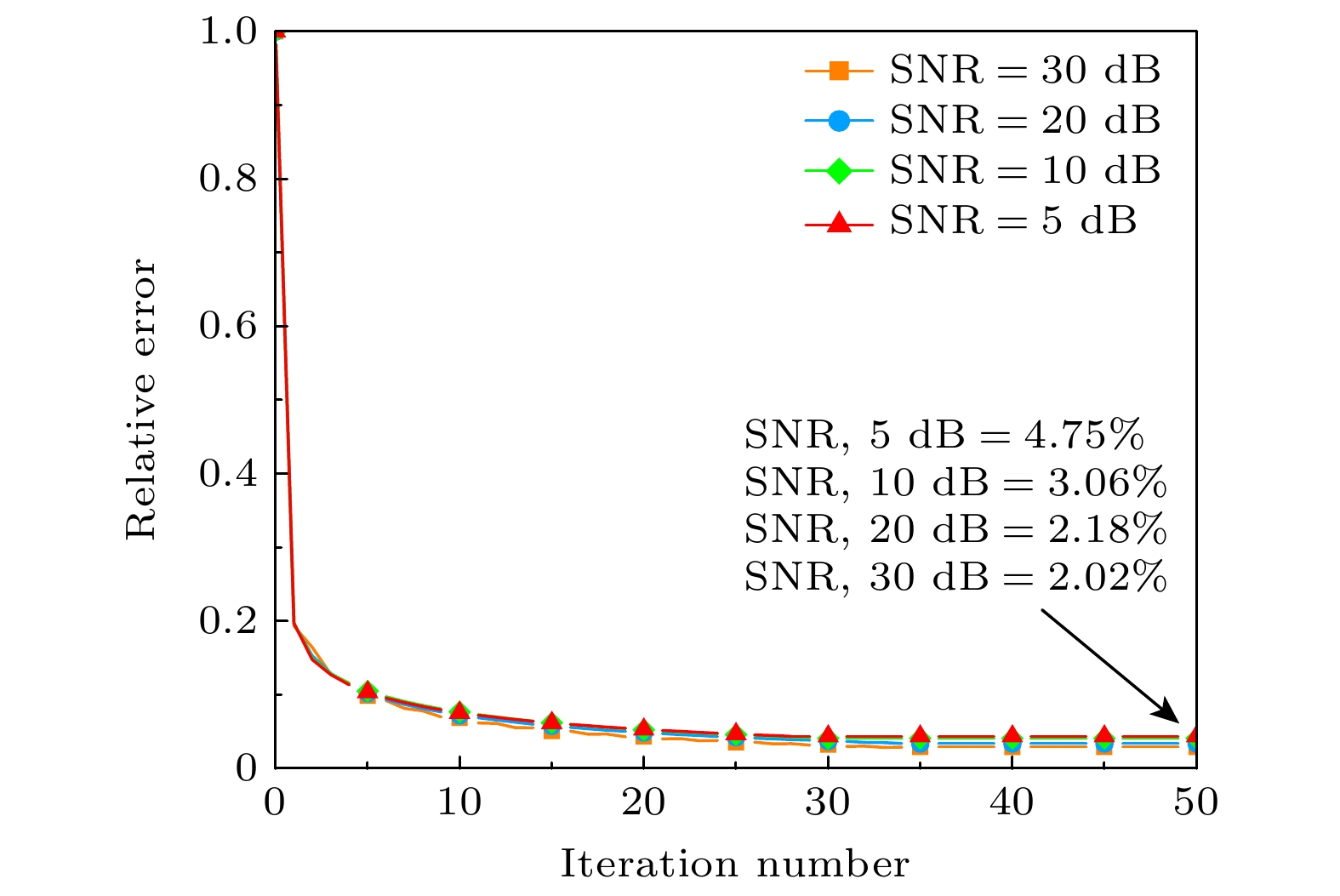
将不同功率的高斯白噪声加入到原始数据中, 形成含有噪声的新数据HSNR. 其中, WGN表示为不同功率水平的高斯白噪声. 根据(16)式, 选取了信噪比(SNR)为5, 10, 20和30 dB的条件进行测试, 并通过图7展示了在不同噪声水平下的磁场分量
$ \left| {{H_x}} \right| $ 分布图. 结果表明, 随着SNR的降低, 噪声功率逐渐增加, 导致磁场图边缘模糊, 图像细节逐渐丢失, 整体分布变得更加杂乱. SNR值为5, 10, 20和30 dB的相对误差分别为4.75%, 3.06%, 2.18% 和 2.02%. 尽管噪声增加, 但源重构的相对误差保持在5%以下, 对噪声有鲁棒性表现如图8所示. -
通过上述分析, 可以验证所提算法的准确性和鲁棒性. 然而, 在实际应用中, 近场测量数据可能会受到环境等多种因素的影响, 从而引入较大的相对误差. 因此, 本节制作了一个简易的芯片模型用于源重构实验. 该芯片的工作频率为1 GHz, 考虑到电磁干扰源通常具有宽带辐射特性, 因此选择2 GHz作为仿真频率.
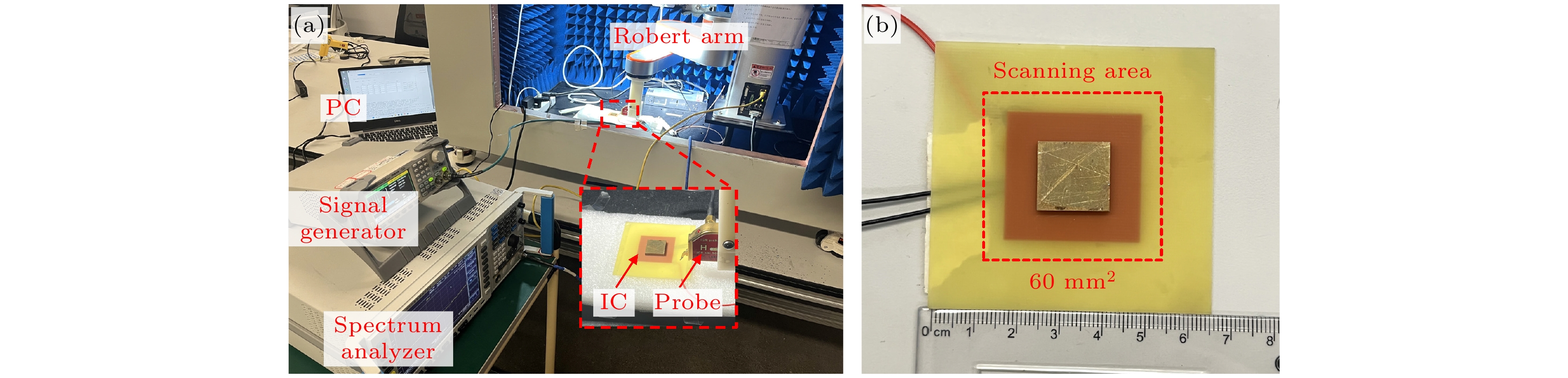
如图9(a)所示, 建立了近场扫描实验系统, 包括信号发生器、频谱仪、PC、扫描设备、DUT和磁场探头. DUT为集成电路(IC). IC的一端通过SMA端口连接至200 ns尖峰脉冲信号, 而另一端接50 Ω负载以模拟真实工作条件. 扫描面积为60 mm×60 mm, 在X和Y方向上的步长均为1.5 mm, 如图9(b)所示. 磁场探头为LANGER EMV Technik ICR近场探头(5 K-6 GHz), 三个磁场分量同时测得. 整个扫描系统由上位机控制, 并通过配备Intel Core i5-8265 U处理器和256 GB存储的主机PC进行数据处理和分析.
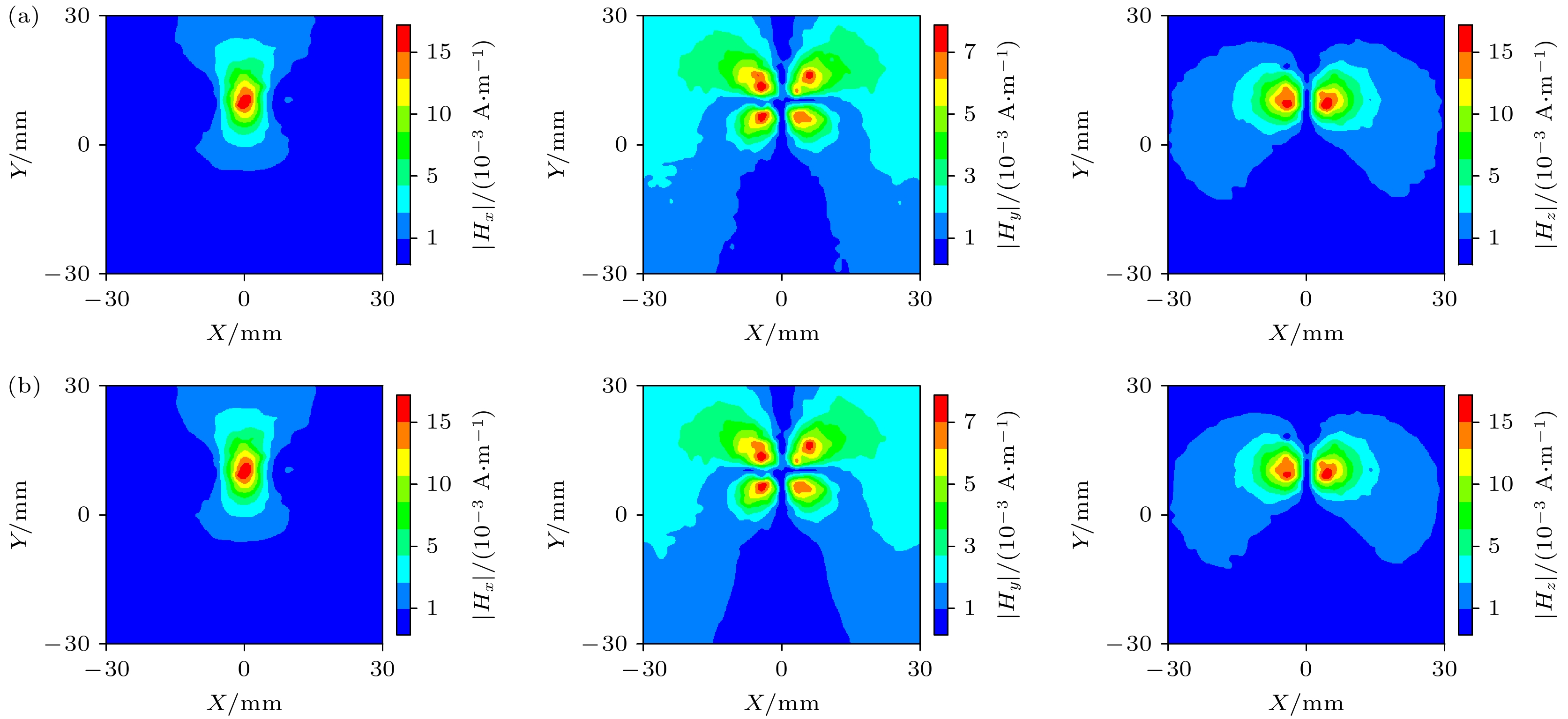
为验证所提方法的实际测试有效性, 选z = 13.22 mm (芯片上方10 mm处, λ/15)作为初始数据进行重构偶极子阵列X. 如图10(a)显示, 在验证平面z = 8.22 mm (芯片上方5 mm处, λ/30), 频率为f = 2 GHz是得到的近场扫描磁场分量
$ \left| {{H_x}} \right| $ ,$ \left| {{H_y}} \right| $ ,$ \left| {{H_z}} \right| $ . 图10(b)展示了采用所提源重构方法计算后得到的$ \left| {{H_x}} \right| $ ,$ \left| {{H_y}} \right| $ ,$ \left| {{H_z}} \right| $ . 最终实测与重构结果的相对误差为2.3%, 低于5%的正常误差范围.测量的近场扫描时间为10800 s (3 h), 而源重构(包括准备阶段95.34 s和迭代阶段97.56 s)在192.9 s内完成. 准备时间是图2的算法流程图的步骤1—3中所花费的时间, 迭代时间是步骤3—9中花费的时间. 迭代的最大次数设置为50次. 根据表1所列, 所提出的方法在35次迭代内实现了2.3%的相对误差, 迭代总时间是单层无相位插值算法的61.7%, 相对误差比双层无相位迭代算法减少了52%.
-
本文提出了一种结合SVD正则化和FISTA的单层无相位辐射源重构算法. 与双层迭代算法和单层插值算法相比, 该方法在重构精度和抗噪性能方面均有所提升. 仿真和实验结果表明, 该算法仅需35次迭代即可稳定收敛, 重构结果与实际数据的相对误差最低可达2.3%, 迭代总时间仅为传统方法的61.7%, 相对误差减少了52%, 验证了其在集成电路电磁干扰源定位中的高效性与鲁棒性. 然而, 当应用于大规模数据时, 算法的计算复杂度显著增加, 且正则化参数的选择依赖经验调优, 这可能影响其在实际场景中的适用性.
基于奇异值分解正则化和快速迭代收缩阈值算法的无相位辐射源重构算法
An algorithm of reconstructing phaseless radiation source based on singular value decomposition regularization and fast iterative shrinkage-thresholding algorithm
-
摘要: 本文提出了一种基于奇异值分解(SVD)正则化和快速迭代收缩阈值算法(FISTA)的单层无相位辐射源重构算法. 该方法能够有效地识别集成电路中的电磁干扰源. 首先, 通过近场扫描获取电磁场数据, 随后利用源重构方法(SRM)在其表面重建等效偶极子模型. 引入SVD正则化项以提高算法的稳定性和抗噪声能力, FISTA技术则加速了算法的收敛速度. 为了验证该方法的准确性和对高斯噪声的鲁棒性, 进行了贴片天线仿真分析和芯片实验测试. 结果表明, 该算法在第35次迭代时达到稳定, 重构结果与仿真结果的相对误差为2.3%, 迭代时间仅为传统方法的61.7%, 相对误差减少了52%.
-
关键词:
- 奇异值分解 /
- 快速迭代收缩阈值算法 /
- 近场扫描 /
- 辐射源重构
Abstract:An algorithm of reconstructing phaseless radiation source based on singular value decomposition (SVD) regularization and fast iterative shrinkage-thresholding algorithm (FISTA) is proposed in this work, aiming at efficiently identifying electromagnetic interference (EMI) sources in integrated circuits (ICs). The method acquires electromagnetic field data through near-field scanning and reconstructs an equivalent dipole array on the surface of the radiation source by using the source reconstruction method (SRM). In the reconstruction process, the SVD regularization term enhances the algorithm's stability and noise resistance, while the FISTA accelerates the convergence speed. In order to validate the effectiveness of the proposed method, dipole array reconstruction is first performed using near-field data at a height of 5 mm for a patch antenna simulation model, followed by analyzing the magnetic field data at a 10 mm validation plane. At the 35th iteration, the total relative error of the reconstruction is 1.21%. The influence of the regularization parameter α on the result is then investigated, and it is found that when α = 0.05 the error is minimized. The method is also tested under different Gaussian white noise conditions, and the relative error is kept below 5%, which demonstrates strong robustness. Finally, the experiments on chips are conducted to verify the method. The proposed method converges stably within 35 iterations, with a relative error of 2.3% in the reconstruction results. The proposed method reduces the total iteration time to 61.7% of the single-layer phaseless interpolation algorithm, while achieving a 52% lower relative error than the double-layer phasless iteration algorithm. The experimental results show that the proposed method can reconstruct phaseless radiation source efficiently and accurately, and has good noise robustness, which is suitable for EMI analysis in ICs. -
-
图 3 贴片天线模型图 (a)三维图; (b)天线结构
Figure 3. Patch antenna model diagram: (a) Three-dimensional diagram; (b) antenna structure.
图 4 在z = 12 mm, f = 2.5 GHz下仿真和源重构的磁场分量幅值结果 (a)仿真的磁场分量幅值; (b)源重构的磁场分量幅值
Figure 4. Magnitude of magnetic field component for simulation and source reconstruction under z = 12 mm, f = 2.5 GHz: (a) Simulated magnetic field component amplitude; (b) magnetic field component amplitude of SRM.
图 5 在z = 12 mm, f = 2.5 GHz下源重构的相对误差 (a) 磁场分量的相对误差
$\sigma_{H_x}, ~\sigma_{H_y}和\sigma_{H_z} $ ; (b)总相对误差σHFigure 5. Relative error of SRM at z = 12 mm, f = 2.5 GHz: (a) Relative error of magnetic field components
$\sigma_{H_x}, ~\sigma_{H_y}\text{ and }\sigma_{H_z} $ ; (b) total relative error σH.
图 6 不同正则化参数对总相对误差的影响
Figure 6. Influence of different regularization parameters on total relative error.
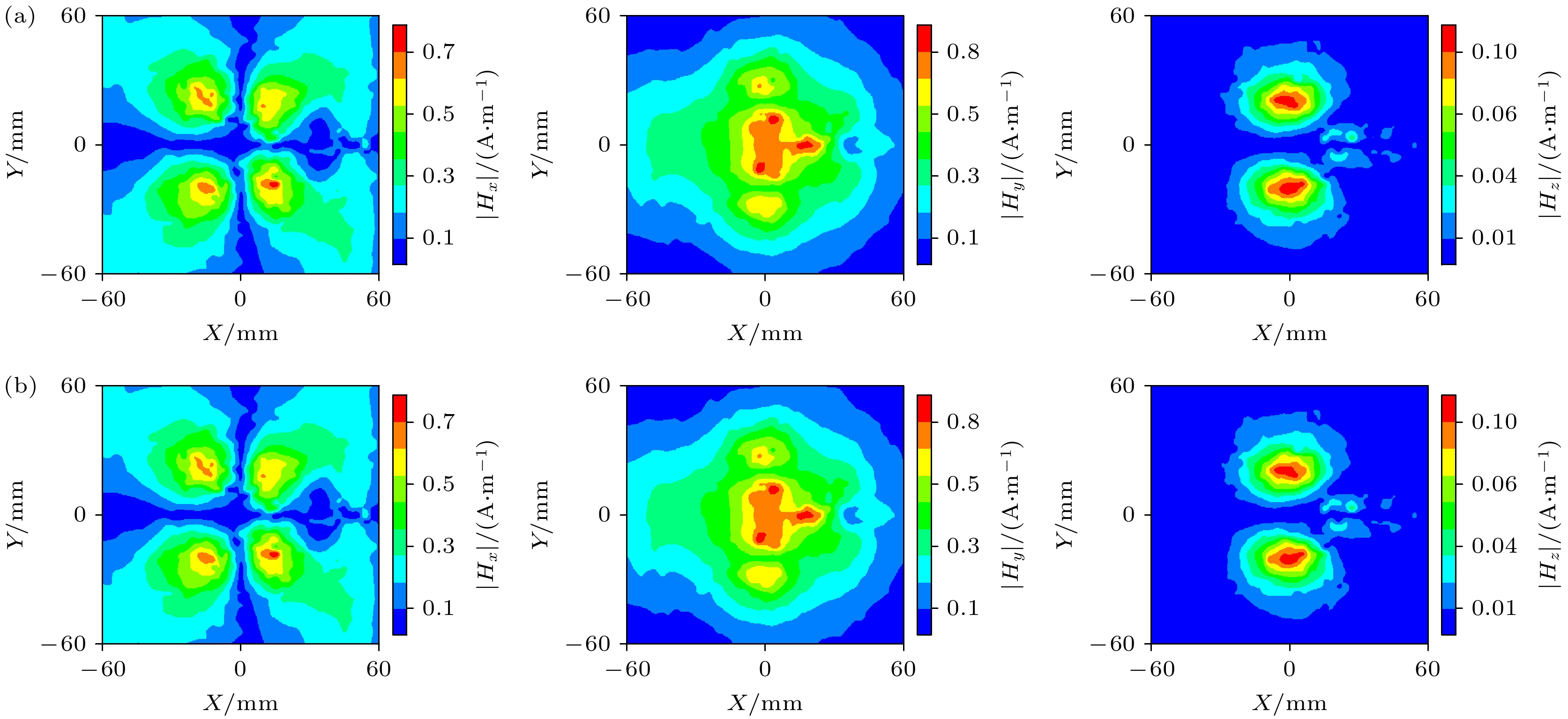
图 7 在不同水平的高斯白噪声下z = 12 mm, f = 2.5 GHz磁场|Hx|幅值 (a) SNR = 5 dB; (b) SNR = 10 dB; (c) SNR = 20 dB; (d) SNR = 30 dB
Figure 7. Magnetic field
$ \left|{H}_{x}\right| $ amplitude under different levels of white Gaussian noise, z = 12 mm, f = 2.5 GHz: (a) SNR = 5 dB; (b) SNR = 10 dB; (c) SNR = 20 dB; (d) SNR = 30 dB.
图 8 加入不同高斯白噪声后总的相对误差
Figure 8. Total relative error after adding different Gaussian white noise.
图 9 近场扫描实验设备 (a)近场扫描装置设备; (b)芯片模型
Figure 9. Near field scanning experimental equipment: (a) Near field scanning equipment; (b) chip model.
图 10 在z = 8.22 mm, f = 2 GHz下近场扫描和源重构的磁场分量幅值 (a)近场扫描的磁场分量幅值; (b)源重构的磁场分量幅值
Figure 10. Amplitude of magnetic field components in near-field scanning and SRM at z = 8.22 mm, f = 2 GHz: (a) Amplitude of magnetic field component in near-field scanning; (b) magnetic field component amplitude of SRM.
-
[1] Schuman C D, Kulkarni S R, Parsa M, Mitchell J P, Date P, Kay B 2022 Nat. Comput. 2 10 doi: 10.1038/s43588-021-00184-y [2] Serpaud S, Boyer A, Dhia S B, Coccetti F 2022 IEEE Trans. Electromagn. Compat. 64 816 doi: 10.1109/TEMC.2021.3136096 [3] Boyer A, Nolhier N, Caignet F, Dhia S B 2022 IEEE Trans. Electromagn. Compat. 64 1230 doi: 10.1109/TEMC.2022.3169183 [4] 曹钟, 杜平安, 聂宝林, 任丹, 张其道 2014 物理学报 63 124102 doi: 10.7498/aps.63.124102 Cao Z, Du P A, Nie B L, Ren D, Zhang Q D 2014 Acta. Phys. Sin. 63 124102 doi: 10.7498/aps.63.124102 [5] Yang R, Wei X C, Shu Y F, Yi D, Yang Y B 2019 IEEE Trans. Antennas Propag. 67 6821 doi: 10.1109/TAP.2019.2927814 [6] Zhang J, Kam K W, Min J, Khilkevich V V, Pommerenke D, Fan J 2013 IEEE Trans Instrum. Meas. 62 648 doi: 10.1109/TIM.2012.2218678 [7] Wang L, Zhang Y, Han F, Zhou J, Liu QH 2020 IEEE Trans. Microwave Theory Tech. 68 4151 doi: 10.1109/TMTT.2020.3006564 [8] Weng H, Beetner D G, DuBroff R E 2011 IEEE Trans. Electromagn. Compat. 53 891 doi: 10.1109/TEMC.2011.2141998 [9] Zuo P, Li Y, Xu Y, Zheng H, Li E P 2019 IEEE Trans. Compon. Packag. Manuf. Technol. 9 329 doi: 10.1109/TCPMT.2018.2829023 [10] Yu Z, Mix J A, Sajuyigbe S, Slattery K P, Fan J 2012 IEEE Trans. Electromagn. Compat. 55 97 [11] Kornprobst J, Mauermayer R A M, Neitz O, Knapp J, Eibert T F 2019 Prog. Electromagn. Res. 165 47 doi: 10.2528/PIER19050904 [12] Yi Z, Zou J, Tian X, Huang Q, Fang W, Shao W, En Y, Gao Y, Han P 2023 IEEE Trans. Electromagn. Compat. 65 879 doi: 10.1109/TEMC.2023.3247681 [13] Regue J R, Ribó M, Garrell J M, Martín A 2001 IEEE Trans. Electromagn. Compat 43 520 doi: 10.1109/15.974631 [14] Han D H, Wei X C, Wang D, Liang W T, Song T H, Gao R X 2024 IEEE Trans. Electromagn. Compat. 66 566 doi: 10.1109/TEMC.2023.3317633 [15] Xiang F P, Li E P, Wei X C, Jin J M 2015 IEEE Trans. Electromagn. Compat. 57 1197 doi: 10.1109/TEMC.2015.2414174 [16] Shu Y F, Wei X C, Fan J, Yang R, Yang Y B 2019 IEEE Trans. Microwave Theory Tech. 67 1790 doi: 10.1109/TMTT.2019.2905238 [17] Zhang J, Fan J 2017 IEEE Trans. Electromagn. Compat. 59 557 doi: 10.1109/TEMC.2016.2638760 [18] Shu Y F, Wei X C, Yang R, Liu E X 2017 IEEE Trans. Electromagn. Compat. 60 937 [19] Yu Z W, Jason M, Sajuyigbe S, Slattery K P, Fan J 2013 IEEE Trans. Electromagn. Compat. 55 97 doi: 10.1109/TEMC.2012.2207726 [20] Beck A, Teboulle M 2009 SIAM J. Imaging Sci. 2 183 doi: 10.1137/080716542 -
计量
- 文章访问数: 58
- HTML全文浏览数: 58
- PDF下载数: 1
- 施引文献: 0