量子密钥分发(quantum key distribution, QKD)以量子物理基本原理为基础, 在通信双方间分发密钥, 确保信息安全^[1,2]. 其安全性不依赖于数学问题的复杂性, 也不受计算能力的限制, 从理论层面上能够实现无条件安全通信^[3]. 1984年, Bennett和Brassard^[1]受量子货币思想启发, 提出了首个QKD协议, 即 BB84 协议. 从1992年第一个32.5 cm的自由空间QKD实验演示^[4]到现在跨越4600 km的天地一体化量子通信网络^[5], 经过30多年理论和实验的发展, QKD已经从实验室逐渐走向现实应用^[6]. 30多年来, 各种QKD协议被提出^[6–8], 根据编码方式的不同主要分为两类: 基于单光子编码的离散变量量子密钥分发(discrete-variable QKD, DV-QKD)和基于光场正交分量编码的连续变量量子密钥分发(continuous-variable QKD, CV-QKD).

CV-QKD将信息编码于光场的正交分量, 采用相干探测技术, 如零差探测或外差探测. 这使得它在中短距离成码率高, 与现有光纤网络兼容性好, 且无需昂贵的单光子探测器. 同时, 其实现成本低、易集成, 能够有效地满足局域网和城域网络的搭建需求, 近年来受到科研人员的广泛关注^[9–12]. 其研究重点主要聚焦于以下三方面: 首要的是确保协议的安全性, 这涵盖了对潜在窃听者Eve可能采取的各类攻击策略的防范, 以及针对实际器件不完美性所带来的现实安全性挑战^[13–23]; 其次是提升协议的性能, 旨在达到更高的密钥生成速率以及实现更远的传输距离^[24–33]; 最后是推动协议物理实现的集成化、小型化和低成本, 这包括探索更为简便的协议方案、拓展协议以支持多用户网络化应用等^[34–43].

尽管CV-QKD在理论和实验方面已取得显著的成就, 但对于真正广泛安全的实际应用仍面临许多关键挑战. 虽然CV-QKD的理论安全性分析已较为完善, 但在实际应用过程中, 存在实际系统与理论模型不匹配的情况, 这会导致安全漏洞的出现, 使系统面临被窃听者攻击的风险. 在确保安全的前提下, 实际的CV-QKD系统致力于在尽可能简化系统结构的基础上实现高性能. 一维(unidimensional, UD) CV-QKD协议仅使用一个调制器(振幅或者相位调制器)来完成信息的编码, 在硬件实现上更为简单, 降低了整体系统的搭建成本. 由于信息编码的维度减少, 所需的随机数生成量也相应减少. 这对于随机数生成资源有限的应用场景尤为重要. 因此, UD CV-QKD对于CV-QKD的小型化和低成本应用具有显著优势. 尤其是在构建大规模量子通信网络时更具吸引力, 通过减少每个节点的成本, 可以更容易地实现网络的扩展和普及^[44–61]. 但目前UD CV-QKD的研究都假定发送端(Alice)具有完全稳定的源, 这在实际中是不现实的. 即使用户可以很好地控制源, 也不可避免地会出现一些误差^[62–65]. 其中, 最主要的源误差是源的强度误差, 比如光脉冲的强度波动、调制器和衰减器的不精确校准以及不可避免的外部环境干扰等都可能导致光源强度误差的产生. 最近, 单路和测量设备独立的两维高斯调制CV-QKD方案(正交振幅和相位都调制)在源强度误差下的现实安全性被研究^[64,65], 有效地促进了协议的实际应用.

为了完善UD CV-QKD的现实安全性, 本文研究了源强度误差对UD CV-QKD协议性能和安全性的影响. 为了使得协议能够在各种现实条件下稳定运行并保障通信安全, 我们对用户的能力做出了三种贴近实际的假设, 并针对这些假设提出了相应的数据优化处理方案, 以减少源误差的影响. 同时, 我们强调, 对于潜在窃听者(Eve)的能力, 并未施加任何限制, 以确保我们的安全分析具有普遍性和严谨性. 进一步, 我们评估了协议在有限码长下的安全性. 由于在协议的实际实现中, 通信双方能交换的量子态数量总是有限的, 因此必须考虑统计涨落和有限码长效应对安全性的影响. 当源误差和有限码长同时存在时, 它们会相互交织并共同影响UD CV-QKD系统的安全性.

本文首先阐述了UD CV-QKD协议方案和安全性, 然后详细地分析了不同现实假设下源误差对UD CV-QKD的影响, 最后综合考虑了源误差和有限码长效应, 以确保系统的实际安全性.

当描述一个CV-QKD协议时, 通常包含两种方案: “准备与测量”(preparation and measurement, PM)和“基于纠缠”(entanglement-based, EB). 在PM方案中, 信息发送方(Alice)会先将经典信息编码到量子态中, 然后通过光信号的形式发送给信息接收方(Bob). Bob接收到信号后, 会进行一系列测量, 以还原出原始的经典信息. 在EB方案中, Alice会生成一个特殊的双模压缩真空态, 并测量其中一个模式的正交分量. 随后, 她将另一个模式发送给Bob, Bob测量相应正交分量, 以完成信息的传递. 在实际应用场景中, 现有的大多数CV-QKD系统都是基于PM方案来实现的. 而EB方案对于协议的安全性分析更加方便.

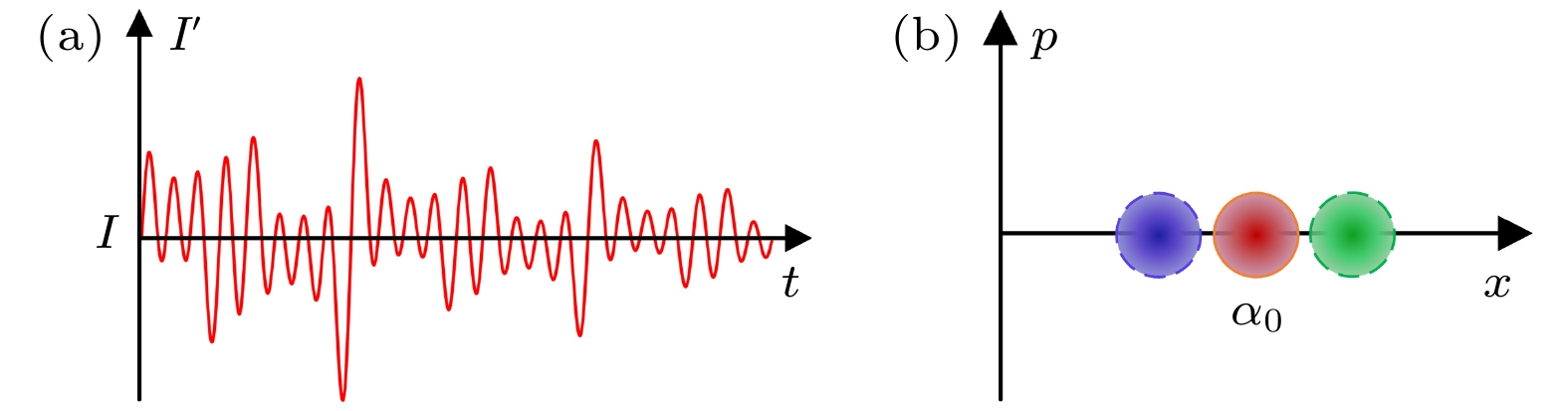
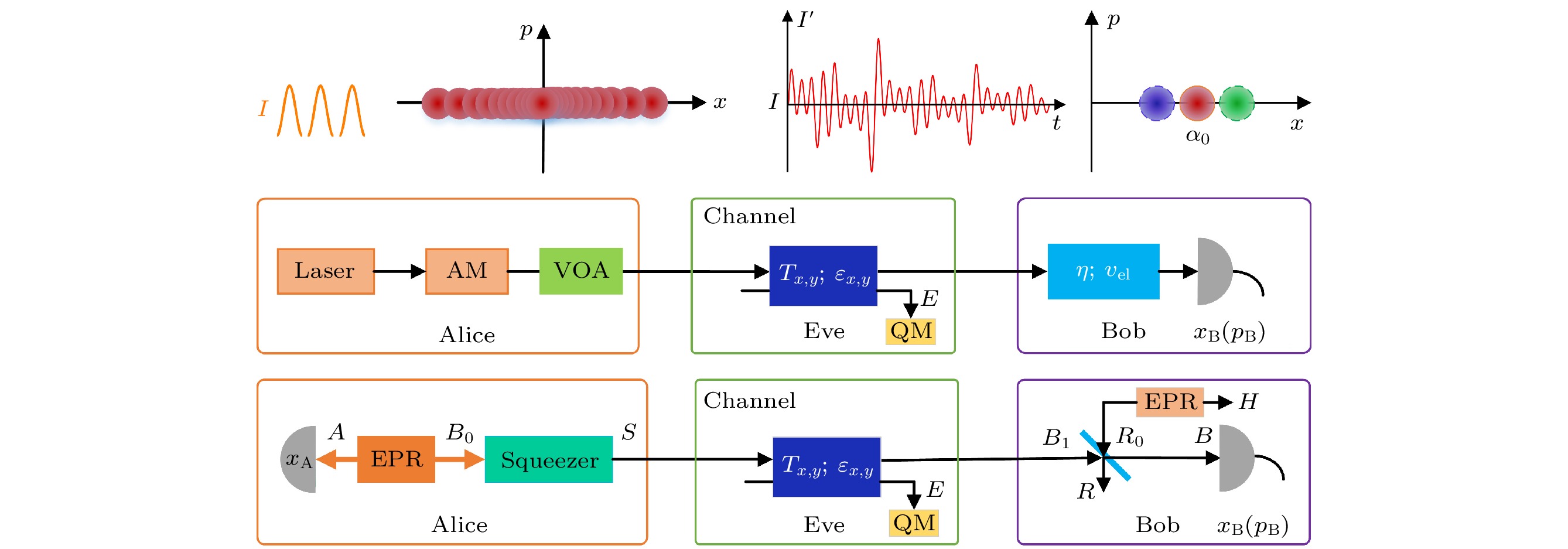
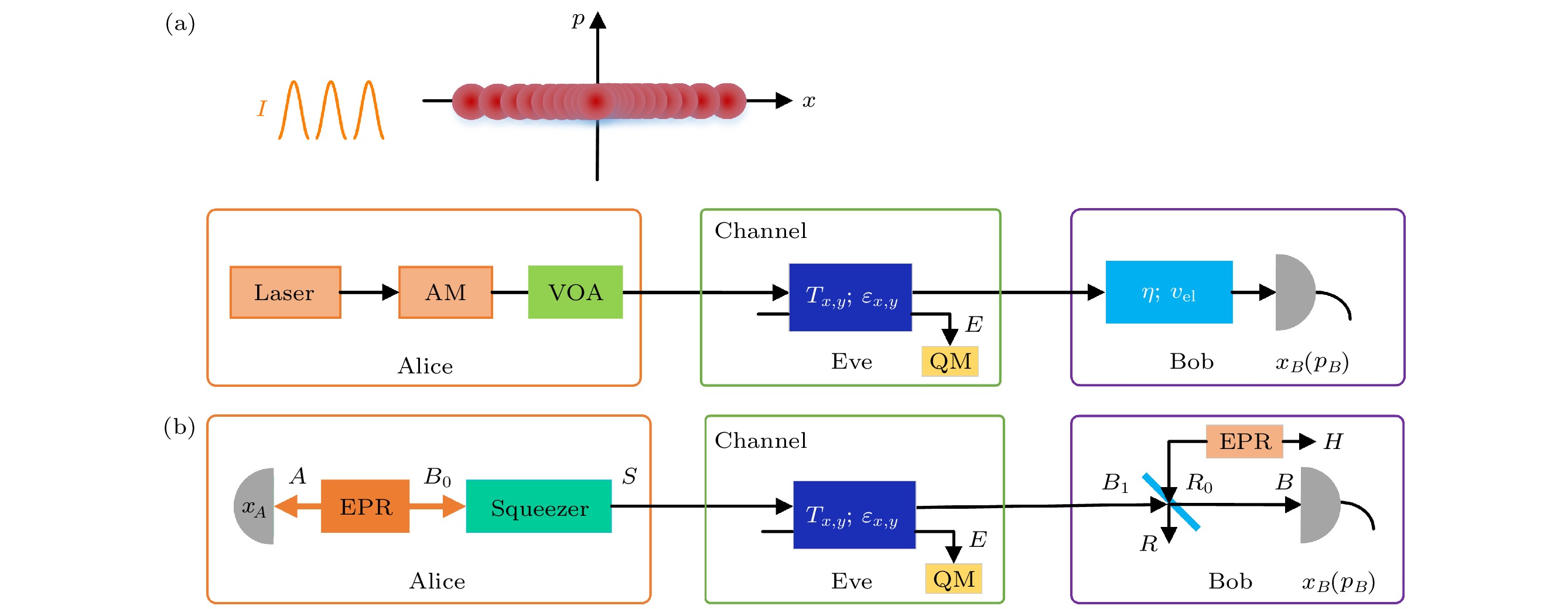
图1(a)展示了一维高斯调制相干态协议的PM方案. 协议的主要步骤包括:

1) 量子态的制备. 在发送端, Alice使用强度为$I$的信号脉冲光准备一系列相干态. 为了完成信息编码, Alice使用一个调制方差为$ {V_{\text{M}}} $的振幅调制器对相干态进行调制, 调制后的量子态在相空间中呈现一维链式结构.

2) 量子态的传输. Alice通过一个不可信的量子信道将调制好的量子态发送出去.

3) 量子态的测量. 探测端Bob接收到信号后, 运用实际的平衡零拍探测器对量子态的正交振幅或者正交相位展开测量.

4) 数据筛选. Bob公开测量正交的选择, Alice只保留与Bob相同的正交分量. 然后Alice和Bob得到一组相互关联的数据.

5) 参数估计. Alice和Bob利用公开信道交换一部分数据, 进行参数估计. 通过对量子信道透射率、额外噪声和正交相位方差等参数的估计, 可以估算协议的密钥率, 判断通信是否安全、有效.

6) 数据协调. 若通信有效, Bob发送一些边信息给Alice, 进行数据协调、纠错, 使得通信双方得到一组完全相同的数据.

7) 私密放大. 通信双方应用哈希函数消除可能泄漏的信息, 得到安全密钥.

为了便于安全性分析, 我们考虑协议等效的EB方案. 如图1(b)所示, Alice准备具有方差$V$的EPR态${\rho _{A{B_0}}}$, 并对自己保留的模式$A$进行零拍探测, 对另外一个模态${B_0}$, 用压缩参数$ r = \ln \sqrt V $的压缩算符(Squeezer)对正交相位进行压缩, 产生模式$S$. 然后Alice将模式$S$通过传输效率为${T_x}$, ${T_y}$, 额外噪声为${\varepsilon _x}$, ${\varepsilon _y}$, 长度为$L$的量子信道发送给Bob. Bob进一步使用传输效率为$\eta $的分束器将接收到的模式${B_1}$转化$B$. 这个转化过程用来模拟探测效率为$\eta $, 电子学噪声为${v_{{\text{el}}}}$的实际零拍探测器. 其中, 电子学噪声通过在分束器的一个端口注入方差为$ {V_{\text{N}}} $的热态$ {\rho _{{R_0}}} $来模拟, 则$ {V_{\text{N}}} = 1 + {{{\nu _{{\text{el}}}}} {/ } {\left( {1{{ - }}\eta } \right)}} $. 然后, Bob使用一个完美的零拍探测器测量模式$B$的正交振幅$x$和部分正交相位$p$, 得到测量结果${x_B}$和${p_B}$. 至此, Alice和Bob获得一组相互关联的数据. 最后经过参数估计、数据协调、私密放大步骤, 通信双方可以提取安全的密钥.

上述两种方案的等价关系已经被证明^[50]. 通过对Alice的零差探测结果乘以一个常数因子, 可以建立UD相干态协议的EB方案和PM方案的一对一等价关系.

利用等价的EB方案, 可以方便地进行密钥速率的计算. 在渐近条件下, 以Bob端的数据为参考端(反向协调), 安全密钥速率的计算公式为^[44]

其中${I_{{{AB}}}}$是Alice和Bob之间的香农互信息; ${\chi _{{{BE}}}}$是Holevo边界, 代表Eve可以从Bob端的数据获取的最大信息量; $\beta $代表数据协调效率.

密钥速率计算的关键是推导出量子态传输过程中系统的协方差矩阵. 起始的EPR态${\rho _{A{B_0}}}$, 对模式${B_0}$进行相位压缩后得到量子态${\rho _{AS}}$, 它的协方差矩阵可以表示为

这时模式$S$的相位正交分量方差为1, 即一个散粒噪声单元. 模式$S$进一步通过量子信道, 发送给Bob, 得到模式${B_1}$, 相应的协方差矩阵变为

其中调制方差$ {V_{\text{M}}} = {V^2} - 1 $, $ {\chi _{{\mathrm{linex}}}} = {{\left( {1 - {T_x}} \right)} {/ } {{T_x}}} + {\varepsilon _x} $代表量子态在正交振幅方向上由信道引入的总噪声(相对于信道的输入端), $ V_y^{{B_1}} $代表模式${B_1}$在正交相位方向上的方差, $ C_y^{{B_1}} $代表模式$A$和${B_1}$在正交相位方向上关联.

在接收端, 模式${B_1}$通过分束器之后, 变为模式$B$. 协方差矩阵$ {{\boldsymbol{\gamma}} _{AB}} $具有如下形式:

其中$ {\chi _{{\mathrm{totx}}}} = {\chi _{{\mathrm{linex}}}} + {\chi _{\hom }}/{T_x} $是相对于信道输入端, 量子态在正交振幅方向上系统引入的总噪声; $ {\chi _{\hom }} = {{\left( {1 - \eta } \right)} {/ } \eta } + {\nu _{{\text{el}}}}/\eta $是相对于Bob输入端, 由于探测器的不完美引入的噪声; $ V_y^B = \eta \left( {V_y^{{B_1}} + {\chi _{\hom }}} \right) $和$ C_y^B = C_y^{{B_1}}\sqrt \eta $是量子态在正交相位方向上的方差和关联.

可以求得互信息${I_{{{AB}}}}$为

Holevo边界${\chi _{{{BE}}}}$定义为

其中$S(\rho )$是量子态$\rho $的冯诺伊曼熵. 基于Eve的纯化, 系统${\rho _{A{B_1}{{E}}}}$为纯态, 有$S({\rho _{A{B_1}}}) = S({\rho _{{E}}})$. 在Bob端进行探测之后, $\rho _{{{ARHE}}}^{{x_B}}$是纯态, 有$S(\rho _{{E}}^{{x_B}}) = S(\rho _{{{ARH}}}^{{x_B}})$. 所以${\chi _{{{BE}}}}$可以进一步写为

其中$g\left( x \right) = \left( {x + 1} \right){\log _2}\left( {x + 1} \right) - x{\log _2}x$.

${\lambda _{1, 2}}$是量子态${\rho _{A{B_1}}}$对应的协方差矩阵$ {{\boldsymbol{\gamma}} _{A{B_1}}} $的辛本征值, 表示为

其中

${\lambda _{3, 4, 5}}$是量子态$\rho _{{{ARH}}}^{{x_B}}$对应的协方差矩阵${\boldsymbol{\gamma}} _{{{ARH}}}^{{x_B}}$的辛本征值, 表示为

其中

基于以上结果, 可以计算密钥速率. 对于上述未知参数$ C_y^{{B_1}} $和$ V_y^{{B_1}} $, $ V_y^{{B_1}} $可以通过在Bob端随机地探测量子态的正交相位分量来估计, 而$ C_y^{{B_1}} $不能被估计, 因为在Alice端起始的量子态在正交相位分量上没有调制. 窃听者Eve可以通过操控$ C_y^{{B_1}} $执行攻击, 然而它的攻击必须符合基本的物理原则. 因此, 未知参数$ C_y^{{B_1}} $可以利用海森伯不确定关系进行限制.

根据海森伯不确定关系, 一个高斯态是物理态, 则其协方差矩阵${\boldsymbol{\gamma}} $必须满足^[66]:

其中

因此, 参数$ C_y^{{B_1}} $和$ V_y^{{B_1}} $可以被限制, 通过如下关系式:

得到抛物线方程:

其中

在理论仿真中, 对于一个固定$ V_y^{{B_1}} $, 可以通过扫描$ C_y^{{B_1}} $, 找到一个$ C_y^{{B_1}{{\mathrm{opt}}} } $, 使得协议的密钥速率最低, 这个密钥率是可获得的安全密钥率^[44,45,50].

上述密钥率的计算基于一个假设, 态的制备过程是完美的. 然而在协议的实际实施过程中, 当Alice准备相干态时, 不可避免地会产生一些误差, 如光源强度误差. 如图2, 实际的光脉冲强度$ I' $随着时间$t$进行变化, 这使得准备发送的目标相干态和实际制备的相干态有偏差.

通过对协议运行中的实际源强度误差建模, 有两种误差来源: 一种是由于源器件(调制器或衰减器)的不精确校准引起的强度偏置; 一种是由于源脉冲强度的不精确控制导致的强度波动. 假设发送者Alice原本打算使用强度为$ I $的信号脉冲光制备一系列相干态, 但在任何时刻${t_i}$, 她实际使用的信号脉冲光强度为$ {I'_i} = I\left( {1 + \varphi } \right)\left( {1 + {\delta _i}} \right) $. $ \varphi $代表强度偏置, 因为在每一轮QKD的传输中, 它的漂移比较缓慢, 可以被视为一个常数. $ {\delta _i} $是强度波动, 其均值为0, 方差为${V_{\text{f}}}$. 由于现实中强度波动的方差远小于调制方差, 因此, 经过调制之后量子态的正交振幅仍然可以近似为高斯分布. 因为$I \propto {\left| \alpha \right|^2}$, Alice实际编码的高斯随机变量是

制备的量子态经过量子信道传输到Bob端, 进行探测后得到:

其中${t_x} = \sqrt {\eta {T_x}} $; ${z_x}$代表噪声项, 服从均值为零, 方差为$\sigma _x^2 = 1 + \eta {T_x}{\varepsilon _x} + {\nu _{{\text{el}}}}$的高斯分布.

下面我们对Alice的能力制定不同的假设, 以适应于各种现实情况, 并提出不同的数据处理方案来保证协议在各种情况下的安全性. 而我们对窃听者(Eve)的能力没有进行任何限定, 即考虑最差的情况, 假设Eve知道每个脉冲的强度边信息.

首先给出最强假设, 也就是Alice知道每个脉冲的强度边信息. 此情形下, 从理论上来说, Alice完全有能力对每个脉冲的误差进行精准校正, 例如对光源进行实时反馈控制. 但这样做会使系统的复杂程度大幅提升, 同时也会增加成本投入. 于是, 我们提出一种新的方案, 即在不增添任何硬件设备的前提下, 仅仅借助简单的数据后处理手段, 可以对安全密钥率进行估算. 具体的操作方法是, 依据强度边信息, Alice直接对她手头的数据$ {x_{{A}}} $做出相应调整, 使其变为$ {x'_{{A}}} $. 如此一来, 信道参数可以被正确估计, 最终的密钥率表达为

其中$ f\left( {{\delta _i}} \right) $是$ {\delta _i} $的概率密度函数, $ {V_{\text{M}}}_i = \left( {1 + \varphi } \right)( 1 + {\delta _i} ){V_{\text{M}}} $. 不难发现, 经过数据修正之后的密钥率近似于理想情况(没有源误差)的密钥率.

在一般情况下, Alice并不能掌握每个脉冲的强度边信息, 在此假定她仅仅了解脉冲强度变化的统计分布情况. 比如, 在QKD正式启动运行前的测试阶段, 对未知参数$ \varphi $和$ {\delta _i} $实施评估. 下面, 我们考虑$ {\delta _i} $的两种常见分布形式: 高斯分布和均匀分布.

为了得到密钥率, Alice和Bob需要公开部分数据对信道参数${T_x}$, ${\varepsilon _x}$进行估计, 假设Alice使用记录的数据$ {x_{{A}}} $进行估计, 那么:

对函数$ \sqrt {1 + {\delta _i}} $在$ {\delta _i} = 0 $附近实施泰勒展开, 从而获得

定义$ {T_{\text{f}}}: = {\left( {1 - {{{V_{\text{f}}}} {/ } 8}} \right)^2} $, 则估计的信道传输效率$ {T'_x} $为

对于额外噪声${\varepsilon '_x}$的精确表达, 可依据下述等价关系实现. 设想起始相干态已被理想制备, 即不存在源误差, 当该相干态经由量子信道$ {T'_x} $, $ {\varepsilon '_x} $完成传输后, Bob所得到的探测结果$ {x'_B} $可重新表示为

此时,

Bob端得到的$ V\left( {{x'_{B}}} \right) $为

建立上述两个方程的等价关系, 得到:

经过简单的代数运算, 得到:

最终得到估计结果为

当源端存在向下强度偏置(即$\varphi \lt 0$)的情况下, 这时:

信道传输效率被低估, 额外噪声被高估, 进而致使估计的密钥率降低, 不过此情形下并不存在安全隐患.

当源端存在一个向上的强度偏置, 即$\varphi \gt 0$, 这时, 信道传输效率可能被高估, 额外噪声被低估, 导致估计的密钥率增加. 由于Eve掌握强度边信息, 其能够利用被低估的噪声, 实施特定的攻击, 比如截取重发攻击, 使得估计的总额外噪声与原始额外噪声数值相等, 以此隐匿攻击行为, 最终引发安全漏洞. 为了避免这个安全漏洞, Alice可以对其所持有的原始数据$ {x_{A}} $予以修正, 得到修正后的数据$ \sqrt {\left( {1 + \varphi } \right)} {x_A} $, 并以此数据进行参数估计, 得到:

这时, 对于$\varphi \lt 0$, 可以得到相比于之前更好的参数估计结果. 而对于$\varphi \gt 0$, 信道传输效率总是被低估, 额外噪声总是被高估, 因此以上提及的潜在安全漏洞可以被克服.

考虑到强度波动$ {\delta _i} $, 由于Eve掌握强度边信息, Alice和Bob只能采用低强度信号脉冲光提取密钥^[65]. 因此, Alice可以进一步扩大自己手中的数据, 以获取更多的低强度脉冲用于密钥提取. 假设Alice进一步调整她的数据为$ \sqrt {\left( {1 + \varphi } \right)d} {x_{A}} $, 其中$ d \geqslant 1 $. 然后, Alice发送低强度信号脉冲的概率为

这时, 参数估计结果为

最终可获得的密钥率为^[64,65]

其中$ \left( {1 - P} \right)H\left( {x_B} \right) $代表不可以用于提取密钥的信息熵(高强度脉冲光). 当$ d $越大时, 则可用于提取密钥的信号数量越多. 然而, 与此同时, 信号传输过程中的损耗估计值以及额外噪声估计值也会相应增大. 因此, 存在一个最佳参数$ {d^{{\text{opt}}}} $使得协议的密钥率达到最大值, 这个可以通过搜索得到.

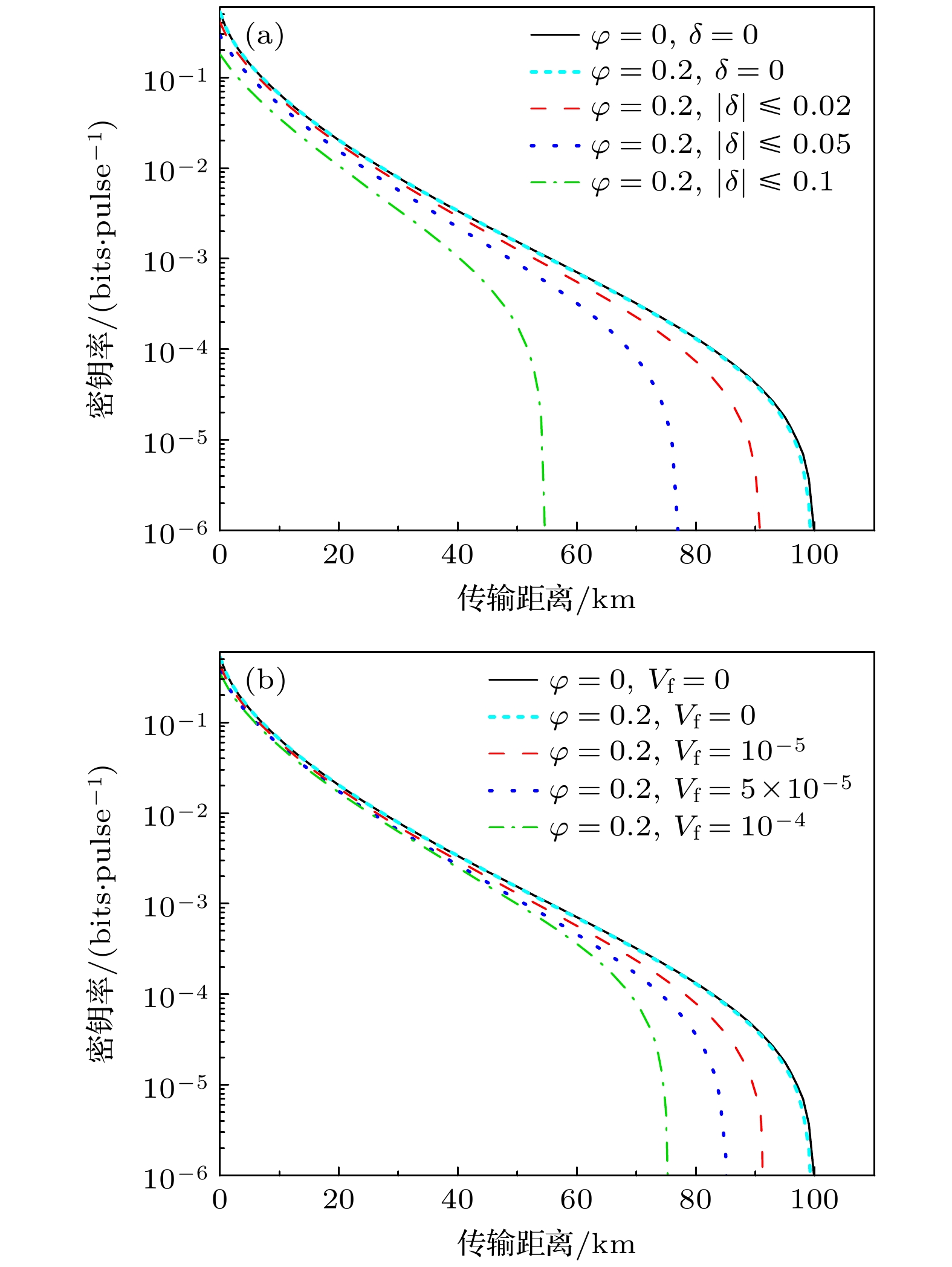
接下来分析不同的源强度误差对协议密钥率的影响. 涉及的仿真系统参数分别设定为$ \beta = 0.{97} $, $ {\varepsilon _x} = 0.03 $, $ \eta = 0.6 $, $ {\nu _{{\text{el}}}} = 0.1 $. 为了公平比较, 采用最优的调制方差$ V_{\text{M}}^{{\text{opt}}} $和$ {d^{{\text{opt}}}} $. 考虑经典的对称的信道, 则$ {T_y} = {T_x} $, $ {\varepsilon _y} = {\varepsilon _x} $, 这时: $ V_y^{{B_1}} = 1 + {T_x}{\varepsilon _x} $. 图3展示了在不同强度偏置和强度波动下, 密钥速率随着传输距离的变化情况. 图3(a)是均匀分布强度波动的结果, 以$ {\delta _i} $的绝对值表示波动范围. 图3(b)是高斯分布强度波动的结果, 以$ {\delta _i} $的方差${V_{\text{f}}}$表示波动强弱. 黑色实线代表没有源强度误差的密钥率. 分析图3可以发现, 在Alice优化调整自身的数据之后, 几乎可以消除光源的强度偏置对协议的影响. 对于一个较大的强度偏置$\varphi = 0.2$, 密钥率几乎没有变化. 这是因为, 经过数据后处理之后, 强度偏置对参数估计结果的影响较小. 强度波动对协议的性能影响较大, 随着波动强度的增加, 协议的密钥率和传输距离快速减少. 说明在协议的实际实施过程中, 源误差不能被忽略不计. 因此, 在协议的实际实施过程中, 必须充分考虑源误差的影响, 并采取相应的措施来减少或消除这些误差.

接下来, 我们探讨一种极端情形, 即不对信号源强度变化的具体概率分布做任何预设假设, 仅假定Alice知晓强度变化范围的上下边界. 具体而言, 假定Alice所对应的信号源脉冲强度变化区间为$ \left[ {{I^{\text{L}}}, {I^{\text{U}}}} \right] $, $ {I^{\text{L}}} $和$ {I^{\text{U}}} $分别代表上下边界. 因为概率分布的具体形式未知, 我们无法像之前的情况那样直接量化Eve可能窃取的信息量. 但是, Alice和Bob可以从低强度脉冲提取密钥. 为了简化, 设定$ I' = gI $, 则$ {I^{{\text{L}}\left( {\text{U}} \right)}} = {g^{{\text{L}}\left( {\text{U}} \right)}}I $. Alice可以采取一种策略: 将她的原始数据$ {x_{A}} $直接调整为上边界值$ \sqrt {{g^{\text{U}}}} {x_{A}} $, 并基于这些调整后的数据进行参数估计和密钥提取. 这种做法的合理性在于, 即便在强度变化范围的最大值处, 协议仍然能够保持其安全性.

当Alice和Bob使用修订后的数据$ \sqrt {{g^{\text{U}}}} {x_{A}} $进行参数估计时, 我们有

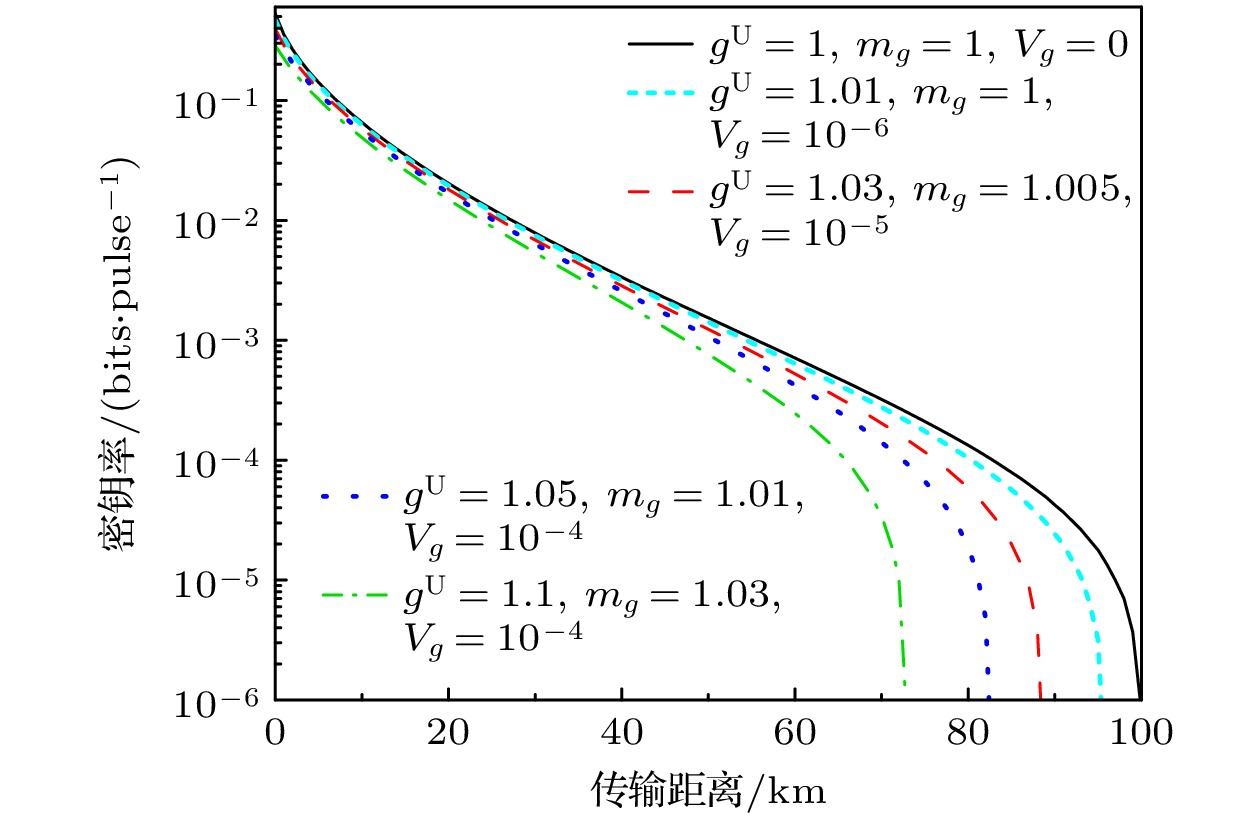
其中$ {T_g} = {m_g}{\left( {1 - {{{V_g}} {/ } {8 m_g^2}}} \right)^2} $, $ {m_g} $和$ {V_g} $是强度变化因子$ g $的固有均值和方差. 最终的密钥率可表达为

图4给出了不同源强度误差下, 协议密钥率随着传输距离的变化情况. 其他参数设定为$ \beta = 0.{97} $, $ {\varepsilon _x} = 0.03 $, $ \eta = 0.6 $, $ {\nu _{{\text{el}}}}=0.1 $. 采用最优调制方差以最大化密钥率. 黑色实线代表没有源强度误差的密钥率. 随着波动区间范围($ {g^{\text{U}}} $)的扩大, 密钥率和传输距离减少. 在短距离处, 影响较少, 但随着传输距离的增加, 影响逐级放大.

在协议的实际实现中, 由于硬件限制、存储容量和计算复杂度等原因, Alice和Bob之间交换的信号总数总是有限的. 接下来, 我们考虑有限码长情形下, 一维连续变量密钥分发协议源误差的影响. 在有限码长场景中, 由于统计波动的影响, 在源误差的基础上, 必须考虑期望值与实际观测值之间可能存在的最大差异. 假设在协议执行期间, Alice与Bob交换的总信号数量记作$N$, 其中$ n $个信号被专门用于密钥的提取, 而剩余的$N - n$个信号则用于系统参数的估计, 密钥速率的计算公式变为^[45]

其中$I_{{{AB}}}^{{\delta _{{\text{PE}}}}}$和$ \chi _{{{BE}}}^{{\delta _{{\text{PE}}}}} $是包含统计波动的互信息和 Holevo边界; $ {\delta _{{\text{PE}}}} $代表参数估计失败的概率; $ \varDelta (n) $是与私密放大有关的修正项, 定义如下:

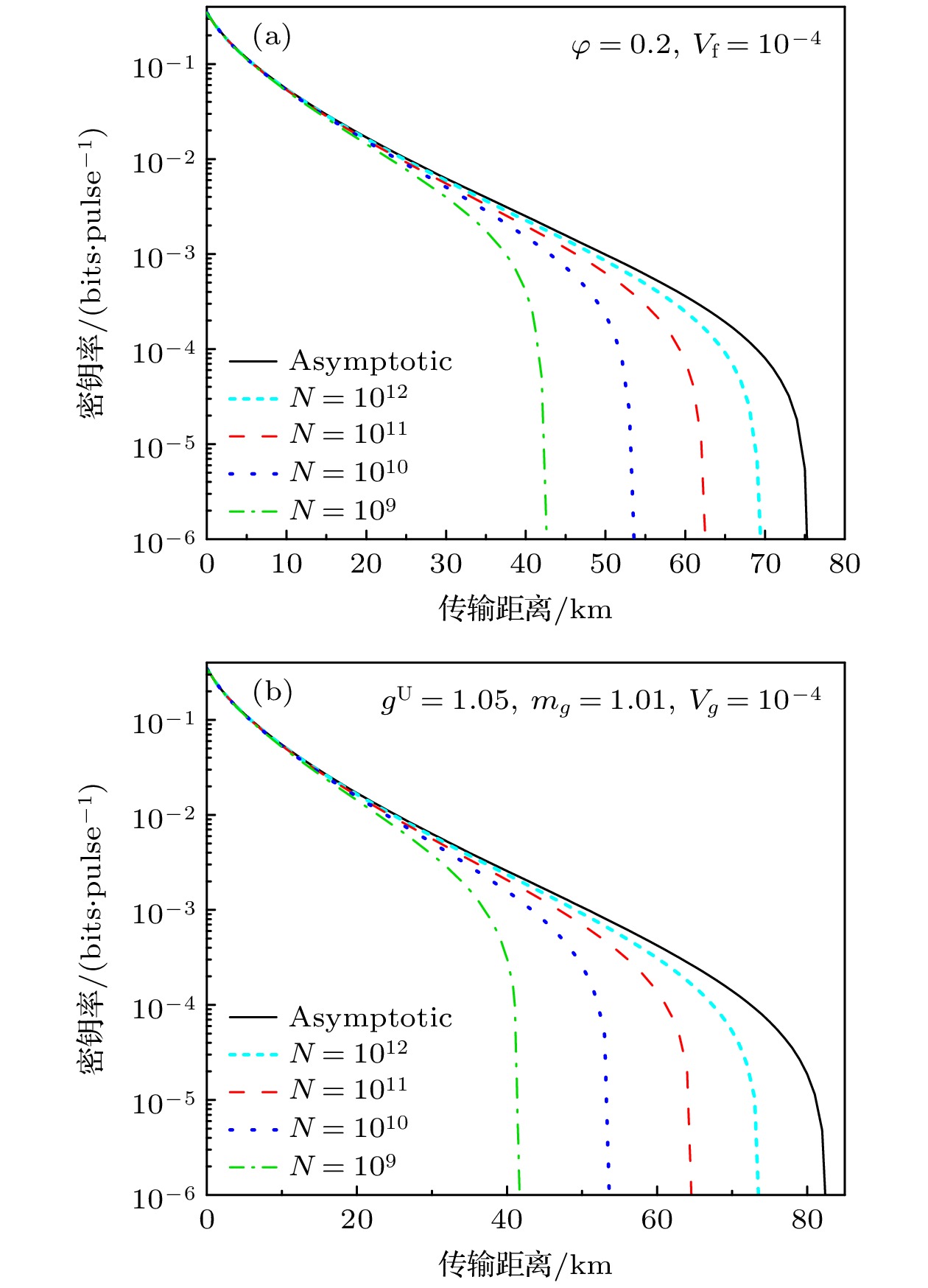
在UD协议中, 除了要估计正交振幅方向上的信道参数$ {T_x} $和$ {\varepsilon _x} $, 还要估计正交相位方差$ V_y^{{B_1}} $. 假设用$ m $关联数据估计信道参数$ {T_x} $和$ {\varepsilon _x} $, 用$ l $数据估计相位方差$ V_y^{{B_1}} $. 在源误差的基础上, 由于统计波动, 参数的估计值和真实值有偏差. 为了保证协议的安全性, 我们考虑最糟糕情况, 采用参数估计边界值, 得到^[45]:

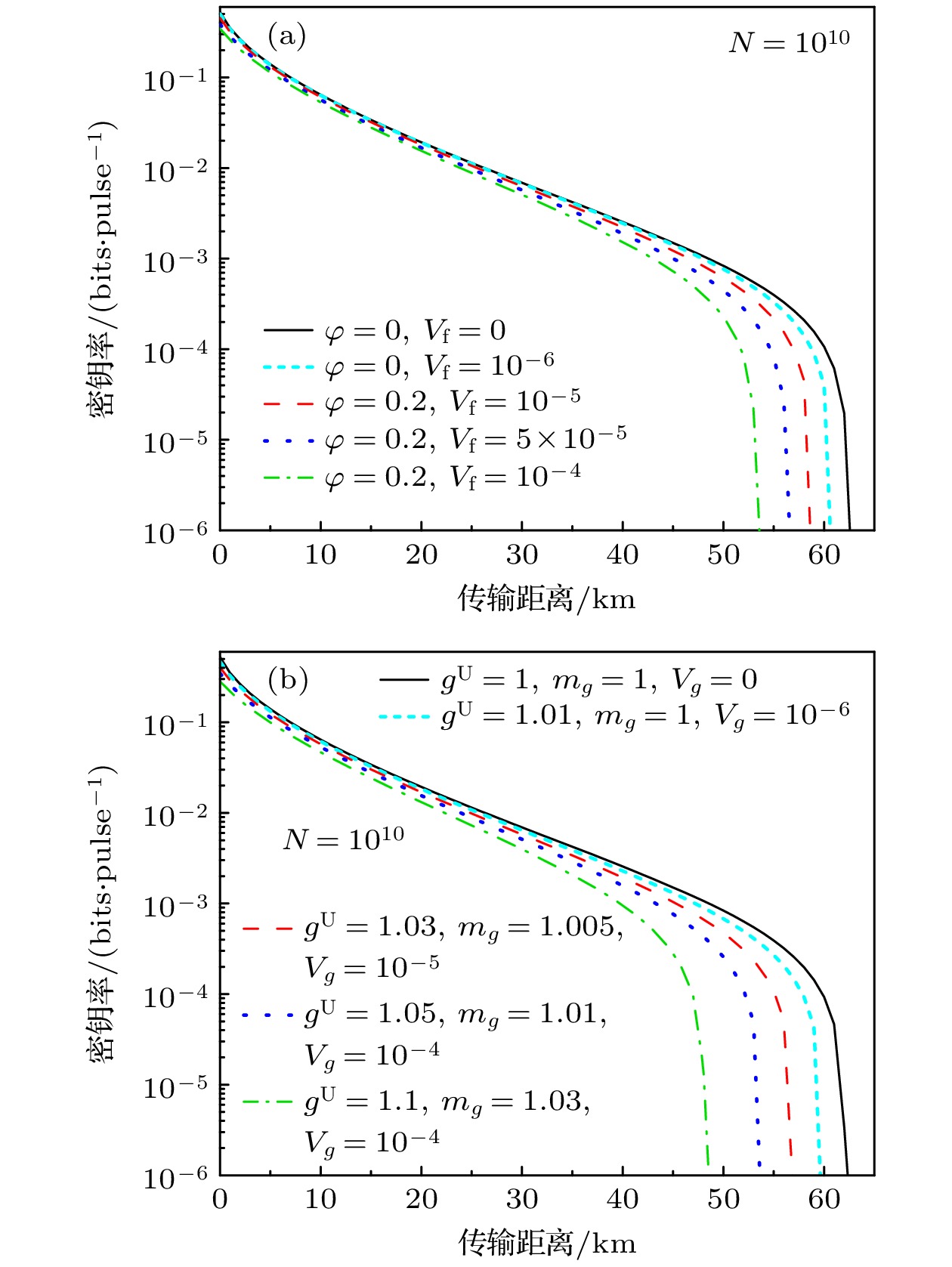
同时考虑源误差和有限码长, 图5对比了不同码长下, 协议的密钥率随着传输距离的变化. 图5(a)代表第二种源误差模型, Alice只知道信号源强度变化的统计分布, 考虑强度偏置$\varphi = 0.2$和具有方差$ {V_{\rm f}} = {10^{ - 4}} $的高斯分布统计波动. 图5(b)代表第三种源误差模型, Alice只知道信号源强度变化的上下边界, 设定源误差参数: ${g^{\mathrm{U}}} = 1.05$, ${m_g} = 1.01$, ${V_g} = {10^{ - 4}}$. 从图5可以发现, 有限码长限制了协议的密钥率和传输距离. 随着信号数量的减少, 可用于参数估计的数据量减少, 产生更大的估计误差, 导致密钥率和传输距离显著减少. 同时, 私密放大步骤也受到限制, 因为需要更多的原始密钥比特来生成相同数量的安全密钥比特. 在源误差存在时, 有限码长效应更加明显, 因为此时可用于参数估计的样本数量有限, 误差的累积导致密钥率的显著下降.

为了进一步研究有限码长下源强度误差的影响, 仿真了信号源脉冲数量$N = {10^{10}}$条件下, 不同强度误差对应的协议密钥率和传输距离, 结果如图6所示. 图6(a)是第二种情况下不同高斯分布源强度波动模型. 图6(b)是第三种情况下不同源误差模型. 从图6可以发现, 尽管有限码长限制了协议的密钥率和传输距离, 但在不同的源误差条件下, 协议仍然是可行的. 对于$N = {10^{10}}$码长, 较大的源误差$\varphi = 0.2$, $ {V_{\text{f}}} = {10^{ - 4}} $, 45 km下可得到大约0.001 bit/pulse的安全密钥率.

本文研究了UD CV-QKD在源强度误差下的现实安全性和性能表现. 结果表明, 源误差对系统的安全性和性能产生了显著影响. 源强度误差可能会为潜在的窃听者提供额外的信息, 从而增加系统的安全性风险. 为了提升协议的现实安全性和减少源误差的影响, 针对不同的现实条件, 提出了不同的数据优化方案. 同时, 研究了有限码长下, 源误差对协议的影响, 验证了具有源强度误差UD CV-QKD的可行性, 为现实环境下UD CV-QKD的安全实施提供了理论依据.

下一步研究, 可以探索更加精确的源误差模型和更高效的数据优化方法, 以提高UD CV-QKD系统的安全性和性能表现. 也可以考虑将UD CV-QKD技术与其他量子通信技术相结合, 以构建更加安全、高效和可靠的量子通信网络系统.