-
安德森局域化现象自1958年首次提出后一直是凝聚态物理领域的研究热点[1]. 当物质波在无序介质中传播时, 系统的波函数被局域在空间中无法扩散, 称为局域态[2,3]; 相反地, 若波函数是分布在整个系统中的, 称为扩展态; 而处于两者之间的状态称为多重分形态[4], 多重分形态不同于经典的局域态和扩展态, 它具有扩展但不遍历的特点. 此外, 迁移率边[5-7]是理解无序系统中电子行为的又一重要概念, 它是一种分离扩展态与局域态的临界能量[8-11]. 通过对迁移率边的研究, 可以深入了解无序系统中的电子行为、相变过程以及材料的导电性等复杂的物理现象. 无序系统中一个最为著名的模型是一维Anbry-André (AA)模型, 它展示了由自对偶性质所导致的所有本征态从扩展态到局域态的转变. 然而此模型中并不存在迁移率边. 随后人们通过引入能量依赖的自对偶机制设计出具有精确迁移 率边的各种广义AA模型, 如具有长程跃迁项的AA模型[12]以及具有特殊在位势的AA模型等. 王玉成等[13]利用数学工具精确地求解了一类马赛克准晶体系, 极大地扩充了具有精确迁移率边的准晶家族. 近些年来, 随着非厄米系统研究的兴起, 人们开始关注无序与非厄米效应的结合, 发现诸如非厄米迁移率边[14,15]、非厄米多体局域化[16]以及非厄米拓扑安德森绝缘体[17]等有趣现象. 非厄米系统因其与厄米系统的显著差异, 为局域化现象的研究开辟了新的方向. 在广义非厄米AA模型中, 发现了局域化转变、实复转变和拓扑相变之间的一致性. 与传统的Anderson模型的局域化不同, 在一维随机无序的非互易Hatano-Nelson模型[18,19]中, 非互易性导致系统在无序环境中出现由扩展相到局域相的转变. 这些现象为非厄米系统的研究提供了新的视角和思路.
在近几十年, 研究封闭系统中的非平衡动力学已经取得了巨大的发展[20,21]. 特别是, 人们在周期驱动系统中发现了很多非驱动系统中所没有的新奇现象[22,23], 例如驱动导致的拓扑量子相变[24-26]、动力学相变[27-29]、时间晶体[30]以及弱遍历性破坏的行为[31,32]等. 对于周期系统来说, 很多现象可以通过分析它们的Floquet哈密顿量
$ H_{\mathrm{F}} $ 来完成, 其演化算符为$ U(T, 0)=\exp[-{\mathrm{i}}H_{\mathrm{F}}T] $ , 这里$ T=2\pi/\omega $ ,$ \omega $ 为驱动频率[33-36]. 近期, Sarkar等[37,38]研究了跃迁项周期驱动的AA模型中的退局域-局域转变. 他们发现周期驱动跃迁项可以导致迁移率边、多重分形态以及CAT态(在质心附近密度分布存在两个局域的峰, 且两个峰值展现等权叠加的特性)的出现, 而这些现象在标准的AA模型中并没有被探测到. 可以发现, 周期驱动方法是研究系统局域化性质的新颖手段. 受到Sarkar的启发, 本文将这一驱动方案应用到非厄米AA模型中讨论其相应的局域化性质, 为系统局域化特性的研究注入了新方法, 同时也为周期驱动技术的应用拓宽了视野. -
本文采用方波式驱动方案来周期驱动一个具有准周期调制的非互易的AA模型, 如图1, 其哈密顿量
$ H(t)=H_0(t)+V $ , 其中动能项势能项
式中,
$ c_{j}^{\dagger}(c_{j}) $ 为费米子在第$ j $ 个格点的产生(湮灭)算符,$ h $ 用来表征非互易强度,$ \mu $ 为在位势的强度,$ \eta $ 控制在位势的调制频率. 当$ \eta $ 为无理数时, 系统为准晶系统, 通常设$ \eta=(\sqrt{5}-1)/2 $ . 当跃迁强度$ {\mathcal{J}(t)}=J $ 不依赖时间时, 系统哈密顿量退化为非互易的AA模型. 在周期边界条件下, 当$ \mu<J{\mathrm{e}}^{|h|} $ 时, 系统中所有的本征态都为扩展态, 相应的能谱都为复数, 而当$ \mu>J{\mathrm{e}}^{|h|} $ 时, 所有的本征态都变为局域态, 相应的能谱都为实值. 可以看出, 这个非互易的AA模型和厄米的AA模型类似, 也不存在迁移率边. 在$ \mu=J{\mathrm{e}}^{|h|} $ 处存在扩展-局域的相变. 本文采用方波式周期驱动方案要求为了数值找到任意频率下的Floquet谱, 首先利用精确对角化找到非厄米哈密顿量
$ H_{\pm}=H[\pm J] $ 的谱和双正交基. 定义$ H_{\pm} $ 的左和右本征态分别为$ |\phi^{{\mathrm{L}}\pm}_p\rangle $ 和$ |\phi^{{\mathrm{R}}\pm}_p\rangle $ , 即$ H_{\pm}|\phi^{{\mathrm{R}}\pm}_p\rangle = \varepsilon_p^{\pm}|\phi^{{\mathrm{R}}\pm}_p\rangle $ 和$ H^{\dagger}_{\pm}|\phi^{{\mathrm{L}}\pm}_p\rangle = \varepsilon_p^{\pm*}|\phi^{{\mathrm{L}}\pm}_p\rangle $ , 且具有双正交性,$ \langle \phi^{{\mathrm{L}}\pm}_p|\phi^{{\mathrm{R}}\pm}_q\rangle=\delta_{pq} $ , 从而可以获得在$ t=T $ 时刻的演化算符[39]其中,
$ c_{pq}=\langle\phi_p^{{\mathrm{L}}+}|\phi_q^{{\mathrm{R}}-}\rangle $ . 利用数值对角化$ U(T, 0) $ , 可以获得其本征值$ \lambda_n={\mathrm{e}}^{-{\mathrm{i}}\varepsilon_{n}^{{\mathrm{F}}}T} $ 和本征态$ |\psi_n\rangle $ . 这里, 本征能量和本征态同时满足$ H_{\mathrm{F}}|\psi_n\rangle=\varepsilon_n^{\mathrm{F}}|\psi_n\rangle $ . 通过研究Floquet哈密顿量$ H_{\mathrm{F}} $ 的本征能谱$ \varepsilon_{n}^{{\mathrm{F}}} $ 和本征态$ |\psi_{n}\rangle $ 可以等效地描述周期驱动系统的局域化性质.引入逆参与率和分形维度
$ D_{q} $ 两个序参量来表征系统的局域化特征. 广义的逆参与率定义为:$ I_ {n}^{(q)}= \displaystyle\sum\nolimits_{j=1}^{{{L}}}|\psi_{n}(j)|^{2 q} $ , 其中$ \psi_{n}(j) $ 表示粒子在第$ n $ 个本征态第$ j $ 个格点上所占据的概率幅. 当$ q=1 $ 时,$ I_{n}^{(1)}=|\psi_{n}(j)|^{2} $ 表示波函数的密度分布; 当$ q=2 $ 时,$ I_{n}^{(2)}=|\psi_{n}(j)|^{4} $ 为逆参与率 (IPR). 由于$ I_{n}^{(q)}\sim L^{-\tau_{q}} $ (这里$ \tau_{q} $ 为缩放指数), 由此给出分形维度的定义为$ D_ {q} = {\tau_{q}}/({q-1}) $ . 对于局域态,$ D_{q}\to 0 $ , 即$ I_{n}^{(q)} $ 为一个不依赖尺寸的有限值. 而对于扩展态来说, 分形维度$ D_{q}\to 1 $ , 相应的$ I_{n}^{(q)} $ 在热力学极限下趋近于零. 而对于多重分形态,$ D_{q}\in(0, 1) $ , 其$ I_{n}^{(q)} $ 在热力学极限下趋于零. 此外, 还可以引入平均逆参与率(MIPR)$ \mathrm{MIPR}= \dfrac{1}{L}\displaystyle\sum\nolimits_{n=1}^{{{L}}}I_{n}^{(2)} $ . 通过标度分析来拟合平均逆参与率:$ \mathrm{MIPR}(1/L)=\tilde{a}\times({1}/{L})^{\tilde{b}}+\tilde{c} $ , 得到相应的拟合参数$ \tilde{a} $ ,$ \tilde{b} $ 和$ \tilde{c} $ . 对于完全局域化区域,$ \tilde{b}\to0 $ ,$ \tilde{c} $ 为有限值. 对于完全扩展区域,$ \tilde{b}\to 1 $ ,$ \tilde{c} $ 趋于0. 当系统中存在多重分形态时,$ \tilde{b}\in(0, 1) $ ,$ \tilde{c} $ 趋于0. 因此, 可以根据$ \tilde{a} $ ,$ \tilde{b} $ 和$ \tilde{c} $ 的取值对其局域化性质进行验证. 另外, 研究表明一些广义的非厄米AA模型中波函数的退局域-局域的转变与能谱的实复转变有一一对应的关系. 全文讨论采用周期边界条件, 选取跃迁强度$ J $ 为能量单位, 即$ J=1 $ , 非互易参数$ h=0.1 $ , 并且考虑弱在位势的情况$ \mu/J=0.05 $ . 利用精确对角化方法计算和讨论Floquet哈密顿量的相关局域化性质. -
本文考虑
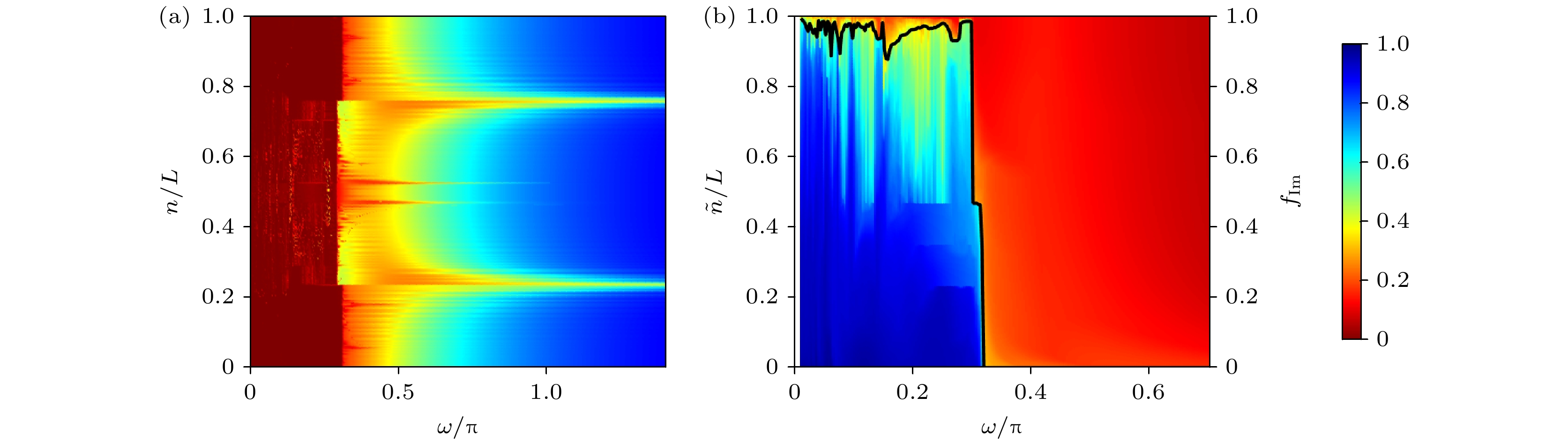
$ J\gg \mu $ 的情况, 这个两段式的驱动方法保证了在高频极限下,$ H_{\mathrm{F}}\approx \displaystyle\int_{0}^{T}H(t){\mathrm{d}}t/T=V $ , 其等效Floquet哈密顿量展现了一个局域相的特征. 相反地, 对于准静态驱动$ \omega\to 0 $ , Floquet本征态表现为扩展态的性质. 因此, 随着$ \omega $ 的变化驱动系统将表现出退局域-局域的转变特性[40]. 图2(a)展示了系统尺寸为$ L=2048 $ 时, 不同能级的逆参与率随着驱动频率$ \omega $ 变化的情况, 图中$ n $ 为能级指标, 能级按照本征能量的实部升序排列. 从图2(a)可以看到在$ \omega=\omega_{\mathrm{c}} \approx 0.318\pi $ 附近存在明显的退局域-局域转变. 当$ \omega > 0.318\pi $ 时, 几乎所有态的逆参与率为接近于1的有限值, 此时系统处于局域相. 在$ \omega < 0.318\pi $ 区域存在两种逆参与率的行为, 即部分态的逆参与率值为趋于0, 部分态为有限值, 表明此时系统中存在迁移率边. 为了进一步确定在驱动频率变化的过程中系统能态的局域化性质, 图2(b)展示了不同能量本征态的分形维度$ D_{2} $ 随着驱动频率$ \omega $ 的变化情况. 这里,$ \tilde{n} $ 为能级指标, 按照相应本征态的逆参与率的值升序排列. 从图2(b)可以看出当$ \omega>\omega_{\mathrm{c}} $ , 所有的本征态的分形维度$ D_2 $ 趋于0, 表明此时系统处于局域相. 而在驱动频率$ \omega $ 从0向$ \omega_{{\mathrm{c}}} $ 转变的过程中, 所有态的分形维度$ D_2 $ 都从趋于1开始, 随着驱动频率的增大, 高逆参与率值区域的本征态的分形维度逐渐减小, 且分形维度减小的区域也开始扩大. 直到趋于退局域-局域转变点附近区域, 可以看到在低逆参与率值的区间, 相应的分形维度$ D_2 $ 趋于1, 对应于扩展态, 在高逆参与率值部分, 存在分形维度$ D_2 $ 趋于0的局域态, 表明此时系统中存在迁移率边. 对于具有中间逆参与率值的本征态, 其分形维度值的分布在$ 0.5 $ 附近, 表明在此处的本征态可能为多分形态. 图2(b)黑色实线展示了系统的复能量占比$ f_{\mathrm{Im}}= N_{\mathrm{Im}}/L $ 随着调制频率$ \omega $ 变化的情况. 这里, 选取截断为$ 10^{-10} $ , 当$ |\mathrm{Im}(\varepsilon_{n}^{{\mathrm{F}}})|<10^{-10} $ , 被认为是机器误差, 并且$ N_{\mathrm{Im}} $ 为具有非零虚部的本征值的数目. 可以看到在低频区系统处于退局域区, 系统绝大多数本征谱为复值, 并且随驱动频率的增加$ f_{\mathrm{Im}} $ 略有减小. 而当$ \omega $ 超过$ \omega_{\mathrm{c}} $ , 此时系统进入到局域区, 所有的态都为局域态, 相应的$ f_{\mathrm{Im}}\to 0 $ . 值得注意的是, 可能的多重分形态所对应的能量为复值. 图中的黑色曲线与局域态和退局域态的边界基本一致, 表明能谱的实-复转变可以表征退局域-局域转变, 且系统中存在迁移率边.另一个值得注意的是, 在能级
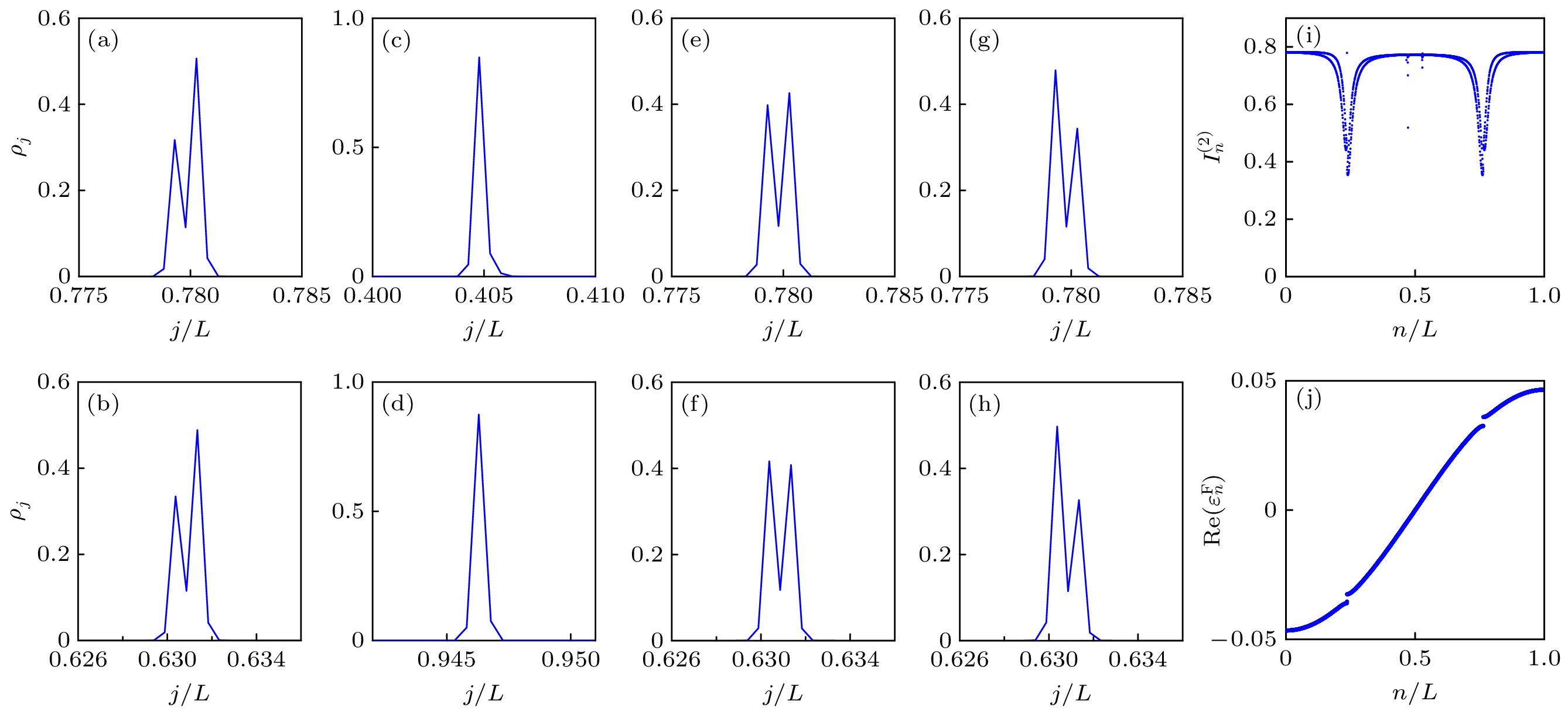
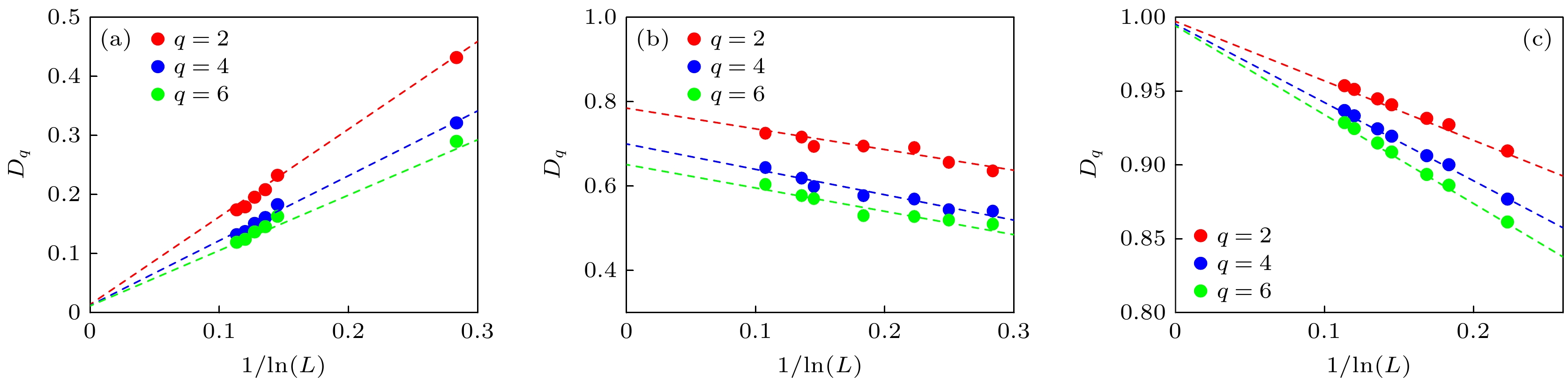
$ n/L\approx0.24 $ 和$ 0.76 $ 附近, 从局域化转变点附近开始向局域区深处延展出两条低逆参与率值的能量区域, 尽管它们的逆参与率值仍然为有限值, 但是明显比周围能态的值小. 图3(a)和图3(b)分别展示了在$ \omega=\pi $ 和$ h=0.1 $ 时, 位于能级$ n/L\approx 0.24 $ 和$ 0.76 $ 处波函数的密度分布$ \rho_{j}=|\psi_j|^2/\Big(\displaystyle \sum\nolimits_j |\psi_j|^2\Big) $ . 可以看到, 能级位于$ n/L\approx 0.24 $ 和$ 0.76 $ 处的密度分布展现出局域的特性, 然而不同于能谱中其他位置的局域态(如图3(c)和图3(d)中$ n/L=1/3 $ 和$ 1/2 $ 处局域态分布的情况), 它们展现了独特的分布结构, 由此造成它们具有更低的逆参与率值. 如图3(i)所示, 在$ n/L\approx 0.24 $ 和$ 0.76 $ 处逆参与率的值有一个明显的降低. 对比于厄米情况($ h=0 $ , 如图3(e)和图3(f)所示), 位于$ n/L\approx 0.24 $ 和$ 0.76 $ 处的密度分布表现为在质心附近两个峰值具有近等权叠加的特点, 被称为CAT态. 而$ h=0.1 $ 的情况, 质心附近两个峰值有着明显的差异, 即右峰明显比左峰高, 这一现象显然是由非互易效应引起的. 改变非厄米参数为$ h=-0.1 $ (如图3(g)和图3(h)所示), 可看出CAT态的峰值变化为左峰高于右峰. 由此可知, 通过调节非厄米参数可以改变CAT态的形式. 从图3(j)所示的$ \omega=\pi $ 和$ h=0.1 $ 时Floquet本征能量实部升序排列的情况来看, Floquet本征能量在局域区都为实能量,$ n/L\approx 0.24 $ 和$ 0.76 $ 位于能隙的位置, 原来有色散的能量在能隙附近逐渐变得平坦, 并且这一特征在$ \omega>\omega_{\mathrm{c}} $ 的区域一直存在. CAT态的存在和其处在能带中的平坦位置有着一定的联系. 在高频极限下, 首先考虑对于Magnus的一阶展开为$ H_{\mathrm{F}}\approx V $ . 因此,$ H_{\mathrm{F}} $ 几乎是对角的, 它的每个特征态都局域在一维链中的某个格点上. 非对角项只会在Magnus高阶展开中产生, 因此它们在高频极限下非常小. 多数情况下, 如果准能量彼此分离得很好, 这些非对角线项将不会改变Floquet谱的性质. 然而, 这一假设在$ n/L\approx 0.24,\; 0.76 $ 附近失效. 这是由于这两处局域态的准能量的能级差近似为零, 此时$ H_{\mathrm{F}} $ 中由$ H_{0} $ 引起的非对角线项虽然小却变得重要, 将导致相邻格点间的局域态发生杂化, 从而在能谱中产生CAT态. 又因为非互易效应的存在导致出现CAT态中的两个密度的非等权叠加. 因此, 这一现象只发生在高频情况下, 对于$ \omega\leqslant \omega_{{\mathrm{c}}} $ , 这一特征是不存在的. 此外, 观察图2(b)可以发现, 在$ \omega \leqslant \omega_{{\mathrm{c}}} $ 的一段频率范围内, 可能存在局域、扩展、多重分形三相共存的区域. 为了确定共存区的存在, 图4(a)—(c)选取$ \omega= 0.235\pi $ 时, 分别展示了$ \tilde{n}/L=0.995 $ ,$ 0.7 $ 和$ 0.2 $ 处的本征波函数对应于不同$ q $ 的分形维度$ D_q $ 随着系统尺寸$ L $ 变化的情况[41]. 可以看到, 对应于不同$ q $ 在$ \tilde{n}/L= 0.995 $ 处的本征波函数的分形维度$ D_q $ 在热力学极限下逐渐趋近于0, 表明此时波函数具有局域态的性质.$ \tilde{n}/L= 0.2 $ 处的波函数的分形维度$ D_q $ 会随着尺寸增大而趋近于1, 表明相应的波函数为扩展态. 而当$ \tilde{n}/L= 0.7 $ 时, 对应于不同$ q $ 的分形维度$ D_q $ 在热力学极限下均处于0和1之间, 很好地展现了多重分形的特点. 由此可见, 系统中存在三相共存的区域.为了进一步验证多重分形态的存在, 图5(a)展示了
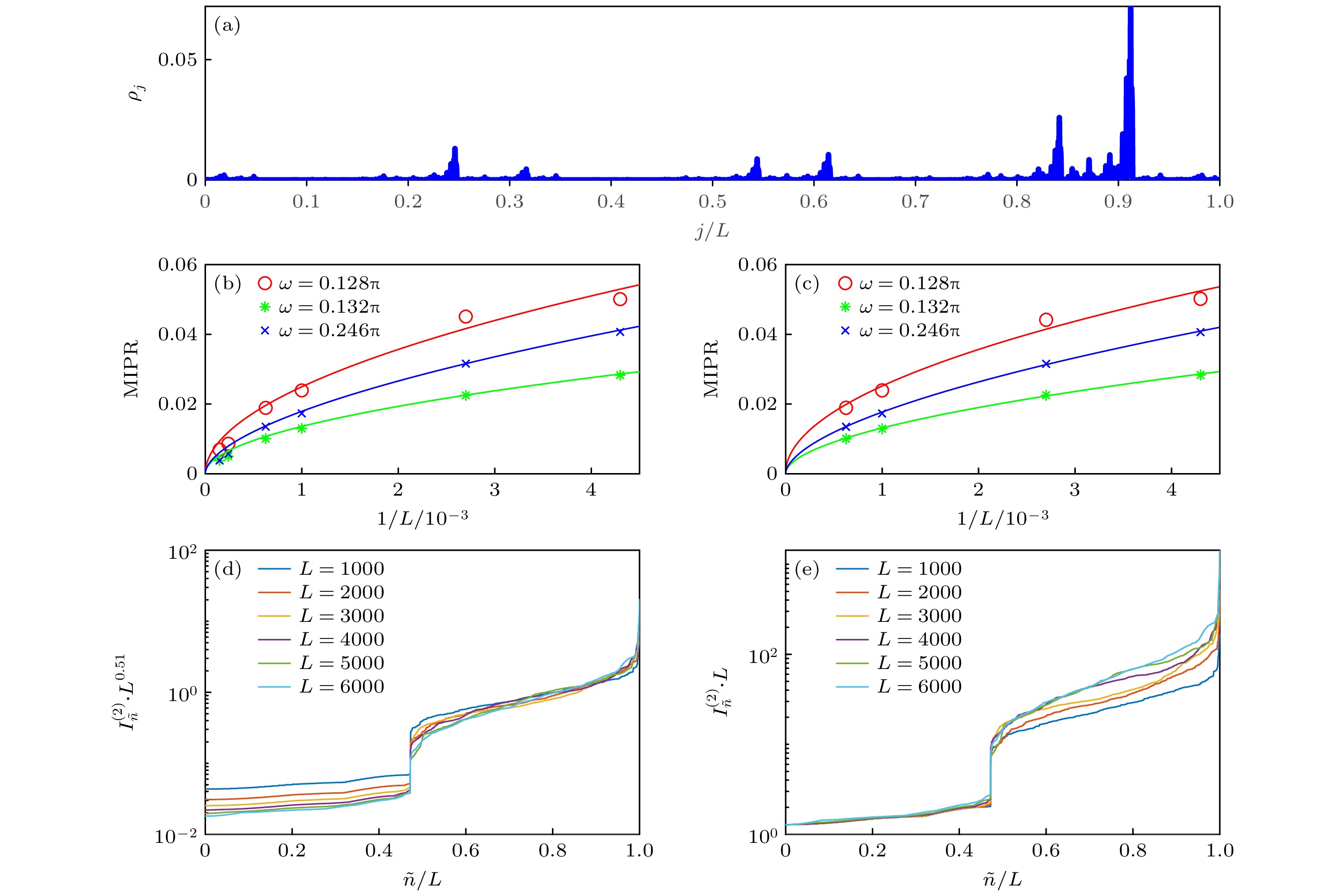
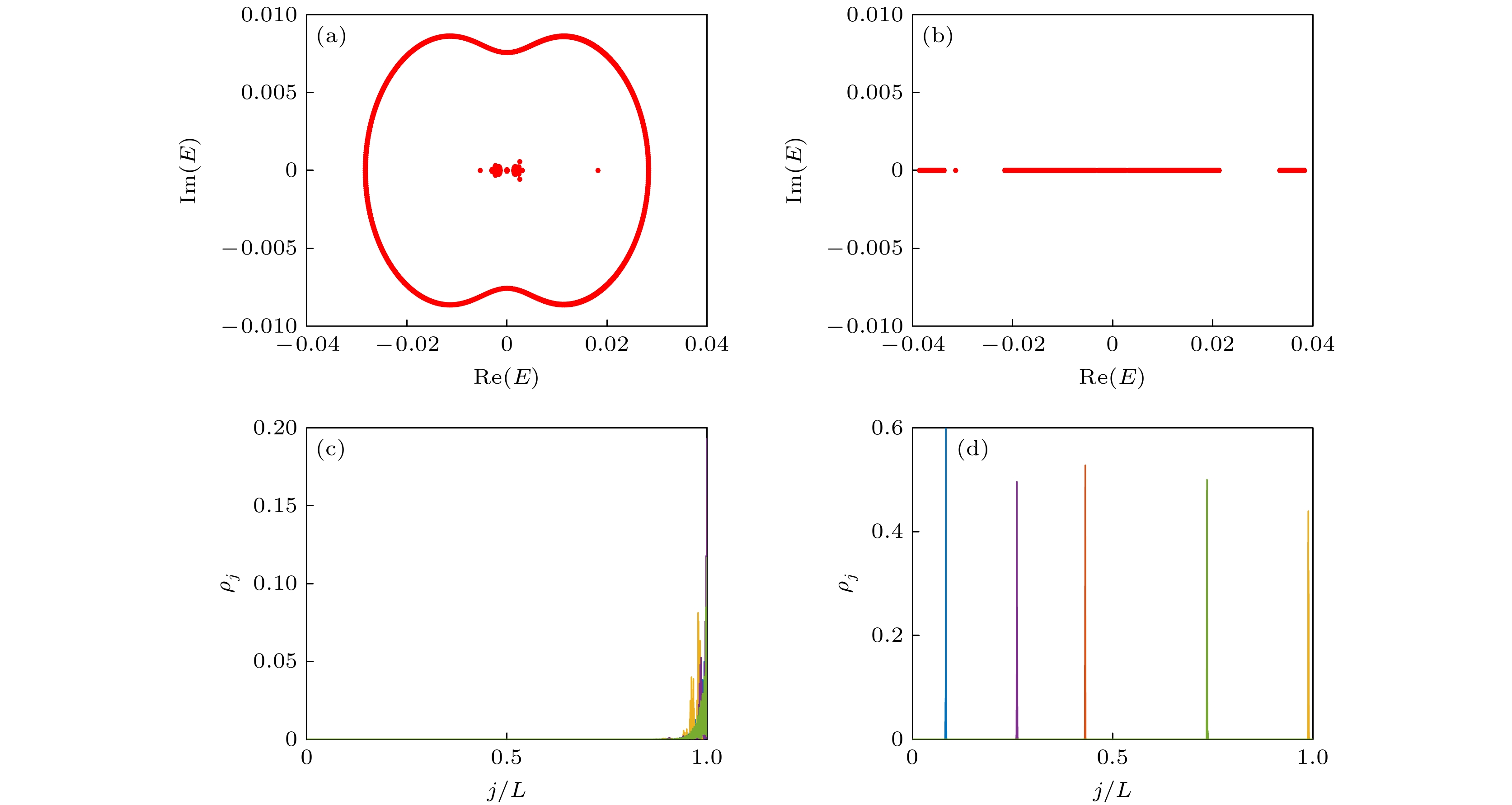
$ \omega=0.132\pi $ ,$ \tilde{n}/L=0.75 $ 处波函数的密度分布$ \rho_j $ , 此时波函数具有扩展但不遍历的特点, 符合多重分形态的特征. 图5(b)对处于存在多重分形区域的MIPR值进行标度分析. 当$ \omega=0.128\pi $ , MIPR标度的拟合参数$ \tilde{a}=0.8889 $ ,$ \tilde{b}=0.518 $ ,$ \tilde{c}\to 0 $ ; 当$ \omega=0.132\pi $ 时, MIPR标度的拟合参数$ \tilde{a}= 0.4693 $ ,$ \tilde{b}=0.514 $ ,$ \tilde{c}\to 0 $ ; 当$ \omega=0.246\pi $ 时, MIPR标度的拟合参数$ \tilde{a}=0.9392 $ ,$ \tilde{b}=0.5742 $ ,$ \tilde{c}\to 0 $ . 表明处于这些频率下, 系统中存在多重分形态. 而多重分形态是具有稳定性的, 图5(c)展示了图5(b) 频率下, 在$ h=0.1 $ 和$ \mu=0.05 $ 附近百分之一的偏差范围内, 随机选取20个数进行无序平均后得到的标度分析图. 当$ \omega=0.128\pi $ 时, MIPR标度的拟合参数$ \tilde{a}=0.8224 $ ,$ \tilde{b}=0.5055 $ ,$ \tilde{c}\to0 $ ; 当$ \omega=0.132\pi $ 时, MIPR标度的拟合参数$ \tilde{a}=0.5335 $ ,$ \tilde{b}=0.5375 $ ,$ \tilde{c}\to 0 $ ; 当$ \omega=0.246\pi $ 时, MIPR标度的拟合参数$ \tilde{a}=0.9509 $ ,$ \tilde{b}=0.5778 $ ,$ \tilde{c}\to 0 $ , 均符合多重分形态的特点, 表明其性质不随参数波动而变化, 进而验证了多重分形态在不同参数下的稳定性. 以频率$ \omega=0.132\pi $ 为例, 在图5(d)和图5(e)中分别展示了在不同尺寸下$ I_{\tilde{n}}^{(2)}\cdot L^{D_{2}} $ 随着$ \tilde{n}/L $ 的变化情况. 可以清晰地看到扩展态和多重分形态之间的边界[42]. 在图5(d)中选取$ D_{2}=0.51 $ , 可以看到, 对于$ \tilde{n}/L> 0.472 $ 的态, 在不同尺寸下,$ I_{\tilde{n}}^{(2)}\cdot L^{D_{2}} $ 都塌缩到一起, 表明这部分态具有多重分形的特征. 作为对比, 在图5(e)中选取$ D_{2}=1 $ , 不同尺寸下$ \tilde{n}/L< 0.472 $ 的态的$ I_{\tilde{n}}^{(2)}\cdot L $ 都塌缩到一起, 这部分态具有扩展态的性质. 由此可以很好地区分扩展和多重分形态的分界线.为了表征非厄米系统的拓扑性质, 在图6(a)和图6(b)中分别展示了处于不同局域相区能谱的特性. 当频率
$ \omega<\omega_{\mathrm{c}} $ ($ \omega=0.132\pi $ )时, 可以发现在具有多重分形态的退局域相中能谱在复空间表现为一个环状结构, 展现了非平庸拓扑特性. 在周期边界条件下密度分布如图5(a)所示, 展现多重分形的特点. 而在开边界条件下, 由于非平庸拓扑特性, 波函数聚集在右边界, 产生非厄米趋肤效应, 如图6(c)所示. 图6(b)展示了当频率$ \omega > \omega_{\mathrm{c}} ( \omega = 0.5\pi $ )时局域相的能谱图, 其中能量均为实值, 展现了拓扑平庸的特点. 从图6(d)可以看到, 在开边界条件下波函数仍然展现局域分布的特点. -
本文研究了周期驱动一个静止状态下处于扩展相的非互易AA模型, 发现通过改变周期驱动的频率可以发生退局域-局域的转变. 当驱动频率
$ \omega>\omega_{\mathrm{c}} $ 时, 系统处于局域相, 并且存在CAT态, 不同于厄米情况, 其本征态的分布存在两个非等权叠加的峰值, 这是由非互易效应导致的. 当$ \omega<\omega_{\mathrm{c}} $ 时, 系统处于退局域相. 驱动频率从0向$ \omega_{\mathrm{c}} $ 增加的过程中, 系统由所有的本征态都为扩展态, 逐渐转变为扩展、局域、临界共存的区域, 直到$ \omega_{\mathrm{c}} $ 处所有的态都变为局域态, 相应的退局域化态的能谱由复值变为最终都为实值, 即Floquet谱的实复转变与退局域-局域转变一致. 然而厄米AA模型中能量均为实值, 不存在实复转变, 并不能体现这一性质. 此外, 由于非厄米特性, 退局域相中波函数在开边界条件下会出现趋肤现象, 而厄米AA模型中并不具有, 体现了非互易模型的独特性. 如(1)式所示的周期驱动非互易AA模型可以利用经典电路的方法来实现. 通过方波电压诱导磁场周期性变化, 从而控制单刀双置开关接入两条分别代表$ H[\pm J] $ 的电路支路进而实现周期驱动[43]. 其中, 每条支路上的非互易耦合可以通过调节电路中电流型负阻抗变换器来实现. 而$ -J $ 的跃迁项可通过负阻抗模块来实现. 准周期势可通过精确调节含电感和电容的接地元件的阻值来实现. 本文通过研究周期驱动非互易准周期调制模型得到了丰富的物理现象, 为周期驱动无序体系提供了思路. 然而, 在干净系统当中也存在局域化现象如Stark模型, 对于周期驱动的Stark体系是否存在扩展到局域的转变以及多重分形态和迁移率边等现象, 值得进一步研究.
周期驱动非互易Aubry-André模型中的多重分形态和迁移率边
Multifractal state and mobility edges in a periodically driven non-reciprocal Aubry-André model
-
摘要: 研究了在非互易Aubry-André模型中由方波式周期驱动所诱导的多重分形态和迁移率边. 通过数值计算逆参与率、能谱的实复转变以及平均逆参与率的标度分析等, 发现在以高于临界频率的驱动下系统展现完全的局域相. 同时在Floquet谱的特定区域存在CAT态, 不同于厄米情况, 其波函数分布的两个峰值展现非等权叠加的特性, 这是由非互易物理所决定的. 而以低于临界频率的驱动下, Floquet谱中存在迁移率边和多重分形态. 该研究结果为周期驱动系统中局域化性质的研究提供了新的视角.Abstract: In this work, we investigate the delocalization-localization transition of Floquet eigenstates in a driven chain with an incommensurate Aubry-André (AA) on-site potential and a small non-reciprocal hopping term that is driven periodically in time. The driving protocol is chosen such that the Floquet Hamiltonian corresponds to a localized phase in the high-frequency limit and a delocalized phase in the low-frequency limit. By numerically calculating the inverse participation ratio and the fractal dimension $D_q$, we identify a clear delocalization-localization transition of the Floquet eigenstates at a critical frequency $\omega_{\rm c}\approx0.318\pi$. This transition aligns with the real-to-complex spectrum transition of the Floquet Hamiltonian. For the driven frequency $\omega \gt \omega_{\mathrm{c}}$, the system resides in a localized phase, and we observe the emergence of CAT states—linear superposition of localized single particle states—in the Floquet spectrum. These states exhibit weight distributions concentrated around a few nearby sites of the chain, forming two peaks of unequal weight due to the non-reciprocal effect, distinguishing them from the Hermitic case. In contrast, for $\omega \lt \omega_{\mathrm{c}}$, we identify the presence of a mobility edge over a range of driving frequencies, separating localized states (above the edge) from multifractal and extended states (below the edge). Notably, multifractal states are observed in the Floquet eigenspectrum across a broad frequency range. Importantly, we highlight that the non-driven, non-reciprocal AA model does not support multifractal states nor a mobility edge in its spectrum. Thus, our findings reveal unique dynamical signatures that do not exist in the non-driven non-Hermitian scenario, providing a fresh perspective on the localization properties of periodically driven systems. Finally, we provide a possible circuit experiment scheme for the periodically driven non-reciprocal AA model. In the following work, we will extend our research to clean systems, such as Stark models, to explore the influence of periodic driving on their localization properties.
-
Key words:
- periodically driven system /
- localization /
- mobility edge /
- non-reciprocal system .
-

-
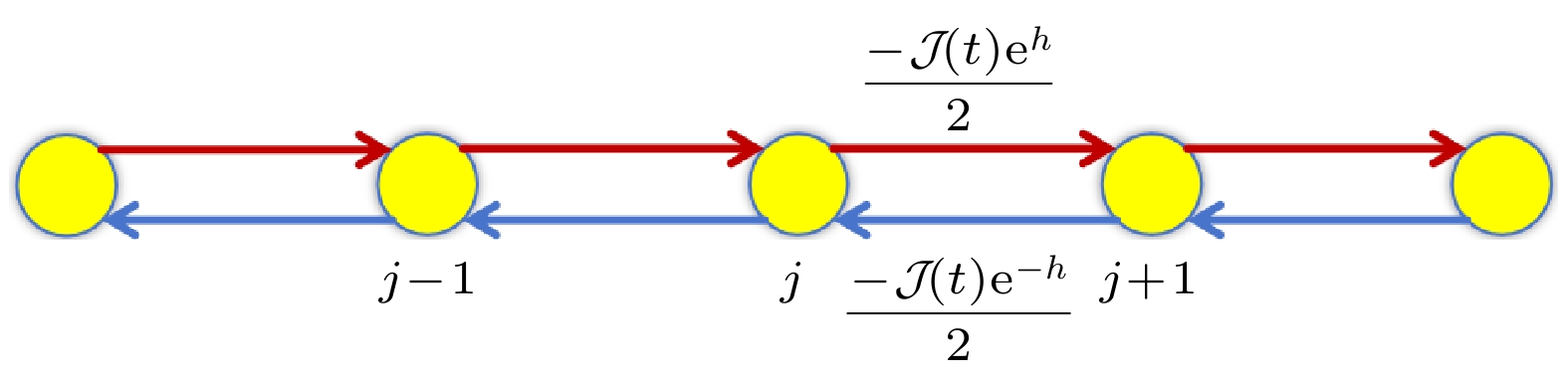
图 1 一维非互易模型示意图. 红线和蓝线代表不同跃迁强度, 其中
$ \mathcal{J}(t) $ 如(1)式所示,$ h $ 代表非互易强度,$ j $ 代表格点Figure 1. Schematic diagram of the one-dimensional non-reciprocal model. The red and blue lines represent different hopping amplitudes,
$ h $ is non-reciprocal amplitudes and$ j $ is the site index.图 2 (a)逆参与率
$ I^{(2)}_{n} $ 随着能级指标$ n/L $ 和频率$ \omega $ 的变化情况(这里, 能量实部升序排列). (b)分形维度$ D_{2} $ 随着能级指标$ \tilde{n}/L $ 和频率$ \omega $ 的变化情况, 以及复能量占比$ f_{\mathrm{Im}} $ (黑色实线)随频率$ \omega $ 的变化图, 其中能级指标$ \tilde{n} $ 以逆参与率值的大小升序排列. 这里$ L=2048 $ Figure 2. (a) Plot of
$ I^{(2)}_{n} $ as a function of the normalized eigenfunction index$ n/L $ and$ \omega $ . Here, the real part of the eigenvalues is ordered in ascending order. (b) Plot of the fractal dimension$ D_{2} $ as a function of$ \tilde{n}/L $ and$ \omega $ , and$ f_{\mathrm{Im}} $ (solid black line) as a function of$ \omega $ , where the energies sort in increasing order of the inverse participation ratio. Here,$ L=2048 $ .图 3 (a), (e)和(g) [(b), (f)和(h)]分别为
$ h=0.1 $ , 0和$ -0.1 $ 时, 位于能级$ n/L\approx0.24 $ ($ n/L\approx0.76 $ )处的密度分布$ \rho_j $ ; (c)和(d)分别为$ h=0.1 $ 时, 能级$ n/L\approx1/3 $ 和$ 1/2 $ 处的密度分布$ \rho_j $ ; (i)$ I_n^{(2)} $ 随着能级$ n/L $ 变化的情况; (j) 能量实部$ \mathrm{Re}(\varepsilon_n^{{\mathrm{F}}}) $ 随着能级指标$ n/L $ 的分布情况. 这里选取$ L=2048 $ 和$ \omega=\pi $ , 并且能级指标按照能量实部升序排列Figure 3. (a), (e), and (g) [(b), (f), and (h)] Plot of the density distributions
$ \rho_j $ at$ n/L\approx0.24 $ ($ n/L\approx0.76 $ ) with$ h=0.1 $ , 0, and$ -0.1 $ , respectively; (c) and (d) plot of$ \rho_j $ with$ h=0.1 $ at$ n/L\approx1/3 $ and$ 1/2 $ , respectively; (i)$ I_n^{(2)} $ as a function of$ n/L $ ; (j) plot of$ \mathrm{Re}(\varepsilon_n^{{\mathrm{F}}}) $ as a function of$ n/L $ . Here,$ L=2048 $ ,$ \omega=\pi $ , and the real part of eigenvalues is ordered in ascending order.图 4 (a)—(c)分别展示了在频率
$ \omega=0.235\pi $ 时, 能级$ \tilde{n}/L\approx 0.995 $ ,$ 0.7 $ 和$ 0.2 $ 处对应于不同$ q $ 的分形维度$ D_q $ 随着尺寸$ 1/\ln{(L)} $ 的变化情况. 这里能级按照逆参与率值的升序排列Figure 4. (a)–(c) Plot of the fractal dimensions
$ D_q $ as a function of$ 1/\ln{(L)} $ with different$ q $ and$ \omega=0.235\pi $ at$ \tilde{n}/L\approx 0.995 $ ,$ 0.7 $ , and$ 0.2 $ , respectively. Here, the energies sort in increasing order of the inverse participation ratio.图 5 (a)频率
$ \omega=0.132\pi $ 时,$ \tilde{n}/L=0.75 $ 处波函数的密度分布$ \rho_j $ ; (b)不同频率处, MIPR的标度分析; (c)图(b)频率下, 在参数$ h=0.1 $ 和$ \mu=0.05 $ 附近随机选取20个数进行无序平均后, MIPR的标度分析; (d), (e)频率$ \omega=0.132\pi $ 时,$ I_{\tilde{n}}^{(2)}\cdot L^{0.51} $ 与$ I_{\tilde{n}}^{(2)}\cdot L $ 随不同尺寸的缩放图. 这里能级按照逆参与率值的升序排列Figure 5. (a) Density distribution
$ \rho_j $ with$ \omega=0.132\pi $ at$ \tilde{n}/L=0.75 $ ; (b) the scaling of the MIPR for different$ \omega $ ; (c) the scaling of MIPR after averaging random 20 parameters near$ h = 0.1 $ and$ \mu = 0.05 $ with the frequency in panel (b); (d), (e) the scaling of$ I_{\tilde{n}}^{(2)}\cdot L^{0.51} $ and$ I_{\tilde{n}}^{(2)}\cdot L $ as a function of$ L $ with$ \omega=0.132\pi $ . Here, the energies sort in increasing order of the inverse participation ratio.图 6 频率
$ \omega=0.132\pi $ (a)和$ \omega=0.5\pi $ (b)时在复空间的能谱图; (c)在开边界条件下, 当频率$ \omega=0.132\pi $ 时环上随机5个能级所对应的密度分布$ \rho_j $ ; (d)在开边界条件下, 当频率$ \omega=0.5\pi $ 时随机5个能级所对应的密度分布$ \rho_j $ , 这里$ L=2048 $ Figure 6. Energy spectrum with
$ \omega=0.132\pi $ (a) and$ \omega=0.5\pi $ (b) in complex space; (c) the density distribution$ \rho_j $ for 5 random energy levels on the ring under open boundary conditions with frequency$ \omega = 0.132\pi $ ; (d) the density distribution$ \rho_j $ for 5 random energy levels under open boundary conditions with frequency$ \omega = 0.5\pi $ . Here,$ L=2048 $ . -
[1] Anderson P W 1958 Phys. Rev. 109 1492 doi: 10.1103/PhysRev.109.1492 [2] Tang L Z, Zhang G Q, Zhang L F, Zhang D W 2021 Phys. Rev. A 103 033325 doi: 10.1103/PhysRevA.103.033325 [3] Schulz M, Hooley C A, Moessner R, Pollmann F 2019 Phys. Rev. Lett. 122 040606 doi: 10.1103/PhysRevLett.122.040606 [4] Lin X S, Chen X M, Guo G C, Gong M 2023 Phys. Rev. B 108 174206 doi: 10.1103/PhysRevB.108.174206 [5] Dai Q, Lu Z P, Xu Z H 2023 Phys. Rev. B 108 144207 doi: 10.1103/PhysRevB.108.144207 [6] Liu H, Lu Z P, Xia X, Xu Z H 2024 New J. Phys. 26 093007 doi: 10.1088/1367-2630/ad7529 [7] Li H, Dong Z L, Longhi S, Liang Q, Xie D Z, Yan B 2022 Phys. Rev. Lett. 129 220403 doi: 10.1103/PhysRevLett.129.220403 [8] Ganeshan S, Pixley J H, Das Sarma S 2015 Phys. Rev. Lett. 114 146601 doi: 10.1103/PhysRevLett.114.146601 [9] Aditya S, Sengupta K, Sen D 2023 Phys. Rev. B 107 035402 doi: 10.1103/PhysRevB.107.035402 [10] Qi R, Cao J P, Jiang X P 2023 Phys. Rev. B 107 224201 doi: 10.1103/PhysRevB.107.224201 [11] Zuo Z W, Kang D W 2022 Phys. Rev. A 106 013305 doi: 10.1103/PhysRevA.106.013305 [12] Xu Z H, Xia X, Chen S 2021 Phys. Rev. B 104 224204 doi: 10.1103/PhysRevB.104.224204 [13] Wang Y C, Xia X, Zhang L, Yao H P, Chen S, You J G, Zhou Q, Liu X J 2020 Phys. Rev. Lett. 125 196604 doi: 10.1103/PhysRevLett.125.196604 [14] Tang Q Y, He Y 2024 Phys. Rev. B 109 224204 doi: 10.1103/PhysRevB.109.224204 [15] Zhou L W 2021 Phys. Rev. Res. 3 033184 doi: 10.1103/PhysRevResearch.3.033184 [16] Liu J H, Xu Z H 2023 Phys. Rev. B 108 184205 doi: 10.1103/PhysRevB.108.184205 [17] Lin Q, Li T Y, Xiao L, Wang K K, Yi W, Xue P 2022 Nat. Commun. 13 3229 doi: 10.1038/s41467-022-30938-9 [18] Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570 doi: 10.1103/PhysRevLett.77.570 [19] Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651 doi: 10.1103/PhysRevB.56.8651 [20] Zhou L W, Wang Q H, Wang H L, Gong J B 2018 Phys. Rev. A 98 022129 doi: 10.1103/PhysRevA.98.022129 [21] Zhou L W, Gong J B 2018 Phys. Rev. A 97 063603 doi: 10.1103/PhysRevA.97.063603 [22] Tiwari V, Bhakuni D S, Sharma A 2024 Phys. Rev. B 109 L161104 doi: 10.1103/PhysRevB.109.L161104 [23] Ji C R, Zhou S D, Xie A, Jiang Z Y, Sheng X H, Ding L, Ke Y G, Wang H Q, Zhuang S L 2023 Phys. Rev. B 108 054310 doi: 10.1103/PhysRevB.108.054310 [24] Mukherjee B, Sen A, Sen D, Sengupta K 2016 Phys. Rev. B 94 155122 doi: 10.1103/PhysRevB.94.155122 [25] Mukherjee B, Mohan P, Sen D, Sengupta K 2018 Phys. Rev. B 97 205415 doi: 10.1103/PhysRevB.97.205415 [26] Mukherjee B 2018 Phys. Rev. B 98 235112 doi: 10.1103/PhysRevB.98.235112 [27] Yang K, Zhou L W, Ma W C, Kong X, Wang P F, Qin X, Rong X, Wang Y, Shi F Z 2019 Phys. Rev. B 100 085308 doi: 10.1103/PhysRevB.100.085308 [28] Zhou L W, Du Q Q 2021 New J. Phys. 23 063041 doi: 10.1088/1367-2630/ac0574 [29] Zhou L W 2019 Phys. Rev. B 100 184314 doi: 10.1103/PhysRevB.100.184314 [30] Else D V, Bauer B, Nayak C 2016 Phys. Rev. Lett. 117 090402 doi: 10.1103/PhysRevLett.117.090402 [31] Mukherjee B, Nandy S, Sen A, Sen D, Sengupta K 2020 Phys. Rev. B 101 245107 doi: 10.1103/PhysRevB.101.245107 [32] Mukherjee B, Sen A, Sen D, Sengupta K 2020 Phys. Rev. B 102 014301 doi: 10.1103/PhysRevB.102.014301 [33] Liu H, Xiong T S, Zhang W, An J H 2019 Phys. Rev. A 100 023622 doi: 10.1103/PhysRevA.100.023622 [34] Wu H, An J H 2020 Phys. Rev. B 102 041119 doi: 10.1103/PhysRevB.102.041119 [35] Wu H, An J H 2022 Phys. Rev. B 105 L121113 doi: 10.1103/PhysRevB.105.L121113 [36] Bai S Y, An J H 2020 Phys. Rev. A 102 060201 doi: 10.1103/PhysRevA.102.060201 [37] Sarkar M, Ghosh R, Sen A, Sengupta K 2021 Phys. Rev. B 103 184309 doi: 10.1103/PhysRevB.103.184309 [38] Sarkar M, Ghosh R, Sen A, Sengupta K 2022 Phys. Rev. B 105 024301 doi: 10.1103/PhysRevB.105.024301 [39] Tong Q J, An J H, Gong J B, Luo H G, Oh C H 2013 Phys. Rev. B 87 201109 doi: 10.1103/PhysRevB.87.201109 [40] Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803 doi: 10.1103/PhysRevLett.126.106803 [41] Ahmed A, Ramachandran A, Khaymovich I M, Sharma A 2022 Phys. Rev. B 106 205119 doi: 10.1103/PhysRevB.106.205119 [42] Roy S, Khaymovich I M, Das A, Moessner R 2018 Sci. Post. Phys. 4 025 doi: 10.21468/SciPostPhys.4.5.025 [43] 成恩宏, 郎利君 2022 物理学报 71 160301 doi: 10.7498/aps.71.20220219 Cheng E H, Lang L J 2022 Acta Phys. Sin. 71 160301 doi: 10.7498/aps.71.20220219 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: