纳米胶体粒子在多孔介质中的输运在许多自然和工业过程中存在. 如含水层内纳米粒子的联合运输^[1,2]、淡水储存^[3]、催化化学反应器^[4,5]、钻井注井作业^[6]、油田开发中水处理^[7]等. 在这些过程中, 胶体粒子与固体基质之间的相互作用通常会导致粒子被捕获, 从而降低胶体浓度并且改变介质性质^[8].

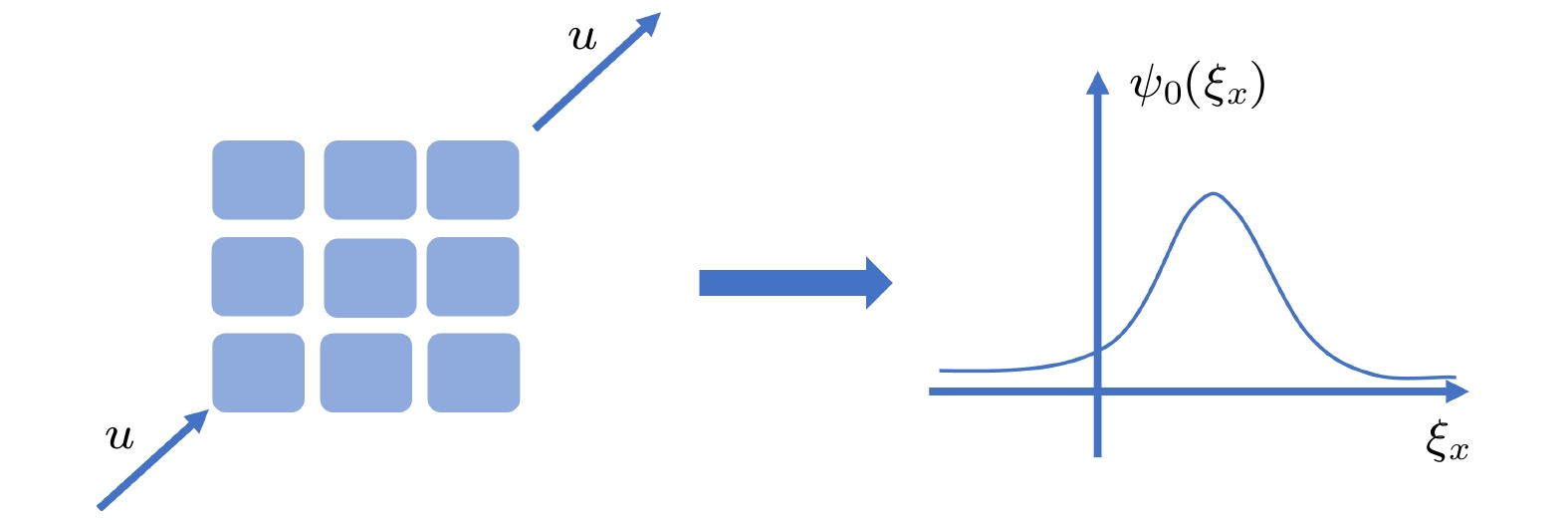
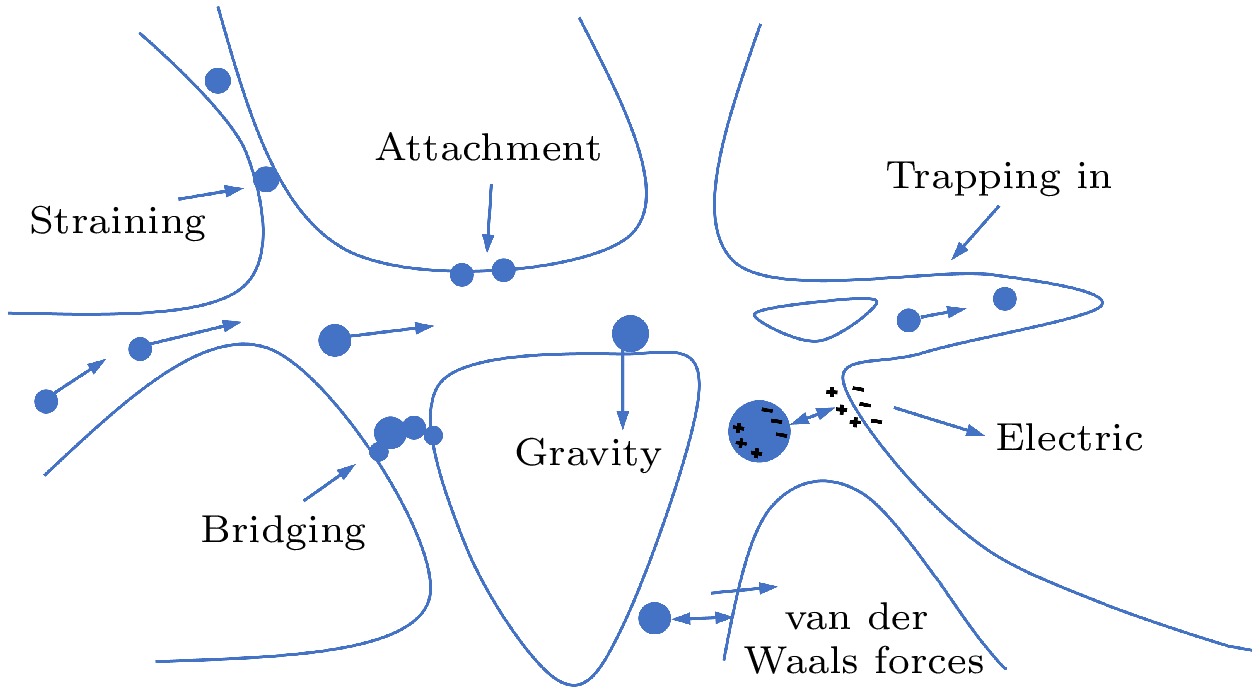
孔隙尺度下多孔介质的胶体粒子输运过程中, 存在范德瓦耳斯力、电场力、重力等相互作用力, 粒子被捕获的机制包括应变、吸附、桥接、扩散等^[9](见图1). 由于多孔介质的复杂性和粒子的多样性, 在孔隙尺度上直接详细描述粒子的输运较为复杂和困难, 但基于该尺度的微观模型能够体现微观机制的影响, 可以与许多实验数据相匹配^[9]. 然而, 孔隙尺度模型中的微观参数不易确定, 难以适用大规模应用场景. 因此, 有必要通过尺度提升方法, 在微观模型的基础上推导纳入微观机制的宏观模型.

一般的尺度提升方法包括直接提升和连续提升两类^[10]. 直接提升方法涉及尺度跳跃, 可能导致宏观方程出现非局部特征^[11], 并且衍生模型中的参数通常受到一些特定假设的限制, 宏观参数的选择可能不唯一^[10]. 特别是存在对流时, 宏观尺度模型预测结果与微观尺度模型预测结果可能有很大差别. 而连续提升方法更具物理性, 在一些物理假设下得到的宏观模型中参数是唯一的, 这些参数的渐近值服从直接提升所获得的关系. 然而, 从数学上证明尺度提升方法的渐近性质及从物理上对其解释较为困难^[12].

另一方面, 近年人们也发展了基于连续假设的宏观数学模型. 质量守恒方程可表示为^[13,14]

其中, $ \phi $是多孔介质孔隙度, C是浓度(单位流体体积中胶体粒子的质量或数量), σ是捕获浓度(单位介质体积捕获的胶体粒子质量或数量), q是通量(单位时间内通过单位面积的胶体粒子质量或数量), u是平均粒子速度, D是扩散系数, $ \varepsilon $是粒子捕获率(单位时间内单位介质体积捕获的胶体粒子质量或数量), $ t $和x分别是时间和空间.

方程(3)是多孔介质粒子捕获过程的直接体现. 为描述该捕获过程, 现有模型大多基于宏观通量来构造捕获率$ \varepsilon $, 常用的两类模型为^[9,15–18]

其中, λ是过滤系数, 表示每单位路径长度的粒子捕获概率^[15]. 模型(4)给出的捕获率与通量相关, 而模型(5)则忽略了扩散和弥散的影响. 两个模型中通量和平均速度的绝对值表示无论流向如何都会发生捕获^[13].

宏观尺度下的捕获过程描述虽然遵循物理规律, 但在解释宏观行为时会出现若干悖论: 1)在系统静止且均匀浓度情况下, 模型(4)和模型(5)无法预测粒子布朗运动导致的捕获; 2)模型(4)容易高估粒子的总路程, 导致捕获率的高估; 3)当过滤系数和扩散系数的乘积较大($ {\boldsymbol{u}} < {\boldsymbol{\lambda}} D $)时, 模型(4)将导致平均粒子运动方向与载液流动方向相反^[8].

上述研究表明, 从描述胶体粒子输运和捕获的微观机制出发, 推导出可靠的大尺度模型具有重要意义. 周知, Boltzmann输运方程(Boltzmann transport equation, BTE)是描述非平衡粒子系统统计行为的可靠模型, 它为建立可行的宏观尺度模型提供了新途径. 实际上, 近期研究者们已经采用Boltzmann方程描述多孔介质中的粒子输送现象. Boltzmann方程采用了粒子速度分布函数$ {\psi _0}\left( {\boldsymbol \xi} \right) $(如图2所示), 反映了粒子通过多孔介质过程中与介质相互作用导致的结果^[19,20], 同时速度分布函数与速度依赖的捕获直接耦合, 体现速度选择性的捕获过程.

基于Boltzmann方程, 通过一定的尺度提升分析方法, 可以推导出相应的宏观模型. 例如, 在浓度变化很小的假设条件下, Russell等^[8,21,22]通过Hilbert空间算子投影和Fourier分析, 从Boltzmann方程推导出一个如(1)式所示的宏观模型, 其中通量和捕获率显式表示为

$ {{\boldsymbol{K}}^{ij}}\left( {i, j = \left\{ {1, 2} \right\}} \right) $是与速度分布函数相关的系数矩阵. 模型(6)和(7)描述了粒子扩散和捕获之间的关系, 可在一定程度上解决上面提到的悖论^[8].

Chapman-Enskog(CE)分析是动理学理论中一个常用的渐近分析方法. 本文拟通过CE分析, 从胶体输运的BTE推导出相应的宏观模型, 该模型不同于传统的宏观对流扩散方程, 能够满足(1)式的质量守恒, 并包含依赖微观捕获机制的延迟项和捕获项, 通量和捕获率表达式能够解决常规宏观模型的悖论.

包含捕获效应的多孔介质胶体输运Boltzmann方程为^[8,21,22]

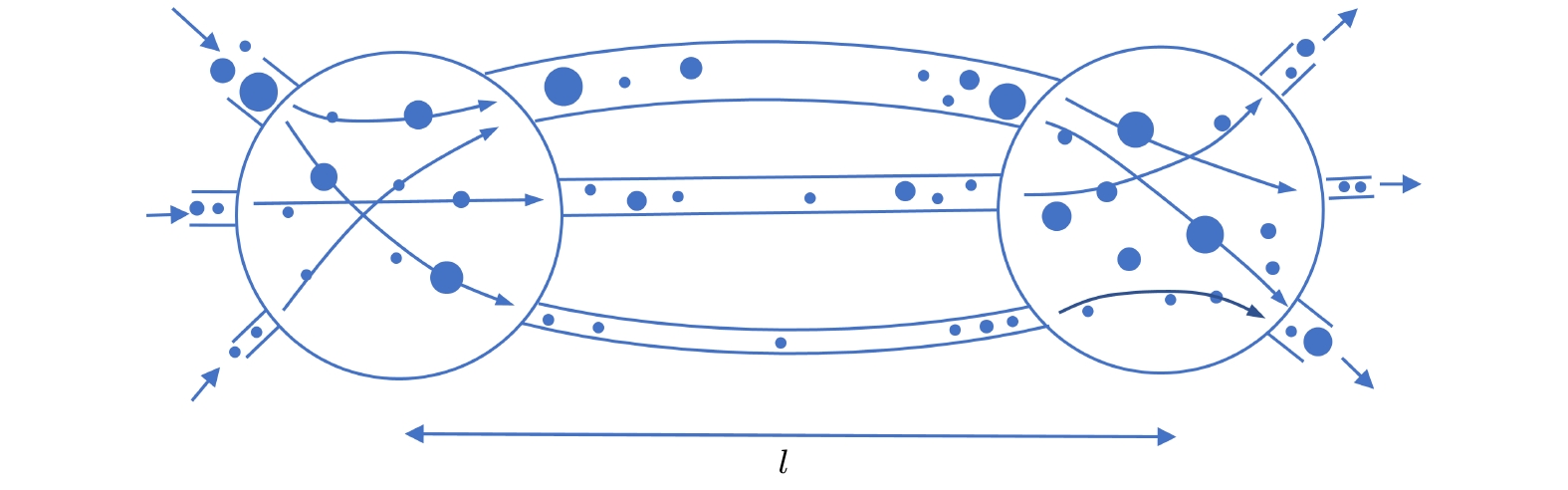
其中, $ \phi $为多孔介质孔隙度, t和x分别是时间和空间, $ {\boldsymbol \xi} $是粒子速度, $ {\boldsymbol{\lambda}} $是过滤系数矢量. $ f\left( {x, {\boldsymbol \xi} , t} \right) $描述了在时刻t、位置$ {\boldsymbol{x}} \in {\mathbb{R}^m} $处, 以速度$ {\boldsymbol \xi} \in {\mathbb{R}^m} $运动的粒子的浓度分布, $ m $代表空间维数. $ {\psi _0}\left( {\boldsymbol \xi} \right) $是在无捕获时平衡状态下的速度分布函数, 满足$ {\psi _0}\left( {\boldsymbol \xi} \right) > 0 $且$ \displaystyle \int {{\psi _0}({\boldsymbol \xi} )} {\text{d}}{\boldsymbol \xi} = 1 $. $ \tau $表示松弛时间, 定义为$ \tau = l/\left\| {\boldsymbol{u }}\right\| $, 其中l是混合长度, $ {\boldsymbol{u}} $是平均粒子速度, 即${\boldsymbol{ u}} = \displaystyle\int {{\boldsymbol \xi} {\psi _0}({\boldsymbol \xi} )} {\text{d}}{\boldsymbol \xi} $. 图3所示为对应的粒子混合过程: 假设平衡分布在某点$ \left( {x, t} \right) $处受到扰动, 粒子行进平均距离为l后到达多孔介质内另一个腔室, 并随着时间的推移松弛到平衡分布, 对应的时间为τ, 即粒子群达到平衡分布的弛豫时间^[21].

与线性化BGK-Boltzmann方程类似^[23], 方程(8)等号右边第1项表示粒子浓度分布趋向平衡浓度分布的“松弛”过程; 不同之处在于等号右边第2项, 即与粒子绝对速度大小成比例的粒子捕获项. 方程(8)从微观尺度上描述了由于粒子捕获而导致的粒子浓度的降低机制.

对方程(8)取零阶矩可以得到质量守恒方程(1), 其中粒子浓度C、粒子通量q和捕获率$ \varepsilon $分别为

通过对Boltzmann方程(8)求零阶矩, 获得了尺度提升的胶体粒子宏观输运模型. 然而, 为使该模型封闭, 需要给出粒子通量q和捕获率$ \varepsilon $的显式表达式. 我们将在第3节通过Chapman-Enskog分析给出.

本节将通过Chapman-Enskog分析从Boltzmann方程(8)推导出相应的宏观模型, 并讨论该模型的一些基本性质.

Chapman-Enskog多尺度展开是分析动理学模型渐近行为的一种方法^[24]. 在该方法中, Boltzmann方程的解表示为一个小参数的级数展开. 类似Russell等^[8,21,22]的做法, 时间取$ t \to t/\phi $, 同时令$ {f^{{\text{eq}}}} = \left( {\displaystyle\int {f{\text{d}}{\boldsymbol \xi} } } \right){\psi _0}({\boldsymbol \xi} ) = C{\psi _0}({\boldsymbol \xi} ) $, $ {f^{{\text{eq}}}} $满足$ \displaystyle\int {{f^{{\text{eq}}}}{\text{d}}{\boldsymbol \xi} } = C $. 于是, Boltzmann方程(8)可以写为

假设与宏观时间相比, 松弛时间τ是一个小的局部常数, 由(12)式可以得到分布的渐近表达式:

其中, $ D = {\partial _{\text{t}}} + {\boldsymbol \xi} \cdot \nabla $为物质导数算子. 对方程(12)求零阶速度矩可得

其中q和$ \varepsilon $分别由(10)式和(11)式给出.

为了闭合表达式, 我们采用渐近展开式(13)来近似函数f. 取f的0阶近似, 即$ f = {f^{{\text{eq}}}} + O\left( \tau \right) $, 此时有

其中$ \left\langle { \cdot , f} \right\rangle = \displaystyle\int { \cdot f{\text{d}}{\boldsymbol \xi} } $. 取f的1阶近似, 则可得到:

和

将(15)式代入(16)式和(17)式, 可得

和

其中, $ \hat {\boldsymbol{u}} = \displaystyle \int {\left| {\boldsymbol \xi} \right|{\psi _0}({\boldsymbol \xi} ){\text{d}}{\boldsymbol \xi} } $表示平衡速度分布的绝对平均速度. 令:

其中, $ R\left( {\boldsymbol{u}} \right) $和$ \bar R\left( {\boldsymbol{u}} \right) $分别表示瞬时速度的变化量和对速度变化量的捕获率. 此时通量q和捕获率ε可以简化表示为

至此, 我们得到了封闭的宏观模型:

假设流体不可压以及速度的时空变化缓慢, 则惯性项$ {\boldsymbol{u }}\cdot \nabla {\boldsymbol{u}} $和$ {\partial _t}{\boldsymbol{u}} $(流动准静态)可以忽略, 此时$ R\left( {\boldsymbol{u}} \right) = \bar R\left({\boldsymbol{ u}} \right) \approx 0 $, 有

宏观模型表示为

此时模型(28)表现为多孔介质中胶体粒子输运的对流-扩散方程(advection-diffusion equation, ADE)形式, 包括依赖于速度分布的扩散项、速度延迟项和反映微观捕获机制的捕获项.

宏观模型(28)与Russell等^[8,21,22]的平均模型(记为R-平均模型)形式相似, 不同之处在于输运系数. R-平均模型由(1)式、(6)式和(7)式表示为

对应的输运系数(记为$ {\boldsymbol{K}}^{{ij}} $)表达式为

Russell等^[8]通过Hilbert空间投影和Fourier分析, 在长波和大时间近似下得到简化模型(29), 这与模型(28)的假设一致. 如果定义新分布$ \psi _0^*({\boldsymbol \xi} ) = {\psi _0}({\boldsymbol \xi} )/\left( {1 + \tau {\boldsymbol{\lambda}} \cdot \left| \xi \right|} \right) $, (30)式右端括号里的值就等于新分布的协方差. 分布$ \psi _0^*({\boldsymbol \xi} ) $量化了宏观尺度下由于捕获和松弛而引起的瞬时速度分布的变化. 而本文模型(28)的输运系数$ {{\boldsymbol{R}}^{ij}} $是在局部平衡近似下导出的, 尽管捕获过程改变速度分布, 但粒子-粒子以及粒子-介质间的相互作用使得速度分布趋化到局部平衡态分布, 而不考虑其他因素影响. 此时由(22)式给出的输运系数$ {{\boldsymbol{R}}^{ij}} $项括号里的值就等于分布$ {\psi _0}(\xi ) $的协方差. 如果扰动很微小以至于对速度分布变化的影响可忽略, 此时本文模型与R-平均模型是近似的, 大大降低输运系数的计算成本.

特别是在一维情况下, 假设速度u ≠ 0, 进一步进行变量替换, 令$ y = \xi /u $, $ {\psi _1}\left( y \right) = {\psi _0}\left( \xi \right)u $, 则$ {\psi _1}\left( y \right) $满足$ \left\langle {1, {\psi _1}\left( y \right)} \right\rangle = 1 $和$ \left\langle {y, {\psi _1}\left( y \right)} \right\rangle = 1 $. 此时系数$ {R_{kl}} $可以写为

显然, 系数$ {R_{ij}}(i, j = \{ 1, 2\} ) $正比于u, 如果$ \lambda $与u无关, 则$ {R_{ij}}/u $与u无关. 特别地, 有效扩散系数$ {R_{11}} $符合$ {R_{11}} = {\alpha _{\text{L}}}u $, 其中, 比例系数$ {\alpha _{\text{L}}} $是粒子分散度. 在本文模型中, $ {\alpha _{\text{L}}} $表示速度分布宽度, 不受粒子捕获的影响.

现在给出模型(28)在一维情况下的无量纲形式. 为此, 我们引入如下无量纲变量:

其中, $ L $为物理特征长度, $ {C_0} $为初始粒子浓度. 相应的无量纲方程可以写为

其中3个无量纲数为

其中$ \theta $称为延迟数, Pe是Peclet数, $ \varOmega $是宏观过滤系数(表示宏观尺度下单位时间的捕获概率). 从(31)式—(33)式可以看出, 这3个无量纲数都与平均速度无关.

进一步假设混合过滤系数$ \lambda l $非常小, 此时(26)式中的第3项可以被忽略, (27)式仅保留第1项, 因此宏观方程可简化为(简化模型A):

与模型(28)相比, 模型(37)没有延迟, 捕获率仅与平均绝对粒子速度以及粒子浓度相关.

如果忽略捕获对非平衡态分布的作用, 方程(27)仅保留第1项, 此时宏观方程(28)简化为(简化模型B):

与模型(28)相比, 模型(38)的延迟被削弱, 宏观捕获则与方程(37)相同.

为了进一步比较本文模型(28)与R-平均模型的宏观系数差异, 不失一般性, 假设$ {\psi _0}\left( {\boldsymbol \xi} \right) $是一个平均值为u及标准方差为$ s $的正态分布, 则可以使用一个表示正速度分布面积的参数α来量化分布偏向正速度的程度, $ \alpha =\displaystyle \int_0^\infty {{\psi _0}\left( {\boldsymbol \xi} \right){\text{d}}{\boldsymbol \xi} } $. 正态分布包含α = 1和α < 1两种情况. 当速度均大于0时, $ \alpha = \displaystyle\int_0^\infty {{\psi _0}\left( {\boldsymbol \xi} \right){\text{d}}{\boldsymbol \xi} } = 1 $, 否则, α < 1.

根据(36)式, 本文模型对应的无量纲参数为

其中$ {\bar R_{12}} = {\bar R_{21}} $, 并且$ {\bar R_{ij}} $都是非负的. 可以看出, 这些宏观参数取决于微观捕获项$ \lambda l $, $ l/L $, 平衡态分布函数$ {\psi _1}\left( y \right) $.

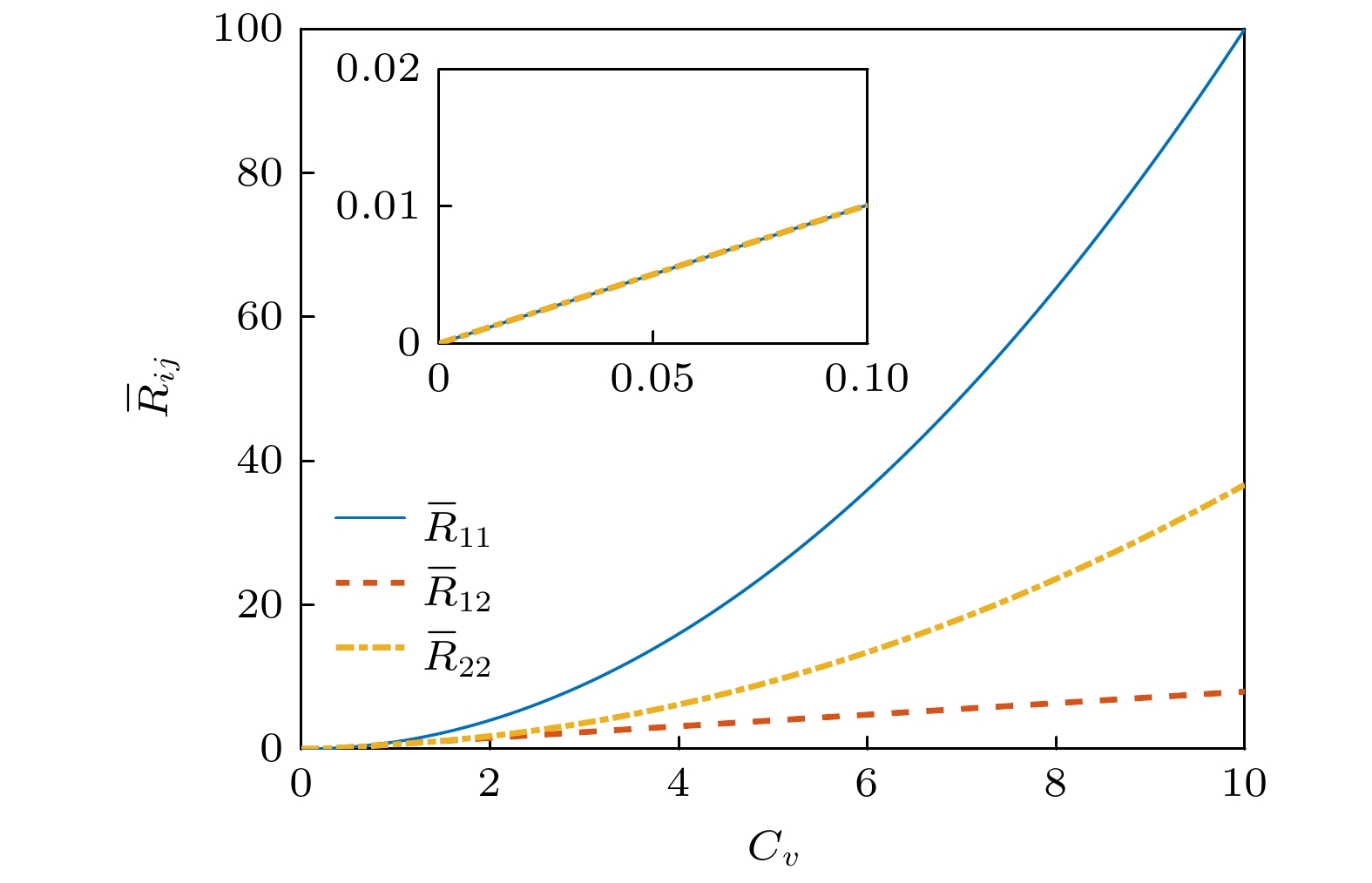
表1列出了α = 1和α < 1时对应的输运系数表达式. 图4所示为速度分布的混合矩$ {\bar R_{ij}} $与系数$ {C_v} = s/u $的关系. 可以发现, $ {\bar R_{11}} = C_v^2 $, 而 $ {\bar R_{12}} $和$ {\bar R_{22}} $随着$ {C_v} $增大的速率均小于$ C_v^2 $的增长 速率.

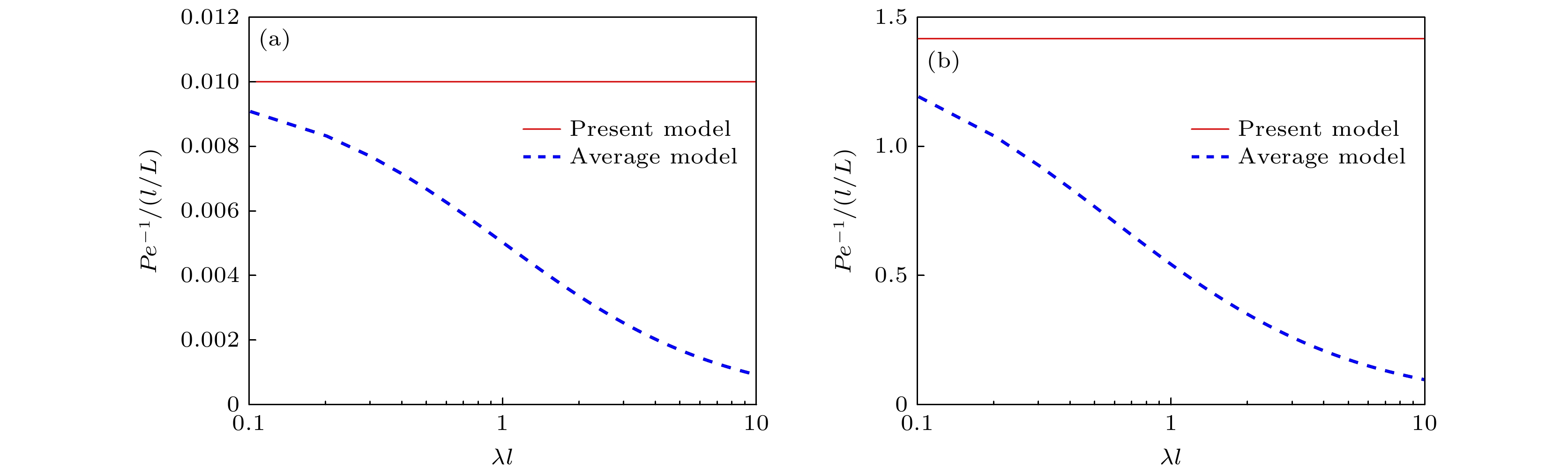
进一步分析本文模型和R-平均模型的宏观系数对混合过滤数$ \lambda l $以及变异系数$ {C_v} $的依赖性. 图5所示为系数$ 1/P{e^*} $与过滤系数$ \lambda l $的关系. $ P{e^*} $定义为$ P{e^*} = (l/L) \cdot Pe = ul/{R_{11}} $, 表示微观尺度下的Peclet数. 图5(a), (b)分别对应α = 1和α < 1两种情况. 可以发现, 本文模型的$ 1/P{e^*} $与$ \lambda l $无关, 仅由平衡态分布的宽度即$ {C_v} $值决定. 这是因为平衡速度分布越宽, 在宏观尺度上的粒子扩散更强. 类似地. R-平均模型的$ 1/P{e^*} $也随$ {C}_{v} $增大而增大. 但是, R-平均模型的$ 1/P{e^*} $依赖$ \lambda l $, 即$ 1/P{e^*} $随着$ \lambda l $的增大而减小. 这是因为粒子捕获改变速度分布的影响大于松弛过程, “打破”了平衡态分布, 降低了速度标准偏差, 从而降低了粒子扩散. 当$ \lambda l $趋于0时, 两个模型的$ 1/P{e^*} $一致.

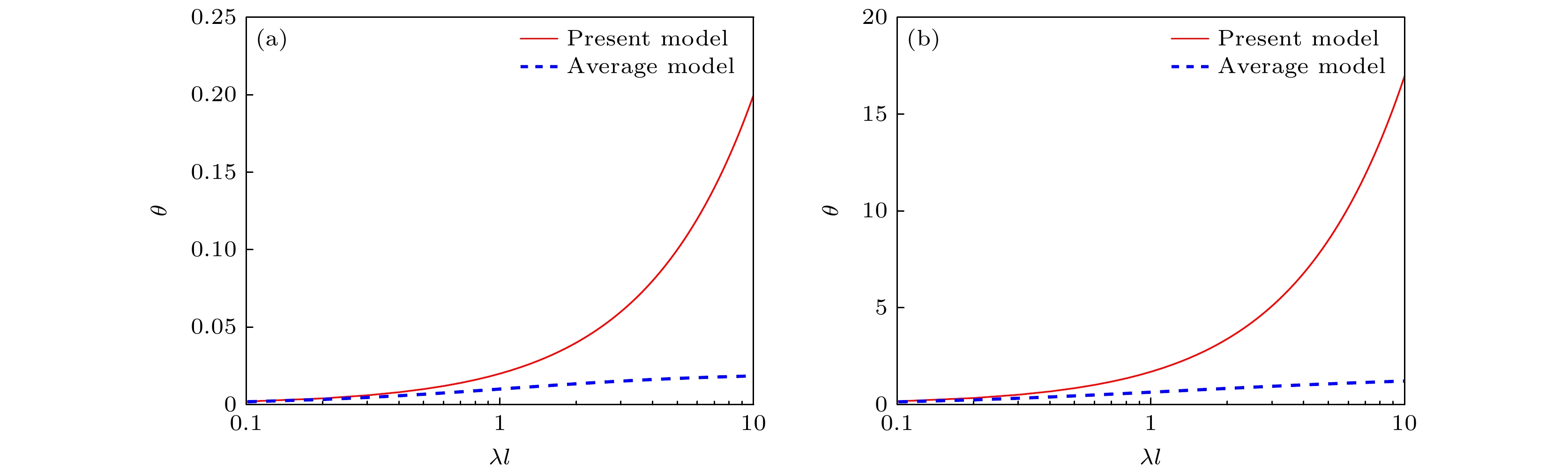
图6所示为延迟数$ \theta $与$ \lambda l $的关系. $ \theta $随$ \lambda l $的增大而增大, 且$ {C_v} $越高, 分布越宽, 表明高速粒子比例越高, 捕获越多, 延迟越大. 这是由于更快的粒子优先到达捕获位点导致宏观尺度上有效平均速度的降低. 当$ \lambda l $趋于0时, 捕获不发生或捕获影响很小, 不产生捕获导致的延迟, 此时两个模型的$ \theta $都趋于0. 随着$ \lambda l $不断增大, 本文模型对$ \lambda l $的线性依赖性使得$ \theta $的增大速度远大于R-平均模型, 而R-平均模型由于扩散的减小, 进一步减小了速度分布的改变, 延迟数变化越来越小, 最终趋于平缓.

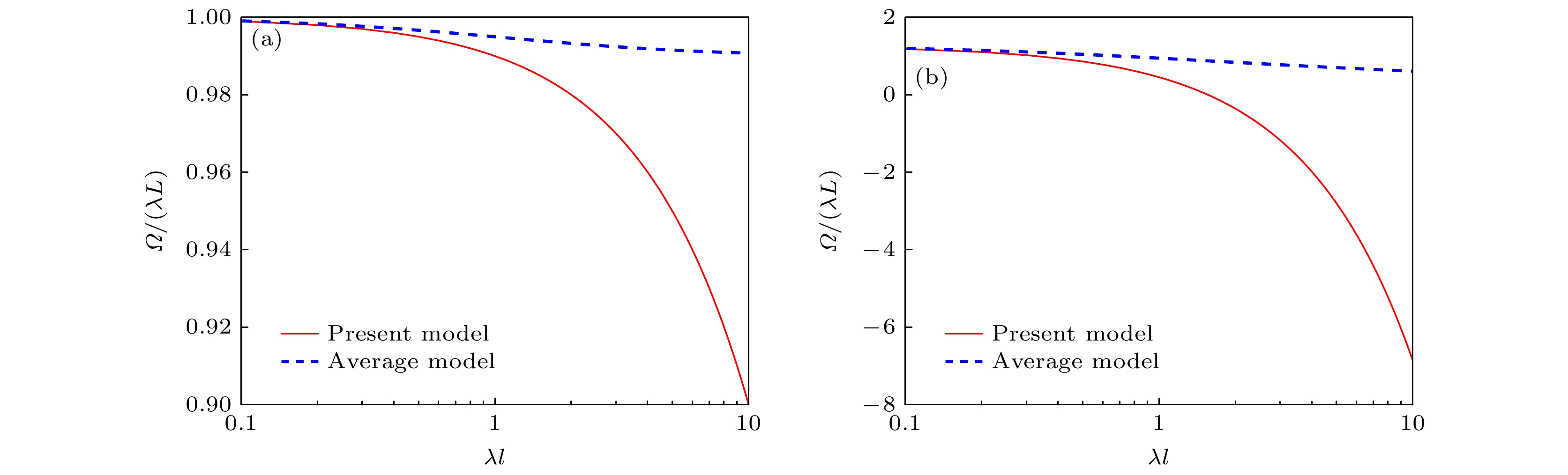
图7所示为系数$ \varPsi = \varOmega /\left( {\lambda L} \right) $随$ \lambda l $的变化. $ \varPsi $表示捕获效率比, 用来衡量宏观捕获率与微观捕获率之间的相对大小关系. 当$ \lambda l $较小时, 对$ {C}_{v}=0.1 $($ \alpha = 1 $)的情况, 速度分布较窄, 粒子捕获相对均匀, 捕获对分布的影响较小, 此时$ \varPsi $接近1, 微观捕获直接体现为宏观捕获, 如图7(a)所示. 当$ {C_v} $增大时, 由于分布变宽, 以及对负速度粒子的捕获, 使得$ \varPsi $在$ \lambda l $较小时大于1, 如图7(b). 随着$ \lambda l $增大, 高速粒子被优先捕获的概率增大, 此时捕获是非均匀的, 粒子被部分捕获, 导致整体捕获转化率开始降低. 同时, 本文模型对$ \lambda l $的线性依赖使得$ \varPsi $的下降速度快于平均模型. 在R-平均模型中, 高捕获率在降低粒子扩散的同时抑制了捕获增长, 使$ \varPsi $比值趋于固定值.

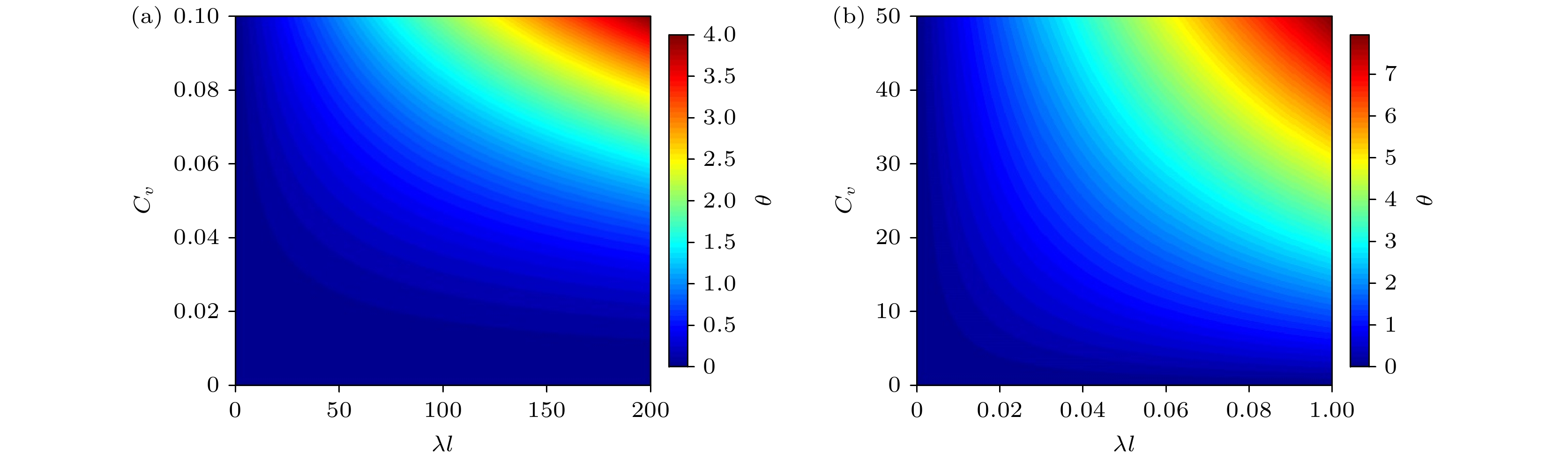
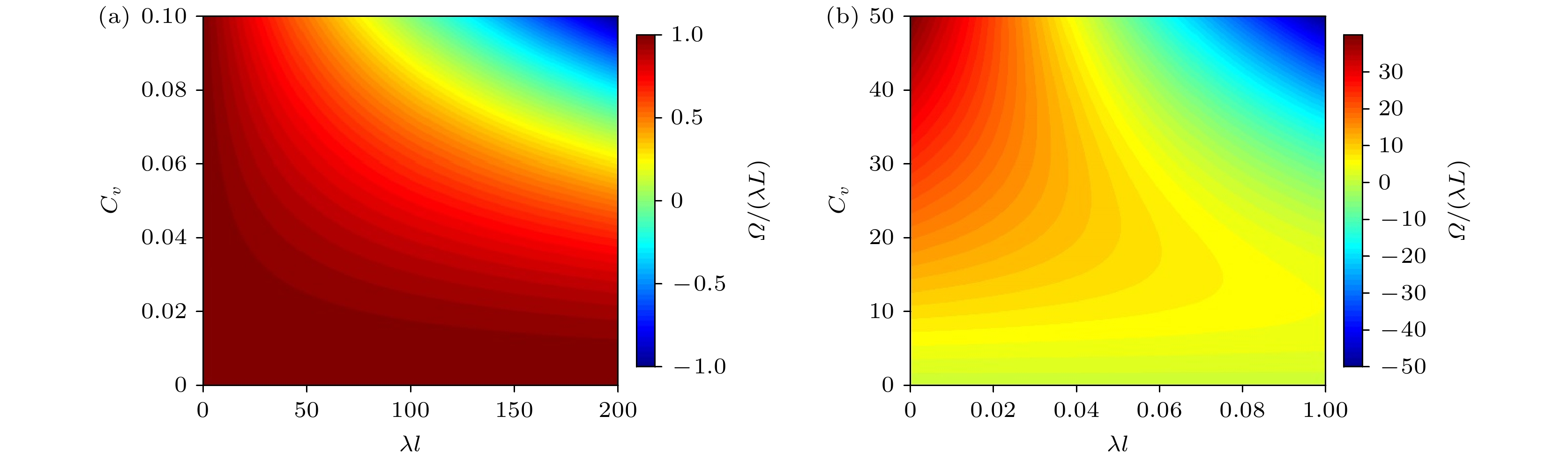
从上述分析可以发现, 本文基于渐近分析得到的宏观模型与R-平均模型在一定情况下相近, 特别是两者都耦合了与速度相关的微观捕获机制, 但本文模型参数更简单. 同时图8和图9分别给出了系数$ \theta $和$ \varPsi $对$ {C_v} $和$ \lambda l $的敏感性分析云图. 从图8可以看出, $ \theta $随着$ {C_v} $和$ \lambda l $增大而增大, 与图6趋势一致. 从图9可以看出, $ \varPsi $随着$ {C_v} $增大而增大, 随着$ \lambda l $增大而减小, 与图7趋势一致. 为保证$ \theta $和$ \varPsi $的数值有效性, $ {C_v} $越小, $ \lambda l $的有效取值范围越大, 或$ \lambda l $越小, $ {C_v} $的有效取值范围越大. 应当指出的是, 当$ \lambda l $趋于无穷时, 本文模型的参数$ \theta $和$ \varOmega $均趋于无穷, 其原因是我们假设可过滤系数较小, 捕获的粒子浓度较低, 同时忽略了过滤系数的变化. 如果进一步考虑非线性效应和非平衡动力学等因素, 则能够耦合更多的信息. 同时由于捕获和扩散的相互作用, 限制了速度分布的宽度. 因此在$ \lambda l $较小时, 宏观系数$ \theta $和$ \varOmega $的数值才符合实际物理意义.

同时, 本模型的3个宏观尺度参数与R-平均模型一样是相互依赖的. 在$ \alpha = 1 $时依赖关系表达式为^[8]

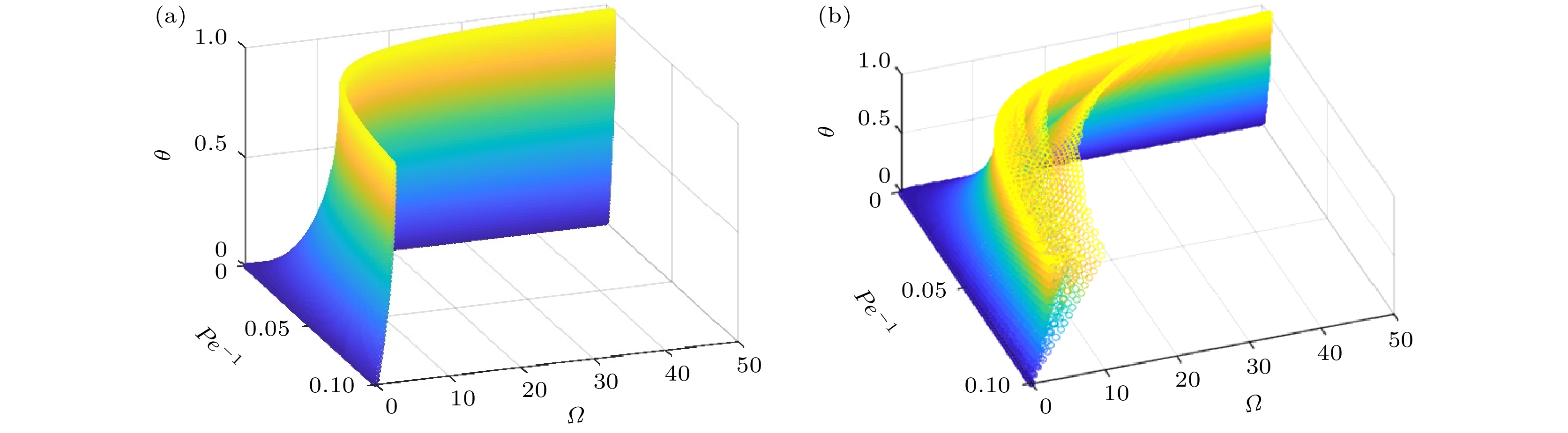
进一步根据微尺度参数$ \left( {\lambda , l, {C_v}} \right) $计算了在$ \alpha = 1 $和时$ \alpha < 1 $相应的宏观参数$ \left( {P{e^{ - 1}}, \theta , \varOmega } \right) $. 图10所示为$ \left( {P{e^{ - 1}}, \theta , \varOmega } \right) $的分布. 可以看出, 当$ \alpha = 1 $时, 该分布是一个二维曲面. 这个可能子空间小于所有正实数组成的三维空间. 当$ \alpha < 1 $时, 由于负速度粒子的影响, 宏观参数空间得到扩展, 但仍小于所有正实数组成的三维空间. 这是由于参数之间的潜在物理联系导致模型只允许某些宏观参数.

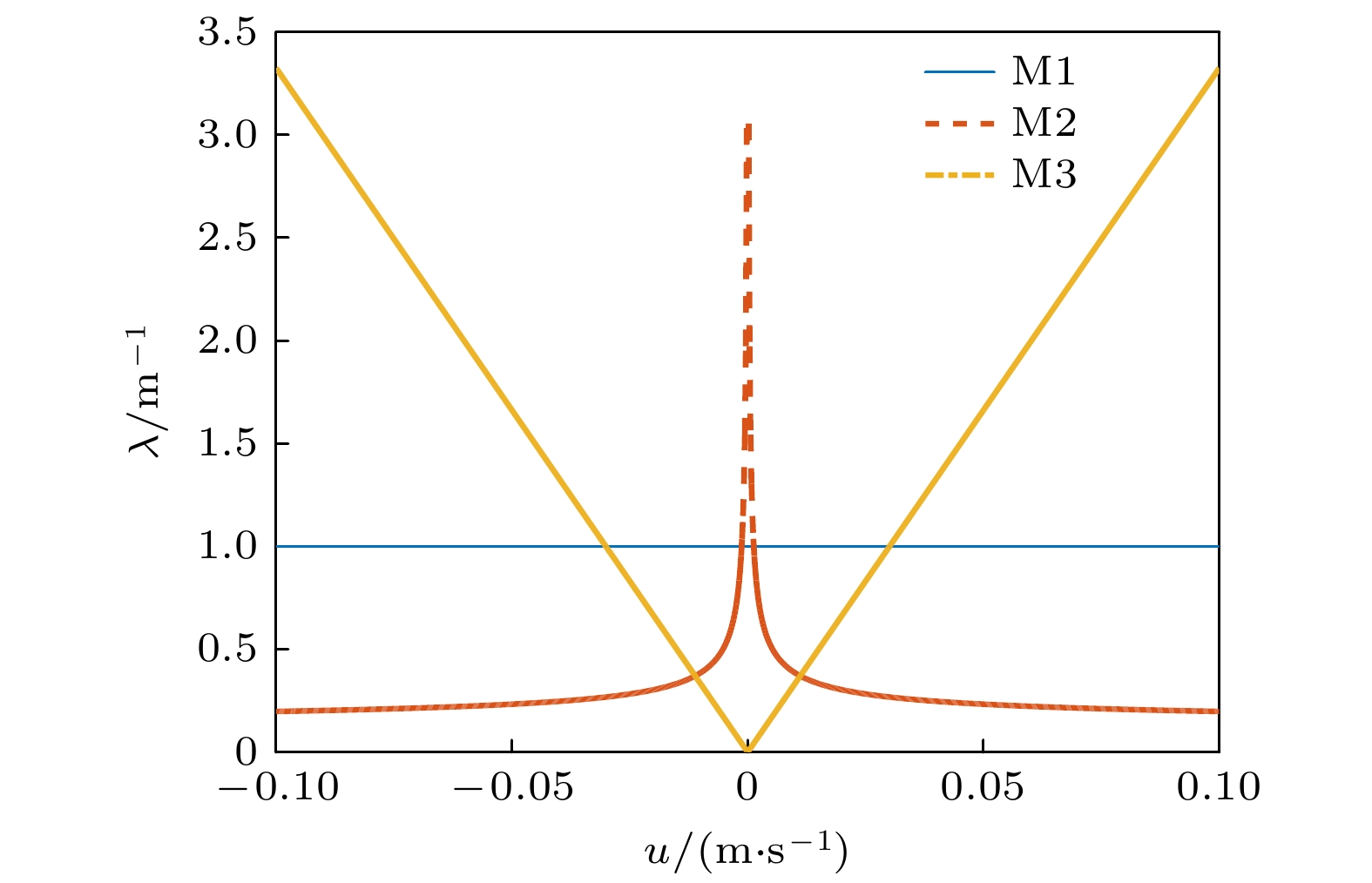
在玻尔兹曼方程(8)中, 过滤系数$ \lambda $反映了应变捕获(straining)作用, 且随着粒径和孔径的不同而变化, 是与距离相关的函数^[25]. 对于其他捕获机制, 可以基于不同的理论构造相关的过滤系数模型^[21]. 下面给出其他两个常见的捕获机制.

首先考虑吸附(attachment)机制, 该机制描述了多孔介质的物理化学性质对粒子捕获的作用. 基于传统胶体过滤理论得到的过滤系数是一个常数, 表示为^[26]

其中, $ {r_{\text{c}}} $表示介质粒子半径, $ \alpha $表示黏附效率, $ {\eta _0}\left( u \right) $表示粒子接近多孔介质的效率, u是平均粒子速度.

第2种机制是惯性捕获(inertial capture), 用于描述非布朗运动粒子的捕获. 在多孔介质中, 以较高速度运动的大粒子更有可能偏离流线, 并与其他粒子碰撞, 导致捕获. 对应的过滤系数也是一个常数, 表示为^[27]

其中, $ {r_{\text{p}}} $是粒子半径, $ {r_{\text{c}}} $是介质粒子半径, $ {\rho _{\text{f}}} $是流体密度, $ \mu $是流体黏度, $ \beta $是捕获过程的特征常数, u是平均粒子速度.

在上面的捕获模型中, 过滤系数$ \lambda $与粒子平均速度以及粒子和介质的性质相关. 尽管底层捕获机制不同, 但统计捕获率的方法相同. 对于图3所示的由平行孔和腔室构成的多孔模型, 假设了应变导致的粒子捕获发生在腔室出口处. 对于其他捕获机制, 则假设捕获发生于穿过平行孔的过程以及在下一个腔室混合的过程.

在本文宏观模型中, 不同捕获机制的过滤系数被视为常数, 因此粒子群的捕获是一种平均效应. 该方法避免了对单个粒子微观过滤系数建模的复杂性, 并能够反映微观捕获机制的总体效应, 具有较好的实用性.

图11给出不同捕获机制对应的过滤系数与平均粒子速度的关系. 对于应变模型M1, 粒子捕获概率与流体速度无关. 对于吸附模型M2, 流体速度越大, 粒子通过单位距离的时间越短, 捕获概率越小. 对于惯性捕获模型M3, 每单位长度粒子捕获的概率随流体速度增大而增大.

接下来, 我们考虑平均速度对不同捕获机制的宏观尺度行为的影响. 图12所示为宏观系数关于平均速度u的敏感性分析. 这里固定混合长度$ l $和平衡态速度分布标准差$ s $, 而平均速度u可以左右平移.

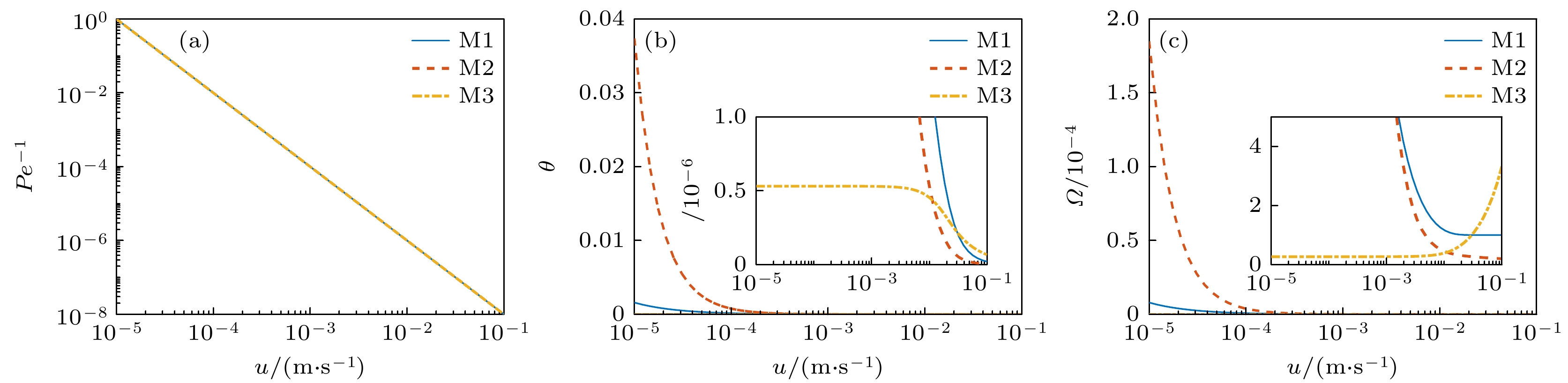
首先, 可以发现$ P{e^{ - 1}} $随平均速度u增大而减小(图12(a)). 随着u增大, 越来越多粒子运动加快, 分布函数能快速松弛到平衡状态, 松弛过程对速度分布的影响越来越小, 因此呈现越来越小的扩散系数. 由于$ P{e^{ - 1}} $与过滤系数无关, 因此3种捕获模型的曲线一致.

从图12(b)可以看到, 应变模型M1、吸附模型M2和惯性捕获模型M3的速度延迟因子$ \theta $与平均速度u具有相关性. 然而这种关系不明确. 首先, $ \theta $应该是非负的, 这是由于无论快速的粒子(M1, M3)还是慢速粒子(M2)被捕获, 都会导致平均速度降低. 随着u的增大, 越来越多的粒子移动变快. 对于应变模型M1, 微观捕获概率不变, 因此扩散减小, 导致延迟也减小; 对于吸附模型M2, 粒子被捕获的概率越来越小, 因此在扩散减小的共同作用下$ \theta $趋于0; 对于惯性捕获模型M3, 粒子被捕获的更多, 而扩散减小, 此时两者的相互作用和竞争决定了宏观系数的变化. 随着速度的继续增大, 扩散影响更大, 导致延迟下降.

图12(c) 所示为宏观过滤系数$ \varOmega $关于平均速度的敏感性分析. 模型M1, M2, M3的微观捕获分别为不变、减小和增大, 而$ \varOmega $分别呈现下降、下降和上升的趋势. 这种关系与3.2节中关于$ \varOmega $的行为分析以及图9(b)一致.

本文第1节介绍了两种常见的宏观尺度上的捕获率表达式(4)和(5). 下面给出相应的描述胶体输运和捕获的宏观方程.

标准模型(Standard Model), 由(1)—(3)式和(5)式表示, 无量纲形式为

Altoé等^[15]提出的修正模型(Altoé Model)由(1)—(4)式表示, 其无量纲形式为

可以发现, 方程(44)不存在延迟, 而方程(45)包含由于捕获和扩散耦合导致的速度延迟. 在我们的模型中, 同样由于速度依赖的粒子捕获率和粒子速度分布耦合产生了速度延迟. 并且速度全正时, 本文模型的捕获率满足(4)式, 与方程(45)的机理相符.

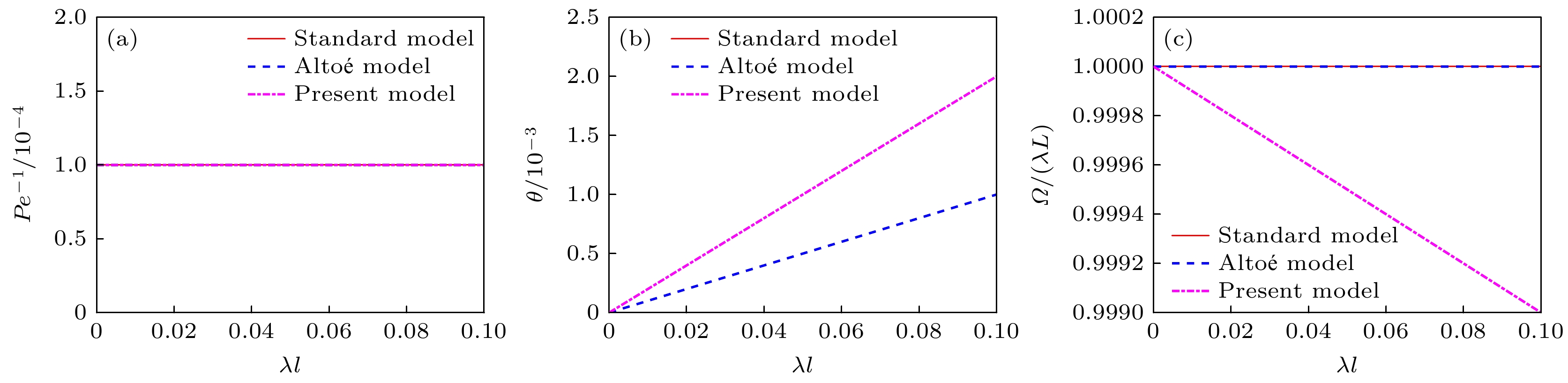
当速度分布均为正值时, 此时分布宽度较窄, 本文在$ \lambda l $为小参数假设下, 可以忽略优先捕获机制的作用以及捕获与扩散的耦合, 此时方程(37)(简化模型A)等同于标准模型(44). 图13所示为在该假设下本文模型与传统模型宏观系数的差异. 可以发现, 二者的宏观扩散是一致的, 延迟数$ \theta $和捕获效率比$ \varPsi={ \varOmega }\text{/(}{ \lambda L}) $的差别在$ {10}^{-3} $量级左右, 这种差异对于低速和低浓度的胶体输运过程来说是可以忽略的.

同样, 当速度分布均为正值时, 假设忽略作用在非平衡态部分的捕获, 此时方程(38)(简化模型B)等同于Altoé修正模型(45). 此时, 延迟的原因来自优先捕获机制造成的平均速度降低, 而非捕获和扩散的耦合原因. 由此造成的捕获是相对均匀的, 因此图13(b)中修正模型的延迟数是本文模型的一半, 且Ψ的值接近1.

本节将讨论本文导出的宏观模型反映微观捕获机制的性质, 以及宏观模型如何解决传统模型存在的悖论, 并分析模型的一致性和局限性.

胶体输运与捕获的动理学模型基于两个假设: 一是粒子速度分布都会向平衡速度分布松弛, 二是粒子捕获与速度绝对值成正比. 基于此微观模型, 我们和Russell等^[8]分别通过不同的提升方法, 推导出不同的宏观模型, 输运系数不同于标准模型和Altoé修正模型. 新模型的系数表达式由粒子速度分布给出, 而非直观的扩散系数和捕获系数. 这种差异源于微观模型(8)中的捕获项, 即与粒子速度相关的捕获率与速度分布的耦合. Russell等^[8]将其定义为优先捕获机制, 即高速粒子能够提前到达滞留位点而被捕获, 进而改变速度分布, 造成有效平均速度的降低以及捕获转化率的降低. 由于无论粒子流向如何均会被捕获, 使得负速度粒子存在时的捕获转化率大于只有正速度粒子的情况. 因此, 我们导出的宏观方程能够捕捉该微观尺度行为.

为了明确优先捕获机制造成的定量差异, 我们考虑半无限多孔介质区域的悬浮液连续注入问题, 相应的边界条件如下:

此时方程的解析解为^[28]

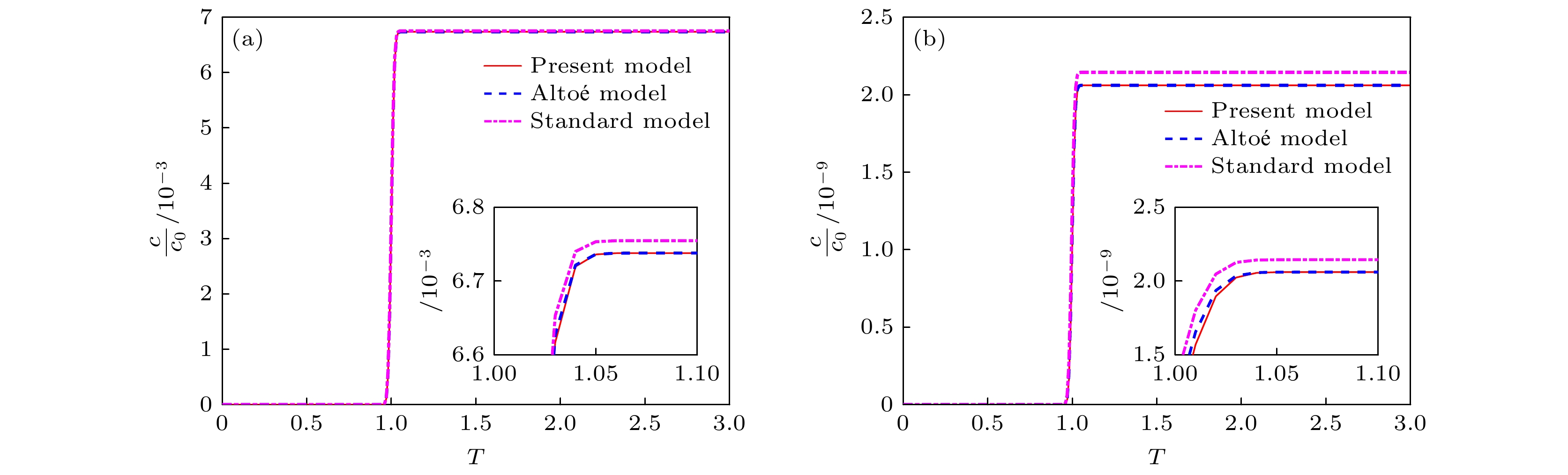
其中, $ v = 1 - \theta $, $ u = v{\left( {1 + 4\varOmega P{e^{ - 1}}/{v^2}} \right)^{1/2}} $.

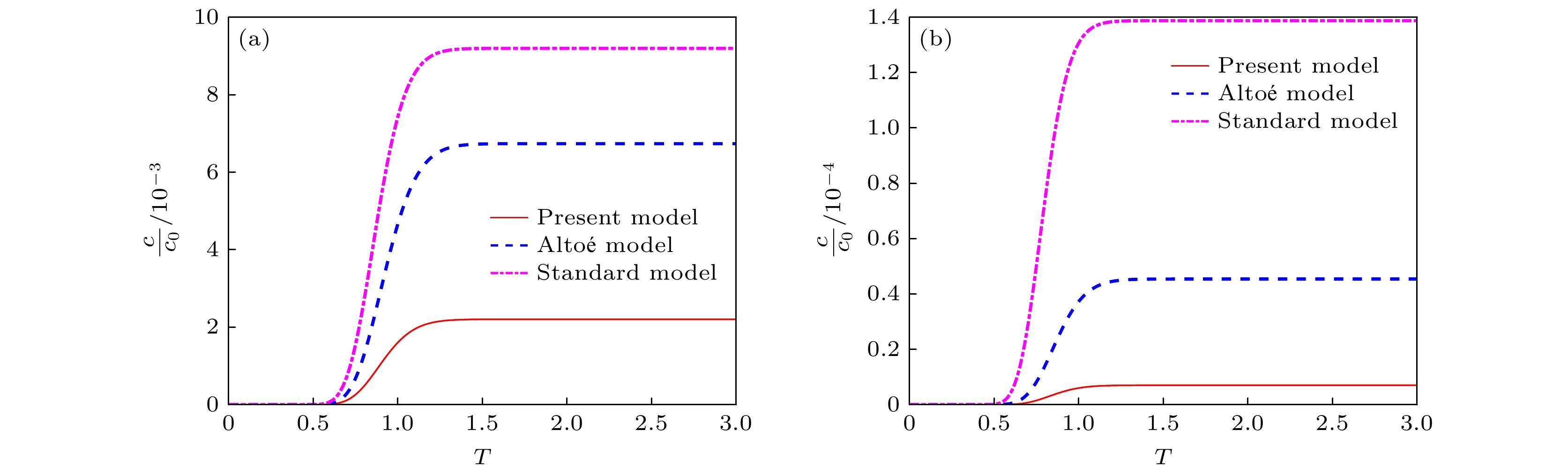
图14所示为粒子正向运动($ \xi > 0 $)时, 本文模型与传统模型的出口浓度随时间的变化. 由于 不存在延迟, 标准模型预测的粒子更早到达出口, 其次是Altoé修正模型, 最后是本模型. 考虑捕获与扩散的耦合作用时, 由于分布较窄以及$ \lambda l $较小, 本文模型与Altoé修正模型达到同样的出口浓度, 且捕获量高于标准模型. 同时, 增大微观捕获率$ \lambda L $, 浓度将会降低更多.

图15所示为存在反向运动粒子时本文模型与传统模型的出口浓度随时间的变化. 同样标准模型预测的粒子更早到达出口, 且捕获量更低; 其次是Altoé修正Model, 最后是本模型. 由于考虑了负速度粒子的捕获, 本文模型预测的捕获量较Altoé校正模型更高. 同时, 增大微观捕获率$ \lambda L $, 捕获与扩散的耦合作用将会增大捕获量. 进一步对比图14和图15可以发现, 速度分布越宽及过滤混合数越大时, 优先捕获机制的效果越明显.

本文的模型部分解决了传统模型的悖论:

第1个悖论是传统ADE模型无法正确描述静止且浓度分布恒定的情况. 但本文模型对于以零为中心的对称平衡速度分布, 由(27)式给出的捕获率表达式中的第1项并不为0, 因此模型能够正确预测布朗运动导致的粒子捕获, 克服了传统模型的这一悖论.

第2个悖论是传统ADE模型会高估捕获率. 这是由于(4)式假设捕获发生在扩散过程中, 高估了粒子的总路程. 而本文并不假设粒子的输运形式, 粒子捕获率是与粒子速度相关的, 尽管在推导出的宏观方程中(26)式前两项仍是对流和扩散相叠加的结果, 但优先捕获机制导致延迟的产生, 使得本文模型能正确预估粒子的行径路程尺度, 从而解决了这一悖论.

传统模型中的第3个悖论是, 捕获或扩散较强时会出现非物理的对流速度. 然而, 通过3.2节的分析可知, 该悖论可以在λl相对小时得到解决, 此时延迟数θ < 1, 宏观捕获率Ω > 0, 悖论不存在.

在3.2节中, 当混合过滤系数相对较小时, 本模型和平均模型相近. 在速度全为正的情况下, 混合过滤系数$ \lambda l $较小时的简化模型A与标准模型一致, 而忽略捕获对非平衡态影响的简化模型B与Altoé修正模型一致. 因此, 标准模型和修正模型可以视为本文模型的特例. 同时. 本文模型又解决了传统模型中存在的部分悖论, 侧面说明了基于Boltzmann方程描述胶体输运与捕获微观过程的合理性, 以及结合局部平衡的尺度提升方法推导出的宏观方程的合理性. 此外, 在考虑反向粒子的捕获时, 本文宏观模型也能够准确捕获这一过程.

应当指出的是, 本文推导过程利用了分布函数的一阶近似. 如果考虑高阶近似, 将会导出更复杂的宏观模型. 同时, 在本研究中, 只考虑了依赖平均速度的过滤系数, 而没有考虑其他因素, 如过滤系数随捕获粒子浓度的变化^[29], 粒子群异质性对捕获的影响^[30], 以及沉积粒子的释放^[31]等. 考虑到这些不同的因素, 需要新的模型描述多孔介质中的胶体输运.

基于描述微观尺度下多孔介质中胶体的输运和捕获的Boltzmann方程, 本文通过Chapman-Enskog分析, 推导出了具有延迟对流速度和线性捕获项的宏观ADE. 该宏观模型包括3个无量纲数: 延迟数θ、逆Peclet数$ P{e^{ - 1}} $和宏观过滤系数Ω. 延迟数θ和宏观过滤系数Ω依赖于微观过滤系数λ, 而$ P{e^{ - 1}} $则是速度分布宽度的结果. 该模型耦合了微观尺度捕获机制, 能够优先捕获高速度运动粒子.

ADE在混合过滤系数λl较小时是有效的, 能够部分解决传统模型的悖论, 并且在某些条件下能恢复到其他模型. 通过对比不同模型的出口浓度曲线, 阐明了优先捕获机制的影响, 即由于依赖粒子速度的捕获项与速度分布函数直接耦合, 导致在宏观行为上出现平流速度的延迟以及可能大于1也可能小于1的捕获效率.