首页
登录
注册
下载:
-
液体电极放电是以溶液作为其中一个 (或两个) 电极的放电形式[1,2], 由于液体良好的导热性可以有效抑制向火花放电的过渡[3], 使得液体电极放电即使在大气压下也可以工作于较为温和的辉光放电阶段[4,5]. 由于等离子体与液体之间的相互作用[6], 液体电极放电会产生大量电子、离子、多种活性粒子[7]和紫外辐射等[8]. 因此, 液体电极放电广泛应用于光谱分析[9]、纳米材料合成[10]、表面改性[11]、水活化[12]、污染控制[13]、催化[14]、医药[15]等多个应用领域.
当液体作阴极时, 等离子体在液面附近呈现为一些丝状接触点[16], 通过静电相互作用, 这些接触点附近的液面会发生扭曲产生一些随机的凸起[17]. 如果放电电流很高, 这些凸起会以小液滴的形式进入等离子体, 从而导致液体中的金属元素发射谱线强度增强[18]. 此外, 根据放电电流和电导率(σ)的不同, 液面上的放电形貌会呈现圆锥状[19,20]、碗状[18]、轴对称喇叭[21]和矩形喇叭[22]. 当液体作阳极时, 放 电产生的电子可以被电负性物质附着形成负离子[22]. 负离子在液面积聚, 会增强负离子层与液面之间的电场[23], 导致液面附近产生一个发光层, 即形成阳极层[24]. 如果负离子均匀分布, 液面会出现圆盘状放电, 即均匀模式[25]. 此外, 在适当的条件下在阳极层中还可以观察到斑图模式, 如弥散盘[24,26]、离散点[27]、条纹[28]、齿轮[29]、轮辐[30]、蜂窝[23]、星状[31]和同心环[32]等结构. 研究发现具体的斑图类型取决于液体电极放电的工作条件[33], 如放电电流[30]、电压幅值[23,34,35]、气体成分[29]、气体流速[36]、气隙宽度[37]、电极温度[38]和液体种类[24]等.
以往对液体电极放电斑图模式的研究大多采用直流电压激励. 事实上, 利用交流电压激励也可以产生斑图模式. Zheng等[35]利用交流电压激励, 通过改变放电功率、气隙宽度、驱动频率以及pH值, 在阳极液面观察到了环状、双环、齿轮状斑图. 在前期工作中, 我们使用初始σ为735 μS/cm的NaCl溶液, 通过交流电压激励在液体电极表面观察到了螺旋斑图[39]. 研究表明, 溶液σ对直流电压激励液体电极放电斑图类型具有重要影响[40], 但其对于交流电压激励放电的模式和斑图影响尚缺乏系统的研究.
针对于此, 本文研究了交流电压激励下大气压液体电极放电的模式. 通过改变液体σ, 研究了各种均匀模式和斑图模式的电学特性、时空演化以及等离子体参数特性, 并基于反应-扩散系统对均匀模式和斑图模式进行数值仿真.
-
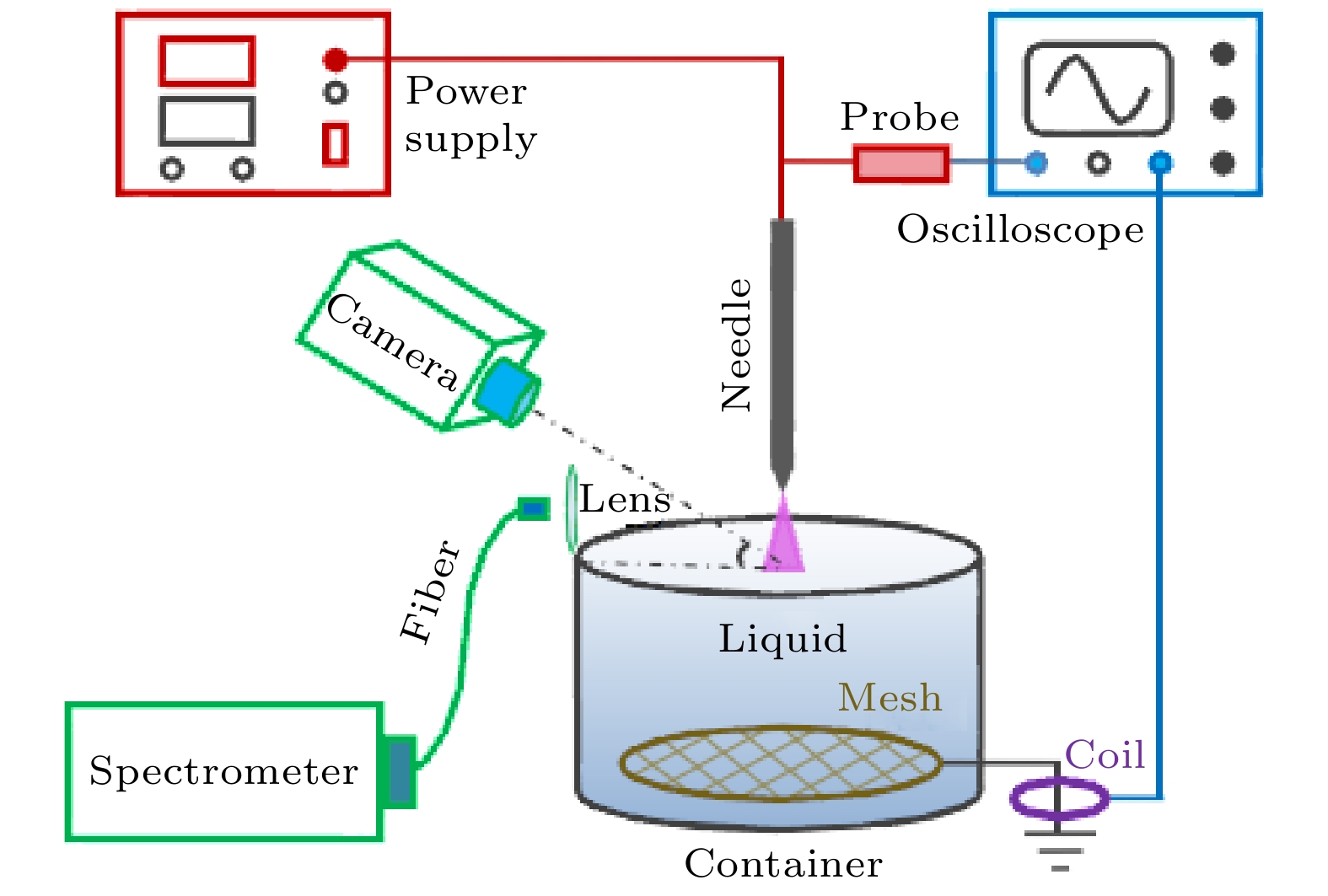
图1为实验装置示意图. 一根直径2.0 mm的钨棒(尖端半径约为400 μm)竖直固定在圆柱形水槽(直径7.5 cm, 高8 cm, 盛满约350 mL溶液)上方, 保持棒尖端到液面距离(电极间距)固定为5.0 mm. 钨棒作为高压电极, 与频率为20 kHz的交流电源 (Suman CTP-2000K)输出端连接. 水槽底部铺有钨网, 作为接地电极. 整个水槽浸泡在一个25 ℃的恒温水箱中, 以保持接地电极的溶液温度恒定(实验中用温度计检测溶液温度波动小于0.1 ℃). 为了获得不同σ的液体, 使用了1.2 μS/cm的去离子水和380 μS/cm的自来水, 对于σ>380 μS/cm的液体用自来水溶解NaCl得到. 溶液的σ由电导率测试仪(lnesa DDSJ-308F)测量. 环境温度为 25 ℃, 湿度为39%. 采用高压探头(Tekronix P6015A)测量钨棒与接地钨网之间的施加电压(气隙电压与液体电极分担电压之和). 采用罗氏线圈(Pearson 8600)测量放电电流. 放电电压和电流波形显示并储存在数字示波器(Tektronix DPO4104)中. 通过配有微距镜头的数码相机(Canon EOS 5D Mark IV)和增强型电荷耦合器件(ICCD) (PI MAX 4)从与水平呈45°的方向对液面上的放电进行拍照. 通过自制的转化器将正弦电压信号变成与之同步的晶体管逻辑(TTL)信号[41], 并用于触发ICCD, 从而实现对放电时空演化的研究. 利用透镜将液面附近放电的发光(仅液面附近的阳极层, 而非整个放电的发光)汇聚到光纤探头的入口, 经由光纤进入光谱仪(Zolix Omni-λ7528i)的入口狭缝中, 通过电荷耦合器件(Zolix DField-Vs-A4)采集放电的发射光谱.
-
随着正弦电压峰值(Up)升高到9.3 kV, 气隙发生击穿放电. 此时形成的放电是很细的丝, 在液面不能观察到任何自组织斑图. 在此基础上, Up逐渐降低到2.3 kV时, 体放电变得弥散, 此时改变溶液σ时液面出现均匀模式和斑图模式, 如图2所示. 可以看出, 当σ = 1.2 μS/cm时, 液面发光呈现圆盘状, 称之为均匀模式[25]. 随着溶液σ的增大, 放电从均匀模式过渡为斑图模式. 最先形成的是齿轮状斑图(σ = 255 μS/cm), 该斑图中部是弥散的圆盘, 其边缘带有多个凸起的齿. 随着σ的增大, 圆盘变小, 但凸起变长, 形成了锯盘状斑图(σ = 380 μS/cm). 此后随着σ的不断增大, 液面上的斑图经历离散点(645 μS/cm)、单臂螺旋(820 μS/cm)及同心圆环(956 μS/cm). 如果进一步增大σ, 放电在液面收缩为一个斑点(图中未给照片) .
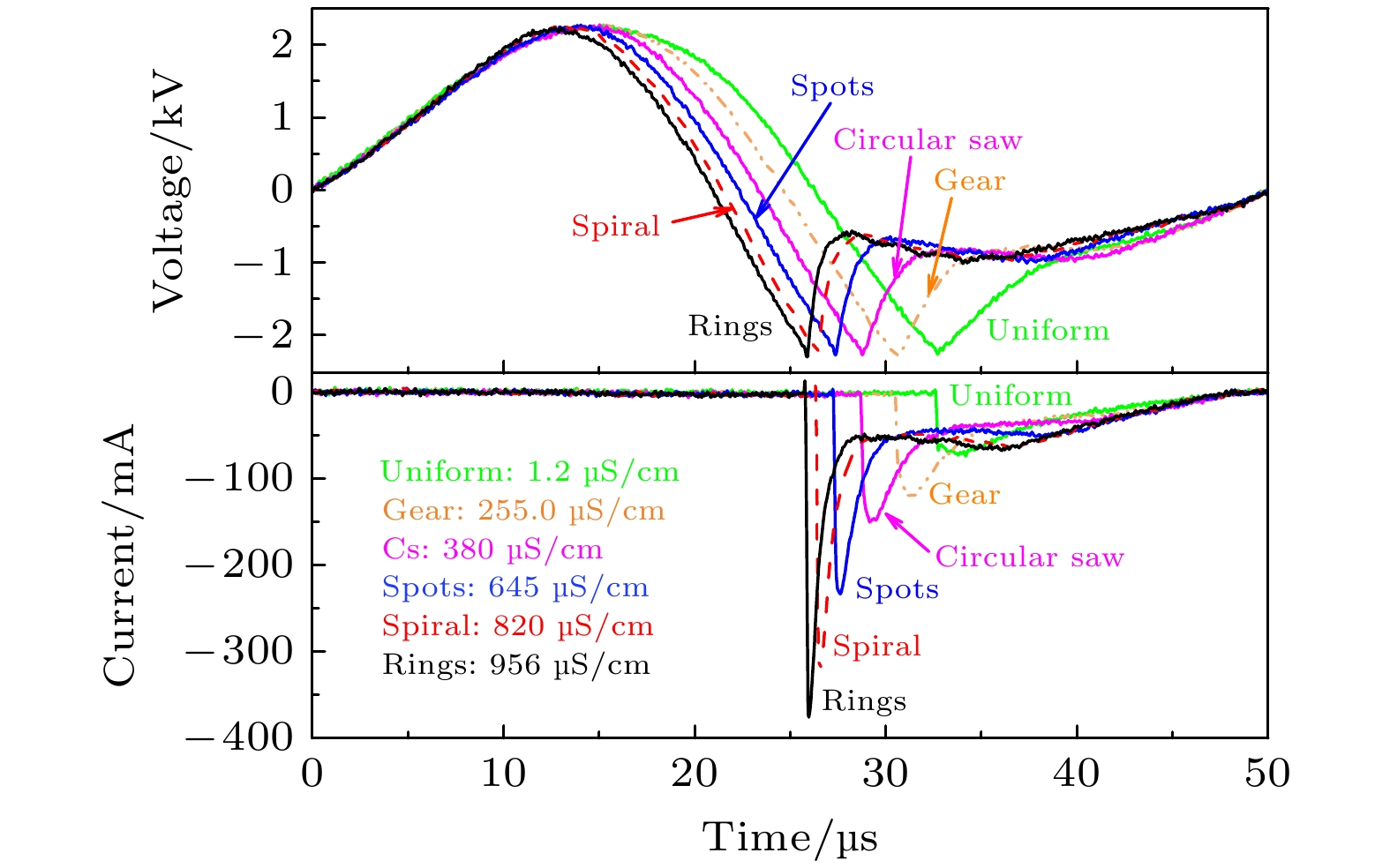
图3所示为不同溶液σ(均匀模式及不同斑图模式)时的施加电压与放电电流波形. 从图3可以看出, 放电仅发生在施加电压的负半周期, 即液体作瞬时阳极时. 放电开始前施加电压以正弦形式随着时间增大, 导致气隙间电场增强, 达到击穿电场后产生放电[42]. 随着等离子体的产生, 气隙电阻迅速减小, 电流迅速增大并达到峰值. 随着溶液σ的增大, 放电回路的总电阻值降低, 所以峰值电流的强度增大. 并且, 随着σ的增大, 液体电极上分担的电压更小, 这意味着相同时刻下气隙分担的电压值更高, 因此能更早地达到击穿条件产生放电, 即在相同的施加电压下, 放电击穿时刻提前. 气体击穿后, 由于放电功率很大, 而电源不是理想的电压源, 因此电压波形会发生扭曲变形. 在放电电流的缓慢减小阶段, 对于均匀模式电流的减小是单调的, 但对于斑图模式电流在减小过程中存在一段几乎不随时间变化的平台阶段. 此外, 随σ的增大, 平台阶段的电流也增大.
利用单次曝光的ICCD(texp = 500 ns)对均匀模式和斑图模式在液面上发光行为的时间演化进行研究, 如图4所示. 在电流的上升时刻A, 不论均匀模式还是斑图模式, 液面上方均出现弥散的圆盘. 这是因为体放电中电子与电负性物质结合形成负离子[22], 这些负离子在电场作用下向液面迁移并沉积在液面上方, 增强了液体电极表面的电场[34]. 此后, 体放电减弱甚至熄灭, 由于负离子仍缓慢地向着阳极层迁移来增强阳极层的电场, 导致圆盘的发光亮度变化不大(B时刻). 对于均匀模式(图4(a)), 在后续的演化过程中, 随放电电流的减小, 到达阳极层的负离子不断减少, 因此液体电极表面的电场不断减弱, 发光强度逐渐减弱(C—E时刻)并最终消失 (F时刻) . 对于斑图模式(图4(b)—(f)), 随着放电进行到平台阶段(时刻C), 液体阳极层开始出现斑图. 斑图在整个平台阶段均存在(时刻D). 此后, 随着电流减小, 这些斑图的边缘逐渐消失(时刻E), 在时刻F完全消失.
由以上过程可知, 斑图存在于电流的平台阶段, 如果没有平台阶段, 则放电仅能形成均匀模式. 此外, 通过拍摄平台阶段的液面图像, 可以避免体放电的干扰, 从而得到清晰的放电照片. 图5(a)为单次曝光ICCD拍摄的D时刻均匀模式和斑图模式的照片. 这个图再次说明随着σ的增大, 放电从均匀模式过渡为斑图模式, 斑图模式经历齿轮、锯盘、五边形排布的分离点、螺旋波和同心环. Rmubach等[25]认为液体阳极层中存在电子碰撞电离和扩散的过程, 即碰撞电离作为活化子, 而扩散和复合作为禁阻子, 通过非线性图灵相互作用而产生斑图[43,44]. 根据上述的图灵反应-扩散模型, 阳极层中电子密度可以表示为拉普拉斯方程的本征函数(方程(1)) , 其在柱坐标系
$ (r, \theta ) $ 中表示如下:其中变量l, m和n是正整数;
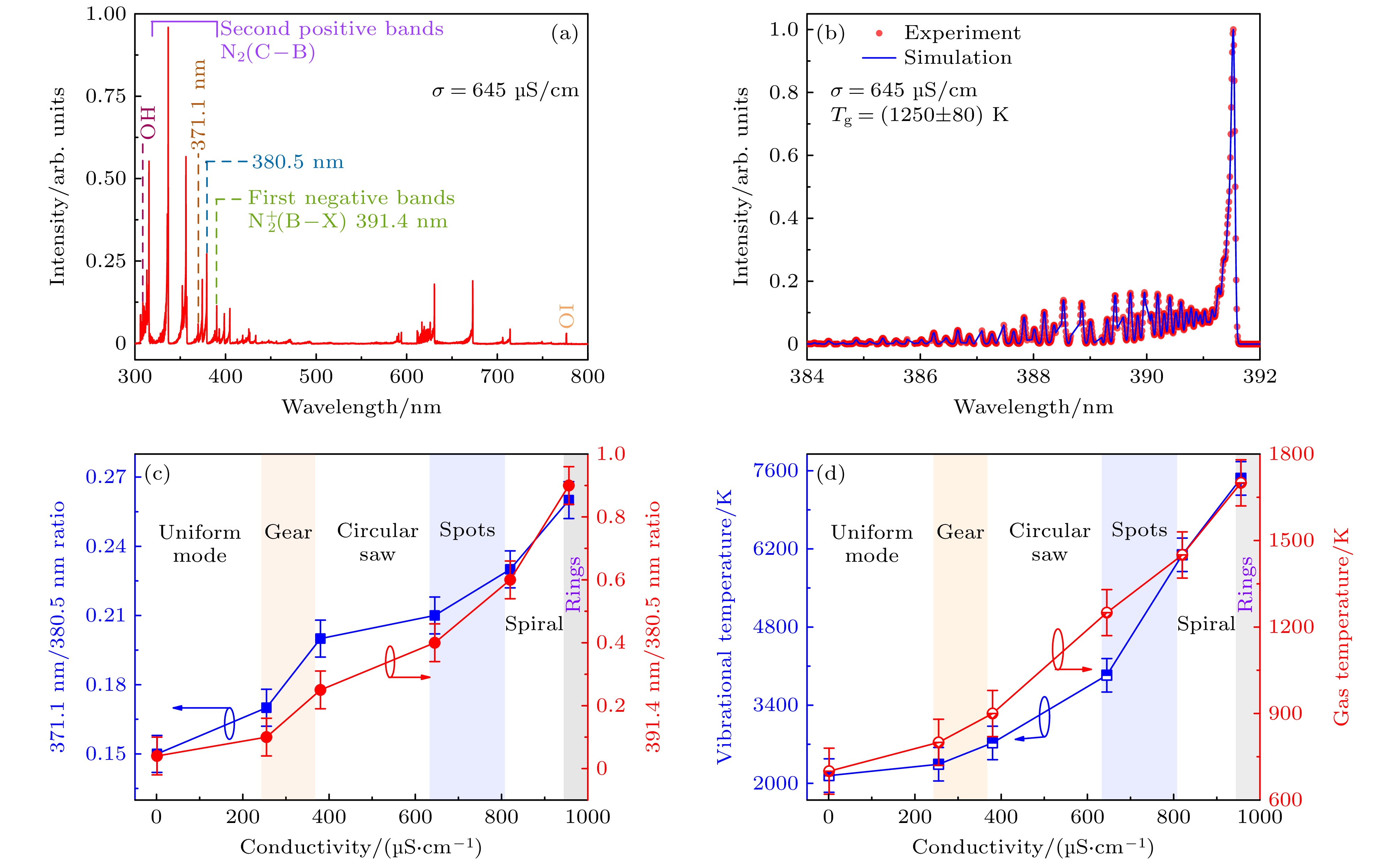
$ {a_{ml}} $ 是m阶贝塞尔函数$ {{\text{J}}_m}\left({{a{}_{ml}}}/{{{r_{\rm p}}}}\right) $ 的第l个零解,$ r_{\rm p} $ 是等离子体的有效半径,$ {A_{ml}} $ 和$ {B_{ml}} $ 是常数, knz = π/2. 使用IDL软件(Interactive Data Language, 6.4 版本) 进行绘制,$ r $ 的取值范围为[0, 2.3], 步长为0.2;$ \theta $ 的取值范围为 [0, 2π], 步长为3.6. 在实验中σ改变会导致电流强度的改变(图3) , 即斑图随σ演化过程中σ和电流强度均在改变. 方程(1)中变量(l与m)值由离子强度(与σ有关)和电流强度决定. 因此, 输出了不同的l与m值的模拟结果, 如图5(b)所示. 可见, 实验获得的均匀模式及各种斑图模式均能得到仿真复现.此外, 采用发射光谱法对自组织斑图演化过程中的等离子体参数进行诊断. 图6(a)为300—800 nm扫描范围内液体表面阳极层(不是整个体放电)的发射光谱. 从图6可以看出, 谱线主要包括OH
$ ({\text{A}}^{2}{{\Sigma}}^{+}\to {\text{X}}^{2}{\Pi}) $ [45],$ {\rm N}_{2}({\text{C}}^{3}{{\Pi}}_{\text{u}}\to{\text{B}}^{3}{{\Pi}}_{\text{g}}) $ [46],$ {\text{N}}_{2}^{+} {(}{\text{B}}^{2}{\Sigma}_{\text{u}}^{+}\to{\text{X}}^{2}{\Sigma}_{\text{g}}^{+}{)} $ 和OI(777.4 nm). 利用Lifbase软件拟合$ {\mathrm{N}}_{2}^{+} $ 的第一负带系$ {(}{\text{B}}^{2}{\Sigma}_{\text{u}}^{+}\to{\text{X}}^{2}{\Sigma}_{\text{g}}^{+}{)} $ 光谱可得到分子转动温度[47], 其近似等于气体温度(Tg)[48,49]. 图6(b)展示了溶液σ为645 μS/cm时, 气体温度的拟合实例. 碰撞-辐射模型表明电子密度(Ne)与电子温度(Te)分别正相关于371.1 nm/380.5 nm和391.4 nm/380.5 nm的强度比[50,51], 所以可以利用谱线强度比研究Ne与Te随溶液σ的变化趋势, 结果图6(c)所示. 采用玻尔兹曼拟合N2的第二正带系可以获得分子振动温度(Tv)[52,53]. 图6(d)为Tg与Tv随σ的变化关系.光谱诊断结果表明液面附近(斑图形成阳极层中) Ne, Te, Tv与Tg均随σ的增大而升高, 即在放电从均匀模式经历齿轮、锯盘、离散点、螺旋波最终过渡到同心环斑图的过程中等离子体参数 (Ne, Te, Tv与Tg) 随σ的增大而升高. 对以上实验现象进行如下定性分析. 随着溶液σ的增大, 放电回路总电阻减小, 因此放电电流峰值增大. 这意味着随着σ的增大, 放电间隙产生了更多的电子, 由于碰撞在电极间产生了更多的电负性物质, 导致在液体表面沉积了更多的负离子. 因此, 随着溶液σ的增大, 液体表面阳极层的电场增强. Te与电场强度呈正相关, 因此阳极层中Te随σ的增大而升高. 此外, 阳极层电场增强, 会导致碰撞电离系数增大, 意味着通过碰撞产生更多的电子, 因此导致Ne也会随着溶液σ的增大而升高. Ne与Te越高, 放电过程中电子通过碰撞传递给中性粒子的能量越多, 因此导致了更高的Tg与Tv, 即也随着溶液σ的增大而升高.
-
本文研究了交流激励大气压液体电极放电中溶液σ对放电模式的影响, 结果表明增大溶液σ, 放电会从均匀模式过渡为斑图模式, 且斑图模式中依次在液面观察到了齿轮、锯盘、五边形排列的离散点、单臂螺旋波和同心圆环等结构. 电压电流波形图表明只有电压的负半周期才会产生放电, 且放电电流随时间快速增大到峰值, 随后缓慢减小. 在电流减小过程中, 均匀模式的减小是单调的, 而斑图模式存在一个平台阶段. σ升高使峰值电流和平台电流增大, 且放电击穿时刻提前. ICCD研究均匀模式和斑图模式的时空演化结果表明, 不论何种放电模式最初液面上均产生的是均匀弥散的圆盘, 而各种非均匀的斑图产生在平台阶段. 基于反应-扩散系统对均匀模式和各种斑图模式进行了模拟仿真, 结果显示离子强度与电流共同影响了放电的模式. 此外, 发射光谱诊断结果表明, 电子温度、电子密度、气体温度及分子振动温度均随σ增大呈上升趋势. 对这一变化趋势进行定性的分析. 本文结果对于大气压液体电极放电斑图动力学的深入研究具有一定参考价值.
交流电压激励液体电极放电中溶液电导率对放电模式的影响
Influence of solution conductivity on discharge mode in alternating-current voltage driven liquid-electrode discharge
-
摘要: 本文利用正弦交流电压激励液体电极放电系统, 通过增大液体电导率(σ), 发现放电从均匀模式过渡为斑图模式, 且斑图模式中依次在液面观察到了齿轮、锯盘、离散点、单臂螺旋和同心圆环等结构. 放电的电压电流波形表明放电仅发生在电压的负半周期(液体作瞬时阳极), 气体击穿后放电电流迅速增大并很快达到峰值然后缓慢减小. 对于均匀模式, 放电电流的减小是单调的; 但对于斑图模式, 放电电流在减小过程中存在一段几乎不随时间变化的平台阶段. 此外, 随σ升高, 峰值电流和平台电流均增大, 且放电击穿时刻提前. 利用增强型电荷耦合设备拍摄了均匀模式和斑图模式在液面附近的时间演化行为, 发现不论何种放电模式最初液面上均产生的是均匀圆盘, 而各种非均匀的斑图是产生在平台阶段. 基于反应-扩散模型, 通过改变离子强度与电流强度(对应变量m和l )对均匀模式和斑图模式进行了数值仿真, 获得了实验对应的放电模式. 此外, 采集了液面附近放电的发射光谱, 计算了与电子温度和电子密度相关的谱线强度比. 通过对光谱进行拟合, 获得了液面附近放电的气体温度和分子振动温度. 研究发现这些等离子体参数随σ的增大(对应着放电模式的变化)而升高.Abstract: A liquid-electrode discharge system excited by an alternating-current sinusoidal voltage is employed to investigate the discharge modes with varying liquid conductivity (σ). The results indicate that with σ increasing, the discharge transitions from the uniform mode to the pattern mode, which undergoes various self-organized patterns such as gear, circular saw, discrete spots, single-arm spiral, and concentric rings on the liquid surface. The voltage and current waveforms reveal that the discharge occurs only in the negative half-cycle of applied voltage (when the liquid acts as the instantaneous anode). After gas breakdown, the discharge current rises rapidly to a peak, and then slowly decreases. For the uniform mode, the current decreases monotonically. However, during the current decreasing in the pattern mode, there appears a plateau in which the current keeps almost invariant with time. As σ increases, the values of the peak current and the plateau increase, and the breakdown moment advances. In addition, fast photography achieved through an intensified charge-coupled device (ICCD) shows that regardless of the discharge mode, a uniform disk is initially generated on the liquid surface, and various non-uniform patterns are formed during the plateau stage. Based on the reaction-diffusion model, numerical simulations are carried out through changing ion strength and current strength, which are related to the variables m and l. The simulated discharge modes are well in line with those obtained in the experiments. Moreover, spectral line intensity ratios related to electron temperature and electron density are determined through the spectra emitted from the discharge near the liquid surface. By fitting the spectra, gas temperature and molecular vibration temperature are obtained, which show an increasing trend with σ increasing.
-
-
图 2 曝光时间texp为0.25 ms, 溶液σ变化时(a)均匀模式和(b)—(f)斑图模式的照片, 其中(b)齿轮模式; (c)锯盘模式; (d)离散点模式; (e)单臂螺旋模式; (f)同心圆环模式
Figure 2. Images of the uniform mode (a) and the self-organized patterns (b)–(f) with varying σ. Panel (b)–(f) correspond to (b) gear, (c) circular saw, (d) discrete spots, (e) single-arm spiral, and (f) concentric rings, respectively. The exposure time (texp) is 0.25 ms.
图 3 溶液σ变化时(不同放电模式)施加电压与放电电流的波形.
Figure 3. Waveforms of applied voltage and discharge current with varying σ (different discharge modes).
图 4 单次曝光ICCD (texp = 500 ns)拍摄液面上放电的时间演化图像(ICCD的门时刻在对应的电流波形中标注) (a) 均匀模式; (b) 齿轮模式; (c) 锯盘模式; (d) 离散点模式; (e) 单臂螺旋模式; (f) 同心圆环模式
Figure 4. Single-shot ICCD images with texp of 500 ns for the discharges on the liquid surface: (a) The uniform mode; (b) gear pattern; (c) circular saw pattern; (d) discrete spots pattern; (e) single-arm spiral pattern; (f) concentric rings pattern. The gate moments of the ICCD are labelled in the corresponding current waveform.
图 5 (a) 单次曝光ICCD (texp = 500 ns) 拍摄的均匀模式和斑图模式的照片; (b) 利用反应-扩散模型获得不同变量(l和m)值的放电模式
Figure 5. (a) Images of the uniform mode and the patterns captured by the ICCD with texp of 500 ns; (b) the discharge modes predicted by the reaction-diffusion model with different values of variables (l and m).
图 6 (a) 300—800 nm扫描范围内来自于液体表面的发射光谱; (b)
$ {\text{N}}_{2}^{+}{(}{\text{B}}^{2}{\Sigma}_{\text{u}}^{+}\to{\text{X}}^{2}{\Sigma}_{\text{g}}^{+}{)} $ 转动谱带拟合实例; (c), (d) Te与Ne (c)及Tv与Tg (d)随σ的变化Figure 6. (a) 300 to 800 nm scanned spectrum emitted from the discharge near the liquid surface; (b) experimental and simulated spectra of
$ {\text{N}}_{2}^{+}{(}{\text{B}}^{2}{\Sigma}_{\text{u}}^{+}\to{\text{X}}^{2}{\Sigma}_{\text{g}}^{+}{)} $ ; (c), (d) Te and Ne (c), Tv and Tg (d) as a function of σ. -
[1] Bruggeman P, Leys C 2009 J. Phys. D: Appl. Phys. 42 053001 doi: 10.1088/0022-3727/42/5/053001 [2] 李雪辰, 耿金伶, 贾鹏英, 吴凯玥, 贾博宇, 康鹏程 2018 物理学报 67 075201 doi: 10.7498/aps.67.20172205 Li X C, Geng J L, Jia P Y, Wu K Y, Jia B Y, Kang P C 2018 Acta Phys. Sin. 67 075201 doi: 10.7498/aps.67.20172205 [3] Saifutdinov A I 2022 Plasma Sources Sci. Technol. 31 094008 doi: 10.1088/1361-6595/ac89a7 [4] Richmonds C, Sankaran R M 2008 Appl. Phys. Lett. 93 131501 doi: 10.1063/1.2988283 [5] Foster J E, Kovach Y E, Lai J, Garcia M C 2020 Plasma Sources Sci. Technol. 29 034004 doi: 10.1088/1361-6595/ab7089 [6] Kovačević V V, Sretenović G B, Obradović B M, Kuraica M M 2022 J. Phys. D: Appl. Phys. 55 473002 doi: 10.1088/1361-6463/ac8a56 [7] 杨双越, 温小琼, 杨天元, 李霄 2024 物理学报 73 075203 doi: 10.7498/aps.73.20231881 Yang S Y, Wen X Q, Yang Y T, Li X 2024 Acta Phys. Sin. 73 075203 doi: 10.7498/aps.73.20231881 [8] Jamróz P, Gręda K, Pohl P, Żyrnicki W 2014 Plasma Chem Plasma Process. 34 25 doi: 10.1007/s11090-013-9503-3 [9] Webb M R, Hieftje G M 2009 Anal. Chem. 81 862 doi: 10.1021/ac801561t [10] Chen Q, Li J S, Li Y F 2015 J. Phys. D: Appl. Phys. 48 424005 doi: 10.1088/0022-3727/48/42/424005 [11] Zheng P C, Liu K M, Wang J M, Dai Y, Yu B, Zhou X J, Hao H G, Luo Y 2012 Appl. Surf. Sci. 259 494 doi: 10.1016/j.apsusc.2012.07.073 [12] Chen Z T, Xu R G, Chen P J, Wang Q 2020 IEEE Trans. Plasma Sci. 48 3455 doi: 10.1109/TPS.2020.3019995 [13] Liang J P, Zhao Z L, Zhou X F, Yang D Z, Yuan H, Wang W C, Qiao J J 2020 Vacuum 181 109644 doi: 10.1016/j.vacuum.2020.109644 [14] Zhang S, Oehrlein G S 2021 J. Phys. D: Appl. Phys. 54 213001 doi: 10.1088/1361-6463/abe572 [15] Vanraes P, Bogaerts A 2021 J. Appl. Phys. 129 220901 doi: 10.1063/5.0044905 [16] Bruggeman P, Ribežl E, Maslani A, Degroote J, Malesevic A, Rego R, Vierendeels J, Leys C 2008 Plasma Sources Sci. Technol. 17 025012 doi: 10.1088/0963-0252/17/2/025012 [17] Shirai N, Suga G, Sasaki K 2020 Plasma Sources Sci. Technol. 29 025007 doi: 10.1088/1361-6595/ab6abc [18] Shirai N, Ichinose K, Uchida S, Tochikubo F 2011 Plasma Sources Sci. Technol. 20 034013 doi: 10.1088/0963-0252/20/3/034013 [19] Bruggeman P, Liu J J, Degroote J, Kong M G, Vierendeels J, Leys C 2008 J. Phys. D: Appl. Phys. 41 215201 doi: 10.1088/0022-3727/41/21/215201 [20] Xu S F, Zhong X X 2015 Phys. Plasmas 22 103519 doi: 10.1063/1.4934710 [21] Xu S F, Zhong X X 2016 Phys. Plasmas 23 010701 doi: 10.1063/1.4939801 [22] Jia P, Gao K, Zhou S, Chen J Y, Wu J C, Wu K Y, Li X C 2021 Plasma Sources Sci. Technol. 30 095021 doi: 10.1088/1361-6595/abde51 [23] Gao K, Wu K Y, Jia P Y, Jia B Y, Kang P C, Li X C 2019 Phys. Plasmas 26 113501 doi: 10.1063/1.5116063 [24] Zhang S Q, Dufour T 2018 Phys. Plasmas 25 073502 doi: 10.1063/1.5030099 [25] Rumbach P, Lindsay A E, Go D B 2019 Plasma Sources Sci. Technol. 28 105014 doi: 10.1088/1361-6595/ab45e4 [26] Shirai N, Ibuka S, Ishii S 2009 Appl. Phys. Express 2 036001 doi: 10.1143/APEX.2.036001 [27] Yang Z M, Kovach Y, Foster J 2021 J. Appl. Phys. 129 163303 doi: 10.1063/5.0043812 [28] Verreycken T, Bruggeman P, Leys C 2009 J. Appl. Phys 105 083312 doi: 10.1063/1.3117223 [29] Shirai N, Uchida S, Tochikubo F 2014 Plasma Sources Sci. Technol. 23 054010 doi: 10.1088/0963-0252/23/5/054010 [30] Li X C, Kang P C, Gao K, Zhou S, Wu K Y, Jia P Y 2020 Plasma Processes Polym. 17 1900223 doi: 10.1002/ppap.201900223 [31] Kovach Y E, Garcia M C, Foster J E 2021 Plasma Sources Sci. Technol. 30 015007 doi: 10.1088/1361-6595/abc815 [32] Li X C, Zhou S, Gao K, Ran J X, Wu K Y, Jia P Y 2022 IEEE Trans. Plasma Sci. 50 1717 doi: 10.1109/TPS.2022.3156027 [33] Qin X R, Feng B W, Wang R Y, Ma Y P X, Zhang Q, Zhong X X 2024 Plasma Processes Polym. 21 2300055 doi: 10.1002/ppap.202300055 [34] Li X C, Geng J L, Jia P Y, Zhang P P, Zhang Q, Li Y R 2017 Phys. Plasmas 24 113504 doi: 10.1063/1.5010209 [35] Zheng P C, Wang X M, Wang J M, Yu B, Liu H D, Zhang B, Yang R 2014 Plasma Sources Sci. Technol. 24 015010 doi: 10.1088/0963-0252/24/1/015010 [36] Srivastava T, Simeni M S, Nayak G, Bruggeman P J 2022 Plasma Sources Sci. Technol. 31 085010 doi: 10.1088/1361-6595/ac83ed [37] Shirai N, Uchida S, Tochikubo F, Ishii S 2011 IEEE Trans. Plasma Sci. 39 2652 doi: 10.1109/TPS.2011.2158324 [38] Chen Y F, Feng B W, Zhang Q, Wang R Y, Ostrikov K (Ken), Zhong X X 2020 Plasma Sci. Technol. 22 055404 doi: 10.1088/2058-6272/ab66e9 [39] Li J M, Zhang X, Tian S, Meng T T, Wan W J, Ran J X, Sun H, Jia P Y, Pang X X, Li X C 2025 Phys. Plasmas 32 032107 doi: 10.1063/5.0249081 [40] Ghimire B, Kolobov V I, Xu K G 2023 Phys. Scr. 98 095602 doi: 10.1088/1402-4896/aceb1c [41] Wu J C, Jia P Y, Ran J X, Chen J Y, Zhang F R, Wu K Y, Zhao N, Ren C H, Yin Z Q, Li X C 2021 Phys. Plasmas 28 073501 doi: 10.1063/5.0047988 [42] Rajzer Y P 1997 Gas Discharge Physicst (Berlin Heidelberg: Springer) p167 [43] Purwins H G, Stollenwerk L 2014 Plasma Phys. Control. Fusion 56 123001 doi: 10.1088/0741-3335/56/12/123001 [44] Trelles J P 2016 J. Phys. D: Appl. Phys. 49 393002 doi: 10.1088/0022-3727/49/39/393002 [45] 陈泽煜, 彭玉彬, 王瑞, 贺永宁, 崔万照 2022 物理学报 71 240702 doi: 10.7498/aps.71.20221385 Chen Z Y, Peng Y B, Wang R, He Y N, Cui W Z 2022 Acta Phys. Sin. 71 240702 doi: 10.7498/aps.71.20221385 [46] 李汉明, 李钢, 李英骏, 李玉同, 张翼, 程涛, 聂超群, 张杰 2008 物理学报 57 0969 doi: 10.7498/aps.57.969 Li H M, Li G, Li Y J, Li Y T, Zhang Y, Cheng T, Nie C Q, Zhang J 2008 Acta Phys. Sin. 57 0969 doi: 10.7498/aps.57.969 [47] 李雪辰, 常媛媛, 刘润甫, 赵欢欢, 狄聪 2013 物理学报 62 165205 doi: 10.7498/aps.62.165205 Li X C, Chang Y Y, Liu R F, Zhao H H, Di C 2013 Acta Phys. Sin. 62 165205 doi: 10.7498/aps.62.165205 [48] Belmonte T, Noël C, Gries T, Martin J, Henrion G 2015 Plasma Sources Sci. Technol. 24 064003 doi: 10.1088/0963-0252/24/6/064003 [49] 张雪雪, 贾鹏英, 冉俊霞, 李金懋, 孙换霞, 李雪辰 2024 物理学报 73 085201 doi: 10.7498/aps.73.20231946 Zhang X X, Jia P Y, Ran J X, Li J M, Sun H X, Li X C 2024 Acta Phys. Sin. 73 085201 doi: 10.7498/aps.73.20231946 [50] Choi J H, Lee T I, Han I, Baik H K, Song K M, Lim Y S, Lee E S 2006 Plasma Sources Sci. Technol. 15 416 doi: 10.1088/0963-0252/15/3/017 [51] Liu Y D, Yan H J, Guo H F, Fan Z H, Wang Y Y, Wu Y, Ren C S 2018 Phys. Plasmas 25 033519 doi: 10.1063/1.5016898 [52] Wu K Y, Liu J N, Wu J C, Chen M, Ran J X, Pang X X, Jia P Y, Li X C, Ren C H 2023 High Volt. 8 1161 doi: 10.1049/hve2.12327 [53] Wu J C, Li X C, Ran J X, Jia H X, Wu K Y, Han G X, Liu J N, Chen J Y, Pang X X, Jia P Y 2023 Plasma Processes Polym. 20 2200188 doi: 10.1002/ppap.202200188 -
图( 6)
计量
- 文章访问数: 29
- HTML全文浏览数: 29
- PDF下载数: 2
- 施引文献: 0